删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

一种压电驱动的三足爬行机器人

本站小编 Free考研考试/2022-01-01


引 言


世界上第一台工业机器人在1954年诞生于美国, 它是由德尔沃设计的一款电子可编程工业机器人, 这就是第一代机器人[1]. 爬行机器人是移动机器人的一种, 按照行动方式可以划分为: 轮式、蠕动式、履带式等[2]. 美国波士顿动力公司[3-5]在美国国防部的资助下, 为美国军方研制了一款步兵班组支援系统, 俗称“BigDog”. 斯坦福大学的工程师们开发出了一款叫做“MicroTugs”的微型爬行机器人[6-7]. 王楠等[8]研制了一种应用于废墟搜救的可变形爬行机器人, 它可以根据实际工作需要实现并排模式、三角模式、直线模式之间变换. 该机器人搭载了包括视频、语音等模块, 可在灾后废墟中高效地搜索幸存者的位置. 田兴华等[9]研制出了仿生小象四足机器人, 提出了3种三自由度混联腿构型用于高速、高承载四足仿生机器人的应用. 沈惠平等[10]研制出了可在水下行走的机器龙虾. 2014年, Chen等[11]研制了一款轮足复合的四足爬行机器人“Quattroped”, 其包含了结构可变的轮腿机构. 张力文等[12]研究建立了软体尺蠖机器人运动构型的准静态求解体系及其运动构型的理论求解与分析. 霍前俊等[13]研究提出了一种结构更简洁、弯曲更灵活、力学性能更好的三腔道仿生软体爬行机器人. 尹铁等[14]设计了一种由压缩空气作为动力驱动的、适应管径1422 mm的内爬行管口组对机器人. 该机器人采用遥控操作控制方式,可以实现前进、后退、紧急停车、涨紧对口等动作. 官文俊等[15]基于仿生学原理和3D打印技术, 将智能材料与液体腔体驱动相结合, 最终实现了SMA丝致动软腔体单次最大位移6 mm的连续伸缩爬行运动. 张丽艳等[16]通过单片机设计制作了适应全地形的六足爬行机器人.

压电陶瓷是一种能够将机械能和电能互相转换的新型功能陶瓷材料. 利用压电陶瓷的正压电效应可以在能量俘获领域发挥作用, Huang等[17]研究了具有电阻?电感谐振电路的非线性能量俘获器的稳态响应机制. Fu等[18]全面综述了利用正压电效应制作的旋转能量俘获器对可穿戴设备、汽车、旋转机器上所发挥的巨大作用. 张东升和胥永晓[19]研究设计出一种压电式海浪能量俘获器用于低频振动的压电能量俘获系统, 将其集成化后可作为海洋无线电设备和传感器的供电装置. 利用压电陶瓷的逆压电效应则可以在机器人驱动领域发挥作用. 李京[20]受节肢动物分节现象的启发,提出并设计了一种微小型谐振式多足压电机器人, 在25 V电压时实现了182.1 mm的最小转向半径. 2019年, Peng等[21]设计了一种微小型双足压电机器人“Milli-Walker”. 该机器人体长仅为6 mm, 主要由一片压电陶瓷和一个整体的双足基体组成, 贺红林等[22]研制了基于谐振驱动的微小型机器人. 2017年, 郑龙龙和李朝东[23-24]提出并设计了一种利用压电双晶片驱动的微小型八足机器人, 可实现一个自由度的弯曲动作. 李魁和徐鉴[25]提出了一种由上下两片压电陶瓷片作动的谐振三足机器人, 依靠异性摩擦实现了3个方向的运动. 2018年, 张卫平等[26-27]研制了一种六足爬行机器人, 其体长125 mm, 宽132 mm, 由3个运动单元节组成. 2019年, Deng等[28]研制了一种腿部为夹心式结构的四足压电机器人. Liu等[29]研制出了采用压电双层膜驱动器并结合惯性冲击式原理(IDM)实现运动的管道机器人. 2010年, 蒋振宇等[30]研制了一种基于双压电膜驱动的微小型足式机器人, 该机器人体长为70 mm, 结构简单. 2017年刘英想等[31]设计了一种实用的小型压电驱动器, 选择梁的3阶弯曲振动模态作为压电驱动器的振动模态, 实验结果表明, 所设计的压电驱动器最高速度可达735 mm/s, 最大输出推力为1.1 N.

目前关于轻型机器人实验研究相对较少, 因此本文在上述爬行机器人研究的基础上, 设计了一种结构简单, 方便使用的三足爬行机器人, 采用更精确的振动力学方法推导了其动力学模型. 建立了输入电压与输出位移的定量关系, 提出了压电片驱动变截面弯折梁的位移模型, 分析了机器人在不同电压、不同频率、不同输入波形、不同运动表面、不同负载下与运动速度之间的关系. 设计实验验证了机器人空载速度最大可达62.8 mm/s, 负载2 g时, 机器人的峰值速度接近53 mm/s. 该机器人虽然最大负载能力有限, 但在负载4 g时速度却可以接近30 mm/s, 在负载6 g时速度也可以达到10 mm/s. 在应用上, 我们可以将质量块换成微型摄像头, 微型传感器等等(市面上的一些微型摄像头, 微型传感器等重量不超过5 g, 尺寸仅为手指甲大小). 当左右两侧输入不对称电压时自由直线行走偏转角度在3°以内. 本文的研究动机是探索轻型机器人的设计及建模方法, 以此为基础, 后续进一步优化和设计以用于微小缝隙内部或者其他微小场所使用.


1.
驱动原理



1.1
压电驱动原理


本文设计了一种三足谐振式弹性腿驱动结构, 由于压电片在周期性电压的驱动下会产生周期性振动, 与之相连的弹性腿也将产生振动, 在压电片的电压驱动频率与弹性腿固有频率相同时, 振动幅度会明显增大, 弹性腿与工作表面发生碰撞, 产生驱动力驱动结构行走. 选取压电片时需要选择合适的压电陶瓷工作模式. 本文采用$ {d_{31}} $模式(施加电压方向与压电片形变方向相垂直). 在给定周期信号的激励下, 压电陶瓷周期性地伸长缩短, 压电片带动机器人产生弯曲变形, 实现弹性足与工作平面接触处的往复运动. 用此原理设计出的机器人具有质量轻, 体积小的特点.


1.2
压电陶瓷驱动机器人的工作原理


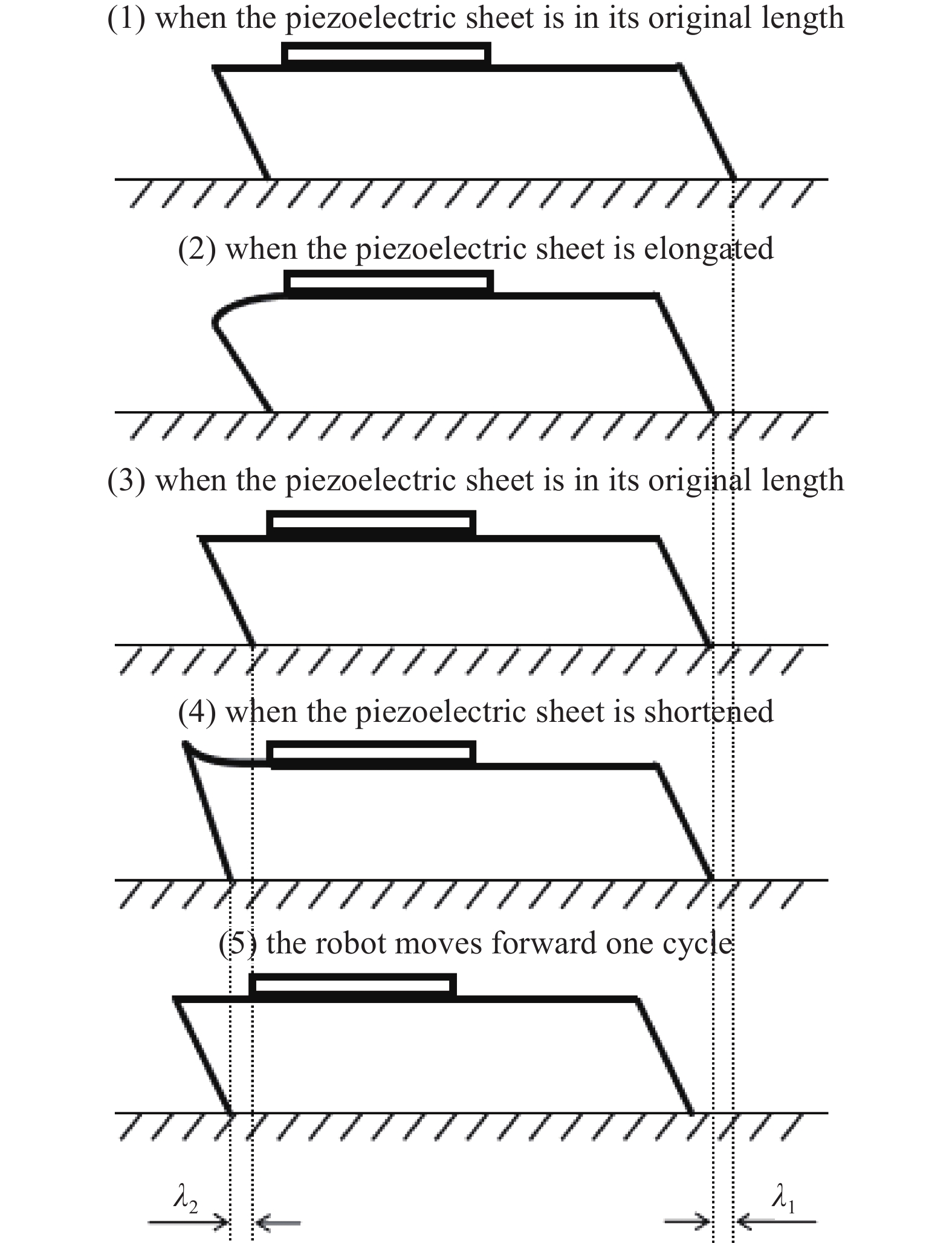
将压电片黏贴在三足爬行机器人的谐振足上, 经过分析可以得到如图1所示的行走原理[30].

(1) 压电片处于初始状态.

(2)压电片受到周期电压驱动信号产生伸长时, 整个结构向下弯曲. 由于摩擦力作用, 前足足端对地面压力增大, 使其保持位置不变, 后足足端抬起, 向前行走$ {lambda _1} $.

(3)压电片受到周期电压驱动信号恢复原长时, 由于前足足端有向上运动的趋势, 对地面压力减小, 后足足端位置不变, 前足足端抬起, 向前行走$ {lambda _1} $.

(4)压电片受到周期电压驱动信号缩短时, 整个结构向上弯曲. 由于摩擦力作用, 后足足端对地面压力增大, 使其保持位置不变, 前足足端抬起, 向前行走$ {lambda _2} $.

(5)压电片受到周期电压驱动信号恢复原长时, 由于摩擦力作用, 前足足端对地面压力增大, 使其保持位置不变, 后足足端抬起, 向前行走$ {lambda _2} $.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-430-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
机器人行走原理[30]



Figure
1.
The walking principle of the robot[30]



下载:
全尺寸图片
幻灯片


本文提出的微小型三足爬行机器人的实物如图2所示, 由压电片、机器人结构本身和谐振式弹性足组成. 机器人结构本身和弹性足为同一构件, 两片压电片分别黏贴在机器人弹性腿的上表面. 首先采用精密加工在弹性铍青铜薄板上切割出机器人整体平面结构, 再将三条弹性足弯折成图2所示的结构. 将驱动元件和执行元件融为一体, 结构非常简单, 适合爬行机器人微小化和批量制造. 机器人身体在压电片作动下产生周期变形, 将振动传递到机器人的腿部. 机器人腿部在振动变形过程中与工作面接触, 使机器人在地面摩擦作用下实现运动.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-430-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
压电驱动的三足爬行机器人实物图



Figure
2.
The experimental photograph of a piezoelectric-driven three-legged crawling robot



下载:
全尺寸图片
幻灯片



2.
整体受力分析及动力学建模


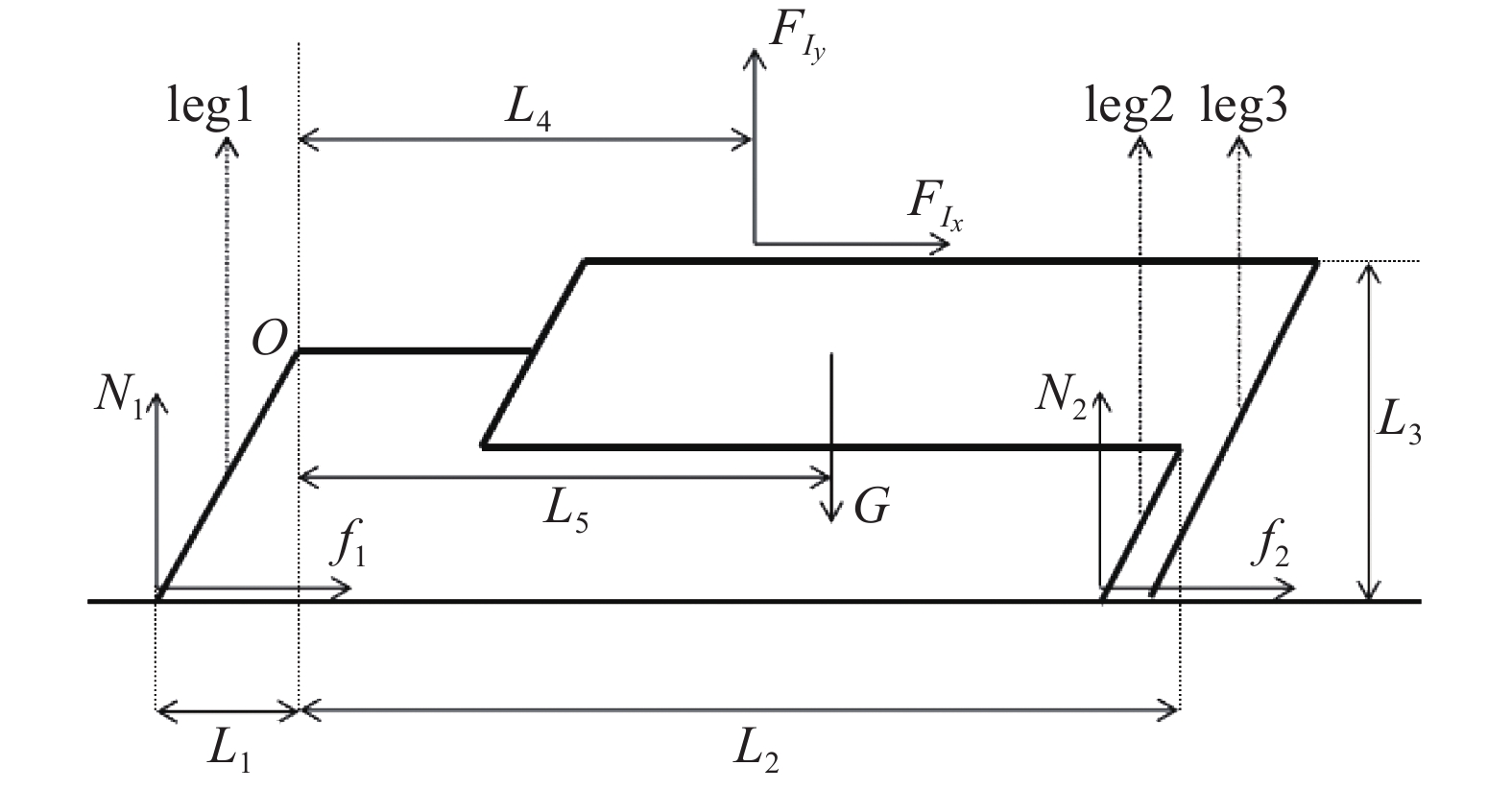
如图3所示, 其中$ {N_1} $, $ {N_2} $为支持力, $ {f_1} $, $ {f_2} $为摩擦力, $ {F_I} $为一片压电片产生的惯性力, $ G $为整体重力, $ u $为机器人与地面间的摩擦系数.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-430-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
整体受力分析示意图



Figure
3.
Overall force analysis



下载:
全尺寸图片
幻灯片


整体受力分析为







$$ {f_1} + 2{f_2} + 2{F_{Ix}} = 0 $$
(1)







$$ {N_1} + 2{N_2} + 2{F_{Iy}} - G = 0 $$
(2)







$$ 2{F_{Iy}}{L_4} + 2{N_2}{L_2} + ({f_1} + 2{f_2}){L_3} - {N_1}{L_1} - G{L_5} = 0 $$
(3)

由式(1) ~ 式(3)可得







$$ {N_1} = G - 2{F_{Iy}} - frac{{2{F_{Ix}}{L_3} + ({L_1} + {L_5})G - 2({L_1} + {L_4}){F_{Iy}}}}{{{L_1} + {L_2}}} $$
(4)







$$ {N_2} = frac{{2{F_{Ix}}{L_3} + ({L_1} + {L_5})G - 2({L_1} + {L_4}){F_{Iy}}}}{{2({L_1} + {L_2})}} $$
(5)







$$ {f_1} = u{N_1} $$
(6)







$$ {f_2} = u{N_2} $$
(7)

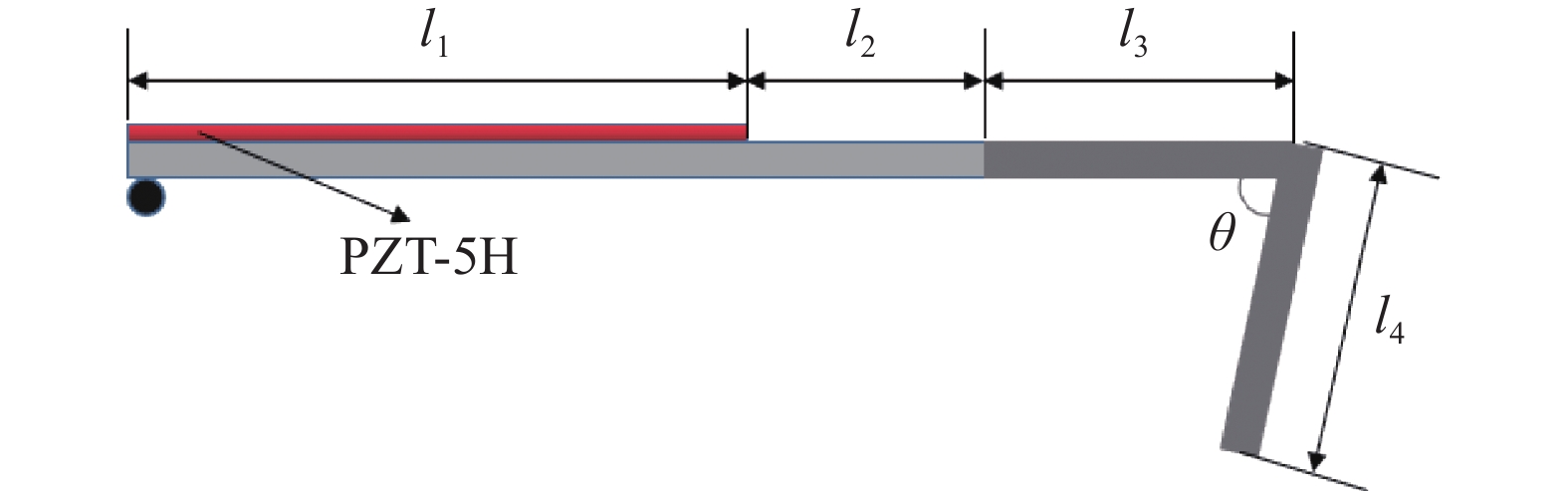
对贴有压电片的压电梁(驱动腿)建模[32], 将机器人整体结构拆分成3个腿部子结构, 对其中一个贴有压电片的子结构建立运动方程. 结构左端由于上下振幅很小(实验验证振动幅值量级为微米级别), 所以左端忽略纵向振动位移, 可以当成水平滑轨结构, 右端为自由端. 如图4所示, 利用哈密顿原理分析振动方程(忽略腿部与地面的碰撞过程).



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-430-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
压电驱动腿示意图



Figure
4.
The diagram of a piezoelectric-driven leg



下载:
全尺寸图片
幻灯片


压电作动器的应力应变关系为







$$ {S_1} = - (z - {z_n})frac{{partial {w^2}(x,t)}}{{partial {x^2}}} $$
(8)







$$ {S_2} = - zfrac{{partial {w^2}(x,t)}}{{partial {x^2}}} $$
(9)

式中, $ z $为纵坐标, $ {z_n} $为中性面







$$ Wint_{ - frac{{{t_b}}}{2}}^{frac{{{t_b}}}{2}} {{sigma ^b}{text{d}}z} + Wint_{frac{{{t_b}}}{2}}^{frac{{{t_b}}}{2} + {t_p}} {{sigma ^p}{text{d}}z} = 0 $$
(10)







$$ Wint_{ - frac{{{t_b}}}{2}}^{frac{{{t_b}}}{2}} {{E_b}(z - {z_n}){text{d}}z} + Wint_{frac{{{t_b}}}{2}}^{frac{{{t_b}}}{2} + {t_p}} {{E_p}(z - {z_n}){text{d}}z} = 0 $$
(11)

其中$ {E_b} $和$ {E_p} $分别为梁和压电片的杨氏模量, $ {sigma ^b} $和$ {sigma ^p} $分别为梁和压电片所受的应力, $ W $为梁和压电片的宽度, $ {t_b} $为梁厚度, $ {t_p} $为压电片厚度, 可得







$$ {z_n} = frac{{{E_p}{t_p}({t_p} + {t_b})}}{{2({E_b}{t_b} + {E_p}{t_p})}} $$
(12)

由式(12)可以得出总势能







$$ begin{split} {
m{delta }}U =& Wleft( {int_0^{{l_1}} {int_{ - frac{{{t_b}}}{2}}^{frac{{{t_b}}}{2}} {{E_b}{S_1}{
m{delta }}{S_1}{
m{d}}z{
m{d}}x} } }
ight) + &WBiggl{{15} {int_0^{{l_1}} {int_{ - frac{{{t_b}}}{2}}^{frac{{{t_b}}}{2} + {t_p}} {left[ {left( {{E_p}{S_1} - {h_{31}}{D_3}}
ight){
m{delta }}{S_1} + }
ight.} } }& {left. {left( {beta _{33}^S{D_3} - {h_{31}}{S_1}}
ight){
m{delta }}{S_1}}
ight]{
m{d}}z{
m{d}}x} Biggl}{15}end{split} $$
(13)

总动能(忽略电场动能)为







$$ T = frac{1}{2}int_0^{{l_1}} {left( {{
ho _b}{t_b} + {
ho _p}{t_p}}
ight)W[{ {w(x,t)} ]^2}} {text{d}}x $$
(14)

总机械虚功为







$$ Delta{W_j} = - cint_0^{{l_1}} {frac{{partial w(x,t)}}{{partial t}}partial w(x,t)} {text{d}}x $$
(15)

总电虚功为







$$ Delta{W_m} = int_0^{{l_1}} {V(x,t)} Delta Q{text{d}}x $$
(16)







$$ Q = oint_{partial V} {D cdot n{text{d}}A}qquad $$
(17)

式中D为电位移向量, $ Q $为电位移, 由式(16)和式(17)可得







$$ Delta {W_m} = Wint_0^{{l_1}} {V(x,t)Delta {D_3}(x,t)} {text{d}}x $$
(18)

由式(13) ~ 式(18), 可得







$$ int_{{t_0}}^{{t_f}} {left[ {Delta T - Delta U + Delta ({W_j} + {W_m})}
ight]{text{d}}t = 0} $$
(19)

将式(19)化简并用欧拉方程, 消除$Delta w(x,t)$和$Delta {D_3}(x,t)$的影响, 考虑当压电片上具有统一的输入电压且与位置无关, 则







$$ V(x,t) = V(t) $$
(20)

由式(8) ~ 式(20)可得(忽略压电陶瓷与铍铜中间基板厚度)

当$ {x_1} in (0,{l_1}) $时







$$ E{I_1}frac{{partial w_1^4(x,t)}}{{partial {x^4}}} + {m_1}frac{{partial w_1^2(x,t)}}{{partial {t^2}}} + cfrac{{partial {w_1}(x,t)}}{{partial t}} = - {M_p}V(t) $$
(21)







$$ {M_p} = - frac{1}{2}bleft( {{t_p} + {t_b} - 2{z_n}}
ight){E_k}{d_{31}} $$
(22)







$$ {E_1}frac{{partial u_1^2(x,t)}}{{partial {x^2}}} - {
ho _b}frac{{partial u_1^2(x,t)}}{{partial {t^2}}} = 0 $$
(23)

当${x_i} in (0,{l_i})$, $i = 2,3$时







$$ E{I_i}frac{{partial w_i^4(x,t)}}{{partial {x^4}}} + {m_i}frac{{partial w_i^2(x,t)}}{{partial {t^2}}} + cfrac{{partial {w_i}(x,t)}}{{partial t}} = 0 $$
(24)







$$ {E_i}frac{{partial u_i^2(x,t)}}{{partial {x^2}}} - {
ho _b}frac{{partial u_i^2(x,t)}}{{partial {t^2}}} = 0 $$
(25)

当$ {x_4} in (0,{l_4}) $时







$$ E{I_4}frac{{partial w_4^4(x,t)}}{{partial {x^4}}} + {m_4}frac{{partial w_4^2(x,t)}}{{partial {t^2}}} + cfrac{{partial {w_4}(x,t)}}{{partial t}} = 0 $$
(26)







$${E_4}frac{{partial u_4^2(x,t)}}{{partial {x^2}}} - {
ho _b}frac{{partial u_4^2(x,t)}}{{partial {t^2}}} = 0 $$
(27)

式中, $ A $为梁横截面积, $ theta $为弯折角度, $ {E_k} $为等效刚度[32], E1, E2, E3, E4分别为各段等效杨氏模量. $ c $为结构阻尼系数







$$ E{I_1} = {W_1}{E_b}{t_b}left(frac{{t_b^2}}{{12}} + frac{{t_p^2}}{4}
ight) + {W_1}{E_p}{t_p}left(frac{{t_p^2}}{{12}} + frac{{t_b^2}}{4}
ight)$$
(28)







$$ E{I_2} = frac{{{E_b}{W_1}t_b^3}}{{12}} $$
(29)







$$ E{I_3} = frac{{{E_b}{W_2}t_b^3}}{{12}} $$
(30)







$$ E{I_4} = frac{{{E_b}{W_2}t_b^3}}{{12}} $$
(31)







$$ {m_1} = {
ho _b}{W_1}{t_b} + {
ho _p}{W_1}{t_p} $$
(32)







$$ {m_2} = {
ho _b}{W_1}{t_b} $$
(33)







$$ {m_3} = {
ho _b}{W_2}{t_b} $$
(34)







$$ {m_4} = {
ho _b}{W_2}{t_b} $$
(35)

式中, $ {z_n} $为等效中性面, $ {W_1} $为第一二段宽度, $ {W_2} $为第三四段宽度, $ V(t) $为电压表达式, $ EI $为抗弯刚度. $ {
ho _b} $为梁密度, $ {
ho _p} $为压电片密度, $ {A_p} $为压电片横截面积.

设横向振动方程的解为$ {w_n}(x,t) = {Y_n}(x){T_n}(t) $, $ n = $$ 1,2,3,4,$可得







$$ begin{split} {Y_n}(x) = &{A_n}{text{sin}}left( {{beta _n}x}
ight) + {B_n}{text{cos}}left( {{beta _n}x}
ight) + &{C_n}{text{sinh}}left( {{beta _n}x}
ight) + {D_n}{text{cosh}}left( {{beta _n}x}
ight) end{split}$$
(36)

设纵向振动方程的解为







$$ {u_n}(x,t) = {U_n}(x){T_n}(t) $$
(37)







$$ {U_n}(x) = {F_n}sin frac{{{w_n}}}{c}x + {G_n}cos frac{{{w_n}}}{c}x $$
(38)







$$ beta _n^4 = frac{{{m_n}{w^2}}}{{E{I_n}}} $$
(39)

An、Bn、Cn、Dn、Fn、Gn均为系数, 当$ {x_1} = 0 $时, 边界条件为







$$ {w_1} = 0 $$
(40)







$$ frac{{partial {w_1}}}{{partial x}} = 0 $$
(41)







$$ frac{{partial {u_1}}}{{partial x}} = 0 $$
(42)

当$ {x_n} = {l_n} $, $ {x_{n + 1}} = 0 $, $ n = 1,2 $时, 连续性边界条件为







$$ {w_n}(x,t) = {w_{n + 1}}(x,t);; $$
(43)







$$ {u_n}(x,t) = {u_{n + 1}}(x,t);; $$
(44)







$$ frac{{partial {w_n}(x,t)}}{{partial x}} = frac{{partial {w_{n + 1}}(x,t)}}{{partial x}} $$
(45)







$$ frac{{partial {u_n}(x,t)}}{{partial x}} = frac{{partial {u_{n + 1}}(x,t)}}{{partial x}} $$
(46)







$$ frac{{partial w_n^2(x,t)}}{{partial {x^2}}} = frac{{partial w_{n + 1}^2(x,t)}}{{partial {x^2}}} $$
(47)







$$ frac{{partial w_n^3(x,t)}}{{partial {x^3}}} = frac{{partial w_{n + 1}^3(x,t)}}{{partial {x^3}}} $$
(48)

当$ {x_3} = {l_3} $,$ {x_4} = 0 $时, 边界条件为







$$ {u_3}(x,t) = {u_4}(x,t)cos theta - {w_4}(x,t)sin theta $$
(49)







$$ {w_3}(x,t) = {w_4}(x,t)cos theta + {u_4}(x,t)sin theta $$
(50)







$$ frac{{partial {w_3}(x,t)}}{{partial x}} = frac{{partial {w_4}(x,t)}}{{partial x}} $$
(51)







$$ frac{{partial w_3^2(x,t)}}{{partial {x^2}}} = frac{{partial w_4^2(x,t)}}{{partial {x^2}}} $$
(52)







$$ frac{{partial {u_3}(x,t)}}{{partial x}} = frac{{partial {u_4}(x,t)}}{{partial x}}cos theta - frac{{partial w_4^3(x,t)}}{{partial {x^3}}}sin theta $$
(53)







$$ frac{{partial w_3^3(x,t)}}{{partial {x^3}}} = frac{{partial w_4^3(x,t)}}{{partial {x^3}}}cos theta + frac{{partial {u_4}(x,t)}}{{partial x}}sin theta $$
(54)

当$ {x_4} = {l_4} $时, 边界条件为







$$ frac{{partial w_4^2(x,t)}}{{partial {x^2}}} = 0 $$
(55)







$$ frac{{partial w_4^3(x,t)}}{{partial {x^3}}} = 0 $$
(56)







$$ frac{{partial {u_4}(x,t)}}{{partial x}} = 0 $$
(57)







$$ w = {beta ^2}sqrt {frac{{E{I_n}}}{{{m_n}}}} $$
(58)

由式(21) ~ 式(58)可以得出压电驱动腿的各阶固有频率$ {w_i} $, 进而求解整个三足爬行机器人的运动过程.


3.
实验验证


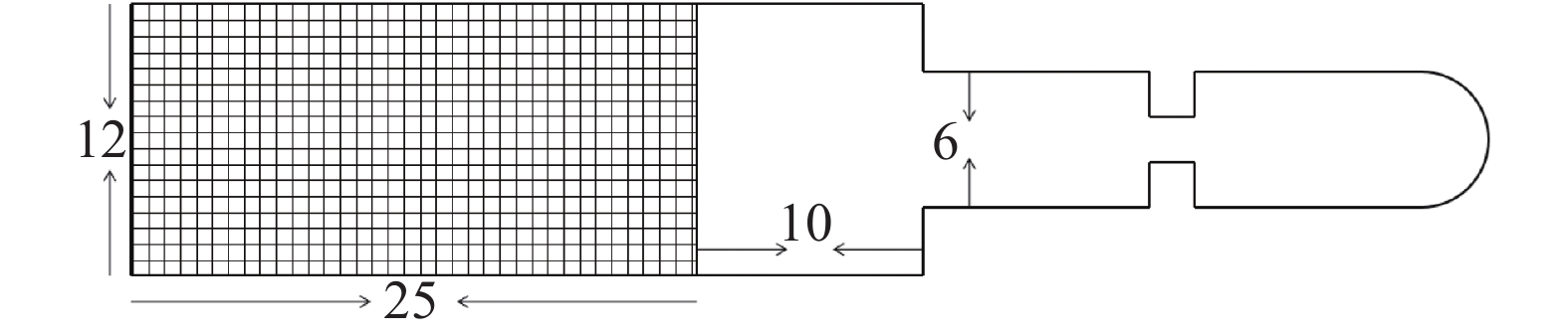
本文选用的压电材料为PZT-5H, 其压电介电常数矩阵、柔度系数矩阵、电场向量以及压电应力常数矩阵参照IEEE标定标准(z方向极化). 设置压电片下方为零电压, 上方输入周期性电压信号. 实验中选用的压电片参数如表1所示, 第1段铍铜基板长25 mm, 宽12 mm, 第2段铍铜基板长为10 mm, 宽为12 mm, 第3段铍铜基板长为15 mm, 宽为6 mm, 第4段铍铜基板长为12 mm, 宽为6 mm, 末端为半径为3 mm的半圆弧, 厚度均为0.2 mm. 周期电压驱动信号选用正弦信号, 压电驱动频率为240 Hz,电压幅值为80 V.




表
1
压电片参数



Table
1.
Parameters of piezoelectric ceramics



table_type1 ">
ParameterValue
PZT-5H size/mm325$ times $12$ times $0.13
Yang's modulus/GPa60
density/(kg·m?3)7800
coupling coefficient/(C·N?1)?3.20×10?10





下载:
导出CSV
|显示表格



为了验证本文所设计三足爬行机器人的工作性能及动力学模型, 设计了相关实验实现不同频率下共振切换使得机器人朝直行, 左转和右转等运动. 实验中机器人总质量为3.5 g, 运动表面材质为树脂复合材料. 根据前面所述建立的机器人振动方程的求解, 设计机器人原型参数如表2所示. 机器人腿部展开俯视图如图5所示, 阴影为黏贴压电片的部分.




表
2
机器人参数表



Table
2.
Parameters of the robot



table_type1 ">
ParameterValue
quality/g3.5
leg bend angle/(°)73
total robot size/mm365×34×10
driving leg size/mm345×12×10
bending leg/mm310×12×0.2





下载:
导出CSV
|显示表格




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-430-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
三足爬行机器人腿部俯视图 (单位: mm)



Figure
5.
Top view of the three-legged crawling robot's one leg (unit: mm)



下载:
全尺寸图片
幻灯片


机器人实验测试仪器如图6所示, 利用信号发生器(品牌为Agilent)生成正弦信号, 将此信号输入功率放大器(型号为HVPA05)模拟输入端, 对信号进行15倍放大后对机器人的压电作动片施加正弦电压信号.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-430-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
实验装置



Figure
6.
Experimental setup



下载:
全尺寸图片
幻灯片


当压电片的驱动电源信号频率为244 Hz时, 与驱动足的固有频率相近, 此时后者的振动幅值会明显增大. 由于人工装配误差等原因会导致机器人左右两侧不对称, 无法行走直线, 所以设计了长度为220 mm的导轨(复合树脂材料)使其沿直线行走, 并记录其行走时间, 便可以得到机器人的实时速度. 如图7所示. 机器人在不加导轨运动时的结果如图8所示, 机器人出发点为A, 结束运动时为B, 经过10次实验, 取实验结果的平均值, 偏移角度为9.54°.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-430-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
机器人行走轨道



Figure
7.
Walking track of the robot



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-430-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
机器人自由运动轨迹



Figure
8.
Free motion trajectory of the robot



下载:
全尺寸图片
幻灯片


本文采用斜面法测量机器人与运动平面之间的摩擦力. 如图9和图10所示, 将机器人放在工作平面上, 将工作平面倾斜, 当机器人刚开始向下运动时, 记录下此时的斜面角度, 即可求出机器人前进和后退时与工作平面间的动摩擦系数. 实验结果表明, 机器人后退时与运动平面的摩擦系数为0.3158, 前进时与运动平面的摩擦系数为0.0712, 机器人正是因为前后摩擦系数不同而产生定向运动.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-430-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
机器人前行时摩擦系数测量



Figure
9.
Measurement of the friction coefficient when the robot moves forward



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-430-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
机器人后退时摩擦系数测量



Figure
10.
Measurement of the friction coefficient when the robot moves backward



下载:
全尺寸图片
幻灯片


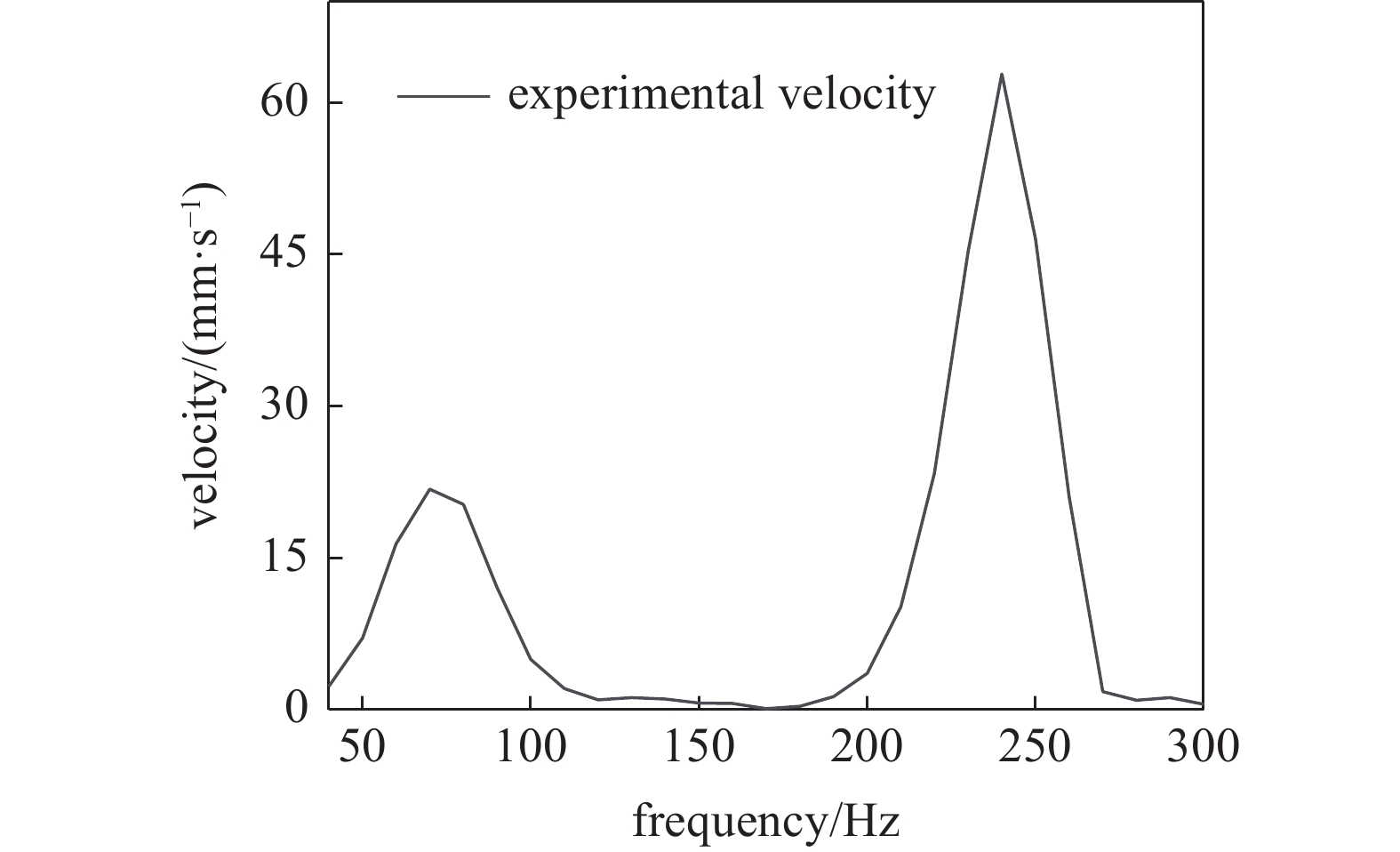
信号电压的频率设置在共振频率附近, 机器人结构厚度为0.2 mm, 保持驱动腿夹角为73°, 驱动电压幅值恒定为80 V. 图11为实验速度结果图, 在激励频率越靠近共振频率时, 机器人的运动速度越快. 在图11中, 驱动足的速度曲线在80 Hz附近存在着一个小的峰值, 这个峰值即对应着谐振足出现的第一个谐振点. 实验曲线中的速度最高峰出现在240 Hz附近, 从图11上可以看出两个谐振点的速度相差较大, 在驱动频率为78 Hz附近的速度不到30 mm/s, 而驱动频率为240 Hz附近的速度接近65 mm/s. 产生这种现象的原因是在低频谐振点, 谐振足的足端竖直位移大于高频谐振点, 水平方向位移偏小, 所以移动速度并不快, 而在第2阶谐振点时, 谐振足足端竖直方向位移偏小,但是水平位移明显大于低频谐振点, 因此速度较快. 从能量守恒角度亦可以说明此现象.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-430-11.jpg'"
class="figure_img
figure_type1 bbb " id="Figure11" />



图
11
机器人的直线运动速度与频率关系



Figure
11.
The relationship between the linear motion speed and frequency of the robot



下载:
全尺寸图片
幻灯片


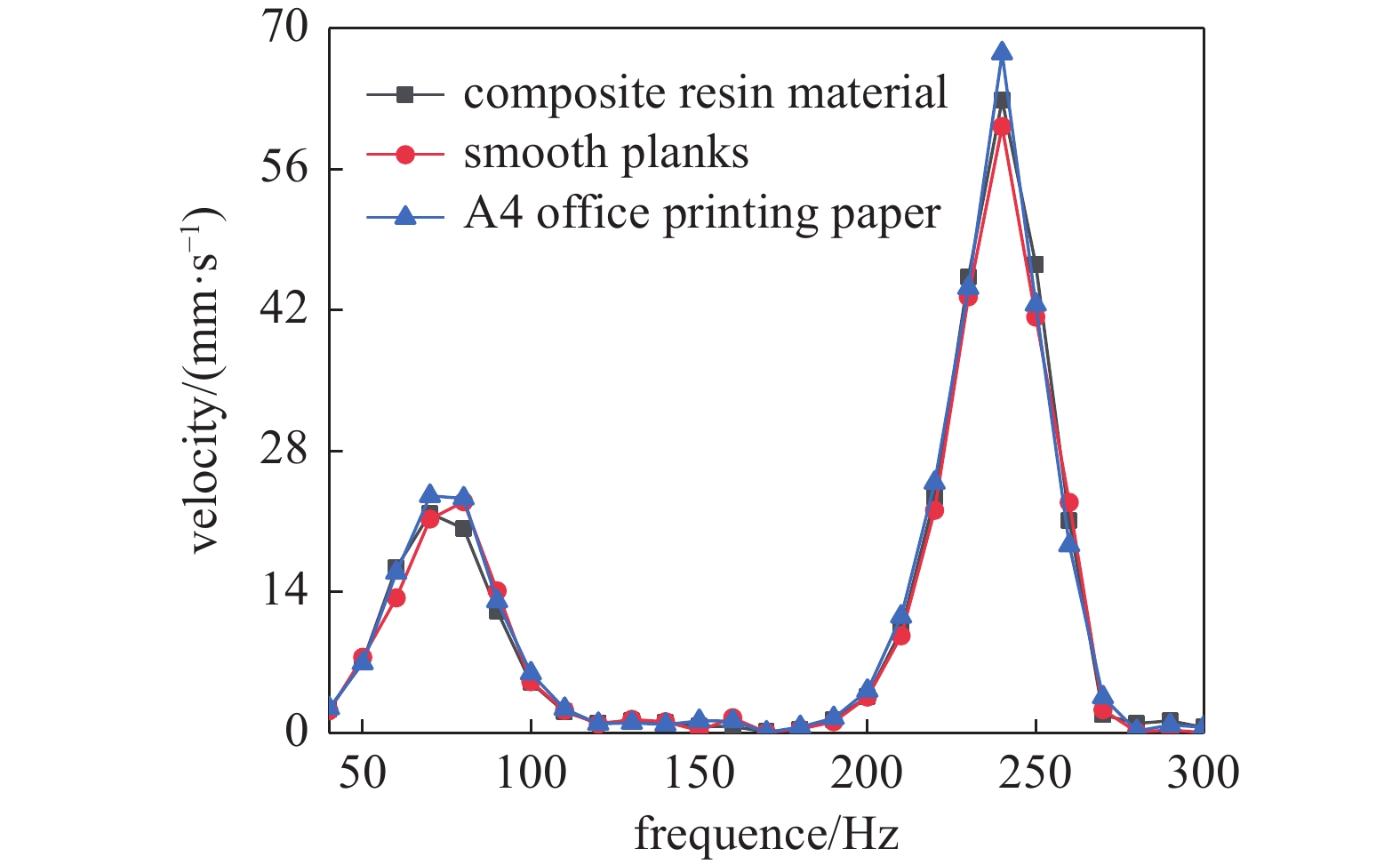
为了研究不同运动表面对机器人速度的影响, 做了3组不同运动表面实验. 实验数据如图12所示, 实验结果表明, 当机器人分别在复合树脂材料, 光滑木板和A4打印纸面上运动时, 速度差别很小. 原因是机器人的速度与机器人腿部前后摩擦系数差有关, 与具体在什么地面无关, 而摩擦系数差和机器人腿部末端与运动平面的接触形式以及腿部弯折角度有关, 所以当弯折角度确定, 前后摩擦系数差不变时, 速度基本相同.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-430-12.jpg'"
class="figure_img
figure_type1 bbb " id="Figure12" />



图
12
机器人在不同运动表面上的速度



Figure
12.
Speeds of the robot on different moving surfaces



下载:
全尺寸图片
幻灯片


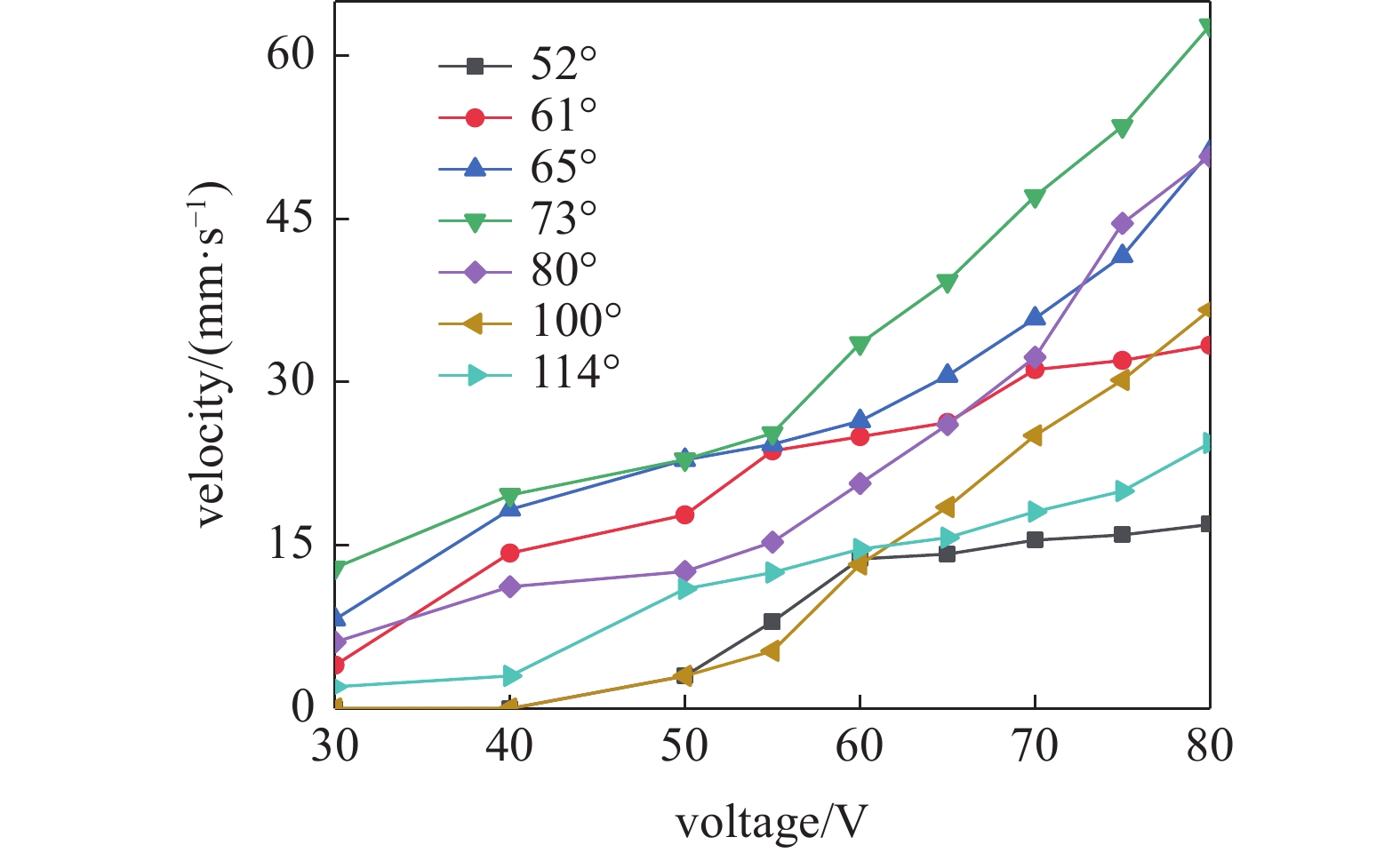
为了研究驱动足弯折角度对机器人运动的影响, 设计了弯折角度为52°, 61°, 65°, 73°80°, 100°和114°等7种谐振机器人分别进行了实验测试. 实验中发现随着弯折角度的增大, 机器人的峰值频率向低频移动, 产生这种现象的原因是随着弯折角度的增大机器人整体的固有频率降低. 在理论计算中也发现峰值频率在向低频移动. 将驱动电压频率与具有不同角度驱动足的机器人的谐振频率相匹配, 并测量其速度. 实验结果如图13所示. 在实验中发现谐振足耦合角超过90°时, 机器人就会向反方向后退行走, 且速度明显低于前进方向速度. 这是由于压电片距离机器人前端距离远, 同样的驱动力下前端位移要大于后端位移, 所以反方向行走速度明显低于前进方向速度. 实验发现在向前行走时驱动腿弯折角度为73°时峰值速度最高, 最大速度可达62.8 mm/s. 反方向行走时驱动腿弯折角度为100°时峰值速度最高, 最大速度为36.6 mm/s.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-430-13.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13" />



图
13
压电驱动腿不同弯曲角度对速度的影响



Figure
13.
Influence of different bending angles of the piezoelectric-driven leg on the speed



下载:
全尺寸图片
幻灯片


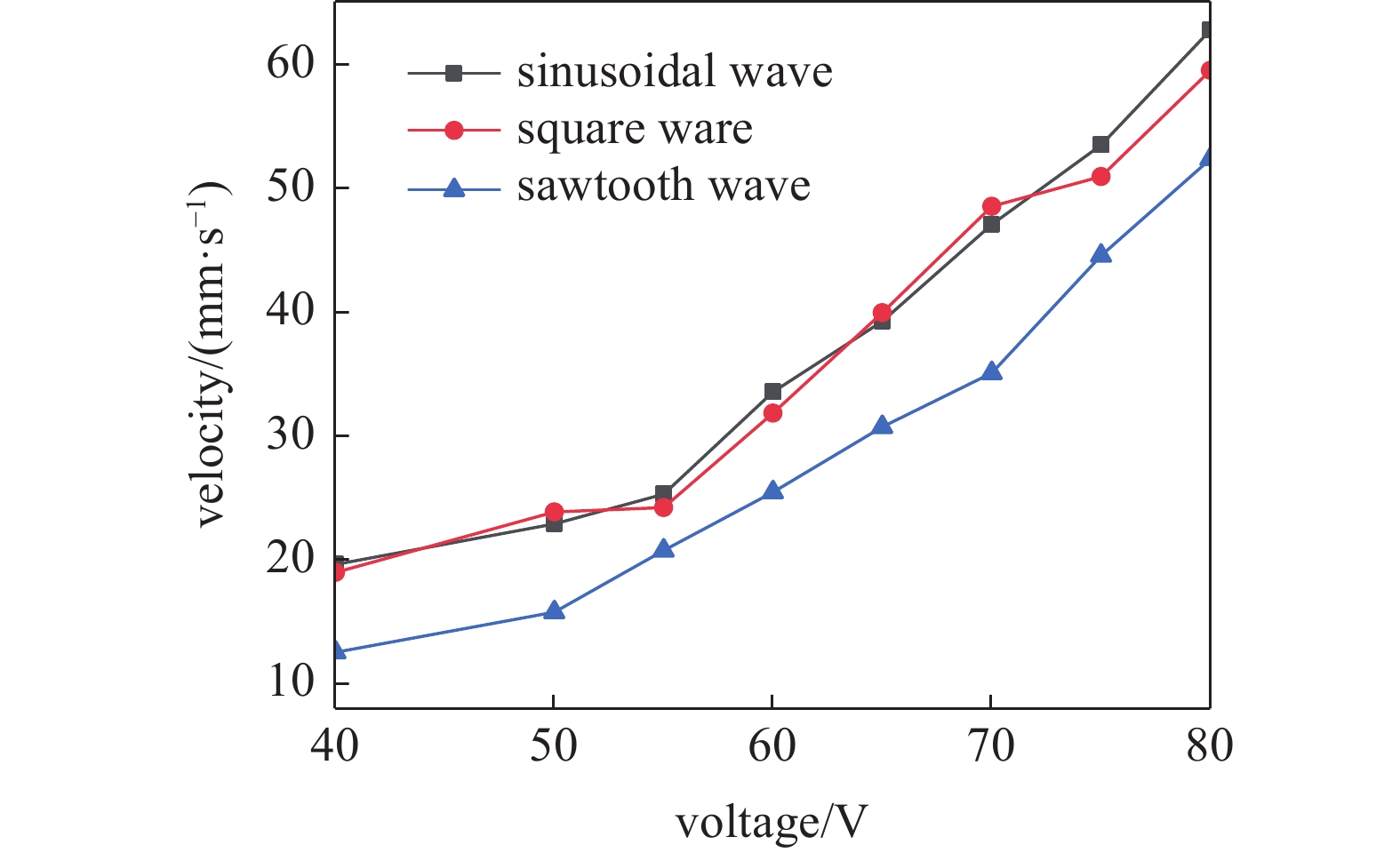
考虑在压电作动下不同输入波形信号对机器人运动的影响, 理论计算结果表明, 只要输入为周期信号, 驱动腿就可以周期性的振动向前行走, 施加给弯折角度为73°的机器人驱动腿的频率240 Hz. 波形设置为正弦波、方波和锯齿波3种, 实验结果如图14所示. 从实验结果中发现当施加信号为正弦波或者为方波时, 速度几乎不受影响, 最大速度为60 mm/s, 而当施加的信号为锯齿波时速度明显降低, 最大速度仅为52.38 mm/s. 究其原因, 从输出功率的角度来考虑当输出信号为正弦波或者方波时, 输出功率相差很小, 并且明显大于锯齿波的输出功率, 所以从实验结果中发现当施加信号为正弦波或者为方波时, 速度几乎不受影响, 最大速度为 60 mm/s, 而当施加的信号为锯齿波时速度明显降低, 最大速度仅为52.38 mm/s.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-430-14.jpg'"
class="figure_img
figure_type1 bbb " id="Figure14" />



图
14
不同输入波形信号对机器人运动的影响



Figure
14.
Influence of different input waveform signals on the motion of the robot



下载:
全尺寸图片
幻灯片


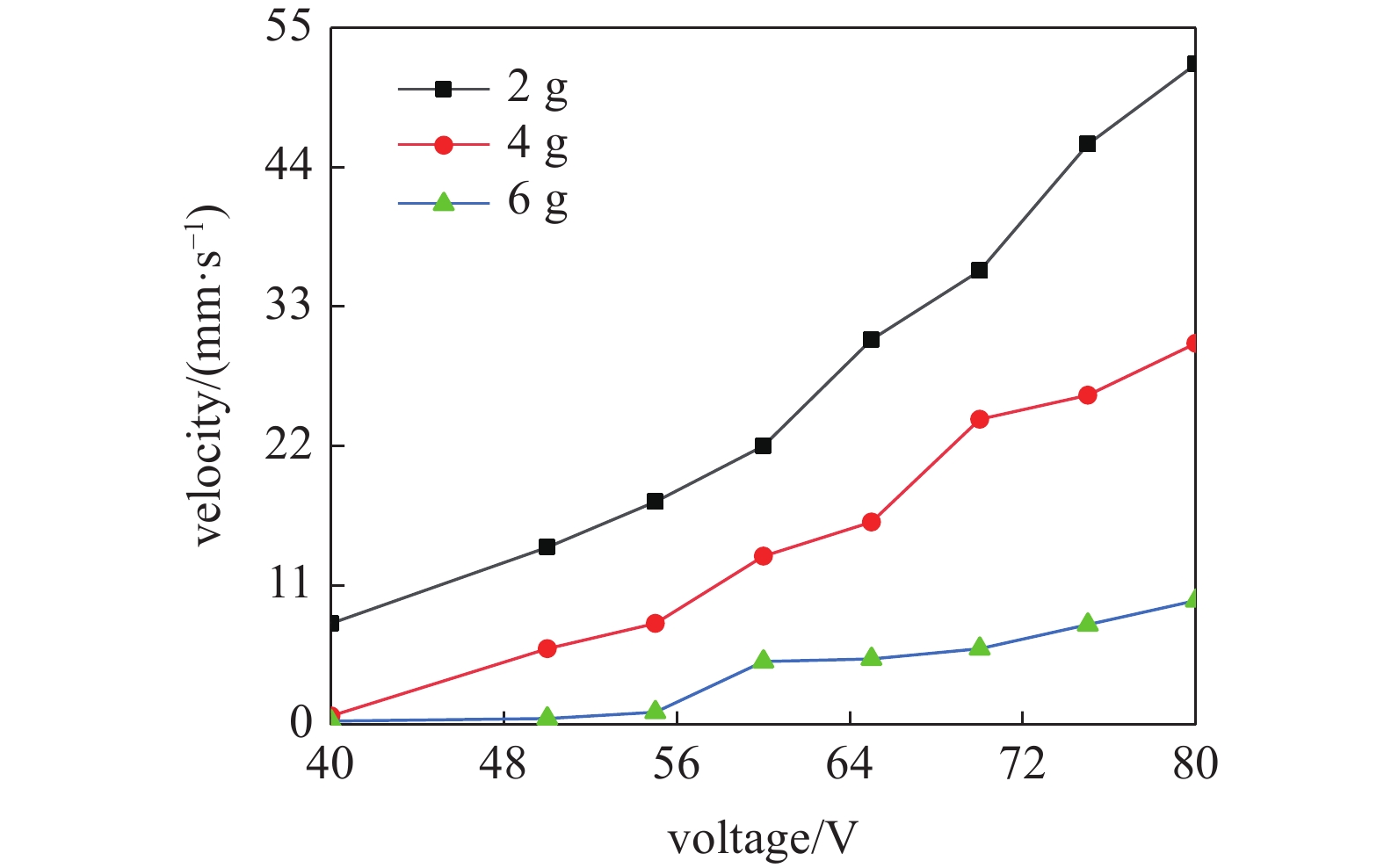
为了测试机器人在负载情况下的实验速度, 在三足机器人的基体上增加一定数量的螺母用来模拟机器人在实际中的负载, 实验照片如图15所示, 实验速度曲线如图16所示. 机器人自重约为3.5 g, 当驱动电压为80 V, 驱动频率为240 Hz, 从图16中可以看出负载重量为2 g时, 机器人的峰值速度接近53 mm/s, 当负载重量为6 g时, 峰值速度降低为9.8 mm/s. 由此可以看出负载质量对机器人运动速度有较大影响, 另外从图16中可以看出, 由于负载的增大, 机器人的速度峰值随之减小. 在240 Hz谐振点附近, 难以实现稳定的运动, 而在80 Hz附近谐振点处可以很容易地实现5 mm/s 甚至更低的稳定速度. 为了测试机器人在不同负载位置情况下的实验速度. 如图17所示, 当负载为2 g时设计了4组不同负载位置的实验, 实验结果表明, 当负载如图17(a)所示时, 机器人会向负载一侧发生转弯, 转弯半径为5.93 cm. 当负载如图17(b)所示时, 机器人也会向负载一侧发生转弯, 转弯半径为5.85 cm. 当负载如图17(c)和图17(d)所示时, 机器人发生倾斜无法正常行走. 因此, 在实际应用中机器人可以在低频下进行稳定低速负载运动工作.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-430-15.jpg'"
class="figure_img
figure_type1 bbb " id="Figure15" />



图
15
机器人负载实物图



Figure
15.
The picture of the robot with the load



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-430-16.jpg'"
class="figure_img
figure_type1 bbb " id="Figure16" />



图
16
机器人在负载下的实验速度曲线



Figure
16.
Experimental speed curves of the robot with different loads



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-430-17-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure17-1" />



17
不同负载位置下的机器人



17.
Robots under different load positions



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-430-17.jpg'"
class="figure_img
figure_type1 bbb " id="Figure17" />



图
17
不同负载位置下的机器人 (续)



Figure
17.
Robots under different load positions (continued)



下载:
全尺寸图片
幻灯片


在实验中当两个谐振足参数完全相同, 驱动频率也相同时机器人就会沿着直线行走. 如图18和图19所示, 当在一个机器人上利用单个谐振足驱动时, 就可以使其在特定的频率下实现左右转弯. 经实验验证, 当机器人身体厚度为0.2 mm, 在80 V电压, 240 Hz的正弦频率驱动下转弯最大半径为150 mm.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-430-18.jpg'"
class="figure_img
figure_type1 bbb " id="Figure18" />



图
18
机器人开始行走位置



Figure
18.
Initial position of the robot



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-430-19.jpg'"
class="figure_img
figure_type1 bbb " id="Figure19" />



图
19
机器人结束行走位置



Figure
19.
Final position of the robot



下载:
全尺寸图片
幻灯片


我们利用单侧电压转弯的特性, 可以消除机器人装配误差产生的直线偏转, 经过实验验证, 当机器人在240 Hz的工作频率下, 右侧电压为80 V, 左侧电压为76 V时, 可以实现不加导轨近似直线运动. 其偏转角度为3°以内.

最后对机器人整体的能耗进行评估, 从功率的角度来考虑, 输出电压为80 V, 输出信号为正弦波时, 实验测得有效电流为107 mA, 有效功率为6.053 W.

用高速摄像机测量得到机器人速度从零到稳定65 mm/s的时间为$ 1 times {10^{ - 5}};{text{s}} $, 即输入到压电片的功为${W_{text{i}}} = {text{6}}{text{.053}} times {text{1}}{{text{0}}^{ - {text{5}}}};{text{J}}$, 对于机器人来说, 从静止到稳定运动的动能变化为${W_{text{o}}} = dfrac{1}{2}m{v^2} = 1.725 times {10^{ - 3}} times ( 65 times $$ {{10}^{ - 3}} )^2 = 7.393 times {10^{ - 6}};{text{J}}$(机器人质量为3.5 g, 最大速度为65 mm/s), 做功效率为${{eta }} = {{{{{W}}_{text{o}}}}}/{{{{{W}}_{text{i}}}}} = {text{0}}{text{.12}}$, 即输入压电片的能量只有12％被用作了机器人的动能. 当机器人稳定运动时, 首先压电片本身用作逆压电效应时就耗散掉了一定的能量(PZT-5H机械品质因子$ Q = 75 $), 其余能量被装配外力产生的机械功, 与运动平面产生的摩擦力做功, 空气摩擦力做功以及机器人运动时上下振动的重力做功等等所耗散掉, 所以输入能量与输出能量平衡, 机器人可以以一个稳定速度稳定运动.


4.
结论


本文设计了一种可以在低频下稳定工作的微小型三足爬行机器人, 分析了其运动机理, 得到了以下结论:

(1)设计了一种新型机器人, 其具有速度快、质量轻等特点. 利用理论力学方法对该三足爬行机器人建立整体受力分析方程, 再用哈密顿原理对变截面、变角度梁建立动力学方程, 最终得到了可求解该三足爬行机器人的压电驱动腿固有频率的方程.

(2)通过实验发现, 当机器人驱动足共振时, 其在二阶固有频率下的直线运动速度明显高于一阶频率. 产生这种现象的原因是在一阶频率谐振点时, 谐振足的足端竖直位移大于高频谐振点, 水平方向位移偏小, 而在二阶谐振点时, 谐振足足端水平位移大于低频谐振点, 而竖直方向位移偏小.

(3)实验发现驱动腿不同弯折角度以及负重大小对机器人速度的影响十分显著. 在过大或者过小的弯折角度条件下, 机器人都无法达到最优速度. 本文通过调整几何参数, 以获得合适的驱动腿弯折角度. 机器人整体重量仅为3.5 g, 在驱动电压为80 V, 负载为2 g时速度可达53 mm/s. 该机器人在工程探测、应急救援等方面具有潜在应用价值.

相关话题/运动 实验 电压 信号 设计
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 仿双髻鲨头部的仿生机器鱼外型设计及其流场特性
    引言随着目前对于水下航行器的各方面研究不断深入,人们逐渐将目光转向自然界中鱼类本身高效、灵活的运动方式上,通过模仿自然界中鱼类的外形特征以及运动方式,并将其成果应用在水下航行器研究中.自仿生机器鱼成为国内外仿生学领域研究热点以来,美国、日本、英国和中国等多个国家的研究机构相继研发成功具备不同鱼种特征 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 磁力耦合道路能量收集设计与动力学分析
    引言智慧城市[1-2]旨在利用互联网、物联网等通讯技术和传感技术构建万物互联的城市,使得城市管理更加有序和高效.智慧交通是智慧城市的重要组成之一.构建智慧交通需要布置大量传感器和网络通讯设备,传统的供能方式主要是电池和有线传输,但存在污染环境、寿命短、成本高、不易维护等问题.道路交通系统中蕴藏着丰富 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 流致振动能量收集的钝头体几何设计研究
    引言能量的循环利用已经成为世界范围内具有重大意义的科学难题.与此同时,能量收集已经成为一种新兴的技术,它可以将环境中冗余的能量转换为电能,在微电子设备的自供能设计领域有着不可限量的应用前景,受到国内外研究者的广泛关注[1-3].风能是一种常见的能源,风力发电机是一种典型的能量转化装置,可用于实现风能 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 线绳驱动转速提升式低频俘能器的设计与研究
    引言由传统化石能源导致的气候变化和环境恶化等问题促使人类寻找一种绿色可再生的清洁能源以实现人类社会的可持续发展[1].低频机械能广泛存在于波浪[2]、桥梁和轨道的振动[3]、人体运动[4]、交通工具的振动[5]、流致振动[6-7]等,被认为是一种具有巨大利用价值的高熵能量[8],并在自供电传感器、工 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 亚毫米球体撞击液滴过程实验研究
    引言物体撞击液面广泛存在于自然界和工业过程,如昆虫水上行走、弹丸入水、湿法喷淋除尘、原料油催化裂化等[1-5].撞击过程包含液滴飞溅、空穴发展、毛细波传播、气体携带等复杂的流动现象[6-11].物体与气?液界面的相互作用对上述过程有重要影响,对物体撞击液面行为的研究能够为相关工业过程参数设计提供理论 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 均匀电场中气泡上升特性的实验研究
    引言强化传热技术在能源动力、石油工程、航空航天、化工等领域具有广泛的应用前景,而利用电场进行强化换热,能够有效减小换热器的体积和重量,提高能源利用效率[1-2].电场强化沸腾换热技术通过电场力控制气泡的生成、脱离、变形与运动[3-5],降低气泡脱离尺寸[6-7],加速气泡脱离频率[8],从而实现换热 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 水中开孔腔流激振荡控制实验研究
    引言空腔流激振荡是工程中常遇到的一类问题,它是指流体在流经开口结构时,边界层在开口前缘发生流动分离并形成不稳定的自由剪切层,在满足一定的流速和几何特征条件下,会引起剪切层发生稳定的自持振荡,产生很强的周期脉动压力,并通常引起高幅值纯音噪声辐射、附加阻力甚至是结构疲劳.以往对空腔流激振荡的研究主要集中 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 倍频激励双转子振动同步机理与实验研究
    引言振动同步可以表征为运动系统根据内部子系统之间的耦合效应调整特征量的变化频率,并使子系统的位移、速度等变量具有一致性和统一性.近年来,由于同步在非线性耦合混沌系统[1-2]、复杂网络系统[3]、多轴控制系统[4-5]、振动筛系统[6-7]等工程技术中具有很高的应用价值和良好的应用前景,已成为国内外 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 致密砂岩逆向渗吸作用距离实验研究
    引言随着常规油气资源的减少,致密油资源成为全球非常规油气勘探开发的热点[1-4],并且北美致密油开发已取得突破性进展[5-7].我国致密油资源丰富、分布广泛,致密油地质储量为2.0×1010t,技术可采储量为2.0×109~2.5×109t[8].我国多数致密油藏具有初始产油量低、产量递减快、衰竭采 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 煤系页岩瓦斯吸附?解吸迟滞效应核磁共振谱实验研究
    引言煤系页岩气俗称瓦斯,是陆相页岩气的重要组成部分之一,主要以吸附态和游离态形式存在.页岩气单井产能并非恒定不变,而是随着累计产量增加而不断递减[1],初期单井产量高递减快,以游离气为主;后期产量稳定,递减慢,以吸附气为主[2],随着煤系页岩瓦斯开采深度不断增加,这一现象愈发明显,而煤系页岩瓦斯吸附 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.