删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

倍频激励双转子振动同步机理与实验研究

本站小编 Free考研考试/2022-01-01


引 言


振动同步可以表征为运动系统根据内部子系统之间的耦合效应调整特征量的变化频率, 并使子系统的位移、速度等变量具有一致性和统一性. 近年来, 由于同步在非线性耦合混沌系统[1-2]、复杂网络系统[3]、多轴控制系统[4-5]、振动筛系统[6-7]等工程技术中具有很高的应用价值和良好的应用前景, 已成为国内外重要科学研究课题之一. 特别是在振动筛分领域, 自20世纪中叶前苏联****Blekhanm首次对两相同激振器同步给出理论解释[8]后, 利用偏心转子同步激励振动质体便开始用于实现物料的筛选与分级. 按照振动筛的振动轨迹分类, 至今共发展了四类振动筛: 圆振动筛、直线同步振动筛、平动椭圆同步振动筛和双轨迹同步振动筛[9]. 在整个振动系统中, 激振电机的同步状态是影响振动筛工作效率的核心因素.

目前针对振动系统同步机理和实验的研究主要侧重于单频激励多电机振动系统. 比如, 赵春雨等[10-11]根据异步电机运动学原理导出以角转速为变量的电磁转矩表达式, 从而进一步探究振动系统在同转速偏心块激励下的动力学行为和同步稳定性理论, 并有效解决了若干工程实际问题. 通过将刚性转子安装在两个弹性阻尼支座上, Sperling等[12]提出一种带有双平面自动平衡装置的转子同步模型, 并根据运动方程进行数值计算后发现, 当转子速度高于系统最大共振转速范围时, 系统可以有效补偿刚性转子的离心力和不平衡力矩从而获得同步振动. Balthazar等[13-14]基于数值模拟定量地分析了非线性振动系统中4个非理想激振器安装于柔性支撑结构的同步运动, 表明在共振频率阶段的Sommerfeld效应显著影响激振电机的同步性. 上述****从振动力学理论角度研究了单频自同步振动系统的同步机理, 但是忽略了系统的机电耦合动力特性. 针对机电耦合诱导的单频振动系统同步传动行为, 侯勇俊等[15-16]考虑电机系统与振动机械系统之间的相互影响, 采用转子动力学理论成功构造三机椭圆振动系统的机电耦合数学模型, 揭示转子与振动质体间同步传动的机电耦合机理. 方潘等[17]在侯勇俊的研究基础上将振动电机视为与摆杆耦合的摆动电机, 并成功把单自由度转子耦合摆装置同步问题转化为研究质体瞬时响应解的存在性和稳定性. 然而, 该系统受限于质体单一振动方向而不适用于实际筛分工程. 所以文献[18-19]更深入探讨了多转子耦合摆电机的多自由度振动同步特性, 并引入相邻交叉耦合控制策略实现系统的椭圆筛分轨迹和零相位控制同步. Zhang等[20-22]运用非线性动力学理论推导了多个同频驱动转子与圆柱滚子耦合的同步运动方程, 并结合实验平台讨论了滚子与转子之间的同步传动机理与动态特性. 以上研究仅仅阐述了由相同激振器驱动振动机械的动力学理论, 将它们应用到振动筛分工程后发现, 物料的筛分能力并没有得到显著提升. 主要原因是不同粒径颗粒在单一频率激励下受到相同激振力作用, 一旦形成筛网堵塞将会影响系统透筛率. 而倍频振动系统单周期内由于受到不同形式的激振力, 物料运动更为活跃的同时有助于减小筛堵概率.

针对振动系统的双频同步行为已有****做出一些试探性研究, 以提高系统物料分级与筛分能力. Modrzewski和Wodzinski[23-24]设计了3种不同类型振动筛用于研究矿物废弃物的分离特性, 实验对比表明双频系统的同步行为和筛选能力优于其他振动结构, 但是缺乏振动系统的理论支撑. 姚运仕等[25-26]则提出了一种采用单电机轮系传动方式实现激振器两种不同频率的强迫同步, 然而受激振器回转振动和箱体振动的影响, 轮系承受较大的冲击载荷和惯性载荷容易引发齿轮疲劳失效. 冯忠绪等[27]引入运动学微分方程阐述了双频振动筛的工作原理, 却并没有对双频振动系统的模型做出修正, 缺陷依然存在. 因此, 有必要采用双频激励多电机自同步振动系统(激振器之间无强迫同步的轮系)来实现双频振动系统的同步运动, 以提高振动筛的寿命与可靠性. 根据振动系统的能量传递过程, 文献[28]引入Lyapunov一次近似理论从数学上证明了双转子二倍频系统实现稳定同步运动是可行的, 但忽视了结构参数变化对系统动力学特性和同步运动状态的影响. Zou等[9,29]虽然根据同步性条件讨论了远共振系统中双电机倍频同步范围, 并从同步控制角度出发利用计算机仿真实现稳定零相位差控制同步, 但是并没有通过数值计算定量探讨系统的内在耦合特性, 同时缺乏实验验证其研究的正确性, 无法全面揭示振动系统的双频同步机理.

综上所述, 现有研究对倍频激励双转子振动同步机理和动力学特性分析尚未明确, 从而对系统的同步溯源缺少充分的理论依据. 本文将围绕倍频振动系统的振动同步机理、同步特征参数定量计算、模拟仿真以及振动实验测试四个方面展开研究. 重点讨论了转子偏心质量、电机安装位置、支撑弹簧刚度以及偏心半径等参数对系统倍频同步状态的影响, 通过实验平台对不同工况下的箱体以及转子动力学特性进行深入比较与分析, 验证了倍频振动同步理论研究的正确性, 为研制新型非常规轨迹的振动机械提供了较好的理论依据.


1.
数学模型及运动微分方程


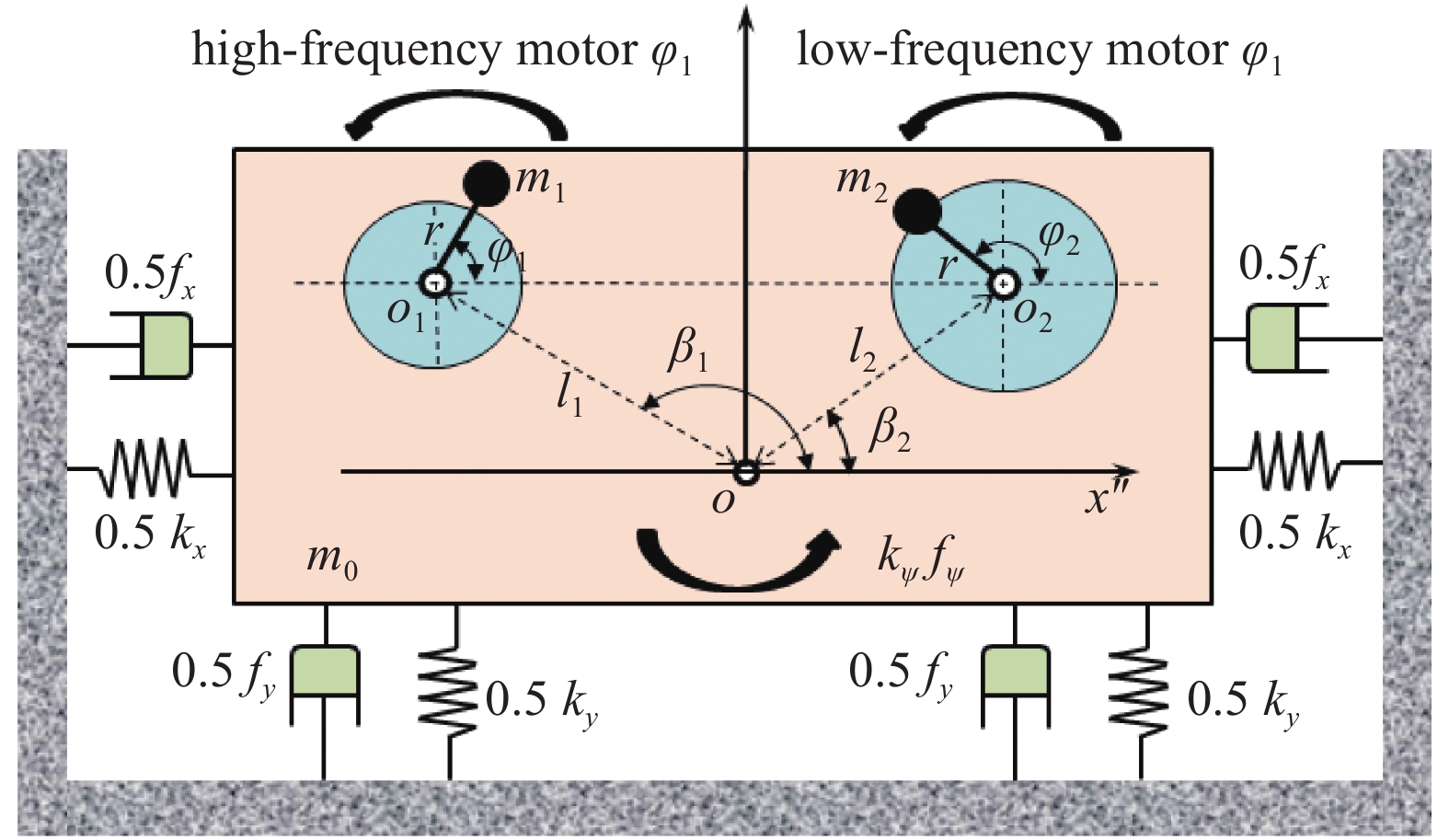
为掌握电机驱动偏心转子之间的倍频同步运动机制, 研究箱体沿各自由度的动力学响应, 本节旨在推导出振动系统的运动微分方程. 如下图1所示为倍频激励双转子振动系统力学模型. 质量为m0的箱体与系统基座之间采用4个压缩弹簧进行弹性连接, 其中弹簧元件沿x, y, ψ自由度的刚度系数分别考虑为kx, ky, kψ, 阻尼系数fx, fy, fψ分别表征弹簧在能量释放和吸收过程中沿x, y, ψ方向上的能量耗散. 高频激振电机(即二极感应电机1)和低频激振电机(即四极感应电机2)固定安装于箱体之上, 分别以转速${dot varphi _i}$(i = 1, 2)驱动质量为mi 的偏心块作同向回转运动. 将两偏心块等效为偏心距均是r的质点, 可以看出振动系统所需的激振力是由转子的离心运动产生. 定义偏心块i绕自身旋转中心oi转动的瞬时相位角为φi; 箱体的瞬时摆动角为ψ; 系统质心至电机轴i的安装距离为li; 直线oio″与坐标轴o″x″之间的夹角为βi. 当两电机在动态坐标系x″o″y″中同步运行时, 固定坐标系xoy可通过图2的多自由度振动系统坐标转换原则得到.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-359-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
倍频激励双转子振动系统数学模型



Figure
1.
Mathematical model of the vibration system actuated with double-frequency and dual-rotor



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-359-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
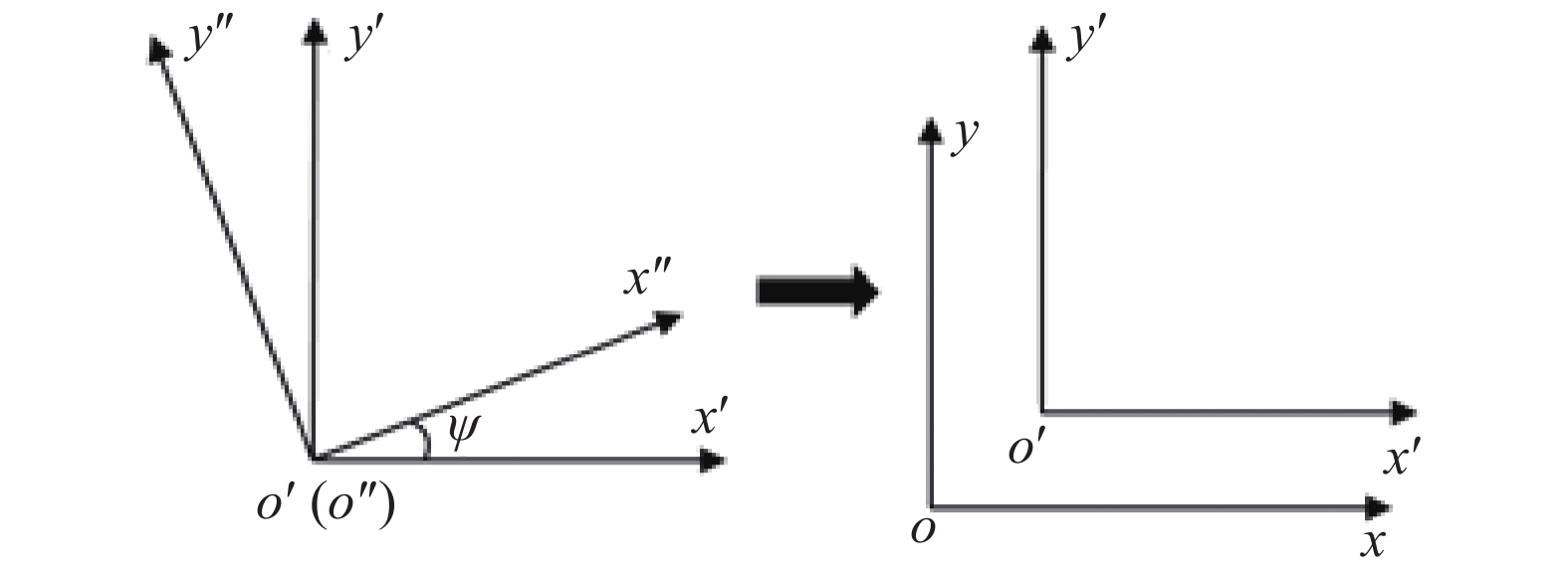
坐标转换原则



Figure
2.
Principle of coordinate transformation



下载:
全尺寸图片
幻灯片


当系统处于振动状态时, 高频转子坐标矩阵Φ1″和低频转子坐标矩阵Φ2″在动态坐标系x″o″y″中可分别描述为







$$left.begin{split} &{{boldsymbol{varPhi }}_1}^{prime prime } = left[ begin{gathered}{l_1}cos {beta _1} + rcos {varphi _1} {l_1}sin {beta _1} + rsin {varphi _1} end{gathered}
ight] &{{boldsymbol{varPhi }}_2}^{prime prime } = left[ begin{gathered}{l_2}cos {beta _2} + rcos {varphi _2} {l_2}sin {beta _2} + rsin {varphi _2} end{gathered}
ight] end{split}
ight} $$
(1)

动态坐标系x″o″y″固定于箱体之上, 实时地跟随系统作位移振动和摆动; 移动坐标系x′o′y′可通过x″o″y″绕质心o″旋转得到; 固定坐标系xoy可通过移动x′o′y′得到. Φi和Φi″的坐标矩阵转换方程为







$$left.begin{split}& {{boldsymbol{varPhi }}_i} = left[ begin{gathered}x y end{gathered}
ight] + {boldsymbol{K}}{{boldsymbol{varPhi }}_i}^{prime prime };&{boldsymbol{K}} = left[ begin{gathered}cos psi ;;; - sin psi sin psi ;;;cos psi end{gathered}
ight] end{split}
ight}$$
(2)

式中, Φi为第i个转子的固定坐标矩阵; [x y]T为系统质心沿x, y方向的幅值矩阵; K为变换矩阵. 根据式(1)和式(2), 获得各转子在平面xoy内的固定坐标







$$ left.begin{split} &{{boldsymbol{varPhi }}_1} = left[ begin{gathered}x + {l_1}cos {text{(}}{beta _1} + psi {text{)}} + rcos {text{(}}{varphi _1} + psi {text{)}} y + {l_1}{text{sin(}}{beta _1} + psi {text{)}} + r{text{sin(}}{varphi _1} + psi {text{)}} end{gathered}
ight] &{{boldsymbol{varPhi }}_2} = left[ begin{gathered}x + {l_2}cos {text{(}}{beta _2} + psi {text{)}} + rcos {text{(}}{varphi _2} + psi {text{)}} y + {l_2}{text{sin(}}{beta _2} + psi {text{)}} + r{text{sin(}}{varphi _2} + psi {text{)}} end{gathered}
ight] end{split}
ight}$$
(3)

分析整个振动系统的能量转化过程, 由转子驱动箱体产生的系统总动能E为







$$ begin{split} &E = frac{1}{2}{m_0}{{dot x}^2} + frac{1}{2}{m_0}{{dot y}^2} + frac{1}{2}{J_{text{m}}}{{dot psi }^2} + frac{1}{2}sumlimits_{i = 1}^2 {{J_i}{{dot varphi }_i}^2} + &qquadfrac{1}{2}sumlimits_{i = 1}^2 {{m_i}{boldsymbol{dot varPhi }}_i^{text{T}}{{{boldsymbol{dot varPhi }}}_i}} end{split} $$
(4)

式中, $dot {()} = {text{d}} {()} /{text{d}}t$; Ji = mir2, 表示偏心块i的转动惯量; Jm = m0le2, 表示箱体的转动惯量; le表示箱体绕质心的等效摆动半径. 若箱体围绕某一平衡位置做周期性同步振动, 其重力与支撑弹簧静止时的初始压力相平衡, 系统可不用考虑重力势能的影响, 总势能U由一系列支撑弹簧的压缩量引起







$$ U = frac{1}{2}{k_x}{x^2} + frac{1}{2}{k_y}{y^2} + frac{1}{2}{k_psi }{psi ^2} $$
(5)

考虑各电机轴的摩擦系数分别是f1, f2, 则由电机轴的摩擦转动以及弹簧能量吸收和释放过程中形成的系统总耗散能D为







$$ D = frac{1}{2}{f_x}{dot x^2} + frac{1}{2}{f_y}{dot y^2} + frac{1}{2}{f_psi }{dot psi ^2} + frac{1}{2}{f_1}{dot varphi _1}^2 + frac{1}{2}{f_2}{dot varphi _2}^2 $$
(6)

倍频激励双电机振动系统是一个完整系统, 将系统的广义坐标矩阵和各自由度的广义力矩阵分别考虑为q = [x y ψ φ1 φ2]和Q = [0 0 0 Me1?Re1 Me2?Re2]. 同时引入下列广义Lagrange方程建立力学模型的运动微分方程[20]







$$ frac{{
m{d}}}{{{
m{d}}t}}left( {frac{{partial E}}{{partial {boldsymbol{dot q}}}}}
ight) - frac{{partial (E - U)}}{{partial {boldsymbol{q}}}} + frac{{partial D}}{{partial {boldsymbol{dot q}}}} = {boldsymbol{Q}} $$
(7)

在振动工程应用中, 箱体的质量远远大于偏心块的质量, 即m0$ gg $mi; 箱体的摆动角度远小于1, 即ψ$ ll $1. 因此可以忽略由激振电机安装误差造成的耦合惯性矩, 把倍频激振器驱动的振动系统视为一个多自由度系统. 将式(4)~式(6)代入方程(7), 并考虑系统总质量M = m0+m1+m2, 获得倍频激励双转子振动系统动力学模型的运动微分方程







$$ left.begin{split} &Mddot x + {f_x}dot x + {k_x}x = sumlimits_{i = 1}^2 {{m_i}r{text{(}}{{dot varphi }_i}^{text{2}}{text{cos}}{varphi _i} + {{ddot varphi }_i}{text{sin}}{varphi _i}{text{)}}} &Mddot y + {f_y}dot y + {k_y}y = sumlimits_{i = 1}^2 {{m_i}r{text{(}}{{dot varphi }_i}^{text{2}}{text{sin}}{varphi _i} - {{ddot varphi }_i}{text{cos}}{varphi _i}{text{)}}} &{J_{text{m}}}ddot psi + {f_psi }dot psi + {k_psi }psi = &qquadsumlimits_{i = 1}^2 {{m_i}r{l_i}{text{[}}{{dot varphi }_i}^{text{2}}{text{sin(}}{varphi _i} - {beta _i}{text{)}} - {{ddot varphi }_i}{text{cos(}}{varphi _i} - {beta _i}{text{)]}}} &{J_1}{{ddot varphi }_1} = {M_{{text{e1}}}} - {R_{{text{e}}1}} + {m_1}r{text{[}}ddot x{text{sin}}{varphi _1} - ddot y{text{cos}}{varphi _1} - &qquad{l_1}ddot psi {text{cos(}}{varphi _1} - {beta _1}{text{)}} - {l_1}{{dot psi }^{text{2}}}{text{sin(}}{varphi _1} - {beta _1}{text{)]}} &{J_2}{{ddot varphi }_2} = {M_{{text{e}}2}} - {R_{{text{e}}2}} + {m_2}r{text{[}}ddot x{text{sin}}{varphi _2} - ddot y{text{cos}}{varphi _2} - &qquad {l_2}ddot psi {text{cos(}}{varphi _2} - {beta _2}{text{)}} - {l_2}{{dot psi }^{text{2}}}{text{sin(}}{varphi _2} - {beta _2}{text{)]}} end{split}
ight} $$
(8)

式中, $ddot {()} = {{text{d}}^{text{2}}} {()} /{text{d}}{t^{text{2}}},;{R_{{text{e}}i}} = {f_i}{dot varphi _i} $, $ {M_{{text{e}}i}} - {R_{{text{e}}i}} $为电机i在考虑阻尼转矩情况下的电磁转矩. 根据方程(8)可知, 前3个等式分别表示箱体沿x方向的水平振动方程, y方向的垂直振动方程以及ψ方向的摆动方程; 后两个等式分别为高频转子和低频转子绕其自身转动轴旋转的运动方程. 激振器之间的倍频同步不仅与箱体沿各自由度的位移振动状态有关, 而且与激振电机的运动特性有关. 因此考虑到箱体与两台电机间的动态耦合效应, 倍频激励双转子振动系统同步研究应视为一个典型的机电耦合动力学问题.


2.
倍频振动同步机理



2.1
系统各自由度响应近似解


式(8)是关于x, y, ψ, φ1, φ2的动力学耦合方程. 若两个转子均以各自额定转速同步振动时, 激振电机作为系统驱动源同样分别以角速度${dot varphi _1}$和${dot varphi _2}$运行. 此时${dot varphi _i}$波动很小, 可对运动微分方程中的角加速度${ddot varphi _i}$忽略不计. 为获得方程的稳态强迫振动响应近似解, 将系统参数分别替换为下列无量纲参数形式







$$ left.begin{split} &{eta _{12}} = {m_1}/{m_2},;{eta _2} = {m_2}/M;&{r_{l1}} = {l_1}/{l_{text{e}}},;{r_{l2}} = {l_2}/{l_{text{e}}} &{r_{text{o}}} = r/{l_{text{e}}},;{lambda _x} = {omega _x}/{omega _{text{m}}};&{lambda _y} = {omega _y}/{omega _{text{m}}},;{lambda _psi } = {omega _psi }/{omega _{text{m}}} &{xi _x} = {f_x}/bigg(2sqrt {{k_x}M}bigg) &{xi _y} = 2{f_y}sqrt {{k_y}M};&{xi _psi } = {f_psi }/bigg(2sqrt {{k_psi }{J_{text{m}}}}bigg) end{split}
ight}$$
(9)

式中, $ {omega _x}{text{ = }}sqrt {{k_x}/M} $, $ {omega _y}{text{ = }}sqrt {{k_y}/M} $, $ {omega _psi }{text{ = }}sqrt {{k_psi }/{J_{text{m}}}} $, ωc (c = x, y, ψ)分别表示振动系统沿c自由度的固有频率; ωm为低频电机的激振频率; λc是振动系统沿c自由度的频率比; ξc是振动系统沿c自由度的粘性阻尼系数. 本文研究超远共振下倍频激励双电机系统的振动同步行为, 其激振频率至少为系统固有频率的3倍及以上, 阻尼系数ξc$ ll $1. 引入式(9)并针对式(8)中箱体的运动方程做出等价变换, 系统沿x, y, ψ自由度的振动微分方程改写为







$$ left.begin{split} &ddot x + 2{xi _x}{omega _x}dot x + {omega _x}^2x = {eta _2}{eta _{12}}r{{dot varphi }_1}^{text{2}}{text{cos}}{varphi _1} + {eta _2}r{{dot varphi }_2}^{text{2}}{text{cos}}{varphi _2} &ddot y + 2{xi _y}{omega _y}dot y + {omega _y}^2y = {eta _2}{eta _{12}}r{{dot varphi }_1}^{text{2}}{text{sin}}{varphi _1} + {eta _2}r{{dot varphi }_2}^{text{2}}{text{sin}}{varphi _2} &ddot psi + 2{xi _psi }{omega _psi }dot psi + {omega _psi }^2psi = {eta _2}{eta _{12}}{r_{text{o}}}{r_{l1}}{{dot varphi }_1}^{text{2}}{text{sin(}}{varphi _1} - {beta _1}{text{)}} + &qquad {eta _2}{r_{text{o}}}{r_{l2}}{{dot varphi }_2}^{text{2}}{text{sin(}}{varphi _2} - {beta _2}{text{)}} end{split}
ight}$$
(10)

采用复变函数规则求解[30], 可推导出箱体的周期性幅值响应解为







$$ left.begin{split} &x = - {eta _2}{eta _{12}}r{
ho _{x1}}{text{cos(}}{varphi _1} + {gamma _{x1}}{text{)}} - {eta _2}r{
ho _{x2}}{text{cos(}}{varphi _2} + {gamma _{x2}}{text{)}} &y = - {eta _2}{eta _{12}}r{
ho _{y1}}{text{sin(}}{varphi _1} + {gamma _{y1}}{text{)}} - {eta _2}r{
ho _{y2}}{text{sin(}}{varphi _2} + {gamma _{y2}}{text{)}} &psi = - {eta _2}{eta _{12}}{r_{text{o}}}{r_{l1}}{
ho _{psi 1}}{text{sin(}}{varphi _1} - {beta _1} + {gamma _{psi 1}}{text{)}} - &qquad {eta _2}{r_{text{o}}}{r_{l2}}{
ho _{psi 2}}{text{sin(}}{varphi _2} - {beta _2} + {gamma _{psi 2}}{text{)}} end{split}
ight}$$
(11)

其中







$$ left.begin{split} &{
ho _{c1}} = frac{1}{{sqrt {{{(1 - {lambda _c^2}/4)}^{text{2}}} + {{({xi _c}{lambda _c})}^{text{2}}}} }} &{
ho _{c2}} = frac{1}{{sqrt {{{{text{(}}1 - {lambda _c^2}{text{)}}}^{text{2}}} + {{{text{(}}2{xi _c}{lambda _c}{text{)}}}^{text{2}}}} }} &{gamma _{c1}} = arctan frac{{{xi _c}{lambda _c}}}{{1 - {lambda _c^{text{2}}}/4}},;{gamma _{c2}} = arctan frac{{2{xi _c}{lambda _c}}}{{1 - {lambda _c^2}}} end{split}
ight}$$
(12)

式中, $ {
ho _{c1}} $, $ {
ho _{c2}} $分别是激振器1和2沿c方向的振幅放大因子; $ {gamma _{c1}} $, $ {gamma _{c2}} $分别是激振器1和2沿c方向的滞后相位角.


2.2
系统倍频自同步准则


通过偏心块间相位差的变化趋势可反映出两台激振电机的同步特性, 从而揭示振动系统的动力学特征. 在同步振动过程中, 以低频电机的特性参数为基准, 两转子的平均相位为φ = (φ1/2+φ2)/2. 高频转子与低频转子的瞬时相位角可分别表示如下







$$left. begin{split}&{varphi _1}{text{ = 2}}(varphi {text{ + }}{alpha _0});&{varphi _2}{text{ = }}varphi - {alpha _0}end{split}
ight}$$
(13)

在单频激励的振动系统中, 其同步稳定性通过转子间的真实相位差值表示. 然而在倍频激励的振动同步系统中, 真实相位差φ1?φ2 = φ+3α0是一个关于时间t的函数, 即φ1?φ2不稳定, 无法用于揭示倍频同步机理. 因此, 考虑到两振动电机的转速关系, 可定义倍频激励振动系统的相位差为







$$ alpha = {varphi _1} - 2{varphi _2} = 4{alpha _0} $$
(14)

依据修正的小参数平均法[10,20], 虽然转子平均角速度$dot varphi $是一个与时间有关的慢变参量, 但是当整个系统处于稳态同步振动时, 依然可以视为在ωm附近周期性波动. 以低频转子的运动特性为基准, 将其最小正周期T作为时域上的积分区间, 此时$dot varphi $在T内积分应视为常数







$$ {omega _{text{m}}} = frac{1}{T}int_t^{t + T} {dot varphi } {text{(}}t{text{)d}}t = {text{const}}{text{.}} $$
(15)

引入扰动参数ε1与ε2分别表征$dot varphi $与$dot alpha $在瞬时状态下的波动程度, 可写为







$$ left. begin{split}&dot varphi {text{ = }}(1{text{ + }}{varepsilon _1}){omega _{text{m}}};;;&dot alpha {text{ = }}{varepsilon _2}{omega _{text{m}}} end{split}
ight}$$
(16)

同时, 确定各激振器的角速度$ {dot varphi _i} $和角加速度$ {ddot varphi _i} $与扰动参数εi的关系







$$ left.begin{split} &{{dot varphi }_1}{text{ = 2}}(1{text{ + }}{varepsilon _1} + {varepsilon _2}){omega _{text{m}}};;;&{{dot varphi }_2}{text{ = }}({text{1 + }}{varepsilon _1} - {varepsilon _2}){omega _{text{m}}} &{{ddot varphi }_1}{text{ = 2}}({{dot varepsilon }_1} + {{dot varepsilon }_2}){omega _{text{m}}};;;&{{ddot varphi }_2}{text{ = }}({{dot varepsilon }_1} - {{dot varepsilon }_2}){omega _{text{m}}} end{split}
ight} $$
(17)

当系统达到同步振动时, 偏心块的转速不产生变化, 说明电机的负载转矩近似等于电磁转矩, 即实际输出转矩与驱动转矩达到动态平衡的状态. 而在能量传递和能量耦合振动过程中, 电机的电磁转矩值是时变的, 需要通过转子1和2在周期T内的微分运动方程的积分平均值来表征. 因此先采用式(11)计算得到参数$ ddot x,;ddot y,;dot psi,;ddot psi$, 然后将其代入方程(8)后两式中并积分求平均, 忽略扰动参数εi的高阶无穷小项的影响, 则两转子的运动平衡方程可以推导出







$$left.begin{split} &{text{2}}{J_1}{omega _{text{m}}}{{dot {bar varepsilon }}_1} + {text{2}}{J_1}{omega _{text{m}}}{{dot {bar varepsilon }}_2} = &qquad a_{11}^prime {{dot {bar varepsilon }}_1} + a_{12}^prime {{dot {bar varepsilon }}_2} - {a_{11}}{{bar varepsilon }_1} - {a_{12}}{{bar varepsilon }_2} + {a_1} = {P_1} &{J_2}{omega _{text{m}}}{{dot {bar varepsilon }}_1} - {J_2}{omega _{text{m}}}{{dot {bar varepsilon }}_2} = &qquad a_{21}^prime {{dot {bar varepsilon }}_1} - a_{22}^prime {{dot {bar varepsilon }}_2} - {a_{21}}{{bar varepsilon }_1} + {a_{22}}{{bar varepsilon }_2} + {a_2} = {P_2} end{split}
ight}$$
(18)

式中







$$ left.begin{split} &a_{11}^prime = a_{12}^prime = {m_2}{r^{text{2}}}{omega _{text{m}}}{W_{{text{c}}1}}&a_{21}^prime = a_{22}^prime ={frac{1}{2}}{m_2}{r^{text{2}}}{omega _{text{m}}}{W_{{text{c}}2}} &{a_{11}} = {text{4}}{m_2}{r^{text{2}}}{omega _{text{m}}}^{text{2}}{W_{{text{s}}1}} + {text{2}}{f_1}{omega _{text{m}}} + &qquad {frac{1}{2}}{m_2}{r^{text{2}}}{omega _{text{m}}}^{text{2}}{H_1}{text{sin}}(bar alpha - {beta _1} + 2{beta _2} - 2{gamma _{psi 2}}) &{a_{12}} = 4{m_2}{r^{text{2}}}{omega _{text{m}}}^{text{2}}{W_{{text{s}}1}} + {text{2}}{f_1}{omega _{text{m}}} - &qquad {frac{1}{2}} {m_2}{r^{text{2}}}{omega _{text{m}}}^{text{2}}{H_1}{text{sin}}(bar alpha - {beta _1} + 2{beta _2} - 2{gamma _{psi 2}}) &{a_1} = {{bar M}_{{text{e}}1}} - {text{2}}{f_1}{omega _{text{m}}} - {text{2}}{m_2}{r^{text{2}}}{omega _{text{m}}}^{text{2}}{W_{{text{s}}1}} - &qquad {frac{1}{4}}{boldsymbol{}}{m_2}{r^{text{2}}}{omega _{text{m}}}^{text{2}}{H_1}{text{sin}}(bar alpha - {beta _1} + 2{beta _2} - 2{gamma _{psi 2}}) &{a_{21}} = {m_2}{r^{text{2}}}{omega _{text{m}}}^{text{2}}{W_{{text{s}}2}} + {f_2}{omega _{text{m}}} - &qquad {text{2}}{m_2}{r^{text{2}}}{omega _{text{m}}}^{text{2}}{H_2}{text{sin(}}bar alpha - {beta _1} + 2{beta _2} + {gamma _{psi 1}} - {gamma _{psi 2}}{text{)}} &{a_{22}} = {m_2}{r^{text{2}}}{omega _{text{m}}}^{text{2}}{W_{{text{s}}2}} + {f_2}{omega _{text{m}}} &{a_2} = {{bar M}_{{{
m{e}}} 2}} - {f_2}{omega _{text{m}}} - {m_2}{r^{text{2}}}{omega _{text{m}}}^{text{2}}{W_{{text{s}}2}} + &qquad {frac{1}{2}} {m_2}{r^{text{2}}}{omega _{text{m}}}^{text{2}}{H_2}{text{sin(}}bar alpha - {beta _1} + 2{beta _2} + {gamma _{psi 1}} - {gamma _{psi 2}}{text{)}} &{W_{{text{c}}1}} = {eta _2}{eta _{12}}^{text{2}}{text{(}}{
ho _{x1}}{text{cos}}{gamma _{x1}} + {
ho _{y1}}{text{cos}}{gamma _{y1}} + {r_{l1}}^{text{2}}{
ho _{psi 1}}{text{cos}}{gamma _{psi 1}}{text{)}} &{W_{{text{s}}1}} = {eta _2}{eta _{12}}^{text{2}}{text{(}}{
ho _{x1}}{text{sin}}{gamma _{x1}} + {
ho _{y1}}{text{sin}}{gamma _{y1}} + {r_{l1}}^{text{2}}{
ho _{psi 1}}{text{sin}}{gamma _{psi 1}}{text{)}} &{H_1} = {eta _{12}}{eta _2}^{text{2}}{r_{text{o}}}{r_{l1}}{r_{l2}}^{text{2}}{
ho _{psi 2}}^{text{2}};&{H_2} = {eta _{12}}{eta _2}^{text{2}}{
ho _{psi 1}}{
ho _{psi 2}}{r_{text{o}}}{r_{l1}}{r_{l2}}^{text{2}} &{W_{{text{c}}2}} = {eta _2}{text{(}}{
ho _{x2}}{text{cos}}{gamma _{x2}} + {
ho _{y2}}{text{cos}}{gamma _{y2}} + {r_{l2}}^{text{2}}{
ho _{psi 2}}{text{cos}}{gamma _{psi 2}}{text{)}} &{W_{{text{s}}2}} = {eta _2}{text{(}}{
ho _{x2}}{text{sin}}{gamma _{x2}} + {
ho _{y2}}{text{sin}}{gamma _{y2}} + {r_{l2}}^{text{2}}{
ho _{psi 2}}{text{sin}}{gamma _{psi 2}}{text{)}} end{split}
ight}$$
(19)

方程(18)中系数ai, aij, a′ij (i = 1, 2; j = 1, 2)是由一系列参数Wsi, Wci, Hi和$bar alpha $共同决定的. 与平均相位φ的变化幅度相比较, 稳态时$ {varepsilon _i},;{dot varepsilon _i},;alpha $的波动范围非常小, 均可看作慢变参量[7]. 因此在方程(18)的积分过程中, 可以取这些参数在一个T内的积分均值$ {bar varepsilon _i},;{dot {bar varepsilon} _i},;bar alpha $用于替换相应的慢变参量, 即







$$ bar {()}= frac{1}{T}int_t^{t + T} { {()}{text{d}}t} $$
(20)

若振动电机分别以各自额定速度${dot varphi _1} approx 2{omega _{text{m}}}$, ${dot varphi _2} approx {omega _{text{m}}}$同步工作, 则${bar M_{{text{e}}i}}$可定义为电磁转矩Mei的积分均值[31], 表示如下







$$left. begin{split}&{bar M_{{text{e}}1}} = {M_1} - {k_1}{text{(}}{bar varepsilon _{text{1}}} + {bar varepsilon _{text{2}}}{text{)}};;;&{bar M_{{text{e}}2}} = {M_2} - {k_2}{text{(}}{bar varepsilon _{text{1}}} - {bar varepsilon _{text{2}}}{text{)}}end{split}
ight}$$
(21)

其中







$$left. begin{split}& {M_i} = {n_{{text{p}}i}}frac{{L_{{text{m}}i}^2U_{text{s}}^2}}{{L_{{text{s}}i}^2{R_{{text{r}}i}}}}{text{(}}{omega _{text{s}}} - {n_{{
m{p}}i}}{omega _i}{text{) }};;;&{k_i} = n_{{text{p}}i}^2frac{{L_{{text{m}}i}^2U_{text{s}}^2}}{{L_{{text{s}}i}^2{omega _{text{s}}}{R_{{text{r}}i}}}}end{split}
ight} $$
(22)

式中, Mi是电机i的输入转矩; ki 是电机i在额定转速运行时的刚度系数; npi 是电机i的磁极对数, np1 = 1, np2 = 2; Lmi和Lsi 分别是电机i的互感系数和定子电感; Rri 是电机i的转子阻抗; Us 是电机额定电压; ωi 是电机i的额定激振频率; ωs 是电网供电频率.

重新整理方程(18), 将其写成与电磁转矩有关的一阶微分方程的矩阵形式







$$ {boldsymbol{P}}dot {bar {boldsymbol{varepsilon}}} = {boldsymbol{Q}}bar {boldsymbol{varepsilon}} + {boldsymbol{R}} $$
(23)

其中







$$ left.begin{split} &{boldsymbol{P}} = left[ {begin{array}{*{20}{c}}{{J_1}{omega _{text{m}}} - a_{11}^prime }&{{text{2}}{J_1}{omega _{text{m}}} - a_{12}^prime } {{J_2}{omega _{text{m}}} - a_{21}^prime }&{ - {J_2}{omega _{text{m}}} + a_{22}^prime } end{array}}
ight];&{boldsymbol{Q}} = left[ {begin{array}{*{20}{c}}{ - {a_{11}}}&{ - {a_{12}}} { - {a_{21}}}&{{a_{22}}} end{array}}
ight] &{boldsymbol{R}} = {left[ {begin{array}{*{20}{c}}{{a_1}}&{{a_2}} end{array}}
ight]^{
m{T}}};&{dot{bar {boldsymbol varepsilon }}} = {left[ {begin{array}{*{20}{c}}{{{dot {bar varepsilon }}_1}}&{{{dot {bar varepsilon }}_2}} end{array}}
ight]^{
m{T}}};&{bar{boldsymbol varepsilon }} = {left[ {begin{array}{*{20}{c}}{{{bar varepsilon }_1}}&{{{bar varepsilon }_2}} end{array}}
ight]^{
m{T}}} end{split}
ight}$$
(24)

式中, 方程(23)称为振动系统耦合方程, 反映了倍频激励下两个偏心块之间的耦合运动关系. P为与转子加速度有关的惯性耦合矩阵; Q为与转子角速度有关的刚度耦合矩阵; R为各电机轴上的电磁转矩与负载转矩之差. 当激振器之间达到稳定的同步振动, 扰动参数矩阵$ {bar{boldsymbol varepsilon }} $和$ {dot{bar {boldsymbol varepsilon }}} $的值与振动电机的激励频率相比可忽略, 其变化量在T内的平均波动是零, 即${dot{bar {boldsymbol varepsilon}}} = bar {boldsymbol{varepsilon}} = {{boldsymbol{0}}}$. 将它代入耦合方程(23), 两电机轴间的平衡转矩方程可以描述为







$$ left.begin{split} &{{bar M}_{{text{e}}1}} + {{bar M}_{{text{e}}2}} - {omega _{text{m}}}{text{(2}}{f_1} + {f_2}{text{)}} - {m_2}{r^{text{2}}}{omega _{text{m}}}^{text{2}}{text{[2}}{W_{{text{s}}1}} + frac{1}{2}{W_{{text{s}}2}} + &qquad{W_{{text{c}}0}}{text{sin(}}bar alpha + {theta _{{text{c}}0}}{text{)}} + {W_{{text{s}}0}}{text{sin(}}bar alpha + {theta _{{text{s}}0}}{text{)]}} = 0 &{{bar M}_{{text{e}}1}} - {{bar M}_{{text{e}}2}} - {omega _{text{m}}}{text{(2}}{f_1} - {f_2}{text{)}} - {m_2}{r^{text{2}}}{omega _{text{m}}}^{text{2}}{text{[2}}{W_{{text{s}}1}} - frac{1}{2}{W_{{text{s}}2}} + &qquad{W_{text{c}}}{text{sin(}}bar alpha + {theta _{text{c}}}{text{)}} + {W_{text{s}}}{text{sin(}}bar alpha + {theta _{text{s}}}{text{)]}} = 0 end{split}
ight} $$
(25)

式中






$$ begin{split} &{W_{text{c}}} = sqrt {{a_{text{c}}}^{text{2}} + {b_{text{c}}}^{text{2}}};&{W_{text{s}}} = sqrt {{a_{text{s}}}^{text{2}} + {b_{text{s}}}^{text{2}}} ; &{W_{{text{c}}0}} = sqrt {{a_{{text{c}}0}}^{text{2}} + {b_{{text{c}}0}}^{text{2}}};&{W_{{text{s}}0}} = sqrt {{a_{{text{s}}0}}^{text{2}} + {b_{{text{s}}0}}^{text{2}}} &{a_{text{c}}} ={frac{1}{4}} {H_1}{text{cos}}({beta _1} - 2{beta _2}){text{cos}}(2{gamma _{psi 2}}) + &qquad {H_2}{text{cos(}}{beta _1} - 2{beta _2}{text{)cos(}}{gamma _{psi 1}} - {gamma _{psi 2}}{text{)}} &{b_{text{c}}} = {frac{1}{4}}- {H_1}{text{sin}}({beta _1} - 2{beta _2}){text{cos}}(2{gamma _{psi 2}}) - &qquad{H_2}{text{sin(}}{beta _1} - 2{beta _2}{text{)cos(}}{gamma _{psi 1}} - {gamma _{psi 2}}{text{)}} end{split} $$







$$ begin{split} &{a_{text{s}}} = -{frac{1}{4}} {H_1}{text{sin(}}{beta _1} - 2{beta _2}){text{sin}}(2{gamma _{psi 2}}) + & {H_2}{text{sin(}}{beta _1} - 2{beta _2}{text{)sin(}}{gamma _{psi 1}} - {gamma _{psi 2}}{text{)}} &{b_{text{s}}} = -{frac{1}{4}} {H_1}{text{cos}}({beta _1} - 2{beta _2}){text{sin}}(2{gamma _{psi 2}}) + &qquad{H_2}{text{cos(}}{beta _1} - 2{beta _2}{text{)sin(}}{gamma _{psi 1}} - {gamma _{psi 2}}{text{)}} &{a_{{text{c}}0}} = {frac{1}{4}}{H_1}{text{cos}}({beta _1} - 2{beta _2}){text{cos}}(2{gamma _{psi 2}}) - &qquad {H_2}{text{cos(}}{beta _1} - 2{beta _2}{text{)cos(}}{gamma _{psi 1}} - {gamma _{psi 2}}{text{)}} &{b_{{text{c}}0}} = -{frac{1}{4}} {H_1}{text{sin}}({beta _1} - 2{beta _2}){text{cos}}(2{gamma _{psi 2}}) + &qquad {H_2}{text{sin(}}{beta _1} - 2{beta _2}{text{)cos(}}{gamma _{psi 1}} - {gamma _{psi 2}}{text{)}} &{a_{{text{s}}0}} = -{frac{1}{4}} {H_1}{text{sin(}}{beta _1} - 2{beta _2}){text{sin}}(2{gamma _{psi 2}} )- &qquad {H_2}{text{sin(}}{beta _1} - 2{beta _2}{text{)sin(}}{gamma _{psi 1}} - {gamma _{psi 2}}{text{)}} &{b_{{text{s}}0}} = -{frac{1}{4}} {H_1}{text{cos}}({beta _1} - 2{beta _2}){text{sin}}(2{gamma _{psi 2}}) - &qquad {H_2}{text{cos(}}{beta _1} - 2{beta _2}{text{)sin(}}{gamma _{psi 1}} - {gamma _{psi 2}}{text{)}} &{theta _{text{c}}} = left{ {begin{array}{*{20}{l}}{arctan ({b_{text{c}}}/{a_{text{c}}}),;{a_{text{c}}} geqslant 0} {{text{π}} + arctan ({b_{text{c}}}/{a_{text{c}}}),;{a_{text{c}}} < 0} end{array}}
ight.; &{theta _{text{s}}} = left{ {begin{array}{*{20}{l}}{arctan ({b_{text{s}}}/{a_{text{s}}}),;{a_{text{s}}} geqslant 0} {{text{π}} + arctan ({b_{text{s}}}/{a_{text{s}}}),;{a_{text{s}}} < 0} end{array}}
ight. &{theta _{{text{c}}0}} = left{ {begin{array}{*{20}{l}}{arctan ({b_{{text{c}}0}}/{a_{{text{c}}0}}),;{a_{{text{c}}0}} geqslant 0} {{text{π}} + arctan ({b_{{text{c}}0}}/{a_{{text{c}}0}}),;{a_{{text{c}}0}} < 0} end{array}}
ight. &;{theta _{{text{s}}0}} = left{ {begin{array}{*{20}{l}}{arctan( {b_{{text{s}}0}}/{a_{{text{s}}0}}),;{a_{text{s0}}} geqslant 0} {{text{π}} + arctan ({b_{{text{s}}0}}/{a_{{text{s}}0}}),;{a_{text{s0}}} < 0} end{array}}
ight. end{split} $$
(26)

通过分析方程(25)可以确定振动系统倍频激励下的自同步准则. 第一式$ {bar M_{{text{e}}1}} + {bar M_{{text{e}}2}} $表示两振动电机的电磁输出转矩之和, ωm(2f1+f2)表示两振动电机轴上的摩擦力矩之和, 其余项表示振动系统在倍频激励下的负载转矩之和. 因此第一式揭示了两电机同步状态下的电磁转矩之和与激振器摩擦力矩以及负载转矩的总和相等. 方程(25)中第二式表示两电机以各自额定激振频率工作时的转矩差分方程. 高频电机与低频电机之间的电磁转矩以弹性振动体为媒介相互传递, 通过调节两个转子之间的瞬时相位差来平衡两个电机输出转矩的差值, 以保证高频转子与低频转子达到倍频自同步状态. 根据上述差分方程并考虑相应的系统结构参数可以反解得到系统同步相位差值$ bar alpha $. 另外Ws与Wc分别是与滞后相位$ {gamma _{ci}} $(c = x, y, ψ; i = 1, 2)有关的正弦系数和余弦系数. 由于箱体的支撑弹簧在各方向的相对阻尼系数ξc普遍较小, 则存在于Ws中与滞后相位有关的正弦项可忽略. 最后, 方程(25)第二式可以进一步整理为







$$left.begin{split} &{T_{text{d}}} = {T_{{text{syn}}}}{text{sin(}}bar alpha + {theta _{text{c}}}{text{) }};;;&bar alpha = arcsin left(frac{{{T_{text{d}}}}}{{{T_{{text{syn}}}}}}
ight) - {theta _{text{c}}} end{split}
ight}$$
(27)

其中







$$ left.begin{split} &{T_{text{d}}} = {T_{{text{r}}1}} - {T_{{text{r}}2}}&{T_{{text{r}}1}} = {{bar M}_{{text{e}}1}} - {text{2}}{f_1}{omega _{text{m}}} - {text{2}}{m_2}{r^{text{2}}}{omega _{text{m}}^{text{2}}}{W_{{text{s}}1}} &{T_{{text{syn}}}} = {m_2}{r^{text{2}}}{omega^{{2}} _{text{m}}}{W_{text{c}}}&{T_{{text{r}}2}} = {{bar M}_{{text{e}}2}} - {f_2}{omega _{text{m}}} -{frac{1}{2}} {m_2}{r^{text{2}}}{omega _{text{m}}^{text{2}}}{W_{{text{s}}2}} end{split}
ight} $$
(28)

式中, Tri为电机i的剩余转矩; Td为两电机间的剩余转矩之差; Tsyn为系统实现倍频同步的同步转矩. 由式(27)可以看出, 振动系统在倍频激励下的同步相位差值$ bar alpha $是由参数Td, Tsyn和θc共同确定的, 而它们又依赖于激振器安装在箱体上的位置结构、偏心质量大小、支撑弹簧刚度等一系列参数. 因此振动系统的结构参数会对转子的倍频同步状态产生影响. 根据三角函数的有界性原则, 获得双转子倍频同步运动准则为







$$ left| {{T_{text{d}}}}
ight| leqslant left| {{T_{{text{syn}}}}}
ight| $$
(29)

作为实现倍频同步振动的必要条件, 两台电机之间输出剩余转矩差的绝对值不能超过系统达到倍频同步的同步转矩. 两台激振器之间的同步转矩越大, 系统实现同步运行越理想, 利用数值解法即可求出式(27)中倍频激励下的同步相位差.

为充分理解具有双频率激励特点的系统同步能力, 规定倍频同步能力指数ξ







$$ xi = left| {frac{{{M_{text{L}}}}}{{{T_{{text{syn}}}}}}}
ight| $$
(30)

式中, $ {M_{text{L}}} = {m_2}{r^{text{2}}}{omega _{text{m}}}^{text{2}}{text{(2}}{W_{{text{s}}1}} + {W_{{text{s}}2}}/2 + {W_{{text{c}}0}} + {W_{{text{s}}0}}{text{)}} $, 表示两振动电机的最大负载转矩. 同步能力指数ξ反映了激振器所承受的最大负载转矩与倍频同步转矩比值的绝对值. 若ξ越趋近于零, 系统获得同步运动的可行性越大.


2.3
系统倍频同步稳定判据


根据式(27)反解得出的相位差可能会存在多解的情况, 其中哪一个值具有同步状态的稳定性, 使得系统能够以二倍激励频率稳定地同步振动, 需要利用Poincare?Lyapunov方法确定[17]. 即考虑Pi存在一组特定参数$ {bar alpha _1},{bar alpha _2}, cdots,{bar alpha _{n - 1}} $, 满足下列n?1阶特征方程







$$ left| begin{gathered}frac{{partial left( {{P_1} - {P_n}}
ight)}}{{partial {alpha _1}}} - delta {text{ }}frac{{partial left( {{P_1} - {P_n}}
ight)}}{{partial {alpha _2}}}{text{ }} cdots {text{ }}frac{{partial left( {{P_1} - {P_n}}
ight)}}{{partial {alpha _{n - 1}}}} frac{{partial left( {{P_2} - {P_n}}
ight)}}{{partial {alpha _1}}}{text{ }}frac{{partial left( {{P_2} - {P_n}}
ight)}}{{partial {alpha _2}}} - delta {text{ }} cdots {text{ }}frac{{partial left( {{P_2} - {P_k}}
ight)}}{{partial {alpha _{n - 1}}}} cdots {text{ }} cdots frac{{partial left( {{P_{n - 1}} - {P_n}}
ight)}}{{partial {alpha _1}}}{text{ }}frac{{partial left( {{P_{n - 1}} - {P_n}}
ight)}}{{partial {alpha _2}}}{text{ }} cdots ;frac{{partial left( {{P_{n - 1}} - {P_n}}
ight)}}{{partial {alpha _{n - 1}}}} - delta end{gathered}
ight| = 0 $$
(31)

若上述行列式的特征根δi (i = 1, 2, ···, n?1)实部全部是负值, 则参数$ {bar alpha _1},{bar alpha _2}, ;cdots,;{bar alpha _{n - 1}} $的值具有唯一性, 系统拥有周期性的稳态响应解; 若所有特征根δi实部至少存在一个是正值, 则系统的响应解是非稳态的; 若所有特征根δi中部分实部是零并且其他根实部均是负值, 则系统的响应解稳定性由中心流形定理界定.

结合式(18)和式(31), 由倍频激励双偏心块的同步稳定判别式可写为







$$ frac{{partial {text{(}}{P_1} - {P_2}{text{)}}}}{{partial bar alpha }} = - {m_2}{r^{text{2}}}{omega _{text{m}}^{text{2}}}{W_{text{c}}}{text{cos(}}bar alpha + {theta _{text{c}}}{text{)}} < 0 $$
(32)

转子同步状态的稳定性决定振动系统的动力学特性, 各自由度的瞬态响应解的稳定性依赖于振动电机的安装参数、支承弹簧的刚度系数和偏心质量等. 系统参数同时满足式(29)和式(32)的前提条件下, 稳定的倍频同步振动能够获得, 即式(27)的稳态相位差$ bar alpha $具有唯一性. 由于$ - {m_2}{r^{text{2}}}{omega _{text{m}}^{text{2}}} $是一个负数, 式(32)简化为







$$ {W_{text{c}}}{text{cos(}}bar alpha + {theta _{text{c}}}{text{)}} > 0 $$
(33)


3.
数值计算与讨论


第2节以数学推导的方式详细探究了倍频转子间的同步性与稳定性判据以及远共振系统的动态耦合机理. 可知, 系统的同步运动特性主要取决于转子的质量比、振动电机位置结构和弹簧刚度等参数. 针对转子同步状态与系统各参数之间的关系, 本节将运用数值计算对其进行定量的讨论. 分析结果为后续倍频激励双转子系统的机电耦合动力学模拟和同步特性实验研究提供重要的理论依据. 为便于计算, 考虑两电机安装距离l1 = l2 = l, 即rl1 = rl2 = rl. 系统基本参数值如下: m0 = 92 kg, m1 = 2 kg, Jm = 10 kg·m2, m2 = 2 ~ 3.5 kg (η2 = 0.02 ~ 0.035), β1 = 2π/3 ~ 5π/6 rad, β2 = π/6 ~ π/3 rad, fx = fy = 300 ~ 3000 N·s/m, fψ = 50 ~ 500 N·m·s/rad (ξx = ξy = ξψ = 0.03 ~ 0.5), kx = ky = 1 × 103 ~ 2 × 107 N/m, kψ = 1 × 102 ~ 5 × 106 N·m/rad (λx = λy = λψ = 0.02 ~ 2.85), l = 0 ~ 3.6 m (rl = 0 ~ 12).


3.1
振动同步范围分析


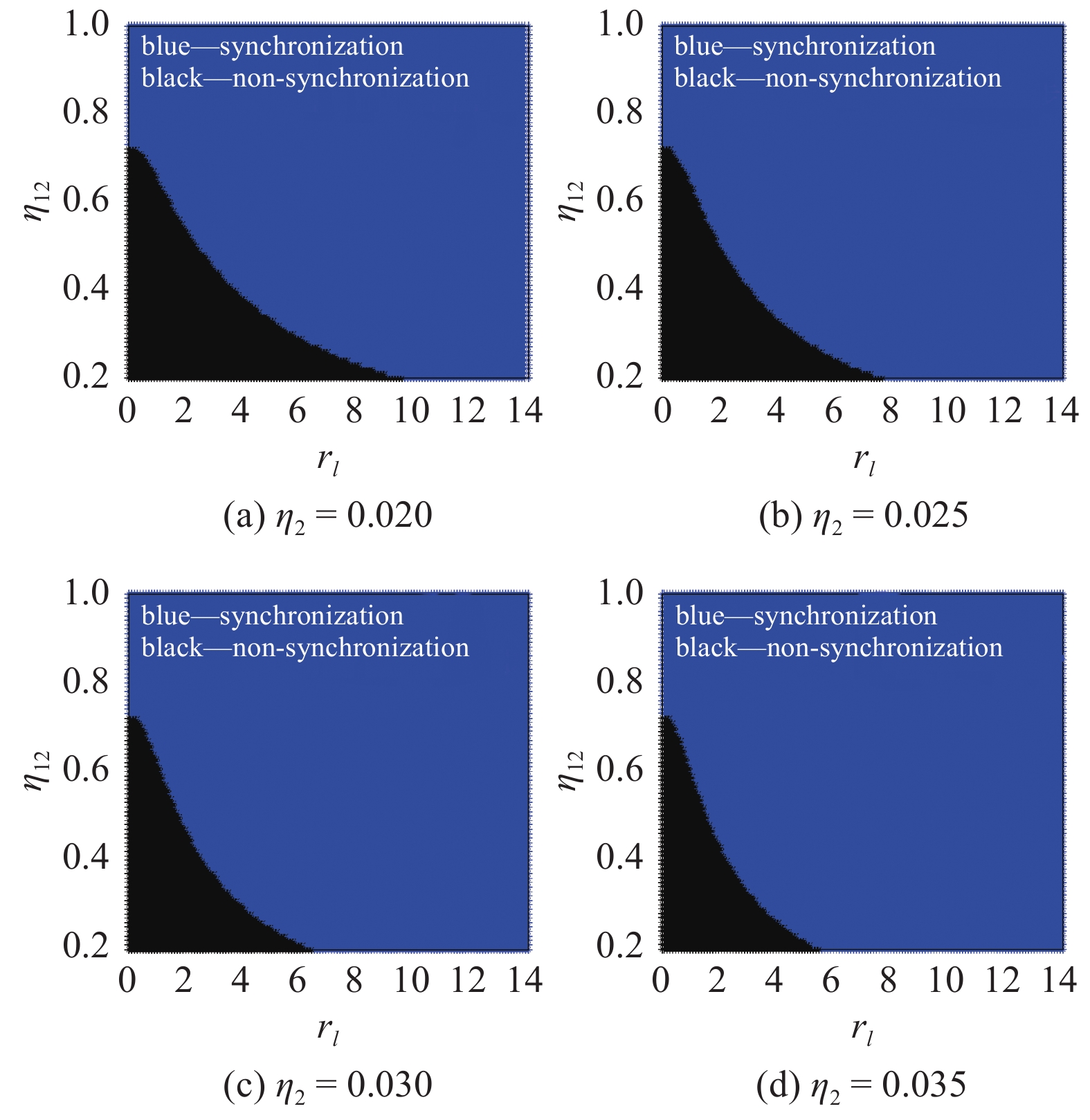
根据式(29), 高频转子与低频转子之间的同步条件可以通过转子输出剩余转矩差和系统同步转矩的关系来反映. 设安装距离rl以及激振器质量比η12为自由变量, 在转子2的不同偏心质量下出现同步运动的区域如图2和图3所示. 当系统结构参数无法满足同步运动准则时的非同步区域用黑色指示标记, 蓝色范围表示系统在此状态下可以出现同步振动. 可见, 倍频激励下双转子同步区域远远大于不适用于同步运动准则的区域. 振动电机轴至系统质心的安装距离与激振器质量比越大, 两电机之间更容易获得倍频同步运动. 同时, 随着低频转子偏心质量的增加, 双频振动系统的非同步范围逐渐减小. 由此可知, 实现不同频率之间同步振动的可行性受结构参数的影响. 在实际工程应用中, 通过选择有效的系统参数, 可以满足振动系统不同的同步特性和工业要求.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-359-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
倍频激励双转子振动同步范围



Figure
3.
Synchronization region of two rotors driven by double-frequency



下载:
全尺寸图片
幻灯片



3.2
倍频同步能力分析


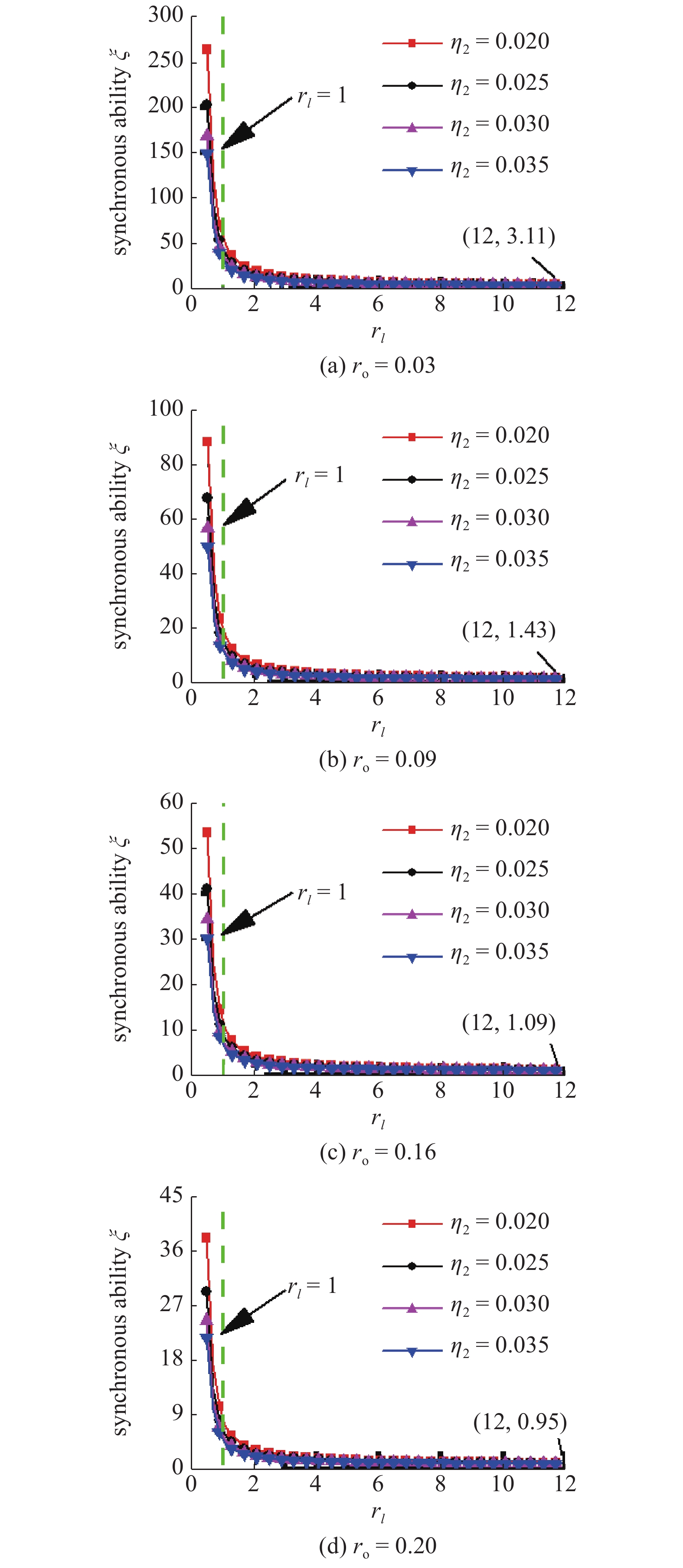
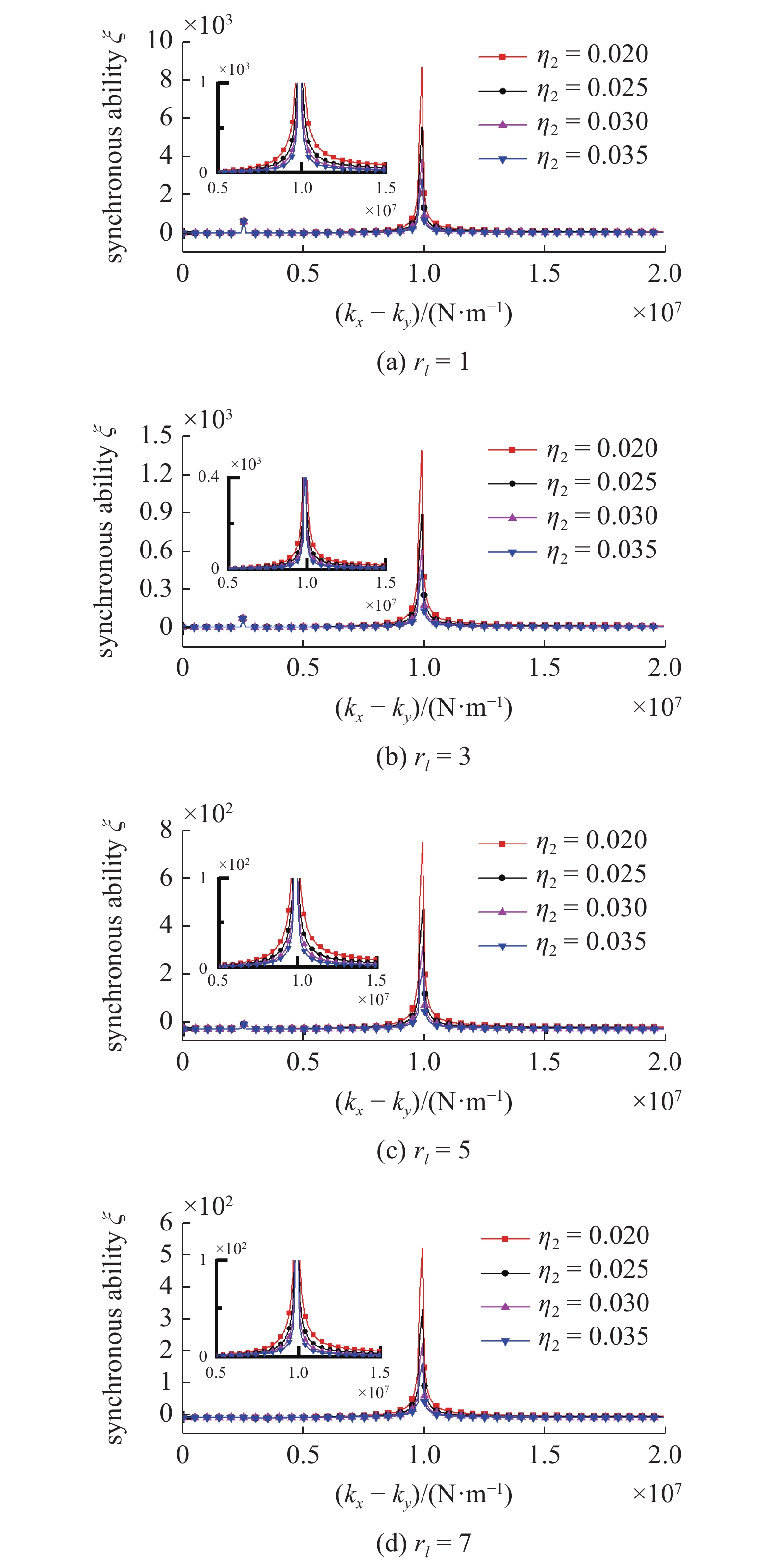
按照式(30), 已利用数值计算方法发现电机在箱体上倾角βi的变化不影响转子倍频同步能力, 本小节不再讨论. 给定β1 = 120°, β2 = 60°, 图4揭示了振动系统在不同转子的偏心质量和偏心半径下, 振动电机的安装距离对倍频转子同步能力指数的变化规律. 可以看出, 随着低频转子质量参数η2的增大, 系统同步指数将会逐渐减小. 意味着增加低频转子的偏心质量有利于提高振动系统的有效激振力, 两电机通过箱体的弹性振动和能量传递使得转子间的耦合量增加, 从而提高系统的同步能力. 同时, 以rl = 1附近为界线, 左边部分的同步指数对rl变化的敏感性程度明显大于右边, 原因在于缩短电机旋转中心至箱体质心的距离容易造成电机间用于平衡自身电磁转矩达到同步状态的可调节量不足. 当rl > 1时, ξ的变化幅度趋于平缓, 并最终以很小的斜率无限接近于零值附近, 表明箱体获得倍频同步振动的可行性也越来越高, 该结果符合3.1节的倍频同步范围分析. 对比图4(a)~4(d), 显示转子的偏心半径参数ro不影响系统同步指数的整体变化趋势, 只改变ξ在相应的ro和rl取值下的值域. 另一方面, 若β2 = 60°, ro = 0.16时, 对于电机距离参数rl分别取1, 3, 5, 7, 质量参数η2分别为0.02, 0.025, 0.03, 0.035时, 不同支撑弹簧刚度值对系统倍频同步能力的影响如图5所示. 可见, 由于振动系统具有两个不同的激励频率, 导致图中共出现两个共振区域, 分别位于2.46 × 106 N/m和9.86 × 106 N/m附近. 此时, 系统各自由度的固有频率和系统的外界激励频率接近, 即系统处于近共振状态, 频率比λx = λy = λψ = 1, 无法出现激振器稳定的倍频同步状态和箱体的周期性振动.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-359-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
当β1 = 120°, β2 = 60°时的倍频同步能力



Figure
4.
Double-frequency synchronization capacity with β1 = 120°, β2 = 60°



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-359-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
当β2 = 60°, ro = 0.16时的倍频同步能力



Figure
5.
Double-frequency synchronization capacity with β2 = 60°, ro = 0.16



下载:
全尺寸图片
幻灯片



3.3
倍频同步转矩分析


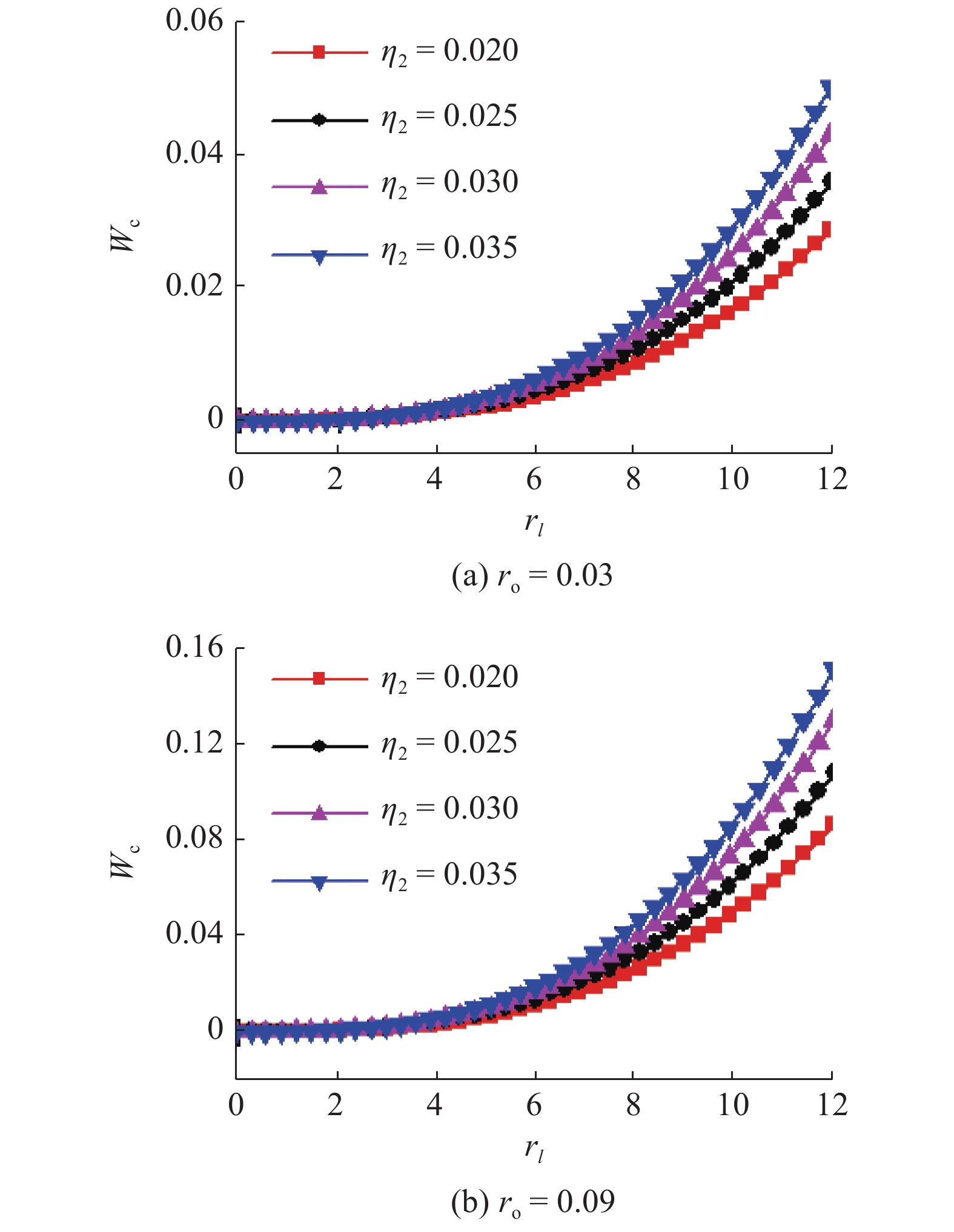
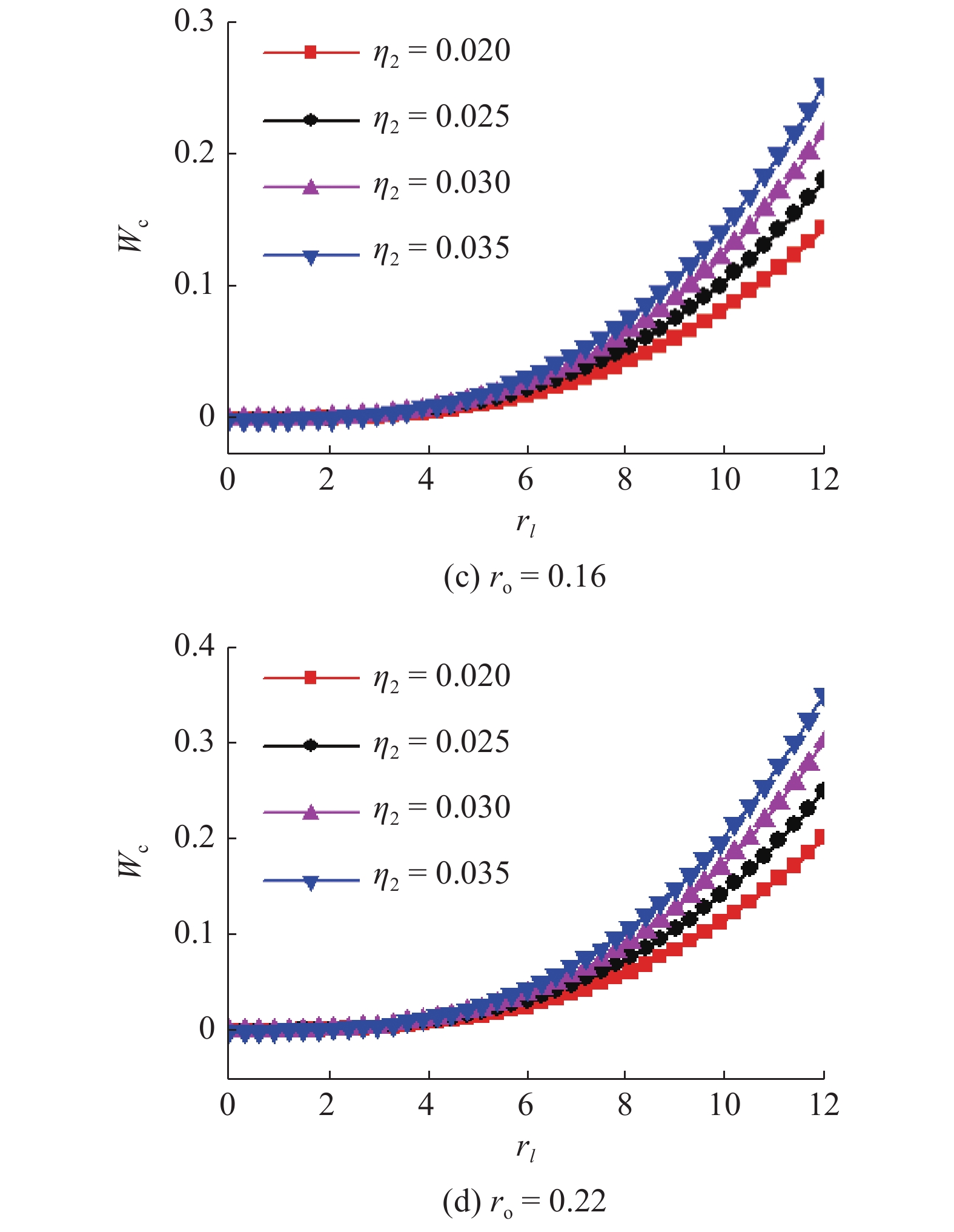
根据振动系统的转矩差分方程(25)第2式和式(27), 高频电机与低频电机通过箱体的弹性耦合以及动能、势能与电能等能量之间的相互转化, 使得偏心块以各自额定转速同步驱动的同时, 其电机轴上的电磁转矩可以达到动态平衡. 因此, 振动系统的倍频同步行为问题可以转换为对电机转矩与结构参数的关系研究. 根据倍频同步准则(29)与同步稳定判别式(33), 倍频同步转矩参数Tsyn由常数$ {m_2}{r^{text{2}}}{omega _{text{m}}^{text{2}}} $和余弦系数Wc两个因式组成, 所以Wc不仅直接影响系统同步转矩的变化, 还决定系统同步运动状态的稳定性, 可将Wc等效为倍频同步转矩. 已确定电机倾斜角βi的取值几乎不影响系统倍频同步转矩. 因此, 如图6所示运用数值计算探究了不同转子的偏心距和偏心质量下, 位置参数rl与倍频同步转矩值的关系. 可以看出, 当rl = 0时, 倍频同步转矩值同样为零, 此时不满足式(29)和式(33), 即两电机无法实现倍频振动. 随着安装距离的不断增加, Wc的值逐渐增大, 表明转子实现同步的能力越容易, 这与3.2节的研究结果相一致. 另外假设rl不变, 倍频同步转矩Wc的值将随着转子2质量的增大而增加, 说明在保证电机所能承受最大负载的前提下, 适当增大低频转子的质量有利于提高系统的同步性. 对比图6(a)~6(d), 讨论了转子的偏心半径ro只会改变Wc在相应的ro和rl取值下的值域, 并不会影响振动系统倍频同步转矩的整体变化趋势.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-359-6-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6-1" />




下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-359-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
当β1 = 120°, β2 = 60°时的倍频同步转矩



Figure
6.
Double-frequency synchronization torque with β2 = 60°, ro = 0.16



下载:
全尺寸图片
幻灯片



3.4
双转子倍频同步状态分析


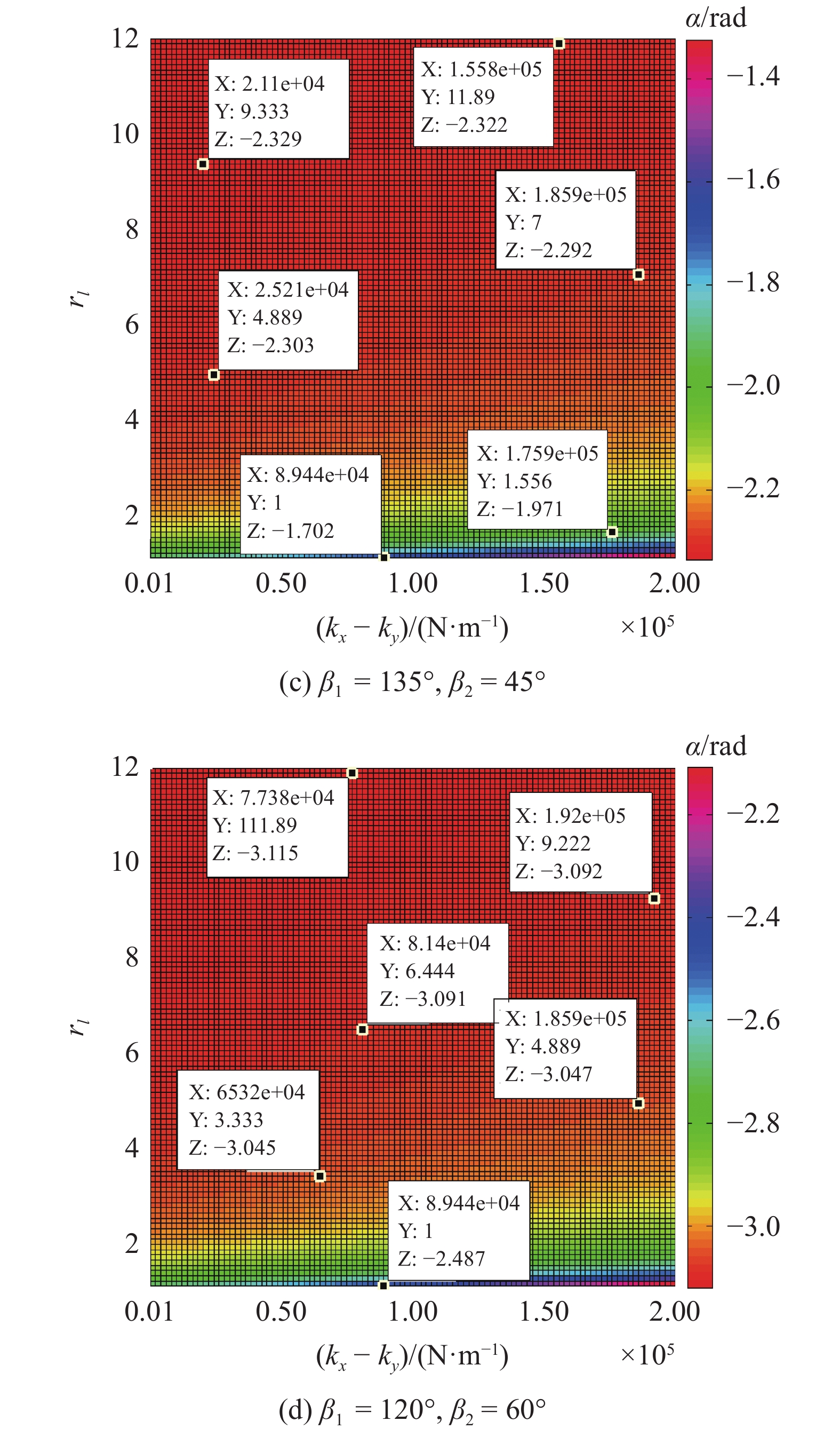
双转子倍频同步运动状态是由高低频振动电机以及刚性箱体之间的耦合振动效应形成的, 其值的稳定性决定了振动系统沿各自由度的位移响应和动力学特性, 是评估系统同步振动的最重要数字特征. 考虑不同的电机倾斜角βi, 根据上述倍频激励双转子同步理论推导, 电机位置结构参数rl、支撑弹簧刚度值kx和ky以及双转子相位差近似稳态值α之间的关系如图7所示, 数值计算的正确性将在接下来的模拟仿真和实验研究中得到验证. 关于机械系统振动类型可分为: 系统1/λc < 0.9时是亚共振系统; 0.9 ≤ 1/λc ≤ 1.1是近共振系统; 1.1 ≤ 1/λc ≤ 3是远共振系统; 1/λc > 3是超远共振系统[22]. 本文考虑系统的kx = ky, kψ可由kx和ky换算得到, kx和ky的取值范围为1 × 103 N/m < kx = ky < 2 × 105 N/m, 即频率比1/λx = 1/λy = 1/λψ > 3.5, 研究对象确定为超远共振系统. 由图7可知, 当β1 = 150°, β2 = 30°时, 随着安装距离rl的增加, 实现倍频振动的稳定同步状态值α在刚度系数不变的情况下逐渐减小并最终趋于?1.55 rad附近. 同时, 考虑rl为一常数, 可见x和y方向弹簧刚度系数的增加几乎不影响两振动电机的稳态相位差值的变化情况. 若改变两振动电机的倾斜角度, 即增加各电机的βi值, 图7(b)的同步状态变化规律类似于图7(a), 但明显两倍频激励的转子相位差的值域发生变化, 此时系统同步状态趋近于?1.96 rad附近. 另外图7(c)和7(d)显示转子在不同的电机倾斜角βi下, 其稳定同步状态值分别锁定在?2.32 rad和?3.12 rad附近. 根据研究结果表明电机斜倾角βi的取值虽然不对振动系统的同步范围、同步能力以及同步转矩值产生影响, 但是对倍频转子的同步行为具有一定的耦合作用. 系统的激振力与同步运动特性依赖于不同相位差值所反映出的动力学特性, 在工程中合理设计振动电机的安装位置可以实现稳定的振动筛分.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-359-7-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7-1" />




下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-359-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
倍频激励双转子相位差近似稳态值



Figure
7.
Double-frequency phase difference between the two rotors in steady state



下载:
全尺寸图片
幻灯片



4.
计算机模拟与分析


为进一步论证倍频激励双转子振动同步理论分析的有效性, 明确两电机在倍频激振源的驱动下各转子与箱体的机电耦合动态特性, 掌握系统倍频振动同步机理, 本节根据多自由度运动微分方程(8)建立了系统的机电耦合动力学仿真模型, 如图8所示. 采用Runge?Kutta算法可求解转子与箱体在超远共振系统中的动态模拟结果. 求解原理如下: 图中x, y, ψ方向的动力学方程模块依次表示箱体质心沿水平方向、竖直方向以及摆动方向上, 以加速度c″ (c = x, y, ψ)作为输出信号的运动微分方程. 同时, 利用积分器分别对其进行一次与二次积分运算, 获取箱体沿c自由度瞬时速度c′ 和瞬时位移c. 在高频振动电机1与低频振动电机2的运动方程中, 分别以各自电磁转矩Mei?Rei作为电机i仿真模型的输入信号, 进而输出转子i的角速度信号$varphi _i^{'}$. 并通过积分器和微分器分别对其进行一次微分和一次积分运算, 获取各转子的瞬时角速度$varphi _i^{''} $和瞬时相位角$ varphi _i$. 最后, 通过引入数据总线模块连续将输出信号继续视为整个振动系统的初始值, 并加入示波模块以更加直观地分析各输出信号的运动特性. 根据此原理, 参照第3节中的系统基本参数作为模型仿真参数, 可实现由激振器和箱体之间的相互耦合所形成的倍频同步运动, 并针对系统的倍频振动特性做出相应分析, 包括: 箱体各方向的运动学研究、转子倍频同步状态研究、转子同步稳定性研究以及振动电机的性能参数分析等. 此外, 两振动电机均考虑为鼠笼式异步激振电机, 电机模型的各电气参数值如下: 高频电机额定功率0.12 kW, 额定电压380 V, 工业电压频率50 Hz, 额定转速(激振频率)314 rad/s, 磁极对数1. 低频电机额定功率0.12 kW, 额定电压380 V, 工业电压频率50 Hz, 额定转速(激振频率)157 rad/s, 磁极对数2.



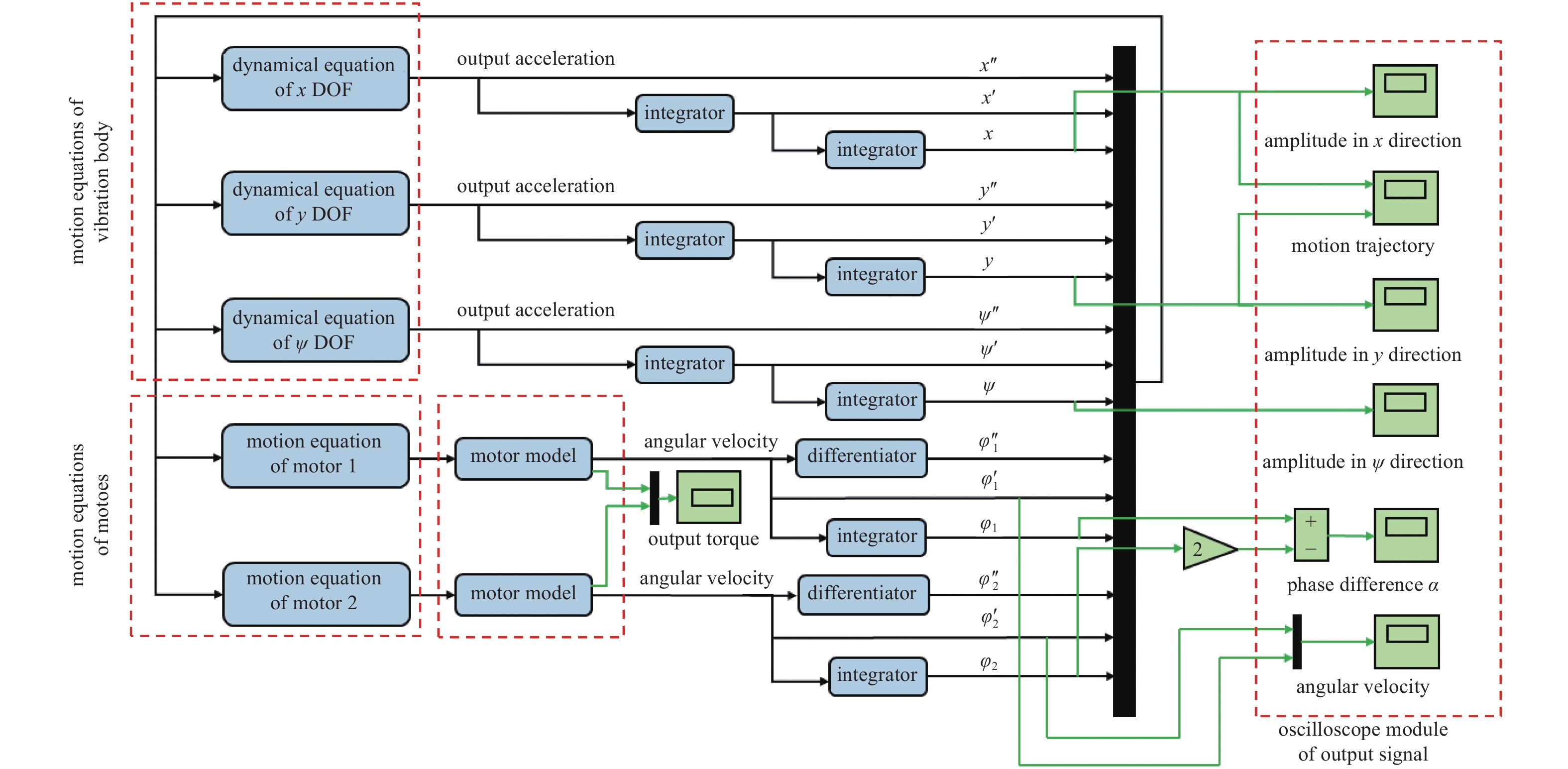onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-359-8.jpg'"
class="figure_img
figure_type2 ccc " id="Figure8" />



图
8
倍频激励双转子振动系统机电耦合动力学仿真模型



Figure
8.
Electromechanical coupling dynamics simulation model of dual-rotor vibration system excited by double-frequency



下载:
全尺寸图片
幻灯片



4.1
β1 = 150°, β2 = 30°, rl = 1.2时的倍频同步特性


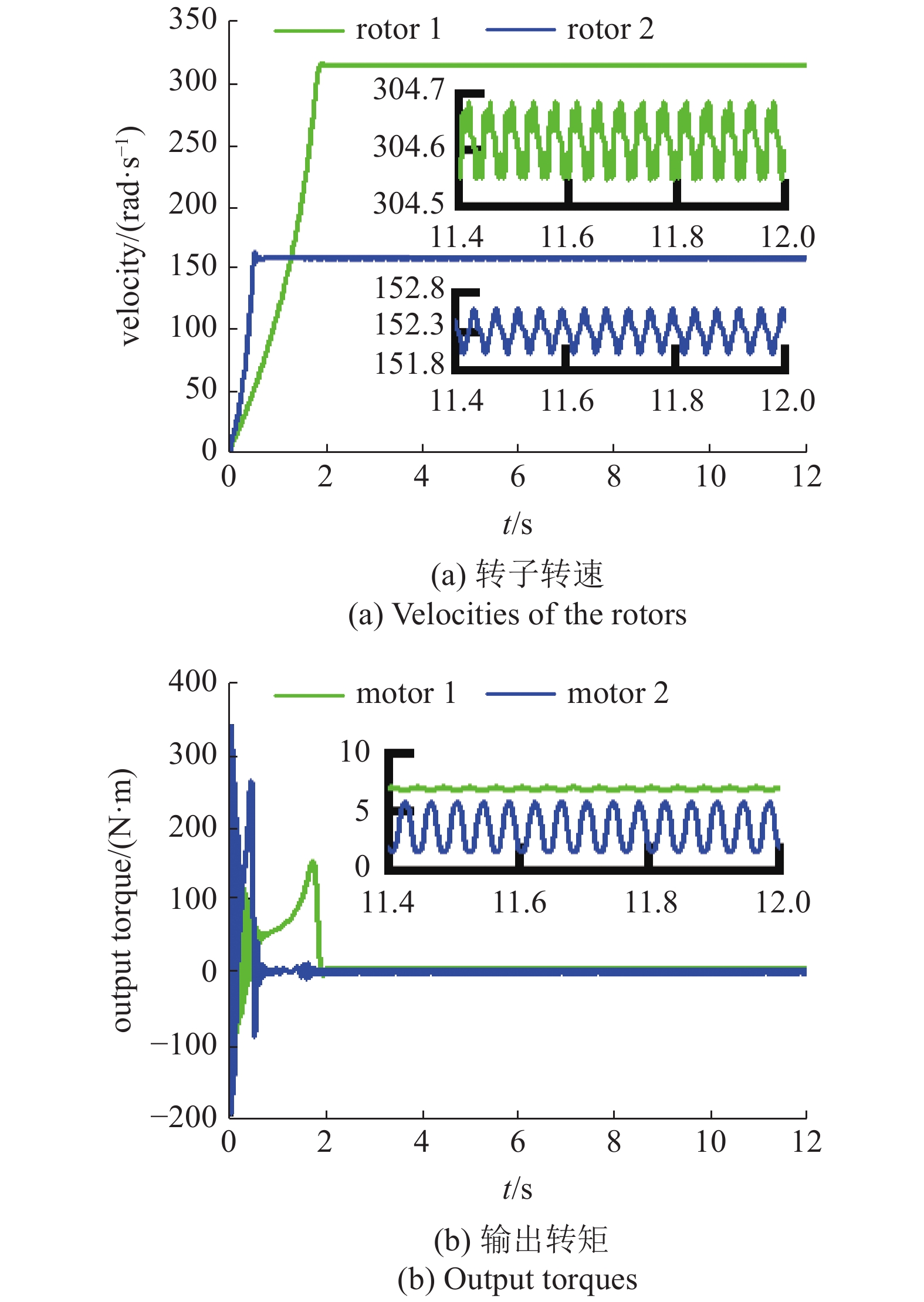
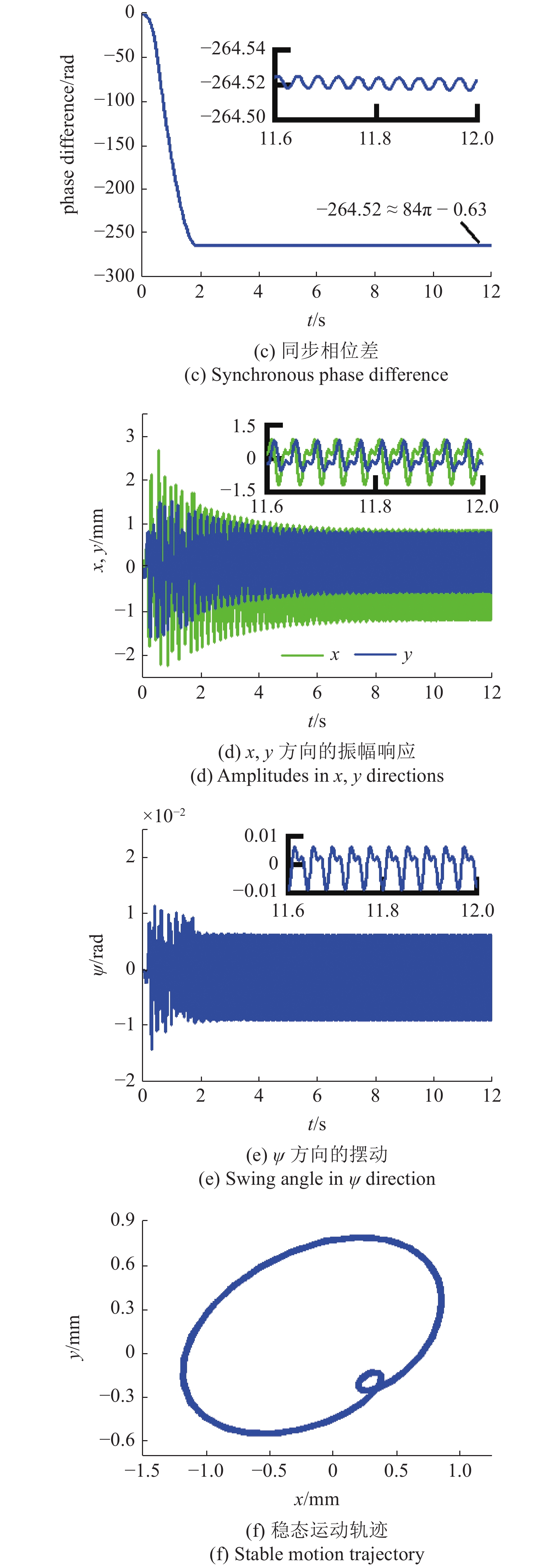
考虑结构参数kx = ky = 89586 N/m, kψ = 13560 N·m/rad (λx = λy = λy = 0.2), m2 = 3 kg (η2 = 0.03, η12 = 0.67), l = 0.36 m (rl = 1.2), 系统倍频同步特性模拟结果如图9所示. 经过计算验证, 此组结构参数符合同步准则和稳定判别式. 如图9(a)所示, 同时对高频振动电机和低频振动电机提供相同动力源, 驱动各转子作同向回转运动. 由于两电机内部性能参数存在一定的差异, 转子1到达额定转速所消耗的时间相对转子2较长, 导致两电机在初始阶段无法以相同转速同步启动, 并且转子1的加速度略小于转子2. 可见低频电机率先以152.3 rad/s到达同步转速状态, 大约运行2 s后, 高频电机的稳态同步转速为304.6 rad/s, 此时系统逐渐获得周期性振动. 将各转子的速度波动范围与振动电机的实际运行速度相比较, 前者远远小于后者, 证明理论分析中将扰动参数看作慢变参量并考虑扰动参数矩阵$ {dot{bar {boldsymbol varepsilon }}} = {bar{boldsymbol varepsilon }} = {{boldsymbol{0}}} $是可行的. 图9(b)为振动电机的输出扭矩情况, 启动阶段时箱体质量较大而施加在激振器旋转轴上的力矩较小, 使得振动电机的输出电磁转矩主要依靠由动力源提供的驱动力而逐渐增大, 并最终分别以7 N·m和3.5 N·m稳定在一个动态平衡的位置. 此时, 可以实现转子由双频激励的同步振动现象. 高频转子和低频转子的自定义稳态同步相位差α近似锁定在?0.63 rad (?264.52 ≈ ?84π?0.63), 如图9(c)所示, 仿真结果与图7(a)的数值计算结果较为接近. 由于该振动系统是一个平面驱动振动系统, 振动电机激励的转子1和转子2均在xoy平面内运动, 沿xoy平面的垂直方向并无其他激振力. 因此图9(d)和9(e)显示箱体仅在x, y与ψ自由度上存在位移响应, 其幅值分别是1.2 mm, 0.8 mm和0.01 rad. 在振动系统从静止到同步运动状态的过渡中, 箱体因共振将存在短暂的混沌运动. 然后随着速度上升, 其质心的稳定轨迹将会显示为如图9(f)所示的内“8”字型.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-359-9-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9-1" />



9
β1 = 150°, β2 = 30°, rl = 1.2时的仿真结果



9.
Simulation result when β1 = 150°, β2 = 30° and rl = 1.2



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-359-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
β1 = 150°, β2 = 30°, rl = 1.2时的仿真结果(续)



Figure
9.
Simulation result when β1 = 150°, β2 = 30° and rl = 1.2 (continued)



下载:
全尺寸图片
幻灯片



4.2
β1 = 142°, β2 = 38°, rl = 1时的倍频同步特性


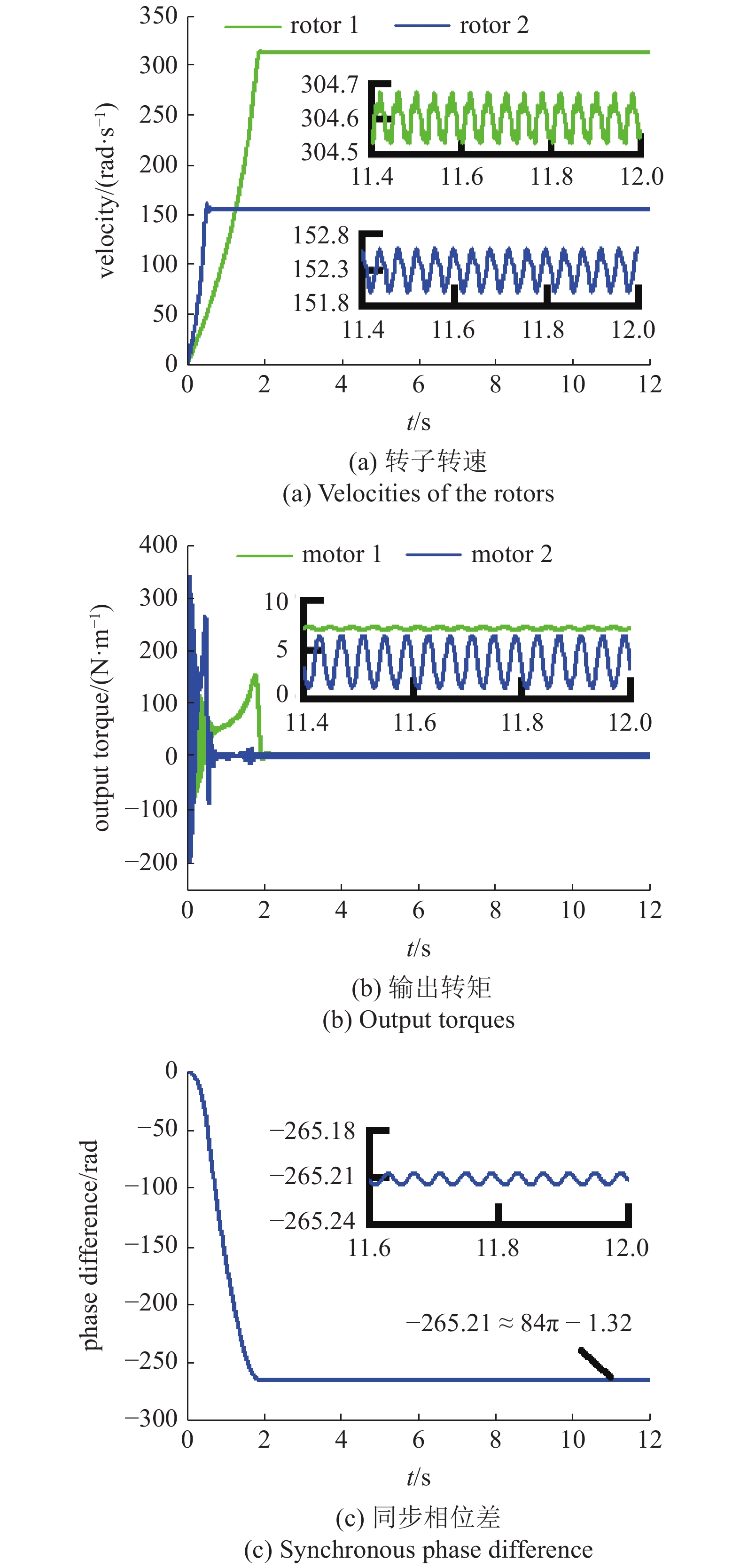
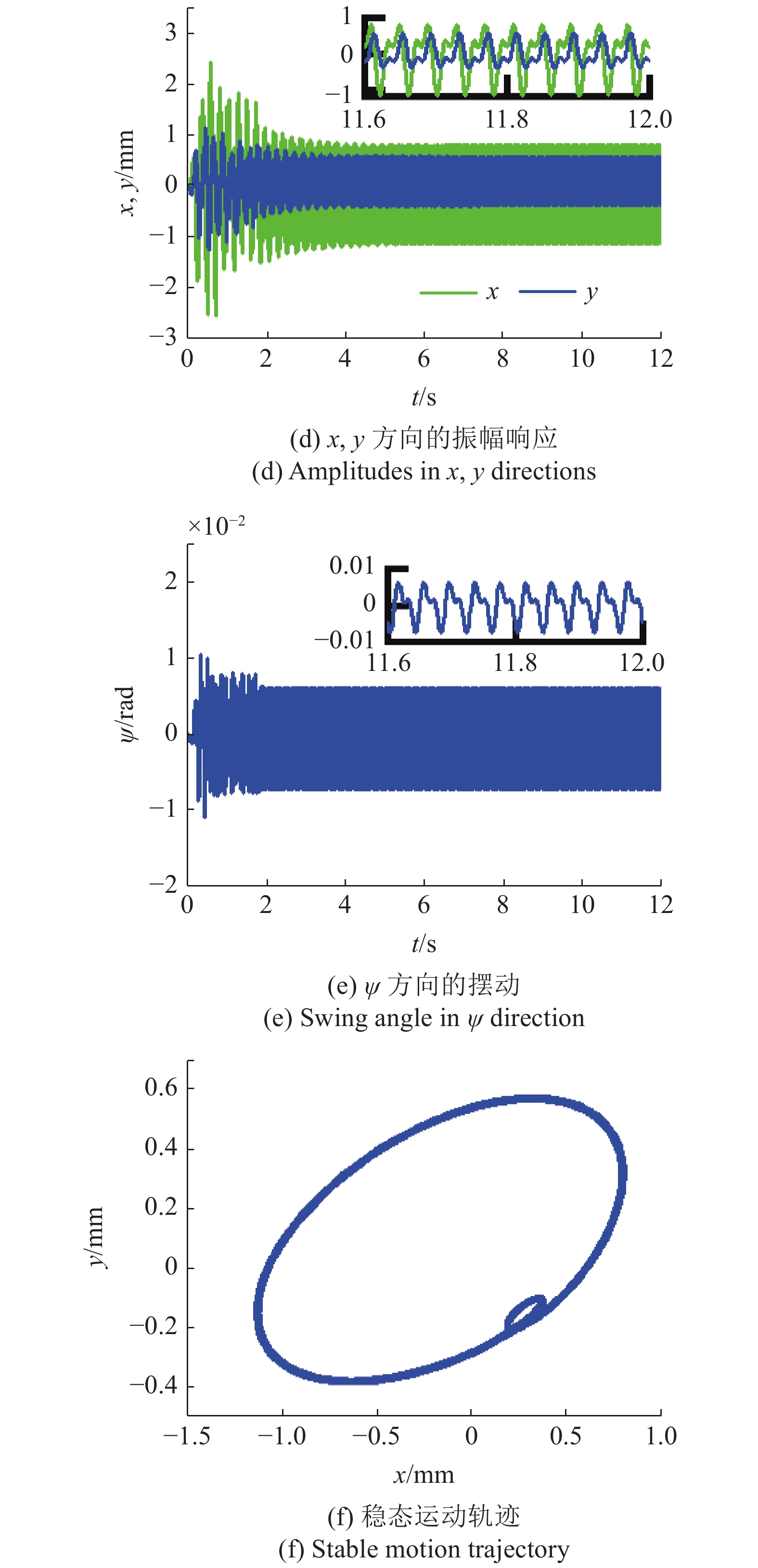
改变电机位置参数并考虑kx = ky = 89586 N/m, kψ = 13560 N·m/rad (λx = λy = λy = 0.2), m2 = 3 kg (η2 = 0.03, η12 = 0.67), l = 0.31 m (rl = 1), 其他系统参数见数值计算部分, 进一步论证机械模型的准确性, 其倍频同步特性模拟结果如图10所示. 将结构参数代入振动系统两个必要条件中进行理论计算, 结果符合关于稳定相位差值的验证标准. 在零时刻同时对高频电机和低频电机提供激振源, 从图10(a)可知转子1的转速上升趋势明显慢于转子2, 这是因为系统所采用的振动电机为一个二极异步电机和一个四极异步电机, 各电机的电气参数存在差异性, 导致转子在到达额定角速度过程中所需的角加速度值不一样. 运行2 s之后两转子逐渐趋于稳态, 其同步转速分别维持在304.6 rad/s和152.3 rad/s. 同时可以看出, 两振动电机在稳态时的速度波动最大值仅为0.3 rad/s, 远小于振动电机的激励频率. 另外, 图10(b)显示为振动电机的输出电磁转矩. 初始时刻由于箱体质量和支撑弹簧的刚度值均较大, 造成箱体无法马上激起振动响应. 随着运行时间增长, 两电机的输出扭矩增大, 并经过共振区后逐渐稳定在7 N·m和4 N·m. 系统处于稳定的倍频同步运动状态, 图10(c)反应转子1与转子2间的相位差α稳定在?1.32 rad (?265.21 ≈ ?84π?1.32). 与图7(b)的理论值相比, 计算结果在允许的误差范围内是吻合的. 此外, 图2-图10(e)揭示了箱体在双频激励下可获得稳定的周期性振动, 各自由度的幅值分别确定为1.1 mm, 0.6 mm与0.008 rad. 最后结合箱体质心沿x和y方向的稳态响应可以得到如图10(f)所示的内“8”型稳态运动轨迹.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-359-10-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10-1" />




下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-359-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
β1 = 142°, β2 = 38°, rl = 1时的仿真结果



Figure
10.
Simulation result when β1 = 150°, β2 = 30° and rl = 1



下载:
全尺寸图片
幻灯片



5.
实验验证


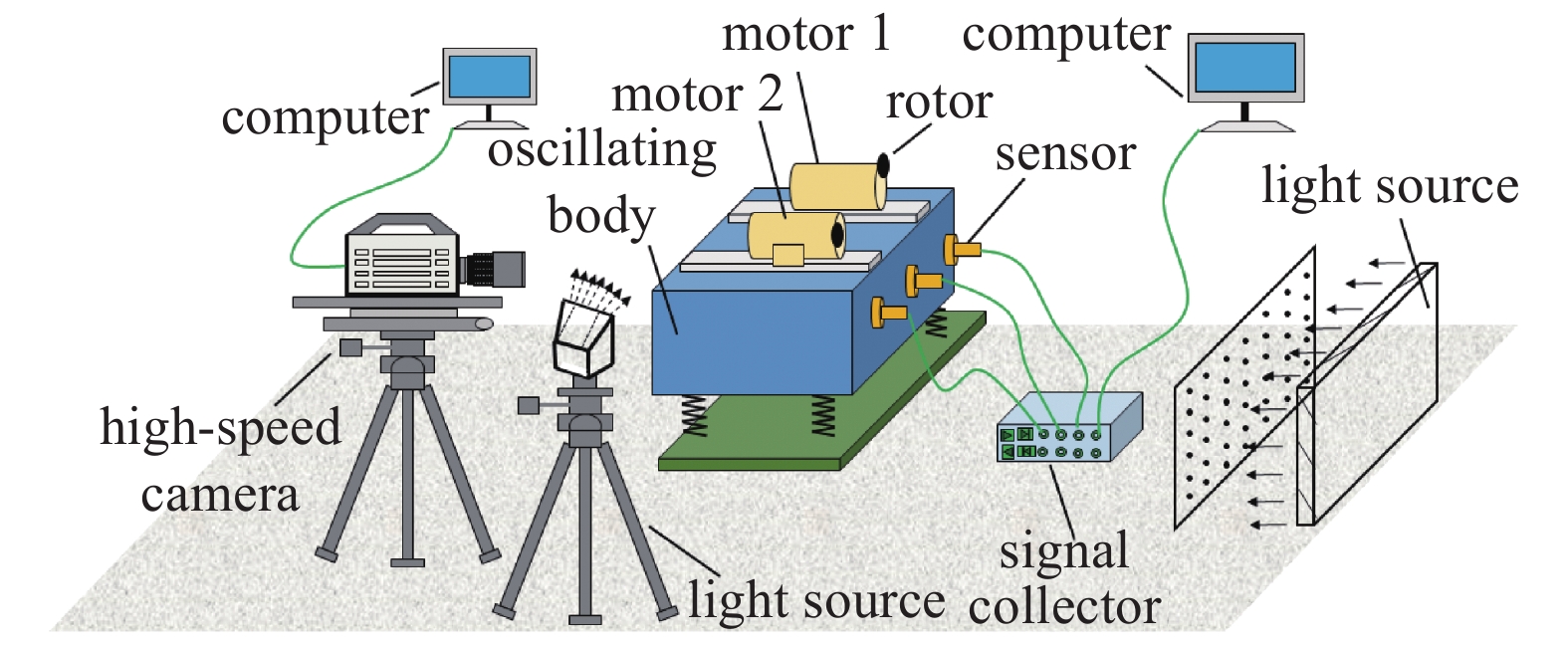
前文已对倍频同步系统的理论推导、数值计算和计算仿真进行详细的研究, 但是研究成果能否应用于振动筛分工程中有待进一步证明. 因此设计倍频激励双转子振动系统试验样机如图11所示. 电机启动时, 机械装置在电机激励偏心块的离心力作用下产生激振力, 其中电机技术参数如表1所示. 箱体在弹簧能量吸收和能量释放过程中发生位移振动和旋转摆动. 随着两电机的回转速度比值逐渐以稳定的两倍关系驱动偏心块, 基于箱体与电机间的弹性耦合效应, 两偏心块将会以恒定相位差值做倍频同步运动, 此时箱体在各方向上做周期性振动. 根据实验样机制定倍频同步实验测试方案, 如图12所示. 实验平台包括同步测试系统、实验样机和动态测试系统. 首先, 在动态测试过程中, 测试点的振动信号由一系列加速度传感器及时采集. 然后通过信号放大器和数据处理系统进行分析得到信号的动态特性. 其次, 在同步测试过程中, 通过高速成像系统准确捕捉高频转子与低频转子在瞬时状态下的相位差, 可以直观地实现稳定同步运动的定量分析. 最后将实验图像传输到计算机进行存储和处理.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-359-11.jpg'"
class="figure_img
figure_type1 bbb " id="Figure11" />



图
11
试验样机: 1 二极振动电机; 2 四极振动电机; 3 偏心块; 4 电机座; 5 钢架; 6 锁紧螺栓; 7 箱体; 8 支撑弹簧; 9 基座



Figure
11.
Experimental prototype: 1 two-pole motor; 2 four-pole motor; 3 eccentric block; 4 motor base; 5 steel frame.; 6 locking bolt; 7 oscillating body; 8 supporting spring; 9 foundation support



下载:
全尺寸图片
幻灯片





表
1
激振电机的技术参数



Table
1.
Technical parameters of the exciting motors



table_type1 ">
ParametersMotor 1Motor 2
model numberYZS-1.5-2YZS-1.5-4
rated voltage/V380380
rated power/kW0.120.12
exciting force/kN1.51.5
velocity/(r·min?1)28601430
pole pairs12
rated frequency/Hz5050
rated current/A0.360.4





下载:
导出CSV
|显示表格




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-359-12.jpg'"
class="figure_img
figure_type1 bbb " id="Figure12" />



图
12
倍频同步振动系统的实验测试方案



Figure
12.
Experimental testing scheme of double-frequency synchronization vibration system



下载:
全尺寸图片
幻灯片



5.1
参数β1 = 150°, β2 = 30°, rl = 1.2的实验结果


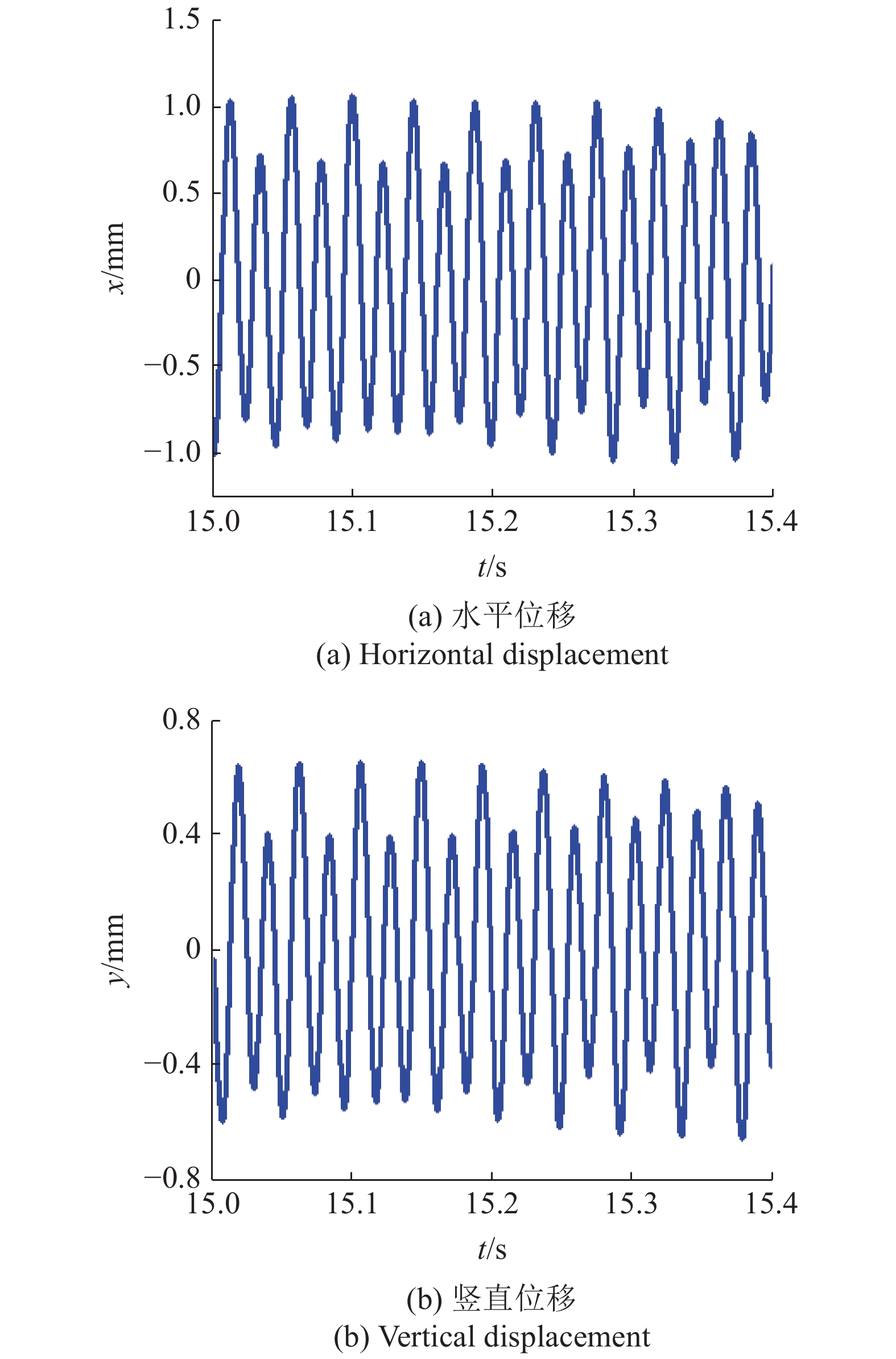
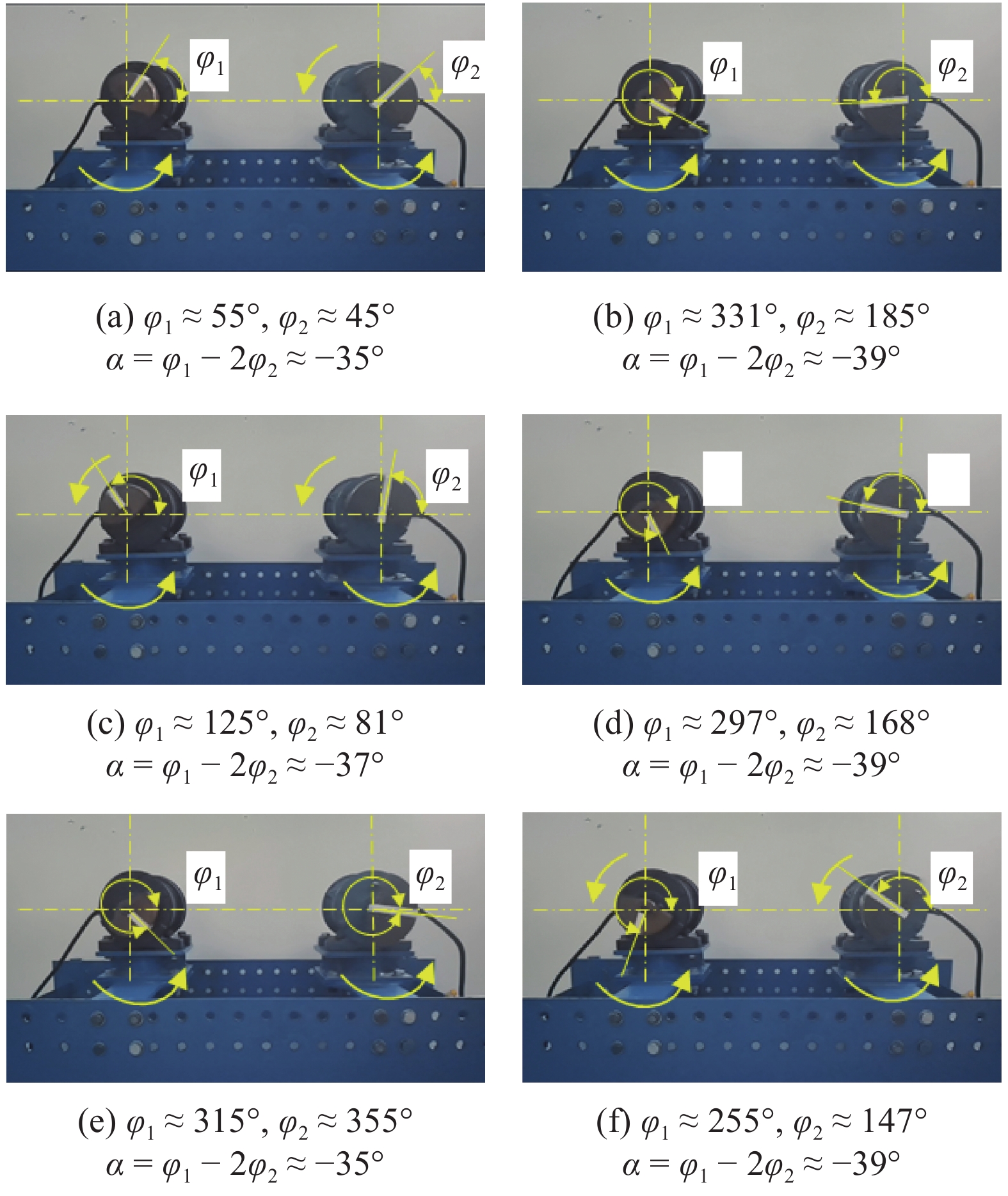
根据图12的实验测试方案, 得到参数β1 = 150°, β2 = 30°, rl = 1.2时的倍频激励双转子振动系统动力学响应和同步运动状态, 如图13和图14所示. 此组结构参数下, 系统动力学响应根据两种不同激励频率叠加所产生的波形可视为近似稳定的周期振动. 箱体沿水平方向的位移单幅值稳定在1.1 mm; 同时振动系统的沿竖直方向位移响应测得0.65 mm. 为实现同向回转双转子倍频同步振动, 箱体不仅必须具有稳定的幅值响应, 还需要两激振电机获得同步运动, 这依赖于偏心转子相位差的稳定性. 如图14所示, 利用高速成像系统精确记录不同瞬时状态的偏心转子位置. 实验测试结果分析表明倍频同步相位差α基本稳定在?39° ~ ?35°(即?0.68 ~ ?0.61 rad), 波动范围很小. 与数值分析和计算机模拟结果对比如表2所示, 确定该工况下的同步状态实验最大误差为9%, 符合振动筛分工程的误差允许范围. 整个机电耦合系统的动能, 势能和电能在同步运行过程中可以产生稳定的动态平衡, 所提出的机械模型能够成功实现倍频同步运动.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-359-13.jpg'"
class="figure_img
figure_type1 bbb " id="Figure13" />



图
13
β1 = 150°, β2 = 30°, rl = 1.2的位移响应



Figure
13.
Displacement responses with β1 = 150°, β2 = 30°, rl = 1.2



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-359-14.jpg'"
class="figure_img
figure_type1 bbb " id="Figure14" />



图
14
β1 = 150°, β2 = 30°, rl = 1.2的同步运动状态: (a) ~ (f) 分别为转子瞬时相位差



Figure
14.
Synchronous motion state with β1 = 150°, β2 = 30°, rl = 1.2: (a) ~ (f) the instantaneous phase differences between rotors



下载:
全尺寸图片
幻灯片





表
2
动力学响应的理论、仿真和实验对比结果



Table
2.
Comparison results among the theories, simulations and experiments of the dynamic responses



table_type1 ">
α /radx /mmy /mm
theoretical value?0.67————
simulation value?0.631.20.72
experimental value?0.611.10.65
error/%98.39.7





下载:
导出CSV
|显示表格



5.2
参数β1 = 142°, β2 = 38°, rl = 1的实验结果


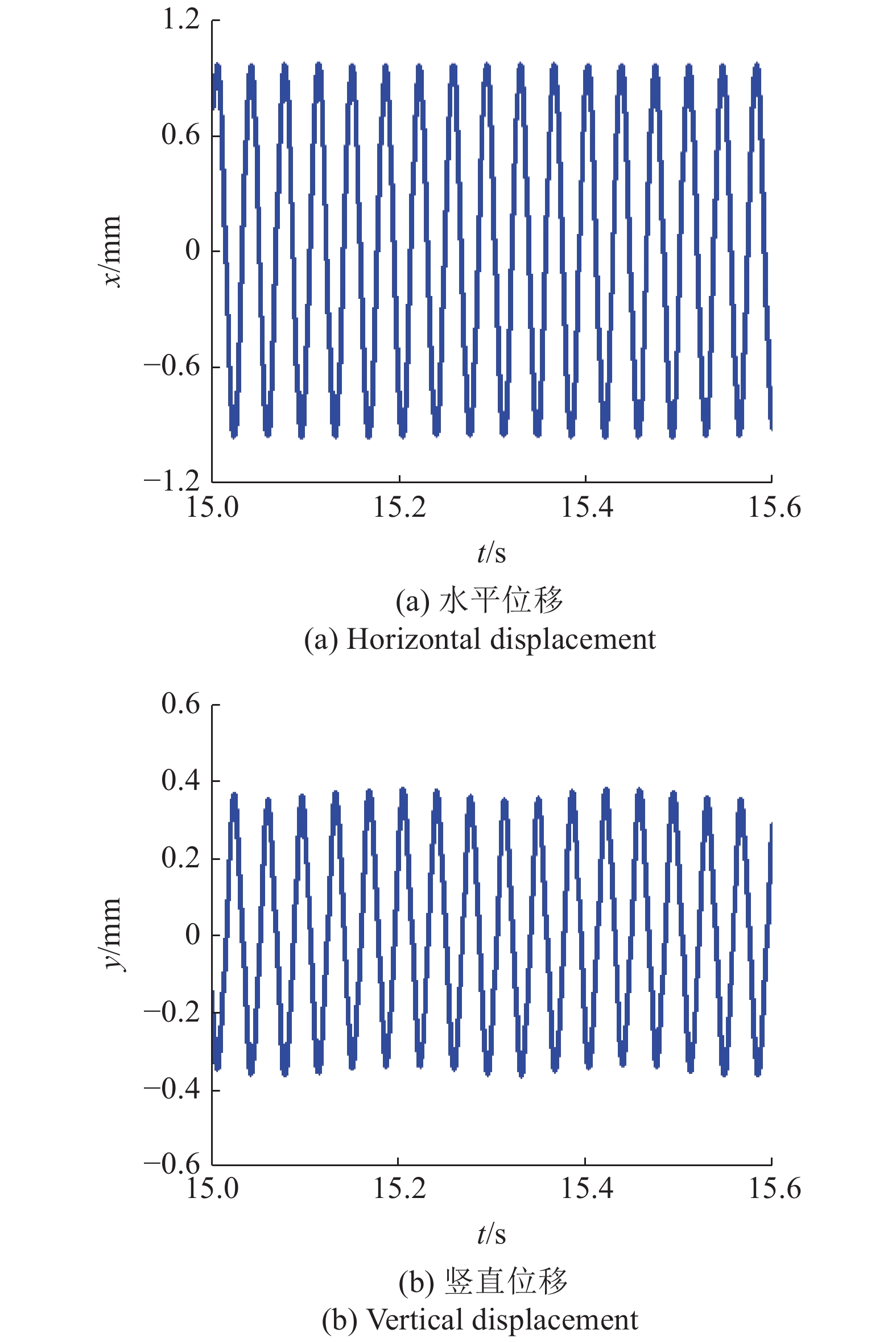
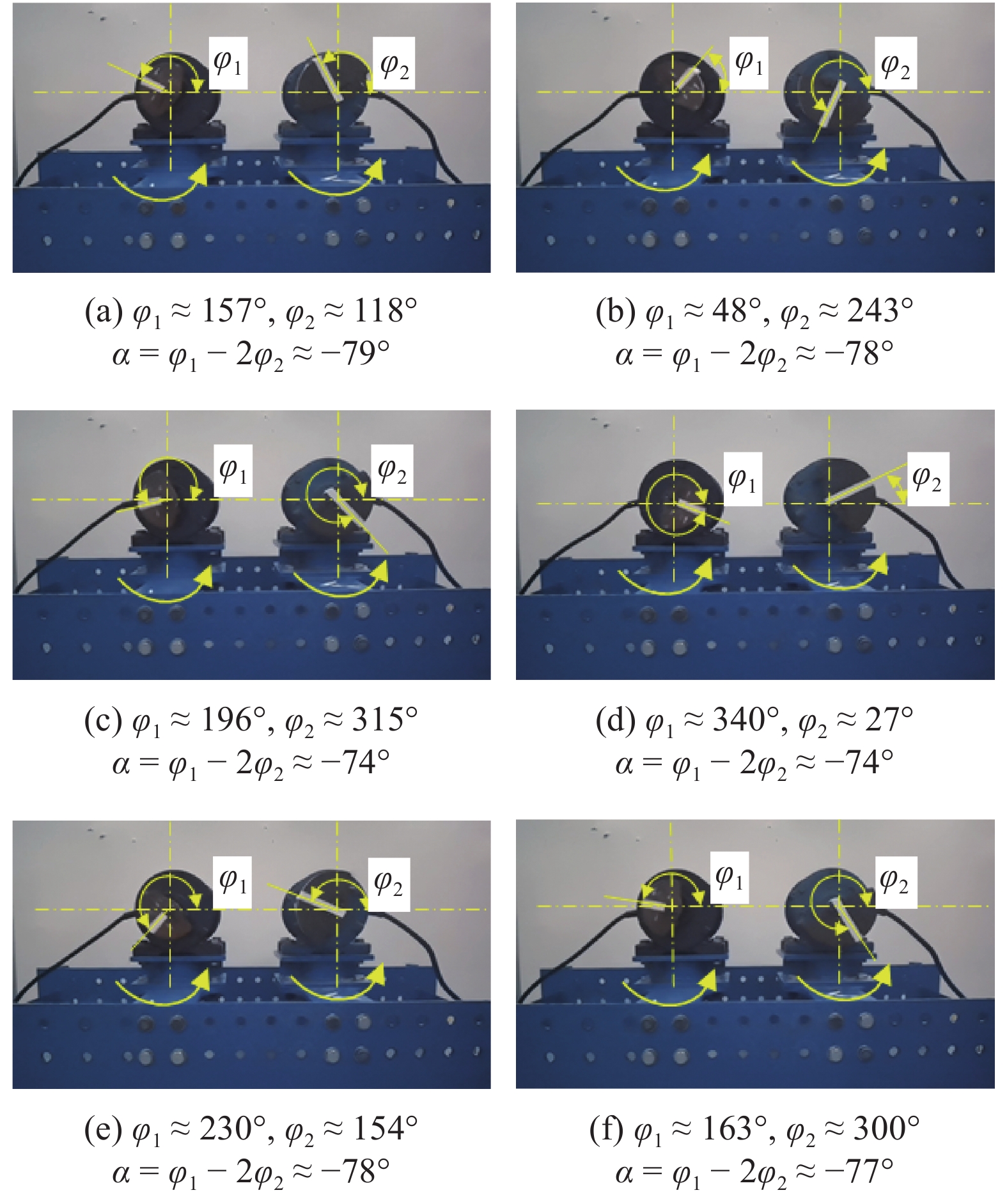
结合实验平台和理论推导, 重新考虑电机安装位置参数β1 = 142°, β2 = 38°, rl = 1, 再次研究了实验系统的机电耦合稳态同步行为, 如图15和图16所示. 运用加速度传感器测得实验测试点沿水平方向的加速度响应, 并在振动分析仪中将加速度值对时间二次积分得到测点的位移振幅为1 mm. 同理, 对振动系统的竖直方向位移响应测得0.4 mm. 此外, 系统6个不同瞬态的偏心转子位置被高速摄像机准确捕捉. 经过对倍频同步状态的分析与计算, 得出不同瞬态的转子相位差值α ≈ ?79° ~ ?74°(即?1.38 ~ ?1.3 rad). 理论、仿真和实验对比结果如表3所示. 无论是箱体的动力学响应还是转子间的同步状态, 实验测试结果与理论推导, 计算机仿真结果基本一致, 并且同步状态的绝对误差为3.3%, 进一步论证了倍频激励双转子振动系统的可行性和正确性. 造成波动误差的原因归纳为: 从振动质体的角度出发, 机械装置施加在电机轴上的负载具有可变性和非均匀性, 这是由于激振电机与箱体之间的耦合作用以及振动系统质量分布的不均匀造成的; 从激振器的角度出发, 实验测试环境的温度和湿度变化对感应电机的各项电气参数会有一定的影响, 比如电机内部转子和定子的电感系数, 阻抗系数, 互感系数等.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-359-15.jpg'"
class="figure_img
figure_type1 bbb " id="Figure15" />



图
15
β1 = 142°, β2 = 38°, rl = 1的位移响应



Figure
15.
Displacement responses with β1 = 142°, β2 = 38°, rl = 1



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/10//lxxb2021-359-16.jpg'"
class="figure_img
figure_type1 bbb " id="Figure16" />



图
16
β1 = 142°, β2 = 38°, rl = 1的同步运动状态: (a) ~ (f) 分别为转子瞬时相位差



Figure
16.
Synchronous motion state with β1 = 150°, β2 = 30°, rl = 1: (a) ~ (f) the instantaneous phase differences between rotors



下载:
全尺寸图片
幻灯片





表
3
动力学响应的理论、仿真和实验对比结果



Table
3.
Comparison results among the theories, simulations and experiments of the dynamic responses



table_type1 ">
α /radx /mmy /mm
theoretical value?1.335————
simulation value?1.3210.45
experimental value?1.381.10.4
error/%3.31011.1





下载:
导出CSV
|显示表格



6.
结 论


本文通过以上理论推导, 数值计算, 仿真研究以及实验验证详细揭示了倍频激励双转子振动系统的自同步机理和动态特征. 重要结论概括如下:

(1)系统倍频同步条件可表征为两台激振器之间输出剩余转矩差的绝对值不能超过倍频同步转矩值, 稳定性判据可通过一个与倍频同步转矩和同步相位差有关的判别式反映;

(2)系统的倍频同步特性主要依赖于安装位置, 激振器的偏心质量, 支撑弹簧刚度值以及偏心半径等参数. 倍频同步能力随着安装距离的不断增加而逐渐接近于零值附近, 电机间用于平衡电磁转矩达到同步状态的耦合量增大, 系统获得倍频同步振动的可行性越来越高;

(3)系统的倍频稳态相位差值在单周期内随着电机位置参数的增大而逐渐趋于平缓, 直至系统同步状态不再受到安装距离变化的影响. 另外电机倾角不影响同步状态的整体变化趋势, 只改变相位差的值域, 系统同步状态在计算模拟与实验研究中得到验证;

(4)与常规同频系统不同, 倍频激励双转子振动系统稳态质心运动轨迹显示为内“8”型, 为研制新型非常规轨迹的振动机械提供了较好的理论依据.

相关话题/系统 电机 运动 实验 质量
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 考虑胎路多点接触的电动汽车?路面耦合系统振动分析
    引言近年来,轮毂电机驱动电动汽车,因传动效率高、便于实现智能控制等优点,得到了广泛关注[1-3],是未来电动汽车的发展方向.但独立驱动电动汽车的动力学与控制也面临诸多新问题,其一是簧下质量大,导致轮胎动载荷增加,轮胎与路面动力学相互作用更加突出.其二是电机激励进一步加剧车轮振动,影响轮胎的接地安全性 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 轮对系统的Hopf分岔研究
    引言近年来随着高速列车运行速度的提高,车辆系统的蛇行失稳问题越发突出,蛇形运动作为车辆系统的固有属性,严重影响着车辆系统的运行平稳性、乘坐舒适性和安全性[1],对车辆系统进行非线性动力学理论方面的研究,不仅可以从车辆动力学角度更加全面地了解蛇形运动,而且对车辆系统的设计与参数优化也具有非常重要的意义 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 致密砂岩逆向渗吸作用距离实验研究
    引言随着常规油气资源的减少,致密油资源成为全球非常规油气勘探开发的热点[1-4],并且北美致密油开发已取得突破性进展[5-7].我国致密油资源丰富、分布广泛,致密油地质储量为2.0×1010t,技术可采储量为2.0×109~2.5×109t[8].我国多数致密油藏具有初始产油量低、产量递减快、衰竭采 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 煤系页岩瓦斯吸附?解吸迟滞效应核磁共振谱实验研究
    引言煤系页岩气俗称瓦斯,是陆相页岩气的重要组成部分之一,主要以吸附态和游离态形式存在.页岩气单井产能并非恒定不变,而是随着累计产量增加而不断递减[1],初期单井产量高递减快,以游离气为主;后期产量稳定,递减慢,以吸附气为主[2],随着煤系页岩瓦斯开采深度不断增加,这一现象愈发明显,而煤系页岩瓦斯吸附 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 固体颗粒对沟槽湍流边界层影响的实验研究
    引言减阻沟槽作为一种被动的减阻方式因其不消耗能源的特点拥有广泛的应用前景.减阻沟槽起源于对于海豚表皮的仿生学研究[1],海豚和鲨鱼表皮存在着微小的,沿着水流方向排列的沟槽结构.这些结构与鲨鱼体表的清洁程度和快速游泳能力有较大的关系[2].顺流沟槽的研究始于20世纪80年代美国兰利研究所[3-5],之 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 挠性航天器太阳翼全局模态动力学建模与实验研究
    引言随着航天领域的发展,现代大型柔性航天器往往安装有诸如大型太阳翼等柔性结构,为了得到可持续的能源,其尺寸日益增大、结构重量越来越轻,太阳翼的弹性振动不可避免地与航天器主体平台的运动相互耦合,这种耦合效应随着太阳翼尺寸的增大显著增强.此时,单个太阳能帆板的模态(假设模态)并不能准确反映整个太阳翼在系 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • DVC中内部散斑质量评价及计算体素点的优化选择
    引言数字体图像相关方法(digitalvolumecorrelation,DVC)是二维数字图像相关方法(two-dimensionaldigitalimagecorrelation,2DDIC)在三维体图像上的拓展.通过比较体成像设备获取的被测试样变形前后数字体图像,该方法可测量物体内部三维全场变 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 半结晶聚合物损伤演化的实验表征与数值模拟1)
    张毅,2),薛世峰,韩丽美,周博,刘建林,贾朋中国石油大学(华东),山东青岛266580EXPERIMENTALCHARACTERIZATIONANDNUMERICALSIMULATIONOFDAMAGEEVOLUTIONINSEMI-CRYSTALLINEPOLYMERS1)ZhangYi,2), ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 张拉整体结构的动力学等效建模与实验验证1)
    陈占魁,罗凯,2),田强北京理工大学宇航学院力学系,北京100081DYNAMICEQUIVALENTMODELINGOFTENSEGRITYSTRUCTURESANDEXPERIMENTALVERIFICATION1)ChenZhankui,LuoKai,2),TianQiangDepartmen ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 湍流边界层等动量区演化机理的实验研究1)
    王超伟*,王康俊*,李彪辉*,姜楠,*,??,2)*天津大学机械工程学院力学系,天津300130??天津市现代工程力学重点实验室,天津300130EXPERIMENTALINVESTIGATIONONTHEEVOLUTIONMECHANISMOFUNIFORMMOMENTUMZONESINTURBU ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.