引言
近年来, 轮毂电机驱动电动汽车, 因传动效率高、便于实现智能控制等优点, 得到了广泛关注[1-3], 是未来电动汽车的发展方向. 但独立驱动电动汽车的动力学与控制也面临诸多新问题, 其一是簧下质量大, 导致轮胎动载荷增加, 轮胎与路面动力学相互作用更加突出. 其二是电机激励进一步加剧车轮振动, 影响轮胎的接地安全性、车辆行驶的平顺性和稳定性.
目前, 关于独立驱动电动汽车的机电耦合振动方面的研究较为丰富, 金智林等[4]针对轮毂电机驱动电动汽车的侧倾稳定性, 分析了不同路面激励下非簧载质量的影响. 张利鹏等[5]建立了分布式驱动动力学模型, 实现了极限工况下整车高速稳定性控制. 平先尧等[6]构造了强跟踪无迹卡尔曼滤波观测器, 提高了四轮独立驱动电动汽车附着系数的识别精度. 张志达等[7]提出了基于故障检测机制的鲁棒自适应UKF算法, 对分布式驱动电动汽车的纵、侧向车速和质心侧偏角进行估计. Qin等[8]针对路面激励引起的不平衡电磁力, 提出了基于动态吸振结构的轮式开关磁阻电机电动汽车的减振方法. Shao等[9]通过对1/4汽车主动悬架和开关磁阻电机模型进行数值模拟, 发现路面不平度与电机气隙偏心率和不平衡残余力高度耦合. Li等[10]针对轮毂电机存在的振动问题, 建立了车辆瞬态动力学机电耦合综合模型, 提出了主动悬架系统多目标优化控制方法. 上述文献多针对电机激励对车辆响应的影响进行研究, 且多将路面作为对车辆的激励, 未涉及电机激励对路面响应的影响, 也未对路面系统进行建模计算.
关于车路相互作用方面, 主要包括路面系统和车路耦合的研究. 路面系统多采用连续体梁[11], 通过Galerkin、有限差分、Newmark、有限元等方法, 研究集中载荷作用下路面动态响应, Froio等[12]研究了无限大Pasternak弹性梁在集中载荷作用下的稳态响应, 通过傅里叶变换得到了一个通用的闭式解析解. Esen[13]采用改进的有限元法, 对功能梯度材料在双参数地基上对Timoshenko梁的横向振动分析. 车路耦合方面, 通过轮胎力将车辆与路面耦合计算[14], 且轮胎多采用单点接触模型, 如Hien等[15]采用有限元法构造运动方程, 弹簧的质量、刚度和车辆阻尼系数假定为高斯随机变量, 研究了具有不确定参数的车辆?弹性支承梁的动力响应. Krishnanunni和Rao[16]提出了车?路系统响应的迭代解耦方法. Li和Yang[17]建立了车路耦合动力学模型, 认为路面振动会给汽车带来二次激励, 影响轮胎动载和附着特性.
针对轮胎与路面接触情况, 多采用单点接触模型, 对实际的胎路接触模型大大简化, 方便计算, 但精度也会降低. 随着数字计算能力的提升, 胎路点接触模型的计算精度, 逐渐受到研究者们的质疑, 车路耦合方面, Yang等[18]提出了改进轮胎滚子接触力学模型, 提高了精度, 但计算量大, 运算速度较慢. 黄晓明和郑彬双[19]针对胎路附着特性研究不足, 提出从时变性、统一性及车辆抗滑需求感应参数等方面深入研究. 孙加亮等[20]针对多柔体系统动力学问题, 提出柔性部件的动力建模与优化. 刘志浩等[21]建立了轮胎欧拉梁模型, 研究轮胎包容性对振动特性的影响. 王立安等[22]建立了1/4汽车与半空间地基耦合振动模型, 采用弹性滚子接触模型反映轮胎包容性, 推导了地表振动位移的解析解. 车桥耦合方面, Zhang等[23]提出了多弹簧接触轮胎模型, 可考虑路面不平顺和车轮跳离路面, 便于车桥耦合动力学分析. Deng等[24]提出了轮胎与桥面的多点接触模型, 通过实验证明多点接触模型精度更高. 车桥耦合中, 桥梁通常取5阶模态即可满足计算要求. 而路面系统, 通常取100阶以上, 计算更为复杂, 且多点接触的车路耦合方面的研究尚不多见. 在非线性路基方面. Ding等[25]等研究考虑几何非线性、水平放置弹性梁的主共振, 表明由非对称弹性支承和几何非线性所引起的软化特性到硬化特性的转变仅存在于第一阶模态响应. Singh和Harsha[26]利用应力函数Galerkin方法研究了夹层板在Pasternak弹性地基上的动力特性. 但以上研究仅采用移动集中力描述车辆载荷, 未考虑胎路多点接触.
独立驱动电动汽车的车轮振动剧烈, 与路面的动力学相互作用更加突出. 但现有研究主要针对传统汽车, 关于电动车轮与路面动力学相互作用的研究尚不多见. 而考虑轮胎与路面的多点接触, 基于非线性地基, 研究独立驱动电动汽车在路面不平顺、电机激励及车路耦合激励的综合作用下的动力学问题, 尚未见文献报道. 鉴于此, 论文建立了基于非线性地基及多点接触的轮毂电机电动汽车?路面系统机电耦合动力学模型, 研究汽车与路面的相互作用机理, 分析非线性地基及多点接触在不同激励形式下对路面和电动汽车响应的影响.
1.
电动汽车?路面系统建模
1.1
车?路系统运动微分方程
车?路系统动力学模型, 如图1所示. 采用二自由度1/4汽车悬架模型描述电动汽车垂向振动; 利用非线性黏弹性地基上有限长Euler?Bernoulli梁模拟道路系统. 路面由各向同性、矩形截面Euler?Bernoulli梁模拟, 地基由三次立方非线性Winkler地基模型[27]模拟. 单位长度梁受到基础的作用力为
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-239-1.jpg'" class="figure_img
figure_type1 bbb " id="Figure1" />
图
1
电动汽车?路面系统动力学模型
Figure
1.
Dynamic model of electric vehicle?road system
下载: 全尺寸图片
幻灯片
$$ P = {k_{{text{r1}}}}{y_{text{r}}} + {k_{{text{r3}}}}{y_{text{r}}}^3 + {c_{ m{r}}}frac{{partial {y_{text{r}}}}}{{partial t}} $$  | (1) |
式中, kr1, kr3分别为地基的线性和非线性弹性系数; cr为地基阻尼系数; yr为路面垂向位移.
假定t = 0时刻汽车位于道路中点, 以速度v沿直线匀速行驶. 利用达朗贝尔原理及Bernoulli?Euler理论, 建立车辆及路面垂向振动微分方程[27]
$$ begin{split}& {m_2}{{ddot y}_2} + {c_2}({{dot y}_2} - {{dot y}_1}) + {k_2}({y_2} - {y_1}) = 0 & ({m_1} + {m_3}){{ddot y}_1} - {c_2}({{dot y}_2} - {{dot y}_1}) - {k_2}({y_2} - {y_1}) + &qquad {text{ }}sumlimits_{i = 1}^n {{c_{{text{t}}i}}({{dot y}_1} - {{dot y}_{0i}} - {{dot y}_{{text{t}}i}})} + sumlimits_{i = 1}^n {{k_{{text{t}}i}}({y_1} - {y_{0i}} - {y_{{text{t}}i}})} = {F_{text{e}}} end{split} $$  | (2) |
$$ begin{split} &EJfrac{{partial {}^4{y_{ m{r}}}}}{{partial {x^4}}} + ho Afrac{{partial {}^2{y_{ m{r}}}}}{{partial {t^2}}} + {k_{{ m{r}}1}}{y_{ m{r}}} + {k_{{ m{r}}3}}{y_{ m{r}}}^3 + &qquad{ m{ }}{c_{ m{r}}}frac{{partial {y_{ m{r}}}}}{{partial t}} = F(t){ m{delta }}(x - vt)end{split}$$  | (3) |
式中, m1, m2分别为非簧载质量和簧载质量, m3为轮毂电机及减速机构质量, y1, y2分别为非簧载质量和簧载质量位移, k2, c2分别为悬架刚度和阻尼系数, Fe为电机垂向激励合力. E为路面材料弹性模量, J为路面截面对中性轴的惯性矩, ρ, A分别为路面密度和横截面积, δ为狄拉克函数, x为汽车行驶方向的位移, v为行驶速度.
F(t)为电动汽车与路面相互作用力, 即轮胎力
$$ begin{split} F = &sumlimits_{i = 1}^n {{c_{{text{t}}i}}({{dot y}_1} - {{dot y}_{0i}} - {{dot y}_{{text{t}}i}})} + {text{ }}sumlimits_{i = 1}^n {{k_{{text{t}}i}}({y_1} - {y_{0i}} - {y_{{text{t}}i}})} - & ({m_1} + {m_2} + {m_3})g end{split} $$  | (4) |
式中, 轮胎与路面为多点接触, n为多点接触数量; yti为轮胎下方各接触点处的路面振动位移, 称之为路面二次激励[27], kti, cti分别为各点接触处轮胎的刚度和阻尼系数. 假定每个接触点的刚度和阻尼系数相同, 即
$$ {k_{{text{t}}i}} = {k_{text{t}}}/n , ;; {c_{{text{t}}i}} = {c_{text{t}}}/n $$  | (5) |
式中, kt, ct为轮胎总的刚度系数和阻尼系数.
y0i为各接触点处的路面不平顺激励, 采用正弦函数描述
$$ {y_{0i}} = {B_0}sin left[frac{{2{text{π}} }}{{{L_0}}}left(vt{text{ + }}frac{{i{L_{text{t}}}}}{{n - 1}} ight) ight],;;i = 0,1,cdots $$  | (6) |
式中, B0, L0分别为路面不平顺幅值及波长, Lt为轮胎接触印迹长度.
汽车参数取为[28]: m1 = 40 kg, m2 = 337.5 kg, m3 = 30 kg, kt = 250 kN/m, k2 = 19.6 kN/m, ct = 375 N·s/m, c2 = 1450 N·s/m, 轮胎印迹Lt = 25.4 mm[24], 车轮滚动半径0.304 4 m[29], 车速v = 20 m/s.
路面系统参数取为[27, 30-31]: 路面宽度、厚度分别为6 m, 0.01 m, 长度L = 160 m; 路面材质为沥青混合料, 密度ρ = 2.5 t/m3, 弹性模型E = 1.6 GN/m2, 路面不平顺参数: L0 = 10 m, B0 = 0.02 m; 地基的线性和非线性弹性系数、地基阻尼系数分别取为kr1 = 8 MN/m2, kr3 = 8 MN/m2, cr = 300
m{k}}{text{N}} cdot {text{s/}}{{text{m}}^2}$
1.2
胎路接触点数的选取
为了合理选取胎路接触点数, 计算得到不同胎路接触点数下的路面响应最大幅值, 根据其收敛性确定接触点数. 模态截断阶数取NM = 200, 轮胎与路面接触点数取1 ~ 8, 行驶速度分别为30, 50, 60和130 km/h, 考虑电机激励与不考虑电机激励时, 接触点数对非线性与线性地基的路面响应最大幅值的影响如图2所示.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-239-2.jpg'" class="figure_img
figure_type1 bbb " id="Figure2" />
图
2
接触点数对路面响应最大幅值的影响
Figure
2.
Effects of the number of contact point on the maximum amplitude of road response
下载: 全尺寸图片
幻灯片
由图2可见, 多点接触较单点接触, 路面响应最大幅值都有所降低:
(1)不考虑电机激励时, 随着接触点数的增大, 路面最大幅值呈现下降趋势. 且当n > 3时, 路面响应最大幅值的相对增量小于0.02%;
(2)考虑单机激励时, 电机激励使得路面响应波动都增大, 且随着车速增加, 路面响应相对降幅增大, 其中车速为130 km/h时, 最大降幅为5.72%, 而车速为30 km/h时, 最大降幅都小于0.8%. 当n > 5时, 路面响应变化较小, 小于1.5%.
综上, 在后续计算中, 胎路接触点数n取为6.
1.3
电机垂向激励
采用四相8/6极开关磁阻电机[29, 32], 每转24个步距, 步进角15°. 电机垂向激励合力由定、转子间的切向力和径向力组成, 其中电磁转矩波动产生切向力, 其表达式为
$$ {F_tau } = {T_{text{e}}}/R $$  | (7) |
式中, R为电机定子半径, Te为电磁转矩.
假设电机相电流I为常数, 且磁路为线性, 则磁极上的径向力为
$$ {F_{text{r}}} = frac{{partial [L(theta ,{l_{ m{g}}}){I^2}/2]}}{{partial {l_{ m{g}}}}} approx - frac{1}{2}{I^2}frac{{L(theta ,{l_{ m{g}}})}}{{{l_{ m{g}}}}} $$  | (8) |
式中, 电感
m{g}}}) $
$$ L(theta ,{l_{ m{g}}}) = {L_{min }} + {K_theta }theta $$  | (9) |
式中, Lmin为最小电感, Kθ为L与θ关系曲线斜率.
定、转子间的气隙长度为
$$ {l_{text{g}}} = sqrt {{b^2} + {{(r{theta _1})}^2}} $$  | (10) |
式中, b为定转子极间最短距离; rθ1转子凸极转过的弧长, r为转子半径, θ1为转子凸极转角.
将式(9)和式(10)代入式(8), 且考虑切向力与径向力的作用周期相同, 得到径向力
$$ {F_{text{r}}} = - dfrac{{{I^2}}}{2}dfrac{{{L_{min }} + {K_theta }dfrac{{a{text{π}} }}{{30}}left({t - nT} ight)}}{{sqrt {{b^2} + {{left(dfrac{{{text{π}} ar}}{{30}} ight)}^2}{{left[t - left(n{text{ + }}dfrac{7}{{20}} ight)T ight]}^2}} }} $$  | (11) |
电机垂向激励合力的解析表达式为
$$ {F_{text{e}}} = left{ begin{array}{l} {F_tau }cos left(dfrac{{a{text{π}} }}{{30}}t ight) + {F_{text{r}}}sin left(dfrac{{a{text{π}} }}{{30}}t ight){text{, }};;nT leqslant t leqslant left(n + dfrac{7}{{20}} ight)T 0 {text{ ,}};;left(n + dfrac{7}{{20}} ight)T < t leqslant left(n + 1 ight)T end{array} ight. $$  | (12) |
式中, T = 60/(aNr)为电磁激励基波周期, a为电机转速, Nr为转子级数.
电机各参数取值为[29, 32]: R = 0.05 m, Te = 165 N·m; b = 1 mm, I = 1 A, Kθ = 82.5, Lmin = 4.95 H, r = 0.047 m, Nr = 6.
2.
路面响应及收敛性判定指标
2.1
路面响应求解
假设路面垂向位移为
$$ {y_{text{r}}}(x,t) = sumlimits_{i = 1}^{NM} {{phi _i}(x){eta _i}(t)} $$  | (13) |
式中,
将式(13)代入式(3), 且两端乘以
$$ begin{split} &sumlimits_{i = 1}^{NM} {left[ ho Afrac{{{{ m{d}}^2}{eta _i}(t)}}{{{ m{d}}{t^2}}} + cfrac{{{ m{d}}{eta _i}(t)}}{{{ m{d}}t}} + {k_{{ m{r1}}}}{eta _i}(t) ight] cdot } int_0^L {{phi _i}(x){phi _j}(x){ m{d}}x{ m{ + }}} &qquad EJsumlimits_{i = 1}^{NM} {{eta _i}(t)} int_0^L {frac{{{{ m{d}}^4}{phi _i}(x)}}{{{ m{d}}{x^4}}}{phi _j}(x){ m{d}}x} + &qquad{k_{{ m{r}}3}}int_0^L {{{left[sumlimits_{i = 1}^{NM} {{eta _i}(t){phi _i}(x)} ight]}^3}{phi _j}(x){ m{d}}x} = { m{ }}&qquadint_0^L {F(t){ m{delta }}(x - vt){phi _j}(x){ m{d}}x} [-15pt]end{split}$$  | (14) |
两端简支边界条件下, 地基梁的模态振型为
$$ {phi _i}(x) = {C_i}sin (i{text{π}} x/L),;;i = 1,2,cdots $$  | (15) |
根据模态振型的正交性, 以及
$$ begin{split} &{{ddot eta }_i}(t) + frac{c}{{ ho A}}{{dot eta }_i}(t) + frac{{EJ{{left( {i{text{π}} } ight)}^4} + {L^4}{k_{{ m{r}}1}}}}{{ ho A{L^4}}}{eta _i}(t) + &qquad{ m{ }}frac{{{k_{{ m{r}}3}}}}{{ ho A}}int_0^L {sumlimits_{i = 1}^{NM} {{{left[ {{phi _i}(x){eta _i}(t)} ight]}^3}{phi _j}(x){ m{d}}x} } = frac{{F(t)}}{{ ho A}}{phi _i}(vt)end{split} $$  | (16) |
对于式(16)中的非线性项积分
ight]}^3}cdot $
m{d}}x$
先将立方非线性项改写
$$ begin{split} &int_0^L {sumlimits_{i = 0}^{NM} {{{left[ {{phi _i}(x){eta _i}(t)} ight]}^3}{phi _j}(x){ m{d}}x} }= sumlimits_{i = 1}^{NM} {sumlimits_{k = 1}^{NM} {sumlimits_{m = 1}^{NM} {{eta _i}(t){eta _k}(t){eta _m}(t) cdot } } } &qquad{ m{ }}int_0^L {{phi _i}(x){phi _k}(x){phi _m}(x){phi _j}(x){ m{d}}x} =&qquad sumlimits_{i = 1}^{NM} {sumlimits_{k = 1}^{NM} {sumlimits_{m = 1}^{NM} {{eta _i}(t){eta _k}(t){eta _m}(t) cdot } } } &qquadint_0^L {sin left(frac{{i{text{π}} x}}{L} ight)} sin left(frac{{k{text{π}} x}}{L} ight)sin left(frac{{m{text{π}} x}}{L} ight)sin (frac{{j{text{π}} x}}{L}){ m{d}}x&qquadj = 1,2,cdots,NM[-13pt]end{split}$$  | (17) |
利用三角函数的积化和公式, 可得式(17)中的积分项为
$$begin{split} &int_0^L {sin left( {frac{{i{text{π}} x}}{L}} ight)} sin left( {frac{{k{text{π}} x}}{L}} ight)sin left( {frac{{m{text{π}} x}}{L}} ight)sin left( {frac{{j{text{π}} x}}{L}} ight){ m{d}}x = &qquadfrac{1}{8}int_0^L {left{ {cos [{text{π}} x(i - k + m - j)/L] + } ight.} &qquadcos [{text{π}} x(i - k - m + j)/L] + cos [{text{π}} x(i - k + m + j)/L] + &qquadcos [{text{π}} x(i - k - m - j)/L] + cos [{text{π}} x(i + k + m - j)/L] + &qquadcos [{text{π}} xleft( {i + k - m + j} ight)/L] + cos [{text{π}} xleft( {i + k + m + j} ight)/L] + &qquadleft. {cos [{text{π}} xleft( {i + k - m - j} ight)/L]} ight}{ m{d}}x[-10pt]end{split}$$  | (18) |
由于
$$ begin{split} &int_0^L {cos left({{text{π}}varDelta x/L} ight)} { m{d}}x = &qquad {text{ }}left{ begin{array}{l} dfrac{{Lsin ({text{π}}varDelta )}}{{{text{π}}varDelta }},;;varDelta {text{ = }}i mp k pm m mp j ne 0 L {text{ }},;;varDelta {text{ = }}i mp k pm m mp j = 0{text{ }} end{array} ight. end{split} $$  | (19) |
式(18)进一步整理为
$$ begin{split}& int_0^L {sin left(frac{{i{text{π}} x}}{L} ight)} sin left(frac{{k{text{π}} x}}{L} ight)sin left(frac{{m{text{π}} x}}{L} ight)sin left(frac{{j{text{π}} x}}{L} ight){text{d}}x {text{ }} =& qquad frac{1}{8}sumlimits_{kk = 1}^8 {{f_{kk}}(i,j,k,m)} end{split} $$  | (20) |
式中,
ight.$
将式(20)代入式(17), 得到
$$ begin{split} &int_0^L {sumlimits_{i = 0}^{NM} {{{left[ {{phi _i}(x){eta _i}(t)} ight]}^3}{phi _j}(x){ m{d}}x} } = &qquadfrac{L}{8}sumlimits_{i = 1}^{NM} {sumlimits_{k = 1}^{NM} {sumlimits_{m = 1}^{NM} {{eta _i}(t){eta _k}(t){eta _m}(t)sumlimits_{kk = 1}^8 {{f_{kk}}(i,j,k,m)} } } } &qquad j = 1,2,cdots,NMend{split}$$  | (21) |
将式(21)代入式(16), 得到非线性地基梁第i阶模态的振动微分方程
$$ begin{split} &{{ddot eta }_i}(t) + frac{c}{{ ho A}}{{dot eta }_i}(t) + frac{{EJ{{left( {i{text{π}} } ight)}^4} + {L^4}{k_{{ m{r}}1}}}}{{ ho A{L^4}}}{eta _i}(t) + &qquadfrac{{L{k_{{ m{r}}3}}}}{{8 ho A}}sumlimits_{i = 1}^{NM} {sumlimits_{k = 1}^{NM} {sumlimits_{m = 1}^{NM} {{eta _i}(t){eta _k}(t){eta _m}(t)} } } sumlimits_{kk = 1}^8 {{f_{kk}}(i,j,k,m)} =&qquad frac{{F(t)}}{{ ho A}}{phi _i}(vt)[-10pt]end{split}$$  | (22) |
式中, 地基梁模态振型
$$ int_0^L {{phi _i^2}left(x ight)} {text{d}}x{text{ = }}int_0^L {C_i^2{{left[ {sin left({frac{{i{text{π}} x}}{L}} ight)} ight]}^2}} {text{d}}x{text{ = 1}} $$  | (23) |
求得
$$ {phi _i}(x) = sqrt {frac{2}{L}} sin left({frac{{i{text{π}} x}}{L}} ight),;;i = 1,2,cdots $$  | (24) |
将式(24)代入式(22), 通过4阶龙格库塔数值方法求解
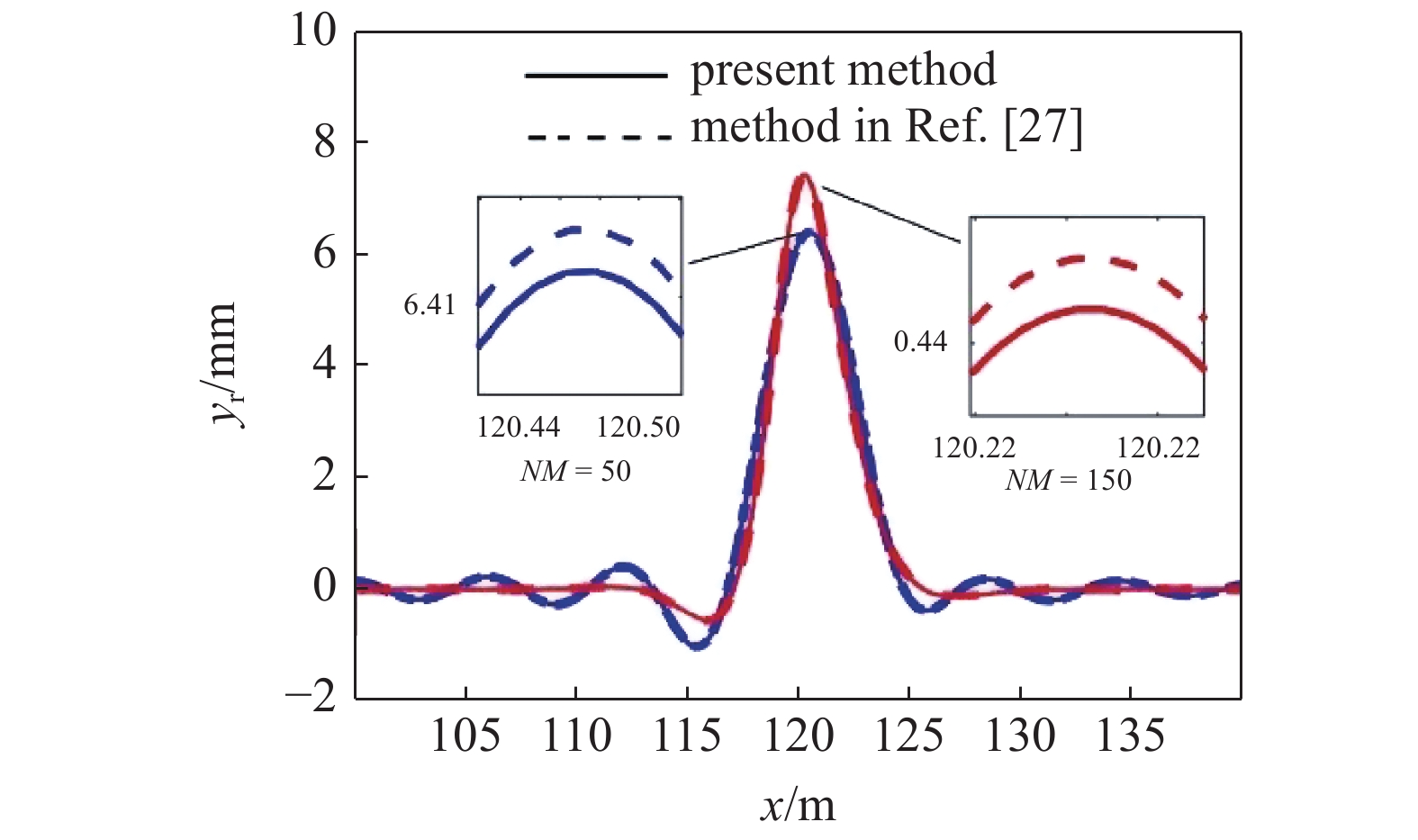
图3所示为本文提出的非线性项积分处理方法与文献[27]的数值积分方法对比, 图中截断阶数分别为50和150, 路面位移最大幅值的相对差别分别为0.16%和0.13%. 证明论文所提出的方法的正确性, 也说明截断阶数越高, 数值积分精度越高, 二者差别越小.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-239-3.jpg'" class="figure_img
figure_type1 bbb " id="Figure3" />
图
3
非线性项积分的求解方法对比
Figure
3.
Comparison of methods for nonlinear integral term
下载: 全尺寸图片
幻灯片
2.2
截断阶数的选取及收敛性判定指标
截断阶数NM越大, 路面响应的精度越高, 但运算耗时也越长. 合理选择截断阶数, 在保证计算精度的同时, 加快运算速度, 具有重要意义. Chen等[33]等研究了集中载荷作用下非线性地基多层梁的Galerkin截断阶数的收敛性. 受此启发, 论文基于非线性地基及胎路多点接触, 分析电动汽车?路面机电耦合系统的Galerkin截断阶数的收敛性.
由式(14)可知, 线弹性地基梁无阻尼、不考虑非线性刚度及路面激励时的固有频率为
$$ {omega _i} = sqrt {frac{{EJ{{left({i{text{π}} } ight)}^4} + {L^4}{k_{{ m{r}}1}}}}{{ ho A{L^4}}}} $$  | (25) |
以相邻频率之间的相对增量为路面响应收敛性的判定指标, 其表达式为
$$ {lambda _i}{text{ = }}frac{{omega _{i{text{ + }}1}^{} - omega _i^{}}}{{omega _i^{}}} times 100{{% }},;;i = 1,2,cdots $$  | (26) |
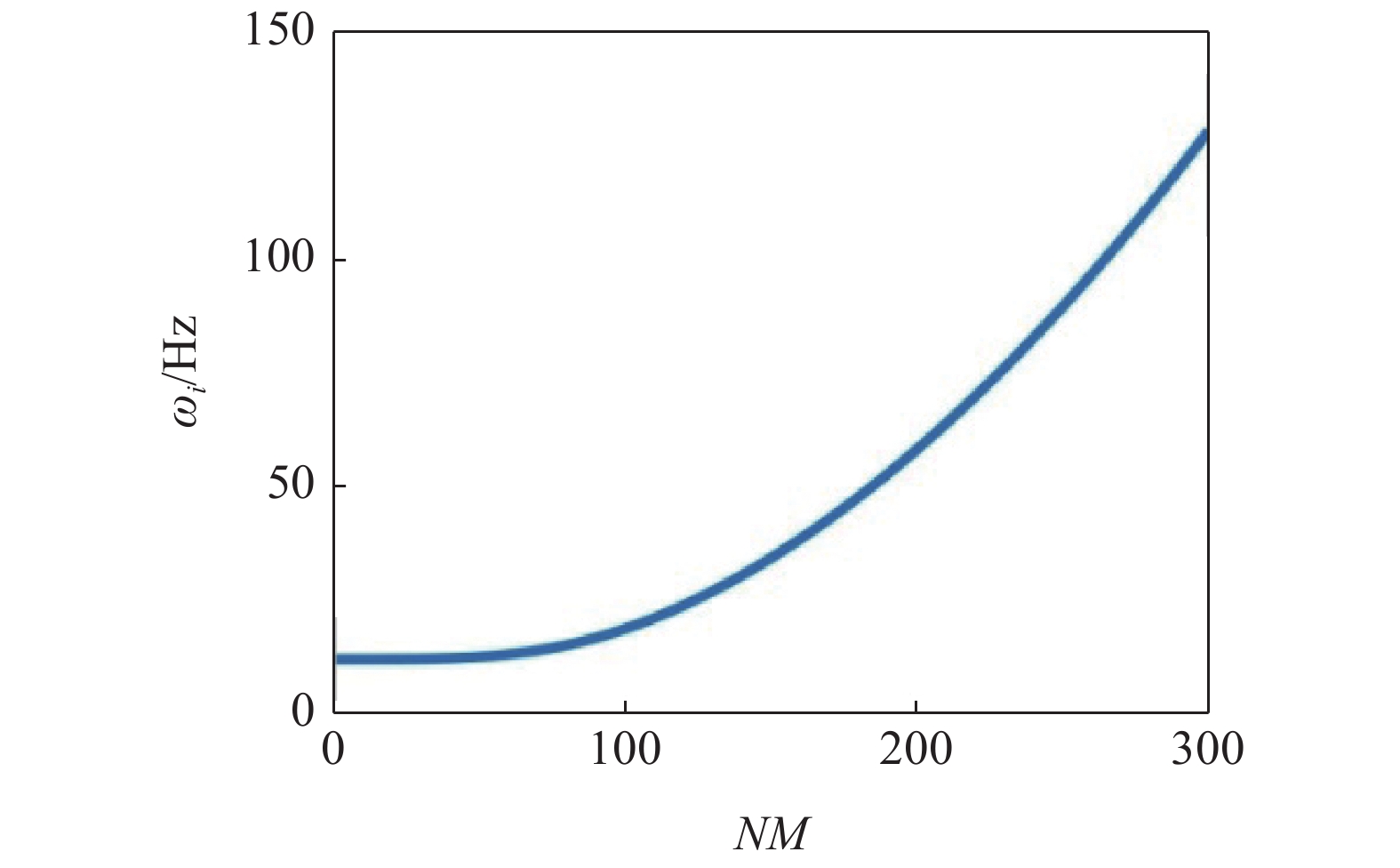
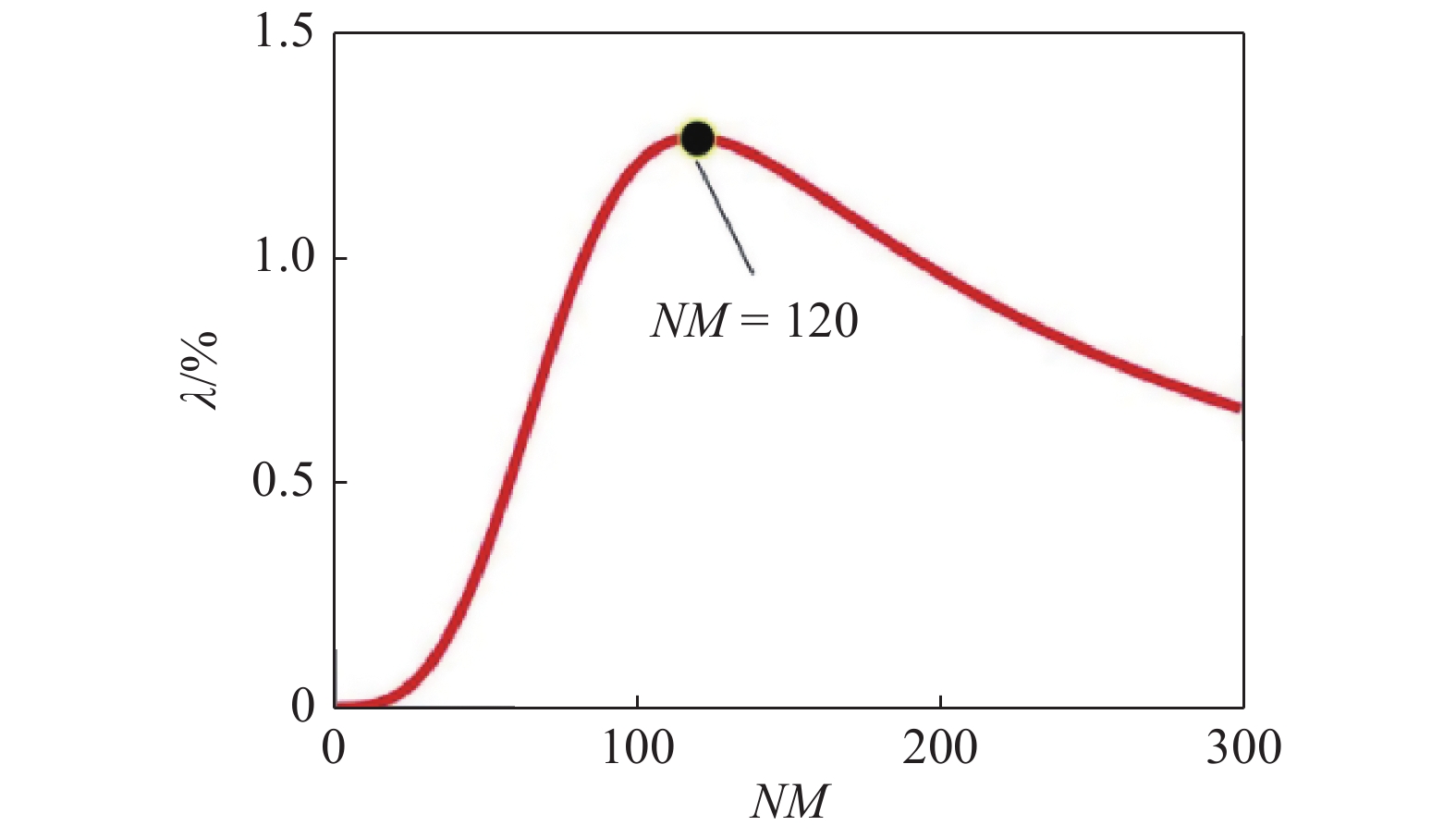
图4所示为线弹性地基梁的固有频率随截断阶数NM的变化曲线, 表1为前300阶固有频率及相邻频率之间的相对差别, 相邻频率之间的相对增量随截断阶数NM的变化曲线如图5示.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-239-4.jpg'" class="figure_img
figure_type1 bbb " id="Figure4" />
图
4
线弹性地基梁的固有频率
Figure
4.
Natural frequency of linear elastic foundation beam
下载: 全尺寸图片
幻灯片
表
1
线弹性地基梁的固有频率及相邻频率差别
Table
1.
Natural frequency and relative differences of adjacent frequencies of linear elastic foundation beam
table_type1 ">
| NM | Frequency/Hz | Difference/% |
| 1 | 11.623 0 | 0 |
| 10 | 11.623 9 | 0.002 6 |
| 20 | 11.636 8 | 0.022 0 |
| 30 | 11.692 8 | 0.075 5 |
| 40 | 11.842 1 | 0.177 0 |
| 50 | 12.150 9 | 0.331 6 |
| 60 | 12.693 2 | 0.529 3 |
| 70 | 13.539 1 | 0.743 7 |
| 80 | 14.742 5 | 0.941 6 |
| 90 | 16.335 2 | 1.096 8 |
| 100 | 18.327 4 | 1.199 0 |
| 110 | 20.714 3 | 1.252 0 |
| 120 | 23.483 4 | 1.266 4 |
| 130 | 26.619 4 | 1.254 1 |
| 140 | 30.107 8 | 1.224 8 |
| 150 | 33.935 7 | 1.186 0 |
| 160 | 38.092 5 | 1.142 3 |
| 170 | 42.569 7 | 1.097 |
| 180 | 47.360 2 | 1.051 9 |
| 190 | 52.458 6 | 1.008 1 |
| 200 | 57.860 7 | 0.966 3 |
| 210 | 63.562 8 | 0.926 7 |
| 220 | 69.562 2 | 0.889 4 |
| 230 | 75.856 7 | 0.854 5 |
| 240 | 82.444 4 | 0.821 7 |
| 250 | 89.323 9 | 0.791 0 |
| 260 | 96.493 9 | 0.762 3 |
| 270 | 103.953 4 | 0.735 5 |
| 280 | 111.701 6 | 0.710 3 |
| 290 | 119.737 7 | 0.686 6 |
| 300 | 128.061 3 | 0.664 4 |
下载: 导出CSV
|显示表格
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-239-5.jpg'" class="figure_img
figure_type1 bbb " id="Figure5" />
图
5
相邻频率的相对增量
Figure
5.
Relative increment of adjacent frequencies
下载: 全尺寸图片
幻灯片
由图4和图5及表1可知:
(1)地基梁的固有频率随着截断阶数NM的增大而增大, 且前60阶具有密频特性, NM大于60时, 固有频率显著增大;
(2)相邻频率之间的相对增量呈现先增后减趋势, NM = 120时, 相对增量达到最大值1.266 4%. NM > 120时, 相对增量逐渐减小, 且NM > 200时, 相对增量都小于1%, 说明截断阶数越高, 相邻频率之间的差别越小, 表明路面响应具有收敛性.
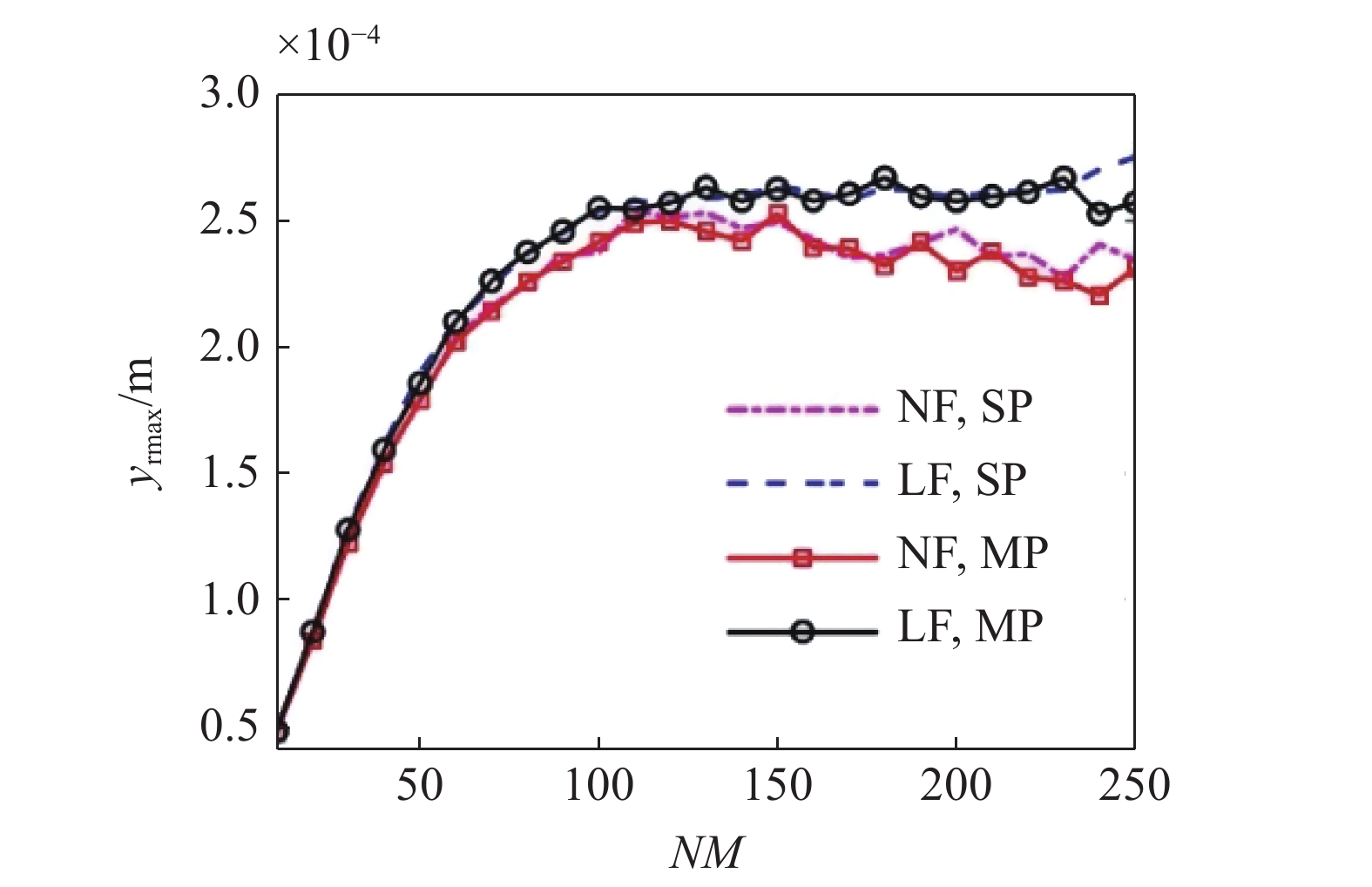
图6所示为路面位移最大幅值随截断阶数NM的变化曲线. 当NM > 120时, 路面垂向位移最大幅值变化较小, 相对差别在3%以内, 且线性地基(linear foundation, LF)与非线性地基(nonlinear foundation, NF)、单点接触(single point, SP)与多点接触(multi-point, MP)的变化趋势一致, 表明NM > 120时, Galerkin截断对于路面位移响应的计算结果相对精确, 也验证了通过式(26)选取截断阶数NM的有效性.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-239-6.jpg'" class="figure_img
figure_type1 bbb " id="Figure6" />
图
6
截断阶数对路面响应最大幅值的影响
Figure
6.
Effects of truncation order on maximum amplitude of road response
下载: 全尺寸图片
幻灯片
3.
系统参数对车辆和路面响应的影响
与以往研究不同[28], 本文在电动汽车?路面系统建模中考虑了非线性地基、胎路多点接触和电机激励, 因此主要分析不同车速和路面不平顺幅值下, 以上3个因素对车辆及路面响应的影响规律.
3.1
非线性地基、多点接触及电机激励对路面响应的影响
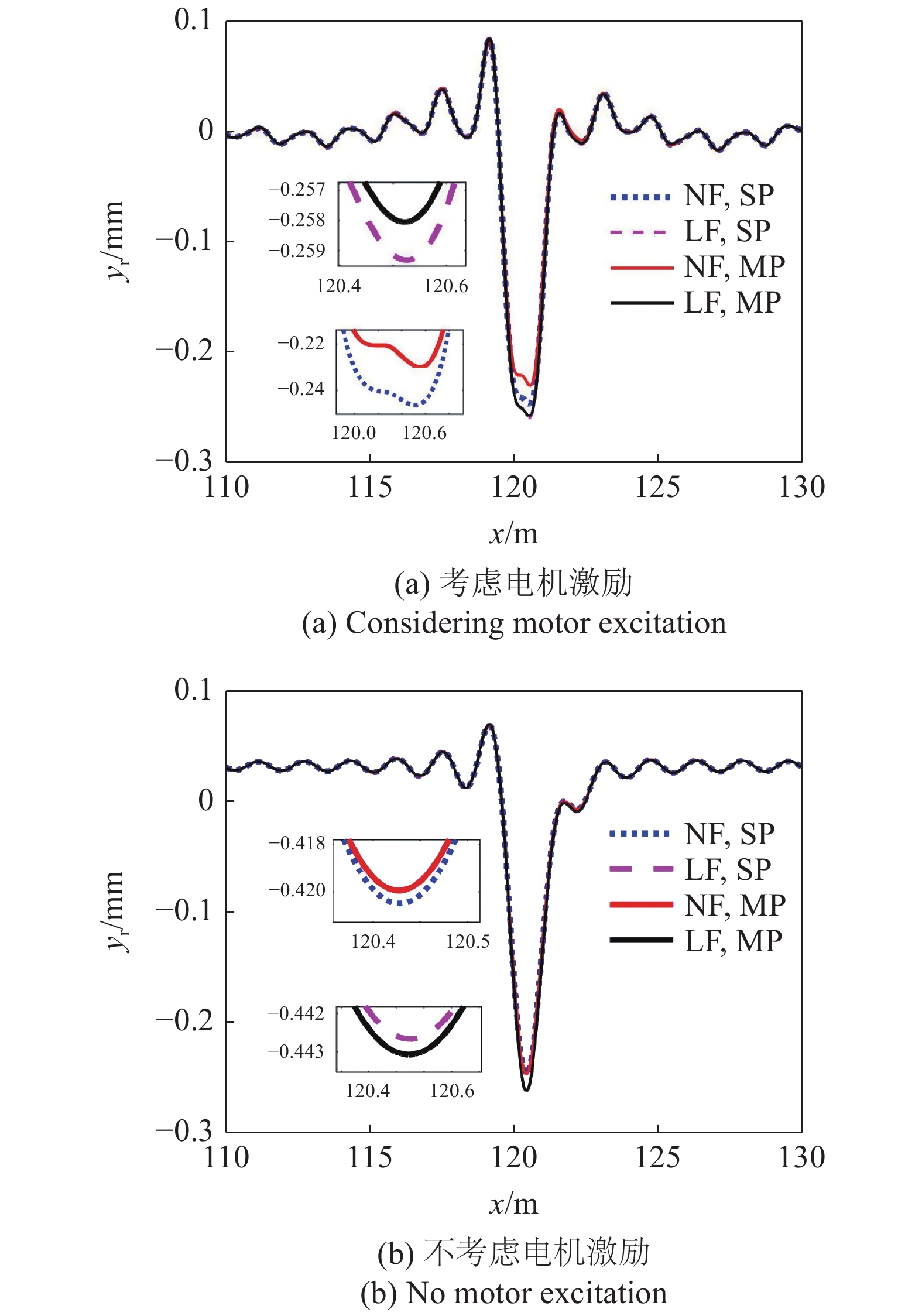
汽车以20 m/s驶过路面某一位置(x = 120 m), 非线性地基与线性地基, 多点接触与单点接触, 以及电机激励对路面垂向位移的影响如图7和图8所示, 路面响应的最大幅值及相对差别见表2.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-239-7.jpg'" class="figure_img
figure_type1 bbb " id="Figure7" />
图
7
B0 = 0.02 m时非线性地基、多点接触及电机激励对路面响应的影响
Figure
7.
Effects of nonlinear foundation and multi-point contact and motor excitation on road response when B0 = 0.02 m
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-239-8.jpg'" class="figure_img
figure_type1 bbb " id="Figure8" />
图
8
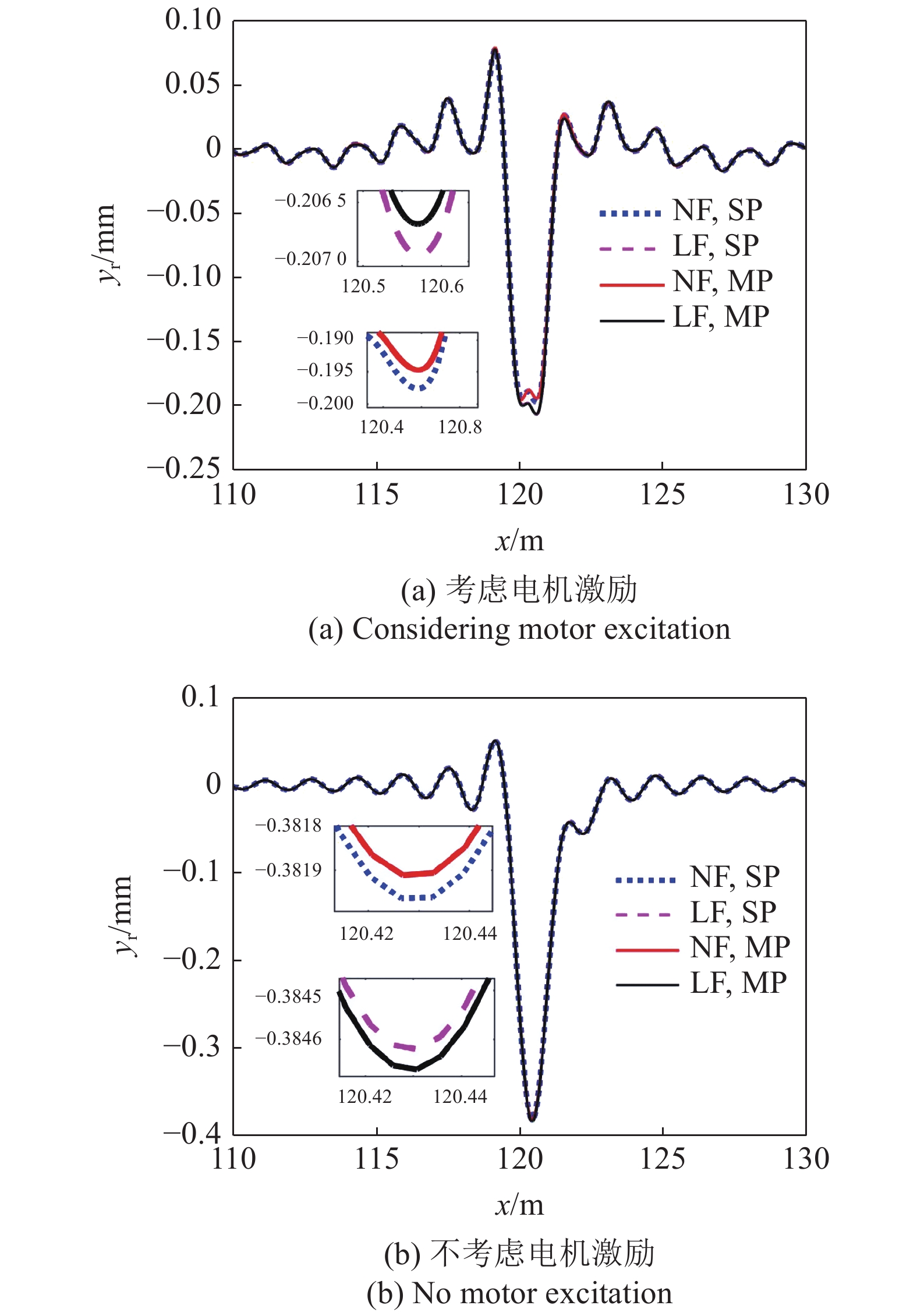
B0 = 0.002 m时非线性地基、多点接触及电机激励对路面响应的影响
Figure
8.
Effects of nonlinear foundation and multi-point contact and motor excitation on road response when B0 = 0.002 m
下载: 全尺寸图片
幻灯片
表
2
路面响应的最大幅值及相对增量
Table
2.
Maximum amplitude of road response and relative difference
table_type2 ">
| B0/m | Motor excitation | NF | LF | Difference between NF and LF | |||||||
| yr(SP)/m | yr(MP)/m | difference | yr(SP)/m | yr(MP)/m | difference | SP | MP | ||||
| 0.02 | √ | 2.468 6 × 10?4 | 2.302 2 × 10?4 | ?6.74% | 2.593 3 × 10?4 | 2.580 6 × 10?4 | ?0.49% | ?4.81% | ?10.79% | ||
| × | 4.205 0 × 10?4 | 4.199 6 × 10?4 | ?0.13% | 4.426 7 × 10?4 | 4.430 9 × 10?4 | 0.09% | ?5.01% | ?5.22% | |||
| difference | 41.29% | 45.18% | ? | 41.42% | 41.76% | ? | ? | ? | |||
| 0.002 | √ | 1.976 6 × 10?4 | 1.957 3 × 10?4 | ?0.98% | 2.069 5 × 10?4 | 2.066 9 × 10?4 | ?0.13% | ?4.49% | ?5.30% | ||
| × | 3.819 7 × 10?4 | 3.819 1 × 10?4 | ?0.02% | 3.846 2 × 10?4 | 3.846 6 × 10?4 | 0.01% | ?0.69% | ?0.71% | |||
| difference | 48.25% | 48.75% | ? | 46.19% | 46.27% | ? | ? | ? | |||
下载: 导出CSV
|显示表格
由图7和图8及表2可知:
(1)胎路多点接触相比于单点接触, 路面响应的最大幅值都有所降低, 且非线性地基与线性地基的变化规律一致. 其中, B0 = 0.02 m时, 考虑电机激励与不考虑电机激励时, 非线性地基的多点接触相比于单点接触, 路面响应最大降幅分别为6.74%和0.13%, B0 = 0.002 m时, 最大降幅分别为0.98%和0.02%. 线性地基的最大降幅都小于0.49%;
(2)非线性地基相比于线性地基, 路面响应的最大幅值都减小, 且多点接触与单点接触的影响规律相似. 但非线性与线性地基的多点接触对路面响应的影响大于单点接触, 其中, B0 = 0.02 m和0.002 m时, 多点接触的最大降幅分别为10.79%和5.30%, 相应的单点接触分别为5.01%和4.49%. 说明路面越粗糙, 非线性地基及线性地基对路面响应的影响增大, 尤其是多点接触的影响更为显著;
(3)考虑电机激励相比于不考虑电机激励, 路面响应的最大幅值明显增大, 其中, B0 = 0.02 m和0.002 m时, 考虑电机激励相比于不考虑电机激励, 非线性地基、多点接触的最大增幅分别为45.18%和48.75%. 非线性地基的单点接触及线性地基都具有相似影响规律. 说明路面较为平滑时, 电机激励的影响更为显著.
3.2
非线性地基、多点接触及电机激励对车辆响应的影响
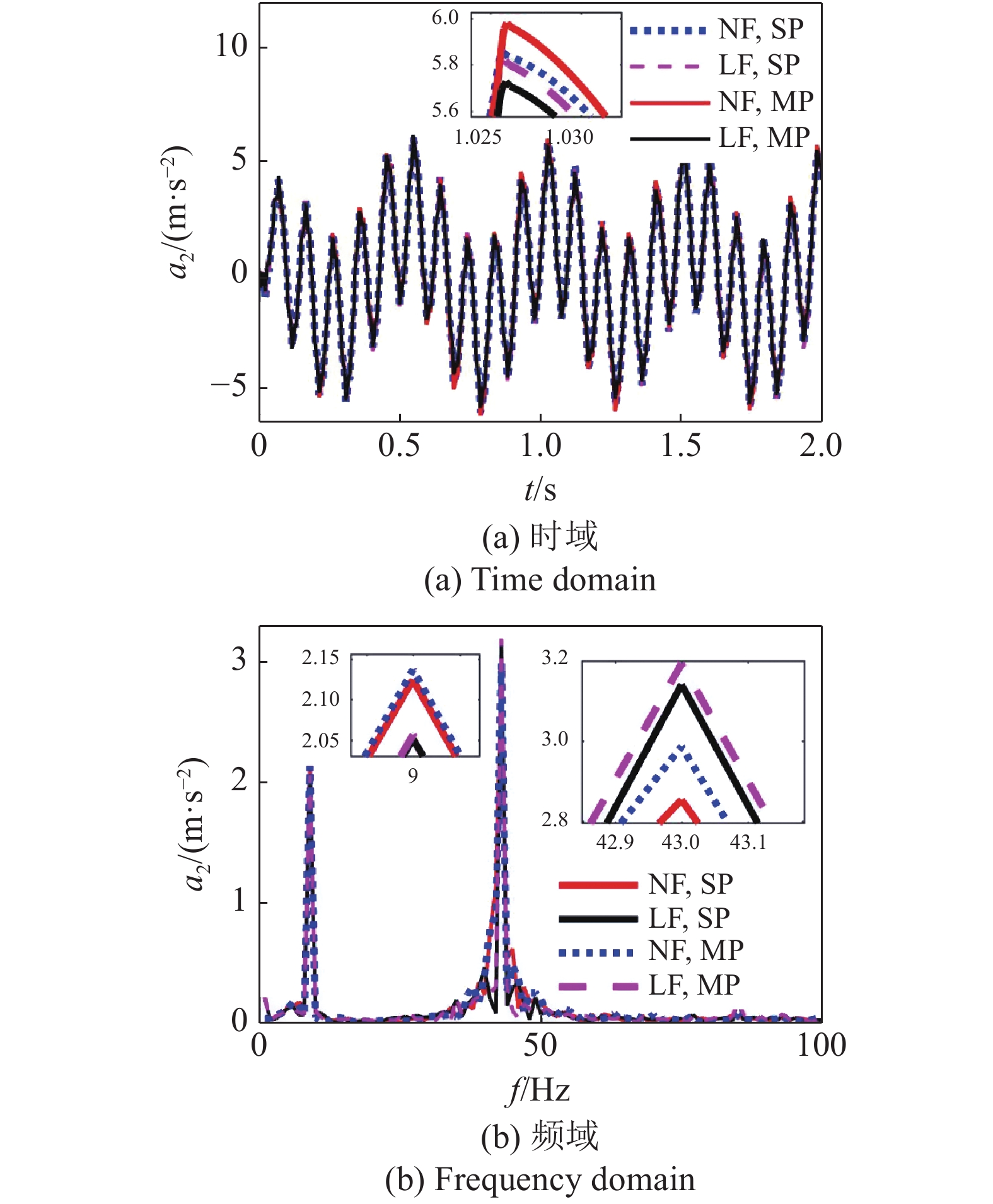
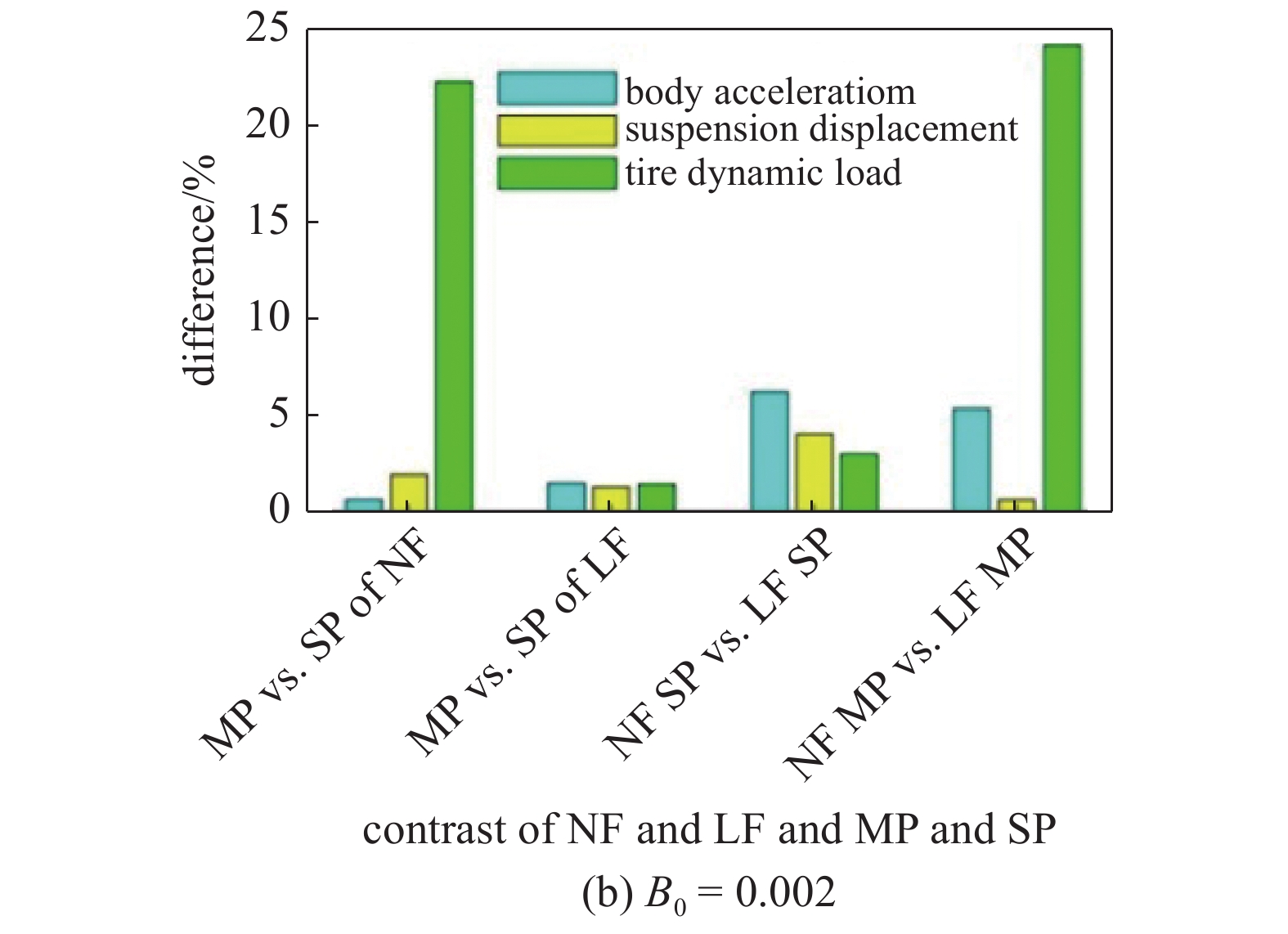
限于篇幅, 论文仅列出路面不平顺幅值B0 = 0.02 m且考虑电机激励时, 非线性地基及多点接触对车辆响应指标的影响, 如图9 ~ 图11示. 图12为B0 = 0.02 m和0.002 m时, 车辆响应指标的相对增量.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-239-9.jpg'" class="figure_img
figure_type1 bbb " id="Figure9" />
图
9
非线性地基及多点接触对车身加速度的影响
Figure
9.
Effects of nonlinear foundation and multi-point contact on acceleration of vehicle body
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-239-11.jpg'" class="figure_img
figure_type1 bbb " id="Figure11" />
图
11
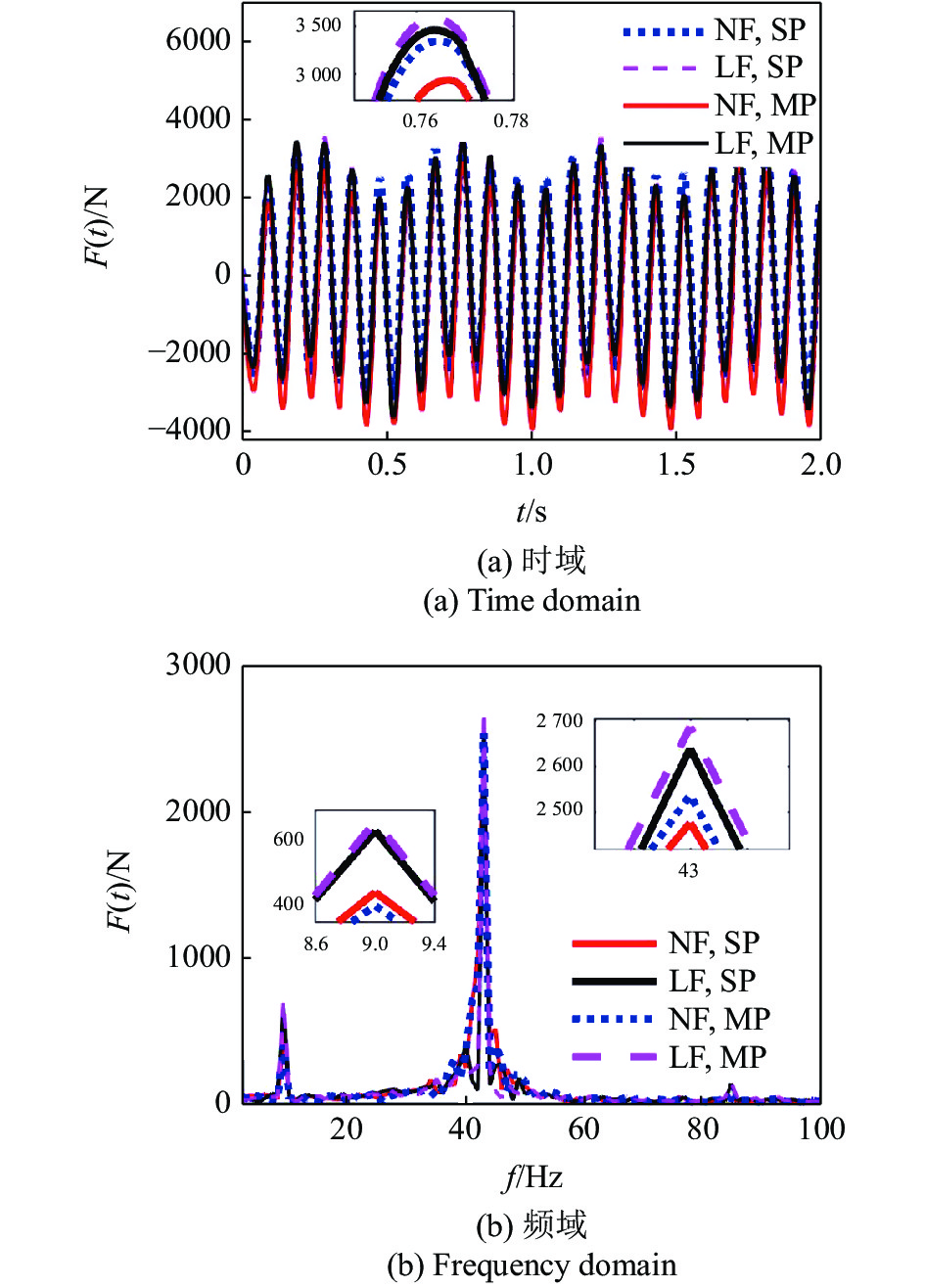
非线性地基及多点接触对轮胎动载荷的影响
Figure
11.
Effects of nonlinear foundation and multi-point contact on tire dynamic load
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-239-12.jpg'" class="figure_img
figure_type1 bbb " id="Figure12" />
图
12
非线性地基及多点接触对车辆响应的相对差别
Figure
12.
Relative differences of nonlinear foundation and multi-point contact on vehicle response
下载: 全尺寸图片
幻灯片
由图9 ~ 图12可见:
(1)从多点接触对车辆响应的影响看, 多点接触相比于单点接触, 车辆响应指标都有所增加, 其中, 轮胎动载荷的影响最大, 考虑电机激励、B0 = 0.02 m和0.002 m时, 非线性地基的最大增幅分别为18.27%和22.31%, 不考虑电机激励时, 最大增幅分别为5.39%和4.76%, 车身加速度和悬架动挠度的影响较小, 最大增幅都小于2.1%. 线性地基与非线性地基的变化趋势相似, 但都低于非线性地基, 最大增量都小于1.5%;
(2)从非线性地基对车辆响应的影响看, 非线性地基的多点接触相比于线性地基, 车辆响应指标都有所增加, 其中, 轮胎动载荷的影响最大, 考虑电机激励、B0 = 0.02 m和0.002 m时, 最大增幅分别为10.19%和24.19%, 车身加速度的影响较小, 最大增幅都小于1.6%;
(3)从频域分析可见, 车辆响应呈现两个明显峰值. 可见, 车身加速度和轮胎动载荷的最大峰值受电机激励的中频(43 Hz)部分的影响较大, 而悬架动挠度受低频(9 Hz)部分的影响较大.
综上可见, 电机激励使得非线性地基及胎路多点接触相比于线性地基及单点接触, 对车辆响应的影响增大, 实际计算时应予以重视.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-239-10.jpg'" class="figure_img
figure_type1 bbb " id="Figure10" />
图
10
非线性地基及多点接触对悬架动挠度的影响
Figure
10.
Effects of nonlinear foundation and multi-point contact on suspension dynamic displacement
下载: 全尺寸图片
幻灯片
3.3
车速对路面和车辆响应的影响
在上述分析的基础上, 本节仅考虑电机激励, 分析不同车速时, 胎路多点接触及非线性地基对车辆及路面响应的影响.
3.3.1
对路面响应的影响
电动汽车在40 ~ 120 km/h行驶速度下, 非线性地基及胎路多点接触对路面响应最大幅值的影响, 如图13示. 为了图示清晰, 图14仅展示车速分别为40, 50和70 km/h时, 路面响应的频域曲线.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-239-13.jpg'" class="figure_img
figure_type1 bbb " id="Figure13" />
图
13
不同车速时非线性地基及胎路多点接触对路面响应最大幅值的影响
Figure
13.
Effects of nonlinear foundation and multi-point contact between tire and road on the maximum amplitude of road response at different speeds
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-239-14.jpg'" class="figure_img
figure_type1 bbb " id="Figure14" />
图
14
不同车速时非线性地基及胎路多点接触对路面响应的频域曲线
Figure
14.
Frequency domain curves of the effects of non-linear foundation and multi-point contact between tire and road on the road response at different speeds
下载: 全尺寸图片
幻灯片
由图13 ~ 图14可知:
(1)不同车速下, 非线性地基相比于线性地基, 路面响应的相对增量随着车速增加而减小, 且多点接触与单点接触变化趋势一致, 其中车速为50 km/h时, 非线性与线性地基的相对增量最大, 为15.8%. 说明中低速行驶时, 非线性地基及多点接触对路面响应的影响应予以关注. 此外, 车速为70 km/h时, 路面不平顺激励频率为1.94 Hz, 接近车身的固有频率, 使得车身加速度增大, 而路面最大位移降低;
(2)从频域响应分析看, 非线性地基与线性地基对路面响应的影响, 随着车速增加而降低, 与图14的影响规律一致; 且路面响应受电机垂向激励的低频部分的影响较大.
综上可见, 电机激励对路面响应的影响最大, 非线性地基的影响次之, 多点接触的影响较小. 尤其是电动汽车中低速行驶在较为粗糙路面时, 电机激励、多点接触及非线性地基对路面响应的综合影响不容忽视.
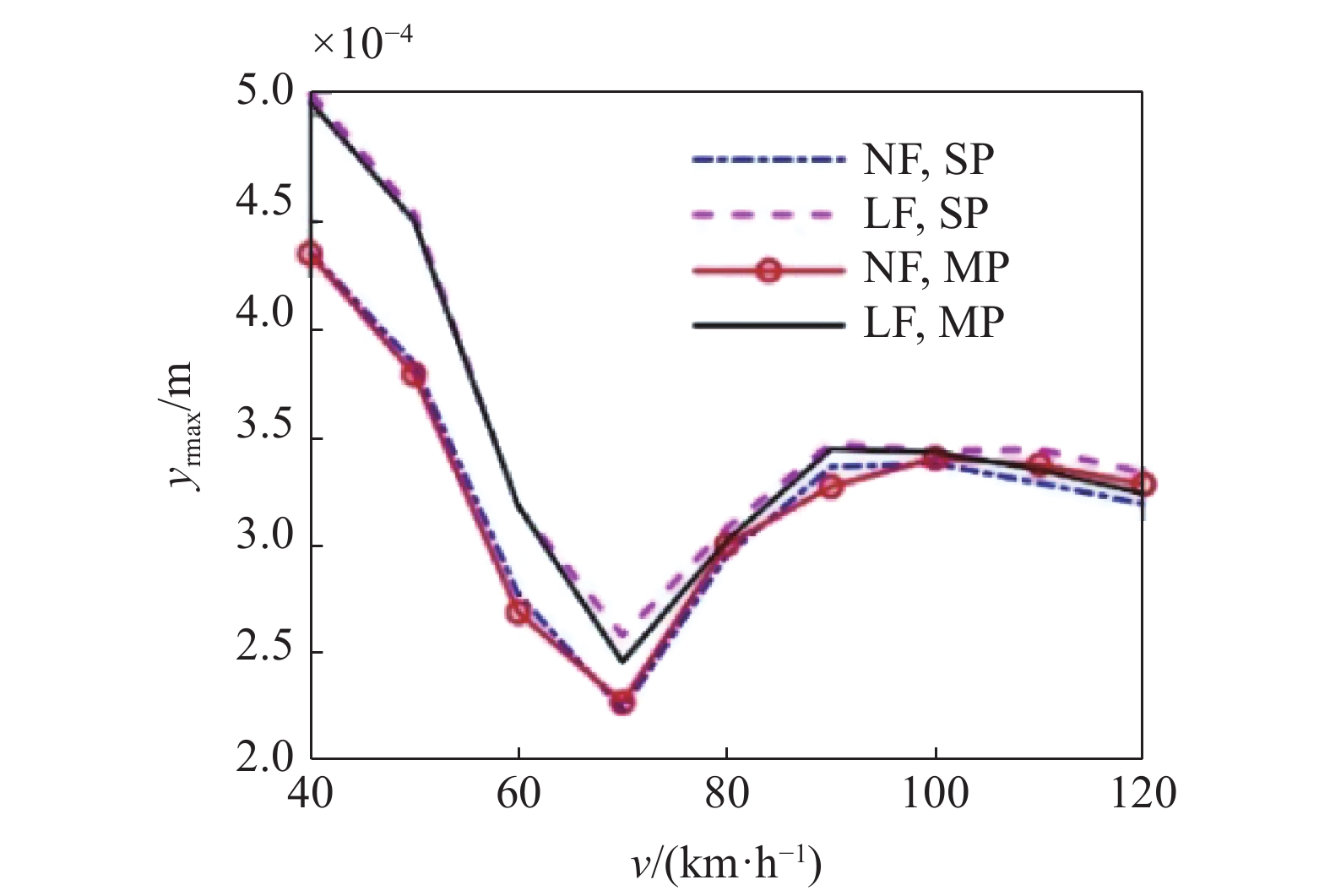
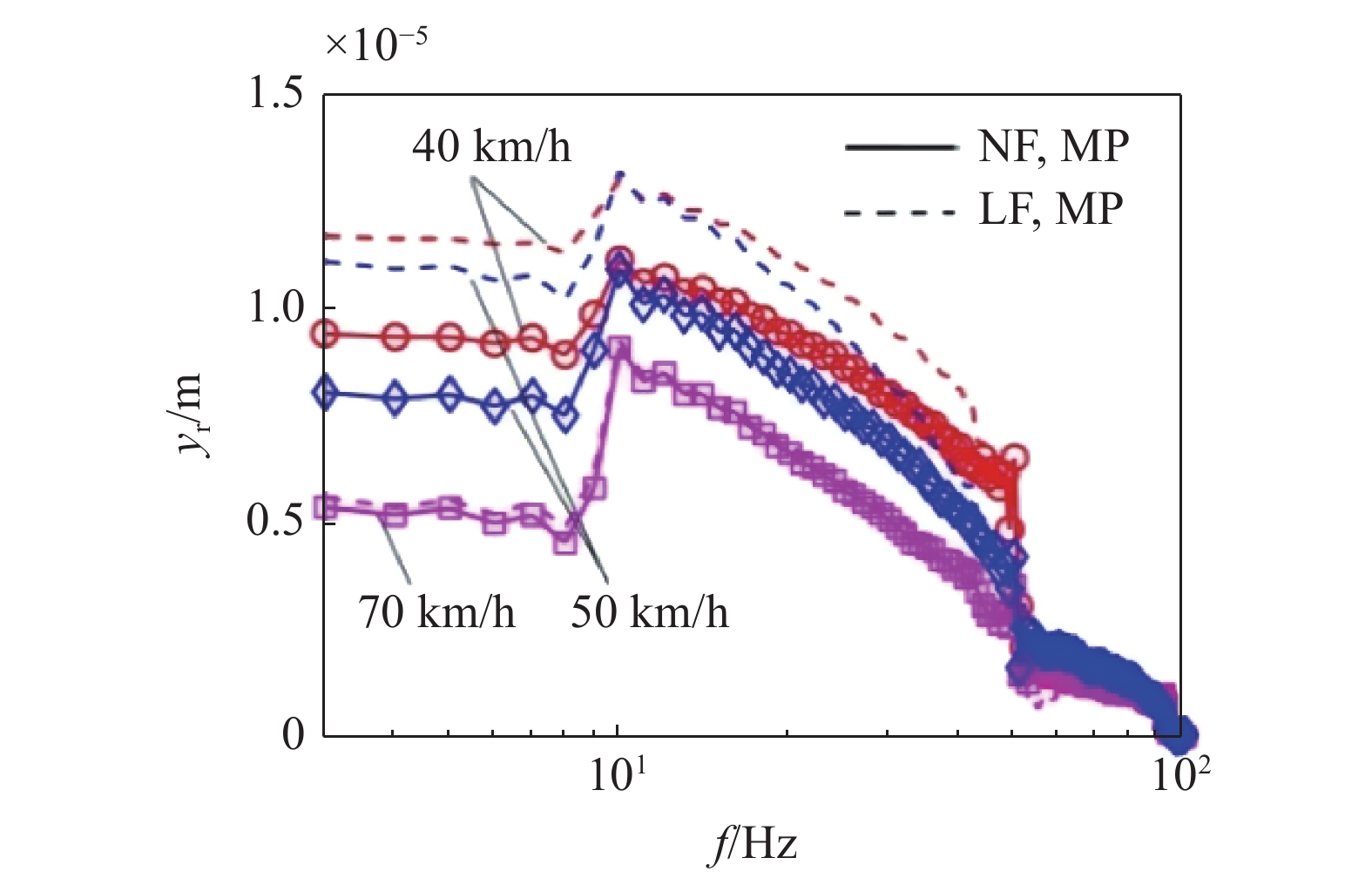
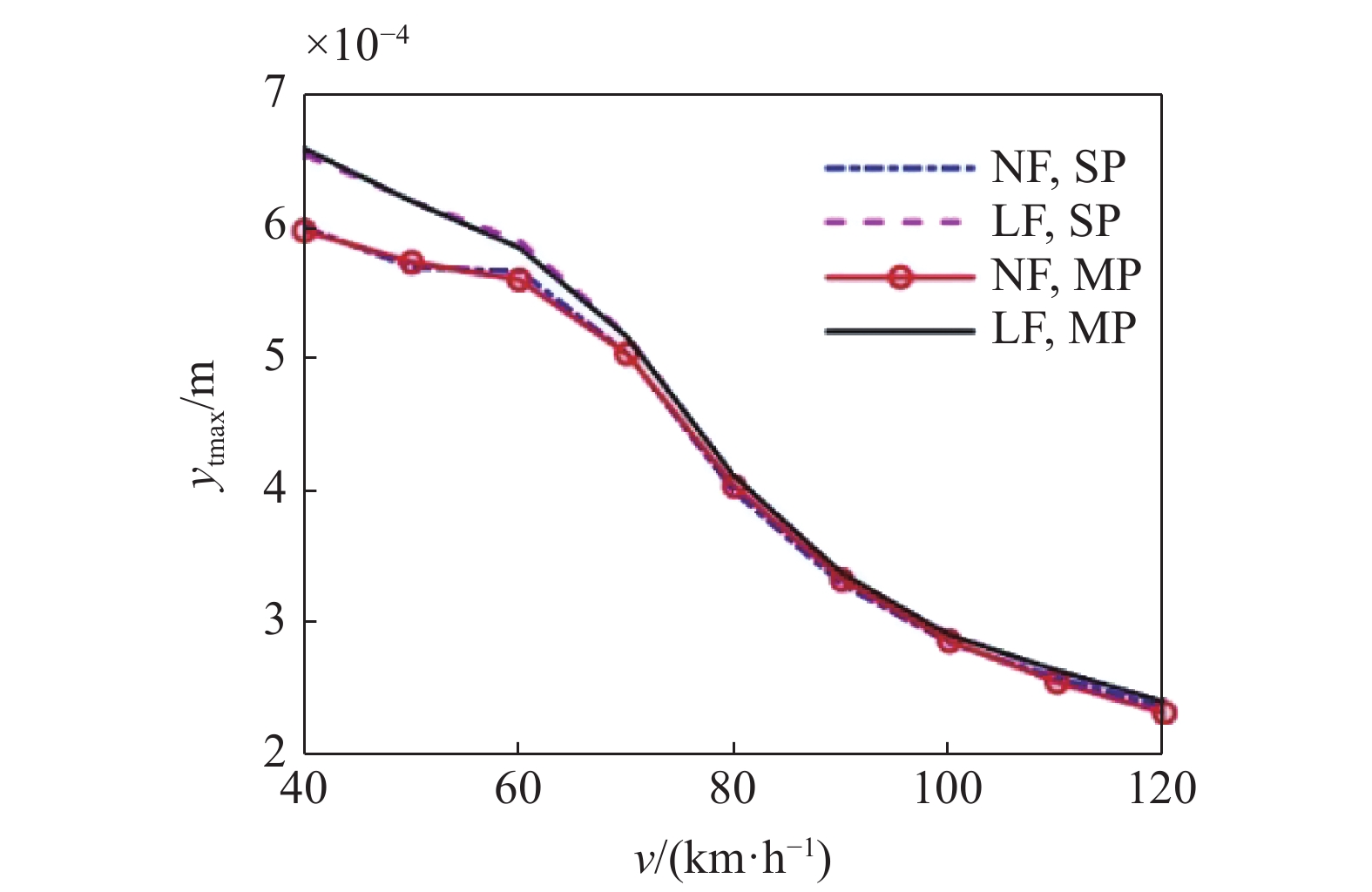
路面二次位移激励受非线性地基、胎路多点接触及电机激励的影响, 如图15所示. 图16为不同速度时, 路面二次位移最大幅值的变化曲线.
由图15 ~ 图16可见:
(1)多点接触相比于单点接触, 对路面二次位移的影响较小, 不同车速下非线性地基的多点接触与单点接触的相对增量都小于2%, 线性地基的变化趋势与之一致;
(2)非线性地基与线性地基对路面二次位移的影响随车速增加而降低, 且多点接触时, 非线性地基相比于线性地基, 路面二次位移最大幅值都有所减小, 其中40 km/h时最大减幅为9.4%, 而60 ~ 120 km/h时都小于5%. 说明中低速行驶时, 非线性地基对路面二次位移的影响较大;
(3)考虑电机激励时, 路面二次位移的最大幅值显著增加, 最大增幅超过60%.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-239-15.jpg'" class="figure_img
figure_type1 bbb " id="Figure15" />
图
15
路面二次位移
Figure
15.
Road secondary displacement
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-239-16.jpg'" class="figure_img
figure_type1 bbb " id="Figure16" />
图
16
不同行驶速度下路面二次位移的最大幅值
Figure
16.
Maximum amplitude of road secondary displacement at different speeds
下载: 全尺寸图片
幻灯片
3.3.2
对车辆响应的影响
车速分别为40 ~ 120 km/h, 考虑电机激励时, 车身加速度、悬架动挠度和轮胎动载荷受非线性地基及多点接触的影响, 如图17. 不同速度下非线性地基及多点接触对车辆响应的最大增幅如图18.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-239-17.jpg'" class="figure_img
figure_type1 bbb " id="Figure17" />
图
17
不同车速下非线性地基及多点接触对车辆响应最大幅值的影响
Figure
17.
Effects of NF and MP on maximum amplitude of vehicle response at different speeds
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-239-18.jpg'" class="figure_img
figure_type1 bbb " id="Figure18" />
图
18
不同车速下非线性地基及多点接触对车辆响应的最大增幅
Figure
18.
Maximum differences of NF and MP on vehicle response at different speeds
下载: 全尺寸图片
幻灯片
由图17 ~ 图18可知:
(1)不同车速下, 多点接触的车辆响应指标的相对增量均大于单点接触. 其中, 轮胎动载荷的相对增量都大于13%, 最大增幅为54.19%, 车身加速度和悬架动挠度的相对增量都小于4%. 而且车速越高, 相对差别越大, 进一步说明限速的必要性;
(2)不同车速下, 非线性地基的车辆响应的相对增幅均大于线性地基. 其中, 轮胎动载荷的影响最大, 高速行驶时最大增幅为43.74%. 悬架动挠度的影响次之, 中低速时最大增幅9.13%, 随着车速的增加, 相对增量减小. 车身加速度的影响较小, 相对增幅都小于5%;
(3)车身加速度、悬架动挠度和轮胎动载荷都在50 ~ 70 km/h区间出现峰值, 主要原因是车辆在该速度区间行驶时, 路面激励与车身固有频率接近, 发生共振所致.
3.4
地基弹性系数对路面和车辆响应的影响
考虑电机激励, 对比分析非线性地基、胎路多点接触(NF, MP)与线性地基、胎路多点接触(LF, MP)下, 地基弹性系数对路面和车辆响应的影响. 分别令kr3和kr1中的一个参数取值不变, 另一个参数分别取8 × 106, 2.4 × 107和4.8 × 107 N·m?2, 地基弹性系数对路面某一位置(x = 120 m处)最大位移的影响如图19所示.
由图19可知, 随着地基线性弹性系数的增大, 路面响应的最大幅值显著降低, 且线性与非线性地基的变化趋势一致, 线性与非线性地基的最大降幅分别为39.8%和38.5%. 地基非线性弹性系数增大时, 线性地基的路面响应不受影响, 非线性地基的路面最大位移略有增加, 最大增幅为1.23%. 可见, 地基线性弹性系数对路面响应的影响大于地基非线性弹性系数. 提升地基弹性系数, 可减小路面最大位移, 对路面使用寿命有利.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-239-19.jpg'" class="figure_img
figure_type1 bbb " id="Figure19" />
图
19
地基弹性系数对路面响应最大幅值的影响
Figure
19.
Effects of foundation elastic coefficient on maximum amplitude of road response
下载: 全尺寸图片
幻灯片
地基弹性系数对车辆响应的最大幅值的影响, 如图20 ~ 图21所示.
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-239-20-1.jpg'" class="figure_img
figure_type1 bbb " id="Figure20-1" />
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-239-20.jpg'" class="figure_img
figure_type1 bbb " id="Figure20" />
图
20
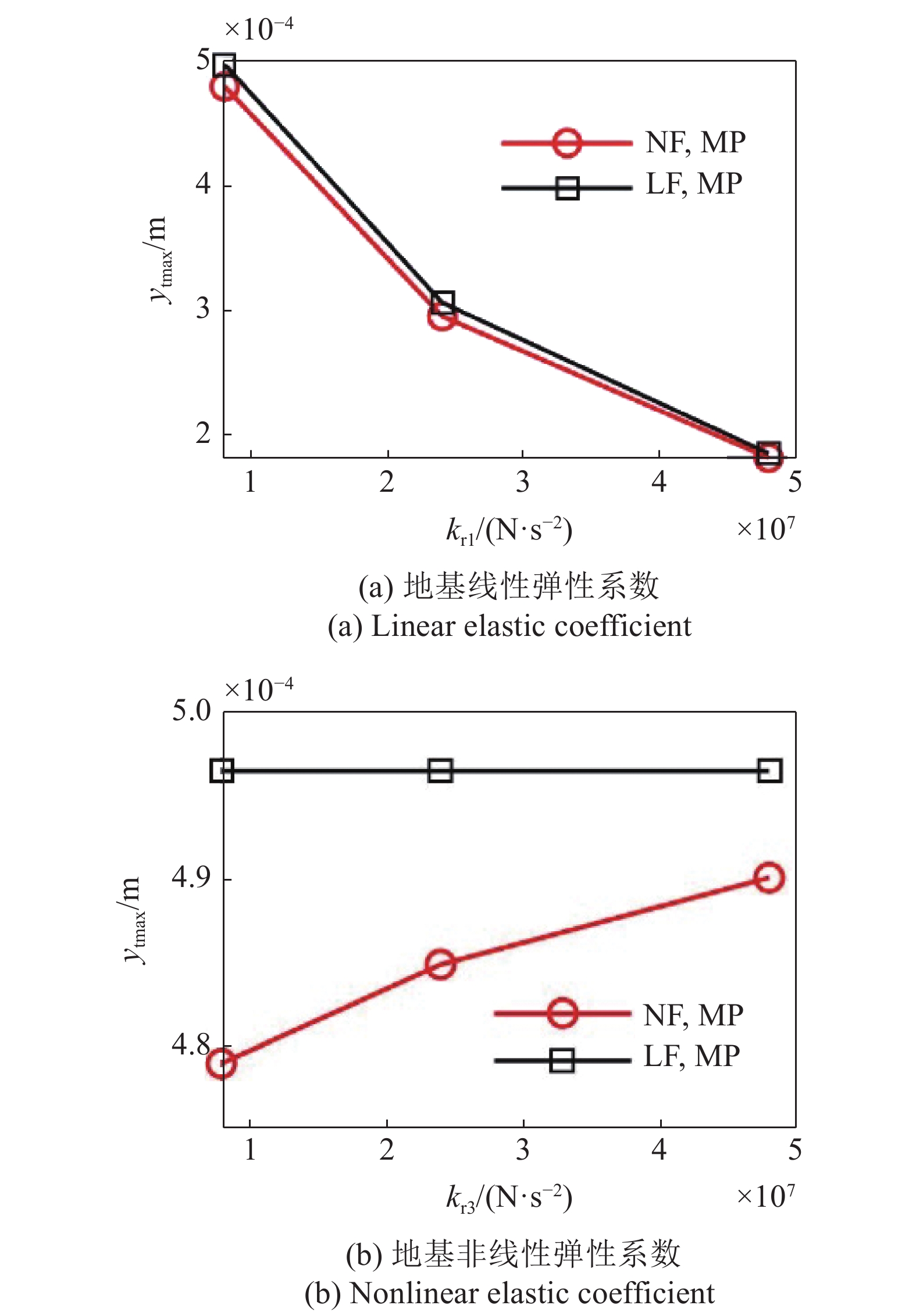
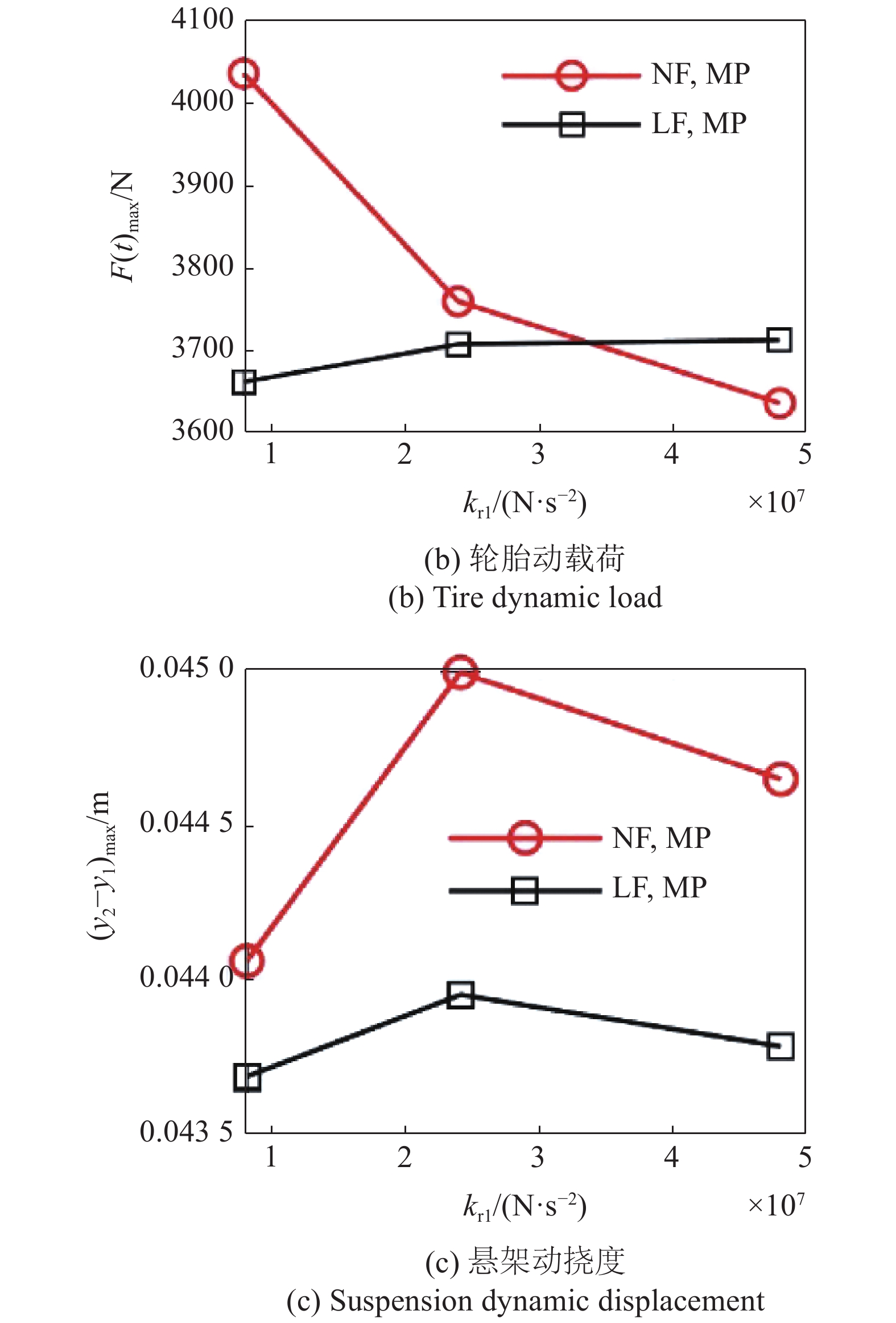
地基线性弹性系数对车辆响应最大幅值的影响
Figure
20.
Effects of foundation linear elastic coefficient on maximum amplitude of vehicle response
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-239-21-1.jpg'" class="figure_img
figure_type1 bbb " id="Figure21-1" />
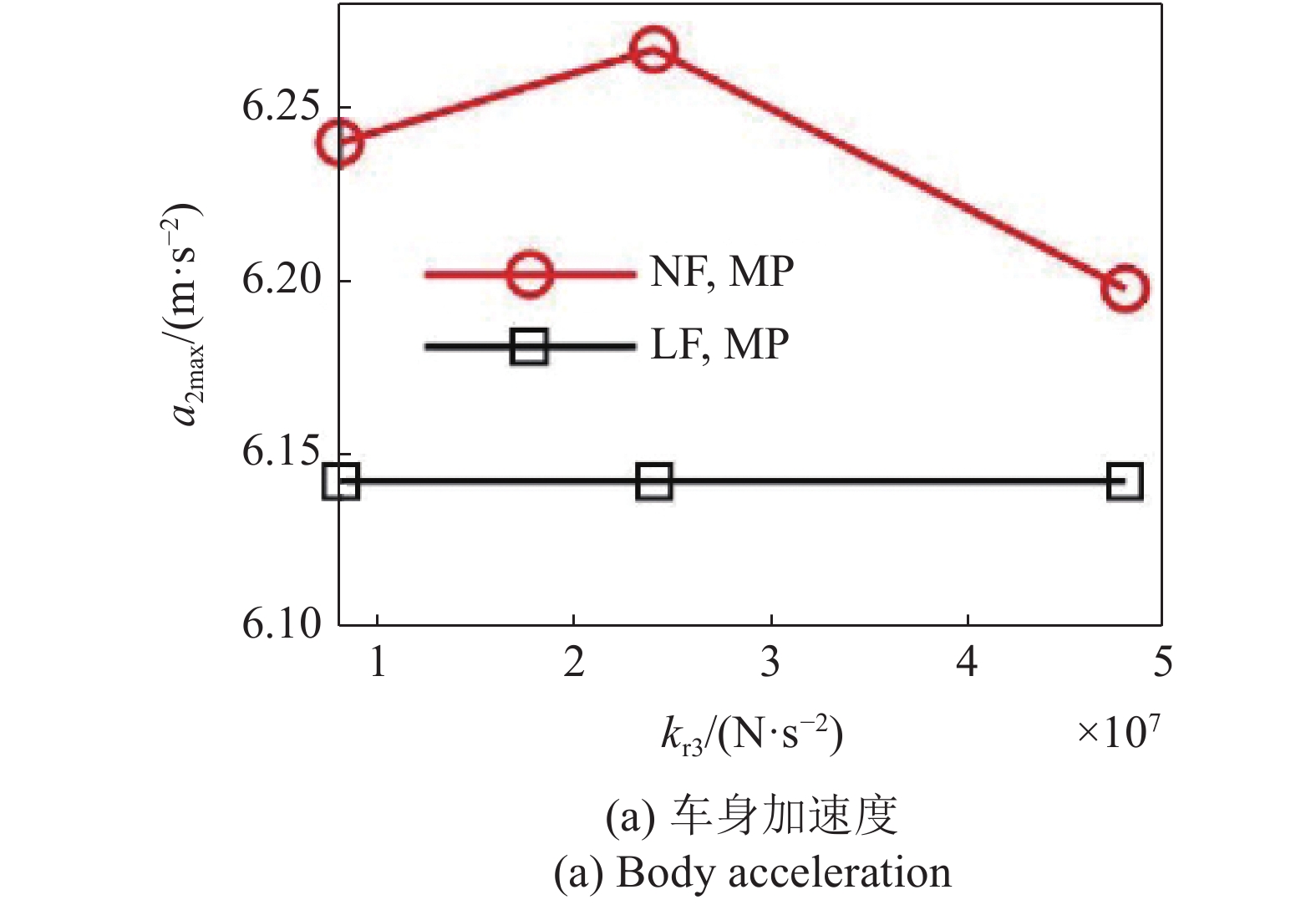
21
地基非线性弹性系数对车辆响应最大幅值影响
21.
Effects of foundation nonlinear elastic coefficient on maximum amplitude of vehicle response
下载: 全尺寸图片
幻灯片
onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/9//lxxb2021-239-21.jpg'" class="figure_img
figure_type1 bbb " id="Figure21" />
图
21
地基非线性弹性系数对车辆响应最大幅值影响(续)
Figure
21.
Effects of foundation nonlinear elastic coefficient on maximum amplitude of vehicle response (continued)
下载: 全尺寸图片
幻灯片
由图20 ~ 图21可见:
(1)从线性弹性系数对车辆响应的影响看, 非线性地基的车辆响应指标的相对增量均大于线性地基, 其中轮胎动载荷的影响最大, 最大增幅为?9.88%, 而车身加速度和悬架动挠度的最大增幅分别为2.63%和2.04%;
(2)从非线性弹性系数的影响看, 非线性地基的车辆响应指标均高于线性地基, 其中, 轮胎动载荷的影响较大, 最大增幅为2.75%, 车身加速度和悬架动挠度的最大增幅分别为?0.68%和1.11%;
(3)地基弹性系数对轮胎动载荷的影响最大, 对悬架动挠度和车身加速度的影响较小. 同时, 增加地基线性弹性系数, 可降低非线性地基的轮胎动载荷, 有利于提升车辆的行驶安全和道路使用寿命.
4.
结论
建立了基于非线性地基及胎路多点接触的电动汽车?路面系统机电耦合动力学模型, 利用Galerkin法推导了非线性地基梁的垂向振动微分方程, 提出了路面截断阶数选取判定指标, 分析了车辆与路面响应受非线性地基、胎路多点接触、电机激励、行驶速度、地基弹性系数的影响规律. 所建模型及研究结果具有较好的理论参考价值, 可为电动汽车垂向动力学分析提供新思路.
(1)推导得到的非线性地基梁非线性项积分的精确表达式, 计算速度快、精度高, 克服了数值积分因积分步长选取影响求解精度的问题以及无量纲变换的繁琐性.
(2)通过判断线弹性地基梁相邻频率间相对增量的最大值, 选取非线性地基?车辆?电机激励耦合系统的路面截断阶数, 简单快捷, 具有可行性.
(3)电机激励对路面响应的影响最大, 非线性地基次之, 多点接触较小. 其中, 电动汽车以中低速行驶在较为粗糙路面时, 电机激励、多点接触及非线性地基对路面响应的综合影响不容忽视.
(4)非线性地基及多点接触对轮胎动载荷的影响最大, 对车身加速度和悬架动挠度的影响较小; 考虑电机激励时, 非线性地基及多点接触对车辆响应的影响增大; 不同车速下, 非线性地基及多点接触对轮胎动载荷的影响最大, 车身加速度和悬架动挠度的影响较小.
(5)地基弹性系数对轮胎动载荷的影响最大, 对悬架动挠度和车身加速度的影响较小. 地基弹性系数对路面响应的影响大于车辆响应. 因此, 增加地基线性弹性系数, 可降低轮胎动载荷及路面响应, 有利于提升车辆的行驶安全和道路使用寿命.
