删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

页岩凝析气藏相平衡的快速准确计算方法

本站小编 Free考研考试/2022-01-01


引 言


随着以煤炭、石油和木柴为代表的传统能源消耗带来的巨量的空气污染日益引起全社会的关注, 天然气作为一种相对较为清洁的能源得到了广泛的重视[1]. 近年来在非常规油气藏勘探和开发技术上的迅猛发展, 使得具有巨大潜在储量但一直得不到有效开发的以页岩气为代表的非常规油气资源成为了投资热点和研究焦点[2]. 中国和北美页岩油气商业开发的成功案例激励了对页岩油气高效开发技术的深入探索, 但经济效益和环境影响上的风险也要求对页岩油气藏中流动和传输机理有更完整彻底的认识[3]. 页岩油气藏中的流体通常为多相多组分复杂流体, 对其各相组成和分布的具有热力学一致性的可靠描述是对其流动和传输行为中物理性质的变化规律进一步分析的必要基础[4]. 对页岩凝析气开发而言, 对其相态转换规律的理解有助于控制相态组成以获得更好的开发效果. 由于页岩油气藏中孔隙尺寸较小, 甚至会有纳米级小孔的广泛分布, 由较强的岩石表面润湿性偏好导致的毛细作用对流体界面性质的影响不容忽视[5]. 因此, 对页岩油气藏中复杂流体的相平衡计算需要建立考虑了毛细作用效应的先进的数值模型, 并设计出快速可靠的算法以应对实际工况中油藏流体包含多达数十种组分的复杂情况. 闪蒸计算是一种预测给定流体混合物的相分配的计算工具, 因其所研究的混合物热力学性质(例如平衡态组成, 密度, 相数, 压力等)在多组分多相流动描述中起着至关重要的作用, 而被视为多组分多相流动模拟中的关键步骤[6]. 在工程上常用的有PT型[7] (恒定压力和温度)和VT型[8] (恒定体积和温度)两种闪蒸计算方法, 而在近几年的学术研究里面, 新兴的VE型[9] (恒定体积和内能)也逐渐受关注. PT型闪蒸计算具有较长的发展历史, 在石油工业中广泛应用, 但VT型闪蒸更适合页岩油气相平衡计算中考虑毛细作用和压力差异的情况, 最近几年在石油工业上有扩大应用的趋势[10]. VE型对变温系统比较方便, 但是因为在工程计算上也有诸多不便, 现在还很少在工业上有应用.

在页岩油气储层中, 由于纳米级孔隙中的空间局限作用以及从微米到纳米的各种规模的孔径分布差异, 储层流体的相平衡往往会产生较大差异[11]. 事实上, 在页岩油气大规模商业开发之前研究者们就已经进行了纳米级多孔介质流体流动的研究, 着眼于该流动现象在化学分离设计, 污染控制或燃料电池中的应用[12]. 在此基础上, 为努力提高页岩油气储层的勘探和开发水平, 着眼于纳米级孔隙中流体的相平衡计算, 并研究相变和相分离现象背后特殊机理已引起了广泛兴趣. 研究发现, 纳米级孔隙中的毛细作用将对受限几何形状中的流体流动的动力学和热力学产生显著作用, 从而改变热力学系统的性质和变化规律[13]. 因此, 需要在页岩油气相平衡计算中基于毛细作用修正热力学分析体系, 从而构造出可靠的闪蒸计算方法以预测相平衡行为.

相平衡计算通常建立在以状态方程为基础的热力学分析上, 在石油工业界中常用的状态方程包括Peng–Robinson 状态方程[14] (P-R状态方程) 和 Soave–Redlich–Kwong[15]状态方程(S-R-K状态方程)两大类, 而其所建立的相平衡热力学分析体系往往具有极强的非线性特征, 对快速准确的相平衡计算带来了挑战. 迭代算法在解决非线性相平衡问题中很流行, 但是相稳定测试和相分离计算在计算上是非常耗时的. 油气田开发的工程实践中, 储藏流体碳氢化合物最多可包含高达数百种物质, 这可能会消耗大量的计算成本, 从而对通过迭代型闪蒸方案进行相平衡建模提出了算法稳定性和能量守恒性的更高要求[16]. 因此, 石油工业界一直在寻求一种可靠且有效的闪蒸计算方法来处理包含大量组分的实际油气藏流体混合物的相平衡分析问题, 从而奠定准确可靠的多组分多相渗流的基础.

Michelsen等[17]于1986年首次提出降秩算法, 并论证了在范德华尔斯混合规则下, 两相闪蒸问题只需要求解3个方程. 该简化方法的中心思想是通过利用二进制交互作用系数(BIC)矩阵的低秩属性来减少非线性方程和未知数的数量. 但是, 该方法假定所有两组分间的相互作用系数均为零, 从而因此严格限制导致了其几乎不适用于实际的储层流体. Jensen和Fredenslund[18]通过引入一种非碳氢化合物组分于实际储层流体中的办法扩展了Michelsen简化法的应用范围. 在该改进算法中, 非碳氢化合物和碳氢化合物之间的非零BIC会减少至只有5个变量, 但该算法的可靠性和适用性仍然受到广泛质疑. 此后, Hendriks[19]提出了广义归约定理, 根据还原变量重新定义了化学势转换后的相平衡问题, 摆脱了对BIC矩阵的限制. 在此基础上, 通过引入截断谱方法, Hendriks和van Bergen[20]使用牛顿?拉夫森迭代法在降维空间中成功模拟了两相平衡. Firoozabadi和Pan[21]基于线性代数的频谱理论, 开发了用于相稳定性测试和相平衡计算的归约模型. 为了进行稳定性分析, 他们发现缩小空间中的切线平面距离(TPD)函数具有更平滑的表面以及唯一的最小值, 这两者都显着提高了其方法的鲁棒性. Li和Johns[22]通过将BIC分解为两部分, 开发了最多包含6个简化参数的归约模型用于快速闪蒸计算. 当所有BIC系数均为零时, 该模型退化为只有3个简化参数的Michelsen简化模型, 或者当非零BIC仅存在于单个组分时, 退化为Jensen和Fredenslund的五简化参数模型. Nichita和Petitfrere[23]设计了具有新型自变量和误差方程组的简化闪蒸公式, 从而简化了Jacobian矩阵的表达式. 与经典的归约方法相比, 它们的方法具有更高的效率, 同时又保持了鲁棒性. Gaganis[24]并没有采用传统的频谱分析方法来分解BIC矩阵, 而是引入了一种新的分解方法以最大程度地降低能量参数的近似误差, 从而可以在给定的精度下以较少的减少变量来执行相平衡计算. 尽管上述简化闪蒸计算方法相较于经典算法显著提升了计算效率, 但是在多组分油藏流体中的相平衡预测准确率始终不尽如人意, 且最近的研究发现简化算法在多组分问题中的加速效果并不明显[25]. 此外, 简化算法在相稳定检测中的表现并不总是准确可靠, 往往错误地刻画了单相区域分界线, 并且会在饱和度等物理量的预测上给出超出物理意义的解.

近年来, 硬件设备和计算能力的飞速提升促使石油工业对油藏模拟提出了更高精度和更大尺度的要求, 而包含千万甚至上亿网格点信息的超大规模油藏模拟器为油气藏流体相平衡算法在鲁棒性和高效性上带来了全新的挑战. 传统的相平衡加速算法无法处理此任务, 研究者将注意力转向了蓬勃发展的人工智能和机器学习技术上. AlexNet在2012年的突破[26]宣布了深度学习时代的开始. 这种技术彻底改变了工业和学术界的各个领域, 包括计算机视觉[27], 自然语言翻译和处理[28], 电子娱乐[29]等, 而很多研究者正在将这种具有深远潜力的新技术应用在石油和天然气工业相关研究中. Vasilyeva等[30]建立了一套优化的深层神经网络, 以了解随机场与储藏关键特征量之间的映射关系, 从而快速计算地下储层的关键特征量以对油藏模拟问题进行粗略的网格逼近. Dang等[31]结合地球化学技术开发了一套深层神经网络, 并以此搭建了一个带状态方程的储层模拟器, 从而可以对低矿化度驱油过程中的不确定性进行评估. 与传统的机器学习方法相比, 深度学习算法由于蕴含了多个隐藏的非线性层可以表征输入特征之间的复杂相关性而在预测准确性和物理一致性上去的了显著进展. 通常, 闪蒸计算中的任务环境是准静态的, 因此经过训练的模型能够捕获特定时间点的分布, 这使得深度学习模型在实际的相平衡计算中成为一种很有希望的选择. 然而, 尽管在该领域中开发基于深度学习的方法的适当性和必要性得到了广泛共识, 但在开发用于加速闪蒸计算的深度学习方法方面仍进行了有限的尝试. 李煜等[7]设计并仔细调试了一个完全连接的深度神经网络, 其选择关键的热力学性质作为输入特征以隐式表示每个组分, 通过训练出的模型代替常规的状态方程表述了输入特征之间的相关热力学规律, 获得了在保证一定预测精度下的计算效率的显著提升. 为了克服有限数量的昂贵实验数据作为训练基准值的问题, Li等[32]改进了深层神经网络结构和相应算法, 以采用NVT型(恒定物质的量、体积和温度)闪蒸计算结果作为训练基准值, 并从两组分问题扩展到了多组分实际储藏流体问题, 且可以考虑更大范围内实际的环境条件. 这些进展已更接近真实的储层复杂流体, 但是所有这些现有的深度学习方法都假设混合物中具有固定的给定数量的组分, 这使得这种模型在广泛的工程实践中往往无用, 因为实际储藏流体具有多变的组分[33]. 因此需要设计一套具有高度自适应性的深度学习算法, 以适应实际页岩油气开发中流体组分和环境参数的多变性和复杂性[34].

本文的结构如图1所示. 基于上述分析, 本工作基于真实气体状态方程, 引入毛细作用构建了具有热力学一致性的NVT型闪蒸计算方法, 通过迭代计算准备了足量数据用于人工智能学习研究, 并通过热力学分析提取了相平衡过程中的关键参数, 设计了高度自适应的深度学习算法和相应的深层神经网络结构, 精细调整了网络参数并选用先进的机器学习技术, 训练出一套可靠稳健的相平衡预测模型, 以期为页岩油气勘探开发中的多组分多相流动过程提供快速准确的相平衡计算结果.



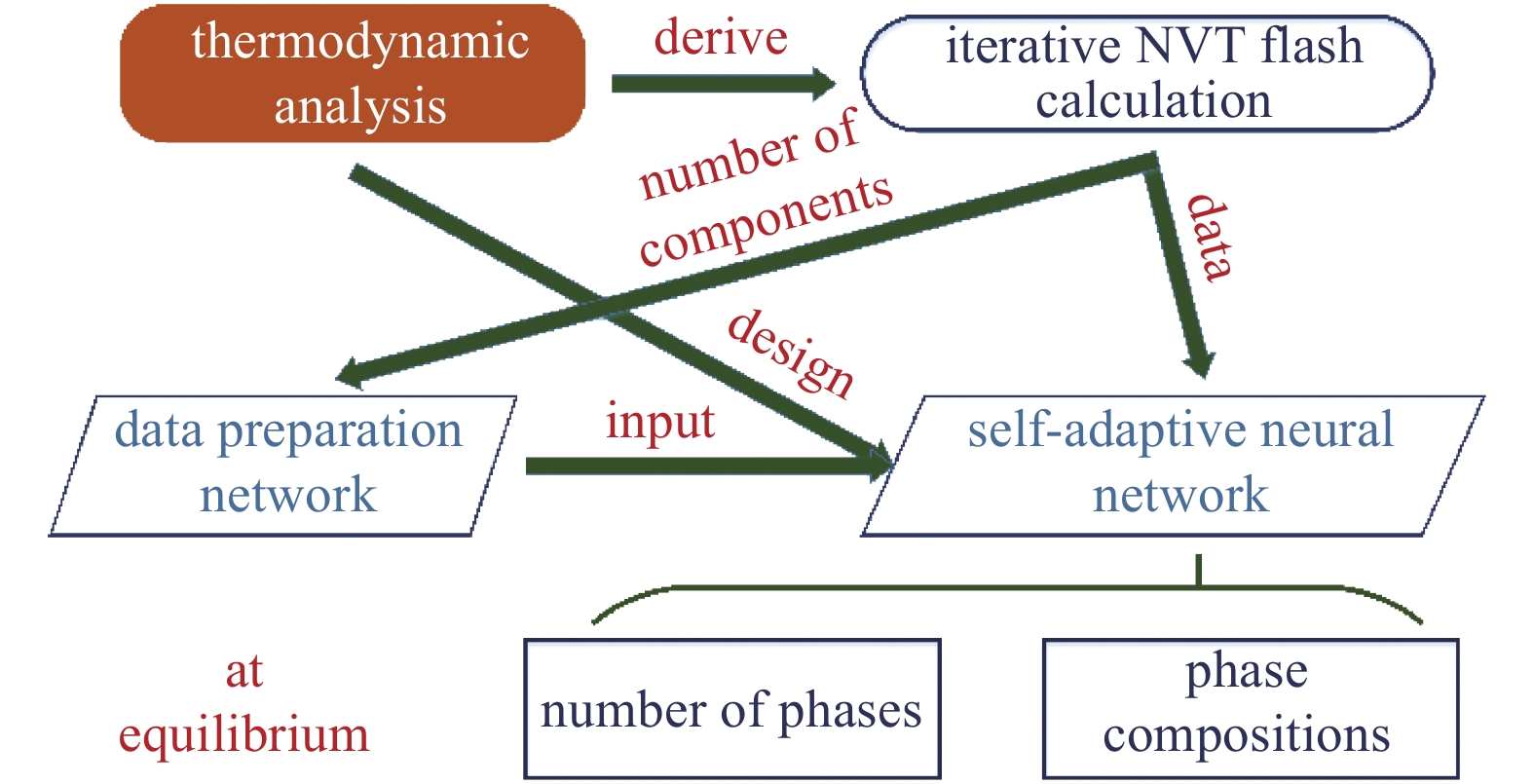onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-229-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
页岩油气相平衡计算体系



Figure
1.
Phase equilibrium calculation scheme for shale gas reservoirs



下载:
全尺寸图片
幻灯片



1.
热力学一致性的NVT型闪蒸计算方法



1.1
基于P-R状态方程的NVT闪蒸计算体系


在NVT型闪蒸计算体系中, 摩尔数和体积通常具有如下守恒性







$$begin{split} & {boldsymbol{N}}^{{
m{G}}}+{boldsymbol{N}}^{{
m{L}}}={boldsymbol{N}}^{{
m{t}}} &{V}^{{
m{G}}}+{V}^{{
m{L}}}={V}^{{
m{t}}} end{split}$$
(1)

式中, $ boldsymbol{N} $为摩尔数, $ V $为体积, 上标G, L和t分别表示气相, 液相和总量. 针对特定相平衡问题, 通常会给定物质的总量${boldsymbol{N}}^{{
m{t}}}={left[{N}_{1}^{{
m{t}}},{N}_{2}^{{
m{t}}},cdots ,{N}_{M}^{{
m{t}}}
ight]}^{mathrm{T}}$, 总体积${V}^{{
m{t}}}$和环境温度$ T $作为条件参数, 其中$ M $表示流体总的组分数目. NVT闪蒸算法和NPT (恒定物质的量、压力和温度)闪蒸算法之间在热力学原理上的基本差异是前者最小化了亥姆霍兹自由能而不是吉布斯自由能, 而气液两相系统的亥姆霍兹自由能由下式给出







$$ F=fleft({boldsymbol{n}}^{{
m{G}}}
ight){V}^{{
m{G}}}+fleft({boldsymbol{n}}^{{
m{L}}}
ight){V}^{{
m{L}}} $$
(2)

式中, $ F $为亥姆霍兹自由能, $ f $为亥姆霍兹自由能密度, $ boldsymbol{n} $为摩尔密度. $ f $随$ boldsymbol{n} $的变化可以由下式计算得到







$$ fleft(boldsymbol{n}
ight)={f}^{text{ideal}}left(boldsymbol{n}
ight)+{f}^{text{repulsion}}left(boldsymbol{n}
ight)+{f}^{text{attraction}}left(boldsymbol{n}
ight) $$
(3)

式中各项基于Peng?Robinson状态方程可得到如下的求解式







$$ {f}^{text{ideal}}left(boldsymbol{n}
ight)=RTsumnolimits_{i=1}^{M}{n}_{i}left({
m{ln}}{n}_{i}-1
ight);;;;;;;;;;;;;;;;; $$
(4)







$$ {f}^{text{repulsion}}left(boldsymbol{n}
ight)=-nRT{
m{ln}}left(1-bn
ight) ;;;;;;;;;;;;;;;;;;;$$
(5)







$$ {f}^{text{attraction}}left(boldsymbol{n}
ight)=frac{aleft(T
ight)n}{2sqrt{2}b}{
m{ln}}left[frac{1+left(1-sqrt{2}
ight)bn}{1+left(1+sqrt{2}
ight)bn}
ight] $$
(6)

在上述方程组中, $ aleft(T
ight) $是Peng?Robinson状态方程中随温度变化的能量系数







$$ aleft(T
ight)=sumnolimits_{i=1}^{M}sumnolimits_{j=1}^{M}{x}_{i}{x}_{j}{left({a}_{i}{a}_{j}
ight)}^{1∕2}left(1-{k}_{ij}
ight) $$
(7)

$ b $是体积系数







$$ b=sumnolimits_{i=1}^{M}{x}_{i}{b}_{i} $$
(8)

式中, 下标$ i $表征第$ i $组分, 而每一组份的能量系数和体积系数可以表示为







$$ {a}_{i}=0.457;24frac{{R}^{2}{T}_{c,i}^{2}}{{P}_{c,i}}{left[1+{m}_{i}left(1-sqrt{{T}_{r,i}}
ight)
ight]}^{2} $$
(9)







$$ {b}_{i}=0.077;80frac{R{T}_{{c}_{i}}}{{P}_{c,i}}qquadqquadqquadqquad $$
(10)

式中, $ {x}_{i} $表示第$ i $组分的摩尔分数, $ {P}_{c} $和$ {T}_{c} $表示临界压力和临界温度, $ {k}_{ij} $表示第$ i $组分和第$ j $组分之间的相互作用系数.


1.2
基于扩散界面法的动力学模型


从热力学第一定律可以推出







$$ begin{array}{c}dfrac{mathrm{d}(U+E)}{mathrm{d}t}=dfrac{mathrm{d}W}{mathrm{d}t}+dfrac{mathrm{d}Q}{mathrm{d}t}end{array} $$
(11)

式中, $ U $表示系统的内能, $ E $表示系统的动能, $ W $表示对系统的做功, $ Q $表示传入系统的热量. 总熵$ S $可以分为两部分, 即系统的熵$ {S}_{text{sys}} $和周围环境的熵$ {S}_{text{surr}} $. 根据熵和热量之间的相互关系







$$ begin{array}{c}mathrm{d}{S}_{text{surr}}=-dfrac{mathrm{d}Q}{T}end{array} $$
(12)

并结合式(11)以及吉布斯关系式







$$ U=F+T{S}_{text{sys}} $$
(13)

可以推导出如下关系式







$$ begin{split}dfrac{mathrm{d}S}{mathrm{d}t} =&dfrac{mathrm{d}{S}_{text{sys}}}{mathrm{d}t}+dfrac{mathrm{d}{S}_{text{surr}}}{mathrm{d}t}=dfrac{mathrm{d}{S}_{text{sys}}}{mathrm{d}t}-dfrac{1}{T}dfrac{mathrm{d}Q}{mathrm{d}t}= & -dfrac{1}{T}dfrac{mathrm{d}(F+E)}{mathrm{d}t}+dfrac{1}{T}dfrac{mathrm{d}W}{mathrm{d}t}end{split} $$
(14)

应用雷诺输运定理和高斯散度定理, 可以得到







$$ begin{split}&frac{mathrm{d}S}{mathrm{d}t} =underset{Vleft(t
ight)}{int }frac{partial s}{partial t}mathrm{d}V+underset{Vleft(t
ight)}{int }nabla left({{boldsymbol{u}}}s
ight)mathrm{d}V& frac{mathrm{d}F}{mathrm{d}t} =underset{Vleft(t
ight)}{int }frac{partial f}{partial t}mathrm{d}V+underset{Vleft(t
ight)}{int }nabla left({{boldsymbol{u}}}f
ight)mathrm{d}Vend{split} $$
(15)

上式中，s, f分别表示熵密度和自由能密度，u表示速度张量.

对两相系统而言, 可以任意选择任一相的体积和摩尔组成作为主要变量, 而另一相的对应物可以通过约束条件(1)进行计算. 例如, 可以选取气相的摩尔组成${{{boldsymbol{N}}}}^{{
m{G}}}$和体积${V}^{{
m{G}}}$为主要变量, 构建如下表达式







$$ frac{partial Fleft({{{boldsymbol{N}}}}^{
m{G}},{V}^{
m{G}}
ight)}{partial {N}_{i}^{
m{G}}}={mu }_{i}left({boldsymbol{n}}^{
m{G}}
ight)-{mu }_{i}left({boldsymbol{n}}^{{
m{L}}}
ight)={mu }_{i}^{
m{G}}-{mu }_{i}^{{
m{L}}} $$
(16)







$$ frac{partial Fleft({{{boldsymbol{N}}}}^{
m{G}},{V}^{
m{G}}
ight)}{partial {V}^{
m{G}}}=Pleft({boldsymbol{n}}^{{
m{L}}}
ight)-Pleft({boldsymbol{n}}^{
m{G}}
ight)={P}^{{
m{L}}}-{P}^{
m{G}} $$
(17)

式中, $ {mu }_{i} $表征第$ i $组分的化学势. 因此, 通过链式法则, 可以构建亥姆霍兹自由能随时间的演进格式为







$$begin{split} frac{partial F}{partial t}=&sumnolimits_{i=1}^{M}frac{partial F}{partial {N}_{i}^{
m{G}}}frac{partial {N}_{i}^{
m{G}}}{partial t}+frac{partial F}{partial {V}^{
m{G}}}frac{partial {V}^{
m{G}}}{partial t}= &sumnolimits_{i=1}^{M}left({mu }_{i}^{
m{G}}-{mu }_{i}^{
m{L}}
ight)frac{partial {N}_{i}^{
m{G}}}{partial t}+left({p}^{
m{L}}-{p}^{
m{G}}
ight)frac{partial {V}^{
m{G}}}{partial t} end{split}$$
(18)

根据昂萨格倒易关系, 可以推出上式中物质的量和熵随时间的变化关系为







$$ begin{split}dfrac{partial {N}_{i}^{
m{G}}}{partial t}=&sumnolimits_{j=1}^{M}{psi }_{i,j}left[{mu }_{j}left({boldsymbol{n}}^{
m{L}}
ight)-{mu }_{j}left({boldsymbol{n}}^{
m{G}}
ight)
ight] +&{psi }_{i,M+1}({p}_{{
m{G}}}-{p}_{{
m{L}}}-{p}_{{
m{c}}})end{split}quad $$
(19)







$$ begin{split}frac{partial {V}^{
m{G}}}{partial t}=&sumnolimits_{j=1}^{M}{psi }_{M+1,j}left[{mu }_{j}left({boldsymbol{n}}^{
m{L}}
ight)-{mu }_{j}left({boldsymbol{n}}^{
m{G}}
ight)
ight] +&{psi }_{M+1,M+1}({p}_{{
m{G}}}-{p}_{{
m{L}}}-{p}_{{
m{c}}})end{split} $$
(20)

式中, $ boldsymbol{varPsi }={left({psi }_{i,j}
ight)}_{i,j=1}^{M+1} $为昂萨格系数矩阵. 为了保证计算效率和准确性, 需要构建与热力学第二定律相一致的能量稳定的动力学系统, 即要保证总亥姆霍兹自由能的耗散特性, 因此需要构建正定的昂萨格系数矩阵. 最简单的办法是设计如下的对角正定矩阵







$$ begin{array}{c}{psi }_{i,i}=dfrac{{D}_{i}{N}_{i}^{{
m{t}}}}{RT},;;i=1,2,cdots ,M;;;;;;end{array} $$
(21)







$$ {psi }_{M+1,M+1}=frac{{C}_{{
m{V}}}^{{
m{G}}}{C}_{{
m{V}}}^{{
m{L}}}{V}^{{
m{t}}}}{{C}_{{
m{V}}}^{{
m{L}}}{p}_{{
m{G}}}+{C}_{{
m{V}}}^{{
m{G}}}{p}_{{
m{L}}}} $$
(22)

并构建物质的量和体积随时间的演进格式为







$$ begin{array}{c}dfrac{partial {N}_{i}^{
m{G}}}{partial t}=dfrac{{D}_{i}{N}_{i}^{{
m{t}}}}{RT}left[{mu }_{i}
ight({boldsymbol{n}}^{
m{L}})-{mu }_{i}({boldsymbol{n}}^{
m{G}}left)
ight],;;i=1,2,cdots ,M end{array} qquad;;;;$$
(23)







$$ begin{array}{c}dfrac{partial {V}^{
m{G}}}{partial t}=dfrac{{C}_{{
m{V}}}^{
m{G}}{C}_{{
m{V}}}^{
m{L}}{V}^{{
m{t}}}}{{C}_{{
m{V}}}^{
m{L}}{p}_{{
m{G}}}+{C}_{{
m{V}}}^{
m{G}}{p}_{{
m{L}}}}({p}_{{
m{G}}}-{p}_{{
m{L}}}-{p}_{{
m{c}}})end{array}qquadqquad;;;; $$
(24)

式中, ${p}_{{
m{c}}}$表示毛细压力.


1.3
考虑毛细作用的闪蒸计算模型


毛细管压力由润湿和非润湿相之间的压差确定, 即${p}_{{
m{c}}}={p}_{{
m{n}}}-{p}_{{
m{w}}}$. 如果由毛细管力所做的功为正, 则两相之间的界面将移向非润湿相, 从而压缩其体积; 否则界面会移向润湿阶段, 这将导致非润湿阶段膨胀. 毛细作用力在一定的单位时间内所做的功可由下式给出







$$begin{split} frac{mathrm{d}W}{mathrm{d}t}=&-{p}_{
m{n}}frac{mathrm{d}{V}_{
m{n}}}{mathrm{d}t}-{p}_{
m{w}}frac{mathrm{d}{V}_{
m{w}}}{mathrm{d}t} =&-{p}_{
m{n}}frac{mathrm{d}{V}_{
m{n}}}{mathrm{d}t}+{p}_{
m{w}}frac{mathrm{d}{V}_{
m{n}}}{mathrm{d}t}=-{p}_{
m{c}}frac{mathrm{d}{V}_{
m{n}}}{mathrm{d}t}end{split}$$
(25)

式中假定毛细压力沿两相界面恒定不变. 计算毛细压力的公式有很多, 闪蒸计算中常用的一个是杨?拉普拉斯方程







$$ begin{array}{c}{p}_{{
m{c}}}=dfrac{2sigma mathrm{c}mathrm{o}mathrm{s}theta }{r}end{array} $$
(26)

式中$ sigma $表示表面张力, 可由下述Weinaug?Katz关系式求得







$$ begin{array}{c}sigma ={left[displaystylesumnolimits_{i=1}^{M}left[boldsymbol{P}{]}_{i}
ight({boldsymbol{n}}_{i,{
m{w}}}-{boldsymbol{n}}_{i,{
m{n}}})
ight]}^{4}end{array} $$
(27)

亥姆霍兹自由能密度的凸分裂是热力学分析中一种通用的方法, 以确保所构建的离散形式具有无条件的能量稳定性. 类似的, 化学势也可以假定为具有两个组成$ {mu }_{i}^{mathrm{c}mathrm{o}mathrm{n}mathrm{v}mathrm{e}mathrm{x}}left(boldsymbol{n}
ight) $和$ {mu }_{i}^{mathrm{c}mathrm{o}mathrm{n}mathrm{c}mathrm{a}mathrm{v}mathrm{e}}left(boldsymbol{n}
ight) $, 可分别计算为







$$ begin{array}{cc}{mu }_{i}^{mathrm{c}mathrm{o}mathrm{n}mathrm{v}mathrm{e}mathrm{x}}left(boldsymbol{n}
ight) =(1+lambda )dfrac{partial {f}^{mathrm{i}mathrm{d}mathrm{e}mathrm{a}mathrm{l}}}{partial {n}_{i}}+dfrac{partial {f}^{mathrm{r}mathrm{e}mathrm{p}mathrm{u}mathrm{l}mathrm{s}mathrm{i}mathrm{o}mathrm{n}}}{partial {n}_{i}}end{array} $$
(28)







$$ begin{array}{cc}{mu }_{i}^{mathrm{c}mathrm{o}mathrm{n}mathrm{c}mathrm{a}mathrm{v}mathrm{e}}left(boldsymbol{n}
ight) =dfrac{partial {f}^{mathrm{a}mathrm{t}mathrm{t}mathrm{r}mathrm{a}mathrm{c}mathrm{t}mathrm{i}mathrm{o}mathrm{n}}}{partial {n}_{i}}-lambda dfrac{partial {f}^{mathrm{i}mathrm{d}mathrm{e}mathrm{a}mathrm{l}}}{partial {n}_{i}};;;;;;;;end{array} $$
(29)

综合考虑热力学一致性和编程计算的简便性, 本算法选用半隐格式构造演化方案, 即对化学式和亥姆霍兹自由能密度的凸组分采用隐式格式, 而对凹组分采用显示格式. 据此, 可以推导出摩尔的量和体积的离散格式为







$$ begin{split}dfrac{{N}_{i,1}^{k+1}-{N}_{i,1}^{k}}{delta t} =&sumnolimits_{j=1}^{M}{psi }_{i,j}left({mu }_{j,2}^{k+1}-{mu }_{j,1}^{k+1}
ight)+&{psi }_{i,M+1}({p}_{1}^{k+1}-{p}_{2}^{k+1}-{p}_{{
m{c}}}^{k+1})quadend{split} $$
(30)







$$ begin{split}frac{{V}_{1}^{k+1}-{V}_{1}^{k}}{delta t} =&sumnolimits_{j=1}^{M}{psi }_{M+1,j}({mu }_{j,2}^{k+1}-{mu }_{j,1}^{k+1})+&{psi }_{M+1,M+1}({p}_{1}^{k+1}-{p}_{2}^{k+1}-{p}_{{
m{c}}}^{k+1})end{split} $$
(31)

式中化学势的半隐格式可以写为







$$ begin{array}{cc}{mu }_{j,1}^{k+1} ={mu }_{j}^{mathrm{c}mathrm{o}boldsymbol{n}mathrm{v}mathrm{e}mathrm{x}}left({boldsymbol{n}}_{1}^{k+1}
ight)+{mu }_{j}^{mathrm{c}mathrm{o}boldsymbol{n}mathrm{c}mathrm{a}mathrm{v}mathrm{e}}left({boldsymbol{n}}_{1}^{k}
ight)end{array} $$
(32)







$$ begin{array}{cc}{mu }_{j,2}^{k+1} ={mu }_{j}^{mathrm{c}mathrm{o}mathrm{n}mathrm{v}mathrm{e}mathrm{x}}left({boldsymbol{n}}_{2}^{k+1}
ight)+{mu }_{j}^{mathrm{c}mathrm{o}mathrm{n}mathrm{c}mathrm{a}mathrm{v}mathrm{e}}left({boldsymbol{n}}_{2}^{k}
ight)end{array} $$
(33)

相对应地, 昂萨格系数矩阵可以构造为







$${boldsymbol{varPsi}} = left[ {begin{array}{*{20}{c}}{boldsymbol{A}}{{{boldsymbol{B}}^{
m{T}}}}end{array}begin{array}{*{20}{c}}{boldsymbol{B}}{boldsymbol{C}}end{array}}
ight]$$
(34)

式中, ${{A}_i}=partial ({mu }_{i,{
m{L}}}-{mu }_{i,{
m{G}}})/partial {N}_{i,{
m{G}}}$, ${{B}_i}=partial ({mu }_{i,{
m{L}}}-{mu }_{i,{
m{G}}})/partial {V}_{
m{G}}= $$ partial ({p}_{
m{G}}-{p}_{
m{L}})/partial {N}_{i,{
m{G}}}$, ${{C}_i}=partial ({p}_{
m{G}}-{p}_{
m{L}})/partial {V}_{
m{G}}$.


2.
深度学习算法加速相平衡计算



2.1
热力学一致性的自适应深层神经网络


如图1所示, 本文提出了一种双网络结构, 以提取输入相平衡数据的热力学关键特征, 并推演输入输出参数之间蕴含的热力学规律, 满足一般页岩油气开发过程中组分数目和工程条件多变的相平衡计算需要.

首先通过第1节提出的NVT型闪蒸计算方法得到带$ N $组分的储层流体闪蒸计算结果, 基于热力学分析提取环境温度$ T $, 总摩尔浓度$ C $以及各组分的临界温度${T}_{{
m{c}},i}$, 临界压力${P}_{{
m{c}},i}$, 偏心因子$ {omega }_{i} $和摩尔分数$ {{textit{z}}}_{i} $作为输入参数, 因此, 输入数据总维度为$ 4N+2 $. 数据准备网络会读取目标流体的组分数目$ M $, 并自动构造输出层维度为$ 4M+2 $, $ M $可以不同于$ N $. 如果$ N<M $, 则将保留训练数据中的所有信息, 并执行数据填充, 通过定义$ M-N $个关键热力学特征为零的虚拟组分, 使得本网络输出的数据集具有$ 4M+2 $的维度. 如果$ N>M $, 则本网络输出的数据集就为输入的训练数据, 但是目标流体的测试数据集中填充$ N-M $个关键热力学特征为零的虚拟组分. 这样, 可以保证第二个神经网络, 即用于相平衡预测的深层神经网络的输入与输出数据维度相同, 从而实现了对组分数多变的实际页岩油气流体相平衡的广泛适用性.

用于相平衡预测的深层神经网络的架构如图2所示. 选用热力学分析得出的关键性质表征流体中的各组分, 并结合温度与摩尔浓度共同作为输入参数. 输出层将得到相稳定测试的结果, 即平衡态时流体中总的相数, 由$ NP $表示, 以及相分离计算的结果, 即平衡态时气相的摩尔组成(${Y}$)和气液比($ mathrm{varphi } $). 每个隐藏层均包含若干个节点, 而每层上训练的模型可以表示为



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-229-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
用于相平衡预测的深层神经网络架构



Figure
2.
Deep neural network for phase equilibrium estimates



下载:
全尺寸图片
幻灯片








$$ {boldsymbol{R}}_{i}={f}_{i}({boldsymbol{W}}_{i}*{boldsymbol{S}}_{i}+{boldsymbol{G}}_{i}) $$
(35)

式中$ {boldsymbol{W}}_{i} $表示第$ i $隐藏层的系数向量, $ {boldsymbol{S}}_{i} $表示第$ i $隐藏层的输入数据集, $ {boldsymbol{G}}_{i} $表示第$ i $隐藏层的偏差, $ {f}_{i} $表示第$ i $隐藏层所用的激活函数, $ {boldsymbol{R}}_{i} $表示第$ i $隐藏层的输出数据集. 对全连接的深层神经网络而言, 上一层的输出数据集通常直接作为下一层的输入数据集, 以总共3层的神经网络为例, 整体的预测模型为







$$ boldsymbol{o}={f}_{3}left{{boldsymbol{W}}_{3}*{f}_{2}left[{boldsymbol{W}}_{2}*{f}_{1}left({boldsymbol{W}}_{1}*{boldsymbol{S}}_{1}+{boldsymbol{G}}_{1}
ight)+{boldsymbol{G}}_{2}
ight]+{boldsymbol{G}}_{3}
ight} $$
(36)

式中$ boldsymbol{o} $表示最终的预测结果, $ {boldsymbol{S}}_{1} $表示第一层的输入数据, $ {boldsymbol{W}}_{1} $, $ {boldsymbol{W}}_{2} $和$ {boldsymbol{W}}_{3} $表示第一、二和三层上的系数向量, $ {boldsymbol{G}}_{1} $, $ {boldsymbol{G}}_{2} $和$ {boldsymbol{G}}_{3} $表示第一、二和三层上的偏差.

本文所提出的自适应性神经网络架构将允许对数据集的填充以统一训练数据集和目标测试数据集, 这对上述训练模型带来了如下修正: 假设$ N<M $, 在数据准备网络中定义了$ M-N $个关键热力学特征为零的虚拟组分, 所以相平预测网络中第一层的输入数据为







$$begin{split}{{boldsymbol{S}}_1} =& Big{ {{T_{{
m{c}},1}},{P_{{
m{c}},1}},{omega _1},{{textit{z}}_1},{T_{{
m{c}},2}},{P_{{
m{c}},2}},{omega _2},{{textit{z}}_2}, cdots ,} &{T_{{
m{c}},N}},{P_{{
m{c}},N}},{omega _N},{{textit{z}}_N},{T_{{
m{c}},{{
m{g}}_1}}},{P_{{
m{c}},{{
m{g}}_1}}},&{omega _{{{
m{g}}_1}}},{{textit{z}}_{{{
m{g}}_1}}},{T_{{
m{c}},{{
m{g}}_2}}},{P_{{
m{c}},{{
m{g}}_2}}},{omega _{{{
m{g}}_2}}},{{textit{z}}_{{{
m{g}}_2}}}, cdots, & {{T_{{
m{c}},{{
m{g}}_{left( {M - N}
ight)}}}},{P_{{
m{c}},{{
m{g}}_{left( {M - N}
ight)}}}},{omega _{{{
m{g}}_{left( {M - N}
ight)}}}},{{textit{z}}_{{{
m{g}}_{left( {M - N}
ight)}}}},T,C} Big}end{split}$$
(37)

式中, 下标g表示虚拟组分.


2.2
适合相平衡预测问题的机器学习技术


过度拟合是深度学习研究中的常见挑战, 这意味着已针对训练数据实现了所得模型的完美性能, 但在验证测试数据的预测表现时只能获得较差的性能. 通常, 如果在深度学习模型(也称为过参数化模型)中包含太多参数, 就会发生此问题. 而多组分相平衡预测, 尤其是真实页岩油气藏流体含有加多组分的情况下, 相平衡预测模型就囊括了超大规模系数矩阵. 通常采用一个附加约束来减少模型的自由度, 以防止过度拟合问题损害的深度学习算法的性能. 过度拟合的一个重要特征是系数参数的范数非常大, 这可能是添加此附加约束的一个角度. 据此, 设计了如下的损失函数形式







$$ L=frac{1}{N}sumnolimits_{n=1}^{N}{Vert boldsymbol{o}-widehat{boldsymbol{o}}Vert }^{2}+lambda {Vert boldsymbol{W}Vert }_{2}^{2} $$
(38)

式中, $ widehat{boldsymbol{o}} $表征真实值, $ boldsymbol{o} $表征预测结果, $ lambda $表征关于系数矩阵$ boldsymbol{W} $的L2正则化系数. 显然, 通过引入此衰减项, 可以在系数矩阵有较大范数的情况下显著修正损失函数, 从而影响训练过程.

真实多组分气藏流体的相平衡预测模型所需的超大规模系数矩阵, 要求合理地赋予初始化的系数以提升训练中的收敛速度, 从而提升深度学习算法的性能和可靠性. 如果在初始化时高估了系数参数, 则会在训练过程中观察到方差的快速增加, 这可能会进一步导致梯度爆炸或消失, 在这种情况下, 训练将永远不会收敛. 相反, 如果系数参数在初始化时被低估, 则方差可能会迅速下降到非常小的值, 这将导致模型复杂性受损甚至最终评估的性能下降. 常用的初始化方法是遵循高斯分布以一定方差进行系数参数的初始化, 以确保每一层的输入和输出方差将保持不变, 这就是常用的Xavier初始化技术, 也在本文中应用于以相平衡预测为目的的深度学习算法设计.

为了准确描述相平衡过程中复杂的热力学规律, 深层神经网络所训练出的模型很难避免高度复杂性带来的过拟合问题, 从而影响到最终的预测效果. Dropout是一种常用办法, 即通过丢弃网络中的某些节点以消去相应的连接关系, 从而显著降低模型的自由度. 如图2所示, 隐藏层中的虚线圆表示dropout消去的节点, 而对应的训练模型改为







$$ {boldsymbol{y}}_{i}={f}_{i}*({boldsymbol{W}}_{i}*{boldsymbol{r}}_{i}*{boldsymbol{S}}_{i}+{boldsymbol{G}}_{i}) $$
(39)

式中$ {boldsymbol{r}}_{i} $为布尔向量. 第$ i $层上的每个节点$ j $都将以保留的概率$ p $或丢弃的概率$ 1-p $进行独立评估. 如果保留该节点, 则对应的$ {r}_{ij} $将为1, 如果将其丢弃, 则$ {r}_{ij} $将为零. 在评估所有节点和连接后, 模型的训练将在dropout后的简化网络上进行. 应该指出的是, 为了保持训练的鲁棒性, 在下一训练周期开始之前, 需要使用初始化的系数将丢弃的节点插入回模型中, 以进行重新的评估和dropout操作.

由于多组分相平衡预测模型的复杂性和所需的巨大训练数据量, 深度学习模型的训练是非常耗时的. 此外, 由于梯度下降的过程会让每一层的参数$ boldsymbol{W} $和$ boldsymbol{G} $都发生变化, 进而使得每一层的线性与非线性计算结果分布产生变化. 后层网络就要不停地去适应这种分布变化, 这个时候就会使得整个网络的学习速率过慢. 此外, 当采用例如sigmoid, tanh等饱和激活函数时, 很容易使得模型训练陷入梯度饱和区, 此时梯度会变得很小甚至接近于0, 参数的更新速度就会减慢, 进而就会放慢网络的收敛速度. 这就是机器学习中常见的内部协变量转移问题(internal covariate shift, ICS). 通常的解决方法是白化, 即使得输入特征分布具有相同的均值与方差, 从而减缓ICS问题的影响. 然而, 白化技术的计算成本太高, 尤其是每一轮训练中的每一层都需要进行此操作, 从而拖慢了训练效率. 此外, 白化过程由于改变了网络每一层的分布, 因而改变了网络层中本身数据的表达能力. 底层网络学习到的参数信息会被白化操作丢失掉. 因此, 本文采用了更先进的批标准化方法(batch normalization, BN),对每一批数据样本计算均值和方法, 进而进行标准化规范每个输入特征值的分布均值为0, 方差为1, 并引入可学习参数以对规范化后的数据进行线性变换以恢复数据本身表达的信息.

输入特征之间强烈的的非线性相关性(在常规闪蒸计算中由基于状态方程的非线性演化方程组表征)在深度学习模型中由激活函数进行表征. 作为表示网络非线性和解决问题能力的关键因素, 激活函数在近些年得到了长足发展. 不同的激活函数有不同的表达形式, 例如ReLU函数可以表示为







$$ fleft(x
ight)=left{begin{array}{cc}0,& text{if};x<0 x,& text{if};xgeqslant 0end{array}
ight. $$
(40)

而Sigmoid函数有如下形式







$$ sigma left(x
ight)=frac{1}{1+{
m{e}}^{-x}} $$
(41)

由于的双网络结构涉及到了数据的填充过程和输入/输出数据的维度变化, 为了保证预测模型仍满足基本的热力学规律, 即每相中所有组分的摩尔分数之和为1的限制条件, Softmax函数恰恰可以实现此目标, 如下所示







$$ {a}_{j}^{L}=dfrac{{{
m{e}}}^{{{textit{z}}}_{j}^{L}}}{displaystylesumnolimits_{k}{{
m{e}}}^{{{textit{z}}}_{k}^{L}}} $$
(42)

式中, $ {a}_{j}^{L} $表示第$ L $层第$ j $个数据的Softmax函数值. 通过计算各相中各组分的摩尔分数的指数和该相中所有组分摩尔分数的指数之和的比值, 可以保证深层神经网络最终输出的摩尔分数满足各相之中和为1的限制条件, 从而保留了热力学的一致性和物理意义.


2.3
神经网络超参调试


采用第1节推导出的具有热力学一致性的NVT迭代闪蒸算法生成了5种组分的Bakken流体, 8种组分的Eagle Ford流体和14种组分的Eagle Ford流体这三种实际储藏流体的相平衡数据, 以供本章的深度学习过程中训练和测试使用. Bakken储藏流体的基本性质数据如表1所示, 两种Eagle Ford储藏流体的化学组成和热力学性质可参见参考文献[32]. 为了在广泛的工程环境条件下得到平滑的相平衡预测曲线, 在环境温度从300 K到850 K, 摩尔密度从10 mol/m3到10000 mol/m 3 的范围内划分了一组$ 301times 301 $的规则网格, 以满足页岩油气藏开发生产中真实的环境条件.




表
1
Bakken储藏流体性质数据



Table
1.
Fluid properties of Bakken reservoir



table_type2 ">
Component${ {textit{z}} }_{,i}$${ {T} }_{{
m{c}},i}$/K		${ {P} }_{{
m{c}},i}$/MPa		$ {omega }_{i} $
C10.250 6190.6064.6000.008
C2 ~ C40.220 0363.304.3100.143
C5 ~ C70.200 0511.563.4210.247
C8 ~ C90.130 0579.343.1320.286
C10+0.199 4788.742.1870.687





下载:
导出CSV
|显示表格



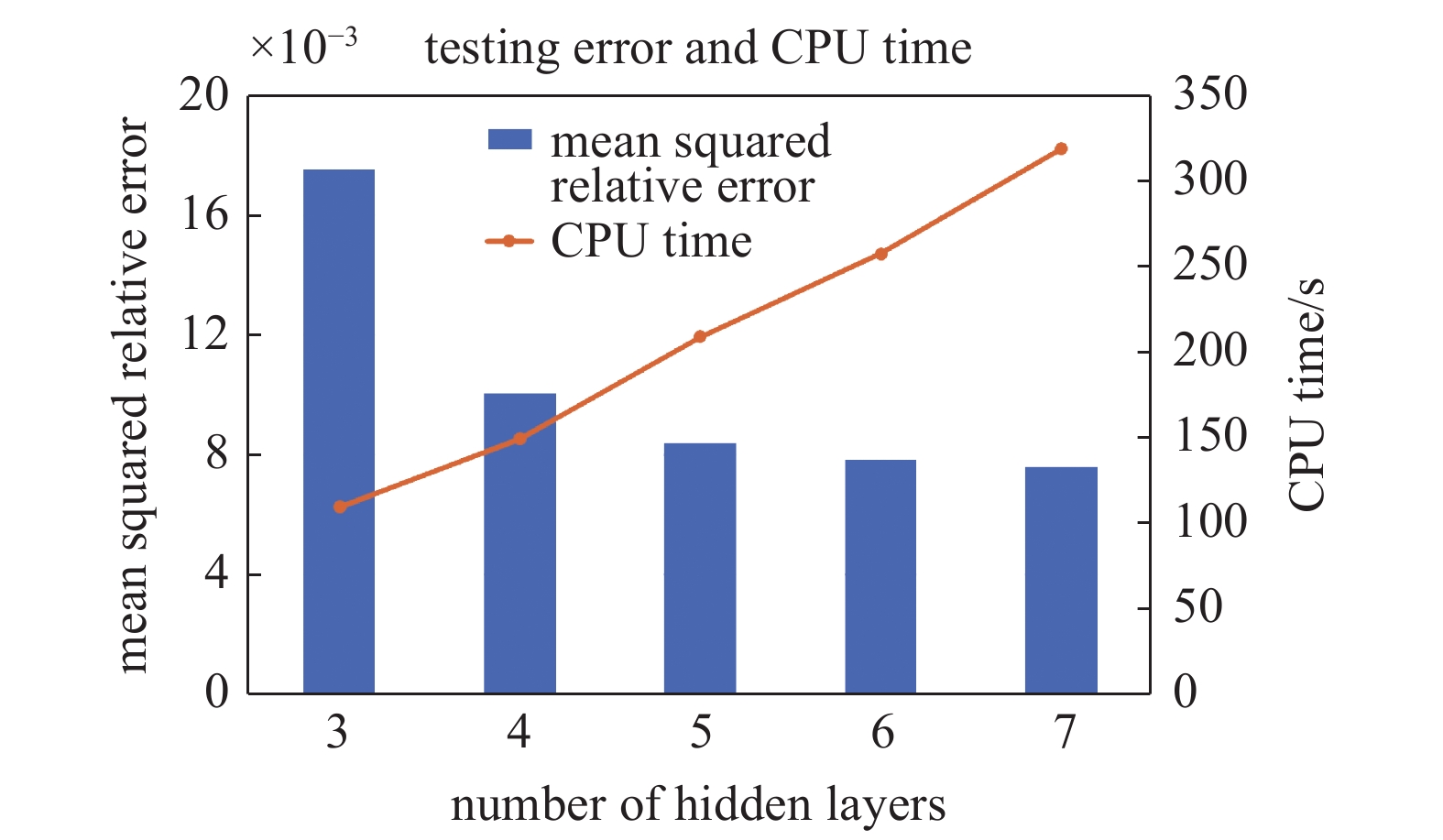
为了准确描述相平衡过程中蕴含的热力学规律, 机器学习训练的模型需要通过隐藏层中各节点的线性组合表征闪蒸计算中用状态方程表征的非线性关系. 因此, 每个隐藏层中的节点数和隐藏层数与训练模型的复杂度直接相关, 从而与训练效率和预测精度紧密相关. 如图3和图4所示, 通过平化的误差均值和计算所用时间来测试每层中节点数目在50 ~ 250范围内以及隐藏层的数目在3 ~ 7之间的性能. 图中的蓝色条状图表示预测结果的平均平方化相对误差, 而橙色折线表示各网络结构所需的学习时间. 从结果比较中可以很容易地看出, 如果网络结构中包含更多节点和隐藏层, 网络复杂度会相对应地增加, 则计算成本将不断增长. 但是, 预测精度的提高会在达到网络构造的某些阈值节点数和层数之后显著放缓, 这表明需要放弃不明显的精度提升以换取更明显的效率提升. 据此分析, 设计了具有6个隐藏层和每层200个节点的深层神经网络用于页岩油气相平衡的快速预测, 以使总体平方化相对误差小于 0.8%, 并且模型训练在普通工作站上使用了可接受的计算时间(几分钟级).



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-229-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
每隐藏层节点数调优



Figure
3.
Tuning on the number of nodes in each hidden layer



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-229-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
隐藏层数调优



Figure
4.
Tuning on the number of hidden layers



下载:
全尺寸图片
幻灯片


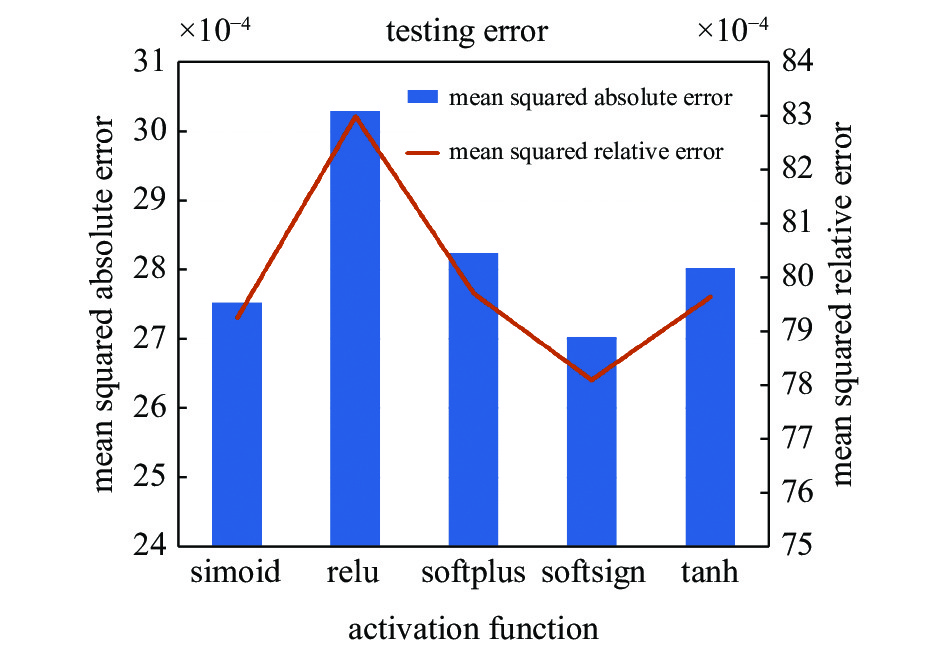
为了更好地在深度学习模型中反映相平衡过程中的热力学规律, 需要找到最合适的激活函数以表征各特征值之间复杂的热力学关系. 选用了5个常用的激活函数Sigmoid, Softplus, Softsign, tanh和ReLU, 通过比较其平方化绝对误差和平方化相对误差来评估对应机器学习模型所具有的预测性能. 如图5所示, 具有4个激活函数Sigmoid, Softplus, Softsign和tanh的网络在测试中表现出相似的预测误差, 而使用ReLU的误差要高一些. 此外, 由于从迭代Flash结果中随机选择了测试数据, 使用不同的批次进行重复测试并去平均值, 以提高对激活函数进行调整的可靠性. 基于此调试结果, 最终选择Softsign函数以构建深层神经网络, 从而更好地保证深度学习算法的可靠性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-229-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
激活函数调优



Figure
5.
Tuning on the activation functions



下载:
全尺寸图片
幻灯片



2.4
预测毛细作用对页岩油气相平衡的影响


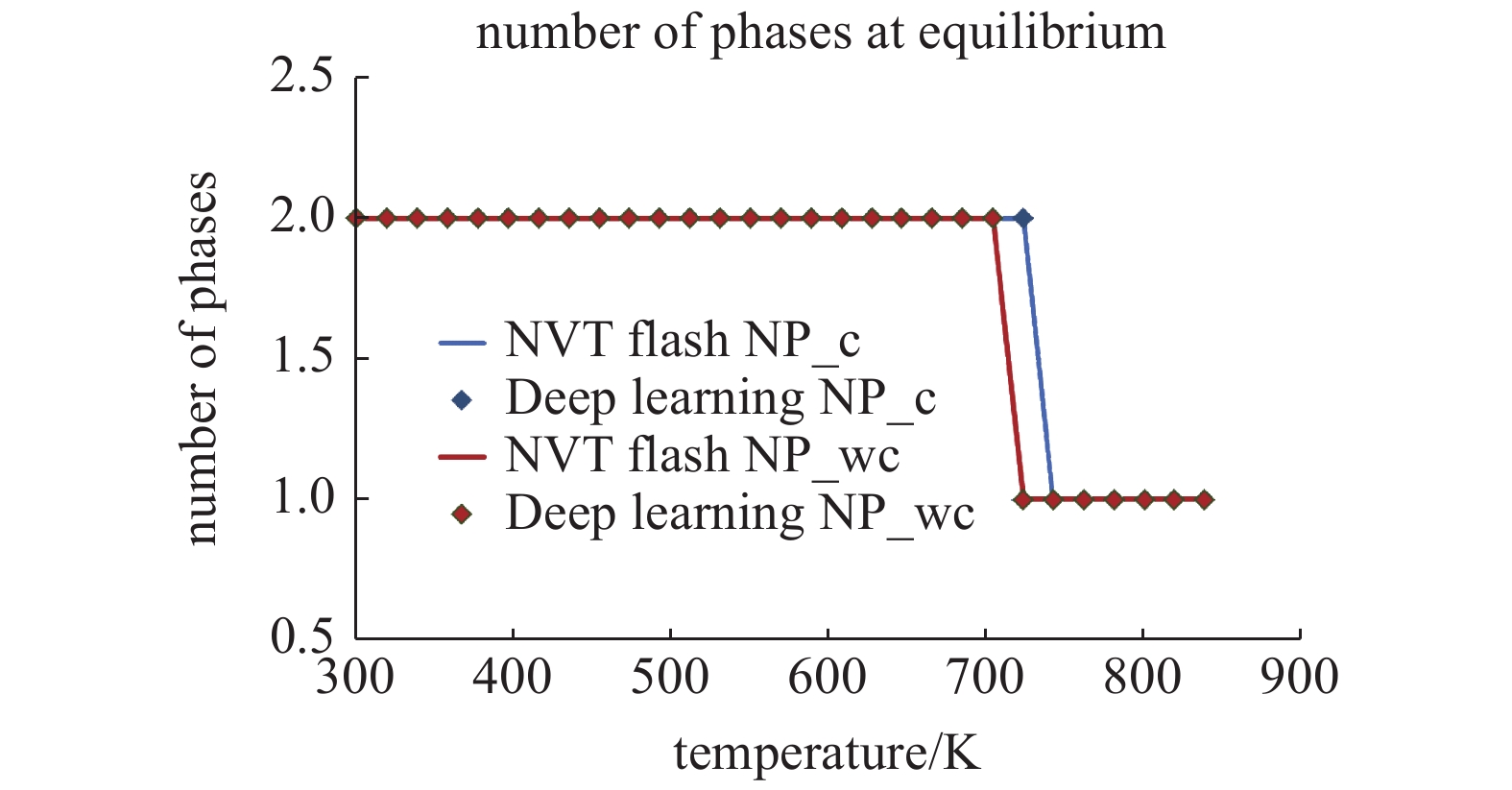
相平衡状态下存在于混合物中的相数是关注的最关键信息, 因为根据此信息可以确定是否需要进行多相流动的模拟结算, 还是单相流动模型已满足需要. 提出的深度学习算法的重要贡献在于将相稳定性测试和相分离计算相结合, 并且在最终输出层中直接预测了处于平衡状态的相数. 在恒定60 mol/m3摩尔浓度的条件下, Bakken储层流体在平衡态的总相数随温度的变化如图6所示. 图中蓝色表示考虑毛细作用时的相数, 用${NP}_{{
m{c}}}$表示, 红色表示不考虑毛细作用时的相数, 用${NP}_{{
m{wc}}}$表示, 菱形标志表示深度学习预测结果, 连续实线表示迭代型NVT闪蒸的计算结果(也是深度学习中的基准数据). 从图中可以明显看出, 无论是否考虑毛细作用, 本文所提出的深度学习算法和神经网络模型都可以很好地预测平衡态时真实储藏流体的总相数, 并且精准捕捉到了流体随着升温从气液两相区向单气相区转变的节点. 值得一提的是, 在毛细作用下这一相变过程被推后了, 即在保持恒定摩尔浓度的前提下, 需要更好的温度以促使流体的完全气化. 这一现象与通常在相包络图中反映的毛细作用对泡点线的压缩和对露点线的扩张效应相吻合.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-229-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
Bakken储层流体在60 mol/m3摩尔浓度时平衡态相数随温度的改变



Figure
6.
Number of phases existing at equilibrium for Bakken reservoir fluids under constant overall mole concentration as 60 mol/m3



下载:
全尺寸图片
幻灯片


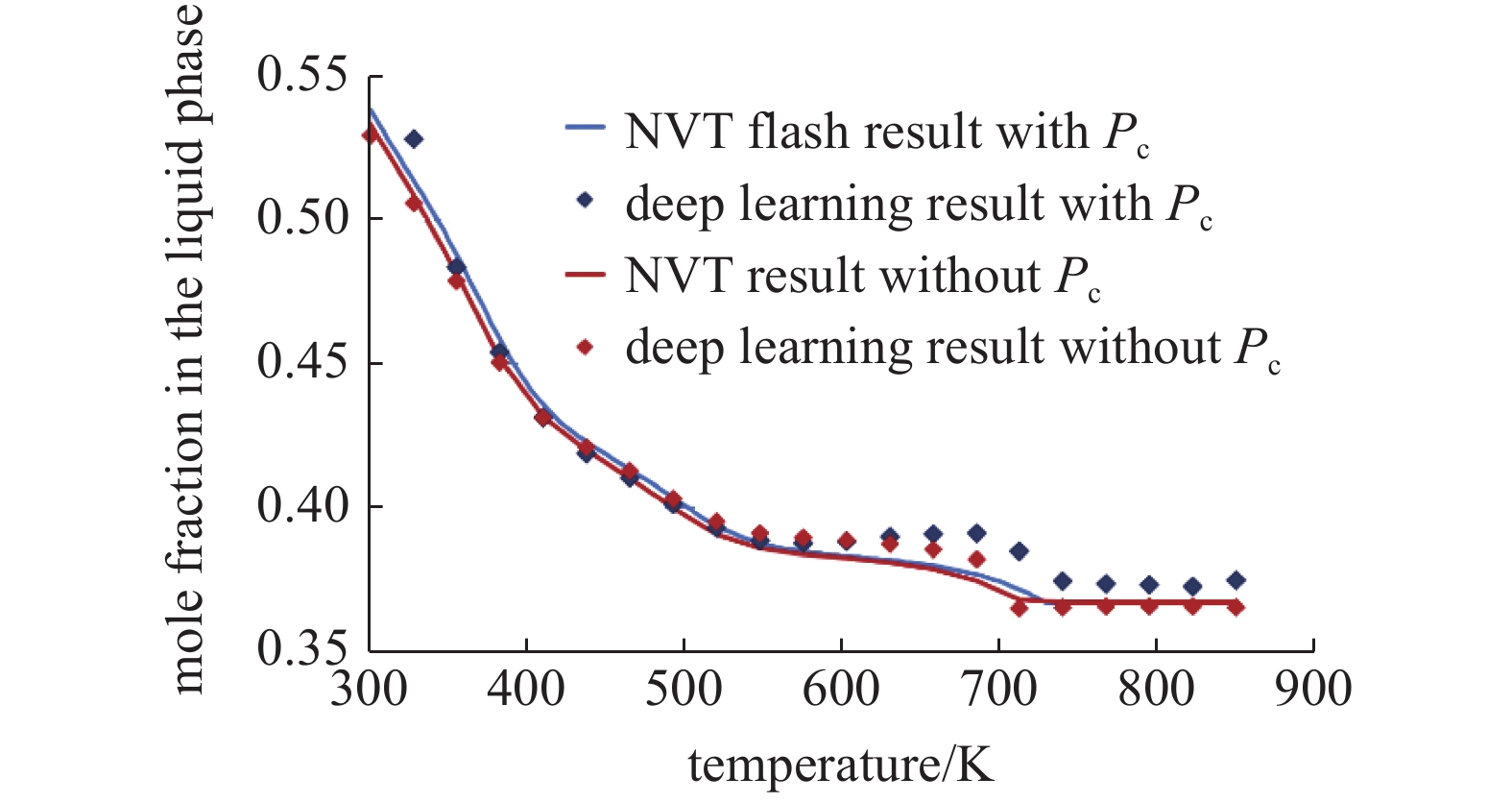
对多组分储藏流体而言, 除了平衡态时的相数之外, 通常还需要计算每个相中各组分的摩尔分数组成从而为后续的多组分多相流模拟提供准确可靠的初场信息, 因此本文所构建的深度学习算法也会输出平衡态摩尔组成的预测结果. 图7在恒定60 mol/m3摩尔浓度的条件下, Bakken储层流体在平衡态时甲烷组分在气相中的摩尔分数随温度的变化. 图中蓝色表示考虑毛细作用时的相分离预测, 红色表示不考虑毛细作用时的相分离预测, 菱形标志表示深度学习预测结果, 连续实线表示迭代型NVT闪蒸的计算结果. 从图中可以看出, 甲烷组分的摩尔分数随温度的升高而在气相中降低, 如果温度超过700 K, 则可以捕捉到明显的相变. 随着Bakken流体混合物从两相区域变为单相区域, 各相的组成摩尔分数将保持不变, 该相变趋势也与图6中的相数变化保持了一致. 此外, 毛细压力对相分离计算的影响也可以在迭代NVT闪蒸计算和训练后的深度学习模型对相平衡状态的预测结果中反映出来, 对不同温度下的各相摩尔组成都造成了影响.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-229-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
Bakken储层流体在60 mol/m3摩尔浓度时甲烷组分在气相的摩尔分数在平衡态随温度的改变



Figure
7.
Mole fraction of C1 component in the vapor phase at equilibrium for Bakken reservoir fluids changing with temperature and under constant overall mole concentration as 60 mol/m3



下载:
全尺寸图片
幻灯片


上述的数值实验和分析论证了本文所提出的深度学习算法的鲁棒性和准确性, 但是采用深度学习算法的核心目的在于提升相平衡计算的效率. 比较了深度学习算法和NVT闪蒸计算方法在考虑毛细作用和不考虑毛细作用的Bakken储层流体相平衡计算中所耗费的时间, 如表2所示. 表2中tflash表示闪蒸计算耗时, tdl表示深度学习耗时, 单位均为秒. ε表示深度学习算法的预测结果与基准值, 即NVT闪蒸计算结果的均方差. 从表中可以明显看出, 本文所提出的深度学习算法相较于迭代型闪蒸计算方法在计算效率上实现了高达数百倍的极大提升, 并且保留了令人满意的预测精度(预测误差在10%以内).




表
2
深度学习算法的表现



Table
2.
Performance of deep learning algorithm



table_type1 ">
Fluidtflash/stdl/s$ mathrm{varepsilon } $
with capillarity22147.80.086
without capillarity20157.50.091





下载:
导出CSV
|显示表格



2.5
带数据填充的自适应神经网络预测效果


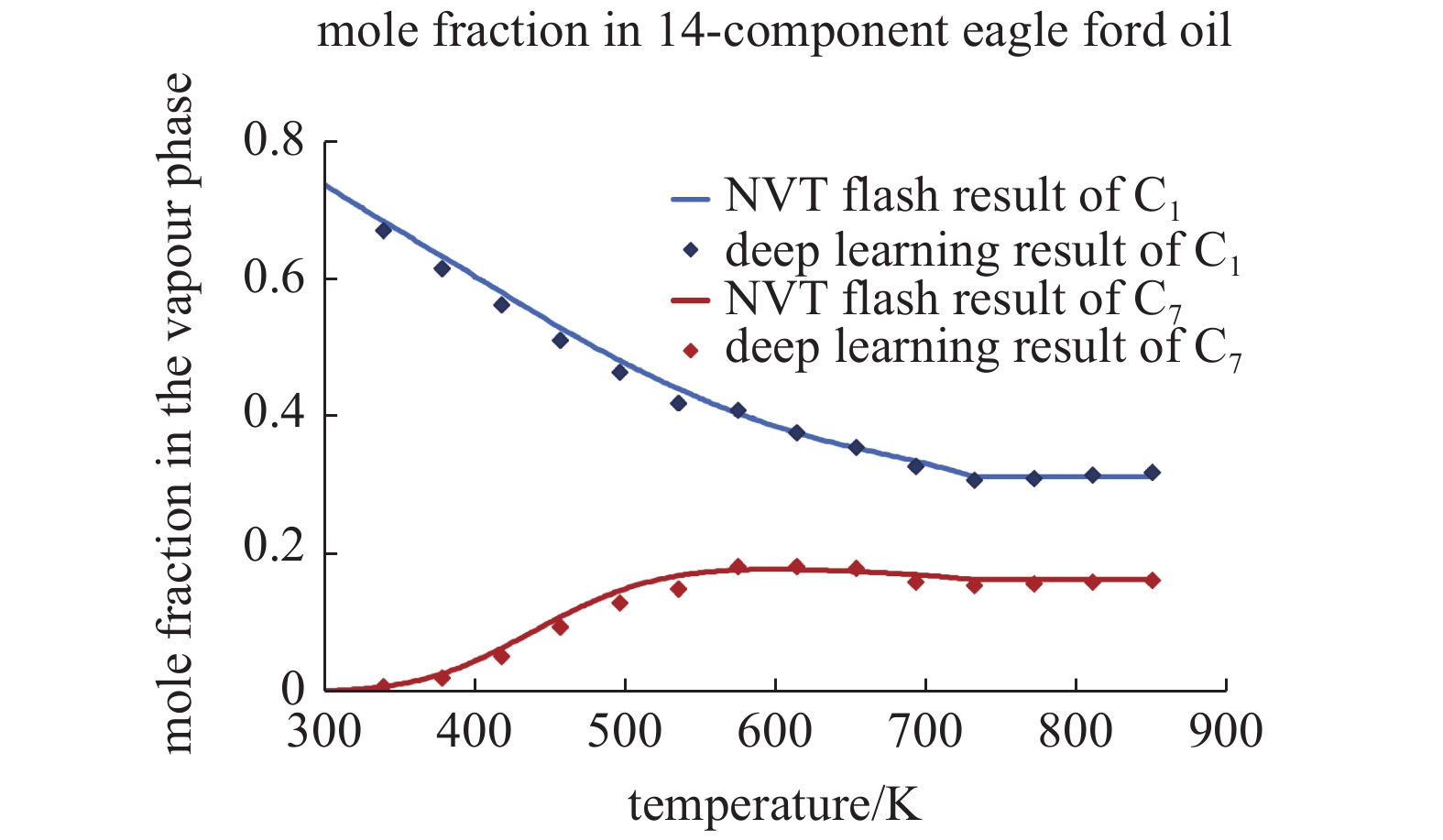
本文所提出的深度学习算法的另一个主要贡献是对流体不同组分数目的自适应性, 从而解决了工程实践中化学组成复杂多变的真实储层流体相平衡预测的难点和挑战. 为了验证此优势, 对8组分Eagle Ford储层流体进行了迭代NVT闪蒸计算以生成相平衡数据作为训练数据集, 并已14组分Eagle Ford储层流体的相平衡预测为目标来训练深度学习模型. 通过数据准备网络将6个虚拟组分和相应的热力学特征填充到训练数据中, 相平衡预测网络的输入维数自动调整为 $ 4times 14+2=58 $. 在恒定343 mol/m3的摩尔浓度条件下, 随机选取了甲烷和庚烷组分在该储层流体平衡态气相中的摩尔分数随温度的变化作为评估变量, 绘制出如图8所示的评价结果. 研究发现, 本文提出的深度学习算法在这两种组分的相平衡预测上均取得了令人满意的结果, 与作为基准值的迭代闪蒸算法吻合较好, 且以各组分在某一相中恒定摩尔分数为表征, 精准地捕捉到了随温度上升的相变过程. 因此, 储层流体化学组成和组分数目多变的实际页岩油气勘探开发工程问题中, 本文所提出的带数据填充的深度学习算法可以有效地解决相平衡分析的瓶颈, 通过对较少组分的较简单储层流体进行迭代闪蒸计算得到一定数量的数据集, 采用该自适应性深度学习算法可以快速得出具有一定精度保证的含有较多组分的较复杂流体相平衡状态预测, 从而为后续的多相渗流和输运建模计算提供高效可靠的热力学基础.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/8//21-229-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
14组分Eagle Ford储层流体在343 mol/m3摩尔浓度时甲烷和庚烷组分在气相的摩尔分数在平衡态随温度的改变



Figure
8.
Mole fraction of C1, C7 components in the vapor phase at equilibrium for 14-component Eagle Ford reservoir fluids changing with temperature and under constant overall mole concentration 343 mol/m3



下载:
全尺寸图片
幻灯片



3.
结 论


本文针对页岩油气勘探开发中相平衡计算这一关乎多组分多相渗流模拟可靠性的关键问题, 基于真实流体状态方程开发了一套具有热力学一致性的NVT型闪蒸计算方法, 基于热力学分析提取了相平衡过程中的关键参数设计了深度学习算法以加速多组分实际流体相平衡计算, 提出了双网络结构以实现在广泛的环境条件下对不同化学组成和组分数目的储层气体的自适应性, 通过对真实储层气体在相平衡态时的总相数和各相的摩尔组成预测论证了本算法中耦合的相稳定测试和相分离计算的准确性, 通过与迭代型闪蒸计算方法的对比论证了深度学习算法的加速效果, 以实际预测结果证实了在页岩油气相平衡计算中考虑毛细作用的影响, 从而为页岩油气勘探开发中涉及多组分多相渗流输运的问题研究提供了快速准确可靠的相分布预测和热力学基础.

相关话题/计算 数据 网络 油气 分数
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 循环神经网络在智能天平研究中的应用
    引言随着航空航天技术的不断发展,高超声速技术受到各个航空航天大国的广泛关注和深入研究,其科学问题具有重要的战略意义[1].对于高超声速飞行器气动外形布局设计和优化问题,高精度气动力测量试验起到决定性作用.激波风洞测力试验可以为高温真实气体效应的研究提供可靠的数据,同时为我国高超声速飞行器研究提供关键 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于Darcy-Stokes耦合模型的多孔介质颗粒悬浮液等效黏性系数计算
    引言颗粒悬浮液广泛存在于自然界及工程应用领域,其黏性特征对悬浮液的流动行为有着重要的影响[1-4].早在1905年,Einstein[5]就研究了低浓度条件下球形固体颗粒对流体黏性的影响,给出了悬浮液等效黏度系数计算的一个强有力的理论框架,并得到了低浓度球形颗粒悬浮液的著名的Einstein黏性公式 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于神经网络的差分方程快速求解方法
    引言近年来,人工神经网络(artificial?neural?networks,ANN),尤其是深度神经网络(deep?neural?networks,DNN)因其在处理和预测高维复杂系统方面的优异能力而被广泛应用于自然语言处理[1]、计算机视觉[2]与图像处理[3]等领域.此外,深度神经网络凭借其 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • DVC中内部散斑质量评价及计算体素点的优化选择
    引言数字体图像相关方法(digitalvolumecorrelation,DVC)是二维数字图像相关方法(two-dimensionaldigitalimagecorrelation,2DDIC)在三维体图像上的拓展.通过比较体成像设备获取的被测试样变形前后数字体图像,该方法可测量物体内部三维全场变 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于人工神经网络的声子晶体逆向设计
    引言声子晶体是一种新型人工周期性复合材料,具有独特的禁带特性,即声波或弹性波在声子晶体中传播时,由于受到周期性结构中波的散射或局部共振的作用,在某些频段范围即带隙内无法传播[1-4].该特性使得声子晶体在工程减振降噪领域具有巨大的应用潜力.声子晶体的拓扑结构和组分材料的属性决定了其带隙特性.因此,根 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • Caputo Δ型分数阶时间尺度Noether定理
    引言分数阶微积分几乎和整数阶微积分同时存在,它的导数和积分的阶数可以是任意数[1].由于分数阶微分方程具有独特的能力来描述自然现象的共同特征?异常行为和记忆效应[2],因此分数阶微分方程能比整数阶微分方程更准确地描述许多实际问题.分数阶微分方程理论是数学的一个重要分支,包括连续分数阶微分方程和离散分 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于分数阶磁流变液阻尼器模型的车辆悬架组合控制
    引言磁流变液阻尼器是利用磁流变液提供可控阻尼力的装置,已广泛应用在车辆悬架[1]、汽车座椅[2]、斜拉索[3]等结构的振动控制中.磁流变液阻尼器通过改变阻尼线圈中的电流强度来改变其磁场强度,能够快速响应并且输出阻尼力.描述磁流变液的力学模型主要有Bingham模型[4-5]、Sigmoid模型[6] ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于数据驱动的流场控制方程的稀疏识别1)
    江昊,王伯福,卢志明,2)上海大学,力学与工程科学学院,上海市应用数学和力学研究所,上海200072DATA-DRIVENSPARSEIDENTIFICATIONOFGOVERNINGEQUATIONSFORFLUIDDYNAMICS1)JiangHao,WangBofu,LuZhiming,2)S ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于组合神经网络的雷诺平均湍流模型 多次修正方法1)
    张珍*,&,叶舒然*,&,岳杰顺*,&,王一伟,*,&,2),黄晨光*,&,***中国科学院力学研究所流固耦合系统力学重点实验室,北京100190&中国科学院大学工程科学学院,北京100049**中国科学 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 考虑颗粒转矩的接触网络诱发各向异性分析1)
    王怡舒*,沈超敏*,刘斯宏,*,2),陈静涛&*河海大学水利水电学院,南京210098&中国建筑第二工程局有限公司,上海200135SHEAR-INDUCEDANISOTROPYANALYSISOFCONTACTNETWORKSINCORPORATINGPARTICL ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.