删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

基于分数阶磁流变液阻尼器模型的车辆悬架组合控制

本站小编 Free考研考试/2022-01-01


引 言


磁流变液阻尼器是利用磁流变液提供可控阻尼力的装置, 已广泛应用在车辆悬架[1]、汽车座椅[2]、斜拉索[3]等结构的振动控制中. 磁流变液阻尼器通过改变阻尼线圈中的电流强度来改变其磁场强度, 能够快速响应并且输出阻尼力. 描述磁流变液的力学模型主要有Bingham模型[4-5]、Sigmoid模型[6]和Bouc-Wen模型[7]等. 其中Bingham模型由于其结构形式简单, 且物理含义明确而被广泛应用. 刘晓梅等[8-9]为解决整数阶Bingham模型不能描述低速时速度?阻尼力滞回特性的缺陷, 提出了磁流变液阻尼器分数阶微分形式的Bingham模型, 可以更好地反应其速度?阻尼力的滞回特性.

为了提高车辆的操控性和乘坐舒适性, ****们对磁流变液阻尼器在车辆悬架中的应用进行了深入研究. 例如, Sharma[10]研究了含有Bingham模型的磁流变液阻尼器悬架, 通过仿真发现半主动控制比被动控制具有更好的稳定性. Tudon-Martinez等[11]研究了基于人工神经网络模型与经典Bingham模型两种不同精度水平的阻尼器模型对车辆悬架的影响. Prabakar等[12]采用Bingham模型和改进的Bouc-Wen模型对含磁流变液阻尼器的车辆悬架的半车模型进行了研究, 结果表明, 具有最优参数的磁流变液阻尼悬架系统比被动悬架性能好一个数量级. 李礼夫等[13]通过对汽车磁流变液半主动悬架控制的研究, 提出了汽车磁流变液半主动悬架预瞄控制方法, 提高了汽车的控制性能.

近年来, 分数阶微积分理论的应用研究发展非常迅速[14-21]. 由于分数阶微积分可以更好的描述材料的记忆特性[22-23], 逐渐成为工程中强有力的建模工具. Vyawahare和Nataraj[24]建立了核反应堆中子扩散的分数阶模型, 消除了经典扩散模型的缺陷, 能够更真实的表示核内中子的运动. Jia和Liu[25]利用分数阶微积分理论建立了带抽头电感的磁耦合升压变换器在连续导通模式下的分数阶数学模型. 陈明等[26]利用少参数分数Zener模型较好地拟合了鲫鱼尾鳍鳍条的松弛特性曲线. 蔡伟和陈文[27]从时间和空间分数阶两个方面概述了不同的分数阶导数声波模型. 陈丙三等[28]建立了磁流变液测试装置的分数阶模型, 且磁流变液的黏弹性可由模型参数获得. Schiessel等[29]、Heymans和Bauwens[30]提出了分数阶单元网络模型和分形流变模型. Niu等[31]采用分数阶磁流变液模型研究了镗杆系统的半主动振动控制.

在利用磁流变液阻尼器进行车辆悬架振动控制的研究方面, Bingham模型大都采用的整数阶模型, 而利用分数阶Bingham模型进行车辆悬架研究的报道还较少. 本文采用分数阶Bingham模型来对磁流变液阻尼器进行建模, 建立含有磁流变液阻尼器的单自由度1/4车辆悬架系统动力学模型. 利用平均法求解悬架系统在半主动控制下的解析解, 并分析控制系统的稳定性. 为改善半主动控制对乘坐舒适性的影响, 提出一种被动控制与半主动控制相结合的组合控制策略.


1.
车辆悬架控制系统模型


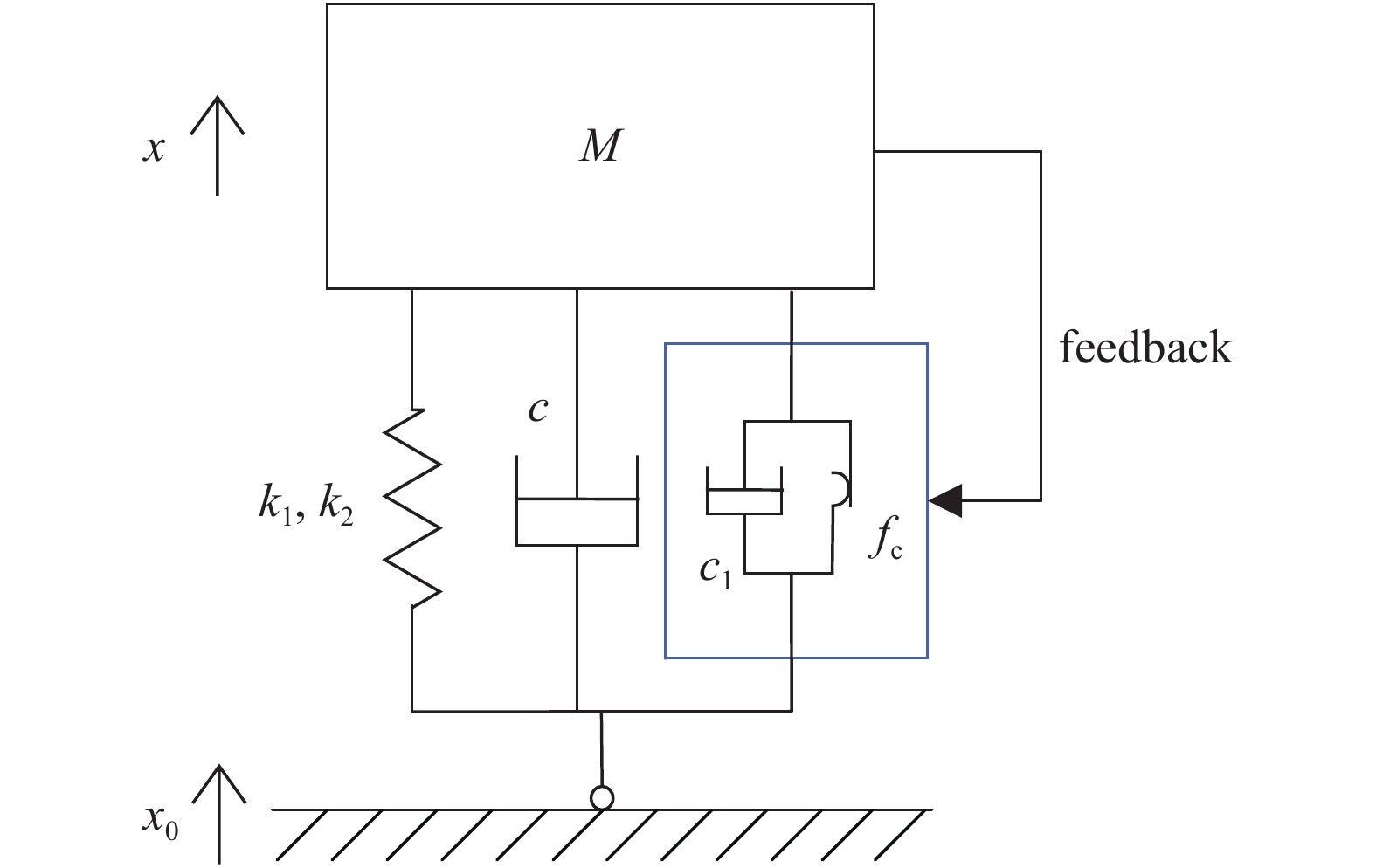
非线性车辆悬架不但可以用较低的成本提高乘坐舒适性[32], 而且可以提高车辆的平顺性[33]. 建立基于磁流变液阻尼器分数阶Bingham模型的单自由度1/4车辆悬架系统模型, 如图1所示. 图中k1和k2分别表示线性刚度和立方刚度, M为簧载质量, c为系统黏性阻尼, x为质量M的位移, ${x_0} = Asin (omega t)$为路面施加在系统上的位移激励, A为激励幅值, $omega $为激励频率. 正弦函数可以用来描述起伏路面施加给车辆悬架的激励, 而起伏路面也是车辆测试中较为常见的一种路面[34].



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-137-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
非线性车辆悬架系统



Figure
1.
Nonlinear vehicle suspension system



下载:
全尺寸图片
幻灯片


图中虚线框内表示分数阶Bingham模型磁流变液阻尼器, 其最大输出阻尼力为







$${F_1} = {f_{
m{c}}}{
m{sgn}} left[ {{D^p}(x - {x_0})}
ight] + {c_1}{D^p}left( {x - {x_0}}
ight)$$
(1)

其中, ${f_{
m{c}}}$为分数阶Bingham模型的库伦阻尼力, $p$和${c_1}$分别为分数阶微分项的阶次和系数.

采用天棚阻尼半主动控制策略, 通过判断簧载质量的运动速度方向和簧载质量与路面的相对运动速度方向来控制磁流变液阻尼器所提供的阻尼力. 系统的运动微分方程为






$$ begin{split}&Mddot{x}+cleft(dot{x}-{dot{x}}_{0}
ight)+{k}_{1}left(x-{x}_{0}
ight)+{k}_{2}{left(x-{x}_{0}
ight)}^{3}+&qquadqquad{f}_{
m{c}}mathrm{sgn}left[{D}^{p}(x-{x}_{0})
ight]+{c}_{1}{D}^{p}left(x-{x}_{0}
ight)=0,&qquadqquaddot{x}left(dot{x}-{dot{x}}_{
m{0}}
ight)geqslant 0end{split};;;tag{2a}$$






$$ begin{split}&Mddot{x}+cleft(dot{x}-{dot{x}}_{0}
ight)+{k}_{1}left(x-{x}_{0}
ight)+{k}_{2}{left(x-{x}_{0}
ight)}^{3}+&qquadqquad b{f}_{
m{c}}mathrm{sgn}left[{D}^{p}(x-{x}_{0})
ight]+b{c}_{1}{D}^{p}left(x-{x}_{0}
ight)=0, &qquadqquaddot{x}left(dot{x}-{dot{x}}_{
m{0}}
ight)<0end{split}tag{2b}$$

其中, b为随磁流变液阻尼器的控制电流而变化的参数, 即半主动控制参数. 当$b = 1$时, 磁流变液阻尼器的输出阻尼力保持不变, 相当于被动控制. 分数阶阶次满足${
m{0 < }}p leqslant 1$. 分数阶微分项采用Caputo定义[35]







$${D^p}left[ {x(t)}
ight] = left{ {begin{array}{*{20}{l}}{dfrac{1}{{Gamma left( {1 - p}
ight)}}displaystyleint_0^t {dfrac{{x'(u)}}{{{{left( {t - u}
ight)}^p}}}} {
m{d}}u,}&{0<p<1}{dfrac{{{
m{d}}x(u)}}{{{
m{d}}t}},}&{p = 1}end{array}}
ight.$$
(3)

其中, $Gamma ({textit{z}})$为Gamma函数, 满足$Gamma ({textit{z}} + 1) = Gamma ({textit{z}})$.


2.
半主动控制下的近似解析解


研究系统在半主动控制下的主共振响应, 即路面施加给悬架系统的激励频率接近系统的固有频率的响应情况. 为了表达激励频率与系统固有频率的接近程度, 引入调谐参数$sigma $, 即${omega ^{
m{2}}} = omega _{
m{0}}^{
m{2}} + varepsilon sigma $, 其中, ${omega _{
m{0}}} = sqrt {{{{k_1}}/M}} $为系统的固有频率.

半主动控制采用天棚阻尼控制策略, 即







$${F_{
m{s}}}{
m{ = }}left{ {begin{array}{*{20}{c}}{{F_1},}&{dot xleft( {dot x - {{dot x}_{
m{0}}}}
ight)geqslant0}{b{F_1},}&{dot xleft( {dot x - {{dot x}_{
m{0}}}}
ight)<0,;;0leqslant b <1}end{array}}
ight.$$
(4)

式(4)中, ${F_{
m{s}}}$为磁流变液阻尼器提供的可控阻尼力.

令$y = x - {x_0}$, 式(2)可以改写为






$$begin{split} ddot y + &2varepsilon mu dot y + omega _0^2y + varepsilon {eta _1}{y^3} + varepsilon {f_{{
m{c1}}}}{
m{sgn}} left[ {{D^p}left( y
ight)}
ight] + & varepsilon {eta _2}{D^p}left( y
ight) = varepsilon fsin left( {omega t}
ight),;;left( {dot y + {{dot x}_{
m{0}}}}
ight)dot y geqslant 0 end{split}tag{5a} $$






$$begin{split} ddot y + &2varepsilon mu dot y + omega _0^2y + varepsilon {eta _1}{y^3} + bvarepsilon {f_{{
m{c1}}}}{
m{sgn}} left[ {{D^p}left( y
ight)}
ight] + & bvarepsilon {eta _2}{D^p}left( y
ight) = varepsilon fsin left( {omega t}
ight),;;left( {dot y + {{dot x}_{
m{0}}}}
ight)dot y < 0 end{split} tag{5b}$$

其中, ${
m{2}}varepsilon mu = {c/M}$, $varepsilon {eta _1} = {{{k_2}}/M}$, $varepsilon {f_{{
m{c1}}}} = {{{f_{
m{c}}}}/M}$, $varepsilon {eta _2} = $$ {{{c_1}}/M}$, $F = MA{omega ^2}$, $varepsilon f = {F/M}$.

设系统(5)在半主动控制下的周期解为






$$y = acos varphi tag{6a};;;;$$






$$dot y = - aomega sin varphi tag{6b}$$

其中, $varphi = omega t + theta $.

天棚阻尼控制策略的控制条件为







$$begin{split}& dot xleft( {dot x - {{dot x}_{
m{0}}}}
ight) = left( {dot y + {{dot x}_{
m{0}}}}
ight)dot y = &qquad a{omega ^2}sqrt {{{left( {a - Asin theta }
ight)}^2} + {{left( {Acos theta }
ight)}^2}} sin varphi sin left( {varphi - beta }
ight) end{split} $$
(7)

其中, $beta = arctan left( {dfrac{{Acos theta }}{{a - Asin theta }}}
ight)$.

当$beta > 0$时, 控制力${F_{
m{s}}}$在一个周期内的变化规律为







$${F_{
m{s}}} = left{ {begin{array}{*{20}{l}} {b{F_1},;;0 < varphi leqslant beta } {{F_1},;;beta < varphi leqslant {
m{{text{π}} }}} {b{F_1},;;{
m{{text{π}} }} < varphi leqslant {
m{{text{π}} }} + beta } {{F_1},;;{
m{{text{π}} }} + beta < varphi leqslant 2{
m{{text{π}} }}} end{array}}
ight.$$
(8)

根据平均法在一个振动周期区间$ left[{
m{0}}, T
ight]$进行积分, 对于周期函数${{T = 2{
m{{text{π}} }}}/omega }$, 可得振幅$a$与相位$theta $的近似解






$$ left. {begin{array}{*{20}{l}}dot{a}=-dfrac{1}{Tomega }{displaystyle {int }_{
m{0}}^{T}left({P}_{1}+b{P}_{2}+b{P}_{3}
ight)mathrm{sin}varphi {
m{d}}t,;; 0<varphi leqslant beta } dot{a}=-dfrac{1}{Tomega }{displaystyle {int }_{
m{0}}^{T}left({P}_{1}+{P}_{2}+{P}_{3}
ight)mathrm{sin}varphi {
m{d}}t,;; beta <varphi leqslant {
m{{text{π}} }}} dot{a}=-dfrac{1}{Tomega }{displaystyle {int }_{
m{0}}^{T}left({P}_{1}+b{P}_{2}+b{P}_{3}
ight)mathrm{sin}varphi {
m{d}}t,;; {
m{{text{π}} }}<varphi leqslant {
m{{text{π}} }}+beta } dot{a}=-dfrac{1}{Tomega }{displaystyle {int }_{
m{0}}^{T}left({P}_{1}+{P}_{2}+{P}_{3}
ight)mathrm{sin}varphi {
m{d}}t,;; {
m{{text{π}} }}+beta <varphi leqslant 2{
m{{text{π}} }}}end{array}}
ight}tag{9a}$$






$$ left. {begin{array}{*{20}{l}}adot{theta }=-dfrac{1}{Tomega }{displaystyle {int }_{
m{0}}^{T}left({P}_{1}+b{P}_{2}+b{P}_{3}
ight)mathrm{cos}varphi {
m{d}}t,;; 0<varphi leqslant beta } adot{theta }=-dfrac{1}{Tomega }{displaystyle {int }_{
m{0}}^{T}left({P}_{1}+{P}_{2}+{P}_{3}
ight)mathrm{cos}varphi {
m{d}}t,;; beta <varphi leqslant {
m{{text{π}} }}} adot{theta }=-dfrac{1}{Tomega }{displaystyle {int }_{
m{0}}^{T}left({P}_{1}+b{P}_{2}+b{P}_{3}
ight)mathrm{cos}varphi {
m{d}}t,;; {
m{{text{π}} }}<varphi leqslant {
m{{text{π}} }}+beta } adot{theta }=-dfrac{1}{Tomega }{displaystyle {int }_{
m{0}}^{T}left({P}_{1}+{P}_{2}+{P}_{3}
ight)mathrm{cos}varphi {
m{d}}t,;; {
m{{text{π}} }}+beta <varphi leqslant 2{
m{{text{π}} }}}end{array}}
ight}tag{9b}$$

其中, ${P_1}left( {a,theta }
ight) = varepsilon fsin left( {varphi - theta }
ight) + varepsilon sigma acos varphi + 2varepsilon mu aomega sin varphi -$$ varepsilon {eta _1}{left( {acos varphi }
ight)^3}$, ${P_{
m{2}}}left( {a,theta }
ight) !=! - varepsilon {f_{{
m{c1}}}}{
m{sgn}} left[ {{D^p}left( {acos varphi }
ight)}
ight]$, ${P_{
m{3}}}left( {a,theta }
ight) = $$ - varepsilon {eta _2}{D^p}left( {acos varphi }
ight)$.

将式(9)表示为







$$left. begin{array}{l} dot a{
m{ = }}{{dot a}_{
m{1}}}{
m{ + }}{{dot a}_2} + {{dot a}_3} adot theta = a{{dot theta }_1} + a{{dot theta }_2} + a{{dot theta }_3} end{array}
ight}$$
(10)

式(10)中的第一部分与无控制时相等, 即






$$begin{split} {{dot a}_1} =& - frac{1}{{{
m{2{text{π}} }}omega }}int_{
m{0}}^{{
m{2{text{π}} }}} {{P_1}left( {a,theta }
ight)sin varphi {
m{d}}varphi } {
m{ = }} & - frac{{varepsilon f}}{{{
m{2}}omega }}{
m{cos}}theta - varepsilon mu a [-12pt] end{split} tag{11a};;$$






$$begin{split} a{{dot theta }_1}{
m{ = }}& - frac{1}{{{
m{2{text{π}} }}omega }}int_{
m{0}}^{{
m{2{text{π}} }}} {{P_1}left( {a,theta }
ight)cos varphi {
m{d}}varphi } = & frac{{varepsilon f}}{{{
m{2}}omega }}{
m{sin}}theta - frac{{varepsilon sigma a}}{{{
m{2}}omega }} + frac{{3varepsilon {eta _1}{a^3}}}{{{
m{8}}omega }} [-12pt] end{split} tag{11b}$$

根据文献[31], 计算稳态响应时分数阶微分项可近似表示为







$${D^p}left( {acos varphi }
ight) = a{omega ^p}cos left( {varphi + frac{{p{
m{{text{π}} }}}}{2}}
ight)$$
(12)

利用式(12)计算式(10)的第2部分, 当 $0 < beta < $$ dfrac{{
m{{text{π}} }}}{2} - dfrac{{p{
m{{text{π}} }}}}{2}$时, 得到






$$begin{split} {{dot a}_2} = &- frac{1}{{Tomega }}int_0^T {left{ { - varepsilon {f_{{
m{c}}1}}{
m{sgn}} left[ {{D^p}left( {acos varphi }
ight)}
ight]}
ight}} sin varphi {
m{d}}t = & frac{{varepsilon {f_{{
m{c1}}}}}}{{2{
m{{text{π}} }}omega }}left( {displaystyleint_0^beta b sin varphi {
m{d}}varphi + int_beta ^{frac{{
m{{text{π}} }}}{2} - frac{{p{
m{{text{π}} }}}}{2}} {sin varphi {
m{d}}varphi } }
ight) + &{
m{ }}frac{{varepsilon {f_{{
m{c1}}}}}}{{2{
m{{text{π}} }}omega }}left[ {int_{frac{{
m{{text{π}} }}}{2} - frac{{p{
m{{text{π}} }}}}{2}}^{
m{{text{π}} }} {left( { - sin varphi }
ight){
m{d}}varphi } + int_{
m{{text{π}} }}^{{
m{{text{π}} + }}beta } {left( { - bsin varphi }
ight)} {
m{d}}varphi }
ight]{
m{ + }} &frac{{varepsilon {f_{{
m{c1}}}}}}{{2{
m{{text{π}} }}omega }}left[ {int_{{
m{{text{π}} + }}beta }^{frac{{3{
m{{text{π}} }}}}{2} - frac{{p{
m{{text{π}} }}}}{2}} {left( { - sin varphi }
ight)} {
m{d}}varphi {
m{ + }}int_{frac{{3{
m{{text{π}} }}}}{2} - frac{{p{
m{{text{π}} }}}}{2}}^{2{
m{{text{π}} }}} {sin varphi {
m{d}}varphi } }
ight] =& frac{{varepsilon {f_{{
m{c1}}}}}}{{2{
m{{text{π}} }}omega }}left[ {left( {2b - 2}
ight) + left( {2 - 2b}
ight)cos beta - 4sin {frac{{p{
m{{text{π}} }}}}{2}} }
ight] end{split} tag{13a}$$






$$begin{split} a{{dot theta }_2} = &- frac{1}{{Tomega }}int_0^T {left{ { - varepsilon {f_{{
m{c}}1}}{
m{sgn}} left[ {{D^p}left( {acos varphi }
ight)}
ight]}
ight}} cos varphi {
m{d}}t = & frac{{varepsilon {f_{{
m{c1}}}}}}{{2{
m{{text{π}} }}omega }}left( {int_0^beta {bcos varphi {
m{d}}varphi } + int_beta ^{frac{{
m{{text{π}} }}}{2} - frac{{p{
m{{text{π}} }}}}{2}} {cos varphi {
m{d}}varphi } }
ight) + & frac{{varepsilon {f_{{
m{c1}}}}}}{{2{
m{{text{π}} }}omega }}left[ {int_{frac{{
m{{text{π}} }}}{2} - frac{{p{
m{{text{π}} }}}}{2}}^{
m{{text{π}} }} {left( { - cos varphi }
ight){
m{d}}varphi } + int_{
m{{text{π}} }}^{{
m{{text{π}} + }}beta } {left( { - bcos varphi }
ight){
m{d}}varphi } }
ight] +& frac{{varepsilon {f_{{
m{c1}}}}}}{{2{
m{{text{π}} }}omega }}left[ {int_{{
m{{text{π}} + }}beta }^{frac{{3{
m{{text{π}} }}}}{2} - frac{{p{
m{{text{π}} }}}}{2}} {left( { - cos varphi }
ight)} {
m{d}}varphi {
m{ + }}int_{frac{{3{
m{{text{π}} }}}}{2} - frac{{p{
m{{text{π}} }}}}{2}}^{2{
m{{text{π}} }}} {cos varphi {
m{d}}varphi } }
ight] cdot& frac{{varepsilon {f_{{
m{c1}}}}}}{{2{
m{{text{π}} }}omega }}left[ {left( {2b - 2}
ight)sin beta + 4cos {frac{{p{
m{{text{π}} }}}}{2}} }
ight] end{split} tag{13b}$$

当$;beta geqslant dfrac{{
m{{text{π}} }}}{2} - dfrac{{p{
m{{text{π}} }}}}{2}$时, 得到






$$begin{split} {{dot a}_2} =& - frac{1}{{Tomega }}int_0^T {left{ { - varepsilon {f_{{
m{c1}}}}{
m{sgn}} left[ {{D^p}left( {acos varphi }
ight)}
ight]}
ight}} sin varphi {
m{d}}t = & frac{{varepsilon {f_{{
m{c1}}}}}}{{2{
m{{text{π}} }}omega }}left[ {int_0^{frac{{
m{{text{π}} }}}{2} - frac{{p{
m{{text{π}} }}}}{2}} {bsin varphi {
m{d}}varphi } + int_{frac{{
m{{text{π}} }}}{2} - frac{{p{
m{{text{π}} }}}}{2}}^beta {left( { - bsin varphi }
ight) {
m{d}}varphi } }
ight]+ & {
m{ }}frac{{varepsilon {f_{{
m{c1}}}}}}{{2{
m{{text{π}} }}omega }}left[ {int_beta ^{
m{{text{π}} }} {left( { - sin varphi }
ight)} {
m{d}}varphi + int_{
m{{text{π}} }}^{frac{{3{
m{{text{π}} }}}}{2} - frac{{p{
m{{text{π}} }}}}{2}} {left( { - bsin varphi }
ight)} {
m{d}}varphi }
ight] +& {
m{ }}frac{{varepsilon {f_{{
m{c1}}}}}}{{2{
m{{text{π}} }}omega }}left[ {int_{frac{{3{
m{{text{π}} }}}}{2} - frac{{p{
m{{text{π}} }}}}{2}}^{{
m{{text{π}} }} + beta } {bsin varphi {
m{d}}varphi } {
m{ + }}int_{{
m{{text{π}} }} + beta }^{2{
m{{text{π}} }}} {sin varphi {
m{d}}varphi } }
ight] =& frac{{varepsilon {f_{{
m{c1}}}}}}{{2{
m{{text{π}} }}omega }}left[ {left( {2b - 2}
ight) + left( {2b - 2}
ight)cos beta - 4bsin {frac{{p{
m{{text{π}} }}}}{2}} }
ight] end{split} tag{14a}$$






$$begin{split} a{{dot theta }_2} =& - frac{1}{{Tomega }}int_0^T {left{ { - varepsilon {f_{{
m{c1}}}}{
m{sgn}} left[ {{D^p}left( {acos varphi }
ight)}
ight]}
ight}} cos varphi {
m{d}}t = & frac{{varepsilon {f_{{
m{c1}}}}}}{{2{
m{{text{π}} }}omega }}left[ {int_0^{frac{{
m{{text{π}} }}}{2} - frac{{p{
m{{text{π}} }}}}{2}} {bcos varphi {
m{d}}varphi } + int_{frac{{
m{{text{π}} }}}{2} - frac{{p{
m{{text{π}} }}}}{2}}^beta {left( { - bcos varphi }
ight){
m{d}}varphi } }
ight] + &frac{{varepsilon {f_{{
m{c1}}}}}}{{2{
m{{text{π}} }}omega }}left[ {int_beta ^{
m{{text{π}} }} {left( { - cos varphi }
ight)} {
m{d}}varphi + int_{
m{{text{π}} }}^{frac{{3{
m{{text{π}} }}}}{2} - frac{{p{
m{{text{π}} }}}}{2}} {left( { - bcos varphi }
ight){
m{d}}varphi } }
ight] +&{
m{ }}frac{{varepsilon {f_{{
m{c1}}}}}}{{2{
m{{text{π}} }}omega }}left[ {int_{frac{{3{
m{{text{π}} }}}}{2} - frac{{p{
m{{text{π}} }}}}{2}}^{{
m{{text{π}} }} + beta } {bcos varphi {
m{d}}varphi } {
m{ + }}int_{{
m{{text{π}} }} + beta }^{2{
m{{text{π}} }}} {cos varphi {
m{d}}varphi } }
ight] =& frac{{varepsilon {f_{{
m{c1}}}}}}{{2{
m{{text{π}} }}omega }}left[ {left( { - 2b + 2}
ight)sin beta + 4bcos {frac{{p{
m{{text{π}} }}}}{2}} }
ight] end{split} tag{14b}$$

利用式(12)计算式(10)的第3部分, 可以得到






$$begin{split}& {{dot a}_3} = - frac{1}{{Tomega }}int_0^T {left[ { - varepsilon {eta _2}{D^p}left( {acos varphi }
ight)}
ight]} sin varphi {
m{d}}t = & frac{{varepsilon {eta _2}a{omega ^p}}}{{2{
m{{text{π}} }}omega }}left[ {int_0^beta {bcos left( {frac{{p{
m{{text{π}} }}}}{2} !+! varphi }
ight)} sin varphi {
m{d}}varphi {
m{ + }}!!int_beta ^{
m{{text{π}} }} {cos left( {frac{{p{
m{{text{π}} }}}}{2} !+! varphi }
ight)} sin varphi {
m{d}}varphi }
ight.!cdot & left. {int_{
m{{text{π}} }}^{{
m{{text{π}} + }}beta } {bcos left( {frac{{p{
m{{text{π}} }}}}{2} + varphi }
ight)} sin varphi {
m{d}}varphi {
m{ + }}int_{{
m{{text{π}} + }}beta }^{2{
m{{text{π}} }}} {cos left( {frac{{p{
m{{text{π}} }}}}{2} + varphi }
ight)} sin varphi {
m{d}}varphi }
ight] = & frac{{varepsilon {eta _2}a{omega ^p}}}{{2{
m{{text{π}} }}omega }}left{ { - frac{1}{2}bleft[ { - cos left( {frac{{p{
m{{text{π}} }}}}{2}}
ight) + cos left( {2beta + frac{{p{
m{{text{π}} }}}}{2}}
ight) + 2beta sin {frac{{p{
m{{text{π}} }}}}{2}} }
ight]}
ight. + & frac{1}{2} {left[ { - cos {frac{{p{
m{{text{π}} }}}}{2}} + cos left( {2beta + frac{{p{
m{{text{π}} }}}}{2}}
ight) + 2left( {beta - {
m{{text{π}} }}}
ight)sin {frac{{p{
m{{text{π}} }}}}{2}} }
ight]} Biggr} [-15pt]end{split} tag{15a}$$






$$begin{split}& a{{dot theta }_3} = - frac{1}{{Tomega }}int_0^T {left[ { - varepsilon {eta _2}{D^p}left( {acos varphi }
ight)}
ight]} cos varphi {
m{d}}t =frac{{varepsilon {eta _2}a{omega ^p}}}{{2{
m{{text{π}} }}omega }} & left[ {int_0^beta {bcos left( {frac{{p{
m{{text{π}} }}}}{2} + varphi }
ight)} cos varphi {
m{d}}varphi {
m{ + }}int_beta ^{
m{{text{π}} }} {cos left( {frac{{p{
m{{text{π}} }}}}{2} + varphi }
ight)} cos varphi {
m{d}}varphi }
ight. + & {
m{ }}left. {int_{
m{{text{π}} }}^{{
m{{text{π}} + }}beta } {bcos left( {frac{{p{
m{{text{π}} }}}}{2} + varphi }
ight)} cos varphi {
m{d}}varphi {
m{ + }}int_{{
m{{text{π}} + }}beta }^{2{
m{{text{π}} }}} {cos left( {frac{{p{
m{{text{π}} }}}}{2} + varphi }
ight)} cos varphi {
m{d}}varphi }
ight] =& frac{{varepsilon {eta _2}a{omega ^p}}}{{2{
m{{text{π}} }}omega }}Biggr{ {left( { - beta + {
m{{text{π}} }}}
ight)cos {frac{{p{
m{{text{π}} }}}}{2}} - cos left( {beta + frac{{p{
m{{text{π}} }}}}{2}}
ight)sin beta } + & b {left[ {beta cos {frac{{p{
m{{text{π}} }}}}{2}} + cos left( {beta + frac{{p{
m{{text{π}} }}}}{2}}
ight)sin beta }
ight]} Biggr} [-15pt]end{split} tag{15b}$$

为简化上面计算结果, 令






$${B_1} = left{ !!!{begin{array}{*{20}{l}} { {left( {2b - 2}
ight) + left( {2 - 2b}
ight)cos beta - 4sin {dfrac{{p{
m{{text{π}} }}}}{2}} } ,;;beta < dfrac{{
m{{text{π}} }}}{2} - dfrac{{p{
m{{text{π}} }}}}{2}} {{left( {2b - 2}
ight) + left( {2b - 2}
ight)cos beta - 4bsin {dfrac{{p{
m{{text{π}} }}}}{2}} } ,;;beta geqslant dfrac{{
m{{text{π}} }}}{2} - dfrac{{p{
m{{text{π}} }}}}{2}} end{array}}
ight.tag{16a}$$






$${B_2} = left{ {begin{array}{*{20}{l}} { {left( {2b - 2}
ight)sin beta + 4cos {dfrac{{p{
m{{text{π}} }}}}{2}} } ,;;beta < dfrac{{
m{{text{π}} }}}{2} - dfrac{{p{
m{{text{π}} }}}}{2}} { {left( { - 2b + 2}
ight)sin beta + 4bcos {dfrac{{p{
m{{text{π}} }}}}{2}} } ,;;beta geqslant dfrac{{
m{{text{π}} }}}{2} - dfrac{{p{
m{{text{π}} }}}}{2}} end{array}}
ight.;;;;;;;;;;;;;tag{16b}$$






$$begin{split} {C_1}{
m{ = }}& { - dfrac{1}{2}bleft[ { - cos {dfrac{{p{
m{{text{π}} }}}}{2}} + cos left( {2beta + dfrac{{p{
m{{text{π}} }}}}{2}}
ight) + 2beta sin {dfrac{{p{
m{{text{π}} }}}}{2}} }
ight]} + & dfrac{1}{2} {left[ { - cos {dfrac{{p{
m{{text{π}} }}}}{2}} + cos left( {2beta + dfrac{{p{
m{{text{π}} }}}}{2}}
ight) + 2left( {beta - {
m{{text{π}} }}}
ight)sin {dfrac{{p{
m{{text{π}} }}}}{2}} }
ight]} end{split} ;;;;;;tag{16c}$$






$$begin{split} {C_{
m{2}}}{
m{ = }}& {left( { - beta + {
m{{text{π}} }}}
ight)cos {frac{{p{
m{{text{π}} }}}}{2}} - cos left( {beta + frac{{p{
m{{text{π}} }}}}{2}}
ight)sin beta } + & b {left[ {beta cos {frac{{p{
m{{text{π}} }}}}{2}} + cos left( {beta + frac{{p{
m{{text{π}} }}}}{2}}
ight)sin beta }
ight]} end{split};;;;;;;;;;;;;;;;tag{16d} $$

将上述计算结果整理为







$$left. begin{array}{l} dot a = - dfrac{{varepsilon f}}{{{
m{2}}omega }}{
m{cos}}theta - varepsilon mu a + dfrac{{varepsilon {f_{{
m{c1}}}}{B_1}}}{{2{
m{{text{π}} }}omega }} + dfrac{{varepsilon {eta _2}a{omega ^p}{C_1}}}{{2{
m{{text{π}} }}omega }} adot theta = dfrac{{varepsilon f}}{{{
m{2}}omega }}{
m{sin}}theta - dfrac{{varepsilon sigma a}}{{{
m{2}}omega }} + dfrac{{3varepsilon {eta _1}{a^3}}}{{{
m{8}}omega }} + dfrac{{varepsilon {f_{{
m{c1}}}}{B_2}}}{{2{
m{{text{π}} }}omega }} + dfrac{{varepsilon {eta _2}a{omega ^p}{C_2}}}{{2{
m{{text{π}} }}omega }} end{array}
ight}$$
(17)

将系统原参数代入式(17), 可以得到







$$left. {begin{array}{*{20}{l}} {dot a = - dfrac{F}{{{
m{2}}Momega }}{
m{cos}}theta - dfrac{{ca}}{{2M}} + dfrac{{{f_{
m{c}}}B}}{{2{
m{{text{π}} }}Momega }} + dfrac{{{c_1}a{omega ^{p - 1}}{C_1}}}{{2{
m{{text{π}} }}M}}} adot theta = dfrac{F}{{{
m{2}}Momega }}{
m{sin}}theta - left( {dfrac{omega }{2} - dfrac{{{k_1}}}{{2Momega }}}
ight)a + dfrac{{3{k_2}{a^3}}}{{{
m{8}}Momega }} + dfrac{{{f_{
m{c}}}{B_2}}}{{2{
m{{text{π}} }}Momega }} + qquaddfrac{{{c_1}a{omega ^{p - 1}}{C_2}}}{{2{
m{{text{π}} }}M}} end{array}}
ight}$$
(18)

当$;beta leqslant 0$时, 控制力${F_{
m{s}}}$在一个周期内的变化规律为







$${F_{
m{s}}} = left{ {begin{array}{*{20}{l}} {{F_1},begin{array}{*{20}{c}} {} end{array}begin{array}{*{20}{c}} {} end{array}0 < varphi leqslant {
m{{text{π}} }} + beta } {b{F_1},begin{array}{*{20}{c}} {} end{array}{
m{{text{π}} }} + beta < varphi leqslant {
m{{text{π}} }}} {{F_1},begin{array}{*{20}{c}} {} end{array}begin{array}{*{20}{c}} {} end{array}{
m{{text{π}} }} < varphi leqslant 2{
m{{text{π}} }} + beta } {b{F_1},begin{array}{*{20}{c}} {} end{array}2{
m{{text{π}} }} + beta < varphi leqslant 2{
m{{text{π}} }}} end{array}}
ight.$$
(19)

利用相同的方法可以得到当$beta leqslant 0$时的振幅$a$与相位$theta $的近似解为







$$left. {begin{array}{*{20}{l}} {dot a = - dfrac{F}{{{
m{2}}Momega }}{
m{cos}}theta - dfrac{{ca}}{{2M}} + dfrac{{{f_{
m{c}}}B{B_1}}}{{2{
m{{text{π}} }}Momega }} + dfrac{{{c_1}a{omega ^{p - 1}}C{C_1}}}{{2{
m{{text{π}} }}M}}} adot theta = dfrac{F}{{{
m{2}}Momega }}{
m{sin}}theta - left( {dfrac{omega }{2} - dfrac{{{k_1}}}{{2Momega }}}
ight)a + dfrac{{3{k_2}{a^3}}}{{{
m{8}}Momega }} + dfrac{{{f_{
m{c}}}B{B_2}}}{{2{
m{{text{π}} }}Momega }} + qquad dfrac{{{c_1}a{omega ^{p - 1}}C{C_2}}}{{2{
m{{text{π}} }}M}} end{array}}
ight}$$
(20)

其中






$$B{B_1} = left{ {begin{array}{*{20}{l}} {left( {2 - 2b}
ight) + left( {2b - 2}
ight)cos beta - 4sin {dfrac{{p{
m{{text{π}} }}}}{2}} } , qquaddfrac{{
m{{text{π}} }}}{2} - dfrac{{p{
m{{text{π}} }}}}{2} < {
m{{text{π}} }} + beta {left( {2 - 2b}
ight) + left( {2 - 2b}
ight)cos beta - 4bsin {dfrac{{p{
m{{text{π}} }}}}{2}} } , qquad {
m{{text{π}} }} + beta leqslant dfrac{{
m{{text{π}} }}}{2} - dfrac{{p{
m{{text{π}} }}}}{2}end{array}}
ight.tag{21a}$$






$$B{B_2} = left{ {begin{array}{*{20}{l}} {left( {2 - 2b}
ight)sin beta + 4cos {dfrac{{p{
m{{text{π}} }}}}{2}} } , qquaddfrac{{
m{{text{π}} }}}{2} - dfrac{{p{
m{{text{π}} }}}}{2} < {
m{{text{π}} }} + beta {left( {2b - 2}
ight)sin beta + 4bcos {dfrac{{p{
m{{text{π}} }}}}{2}} } , qquad {
m{{text{π}} }} + beta leqslant dfrac{{
m{{text{π}} }}}{2} - dfrac{{p{
m{{text{π}} }}}}{2} end{array}}
ight.;;;;;;;;;;;;;;;;;;tag{21b}$$






$$begin{split} C{C_{
m{1}}}{
m{ = }}& {dfrac{1}{2}bleft[ { - cos {dfrac{{p{
m{{text{π}} }}}}{2}} + cos left( {2beta + dfrac{{p{
m{{text{π}} }}}}{2}}
ight) + 2beta sin {dfrac{{p{
m{{text{π}} }}}}{2}} }
ight]} + & dfrac{1}{2} {left[ {cos {dfrac{{p{
m{{text{π}} }}}}{2}} - cos left( {2beta + dfrac{{p{
m{{text{π}} }}}}{2}}
ight) - 2left( {beta + {
m{{text{π}} }}}
ight)sin {dfrac{{p{
m{{text{π}} }}}}{2}} }
ight]} end{split} tag{21c}$$






$$begin{split} C{C_{
m{2}}}{
m{ = }}& {left( {beta + {
m{{text{π}} }}}
ight)cos {frac{{p{
m{{text{π}} }}}}{2}} + cos left( {beta + frac{{p{
m{{text{π}} }}}}{2}}
ight)sin beta } - & b {left[ {beta cos {frac{{p{
m{{text{π}} }}}}{2}} + cos left( {beta + frac{{p{
m{{text{π}} }}}}{2}}
ight)sin beta }
ight]} end{split} ;;;;;;;;;;;;;;;;tag{21d}$$


3.
定常解及其稳定性分析



3.1
半主动控制的定常解


研究系统的定常解, 设$bar a$和$bar theta $分别是稳态解相对应的振幅和相位, 令式(18)中的$dot a = 0$, $adot theta = 0$, 可得系统在$;beta > 0$时的定常解为






$$F{
m{cos}}bar theta = - comega bar a + frac{{{f_{
m{c}}}}}{{
m{{text{π}} }}}{B_1} + frac{{{c_1}bar a{omega ^p}}}{{
m{{text{π}} }}}{C_1}tag{22a}qquadqquad;;;;;;$$






$$F{
m{sin}}bar theta = left( {M{omega ^2} - {k_1}}
ight)bar a - frac{{3{k_2}{{bar a}^3}}}{{
m{4}}} - frac{{{f_{
m{c}}}}}{{
m{{text{π}} }}}{B_2} - frac{{{c_1}bar a{omega ^p}}}{{
m{{text{π}} }}}{C_2}tag{22b}$$

将$F = MA{omega ^2}$代入式(22)中并消去$bar theta $, 可以得到系统在半主动控制下且$beta > 0$时的幅频响应方程和相频响应方程为






$$begin{split} {left( {MA{omega ^2}}
ight)^2} =& {left[ { - comega bar a + frac{{{f_{
m{c}}}}}{{
m{{text{π}} }}}{B_1} + frac{{{c_1}bar a{omega ^p}}}{{
m{{text{π}} }}}{C_1}}
ight]^2} + & {left[ {left( {M{omega ^2} - {k_1}}
ight)bar a - frac{{3{k_2}{{bar a}^3}}}{{
m{4}}} - frac{{{f_{
m{c}}}}}{{
m{{text{π}} }}}{B_2} - frac{{{c_1}bar a{omega ^p}}}{{
m{{text{π}} }}}{C_2}}
ight]^2} end{split} tag{23a}$$






$$tan bar theta {
m{ = }}dfrac{{left( {M{omega ^2} - {k_1}}
ight)bar a - dfrac{{3{k_2}{{bar a}^3}}}{{
m{4}}} - dfrac{{{f_{
m{c}}}}}{{
m{{text{π}} }}}{B_2} - dfrac{{{c_1}bar a{omega ^p}}}{{
m{{text{π}} }}}{C_2}}}{{ - comega bar a + dfrac{{{f_{
m{c}}}}}{{
m{{text{π}} }}}{B_1} + dfrac{{{c_1}bar a{omega ^p}}}{{
m{{text{π}} }}}{C_1}}}tag{23b}$$

令式(20)中的$dot a = 0$, $adot theta = 0$, 可得系统在$beta leqslant 0$时定常解为






$$F{
m{cos}}bar theta = - comega bar a + dfrac{{{f_{
m{c}}}}}{{
m{{text{π}} }}}B{B_1} + dfrac{{{c_1}bar a{omega ^p}}}{{
m{{text{π}} }}}C{C_1}tag{24a}qquadqquad$$






$$F{
m{sin}}bar theta = left( {M{omega ^2} - {k_1}}
ight)bar a - frac{{3{k_2}{{bar a}^3}}}{{
m{4}}} - frac{{{f_{
m{c}}}}}{{
m{{text{π}} }}}B{B_2} - frac{{{c_1}bar a{omega ^p}}}{{
m{{text{π}} }}}C{C_2}tag{24b}$$

同样将$F = MA{omega ^2}$代入式(24)中并消去${bar theta _1}$, 得到系统在$beta leqslant 0$时的幅频响应方程和相频响应方程为






$$begin{split}& {left( {MA{omega ^2}}
ight)^2} = {left( { - comega bar a + frac{{{f_{
m{c}}}}}{{
m{{text{π}} }}}B{B_1} + frac{{{c_1}bar a{omega ^p}}}{{
m{{text{π}} }}}C{C_1}}
ight)^2} + &qquad {left[ {left( {M{omega ^2} - {k_1}}
ight)bar a - frac{{3{k_2}{{bar a}^3}}}{{
m{4}}} - frac{{{f_{
m{c}}}}}{{
m{{text{π}} }}}B{B_2} - frac{{{c_1}bar a{omega ^p}}}{{
m{{text{π}} }}}C{C_2}}
ight]^2} end{split} tag{25a}$$






$$tan bar theta {
m{ = }}dfrac{{left( {M{omega ^2} - {k_1}}
ight)bar a - dfrac{{3{k_2}{{bar a}^3}}}{{
m{4}}} - dfrac{{{f_{
m{c}}}}}{{
m{{text{π}} }}}B{B_2} - dfrac{{{c_1}bar a{omega ^p}}}{{
m{{text{π}} }}}C{C_2}}}{{ - comega bar a + dfrac{{{f_{
m{c}}}}}{{
m{{text{π}} }}}B{B_1} + dfrac{{{c_1}bar a{omega ^p}}}{{
m{{text{π}} }}}C{C_{_1}}}}tag{25b}$$


3.2
半主动控制下的稳定性分析


分析定常解的稳定性, 令$a = bar a + Delta a$, $theta = bar theta + Delta theta $, 当$;beta > 0$时, 代入式(18)中进行线性化可以得到






$$frac{{{
m{d}}Delta a}}{{{
m{d}}t}} = left( { - frac{c}{{2M}} + frac{{{c_1}{omega ^{p - 1}}{C_1}}}{{{
m{2{text{π}} }}M}}}
ight)Delta a + frac{{MA{omega ^2}sin bar theta }}{{{
m{2}}Momega }}Delta theta tag{26a}$$






$$begin{split} dfrac{{{
m{d}}Delta theta }}{{{
m{d}}t}} =& left( { - dfrac{{MA{omega ^2}{
m{sin}}bar theta }}{{{
m{2}}Momega {{bar a}^2}}} + dfrac{{3{k_2}bar a}}{{4Momega }} - dfrac{{{f_{
m{c}}}}}{{{
m{2{text{π}} }}Momega {{bar a}^2}}}{B_2}}
ight)Delta a + & dfrac{{MA{omega ^2}cos bar theta }}{{{
m{2}}Momega bar a}}Delta theta end{split} tag{26b}$$

进一步得到系统的特征行列式为







$$Delta left[ {begin{array}{*{20}{c}} { - dfrac{c}{{2M}} + dfrac{{{c_1}{omega ^{p - 1}}{C_1}}}{{{
m{2{text{π}} }}M}} - lambda }&{dfrac{{{S_1}}}{{{
m{2}}Momega }}} S&{dfrac{{{S_2}}}{{2Momega bar a}} - lambda } end{array}}
ight] = 0$$
(27)

其中






$$begin{split}&{S_1} = left( {M{omega ^2} - {k_1}}
ight)bar a - dfrac{{3{k_2}{{bar a}^3}}}{{
m{4}}} - dfrac{{{f_{
m{c}}}}}{{
m{{text{π}} }}}{B_2} - dfrac{{{c_1}bar a{omega ^p}}}{{
m{{text{π}} }}}{C_2}&{S_2} = - comega bar a + frac{{{f_{
m{c}}}}}{{
m{{text{π}} }}}{B_1} + frac{{{c_1}bar a{omega ^p}}}{{
m{{text{π}} }}}{C_1}&S = - frac{{{S_1}}}{{{
m{2}}Momega {{bar a}^2}}} + frac{{3{k_2}bar a}}{{4Momega }} - frac{{{f_{
m{c}}}}}{{{
m{2{text{π}} }}Momega {{bar a}^2}}}cos frac{{p{
m{{text{π}} }}}}{2}end{split} $$

将式(27)展开, 得到系统的特征方程为







$${lambda ^2} + Plambda + Q = 0$$
(28)

其中






$$begin{split}P{
m{ = }}&frac{c}{{2M}} - frac{{{c_1}{C_1}{omega ^{p - 1}}}}{{2{
m{{text{π}} }}M}} - frac{{{S_2}}}{{2Momega bar a}} Q =& - frac{{3{S_1}{k_2}bar a}}{{8{M^2}{omega ^2}}} + frac{{S_1^2}}{{4{M^2}{omega ^2}{{bar a}^2}}} - frac{{c{S_2}}}{{4{M^2}omega bar a}} + & frac{{{c_1}{C_1}{S_2}{omega ^{p - 2}}}}{{4{
m{{text{π}} }}{M^2}bar a}} + frac{{{S_1}{f_{
m{c}}}}}{{{
m{4{text{π}} }}{M^2}{omega ^2}{{bar a}^2}}}cos {frac{{p{
m{{text{π}} }}}}{2}} end{split} $$

同理, 当$beta leqslant 0$时, 系统的特征行列式为







$$det left[ {begin{array}{*{20}{c}} { - dfrac{c}{{2M}} + dfrac{{{c_1}{omega ^{p - 1}}C{C_1}}}{{{
m{2{text{π}} }}M}} - lambda }&{dfrac{{S{S_1}}}{{{
m{2}}Momega }}} {SS}&{dfrac{{S{S_2}}}{{2Momega bar a}} - lambda } end{array}}
ight] = 0$$
(29)

其中






$$begin{split} &S{S_1} = left( {M{omega ^2} - {k_1}}
ight)bar a - frac{{3{k_2}{{bar a}^3}}}{{
m{4}}} - frac{{{f_{
m{c}}}}}{{
m{{text{π}} }}}B{B_2} - frac{{{c_1}bar a{omega ^p}}}{{
m{{text{π}} }}}C{C_2}&S{S_2} = - comega bar a + frac{{{f_{
m{c}}}}}{{
m{{text{π}} }}}B{B_1} + frac{{{c_1}bar a{omega ^p}}}{{
m{{text{π}} }}}C{C_1}&SS = - frac{{S{S_1}}}{{{
m{2}}Momega {{bar a}^2}}} + frac{{3{k_2}bar a}}{{4Momega }} - frac{{{f_{
m{c}}}}}{{{
m{2{text{π}} }}Momega {{bar a}^2}}}cos frac{{p{
m{{text{π}} }}}}{2}end{split}$$

将式(29)展开, 得到系统的特征方程为







$${lambda ^2} + Plambda + Q = 0$$
(30)

其中 $P{
m{ = }}dfrac{c}{{2M}} - dfrac{{{c_1}C{C_1}{omega ^{p - 1}}}}{{2{
m{{text{π}} }}M}} - dfrac{{S{S_2}}}{{2Momega bar a}}$






$$begin{split} Q =& - dfrac{{3S{S_1}{k_2}bar a}}{{8{M^2}{omega ^2}}} + dfrac{{SS_1^2}}{{4{M^2}{omega ^2}{{bar a}^2}}} - dfrac{{cS{S_2}}}{{4{M^2}omega bar a}} + & dfrac{{{c_1}C{C_1}S{S_2}{omega ^{p - 2}}}}{{4{
m{{text{π}} }}{M^2}bar a}} + dfrac{{S{S_1}{f_{
m{c}}}}}{{{
m{4{text{π}} }}{M^2}{omega ^2}{{bar a}^2}}}cos {dfrac{{p{
m{{text{π}} }}}}{2}} end{split} $$

经分析可知$P$恒大于零, 根据李雅普诺夫稳定性理论, $P > 0$, $Q > 0$是奇点$left( {bar a,bar theta }
ight)$渐进稳定的充分条件. 因此系统的定常解的稳定性条件为







$$Q > 0$$
(31)

且当系统有多值解时, 中间的一支解为不稳定解.


4.
数值解验证


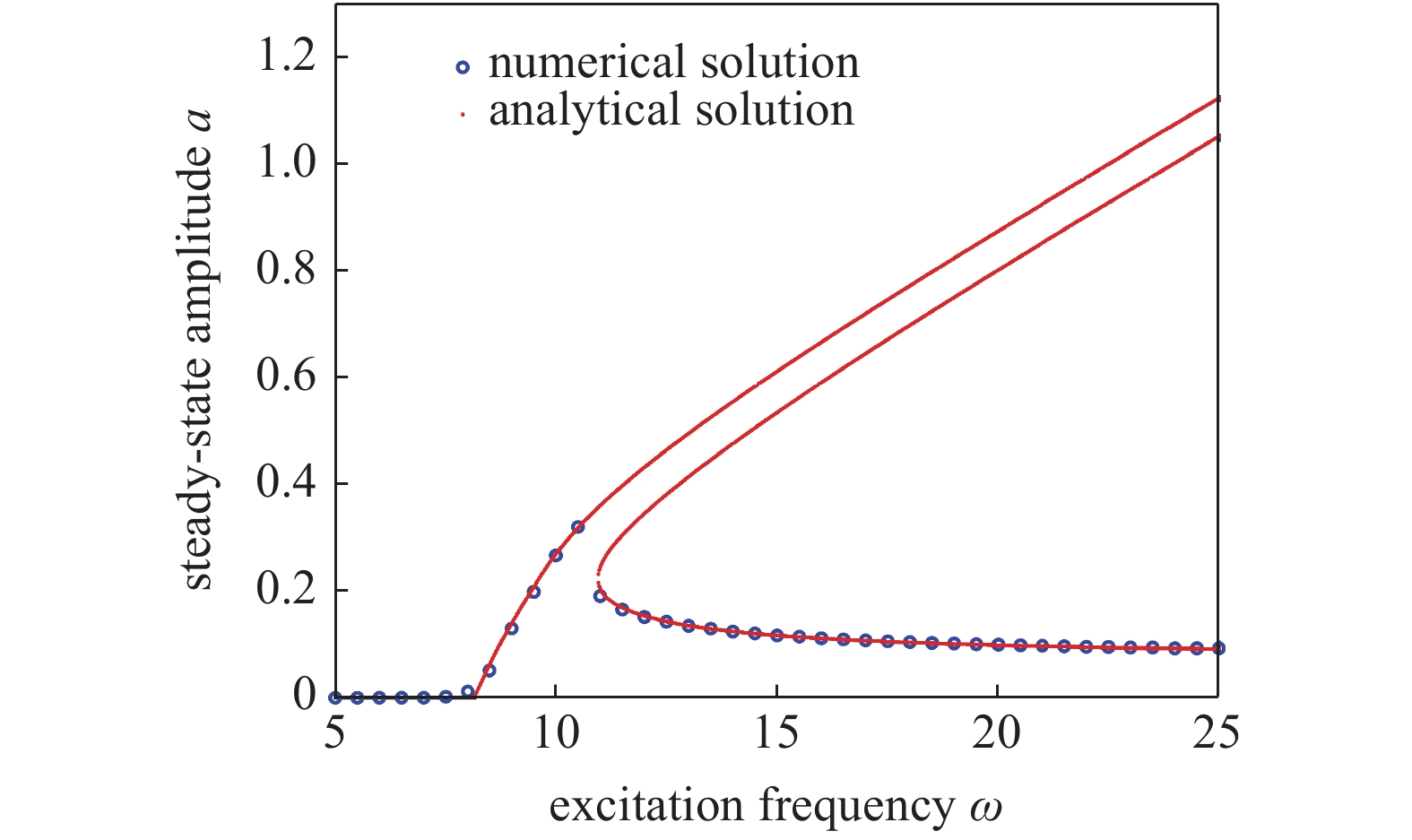
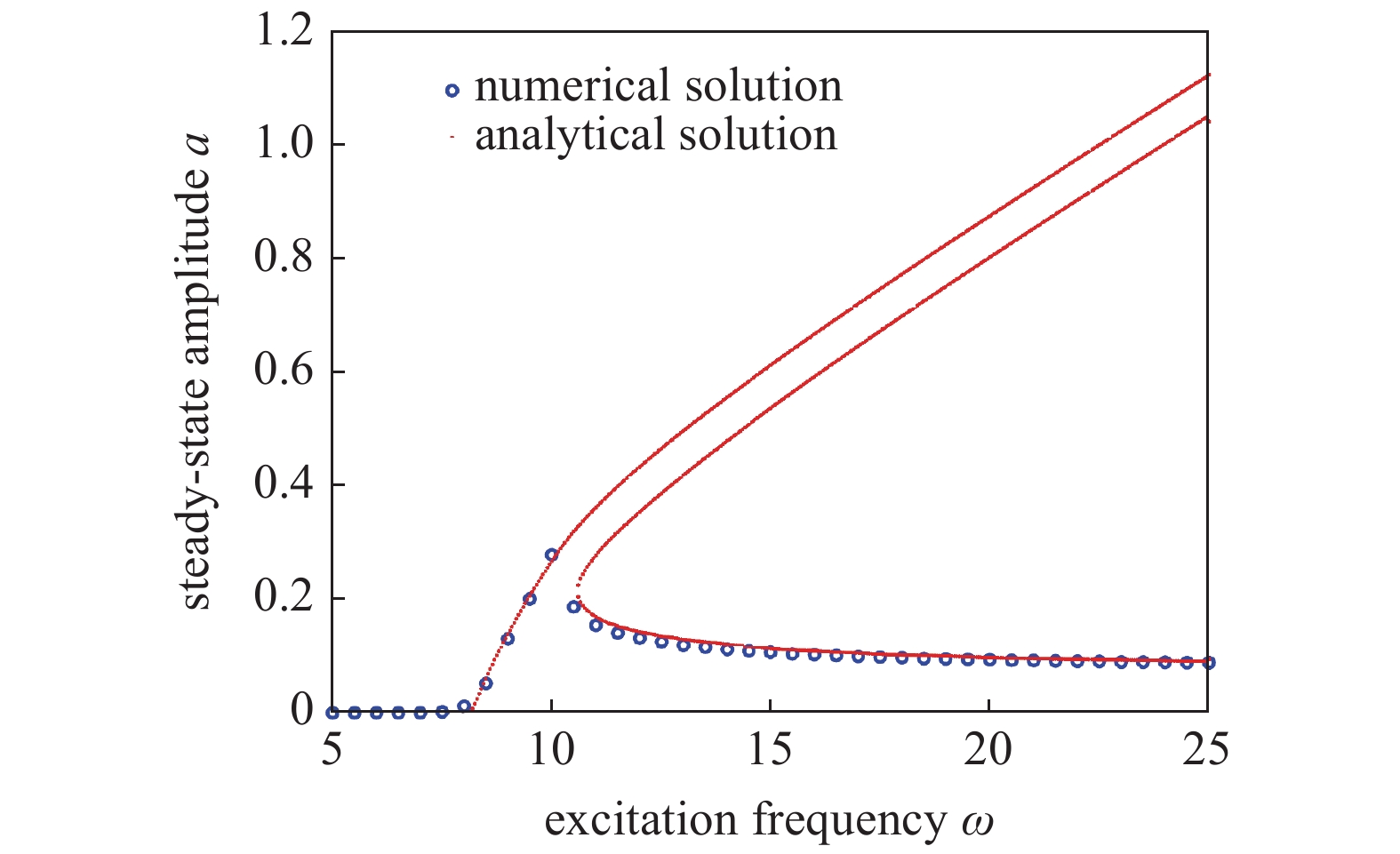
选择一组参数验证解析解的正确性. 选择文献[8, 36-38]中的参数值, 悬架系统的具体参数选择为: $M = {
m{240;kg}}$, $c = {
m{50;Ncdot s/m}}$, ${k_1} = 1{
m{5}};000;{
m{N/m}}$, ${k_2} = $$ {
m{15}}0;000;{
m{N/}}{{
m{m}}^{
m{3}}}$, 磁流变液阻尼器的参数选择为: ${c_1} = $$ 300;{
m{Ncdot s/m}}$, $p = 0.8{
m{4}}$, ${f_{
m{c}}} = 1000;{
m{N}}$. 路面激励幅值为$A = {
m{0}}{
m{.08}}$ m. 通过Matlab对系统进行数值计算, 利用幂级数法[35]绘制幅频响应曲线, 时间总长设定为150 s, 步长设定为0.001 s, 并将后30 s响应的最大值作为稳态响应的峰值. 当悬架系统在被动控制即$b = 1$时, 其数值计算结果如图2所示. 根据式(23a)和式(25a)的幅频响应方程, 利用系统的近似解析解将幅频曲线也绘制在图2中. 当悬架系统在半主动控制下即$b = 0.1$时的对比结果如图3所示. 从图中可以看出近似解析解和数值解具有较好的一致性, 从而验证了半主动控制解析解计算过程的正确性. 从图2中数值解可以看出当激励频率比较小时, 幅频曲线的幅值响应很小, 出现这种现象的原因是当激励频率较小时, 传递到磁流变液阻尼器的外力不足以克服其内部的剪切摩擦力${f_{
m{c}}}$, 此时的磁流变液阻尼器几乎没有运动, 即悬架的簧载质量与路面的相对位移很小. 由于在车辆悬架系统中存在限位块, 当系统有多解现象时幅值大的上支渐进稳定解在实际应用中并不会出现.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-137-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
系统在被动控制下的幅频响应



Figure
2.
Amplitude-frequency response of system under passive control



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-137-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
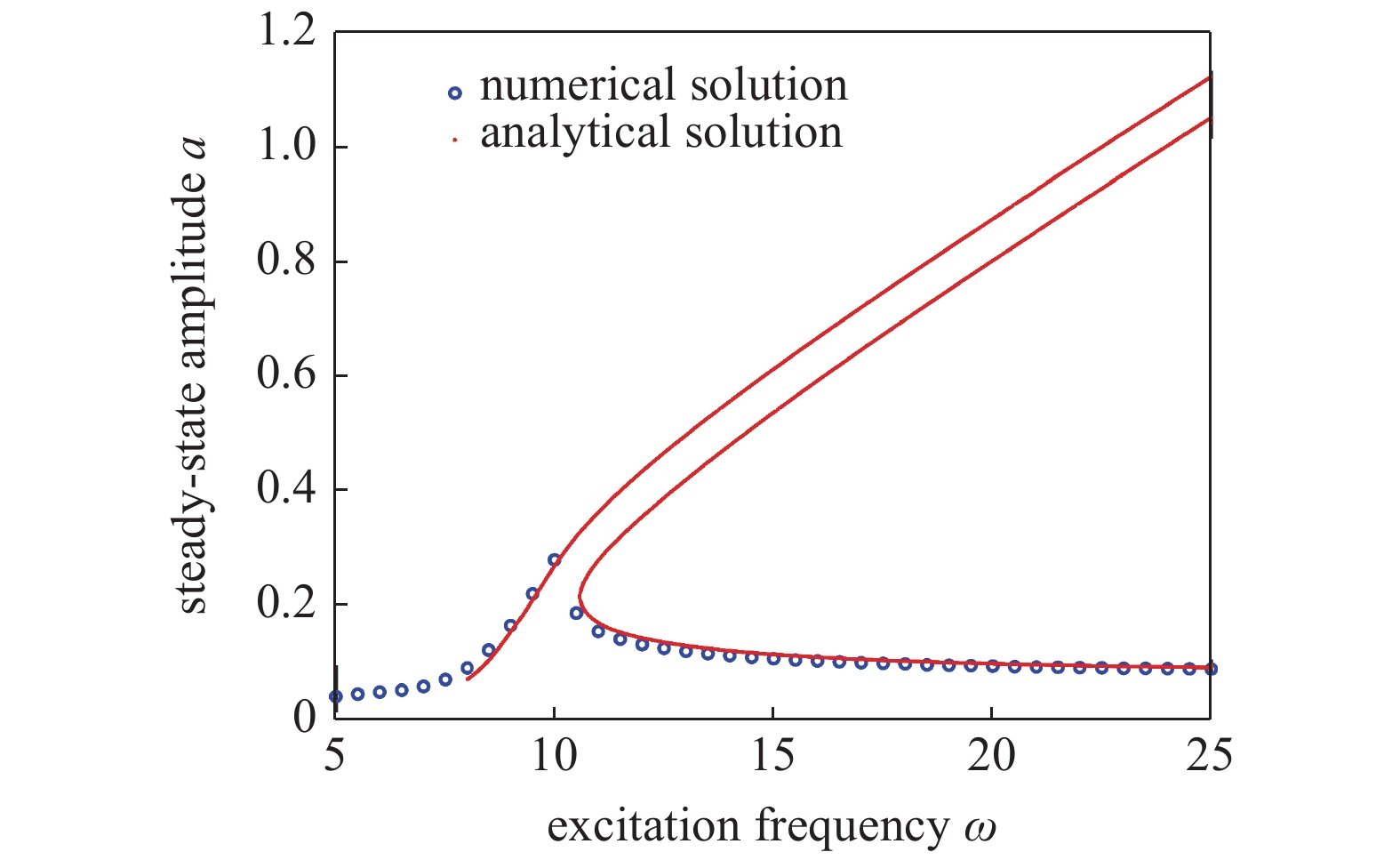
系统在半主动控制下的幅频响应



Figure
3.
Amplitude-frequency response of system under semi-active control



下载:
全尺寸图片
幻灯片



5.
半主动控制对乘坐舒适性的影响


基于单自由度车辆悬架模型研究半主动控制对车辆乘坐舒适性的影响, 仅考虑垂直方向的振动控制效果. 接下来通过比较悬架系统在半主动控制和被动控制下的簧载质量垂直方向的加速度均方根值来说明半主动控制对车辆乘坐舒适性方面的影响. 首先对簧载质量的加速度时间历程进行频谱分析, 得到功率谱密度函数${G_{
m{a}}}left( f
ight)$, 然后根据下式计算加速度均方根值[39]







$${a_{
m{s}}} = sqrt {int_{{
m{0}}{
m{.5}}}^{{
m{80}}} {{W^2}left( f
ight){G_{
m{a}}}left( f
ight){
m{d}}f} } $$
(32)

其中, $Wleft( f
ight)$为频率加权函数







$$Wleft( f
ight) = left{ {begin{array}{*{20}{l}} {0.5}, {f/4}, 1, {12.5/f} ,end{array}}
ight.begin{array}{*{20}{l}} { {0.5 leqslant f < 2} } { {2 leqslant f < 4} } { {4 leqslant f < 12.5} } { {12.5 leqslant f < 80} } end{array}$$
(33)

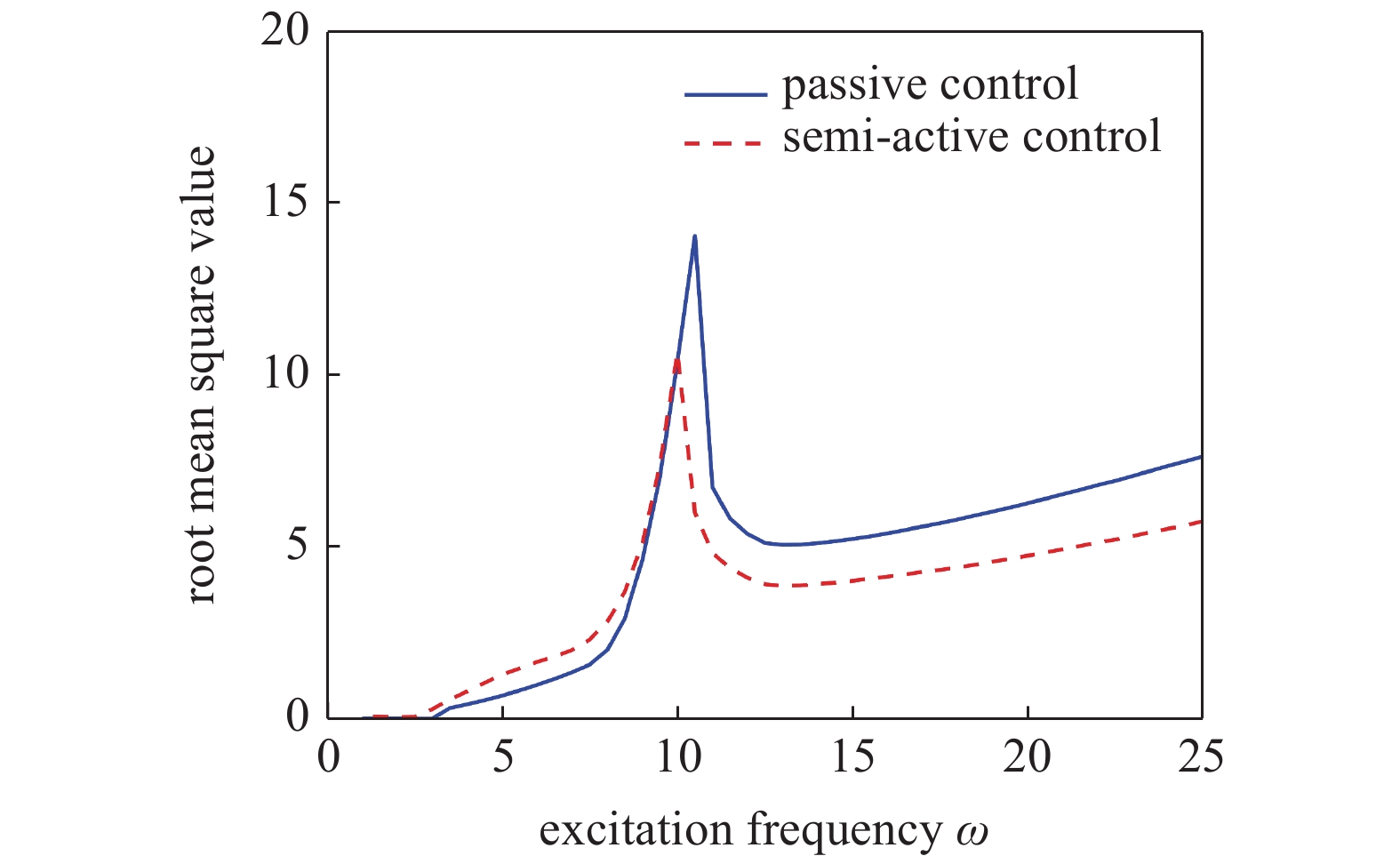
利用数值计算得到悬架系统在被动控制和半主动控制下, 簧载质量的加速度均方根值对比图, 如图4所示. 横坐标为激励频率, 纵坐标为簧载质量的加速度均方根值, 半主动控制参数$b = 0.1$, 振动分析时间选择120 s, 其他参数值保持不变. 从图4中可以发现悬架在半主动控制下, 当路面激励频率较小时, 簧载质量的加速度均方根值反而比被动控制时还大, 说明在车辆悬架的低频激励区域, 基于磁流变液阻尼器的半主动控制无法起到提高乘坐舒适性的作用. 而当路面激励频率较大时, 半主动控制在提高乘坐舒适性方面起到了很好的作用.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-137-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
加速度均方根值



Figure
4.
RMS of acceleration



下载:
全尺寸图片
幻灯片


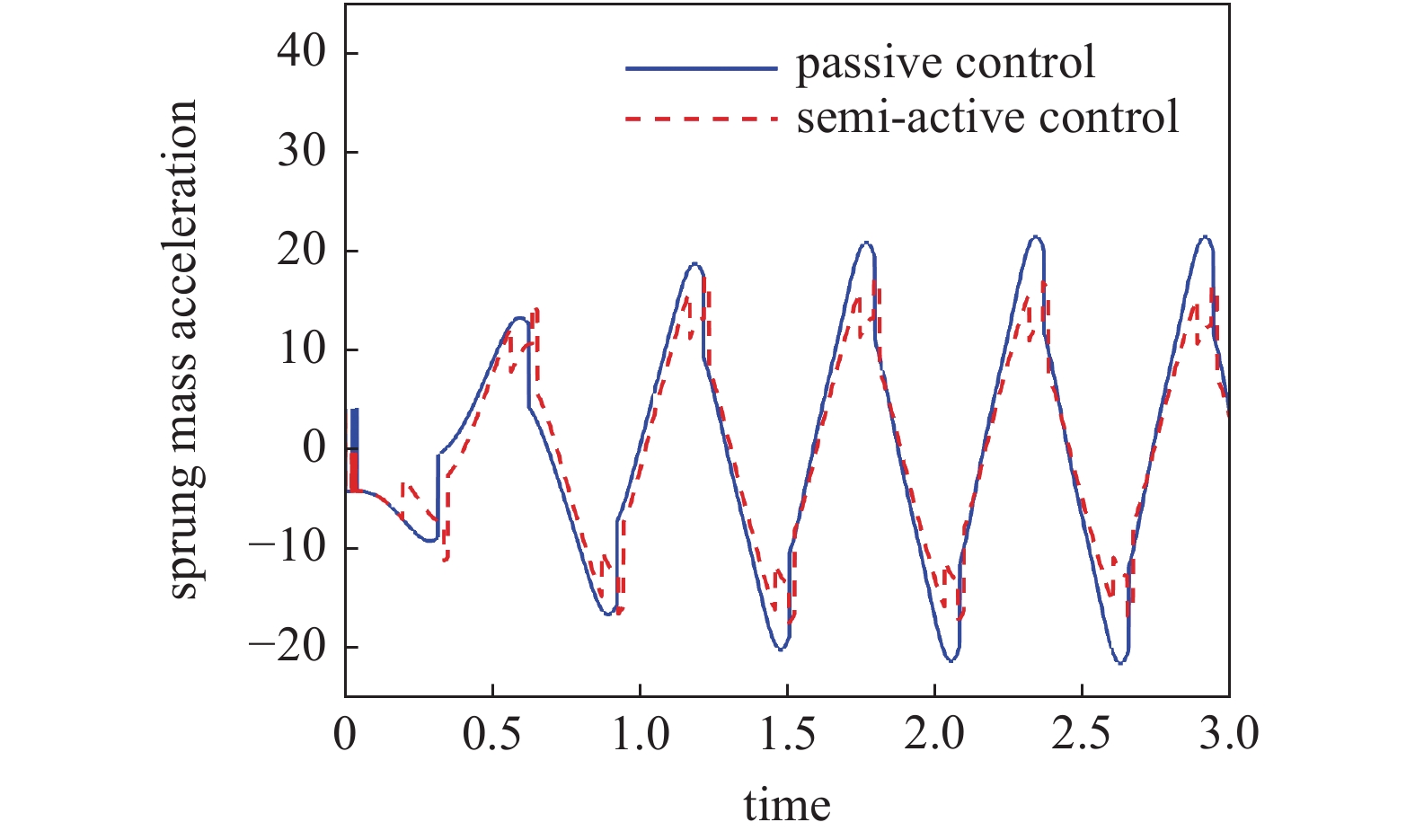
当激励频率在主共振频率附近$omega = 11;{
m{rad/s}}$时, 半主动控制参数为$b = 0.1$和被动控制时的簧载质量的加速度时间历程对比图如图5所示, 图中截取了前3 s的加速度时间历程, 其他参数值与第4节相同. 从图5中可以看出, 在该频率的激励下半主动控制能有效降低簧载质量的加速度峰值, 从而提高了车辆的乘坐舒适性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-137-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
簧载质量的加速度时间历程



Figure
5.
Acceleration time history of sprung mass



下载:
全尺寸图片
幻灯片


为了解决半主动控制会在低频激励区域降低乘坐舒适性的问题, 采用一种组合控制策略, 即当路面的外激励频率小于切换频率时, 悬架系统采用被动控制策略进行振动控制; 而当外激励频率值大于切换频率时, 悬架采用半主动控制策略进行振动控制.

当$b = 1$时, 即被动控制的幅频响应方程为







$$begin{gathered} {left( {MA{omega ^2}}
ight)^2} = left{ {{{left[ { - omega left( {c + {c_1}{omega ^{p - 1}}sin {frac{{p{
m{{text{π}} }}}}{2}} }
ight) - frac{{4{f_{
m{c}}}}}{{bar a{
m{{text{π}} }}}}sin {frac{{p{
m{{text{π}} }}}}{2}} }
ight]}^2}}
ight. + left. {{{left( { - frac{{4{f_{
m{c}}}}}{{bar a{
m{{text{π}} }}}}cos {frac{{p{
m{{text{π}} }}}}{2}} - {k_1} + M{omega ^2} - frac{{3{k_2}{{bar a}^2}}}{4} - {c_1}{omega ^p}cos {frac{{p{
m{{text{π}} }}}}{2}} }
ight)}^2}}
ight}{{bar a}^2} end{gathered} $$
(34)

根据式(34)以及半主动控制参数为b = 0.1时的幅频响应方程, 可以得到两条幅频响应曲线在固有频率附近的交点对应的频率为: ${omega _{
m{i}}} = 9.54$ rad/s. 将该幅频响应曲线交点对应的频率作为组合控制的切换频率. 利用数值解和解析解分别绘制悬架系统在组合控制下的幅频响应曲线, 如图6所示. 从图中可以看出数值解与解析解具有较好的一致性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-137-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
系统在组合控制下的幅频响应



Figure
6.
Amplitude-frequence response curves of system under combined control



下载:
全尺寸图片
幻灯片



6.
组合控制的振动控制效果分析


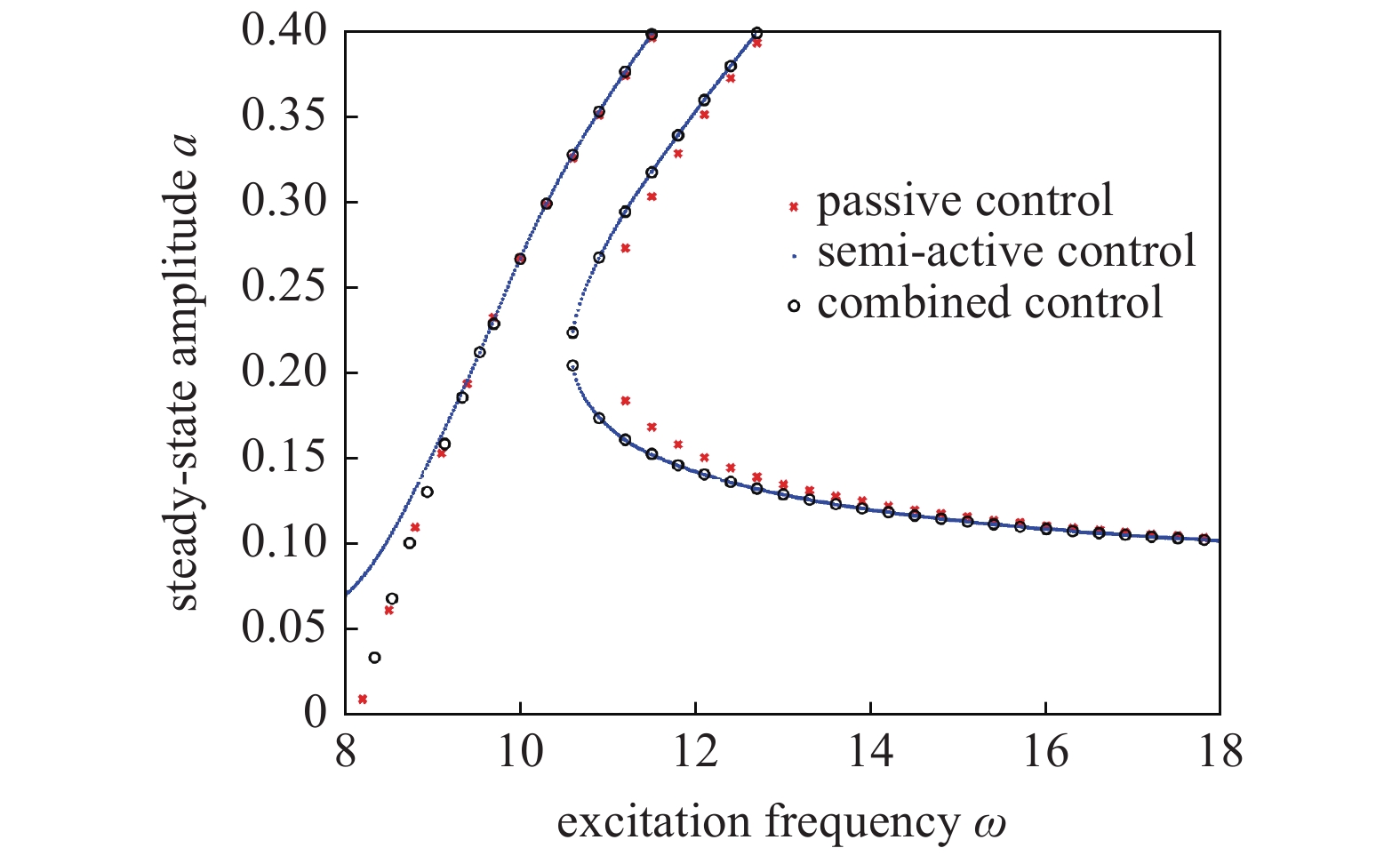
为了验证组合控制的振动效果, 利用近似解析解分别得到悬架系统在被动控制、半主动控制以及组合控制下的幅频响应曲线, 如图7所示. 其中, 半主动控制参数为b = 0.1. 当系统有多解时, 仅考虑最下面一支稳定解的结果. 从图7中可以看出, 悬架系统在组合控制下的主共振振幅最小. 而当激励频率增大到一定程度, 半主动控制将失去对振幅的抑制作用, 效果将又和被动控制一致.

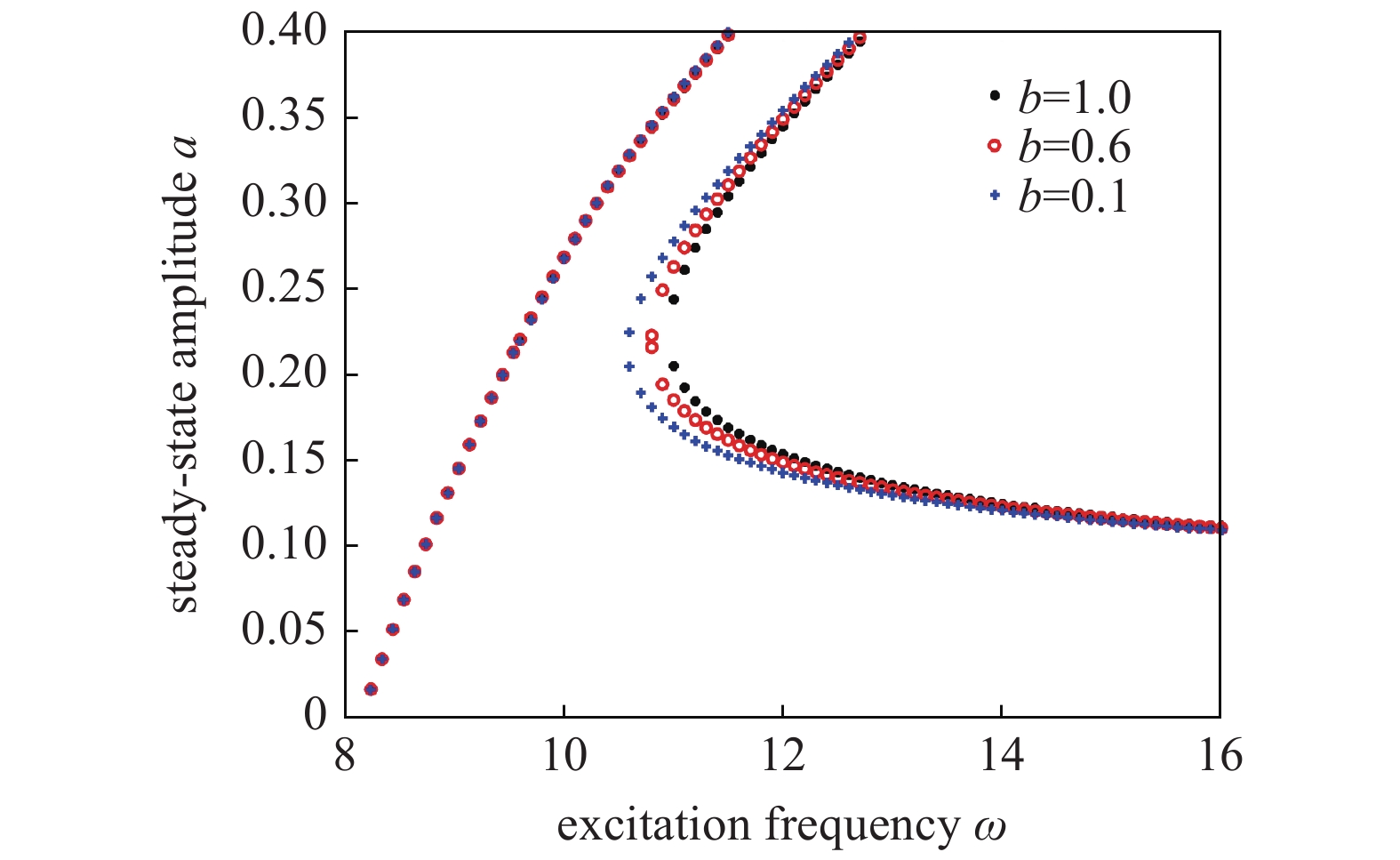
为了研究半主动控制参数b对悬架系统在组合控制下的影响, 分别选取b = 0.1, b = 0.6, b = 1时, 利用近似解析解得到系统的幅频响应曲线, 如图8所示. 同样仅考虑最下面一支稳定解的结果, 从图8中可以看出, 半主动控制参数$b$值越小, 系统的主共振幅值越小. 在频率$omega = 11;{
m{rad/s}}$时, 当$b = 0.1$时共振幅值为0.169 8 m; 当$b = 1$时, 即悬架系统在被动控制作用下时, 共振幅值为0.205 1 m. 悬架系统在组合控制作用下的共振峰值比被动控制的共振幅值减小了约0.035 3 m.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-137-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
不同控制策略下的幅频响应



Figure
7.
Amplitude-frequence response curves under different control strategies



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/7//21-137-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
b变化时对组合控制的影响



Figure
8.
Effect of combined control with different b



下载:
全尺寸图片
幻灯片



7.
结论


本文将磁流变液阻尼器的分数阶Bingham模型应用到单自由度1/4车辆悬架系统的动力学分析中, 研究了悬架系统的振动控制. 通过平均法研究了系统在半主动控制下的主共振响应, 得到了系统的近似解析解, 并通过数值解验证了近似解析解的正确性. 通过比较悬架系统在半主动控制和被动控制作用下的簧载质量垂直方向的加速度均方根值, 说明了半主动控制在路面激励频率小于固有频率附近的切换频率时反而会降低车辆的乘坐舒适性, 继而提出了一种被动控制与半主动控制相结合的组合控制策略, 并利用系统在被动控制和半主动控制下的两条幅频响应曲线在固有频率附近的交点对应的频率作为切换频率. 分析结果表明, 该组合控制策略不但可以提高乘坐舒适性, 还可以有效抑制悬架系统的主共振振动幅值. 为分数阶磁流变液阻尼器模型在车辆悬架中的应用提供了参考.

相关话题/控制 系统 车辆 分数 质量

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.