,2)西北工业大学深圳研究院, 广东深圳 518057;西北工业大学航天学院, 西安 710072A ROBUST STABILIZATION CONTROL FOR DUAL-ARM SPACE ROBOT CAPTURING TUMBLING TARGET1)
Xia Pengcheng, Luo Jianjun, Wang Mingming,2)Research & Development Institute of Northwestern Polytechnical University in Shenzhen, Shenzhen 518057, Guangdong, China;School of Astronautica, Northwestern Polytechnical University, Xi'an 710072, China通讯作者: 2)王明明, 副教授, 主要研究方向: 空间机器人运动规划与控制. E-mail:mwang@nwpu.edu.cn
收稿日期:2020-12-24接受日期:2021-02-8网络出版日期:2021-04-08
| 基金资助: |
Received:2020-12-24Accepted:2021-02-8Online:2021-04-08
作者简介 About authors
摘要
针对空间双臂机器人抓捕翻滚目标的稳定控制问题, 由于目标惯性参数的不确定性以及双臂同时作用于目标存在内力挤压, 已有的稳定控制方法无法有效地约束机械臂末端与目标的接触力与力矩, 无法保证控制过程中抓捕点处的接触安全. 为此, 本文考虑被抓捕目标惯性参数不确定性与双臂内力挤压对抓捕后阶段组合体稳定控制的影响, 提出了一种保证接触安全的鲁棒稳定控制方法. 首先, 根据目标的有界不确定性构造鲁棒正不变集, 同时考虑双臂与目标接触内力的影响, 利用预测控制方法在该不变集内规划控制目标运动的虚拟接触力与力矩. 然后, 根据目标动力学模型以及空间双臂机器人的运动约束, 规划空间双臂机器人的鲁棒安全期望运动轨迹. 最后, 利用障碍李雅普诺夫函数构造跟踪控制器, 使空间双臂机器人有效地跟踪期望轨迹, 从而使得翻滚目标运动受到等效于虚拟控制律的作用, 在保证接触安全的同时实现鲁棒的稳定控制. 通过空间双臂机器人稳定翻滚目标的仿真算例验证了所提方法的有效性.
关键词：
Abstract
Due to the inaccurate inertia parameters of the captured tumbling target and the internal wrenches at the grasping points, the motion of the space robot stabilizing the tumbling target cannot be planned and controlled effectively in the post-capture phase. In the existing studies, it is risky to track the desired trajectory planned by inaccurate parameters, which cannot restrain the contact wrenches and guarantee the safety of the grasping points. In order to control the post-capture dual-arm space robot safely, a robust control scheme is proposed for the dual-arm space robot capturing a tumbling target in this paper, where the influences of the inaccurate target inertia parameters and the internal wrenches at the grasping points are considered. First, a robust invariant set is constructed considering the influences of the inaccurate target parameters and internal stress wrenches. Then, to plan a safe desired motion for the dual-arm space robot, a virtual robust control law for the captured target is developed, where the desired trajectory of the target is planned within the constructed invariant sets. By the motion constraints between the space robot and the target, a robust desired trajectory of the dual-arm space robot is obtained. A barrier Lyapunov function based constrained controller is developed to track the robust trajectory efficiently. By tracking the robust trajectory with prescribed control performance, the designed virtual control law is applied to stabilize the captured target. During the stabilization control process, the measured contact wrenches can be restrained by the proposed scheme effectively, which guarantees the safety of the grasping points and the reliability of the stabilization control. The effectiveness of the proposed scheme is validated via the digital simulations, where a non-cooperative tumbling target is stabilized by a dual-arm space robot.
Keywords：
PDF (1564KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
夏鹏程, 罗建军, 王明明. 空间双臂机器人抓捕翻滚目标后的鲁棒稳定控制1). 力学学报[J], 2021, 53(4): 1138-1155 DOI:10.6052/0459-1879-20-449
Xia Pengcheng, Luo Jianjun, Wang Mingming.
引言
在轨维修失效卫星是当前空间机器人在轨服务的重要应用场景[1]. 空间机器人抓捕翻滚目标技术是在轨服务所需的关键技术之一[2-3]. 一般将空间机器人抓捕目标的过程分为抓捕前, 抓捕中和抓捕后3个阶段. 在抓捕后阶段, 如何保证机械臂末端与目标接触力/力矩在安全范围内稳定和操控目标是空间机器人在轨服务的难点之一.考虑到抓捕后阶段任务的安全性和复杂度, 空间机器人的抓捕控制通常分为期望运动轨迹规划和轨迹跟踪控制两个过程. 对于惯性参数已知的目标, 抓捕后的轨迹规划问题通常被转换为优化问题求解[4]. Dimitrov等[5-8]从能量守恒约束的角度规划了抓捕后阶段的期望运动轨迹. 王明明等[9-11]则利用样条曲线对机器人关节运动进行参数化处理, 规划了时间最优的空间机器人运动轨迹. 余敏等[12-14]针对空间双臂机器人提出了一种协调基座与机械臂运动的轨迹规划方法. 在实际应用中, 因为无法提前准确地获得翻滚目标的惯性参数, 通常利用其估值实现轨迹规划与跟踪控制. 由于被抓捕目标的惯性参数存在不确定性, 抓捕了翻滚目标的空间机器人并不能有效地跟踪规划的期望运动轨迹. 为了解决这一问题, 研究者们针对目标与空间机器人构成的组合体提出了自适应控制策略[15-17]. 然而上述针对组合体提出的控制方法并未考虑控制过程中因目标与机械臂末端交互而产生的接触安全问题.
当空间多臂机器人跟踪期望运动轨迹时, 由于目标惯性参数具有不确定性以及抓捕矩阵零空间内多臂之间拉扯与挤压内力的影响, 空间机器人末端的接触力/力矩可能无法满足规划的安全接触约束[18-19]. 为了保证机械臂末端的接触安全, 减小交互过程中的接触力/力矩, 空间机器人的研究****引入了地面机器人的阻抗控制方法[20-22]. Abiko等[23-27]基于阻抗控制方法设计了跟踪控制器, 通过设计关节的控制力矩, 将机械臂末端运动与接触力之间的关系等效于一个质量-弹簧-阻尼系统, 有效地调整了目标与机械臂末端的接触情况. 为了提高阻抗控制效率, Stolfi等[28-29]提出了仅对产生接触的运动方向采用阻抗控制的混合控制策略. Xia等[30]提出了一种根据末端接触情况调整期望运动的方法, 通过调整期望运动轨迹的方式保证末端接触的安全. 上述研究仅利用机器人力控制方法被动地调整了交互过程中的接触力与力矩, 而并未在最初设计期望运动轨迹的过程中预先考虑目标惯性参数不确定性的影响, 从而无法有效地约束接触力与力矩, 进而保证接触安全. 在近年的研究中, 为了主动地处理因模型不确定性而产生的接触安全问题, Gangapersaud等[31-32]针对模型不确定性有界的情况, 设计了考虑模型不确定性的期望运动轨迹以及跟踪控制器.
为了有效地约束空间双臂机器人稳定和操控翻滚目标运动过程中的接触力与力矩, 保证抓捕点处的接触安全, 本文提出了一种考虑目标惯性不确定性与抓捕点处内力的接触安全鲁棒控制方法. 首先, 利用目标惯性参数的估值, 设计稳定控制的标称运动. 在此基础上, 考虑目标不确定性以及内力的影响, 构造目标运动包络的鲁棒不变集. 在不变集内设计控制目标运动稳定的虚拟鲁棒控制律. 随后, 根据该控制律与运动约束生成组合体的期望运动. 最后, 基于障碍李雅普诺夫函数设计了跟踪控制器, 使得空间机器人能够在设计的控制性能约束范围内有效地跟踪期望运动轨迹、翻滚目标的运动受到等效于虚拟控制律的接触力/力矩, 从而保证控制过程中的接触安全.
1 抓捕翻滚目标后的组合体建模
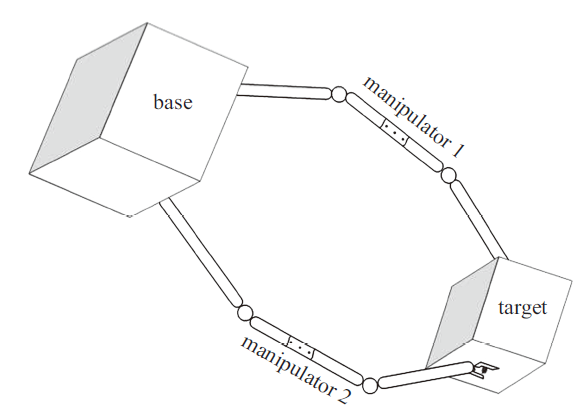
鉴于七自由度机械臂具有冗余度、方便完成多目标的空间操控任务, 本文中空间机器人由两个对称安装的七自由度刚性机械臂与一个六自由度运动的可控基座组成. 翻滚目标与空间双臂机器人在抓捕点处连接形成组合体, 如图1所示.图1
新窗口打开|下载原图ZIP|生成PPT图1空间机器人抓捕后示意图
Fig.1Snapshot of space robot after capturing target
两个七自由度机械臂各关节旋转的角速度分别为${\dot{{\theta }}}_1 $和${\dot{{\theta }}}_{2} $, 基座的线速度和角速度分别为${v}_{b} $和${\omega}_{b} $. 为了方便动力学模型的建立, 将这些状态量组合为一个广义向量, ${\dot{{q}}}=\left[{v}_{b}^{T}, \omega_{b}^{T},\dot{{\theta }}_1^{T},\dot{{\theta }}_2^{T}\right]^{T}$. 在空间机器人的本体坐标系内建立如下的动力学模型
式中, ${M}$为机械臂与基座的惯性矩阵, ${c}_{1} $为非线性项. ${u}_0 =\left[{u}_{b}^{T},\tau_{1}^{T},\tau_{2}^{T}\right]^{T}$为空间双臂机器人的控制输入, 其中${u}_{b} =\left[{F}_{b}^{T},\tau_{b} ^{T}\right]^{T}$为基座的控制力与力矩, ${\tau }_{1} $和${\tau }_2 $为机械臂的关节控制力矩. ${J}_{ce} $是空间双臂机器人末端的雅可比矩阵, 由双臂各自的末端雅可比矩阵共同组成. ${f}_{e} =\left[{F}_{{e1}}^{T},\tau_{{e1}}^{T},{F}_{{e2}}^{T},\tau_{{e2}}^{T}\right]^{T}$为双机械臂末端所受到的接触力与力矩, 可以通过机械臂末端的力传感器测得.
根据机械臂末端的速度${v}_{{e1}} $, ${v}_{{e2}}$和角速度${w}_{{e1}} $, ${w}_{{e2}} $, 定义空间双臂机器人末端的广义速度向量${\dot{{x}}}_{e}=\left[{v}_{{e1}}^{T},{w}_{{e1}} ^{T},{v}_{{e2}}^{T},{w}_{{e2}}^{T}\right]^{T}$. 类似地, 根据目标质心的速度${v}_{t}$与角速度${w}_{t} $, 定义目标的广义速度${\dot{{x}}}_{t} =\left[{v}_{t}^{T},{w}_{t}^{T}\right]^{T}$. 在抓捕后阶段, 目标与空间机器人形成组合体, ${\dot{{q}}}$, ${\dot{{x}}}_{e}$与${\dot{{x}}}_{t} $满足如下运动学约束
式中, ${J}_{te} $目标质心到抓捕点的雅可比矩阵. 为了方便描述, 对于向量${x}\in {R}^{3}$, ${x}^{\times }$表示为与其对应的反对称矩阵. 根据向量${x}_{1} ,{x}_{2} \in {R}^{3}$, 定义如下运算
目标的六自由度运动规律可以表述为如下的形式
式中, ${I}_{t} $为翻滚目标的惯性矩阵. 由于目标与空间机器人固连, 目标的运动受到接触力/力矩的影响. 将式(1)和式(4)联立, 可以得到组合体的闭链动力学方程
2 接触安全因素分析与处理
为了有效地约束空间双臂机器人抓捕和稳定翻滚目标运动过程中的接触力/力矩, 保证抓捕点处的接触安全, 需要对影响接触安全的因素进行相应的分析.2.1 目标惯性参数不确定性影响分析
由于翻滚目标的惯性参数无法提前准确地测量, 因此存在不确定性. 一般利用其惯性参数的估值设计期望的运动轨迹. 首先, 利用多项式将目标的运动空间进行参数化处理. 随后, 根据式(4)中的目标动力学方程, 将标称运动的规划问题转化为如下优化问题, 可得式中, ${\varepsilon }$为目标运动状态与最终期望之间的误差, $T_{0}$为运动时间, $\lambda_{1} $和$\lambda_2 $为权重因子, ${f}_{\max } $为接触力/力矩的安全约束, ${x}_{t min} $和${x}_{t max}$为运动状态的上下界. 通过求解上述优化问题, 可以得到目标运动的期望轨迹. 最终, 利用目标与机械臂的运动学约束, 求解得到组合体中机械臂关节与基座的期望运动轨迹. 由目标的动力学方程可知, 对于惯性参数已知的目标, 当跟踪控制器有效地跟踪上规划的期望轨迹时, 目标将受到规划的接触力/力矩作用.
对于惯性参数无法准确获知的目标, 由于不确定性的影响, 动力学模型中与目标惯性参数相关的项存在如下的关系
式中, ${J}_{te} $和${\hat{{J}}}_{te}$分别表示雅可比矩阵的真值与估值, $\Delta {J}_{te}$为雅可比矩阵的偏差. 类似地, ${I}_{t} $和${\hat{{I}}}_{t} $分别表示目标惯性矩阵的真值与估值, $\Delta {I}_{t}$为二者之间的偏差. 根据式(2)中的运动学约束, 目标的估计速度${\hat{{\dot{{x}}}}}_{t}$与真实速度${\dot{{x}}}_{t} $之间满足如下关系
因此, 在抓捕后阶段, 根据双臂机器人末端的速度无法准确地估计目标质心的运动速度. 此外, 由于雅可比矩阵${J}_{te}$的真值无法获得, 接触力/力矩对目标运动的实际作用效果存在偏差.
综上分析, 当空间机器人有效地跟踪上利用目标估计参数规划参考的期望轨迹时, 根据目标的动力学方程式(4), 有以下的关系
式中, ${w}_{t}$为目标惯性参数不确定对估计动力学模型产生的影响. $\Delta {f}_{e}$为接触力/力矩的实际值${f}_{e} $和规划值${f}_{{ep}}$之间的误差. 当空间机器人有效地跟踪利用估计参数规划的期望运动时, 由于不确定的目标惯性参数影响, 空间机器人末端与目标交互的过程无法满足规划的接触力/力矩约束, 控制过程存在接触安全问题. 因此, 有必要在规划的过程中考虑目标不确定性的影响, 使得空间机器人在跟踪期望轨迹时能够保证接触的安全.
2.2 机械臂末端内力影响分析
当空间机器人的双臂同时作用于非合作目标时, 描述末端接触力/力矩的${f}_{e} $和作用于目标质心运动的向量${F}_{E} $满足如下的关系式中, ${F}_{E} $为控制目标运动的有效力与力矩. 与空间单臂机器人不同, 当两个机械臂同时作用于目标时, 在雅可比矩阵${J}_{te}$的零空间内会产生不影响目标运动的无效力与力矩${F}_{I}$即内力, 其表达式如下
式中, $† $表示矩阵的广义逆, ${I}$为单位矩阵. 内力${F}_{I} $反应了多个机械臂与目标之间的拉扯与挤压. ${F}_{I}$仅对机械臂末端的接触力/力矩产生影响. 因此, 为了抓捕点处机械臂末端与目标接触的安全, 还需要在规划期望轨迹的过程中考虑内力的影响.
3 鲁棒运动轨迹规划
经上分析可知, 为了保证稳定过程中抓捕点处的接触安全, 需要在规划期望运动的过程中考虑目标不确定性以及内力的影响, 以便空间机器人能在约束的接触力/力矩内安全有效地跟踪期望运动, 保证控制过程中抓捕点处的接触安全. 为此, 本文提出了一种考虑目标有界不确定性以及内力影响的鲁棒轨迹规划方法.根据动力学方程(4)可知, 目标的期望运动可以通过规划期望的接触力与力矩得到. 因此可以将接触力/力矩视为虚拟的控制量, 针对目标运动设计虚拟的鲁棒控制律, 即可根据式(4)得到考虑目标不确定性的目标期望运动轨迹. 在此基础上, 根据式(2)中的运动约束, 可求解得到组合体中空间双臂机器人关节与基座的期望运动轨迹.
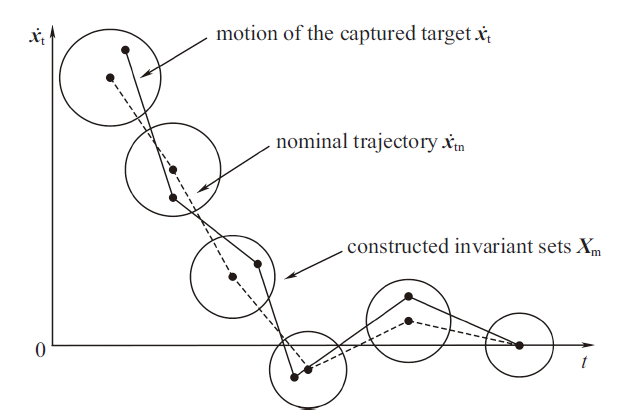
本文采用鲁棒预测控制方法设计虚拟控制律. 如图2所示, 首先, 利用目标惯性参数的估值, 根据式(6)规划满足任务要求的标称运动轨迹${\dot{{x}}}_{tn} $. 随后, 根据标称运动构造考虑不确定性的不变集序列$X_{m} $, 构造目标运动包络. 最终, 在不变集内考虑机械臂末端内力的影响, 设计虚拟控制目标运动的鲁棒控制律, 控制受到有界不确定性影响的系统在状态约束范围内逼近规划的标称运动.
图2
新窗口打开|下载原图ZIP|生成PPT图2基于虚拟控制律的控制过程示意图
Fig.2Schematic diagram of the virtual control law
为了描述控制受到有界不确定性影响的系统逼近标称运动轨迹的过程, 首先对目标的动力学进行离散化处理
式中, ${\dot{{x}}}_{t}^{+}$代表下一时刻的状态, $\Delta t$为离散时间, ${I}$为单位矩阵. 控制目标运动逼近标称运动的过程可以被描述为如下的优化问题
式中, ${e}_{r} \left( i \right)$和${f}_{re}\left( i \right)$为$N$步预测控制控制中标称与实际运动轨迹的误差. ${f}_{{en}} \left( i \right)$为与标称轨迹对应的标称控制律, ${f}_{{en}} \left( i\right)$代表了双臂末端作用于目标的虚拟接触力与力矩. ${Q}_{r} $和${R}_{r} $为正定矩阵, $V_{f}$为终端代价函数. 将求解得到的式(19)的最优值记作$V_{r}^{0}$.
3.1 目标惯性不确定性与机械臂末端内力处理
为了考虑目标与双臂之间的拉扯、挤压对于末端接触力/力矩的影响, 利用雅可比矩阵${J}_{te}$以及其零空间可以构造如下的正定矩阵为了使得目标的运动状态在受到其惯性参数有界不确定性影响时仍能够处于状态约束范围内, 本文构造了目标运动包络的鲁棒正不变集. 当目标的运动状态处于该鲁棒正不变集内时, 即便受到惯性参数不确定性影响仍能处于该集合内. 因此在满足状态约束的不变集内控制翻滚目标运动, 目标的运动状态够满足规划的状态约束. 为了方便构造不变集, 根据标称轨迹${\dot{{x}}}_{tn} $定义如下集合的序列, 即$X_l \left( {{\bar{{\dot{{x}}}}}_{tn} } \right)$
根据目标状态以及接触力/力矩的约束, 考虑目标不确定性的有界性, 可以构造不变集序列$X_{m} \left({{\bar{{\dot{{x}}}}}_{tn} } \right)$, 构造过程详见附录与参考文献[33].
3.2 鲁棒轨迹生成
为了在求解式(19)中优化问题的过程中考虑目标不确定性以及机械臂末端内力影响, 快速地生成鲁棒的期望运动轨迹, 本文采用将此$N$步预测控制问题拆分为$N$次的单步预测控制问题求解. 进行单步预测控制时, 根据当前的状态设计如下的反馈控制律式中, ${K}$为待求解的控制参数, ${K}_{o}={f}_{{en}} $. 为了保证求解效率, 令${z}=\left[{e}_{r}^{+T}, {f}_{{er}}^{+T}\right]^{T}$, 将单步预测控制问题转化为如下的线性矩阵不等式形式
式中
通过对式(26)中的控制问题迭代求解, 即可得到鲁棒的虚拟控制律. 根据目标的标称模型式(4)和虚拟控制律, 得到考虑目标惯性不确定性与机械臂末端内力影响的鲁棒目标期望运动轨迹${\dot{{x}}}_{r}$. 鉴于空间机器人与目标满足式(2)中的运动学约束. 通过求解满足约束的逆运动学, 即可得到与鲁棒的目标期望运动轨迹${\dot{{x}}}_{r} $对应的空间机器人关节与基座期望运动轨迹${\dot{{q}}}_{r} $. 由于目标的运动受到机械臂末端接触力与力矩的影响, 当空间机器人有效地跟踪上期望运动轨迹时, 目标运动受到等效于鲁棒控制律的接触力与力矩作用, 从而约束了抓捕点处产生的接触力与力矩, 保证了接触安全.
4 基于障碍李雅普诺夫函数的跟踪控制器设计
为了约束控制过程中抓捕点处的接触力/力矩, 空间双臂机器人需要有效地跟踪期望运动轨迹. 本文基于障碍李雅普诺夫函数[34]设计了跟踪期望运动轨迹的控制器.定义关节与基座跟踪运动轨迹的误差为: ${e}_{s} ={q}-{q}_{r} $和${z}_{s} ={\dot{{q}}}-{\alpha }_{s} $, 其中${\alpha }_{s} $为设计的中间控制量. 为了保证跟踪性能, 为状态量设计如下形式的约束
式中, ${k}_{c} $为由正数组成的控制性能约束向量. 对空间双臂机器人构造如下的障碍李雅普诺夫函数
式中, $n$为被控状态量${\dot{{q}}}$的分量数目, $i$为向量的分量下标. 对式(31)中的李雅普诺夫函数求导可得
利用如下的不等式
式中, $\lambda $为正数. 根据控制参数${k}_{e} \in {R}^{20}$, 可以设计中间控制量${\alpha }_{s} \in {R}^{20}$如下
利用退步法构造控制空间双臂机器人跟踪期望运动轨迹的李雅普诺夫函数如下
对该李雅普诺夫函数求导可得
设计空间双臂机器人的控制律如下
式中, ${k}_{z} ={diag}\left( {k_{z1},k_{z2},\cdots ,k_{zn} } \right)$为正定矩阵. 将该控制律代入李雅普诺夫函数$V_{2} $的导数中, 得到$\dot{{V}}_{2} \leqslant 0$. 进而可以得到如下关系
式中, $V_{2} \left( t \right)$和$V_{2}(0)$分别为$t$时刻与初始时刻的李雅普诺夫函数. 根据式(38)由此可以推导得到
对不等式两边进行指数化处理
整理后可得到跟踪误差满足如下的约束关系
利用此跟踪控制器, 可以在设定的约束性能范围内有效地跟踪期望运动轨迹.
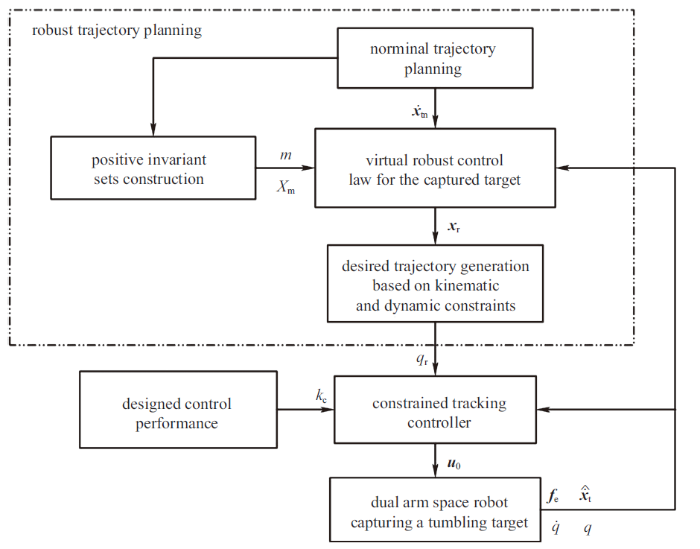
综上, 本文通过设计虚拟鲁棒控制律规划鲁棒的期望运动轨迹, 随后, 在约束性能范围内有效地跟踪期望轨迹, 使得目标运动能够受到等效于虚拟鲁棒控制律的接触力/力矩控制, 从而约束抓捕点处的接触力/力矩, 保证接触安全的同时实现抓捕后阶段的鲁棒稳定控制, 该鲁棒控制方法的结构如图3所示.
图3
新窗口打开|下载原图ZIP|生成PPT图3鲁棒稳定控制方法结构图
Fig.3Schematic diagram of the proposed control scheme
5 仿真验证
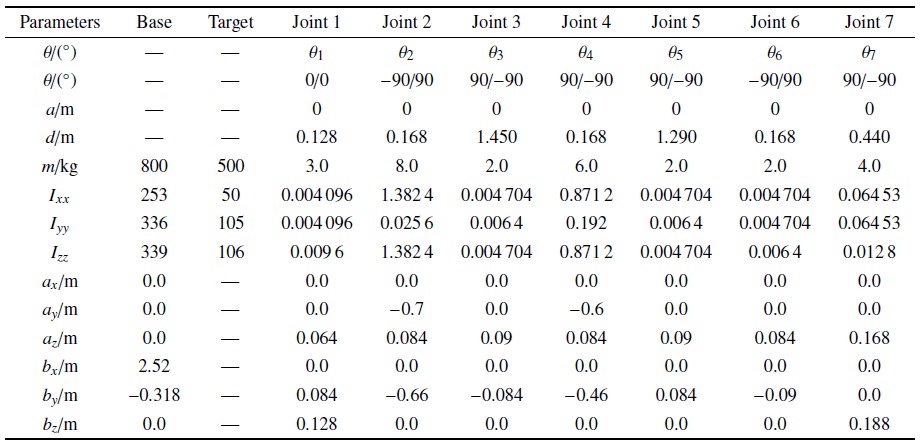
为了验证所提鲁棒稳定控制方法的有效性, 本节利用该方法设计了稳定翻滚目标的仿真算例和两组对照组. 抓捕后阶段组合体的动力学与运动学参数如表1所示. 估计的惯性参数为真实值的85${\%}$. 双臂末端的接触力/力矩安全约束分别为$[-20,20]$ N与$[-20, 20]$ N$\cdot$m. 翻滚目标的运动速度为$[0.05,0.18,-0.22]$ m/s, 角速度为$[0.05,$ $-0.28,$ $-0.18]$ rad/s, 两个抓捕点在目标本体坐标系上的位置分别为$[0,0.5,0]^{T}$ m和$[0,-0.5,0]^{T}$ m. 为了规划目标的期望稳定运动, 首先利用$n$阶多项式对目标运动的速度以及角速度进行参数化处理. 根据目标惯性参数的估计值建立式(6)和式(7)中的优化问题, 通过求解优化问题得到参考的期望运动轨迹.Table 1
表1
表1组合体运动学和动力学参数
Table 1
 |
新窗口打开|下载CSV
在两组对照组中, 空间双臂机器人跟踪利用估计参数设计参考的期望轨迹. 在对照组1中, 利用如下的PD控制器跟踪参考期望运动轨迹, 可得
式中, ${\dot{{e}}}_{s} =\left[{\dot{{e}}}_{b}^{T} ,{\dot{{e}}}_{{q1}}^{T} ,{\dot{{e}}}_{{q2}}^{T} \right]^{T}$为速度跟踪误差, 控制参数${K}_{p} =-{diag}({I}_{12}, 0.6{I}_6 )$, ${K}_{d} =-{diag}(3{I}_{12},2{I}_6 )$, ${I}_{12}$和${I}_6 $分别是维度为12和6的单位矩阵.
在对照组2中, 利用该控制器跟踪参考期望运动轨迹. 约束跟踪控制器的控制参数选择如下
$\begin{eqnarray*} n=20,\ \ k_{{e}i} =1,\ \ k_{{z}i} =3,\ \ k_{{c}i} =1.5 \end{eqnarray*}$
本文所提约束跟踪控制器的控制性能以及有效性, 可以通过对比对照组1, 2的仿真结果予以验证.
所提鲁棒控制方法采用同样的约束跟踪控制器. 选择目标速度为零的状态序列作为标称轨迹. 同时令$N=20$, $\Delta t=0.01$ s, ${Q}_{r} $为单位阵. 由抓捕点的位置可知, ${R}_{r} $是正定的. 本文所提鲁棒稳定控制方法的有效性, 可以通过对比对照组1与所提方法的仿真结果予以验证.
图4$\sim\!$图6分别展示了对照组1, 2以及所提方法翻滚目标的运动情况. 仿真结果显示, 对照组方法和本文所提的鲁棒控制方法均能够有效地控制空间双臂机器人稳定翻滚目标的运动. 对照组中利用PD控制器直接跟踪参考期望轨迹需要5.5 s实现目标运动稳定, 利用所提的鲁棒稳定控制方法可以在3.2 s内实现翻滚目标的稳定.
图4
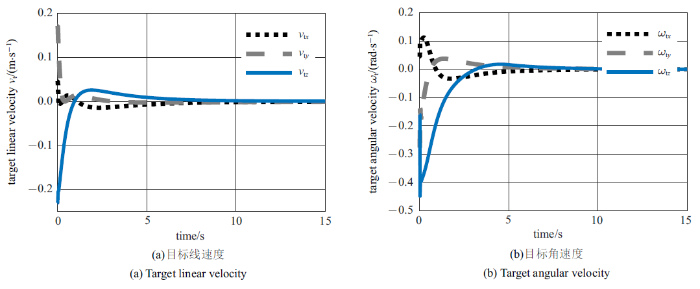新窗口打开|下载原图ZIP|生成PPT图4利用PD控制器直接跟踪参考期望轨迹稳定目标运动时目标的运动速度
Fig.4Velocities of the target when space robot tracks the estimated trajectory with PD controller
图5
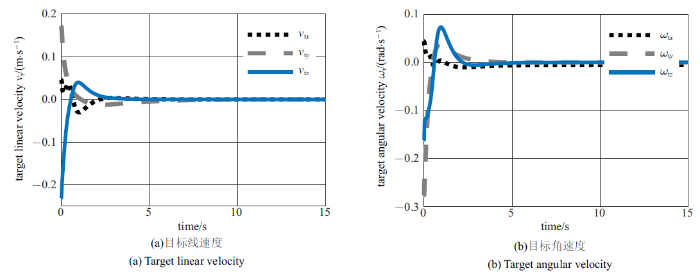新窗口打开|下载原图ZIP|生成PPT图5利用约束跟踪控制器直接跟踪参考期望轨迹稳定目标运动时目标的运动速度
Fig.5Velocities of the target when space robot tracks the estimated trajectory with the constrained tracking controller
图6
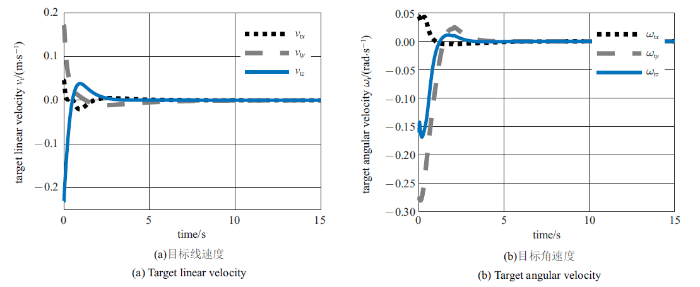新窗口打开|下载原图ZIP|生成PPT图6利用所提鲁棒控制方法稳定目标运动时目标的运动速度
Fig.6Velocities of the target under the control of the proposed robust scheme
图7$\sim\!$图9展示了稳定翻滚目标运动过程中空间双臂机器人的关节速度跟踪误差. 由仿真结果可知, PD和所提约束跟踪控制器均有效地跟踪了期望运动. 在稳定过程中, PD和约束跟踪控制器分别用了6 s和4 s将关节角速度的跟踪误差收敛至10$^{-3}$数量级以内. 由图8和图9中的结果可知, 约束跟踪控制器能在约束的性能范围内控制跟踪误差收敛, 跟踪不同期望运动轨迹时能够保证误差收敛的速度.
图7
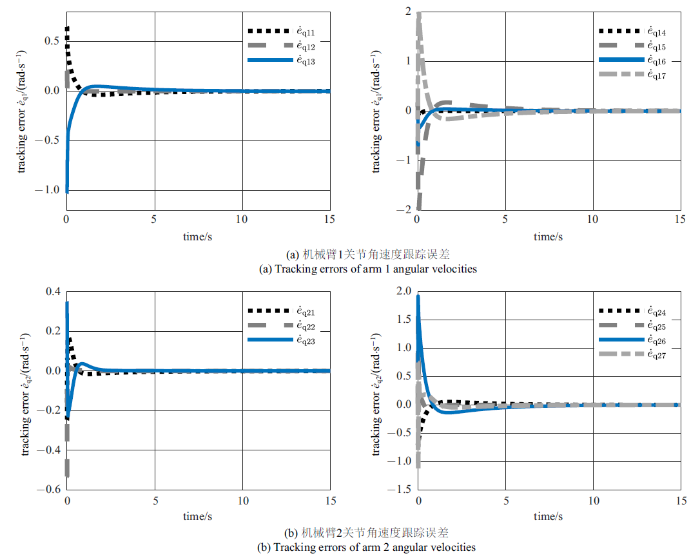新窗口打开|下载原图ZIP|生成PPT图7利用PD控制器直接跟踪参考期望轨迹稳定目标运动时的关节角速度跟踪误差
Fig.7Tracking errors of the joint angular velocities tracking estimated trajectory with PD controller
图8
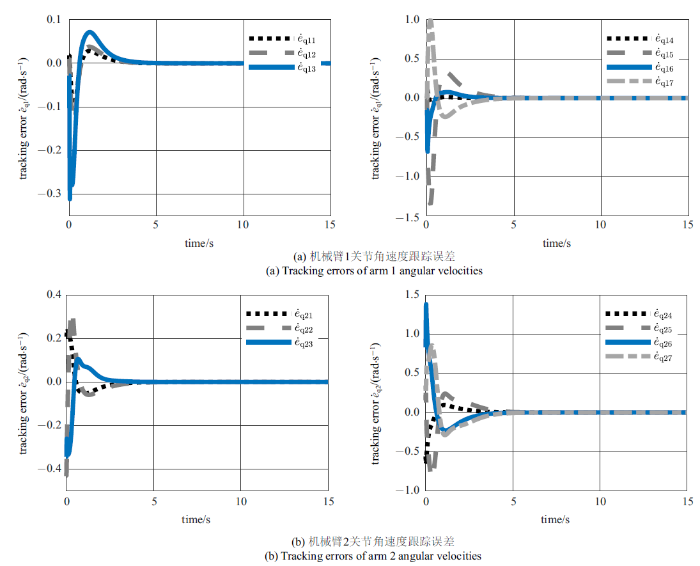新窗口打开|下载原图ZIP|生成PPT图8利用约束跟踪控制器直接跟踪参考期望轨迹稳定目标运动时的关节角速度跟踪误差
Fig.8Tracking errors of the joint angular velocities tracking estimated trajectory with the constrained tracking controller
图9
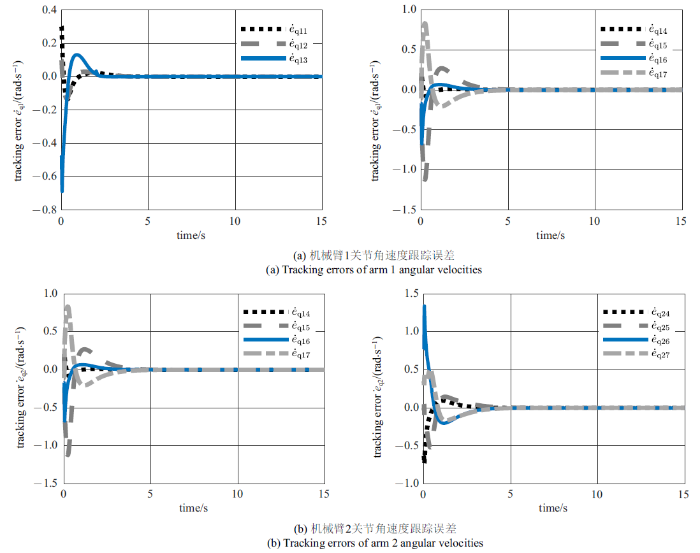新窗口打开|下载原图ZIP|生成PPT图9利用所提鲁棒控制方法稳定翻滚目标时机械臂的关节角速度跟踪误差
Fig.9Tracking errors of the joint angular velocities under the control of the proposed robust scheme
图10$\sim\!$图12展示了对照组1, 2和所提控制方法稳定翻滚目标运动时末端的接触力/力矩. 由于抓捕初始时刻抓捕点处与机械臂末端存在不可估计的加速度差, 在抓捕后阶段的开始, 目标与机械臂末端会因为连接后的稳定控制产生冲击. 对比图10和图11的仿真结果可知, 采用不同的跟踪控制器, 机械臂末端与目标交互过程中产生的接触力/力矩会因为控制效果而不同. 结合图7 $\sim\!$图9中的结果可知, 与利用PD控制器跟踪期望运动轨迹的情况相对比, 利用约束跟踪控制器跟踪期望运动轨迹时的跟踪误差范围较小, 约束控制器可以有效地处理初始冲击对目标运动加速度产生的影响, 能有效地控制空间双臂机器人跟踪期望运动轨迹, 在抓捕点处产生较小的接触力/力矩. 此外, 由图10和图11的仿真结果可知, 由于对照组参考期望运动轨迹并未考虑目标不确定性与内力的影响, 稳定过程中机械臂末端的接触力/力矩可能无法满足规划的约束.
图10
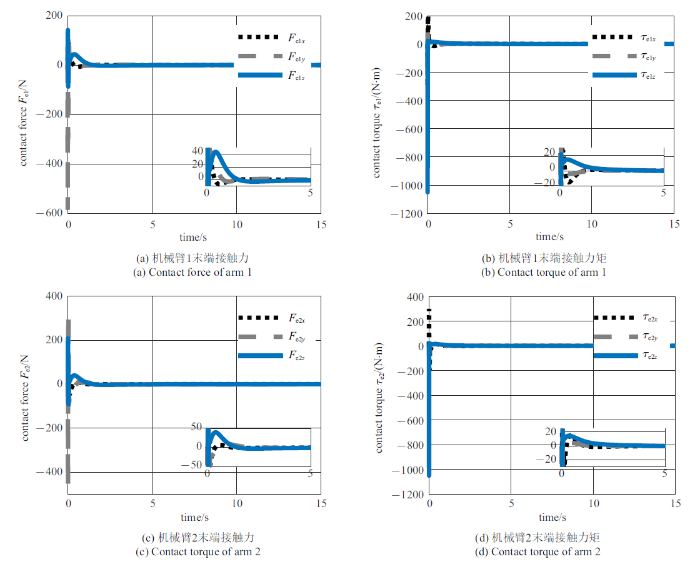新窗口打开|下载原图ZIP|生成PPT图10利用PD控制器直接跟踪参考期望轨迹稳定目标运动时机械臂末端的接触情况
Fig.10Contact wrenches of the manipulators tracking the estimated trajectory with PD controller
图11
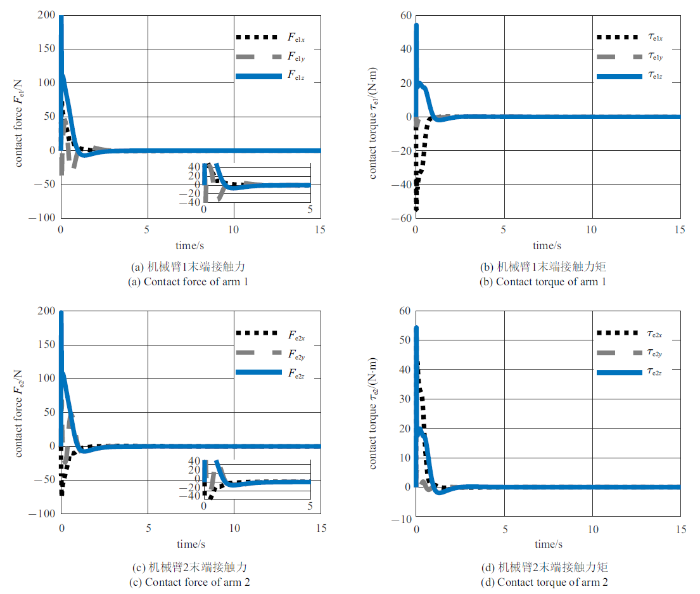新窗口打开|下载原图ZIP|生成PPT图11利用约束跟踪控制器直接跟踪参考期望轨迹稳定目标运动时机械臂末端的接触情况
Fig.11Contact wrenches of the manipulators tracking the estimated trajectory with the constrained tracking controller
图12
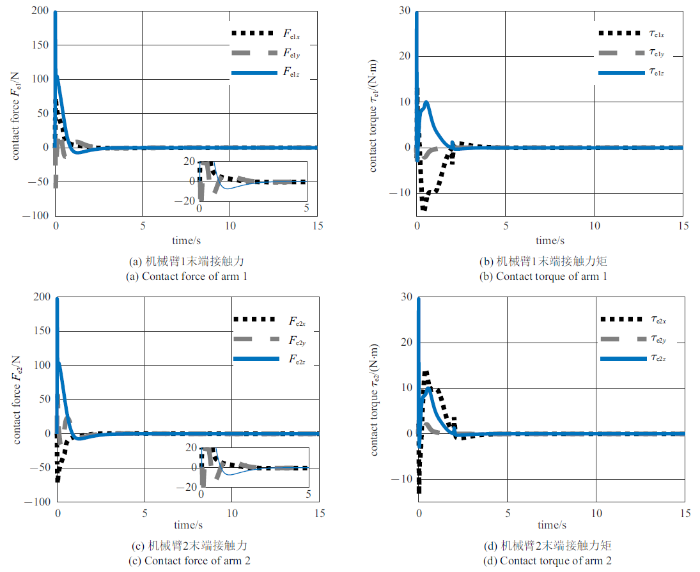新窗口打开|下载原图ZIP|生成PPT图12利用所提鲁棒控制方法稳定翻滚目标时机械臂末端的接触情况
Fig.12Contact wrenches of the manipulators under the control of the proposed robust scheme
图12展示了利用所提鲁棒控制方法稳定目标运动时机械臂末端受到的接触力/力矩. 由图中结果可知, 所提控制方法在稳定翻滚目标的过程中, 在0.6 s后空间机器人双臂末端的接触力/力矩满足安全约束$[-20, 20]$ N与$[-20, 20]$ N$\cdot$m, 保证了接触安全. 对比对照组的结果可知, 经过初始冲击后所提方法可以有效地约束末端的接触力/力矩在$[-20, 20]$ N与$[-20,20]$ N$\cdot$m的范围以内. 当目标的不确定性在估计的边界以内时, 所提方法可以有效地约束末端的接触力/力矩, 保证抓捕后阶段翻滚目标稳定时的接触安全.
图13$\sim\!$图15展示了控制过程中的控制输入. 由图13的仿真结果可以看出, PD控制器为了跟踪上期望运动轨迹, 在初始的1 s内, 控制输入在输入饱和的约束范围$[-300, 300]$ N与$[-300, 300]$ N$\cdot$m内振荡. 由图14和图15的仿真结果可知, 与利用PD控制器跟踪期望运动相比, 约束跟踪控制器控制输入收敛平缓. 此外, 跟踪鲁棒轨迹使得机械臂的控制力矩范围由$[-160,150]$ N$\cdot$m下降至$[-100,80]$ N$\cdot$m. 综上仿真结果, 所提控制方法可以在输入饱和的约束范围内有效地稳定翻滚目标.
图13
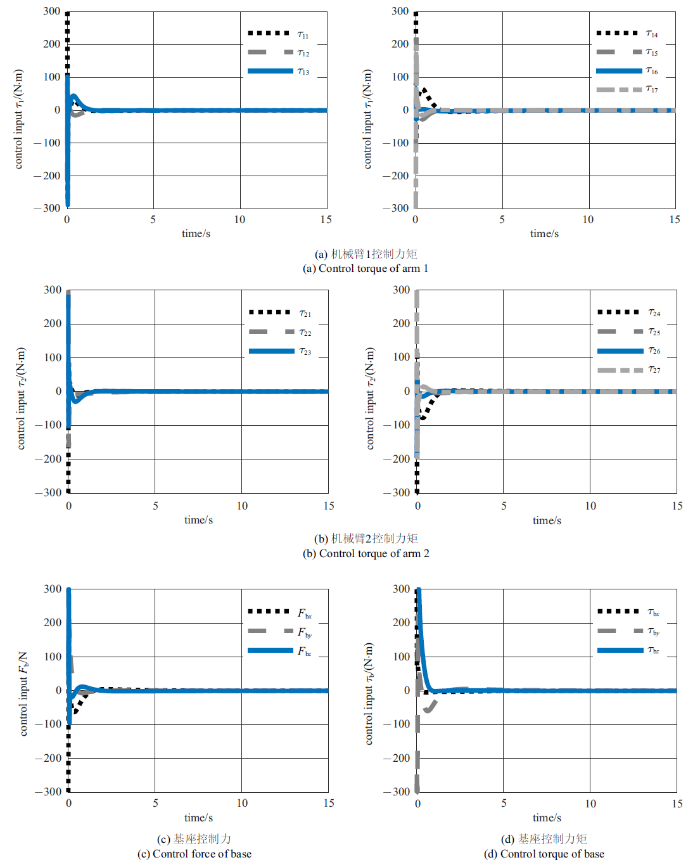新窗口打开|下载原图ZIP|生成PPT图13利用PD控制器直接跟踪参考期望轨迹稳定目标运动时的控制输入
Fig.13Control inputs of the manipulators tracking the estimated trajectory with PD controller
图14
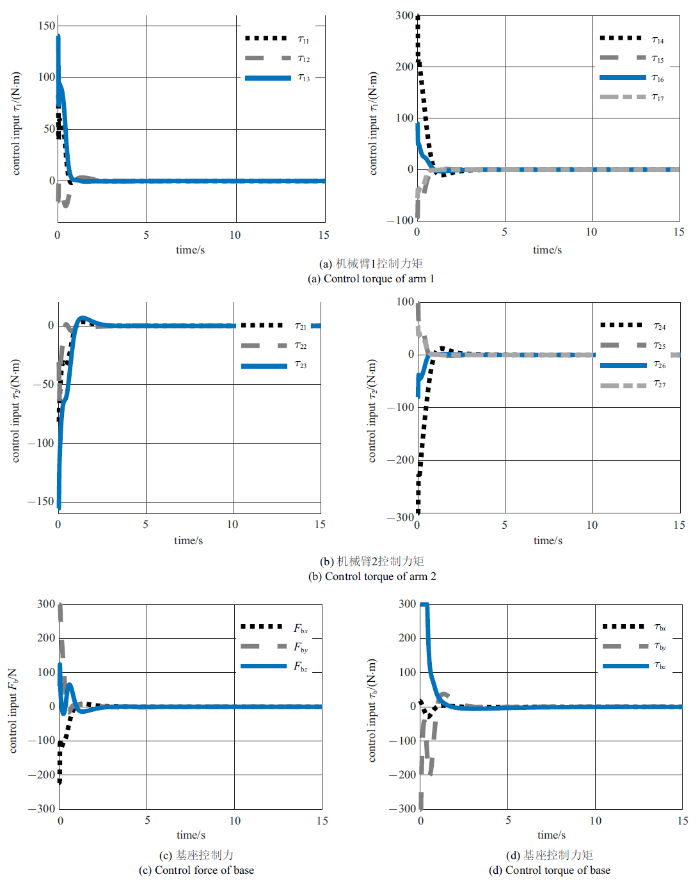新窗口打开|下载原图ZIP|生成PPT图14利用约束跟踪控制器直接跟踪参考期望轨迹稳定目标运动时的控制输入
Fig.14Control inputs of the manipulators tracking the estimated trajectory with the constrained tracking controller
图15
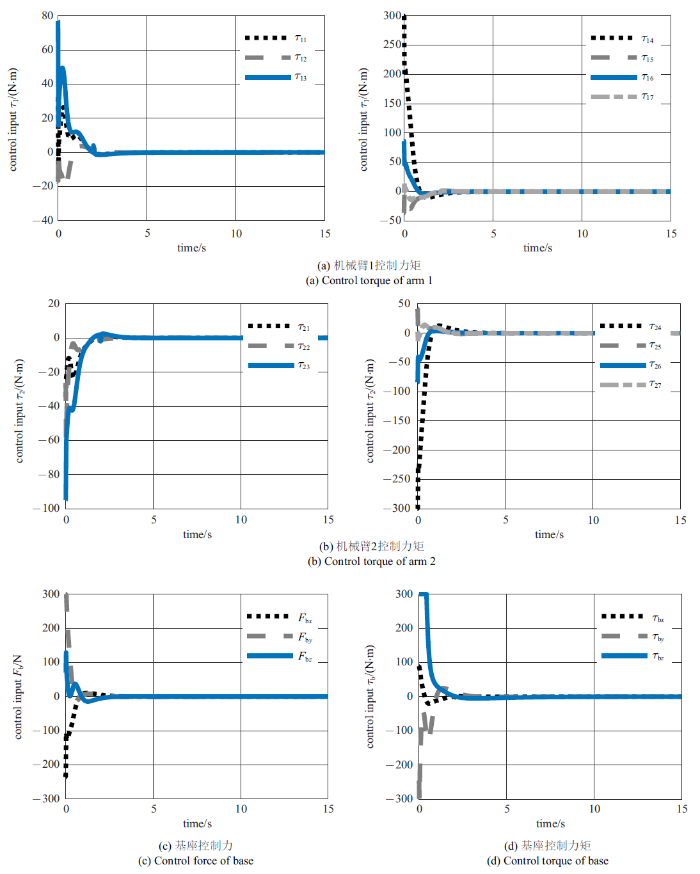新窗口打开|下载原图ZIP|生成PPT图15利用所提鲁棒控制方法稳定翻滚目标时机械臂末端的接触情况
Fig.15Control inputs of the manipulators under the control of the proposed robust scheme
6 结论
本文针对抓捕翻滚目标后的空间双臂机器人提出了一种考虑目标惯性不确定性与抓捕点处内力的鲁棒安全稳定控制方法, 总结如下:(1) 通过设计控制目标运动的虚拟鲁棒控制律, 考虑了目标惯性参数不确定性以及机械臂末端内力对抓捕后控制的影响, 规划了考虑接触安全的空间双臂机器人期望运动轨迹.
(2) 在设计的控制性能约束内有效地跟踪规划的运动轨迹, 使得目标运动受到等效虚拟控制律的作用, 在提高了控制可靠性的同时约束了末端的接触力/力矩, 保证了控制过程中抓捕点处的接触安全.
(3) 仿真结果表明, 当目标惯性参数不确定性产生的影响在预估范围内时, 鲁棒控制方法能够有效地约束接触力/力矩, 保证抓捕后阶段控制过程中目标与空间机器人的接触安全.
附录 鲁棒正不变集构造
选取函数$V_{f}'$以及对应的控制律构造标称系统的局部李雅普诺夫函数, 使得$\beta V_{f} '$等于$V_{f} $. 对于终端约束$\mathbb{X}_{f} :=\left\{ {V_{f} '<\alpha } \right\}$, 由如下引理1[33]可知, 式(19)中的优化问题不需要终端代价函数. (注: 附录中的引理均来自于参考文献[33]中的3.6节Tube-Based MPC of Nonlinear Systems).引理 1: 对于所有的$l>0$, 存在一个$\beta_{c} :=l/\alpha $, 如果$\beta >\beta_{c} $, 那么对于$X_l \left( {{\bar{{\dot{{x}}}}}_{tn} }\right)$中的终端状态都会满足终端约束$\mathbb{X}_{f} $.
为了构造针对干扰${w}$的$X_{m} \left( {{\bar{{\dot{{x}}}}}_{tn} } \right)$, 首先引入如下关于$V_{r}^{0}$的3个引理[33].
引理 2: 如果$\beta >\beta_{c} $, 则存在常数$c_{{r}1}$和$c_{{r}2} $满足下关系:
(1) 对于状态${\dot{{x}}}_{t} $, $V_{r}^{0}\geqslant c_{{r}1} \left| {{\dot{{x}}}_{t} -{\dot{{x}}}_{tn} } \right|^{2}$;
(2) 对于状态${\dot{{x}}}_{t} $, $V_{r}^{0}\leqslant c_{{r}2} \left| {{\dot{{x}}}_{t} -{\dot{{x}}}_{tn} } \right|^{2}$;
(3) 当标称系统状态处于$X_l \left( {{\bar{{\dot{{x}}}}}_{tn} } \right)$内时, 有$V_{r} ^{0}\left( {{\dot{{x}}}_{t}^{+}} \right)\leqslant V_{r} ^{0}\left( {{\dot{{x}}}_{t} } \right)-c_{{r}1} \left| {{\dot{{x}}}_{t} -{\dot{{x}}}_{tn} } \right|^{2}$, 式中${\dot{{x}}}_{t} ^{+}$为下一时刻标称系统运动状态的估计值.
由引理2可推导得到
$\begin{eqnarray*} V_{r}^{0}\left( {{\dot{{x}}}_{t}^{+}} \right)\leqslant V_{r}^{0}\left( {{\dot{{x}}}_{t} } \right)-\sum\limits_{i=0}^{N-1} {\left[ {{\dot{{x}}}_{t} \left( i \right)^{T}{\dot{{x}}}_{t} \left( i \right)+{f}_{e} \left( i \right)^{T}{f}_{e} \left( i \right)} \right]} \end{eqnarray*}$
因此, 被控的系统在$X_l \left( {{\bar{{\dot{{x}}}}}_{tn} } \right)$是渐近稳定的. 由于$X_l \left( {{\bar{{\dot{{x}}}}}_{tn} } \right)$的范围太大, 为了实现鲁棒控制, 需要将系统的运动约束在一个与干扰${w}$相关的更小的$X_{m} \left( {{\bar{{\dot{{x}}}}}_{tn} } \right)$.
引理 3: 如果$\beta >\beta_{c} $则$V_{r}^{0}$具有如下性质
(1) 对于$X_{m} \left( {{\bar{{\dot{{x}}}}}_{tn} } \right)$内的状态${\dot{{x}}}_{t} $, 有$V_{r}^{0}\left( {{\dot{{x}}}_{t}^{+}} \right)\leqslant \gamma V_{r} ^{0}\left( {{\dot{{x}}}_{t} } \right)$, 其中$\gamma :=c_{{r}1} /c_{{r}2} $;
(2) 当状态在$X_l \left( {{\bar{{\dot{{x}}}}}_{tn} } \right)$内时, ${\dot{{x}}}_{t} $到$V_{t} ^{0}$的映射是李普希兹连续的且存在李普希兹常数$c_{3} >0$;
(3) $\oplus $为集合加法, 当状态在$\left( {X_l \left( {{\bar{{\dot{{x}}}}}_{tn} } \right)\oplus \mathbb{W}} \right)$内时, 有$V_{r}^{0}\left( {{\dot{{x}}}_{t} ^{+}} \right)\leqslant \gamma V_{r}^{0}\left( {{\dot{{x}}}_{t} } \right)+c_{3} {W}_{t} $.
引理 4: 如果$\beta >\beta_{c} $, 对于在$X_{m} \left( {{\bar{{\dot{{x}}}}}_{tn} } \right)$内的状态${\dot{{x}}}_{t} $, 如果$V_{r} ^{0}\left( {{\dot{{x}}}_{t} } \right)<m<l$, 则满足$V_{t}^{0}\left( {{\dot{{x}}}_{t}^{+}} \right)<m$, 其中$m\ge \left( {c_{3} /\left( {1-\gamma } \right)} \right)\left| \mathbb{W} \right|$, $\left| \mathbb{W} \right|:=\max \left\{ {W_{t} \vert W_{t} \in \mathbb{W}} \right\}$.
当定义$X_{m} \left( {{\bar{{\dot{{x}}}}}_{tn} } \right)$的$m$满足如下约束时
$\begin{eqnarray*} m\geqslant \left( {c_{3} /\left( {1-\gamma } \right)} \right)\left| \mathbb{W} \right| \end{eqnarray*}$
由引理3和4可知, $X_{m} \left( {{\bar{{\dot{{x}}}}}_{tn} } \right)$内状态对所受到的目标惯性参数不确定性影响是鲁棒正不变的. 当$X_{m} \left( {{\bar{{\dot{{x}}}}}_{tn} } \right)$内的状态${\dot{{x}}}_{t} $满足规划的状态约束时, $X_{m} \left( {{\bar{{\dot{{x}}}}}_{tn} } \right)$为构造目标运动包络的不变集序列.
为了保证控制过程的安全, 虚拟控制律需要在$X_{m} \left( {{\bar{{\dot{{x}}}}}_{tn} } \right)$内控制目标的运动. 同时, 考虑到目标惯性参数不确定性影响, 直接在期望的运动约束范围内构造不变集可能使得系统的运动违反约束. 因此还需要对限制标称系统运动的约束进行如下的压缩, 以保证控制过程的安全
$\begin{eqnarray*} \left. {{\begin{array}{*{20}c} {\alpha_{o} {\dot{{x}}}_{{tL}} \leqslant {\dot{{x}}}_{t} \leqslant \alpha_{o} {\dot{{x}}}_{{tU}} } \hfill \\ {\theta_{o} {f}_{{eL}} \leqslant {f}_{e} \leqslant \theta _{o} {f}_{{eU}} } \hfill \\ \end{array} }} \right. \end{eqnarray*}$
式中, $\alpha_{o} $和$\theta_{o} $为调整约束范围的常数, 根据离散模型式(16), 通过打靶法求得. ${\dot{{x}}}_{{tU}} $和${\dot{{x}}}_{{tL}} $为状态约束的上、下界. 类似地, ${f}_{{eU}} $和${f}_{{eL}} $为接触力与力矩的安全约束上、下界. 在此基础上利用打靶法, 可以得到构造$X_{m} \left( {{\bar{{\dot{{x}}}}}_{tn} } \right)$的参数$c_{3} $, $\gamma $和$\left| \mathbb{W} \right|$的保守估计值.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 4]
[本文引用: 1]
