黄广靖, 戴玉婷^,2), 杨超北京航空航天大学航空科学与工程学院, 北京 100191

PLASMA-BASED FLOW CONTROL ON PITCHING AIRFOIL AT LOW REYNOLDS NUMBER ¹⁾

Huang Guangjing, Dai Yuting^,2), Yang ChaoSchool of Aeronautic Science and Engineering, Beihang University, Beijing 100191, China

通讯作者: 2)戴玉婷, 副教授, 主要研究方向: 气动弹性力学. E-mail:yutingdai@buaa.edu.cn

收稿日期:2020-06-1接受日期:2020-10-20网络出版日期:2021-12-31

基金资助:

1)国家自然科学基金资助项目.11672018

Received:2020-06-1Accepted:2020-10-20Online:2021-12-31
作者简介 About authors


摘要
针对低雷诺数翼型气动性能差的特点, 通过介质阻挡放电(dielectric barrier discharge, DBD)等离子体激励控制的方法, 提高翼型低雷诺数下的气动特性,改善其流场结构. 采用二维准直接数值模拟方法求解非定常不可压Navier-Stokes方程,对具有俯仰运动的NACA0012翼型的低雷诺数流动展开数值模拟.同时将介质阻挡放电激励对流动的作用以彻体力源项的形式加入Navier-Stokes方程,通过数值模拟探究稳态DBD等离子体激励对俯仰振荡NACA0012翼型气动特性和流场特性的影响.为了进行流动控制, 分别在上下表面的前缘和后缘处安装DBD等离子体激励器,并提出四种激励器的开环控制策略,通过对比研究了这些控制策略在不同雷诺数、不同减缩频率以及激励位置下的控制效果.通过流场结构和动态压强分析了等离子体进行流场控制的机理. 结果表明,前缘DBD控制中控制策略B(负攻角时开启上表面激励器,正攻角时开启下表面激励器)效果最好,后缘DBD控制中控制策略C(逆时针旋转时开启上表面激励器,顺时针旋转时开启下表面激励器)效果最好,前缘DBD控制效果会随着减缩频率的增大而下降, 同时会导致阻力增大.而后缘DBD控制可以减小压差阻力, 优于前缘DBD控制,对于计算的所有减缩频率(5.01~11.82)都有较好的增升减阻效果.在不同雷诺数下, DBD控制的增升效果较为稳定, 而减阻效果随着雷诺数的降低而变差,这是由流体黏性效应增强导致的.
关键词： 等离子体;低雷诺数;俯仰振荡;流动控制;增升减阻

Abstract
To improve the poor aerodynamic performance of pitching airfoils at low Reynolds number, the paper developed a control strategy based on the dielectric barrier discharge (DBD) plasma control. The 2D quasi direct numerical simulation method was applied to solve the unsteady incompressible Navier-Stokes equations around an oscillating NACA0012 airfoil at low Reynolds number. Equations for plasma flow control are added to the momentum equations in the Openfoam solver as a source term. The effects of steady DBD plasma actuation on the aerodynamic force characteristics of an oscillating NACA0012 airfoil are investigated. The DBD plasma actuators are located at the leading edge and trailing edge of the upper and lower airfoil surfaces, respectively. And four open-loop control strategies for the actuators were proposed. The flow control effects of these control strategies with different Reynold numbers, reduced frequency and the positions of plasma actuators are compared. The mechanisms of plasma flow control is analyzed by the flow field structures and dynamic pressure distribution. Results indicate the effect of control strategy B (switch on actuator located on the upper surface at negative angle of attack, and switch on actuator located on the lower surface at positive angle of attack) is best when the plasma actuators located at leading edge of airfoil, and control strategy C (switch on actuator mounted on the upper surface during counterclockwise rotation stage, switch on actuator mounted on the lower surface during clockwise rotation stage) has best effect when the plasma actuators located at the trailing edge of airfoil. When the plasma actuators located at leading edge, the flow control effect will decrease as the reduced frequency increases, and it also increase airfoil's drag. For the trailing edge plasma cases, the pressure drag may decrease, which is better than the leading edge plasma cases. Meanwhile, the trailing edge DBD plasma control has good effect of enhancing lift and reducing drag for all the calculated reduced frequency ranges (5.01~11.82). The lift enhancement effects of DBD flow control are good at different Reynolds numbers. However, due to the flow viscosity effect enhancement, the drag reduction effects of DBD flow control become worse with decreasing Reynolds numbers.
Keywords：plasma;low Reynolds number;pitching airfoil;flow control;lift enhancement and drag reduction


PDF (187147KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
黄广靖, 戴玉婷, 杨超. 低雷诺数俯仰振荡翼型等离子体流动控制 ¹⁾. 力学学报[J], 2021, 53(1): 136-155 DOI:10.6052/0459-1879-20-183
Huang Guangjing, Dai Yuting, Yang Chao. PLASMA-BASED FLOW CONTROL ON PITCHING AIRFOIL AT LOW REYNOLDS NUMBER ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2021, 53(1): 136-155 DOI:10.6052/0459-1879-20-183

引言

近年来随着微小型无人机(micro air vehicles, MAV)在军事和民用方面的广泛应用^[1-2], 比如侦查、监测、通信等,低雷诺数($Re =10^{3}$~$10^{5})$下的空气动力学问题成为研究的热点之一. 微小型无人机由于特征尺寸小、飞行速度低,使得该飞行器的流动特性与常规飞行器大有不同. MAV中小攻角的绕翼流动主要为层流, 以至于其很难抵抗逆压梯度而产生流动分离, 形成层流分离泡. 随着雷诺数的减小, 层流分离泡不断增大并逐步向前缘移动, 导致升力系数下降、阻力系数骤增,气动性能急剧下降^[3-4]. 这些独特的气动特性严重阻碍了微小型飞行器的发展. 为了使其获得更好的气动特性和更高的机动性, 在微小型飞行器设计中, 采用合适的主动流动控制方法来改善翼型低雷诺数下的流场结构, 提高气动性能变得急需而迫切^[5].

微小型飞行器的绕翼流动存在复杂的非定常流动现象, 并且这些现象受沉浮、俯仰或拍打等机翼运动的影响. 近年来, 很多****对低雷诺数绕振荡机翼的气动特性进行了研究. Cleaver等^[6]通过气动力测量和粒子图像测速技术研究了雷诺数10,000下具有15$^\circ$ 攻角的沉浮振荡NACA0012翼型的气动力特性, 沉浮振荡幅值范围为2.5%,$\sim$ 20%的弦长. 研究表明,翼型的沉浮振荡可以有效地增升减阻. Tuncer和Platzer^[7]通过数值模拟研究了NACA0012翼型在不同拍打幅值和频率作用下的尾迹涡结构的形成、分离特性、平均气动力和推进效率. 研究表明由于前缘涡的存在, 高频沉浮振荡可以获得较高的推力系数但推进效率会降低; 而在一定条件下,拍打振荡可以在较高推进效率的前提下获得较高的推力系数. Amiralaei等^[8]研究了雷诺数处于555~5000范围时减缩频率、振荡幅值和雷诺数等非定常参数对谐波俯仰振荡翼型气动特性的影响. 研究表明这些非定常参数对翼型附近涡结构的数量和强度有较强的影响,进而影响气动力特性, 因此应慎重地选择这些非定常参数来取得较好的升力特性.

等离子体激励控制是近年来发展较快的主动控制技术,其主要原理是利用高伏电压作用于等离子体激励器击穿局部气体, 将气体电离化,带电粒子在电场的作用下与其他中性分子发生碰撞, 对流场形成可控的扰动^[9].该流动控制技术与传统流动控制手段相比, 具有无移动部件, 结构简单, 响应速度快,附加质量小以及功耗低的特点^[10], 可以实现增升、减阻、延缓分离等控制效果.

等离子体激励控制技术目前已被应用于旋翼叶片流动控制^[11]、静止和振荡机翼的增升控制^[12-14]、等离子体虚拟气动襟翼^[15-17]、翼型动态失速控制^[18]、三角翼前缘涡控制^[19]等实验研究中,相关****也通过数值模拟的方法对等离子体流动控制技术进行了研究.关于等离子体区域的处理较为简便的方法是将因粒子碰撞产生的动量传递效应简化为一种作用于流体的电场力,并将其以彻体力源项的形式与Navier-Stokes方程耦合求解,文献[20,21,22,23,24]基于不同的假设条件, 分别提出了不同的简化模型.

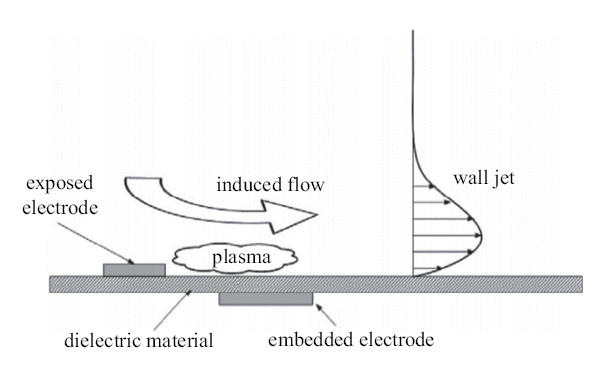
本文采用交流介质阻挡放电激励器产生等离子体激励,典型的表面DBD激励器如图1所示^[25], 由绝缘介质和其两侧非对称布置的高低电压电极组成,其典型工作频率范围为1~10 kHz, 电压幅值范围为5~10 kV. 普遍认为,毫秒等离子体激励彻体力效应占主导^[26],因此本文使用Shyy等^[22]提出的简化模型计算等离子体激励产生的彻体力.目前关于低雷诺数等离子体流动控制的数值仿真研究取得了一定的进展.Rizzetta和Visbal^[27]利用大涡模拟技术研究了雷诺数60,000下攻角为4$^\circ$的SD7003翼型的阵风减缓控制,研究表明采用等离子体控制可以有效地减缓阵风带来的不利影响,提升静止翼型的气动性能;其后研究了等离子体控制对雷诺数30,000和60,000下的拍动翼型气动特性的影响,研究表明等离子体控制可以减缓流动分离, 阻力减小80%,升阻比增大5倍^[28].Mukherjee和Roy^[29]利用大涡模拟技术模拟了雷诺数$1.35\times10^{5}$下的俯仰振荡NACA0012翼型的流动并探究了等离子体激励的控制效果,结果表明在翼型表面合适的位置布置等离子体激励器, 可以实现增升减阻的效果.Mahboubidoust等^[30]对雷诺数12,000下的振荡NACA0012翼型的二维不可压层流流动进行了数值研究,分别对前缘和后缘两个不同位置施加等离子体激励,结果表明等离子体控制可以提升俯仰振荡翼型的气动性能,但是对拍动翼型的气动性能没有积极的控制效果,相对于在其他位置施加等离子体激励, 在后缘施加等离子体激励具有更好的控制效果,同时也发现等离子体激励在不同的运动行程中控制效果也存在明显的差异. 因此,展开对等离子体控制策略和控制机理的研究是有必要的.

图1

新窗口打开|下载原图ZIP|生成PPT
图1典型的表面DBD激励器示意图

Fig.1A schematic of the SDBD configuration



Kojima等^[31]采用三维隐式大涡模拟和二维层流模型模拟了不同厚度翼型低雷诺数下层流分离效应,结果显示在$Re<30 000$时, 层流模型和大涡模拟方法获得中小攻角下的气动特性和流场特性具有较好的一致性.因此, 本文采用二维层流不可压模型对俯仰振荡NACA0012翼型的低雷诺数流动展开数值模拟,使用文献[22]的简化模型计算等离子体激励产生的彻体力, 将其作为动量方程的源项进行耦合求解.在翼型上下表面的前后缘分别对称布置DBD激励器, 提出四种不同的开环控制策略,通过对比研究了这四种开环控制策略在不同减缩频率、激励位置和雷诺数下的控制效果和原因.

1 研究方法

1.1 控制方程和数值方法

准直接数值模拟方法(quasi-DNS)被越来越广泛地应用于复杂流动的数值模拟.传统意义的DNS需要较密的计算网格和高阶数值离散格式, 导致其计算效率较差.而准DNS计算所需的网格单元较少, 空间离散和时间离散均采用二阶离散格式,以快速得到精确但未对所有尺度湍流进行解析的流动仿真结果^[32].对于二维非定常层流不可压流动, 其基本控制方程为

(1)$\begin{eqnarray} &&\nabla \cdot {U}=0 \end{eqnarray}$
(2)$\begin{eqnarray} \rho \frac{D{U}}{Dt}=-\nabla p+\mu \nabla^{2}{U}+{b} \end{eqnarray}$
其中, ${U}$为速度矢量, $\rho $为流体密度, $p$为压强, $\mu $为动力黏性系数, ${b}$为等离子体激励彻体力.

数值方法采用基于单元中心格式的有限体积法求解上述控制方程, 瞬态项采用欧拉向后二阶隐式离散格式, 对流项采用二阶线性迎风离散格式, 扩散项采用基于线性插值和显式非正交修正的面法向梯度格式的二阶精度格式进行离散. 本文采用PISO (pressure-implicit with splitting of operators)算法处理压力速度耦合问题, 压强方程采用多重网格求解器(geometric algebraic multi-grid, GAMG)进行离散矩阵的求解, 速度方程采用不完全LU光顺求解器(diagonal incomplete-LU, DILU)进行离散矩阵的求解.

1.2 DBD等离子体数值模型

交流介质阻挡放电激励器激励彻体力效应占主导, 因此下面给出等离子体激励彻体力的数值模型的描述. 表面DBD激励器的电场线一般在阴极附近聚集, 在阳极附近近似均匀分布, 在除了阴极附近的大部分区域电场线可以看作是平行的. 因此可以假设电场强度在空间上是线性变化的, 并且随着与电极距离的增大, 电场强度不断减弱. 电场强度的变化关系可以写为

(3)$\begin{eqnarray} \left| E \right|=E_{0} -k_{1} x-k_{2} y \end{eqnarray}$
其中, $E_{0} ={V}/{d}$, $d$为两个电极水平方向之间的距离, $V$为电极之间施加的均方根电压值. 系数$k_{1} $和$k_{2}$可根据击穿电场强度$E_{b} $计算得到

(4)$\begin{eqnarray} k_{1} =\frac{E_{0} -E_{b} }{b},\ \ k_{2} =\frac{E_{0} -E_{b} }{a} \end{eqnarray}$
其中, $a$为等离子体激励区域的高度, $b$为等离子体区域的宽度. 电场强度的分量形式为

(5)$\begin{eqnarray} E_{x} =\frac{Ek_{2} }{\sqrt {k_{1}^{2} +k_{2}^{2} } },\ \ E_{y} =\frac{Ek_{1} }{\sqrt {k_{1}^{2} +k_{2}^{2} } } \end{eqnarray}$
于是, 等离子体激励彻体力分量为

(6)$\begin{eqnarray} \left.\begin{array}{l} b_{x} =\vartheta \alpha \rho_{c} e_{c} \Delta tE_{x} \delta \\ b_{y} =\vartheta \alpha \rho_{c} e_{c} \Delta tE_{y} \delta \\ \end{array}\right\} \end{eqnarray}$
其中, $\vartheta $为交流电压的频率, $\alpha $为粒子碰撞效率因子, $\rho_{c}$为电子数密度, $e_{c} $为电子电荷量, $\Delta t$为等离子体放电时间. $\delta$为狄拉克函数表征等离子体激励彻体力只在等离子体存在的区域存在

(7)$\begin{eqnarray} \delta =\left\{\begin{array}{l@{\quad}l} 1, & E>E_{cr}\\ 0, & E\leqslant E_{cr}\\ \end{array} \right. \end{eqnarray}$
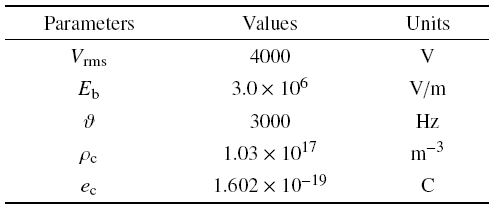
其中, $E_{cr} $即为击穿电场强度$E_{b} $. 本文中使用的等离子体模型的相关参数如表1所示.


Table 1
Table 1Parameters for plasma modeling

新窗口打开|下载CSV

1.3 数值计算模型

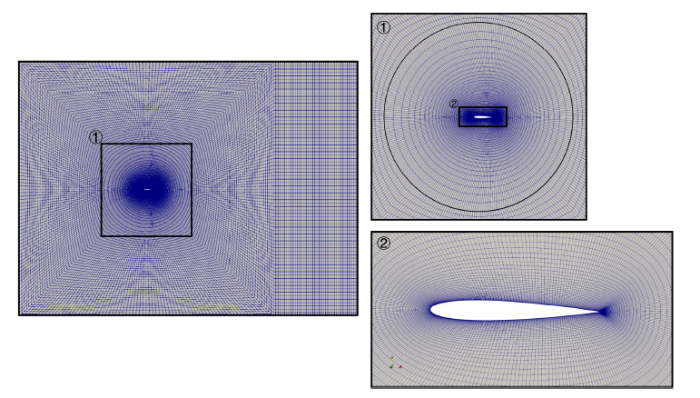
计算采用NACA0012翼型, 翼型弦长为$c=1$ m. 本文采用O型网格,为了处理翼型俯仰运动带来的网格变形问题, 本文在距离俯仰轴$5c$处定义滑移网格交界面, 将计算网格分为内域和外域两部分.内域网格随翼型进行刚体运动, 外域网格保持静止, 以避免翼型运动带来的网格变形问题. 计算所用网格如图2所示.

计算中, 翼型表面采用无滑移壁面条件, 入口距离翼型15$c$, 采用速度入口作为边界条件, 出口距离翼型25$c$, 采用压力出口作为边界条件, 上下壁面距离翼型15$c$, 采用对称边界条件. NACA0012翼型的俯仰轴位于距翼型前缘1/4弦长处, 俯仰振荡形式为

(8)$\begin{eqnarray} \alpha (t)=A\sin (\omega t) \end{eqnarray}$
式中, $A$为俯仰运动的幅值(顺时针为正), $\omega =2\pi f$, f为俯仰运动的频率.

图2

新窗口打开|下载原图ZIP|生成PPT
图2NACA0012翼型计算网格

Fig.2Computational grids of NACA0012 airfoil

2 算例验证

2.1 等离子体数值模型验证

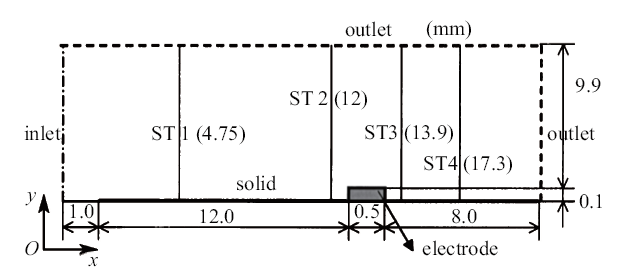
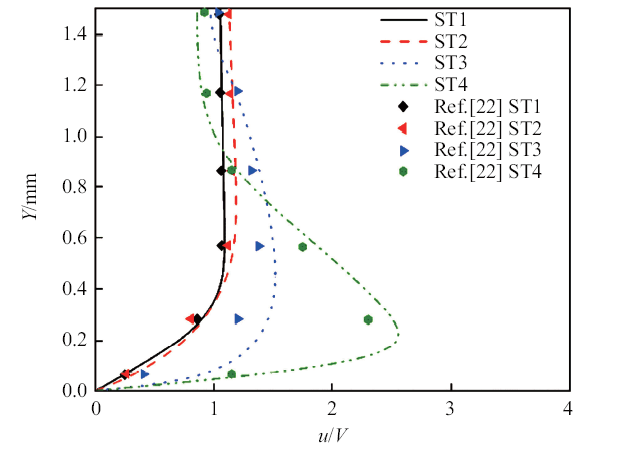
本文将等离子体控制以彻体力形式加在相应流体控制区域. 为了验证DBD等离子体数值模型实现的准确性, 本文采用文献[22]中的平板算例进行验证. 该算例计算域如图3所示. 四个不同流向位置的速度型分布曲线如图4所示.本文所使用计算程序得到的不同流线位置的速度型分布与文献参考值吻合很好, 表明了DBD等离子体数值模型实现的准确性.

图3

新窗口打开|下载原图ZIP|生成PPT
图3平板流动计算域与边界条件设置

Fig.3Computational domain and boundary conditions of the flat plate flow

图4

新窗口打开|下载原图ZIP|生成PPT
图4不同流向位置速度型分布结果与文献[22]比较

Fig.4Comparison of Ref.[22] data and numerical results

2.2 低雷诺数动态气动力计算结果验证

为了验证滑移网格和流体模型处理翼型俯仰振荡运动的准确性, 本文采用NACA0012翼型进行验证, 雷诺数为12 000, 俯仰运动的幅值为2$^\circ$, 减缩频率($k=\pi fc/U)$为6.68. 将滑移网格方法与文献[30]中的动网格方法进行对比.同时采用表2中三种不同的网格进行网格无关性试验, 三种网格均满足$y^{+}<1$.


Table 2
Table 2Parameters for three different grids

新窗口打开|下载CSV

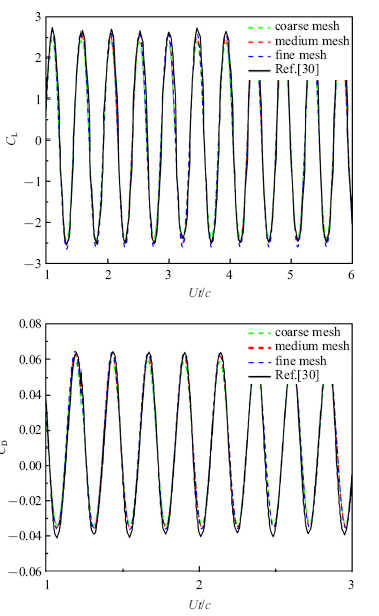
翼型俯仰振荡的升力、阻力系数变化曲线如图5所示. 由图5可知, 中等网格和细网格的升力系数曲线和阻力系数曲线均吻合得很好, 故采用中等网格进行后续的计算. 而且,通过滑移网格方法计算的气动力响应与文献中采用动网格技术得到的结果吻合得很好, 升阻力系数最大误差分别为5%和2.8%. 表明本文采用的滑移网格方法和流体准直接数值模型方法能够准确地模拟翼型俯仰振荡下的气动特性和流场特性.

图5

新窗口打开|下载原图ZIP|生成PPT
图5升力、阻力系数时间变化曲线与文献[30]比较

Fig.5Lift and drag coefficients, comparison of present work and Ref.[30]

3 结果分析与讨论

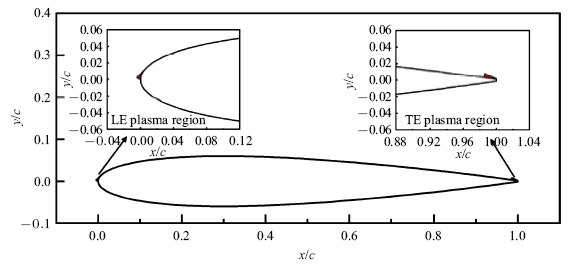
本文重点研究了不同雷诺数、不同等离子体激励器布置位置、不同等离子体激励控制策略(基准(baseline):无DBD激励; DBD常开控制(DBD-NO): 上下表面DBD激励在整个周期开启;DBD控制策略A (DBD-A): 正攻角(顺时针为正)时开启上表面DBD激励,负攻角时开启下表面DBD激励; DBD控制策略B (DBD-B): 负攻角时开启上表面DBD激励,正攻角时开启下表面DBD激励; DBD控制策略C (DBD-C):顺时针旋转时开启上表面DBD激励, 逆时针旋转时开启下表面DBD激励;DBD控制策略D (DBD-D): 逆时针旋转时开启上表面DBD激励,顺时针旋转时开启下表面DBD激励)对振幅为8$^\circ$ ,减缩频率分别为5.01, 6.68, 8.88和11.82的俯仰振荡翼型的气动力特性和流场结构的影响.等离子体激励器对称的布置在翼型前缘(LE)的上下表面或后缘(TE)的上下表面.具体位置如图6所示, 图中红色三角区域为等离子体区域, 该区域高为0.005 m,宽为0.015 m. 首先计算雷诺数12,000下, 不同的等离子体激励器布置位置、俯仰振荡减缩频率和等离子体控制策略对俯仰振荡翼型气动力特性和流场结果的影响,之后针对增升减阻效果较好的控制策略计算不同雷诺数下的气动力特性进行对比分析.为了得到稳定的计算结果, 每个工况计算15个周期,取最后的10个周期的计算结果进行平均.

3.1 前缘DBD流动控制结果及机理分析

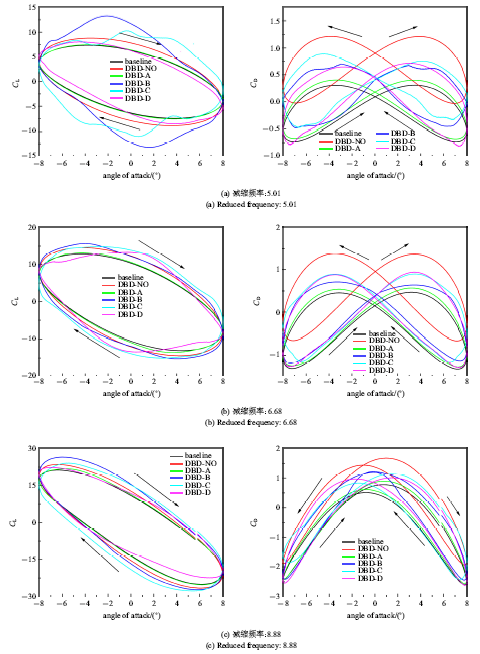
图7给出了前缘DBD激励在一个振荡周期内的气动力系数随攻角的变化曲线.不同的控制策略对气动力特性的影响存在明显的差异,DBD常开控制在不同的减缩频率下都有一定的增升效果,但是同时也会导致阻力系数的增大. 相较于基准情况, 控制策略A和D的增升效果较差,均不如DBD常开控制的增升效果, 尤其是控制策略A无任何增升效果, 反而会增大阻力.控制策略B和C均有较好的增升效果, 与DBD常开控制相比阻力系数也大幅降低.图 8给出了前缘DBD激励控制下相对于基准情况的最大升力系数和平均阻力系数变化率随减缩频率的变化曲线.可见, 在进行DBD流动控制时选择合适的控制策略可以大幅提升流动控制的效果. 同时,随着减缩频率的增大, 前缘DBD激励幅值相对于俯仰振荡扰动变小, 增升效果逐渐变差.减缩频率为5.01时前缘DBD激励有较好的增升效果,尤其是控制策略B在逆时针旋转阶段和顺时针旋转阶段中均有80%的增幅,但是在取得较好增升效果的同时平均阻力相对于基准工况增大150%,与DBD常开控制情况相比平均阻力增幅从360%下降到150%. 综合来看,控制策略B是前缘DBD控制的最优控制策略.

下面对前缘DBD控制策略B一个周期内的气动力变化进行研究,并从流场结构和压强分布的角度对气动力变化进行分析.图9和图10分别给出了减缩频率5.01和11.82下一个周期内攻角、基准和前缘DBD控制策略B升力系数随时间变化曲线,并将0.125$T$, 0.375$T$, 0.625$T$和0.875$T$这四个时刻分别标记为(a), (b), (c)和(d).图11和图12分别给出了减缩频率5.01下基准和前缘DBD控制策略B四个时刻下的流场结构.图13给出了减缩频率5.01下两种工况四个时刻下的压强分布曲线.

图6

新窗口打开|下载原图ZIP|生成PPT
图6前后缘等离子体区域

Fig.6Leading edge and trailing edge plasma region

图7

新窗口打开|下载原图ZIP|生成PPT
图7前缘DBD控制气动力随攻角变化曲线

Fig.7Aerodynamic coefficient during an oscillation cycle of leading edge DBD plasma control

图7

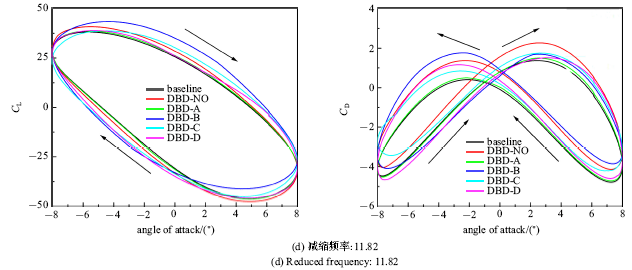新窗口打开|下载原图ZIP|生成PPT
图7前缘DBD控制气动力随攻角变化曲线(续)

Fig.7Aerodynamic coefficient during an oscillation cycle of leading edge DBD plasma control (continued)

图8

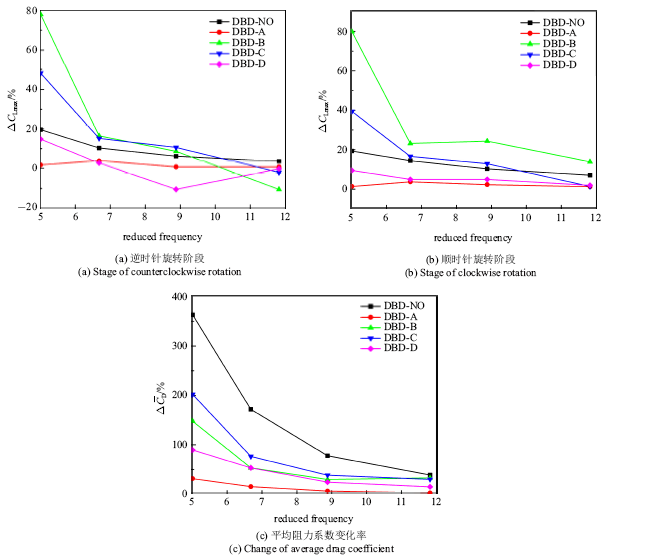新窗口打开|下载原图ZIP|生成PPT
图8前缘DBD控制最大升力系数和平均阻力系数变化率随减缩频率的变化曲线

Fig.8Rate of max lift coefficient and average drag coefficient change as reduced frequency with plasma at leading edge

图9

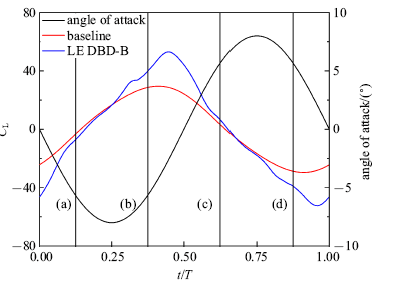新窗口打开|下载原图ZIP|生成PPT
图9减缩频率5.01时升力系数随时间变化曲线

Fig.9Lift coefficient as time with $k=5.01$

图10

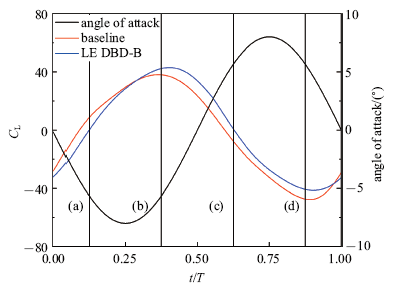新窗口打开|下载原图ZIP|生成PPT
图10减缩频率11.82时升力系数随时间变化曲线

Fig.10Lift coefficient as time with $k=11.82$

图11

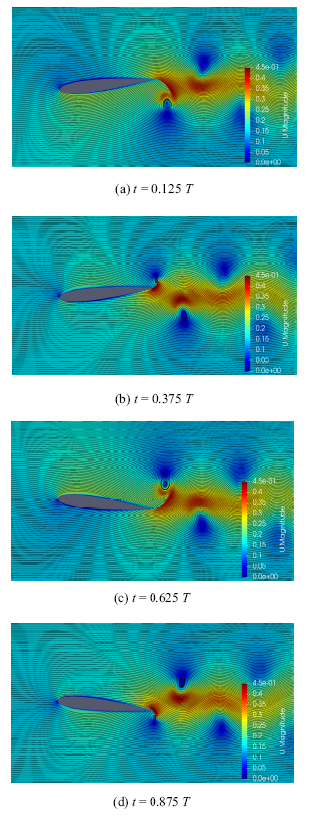
新窗口打开|下载原图ZIP|生成PPT
图11减缩频率5.01时基准流场结构

Fig.11Flow field structure of baseline with $k=5.01$



减缩频率为5.01时, (a)时刻攻角为$-$5.656$^\circ$ , 翼型继续向下低头运动.基准工况在翼型的下表面前半部分产生了低压区, 然而由于翼型的俯仰运动,后缘处脱落一个顺时针涡, 加速了翼型上表面后半部分的流动,同时在翼型上表面后半部分也产生了低压区(图13(a)),抵消了部分由于负攻角产生的负升力.

前缘DBD控制策略B此时上表面DBD激励开启, 会对上表面前缘附近的流体进行加速,在上表面前缘附近形成吸力峰,同时之前下表面DBD激励启动时产生的顺时针涡移动到下表面0.8$c$处并在该处也形成了一个吸力峰(图12(a)),该吸力峰的幅值及范围更大, 该减缩频率较小,俯仰运动产生的流场扰动小于DBD激励产生的加速效应, 因此相对于基准,前缘控制策略B在(a)时刻负升力更大.

图12

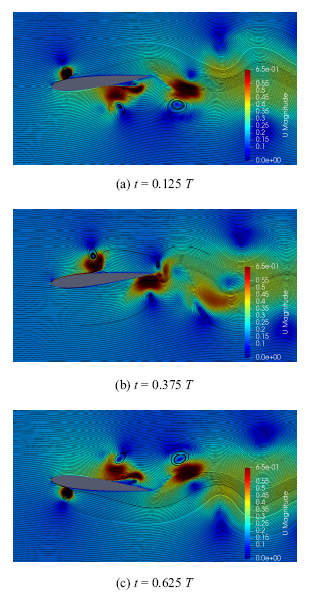
新窗口打开|下载原图ZIP|生成PPT
图12减缩频率5.01时前缘DBD控制策略B流场结构

Fig.12Flow field structure of leading edge DBD control strategy B with $k=5.01$



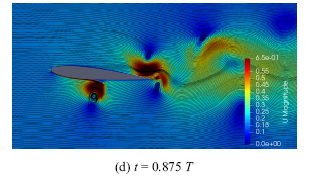
(b)时刻攻角为$-$5.656$^\circ$ , 翼型抬头向上运动.基准工况此时翼型后半部分向下运动, 翼型上表面后半部分会吸引更多的流体, 从而带动整个上翼面的流动, 使得翼型上表面压强整体减小;前缘DBD控制策略B上表面DBD激励产生的逆时针涡向下游移动(图12(b)),使得上表面前半部分压强降低, 同时下表面顺时针涡移动到后缘附近,由于该涡的作用在该涡的上游由于翼型抬头运动产生的$y$方向速度被削弱,在该涡上游附近产生一个高压区,同时由于后缘处顺时针涡的存在压强在后缘附近又迅速减小.基准工况和前缘控制策略B在(c)(d)时刻的气动特性和流场结构基本与(a)(b)时刻相反.

图12

新窗口打开|下载原图ZIP|生成PPT
图12减缩频率5.01时前缘DBD控制策略B流场结构(续)

Fig.12Flow field structure of leading edge DBD control strategy B with $k=5.01$ (continued)



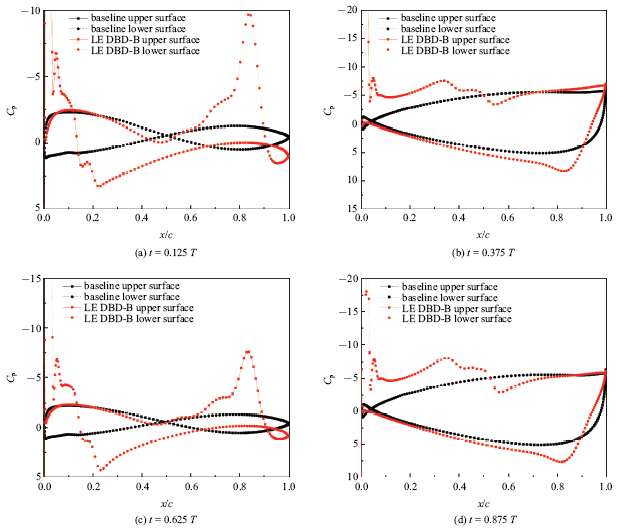
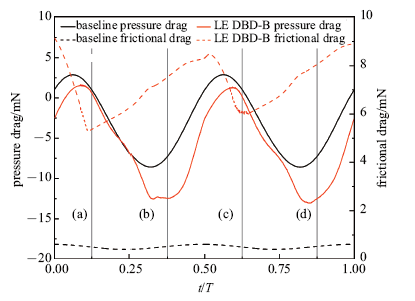
图14给出了减缩频率5.01下两种工况摩擦阻力和压差阻力随时间变化曲线,单个周期内基准平均压差阻力为$-$0.003 N, 平均摩擦阻力为0.000 5 N;前缘DBD控制策略B平均压差阻力为$-$0.005 9 N, 平均摩擦阻力为0.007 2 N.前缘DBD激励由于其对壁面附近流体的加速效应, 流体法向速度梯度增大,导致摩擦阻力增大. 如图13(b)所示, (b)时刻相较于基准工况,前缘DBD控制策略B上表面压强分布更加平缓, 下表面压强分布更加陡峭,使得压差阻力明显减小, 而前缘DBD控制策略B由于图12(b)所示的后缘涡结构的影响,下表面后缘附近压强迅速降低, 导致压差阻力降幅减小, 最终导致平均阻力增大.

图13

新窗口打开|下载原图ZIP|生成PPT
图13减缩频率5.01时压强分布曲线

Fig.13Pressure distribution curve with $k=5.01$

图14

新窗口打开|下载原图ZIP|生成PPT
图14减缩频率5.01时压差阻力和摩擦阻力随时间变化曲线

Fig.14Pressure drag and frictional drag curves as time with $k=5.01$



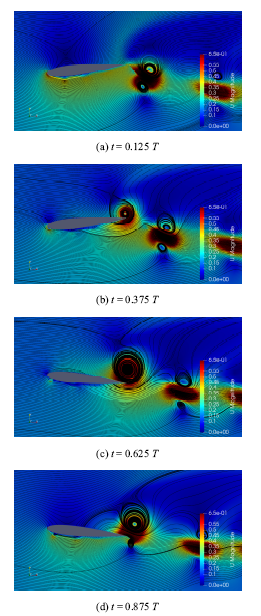
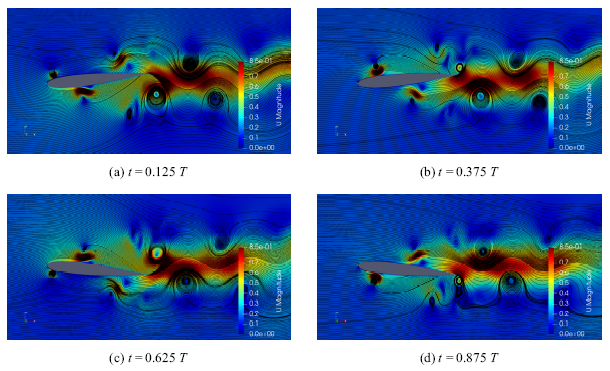
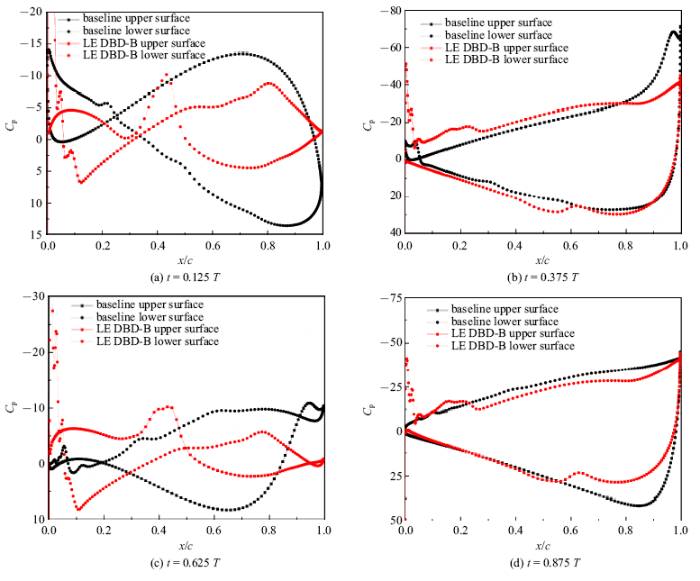
图15和图16分别给出了减缩频率11.82下基准和前缘DBD控制策略B四个时刻下的流场结构.图17给出了减缩频率11.82下两种工况四个时刻下的压强分布曲线.减缩频率为11.82时,(a)时刻两种工况的气动力特性和压强分布由翼型俯仰运动扰动为主导,压强分布曲线呈现$\infty $形, 同时由于负攻角, 基准工况在下表面前缘出现吸力峰,而前缘DBD控制策略B上表面的DBD激励抑制了下表面前缘吸力峰的形成, 除此之外,由于减缩频率的增大,上个周期下表面前缘DBD激励产生的逆时针涡仅移动到翼型中部(图16(a)),在下表面中部附近形成一个小的吸力峰.(b)时刻两个工况的气动力特性由翼型后缘涡主导,而前缘DBD控制策略B上个周期上表面前缘DBD激励产生的逆时针涡与翼型抬头运动甩出的后缘涡相互抑制(图16(b)),减小了后缘涡的强度,同时前缘DBD激励加速了上表面前缘附近的流动且抑制了翼型下表面的前缘吸力峰,最终前缘DBD控制策略B升力小幅增大.前缘DBD控制策略B在(c)(d)时刻的气动特性和流场结构基本与(a)(b)时刻相反.基准工况在(c)(d)时刻在下表面前缘附近产生了逆时针小涡(图15(c)图15(d)),该涡结构抑制了上表面的吸力峰,导致在(d)时刻基准工况的负升力大小超过前缘DBD控制策略B.

图15

新窗口打开|下载原图ZIP|生成PPT
图15减缩频率11.82时基准流场结构

Fig.15Flow field structure of baseline with $k=11.82$

图16

新窗口打开|下载原图ZIP|生成PPT
图16减缩频率11.82时前缘DBD控制策略B流场结构

Fig.16Flow field structure of leading edge DBD control strategy B with $k=11.82$

图17

新窗口打开|下载原图ZIP|生成PPT
图17减缩频率11.82时压强分布曲线

Fig.17Pressure distribution curve with $k=11.82$

3.2 后缘DBD流动控制结果及机理分

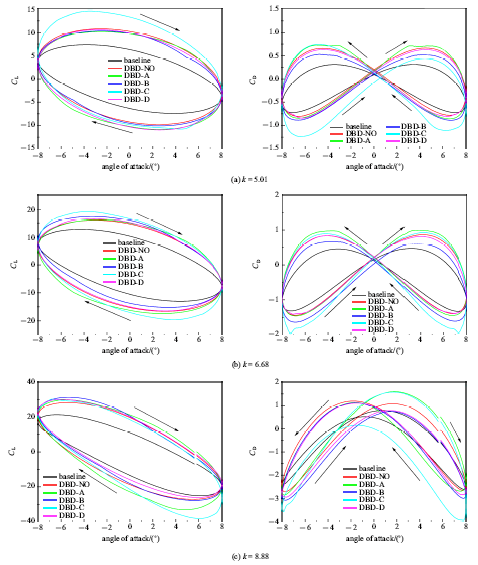
图18给出了后缘DBD激励在一个振荡周期内的气动力系数随攻角的变化曲线.后缘DBD控制效果明显优于前缘DBD激励,后缘DBD在所有的减缩频率下均有较为明显的增升效果, 同时阻力系数不存在明显的增大, 甚至出现了明显的降低.

图18

新窗口打开|下载原图ZIP|生成PPT
图18后缘DBD控制气动力随攻角变化曲线

Fig.18Aerodynamic coefficient during an oscillation cycle of trailing edge DBD plasma control

图18

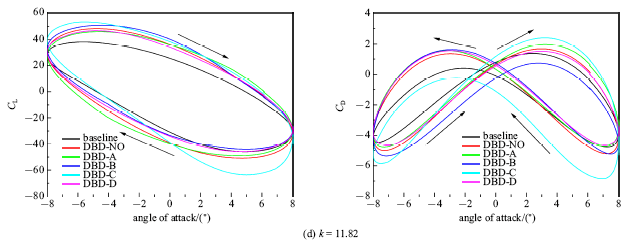
新窗口打开|下载原图ZIP|生成PPT
图18后缘DBD控制气动力随攻角变化曲线(续)

Fig.18Aerodynamic coefficient during an oscillation cycle of trailing edge DBD plasma control (continued)



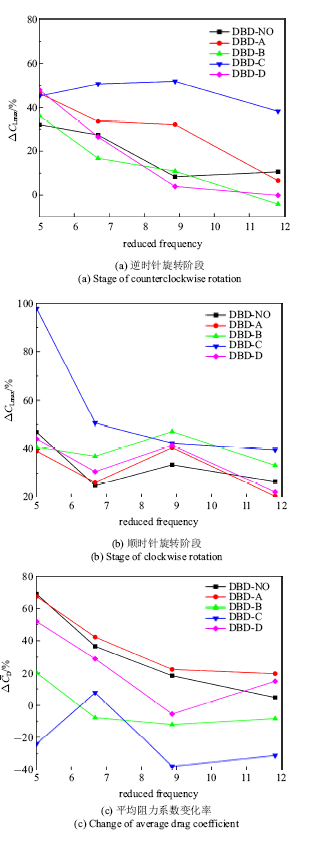
图19给出了后缘DBD激励控制下相对于基准情况的最大升力系数和平均阻力系数变化率随减缩频率的变化曲线.可见, 对于后缘DBD控制, 不同的控制策略均有较好的增升效果,逆时针旋转阶段的最大升力系数变化率与前缘DBD控制一样随着减缩频率的增大而减小,但是采用合适的控制策略可以解决这个问题. 对于后缘DBD控制,控制策略C的增升减阻效果明显优于其他控制策略.控制策略C在不同的减缩频率下均有较为稳定的增升效果, 幅度在40%以上,尤其是减缩频率为5.01时最大升力系数增幅高达100%.不同的控制策略对阻力系数的影响存在明显的差异,控制策略A和D在升力增大的同时也会导致阻力系数的增大;而控制策略B和C在大部分减缩频率下平均阻力系数变化率为负值,即使在某些减缩频率下平均阻力系数增大, 其增幅也远小于最大升力系数的增幅,尤其是控制策略C平均阻力系数减幅基本在20%以上. 综合来看,控制策略C是后缘DBD控制的最优控制策略.

图19

新窗口打开|下载原图ZIP|生成PPT
图19后缘DBD控制最大升力系数和平均阻力系数变化率随减缩频率的变化曲线

Fig.19The rate of max lift coefficient and average drag coefficient change as reduced frequency with plasma at trailing edge



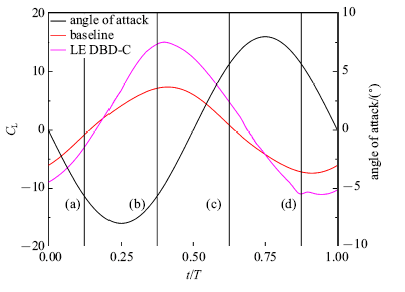
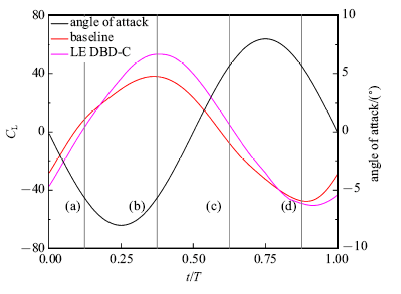
下面对后缘DBD控制策略C一个周期内的气动力变化进行研究, 并从流场结构和压强分布的角度对气动力变化进行分析.图20和图21分别给出了减缩频率5.01和11.82下一个周期内攻角、基准和后缘DBD控制策略C升力系数随时间变化曲线,并将0.125$T$, 0.375$T$, 0.625$T$和0.875$T$这四个时刻分别标记为(a)(b)(c)和(d).图22给出了减缩频率5.01下后缘DBD控制策略C四个时刻下的流场结构.图23给出了减缩频率5.01下两种工况四个时刻下的压强分布曲线.

图20

新窗口打开|下载原图ZIP|生成PPT
图20减缩频率5.01升力系数随时间变化曲线

Fig.20Lift coefficient as time with $k=5.01$

图21

新窗口打开|下载原图ZIP|生成PPT
图21减缩频率11.82升力系数随时间变化曲线

Fig.21Lift coefficient as time with $k=11.82$

图22

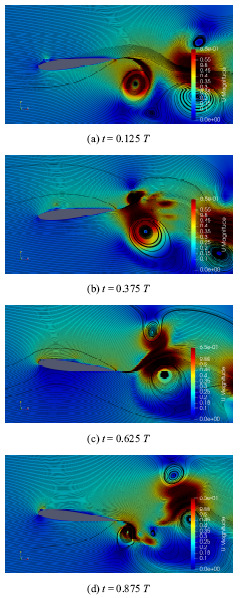
新窗口打开|下载原图ZIP|生成PPT
图22减缩频率5.01时后缘DBD控制策略C流场结构

Fig.22Flow field structure of trailing edge DBD control strategy C with $k=5.01$



减缩频率为5.01时, (a)时刻攻角为$-$5.656$^\circ$ , 翼型继续向下低头运动.后缘DBD控制策略C此时下表面DBD激励开启,在后缘DBD激励和翼型低头运动的共同作用下,在后缘的右下方产生了一个顺时针涡(图22(a)),该涡带动翼型下表面后半部分流体加速,因此在翼型下表面后缘附近出现了一个很大的低压区,使得后缘DBD控制策略C在此时刻的负升力最大. (b)时刻攻角为$-$5.656$^\circ$ ,翼型抬头向上运动. 后缘DBD控制策略C此时上表面后缘DBD激励开启,因此在后缘产生了很大的吸力峰,同时后缘右下方的顺时针涡削弱翼型抬头运动产生的$y$方向速度,使得翼型下表面后缘附近的压强增大, 进一步提升了正升力.后缘DBD控制策略C在(c)(d)时刻由于正攻角的原因均在上表面前缘产生了一个吸力峰,而(a)(b)时刻由于上表面前缘顺时针小涡的存在(图22),并没有在下表面前缘产生吸力峰.

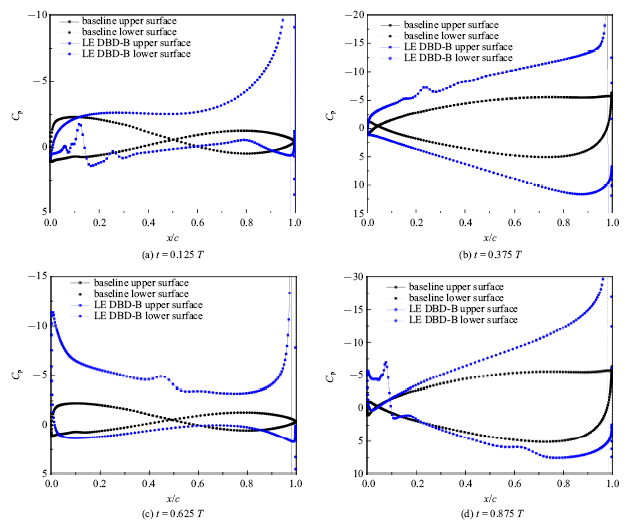
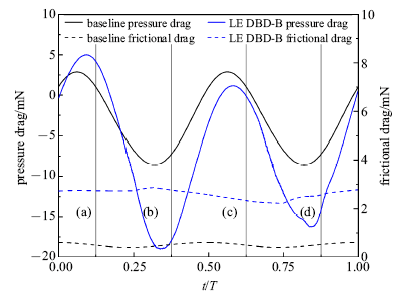
图24给出了减缩频率5.01下两种工况摩擦阻力和压差阻力随时间变化曲线,单个周期内基准平均压差阻力为$-$0.003 N, 平均摩擦阻力为0.000 5 N;后缘DBD控制策略C平均压差阻力为$-$0.006 8 N, 平均摩擦阻力为0.002 6 N.由于后缘DBD激励仅影响后缘附近, 影响区域较小,因此摩擦阻力增大幅度明显比前缘DBD控制策略B小. 如图23(b)所示,(b)时刻相较于基准工况, 后缘DBD控制策略C上表面压强分布更加平缓,下表面压强分布更加陡峭, 使得压差阻力明显减小.

图23

新窗口打开|下载原图ZIP|生成PPT
图23减缩频率5.01时压强分布曲线

Fig.23Pressure distribution curve with $k=5.01$

图24

新窗口打开|下载原图ZIP|生成PPT
图24减缩频率5.01时压差阻力和摩擦阻力随时间变化曲线

Fig.24Pressure drag and frictional drag curves as time with $k=5.01$

图25

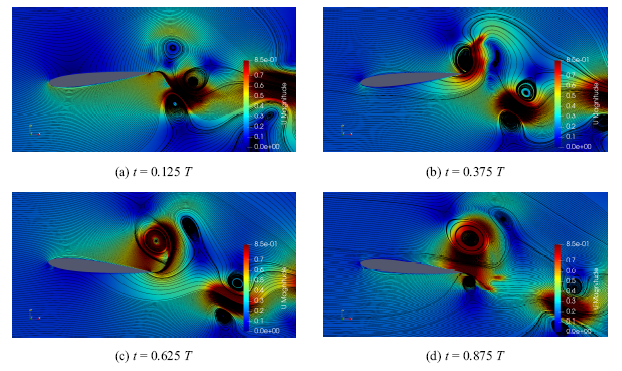
新窗口打开|下载原图ZIP|生成PPT
图25减缩频率11.82时后缘DBD控制策略C流场结构

Fig.25Flow field structure of trailing edge DBD control strategy C with $k=11.82$

图26

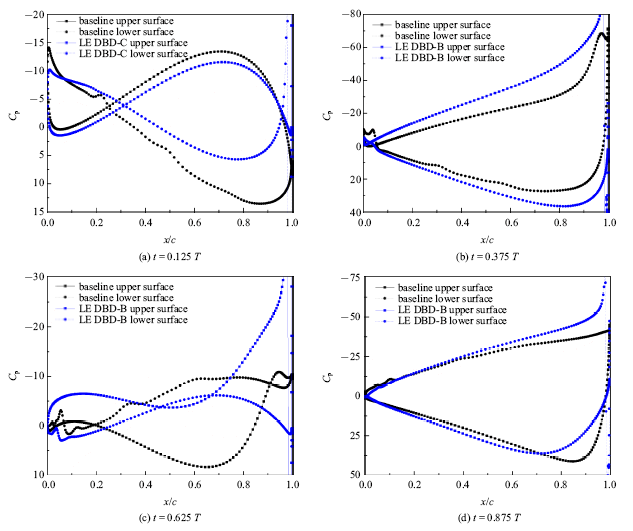
新窗口打开|下载原图ZIP|生成PPT
图26减缩频率11.82时压强分布曲线

Fig.26Pressure distribution curve with $k=11.82$



图25给出了减缩频率11.82下后缘DBD控制策略C四个时刻下的流场结构,图26给出了减缩频率11.82下两种工况四个时刻下的压强分布曲线.(a)时刻三种工况的气动力特性和压强分布由翼型俯仰运动扰动为主导,压强分布曲线呈现$\infty $形, 同时由于负攻角,基准工况和后缘DBD控制策略C在下表面前缘不同程度的出现吸力峰.(b)时刻三个工况的气动力特性由翼型后缘涡主导,后缘DBD控制策略C上表面的DBD激励使得翼型抬头运动在后缘甩出的逆时针涡强度变大(图25(b)),使得后缘DBD控制策略C的升力大幅提升.后缘DBD控制策略C在(b)时刻生成的后缘涡不断向上移动,在(c)时刻移动到后缘的上方(图25(c)), 由于该涡的强度较大,在上表面后缘附近产生了一个范围很大的低压区, 正升力增大,(d)时刻气动特性与(b)时刻大体相反, 下表面后缘附近卷起顺时针涡,在下表面后缘附近造成低压区,然而由于上表面后缘上方的逆时针涡依然存在(图25(d)), 导致上表面高压区压强降低,升力增大幅度降低.

3.3 雷诺数对DBD流动控制效果的影响

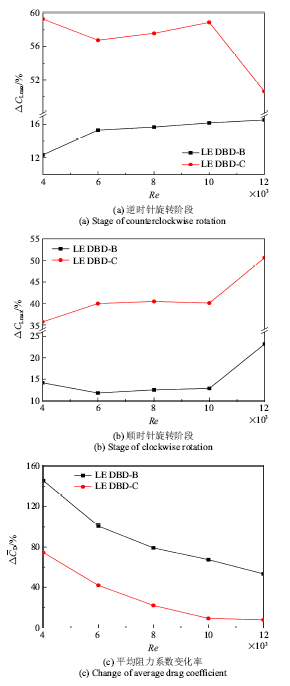
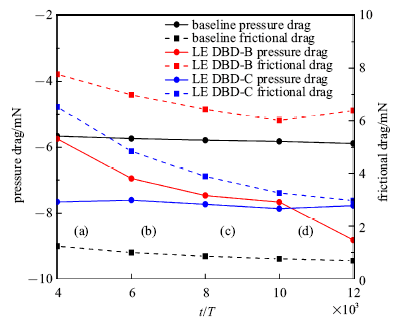
本节通过计算雷诺数分别为4000, 6000, 8000, 10 000和12 000时三种控制策略(基准、前缘控制策略B和后缘控制策略C)作用下幅值为8$^\circ$、减缩频率为6.68的俯仰振荡NACA0012翼型的气动特性来研究雷诺数对DBD流动控制效果的影响.图27给出了这两种控制策略相对于基准情况最大升力系数和平均阻力系数变化率随雷诺数的变化曲线,两种控制策略的最大升力系数变化率在逆时针旋转阶段和顺时针旋转阶段随雷诺数的变化都较为稳定.后缘DBD控制策略C增升效果明显好于前缘DBD控制策略B. 在逆时针旋转阶段,后缘控制策略C的增升幅度稳定在55%左右,前缘控制策略B的增升幅度稳定在15%左右; 在顺时针旋转阶段,后缘控制策略C的增升幅度稳定在40%左右,前缘控制策略B的增升幅度稳定在13%左右.两种控制策略的平均阻力系数变化率随着雷诺数的增大而减小.图28给出了三种情况平均压差阻力和平均摩擦阻力随雷诺数的变化曲线.两种控制策略的平均压差阻力均低于基准情况, 后缘控制策略C的平均压差阻力更小.基准和后缘控制策略C的平均压差阻力随雷诺数变化基本不变,而前缘控制策略B的平均压差阻力随着雷诺数的增大而减小.三种情况的摩擦阻力都随着雷诺数的增大而减小, 这是因为随着雷诺数的增大,流体的黏性效应减弱, 其中后缘控制策略C平均摩擦阻力的下降速度最快.针对雷诺数降低, 平均摩擦阻力增大, DBD控制减阻效果变差可通过减小DBD强度,适当减弱等离子体对流体的加速效应来改善.

图27

新窗口打开|下载原图ZIP|生成PPT
图27最大升力系数和平均阻力系数变化率随雷诺数的变化曲线

Fig.27Rate of max lift coefficient and average drag coefficient change as Reynold numbers

图28

新窗口打开|下载原图ZIP|生成PPT
图28平均压差阻力和平均摩擦阻力随雷诺数变化曲线

Fig.28Average pressure drag and average frictional drag curves as Reynold numbers

4 结论

本文采用非定常数值模拟手段, 以俯仰振荡NACA0012翼型为研究对象,对比研究了不同开环控制策略在不同俯仰振荡减缩频率、不同DBD激励布置位置和不同雷诺数下的控制效果,并通过从气动力特性、流场结构和压强分布等角度的细致分析, 得到以下结论:

(1)采用一定的控制策略能够提升流动控制效果,前缘DBD控制策略B和后缘DBD控制策略C的增升减阻效果均明显优于DBD常开控制的情况.针对不同的DBD激励布置位置和不同的俯仰振荡运动减缩频率, 最优控制策略也不同.

(2)前缘DBD控制策略B只对较小的减缩频率具有较好的增升效果. 减缩频率增大后,俯仰运动甩出的后缘涡会产生很大的升力,而前缘DBD控制策略B上个周期DBD激励产生的涡结构会减小后缘涡的强度,导致增升效果减小. 同时前缘DBD控制往往会使平均阻力增大,这是由于DBD激励对壁面附近流体的加速效应, 流体法向速度梯度增大,使摩擦阻力增大, 另外由于DBD激励产生的涡结构移动到后缘, 导致压差阻力降幅减小,难以抵消摩擦阻力的增幅.

(3)后缘DBD控制策略C在所有的减缩频率都有较好的增升减阻效果. 由于后缘DBD激励产生的后缘涡在后缘上下表面形成较大的压强差导致升力增大, 该涡结构也导致压差阻力大幅降低.

(4) DBD控制的增升效果随着雷诺数的变化较为稳定, 而DBD控制的减阻效果会随着雷诺数的降低而变差, 这主要是由于雷诺数降低, 流体的黏性效应增强导致的. 可通过适当降低DBD强度来改善DBD控制的减阻效果.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] Mueller TJ , DeLaurier JD. Aerodynamics of small vehicles
Annual Review of Fluid Mechanics, 2003,35(1):89-111
[本文引用: 1]

[2] Shyy W, Aono H, Chimakurthi SK , et al. Recent progress in flapping wing aerodynamics and aeroelasticity
Progress in Aerospace Sciences, 2010,46(7):284-327
[本文引用: 1]

[3] Shyy W, Lian Y, Tang J , et al. Aerodynamics of Low Reynolds Number Flyers. New York: Cambridge University Press, 2008
[本文引用: 1]

[4] 刘强, 刘周, 白鹏 等. 低雷诺数翼型蒙皮主动振动气动特性及流场结构数值研究
力学学报, 2016,48(2):269-277.
[本文引用: 1]

( Liu Qiang, Liu Zhou, Bai Peng , et al. Numerical study about aerodynamic characteristics and flow field structures for a skin of airfoil with active oscillation at low Reynolds number
Chinese Journal of Theoretical and Applied Mechanics, 2016,48(2):269-277 (in Chinese))
[本文引用: 1]

[5] Kang W, Lei P, Zhang J , et al. Effects of local oscillation of airfoil surface on lift enhancement at low Reynolds number
Journal of Fluids and Structures, 2015,57:49-65
[本文引用: 1]

[6] David C, Wang ZJ, Gursul I . Lift enhancement on oscillating airfoils//39th
AIAA Fluid Dynamics Conference. 2009
[本文引用: 1]

[7] Tuncer IH, Platzer MF . Computational study of flapping airfoil aerodynamics
Journal of Aircraft, 2000,37(3):514-520
[本文引用: 1]

[8] Amiralaei MR, Alighanbari H, Hashemi SM . An investigation into the effects of unsteady parameters on the aerodynamics of a low Reynolds number pitching airfoil
Journal of Fluids and Structures, 2010,26(6):979-993
[本文引用: 1]

[9] 杨鹤森, 赵光银, 梁华 . 翼型动态失速影响因素及流动控制研究进展
航空学报, 2020,41:023605
[本文引用: 1]

(Yang Hesen, Zhao Guangyin, Liang Hua. Research progress and influence factors of airfoil dynamic stall flow control
Acta Aeronautica et Astronautica Sinica, 2020,41:023605 (in Chinese))
[本文引用: 1]

[10] Cattafesta III LN, Sheplak M . Actuators for active flow control
Annual Review of Fluid Mechanics, 2011,43:247-272
[本文引用: 1]

[11] Lorber P, McCormick D, Anderson T, et al. Rotorcraft retreating blade stall control//Fluids 2000 Conference and Exhibit
2000: 2475
[本文引用: 1]

[12] Corke T, Jumper E, Post M , et al. Application of weakly-ionized plasmas as wing flow-control devices//40th AIAA Aerospace Sciences Meeting & Exhibit
2002: 350
[本文引用: 1]

[13] Post ML, Corke TC . Separation control on high angle of attack airfoil using plasma actuators
AIAA Journal, 2004,42(11):2177-2184


[14] Post ML, Corke TC. Separation control using plasmas actuators stationary and oscillating airfoils//AIA
2004 -0841. Reston: AIAA2004, 2004
[本文引用: 1]

[15] Feng LH, Choi KS, Wang JJ . Flow control over an airfoil using virtual Gurney flaps
Journal of Fluid Mechanics, 2015,767:595-626
[本文引用: 1]

[16] Feng LH, Jukes TN, Choi KS , et al. Flow control over a NACA 0012 airfoil using dielectric-barrier-discharge plasma actuator with a Gurney flap
Experiments in Fluids, 2012,52(6):1533-1546


[17] 冯立好, 王晋军 , Kwing-So C. 等离子体环量控制翼型增升的实验研究
力学学报, 2013,45(6):815-821.
[本文引用: 1]

( Feng Lihao, Wang Jinjun, Kwing-So C . Experimental investigation on lift increment of a plasma circulation control airfoil
Chinese Journal of Theoretical and Applied Mechanics, 2013,45(6):815-821 (in Chinese))
[本文引用: 1]

[18] 张卫国, 史喆羽, 李国强 等. 风力机翼动态失速等离子体流动控制数值研究
力学学报, 已录用.
[本文引用: 1]

( Zhang Weiguo, Shi Zheyu, Li Guoqiang, et al. Numerical study of dynamic stall flow control for wind turbine airfoil using plasma actuator
Chinese Journal of Theoretical and Applied Mechanics, in press (in Chinese))
[本文引用: 1]

[19] 牛中国, 赵光银, 梁华 等. 三角翼DBD等离子体流动控制研究进展
航空学报, 2019,40(3):022201
[本文引用: 1]

(Niu Zhongguo, Zhao Guangyin, Liang Hua, et al. A review of vortical flow control over delta wings using DBD plasma actuation
Acta Aeronautica et Astronautica Sinica, 2019,40(3):022201 (in Chinese))
[本文引用: 1]

[20] Massines F, Rabehi A, Decomps P , et al. Experimental and theoretical study of a glow discharge at atmospheric pressure controlled by dielectric barrier
Journal of Applied Physics, 1998,83(6):2950-2957
[本文引用: 1]

[21] Orlov DM . Modelling and simulation of single dielectric barrier discharge plasma actuators. [PhD Thesis]
Indiana: The University of Notre Dame
[本文引用: 1]

[22] Shyy W, Jayaraman B, Andersson A . Modeling of glow discharge-induced fluid dynamics
Journal of Applied Physics, 2002,92(11):6434-6443
[本文引用: 6]

[23] Suzen Y, Huang G, Jacob J , et al. Numerical simulations of plasma based flow control applications//35th AIAA Fluid Dynamics Conference and
Exhibit. 2005: 4633
[本文引用: 1]

[24] Roth JR, Sherman DM, Wilkinson SP . Electrohydrodynamic flow control with a glow-discharge surface plasma
AIAA Journal, 2000,38(7):1166-1172
[本文引用: 1]

[25] Zhang PF, Liu AB, Wang JJ . Aerodynamic modification of a NACA 0012 Airfoil by Trailing-Edge Plasma Gurney Flap
AIAA Journal, 2009,47(10):2467-2474
[本文引用: 1]

[26] 梁华, 李应红, 吴云 等. 等离子体气动激励的数值仿真
高电压技术, 2009,35(5):1071-1076.
[本文引用: 1]

( Liang Hua, Li Yinghong, Wu Yun , et al. Numerical simulation of plasma aerodynamic actuation
High Voltage Engineering, 2009,35(5):1071-1076 (in Chinese))
[本文引用: 1]

[27] Rizzetta DP, Visbal MR . Exploration of plasma-based control for low-Reynolds number airfoil/gust interaction
International Journal of Computational Fluid Dynamics, 2011,25(10):509-533
[本文引用: 1]

[28] Rizzetta DP, Visbal MR . Effect of plasma-based control on low-Reynolds-number flapping airfoil performance
AIAA Journal, 2012,50(1):131-147
[本文引用: 1]

[29] Mukherjee S, Roy S . Enhancement of lift and drag characteristics of an oscillating airfoil in deep dynamic stall using plasma actuation//50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition
2012: 702
[本文引用: 1]

[30] Mahboubidoust A, Ramiar A, Dardel M . Investigation of steady plasma actuation effect on aerodynamic coefficients of oscillating airfoil at low Reynolds number
Theoretical and Applied Mechanics Letters, 2017,7(4):185-198
[本文引用: 4]

[31] Kojima R, Nonomura T, Oyama A , et al. Large-eddy simulation of low-Reynolds-number flow over thick and thin NACA airfoils
Journal of Aircraft, 2013,50(1):187-196
[本文引用: 1]

[32] Lecrivain G, Rayan R, Hurtado A , et al. Using quasi-DNS to investigate the deposition of elongated aerosol particles in a wavy channel flow
Computers & Fluids, 2016,124:78-85
[本文引用: 1]