Ievgen Mochalin^*,?, 林静雯^*, 蔡建程^,*,?,2), VolodymyrBrazhenko^*,?, 鄂世举^*,?*浙江师范大学工学院, 浙江金华 321004
^?浙江省城市轨道交通智能运维技术与装备重点实验室, 浙江金华 321005

MODELLING AND CALCULATION OF THE TURBULENT BOUNDARY LAYER ON A ROTATING CYLINDER SURFACE WITH STRONG SUCTION ¹⁾

Ievgen Mochalin^*,?, Lin Jingwen^*, Cai Jiancheng^,*,?,2), Volodymyr Brazhenko^*,?, E Shiju^*,?*College of Engineering, Zhejiang Normal University, Jinhua 321004, Zhejiang, China
^?Key Laboratory of Urban Rail Transit Intelligent Operation and Maintenance Technology & Equipment of Zhejiang Province, Jinhua 321005, Zhejiang, China

通讯作者: 2)蔡建程, 工学博士, 主要从事流体机械内流、流动噪声、振动与声学的研究. E-mail:cai_jiancheng@foxmail.com

收稿日期:2020-02-9接受日期:2020-02-9网络出版日期:2020-09-18

基金资助:

1)国家自然科学基金.51976201 浙江省自然科学基金.LY18E060006 国家级大学生创新创业训练.201910345049

Received:2020-02-9Accepted:2020-02-9Online:2020-09-18
作者简介 About authors


摘要
提出了湍流边界层的一种简单、快速计算方法, 用以求解强吸气作用下旋转圆筒表面边界层流动. 首先, 理论分析了同心圆筒间的旋转流体运动, 外筒静止、内筒旋转且为多孔吸气条件. 强吸气情况下旋转流动主要表现为内筒壁面附近的边界层流动, 基于这一事实得到了周向速度分布的解析表达式. 其次, 通过引入新参数扩展Cebeci-Smith代数湍流模型, 使其能考虑流线曲率、壁面吸气、低Reynolds数效应等因素. 针对这些因素的综合影响, 采用解析修正和经验参数对模型进行调整. 同时, 基于Reynolds应力湍流模型的仿真结果, 校准代数湍流模型中的经验参数. 最后, 给出基于广义Cebeci-Smith湍流模型的旋转壁面边界层流动的迭代算法, 该算法适用于需要特殊迭代过程的轴向及周向流动均匀情况. 计算了不同旋转速度和吸气强度组合工况下的边界层流动, 其周向速度和湍流强度分布与基于Reynolds应力湍流模型的计算结果非常接近. 并且表明, 当Reynolds应力湍流模型数值模拟预测内筒边界层为稳定层流时, 该方法也再现了相同初始条件下的层流边界层.
关键词： 湍流边界层;旋转同心圆筒;壁面吸气;Cebeci-Smith代数湍流模型

Abstract
A simple, fast and adequate approach to the turbulent boundary layer calculation on the surface of a rotating permeable cylinder has been elaborated for the case of a strong suction through the cylinder surface. Firstly, the rotational gap flow between two concentric cylinders was analyzed theoretically; the outer cylinder is stationary, and the inner porous cylinder is rotating with suction condition. Based on the fact that the stationary outer cylinder does not influence the flow near the rotating inner one, it can be treated as a boundary layer on the surface of rotating permeable cylinder, and an analytical expression for the circumferential velocity distribution is obtained. Secondly, the Cebeci-Smith two-layer algebraic turbulence model has been adjusted to account for centrifugal force field (streamlines curvature), wall suction, and low-Reynolds-number effects. Analytical corrections and empirical coefficients are used to tune the model for the specific conditions of coupled influence of the factors mentioned above. The calibration database was used which has been obtained by detailed numerical simulation based on the Reynolds stress turbulent model. The numerical simulation approach has been comprehensively verified in the known study for the specific flow conditions under consideration. Finally, the solution algorithm based on generalized Cebeci-Smith two-layer algebraic turbulence model was offered to solve the boundary layer flow over the rotating porous cylinder surface. The algorithm is suited for the situation of flow uniformity in the azimuthal and axial directions that required a special iterative procedure to be elaborated. The results of the algebraic turbulence model with different combinations of the rotational speed and the suction velocity agree well with the simulation results of the Reynolds stress turbulent model. It is demonstrated that the method developed reproduces also the laminar boundary layer at the same initial conditions when the detailed numerical simulation predicts the stable laminar flow in the inner cylinder boundary layer.
Keywords：turbulent boundary layer;concentric rotating cylinders;wall suction;Cebeci-Smith algebraic turbulence model


PDF (1732KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
Ievgen Mochalin, 林静雯, 蔡建程, VolodymyrBrazhenko, 鄂世举. 强吸气旋转圆筒壁面湍流边界层建模及计算 ¹⁾. 力学学报[J], 2020, 52(5): 1323-1333 DOI:10.6052/0459-1879-20-032
Ievgen Mochalin, Lin Jingwen, Cai Jiancheng, Volodymyr Brazhenko, E Shiju. MODELLING AND CALCULATION OF THE TURBULENT BOUNDARY LAYER ON A ROTATING CYLINDER SURFACE WITH STRONG SUCTION ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2020, 52(5): 1323-1333 DOI:10.6052/0459-1879-20-032

引言

旋转可渗透圆柱外的流动是在Taylor-Couette流动的基础上叠加径向穿透流动^[1-2], 它具有很多应用, 旋转过滤是一个典型例子^[3-5]. 含杂质溶液通过旋转圆筒膜可以大为提高过滤效率, 并且旋转膜表面的固相沉积率低不容易阻塞, 因此有****专门分析旋转过滤圆柱表面的流体运动^[6-10].

旋转柱体的冷却是Taylor-Couette流动的另一个研究方向, Fénot等^[11]综述了转子-静子系统中的同心圆筒间隙内的不可压缩流动与换热问题研究. Mochalin等^[12]研究了外筒静止、内筒旋转工况下的间隙流动, 发现内筒做成完全多孔或是条状多孔可以使换热效率提高1.5倍. 因此, 研究旋转多孔圆筒表面附近的流动很有意义.

旋转圆筒外的流动由于受到离心不稳定的作用, 会导致二次涡流即Taylor涡的产生. 对于同心不可渗透圆筒间的流动, 在较低的旋转速度时就能发生流动不稳定性, 体现为轴对称Taylor涡的产生, 随着旋转速度的提高, 流动模式会改变^[13]. 对于经典Taylor-Couette流动, 相比于由离心不稳定引起的Taylor涡产生, 两圆筒间的流动由层流到湍流的转捩发生较迟. 通过多孔圆筒引入径向穿透流, 可以使间隙流动变得稳定, 从而Taylor涡的产生大为延后^[14-15]. Mochalin和Khalatov^[16]的研究表明强吸气穿透流可以防止Taylor涡的产生直到非常大的旋转速度, 并且发现旋转吸气圆筒壁面引起的旋转流体运动集中在其壁面附近, 而外面静止圆筒对里边旋转圆筒附近的流动影响很小, 所以旋转流动可以视为旋转多孔圆筒表面的边界层流动. 边界层厚度依赖于旋转速度和径向穿透流强度.

研究表明, 多孔壁面径向流可以使边界层从层流转捩到湍流发生在离心不稳定(Taylor涡)之前, 这就为边界层湍流强度控制提供了新思路. 旋转壁面流动具有很多应用价值, 比如相分离、表面冷却等^[12,16]. 所以, 有必要研究旋转多孔圆筒表面的湍流边界层流动.

Mochalin和Khalatov^[16]通过求解Reynolds平均Navier-Stokes方程和Reynolds应力湍流模型, 研究了同心圆筒间的流动. 梁田等^[17]则利用Spalart-Allmaras湍流模型计算边界层抽气, 进行叶栅角区分离流动控制的研究. 在这些研究中, 近壁面流动使用非常稠密的低Reynolds数计算网格, 计算量大. 本文的研究目标是对于强吸气旋转壁面流动使用简单而可靠的预测方法, 并提供计算步骤. 其研究思路是使用恰当的代数湍流模型, 基于详细数值模拟结果进行代数湍流模型参数的调整和校准, 使其适用于一定工况范围.

1 强吸气壁面旋转流动速度分布的解析表达式

1.1 基本假设与无量纲参数化

本文所研究的同心圆筒间流动为半径$R$外的多孔圆柱壁外的稳定流动(在离心不稳定发生之前). 旋转流体运动主要集中在厚度为$\delta $的边界层内. 多孔壁面吸气, 假设均匀吸气速度分布$V_{\rm s} $. 旋转流动认为在轴向不变化, 即$V_z \equiv 0$, $\partial / {\partial z\equiv 0}$, 且轴对称即$\partial / {\partial \varphi \equiv 0}$ $(\varphi $为方位角).

旋转流动可使用Reynolds平均Navier-Stokes (N-S)方程联合连续方程进行描述. 显然, 使用柱坐标系$(r,\varphi ,z)$更为方便, 在柱坐标系下稳态不可压缩N-S方程

(1) $ \begin{eqnarray} \label{eq1} && \frac{\partial }{\partial r}\left( {rV_r V_\varphi } \right)=\frac{\partial }{\partial r}\left( {r\nu _{\rm e} \frac{\partial V_\varphi }{\partial r}} \right)+\nu _{\rm e} \frac{\partial V_\varphi }{\partial r}- r\frac{\partial }{\partial r}\left( {\frac{\nu _{\rm e} V_\varphi }{r}} \right)- \\&&\qquad\frac{2\nu _{\rm e} V_\nu }{r}-V_\varphi V_r \end{eqnarray} $
式中, $V_r$, $V_\varphi $分别为径向和周向的平均速度, $\rho$为流休密度, $\nu _{\rm e}$为流体的有效运动黏度, 它等于分子黏性$\nu $和湍流黏性$\nu _{\rm t} $之和, $\nu _{\rm e} =\nu +\nu _{\rm t} $.

连续方程为

(2) $ \begin{eqnarray} \label{eq2} \frac{\partial }{\partial r}\left( {rV_r } \right)\mbox{=0} \end{eqnarray} $
积分上述方程, 注意到壁面$V_r (R)=V_{\rm s} $条件, 得到

(3) $ \begin{eqnarray} \label{eq3} rV_r ={\rm const}=-RV_{\rm s} \end{eqnarray}$
利用式(2), 方程(1)可以转化成

(4) $ \begin{eqnarray} \label{eq4} \frac{\partial }{\partial r}\left( {r^2V_r V_\varphi } \right)= \frac{\partial }{\partial r}\left( {r^2\nu _{\rm e} \frac{\partial V_\varphi }{\partial r}-r\nu _{\rm e} V_\varphi } \right)-rV_\varphi \frac{\partial \nu _{\rm e} }{\partial r} \end{eqnarray} $
在本文中, 边界层的计算在径向划分为多个微元段$\Delta r$, 在每一段中$\nu _{\rm e}$认为是常数. 遵循这一假设, 式(4)中最后一项在每个微元段可以忽略. 进一步对式(4)中最后一项在整个边界层内都忽略, 这是附加的假设. 其有效性将从本文方法的结果与详细的数值仿真结果相比较看出. 利用式(3)以及上述假设, 积分式(4), 得到

(5) $ \begin{eqnarray} \label{eq5} -rRV_{\rm s} V_\varphi -r^2\nu _{\rm e} \frac{\partial V_\varphi }{\partial r}+r\nu _{\rm e} V_\varphi =C \end{eqnarray}$
上式中的积分常数$C$可由旋转壁面的边界条件

(6) $ \begin{eqnarray} \label{eq6} r=R:\ \ V_\varphi =\varOmega R=W,\ \ \nu _{\rm t} =0,\ \ \nu _{\rm e} =\nu \end{eqnarray}$
确定, 其中$\varOmega $为壁面旋转角速度. 式(5)中的速度梯度可用壁面处的摩擦应力

(7) $ \begin{eqnarray} \label{eq7} \tau _{\rm w} =\left| {\rho \nu \left( {\frac{\partial V_\varphi }{\partial r}-\frac{V_\varphi }{r}} \right)_{r=R} } \right| \end{eqnarray}$
来表示.

利用摩擦速度的概念$V_{\rm w} =\sqrt {{\tau _{\rm w} } / \rho } $, 从式(7)出发, 注意到边界条件(6), 得到

(8) $ \begin{eqnarray} \label{eq8} \left. {\frac{\partial V_\varphi }{\partial r}} \right|_{r=R} =-\frac{V_{\rm w}^2 }{\nu }+\frac{W}{R} \end{eqnarray}$
联合式(5)、式(6)和式(8), 得到

(9) $ \begin{eqnarray} \label{eq9} -rRV_{\rm s} V_\varphi -r^2\nu _{\rm e} \frac{\partial V_\varphi }{\partial r}+r\nu _{\rm e} V_\varphi =-V_{\rm s} R^2 W+R^2 V_{\rm w}^2 \end{eqnarray}$
为了得到无量纲表达, 使用圆筒半径$R$、壁面旋转速度$W$和动压作为长度、速度和压力的参考量, 通过下式定义无量纲量

(10) $ \begin{eqnarray} \label{eq10} r=R\xi , V_r =Wu_r , V_\varphi =Wu_\varphi , p=\rho W^2q \end{eqnarray}$
其中, $\xi $为无量纲径向坐标, $u_r$, $u_\varphi $为无量纲径向和周向速度, $q$为无量纲压力. 从而得到无量纲化的式(9)为

(11) $ \begin{eqnarray} \label{eq11} && -R^2u_{\rm s} W^2r\xi u_\varphi -RW(\nu +\nu _{\rm t} )\xi ^2\frac{\partial u_\varphi }{\partial y}+ \\&&\qquad RW(\nu +\nu _{\rm t} )\xi u_\varphi =-u_{\rm s} R^2W^2+R^2W^2u_{\rm w}^2 \end{eqnarray}$
式中, $u_{\rm w} ={V_{\rm w} } / W$为无量纲摩擦速度, $u_{\rm s} ={V_{\rm s} } / W$为无量纲吸气速度. 式(11)两边同除以$RW$, 得到

(12) $ \begin{eqnarray} \label{eq12} &&(1+\tilde{{\nu }}_{\rm t} )\xi ^2\frac{{\rm d}u_\varphi }{{\rm d}y}-(1+\tilde{{\nu }}_{\rm t} )\xi u_\varphi + u_{\rm s} Re_\varphi \xi u_\varphi = \\&&\qquad u_{\rm s} Re_\varphi -Re_\varphi u_{\rm w}^2 \end{eqnarray}$
式中, $\tilde{{\nu }}_{\rm t} ={\nu _{\rm t} } / \nu $为湍流黏性比, $Re_\varphi ={WR} / \nu $为旋转Reynolds数. 为表征吸气强度, 再引入径向Reynolds数$Re_r ={V_{\rm s} R} / \nu =u_{\rm s} Re_\varphi $.

为求解式(12), 将旋转圆柱壁面法向的边界层分成足够小间隔$\Delta \xi _i $, 在每个间隔内湍流黏性看成为常数, 式(12)简化为

$$\begin{eqnarray*} \frac{\rm d}{{\rm d}\xi }\left[ {(1+\tilde{{\nu }}_{\rm t} )\xi ^{\frac{Re_r}{1+\tilde{{\nu }}_{\rm t} }-1}u_\varphi } \right]=\left( {Re_r -Re_\varphi u_{\rm w}^2 }\right)\xi ^{\frac{Re_r}{1+\tilde{{\nu }}_{\rm t} }-3} \end{eqnarray*}$$

积分后得到

(13) $ \begin{eqnarray} \label{eq13} (1+\tilde{{\nu }}_{\rm t} )\xi^{\frac{Re_r }{1+\tilde{{\nu }}_{\rm t} }-1}u_\varphi =\frac{{Re_r -Re_\varphi u_{\rm w}^2 } }{\dfrac{Re_r }{1+\tilde{{\nu}}_{\rm t} }-2}\xi ^{\frac{Re_r }{1+\tilde{{\nu }}_{\rm t} }-2}+C \end{eqnarray}$
积分常数$C$由下列边界条件得到

(14) $ \begin{eqnarray} \label{eq14} u_\varphi (\xi _{0i} )=u_{\varphi i} \ \ (i=1,2,\cdots ,N) \end{eqnarray}$
式中$\xi _{0i} ,u_{\varphi i} $分别为无量纲径向距离和每个径向间隔$\Delta \xi _i $的周向速度; 对于第一步, 由式(6)、式(10)可知$\xi _{01} =1, u_{\varphi 1} =1$. 把式(14)代入式(13), 得到常数$C$的定义

(15) $ \begin{eqnarray} \label{eq15} C=(1+\tilde{{\nu }}_{\rm t} )\xi _{0i}^{{\frac{Re_r }{1+\tilde{{\nu }}_{\rm t} }-1} } u_{\varphi i}-\frac{Re_r -Re_\varphi u_{\rm w}^2}{\dfrac{Re_r }{1+\tilde{{\nu }}_{\rm t}}-2}\xi _{0i}^{\frac{Re_r }{1+\tilde{{\nu }}_{\rm t}}-2} \end{eqnarray}$
因此, 在每个间隔内$\xi \in [\xi _{0i} ,\xi _{0i} +\Delta \xi _i ]$, 周向速度可由式(13)、式(15)得到

(16) $ \begin{eqnarray} \label{eq16} &&u_\varphi =\left( {\frac{\xi _{0i} }{\xi }} \right)^{{\frac{Re_r }{1+\tilde{{\nu }}_{\rm t} }-1}}u_{\varphi i} +\frac{Re_r -Re_\varphi u_{\rm w}^2 }{Re_r -2(1+\tilde{{\nu }}_{\rm t} )}\frac{1}{\xi }\cdot \\&&\qquad\left[ {1-\left( {\frac{\xi _{0i} }{\xi }} \right)^{{\frac{Re_r }{1+\tilde{{\nu }}_{\rm t} }-2} }} \right] \end{eqnarray}$

1.2 圆筒表面摩擦应力

壁面吸气使得两个圆柱面间流动的Taylor涡产生大为滞后. 这意味着径向Reynolds数($Re_{r})$足够大时, 两圆柱面间流动为层流流动, 其周向流动速度分布可表示为^[16]

(17) $ \begin{eqnarray} \label{eq17} u_\varphi =\xi ^{1-Re_r } \end{eqnarray}$
上式沿径向求导, 得到

$$\begin{eqnarray*} \frac{\partial u_\varphi }{\partial \xi }=\left( {1-Re_r } \right)\xi ^{-Re_r} \end{eqnarray*}$$

由该速度分布, 进而可以得到摩擦系数

(18) $ \begin{eqnarray} \label{eq18} c_{\rm f} ={\tau _{\rm w} } \Bigg/ {\left( {\frac{1}{2}\rho W^2} \right)}=2u_{\rm s} \end{eqnarray}$
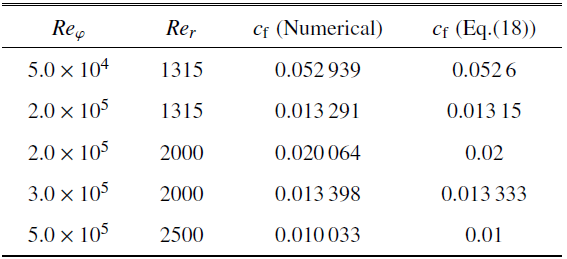
表1给出了所考虑的旋转圆筒壁面摩擦系数. 表中的数值仿真按文献^[16]中的方法得到, 可以看出由式(18)得到的结果与数值仿真结果非常接近, 误差在1%之内. 表1中的第1、3行的$Re_{\varphi}$, $Re_{r}$组合, 其流态为层流, 其余为湍流. 基于此, 式(18)可以应用于旋转同心圆筒间的湍流流动. 所以, 有如下关系式

(19) $ \begin{eqnarray} \label{eq19} u_{\rm w}^2 =\frac{c_{\rm f} }{2}=u_{\rm s} \end{eqnarray}$
Table 1
表1
表1强吸气旋转圆筒表面摩擦应力
Table 1Friction coefficient values on the surface of a rotating cylinder with strong suction

新窗口打开|下载CSV

利用式(19)可以化简式(16), 得到

(20) $ \begin{eqnarray} \label{eq20} u_\varphi =\left( {\frac{\xi _{0i} }{\xi }} \right)^{{\frac{Re_r }{1+\tilde{{\nu }}_{\rm t} }-1}}u_{\varphi i} \end{eqnarray}$
这里顺便指出, 已有的对吹吸气槽道湍流的研究表明吹气可以使壁面阻力系数下降, 而吸气会使壁面阻力系数上升^[18-19], 而高频周期吹气扰动在狭缝下游产生明显的减阻效果^[20], 另外通过在平板壁面施加不同频率振幅的周期性扰动, 能进行湍流边界层的主动控制减阻^[21]. 表1的第2行和第3行表明, 固定旋转速度($Re_\varphi $一定)的前提下, 摩擦系数随着吸气强度$Re_r$的增加而增加. 而随旋转速度$Re_\varphi $的提高, 摩擦系数下降. 所以当$Re_\varphi$和$Re_r $同时提高时, 摩擦系数有可能下降.

2 代数湍流模型

2.1 湍流黏性的基本关系式

壁面吸气可以延迟边界层从层流到湍流的转捩^[22-25]. 本文研究边界层除吸气外还涉及离心力和旋转对称等因素影响. 文献^[16]中的数值仿真诚然可以考虑这些因素, 但计算量过大. 本文提供更为快捷的代数湍流型模型, 以求解旋转边界层. 思路如下: 寻找一个合适的代数湍流模型, 根据新增加的影响因素进行改进, 并依据特定的情况用实验或计算数值结果进行参数校准.

本文依据Cebeci-Smith(CS)湍流模型^[26], 校准数据使用文献^[16]的结果. CS模型能考虑压力梯度、壁面吸(吹)气、可压缩性和低Reynolds数效应等因素的影响. 对每个影响因素, 分别引入一个因子(经验参数或是含经验参数的表达式), 然后耦合所有的因子.

平板流动的经典CS两层湍流模型可以表述如下

(21) $ \begin{eqnarray} \label{eq21} &&\nu _{\rm t} =\left\{ {\begin{array}{ll} \nu _{\rm ti} ,& y\leqslant y_{\rm m} \\ \nu _{\rm to} ,& y>y_{\rm m} \\ \end{array}} \right. \end{eqnarray} $
(22) $ \begin{eqnarray} \label{eq22} \nu _{\rm ti} =l_{\rm m}^2 \left[ {\left( {\frac{\partial V_x }{\partial y}} \right)^2+\left( {\frac{\partial V_y }{\partial x}} \right)^2} \right]^{{1}/{2}} \end{eqnarray}$
(23) $ \begin{eqnarray} \label{eq23} l_{\rm m} =\kappa y\left[ {1-\exp \left( {-y^+/A_\ast } \right)} \right] \end{eqnarray}$
(24) $ \begin{eqnarray} \label{eq24} \nu _{\rm to} =kV_{\rm m} \delta ^\ast \end{eqnarray}$
(25) $ \begin{eqnarray} \label{eq25} \delta ^\ast =\int_0^\delta {\left( {1-\frac{V_x }{V_{\rm m} }} \right)}{\rm d}y \end{eqnarray}$
式中$\nu _{\rm ti}$, $\nu _{\rm to} $为湍流边界层内层与外层的湍流运动黏性系数; $y_{\rm m} $为$\nu _{\rm ti} =\nu _{\rm to} $时的壁面法向距离; $V_x$, $V_y$为流向和横向的速度; $l_{\rm m}$为Prandtl混合长度; $y$为离壁面的法向距离; $V_{\rm m}$为边界层厚度$\delta $内的最大速度; $\delta ^\ast $为边界层位移厚度. 无量纲距离$y^+$定义为

(26) $ \begin{eqnarray} \label{eq26} y^+=\frac{V_{\rm w} y}{\nu } \end{eqnarray}$
经验参数

(27) $ \begin{eqnarray} \label{eq27} \kappa =0.41,\ \ k=0.016 8,\ \ A_\ast =26 \end{eqnarray}$
式(22)可从下式

(28) $ \begin{eqnarray} \label{eq28} \nu _{\rm t} = l_{\rm m}^2 \sqrt {2{\dot{{ S}}}:{\dot{{ S}}}} \end{eqnarray}$
式中, ${\dot{{ S}}}$为应变率张量, $:$表示张量二次缩并, 通过数量级分析忽略其中一些项而得到, 详细推导可参见文献^[24].

广义的CS模型^[26]可以考虑如下因素: 趋于边界层外界线时湍流强度的衰减、 外层低Reynolds数对湍流涡的影响、 壁面吸(吹)气、 压力梯度、 可压缩性. 本文不考虑最后两个因素, 仅考虑前3者.

边界层外层界线附近湍流强度的衰减, 由Klebanoff间歇系数来表示

(29) $ \begin{eqnarray} \label{eq29} F_{\rm kl} (y,\delta )=\left[ {1+5.5\left( {\frac{y}{\delta }} \right)^6} \right]^{-1} \end{eqnarray}$
用它乘式(24)右端.

低Reynolds数的影响通过改变式(24)右端的Clauser系数$k$实现

(30) $ \begin{eqnarray} \label{eq30} k=0.0168\frac{1.55}{1+\varPi _0 } \end{eqnarray}$
式中尾迹参数$\varPi _0 $由Schlichting^[24]建议为

(31) $ \begin{eqnarray} \label{eq31} \left. \begin{array}{ll} \varPi _0 =0.55\left[ {1-\exp \left( {-0.243\sqrt {z_1 } -0.298z_1 } \right)} \right] \\ z_1 =\dfrac{Re^{\ast \ast }}{425}-1 \\ \end{array} \right\} \end{eqnarray} $
式中

(32) $ \begin{eqnarray} \label{eq32} Re^{\ast \ast }={V_{\rm m} \delta ^{\ast \ast }} / \nu \end{eqnarray} $
$\delta ^{\ast \ast }$为动量厚度

(33) $ \begin{eqnarray} \label{eq33} \delta ^{\ast \ast }=\int_0^\delta {\frac{V_x }{V_{\rm m} }\left( {1-\frac{V_x }{V_{\rm m} }} \right){\rm d}y} \end{eqnarray}$
广义CS模型中通过改变式(23)参数$A^\ast $以考虑壁面吸气的影响

(34) $ \begin{eqnarray} \label{eq34} A_\ast =26\left[ {\exp \left( {C_1 \frac{-V_{\rm s} }{V_{\rm w} }} \right)} \right]^{-{1}/{2}},\ \ C_1 =11.8 \end{eqnarray} $
CS模型中并没有考虑流线曲率的影响, 流线曲率会产生离心力. 本文利用Bradshaw^[27]的思想, 这一思想被许多****所采纳^[28-30], 它把流线曲率的影响与浮力效应相类比, 引入Richardson数$Ri$ (表示由于离心力和速度梯度产生的湍流能量之比)到湍流黏性系数中

(35) $ \begin{eqnarray} \label{eq35} \nu _{\rm t} =\nu _{t0} \left( 1-\beta Ri\right)^{2m} \end{eqnarray}$
式中, $\nu _{\rm t0} $为不考虑流线曲率的湍流黏性, $\beta$, $m$为经验常数. $\beta$, $m$的选择依赖于用于校准的剪切流, 这将在下文中简述. 根据Bradshaw^[27]的建议, 对于具有周向和轴向分量的旋涡流动

(36) $ \begin{eqnarray} \label{eq36} Ri=\frac{2\dfrac{V_\varphi }{r^2}\dfrac{\partial (V_\varphi r)}{\partial r}}{\left( {\dfrac{\partial V_z }{\partial r}} \right)^2+\left( {\dfrac{1}{r}\dfrac{\partial (V_\varphi r)}{\partial r}} \right)^2} \end{eqnarray}$
所以, 在广义CS模型中, 考虑到趋于边界层外界线时湍流强度的衰减、外层内低Reynolds数对湍流涡的影响、流线曲率、壁面吸(吹)气等方面后, 式(22)和式(24)改写为

(37) $ \begin{eqnarray} \label{eq37} &&\nu _{\rm ti} =l_{\rm m}^2 \sqrt {2{\dot{{ S}}}:{\dot{{ S}}}} \left( {1-\beta Ri } \right)^{2m} \end{eqnarray}$
(38) $ \begin{eqnarray} \label{eq38} \nu _{\rm to} =k\delta ^\ast V_{\rm m} F_{\rm kl} \left( {1-\beta Ri } \right)^{2m} \end{eqnarray}$
式(23)中的$A_\ast $由式(34)给出, 而式(38)中的$k$由式(30)~式(33)得到而不是式(27)中的常数0.016 8. 式(38)中的Klebanoff 函数$F_{\rm kl} $由式(29)给出.

对于轴对称二维流动, 式(37)中的$\sqrt {2{\dot{{ S}}}:{\dot{{ S}}}} $可以用平均流的速度梯度表示为

$$\begin{eqnarray*} \sqrt {2{\dot{{ S}}}:{\dot{{ S}}}} =\left[ {\left( {\frac{\partial V_\varphi }{\partial r}-\frac{V_\varphi }{r}} \right)^2+2\left( {\frac{\partial V_r }{\partial r}} \right)^2+2\left( {\frac{V_r }{r}} \right)^2} \right]^{{1}/{2}} \end{eqnarray*}$$

利用式(3)和式(10), 上式可以写为

(39) $ \begin{eqnarray} \label{eq39} \sqrt {2{\dot{{ S}}}:{\dot{{ S}}}} =\frac{W}{R}\left[ {\left( {\frac{\partial u_\varphi }{\partial \xi }-\frac{u_\varphi }{\xi }} \right)^2+4\left( {\frac{u_{\rm s} }{\xi ^2}} \right)^2} \right]^{{1}/{2}} \end{eqnarray} $
对于壁面法向距离$y$及无量纲壁面距离$y^{+}$式(26)有

(40) $ \begin{eqnarray} \label{eq40} \left. \begin{array}{ll} y=r-R=R(\xi -1)\\ y^+=\dfrac{u_{\rm w} WR(\xi -1)}{\nu }=u_{\rm w} Re_\varphi (\xi -1) \\ \end{array} \right\} \end{eqnarray}$
由式(23)、式(34)、式(39)、式(40), 边界层内层湍流黏性式(37)可写为

(41) $ \begin{eqnarray} \label{eq41} && \tilde{{\nu }}_{\rm ti} =\kappa ^2(\xi -1)^2\left[ {1-\exp \left( {\frac{-u_{\rm w} Re_\varphi (\xi -1)}{A_\ast }} \right)} \right]^2\cdot \\&&\qquad Re_\varphi \left[ {\left( {\frac{\partial u_\varphi }{\partial \xi }-\frac{u_\varphi }{\xi }} \right)^2+4\left( {\frac{u_{\rm s} }{\xi ^2}} \right)^2} \right]^{{1}/{2}}\cdot \\&&\qquad \left( {1-\beta Ri } \right)^{2m} \end{eqnarray} $
(42) $ \begin{eqnarray} \label{eq42} A_\ast =26\exp \left( {C_1 \frac{u_{\rm s} }{2u_{\rm w} }} \right) \end{eqnarray} $
经验参数$\beta$, $m$, $C_1 $的选择在2.3节讨论.

对于式(36)的Richardson数, 考虑到$\xi \approx 1$, 有

(43) $ \begin{eqnarray} \label{eq43} Ri ={2u_\varphi } / {\left( {{\partial u_\varphi } / {\partial \xi }} \right)} \end{eqnarray}$
对所研究的问题$V_{\rm m} =W$, 所以由式(38)可以得到边界层外层的黏性系数

(44) $ \begin{eqnarray} \label{eq44} \tilde{{\nu }}_{\rm to} =k\tilde{{\delta }}^\ast Re_\varphi F_{\rm kl} \left( {1-\beta Ri } \right)^{2m} \end{eqnarray} $
式中无量纲位移厚度$\tilde{{\delta }}^\ast ={\delta ^\ast } / R$ (其他的无量纲厚度$\tilde{{\delta }},\tilde{{\delta }}^{\ast \ast}$定义类似). 式(44)中系数$k$由式(30)、式(31)确定. 由式(32)得到

(45) $ \begin{eqnarray} \label{eq45} Re^{\ast \ast }=\frac{W\delta ^{\ast \ast }}{\nu }=Re_\varphi \tilde{{\delta }}^{\ast \ast } \end{eqnarray} $
由式(29)给出Klebanoff 间歇系数$F_{\rm kl} $.

(46) $ \begin{eqnarray} \label{eq46} F_{\rm kl} =\left[ {1+5.5\left( {\frac{\xi -1}{\tilde{{\delta }}}} \right)^6} \right]^{-1} \end{eqnarray} $
由于研究对象为旋转流动, 定义位移厚度应使用相对速度$W-V_\varphi $, 式(25)可写为

(47) $ \begin{eqnarray} \label{eq47} \tilde{{\delta }}^\ast =\int_1^{1+\tilde{{\delta }}} {u_\varphi {\rm d}\xi } \end{eqnarray}$
动量厚度

(48) $ \begin{eqnarray} \label{eq48} \tilde{{\delta }}^{\ast \ast }=\int_1^{1+\tilde{{\delta }}} {u_\varphi \left( {1-u_\varphi } \right) {\rm d}\xi } \end{eqnarray}$

2.2 外层湍流黏性公式的修正

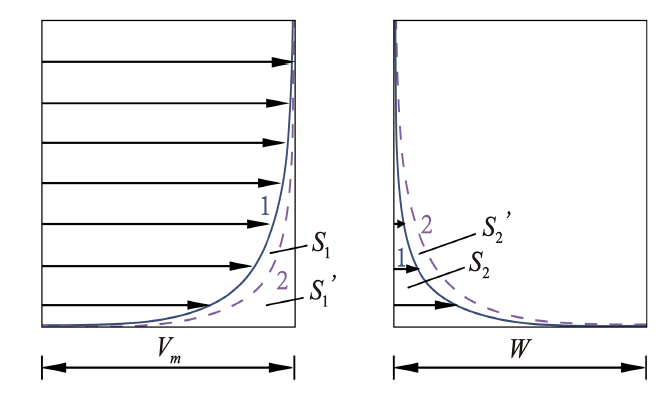
本文研究的旋转圆管壁面边界层与平板边界层有区别, 其轴对称性使计算需特殊处理. 对于平板边界层, 边界层从平板前缘点开始, 向下游(纵向)发展. 下游各横截面上边界层厚度、位移厚度和动量厚度由上一横截面上信息计算得到, 这是因为平板边界层沿纵向是抛物型偏微分方程. 对于本文中的旋转轴对称边界层, 由于初值未知, 因此需要使用迭代方法计算, 即先设置初始猜想值, 通过迭代收敛求解边界层.

下面进行迭代求解的说明. 图1示意了静止壁面和旋转壁面边界层速度分布. 实线下的面积记为$S_1$, $S_2$, 虚线下的面积记为${S}'_1$, ${S}'_2 $. 如果黏性增加, 则将导致层与层之间的动量交换. 对于静止的平板边界层: $\delta _1^\ast ={S_1 }/{V_{\rm m} }$, ${\delta}_1^{'\ast} ={{S}'_1 }/{V_{\rm m} }$.

图1

新窗口打开|下载原图ZIP|生成PPT
图1静止壁面(左)和旋转壁面(右)边界层: 1 -- $\nu _{\rm t} $小; 2 -- $\nu _{\rm t} $大

Fig.1Typical velocity profiles in the boundary layers on a stationary surface (Left) and a rotating cylinder surface (Right): 1 -- less $\nu _{\rm t} $ values; 2 -- greater $\nu _{\rm t} $ values



而对于旋转边界层

$$\begin{eqnarray*} \delta _2^\ast =\frac{S_2 }{W},\ \ {\delta}_2^{'\ast} =\frac{{S}'_2}{W} \end{eqnarray*}$$

显然${\delta }_1^{'\ast} <\delta _1^\ast $而${\delta }_2^{'\ast} >\delta _2^\ast$. 如果位移厚度的初始值过大, 意味着湍流黏性值估计过高, 从而会得到静止壁面位移厚度计算值减小, 进入下一个迭代, 反之亦然, 所以迭代过程中得以校正. 对于旋转圆筒壁面的边界层, 趋势相反. 当位移厚度$\tilde{{\delta }}_0^\ast $估计好后, 从式(44)可以得到

(49) $ \begin{eqnarray} \label{eq49} \tilde{{\nu }}_{\rm to} =k\frac{\left( {\tilde{{\delta }}_0^\ast }\right)^2}{\tilde{{\delta }}^\ast }Re_\varphi F_{\rm kl} \left( {1-\beta Ri } \right)^{2m} \end{eqnarray} $
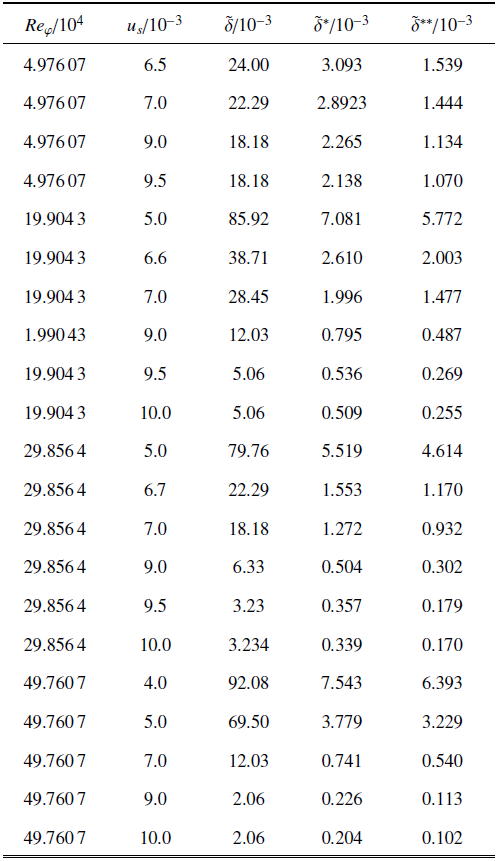
边界层位移厚度的计算依赖于式(12)所描述的$u_\varphi $速度分布. 由式(19) $u_{\rm w}^2 =u_{\rm s} $可知无量纲位移厚度主要依赖于$u_{\rm s} $和$Re_\varphi $. 对$R=0.11$ m以空气为介质和$R=0.055$ m以水为介质的情况, 在适用于低Reynolds数的计算网格上使用Reynolds应力湍流模型进行数值仿真, 得到不同$u_{\rm s}$, $Re_\varphi $组合的边界层厚度(见表2), 基于此建立$\tilde{{\delta }}_0^\ast (u_{\rm s} ,Re_\varphi )$的关联公式.

Table 2
表2
表2旋转吸气圆筒表面无量纲边界层厚度
Table 2Values of the dimensionless boundary layer thicknesses on the surface of a rotating suction cylinder

新窗口打开|下载CSV

对表2中的数据分析拟合, 得到无量纲位移厚度

(50) $ \begin{eqnarray} \label{eq50} &&\tilde{{\delta }}_0^\ast \left( {u_{\rm s} ,Re_\varphi } \right)= \\&&\qquad ( 5.940 2\times 10^{-12}-8.032 1\times 10^{-18}Re_\varphi ) u_{\rm s}^{- 4} + \\&&\qquad7.059 1\times 10^{-9}Re_\varphi -8.193 5Re_\varphi ^{1 / 2} + \\&&\qquad2.3262\times 10^{-3} \end{eqnarray} $
无量纲厚度

(51) $ \begin{eqnarray} \label{eq51} && \tilde{{\delta }}_0 (u_{\rm s} ,Re_\varphi )= \\&&\qquad( 2.765 4\times 10^{-13}-1.121 7\times 10^{-19}Re_\varphi ) u_{\rm s}^{-5}- \\&&\qquad 2.336 3\times 10^{-8}Re_\varphi +0.010 5 \end{eqnarray}$
通过上两式得到相应边界层厚度的初始估计值.

边界层形状因子${(\tilde{{\delta }}_0^\ast } / {\tilde{{\delta }}_0^{\ast\ast } })$在所考虑的$u_{\rm s}$, $Re_\varphi $范围内是变化的. 使用常数形状因子作为第一次迭代时的近似

(52) $ \begin{eqnarray} \label{eq52} \tilde{{\delta }}_0^{\ast \ast } =0.625\tilde{{\delta }}_0^\ast \end{eqnarray}$
式(49)~式(52)作为轴对称旋转边界层迭代求解的初值.

2.3 流线曲率和壁面吸气所对应的经验参数选取

由流线曲率以及相应的离心力对湍流影响由Bradshaw修正式(35)得到, 结合到式(41)和式(44)式中进行内层和外层湍流黏性修正. 对于经验参数$m$, 取$m=1$. $\beta $依赖壁面曲率、吸气率和旋转速度. 从黏性底层到湍流强烈的外层, $\beta$的变化与形状因子${\tilde{{\delta }}_0^\ast } / {\tilde{{\delta }}_0^{\ast\ast } }$有关, 详细的流场数值模拟表明如下的$\beta $取值较合理

(53) $ \begin{eqnarray} \label{eq53} \beta =0.135\left( {\frac{\tilde{{\delta }}^\ast }{\tilde{{\delta }}^{\ast \ast }}-0.5} \right)^{-10} \end{eqnarray} $
吸气对边界层的影响通过式(41)中的经验参数$A_\ast $修正. $A_\ast $指数形式的式(42)中系数$C_{1}$在平板边界层的CS模型中取$C_1 =11.8$. 对于本文研究的旋转边界层, $C_{1}$与边界层中的湍流程度有关, 而${\tilde{{\delta }}^\ast } / {\tilde{{\delta }}^{\ast \ast }}$与湍流程度密切相关. 对于层流边界层, ${\tilde{{\delta }}^\ast } / {\tilde{{\delta }}^{\ast \ast }}=2$. 湍流黏性为$\tilde{{\nu }}_{\rm t} =0$, 从式(41)和式(42)可知$C_1 \to \infty $; 对于本文研究的已经发展的湍流边界层${\tilde{{\delta }}^\ast } / {\tilde{{\delta }}^{\ast \ast }\approx 1.17}$, $C_1 \approx 11$. 通过详细数值模拟的流场数据的校核标定, 表明$C_{1}$的较好近似

(54) $ \begin{eqnarray} \label{eq54} C_1 =5.35\times 10^{-4}\left( {\frac{\tilde{{\delta }}^\ast }{\tilde{{\delta }}^{\ast \ast }}} \right)^{18.5}+11.217 \end{eqnarray}$
这与上述两个极限情况吻合良好.

注意到系数$\beta $和$C_{1}$校核与形状因子${\tilde{{\delta }}^\ast } / {\tilde{{\delta }}^{\ast \ast }}$的确定是耦合的: 一方面$\beta $和$C_{1}$依赖于形状因子${\tilde{{\delta }}^\ast } / {\tilde{{\delta }}^{\ast \ast }}$的值, 而反过来$\beta $和$C_{1}$值的选择又影响形状因子${\tilde{{\delta }}^\ast } / {\tilde{{\delta }}^{\ast \ast }}$的值. 基于已验证详细的数值模拟结果, 计算形状因子${\tilde{{\delta }}^\ast } / {\tilde{{\delta }}^{\ast \ast }}$值, 建立标定所需数据库. 对于不同$Re_\varphi $和$u_{\rm s} $的组合, 使用所建立的近似方法进行不同$\beta $和$C_{1}$参数组合的试算, 求得相应的${\tilde{{\delta }}^\ast } / {\tilde{{\delta }}^{\ast \ast }}$值. 然后根据梯度下降法改变$\beta $和$C_{1}$取值, 使详细数值模拟得到的${\tilde{{\delta }}^\ast } / {\tilde{{\delta }}^{\ast \ast }}$与基于代数湍流模型方法得到的${\tilde{{\delta }}^\ast } / {\tilde{{\delta }}^{\ast \ast }}$之差在容许误差之内. 有了$\beta $和$C_{1}$离散形式参数值集后, 对其进行拟合, 得到最小二乘拟合函数$\beta ({\tilde{{\delta }}^\ast } / {\tilde{{\delta }}^{\ast \ast })}$、$C_1 ({\tilde{{\delta }}^\ast } / {\tilde{{\delta }}^{\ast \ast })}$, 其结果见式(53)和式(54).

尾迹参数$\varPi _0 $使用经典公式(31), 它对壁面曲率和吸气的依赖通过合理选择参数$\beta $和$C_1 $体现.

3 算法及验证

3.1 迭代计算过程

边界层流动方程(20)的近似解以及上述定义代数湍流模型的方程, 表明可以用迭代法求解吸气旋转圆筒壁面的边界层流动. 主要步骤如下.

(1) 确定下列参数的初始值:

由式(20)旋转Reynolds数$Re_\varphi $; 无量纲吸气速度$u_{\rm s} $; 径向空间步长$k_r$; 径向最大的无量纲尺寸$\tilde{{h}}=\xi _{\max } $; 无量纲位移厚度计算迭代容差$\varepsilon ^\ast $.

(2)第一步计算:

(a)从式(19)得到无量纲摩擦速度$u_{\rm w} $;

(b)由式(50)预测无量纲边界层位移厚度$\tilde{{\delta }}_0^\ast $;

(c)由式(51)和式(52)预测无量纲边界层厚度和动量厚度$\tilde{{\delta }}_0$和$\tilde{{\delta }}_0^{\ast \ast } $;

(3) $\tilde{{\delta }}_0$, $\tilde{{\delta }}_0^\ast$, $\tilde{{\delta }}_0^{\ast\ast } $作为$\tilde{{\delta }}$, $\tilde{{\delta }}^\ast$, $\tilde{{\delta }}^{\ast \ast }$的初始近似.

(4)无量纲周向速度和径向坐标的初始值设置为$u_{\varphi 0} =1, \xi _{0,0} =1$. 根据式(8)和式(10)得初始导数值${(\partial u_\varphi } / {\partial \xi })_0 =1-Re_\varphi u_{\rm w}^2 $.

(5)第一层壁面距离由条件$y_1^+ =0.5$以及$y^+$的定义式(26), 得到$\Delta \xi _0 =\xi _1 -1={y^+}/({u_{\rm w} Re_\varphi })$.

(6)尾迹参数$\varPi _0 $、系数$k$, 以及系数$\beta$, $C_1 $由式(30)、式(31)、式(45)、式(53)得到.

(7)边界层内层计算循环:

(a)设置$\kappa =0.41$和$m=1$, 当前步的湍流黏性$\tilde{{\nu }}_{\rm ti}$由式(41)~式(43)得到;

(b)外层湍流黏性$\tilde{{\nu }}_{\rm to} $由式(43)、式(46)、式(49)计算得到;

(c) $\tilde{{\nu }}_{\rm ti}$, $\tilde{{\nu }}_{\rm to} $两者的较小值作为$\tilde{{\nu}}_{\rm t} $取值;

(d)当前步结束时设置坐标值$\xi _{1i} =\min(\xi _{0i} +\Delta \xi _i$, $\tilde{h})$, 周向速度$u_{\varphi (i+1)} $由式(20)得到;

(e)当前步结束时计算导数${\partial u_\varphi } / {\partial \xi }$

$$\begin{eqnarray*} \left( {{\partial u_\varphi } / {\partial \xi }} \right)\vert _{i+1} ={\left( {u_{\xi (i+1)} -u_{\xi i} } \right)} / {\Delta \xi _i }, \end{eqnarray*}$$

下一步长

$$\begin{eqnarray*} \Delta \xi _{i+1} =\min \left( {\Delta \xi _i \cdot k_r , 0.1\left( {\tilde{{h}}-1} \right)} \right); \end{eqnarray*}$$

(f)检查是否已经到达内层边界$\left( {\tilde{{\nu }}_{\rm t} \geqslant \tilde{{\nu }}_{\rm to}} \right)$, 如果满足该条件, 那么内层计算结束, 否则回到(a)计算下一层.

(8)下面几步为边界层外层计算循环:

(a)当前步计算初始湍流黏性由式(30)、式(31)、式(43)、式(45)、式(46)、式(49)得到;

(b)该步结束时的坐标$\xi _{i+1} =\min \left( {\xi _i +\Delta \xi _i , \tilde{{h}}} \right)$, 周向速度$u_{\varphi (i+1)} $由式(20)得到;

(c)当前步结束时计算导数${\partial u_\varphi } / {\partial \xi }$:

$$\begin{eqnarray*} \left( {{\partial u_\varphi } / {\partial \xi }} \right)\vert _{i+1} ={\left( {u_{\xi (i+1)} -u_{\xi i} } \right)} / {\Delta \xi _i }, \end{eqnarray*}$$

下一步长

$$\begin{eqnarray*} \Delta \xi _{i+1} =\min \left( {\Delta \xi _i \cdot k_r , 0.1\left( {\tilde{{h}}-1} \right)} \right); \end{eqnarray*}$$

(d)当达到区域边界时, 计算结束, 否则回到(a)继续计算.

(9) $\tilde{{\delta }}$的改进值由关系$u_\varphi (1+\tilde{{\delta }})=0.001$得到, $\tilde{{\delta }}^\ast ,\tilde{{\delta }}^{\ast \ast }$的校正值由式(47)和式(48)计算得到.

(10)检验精度${\left| {\tilde{{\delta }}_{i+1}^\ast -\tilde{{\delta }}_i^\ast } \right|} / {\max \left( {\tilde{{\delta }}_{i+1}^\ast ,\tilde{{\delta }}_i^\ast } \right)}\leqslant \varepsilon ^\ast $, 如果满足则停止计算, 否则回到(4)进行下一轮迭代.

3.2 迭代计算方法的验证

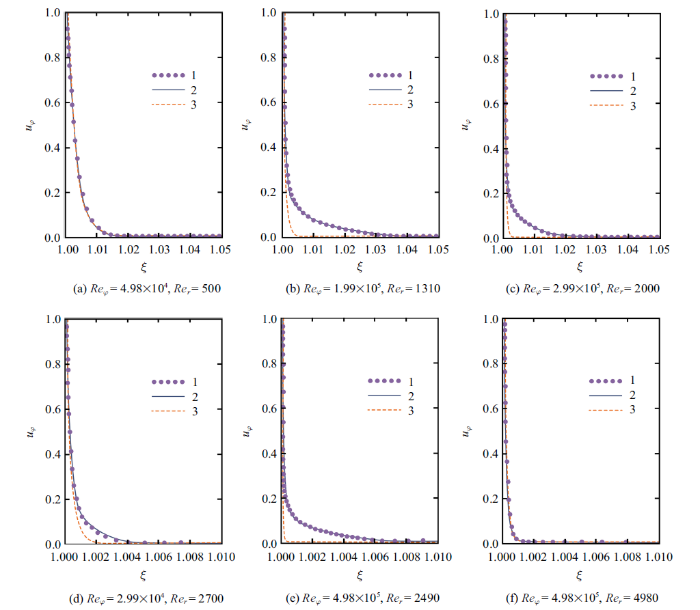
为了验证上述方法的正确性, 对比本文的代数湍流模型和详细流场数值模拟得到的边界层周向速度, 其结果如图2所示. 图中也包括由式(17)描述的层流边界层. $Re_\varphi$和$Re_r$的组合覆盖层流边界层和离心不稳定发生前的湍流边界层. 图2中的$Re_\varphi$和$Re_r$组合并不是用于校准湍流模型参数的$Re_\varphi$和$Re_r $组合.

图2

新窗口打开|下载原图ZIP|生成PPT
图2旋转圆筒壁面边界层的平均速度分布: 1 -- Reynolds应力湍流模型的数值仿真结果; 2 -- 本文代数湍流模型结果; 3 -- 层流边界层, 即式(17)

Fig.2Mean velocity profiles in the boundary layer on the surface of a rotating suction cylinder: 1 -- detailed numerical simulation, RSM turbulence model; 2 -- application of the algebraic turbulence model; 3 -- laminar profile, equation~(17)



从图2可以看出, 本文的代数湍流模型所预测的旋转圆筒周向速度与Reynolds应力微分形式湍流模型的详细数值模拟得到的结果几乎一致. 并且它也能预测强吸气条件下的层流边界层速度分布, 见图2(f).

图3显示了边界层内的湍流黏性分布, 可以看出代数湍流模型的预测结果与Reynolds应力模型的数值计算结果比较接近. 其中图3(a)为层流边界层, 理论上湍流黏性为0, 本文的代数湍流模型的湍流黏性预测值也非常小.

图3

新窗口打开|下载原图ZIP|生成PPT
图3湍流黏性: 1 -- Reynolds应力湍流模型的数值仿真结果; 2 -- 本文代数湍流模型结果

Fig.3Turbulent viscosity ratio profiles: 1 -- detailed numerical simulation, RSM turbulence model; 2 -- application of the algebraic turbulence model



以上流场结果也证实, 对于强吸气旋转圆筒Couette流动, 其主要流动为旋转圆筒壁附近的边界层流动. 随着旋转Reynolds数$Re_\varphi $的增大, 湍流及离心不稳定性增强. 吸气量减弱(即$Re_r $减小), 边界层增厚, 边界层内湍流强度增大. 在大$Re_r $情况下, 离心不稳定发生大为延后. 因此, 可以通过合适的$Re_\varphi$和$Re_r $组合来控制边界层的厚度和湍流强度, 具有很好的创新实用价值.

4 结论

本文针对吸气旋转壁面的湍流边界层流动建立了代数湍流模型. 基于Cebeci-Smith两层代数湍流模型, 通过推导分析, 对其进行修正和经验参数的调整, 用以考虑离心力场(流线曲率)和壁面吸气等因素的影响. 利用Reynolds应力湍流模型的详细数值模拟得到的流场, 校准Cebeci-Smith代数模型的经验参数.

建立了壁面吸气条件下轴对称旋转壁面边界层的迭代算法, 它容易用计算机程序实现. 该迭代算法能用于离心失稳(Taylor涡)发生前的层流及湍流边界层计算. 在旋转多孔圆筒强吸气条件下, 离心不稳定在较大的旋转速度($Re_\varphi \sim 10^5)$条件下发生, 通过调整吸气强度可以控制边界层厚度和湍流强度. 这为旋转壁面的剪切力、动量传递、传热和传质的控制提供了新思路. 本研究可应用于动态旋转过滤、转子轴的热保护、新型旋转热交换器等领域.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] Wilkinson N, Dutcher CS. Taylor-Couette flow with radial fluid injection
The Review of Scientific Instruments, 2017,88(8):1-9
[本文引用: 1]

[2] Min K, Lueptow RM. Hydrodynamic stability of viscous flow between rotating porous cylinders with radial flow
Physics of Fluids, 1994,6(1):144-151
DOIURL [本文引用: 1]

[3] Wereley ST, Akonur A, Lueptow RM. Particle--fluid velocities and fouling in rotating filtration of a suspension
Journal of Membrane Science, 2002,209(2):469-484
[本文引用: 1]

[4] Ji P, Motin A, Shan W, et al. Dynamic crossflow filtration with a rotating tubular membrane: Using centripetal force to decrease fouling by buoyant particles
Chemical Engineering Research and Design, 2016,106(6):101-114


[5] Jaffrin1 MY, Ding L. A review of rotating and vibrating membranes systems: advantages and drawbacks
Journal of Membrane and Separation Technology, 2015,4(3):134-148
[本文引用: 1]

[6] Motin A, Tarabara VV, Bénard A. Numerical investigation of the performance and hydrodynamics of a rotating tubular membrane used for liquid--liquid separation
Journal of Membrane Science, 2015,473(3):245-255
[本文引用: 1]

[7] Zheng J, Cai J, Wang D, et al. Suspended particle motion close to the surface of rotating cylindrical filtering membrane
Physics of Fluids, 2019,31(5):1-10


[8] 刘难生, 董宇红, 陆夕云 等. 旋转同心圆筒间Couette-Taylor流动的数值模拟
中国科学技术大学学报, 2002,32(1):91-97


( Liu Nansheng, Dong Yuhong, Lu Xiyun, et al. Numerical simulation of the Couette-Taylor flow between two concentric rotating cylinders
Journal of University of Science and Technology of China, 2002,32(1):91-97 (in Chinese))


[9] 冯俊杰, 毛玉红, 叶强 等. Taylor-Couette流场特性的PIV测量及数值模拟
实验流体力学, 2016,30(2):67-74


( Feng Junjie, Mao Yuhong, Ye Qiang, et al. PIV measurement and numerical simulation of Taylor-Couette flow
Journal of Experiments in Fluid Mechanics, 2016,30(2):67-74 (in Chinese))


[10] 蔡利亚. 同轴圆柱间旋转流动Taylor-Couette流的数值模拟
辽宁工业大学学报(自然科学版), 2007,27(3):206-210
[本文引用: 1]

( Cai Liya. Numerical simulation of Taylor-Couette flow between two coaxial rotating cylinders
Journal of Liaoning Institute of Technology, 2007,27(3):206-210 (in Chinese))
[本文引用: 1]

[11] Fénot M, Bertin Y, Dorignac E, et al. A review of heat transfer between concentric rotating cylinders with or without axial flow
International Journal of Thermal Sciences, 2011,50(7):1138-1155
[本文引用: 1]

[12] Mochalin I, E SJ, Wang D, et al. Numerical study of heat transfer in a Taylor-Couette system with forced radial throughflow
International Journal of Thermal Sciences, 2020,147(3):1-10
[本文引用: 2]

[13] Andereck CD, Liu SS, Swinney HL. Flow regimes in a circular Couette system with independently rotating cylinders
Journal of Fluid Mechanics, 1986,164(3):155-183
[本文引用: 1]

[14] Johnson EC, Lueptow RM. Hydrodynamic stability of flow between rotating porous cylinders with radial and axial flow
Physics of Fluids, 1997,9(12):3687-3696
[本文引用: 1]

[15] Serre E, Sprague MA, Lueptow RM. Stability of Taylor--Couette flow in a finite-length cavity with radial throughflow
Physics of Fluids, 2008,20(3):65-69
[本文引用: 1]

[16] Mochalin IV, Khalatov AA. Centrifugal instability and turbulence development in Taylor--Couette flow with forced radial throughflow of high intensity
Physics of Fluids, 2015,27(9):1-9
[本文引用: 7]

[17] 梁田, 刘波, 茅晓晨. 附面层抽吸对叶栅角区分离流动的控制研究
推进技术, 2019,40(9):1972-1981
[本文引用: 1]

( Liang Tian, Liu Bo, Mao Xiaochen. Investigation of corner separation control for cascade with boundary layer suction
Journal of Propulsion Technology, 2019,40(9):1972-1981 (in Chinese))
[本文引用: 1]

[18] Kametani Y, Fukagata K. Direct numerical simulation of spatially developing turbulent boundary layers with uniform blowing or suction
Journal of Fluid Mechanics, 2011,681(8):154-172
[本文引用: 1]

[19] 郑连存, 邓学蓥, 范玉妹. 特定抽吸/喷注下幂律流体平板边界层问题
力学学报, 2001,33(5):675-678
[本文引用: 1]

( Zheng Liancun, Deng Xueying, Fan Yumei. Flat plate boundary layer problems with special suction/injection conditions in power law fluid
Acta Mechanica Sinica, 2001,33(5):675-678 (in Chinese))
[本文引用: 1]

[20] 王艳平, 郭昊, 刘沛清 等. 高频吹气扰动影响近壁区拟序结构统计特性的实验研究
力学学报, 2015,47(4):571-579
[本文引用: 1]

( Wang Yanpin, Guo Hao, Liu Peiqing, et al. Effects of high frequency blowing perturbation on a turbulent boundary layer
Chinese Journal of Theoretical and Applied Mechanics, 2015,47(4):571-579 (in Chinese))
[本文引用: 1]

[21] 王帅杰, 崔晓通, 白建侠 等. 减阻工况下壁面周期扰动对湍流边界层多尺度的影响
力学学报, 2019,51(3):767-774
[本文引用: 1]

( Wang Shuaijie, Cui Xiaotong, Bai Jianxia, et al. The effect of periodic perturbation on multi scales in a turbulent boundary layer flow under drag reduction
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(3):767-774 (in Chinese))
[本文引用: 1]

[22] Fransson JHM, Konieczny P, Alfredsson PH. Flow around a porous cylinder subject to continuous suction or blowing
Journal of Fluids and Structures, 2004,19(8):1031-1048
[本文引用: 1]

[23] Kim K, Sung HJ, Chung MK. Assessment of local blowing and suction in a turbulent boundary layer
AIAA Journal, 2001,40(1):175-177


[24] Schlichting H, Gersten K. Boundary-Layer Theory
Berlin Heidelberg: Springer-Verlag, 2017
[本文引用: 2]

[25] Trip R, Fransson JHM. Boundary layer modification by means of wall suction and the effect on the wake behind a rectangular forebody
Physics of Fluids, 2014,26(12):1-18
[本文引用: 1]

[26] Cebeci T. Analysis of Turbulent Flows with Computer Programs
Oxford, UK: Butterworth-Heinemann, 2013
[本文引用: 2]

[27] Bradshaw P. The analogy between streamline curvature and buoyancy in turbulent shear flow
Journal of Fluid Mechanics, 1969,36(1):177-191
[本文引用: 2]

[28] Chen H, Zhang B. Fluid flow and mixed convection heat transfer in a rotating curved pipe
International Journal of Thermal Sciences, 2003,42(11):1047-1059
[本文引用: 1]

[29] Weigand B, Beer H. On the universality of the velocity profiles of a turbulent flow in an axially rotating pipe
Applied Scientific Research, 1994,52(2):115-132
DOIURL

[30] Kikuyama K, Murakami M, Nishibori K, et al. Flow in an axially rotating pipe: A calculation of flow in the saturated region
JSME International Journal, 1983,26(214):506-513
[本文引用: 1]