郭慧吉, 狄宏规
, 2) , 周顺华, 何超, 张小会同济大学上海市轨道交通结构耐久与系统安全重点实验室, 上海 201804
WAVE FUNCTIONS METHOD FOR CALCULATING THE DYNAMIC RESPONSE OF A TUNNEL IN UNSATURATED SOIL 1) Guo Huiji, Di Honggui
, 2) , Zhou Shunhua, He Chao, Zhang XiaohuiShanghai Key Laboratory of Rail Infrastructure Durability and System Safety, Tongii University, Shanghai 201804, China
通讯作者: 2)狄宏规, 助理教授, 主要研究方向: 轨道交通隧道系统动力学. E-mail:
2012dihonggui@tongji.edu.cn 收稿日期: 2019-10-11
接受日期: 2020-02-17
网络出版日期: 2020-03-18
基金资助: 1)国家自然科学基金资助项目 .51808405
Received: 2019-10-11
Accepted: 2020-02-17
Online: 2020-03-18
作者简介 About authors
摘要 针对非饱和地基土中埋置隧道的三维动力响应计算问题, 提出了波函数法.采用无限长的Flügge薄壁圆柱壳模拟圆形隧道衬砌,采用流、固、气组成的三相介质模拟非饱和地基土体.分别采用分离变量法以及Helmholtz矢量分解定理求解薄壁圆柱壳的振动控制方程与非饱和土的波动方程.根据隧-土交界面与地表面处的应力、位移以及孔隙流体压力等边界条件,利用平面波与柱面波的转换性质,实现了隧道内作用单位简谐载荷时隧道衬砌与土体系统动力响应的耦合求解.通过与既有单相弹性介质2.5维有限元-边界元法、两相饱和多孔介质2.5维有限元-边界元法以及三相非饱和介质Pip in Pip半解析法的计算结果进行对比, 验证了本文计算方法的可靠性. 最后,基于该方法, 通过算例分析了不同饱和度下非饱和土-隧道系统的动力响应特征.结果表明, 饱和度对土体动位移与超孔隙水压力的幅值响应有较大影响.该方法的非饱和地基土参数退化后,也可用来计算和分析饱和地基土或单相弹性地基土与隧道系统的动力响应.
关键词： 非饱和土 ;
Flügge圆柱壳 ;
波函数转换 ;
饱和度 Abstract This paper presents a wave functions method to calculate the three dimensional dynamic interaction between a circular tunnel and the surrounding unsaturated foundation soil. The tunnel lining is conceptualized as an infinite Flügge cylindrical shell, and the unsaturated foundation soil is conceptualized as a three-phase medium consisting of fluid, solid and gas. The motion equations of infinite Flügge cylindrical shell are solved by the separation of variable method, and the Helmholtz decomposition theorem is used to solve the unsaturated soil governing equations. Based on the boundary conditions of displacement, stress and pore fluid pressure at the unsaturated soil-tunnel interface and the ground surface, the dynamic interaction between the unsaturated soil and circular tunnel is solved when the tunnel invert subjected to a unit harmonic load. The transformation properties of plane wave functions and cylindrical wave functions are used to apply the boundary conditions expressed in both the rectangular and cylindrical coordinate systems before the coupling. The proposed method is verified by comparing with the results obtained by the existing 2.5 dimensional coupled FE-BE method for single phase elastic medium, 2.5 dimensional coupled FE-BE method for two phase saturated porous medium and Pip in Pip semi analytical method for three-phase unsaturated medium. Finally, by using the proposed method, the dynamic response of the unsaturated soil-tunnel system under different soil saturations is analyzed by a case study. The results show that saturation has a great effect on the dynamic response amplitude of soil displacement and excess pore water pressure. Because the three-phase medium simulating unsaturated soil can be reduced to two-phase medium or single-phase medium, this method can also be used to calculate and analyze the dynamic response of a circular tunnel buried in two-phase saturated soil or in single-phase elastic soil after the degeneration of the calculation parameters of unsaturated soil.
Keywords： unsaturated soil ;
Flügge cylindrical shell ;
wave functions transformation ;
saturation PDF (777KB) 元数据 多维度评价 相关文章 导出 EndNote |
Ris |
Bibtex 收藏本文 本文引用格式 郭慧吉, 狄宏规, 周顺华, 何超, 张小会. 非饱和土-隧道系统动力响应计算的波函数法
1) .
力学学报 [J], 2020, 52(2): 591-602 DOI:
10.6052/0459-1879-19-280 Guo Huiji, Di Honggui, Zhou Shunhua, He Chao, Zhang Xiaohui.
WAVE FUNCTIONS METHOD FOR CALCULATING THE DYNAMIC RESPONSE OF A TUNNEL IN UNSATURATED SOIL 1) .
Chinese Journal of Theoretical and Applied Mechanics [J], 2020, 52(2): 591-602 DOI:
10.6052/0459-1879-19-280 引言 地下列车运行时, 轮轨冲击振动会经由轨道、隧道传至地基土体, 引起地基土和周边建(构)筑物的振动
[1 ] . 随着地下铁道的快速发展,地下列车运行引起的环境振动问题和软土隧道沉降问题日益凸显
[2 -4 ] .
Metrikine等
[5 ] 将隧道视为埋置于弹性土体中的欧拉梁, 建立了二维解析模型, 探讨了隧道及地表在恒定、移动简谐载荷和随机载荷作用下的动力响应. Forrest和Hunt
[6 ] 采用薄壁圆柱壳模拟隧道, 弹性圆土柱模拟地基, 提出了隧道-土体系统动力响应三维半解析计算方法, 即PiP半解析法.Yuan等
[7 ] 将隧道简化为埋置在弹性半空间的中空圆柱体, 基于平面波和柱面波转换, 获得了弹性半空间埋置单洞隧道的动力响应闭合解.He等
[8 ] 通过引入波的平移公式, 提出了单相弹性半空间中埋置双洞隧道系统动力响应的基本解. 数值法方面, Thiede等
[9 ] 采用二维有限元法研究了地铁列车振动响应问题.Bian等
[10 ] 采用2.5维有限元法研究了地铁列车运行引起的地基振动.Sheng等
[11 ] 采用波数离散法, 建立了2.5维波数有限元-边界元法, 研究了地面和地下列车载荷引起的振动响应问题.Degrande等
[12 ] 基于Floquet变换, 提出了周期性有限元-边界元法, 并用于振动预测; Hung和Yang
[13 ] 采用无限域模拟地基, 提出了2.5维有限元-无限元法, 模拟地下列车运行引起的地表振动. 此外, 针对富水地层的隧道, 相关****采用Biot饱和多孔介质模拟饱和土体, 对上述模型或方法进行了发展和改进: 如饱和全空间的PiP半解析法
[14 -15 ] ;-饱和半空间的波面转换闭合解
[16 -17 ] 以及饱和半空间的2.5维有限元-边界元法
[18 -20 ] 等.
然而, 采用单相或两相介质难以模拟地基土的实际情况, 需考虑饱和度对动力响应的影响
[21 -22 ] . 徐明江
[23 ] 基于V-G模型, 建立了非饱和土的动力控制方程, 求解了非饱和土地基与基础的动力响应.高广运等
[24 ] 、李伟华等
[25 ] 基于非饱和介质波动理论, 采用有限元法研究了移动载荷作用下路基和地基的动力响应.郭鹏飞等
[26 ] 、章敏等
[27 ] 基于非饱和土的动力控制方程, 分析了非饱和土中桩基的动力响应问题. 但受计算方法限制, 目前对于非饱和土-隧道系统动力响应的研究较少.刘洪波
[28 ] 等提出了简谐载荷作用下非饱和土中深埋圆形隧洞系统动力响应的2维解析解.考虑到2维计算方法无法考虑系统的3维动力特性, 狄宏规
[29 ] 等在文献
[15 ] 的基础上,进一步提出了非饱和土-隧道系统动力响应计算的3维PiP半解析法.但上述2维或3维解
[28 -29 ] 均假定隧道外的土体外径为无穷大, 即均为全空间算法, 故无法获得真实半空间地基表面的动力响应.
为研究非饱和半空间中埋置圆形隧道系统的动力响应问题,本文将圆形隧道视为Flügge薄壁圆柱壳, 隧道外的非饱和地基土简化为由流、固、气组成的三相介质,分别采用分离变量法求解圆柱壳的振动控制方程, Helmholtz矢量分解定理求解非饱和土的波动方程, 并基于隧-土交界面处及地表等边界条件, 利用平面波和柱面波的转换进行耦合求解, 提出了移动简谐载荷下非饱和半空间地基中埋置圆形隧道动力响应计算的波函数法, 基于该方法, 探讨了非饱和地基土-隧道系统的动力响应特征.
1 控制方程和求解 将隧道衬砌简化为无限长的Flügge薄壁圆柱壳, 壳体由均质、各向同性、线弹性材料组成.将非饱和地基土简化为由流、固、气组成的三相介质.计算过程中包括
图1 所示的圆柱坐标系($r$, $\theta$, $z)$和直角坐标系($x$, $y$, $z)$两种坐标系. 图中, $O_{1}$, $O_{2}$, $O_{3}$, $O_{4}$为4个观测点:-$O_{1}$点位于载荷作用点正上方地表, $O_{3}$点位于载荷作用点下方隧道底部, $O_{2}$, $O_{4}$点分别位于$O_{1}$, $O_{3}$左侧20 m处.
图1 新窗口打开 |
下载原图ZIP |
生成PPT 图1非饱和土-隧道系统及坐标系 Fig. 1Unsaturated soil-tunnel system and coordinate 图中: $q$代表激振载荷; $v_{0}$代表载荷移动速度; $d$代表隧道中心线距离地表竖直距离; $r_{1}$代表隧道衬砌半径.
1.1 衬砌振动控制方程 隧道衬砌视为Flügge薄壁圆柱壳, 利用分离变量法对壳体控制方程进行求解, 可得简谐载荷作用下壳体平衡方程的矩阵表达式
[6 ] (1) $ \begin{eqnarray} \label{eq1} \left[ {{\begin{array}{*{20}c} {\hat{{\tilde{{U}}}}_{mz} } \\ {\hat{{\tilde{{U}}}}_{m\theta } } \\ {-\hat{{\tilde{{U}}}}_{mr} } \\ \end{array} }} \right]=S^{-1}\left[ {{\begin{array}{*{20}c} {\hat{{\tilde{{q}}}}_{mz} } \\ {\hat{{\tilde{{q}}}}_{m\theta } } \\ {\hat{{\tilde{{q}}}}_{mr} } \\ \end{array} }} \right] \end{eqnarray}$ 式中, 上标"\^{}"代表$z$方向所对应的波数域; 上标"$\sim$"表示时间$t$所对应的频域; $m$表示环向模态; $\hat{{\tilde{{U}}}}_{mz}$,$\hat{{\tilde{{U}}}}_{m\theta}$, $\hat{{\tilde{{U}}}}_{mr}$和$\hat{{\tilde{{q}}}}_{mz}$, $\hat{{\tilde{{q}}}}_{m\theta }$,$\hat{{\tilde{{q}}}}_{mr}$分别表示在频域-波数域内位移和应力在单个环向模态数$m$下的物理量;式(1)各变量表达式详见附录A.
1.2 非饱和地基土波动方程 将非饱和地基土视为流、固、气组成的三相介质, 其实用波动方程如下
[23 ] (2a) $ \begin{eqnarray} \label{eq2} \left. {\begin{array}{l} \mu \nabla ^2u_{\rm b} +(\lambda +\mu )\nabla \nabla \cdot u_{\rm b} -a\gamma \nabla p_{\rm l} -a(1-\gamma )\nabla p_{\rm g} =\\ \qquad {\mathop{\rho}\limits^\smallfrown}_{\rm s} u_{\rm b}{''}+{\mathop{\rho}\limits^\smallfrown}_{\rm l} u_{\rm l}{''}+{\mathop{\rho}\limits^\smallfrown}_{\rm g} u_{\rm g}{''} \\ -\nabla p_{\rm l} =b_{\rm l} (u_{\rm l} '-u_{\rm b} ')+\rho _{\rm l} u_{\rm l}{''} \\ -\nabla p_{\rm g} =b_{\rm g} (u_{\rm g} '-u_{\rm b} ')+\rho _{\rm g} u_{\rm g}{''} \\ \end{array}} \right\}\quad \end{eqnarray} $ 式中, $a=1-K_{\rm b} /K_{\rm s}$, $K_{\rm b} =\lambda +2\mu /3$,$b_{\rm l}=n_0 S_r \eta _{\rm l} /(k_{{\rm rl}} \kappa )$, $b_{\rm g} =n_0 (1-S_r )\eta_{\rm l} /(k_{{\rm rg}} \kappa)$, ${\mathop{\rho}\limits^\smallfrown}_{\rm s} =(1-n_0 )\rho_{\rm s}$, ${\mathop{\rho}\limits^\smallfrown}_{\rm g} =n_0 (1-S_r )\rho _{\rm g}$, ${\mathop{\rho}\limits^\smallfrown}_{\rm l} =n_0 S_r \rho _{\rm l} $; 下标s, b, l, g分别代表土颗粒、土骨架、孔隙水以及气体物理量的分量; 上标"'"、"''"分别表示一阶、二阶导; $u$表示位移矢量; $p$表示流体压力; $\rho $表示密度; $\lambda $, $\mu$为土骨架Lame常数; $\gamma $为有效应力系数. $K$为压缩模量; $n_{0}$, $S_{r}$分别为土体孔隙率与饱和度;$\eta$为流体黏滞系数; $k_{\rm rl}$, $k_{\rm rg}$分别为液体和气体渗透系数; $\kappa $为土的渗透率.
非饱和土中流体和气体的渗流连续性方程为
(2b) $ \begin{eqnarray} \label{eq2b} \left.{\begin{array}{l} -p_{\rm l} '=a_{11} \nabla \cdot u_{\rm b} '+a_{12} \nabla \cdot u_{\rm l} '+a_{13} \nabla \cdot u_{\rm g} ' \\ -p_{\rm g} '=a_{21} \nabla \cdot u_{\rm b} '+a_{22} \nabla \cdot u_{\rm l} '+a_{23} \nabla \cdot u_{\rm g} ' \\ \end{array}} \right. \end{eqnarray}$ 式中, $a_{11}$, $a_{12}$, $a_{13}$, $a_{21}$, $a_{22}$, $a_{23}$表达式见附录B.
通过引入非饱和多孔介质的平均密度
(3a) $ \begin{eqnarray} \label{eq3a} \rho =(1-n_0 )\rho _{\rm s} +n_0 S_r \rho _{\rm l} +n_0 (1-S_r )\rho _{\rm g} \end{eqnarray} $ 孔隙水与固体骨架的相对位移
(3b) $ \begin{eqnarray} \label{eq3b} v=n_0 S_r (u_{\rm l} -u_{\rm b} ) \end{eqnarray} $ 气体与固体骨架间的相对位移
(3c) $ \begin{eqnarray} \label{eq3c} w=n_0 (1-S_r )(u_{\rm g} -u_{\rm b} ) \end{eqnarray} $ 将上述波动方程方程(2a)写成$u_{\rm b}-v-w$的表达形式有
(4a) $ \begin{eqnarray} \label{eq4a} \left. {\begin{array}{l} \mu \nabla ^2u_{\rm b} +(\lambda _c +\mu )\nabla (\nabla \cdot u_{\rm b} )+M\nabla (\nabla \cdot v)+ \\ \qquad N\nabla (\nabla \cdot w)=\rho u_{\rm b}{''}+\rho _{\rm l} v^{''}+\rho _{\rm g} w^{''} \\ b_{11} \nabla (\nabla \cdot u_{\rm b} )+b_{12} \nabla (\nabla \cdot v)+b_{13} \nabla (\nabla \cdot w)= \\ \qquad \rho _{\rm l} u_{\rm b}{''}+\vartheta _{\rm l} v^{''}+d_{\rm l} v' \\ b_{21} \nabla (\nabla \cdot u_{\rm b} )+b_{22} \nabla (\nabla \cdot v)+b_{23} \nabla (\nabla \cdot w)= \\ \qquad \rho _{\rm g} u_{\rm b}{''}+\vartheta _{\rm g} w^{''}+d_{\rm g} w' \\ \end{array}} \right\} \end{eqnarray} $ 渗流连续性方程(2b)写成$u_{\rm b}-v-w$的表达形式有
(4b) $ \begin{eqnarray} \label{eq8} \left. {\begin{array}{l} -p_{\rm l} =b_{11} \nabla \cdot u_{\rm b} +b_{12} \nabla \cdot v+b_{13} \nabla \cdot w \\ -p_{\rm g} =b_{21} \nabla \cdot u_{\rm b} +b_{22} \nabla \cdot v+b_{23} \nabla \cdot w \\ \end{array}} \right\} \end{eqnarray} $ 土体总应力表达式
(4c) $ \begin{eqnarray} \label{eq9} \left. {\begin{array}{l} \sigma _{ij} =\lambda e\delta _{ij} +2\mu \varepsilon _{ij} -\delta _{ij} ap \\ p=\gamma p_{\rm l} +(1-\gamma )p_{\rm g} \\ \end{array}} \right\} \end{eqnarray} $ 式中, $\sigma_{ij}$为土单元总应力; $e$为体积应变; $\varepsilon_{ij}$为应变分量; $\delta_{ij}$为克罗内克符号;
$p$为等效孔隙流体压力. 其余各参数具体表达式见附录C.
根据Helmholtz矢量分解定理, 式(4)中土骨架位移$u_{\rm b}$和流体、气体相对于骨架的位移$v$, $w$,用标量势和矢量势分别表示为
(5) $ \begin{eqnarray} \label{eq10} \left. {\begin{array}{l} u_{\rm b} =\nabla \times ({\rm e}_z \varphi _{{\rm SH}} )+\nabla \times \nabla \times ({\rm e}_z \varphi _{{\rm SV}} )+\nabla \varphi _{\rm P} \\ v=\nabla \times ({\rm e}_z \phi _{{\rm SH}} )+\nabla \times \nabla \times ({\rm e}_z \phi _{{\rm SV}} )+\nabla \phi _{\rm P} \\ w=\nabla \times ({\rm e}_z \chi _{{\rm SH}} )+\nabla \times \nabla \times ({\rm e}_z \chi _{{\rm SV}} )+\nabla \chi _{\rm P} \\ \end{array}} \right\} \end{eqnarray}$ 式中, 下标SH, SV, P分别代表SH, SV, P波的分量$\varphi$, $\phi$, $\chi $分别为土骨架部分、液体部分以及气体部分的势函数. ${\rm e}_z$表示$z$方向单位向量.
考虑稳态响应, 将式(5)代入式(4a), 对时间$t$进行Fourier变换至频域后, 得到如下两组方程
(6) $ \begin{eqnarray} \left. \begin{array}{l} \left[ \begin{array}{l} (\lambda _c +2\mu )\nabla ^2+ \omega^2\rho, M\nabla ^2+ \omega^2\rho_{\rm l}, N\nabla ^2+ \omega^2\rho _{\rm g} \\ b_{11} \nabla ^2+ \omega^2\rho _{\rm l}, b_{12} \nabla ^2+ \omega^2\vartheta _{\rm l} -{\rm i} \omega d_{\rm l}, b_{13} \nabla ^2 \\ b_{21} \nabla ^2+ \omega^2\rho _{\rm g}, b_{22} \nabla ^2, b_{23}\nabla ^2+ \omega^2\vartheta _{\rm g} -{\rm i} \omega d_{\rm g} \\ \end{array} \right]\cdot\\ \qquad \left[ \begin{array}{*{20}c} {\tilde{{\varphi }}_{\rm P} } \\ {\tilde{{\phi }}_{\rm P} } \\ {\tilde{{\chi }}_{\rm P} } \\ \end{array}\right]=0 \\ \left[ \begin{array}{l} \mu \nabla ^2+ \omega^2\rho, \omega^2\rho _{\rm l}, \omega^2\rho_{\rm g} \\ \omega^2\rho _{\rm l}, \omega^2\vartheta _{\rm l} -{\rm i} \omega d_{\rm l}, 0 \\ \omega^2\rho _{\rm g}, 0, \omega^2\vartheta _{\rm g} -{\rm i} \omega d_{\rm g} \\ \end{array} \right]\left[ \begin{array}{*{20}c} {\tilde{{\varphi }}_{{\rm SH,SV}} } \\ {\tilde{{\phi }}_{{\rm SH,SV}} } \\ {\tilde{{\chi }}_{{\rm SH,SV}} } \\ \end{array} \right]=0 \\ \end{array}\right\} \end{eqnarray}$ 式中$ \omega$为角频率.
为满足微分方程组(6)有非零解, 则需满足系数矩阵行列式为0的条件, 得
(7) $ \begin{eqnarray} \label{eq7} \left.\begin{array}{l} (Ba\nabla ^6+Bb\nabla ^4+Bc\nabla ^2+Bd)\tilde{{\varphi }}_{\rm P} =0\\ (\nabla ^2+Be)\tilde{{\varphi }}_{{\rm SH,SV}} =0 \\ \end{array}\right\} \end{eqnarray}$ 式中, $Ba$, $Bb$, $Bc$, $Bd$, $Be$表达式见附录D.
根据式(7), 可得如下两组Helmholtz方程
(8) $ \left.\begin{array}{l} (\nabla ^2+k_{{\rm p1,p2,p3}}^2 )\tilde{{\varphi }}_{{\rm P1,P2,P3}} =0 \\ (\nabla ^2+k_{\rm s}^2 )\tilde{{\varphi }}_{{\rm SH,SV}} =0 \\ \end{array}\right\} $ 式中, $k_{\rm p1}$, $k_{\rm p2}$, $k_{\rm p3}$分别为非饱和地基中的纵波波数; $k_{\rm s}$为非饱和地基中的横波波数.
利用式(6)、式(8), 经推导整理, 各势函数可表达为
(9) $ \begin{eqnarray} \label{eq13} \left.\begin{array}{l} \tilde{{\varphi}}_{\rm P} =\tilde{{\varphi}}_{{\rm P}1} {\rm +}\tilde{{\varphi}}_{{\rm P}2} {\rm +}\tilde{{\varphi}}_{{\rm P}3} \\ \tilde{{\phi}}_{\rm P} =\tilde{{\phi}}_{{\rm P}1} {\rm +}\tilde{{\phi}}_{{\rm P}2} {\rm +}\tilde{{\phi}}_{{\rm P}3} =\mu_{1{\rm l}} \tilde{{\varphi}}_{{\rm P}1} {\rm +\mu }_{2{\rm l}} \tilde{{\varphi}}_{{\rm P}2} {\rm +\mu }_{3{\rm l}} \tilde{{\varphi}}_{{\rm P}3} \\ \tilde{{\chi }}_{\rm P} =\tilde{{\chi }}_{{\rm P}1} {\rm +}\tilde{{\chi }}_{{\rm P}2} {\rm +}\tilde{{\chi }}_{{\rm P}3} =\mu_{1{\rm g}} \tilde{{\varphi}}_{{\rm P}1} {\rm +\mu }_{2{\rm g}} \tilde{{\varphi}}_{{\rm P}2} {\rm +\mu }_{3{\rm g}} \tilde{{\varphi}}_{{\rm P}3} \\ \tilde{{\phi}}_{{\rm SH}} =\mu_{{\rm sl}} \tilde{{\varphi}}_{{\rm SH}} ,\tilde{{\chi }}_{{\rm SH}} =\mu_{{\rm sl}} \tilde{{\varphi}}_{{\rm SH}} \\ \tilde{{\phi}}_{{\rm SV}} =\mu_{{\rm sg}} \tilde{{\varphi}}_{{\rm SV}} ,\tilde{{\chi }}_{{\rm SV}} =\mu_{{\rm sg}} \tilde{{\varphi}}_{{\rm SV}} \\ \end{array}\right\} \end{eqnarray}$ 式中, $\mu _{\rm 1l}$, $\mu _{\rm 2l}$, $\mu _{\rm 3l}$, $\mu _{\rm 1g}$, $\mu_{\rm 2g}$, $\mu _{\rm 3g}$, $\mu _{\rm sl}$, $\mu _{\rm sg}$的表达式见附录E.
由于隧道埋置的非饱和半空间中存在两个散射面, 即圆柱形隧道外表面以及地表水平面, 因此总的波场中包括外行的柱面波以及下行的平面波两种波.参考文献
[16 ] 并结合式(9), 可得到直角坐标系下下行面波的位移势函数为
(10a) $ \begin{eqnarray} \left.\begin{array}{l} \hat{{\bar{{\tilde{{U}}}}}}_1^d =\nabla \times ({\rm e}_z \hat{{\bar{{\tilde{{\varphi }}}}}}_{{\rm SH}} )=\left[ {{\rm i}k_y, {\rm i}k_{{\rm s}x}}, 0 \right]{\rm e}^{-{\rm i}k_{{\rm s}x} x} \\ \hat{{\bar{{\tilde{{U}}}}}}_2^d =\nabla \times \nabla \times ({\rm e}_z \hat{{\bar{{\tilde{{\varphi }}}}}}_{{\rm SV}} )=\\\qquad \left[ {k_zk_{{\rm s}x}, -k_z k_y, k_y^2 +k_{{\rm s}x}^2 } \right]{\rm e}^{-{\rm i}k_{{\rm s}x} x} \\ \hat{{\bar{{\tilde{{U}}}}}}_3^d =\nabla \hat{{\bar{{\tilde{{\varphi}}}}}}_{{\rm P}1} =\left[ {-{\rm i}k_{{\rm p1}x}, {\rm i}k_y, {\rm i}k_z } \right]{\rm e}^{-{\rm i}k_{{\rm p1}x} x} \\ \hat{{\bar{{\tilde{{U}}}}}}_4^d =\nabla \hat{{\bar{{\tilde{{\varphi }}}}}}_{{\rm P}2} =\left[ {-{\rm i}k_{{\rm p2}x}, {\rm i}k_y, {\rm i}k_z } \right]{\rm e}^{-{\rm i}k_{{\rm p2}x} x} \\ \hat{{\bar{{\tilde{{U}}}}}}_5^d =\nabla \hat{{\bar{{\tilde{{\varphi}}}}}}_{{\rm P}3} =\left[ {-{\rm i}k_{{\rm p3}x}, {\rm i}k_y, {\rm i}k_z } \right]{\rm e}^{-{\rm i}k_{{\rm p3}x} x} \\ \end{array}\right\} \end{eqnarray} $ 式中, "--"代表$y$向波数域; $\hat{{\bar{{\tilde{{U}}}}}}_1^d$, $\hat{{\bar{{\tilde{{U}}}}}}_2^d$, $\hat{{\bar{{\tilde{{U}}}}}}_3^d$, $\hat{{\bar{{\tilde{{U}}}}}}_4^d$, $\hat{{\bar{{\tilde{{U}}}}}}_5^d$分别为SH, SV, P1, P2, P3波直角坐标下频域波数域中下行波的位移势函数; $k_{y}$, $k_{z}$分别为$y$向与$z$向波数; $k_{{\rm s}x} =\sqrt {k_{\rm s}^2 -k_y^2-k_z^2 } $为S波$x$向波数, 且虚数部非负; $k_{{\rm p}1,2,3 x} =\sqrt {k_{{\rm p}1,2,3}^2 -k_y^2 -k_z^2 } $为P波$x$向波数, 且虚数部非负.直角坐标下上行波位移势函数$\hat{{\bar{{\tilde{{U}}}}}}^u$只需将式(10a)中$k_{{\rm s}x}$, $k_{{\rm p}1,2,3 x}$替换为$-k_{{\rm s}x}$, $-k_{{\rm p}1,2,3 x}$即可.
圆柱坐标系下外行波的位移势函数为
(10b) $ \begin{eqnarray} \left.\begin{array}{l} \hat{{\tilde{{U}}}}_{m1}^o =\nabla \times ({\rm e}_z \hat{{\tilde{{\varphi }}}}_{m{\rm SH}} )= \\ \quad \left[ {\dfrac{{\rm i}m}{r}H_m^{(1)} (k_{{\rm s}r} r), k_{{\rm s}r} H_m^{(1)'} (k_{{\rm s}r} r),0} \right]{\rm e}^{{\rm i}m\theta } \\ \hat{{\tilde{{U}}}}_{m2}^o =\nabla \times \nabla \times ({\rm e}_z \hat{{\tilde{{\varphi }}}}_{m{\rm SV}} )= \\ \quad \left[ {{\rm i}k_z k_{{\rm s}r} H_m^{(1)'} (k_{{\rm s}r} r),\dfrac{-mk_z }{r}H_m^{(1)} (k_{{\rm s}r} r),k_{{\rm s}r}^2 H_m^{(1)} (k_{{\rm s}r} r)} \right]{\rm e}^{{\rm i}m\theta } \\ \hat{{\tilde{{U}}}}_{m3}^o =\nabla \hat{{\tilde{{\varphi }}}}_{m{\rm P}1} = \\ \quad \left[ {k_{{\rm p}1r} H_m^{(1)'} (k_{{\rm p}1r} r),\dfrac{{\rm i}m}{r}H_m^{(1)} (k_{{\rm p1}r} r),{\rm i}k_z H_m^{(1)} (k_{{\rm p}1r} r)} \right]{\rm e}^{{\rm i}m\theta } \\ \hat{{\tilde{{U}}}}_{m4}^o =\nabla \hat{{\tilde{{\varphi }}}}_{m{\rm P}2} = \\ \quad \left[ {k_{{\rm p}2r} H_m^{(1)'} (k_{{\rm p}2r} r),\dfrac{{\rm i}m}{r}H_m^{(1)} (k_{{\rm p}2r} r),{\rm i}k_z H_m^{(1)} (k_{{\rm p}2r} r)} \right]{\rm e}^{{\rm i}m\theta } \\ \hat{{\tilde{{U}}}}_{m5}^o =\nabla \hat{{\tilde{{\varphi }}}}_{m{\rm P}3} = \\ \quad \left[ {k_{{\rm p}3r} H_m^{(1)'} (k_{{\rm p}3r} r),\dfrac{{\rm i}m}{r}H_m^{(1)} (k_{{\rm p}3r} r),{\rm i}k_z H_m^{(1)} (k_{{\rm p}3r} r)} \right]{\rm e}^{{\rm i}m\theta } \\ \end{array}\right\}\\&& \end{eqnarray} $ 式中, $\hat{{\tilde{{U}}}}_{m1}^o$, $\hat{{\tilde{{U}}}}_{m2}^o$, $\hat{{\tilde{{U}}}}_{m3}^o$, $\hat{{\tilde{{U}}}}_{m4}^o$, $\hat{{\tilde{{U}}}}_{m5}^o $分别为SH, SV, P1, P2, P3波圆柱坐标下频域波数域中外行波的位移势函数; $H_m^{(1)}$为第一类Hankel函数; $k_{{\rm s}r} =\sqrt {k_{\rm s}^2 -k_z^2 } $为S波$r$向波数, 且虚数部非负; $k_{{\rm p}1,2,3 r} =\sqrt {k_{{\rm p}1,2,3}^2 -k_z^2 } $为P波$r$向波数, 且虚数部非负. 圆柱坐标下内行行波位移势函数$\hat{{\tilde{{U}}}}_m^r $只需将式(10b)中$H_m^{(1)} $替换为第一类Bessel函数J$_m^{(1)}$即可.
将式(10)代入式(4b)得直角坐标系与圆柱坐标系下孔压的表达式, 如式(11)所示
(11a) $ \left.\begin{array}{l} \hat{{\bar{{\tilde{{\vartheta }}}}}}_{{\rm 3}}^d =A_{{\rm p}1}^{\rm l} \nabla ^2\hat{{\bar{{\tilde{{\varphi }}}}}}_{{\rm P}1} =-A_{{\rm p}1}^{\rm l} k_{{\rm p}1}^2 {\rm e}^{-{\rm i}k_{{\rm p}1x} x} \\ \hat{{\bar{{\tilde{{\vartheta }}}}}}_{{\rm 4}}^d =A_{{\rm p}2}^{\rm l} \nabla ^2\hat{{\bar{{\tilde{{\varphi }}}}}}_{{\rm P}1} =-A_{{\rm p}2}^{\rm l} k_{{\rm p}2}^2 {\rm e}^{-{\rm i}k_{{\rm p}2x} x} \\ \hat{{\bar{{\tilde{{\vartheta }}}}}}_{{\rm 5}}^d =A_{{\rm p}3}^{\rm l} \nabla ^2\hat{{\bar{{\tilde{{\varphi }}}}}}_{{\rm P}1} =-A_{{\rm p}3}^{\rm l} k_{{\rm p}3}^2 {\rm e}^{-{\rm i}k_{{\rm p}3x} x} \\ \hat{{\tilde{{\vartheta }}}}_{m3}^o =A_{{\rm p}1}^{\rm l} \nabla ^2\hat{{\tilde{{\varphi }}}}_{m{\rm P}1} =-A_{{\rm p}1}^{\rm l} k_{{\rm p}1}^2 H_m^{(1)} (k_{{\rm p}r1} r){\rm e}^{{\rm i}m\theta } \\ \hat{{\tilde{{\vartheta }}}}_{m4}^o =A_{{\rm p}2}^{\rm l} \nabla ^2\hat{{\tilde{{\varphi }}}}_{m{\rm P}1} =-A_{{\rm p}2}^{\rm l} k_{{\rm p}2}^2 H_m^{(1)} (k_{{\rm p}r2} r){\rm e}^{{\rm i}m\theta } \\ \hat{{\tilde{{\vartheta }}}}_{m5}^o =A_{{\rm p}3}^{\rm l} \nabla ^2\hat{{\tilde{{\varphi }}}}_{m{\rm P}1} =-A_{{\rm p}3}^{\rm l} k_{{\rm p}3}^2 H_m^{(1)} (k_{{\rm p}r3} r){\rm e}^{{\rm i}m\theta } \\ \end{array}\right\} $ (11b) $ \left.\begin{array}{l} \hat{{\bar{{\tilde{{\vartheta }}}}}}_{{\rm g 3}}^d =A_{{\rm p}1}^{\rm g} \nabla ^2\hat{{\bar{{\tilde{{\varphi }}}}}}_{{\rm P}1} =-A_{{\rm p}1}^{\rm g} k_{{\rm p}1}^2 {\rm e}^{-{\rm i}k_{{\rm p}1x} x} \\ \hat{{\bar{{\tilde{{\vartheta }}}}}}_{{\rm g 4}}^d =A_{{\rm p}2}^{\rm g} \nabla ^2\hat{{\bar{{\tilde{{\varphi }}}}}}_{{\rm P}1} =-A_{{\rm p}2}^{\rm g} k_{{\rm p}2}^2 {\rm e}^{-{\rm i}k_{{\rm p}2x} x} \\ \hat{{\bar{{\tilde{{\vartheta }}}}}}_{{\rm g 5}}^d =A_{{\rm p}3}^{\rm g} \nabla ^2\hat{{\bar{{\tilde{{\varphi }}}}}}_{m{\rm P}1} =-A_{{\rm p}3}^{\rm g} k_{{\rm p}3}^2 {\rm e}^{-{\rm i}k_{{\rm p}2x} x} \\ \hat{{\tilde{{\vartheta }}}}_{{\rm g }m3}^o =A_{{\rm p}1}^{\rm g} \nabla ^2\hat{{\tilde{{\varphi }}}}_{m{\rm P}1} =-A_{{\rm p}1}^{\rm g} k_{{\rm p}1}^2 H_m^{(1)} (k_{{\rm p}r1} r){\rm e}^{{\rm i}m\theta } \\ \hat{{\tilde{{\vartheta }}}}_{{\rm g }m4}^o =A_{{\rm p}2}^{\rm g} \nabla ^2\hat{{\tilde{{\varphi }}}}_{m{\rm P}1} =-A_{{\rm p}2}^{\rm g} k_{{\rm p}2}^2 H_m^{(1)} (k_{{\rm p}r2} r){\rm e}^{{\rm i}m\theta } \\ \hat{{\tilde{{\vartheta }}}}_{{\rm g }m5}^o =A_{{\rm p}3}^{\rm g} \nabla ^2\hat{{\tilde{{\varphi }}}}_{m{\rm P}1} =-A_{{\rm p}3}^{\rm g} k_{{\rm p}3}^2 H_m^{(1)} (k_{{\rm p}r3} r){\rm e}^{{\rm i}m\theta } \\ \end{array}\right\} $ 式中, $\hat{{\bar{{\tilde{{\vartheta }}}}}}_{{\rm 3}}^d$, $\hat{{\bar{{\tilde{{\vartheta }}}}}}_{{\rm 4}}^d$, $\hat{{\bar{{\tilde{{\vartheta }}}}}}_{{\rm 5}}^d $分别为P1, P2,P3波直角坐标下频域波数域中下行波的孔隙水压力势函数; $\hat{{\bar{{\tilde{{\vartheta }}}}}}_{{\rm g 3}}^d$, $\hat{{\bar{{\tilde{{\vartheta }}}}}}_{{\rm g 4}}^d$, $\hat{{\bar{{\tilde{{\vartheta }}}}}}_{{\rm g 5}}^d $分别为P1, P2,P3波直角坐标下频域波数域中下行波的气体压力势函数; $\hat{{\tilde{{\vartheta }}}}_{m{\rm 3}}^o$, $\hat{{\tilde{{\vartheta }}}}_{m{\rm 4}}^o$, $\hat{{\tilde{{\vartheta }}}}_{m{\rm 5}}^o $分别为P1, P2, P3波圆柱坐标下频域波数域中外行波的孔隙水压力势函数; $\hat{{\tilde{{\vartheta }}}}_{{\rm g }m3}^o$, $\hat{{\tilde{{\vartheta }}}}_{{\rm g }m4}^o$, $\hat{{\tilde{{\vartheta }}}}_{{\rm g }m5}^o$分别为P1, P2, P3波圆柱坐标下频域波数域中外行波的气体压力势函数; $A_{{\rm p}1,2,3}^{\rm l} ,A_{{\rm p}1,2,3}^{\rm g} $表达式见附录F.
将式(10)、式(11)代入式(4c)得直角坐标系下SH, SV, P1, P2, P3频域波数域中下行波的总应力势函数$\hat{{\bar{{\tilde{{\varPsi }}}}}}_1^d$, $\hat{{\bar{{\tilde{{\varPsi }}}}}}_2^d$, $\hat{{\bar{{\tilde{{\varPsi }}}}}}_3^d$, $\hat{{\bar{{\tilde{{\varPsi }}}}}}_4^d$, $\hat{{\bar{{\tilde{{\varPsi }}}}}}_5^d $表达式, 以及圆柱坐标系下SH, SV, P1, P2, P3频域波数域中外行波的总应力势函数$\hat{{\bar{{\tilde{{\varPsi }}}}}}_{m1}^o$, $\hat{{\bar{{\tilde{{\varPsi }}}}}}_{m2}^o$, $\hat{{\bar{{\tilde{{\varPsi }}}}}}_{m3}^o$, $\hat{{\bar{{\tilde{{\varPsi }}}}}}_{m4}^o$, $\hat{{\bar{{\tilde{{\varPsi }}}}}}_{m5}^o $表达式,分别为
(12a) $ \begin{eqnarray} \label{eq3} &&\left.\begin{array}{l} \hat{{\bar{{\tilde{{\varPsi }}}}}}_1^d =\Big[2k_y k_{{\rm s}x} ,\ k_{{\rm s}x}^2 -k_y^2 ,\ -k_z k_y \Big]\mu {\rm e}^{-{\rm i}k_{{\rm s}x} x} \\ \hat{{\bar{{\tilde{{\varPsi }}}}}}_2^d =\Big[-2{\rm i}k_z k_{{\rm s}x}^2 ,\ 2ik_z k_y k_{{\rm s}x} ,\ -{\rm i}k_{{\rm s}x} (k_y^2 +k_{{\rm s}x}^2 -k_z^2 )\Big]\cdot\\\qquad \mu {\rm e}^{-{\rm i}k_{{\rm s}x} x} \\ \hat{{\bar{{\tilde{{\varPsi }}}}}}_3^d =\Big[-2k_{{\rm p}1x}^2 -(\lambda -E1-E4)k_{{\rm p}1}^2/\mu ,\ 2k_y k_{{\rm p}1x} ,\\\qquad2k_z k_{{\rm p}1x} \Big]\mu {\rm e}^{-{\rm i}k_{{\rm p}1x} x} \\ \hat{{\bar{{\tilde{{\varPsi }}}}}}_4^d =\Big[-2k_{{\rm p}2x}^2 -(\lambda -E2-E5)k_{{\rm p}2}^2/\mu ,\ 2k_y k_{{\rm p}2x} ,\\\qquad2k_z k_{{\rm p}2x} \Big]\mu {\rm e}^{-{\rm i}k_{{\rm p}2x} x} \\ \hat{{\bar{{\tilde{{\varPsi }}}}}}_5^d =\Big[-2k_{{\rm p}3x}^2 -(\lambda -E3-E6)k_{{\rm p}3}^2/\mu ,\ 2k_y k_{{\rm p}3x} ,\\\qquad 2k_z k_{{\rm p}3x} \Big]\mu {\rm e}^{-{\rm i}k_{{\rm p}3x} x} \\ \end{array}\right\} \end{eqnarray} $ (12b) $ \begin{eqnarray} \label{eq12b} \left.\begin{array}{l} \hat{{\tilde{{\varPsi }}}}_{m1}^o =\bigg[\dfrac{2{\rm i}m}{r^2}\Big(k_{{\rm s}r} rH_m^{(1)'} (k_{{\rm s}r} r)-H_m^{(1)} (k_{{\rm s}r} r)\Big),\ \\\\qquad -k_{{\rm s}r} ^2\Big(2H_m^{(1)''} (k_{{\rm s}r} r)+ H_m^{(1)} (k_{{\rm s}r} r)\Big),\ \\\\qquad \dfrac{-mk_z }{r}H_m^{(1)} (k_{{\rm s}r} r)\bigg]\mu {\rm e}^{{\rm i}m\theta } \\\ \hat{{\tilde{{\varPsi }}}}_{m2}^o =\bigg[2{\rm i}k_z k_{{\rm s}r} ^2H_m^{(1)''} (k_{{\rm s}r} r),\ \dfrac{2mk_z }{r^2}\Big(H_m^{(1)} (k_{{\rm s}r} r)-\\\\qquad k_{{\rm s}r} rH_m^{(1)'} (k_{{\rm s}r} r)\Big),\ k_{{\rm s}r} (k_{\rm s}^2 -2k_z ^2)H_m^{(1)'} (k_{{\rm s}r} r)\bigg]\mu {\rm e}^{{\rm i}m\theta } \\\ \hat{{\tilde{{\varPsi }}}}_{m3}^o =\bigg[\Big\{-(\lambda -E1-E4)k_{{\rm p}1}^2 /\mu \Big\}H_m^{(1)} (k_{{\rm p}1r} r)+\\\\qquad2k_{{\rm p}1r}^2 H_m^{(1)''} (k_{{\rm p}1r} r),\ \dfrac{-2{\rm i}m}{r^2}\Big(H_m^{(1)} (k_{{\rm p}1r} r)-\\\\qquad k_{{\rm p}1r} rH_m^{(1)'} (k_{{\rm p}1r} r)\Big),\ 2{\rm i}k_z k_{{\rm p}1r} H_m^{(1)'} (k_{{\rm p}1r} r)\bigg]\mu {\rm e}^{{\rm i}m\theta } \\\ \hat{{\tilde{{\varPsi }}}}_{m4}^o =\bigg[\Big[-(\lambda -E{\rm 2}-E{\rm 5})k_{{\rm p}2}^2 /\mu \Big]H_m^{(1)} (k_{{\rm p}2r} r)+\\\\qquad 2k_{{\rm p}1r}^2 H_m^{(1)''} (k_{{\rm p}2r} r),\ \dfrac{-2{\rm i}m}{r^2}\Big(H_m^{(1)} (k_{{\rm p}2r} r)-\\\\qquad k_{{\rm p}2r} rH_m^{(1)'} (k_{{\rm p}2r} r)\Big),\ 2{\rm i}k_z k_{{\rm p}2r} H_m^{(1)'} (k_{{\rm p}2r} r)\bigg]\mu {\rm e}^{{\rm i}m\theta }\\ \hat{{\tilde{{\varPsi }}}}_{m5}^o =\bigg[\Big[-(\lambda -E{\rm 3}-E{\rm 6})k_{{\rm p}3}^2 /\mu \Big]H_m^{(1)} (k_{{\rm p}3r} r)+\\\\qquad 2k_{{\rm p}1r}^2 H_m^{(1)''} (k_{{\rm p}3r} r),\ \dfrac{-2{\rm i}m}{r^2}\Big(H_m^{(1)} (k_{{\rm p}3r} r)-\\\\qquad k_{{\rm p}3r} rH_m^{(1)'} (k_{{\rm p}3r} r){\rm \Big),\ }2{\rm i}k_z k_{{\rm p}3r} H_m^{(1)'} (k_{{\rm p}3r} r)\bigg]\mu {\rm e}^{{\rm i}m\theta } \\ \end{array}\right\} \\&& \end{eqnarray} $ 式中, $E$1, $E$2, $E$3, $E$4, $E$5, $E$6表达式见附录G.
根据圆柱坐标系与直角坐标系下各类波的位移, 孔压以及应力函数表达式,得位移总场$\hat{{\tilde{{u}}}}$, 孔压总场$\hat{{\tilde{{p}}}}_{\rm l,g}$以及应力总场$\hat{{\tilde{{\tau }}}}$的频域-波数域表达式, 如式(13)所示
(13a) $ \begin{eqnarray} \label{eq5} &&\hat{{\tilde{{u}}}}=\dfrac{1}{2\pi }\displaystyle\int_{-\infty }^\infty {\displaystyle\sum\limits_{j=1}^5 {X_j^z } } \hat{{\bar{{\tilde{{U}}}}}}_j^d {\rm e}^{{\rm i}k_yy}{\rm d}k_y+\displaystyle\sum\limits_{m=-\infty }^\infty {\displaystyle\sum\limits_{j=1}^5 {X_{mj}^c \hat{{\tilde{{U}}}}_{m1}^o } } \end{eqnarray} $ (13b) $ \begin{eqnarray} \hat{{\tilde{{p}}}}_{{\rm ,g}} =\dfrac{1}{2\pi }\int_{-\infty }^\infty {\displaystyle\sum\limits_{j=3}^5 {X_j^z } } \hat{{\bar{{\tilde{{\vartheta }}}}}}_{{\rm ,g }j}^d {\rm e}^{{\rm i}k_yy}{\rm d}k_y\!+\!\displaystyle\sum\limits_{m=-\infty }^\infty {\displaystyle\sum\limits_{j=3}^5 {X_{mj}^c \hat{{\tilde{{\vartheta }}}}_{{\rm ,g }mj}^o } } \end{eqnarray} $ (13c) $ \begin{eqnarray} \hat{{\tilde{{\tau }}}}=\frac{1}{2\pi }\displaystyle\int_{-\infty }^\infty {\displaystyle\sum\limits_{j=1}^5 {X_j^z } } \hat{{\bar{{\tilde{{\varPsi }}}}}}_j^d {\rm e}^{{\rm i}k_yy}{\rm d}k_y+\displaystyle\sum\limits_{m=-\infty }^\infty {\displaystyle\sum\limits_{j=1}^5 {X_{mj}^c \hat{{\tilde{{\varPsi }}}}_{mj}^o } } \end{eqnarray} $ 式中, $X_j^z$ $(j=1$, 2, 3, 4, 5)分别为直角坐标下中SH, SV, P1, P2, P3波势函数的待定系数; $X_{mj}^c$ $(j=1$, 2, 3, 4, 5; $m$数值计算取$-20\sim 20$范围内的整数)为圆柱坐标下中SH, SV, P1, P2, P3波势函数的待定系数.
为满足柱面波与平面波在同一边界条件的耦合求解, 引入Bessel函数与指数函数间的转化关系
[8 ] , 如式(14)所示
(14a) $ H_m^{(1)} (k_r r){\rm e}^{{\rm i}m\theta }=\frac{1}{\pi }\int_{-\infty }^\infty {\frac{{\rm i}^{-m}{\rm e}^{{\rm i}m\beta }}{k_x }} {\rm e}^{{\rm i(}k_x x+k_y y)}{\rm d}k_y $ (14b) $ {\rm e}^{{\rm i(}-k_x x+k_y y)}=\displaystyle\sum\limits_{m=-\infty }^\infty {{\rm i}^{-m}J_m^{(1)} (k_r r){\rm e}^{{\rm i}(m\theta +m\beta )}} $ 式中 $\beta =\arcsin (k_y /k_r )$.
将式(14)代入式(10) $\sim\!$式(12)得柱面波函数与平面波函数间的转化关系, 如式(15)所示
(15) $ \begin{eqnarray} \label{eq15} \left.\begin{array}{l} \left( {{\begin{array}{*{20}c} {\hat{{\tilde{{U}}}}_{mj}^o } \\ {\hat{{\tilde{{\varPsi }}}}_{mj}^o } \\ {\hat{{\tilde{{\vartheta }}}}_{{\rm,g}mj}^o } \\ \end{array} }} \right)=\dfrac{1}{\pi }\displaystyle\int_{-\infty }^\infty {\frac{I_{mj} (k_y ,\omega )}{h_j }} \left( {{\begin{array}{*{20}c} {\hat{{\bar{{\tilde{{U}}}}}}_j^u } \\ {\hat{{\bar{{\tilde{{\varPsi }}}}}}_j^u } \\ {\hat{{\bar{{\tilde{{\vartheta }}}}}}_{{\rm , g}j}^u } \\ \end{array} }} \right){\rm e}^{{\rm i}k_yy}{\rm d}k_y \\[8mm] \left( {{\begin{array}{*{20}c} {\hat{{\bar{{\tilde{{U}}}}}}_j^d } \\ {\hat{{\bar{{\tilde{{\varPsi }}}}}}_j^d } \\ {\hat{{\bar{{\tilde{{\vartheta }}}}}}_{{\rm , g}j}^d } \\ \end{array} }} \right){\rm e}^{{\rm i}k_yy}=\displaystyle\sum\limits_{m=-\infty }^\infty {\left( {{\begin{array}{*{20}c} {\hat{{\tilde{{U}}}}_{mj}^r } \\ {\hat{{\tilde{{\varPsi }}}}_{mj}^r } \\ {\hat{{\tilde{{\vartheta }}}}_{{\rm , g}mj}^r } \\ \end{array} }} \right)I_{mj} (k_y ,\omega )} \\ \end{array}\right\} \end{eqnarray}$ 式中, $I_{mj} (k_y ,\omega )$, $h_j $表达式见附录H.
假定地表应力为0且地表为透水边界, 结合式(13)和式(15), 可得
(16) $ \begin{eqnarray} \label{eq16} \left. {\begin{array}{l} \left( {\displaystyle\sum\limits_{j=1}^5 {\left(X_j^z \hat{{\bar{{\tilde{{\varPsi}}}}}}_j^d +2\dfrac{\hat{{\bar{{\tilde{{\varPsi}}}}}}_j^u }{h_j }\displaystyle\sum\limits_{m=-N}^N {I_{mj} X_{mj}^c } \right)} } \right)_{x=d} =0 \\[6mm] \left( {\displaystyle\sum\limits_{j=3}^5 {\left(X_j^z \hat{{\bar{{\tilde{{\vartheta }}}}}}_{{\rm ,g }j}^d +2\dfrac{\hat{{\bar{{\tilde{{\vartheta }}}}}}_{{\rm ,g }j}^u }{h_j }\displaystyle\sum\limits_{m=-N}^N {I_{mj} X_{mj}^c } \right)} } \right)_{x=d} =0 \\ \end{array}} \right\} \end{eqnarray}$ 由式(16)得
(17) $ \begin{eqnarray} \label{eq17} X_j^z =\displaystyle\sum\limits_{j'=1}^5 {\frac{K_{jj'} }{h_{j'} }} \displaystyle\sum\limits_{m=-N}^N {I_{mj'} X_{mj'}^c } \end{eqnarray}$ 式中, $K_{jj'} $见附录I.
将式(17)代入式(13)得圆柱坐标下总场表达式如下
(18) $ \left. \begin{array}{l} \hat{{\tilde{{u}}}}_m =\left[ \begin{array}{*{20}c} {\hat{{\tilde{{U}}}}_{mz} } \\ {\hat{{\tilde{{U}}}}_{m\theta } } \\ {-\hat{{\tilde{{U}}}}_{mr} } \\ \end{array} \right]=\displaystyle\sum\limits_{j=1}^5 \Bigg(X_{mj}^c \hat{{\tilde{{U}}}}_{mj}^o + \dfrac{1}{2\pi }\int_{-\infty }^\infty I_{mj} (k_y ,\omega )\cdot \\\qquad \hat{{\tilde{{U}}}}_{mj}^r \displaystyle\sum\limits_{j'=1}^5 {\dfrac{K_{jj'} }{h_{j'} }} \displaystyle\sum\limits_{n=-N}^N {I_{nj'} X_{nj'}^c {\rm d}k_y} \Bigg) \\ \hat{{\tilde{{\tau }}}}_m =\left[ \begin{array}{*{20}c} {-\hat{{\tilde{{\varPsi }}}}_{mz} } \\ {-\hat{{\tilde{{\varPsi }}}}_{m\theta } } \\ {\hat{{\tilde{{\varPsi }}}}_{mr} } \\ \end{array} \right]=\displaystyle\sum\limits_{j=1}^5 \Bigg(X_{mj}^c \hat{{\tilde{{\varPsi }}}}_{mj}^o + \dfrac{1}{2\pi }\int_{-\infty }^\infty I_{mj} (k_y ,\omega )\cdot \\\qquad \hat{{\tilde{{\varPsi }}}}_{mj}^r \displaystyle\sum\limits_{j'=1}^5 \dfrac{K_{jj'}}{h_{j'} } \displaystyle\sum\limits_{n=-N}^N I_{nj'} X_{nj'}^c {\rm d}k_y\Bigg) \\ \end{array}\right\} $ \subsection{耦合求解
根据式(1)壳体的平衡方程, 利用隧道与地基土交界面处的位移与应力的连续性条件,可得
(19) $ \begin{eqnarray} \label{eq19} S\left[ {{\begin{array}{*{20}c} {\hat{{\tilde{{U}}}}_{mz}} \\ {\hat{{\tilde{{U}}}}_{m\theta }} \\ {-\hat{{\tilde{{U}}}}_{mr}} \\ \end{array} }} \right]_{r=r_1 } {\rm +}\left[ {{\begin{array}{*{20}c} {-\hat{{\tilde{{\varPsi }}}}_{mz} } \\ {-\hat{{\tilde{{\varPsi }}}}_{m\theta } } \\ {\hat{{\tilde{{\varPsi }}}}_{mr} } \\ \end{array} }} \right]_{r=r_1 } =\left[ {{\begin{array}{*{20}c} {\hat{{\tilde{{q}}}}_{mz} } \\ {\hat{{\tilde{{q}}}}_{m\theta } } \\ {\hat{{\tilde{{q}}}}_{mr} } \\ \end{array} }} \right] \end{eqnarray}$ 假设隧道衬砌不透水, 不透气, 则隧, 土交界面土体孔压和气压的法向导数为0, 即
(20) $ \begin{eqnarray} \label{eq20} \left( {\frac{\partial \hat{{\tilde{{\vartheta }}}}_{\rm l} }{\partial r}} \right)_{r=r_1 } =0{\rm , }\left( {\frac{\partial \hat{{\tilde{{\vartheta }}}}_{\rm g} }{\partial r}} \right)_{r=r_1 } =0 \end{eqnarray}$ 结合式(19)和式(20), 可求解得到待定系数$X_j^z$, $X_{mj}^c $, 将待定系数代入式(13), 即可得到半空间整个场函数. 由于载荷为移动载荷,令$z_{0}=z-v_{0}t$, 则位移和应力分量变成与时间无关的量,即随点载荷一起移动的坐标系($x$, $y$, $z_{0})$下, 该问题成了一个稳态问题
[15 ] .通过双重傅里叶逆变换, 即可得到时域和空间域中系统的动力响应.
2 算法的验证 在本文提出的非饱和地基土-隧道动力响应计算方法中, 若将非饱和地基土参数$S_{r}$, $S_{e}$趋近于1, $A_{\rm s}$趋近于0,则地基土可退化为两相饱和地基土; 若将非饱和地基土参数$S_{r}$趋近于$S_{w0}$, 孔隙率$n_{0}$趋近于0, 则地基土退化为单相弹性地基土
[30 ] . 为验证本文算法的可靠性, 将本文方法的计算结果分别与既有的2.5维有限元-边界元法以及全空间PiP半解析法的计算结果进行对比分析.
2.1 单相弹性地基土 令$S_{r}=0.06$, $n_{0}=0.001$, 将本文计算方法中的地基土体退化为单相弹性地基土, 与既有文献
[31 ,32 ] 中的2.5维有限元-边界元法进行对比, 计算参数参考文献
[31 ] . 固定单位简谐载荷作用于隧道仰拱($x=-2.75$ m, $y=0$ m, $z=0$ m)处, 分别取地表两个观察点($O_{1}$: $x=10$ m, $y=0$ m, $z=0$ m; $O_{2}$: $x=10$ m, $y=20$ m, $z=0$ m)进行对比验证, 土体竖向位移响应随频率的变化曲线如
图2 所示. 可以看到, 本文算法的计算结果与既有单相弹性地基土的2.5维有限元-边界元法的计算结果吻合较好,验证了将非饱和地基土退化为单相弹性地基土时, 本文方法计算结果的可靠性.
2.2 两相饱和地基土 令$S_{r}=0.999$, $A_{\rm s}=0$, 将本文的非饱和地基土退化为两相饱和地基土, 与既有的饱和地基土2.5维有限元-边界元法进行对比, 计算参数参考文献
[20 ] . 计算时移动单位简谐载荷($v_{0}=16.7$ m/s, $f_{0}=20$ Hz)作用于隧道仰拱($x=-2.75$ m, $y=0$ m, $z_{0}=z-v_{0}t=0$ m)处.
图3 给出了隧道底部土体位移与孔压幅值沿隧道轴向的分布. 从
图3 可以看到, 本文方法的计算结果与既有的饱和土2.5维有限元-边界元法的计算结果吻合较好, 验证了将本文计算方法中非饱和地基土退化为两相饱和地基土时,本文方法计算结果的可靠性.
图2 新窗口打开 |
下载原图ZIP |
生成PPT 图2退化后算法的验证(非饱和地基土退化为单相弹性地基土) Fig. 2Verification of the method after the unsaturated soil degenerate into single-phase elastic soil 图3 新窗口打开 |
下载原图ZIP |
生成PPT 图3退化后算法的验证(非饱和地基土退化为饱和地基土) Fig. 3Verification of the method after the unsaturated soil degenerate into two-phase saturated soil 2.3 全空间非饱和地基土 进一步验证本文提出的非饱和半空间地基土-隧道系统动力响应计算方法的可靠性. 由于既有文献中未见关于非饱和半空间地基土-隧道系统动力响应的研究, 为此, 选取既有的非饱和全空间地基土的PiP半解析法
[29 ] 进行对比验证.分别选取隧道中心线距离地表竖直距离$d=25$ m与$d=5$ m时进行计算和对比分析, 隧道半径$r_{1}=3$ m, 隧道衬砌厚度$h=0.25$ m. 隧道衬砌为混凝土材料, 其杨氏模量$E_{t}=50$ GPa, 泊松比$\upsilon_{t}=0.3$, 密度$\rho_{t}=2500$ kg/m$^{3}$, 材料阻尼为$\beta_{t}=0.03$. 非饱和土的参数参考文献
[23 , 33 ] . 计算移动单位简谐载荷($v_{0}=16.7$ m/s, $f_{0}=20$ Hz)作用于隧道仰拱($x=-2.75$ m, $y=0$ m, $z_{0}=0$ m)处时, 隧道底部土体的动力响应, 结果如
图4 所示. 由
图4 可以发现, 本文方法计算的隧道底部土体的动力响应与全空间PiP半解析法的计算结果基本吻合,验证了本文计算方法的可靠性.
图4 新窗口打开 |
下载原图ZIP |
生成PPT 图4非饱和地基土对比验证 Fig. 4Verification by comparison with the results obtained by existing tunnel model 3 算例分析 基于本文提出的算法,重点研究固定简谐载荷作用下饱和度对地基土-隧道系统动力响应的影响.圆形隧道衬砌和非饱和地基土计算参数如
表1 所示, 其中,隧道衬砌计算参数参考文献
[33 ] 中上海地铁参数,非饱和地基土参考文献
[23 ] 给出的砂土参数, 如
表1 所示.
图5 给出了固定简谐载荷作用于隧道仰拱($x=-2.75$ m, $y=0$ m,$z_{0}=z-v_{0}t=0$ m)处时, 不同位置处($O_{1}$, $O_{2}$, $O_{3}$, $O_{4})$土体竖向位移幅值随激振频率$f_{0}$的变化曲线,计算时考虑了不同的饱和度($S_{r}=1$, 0.9, 0.7, 0.5). 由
图5 可以看到,在相同的激振频率但不同的饱和度下, 土体竖向位移幅值存在差异,这是由于饱和度的改变一方面会引起土体有效应力的改变,另一方面会引起土体动剪切模量的变化,两者共同作用使得不同饱和度状态下土体位移幅值存在差异.
Table 1 表1 表1 隧道衬砌和非饱和土计算参数
Table 1
Calculation parameters of tunnel lining and unsaturated foundation soil 新窗口打开 |
下载CSV 图5 新窗口打开 |
下载原图ZIP |
生成PPT 图5不同地表观测点位移频响曲线 Fig. 5Frequency response curves of soil displacement of different observation points on ground surface 从
图5 中还可以看到, 土体竖向位移随载荷激振频率的变化曲线呈现出明显的震荡现象,这主要是由于地表瑞雷面波和横, 纵波的干涉效应所致
[6 ] .同时在不同饱和度下, 竖向位移频响曲线极值点出现位置的不同.根据Forrest等
[6 ] 的研究,频响曲线极值点出现的位置与土体中波的传播速度存在相关性.而从非饱和土控制方程求解中可得, 弹性波波速表达式$c=\omega /Re(k)$中$k$值与饱和度存在关联.因此, 土体饱和度的变化会引起频响函数极值点位置的改变.
图6 为不同饱和度下隧道下方观测点$O_{3}$和$O_{4}$处土体超孔隙水压力的频响曲线. 由
图6 可以看到, 饱和度越小,土体超孔隙水压力越小. 此外, 还可以看到, 当饱和度从1.0变为0.9时,超孔隙水压力下降幅度大, 其原因在于当土体饱和度接近1时,气体以闭气泡形式存在于液体中, 由于气体的体积模量远小于液体的体积模量,因此随着气体的含量的增大, 等效孔隙流体的体积模量迅速下降,使得等效孔隙流体分担的力减小, 造成超孔隙水压力迅速下降. 综合
图5 和
图6 可知,饱和度对系统动力响应存在较大影响, 对于非饱和地基土,计算隧道动力响应时应考虑饱和度的影响.
图6 新窗口打开 |
下载原图ZIP |
生成PPT 图6不同观测点超孔隙水压力频响曲线 Fig. 6Frequency response curves of pore water pressure at different observation points 4 结论 (1)本文提出了非饱和土-隧道系统动力响应计算的波函数法. 该方法的计算结果与既有的2.5维有限元-边界元法以及全空间PiP半解析法的计算结果均吻合较好, 验证了本文计算方法的可靠性.
(2)算例分析结果表明, 饱和度对土体位移与超孔隙水压力的幅值有较大影响. 因此, 对于非饱和地层中的隧道系统, 计算其系统动力响应时, 将土体视为三相介质而非单相介质或两相介质是有必要的.
(3)本文算法中的三相介质(非饱和地基土)可退化为两相介质(饱和地基土)或单相介质(弹性地基土). 通过参数退化, 结合位移应力协调以及渗流连续等条件,该方法可进一步发展为单相弹性地基土, 饱和地基土, 非饱和地基土并存条件下分层地基土-隧道系统动力计算方法.
附录 附录A \begin{eqnarray*} && S=\frac{-r_1 (1-\upsilon^2 )}{Eh}\left[ {{\begin{array}{*{20}c} {s_{11} } & {s_{12} } & {s_{13} } {s_{21} } & {s_{22} } & {s_{23} } \\ {s_{31} } & {s_{32} } & {s_{33} } \\ \end{array} }} \right] \\ &&s_{11} =\frac{\rho _t r_1 (1-\upsilon ^2)}{E}\omega ^2-r_1 \xi ^2-\frac{(1-\upsilon )}{2r_1 }\left(1+\frac{h^2}{12r_1^2 }\right)m^2\\ &&s_{12} =-\frac{(1+\upsilon )}{2}\xi m\\ &&s_{13} =-\upsilon {\rm i}\xi +\frac{h^2}{12}({\rm i}\xi )^3+\frac{h^2}{12r_1^2 }\frac{(1-\upsilon )}{2}{\rm i}\xi m^2\\ &&s_{21} =-\frac{(1+\upsilon )}{2}\xi m\\ &&s_{22} =\frac{\rho _t r{ }_1(1-\upsilon ^2)}{E}\omega ^2-\frac{r_1 (1-\upsilon )}{2}\left(1+\frac{h^2}{4r_1^2 }\right)\xi ^2-\frac{1}{r_1}m^2 \\ &&s_{23} =-\frac{\rm i}{r_1}m-{\rm i}\frac{h^2}{12}\frac{(3-\upsilon )}{2r_1 }\xi ^2m,\\ &&s_{31} =\upsilon {\rm i}\xi -\frac{h^2}{12}({\rm i}\xi )^3-\frac{h^2}{12r_1^2 }\frac{(1-\upsilon )}{2}{\rm i}\xi m^2 \\ &&s_{32} =\frac{{\rm i}}{r_1 }m+{\rm i}\frac{h^2}{12}\frac{(3-\upsilon )}{2r_1 }\xi ^2m \\ &&s_{33} =\frac{\rho _t r_1 (1-\upsilon ^2)}{E}\omega ^2-\frac{h^2}{12}\left(r_1 \xi ^4+\frac{2}{r_1 }\xi ^2m^2+\frac{1}{r_1^3 }m^4\right)- \\&&\qquad\frac{1}{r_1 }+\frac{h^2}{12r_1^3 }(2m^2-1) \\ &&\hat{{\tilde{{q}}}}_{mz} =0,\ \hat{{\tilde{{q}}}}_{m\theta } =0,\ \hat{{\tilde{{q}}}}_{mr} =\frac{1}{r_1 }\delta (\omega -2\pi f_0 +k_z v_0 ){\rm e}^{-{\rm i}m\pi } \end{eqnarray*}
其中, $\xi$为壳$z$方向波数; $h$为壳的厚度; $E$为壳体杨氏模量; $\nu$为壳体泊松比;$\rho_{t}$为壳体密度; $q_{r}$, $q_{\theta }$, $q_{z}$分别为衬砌壳中心面沿$r$, $\theta$,$z$向的净应力; $f_{0}$为激振频率.
附录B \begin{eqnarray*} && a_{11} =\frac{c_1 A_{22}}{A_{11} A_{22} -A_{12} A_{21} },\ \ a_{12} =\frac{A_{22} A_{13} -A_{12} A_{23} }{A_{11} A_{22} -A_{12} A_{21} }\\ && a_{13} =\frac{A_{22} A_{14} -A_{12} A_{24} }{A_{11} A_{22} -A_{12} A_{21} },\ \ a_{21} =-\frac{c_1 A_{21} }{A_{11} A_{22} -A_{12} A_{21} }\\ && a_{22} =\frac{A_{11} A_{23} -A_{21} A_{13} }{A_{11} A_{22} -A_{12} A_{21} },\ \ a_{23} =\frac{A_{11} A_{24} -A_{21} A_{14} }{A_{11} A_{22} -A_{12} A_{21} } \\ && A_{11} =\frac{c_2 \gamma -n_0 S_r }{K_{\rm s} }+\frac{n_0 S_r }{K_{\rm l} }\\&&A_{12} =\frac{c_2 \left(1-\gamma \right)-n_0 \left(1-S_r \right)}{K_{\rm s} }+\frac{n_0 \left(1-S_r \right)}{K_{\rm g} }\\ && A_{13} =n_0 S_r ,\ \ A_{14} =n_0 \left(1-S_r \right),\ \ A_{21} =A_s -\frac{S_r \left(1-S_r \right)}{K_{\rm l} }\\ && A_{22} =\frac{S_r \left(1-S_r \right)}{K_{\rm g} }-A_s\ \ A_{23} =-A_{24} =-S_r \left(1-S_r \right) \\ && c_1 =1-n_0 -\frac{K_{\rm b} }{K_{\rm s} },\ \ c_2 =1-\frac{K_{\rm b} }{K_{\rm s} }\\&&A_s =-\alpha _1 \alpha _2 \alpha _3 \left(1-S_{w0} \right)\left(S_e \right)^{\frac{\alpha _2 +1}{\alpha _2 }}\left[\left(S_e \right)^{-\frac{1}{\alpha _2 }}-1\right]^{\frac{\alpha _3 -1}{\alpha _3 }} \\ && K_{\rm b} =\lambda +\frac{2}{3}\mu ,\ \ S_e =\frac{S_r -S_{w0} }{1-S_{w0} }\\&&\mu =\mu _s +\frac{2050}{\alpha }\ln \left(\sqrt {Se^{-2}-1} +Se^{-1}\right)\tan \varphi\\&& \lambda =\frac{2\upsilon _s \mu }{1-2\upsilon _s } \end{eqnarray*}
其中, $S_{w0} $为液体的约束饱和度; $\alpha_{1}$, $\alpha_{2}$, $\alpha_{3}$分别为拟合参数, $\upsilon_{\rm s} $为土体泊松比; $\varphi $土饱和时的内摩擦角; $\mu_{\rm s}$分别为土体饱和状态下的动剪切模量.
附录C \begin{eqnarray*} &&\lambda _c =\lambda +c_2 \gamma b_{11} +c_2 \left(1-\gamma \right)b_{21}\\&& M=c_2 \gamma b_{12} +c_2 \left(1-\gamma \right)b_{22} \\&& N=c_2 \gamma b_{13} +c_2 \left(1-\gamma \right)b_{23} ,\ \ b_{11} =\frac{c_2 A_{22} }{A_{11} A_{22} -A_{12} A_{21} }\\&&b_{12} =\frac{1}{n_0 S_r}a_{12},\ \ b_{13} =\frac{1}{n_0(1-S_r)}a_{13}\\&&b_{21} =-\frac{c_2 A_{21} }{A_{11} A_{22} -A_{12} A_{21} },\ \ b_{22} =\frac{1}{n_0 S_r}a_{22}\\&&b_{23} =\frac{1}{n_0(1-S_r)}a_{23},\ \ \vartheta _{\rm l} =\frac{\rho _{\rm l} }{n_0 S_r}\\&&\vartheta _{\rm g} =\frac{\rho _{\rm g} }{n_0 \left(1-S_r \right)},\ \ d_{\rm l} =\frac{\eta _{\rm l} }{k_{{\rm rl}} \kappa },\ \ d_{\rm g} =\frac{\eta _{\rm g} }{k_{{\rm rg}} \kappa }\\ && k_{{\rm rl}} =\sqrt {S_e } \left\{ {1-[1-\left(S_e \right)^{1/\alpha _2 }]^{\alpha _2 }} \right\}^2\\&&k_{{\rm rg}} =\sqrt {1-S_e } [1-\left(S_e \right)^{1/\alpha _2 }]^{2\alpha _2 } \end{eqnarray*}
附录D \begin{eqnarray*} &&D_1 =\lambda _c +2\mu ,D_2 =M,D_3 =N,D_4 =b_{11} ,D_5 =b_{12}\\ && D_6 =b_{13}, D_7 =b_{21}, D_8 =b_{22} ,D_9 =b_{23} ,C_1 =\omega ^2\rho\\ &&C_2 =\omega ^2\rho _{\rm l}, C_3 =\omega ^2\rho _{\rm g}, C_4 =\omega ^2\rho _{\rm l}, C_5 =\omega ^2\vartheta _1 -{\rm i}\omega d_{\rm l}\\&&C_6 =0,C_7 =\omega ^2\rho _{\rm g}, C_8 =0,C_9 =\omega ^2\vartheta _{\rm g} -{\rm i}\omega d_{\rm g}\\ && Ba=D_1 D_5 D_9 +D_2 D_6 D_7 +D_3 D_4 D_8 -(D_3 D_5 D_7 +\\ &&\qquad D_1 D_6 D_8 +D_2 D_4 D_9 )\\ && Bb=D_1 D_5 C_9 +D_1 D_9 C_5 +D_5 D_9 C_1 +D_2 D_6 C_7 +\\ &&\qquad D_2 D_7 C_6 + D_6 D_7 C_2 + D_3 D_4 C_8 +D_3 D_8 C_4 +\\ &&\qquad D_4 D_8 C_3 -(D_3 D_5 C_7 + D_3 D_7 C_5 +D_5 D_7 C_3 +\\ &&\qquad D_1 D_6 C_8 +D_1 D_8 C_6 +D_6 D_8 C_1 + D_2 D_4 C_9 +\\ &&\qquad D_2 D_9 C_4 +D_4 D_9 C_2 ) \\ && Bc=D_1 C_5 C_9 +D_5 C_1 C_9 +D_9 C_1 C_5 +D_2 C_6 C_7 +\\ &&\qquad D_6 C_2 C_7 + D_7 C_2 C_6 + D_3 C_4 C_8 +D_4 C_3 C_8 +\\ &&\qquad D_8 C_3 C_4 -(D_3 C_5 C_7 + D_5 C_3 C_7 + D_7 C_3 C_5 +\\ &&\qquad D_1 C_6 C_8 +D_6 C_1 C_8 +D_8 C_1 C_6 + D_2 C_4 C_9 +\\ &&\qquad D_4 C_2 C_9 +D_9 C_2 C_4 ) \\ && Bd=C_1 C_5 C_9 +C_2 C_6 C_7 +C_3 C_4 C_8 -(C_3 C_5 C_7 +\\ &&\qquad C_1 C_6 C_8 + C_2 C_4 C_9 ) \\ && Be=\frac{C_1 C_5 C_9 -C_3 C_5 C_7 -C_2 C_4 C_9 }{\mu C_5 C_9 } \end{eqnarray*}
附录E \begin{eqnarray*} && Bx1=D1\ast \left(-1\ast k_{{\rm p}1}^2 \right)+C1, Bx2=D2\ast \left(-1\ast k_{{\rm p}1}^2 \right)+C2\\ && Bx3=D3\ast \left(-1\ast k_{{\rm p}1}^2 \right)+C3, Bx4=D4\ast \left(-1\ast k_{{\rm p}1}^2 \right)+C4 \\ && Bx5=D5\ast \left(-1\ast k_{{\rm p}1}^2 \right)+C5, Bx6=D6\ast \left(-1\ast k_{{\rm p}1}^2 \right)+C6 \\ && By1=D1\ast \left(-1\ast k_{{\rm p}2}^2 \right)+C1, By2=D2\ast \left(-1\ast k_{{\rm p}2}^2 \right)+C2 \\ && By3=D3\ast \left(-1\ast k_{{\rm p}2}^2 \right)+C3, By4=D4\ast \left(-1\ast k_{{\rm p}2}^2 \right)+C4 \\ && By5=D5\ast \left(-1\ast k_{{\rm p}2}^2 \right)+C5, By6=D6\ast \left(-1\ast k_{{\rm p}2}^2 \right)+C6 \\ && Bz1=D1\ast \left(-1\ast k_{{\rm p}3}^2 \right)+C1, Bz2=D2\ast \left(-1\ast k_{{\rm p}3}^2 \right)+C2 \\ && Bz3=D3\ast \left(-1\ast k_{{\rm p}3}^2 \right)+C3, Bz4=D4\ast \left(-1\ast k_{{\rm p}3}^2 \right)+C4 \\ && Bz5=D5\ast \left(-1\ast k_{{\rm p}3}^2 \right)+C5, Bz6=D6\ast \left(-1\ast k_{{\rm p}3}^2 \right)+C6 \\ && \mu_{{\rm 1l}} =\frac{Bx3\ast Bx4-Bx1\ast Bx6}{Bx2\ast Bx6-Bx3\ast Bx5}\\&&\mu_{{\rm 2l}} =\frac{By3\ast By4-By1\ast By6}{By2\ast By6-By3\ast By5}\\ && \mu_{{\rm 3l}} =\frac{Bz3\ast Bz4-Bz1\ast Bz6}{Bz2\ast Bz6-Bz3\ast Bz5}\\&&\mu_{{\rm 1g}} =\frac{Bx2\ast Bx4-Bx1\ast Bx5}{Bx3\ast Bx5-Bx2\ast Bx6} \\ && \mu_{{\rm 2g}} =\frac{By2\ast By4-By1\ast By5}{By3\ast By5-By2\ast By6}\\&&\mu_{{\rm 3g}} =\frac{Bz2\ast Bz4-Bz1\ast Bz5}{Bz3\ast Bz5-Bz2\ast Bz6} \\ && \mu_{{\rm sl}} =-\frac{C4}{C5},\mu_{{\rm sg}} =-\frac{C7}{C9} \end{eqnarray*}
附录F \begin{eqnarray*} && A_{{\rm p}1}^{\rm l} =-(b_{11} +b_{12} \mu_{1{\rm l}} +b_{13}\mu_{1{\rm g}})\\ && A_{{\rm p}2}^{\rm l} =-(b_{11} +b_{12} \mu_{2{\rm l}} +b_{13} \mu_{2{\rm g}}) \\ && A_{{\rm p}3}^{\rm l} =-(b_{11} +b_{12} \mu_{3{\rm l}} +b_{13}\mu_{3{\rm g}})\\ && A_{{\rm p}1}^{\rm g} =-(b_{21} +b_{22} \mu_{1{\rm l}} +b_{23} \mu_{1{\rm g}})\\ && A_{{\rm p}2}^{\rm g} =-(b_{21} +b_{22} \mu_{2{\rm l}} +b_{23}\mu_{2{\rm g}})\\ && A_{{\rm p}3}^{\rm g} =-(b_{21} +b_{22} \mu_{3{\rm l}} +b_{23} {\rm \mu }_{3{\rm g}}) \end{eqnarray*}
附录G \begin{eqnarray*} && E1=-a\gamma \left(b_{11} +b_{12} \mu_{1{\rm l}} +b_{13} \mu_{1{\rm g}} \right),\\ &&E4=-a\left(1-\gamma \right)\left(b_{21} +b_{22} \mu_{1{\rm l}}+b_{23} \mu_{1{\rm g}} \right) \\ && E2=-a\gamma \left(b_{11} +b_{12} \mu_{2{\rm l}} +b_{13} \mu_{2{\rm g}} \right),\\ &&E5=-a\left(1-\gamma \right)\left(b_{21} +b_{22} \mu_{2{\rm l}}+b_{23} \mu_{2{\rm g}} \right) \\ && E3=-a\gamma \left(b_{11} +b_{12} \mu_{3{\rm l}} +b_{13} \mu_{3{\rm g}} \right),\\ &&E6=-a\left(1-\gamma \right)\left(b_{21} +b_{22} \mu_{3{\rm l}}+b_{23} \mu_{3{\rm g}} \right) \end{eqnarray*}
附录H \begin{eqnarray*} &&I_{mj} ={\rm i}^{-m}\cdot\\&&\quad \left\{ {{\begin{array}{*{20}l} {{\rm e}^{{\rm i}m\beta _{\rm s} }}, \\ {{\rm e}^{{\rm i}m\beta _{\rm s} }} , \\ {{\rm e}^{{\rm i}m\beta _{{\rm p}1} }}, \\ {{\rm e}^{{\rm i}m\beta _{{\rm p}2} }}, \\ {{\rm e}^{{\rm i}m\beta _{{\rm p}3} }}, \\ \end{array}}} \right.{\begin{array}{*{20}l} {\beta _s =\arcsin \left(k_y /k_{{\rm s}r} \right)}, \\ {\beta _s =\arcsin \left(k_y /k_{{\rm s}r} \right)}, \\ {\beta _{p1} =\arcsin \left(k_y /k_{{\rm p}1r} \right)} , \\ {\beta _{p2} =\arcsin \left(k_y /k_{{\rm p}2r} \right)}, \\ {\beta _{p3} =\arcsin \left(k_y /k_{{\rm p}3r} \right)} , \\ \end{array} }{\begin{array}{*{20}l} {h_j =k_{{\rm s}x} }, \\ {h_j =k_{{\rm s}x} } , \\ {h_j =k_{{\rm p}1x} } , \\ {h_j =k_{{\rm p}2x} }, \\ {h_j =k_{{\rm p}3x} } , \\ \end{array}}{\begin{array}{*{20}l} {j=1} \\ {j=2} \\ {j=3} \\ {j=4} \\ {j=5} \\ \end{array} } \end{eqnarray*}
附录I \begin{eqnarray*} \left[ {K_{jj'} } \right]=-2\left[ {{\begin{array}{*{20}c} {\hat{{\bar{{\tilde{{\varPsi}}}}}}_1^d } & {\hat{{\bar{{\tilde{{\varPsi}}}}}}_2^d } & {\hat{{\bar{{\tilde{{\varPsi}}}}}}_3^d } & {\hat{{\bar{{\tilde{{\varPsi}}}}}}_4^d } & {\hat{{\bar{{\tilde{{\varPsi}}}}}}_5^d } \\ 0 & 0 & {\hat{{\bar{{\tilde{{\vartheta }}}}}}_{{\rm 3}}^d } & {\hat{{\bar{{\tilde{{\vartheta }}}}}}_{{\rm 4}}^d } & {\hat{{\bar{{\tilde{{\vartheta }}}}}}_{{\rm 5}}^d } \\ 0 & 0 & {\hat{{\bar{{\tilde{{\vartheta }}}}}}_{{\rm g 3}}^d } & {\hat{{\bar{{\tilde{{\vartheta }}}}}}_{{\rm g 4}}^d } & {\hat{{\bar{{\tilde{{\vartheta }}}}}}_{{\rm g 5}}^d } \\ \end{array} }} \right]^{-1}\left[ {{\begin{array}{*{20}c} {\hat{{\bar{{\tilde{{\varPsi}}}}}}_1^u } & {\hat{{\bar{{\tilde{{\varPsi}}}}}}_2^u } & {\hat{{\bar{{\tilde{{\varPsi}}}}}}_3^u } & {\hat{{\bar{{\tilde{{\varPsi}}}}}}_4^u } & {\hat{{\bar{{\tilde{{\varPsi}}}}}}_5^u } \\ 0 & 0 & {\hat{{\bar{{\tilde{{\vartheta }}}}}}_{{\rm 3}}^u } & {\hat{{\bar{{\tilde{{\vartheta }}}}}}_{{\rm 4}}^u } & {\hat{{\bar{{\tilde{{\vartheta }}}}}}_{{\rm 5}}^u } \\ 0 & 0 & {\hat{{\bar{{\tilde{{\vartheta }}}}}}_{{\rm g 3}}^u } & {\hat{{\bar{{\tilde{{\vartheta }}}}}}_{{\rm g 4}}^u } & {\hat{{\bar{{\tilde{{\vartheta }}}}}}_{{\rm g 5}}^u } \\ \end{array} }} \right] \end{eqnarray*}
[1] Lai CG Callerio A Faccioli E et al . Prediction of railway-induced ground vibrations in tunnelsJournal of Vibration and Acoustics , 2005 ,127(5 ):503 -514 [本文引用: 1] [2] Abul-Husn NS Sutak M Milne B et al . Measurement of building foundation and ground-borne vibrations due to surface trains and subwaysEngineering Structures , 2013 ,53(10 ):102 -111 [本文引用: 1] [3] Zhou SH Di HG Xiao JH et al . Differential settlement and induced structural damage in a cut-and-cover subway tunnel in a soft depositJ. Perform Constr Facil , 2016 ,30(5 ):04016028 [4] Huang X Huang HW Zhang J Tunnelling and Underground Space Technology , 2012 ,31:20 -32 [本文引用: 1] [5] Metrikine AV Vrouwenvelder ACWM Journal of Sound and Vibration , 2000 ,234(1 ):43 -66 [本文引用: 1] [6] Forrest JA Hunt HEM Journal of Sound and Vibration , 2006 ,294(4/5 ):678 -705 [本文引用: 4] [7] Yuan ZH Bostr?m A Cai YQ Journal of Sound and Vibration , 2017 ,387:177 -193 [本文引用: 1] [8] He C Zhou SH Guo PJ et al . Three-dimensional analytical model for the dynamic interaction of twin tunnels in a homogeneous half-spaceActa Mech , 2019 ,230:1159 -1179 [本文引用: 2] [9] Thiede R Natke HG Soil Dynamics and Earthquake Engineering V First Int Conf Soil Dyn Earthquake , 1991 : 672 -682 [本文引用: 1] [10] Bian XC Jin WF Jiang HG SCIENCE A ( Applied Physics and Engineering ), 2012 ,13(11 ):870 -876 [本文引用: 1] [11] Sheng X Jones CJC Thompson DJ Mathematical Physical and Engineering Sciences , 2005 ,461:2043 -2070 [本文引用: 1] [12] Degrande G Clouteau D Othman R et al . A numerical model for ground-borne vibrations from underground railway traffic based on a periodic finite element-boundary element formulationJournal of Sound and Vibration , 2006 ,293(3-5 ):645 -666 [本文引用: 1] [13] Hung HH Yang YB Earthquake Engineering and Engineering Vibration , 2010 ,9(3 ):327 -335 [本文引用: 1] [14] 曾晨 , 孙宏磊 , 蔡袁强 等 . 简谐载荷作用下饱和土体中圆形衬砌隧道三维动力响应分析岩土力学 , 2014 ,35(4 ):1147 -1156 [本文引用: 1] ( Zeng Chen Sun Honglei Cai Yuanqinag et al . Analysis of three-dimensional dynamic response of a circular lining tunnel in saturated soil to harmonic loadingRock and Soil Mechanics , 2014 ,35(4 ):1147 -1156 (in Chinese)) [本文引用: 1] [15] Di HG Zhou SH Luo Z et al . A vehicle-track-tunnel-soil model for evaluating the dynamic response of a double-line metro tunnel in a poroelastic half-spaceComputers and Geotechnics , 2018 ,101:245 -363 [本文引用: 3] [16] He C Zhou SH Di HG et al . Analytical method for calculation of ground vibration from a tunnel embedded in a multi-layered half-spaceComputers and Geotechnics , 2018 ,99:149 -164 [本文引用: 2] [17] He C Zhou SH Guo PJ et al . Theoretical modelling of the dynamic interaction between twin tunnels in a multi-layered half-spaceJournal of Sound and Vibration , 2019 ,456:65 -85 [本文引用: 1] [18] 何超 , 周顺华 , 狄宏规 等 . 饱和土-隧道动力响应的2.5维有限元-边界元耦合模型力学学报 , 2017 ,49(1 ):126 -136 [本文引用: 1] ( He Chao Zhou Shunhua Di Honggui et al . A 2.5D coupled FE-BE model for the dynamic interaction between tunnel and saturated soilChinese Journal of Theoretical and Applied Mechanics , 2017 ,49(1 ):126 -136 (in Chinese)) [本文引用: 1] [19] He C Zhou SH Di HG et al . A 2.5-D coupled FE-BE model for the dynamic interaction between saturated soil and longitudinally invariant structuresComputers and Geotechnics , 2017 ,82:211 -222 [20] He C Zhou SH Guo PJ et al . Modelling of ground vibration from tunnels in a poroelastic half-space using a 2.5-D FE-BE formulationTunnelling and Underground Space Technology , 2018 ,82:211 -221 [本文引用: 2] [21] 郭家禄 , 施萍 . 非饱和粘性土的动力特性水利水运工程学报 , 1987 (3 ):85 -91 [本文引用: 1] ( Guo Jialu Shi Ping Hydro-Science and Engineering , 1987 (3 ):85 -91 (in Chinese)) [本文引用: 1] [22] 陈少林 , 赵宇昕 . 一种三维饱和土-基础-结构动力相互作用分析方法力学学报 , 2016 ,48(6 ):1362 -1371 [本文引用: 1] ( Chen Shaolin Zhao Yuxin Chinese Journal of Theoretical and Applied Mechanics , 2016 ,48(6 ):1362 -1371 (in Chinese)) [本文引用: 1] [23] 徐明江 . 非饱和土地基与基础的动力响应研究. [博士论文]广州: 华南理工大学 , 2010 [本文引用: 4] ( Mingjiang Xu Guangzhou: South China University Technology , 2010 (in Chinese)) [本文引用: 4] [24] 高广运 , 姚哨峰 , 孙雨明 等 . 2.5维有限元分析高铁载荷诱发非饱和土地面振动同济大学学报(自然科学版) , 2019 ,47(7 ):957 -966 [本文引用: 1] ( Gao Guangyun Yao Shaofeng Sun Yuming et al . Unsaturated ground vibration induced by high-speed train loads based on 2.5D finite element methodJournal of Tongji University , 2019 ,47(7 ):957 -966 (in Chinese)) [本文引用: 1] [25] 李伟华 , 王文强 . 非饱和土地基振动响应分析振动与冲击 , 2019 ,38(12 ):182 -190 [本文引用: 1] ( Li Weihua Wang Wenqiang Journal of Vibration and Shock , 2019 ,38(12 ):182 -190 (in Chinese)) [本文引用: 1] [26] 郭鹏飞 , 周顺华 , 杨龙才 等 . 考虑横向惯性效应的非饱和土中单桩的竖向动力响应力学学报 , 2017 ,49(2 ):344 -358 [本文引用: 1] ( Guo Pengfei Zhou Shunhua Yang Longcai et al . Analytical solution of the vertical dynamic response of rock-socked pile considering transverse inertial effect in unsaturated soilChinese Journal of Theoretical and Applied Mechanics , 2017 ,49(2 ):113 -127 (in Chinese)) [本文引用: 1] [27] 章敏 , 王星华 , 冯国瑞 . 非饱和土中端承桩水平振动特性研究岩土力学 , 2015 (2 ):409 -422 [本文引用: 1] ( Zhang Min Wang Xinghua Feng Guorui Rock and Soil Mechanics , 2015 (2 ):409 -422 (in Chinese)) [本文引用: 1] [28] 刘洪波 , 刘洁 , 闻敏杰 . 深埋圆形隧洞非饱和土-衬砌结构系统的动力特性振动与冲击 , 2016 ,35(13 ):36 -41 [本文引用: 2] ( Liu Hongbo Liu Jie Wen Minjie Journal of Vibration and Shock , 2016 ,35(13 ):36 -41 (in Chinese)) [本文引用: 2] [29] 狄宏规 , 郭慧吉 , 王炳龙 等 . 非饱和全空间埋置隧道动力响应壳柱法半解析模型同济大学学报 (自然科学版) , 2020 ,48(3 ):1 -7 [本文引用: 3] ( Di Honggui Guo Huiji Wang Binglong et al . A semi-analytical shellcylinder model for calculating the dynamic response of a circular tunnel buried in an unsaturated full-space. Journal of Tongji University (Natural Science , 2020 ,48(3 ):1 -7 (in Chinese)) [本文引用: 3] [30] 章敏 . 非饱和土中桩的动力响应与循环载荷试验研究. [博士论文]长沙: 中南大学 , 2013 [本文引用: 1] ( Zhang Min Changsha: Central South University , 2013 (in Chinese)) [本文引用: 1] [31] He C Zhou SH Guo PJ Construction and Building Materials , 2019 ,223:69 -80 [本文引用: 2] [32] Hussein MFM Fran?ois S Schevenels M et al . The fictitious force method for efficient calculation of vibration from a tunnel embedded in a multi-layered half-space.J. Sound Vib , 2014 ,333:6996 -7018 [本文引用: 1] [33] Di HG Zhou SH He C et al . Three-dimensional multilayer cylindrical tunnel model for calculating train-induced dynamic stress in saturated soilsComputers and Geotechnics , 2016 ,80:333 -345 [本文引用: 2] 
,2), 周顺华, 何超, 张小会同济大学上海市轨道交通结构耐久与系统安全重点实验室, 上海 201804
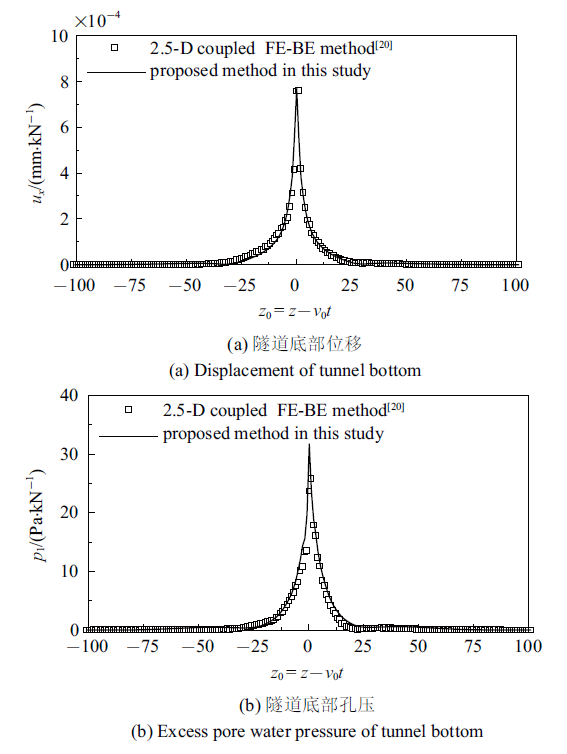新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT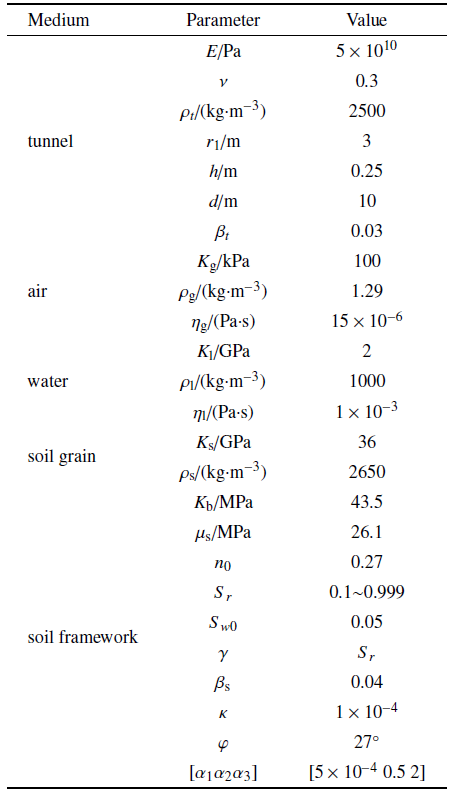
新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT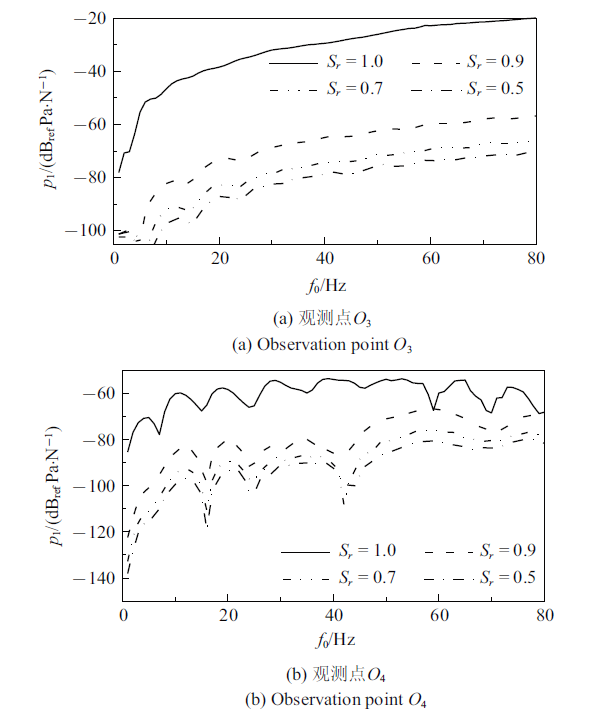
新窗口打开|下载原图ZIP|生成PPT
