,2)南京航空航天大学机械结构力学及控制国家重点实验室, 南京210016RESEARCH ON SPONTANEOUS ACTION POTENTIAL INDUCED BY CHANNEL NOISE IN MORRIS-LECAR SYSTEM 1)
Yang Li, Xianbin Liu,2)State Key Laboratory of Mechanics and Control of Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China通讯作者: 2) 刘先斌, 教授, 主要研究方向: 动力学与控制, 随机分岔, 随机动力学, 随机振动. E-mail:xbliu@nuaa.edu.cn
收稿日期:2019-10-23接受日期:2019-12-7网络出版日期:2020-01-18
| 基金资助: |
Received:2019-10-23Accepted:2019-12-7Online:2020-01-18
作者简介 About authors
摘要
在生物物理学中, 越来越多的现象是由于分段确定性的动力系统与连续时间马氏过程之间的耦合作用而产生的. 因为这种耦合性, 相关的数学模型更适合取为随机混合系统而不是扩散过程(基于It?随机微分方程). 本文从理论上和数值上研究了在弱噪声条件下无鞍点状态的随机混合Morris-Lecar系统中, 由通道噪声诱导的自发性放电现象. 一个动作电位的初始阶段可视为噪声诱导的逃逸事件, 其最优路径和拟势可由辅助Hamilton系统给出. 由于系统不存在鞍点, 因此可选择虚拟分界线(ghost separatrix)为阈值, 研究噪声诱导的自静息态的逃逸事件. 通过计算在阈值处的拟势, 便可发现其值有一个明显的最小值, 其作用类似于鞍点. 通过改进的Monte Carlo模拟方法, 计算了历程概率分布, 其结果对初始阶段和兴奋阶段的理论解均给出了验证. 此外, 基于前人将拟势等高线作为阈值的另一种选择, 我们对两种阈值取法的优劣性进行了比较. 最后, 本文研究了钠离子和钾离子通道噪声的不同组合对最优路径和拟势的影响. 结果表明: 钾离子通道噪声在自发性放电过程中起主导作用, 且两种噪声强度存在一个最优比例能使总的噪声强度达到最小.
关键词：
Abstract
There are a growing number of problems in biological physics involving the coupling between a piecewise deterministic dynamical system and a continuous time Markov process, which is more appropriate to be modeled as a stochastic hybrid system than a diffusion process. Specifically, we investigate the spontaneous action potential induced by channel noise in stochastic hybrid Morris-Lecar system without a saddle state both theoretically and numerically in the case of weak noise. The initiation phase of an action potential can be regarded as an event of noise induced escape, for which the optimal paths and then the quasi-potential are computed via an auxiliary Hamiltonian system. Due to the absence of the saddle point, the ghost separatrix is chosen as threshold for studying the transition events from the resting state. Through evaluating the quasi-potential on the threshold, we have found an obvious minimum that acts similarly as a saddle point. Prehistory probability distribution has been performed by improved Monte Carlo simulation, which confirmed the theoretical results for not only the initial phase but also the excitable phase. In addition, the contour line of quasi-potential as another choice of threshold selected by previous researchers has been introduced and their advantages and disadvantages are compared. Finally, the impacts on patterns of optimal paths and quasi-potential about various combinations of Na$^{+}$ and K$^{+}$ channel noise are studied thoroughly. The results shows that it is the fluctuation of K$^{+}$ channel that plays the dominant role in the process of spontaneous excitability and there exists an optimal ratio for the two channel noises which minimizes the fluctuation strength.
Keywords：
PDF (5354KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
李扬, 刘先斌. Morris-Lecar系统中通道噪声诱导的自发性动作电位研究 1). 力学学报[J], 2020, 52(1): 184-195 DOI:10.6052/0459-1879-19-294
Yang Li, Xianbin Liu.
引言
在生物物理学中, 有越来越多的现象源于分段确定性动力系统和连续时间马氏过程的耦合作用, 其数学模型为随机混合系统(stochastic hybrid system). 例如遗传开关现象[1-2], 电力驱动的细胞内运输[3-4], 随机神经元网络[5-9]和随机离子通道等等[10-12]. 此时, 由于连续状态和离散状态之间的耦合特性, 使得混合系统比随机微分方程更难处理. 虽然可以通过采用扩散近似方法得到相应混合系统的扩散过程近似, 但是众所周知, 如果考虑亚稳态动力学行为, 除了在接近分岔极限[13]的特殊情况之外, 该方法通常会产生显著的误差[1,14-15]. 此外, 恰恰是由于开通道数的离散特性, 混合系统比连续系统更符合实际物理模型. 因此, 为了揭示实际模型的内在动力学行为, 直接处理原始的混合系统是必要且本质的.很多混合系统均可表现出可激性(excitability)特征, 此时即便是很小的随机扰动也可能对其动力学行为产生深远的影响, 如自发性动作电位(spontaneous action potential)现象. 一般意义下, 如果偏离静息态的一个小扰动能够导致其电位在返回静息态之前出现一个大的偏差, 即称产生了一个动作电位[16]. 通常, 自发性动作电位可以分为两个阶段: 初始阶段和兴奋阶段. 初始阶段是指系统在噪声驱动下从静息态到运动到某个阈值(threshold)的过程, 因此可视为噪声诱导的离出(exit)事件或逃逸事件. 这个阶段, 由于噪声强度较弱, 将花费相当长的时间. 一旦达到阈值, 系统将沿着确定性流演化, 直至返回静息态,此为兴奋阶段. 与前者相比, 兴奋阶段是暂态的, 其运动轨迹仅受确定性动力学运动规律控制. 因此, 只要能够准确刻画初始阶段的离出行为, 便可清晰地描述整个动作电位.
事实上, Freidlin和Wentzell[17]所建立的大偏差理论(large deviation theory)已被广泛应用于分析弱噪声对具有多种极限集——不动点[18-19]、极限环[20-21]和奇怪吸引子[22-23]等系统的长期动力学行为的影响.依据大偏差理论中定义的作用(量)泛函(action functional)的概念, 通过它在任一绝对连续函数处的值能够得到任一随机轨线通过该函数附近时其难易程度的量度. 根据自吸引子出发所有路径集合上作用泛函的驻值, 便可以确定最优的离出路径,即系统以最大的概率沿着该路径移动.
基于大偏差理论, 人们对噪声诱导的逃逸问题进行了大量的研究, 但主要结果限于阈值具有明确定义的情况, 一般为系统鞍点的稳定流形, 此时最优路径则为连接吸引子和鞍点的异宿轨道[24]. 然而遗憾的是, 很多系统在相空间中并没有鞍点. 因此为了研究这些离出问题, 必须定义合适的阈值. 近期, Chen等[25]和Khovanov等[26]通过选择虚拟分界线作为FitzHugh-Nagumo系统的阈值, 描述了其离出方案和有限噪声效应. Carson等[27]研究了通道涨落引起的Hodgkin-Huxley模型的放电事件, 并通过一维郎之万(Langevin)近似计算了其平均放电频率. James等[28]将该模型简化为只保留简单的钠离子通道噪声的模型, 并计算出平均首次离出时间的精确表达式.基于Hodgkin-Huxley模型同时保留钠离子和钾离子通道噪声的另一种简化系统, 此时其相应的确定性模型只有一个稳定的不动点, Brooks等[12]发现了拟环(quasi-cycle)的出现. Newby[11]利用WKB近似方法对同一系统进行了研究,得到了离出路径满足的Hamilton表述. 本文以他们的工作为基础, 重点研究了该模型在自定义阈值下的自发性动作电位, 并讨论了通道数对可激系统动力学行为的影响.
迄今为止, 用于计算拟势的主要方法是WKB近似, 它被广泛应用于研究扩散过程、生灭控制方程和随机混合系统中的逃逸事件. 此外, 本文采用的数值方法包括几何最小作用量法(geometric minimum action method, GMAM)[29]和有序逆风法(ordered upwind method, OUM)[30]. 它们均基于几何作用概念, 即将作用泛函的时间参数化转化为弧长, 从而可将关于无穷时间的积分简化为有限长度的积分. GMAM可用于求解具有固定端点的最优路径和它的作用泛函, 而OUM可用于计算离散化的相空间节点上的拟势.
本文具体组织如下: 第2节介绍了随机混合Morris-Lecar模型, 第3节中给出了极值路径满足的辅助Hamilton系统和改进的混合系统的Monte Carlo模拟算法. 通过定义虚拟分界线为阈值, 第4节研究了系统的自发性放电现象. 在第5节中, 通过改变钠离子和钾离子通道数, 我们详细讨论了不同噪声组合对系统拟势和最优路径的影响. 结论见第6节.
1 随机模型
本文所研究的模型最初由Hodgkin 和Huxley[31]提出并用于描述鱿鱼巨轴突的膜电位, Newby[11]将其简化为只考虑单通道钠离子和钾离子的情形, 出于论文的完整性考虑, 我们简述其模型结构. 首先,膜电位$v$的演化受控于离子电流和外加刺激电流$I_{\rm app} $, 即其中, $n=0,1,2,\cdots ,N$和$m=0,1,2,\cdots ,M$分别表示钠离子和钾离子的开通道数, 函数$f_i (v)=g_i \left( {v_i -v} \right)$, $i=$ Na,K, leak分别决定了钠离子和钾离子电流和漏泄电流. 钠离子和钾离子开闭状态的切换取决于
其中, $a_{\rm Na}(v)=\exp\left[4\left(\gamma _{\rm Na} v+\kappa_{\rm Na} \right) \right]$, $b_{\rm Na} =1$, $a_{\rm K} (v)=\exp\left( \gamma _{\rm K} v+\kappa _{\rm K}\right)$和$b_{\rm K} (v)=\exp\left(-\gamma _{\rm K} v-\kappa _{\rm K}\right)$. 由此可见, 电位$v$的演化受控于方程(1). 在两次相邻跳跃之间, 其值是确定性的, 但会通过影响转移率反过来修正随机的跳跃时间, 因此它们之间是耦合的.
根据耦合过程的马氏性, 其概率密度函数$p$ $(v,m,n,t)$满足下面Chapman-Kolmogorov (CK)方程[9]
其中的算子定义如下
而转移率分别为
假设$\beta _{\rm Na} $和$M$均很大且满足$\varepsilon =\beta _{\rm Na}^{-1}$, $M^{-1}=\varphi \varepsilon $. 此外, 可将$w=m / M$视为第二个状态变量, 在弱噪声极限$\varepsilon \to 0$时, 系统恢复为确定性的Morris-Lecar方程[32]
其中, $x_\infty (v)=\left\{1+\tanh\left[2\left( \gamma_{\rm Na} v+\kappa _{\rm Na}\right)\right]\right\}\big/2$, $w_\infty (v)=\left[1+\tanh\left( \gamma _{\rm K} v+\kappa _{\rm K} \right) \right]\big/2$和$\tau _w (v)=2\big/\beta _{\rm K} \cosh\left(\gamma _{\rm K} v+\kappa _{\rm K} \right)$. $\beta _{\rm K} $和$\beta _{\rm Na}$决定了钾离子和钠离子通道开闭的快慢, 通常有$\beta _{\rm K} \ll \beta _{\rm Na} $, 意味着钠离子通道的开闭远快于钾离子.
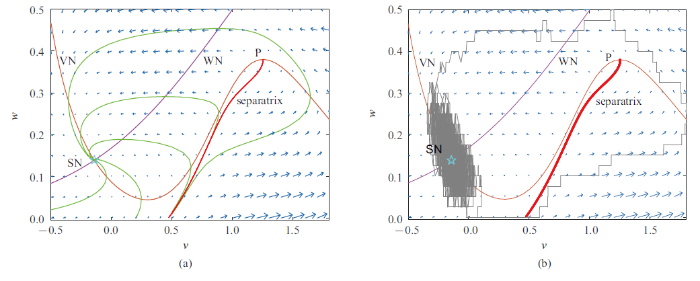
在研究随机模型之前, 需要先考察由方程(6)定义的确定性系统的动力学行为, 方程中的参数见附录. 如图1(a)所示, 棕色和粉红色曲线分别代表$v$零倾线和$w$零倾线, 它们相交于一个全局稳定的平衡点SN, 图中的小箭头指明了向量场的变化趋势.此外依据四阶龙格-库塔法, 图中给出了5条具有代表性的确定性路径, 即图中的绿色曲线. 通过观察, 可以发现, 虽然所有的路径最终都收敛于SN, 但从不同的初始点出发, 它们之间存在着本质上的区别. 其中一些迅速而直接地衰减到SN, 而另外的则先向右移动, 直至到达$v$零倾线的右支, 然后向左转, 这样便产生了一个动作电位. 图中的红色粗体曲线称为虚拟分界线(ghost separatrix)[33], 它是通过$v$零倾线的顶点$P$时间后向积分得到的. 可以看出, 初始点位于此分界线左侧的路径, 运动的振幅较小, 而右侧对应于大振幅运动. 在图1(a)中, 右侧三条路径的初始位置之间的差异仅为0.01, 很难区分, 但在这些路径的中间位置上则出现了宏观上的有限距离. 因此, 这条曲线起到了拟阈值的作用[16].
图 1
新窗口打开|下载原图ZIP|生成PPT图 1向量场、确定性轨线和随机轨线. 棕色和粉红色曲线分别表示$v$零倾线和$w$零倾线, SN为不动点, 绿色曲线是确定性路径, 红色粗体线指代分界线, 小箭头代表向量场的方向. 一条代表性随机轨道表示为灰色锯齿线, 里面包含一次自发性动作电位
Fig. 1Vector field, deterministic and stochastic trajectories. Brown and pink curves indicate the $v$-nullcline and $w$-nullcline respectively. SN denotes the fixed point, the green curves show the deterministic paths, the red bold line suggests the ghost separatrix, and the small arrows represent directions of vector field. A representative stochastic trajectory has been denoted by gray zigzag line, containing a spontaneous action potential
在图1(b)中, 灰色锯齿形曲线是一条具有代表性的表示自发性动作电位的随机路径. 由于SN的吸引性和较弱的噪声强度, 系统将长期在SN附近徘徊. 随后在某个偶然的时刻, 它会跃过阈值, 然后再次沿着确定的路径返回到SN. 这整个过程构成一个自发性动作电位.
2 理论分析与数值模拟方法
2.1 WKB近似
随机混合Morris-Lecar的WKB近似的结果已由Newby导出[11]. 出于论文完整性的考虑, 我们简述其主要结果以便于后面的理论分析及数值计算, 并给出几点重要的评述.在弱噪声条件下, 假设平稳概率密度具有下面近似的形式
这里$C\left( {v,w} \right)$是前因子项, 本文不予讨论. $r\left( {n\vert v,w} \right)$是已知$v,w$后$n$的条件概率分布. $W\left( {v,w} \right)$称为拟势, 它度量了系统在随机激励下抵达相空间中某一位置的困难程度. 将方程(7)代入平稳CK方程并合并所有$\varepsilon$的最高阶项系数得到Hamilton-Jacobi方程
根据特征线法可知, 这一方程的解由一个辅助Hamilton系统生成
通过积分可以得到每条特征线上的拟势, 即
对于WKB近似的形式及结果, 我们认为有必要给出以下三个重要的评述:
首先, 相比于扩散过程, 方程(7)的形式多了一项$r\left( {n\vert v,w} \right)$, 这是因为系统中存在离散变量. 由此, 概率密度的归一化条件不能像扩散过程那样进行直接积分且其积分值等于1, 而必须先对离散变量求和然后再对连续变量进行积分.
其次, 若在方程(9)中令${p}={\bf 0}$, 则辅助Hamilton方程恢复为确定性的Morris-Lecar系统, 这意味着动量${p}$度量了离出的极值路径与确定性流之间的距离. 就是说, 它刻画了噪声在驱动系统离出的过程中所扮演的角色. 因此, 与随机微分系统的情形类似, 可将动量值视为噪声影响的一个指示器.
第三, 作者已严格证明了混合系统一定不满足细致平衡条件的事实[14], 这一结论与扩散过程的相关结论有着本质的区别. 对于混合系统, 离出路径不会出现可以简单地视为确定性流的时间反向的情况. 于是, 尖点和焦散线等奇异性[34]的出现会更为普遍, 这源于由极值路径所追溯的流形出现折叠的特性, 并因此导致拟势的多值性[35].
2.2 Monte Carlo模拟
基于Gillespie算法[36]的Monte Carlo模拟的基本原理是通过计算随机跳跃时间和状态转移来演化样本轨迹. Bressloff[8]和Newby[11]分别描述了他们算法的主要步骤, 并应用于神经网络和Morris-Lecar等模型. 然而, 他们的方法得以实施均有一个前提条件, 即要求方程$\dot{v}=I_{\rm ion}(v,m,n)$对固定的$m$, $n$有显式解, 因此很难推广到更复杂的系统. 在此我们提出一种适用于几乎所有随机混合系统的新算法, 并且此方法能够计算出足够精确的跳跃时间, 从而可以近似到任何期望的精度.为了计算下一次跳跃时间, 我们需要考虑四种可能的转移: $n\to n\pm 1$和$m\to m\pm 1$. 在开通道数的两次相邻跳跃之间, 电位的演化受控于确定性动力学$\dot{v}=I_{\rm ion}(v,m,n)$. 此处求解的主要的困难来源于转移率和电位的耦合关系. 为了解决这个问题, 定义
从而可以得到具有初始条件$v\left( 0 \right)=v_0 $和$G\left( 0\right)=0$的微分方程组
只需要提供时间步长$h$和两个均匀分布随机变量$Y$和$r$, 当下列条件满足时
跳跃时间和电位的估计就可由$\tau \approx kh$和$v\left( \tau \right)\approx v\left( {kh} \right)$给出. 为了确定所发生的转移是4种可能中的哪一种, 变量$a$定义为满足下列不等式的最小整数
其中$a=1,2,3,4$分别对应于以下4种转移行为: $n\to n+1$, $n\to n-1$, $m\to m+1$, $m\to m-1$. 至此可以看出, 通过将函数$F$的积分定义为一个新的变量, 不需要像前人一样解析计算出$v$的表达式, 而是将其转化为一个微分方程组来同时进行数值积分, 因此这一方法是通用的.
3 不同阈值下的自发性动作电位
如前所述, 自发性动作电位可分为两个阶段: 初始阶段和兴奋阶段. 由于噪声强度较弱, 系统将在吸引子附近游荡很长时间, 随后, 它将离开静息态, 并在某个随机时间穿过阈值. 一旦到达阈值, 它将沿着确定性轨迹返回到吸引子. 此时便意味着一个动作电位出现了. 事实上, 初始阶段的本质是: 在给定阈值的条件下, 由噪声诱导的从吸引域中的逃逸事件(离出问题).迄今为止, 我们应该能够意识到阈值的重要性！因为它决定了什么样的动力学行为意味着一次放电. 如果相空间中存在鞍点, 那么其稳定流形自然起到阈值的作用, 最优路径就是连接吸引子和鞍点的路径, 即异宿轨道. 穿过鞍点后, 系统会沿着鞍点的不稳定流形运动.然而遗憾的是, 对于不具有鞍点的系统(如本文中的模型), 很难定义这样一个阈值. 尽管如此, 本文的系统与具有鞍点的系统有很多相同的动力学特征. 为了了解这一事实, 我们需要首先选择一个具有规范定义的阈值来观察初始逃逸事件. 考虑到第2节中关于模型的确定性动力学的分析, 虚拟分界线在自发性动作电位中起着重要作用. 如果系统受噪声的驱动下穿过分界线, 那么系统之后将几乎沿着确定性轨迹绕一个大圈回到不动点, 形成一个电位的尖峰. 从这一点来看, 把此分界线看成阈值是合理的.
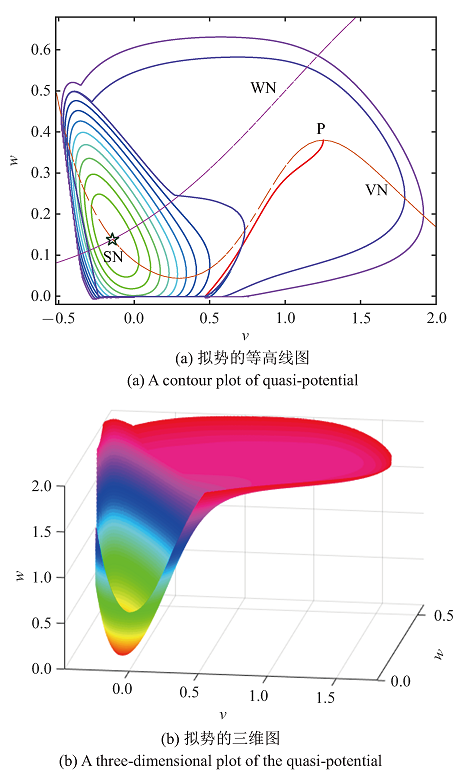
在考察离出路径之前, 我们先来考察系统的拟势. 依据OUM可计算出相关区域的拟势, 其结果由图2所示的等高线和三维图给出. 值得注意的是, 该数值方法是通过从不动点开始逐次更新相邻节点的值来计算规则网格上的拟势, 其结果必然是拟势的全局最小值. 对于此系统, 用$800\times 800$的网格覆盖区域$\left[ {-0.5,1.8} \right]\times \left[ {0,0.6}\right]$足够精确. 图2(b)所示, SN附近存在一个很深的势阱, 在势阱右上方有一个很大的平坦区域, 拟势几乎保持不变, 随后在远处迅速增长. 我们注意到, 图2(a)中在$w=0$处有一个拟势的截痕, 这是因为$w$表示钾离子的开通道数的比例, 不可能是负的.
图 2
新窗口打开|下载原图ZIP|生成PPT图 2利用OUM在$800\times 800$的网格上计算的拟势
Fig. 2Quasi-potential calculated by OUM on a $800\times 800$ grid
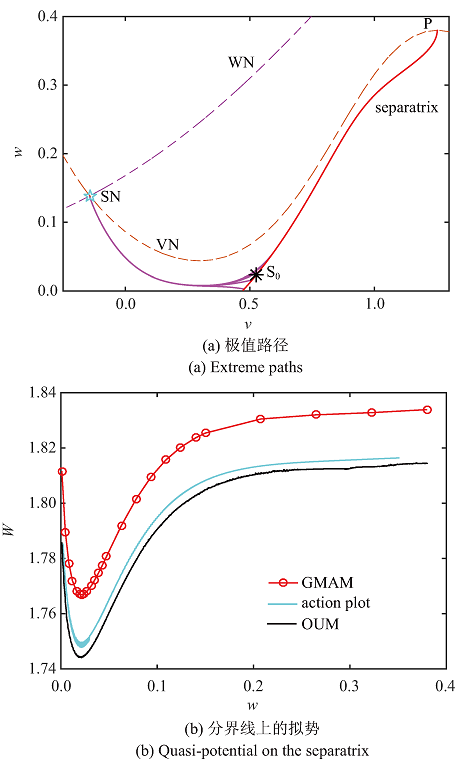
由辅助Hamilton系统(9)的解所刻画的轨迹, 在$t_0 \to -\infty $时起始于SN的条件下, 在四维扩展相空间中张成二维不稳定拉格朗日流形.这些路径在坐标空间上的投影决定了极值路径的模式. 在扩展的相空间中, 由于增加了两个不稳定维度, 原来的稳定不动点转化为鞍点. 为了描述极限路径的模式, 我们使用作用量图(action plot)[23]方法求解辅助Hamilton系统的初值问题. 在二维拉格朗日流形上选取均匀分布于以SN为中心半径为0.001的圆周上的点为初始点, 并且每条极值路径可由初始点的角位置参数化, 与拟势的特征线方程(10)一起积分, 直到阈值后终止. 其中几条具有代表性的极值路径如图3(a)所示, 它们起始时极为接近, 在到达分界线前散开. 当极值路径触碰到分界线时, 该点的拟势值便被记录, 因此我们能够得到分界线上所有点的拟势, 其与$w$的函数关系由图3(b)给出. 此外, 利用插值原理, 前面的OUM方法的结果也可以用于计算阈值处的拟势, 其结果如图3(b)中的黑线所示. 可以看出, 两种方法的结果吻合得相当好.
图 3
新窗口打开|下载原图ZIP|生成PPT图 3选取分界线为阈值
Fig. 3The separatrix chosen as threshold
GMAM是另一种计算拟势的方法. 其主要思想是在两个端点给定的条件下计算连接此两点的最优路径及其上的作用泛函. 我们将一个端点选在SN, 另一个位于分界线, 通过不断改变分界线上的点以计算不同位置的拟势值. 为了提高计算效率, 这一方法的误差会比前两个结果稍大一些, 但仍在可接受范围内. 从图3(b)中可以看出, 分界线上的拟势在$w\approx 0.023$ (对应于左图中的S$_{0}$点)附近存在明显的最小值. 对于双稳态系统, 鞍点一般是边界上拟势的最小值点, 因此离出行为总发生在鞍点. 对于本文的模型, 尽管不存在鞍点, 但是S$_{0}$有着类似于鞍点的 作用.
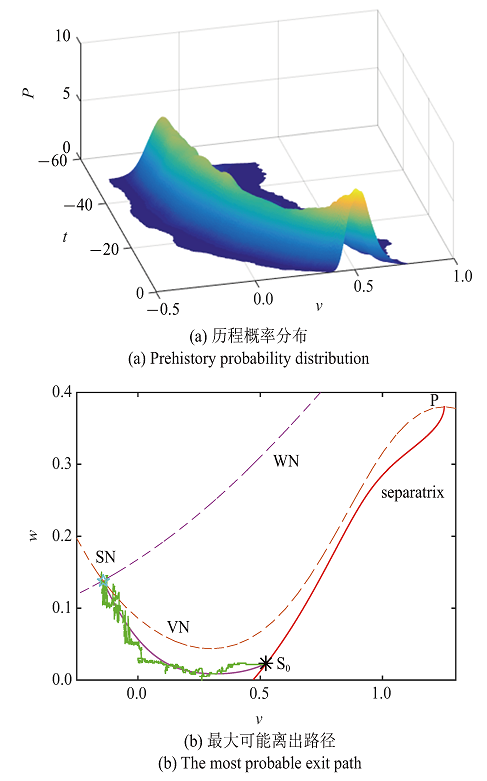
为了验证我们之前的理论结果, 现采用历程概率分布方法模拟涨落路径的分布. 这一概念由Dykman[37]首先提出, 历程概率分布$P_{\rm h} \left( {{x},t\vert {x}_{\rm f} ,t_{\rm f} } \right)$被定义为三时刻转移概率$P_{\rm h} \left( {{x}_{\rm f} ,t_{\rm f}; {x},t\vert {x}_i ,t_i } \right)$与两时刻转移概率$P_{\rm h} \left( {{x}_{\rm f} ,t_{\rm f} \vert {x}_i ,t_i } \right)$之比, 初始时刻$t_i $被设为$-\infty $, 从而$t_i $和${x}_i $均可从表达式中去掉. 这一分布包含了系统到达${x}_{\rm f} $之前关于系统演化的所有信息. 根据大偏差理论, 系统会以压倒性的概率通过最优路径的邻域, 因此历程概率分布将在最优路径附近达到峰值. 为了观察系统的动力学行为, 我们固定终点时间为$t_{\rm f} =0$并向前追溯. 基于第2节中改进的Monte Carlo算法, 可以得到众多从SN出发直至阈值的随机路径. 根据核密度估计, 最终得到历程概率分布的结果如图4(a)所示. 自这些轨迹的样本集合中, 提取每一时刻历程概率分布的最大值位置, 如图4(b)所示, 其结果与GMAM计算的最优路径的理论值吻合得相当好. 此外, 这一结果证实了我们之前的观点, 即离出位置集中在S$_{0}$上.
前面的研究表明, 将自SN出发到分界线的最优路径作为动作电位的初始阶段是合理的. 然而, 为了说明以分界线作为阈值的合理性, 还应该观察系统在越过分界线后是否存在大振幅运动, 并且其结果是否与模拟结果一致. 为了观察系统的放电特性,将离出路径进一步延伸, 允许最优路径触及$v$零倾线的右分支, 看看本文的分析是否成立?
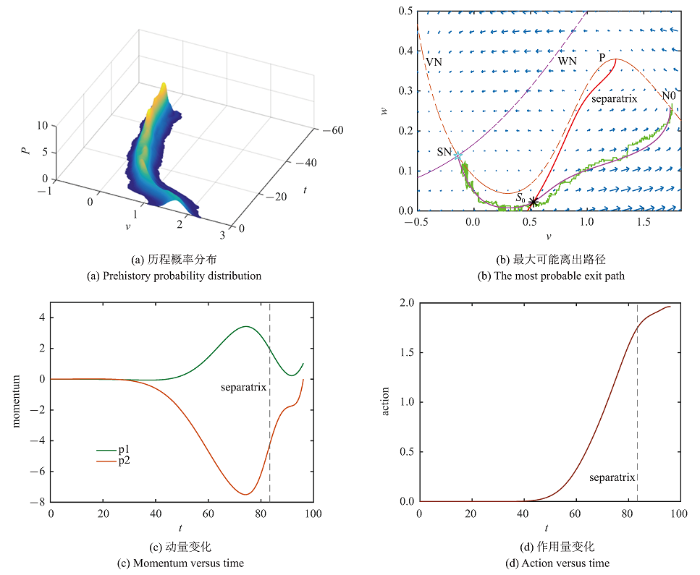
首先, 通过对随机轨道样本进行积分直到$v$零倾线右支, 经统计可得其历程概率分布如图5(a)所示. 提取该分布的峰顶线, 所得结果如图5(b)所示, 曲线在穿过分界线的时候非常接近S$_{0}$. 另一方面, 由GMAM给出的极值路径的理论解自SN开始, 至S$_{0}$结束, 进一步可延伸至$v$零倾线的N$_{0}$点. 从图中可以看出, 理论解与数值模拟结果非常吻合, 这说明将分界线作为阈值不仅对初始阶段是合理的, 对兴奋阶段同样合理. 图5(b)中所示的小箭头表示确定性向量场的方向, 可以看出, 在穿过分界线后, 最优路径与确定性流的方向很接近. 我们换个角度观察动量随时间变化情况, 即图5(c). 可以看出最优路径穿越阈值后, 动量值迅速衰减. 如前所述, 动量本质上是对涨落路径偏离确定性流的程度的度量, 动量的衰减这一现象正说明离出路径接近于确定性轨线这一事实. 此外, 拟势的值源于动量的积分, 而拟势在分界线右边变化缓慢, 这也与OUM的结果一致. 因此, 当系统到达N$_{0}$后, 几乎沿确定性轨迹返回到SN, 发生一次完整的放电现象.
图 4
新窗口打开|下载原图ZIP|生成PPT图 4理论计算与数值结果的最优路径对比
Fig. 4The comparison for the optimal paths between the theoretical and numerical results
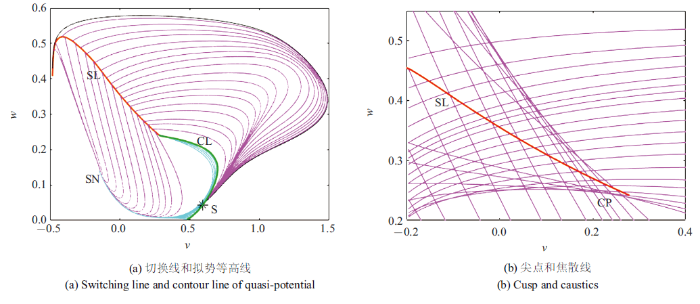
根据图2中拟势的形状可知, 若系统能够跃出势阱, 则其后续运动在平坦区域的能量消耗很小. 因此, Newby选择势阱与平坦区域的接合处作为阈值, 将从势阱中的逃逸视为起始阶段[11]. 其具体操作如下: 首先, 如图6所示, 相空间中存在一个尖点(cusp point, CP), 延伸出两条焦散线(caustics)和一条切换线(switching line, SL). 这一现象的出现是由于拉格朗日流形在扩展相空间中的折叠结构, 使得其在坐标空间上的投影具有多值性[21]. 而拟势取全局最小值, 由此会导致拟势在切换线上的不可微性, 出现一条折痕. 因此, 到达SL两侧两点的最优路径在拓扑上是完全不同的. 于是, 可以选择SL作为阈值的一部分, 另一部分由尖点的拟势等高线(contour line, CL)提供, 分别用粗体的棕色和绿色曲线表示. 可以看出最终进入平坦区域的极值路径在穿过CL时几乎都位于某个S点附近.
图 5
新窗口打开|下载原图ZIP|生成PPT图 5初始阶段和兴奋阶段的最优路径及其动量、作用量
Fig. 5The optimal path as well as the momentum, the action for initial and excitation phase
图 6
新窗口打开|下载原图ZIP|生成PPT图 6另一种阈值选择
Fig. 6Another choice for threshold
在结束这一节之前, 我们比较一下这两种阈值选择的差别. 首先, 以分界线为阈值更多的是关注确定性系统的行为, 而第二种主要考虑的是拟势的结构. 另外, 前者只承认大振幅运动为一次放电现象, 这实际上更符合动力学的观点. 更重要的是, 由于鞍点的拟势在整个边界上取最小值, 使得在弱噪声极限情况下, 最优路径必然会通过鞍点, 因此鞍点状态在逃逸问题中起着至关重要的作用. 但是, 由于选择拟势等高线作为阈值, CL上的每个点具有相同的概率, 这削弱了S的特殊意义. 综合来看, 我们认为将分界线作为阈值更为合理. 最后, 需要强调的是, 这两种选择的平均首次离出时间几乎是相同的, 因为它们都在拟势的平坦区域, 具有几乎相等的拟势.
4 不同噪声组合下的影响
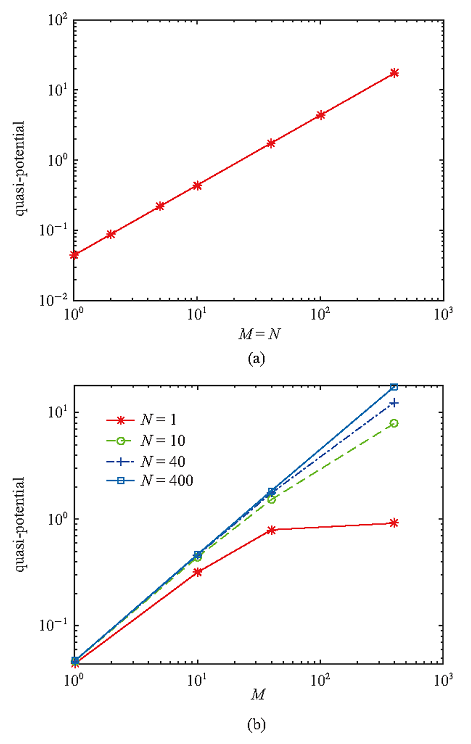
迄今为止, 我们研究了随机混合Morris-Lecar系统对于不同阈值在$M=N=40$的情况下自发性放电现象. 本节, 我们将分析钠离子和钾离子噪声的各种不同组合, 即不同的$M$和$N$的值将如何影响离出方案和拟势形状.首先为探索$M$和$N$量级的影响, 令$M=N$. 可以发现, 当具有不同$M$和$N$值和相同初始点时, 极值路径完全一致. 然而, 当使用GMAM计算分界线上SN到S$_{0}$的最优路径时, 拟势却发生了明显的变化, 如图7(a)所示, 拟势与$M$, $N$的量级呈严格的正比关系. 换句话说, $M$, $N$的量级线性地决定了势阱的深度. 这一事实很好理解, 因为如果$M$和$N$的值很大, 那么由$m$和$n$的加减所带来的变化对$v$的导数影响很小, 于是便导致了更大的逃逸难度.
另一方面, 通过研究$M$和$N$值的不同组合, 以确定何种涨落对整个逃逸过程的贡献更大. 首先观察分界线上的拟势与$M$, $N$的不同组合之间的关系. 将$N$分别取为1, 10, 40, 400, 拟势与$M=1$, 10, 40, 400之间的4条折线关系如图7(b)所示. 可以看出,如果固定$N$, 则拟势将随着$M$的增大而显著增大. 当然, 也存在一个$N=1$时的特殊情况, 即拟势自$M=40$到$M=400$时增大得不明显. 不过, 这一现象也是可以理解的, 若$M$与$N$的比值过大, 钾离子的涨落便会足够小.
图 7
新窗口打开|下载原图ZIP|生成PPT图 7$M$和$N$不同组合下拟势的对比
Fig. 7Comparison for quasi-potential with various combinations of $M$ and $N$
另一个角度, 通过固定$M$我们可以分析钠离子通道噪声对拟势的影响. 若$M=1$, 则当$N$取不同值时, 拟势值几乎无法区分. 此外, 当$M$的值较大时, 在$N<M$的条件下, $N$的增大会导致拟势的明显增长. 然而, 当$N$接近或大于$M$时, 拟势随$N$的增大几乎没有明显的增长. 也就是说, 如果初始时$M=N$, 则增大$M$的贡献远远大于增大$N$的贡献. 因此, 此时控制势阱深度的因素是钾离子通道噪声.
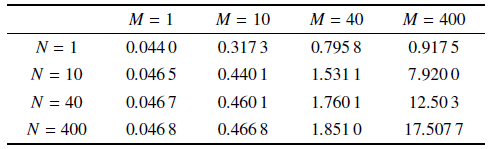
事实上, 根据表1中的数据, 我们从另一个方面也可以发现这些特性. 对角线显示了前文中的线性关系. 此外, 当我们观察另一条对角线就会发现另一个更有趣的性质-$M$和$N$的乘积保持不变而拟势存在明显的最大值, 即, 存在一个能使涨落强度最小的$M$与$N$的最优比例. 我们可以利用这一性质控制噪声强度的大小. 另外可以发现, 在这个最优值的条件下$M$是$N$的数倍, 这也从另一方面证实了钾离子通道噪声的主导作用.
Table 1
表 1
表 1$M$和$N$不同组合下分界线上S$_{0}$的拟势
Table 1
 |
新窗口打开|下载CSV
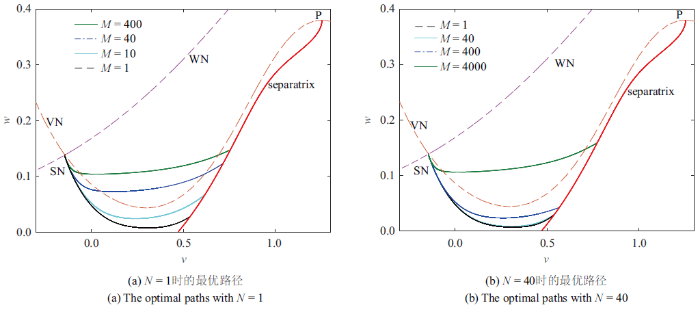
接下来, 通过调整$M$和$N$的相对大小, 我们观察钠离子和钾离子通道噪声如何分别影响离出路径. 对不同的$M$, 将8种情况分为$N=1$和$N=40$两组, 它们的最优路径分别如图8所示. 可以看出, 最优路径的动力学行为由$M$和$N$的比值决定, 与量级无关. 如果$M$远大于$N$, 则最优路径接近水平线. 当$M$大于或者几乎等于$N$时, 最优路径位于$v$零倾线以下. 若初始时$M=N$, 则增大$M$会显著改变最优路径的形状, 而$N$的增大所引起的改变很小. 类似于拟势与通道噪声强度比值的关系, 最优路径也主要取决于钾离子通道噪声. 最后我们指出, 在具有快慢尺度的扩散过程里存在类似的现象, 即调整快慢方向的噪声强度比例可以控制最优路径水平或弯曲. 实际上, 快变方向的噪声较强时, 系统能够直接克服水平势垒从而沿水平方向离出, 而快变方向噪声较弱时无法克服, 因此只能沿着快变方向零倾线离出, 表现为弯曲的最优路径. 在文献[38]中对一相对简单的快慢尺度扩散过程给出了理论解释, 本文研究的模型虽为混合系统, 但仍具有快慢特性, 因此出现了类似的现象.
图 8
新窗口打开|下载原图ZIP|生成PPT图 8$M$和$N$不同组合下最优路径的对比
Fig. 8Comparison for the optimal paths with various combinations of $M$ and $N$
5 结论
本文研究了因为系统缺乏鞍点状态而没有明确阈值的随机混合Morris-Lecar系统的自发性动作电位. 通过定义虚拟分界线为拟阈值, 可以将一次放电行为分解为一个长时间的初始阶段和一个暂态的兴奋阶段. 前者可以看成是噪声诱导的逃逸事件, 而后者则几乎会沿着确定性的路径在大范围运动后回到静息态. 通过三种不同的数值方法, 即GMAM、OUM和作用量图方法, 计算得出阈值上的拟势, 发现结果存在明显的最小值. 由此可以肯定离出位置几乎集中于这个点附近, 因此可以断定该点发挥着类似鞍点的作用. 通过改进的蒙特卡罗方法我们对历程概率分布进行了模拟, 验证了我们前面使用理论方法得到的最优路径和离出位置的结果. 另外, 针对前人所给出的另一种阈值取法, 即切换线和尖点拟势等高线的组合, 我们比较了两种选择的优劣性, 并认为, 从动力学的角度来讲, 前者更具有实际物理意义.最后, 研究表明, $M$, $N$的量级严重影响势阱的深度, 并且它们之间呈现严格的线性关系. 此外, $M$和$N$的不同组合对最优路径的模式和拟势有着显著影响, 钾离子通道噪声在自发性动作电位过程中起主导作用. 研究还发现, 存在一个$M$和$N$的最优比值, 能使涨落强度达到最小.
附录
参数值$v_{\rm Na } =3.7, \ \ g_{\rm Na } =0.22, \ \ v_{\rm K} =-0.9, \ \ g_{\rm K} =0.4, \ \ v_{\rm leak} =-0.36, \ \ g_{\rm leak} =0.1, \ \ \beta _{\rm K} =0.04, \ \ I_{\rm app} =0.06, \ \ \gamma _{\rm Na } =1.22, \ \ \kappa _{\rm Na } =-1.188, \ \ \gamma _{\rm K} =0.8, \ \ \kappa _{\rm K} =-0.8, \ \ M=40, \ \ N=40. $}
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 5]
[本文引用: 2]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
