,2), 律梦泽同济大学土木工程防灾国家重点实验室 土木工程学院,上海 200092A NEW METHOD FOR THE PROBABILITY DENSITY OF MAXIMUM ABSOLUTE VALUE OF A MARKOV PROCESS1)
Chen Jianbing,2), Lü MengzeState Key Laboratory of Disaster Reduction in Civil Engineering & College of Civil Engineering, Tongji University, Shanghai 200092, China通讯作者: 2)陈建兵，教授，主要研究方向：随机动力学、结构非线性分析与工程可靠性. E-mail:chenjb@tongji.edu.cn
收稿日期:2019-04-25网络出版日期:2019-09-18
| 基金资助: |
Received:2019-04-25Online:2019-09-18
作者简介 About authors
摘要
随机过程或随机系统响应的最大绝对值概率分布往往是科学与工程中关心的重要挑战性问题.本文从理论与数值上进行了Markov过程的时变最大绝对值过程及其概率分布研究.文中,通过引入扩展状态向量,构造了最大绝对值$\!$-$\!$-$\!$状态量联合向量过程,由此将不具有Markov性的最大值过程转化为具有Markov性的向量随机过程.在此基础上,通过最大绝对值$\!$-$\!$-$\!$状态量之间的关系,建立了联合向量过程的转移概率密度函数.进而,结合Chapman-Kolmogorov方程和路径积分方法,提出了最大绝对值概率密度函数求解的数值方法.由此,可以得到Markov过程最大绝对值过程的时变概率密度函数,可进一步用于结构动力可靠度分析等.通过数值算例,验证了本文所提方法的有效性. 该方法有望推广到更一般随机系统的极值分布估计之中.
关键词：
Abstract
The probability distribution of maximum absolute value of stochastic processes or responses of stochastic systems is a significant problem in various science and engineering fields. In the present paper, theoretical and numerical studies on the time-variant extreme value process and its probability distribution of Markov process are performed. An augmented vector process is constructed by combining the maximum absolute value process and its underlying Markov process. Thereby, the non-Markov maximum absolute value process is converted to a Markov vector process. The transitional probability density function of the augmented vector process is derived based on the relationship between the maximum absolute process and the underlying state process. Further, by incorporating the Chapman-Kolmogorov equation and the path integral solution method, the numerical methods for the probability density function of the maximum absolute value is proposed. Consequently, the time-variant probability density function of the maximum absolute of a Markov process can be obtained, and can be applied, e.g., to the evaluation of dynamic reliability of engineering structures. Numerical examples are illustrated, demonstrating the effectiveness of the proposed method. The proposed method is potentially to be extended for the estimation of extreme value distribution of more general stochastic systems.
Keywords：
PDF (11863KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
陈建兵, 律梦泽. 一类Markov过程的最大绝对值过程概率密度求解的新方法1). 力学学报[J], 2019, 51(5): 1437-1447 DOI:10.6052/0459-1879-19-104
Chen Jianbing, Lü Mengze.
引言
在科学与工程的诸多领域中,随机过程或系统随机响应的极值分布对把握系统的性态乃至进行系统设计至关重要. 例如,在物理学[1]、生物学[2]、经济学[3]、人口学[4]、地理学[5]及土木工程[6-7]中,人们常常关注的首次超越概率问题,即可转化为极值分布问题进行求解. 因此,很早以来极值分布问题就得到了国内外研究者的关注[8-9],并取得了重要进展. 例如,对于独立随机变量序列与平稳随机序列极值分布的渐进性质,人们已有较为清晰的认识[10];对于平稳窄带过程,其峰的概率分布近似为Rayleigh分布[11]. 然而,对于一般随机过程的极值分布特征及其解析解或数值求解方法,迄今为止依然所知甚少[10].即使对于Markov过程,其极值分布性质及求解方法亦具有高度挑战性. 例如,作为一类最简单的Markov过程,Brown运动过程最大值的概率分布具有半正态分布形式[12-13],但Brown运动的最大绝对值分布精确解则迄今未见报道. 获得极值分布的另一思路是针对某一给定的阈值,施加吸收边界条件,求解其在某一时刻之前未超过这一阈值的剩余概率[14-15]. 对于极少数特殊过程,人们获得了剩余概率解析解[12,16-17]. 但对于更一般的Markov过程,给定阈值下的剩余概率解析解或数值解均十分困难. 而且,在数值求解中,吸收边界条件通常是针对某一确定性阈值,而在大多数实际问题中,阈值可能为随机变量[6],因而需要多次求解,从而带来很大的计算工作量. 近年来,对于更为一般的随机系统响应,基于广义密度演化方程[18-19]的极值分布方法提供了新的途径[20].
事实上,对于Markov过程,求解其时变极值过程的概率密度与求解某一阈值下的剩余概率是等价的. 但是,前者不依赖于阈值的选取. 因此,对于科学与工程实际中的首次超越问题,一旦获得了时变极值过程的概率分布,即可直接通过积分得到系统在确定性或随机阈值下的时变可靠度. 遗憾的是,时变极值过程的概率密度解析解难以获取. 尽管通过Monte Carlo模拟求解Itô随机微分方程可以给出估计[21-24],但为了保证低失效概率时必须的尾部精度,往往需要难以承受的巨大计算工作量.
针对Markov过程,本文提出了一类获取时变最大绝对值过程概率密度的新方法. 事实上,尽管Markov过程的时变最大绝对值过程本身并非Markov过程,但引入状态量可以构造一个具有Markov性的增广向量过程. 进而,结合Chapman-Kolmogorov方程,可实现其联合概率密度的数值求解,由此获得最大绝对值过程的概率密度. 通过典型数值算例分析,验证了本文建议方法的有效性. 该方法有望推广到更一般随机系统的分析之中.
1 最大绝对值过程与最大绝对值-状态量联合向量过程
考虑随机过程$X(t) $,其时变极值过程可定义为其中${\rm ext}\left\{, \cdot ,\right\}$表示取极值. 根据所关心的实际问题,该极值可能是最大值、最小值或最大绝对值等. 显然,从样本特征看,时变极值过程$Z\left( t \right)$是一个单调变化的随机过程.
研究时变极值过程具有重要的工程意义. 例如,在首次超越破坏问题中,若将系统的首次超越破坏考虑为双壁问题[25],则结构可靠度可以表示为
其中,${\rm Pr}\left\{ ,\cdot ,\right\}$表示随机事件发生的概率. 此时,若定义$Z(t) $为$X(t)$的最大绝对值过程,即
则由此可得首次超越破坏问题的可靠度为
其中,$p_Z \left( {z,t} \right)$为$Z(t) $的概率密度,应注意到它是时变的.
遗憾的是,如前所述,对于一般的随机过程,除了极特殊的情况,难以获得其时变极值过程概率密度的解析表达[12,16-17].
事实上,即使$X(t) $为Markov过程,其时变极值过程$Z\left( t\right)$也并非Markov过程. 为了更清楚地说明这一点,考虑具有如下运动方程的随机过程$X(t) $
其中,$f\left( \cdot \right)$与$g\left( \cdot \right)$为确定性函数;$\xi(t) $为Gauss白噪声过程,即$E\left[ {\xi (t) }\right] = 0$, $E\left[ {\xi (t) \xi \left( {t + \tau } \right)}\right] = D\delta \left( \tau \right)$. 这里$E\left( \cdot\right)$为期望算子,$D$为白噪声强度. 式(5)亦可写为Itô随机微分方程的形式
其中$W(t) $为Brown运动过程,满足$E\left[ {d W\left( t \right)} \right] = 0$,$E\left\{ {\left[ {d W(t) }\right]^2} \right\} = Dd t$. 如所周知,由Itô随机微分方程 (6)确定的随机过程$X(t) $是Markov过程[26].
若从时间离散格式考虑这一问题将更为清晰. 在任意时刻$t$,若已知$X\left( t\right)$的信息,则由于$X(t) $的Markov性,对于无穷小的时间增量$\Delta t$,$X\left( {t + \Delta t} \right)$的概率信息可以完全确定. 然而,对于由式(3)给出的最大绝对值过程$Z(t) $,$Z\left( {t + \Delta t} \right)$等于$Z(t) $或$\left| {X\left( {t + \Delta t} \right)} \right|$,即
这意味着同时需要$Z(t) $与$X\left( t\right)$的信息才可以确定$Z\left( {t + \Delta t} \right)$,仅仅知道$Z\left( t\right)$的信息不足以确定$Z\left( {t + \Delta t} \right)$. 因此,随机过程$Z(t) $本身并非Markov过程.
然而,从上述分析可见,若引入最大绝对 值$\!$-$\!$-$\!$状态量联合向量过程$\left( {Z\left( t\right),X(t) } \right)^{\rm T}$,则由式(7)可知, $\left( {Z\left( {t + \Delta t} \right),X\left( {t + \Delta t} \right)} \right)^{\rm T}$的概率信息仅取决于$\left( {Z(t) ,X\left( t \right)} \right)^{\rm T}$, 因此$\left({Z(t) ,X\left( t \right)} \right)^{\rm T}$是一个Markov向量过程.
尽管对于一般系统获取上述联合向量过程的概率密度解析解较为困难,但通过构造上述具有Markov性的联合向量过程,为最大绝对值的概率密度函数的数值求解提供了可能.
2 最大绝对值$\!$-$\!$-$\!$状态量联合向量过程时变概率密度函数的数值求解方法
2.1 一维随机过程的最大绝对值$\!$-$\!$-$\!$状态量联合向量过程
由于最大绝对值$\!$-$\!$-$\!$状态量联合向量过程的Markov性,可以采用多种数值方法求解其联合概率密度函数.例如,基于Chapman-Kolmogorov方程,可以由路径积分通过数值方法求解Markov向量过程$\left( {Z(t) , X(t) }\right)^{\rm T}$的联合概率密度,进而由边缘概率密度积分获得最大绝对值过程$Z(t) $的概率密度函数.由于Markov性,向量过程$\left( {Z(t) ,X(t) }\right)^{\rm T}$的转移概率密度满足Chapman-Kolmogorov方程,即
其中,$t_1 $,$t_{2} $与$t_{3} $是任意三个不同的时刻; $p_{ZX}\left( {z_2 ,x_2 ,t_2 \vert z_1 ,x_1 ,t_1 } \right)$为在$t_1$时刻处于状态$\left( {z_1 ,x_1 } \right)$的条件下$t_{2}$时刻处于状态$\left( {z_2 ,x_2 } \right)$的概率密度,即转移概率密度,其余符号意义类似.
根据式(8),可以通过下式逐步积分求解获得向量过程$\left( {Z\left( t\right),X(t) } \right)^{\rm T}$的联合概率密度
其中,$p_{ZX} \left( {z,x,t} \right)$为向量过程$\left( {Z\left( t\right),X(t) } \right)^{\rm T}$的联合概率密度;$\tau >0$是很小的时间增量. 根据式(1),初始条件为
其中,$\delta \left( \cdot \right)$为Dirac $\delta $函数;$p_X \left( {x,0}\right)$为$X\left( 0 \right)$的概率密度. 如果随机过程$X\left( t\right)$具有确定性初值,例如$X\left( 0 \right) = x_0 $,则$p_X \left( {x,0}\right) = \delta \left( {x - x_0 } \right)$. 因此,若转移概率密度函数$p_{ZX}\left( {z,x,t + \tau \vert {z}',{x}',t}\right)$已知,即可逐步积分求解式(9)以获得$p_{ZX} \left( {z,x,t}\right)$,此即路径积分法的基本思想[27].
一旦得到$p_{ZX} \left( {z,x,t} \right)$,即可进一步获得时变极值过程$Z\left(t \right)$的概率密度
同时,随机过程$X(t) $的概率密度亦可由边缘概率密度积分获得
对于状态量$X(t) $,根据式(6),当时间增量很小时,可采用短时Gauss分布作为转移概率密度$p_X \left( {x,t + \tau \vert {x}',t} \right)$的近似解析表达[28]
另一方面,若考虑$X(t) $的最大绝对值过程$Z\left( t \right)$,对于很小的时间增量$\tau $,在$\left\{ {Z(t) ={z}',X\left( {t + \tau } \right) = x} \right\}$的条件下$Z(t) = z$的概率密度为$p_{Z\vert X} \left( {z,t +\tau ;x\vert {z}',t} \right)$. 那么,根据式(7),将可能存在两种情况：(1) 若${z}' > \left| x \right|$,则有$z ={z}'$;(2) 若${z}' \le qslant \left| x \right|$,则有$z = \left| x \right|$. 因此,我们有
根据全概率定理,向量过程$\left( {Z(t) ,X(t) }\right)^{\rm T}$的转移概率密度$p_{ZX} \left( {z,x,t + \tau \vert{z}',{x}',t} \right)$为
将式(14)代入式(15)有
其中,$u\left( \cdot \right)$为单位阶跃函数;$p_X \left( {x,t + \tau \vert {x}',t}\right)$已由式(13)给出.
2.2 多维随机过程的最大绝对值$\!$-$\!$-$\!$状态量联合向量过程
上述思想可以扩展到多维Markov过程最大绝对值的概率密度求解之中. 不失一般性,考虑一个$n$维Markov向量过程$X(t) = \left( {X_1 (t) , \cdots , X_n (t) }\right)^{\rm T}$. 若所关心的量是其中的第$l$个分量$X_l (t) ,\;l=1,2, \cdots , n$,并记其最大绝对值过程为则与上一节类似,可知$\left( {Z_l (t) ,{\pmb X}^{\rm T}(t) } \right)^{\rm T}$是一个$n + 1$维Markov向量过程.
记向量过程$\left( {Z_l (t) , {\pmb X}^{\rm T}\left( t\right)} \right)^{\rm T}$的转移概率密度为$p_{Z_l { X}} \left( {z_l,{\pmb x},t + \tau \vert {z}'_l ,{\pmb x}', t}\right)$,可将式(14)与式(15)扩展至高维情形,有
其中,$p_{ X} \left( {{\pmb x},t + \tau \vert {\pmb x}',t} \right)$为$n$维Markov过程${\pmb X}\left( t \right)$的转移概率密度.
因此,一旦获得了向量过程$\left( {Z_l (t) ,{\pmb X}^{\rm T}(t) }\right)^{\rm T}$的转移概率密度函数,其联合概率密度即可通过路径积分采用数值方法求解获得,即
其初值为
其中,$p_{ X} \left( {{\pmb x},0} \right)$为${\pmb X}\left(0 \right)$的概率密度. 若$n$维过程${\pmb X}\left( t\right)$具有确定性初值,例如${\pmb X}\left( 0 \right) = {\pmb x}_0$,则$p_{ X} \left( {{\pmb x},0} \right)=\delta ({\pmb x}-{\pmb x}_0)$.
进一步地,可以积分获得最大绝对值过程$Z_l (t) $的概率密度
进而可通过式(4)进行可靠度计算.
对于时变极值过程概率密度的路径积分求解的具体数值实现格式,文献[29,30]中已经进行了详细阐述. 值得指出的是,由于式(16)和式(18)中含有Dirac$\delta $函数,因此,在数值上概率密度函数是稀疏的. 亦即,虽然看起来由于引入了绝对值最大值而使得维数增大了一维,但其稀疏性使得实际数值处理的维度不变. 限于篇幅,这里不再赘述.
3 数值算例
本节将通过几个具体数值算例对上述方法加以说明和验证.3.1 Brown运动过程的最大绝对值
考虑Brown运动过程$W(t) $,即$W\left( 0 \right) = 0$,且对于任意$\tau > 0$,有$W\left( {t + \tau } \right) - W(t) \sim N\left( {0,D\tau } \right)$, $E\left[ {W(t)W\left( {t + \tau } \right)} \right] = Dt$,其中$D$为白噪声强度[26]. Brown运动过程$W\left( t\right)$服从Gauss分布,即
其在任意时间增量$\tau $下的转移概率密度为
记$Z(t) $为$W\left( t \right)$的最大绝对值过程. 根据式(16),最大绝对值$\!$-$\!$-$\!$状态量联合向量过程$\left( {Z(t) ,W(t) } \right)^{\rm T}$的转移概率密度函数为
由此,可以通过式(9)与式(10)对向量过程$\left( {Z(t) ,W\left( t\right)} \right)^{\rm T}$的联合概率密度$p_{ZW} \left( {z,w,t}\right)$进行数值求解,进而获得$Z(t) $的概率密度$p_Z \left( {z,t}\right)$.
在本例中,取白噪声强度$D = 1$,时间步长$\Delta t = 0.02$,求解域为$z \in\left[ {0,15} \right]$,$x \in \left[ { - 15,15}\right]$,网格尺寸$\Delta z = \Delta x = 0.02$. 通过数值求解可得,在$t \in\left[ {4,10} \right]$内$W(t) $与$Z\left( t\right)$的概率密度曲面如图1所示.
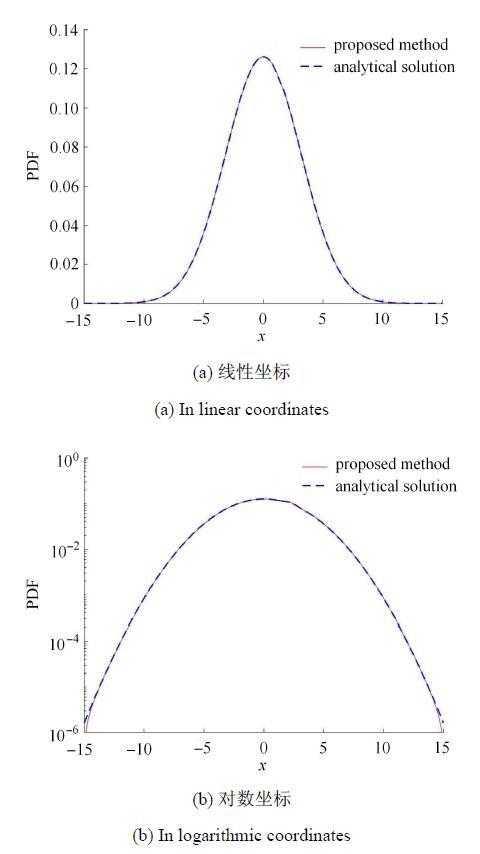
在$t= 10$时刻,$W\left( t \right)$的概率密度数值解与解析解式(22)的对比如图2所示. 从图中可见,二者高度吻合.
图1
新窗口打开|下载原图ZIP|生成PPT图1Brown运动过程$W(t) $及其最大绝对值过程$Z\left( t \right)$的概率密度曲面
Fig. 1The PDF surfaces of $W(t) $and $Z(t) $of the Brownian motion process
图2
新窗口打开|下载原图ZIP|生成PPT图2Brown运动过程$W(t) $的概率密度数值结果与解析解的对比
Fig. 2The comparison between the numerical and analytical solution of PDF of Brownian motion process $W(t) $
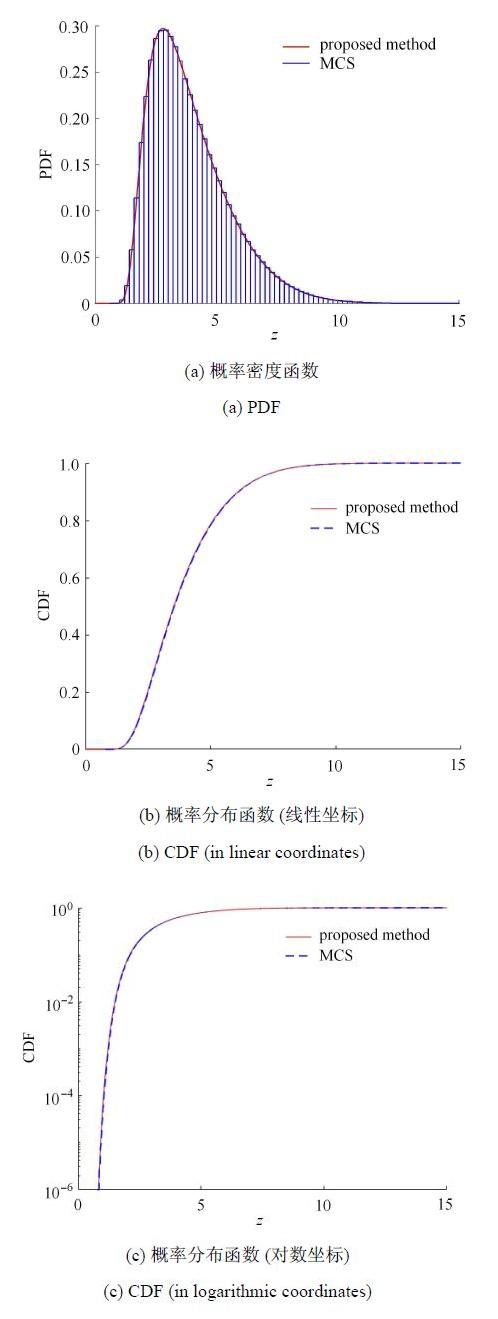
另一方面,尽管Brown运动最大值的概率密度函数解析解已知为半正态形式分布[13],但其最大绝对值过程$Z\left(t \right)$的概率密度解析解迄今未知. 因此,将本文方法获得的结果与Monte Carlo模拟(MCS)获得的概率密度函数(PDF)与概率分布函数(CDF)进行比较. 取随机抽样次数10$^{6}$次,结果如图3所示. 从图中可见,本文建议方法具有很高的精度.
图3
新窗口打开|下载原图ZIP|生成PPT图3采用本文方法获得的Brown运动的最大绝对值过程$Z\left( t \right)$的概率密度与概率分布与Monte Carlo结果的对比
Fig. 3The comparison between the proposed method and MCS for the PDF and CDF of $Z(t) $of Brownian motion process
从图中可见,本文方法的数值结果与10$^{6}$次Monte Carlo模拟的结果吻合很好. 在MonteCarlo模拟尾部考虑30%变异系数的情况下(此时,Monte Carlo模拟结果尾部误差为模拟次数倒数即$1 / 0.3^2 \approx10$倍),可以认为本文建议的方法可以达到10$^{ - 5}$或更高的计算精度.
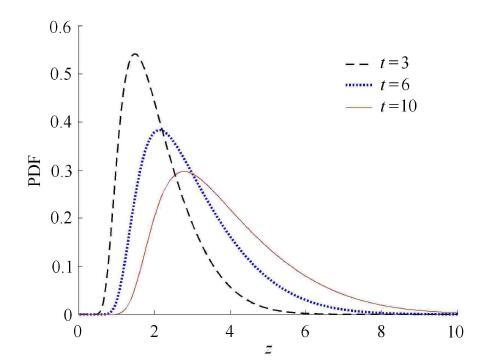
图4给出了3个不同时刻下最大绝对值过程的概率密度数值结果.
图4
新窗口打开|下载原图ZIP|生成PPT图4Brown运动的最大绝对值过程$Z\left( t \right)$的概率密度在不同时刻下的对比
Fig. 4The PDF of $Z(t) $of Brownian motion process at different time instants
从图中可见,随着时间的推移,最大绝对值过程$Z\left( t \right)$的概率密度的峰值逐渐向右移动,这正符合$Z\left( t\right)$单调不减的样本特征. 另一方面,其峰值逐渐变低,即概率密度呈扩散的趋势,这是由于Brown运动过程的 扩散特征(即不会趋于稳态)导致的.值得指出,Brown运动最大值过程的概率分布是半正态形式[13],虽然其概率密度函数也随着时间增长而峰值降低、范围变宽,但峰值点始终在原点,这与上述最大绝对值概率分布特征具有显著区别.
3.2 一维非线性标量扩散过程的最大绝对值分布
考虑一类一维非线性标量扩散过程$X\left( t \right)$,其Itô随机微分方程为[31]其中,$\alpha $为非线性系数;$W\left( t \right)$为白噪声强度为$D$的Brown运动过程. 当$t \to \infty $时,$X\left( t \right)$的概率密度存在稳态解[31]
其中$C$为归一化常数
如前所述,对于很小的时间增量$\tau $,$X\left( t\right)$的转移概率密度可采用近似Gauss分布
记$Z(t) $为$X\left( t\right)$的最大绝对值过程,由式(3)定义. 根据式(16),最大绝对值-状态量联合向量过程$\left( {Z(t) ,X(t) } \right)^{\rm T}$的转移概率密度可以写为
由此,可以通过式(9)与式(10)对向量过程$\left( {Z(t) ,X\left( t \right)} \right)^{\rm T}$的联合概率密度函数$p_{ZX} \left( {z,x,t} \right)$进行数值求解,进而获得最大绝对值过程$Z\left( t\right)$的概率密度$p_Z \left( {z,t} \right)$.
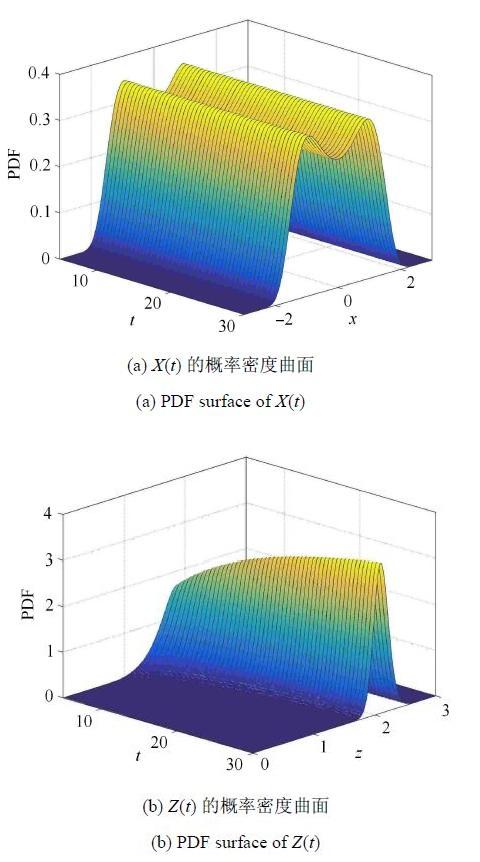
在本例中,取初值$x_0 = 0$,非线性系数$\alpha = 0.1$,白噪声强度$D =1$,时间步长$\Delta t = 0.02$,求解域为$z \in \left[ {0, 5}\right]$,$x \in \left[ { - 5, 5} \right]$,网格尺寸$\Delta z = \Delta x = 0.05$. 通过数值求解可得在$t \in \left[ { 5, 30} \right]$内$X\left(t \right)$与$Z(t) $的概率密度曲面如图5所示.
图5
新窗口打开|下载原图ZIP|生成PPT图5一维非线性标量扩散过程$X(t) $及其最大绝对值过程$Z\left( t \right)$的概率密度曲面
Fig. 5The PDF surfaces of $X(t) $and $Z(t) $of a one-dimensional non-linear scalar diffusion process
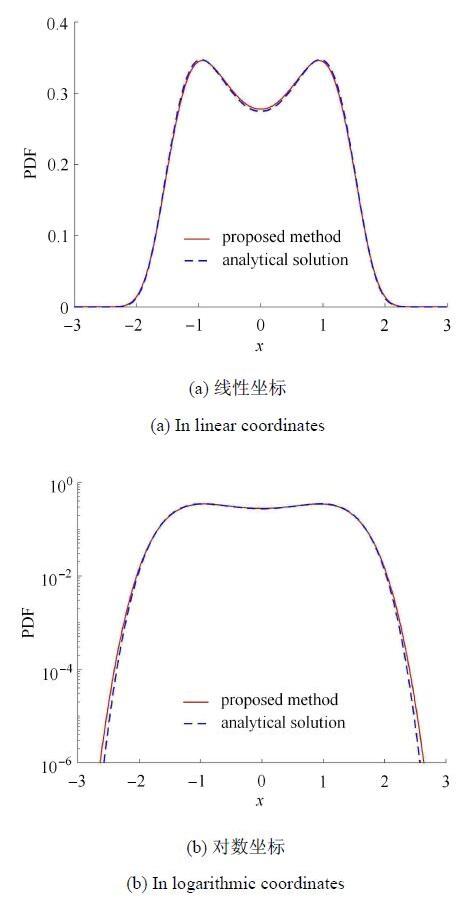
在$t = 30$时刻,$X\left( t \right)$的概率密度数值解与稳态解析解式(26)的对比如图6所示. 可见,数值解具有很高的精度. 这一结果,可以从侧面验证本文程序编制的正确性.
图6
新窗口打开|下载原图ZIP|生成PPT图6一维非线性标量扩散过程$X\left( t \right)$的概率密度数值结果与稳态解析解的对比
Fig. 6The comparison between the numerical and analytical solution of PDF of a one-dimensional non-linear scalar diffusion process $X(t)$
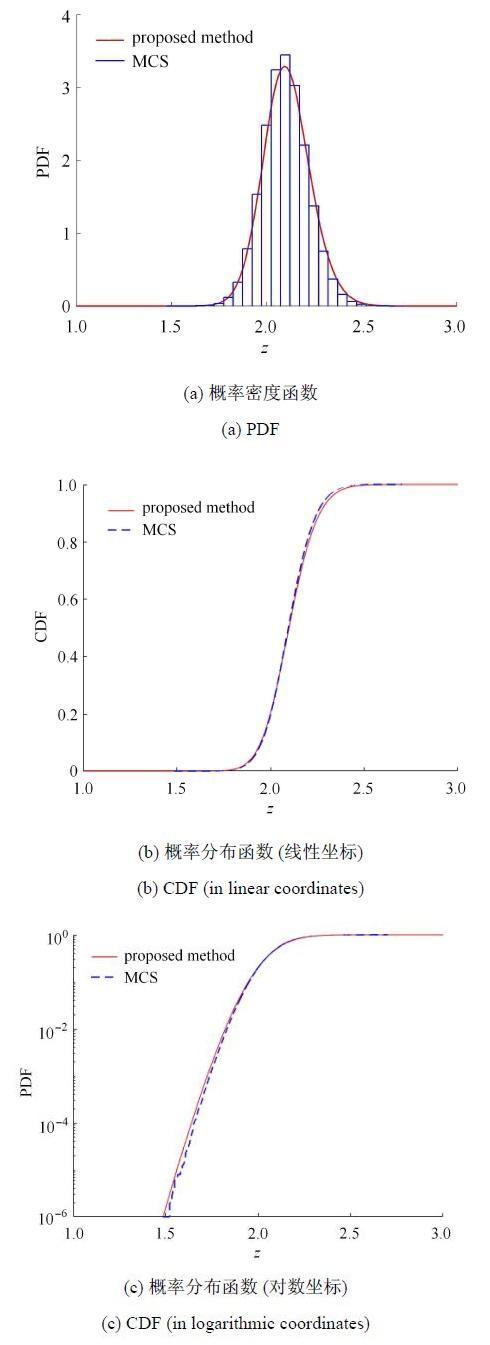
另一方面,将本文方法获得的最大绝对值过程的概率密度函数和概率分布函数与Monte Carlo结果进行比较. 取随机抽样次数为10$^{6}$次,结果如图7所示. 其中,在Monte Carlo模拟中,随机微分方程的数值求解采用 二阶随机Runge-Kutta算法[22],该方法具有二阶强收敛性. 从图7中可见,无论是概率密度还是概率分布,本文建议方法均具有很高的精度. 特别是概率分布函数的尾部(图7(c)),可见在考虑Monte Carlo模拟结果30%变异性的范围内,本文结果在10$^{ - 5}$的精度水平得到了验证.另外,采用MatLab编写程序并运行,本文方法共耗时15.99,s,10$^{6}$次Monte Carlo模拟共耗时309.35,s.可见,在相同量级甚至更高的精度要求下,本文方法的计算效率显著高于Monte Carlo模拟的效率.
图7
新窗口打开|下载原图ZIP|生成PPT图7一维非线性标量扩散过程的最大绝对值过程$Z\left( t \right)$的概率密度与概率分布数值结果与Monte Carlo结果的对比
Fig. 7The comparison between the proposed method and MCS for the PDF and CDF of $Z(t) $of a one-dimensional non-linear scalar diffusion process
此外,取3个不同时刻下最大绝对值过程$Z\left( t \right)$的概率密度数值结果进行比较,结果如图8所示.
图8
新窗口打开|下载原图ZIP|生成PPT图8不同时刻下的一维非线性标量扩散过程的最大绝对值过程$Z\left( t \right)$的概率密度
Fig. 8The PDF of $Z(t) $of a one-dimensional non-linear scalar diffusion process at different time instants
由图8可见,随着时间的推移,最大绝对值过程$Z\left( t \right)$的概率密度的峰值逐渐向右移动,这与图4中所呈现出的特征是一致的.所不同的是,其分布逐渐变窄,峰值逐渐变高,这是由于该一维非线性标量扩散过程逐渐趋于稳态所导致的.
3.3 白噪声激励下Duffing振子的位移最大绝对值
考虑Gauss白噪声激励下的单自由度Duffing振子[32],其运动方程为其中,$\gamma > 0$为线性阻尼系数;$\varepsilon > 0$为非线性刚度系数;$D$为白噪声强度;$\xi \left( t\right)$为标准Gauss白噪声过程. 记$\dot {X}(t) = V\left( t\right)$,则该振子的响应可视为二维Markov向量过程${\pmb Y}\left( t \right) = \left( {X(t) ,V(t) } \right)^{\rm T}$,其Itô随机微分方程如下
其中$W(t) $为Brown运动过程.
如前所述,对于很小的时间增量$\tau $,向量过程${\pmb Y}\left( t\right)$的转移概率密度可以采用Gauss近似[28]
依然记$Z(t) $为位移过程$X\left( t \right)$的最大绝对值过程,由式(3)定义.根据式(18),位移最大绝对值$\!$-$\!$-$\!$状态向量联合向量过程$\left( {Z(t) ,{\pmb Y}^{\rm T}(t) } \right)^{\rm T}$的转移概率密度为
由此,可通过式(19)与式(20)对向量过程$\left( {Z(t) ,{\pmb Y}^{\rm T}(t) } \right)^{\rm T}$的联合概率密度$p_{Z{ Y}} \left( {z,x,v,t} \right)$进行数值求解,进而获得最大绝对值过程$Z\left( t\right)$的概率密度$p_Z \left( {z,t} \right)$.前已指出,尽管对于一般的多维问题,采用路径积分的计算效率较低,然而在该问题的数值实现中,由于存在$u\left(\cdot \right)$与$\delta \left( \cdot\right)$函数,最大绝对值$\!$-$\!$-$\!$状态量联合向量过程的转移概率密度是稀疏的,因此可以有效降低其数值存储与计算成本[29].
在本例中,取初值$x_0 = 0$,$v_0 = 0$,线性阻尼系数$\gamma =0.5$,非线性刚度系数$\varepsilon = 0.3$,白噪声强度$D = 1$,时间步长$\Delta t = 0.02$,求解域为$z \in \left[ {0, 5} \right]$,$x \in \left[ { - 5, 5} \right]$,$v \in \left[ { - 7, 7} \right]$,网格尺寸$\Delta z = \Delta x = \Delta v = 0.05$. 通过数 值求解,可得在$t \in \left[ { 5, 30} \right]$内$X\left( t\right)$与$Z(t) $的概率密度曲面如图9所示.
图9
新窗口打开|下载原图ZIP|生成PPT图9Duffing振子位移响应过程$X(t) $及其最大绝对值过程$Z\left( t \right)$的概率密度曲面
Fig. 9The PDF surfaces of $X(t) $and $Z(t) $of Duffing oscillator
在$t = 30$时刻,将本文方法获得的最大绝对值过程$Z\left( t\right)$的概率密度函数(PDF)和概率分布函数(CDF)与Monte Carlo结果进行比较,取随机抽样次数10$^{6}$次,结果如图10所示. 其中,在Monte Carlo模拟中,随机微分方程的数值求解采用二阶随机Runge-Kutta算法[22].
图10
新窗口打开|下载原图ZIP|生成PPT图10Duffing振子位移响应过程的最大绝对值过程$Z\left( t \right)$的概率密度与概率分布数值分析结果与Monte Carlo结果的对比
Fig. 10The comparison between the proposed method and MCS for the PDF and CDF of $Z(t) $of Duffing oscillator
由以上图中的对比可以看出,最大绝对值概率密度的数值结果与Monte Carlo结果吻合良好.与图7中类似,尾部精度可达至少10$^{ - 5}$量级的水平.特别是,本文建议方法在尾部也具有很高的精度,可以进一步应用于系统可靠度的计算当中.
上述基本思想,有望进一步结合Fokker-Planck-Kolmogorov方程降维方法、即基于物理驱动的概率密度群演化方法[33-35],将其推广到一般多自由度非线性系统响应的最大绝对值及可靠度分析之中.
4 结论
本文提出了一类求解Markov过程的最大绝对值时变概率密度函数的数值方法. 在该方法中,定义了Markov过程的时变最大绝对值过程,进而构造最大绝对值$\!$-$\!$-$\!$状态量联合向量过程,从而将一个非Markov过程转化为Markov向量过程. 在此基础上,基于Chapman-Kolmogorov方程与路径积分方法,提出了最大绝对值$\!$-$\!$-$\!$状态量联合概率密度的数值求解算法. 通过具体数值算例,对该方法的有效性进行了验证. 主要结论有：(1)本文建议方法可以获得Markov过程最大绝对值的时变概率密度数值解,且理论上适用于一般的线性或非线性、一维或多维随机动力系统.
(2) 该方法的数值结果具有很高的精度. 在概率密度尾部甚至可以达到10$^{ -4}$$\sim$10$^{ - 5}$或更高的计算精度,这对于工程结构可靠度的计算具有重要意义.
(3)对于低维问题,该方法具有理想的计算效率. 由于最大绝对值---状态量联合向量过程的转移概率密度的稀疏性,可以通过数值处理获得较高的数值存储与计算效率.
本文的基本思想可以进一步扩展至更复杂的随机动力系统,例如高维、非白噪声激励、非Markov过程等. 对此,尚需进一步开展深入研究.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 3]
[本文引用: 3]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
