,2), 朱凌云天津工业大学 机械工程学院 天津 300387;天津工业大学天津市现代机电装备技术重点实验室 天津 300387 天津 300387RESEARCH ON MULTI-STABILITY CHARACTERISTICS OF GEAR TRANSMISSION SYSTEM WITH TWO-SPACE COUPLING1)
Shi Jianfei, Gou Xiangfeng,2), Zhu LingyunSchool of Mechanical Engineering, Tiangong University, Tianjin 300387, China;Tianjin Key Laboratory of Modern Mechatronics Equipment Technology, Tiangong University, Tianjin 300387, China通讯作者: 2) 苟向锋, 教授, 主要研究方向：机械系统动力学.E-mail:20150022@tjpu.edu.cn
收稿日期:2019-04-15网络出版日期:2019-09-18
| 基金资助: |
Received:2019-04-15Online:2019-09-18
作者简介 About authors
摘要
通过将系统参数定义为参数变量, 构成参数空间,研究齿轮传动系统在参数空间和状态空间耦合下的非线性全局动力学特性,以及多参数、多初值和多稳态行为之间的关联特性.首先设计了一个两空间耦合下非线性系统多稳态行为的计算和辨识方法.其次,基于该方法并结合相图、Poincaré映射图、分岔图、最大Lyapunov指数、吸引域等,研究齿轮传动系统在不同参数平面上多稳态行为的存在区域和分布特性,以及多稳态行为在状态平面上的分布特性,揭示了参数平面和状态平面上系统可能隐藏的多稳态行为和分岔,并分析了多稳态行为的形成机理. 结果发现,两空间耦合下系统在参数平面上存在大量多稳态行为并呈"带状"分布, 状态平面上多稳态行为出现两种不同的侵蚀现象, 即内部侵蚀和边界侵蚀.分岔点或分岔曲线对初值的敏感性导致多稳态行为的出现.当齿侧间隙和误差波动在较小的范围内变化时,系统全局动力学特性受间隙和误差扰动的影响较小,受啮合频率的影响较大.两空间耦合下系统全局动力学特性变得丰富和复杂.
关键词：
Abstract
By defining the system parameters as parameter variables and forming the parameter space, the nonlinear global dynamics of the gear transmission system under the coupling of parameter space and state space are studied in detail in this work. The correlative relationship between multiple parameters, multiple initial values and multiple stable behaviors is also obtained. Firstly, a method for calculating and identifying the multi-stable behavior of a nonlinear system under the coupling of two spaces is designed. Secondly, based on the designed method and combined with phase diagram, Poincaré map, bifurcation diagram, top Lyapunov exponent and basin of attraction, the existence and distribution of multi-stable behavior for the gear transmission system in different parameter planes are investigated numerically to better understand the motion mechanism of the system. In addition, the distribution characteristic of multi-stable behavior in the state plane is also studied on the base of the cell-to-cell mapping method. The multi-stable behavior and bifurcation that may be hidden in the parametric plane and the state plane are fully revealed. The formation mechanism of multi-stable behavior is analyzed as well. The results show that there are a large number of multiple stable behaviors which are banded distribution in the parametric planes of the gear system under the coupling of two spaces. Two different erosion phenomena, such as internal erosion and boundary erosion, are clearly observed in the state plane. The sensitivity of bifurcation points or bifurcation curves to initial values leads to the occurrence of multi-stable behavior. When the amplitude of backlash or error fluctuation changes in a small range, the global dynamic characteristics of the gear system are less affected by the backlash or error disturbance. However, the global dynamic characteristics are greatly affected by the meshing frequency. Global dynamic characteristics of the gear system become rich and complex under two-space coupling.
Keywords：
PDF (23437KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
石建飞, 苟向锋, 朱凌云. 两空间耦合下齿轮传动系统多稳态特性研究1). 力学学报[J], 2019, 51(5): 1489-1499 DOI:10.6052/0459-1879-19-093
Shi Jianfei, Gou Xiangfeng, Zhu Lingyun.
引言
由于时变啮合刚度、动态传递误差及齿侧间隙等,齿轮传动系统已成为一种典型的含多参数的非光滑非线性系统[1-4],其运动的稳定性、安全性及可靠性是影响机组正常工作的关键因素[5-7]. 一个非线性系统,其运动方程主要由系统参数和状态变量按照一定的数学关系构成,故系统参数和状态变量初值共同决定着非线性系统的动力学特性及其演变规律.因此,多参数和多初值之间的耦合关系和关联规律对非线性系统动力学特性的影响不可忽略.为了全面掌握齿轮传动系统运动机理、揭示其全局动力学特性,将系统参数定义为参数变量, 构成参数空间,研究参数空间与状态空间耦合下齿轮传动系统的非线性动力学特性是非常有必要的.
近年来,很多国内外****研究了各种非线性系统在两参数平面上的动力学行为及其分岔,如交通网络[8]、电路[9]、经济[10]、生物[11]以及冲击振动[12-16]等系统, 并获得很多有价值的研究成果.在齿轮传动系统方面,Mason等[17,18]基于双参数法研究了参数平面上擦边分岔曲线对齿轮系统全局动力学特性的影响,发现参数平面上可达边界鞍结点主要由擦边分岔或鞍结分岔产生.Xiang等[19]研究了含多个非线性参数的行星齿轮系统的动力学特性,发现选择合理的系统参数, 可以避免混沌运动对齿轮系统振动特性的影响.Gou等[20]研究单自由度直齿轮系统在参数平面上的分岔转迁过程,得到了参数平面上不同运动的连续存在区域.郜志英等[21]研究了非线性单级齿轮系统在参数平面内周期运动和混沌运动的分岔结构,得到了不同参数平面内的域界,并通过多项式拟合得到了周期运动稳定参数域和混沌吸引子的激变点.林何等[22]考虑了锥齿轮系统在参数域界结构中的稳态特性,数值分析了系统在多参数域共同激励下的动态分岔行为.苟向锋等[23]通过计算齿轮--转子系统在双参数平面上动力学行为分布图,得到系统双参数变化的周期运动和非周期运动的分布规律和分岔特性.以上文献对齿轮系统在参数平面上的动力学特性进行了广泛的研究,但这些研究只考虑系统在参数平面上的动力学特性,忽略状态空间的影响(忽略初值变化的影响). 因此,参数平面上可能存在的多稳态行为(共存吸引子)的存在区域及其分岔没有完全被揭示,一些潜在的动力学行为或分岔可能被隐藏,参数平面上一些重要的信息被丢失, 导致分析结果的精确性得不到保障.故参数空间和状态空间的耦合特性必须考虑.
很多研究发现在非线性齿轮传动系统中存在大量的多稳态行为(共存吸引子)[24-26], 包括周期与周期共存, 周期与混沌共存等.这些共存的动力学行为中, 只有部分动力学行为是稳定的、安全的,其余部分是不稳定的, 可能导致系统运动的动态失稳[27-31]. 可见,多稳态行为或共存吸引子对非线性系统的全局动力学特性至关重要.
本文研究了参数平面与状态平面耦合下单自由度齿轮传动系统的全局动力学特性.首先,设计了一个非线性系统在参数平面和状态平面耦合下多稳态行为的计算和辨识方法,并采用变步长四阶Runge-Kutta法对系统进行数值求解. 其次, 基于该方法,并结合相图、Poincaré映射图、最大Lyapunov指数(top lyapunov exponent, TLE)、吸引域等,研究了齿轮传动系统在参数平面上多稳态行为的分布特性;基于胞映射法[20]研究多稳态行为在状态平面上的分布特性以及其吸引域的演变规律.
1 齿轮传动系统非线性动力学模型
单级齿轮传动系统的简化物理模型如图1所示. 图中, $\theta _i $,$r_{{\rm b}i} $, $I_i $和$T_i (i =1,2)$分别表示主、从动齿轮的扭转角位移、基圆半径、转动惯量和转矩;$k(t)$和$e(t)$分别为齿轮副 的时变啮合刚度和综合传递误差,其中$t$为时间; $c_{\rm g} $为齿轮副的啮合阻尼; $D_1$为齿侧间隙的一半. 根据文献[20],单自由度齿轮传动系统的量纲一化运动微分方程为图1
新窗口打开|下载原图ZIP|生成PPT图1齿轮副简化物理模型
Fig. 1Simplified physical model of gear system
式中, $x$, $\dot {x}$, $\ddot{x}$分别为相对位移、速度和加速度,$\xi $为阻尼比, $k$为啮合刚度波动幅值,$\varepsilon $为综合传递误差波动幅值, $F$为转矩,$\omega $为啮合频率, $f(x)$为非线性间隙函数, 可表示为
其中, $D$为量纲一齿侧间隙的一半.
单自由度齿轮传动系统基本参数为：主、从动轮齿数分别为30和60,齿宽分别为100和95 mm, 模数$m$= 3 mm, 压力角$\alpha = 20^ \circ $,间隙2$D$= 0.02 mm. 式(1)中,单级齿轮传动系统非线性动力学模型包含6个动力学参数, 其中,阻尼比$\xi$、刚度波动幅值$k$、误差波动幅值$\varepsilon$、齿侧间隙$D$为齿轮系统结构参数, 啮合频率$\omega$和转矩$F$为系统运动参数.
2 参数平面和状态平面耦合下多稳态行为的辨识方法
针对一个非线性系统, 任意选择两个参数$u_{1}$和$u_{2}$作为参数变量,由这两个参数变量构成 一个参数平面$\varSigma $= ($u_{1}$,$u_{2})$. 在状态空间定义一个Poincaré~截面$\varPi = \left\{{(x,\dot {x},t)\vert \bmod \;(t,T) = 0} \right\}$, 在截面$\varPi$上选择一个有界区域$\varOmega $= ($x$,$\dot{x})$作为考察状态平面. 参数平面$\varSigma$和状态平面$\varOmega$耦合下非线性系统全局动力学行为的计算和辨识方法描述如下.首先, 将参数平面$\varSigma $划分为$m\times m$= $M$个小网格,建立参数子平面$\varSigma _{i}(i$= 1,2,$\cdots$,$M$),每一个小网格代表一个参数子平面.假设用每一个参数子平面中心点的全局动力学特性代表整个参数子平面的全局动力学特性,通过计算所有参数子平面中心点的全局特性, 可得整个参数平面$\varSigma$上的全局动力学特性.
其次, 将状态平面$\varOmega $划分为$n\times n$= $N$个小网格,建立状态子平面$\varOmega _{j}(j$= 1,2,$\cdots$,$N$),每一个状态子平面代表一组初始值,假设用状态子平面中心点的值代表这个初始值,则在有界状态平面$\varOmega $内有$N$个初始值需要被考察.
最后, 采用变步长四阶Runge-Kutta法数值求解非线性系统,计算每一个参数 子平面$\varSigma _{i}$在状态平面$\varOmega$内所有初值下的全局动力学特性, 通过计算每个解的最大Lyapunov指数(TLE)判断其稳定性, 对每一个$\varSigma _{i}$,在状态平面$\varOmega $内, 系统可能存在多个稳态解共存情况.当所有参数子平面$\varSigma _{i}(i$=1,2,$\cdots$,$M$)在状态平面$\varOmega$内的全局动力学特性被计算完后, 可得系统在整个参数平面$\varSigma$上的全局动力学特性,进而得到系统在参数平面和状态平面耦合下多稳态行为在参数平面上的分布特性,基于胞映射方法可得每一个参数子平面在状态平面上多稳态行为的分布特性及吸引域.
此外, 参数平面$\varSigma $和状态平面$\varOmega $一定时,随着网格数量($N$或$M$)的增大, 其计算精度越高,但计算量和计算时间也将呈指数倍地增大. 因此,在计算时应根据实际需求选择合理的网格数量.
3 单参数变量与状态平面的耦合特性
方程(1)中, 以啮合频率$\omega $(0.4$<$$\omega$$<$1.2)作为参数变量, 构成一维参数空间, 其他参数$F$= 0.05, $\xi $= 0.01, $k$= 0.1, $\varepsilon$= 0.2, $D$= 1.0固定. 状态平面$\varOmega = \{(x,\dot {x})\vert-2.0 \le x \le 2.0,-2.0 \le \dot {x} \le 2.0\}$被划分为20$\times $20 = 400个小网格,每一个小网格代表一个初值点, 针对每一组系统参数值,计算其在$\varOmega $内400个初值条件下的全局动力学特性,可得系统在参数$\omega $与状态平面$\varOmega$耦合下的全局动力学特性.为了对比, 图2给出了系统在不考虑状态平面$\varOmega$时相对位移$x$随$\omega $增大的分岔图和相应的TLE谱.TLE值用来判断系统解稳定性, 当TLE $<$0时,系统表现为稳定的周期运动; 当TLE $>$0时, 系统表现为不稳定的混沌运动; 当TLE = 0时, 系统发生分岔. 图2中, 随啮合频率的增大,系统动力学行为分别在B1和B2点发生两次跳跃, 随后经倍周期分岔序列进入混沌状态. 在跳跃点或分岔点附近, 系统TLE值近似为0,在混沌区域, 系统TLE值大于0. 可见, 不考虑状态平面$\varOmega$时系统动力学行为和分岔过程比较简单且单一.
图2
新窗口打开|下载原图ZIP|生成PPT图2不考虑状态平面$\varOmega$时随$\omega $增大的分岔图和TLE谱
Fig. 2Bifurcation diagram and corresponding TLE spectrum of the system with the increase in $\omega$without considering the state plane $\varOmega $
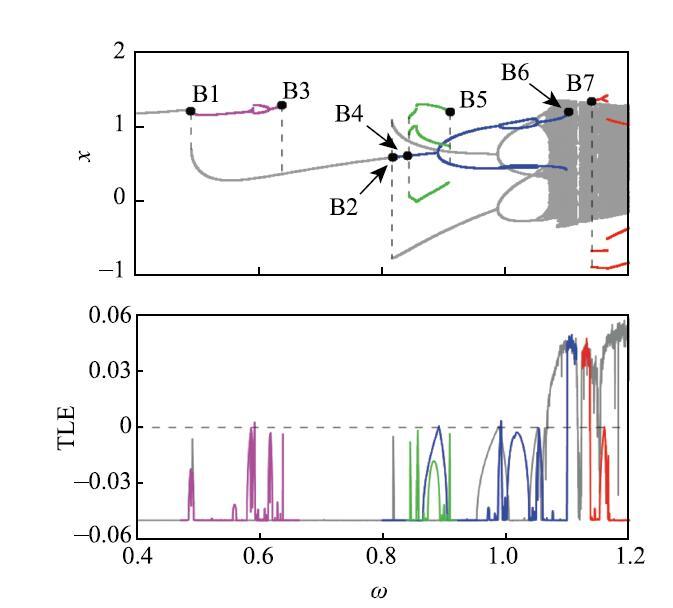
图3为单参数$\omega $与状态平面$\varOmega$耦合下系统随$\omega $增大的分岔图和相应的TLE谱.图中不同的颜色表示共存的动力学行为或分岔分支,每个分岔分支及其对应的TLE用相同颜色表示,TLE值用来判断解的稳定性或分岔. 对比图2,系统动力学行为和分岔变得较为复杂, 一些潜在的、隐藏的动力学特性,如周期跳跃、 倍化分岔和鞍结分岔以及各种周期行为等被完全揭示. B1点,稳定的周期1运动出现两条分支(灰色和品红色),该周期1运动在一部分初值范围内发生周期跳跃(灰色),而在另一部分初值范围内持续存在并经过一次倍化分岔和逆倍化分岔后在B3点消失(品红色).可见, 分岔点对初值的敏感性引起共存吸引子或多稳态行为.在B1和B3点之间,系统出现2个周期1共存或1个周期1与1个周期2共存的情况,其在状态平面$\varOmega $上的分布特性分别如图4(a)和图4(b)所示,其中"+"和"$\times $"表示Poincaré映射点或吸引子,P1和Q1表示两个不同的周期1行为, Q2表示周期2行为,浅灰色为P1的吸引域, 黑色为Q1或Q2的吸引域,对应相空间轨迹分别如图5(a)和图5(b)所示, 两运动轨迹的振动幅值不同,P1相对较小.
图3
新窗口打开|下载原图ZIP|生成PPT图3参数$\omega$与状态平面$\varOmega$耦合下的分岔图和TLE
Fig. 3Bifurcation diagram and corresponding TLE spectrum under coupling of the parameter $\omega$and the state plane $\varOmega$
图4
新窗口打开|下载原图ZIP|生成PPT图4随啮合频率$\omega $增大的吸引域
Fig. 4Basins of attraction of the system with the increase in $\omega $
图5
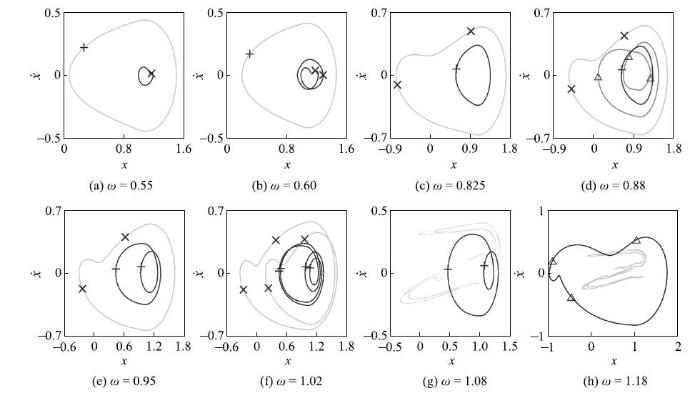
新窗口打开|下载原图ZIP|生成PPT图5多初值下随$\omega $变化的相图和Poincaré截面图
Fig. 5Phase portraits and Poincaré maps of the system with the change of $\omega $under multi-initial value
与B1点相似, 在B2点,稳定的周期1运动在部分初值范围内发生周期跳跃并转迁为周期2运动(灰色),随后该周 期2运动经倍周期序列进入混沌,而在另一部分初值范围内该周期1运动持续存在(蓝色).分岔点B2对初值具有敏感性, 引起多稳态行为, 在B2和B4点之间,系统存在1个周期1(P1)和1个周期2(Q2)共存 情况,其在状态平面上的分布特性如图4(c)所示, 图中浅灰色为P1的吸引域,黑色为Q2的吸引域, 对应相轨 迹如图5(c)所示.
分岔点B4对初值具有敏感性,蓝色周期1运动在部分初值范围内转迁为绿色周期3运动,随后该周期3运动在B5点消失;而在另一部分初值范围内该蓝色周期1运动持续存在,随后经两次倍化分岔转迁为周期4运动, 后经逆倍化分岔退化为周期2运动,最终在B6点消失. 在B4和B5点之间,系统存在1个周期1(P1)、周期2(Q2)和周期3(P3)共存情况,其在状态平面上的分布特性如 图4(d)所示, 图中"$\Delta$"表示周期3吸引子, 浅灰色为P1的吸引域, 深灰色为P3的吸引域,黑色为Q2的吸引域, 对应相轨迹如图5(d)所示.由于蓝色周期1运动发生倍化分岔,在B5点之前较小区域内系统存在2个周期2(P2和Q2)和1个周期3(P3)共存情况,其在状态平面上的分布特性见图4(e), 图中浅灰色表示P2的吸引域,深灰色表示P3的吸引域, 黑色表示Q2的吸引域.
在B5和B6点之间,系统分别存在2个周期2(P2和Q2)共存、2个周期4(P4和Q4)共存、1个周期2(P2)和混沌共存的情况, 其在状态平面上的分布特性分别如图4(f) $\sim$图4(h)所示,图中浅灰色为P2或P4的吸引域, 黑色为Q2和Q4或混沌的吸引域,对应相轨迹分别如图5(e)$\sim$图5(g)所示, 灰色表示混沌吸引子.
在B7点, 混沌运动在部分初值范围内经鞍结分岔退化为周期3运动,随后该周期3运动经历一次倍化分岔和周期跳跃后转迁为周期3运动,在该参数范围内系统存在周期3(P3)和混沌运动共存,其在状态平面上的分布特性如图4(i)所示, 图中浅灰色表示P3的吸引域,黑色表示混沌的吸引域, 对应相轨迹如图5(h)所示,图中灰色表示混沌吸 引子.
综上所述, 单参数$\omega $与状态平面$\varOmega $耦合下,一些隐藏的分岔点和动力学行为被完全揭示,各种类型的多稳态行为被得到, 分岔点与多稳态行为的共存被发现.
隐藏分岔点对初值的敏感性是引起多稳态行为或共存吸引子的主要原因,如分岔点B1、B2、B4、B7等, 这些分岔点不仅改变了共存吸引子的数量,而且改变了其在状态平面上的分布特性. 此外, 当$\omega$较小时, 系统表现为稳定的周期1行为, 系统全局动力学稳定性较强,随$\omega $增大系统出现了多稳态行为以及混沌,系统全局动力学稳定性变弱.
4 参数平面与状态平面的耦合特性
由3节的分析可知,啮合频率作为一种运动参数对齿轮传动系统的全局动力学特性及其演变规律有重要影响.由于齿侧间隙和综合传递误差是引起齿轮系统非线性振动的主要因素,以系统两个结构参数(齿侧间隙$D$和误差波动幅值$\varepsilon$)和一个运动参数(啮合频率$\omega $)为控制参数,基于第2节方法, 分别研究齿轮传动系统在参数平面$\omega$-D与状态平面$\varOmega $耦合下、参数平面$\omega$-$\varepsilon $与状态平面$\varOmega $耦合下的全局动力学特性.对一个给定的参数平面$\omega $-$D$或$\omega$-$\varepsilon $, 将该参数平面网格划分为1000$\times$1000个小方格, 每一个小网格代表一组参数值.4.1 参数平面$\omega $-$D$与状态平面$\varOmega$的耦合特性
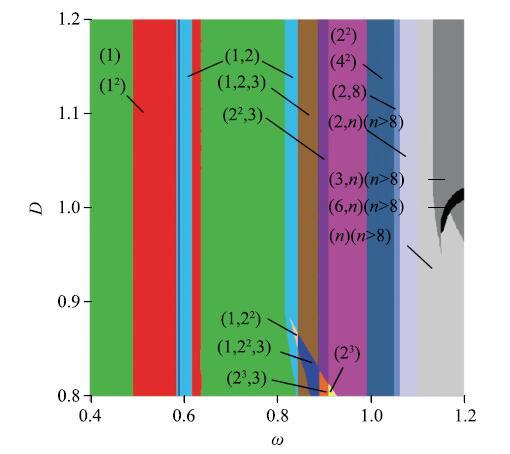
图6为参数平面$\omega $-D与状态平面$\varOmega$耦合下齿轮传动系统在$\omega $-D上多稳态行为的分布图.图中不同的颜色表示不同类型的多稳态行为(共存行为),并用相应的符号标记, 如青绿色表示在$\varOmega $内只有1个周期1运动,并用符号(1)标记; 深灰色表示在$\varOmega$内有1个周期3运动和1个周期$n$运动共存, 并用符号(2,$n)(n$$>$8)标记,$n$表示周期数大于8的周期行为或混沌; 以此类推, 其对应关系详见表1.图6
新窗口打开|下载原图ZIP|生成PPT图6参数平面$\omega $-D与状态平面$\varOmega$耦合下系统多稳态分布图
Fig. 6Distribution diagram of multi-stable behavior of the system in the parameters plane under coupling of the parameter plane$\omega $-D and the state plane $\varOmega $
Table 1
表1
表1
Table 1
 |
新窗口打开|下载CSV
由图6可知, 参数平面与状态平面耦合下, 系统在参数平面$\omega$-$D$上可能隐藏的动力学行为被完全揭示,各种类型的多稳态行为以及其连续的存在区域被得到,这些存在区域成"带状"分布, 表明在一定啮合频率$\omega$下, 系统全局动力学行为受间隙$D$变化的影响较小,受啮合频率变化的影响较大. 不同区域之间的边界曲线表示分岔曲线,类似于3节的分析,这些分岔曲线对初值的敏感依赖性导致各种类型的多稳态行为,图3为图6中当间隙值取$D$= 1.0的一种特殊情况, 平面$\omega$-D上各种类型的多稳态行为在平面$\varOmega $上的分布特性与图4相似.
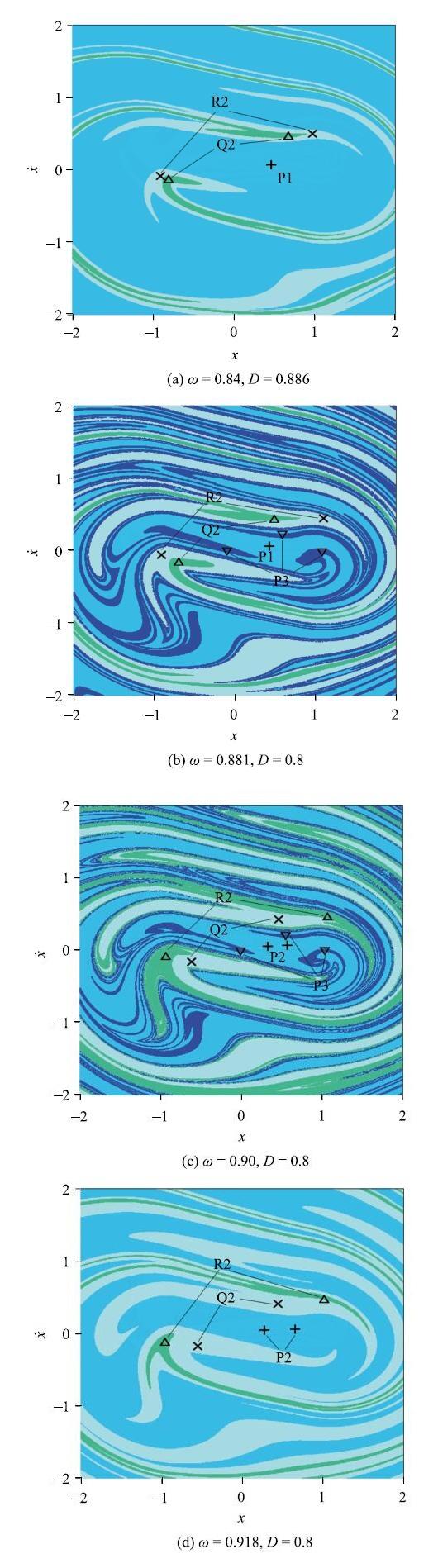
当啮合频率在$\omega $= 0.9附近、间隙值在$D$=0.81附近取值时, 系统全局动力学特性较为复杂, 参数平面上系统存在(1,2$^{2})$、(1,2$^{2}$,3)、(2$^{3}$,3)、(2$^{3})$等多稳态行为的存在区域, 其在状态平面上的分布特性分别如图7(a) $\sim$图7(d)所示,图中各共存吸引子的吸引域相互缠绕在一起,初值的微小扰动都有可能使系统运动在不同的周期响应之间相互切换,加剧齿轮副间的振动冲击.
图7
新窗口打开|下载原图ZIP|生成PPT图7吸引域图
Fig. 7Basins of attraction of the system
此外, 相比图7(a), 在图7(b)中,系统在天蓝色周期1行为(P1)的吸引域内出现了新的蓝色周期3行为(P3),即P3由P1在部分初值范围内产生,P1的吸引域(天蓝色)被P3的吸引域(蓝色)侵蚀,我们把这种吸引域的侵蚀定义为内部侵蚀. 相似地,在图4中, 随着各种多稳态行为的出现,其在状态平面上吸引域的侵蚀均为内部侵蚀.
当啮合频率较小时, 系统表现为简单的周期1行为或周期1与周期2行为共存,系统的工作性能较为平稳. 当啮合频率较大时,系统存在多种不同类型的周期行为共存以及周期行为与混沌共存,齿轮传动系统动力学行为相对较为复杂.
4.2 参数平面$\omega $-$\varepsilon $与状态平面$\varOmega $的耦合特性
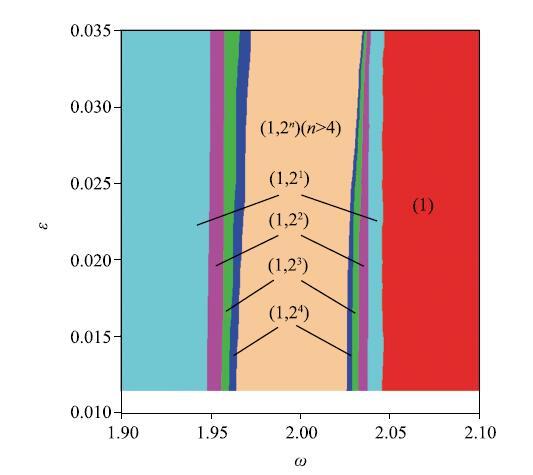
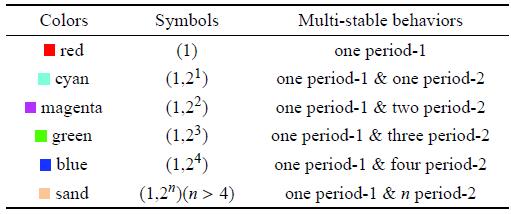
图8为参数平面$\omega $-$\varepsilon $与状态平面$\varOmega$耦合下齿轮系统在$\omega $-$\varepsilon$上多稳态行为的分布图,图中不同颜色与其所代表多稳态行为之间的对应关系详见表2.图8
新窗口打开|下载原图ZIP|生成PPT图8参数平面$\omega-\varepsilon $与状态平面$\varOmega$耦合下系统多稳态分布图
Fig. 8Distribution diagram of multi-stable behavior of the system in the parameters plane under coupling of the parameter plane$\omega $-$\varepsilon $and the state plane $\varOmega $
Table 2
表2
表2
Table 2
 |
新窗口打开|下载CSV
与图6相似, 在图8中,各种多稳态行为或共存吸引子在参数平面上的存在区域成"带状"分布,当误差波动幅值在较小的范围内扰动时,齿轮传动系统的动力学行为受误差波动幅值变化的影响较小,受啮合频率变化的影响较大. 随啮合频率增大, 参数平面$\omega$-$\varepsilon $上共存周期2行为的数量逐渐增多. 计算发现,当啮合频率在$\omega $= 2.0附近时,共存周期2行为的数量达到最多, 由于其在参数平面$\omega$-$\varepsilon $上存在区域非常小, 而且类型较多,图8没有给出其详细存在区域. 随着啮合频率进一步增大,共存周期2行为的数量开始逐渐减小, 当$\omega $$>$2.05时,周期2行为已全部消失, 参数平面$\omega $-$\varepsilon$上系统只存在一个稳定的周期1行为(红色区域),此时系统全局动力学特性较为简单且稳定.
为了进一步分析多稳态行为在状态平面上的分布特性及其演变规律, 图8中,固定误差波 动幅值$\varepsilon $= 0.02,取仿真啮合频率值$\omega $= 1.946, 1.950 5, 1.96, 1.9606, 1.960 9, 1.975 2, 计算各共存行为在状态平面$\varOmega$上的分布特性如图9所示.
图9
新窗口打开|下载原图ZIP|生成PPT图9$\varepsilon $= 0.02时随啮合频率$\omega $变化的吸引域
Fig. 9Basins of attraction of the system with the change of $\omega $
由图9可见, $\omega $= 1.946时, 状态平面$\varOmega$上系统存在1个周期1行为和1个周期2行为, 符号"+"代表周期1的吸引子,其吸引域用红色表示, "$\times $"代表周期2的吸引子,其吸引域用浅灰色表示, 周期2吸引子"$\times$"与周期1吸引子"+"分布在一条直线上, 如图9(a)所示.随$\omega $增大到$\omega $= 1.9505时,如图9(b)所示, 状态平面$\varOmega$上系统存在1个周期1行为和2个周期2行为, "$\Delta$"代表新出现的周期2行为的吸引子, 且与旧的吸引子"$\times$"和"+"分布在一条直线上. 黄色表示新出现周期2吸引子的吸引域,且黄色区域是在红色区域和浅灰色区域的边界处产生,红色区域和浅灰色区域被黄色区域侵蚀, 不同于4.1节的内部侵蚀,我们把这种侵蚀定义为边界侵 蚀(在现有文献中很少见有这种侵蚀方式).随$\omega $继续增大, $\omega $=1.96时(见图9(c)), 状态平面$\varOmega$内系统存在1个周期1行为和3个周期2行为共存, "$\nabla$"代表新出现的周期2行为的吸引子, 且与旧的吸引子"$\times $","+"和"$\Delta $"分布在一条直线上,天蓝色区域为新出现的周期2行为吸引子的吸引域,且在黄色区域和浅灰色区 域的边界处产生, 为边界侵蚀. $\omega$= 1.960 6时(见图9(d)), 状态平面$\varOmega$内系统存在1个周期1行为和4个周期2行为共存(用5不同种颜色区分),黄绿色区域为新出现的 周期2吸引子的吸引域,且在天蓝色区域和浅灰色区域的边界处产生, 为边界侵蚀.计算发现随着共存周期2行为数量的增多, 其相应吸引域面积不断收缩,共存吸引子相互靠近 并挤在一起, 使共存吸引子很难清晰地显示,但所有共存的吸引子分布在一条直线上, 故图9(d)没有具体给出新出现的周期2行为的吸引子, 只给出吸引子的分布位置,如图中线段(下同), 不 同的周期2行为用不同颜色的吸引域区分.$\omega $= 1.960 9时(见图9(e)), 状态平面$\varOmega$内系统存在1个周期1行为和5个周期2行为共存(用6种不同颜色区分),浅粉色 区域为新出现的周期2行为吸引子的吸引域,在黄绿色和浅灰色的边界处产生. $\omega $= 1.975 2时,如图9(f)所示, 在$\varOmega$内系统存在1个周期1行为和10个周期2行为共存(用11种不同颜色区分).随啮合频率增大, 周期2行为的数量不断增多,其在状态平面上吸引域的面积不但缩小, 且具有相似的拓扑结构,限于篇幅, 本文没有给出全部吸引域图.
对比图9(a) $\sim$图9(f), 当啮合频率在较小范围内不断增大时,在周期1和周期2行为(红色和浅灰色)之间的区域内,系统连续出现了新的周期2行为, 且在各吸引域的边界处产生,出现了边界侵蚀. 随着共存周期2行为数量的增加, 其吸引域面积不断缩小,但具有相似的拓扑结构.周期2行为连续不断的出现使齿轮传动系统的非线性振动特性变得非常复杂,初值的轻微扰动都将引起系统运动状态发生突变, 加强振动, 进而影响系统工作的平稳性.
4.3 研究方法和结果的对比
文献[7,8,9,10,11,12,13,14]基于Runge-Kutta法研究了各种非线性系统在双参数平面上的分岔特性和不同动力学行为包括周期行为和混沌的连续存在区域,其中文献[14]基于网格划分的思想设计了非线性系统多参数分岔的计算方法,并分析了Duffing系统在双参数平面上的分岔特性.以上这些研究对本文方法的研究非常重要,但目前文献只考虑单一初值下系统在参数平面上的动力学特性,并没有考虑多初值(状态空间)对系统全局动力学特性的影响.文献[15,16,17,18,19,20,21]基于Runge-Kutta法数值得到齿轮传动系统在双参数平面上各种动力学行为的存在区域以及分岔曲线,但没有揭示齿轮传动系统在参数平面上可能隐藏的分岔曲线或动力学行为.文献[22-23,26]基于胞映射法揭示了齿轮传动系统在状态空间各共存吸引子的吸引域,但没有分析参数平面上共存吸引子的分布特性.这些文献的研究结果对本文分析结果同样非常重要.本文基于齿轮传动系统多参数和非线性特性,将参数空间和状态空间耦合在一起,基于变步长四阶Runge-Kutta法数值研究了齿轮传动系统在两空间耦合下的全局动力学特性,为系统动力学行为的预测、控制以及更全面地掌握系统运动机理提供理论基础.
5 结论
针对多参数非线性系统,设计了一个计算和辨识参数平面与状态平面耦合下多稳态行为的方法,分别研究了齿轮传动系统在单参数与状态平面耦合下、参数平面与状态平面耦合下的全局动力学特性,揭示了参数平面上多稳态行为的分布特性,以及状态平面上多稳态行为的分布特性, 主要结论如下：(1)参数平面与状态平面耦合下,齿轮系统在参数平面上可能隐藏的动力学行为和分岔被完全揭示,各种类型多稳态行为的连续存在区域被得到.分岔点或分岔曲线对初值的敏感性是产生多稳态行为的主要原因,如参数平面上不同多稳态行为存在区域的边界曲线.
(2)状态平面上, 多稳态行为的两种不同的侵蚀现象被发现,即内部侵蚀和边界侵蚀.这两种不同的侵蚀现象使齿轮系统多稳态行为和全局动力学特性变得丰富和复杂.
(3)若齿轮系统的齿侧间隙或误差波动幅值在较小范围内扰动,系统的全局动力学特性受间隙或误差变化的影响较小,而受啮合频率变化的影响较大. 当啮合频率较小时,齿轮系统全局动力学特性较为简单且稳定; 随着啮合频率的增大,系统运动特性逐渐失稳, 且全局动力学特性变得复杂.
本文的研究为齿轮传动系统动力学行为的评价和控制、以及系统设计参数的选择具有一定的参考价值,也为其它非线性系统的深入研究提供了一种新的分析思路和方法.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 2]
[本文引用: 2]
[本文引用: 2]
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 2]
[本文引用: 2]
[本文引用: 2]
[本文引用: 4]
[本文引用: 2]
[本文引用: 2]
[本文引用: 2]
[本文引用: 2]
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
