配置柔顺机构空间机器人双臂捕获卫星操作力学模拟及基于神经网络的全阶滑模避撞柔顺控制 1)

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-01

朱安, 陈力^,²⁾福州大学机械工程及自动化学院,福州 350116

MECHANICAL SIMULATION AND FULL ORDER SLIDING MODE COLLISION AVOIDANCE COMPLIANT CONTROL BASED ON NEURAL NETWORK OF DUAL-ARM SPACE ROBOT WITH COMPLIANT MECHANISM CAPTURING SATELLITE ¹⁾

Zhu An, Chen Li^,²⁾College of Mechanical Engineering and Automation, Fuzhou University, Fuzhou 350116, China

通讯作者: *陈力,教授,主要研究方向：空间机器人系统动力学与控制. E-mail：chnle@fzu.edu.cn

收稿日期:2018-12-3接受日期:2019-02-1网络出版日期:2019-07-18

基金资助:

1)国家自然科学基金.11372073
国家自然科学基金.11072061
福建省工业机器人基础部件技术重大研发平台.2014H21010011

Received:2018-12-3Accepted:2019-02-1Online:2019-07-18
作者简介 About authors

摘要
讨论了空间机器人双臂捕获卫星操作过程避免关节冲击破坏的避撞柔顺控制问题. 为此在关节电机与机械臂之间设计了一种旋转型串联弹性执行器(rotatory series elastic actuator, RSEA)--柔顺机构,其作用在于：(1) 通过其内置弹簧的拉伸或压缩变形来吸收捕获操作过程中被捕获卫星对空间机器人关节产生的冲击能量;(2) 可以利用合理设计的与之配合的避撞柔顺控制策略来保证关节冲击力矩受限在安全范围. 首先,利用第二类Lagrange方程分别建立了捕获操作前含柔顺机构双臂空间机器人的开环分系统动力学模型与目标卫星的分系统动力学模型;之后,基于系统动量守恒关系、闭链系统位置与速度几何约束关系,获得了捕获操作后空间机器人与被捕获卫星闭链混合体系统综合动力学方程; 最后,基于RBF神经网络提出了一种捕获操作后两者混合体系统镇定运动的全阶终端滑模避撞柔顺控制方案. 所提方案结合柔顺机构在有效吸收、缓冲被捕获卫星冲击能量的同时,还在冲击能量过大时适时开、关空间机器人关节驱动器,以避免关节驱动器过载、破坏;此外,还通过最小权值范数法分配了机械臂各关节力矩,以保证双臂协调操作. Lyapunov稳定性理论证明了系统的全局稳定性,系统计算机数值仿真也验证了上述避撞柔顺控制策略的有效性.
关键词： 柔顺机构;空间机器人;双臂捕获卫星操作;力学模拟;避撞柔顺控制

Abstract
The problem of collision avoidance compliance control for dual-arm space robot to protect joint due to impact in the process of capturing satellite is discussed. For this reason, a rotatory series elastic actuator (RSEA), a compliant mechanism, is designed between the joint motor and the manipulator. It has two functions: firstly, the impact energy of satellite to robot joints can be absorbed by RSEA's built-in spring through stretching or compressing in the capture operation; secondly, the impact torque of the joints can be limited in the safe range by reasonably designing a matching collision avoidance compliance control strategy. First of all, the dual-arm space robot with compliant mechanism open-loop subsystem dynamics model and the target satellite subsystem dynamics model are established before capture operation by the second Lagrange equation. Then, based on the momentum conservation and geometric constraints of the position and velocity of the closed-chain system, the closed-chain hybrid system of the space robot and the captured satellite is obtained after the capture operation. Finally, for calm control the hybrid system, based on RBF neural network, a full-order terminal sliding mode collision avoidance compliance control scheme is proposed. The proposed scheme not only can effectively absorb and buffer the impact energy in the capture operation, but can turn on or off the space robot's joint motor timely when the impact energy is too large, so as to avoid overload and damage of the joint actuator. In addition, the joint torques are allocated by the minimum weight norm theory to ensure the coordinated operation between manipulators. The global stability of the system is proved by the Lyapunov theory. At last, the effectiveness of the collision avoidance compliance control strategy is verified by computer simulation.
Keywords：compliance mechanisms;space robots;dual-arm capture satellite operations;mechanical simulation;collision avoidance compliance control

PDF (3024KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex 收藏本文
本文引用格式
朱安, 陈力. 配置柔顺机构空间机器人双臂捕获卫星操作力学模拟及基于神经网络的全阶滑模避撞柔顺控制 ¹⁾. 力学学报[J], 2019, 51(4): 1156-1169 DOI:10.6052/0459-1879-18-407
Zhu An, Chen Li. MECHANICAL SIMULATION AND FULL ORDER SLIDING MODE COLLISION AVOIDANCE COMPLIANT CONTROL BASED ON NEURAL NETWORK OF DUAL-ARM SPACE ROBOT WITH COMPLIANT MECHANISM CAPTURING SATELLITE ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2019, 51(4): 1156-1169 DOI:10.6052/0459-1879-18-407

引言

随着人类对太空探索的不断深入,空间站的组装与维修,故障卫星的回收、太空垃圾的清理等任务已经成为各国关注的热点. 由于太空环境极其恶劣,让宇航员去完成上述任务不但所需费用高昂,而且宇航员也会面临许多危险,因此如何更好地让空间机器人代替宇航员完成上述任务被越来越多的****关注^[1-8]. 相较于单臂空间机器人系统,双臂空间机器人系统由于具有更高灵活性,更大的负载能力,能执行更加复杂的任务,因而正在逐渐成为空间机器人捕获操作研究的重点^[9-14]. 目前比较成熟的双臂或多臂空间机器人系统包括：已装配到国际空间站上的双臂空间机器人系统Dextre^[15]、Robonaut2^[16]; Maryland大学研制的遥控操作飞行机器人系统 Ranger^[17];美国正在研制的能对大多数非合作航天器进行捕获和维修的多臂空间机器人系统FREND^[18].

一般情况下,双臂空间机器人在轨捕获卫星的过程可分为：(1)对被捕获卫星进行观测,估计其相应的物理参数并对捕获路径进行规划;(2)让空间机器人逐渐的靠近被捕获卫星,进行捕获阶段的准备;(3)空间机器人末端执行器与被捕获卫星上的捕获点接触、碰撞;(4)捕获完成后,对空间机器人与被捕获卫星形成的混合体系统进行镇定控制. 双臂空间机器人捕获卫星操作过程存在非完整动力学约束,动量、动量矩与能量传递变化,捕获前后结构开、闭环变拓扑,闭环接触几何、运动学约束共存等问题,因此对双臂空间机器人进行研究将相对困难. Takahashi等^[19]研究了被捕获目标与双臂空间机器人发生碰撞后对机器人产生的影响;徐文福等^[20]研究了双臂空间机器人捕获目标的自主路径规划问题;董楸煌等^[21]研究了空间机器人捕获卫星过程的碰撞动力学模拟及镇定控制问题;程靖等^[22]研究了双臂空间机器人捕获卫星的力学分析与镇定控制;Jia等^[23]研究了闭链双臂空间机器人控制问题,并提出了一种自适应控制方法.

通常,在捕获操作的第3阶段,空间机器人会受到很大的冲击载荷,而关节是其最薄弱的部分,若不对关节进行保护很有可能造成捕获操作失败. 对空间机器人捕获卫星操作的研究虽然受到了众多****的关注,但大多数****的研究点都在对捕获碰撞过程的分析和对捕获完成后混合体系统的控制问题上. 值得注意的是,空间机器人的关节电机是其较为脆弱的部分,在捕获操作过程中由于机械臂末端会与卫星会发生碰撞从而导致关节电机承受较大的冲击力矩,然而关节电机能承受的冲击力矩是有限的,一旦其所受冲击力矩超过极限值,关节电机将会失效,从而导致捕获操作的失败甚至空间机器人的损坏. 因此,在空间机器人捕获卫星操作过程中是否对关节电机进行保护将决定捕获操作的成功与否,而本文的创新点就在于如何在空间机器人捕获卫星操作过程中实现对其关节电机的保护及捕获操作完成后在保护关节电机的情况下实现对在混合体系统的快速镇定控制. SEA (series elastic actuator)传动装置可以在机器人与外界环境发生碰撞时很好地保护机器人的关节^[24-26]. 本文提出一种RSEA (rotatory series elastic actuator)传动装置,使其可满足双臂空间机器人捕获卫星操作的要求. 由于RSEA传动装置的加入,空间机器人的关节具有一定的柔性,其将会使空间机器人机械臂在运动的过程中发生弹性振动,而弹性振动严重时有可能会使系统失稳,导致捕获的失败.

为了抑制弹性振动,考虑基于奇异摄动理论,将混合体系统分为快变子和慢变子系统,针对快变子系统,采用速度差值反馈控制策略^[27]. 由于空间机器人载体姿态的控制会不断的消耗液体燃料导致其质量不断地发生变化;另外恶劣的太空环境会使空间机器人系统参数摄动, 例如机械臂向阳面和背阳面的温度分布不均会导致机械臂质心发生变化等. 因此,一般情况下,建立的空间机器人系统动力学模型是存在误差的. 虽然消除建模误差的方法有很多,例如自适应控制,但其参数可调性较差;而RBF神经网络可以任意精度逼近非线性项^[28-29], 故综合考虑下,采用其弥合因建模误差引入的不确定项. 由于滑模控制具有良好的鲁棒性而应用广泛,但传统滑模控制因存在切换项导致抖振问题不可避免,而全阶滑模控制不存在切换项,因此其可以在保持传统滑模控制鲁棒性强优点的同时,还能克服抖振的问题^[30];空间机器人捕获卫星后要求其能快速镇定,而终端滑模控制可以实现系统在有限时间内收敛^[31-33],因此其引入可以使系统快满足这一要求. 故基于上述描述,针对慢变子系统,提出一种基于RBF神经网络的全阶终端滑模控制策略.

为了在双臂空间机器人捕获卫星操作过程中保护其关节电机,本文提出一种由RSEA传动装置构成的柔顺机构;根据第二类Lagrange方程分别得到双臂空间机器人系统和被捕获卫星系统的动力学方程;利用力的传递关系及动量守恒定律,研究了机械臂末端与被捕获目标卫星发生碰撞的冲击效应;然后结合牛顿第三定律以及捕获位置的线速度和角速度约束,获得了混合体系统动力学方程;最后通过对含RSEA传动装置的双臂空间机器人捕获卫星操作过程进行仿真分析,验证了RSEA的抗冲击性能及所提策略的有效性.

1 柔顺装置结构及避撞策略

含柔顺装置的双臂空间机器人机械臂的主动关节由电机通过RSEA 传动装置驱动,所设计的RSEA传动装置结构见图1. 其由输入圆盘(与外部电机相连)、传动弹簧组、支撑中轴、负载空心轴和扫臂构成. 扫臂为星形且3只扫臂呈120$^{\circ}$均布,扫臂的空心轴通过轴承与固定在输入圆盘上的支撑中轴连接;3组线弹簧呈内接等边三角形布置,安装在输入圆盘的附加挡块和扫臂之间,每组弹簧有2根,共同驱动1只扫臂. 图中$ {R}$为扫臂的有效半径,$ {r}$为弹簧的半径.

图1

新窗口打开|下载原图ZIP|生成PPT
图1RSEA传动装置结构图

Fig. 1Structure of RSEA

在捕获阶段,机械臂末端与被捕获卫星发生碰撞,机械臂关节处会产生很大的冲击力矩,该力矩先作用在RSEA传动装置的扫臂上, 扫臂再把力传递给弹簧使得弹簧压缩或拉伸,从而把碰撞产生的能量存储在弹簧里,实现对关节的保护. 在镇定控制阶段,由于碰撞时产生的碰撞冲击效应,电机开启时关节也会受到冲击力矩,若力矩超过关节所能承受的极限而不关停电机,关节很可能会发生损坏. 但由于闭链约束的存在,若仅仅关闭超过极限力矩的电机,混合体系统将会形成欠驱动系统,由于其他电机仍在正常工作,此时该关节所受的冲击力矩将不会减小. 因此,需要根据关节所能承受的极限力矩设置一个关机力矩阀值让所有电机都关停. 当检测到某个关节所受冲击力矩超过所设关机力矩阀值后所有电机都关停,由于RSEA传动装置的存在,其内部被压缩的弹簧将会提供弹力来减小关节所受冲击力矩. 然而,在实际操作中,如果只设定一个关机力矩阀值,电机将会频繁的开关机,这很容易造成电机的损坏. 由此,本文所提的柔顺控制策略同时设置了电机关机力矩阀值和开机力矩阀值. 当关节所受力矩超过关机力矩阀值时,电机关停;当关节所受力矩低于开机力矩阀值时,电机再次开机.

2 空间机器人捕获卫星操作过程的碰撞分析

2.1 空间机器人与被捕获卫星动力学建模

空间机器人系统与被捕获卫星系统如图2所示.其中$O_0$, $O_i$ $(i = 1, 2, \cdots, 6)$, $O_{s} $分别为载体质心、各关节铰中心、卫星质心;$b_{L}$, $b_{R} $分别为左、右机械臂末端;$b'_{L}$, $b'_{R}$分别为卫星左、右把手末端;$XOY$为系统随轨道平动的惯性参考坐标系;$x_{0}O_{0} y_{0} $, $x_{s} O_{s} y_{s}$分别为固定在载体质心、被捕获卫星质心上的坐标系;$x_i O_i y_i$ $(i = 1, 2, \cdots, 6 )$是固定在关节铰中心的连杆坐标系. 文中所用符号定义如下：$m_{ 0} , I_{ 0}, L_{ 0} $分别为载体质量、转动惯量和质心$O_0 $到$O_1$或$O_4$的距离;$m_{s}, I_{s}, d_{s} $分别为卫星的质量、转动惯量和质心到两端末端把手的距离;$m_i$, $I_i$, $L_i $ $(i = 1, 2, \cdots, 6)$分别为第$i$个机械臂的质量、转动惯量、长度; $I_{{m}i}$ $(i = 1, 2, \cdots, 6)$ 为第$i$个电机转子的转动惯量;$d_i $ $(i = 1, 2, \cdots, 6)$为第$i$个关节铰中心到机械臂$i$质心的距离; $k_{{s}i}$ $(i = 1, 2, \cdots, 6 )$为第$i$个RSEA传动装置中弹簧的刚度;$\theta _{0}$, $\theta _i$, $\theta _{s}$, $\theta _{{m}i}$ $(i = 1, 2, \cdots, 6 )$分别为载体姿态角、机械臂转角、卫星姿态角和电机转子转角;$\psi _1$, $\psi _2 $分别为载体质心$O_0 $分别与$O_1 ,\;O_4 $连线相对$x_0 $轴的夹角.

图2

新窗口打开|下载原图ZIP|生成PPT
图2含RSEA的双臂空间机器人系统及被捕获卫星系统

Fig. 2Dual-arm space robot with RSEA and satellite systems

定义空间机器人系统广义坐标列向量为${\pmb q}_{r} = [x_0 ,y_0 ,\theta _0 , {\pmb \theta }_{ L}^{T}, {\pmb \theta }_{R}^{T} ]^{T}$, ${\pmb \theta }_{L} = [ \theta _1 ,\theta _2 ,\theta _3 ]^{T}$, ${\pmb \theta }_{R} = [ \theta _4 ,\theta _5 ,\theta _6 ]^{T}$;定义卫星系统广义坐标列向量为${\pmb q}_{s} =[x_{s} ,y_{s} ,\theta _{s} ]^{T}$;定义${\pmb e}_x^{(i)}$ $(i = 0, 1, \cdots ,6)$, ${\pmb e}_x^{({s})} $分别为空间机器人各连体坐标系、卫星坐标主轴方向的单位向量,${\pmb e}_x^{({L})}$, ${\pmb e}_x^{({R})} $分别为$O_0 $与$O_1 ,\;O_4 $连线方向上的单位向量. 由此,可将空间机器人载体质心位置矢径${\pmb r}_0 $,各机械臂质心位置矢径${\pmb r}_i$ $(i = 1, 2, \cdots, 6)$,机械臂左、右末端位置矢径${\pmb r}_{{bL}}$, ${\pmb r}_{{bR}} $,被捕获卫星质心位置矢径${\pmb r}_{s} $,被捕获卫星末端把手位置矢径${\pmb r}'_{{ bL}}$, ${\pmb r}'_{{bR}} $表示为

(1)$ \left.\!\!\begin{array} {\pmb r}_0 =(x_0 ,y_0 )^{T} \\ {\pmb r}_1 = {\pmb r}_0 + L_0 {\pmb e}_x^{({L})} + d_1 {\pmb e}_x^{(1)} \\ {\pmb r}_2 = {\pmb r}_0 + L_0 {\pmb e}_x^{({L})} + L_1 {\pmb e}_x^{(1)} + d_2 {\pmb e}_x^{(2)} \\ {\pmb r}_3 = {\pmb r}_0 + L_0 {\pmb e}_x^{({L})} + L_1 {\pmb e}_x^{(1)} + L_2 {\pmb e}_x^{(2)} + d_3 {\pmb e}_x^{(3)} \\ {\pmb r}_4 = {\pmb r}_0 + L_0 {\pmb e}_x^{({R})} + d_4 {\pmb e}_x^{(4)} \\ {\pmb r}_5 = {\pmb r}_0 + L_0 {\pmb e}_x^{({R})} + L_4 {\pmb e}_x^{(4)} + d_5 {\pmb e}_x^{(5)} \\ {\pmb r}_6 = {\pmb r}_0 + L_0 {\pmb e}_x^{({R})} + L_4 {\pmb e}_x^{(4)} + L_5 {\pmb e}_x^{(5)} + d_6 {\pmb e}_x^{(6)} \\ {\pmb r}_{s} = (x_{s} ,y_{s} ) \end{array}\!\!\right\} $

(2)$ \left.\begin{array} {\pmb r}_{{bL}} = {\pmb r}_0 + L_0 {\pmb e}_x^{({L})} + L_1 {\pmb e}_x^{(1)} + L_2 {\pmb e}_x^{(2)} + L_3 {\pmb e}_x^{(3)} \\ {\pmb r}_{{bR}} = {\pmb r}_0 + L_0 {\pmb e}_x^{({R})} + L_4 {\pmb e}_x^{(4)} + L_5 {\pmb e}_x^{(5)} + L_6 {\pmb e}_x^{(6)} \\ {\pmb r}'_{{bL}} = {\pmb r}_{s}-d_{s} {\pmb e}_x^{({s})} \\ {\pmb r}'_{{bR}} = {\pmb r }_{s} + d_{s} {\pmb e }_x^{({s})} \end{array}\!\!\right\} $

其中,$x_0, y_0 $为基座质心坐标,$x_{s}, y_{s} $为卫星质心坐标. 对式(1)求导可得空间机器人系统动能$T_{r} $与卫星系统动能$T_{s} $分别为

(3)$ \left.\begin{array} T_{r} = \sum _{i = 0}^6 \Big(\dfrac{1}{2} I_i \omega _i^2 + \dfrac{1}{2}m_i \dot{\pmb r}_i^2 \Big ) + \sum_{j = 1}^6 \Big (\dfrac{1}{2}I_{{m}j} \omega _{{m}j}^2 \Big ) \\ T_{s} = \dfrac{1}{2}I_{s} \omega _{s}^{2} + \dfrac{1}{2}m_{s} \dot {r}_{s}^{2} \end{array}\!\!\right\} $

其中,$\omega _i$ $(i = 1, 2, \cdots, 6)$, $\omega _{{m}j}$ $(j = 1, 2, \cdots, 6)$, $\omega _{s}$分别为载体与各机械臂、电机转子、卫星的角速度.

对式(2)求导可得空间机器人末端速度、卫星把手速度与广义速度的关系为

(4)$\left.\begin{array} {\pmb S}_{b} = {\pmb J}_{r} \dot {\pmb q}_{r} \\ {\pmb S}'_{b} = {\pmb J}_{s} \dot {\pmb q}_{s} \end{array}\!\! \right\}$

其中,${\pmb S}_{b} = [\dot {x}_{{bL}} ,\dot {y}_{{bL}} ,\dot {\theta }_{{bL}} ,\dot {x}_{{bR}}, \dot {y}_{{bR}} ,\dot {\theta }_{{bR}} ]^{T}$, ${\pmb S}'_{b} = [\dot {x}'_{bL} , \dot {y}'_{bL}$, $\dot {\theta }'_{bL}, \dot {x}'_{bR}, \dot {y}'_{bR}, \dot {\theta }'_{bR} ]^{T}$分别为机械臂末端$b_{L} $和$b_{R} $, $b'_{L} $和$b'_{R} $上的线速度和角速度列向量;${\pmb J}_{r} \in {\pmb R}^{6\times 9}$, ${\pmb J}_{s} \in {\pmb R}^{6\times 3}$为空间机器人末端、卫星把手对应的运动Jacobian矩阵.

若忽略太空的微重力,空间机器人的势能只来源于RSEA的弹性势能. 因此空间机器人系统势能$U_{r} $与卫星系统势能$U_{s} $分别为

(5)$\left.\begin{array}{l} U_{r} = \sum_{i = 1}^6 \Big [ \dfrac{3}{2}k_{si}(\Delta x_{Li}^2 + \Delta x_{Ri}^2 ) \Big ] \\ U_{s} = 0 \end{array}\!\! \right\} $

其中, $\Delta x_{{L}i} = x(\phi _i )$, $\Delta x_{{R}i} =-x(\phi _i )$, $x(\phi _i ) = R\sin \phi _i $ $(i = 0, 1, \cdots, 6)$;$x(\phi _i )$为第$i$个RSEA传动装置的一个挡块上弹簧的变形量,$\Delta x_{Li} $为左侧弹簧变形量,$\Delta x_{Ri} $为右侧弹簧变形量,$\phi _i $为输入圆盘与扫臂之间的角度差.

结合式(3) ~式(5)和第二类Lagrange方程,可得未发生碰撞前含RSEA传动装置的双臂空间机器人系统与卫星系统动力学方程分别为

(6a)$ {\pmb D}_{r}({\pmb q}_{r})\ddot{\pmb q}_{r}+{\pmb C}_{r}({\pmb q}_{r}, \dot{\pmb q}_{r})\dot{\pmb q}_{r}={\pmb \tau}_{r}+{\pmb J}^{T}_{r}{\pmb F}_{r} $

(6b)$ {\pmb I}_{m}\ddot{\pmb q}_{m}+ {\pmb K}({\pmb q}_{m}-{\pmb q}_{\theta } ) = {\pmb \tau }_{m} $

(6c)$ {\pmb K}({\pmb q}_{m}-{\pmb q}_{\theta } ) = {\pmb \tau }_{\theta } $

(7)$ {\pmb D}_{s}\ddot{\pmb q}_{s}={\pmb J}^{T}_{s} {\pmb F}_{r} $

式中,${\pmb D}_{r} \in {\pmb R}^{9\times 9}$, ${\pmb D}_{s} \in {\pmb R}^{3\times 3}$分别为空间机器人与卫星对称、正定的惯量矩阵, ${\pmb C}_{r} \dot {\pmb q}_{r} \in {\pmb R}^{9\times 1}$为空间机器人包含科氏力、离心力矩阵;${\pmb q}_{m} = [\theta _{{m1}}$, $\theta _{{m2}}$, $\theta _{{m3}}$, $\theta _{{m4}}$, $\theta _{{m5}}$, $\theta _{{m6}} ]^{T}$,${\pmb q}_{\theta } = [\theta _1 ,\theta _2 ,\theta _3 ,\theta _4 ,\theta _5 ,\theta _6 ]^ {T}$;${\pmb \tau }_{R} = [{\pmb \tau }_{B}^{T} , {\pmb \tau }_{L}^{T} , {\pmb \tau }_{R}^{T} ]^{T}$为基座及各机械臂控制力矩列向量,${\pmb \tau }_{B} = [0,0,\tau _0 ]^{ T}$为基座控制力矩列向量,${\pmb \tau }_{L} = [\tau _1 ,\tau _2 ,\tau _3 ]^{T}$, $ {\pmb \tau }_{ R} = [ \tau _4 ,\tau _5 ,\tau _6 ]^{T}$分别为左、右侧机械臂控制力矩列向量,${\pmb \tau }_{m} = [\tau _{{m1}} ,\tau _{{m2}} ,\tau _{{m3}} ,\tau _{{m4}} ,\tau _{{m5}} ,\tau _{{m6}} ]^{T}$为电机输出力矩列向量,${\pmb \tau }_{\theta } = [ {\pmb \tau }_{L}^{T} , {\pmb \tau }_{R}^{T} ]^{T}$;${\pmb I }_{m} ={diag} (I_{{m1}} ,I_{{m2}} ,I_{{m3}} ,I_{{m4}} ,I_{{m5}} ,I_{{m6}} )$为电机转子转动惯量矩阵;${\pmb K} ={diag} (k_1 ,k_2 ,k_3 ,k_4 ,k_5 ,k_6 )$为关节等效刚度矩阵,具体计算公式在仿真处给出;${\pmb F }_{r} $, $ {\pmb F}'_{r} \in {\pmb R }^{6\times 1}$分别为空间机器人和卫星上的相互作用力、力矩列向量,且有${\pmb F }_{r} = -{\pmb F }'_{ r} $.

2.2 空间机器人捕获卫星操作过程的碰撞冲击效应分析

捕获操作过程中,双臂空间机器人与被捕获卫星发生碰撞,由于相互作用力的存在,各自的运动状态会发生变化. 卫星把手上的力可分解为

(8)$ {\pmb F }'_{r} =({\pmb J }_{s}^{T} ) + {\pmb M }_{s} \ddot{\pmb q }_{s} + {\pmb F }_{I} $

其中,$({\pmb J }_{s}^{T} )^ + $表示${\pmb J }_{s}^{T} $的伪逆,其定义为：$({\pmb J }_{ s}^{T} )^ + = {\pmb J }_{s} ({\pmb J }_{s}^{T} {\pmb J }_{s} )^{-1}$. ${\pmb F }_{ I} $为在碰撞时间内左右机械臂非协调运动导致对卫星的压紧力或拉力,定义在$ {\pmb J}_{s}^{T} $零空间内,有${\pmb J }_{s}^{T} {\pmb F }_{I} = 0$. 由式(6a)、式(7)、式(8)可得

(9)$ {\pmb D }_{r}({\pmb q }_{r} ) \ddot {\pmb q }_{r} + {\pmb C }_{r} ({\pmb q }_{r} ,\dot {\pmb q }_{r} ) \dot{\pmb q }_{r} = {\pmb \tau }_{r}-{\pmb J }_{r}^{T} ({\pmb J }_{s}^{T} )^ + {\pmb M }_{s} \ddot {\pmb q}_{s}-{\pmb J}_{R}^{T} {\pmb F}_{I} $

捕获操作完成后,空间机器人与被捕获卫星锁紧固连形成闭链系统. 在闭链系统内,机器人左机械臂末端矢径${\pmb r}_{{bL}} $与卫星左把手矢径${\pmb r}'_{{bL}} $可表示为

(10)$\left. \begin{array}{l} {\pmb r}_{{bL}}(t_0 + \Delta t ) = {\pmb r }_{{OL}} + L_1 {\pmb e }_x^{(1)} + L_2 {\pmb e }_x^{(2)} + L_3 {\pmb e }_x^{(3)} \\ {\pmb r }'_{{bL}} ( t_0 + \Delta t ) = {\pmb r }_{{OR}} + L_4 {\pmb e }_x^{(4)} + L_5 {\pmb e}_x^{(5)} + (L_6 + 2d_{s} ){\pmb e }_x^{(3)} \end{array} \!\! \right\} $

其中,${\pmb r}_{{OL}} = (x_{{OL}} ,y_{{OL}} )^{T}$, ${\pmb r}_{{OR}} = (x_{{OR}} ,y_{{OR}} )^{T}$分别为基座质心${ O}_0 $到${ O}_1 $, ${O}_4 $的矢径. 对式(10)求导得

(11)$ \left. \begin{array}{l} \dot{\pmb r}_{{bL}}(t_0 + \Delta t) = \dot {\pmb r}_{{OL}} + L_1 \dot{\pmb e}_x^{(1)} + L_2 \dot{\pmb e}_x^{(2)} + L_3 \dot{\pmb e}_x^{(3)} \\ \dot {\pmb r}'_{{bL}} ( t_0 + \Delta t ) = \dot{\pmb r}_{{OR}} + L_4 \dot {\pmb e}_x^{(4)} + L_5 \dot {\pmb e}_x^{(5)} + (L_6 + 2d_{s} ) \dot{\pmb e}_x^{(3)} \end{array} \!\! \right\} $

捕获操作完成后满足相关点的位置约束和速度约束

(12a)$ {\pmb r}_{{bL}} (t_0 +\Delta t) = {\pmb r}'_{{bL}} ( t_0 + \Delta t ) $

(12b)$ \dot{\pmb r}_{{bL}}(t_0 + \Delta t) = \dot {\pmb r}'_{{bL}} ( t_0 + \Delta t) $

结合式(10) $\sim $式(12b)可得左、右臂广义坐标与广义速度存在如下关系

(13a)$ \theta _1 + \theta _2 + \theta _3 = \theta _4 + \theta _5 + \theta _6 + k \pi $

(13b)$ \dot {\theta }_1 + \dot {\theta }_2 + \dot {\theta }_3 = \dot {\theta }_4 + \dot {\theta }_5 + \dot {\theta }_6 $

由六边形内角和定理可计算出$k =-1$. 可把式(12b)和式(13b)重新写成

(14)$\left.\begin{array} {\pmb J}_{{OL1}} \dot{\pmb \theta }_{L} = {\pmb J}_{{OR1}} \dot {\pmb \theta }_{R} \\ \dot {\theta }_1 + \dot {\theta }_2 + \dot {\theta }_3-\dot {\theta }_4-\dot {\theta }_5-\dot {\theta }_6 = 0 \end{array}\!\! \right\}$

式中,${\pmb J}_{{OL1}} \in {\pmb R}^{2\times 3}$, ${\pmb J}_{{OR1}} \in {\pmb R}^{2\times 3}$分别为基座连体坐标系下两个运动相关点对应的运动Jacobian矩阵. 可把式(14)合并为

(15)${\pmb J}_{{OL}} \dot{\pmb \theta}_{L} = {\pmb J}_{{OR}} \dot {\pmb \theta }_{R}$

式中,${\pmb J}_{{OL}} = [{\pmb J}_{{OL1}}^{T}$, ${\pmb E}_{3\times 1} ]^{T}$, ${\pmb J}_{{OR}}= [{\pmb J}_{{OR1}}^{T}$, ${\pmb E}_{3\times 1} ]^{T}$,${\pmb E}_{{m}\times {n}} $表示${ m}\times { n}$阶元素均为1的矩阵. 设${\pmb q}_{L} = [x_0 ,y_0 ,\theta _0 ,{\pmb \theta }_{L}^{T} ]^{T}$为闭链系统广义坐标列向量,由式(15)可得

(16)$\dot {\pmb q}_{r} = {\pmb U}^{T} \dot {\pmb q}_{L}$

式中,${\pmb U} = [{\pmb E}_{6\times 6}$, ${\pmb U}_{1}^{T} ], {\pmb U}_1 = [{\pmb 0}_{3\times 3} , {\pmb J}_{{OR}}^{-1} {\pmb J}_{{OL}} ]$.

捕获操作完成后,式(4)依然成立,由相关点的速度约束得

(17)${\pmb J}_{{rL1}} \dot {\pmb q}_{L}(t) = {\pmb J}_{{sL1}} \dot {\pmb q}_{s} (t) $

式中,${\pmb J}_{{rL1}} \in {\pmb R}^{2\times 6}$, ${\pmb J}_{{sL1}} \in {\pmb R}^{2\times 3}$分别为机器人左臂末端点、被捕获卫星左把手在惯性参考坐标系下对应的运动Jacobian矩阵. 把式(15)、式(17)合并为

(18)${\pmb J}_{{rL}} \dot {\pmb q}_{L}(t) = {\pmb J}_{{sL}} \dot {\pmb q}_{s} (t) $

式中,${\pmb J}_{{rL}} = [{\pmb J}_{{rL1}}^{T} , {\pmb G}_1^{T} ]^{T}, {\pmb G}_1 = [{\pmb 0}_{1\times 2} ,{\pmb E}_{1\times 4} ]$;${\pmb J}_{{sL}} = [{\pmb J}_{{sL1}}^{T} ,{\pmb G}_2^{T} ]^{T}$,${\pmb G}_2 = [{\bf 0}_{1\times 2} ,1]$. 由式(18)可得

(19)$\dot {\pmb q}_{s}(t_0 + \Delta t) = {\pmb J}_{{sL}}^{-1} {\pmb J}_{{rL}} \dot {\pmb q}_{L} (t_0 + \Delta t) $

对式(6a)、式(7)两端积分得

(20)$ \left.\begin{array}{l} \int_{t_0 }^{t_0 + \Delta t} \left[ {{\pmb D}_{r}({\pmb q}_{r} ) \ddot{\pmb q}_{r} + {\pmb C}_{r} ( {\pmb q}_{r},\dot{\pmb q}_{r} ) \dot {\pmb q}_{r} } \right]{d} t =\\ \qquad \int_{t_0 }^{t_0 + \Delta t} ( {\pmb \tau }_{r} + {\pmb J}_{r}^{T} {\pmb F}_{r} ){d} t \\ \int_{t_0 }^{t_0 + \Delta t} {\pmb D}_{s} \ddot {\pmb q}_{s} {d}t = \int_{t_0 }^{t_0 + \Delta t} {\pmb J}_{s}^{T} {\pmb F}'_{R} {d} t \end{array} \!\! \right\} $

式中,$t_0 $为碰撞前的时刻. 由于碰撞时间$\Delta t$很短,在这一时段可认为系统的广义坐标未发生突变,仅有广义速度和广义加速度发生了突变. 为了保护关节电机,捕获碰撞阶段电机处于关机状态,因此式(20)可以近似为

(21a)$ {\pmb D}_{r} \left[ { \dot{\pmb q}_{r} ( t_{0} + \Delta t ) - \dot {\pmb q }_{r} (t_0 )} \right] = {\pmb J}_{r}^{T} {\pmb f}_{r} $

(21b)$ {\pmb D}_{s} \left[ { \dot{\pmb q}_{s} (t_{0} + \Delta t)-\dot {\pmb q}_{s} (t_0 )} \right] = {\pmb J}_{s}^{T} {\pmb f}'_{r} $

式中,${\pmb f}_{r} = \int_{t_0 }^{t_0 + \Delta t} {\pmb F}_{r} {d}t$, ${\pmb f}'_{r} = \int_{t_0 }^{t_0 + \Delta t} {\pmb F}'_{r} {d}t$为碰撞冲量,且满足关系${\pmb f}_{ r} =-{\pmb f}'_{r} $. 由${\pmb f}_{r}$, ${\pmb f}'_{r} $的关系,式(21a)、式(21b)可合并成如下形式

(22)$ \begin{array}{l} {\pmb D}_{r} \left[ { \dot {\pmb q}_{r}(t_{0} + \Delta t)-\dot{\pmb q}_{r} (t_0 )} \right] + \\ \qquad {\pmb J}_{r}^{T} ({\pmb J}_{s}^{T} )^ + {\pmb D}_{s} \left[ { \dot {\pmb q}_{s} (t_{0} + \Delta t )-\dot{\pmb q}_{s} (t_0 )} \right] = {\bf 0} \end{array} $

将式(16)、式(19)代入式(22)可得

(23)$ \begin{array}{l} {\pmb U \pmb D}_{r} {\pmb U}^{T}\left[ { \dot {\pmb q}_{L}(t_0 + \Delta t)- \dot {\pmb q}_{L} (t_0 )} \right] + \\ \qquad {\pmb U\pmb J}_{r}^{T} ({\pmb J}_{s}^{T} )^ + {\pmb D}_{s} \left[ {{\pmb J}_{{sL}}^{-1} {\pmb J}_{{rL}} \dot {\pmb q}_{L} (t_0 + \Delta t)- \dot {\pmb q}_{s} (t_0 )} \right] = {\bf 0} \end{array} $

由式(23)可解出

(24)$\dot{\pmb q}_{L}(t_0 + \Delta t) = {\pmb A}^{-1}\left[ {{\pmb L}\dot {\pmb q}_{L} (t_0 ) + {\pmb B}\dot {\pmb q}_{s} (t_0 )} \right] $

式中,${\pmb L} = {\pmb U\pmb D}_{r} {\pmb U}^{T}$, $ {\pmb A} = {\pmb L} + {\pmb B\pmb J}_{{sL}}^{-1} {\pmb J}_{{rL}} $, ${\pmb B} = {\pmb U \pmb J}_{ r}^{T} ({\pmb J}_{s}^{T} )^ + {\pmb D}_{s} $. 把式(16)、式(24)代入式(21a)得

(25)${\pmb f}_{r} =({\pmb J}_{r}^{T} )^ + {\pmb D}_{r} \left[ {({\pmb U}^{T}{\pmb A}^{-1}{\pmb L}-{\pmb U}^{T}) \dot{\pmb q}_{L} (t_0 ) + {\pmb U}^{T}{\pmb A}^{-1}{\pmb B}\dot{\pmb q}_{s} (t_0 )} \right] $

由于$\Delta t$非常小,可以把碰撞力${\pmb F}_{r} $近似为

(26)${\pmb F}_{r} = \dfrac{{\pmb f}_{r} }{\Delta t}$

2.3 完全能控形式的闭链混合体系统动力学模型

对式(16)、式(19)求导并整理得

(27)$\left.\begin{array}{l} \ddot{\pmb q}_{r} = \dot{\pmb U}^{T} \dot {\pmb q}_{L} + {\pmb U}^{T}\ddot{\pmb q}_{L} \\ \ddot{\pmb q}_{s} = {\pmb J}_{{sL}}^{-1}(\dot{\pmb J}_{{rL}} \dot{\pmb q}_{L} + {\pmb J}_{{rL}} \ddot{\pmb q}_{L}-\dot {\pmb J}_{{sL}} {\pmb J}_{{sL}}^{ -1} {\pmb J}_{{rL}} \dot{\pmb q}_{L} ) \end{array} \!\!\right\} $

将式(16)、式(19)、式(27)代入式(9)并整理得

(28)${\pmb D}_{h} \ddot{\pmb q}_{L}-{\pmb C}_{h} \dot{\pmb q}_{L} = {\pmb \tau }_{h}-{\pmb F}_{{Ih}}$

其中

$ {\pmb D}_{h} = {\pmb L} + {\pmb B\pmb J}_{{sL}}^{-1} {\pmb J}_{{rL}} \\ {\pmb C}_{ h} = {\pmb U \pmb C}_{r} {\pmb U}^{T} + {\pmb U \pmb D}_{r} \dot{\pmb U}^{T} + {\pmb B\pmb J}_{{sL}}^{-1} (\dot{\pmb J}_{{rL}}-\dot{\pmb J}_{{sL}} {\pmb J}_{{sL}}^{ -1} {\pmb J}_{{rL}} )\\ {\pmb \tau }_{h} = {\pmb U\pmb \tau }_{r} , \ \ {\pmb F}_{{Ih}} = {\pmb U\pmb J}_{r}^{T} {\pmb F}_{I} $

将${\pmb \tau }_{h} $, ${\pmb F}_{{Ih}} $进行如下分块

(29)$\left. \begin{array}{l} {\pmb \tau }_{h} = [{\pmb \tau }_{{ha}}^{T} ,{\pmb \tau }_{{hb}}^{T} ]^{T} \\ {\pmb F}_{{Ih}} = [{\pmb F}_{{Iha}}^{T} ,{\pmb F}_{{Iha}}^{T} ]^{T} \end{array} \!\! \right\}$

其中,${\pmb \tau }_{{ha}} \in {\pmb R}^{3\times 1},{\pmb \tau }_{{hb}} \in {\pmb R}^{3\times 1},{\pmb F}_{{Iha}} \in {\pmb R}^{2\times 1},{\pmb F}_{{Iha}} \in {\pmb R}^{4\times 1}$. 将${\pmb U}$和$ {\pmb J}_{r} $的表达式代入到${\pmb \tau }_{h} $和${\pmb F}_{{Ih}} $的表达式中可得

(30)$\left. \begin{array}{l} {\pmb \tau }_{{ha}} = [0,0,\tau _0 ]^{T} \\ {\pmb \tau }_{{hb}} = {\pmb \varLambda }[{\pmb \tau }_{L}^{T} ,{\pmb \tau}_{R}^{T} ]^{T} \end{array} \right\}$

(31)${\pmb F}_{{Ih}} = [0,0,{\pmb F}_{{Ihb}}^{T} ]^{T}$

式中, ${\pmb \varLambda } = [{\pmb E}_{3\times 3} ,({\pmb J}_{{OR}}^{-1} {\pmb J}_{{OL}} )^{ T}]$. 对式(28)进行如下分块

(32)$ \left[ \!\! \begin{array}{cc} {\pmb D}_{{h11}} & {\pmb D}_{{h12}} \\ {\pmb D}_{{h21}} & {\pmb D}_{{h22}} \end{array} \!\! \right]\left[\!\!\begin{array}{c} {\ddot{\pmb q}_{N} } \\ {\ddot{\pmb q}_{c} } \end{array} \!\! \right] + \left[\!\! \begin{array}{cc} {\pmb C}_{{h11}} &{\pmb C}_{{h12}} \\ {\pmb C}_{{h21}} & {\pmb C}_{{h22}} \end{array} \!\! \right]\left[\!\!\begin{array}{c} \dot{\pmb q}_{N}\\ \dot{\pmb q}_{c} \end{array} \!\! \right] = \\ \qquad \left[\!\!\begin{array}{c} {\bf 0}_{2\times 1} \\ {\pmb \tau }_{c} \end{array} \!\! \right]-\left[\!\!\begin{array}{c} {\bf 0}_{2\times 1} \\ {\pmb F}_{{Ihb}} \end{array} \!\!\right]$

式中,${\pmb D}_{{h11}} \in {\pmb R}^{2\times 2}$,${\pmb D}_{{h12}} \in {\pmb R}^{2\times 4}\\, {\pmb D}_{{h21}} \in {\pmb R}^{4\times 2}$,${\pmb D}_{{h22}} \in {\pmb R}^{4\times 4}\\ , {\pmb C}_{{ h11}} \in {\pmb R}^{2\times 2}$,${\pmb C}_{{h12}} \in {\pmb R}^{2\times 4}$,${\pmb C}_{{h21}} \in {\pmb R}^{4\times 2}\\ , {\pmb C}_{{h22}} \in {\pmb R}^{4\times 4}$,${\pmb q}_{N} = [x_0 ,y_0 ]^{T}$,${\pmb q}_{c} = [\theta _0,{\pmb \theta }_{L}^{T} ]^{T}$,${\pmb \tau }_{c} = [\tau _0 , {\pmb \tau }_{{hb}} ]^{T}$.

捕获操作完成后机械臂末端执行器与被捕获卫星把手锁紧,因此内力项对闭链混合体系统运动无影响. 由于闭链混合体系统不受外力作用,通过观察发现$ {\pmb C}_{{h11}} $和${\pmb C}_{{h21}} $的元素均为零,故可解得完全能控形式的闭链混合体系统动力学模型为

(33a)$ {\pmb D}_{c} \ddot{\pmb q}_{c} + {\pmb C}_{c} \dot{\pmb q}_{c} = {\pmb \tau }_{c} $

(33b)$ {\pmb I}_{m} \ddot{\pmb q}_{m} + {\pmb K}( {\pmb q}_{m}-{\pmb q}_{ \theta } ) = {\pmb \tau }_{m} $

(33c)$ {\pmb K}({\pmb q}_{m}-{\pmb q}_{\theta } ) = {\pmb \tau }_{\theta } $

式中, ${\pmb D}_{c} = {\pmb D}_{{h22}}-{\pmb D}_{{h21}} {\pmb D}_{{h11}}^{-1} {\pmb D}_{{h12}}$, ${\pmb C}_{c} = {\pmb C}_{{h22}}-{\pmb D}_{{h21}} {\pmb D}_{{ h11}}^{-1} {\pmb C}_{{h12}} $.

3 控制器的设计

3.1 快变子系统控制器设计

由于RSEA传动装置的引入,空间机器人关节具有一定的柔性,这将会使得机械臂在运动的过程中发生弹性振动,为了抑制这个弹性振动,基于奇异摄动理论,将闭链混合体系统分为快变子系统和慢变子系统分别进行控制. 基于此,关节电机输出力矩可以表示为

(34)${\pmb \tau }_{m} = {\pmb \tau }_{s} + {\pmb \tau }_{f}$

式中,${\pmb \tau }_{f} \in {\pmb R}^{6\times 1}$为快变子系统力矩,${\pmb \tau }_{s} \in {\pmb R}^{6\times 1}$为慢变子系统力矩.

令系统"快变"量为${\pmb T}_{\theta } = {\pmb K}( {\pmb q}_{m}-{\pmb q}_{\theta } )$,定义正比例因子$\varepsilon $及正定的对角矩阵${\pmb K}_1 $,取值满足如下关系

(35)${\pmb K} = \dfrac{{\pmb K}_1 }{\varepsilon ^2}$

因此可将式(33b)、式(33c)重写为如下形式

(36)$\varepsilon ^2\ddot{\pmb T}_{\theta } = {\pmb I}_{m}^{-1} {\pmb K}_1({\pmb \tau }_{m}-{\pmb I}_{m} \ddot{\pmb q}_{\theta }-{\pmb T}_{\theta } ) $

采用速度差值反馈器来设计如下形式的快变子控制方法

(37)${\pmb \tau }_{f} =-{\pmb K}_{f}(\dot {\pmb q}_{m}-\dot{\pmb q}_{\theta } ) $

式中,${\pmb K}_{f} = K_2 / \varepsilon $,${\pmb K}_2 \in {\pmb R}^{6\times 6}$为正定对角矩阵. 将式(34)、式(37)代入式(36) 得

(38)$\varepsilon ^2{\pmb I}_{m} \ddot{\pmb T}_{\theta } + \varepsilon {\pmb K}_2 \dot{\pmb T}_{\theta } + {\pmb K}_1 {\pmb T}_{\theta } = {\pmb K}_1({\pmb \tau }_{s}-{\pmb I}_{m} \ddot{\pmb q}_{\theta } ) $

当$\varepsilon \to 0$时,关节的增广刚度${\pmb K} \to \infty $,由式(33)和式(34)可解出慢变子系统动力学方程

(39)${\pmb D}_{{c\theta }} \ddot{\pmb q}_{c} + {\pmb C}_{{c\theta }} \dot{\pmb q}_{c} = {\pmb \tau }_{{s\theta }}$

式中,${\pmb D}_{{c\theta }} = {\pmb D}_{c} + {\pmb I}_{{m\theta }} $;${\pmb C}_{{c\theta }} $为${\pmb q}_{m} = {\pmb q}_{\theta } $时${\pmb C}_{c} $对应的新矩阵;${\pmb I}_{{m\theta }} = [{\pmb 0}_{4\times 1} ,{\pmb I}_{{m\theta I}} ]^{T} $, ${\pmb I}_{{m\theta I}} = [ {\pmb 0 }_{3\times 1} ,({\pmb \varLambda \pmb I}_{m} )^{T}]^{T}$, $ {\pmb \tau }_{{s\theta }} = [\tau _0 ,({\pmb \varLambda \pmb\tau }_{s} )^{T}]^{T}$.

3.2 慢变子系统控制器设计

系统的不确定参数可以简化为

(40)$\left.\begin{array} \Delta {\pmb D}_{{c\theta }} = {\pmb D}_{{c\theta }}-\hat {\pmb D}_{{c\theta }} \\ \Delta {\pmb C}_{{c\theta }} = {\pmb C}_{{c\theta }}-\hat{\pmb C}_{{c\theta }} \end{array} \right\}$

式中,$ \hat{\pmb D}_{{c\theta }} $, $ \hat {\pmb C}_{{c\theta }} $分别为${\pmb D}_{{c\theta }} $, $ {\pmb C}_{{c\theta }} $的估计值.

性质1 $ \hat {\pmb D}_{{c\theta }} $是正定对称阵,且满足一致有界性. 即$\lambda _1 \leqslant \left\| {{\pmb D}_{{c\theta }} } \right\| \leqslant \lambda _2 $, $0 < \lambda _1 < \lambda _2 $.

将式(40)代入式(39)得

(41)$\hat{\pmb D}_{{c\theta }} \ddot{\pmb q}_{c} + \hat {\pmb C}_{{c\theta }} \dot{\pmb q}_{c} + {\pmb \rho }(t) = {\pmb \tau }_{{s\theta }}$

式中,${\pmb \rho }(t) =\Delta {\pmb D}_{{c\theta }} \ddot{\pmb q}_{c} + \Delta {\pmb C}_{{ c\theta }} \dot{\pmb q}_{c} $为系统不确定量.

假设1 系统不确定量${\pmb \rho }(t)$是有界的,即$\left\| {{\pmb \rho }(t)} \right\| \leqslant b_1 ,b_1 > 0$;定义${\pmb \rho }_1 (t) = {\pmb D}_{{c\theta }}^{-1} {\pmb \rho }(t)$,假设$ \dot{\pmb \rho }_1 (t)$也是有界的,即$\left\| {\dot{\pmb \rho }_1 (t)} \right\| \leqslant b_2 ,b_2 > 0$.

引理1^[30] \ \ 若定义一个连续、正定的函数$V(t)$满足如下条件

(42)$\dot {V}(t) \leqslant-\alpha V^k(t),\forall t > t_0 ,V(t_0 ) \geqslant 0$

式中,$\alpha > 0, 0 < k < 1$. 对于任给的$t_0 $都有

(43)$ \left.\begin{array} V^{1-k}(t) = V^{1-k}(t_0 )-\alpha(1-k)(t-t_0 ),\;t_0 \leqslant t \leqslant t_1 \\ V(t) = 0,\;\forall t \geqslant t_1 \end{array} \right\} $

定义闭链混合体系统的期望位置、速度、加速度分别为${\pmb q}_{{cd}}$, $\dot{\pmb q}_{{cd}}$, $\ddot{\pmb q}_{{cd}} \in {\pmb R}^{4\times 1}$,假设${\pmb q}_{{cd}}$, $\dot {\pmb q}_{{cd}}$, $ \ddot{\pmb q}_{{cd}} $都是有界的,则可得系统的位置、速度、加速度误差分别为

(44)${\pmb e} = {\pmb q}_{c}-{\pmb q}_{{cd}} , \ \ \dot{\pmb e} = \dot{\pmb q}_{c}- \dot {\pmb q}_{{cd}} , \ \ \ddot{\pmb e} = \ddot{\pmb q}_{c}-\ddot{\pmb q}_{{cd}}$

基于式(44),设计如下全阶终端滑模变量

(45)$ {\pmb S} = \ddot{\pmb e} + {\pmb \eta }_2 {sig}( \dot{\pmb e})^{\chi _2 } + {\pmb \eta }_1 {sig} ({\pmb e})^{\chi _1 } $

式中,${\pmb \eta }_i = {diag}[\eta _{i1} ,\eta _{i2} ,\eta _{i3} ,\eta _{i4} ](i = 1,2)$,${\pmb \eta }_i $的取值需使相关多项式$p^2 + \eta _{2j} p + \eta _{1j} (j = 1,2, 3,4)$满足Hurwitz判据;$0 < \chi _1 < 1$, $\chi _2 = {2\chi _1 }/ (1 + \chi _1 )$;${sig}({\pmb y})^\chi = [\vert y_1 \vert ^\chi {sgn} ( y_1 ), \vert y_2 \vert ^\chi {sgn}( y_2 ), \cdots, \vert y_{n} \vert ^\chi {sgn}( y_{n} )]^{T}$, ${\pmb y} = [y_1 ,y_2 , \cdots , y_{n} ]^{T}$.

由于$\dot{\pmb \rho }_1 (t)$未知,因此采用RBF神经网络对其逼近. 假设存在一个理想的权值矩阵${\pmb W}^{ \ast }$使得$\dot{\pmb \rho }_1 (t)$可以被逼近为

(46)$ \dot{\pmb \rho }_1(t) = {\pmb W}^{\ast {T}}\phi ({\pmb y}) + {\pmb \delta } $

式中,${\pmb W}^\ast = [w_1 ,w_2 , \cdots ,w_p ]^{T}$,$p$为一个隐含层中神经元的个数;${\pmb y} = [{\pmb e}^{T},\dot{\pmb e}^{T}, \ddot {\pmb e}^{T}]^{T}$为神经网络输入量;${\pmb \delta }$为神经网络的逼近误差,且满足$\left\| {\pmb \delta } \right\| \leqslant \delta _{N} $;$\phi ({\pmb y}) = [\phi _{\;1} ({\pmb y}),\phi _{\;2} ({\pmb y}), \cdots ,\ phi _p ({\pmb y})]^{T}$为高斯基函数,其表达式为

(47)$ \phi _{\;i}({\pmb y}) ={exp}\left[ {\dfrac{-({\pmb y}-{\pmb \nu }_i )^{T}({\pmb y}-{\pmb \nu }_i )}{2\varpi _i }} \right], \ \ i = 1,2, \cdots,p $

式中,${\pmb \nu }_i = [\nu _{i1} ,\nu _{i2} , \cdots , \nu _{i12} ]^{T}$和$\varpi _i $分别为高斯基函数的中心和宽度.

基于式(15) $\sim $式(47)设计控制力矩${\pmb \tau }_{{s\theta }} $为

(48a)$ {\pmb \tau }_{{s\theta }} = \hat {\pmb D}_{{c\theta }} ({\pmb \tau }_{{ s\theta 0}} + {\pmb \tau }_{{s\theta 1}} + {\pmb \tau }_{{s\theta 2}} ) $

(48b)$ {\pmb \tau }_{{s\theta 0}} = \hat {\pmb D}_{{c\theta }}^{-1} \hat{\pmb C}_{{c\theta }} \dot{\pmb q}_{c} + \ddot{\pmb q}_{{cd}} $

(48c)$ {\pmb \tau }_{{s\theta 1}} =-{\pmb \eta }_2 {sig} ( \dot {\pmb e})^{\chi _2 }-{\pmb \eta }_1 {sig} ({\pmb e})^{\chi _1 } $

(48d)$ \dot{\pmb \tau }_{{s\theta 2}} = \hat {\pmb W}^{T}\phi ({\pmb y})-(\xi _1 + \xi _2 + \xi _3 ){\pmb u}_s $

式中,$ \hat{\pmb W}$为${\pmb W}^\ast $的估计值,$\xi _1 > \delta _{N} $,$\xi _2 ,\xi _3 > 0$,${\pmb \tau }_{{s\theta 2}} (0) = {\bf 0}_{4\times 1} $,${\pmb u}_s $定义如下

(49)${\pmb u}_s = \left\{ \begin{array}{cc} \dfrac{\pmb S}{\left\| {\pmb S} \right\|} , & \left\| {\pmb S} \right\| \ne 0 \\ {\bf 0} , & \left\| {\pmb S} \right\| = 0 \end{array} \right.$

$\hat {\pmb W}$的自适应率采取如下形式

(50) $ \dot{ \hat{\pmb W}} =-\dot{ \tilde {\pmb W}} =-\dfrac{1}{\mu }\phi({\pmb y}){\pmb S}^{T} $

式中,$\tilde {\pmb W}= {\pmb W}^\ast-\hat {\pmb W},\mu > 0$.

定理1 对于给定的慢变子系统方程(41),假如全阶终端滑模变量采用式(45)所示形式,控制率采用式(48)所示形式,神经网络自适应率采用式(50)所示形式,则可保证系统在有限时间内收敛到零.

证明选取如下形式的Lyapunov函数

(51)$V_1 = \dfrac{1}{2}{\pmb S}^{T}{\pmb S} + \dfrac{1}{2}{trace}( \mu \tilde {\pmb W}^{T} \tilde {\pmb W})$

对$V_1 $求导得

(52)$\dot {V}_1 = {\pmb S}^{T}\dot{\pmb S} +{trace}( \mu \tilde {\pmb W}^{T}\dot{ \tilde {\pmb W}})$

由式(41)、式(45)、式(48a) $\sim $式(48c)得

(53)$ {\pmb S} = \hat{\pmb D}_{{c\theta }}^{-1} [ \hat {\pmb D}_{{c\theta }}({\pmb \tau }_{{s\theta 0}} + {\pmb \tau }_{{s\theta 1}} + {\pmb \tau }_{{s\theta 2}} )-{\pmb \rho }(t)-\hat{\pmb C}_{{c\theta }} \dot{\pmb q}_{c} ]- \\ \qquad \ddot{\pmb q}_{{cd}} + {\pmb \eta }_2 {sig} ( \dot {\pmb e})^{\chi _2 } + {\pmb \eta }_1 sig({\pmb e})^{\chi _1 } = {\pmb \tau }_{{s\theta 2}}-{\pmb \rho }_1 (t) $

对式(53)求导并将式(46)、式(48d)代入得

(54)$ \begin{array}\dot{\pmb S} = \dot{\pmb \tau }_{{s\theta 2}}-\dot {\pmb \rho }_1(t)=\\ \qquad -\tilde {\pmb W}{\pmb \phi} ({\pmb y})-(\xi _1 + \xi _2 + \xi _3 ){\pmb u}_s-{\pmb \delta } \end{array} $

将式(50)、式(54)代入式(52)得

(55)$ \begin{array}\dot {V}_1 = {\pmb S }^{T}[-\tilde {\pmb W}^{T}{\pmb\phi}({\pmb y})-(\xi _1 + \xi _2 + \xi _3 ){\pmb u}_s-{\pmb \delta }] + \\ \qquad {trace} (\tilde{\pmb W}^{T}{\pmb\phi} ({\pmb y})S^{T}) =\\ \qquad -{\pmb S}^{T}(\xi _1 + \xi _2 + \xi _3 ){\pmb u}_s-{\pmb S}^{T}{\pmb \delta } \leqslant -(\xi _2 + \xi _3 )\left\| {\pmb S} \right\| \end{array} $

由于$\xi _2 ,\xi _3 > 0$, $ \| {\pmb S} \| > 0$,故$\dot {V}_1 < 0$. 因此可得$\ddot{\pmb e},\; \dot {\pmb e},\;{\pmb e},\; \tilde{\pmb W}$都是有界的.

上述过程证明了${\pmb S},\ddot{\pmb e}, \dot{\pmb e},{\pmb e}, \tilde {\pmb W}$是有界的,接下来将证明${\pmb S}, \ddot {\pmb e},\dot{\pmb e},{\pmb e}$可在有限时间内收敛.

由于高斯基函数${0} < \phi _{\;i} ({\pmb y}) < 1$, $i = 1,2, \cdots ,p$, 因此可得

(56)$\left\| {{\pmb\phi}({\pmb y})} \right\| \leqslant \sqrt p $

由F范数的性质可得

(57)$ \left\| { \tilde{\pmb W}^{T}{\pmb\phi}({\pmb y})} \right\|_{F} \leqslant \left\| { \tilde{\pmb W}^{T}} \right\|_{F} \left\| { {\pmb\phi} ({\pmb y})} \right\| $

由于上一步已经证明$\left\| { \tilde {\pmb W}^{T}} \right\|_{F} $是有界的,因此通过式(56)、式(57)可知$\left\| { \tilde {\pmb W}^{T}{\pmb\phi} ({\pmb y})} \right\|_{ F} $是有界的. 若取$\xi _2 \geqslant \left\| { \tilde {\pmb W}^{T}{\pmb\phi} ({\pmb y})} \right\|_{F} $,取如下形式的Lyapunov函数

(58)$V_2 = \dfrac{1}{2}{\pmb S}^{T}{\pmb S}$

对$V_2 $求导并代入式(54)得

(59)$ \begin{array}\dot {V}_2 = {\pmb S}^{T}[-\tilde {\pmb W}^{T}{\pmb\phi}({\pmb y})-(\xi _1 + \xi _2 + \xi _3 ){\pmb u}_s-{\pmb \delta }] = \\ \qquad -{\pmb S}^{T} \tilde {\pmb W}^{T}{\pmb\phi} ({\pmb y})-{\pmb S}^{T}(\xi _1 + \xi _2 + \xi _3 ){\pmb u}_s-{\pmb S}^{T}{\pmb \delta } \end{array} $

由于$\xi _1 > \delta _{N} , \xi _2 \geqslant \left\| { \tilde {\pmb W}^{T}{\pmb \phi} ({\pmb y})} \right\|_{F} ,\xi _2 > 0$,可得

(60)$\dot {V}_2 \leqslant \xi _3 \left\| {\pmb S} \right\| \leqslant-\sqrt 2 \xi _3 V_2^{1 / 2}$

因此,由引理1得$V_2 $将在有限时间内收敛到零,进一步可知${\pmb S},\; \ddot {\pmb e},\;\dot{\pmb e},\;{\pmb e}$将在有限时间内收敛到零.

由式(39)可知对快变子系统进行控制需要输入$\tau _{s} $,但实际设计的是$\tau _{{s\theta }} $,因此把${\pmb \tau }_{{s\theta }} $分解为${\pmb \tau }_{{s\theta }} = [\tau _0 ,{\pmb \tau }_{{bs\theta }} ^{T}]^{T}$,其中${\pmb \tau }_{{bs\theta }} \in {\pmb R}^{3\times 1}$. 由前给出${\pmb \tau }_{{s\theta }} $与${\pmb \tau }_{s} $的关系,结合加权最小范数法,可解得

(61)${\pmb \tau }_{s} = {\pmb \varXi \pmb \varLambda }^{T}( {\pmb \varLambda \pmb \varXi\pmb \varLambda }^{T})^{-1}{\pmb \tau }_{{bs\theta }}$

式中,${\pmb \varXi } \in {\pmb R}^{6\times 6}$为对称正定的权值矩阵.

4 数值仿真

4.1 碰撞过程中RSEA抗冲击性能模拟

采用图2的双臂空间机器人系统及卫星系统进行数值仿真. 双臂空间机器人系统参数：$ {m}_0 = 50$ kg, $ {m}_i = 5$ kg $(i= 1,2,4,5)$, ${m}_j = 2$ kg $(j = 3,6)$, $L_i = 1$ m\;$(i = 1,2,4,5)$, $L_j = 0.5$ m\;$(j = 3,6)$, $d_i = 0.5$ m\;$(i = 1,2,4,5)$, $d_j = 0.25$ m\;$(j= 3,6)$, $I_0 = 34$ kg$\cdot$ m$^2$, $I_i = 1$ kg$\cdot$ m$^2$ $(i = 1,2,4,6)$, $I_j = 0.5$ kg$ \cdot $ m$^2$ $(j = 3,6)$, $I_{{m}\;i} = 0.05$ kg$\cdot $ m$^2$ ($i = 1,2, \cdots,6)$, $k_{{s}\;i} = 1000$ N/m $(i = 1,2, \cdots, 6)$, $\psi _1 = 2.791$ rad, $\psi _2 = 0.349$ rad. 被捕获卫星系统的参数为：$m_{s} = 5$ kg,$d_{s} = 0.25$ m,$I_{s} = 3$ kg $\cdot$ m$^2$. 双臂空间机器人碰撞前的初始位置为$ {\pmb q}_{r} (t_0 ) = (0.3, 0.3, 10^\circ, 120^\circ,-60^\circ,-60^\circ, 60^\circ, 60^\circ, 60^\circ)^{ T}$关节等效刚度的计算公式^[24]为

(62)$ {\pmb K} = 2{\pmb K}_{s}(3R^2 + r^2)(2\cos ^2{\pmb \varphi }-1) $

式中, $ {\pmb K}_{s} = {diag} (k_{s1} ,k_{s2} ,k_{s3} ,k_{s4} ,k_{s5} ,k_{s6} )$, $ {R} = 0.1$ m, $r = 0.01$ m. ${\pmb \varphi }$为机械臂末端施加载荷$ {\pmb F}_{r}$ = [20 N, 20 N, 0, $- 20$ N, $-20$ N ,0]$^{T}$时扫臂的转角,仿真时取${\pmb \varphi } = {diag} (3^{\circ}, 2^{\circ}, 1^{\circ}, -3^{\circ},-2^{\circ},-1^{\circ})$.

为了验证RSEA传动装置的抗冲击性能,仿真时采用多组卫星速度对碰撞过程中的关节力矩进行仿真模拟,结果如表1所示. 其中卫星速度前两项单位为m/s,后一项单位为rad/s.

Table 1
表1
表1卫星不同初速度下RSEA的抗冲击性能比较
Table 1RSEA impact resistance at different satellite initial velocities

新窗口打开|下载CSV

由表1可看出,在碰撞过程中,对卫星不同的初速,RSEA都能有效的减小空间机器人关节所受冲击力矩,从而达到保护关节的作用.

4.2 捕获过程中避撞柔顺控制策略性能模拟

避撞柔顺控制策略参数如下: ${\pmb \eta }_1 ={diag }(5,5,5,5)$, ${\pmb \eta }_2 ={diag} (5,5,5,5)$, $\chi _1 = 9 / {23}$, $\chi _2 = 9 /{16}$, $\xi _i = 1\;(i = 1,2,3)$, $\mu = 50$, $\varepsilon = 0.5$, ${\pmb K }_2 = {diag} (5,5,5,5,5,5) $. 高斯基函数中心为$-2, -1, 0, 1, 2$; 宽度为0.8. 双臂空间机器人碰撞前的初始位置如4.1,被捕获卫星碰撞前的初始速度$\dot {\pmb q}_{s} (0) = [0.5$ m/s, 0.5 m/s, 0.35 rad/s]$^{T}$,仿真时间为 10 s.

为了突出避撞柔顺控制策略可以在捕获中满足多种电机的需求,本次采用两组力矩阀值进行仿真. 首先假设第一组关节电机能承受 40 N$\cdot$m的冲击力矩,第二组关节电机能承受 30 N$\cdot $m的冲击力矩. 关机阀值选取的原则为不能超过电机所能承受的极限力矩;而开机阀值的选取遵循两个原则：一是电机不能受到损害,二是实现快速镇定控制. 若开机阀值选取过大,其与关机阀值的差值就相对较小,电机会频繁的开关机,这对电机是非常不利的;若开机阀值选取过小,其与关机阀值的差值就相对较大,此时电机关停时间会过长,进而延长镇定控制的时间. 通过对多组阀值数值仿真的结果分析,采用第一组仿真的关机阀值为${F}_{M} = 35$ N$\cdot$m,开机阀值为${F}_{m} = 10$ N$\cdot $m;第二组仿真的关机阀值为${F}_{M} = 25$ N$ \cdot $m, 开机阀值为${F}_{m} = 10$ N$\cdot$m.

图3为不开启避撞柔顺控制关节冲击力矩;图4 $\sim $图9为第一组仿真的结果;图10 $\sim $图15为第二组仿真的结果.

图3

新窗口打开|下载原图ZIP|生成PPT
图3不开启避撞柔顺控制关节力矩

Fig. 3Joint impact torque on closing avoidance collision and compliant control

图4

新窗口打开|下载原图ZIP|生成PPT
图4电机信号 $(F_{ M} = 35$\,N$\cdot$m, $F_{ m} = 10$\,N$\cdot$m)

Fig. 4Switch signal of joint motor $(F_{ M} = 35$\,N$\cdot$m, $F_{ m} = 10$\,N$\cdot$m)

图5

新窗口打开|下载原图ZIP|生成PPT
图5开启避撞柔顺控制关节力矩 $(F_{M} = 35$ N$\cdot$m, $F_{m}=10$ N$\cdot$m)

Fig. 5Joint impact torque on opening avoidance collision and compliant control $(F_{M} = 35$ N$\cdot$m, $F_{m}=10$ N$\cdot$m)

图6

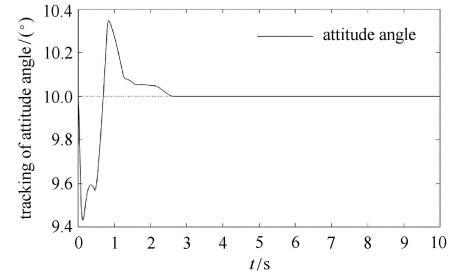
新窗口打开|下载原图ZIP|生成PPT
图6开启避撞柔顺控制姿态角$(F_{M} = 35$ N$\cdot$m, $F_{m}=10$ N$\cdot$m)

Fig. 6Attitude angle tracking on opening avoidance collision and compliant control $(F_{M} = 35$ N$\cdot$m, $F_{m}=10$ N$\cdot$m)

图7

新窗口打开|下载原图ZIP|生成PPT
图7开启避撞柔顺控制关节角 $(F_{M} = 35$ N$\cdot$m, $F_{m}=10$ N$\cdot$m)

Fig. 7Joint angle tracking on opening avoidance collision and compliant control $(F_{M} = 35$ N$\cdot$m, $F_{m}=10$ N$\cdot$m)

图8

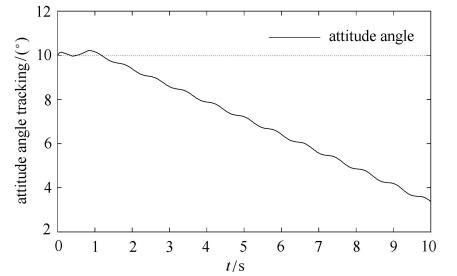新窗口打开|下载原图ZIP|生成PPT
图8关闭快变子控制器载体姿态角$(F_{M} = 35$ N$\cdot$m, $F_{m}=10$ N$\cdot$m)

Fig. 8Attitude angle on closing fast controller $(F_{M} = 35$ N$\cdot$m, $F_{m}=10$ N$\cdot$m)

图9

新窗口打开|下载原图ZIP|生成PPT
图9关闭快变子控制器关节角$(F_{M} = 35$ N$\cdot$m, $F_{m}=10$ N$\cdot$m)

Fig. 9Joint angle on closing fast controller $(F_{M} = 35$ N$\cdot$m, $F_{m}=10$ N$\cdot$m)

图10

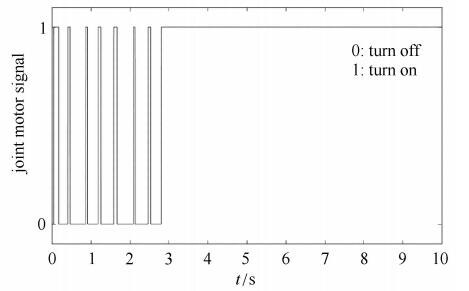新窗口打开|下载原图ZIP|生成PPT
图10电机信号$(F_{M} = 25$ N$\cdot$m, $F_{m}=10$ N$\cdot$m)

Fig. 10Switch signal of joint motor $(F_{M} = 25$ N$\cdot$m, $F_{m}=10$ N$\cdot$m)

图11

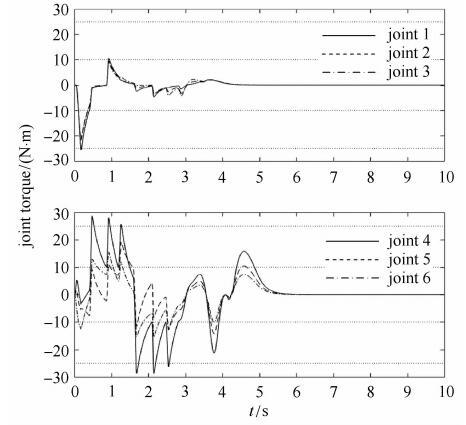新窗口打开|下载原图ZIP|生成PPT
图11开启避撞柔顺控制关节力矩$(F_{M} = 25$ N$\cdot$m, $F_{m}=10$ N$\cdot$m)

Fig. 11Joint impact torque on opening avoidance collision and compliant control $(F_{M} = 25$ N$\cdot$m, $F_{m}=10$ N$\cdot$m)

图12

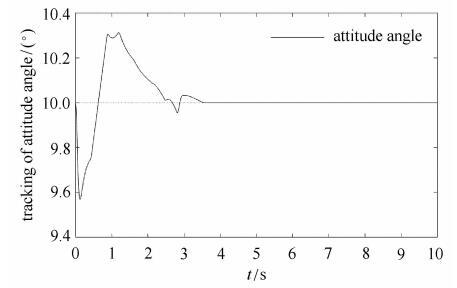
新窗口打开|下载原图ZIP|生成PPT
图12开启避撞柔顺控制姿态角$(F_{M} = 25$ N$\cdot$m, $F_{m}=10$ N$\cdot$m)

Fig. 12Attitude angle tracking on opening avoidance collision and compliant control$(F_{M} = 25$ N$\cdot$m, $F_{m}=10$ N$\cdot$m)

图13

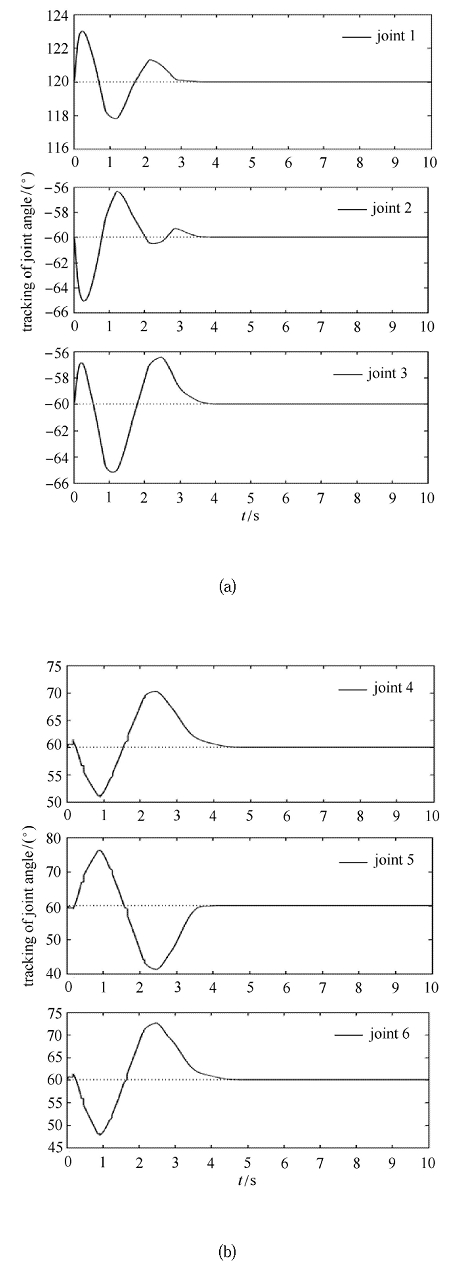新窗口打开|下载原图ZIP|生成PPT
图13开启避撞柔顺控制关节$(F_{M} = 25$ N$\cdot$m, $F_{m}=10$ N$\cdot$m)

Fig. 13Joint angle tracking on opening avoidance collision and compliant control $(F_{M} = 25$ N$\cdot$m, $F_{m}=10$ N$\cdot$m)

图14

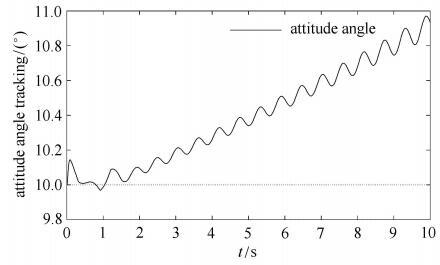新窗口打开|下载原图ZIP|生成PPT
图14关闭快变子控制器载体姿态角$(F_{M} = 25$ N$\cdot$m, $F_{m}=10$ N$\cdot$m)

Fig. 14Attitude angle on closing fast ontroller \\ $(F_{M} = 25$ N$\cdot$m, $F_{ m}=10$ N$\cdot$m)

图15

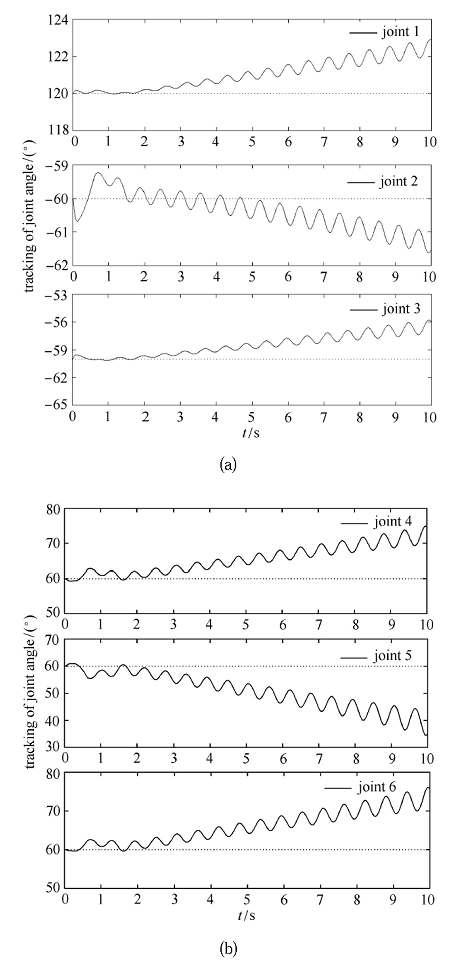新窗口打开|下载原图ZIP|生成PPT
图15关闭快变子控制器关节角$(F_{M} = 25$ N$\cdot$m, $F_{m}=10$ N$\cdot$m)

Fig. 15Joint angle on closing fast controller \\ $(F_{M} = 25$ N$\cdot$m, $F_{ m}=10$ N$\cdot$m)

5 结论

为了在空间机器人捕获卫星的中保护关节不受冲击破坏且实现捕获后的镇定控制,本文设计了一种RSEA传动装置且提出了一种与之配合的避撞柔顺控制策略. 从仿真结果来看,RSEA在碰撞过程中具有较好的抗冲击性能;避撞柔顺控制策略也可以很好的限制关节力矩,且能使系统镇定. 根据所设置的关机力矩阀值不同,系统达到镇定的电机开关次数和所花时间也不同. 其规律大致为：设置的关机力矩阀值小,电机开关次数多,系统镇定所花时间长;设置的关机力矩阀值大,电机开关次数少,系统镇定所花时间短. 因此,我们根据关节所能承受的极限力矩值,在保证足够安全系数的前提下,合理的设置关节力矩阀值,使得即可以在捕获过程中保护关节,又可以在捕获后实现快速镇定.

参考文献原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]

Lim

, Chung

. Dynamic analysis of a tethered satellite system for space debris capture
Nonlinear Dynamics, 2018,94(4):2391-2408

DOI [本文引用: 1]

[2]

尹婷婷, 邓子辰, 胡伟鹏等. 空间刚性杆——弹簧组合结构轨道、姿态耦合动力学分析
力学学报, 2018,50(1):87-98

( Yin

Tingting

, Deng

Zichen

, Hu

Weipeng

, et al. Dynamic modelling and simulation of orbit and attitude coupling problems for structure combined of spatial rigid rods and spring
Chinese Journal of Theoretical and Applied Mechanics, 2018,50(1):87-98 (in Chinese))

[3]

岳宝增, 于嘉瑞, 吴文军 . 多储液腔航天器刚液耦合动力学与复合控制
力学学报, 2017,49(2):390-396

( Yue

Baozeng

, Yu

Jiarui

, Wu

Wenjun

. Rigid and liquid coupling dynamics and hybrid control of spacecraft with multiple propellanttanks
Chinese Journal of Theoretical and Applied Mechanics, 2017,49(2):390-396 (in Chinese))

[4]

Daniel

, Carole

. On-orbit upgrade and repair: the hubble spacetelescope example
Journal of Spacecraft and Rockets, 2006,43(3):614-625

DOI URL

[5]

Floresabad

, Ma

, Pham

, et al. A review of space robotics technologies for on-orbit servicing
Progress in Aerospace Sciences, 2014,68(8):1-26

DOI URL

[6]

, Liang

, Li

, et al. A universal on-orbit servicing system used in the geostationary orbit
Advances in Space Research, 2011,48(1):95-119

DOI URL

[7]

Chen

, Huang

, Cai

, et al. A non-cooperative target grasping position prediction model for tethered space robot
Aerospace Science and Technology, 2016,58:571-581

DOI URL

[8]

王靖森, 刘晓峰, 段柳成等. 考虑关节摩擦的空间机器人动力学建模与参数辨识
力学季刊, 2015,36(4):594-601

[本文引用: 1]

( Wang

Jingsen

, Liu

Xiaofeng

, Duan

Liucheng

, et al. Dynamic modeling and parameter identification of a space robot considering joint friction
Chinese Quarter of Mechanics, 2015,36(4):594-601 (in Chinese))

[本文引用: 1]

[9]

郭闻昊, 王天舒 . 空间机器人抓捕目标星碰撞前构型优化
宇航学报, 2015,36(4):390-396

DOI Magsci [本文引用: 1]

空间双臂机器人抓捕目标星会导致碰撞，针对碰撞引起机器人系统基座姿态变化的问题，提出一种基于粒子群算法的碰撞前构型优化方法。该方法首先给出了碰撞前和碰撞后的动力学模型，然后根据冲量—动量方程推导出碰撞阶段动力学方程，最后提出基于粒子群算法的最优碰撞前构型规划数值方法，使碰撞对机器人系统角动量的影响尽量小。通过计算校验了该方法的有效性，找到了用于空间机器人抓捕目标星的较理想的碰撞前构型。

( Guo

Wenhao

, Wang

Tianshu

. Pre-impact configuration optimization for a space robot capturing target satellite
Journal of Astronautics, 2015,36(4):390-396 (in Chinese))

DOI Magsci [本文引用: 1]

赵金刚, 戈新生 . 动态规划求解空间双臂机器人非完整运动最优控制问题
力学季刊, 2016(2):225-233

( Zhao

Jingang

, Ge

Xinsheng

. Dynamic programming for solving the optimal nonholonomic motion control problem of the bi-arm space robot
Chinese Quarterly of Mechanics, 2016(2):225-233 (in Chinese))

[11]

Davide

, Marco

, Andrea

, et al. Occlusion-free visual servoing for the shared autonomy teleoperation of dual-arm robots
IEEE Robotics and Automation Letters, 2018,3(2):796-803

DOI URL

[12]

Stolfi

, Gasbarri

, Sabatini

. A combined impedance-PD approach for controlling a dual-arm space manipulator in the capture of a non-cooperative target
Acta Astronautica, 2017,139:243-253

DOI URL

[13]

Zarafshan

, Moosavian

SAA

, Papadopoulos

. Adaptive hybrid suppression control of space free-flying robots with flexible appendages
Robotica, 2016,34(7):1-22

[14]

Abdul Hafez

, Mithun

, Anurag

, et al. Reactionless visual servoing of a multi-arm space robot combined with other manipulation tasks
Robotics and Autonomous Systems, 2017,91:1-10

DOI URL [本文引用: 1]

[15]

Coleshill

, Oshinowo

, Rembala

, et al. Dextre: Improving maintenance operations on the international space station
Acta Astronautica, 2009,64(9/10):869-874

DOI URL [本文引用: 1]

[16]

Diftler

, Mehling

, Abdallah

, et al. Robonaut 2 - The first humanoid robot in space
//IEEE International Conference on Robotics and Automation. Piscataway, NJ, USA: IEEE, 2011: 2178-2183

[本文引用: 1]

[17]

Sabelli

, Akin

, Carignan

. Selecting impedance parameters for the ranger 8-DoF dexterous space manipulator
//AIAA Aerospace Conference and Exhibit. Reston, VA, USA: AIAA, 2007: 1-15

[本文引用: 1]

[18]

Debus

, Dougherty

. Overview and performance of the frontend robotics enabling near-term demonstration (FREND) robotic arm//AIAA Infotech@Aerospace Conference
Reston, VA, USA: AIAA, 2009: AIAA 2009-1870

[本文引用: 1]

[19]

Takahashi

, Ise

, Sato

, et al. Hydrid simulation of a dual-arm space robot colliding with a floating object
//IEEE International Conference on Robotics and Automation. Piscataway, UAS: IEEE, 2008: 1202-1206

[本文引用: 1]

[20]

徐文福, 刘厚德, 李成等. 双臂空间机器人捕获运动目标的自主路径规划
机器人, 2012,34(6):704-714

DOI Magsci [本文引用: 1]

针对双臂空间机器人系统捕获运动目标的规划问题，提出了自由漂浮和基座姿态受控两种模式下的自主路径规划方法．首先根据手眼相机测量结果，规划各机械臂末端的运动速度，然后采用阻尼最小二乘法求解所推导的微分运动学方程，得出各关节的期望角度和期望角速度，作为关节控制器的输入，直到满足抓捕条件．最后建立了双臂空间机器人系统的多体动力学模型并开展仿真研究，仿真结果证明了所提方法的有效性．

( Xu

Wengfu

, Liu

Houde

, Li

Chen

, et al. Autonomous path planning of dual-arm space robot for capturing moving target
Robot, 2012,34(6):704-714 (in Chinese))

DOI Magsci [本文引用: 1]

董楸煌, 陈力 . 空间机械臂捕获卫星过程的碰撞动力学模拟及镇定运动的鲁棒控制
计算力学学报, 2014(3):315-321

[本文引用: 1]

( Dong

Qiuhuang

, Chen

. Impact dynamics simulation and robust control for stabilizing of a space manipulator capturing satellite
Chinese Journal of Computational Mechanics, 2014(3):315-321 (in Chinese))

[本文引用: 1]

[22]

程靖, 陈力 . 空间机器人双臂捕获卫星力学分析及镇定控制
力学学报, 2016,48(4):832-842

DOI Magsci [本文引用: 1]

随着航天技术的发展，空间机器人要求具有对非合作卫星的在轨捕获能力. 双臂空间机器人与单臂空间机器人相比在这方面显然更具有优势. 然而由于太空环境的复杂性，使得空间机器人双臂捕获非合作卫星操作过程的动力学与控制问题表现出下述特点：非完整动力学约束，动量、动量矩与能量传递变化，捕获前后结构开、闭环变拓扑，与闭环接触几何、运动学约束多者共存. 因此空间机器人双臂捕获卫星技术相关动力学与控制问题变得极其复杂. 为此，讨论了双臂空间机器人捕获自旋卫星过程的动力学演化模拟，以及捕获操作后其不稳定闭链混合体系统的镇定控制问题. 首先，利用拉格朗日第二类方程建立了捕获操作前双臂空间机器人的开环系统动力学模型，利用牛顿-欧拉法建立了目标卫星的系统动力学模型；在此基础上基于动量守恒定律、力的传递规律，经过积分与简化处理分析、求解了双臂空间机器人捕获目标卫星后受到的碰撞冲击效应，给出了合适的捕获操作策略. 根据闭链系统的闭环约束几何及运动学关系获得了闭合链约束方程，推导了捕获操作后闭链混合体系统的动力学方程. 最后基于该动力学方程针对捕获操作结束后失稳的闭链混合体系统，设计了镇定运动模糊H∞ 控制方案. 提出的方案利用模糊逻辑环节克服参数不确定影响，由H∞ 鲁棒控制项消除逼近误差来保证系统控制精度；通过最小权值范数法分配各臂关节力矩，以保证两臂协同操作. 李雅普诺夫稳定性理论证明了系统的全局稳定性. 最后通过数值仿真实验模拟、分析了碰撞冲击响应，并验证了上述镇定运动控制方案的有效性.

( Cheng

Jing

, Chen

. Mechanical analysis and calm control of dual-arm space robot for capturing a satellite
Chinese Journal of Theoretical and Applied Mechanics, 2016,48(4):832-842 (in Chinese))

DOI Magsci [本文引用: 1]

Jia

, Hu

, Xu

. Dynamics and adaptive control of a dual-arm space robot with closed-loop constraints and uncertain inertial parameters
Acta Mechanica Sinica, 2014,30(1):112-124

DOI URL [本文引用: 1]

[24]

张秀丽, 谷小旭, 赵洪福等. 一种基于串联弹性驱动器的柔顺机械臂设计
机器人, 2016,38(4):385-394

DOI Magsci [本文引用: 2]

为了应对工作环境的动态变化以及人机交互的不确定性，设计了基于被动柔顺结构和主动柔顺控制的柔顺机械臂SoftArm II．在关节电机和连杆之间加入串联弹性驱动器（SEA）传动模块，SEA传动模块由线弹簧周向均布构成；建立了3DOF柔顺机械臂的运动学/动力学模型以及系统刚度模型，基于系统刚度模型提出工作空间典型位姿下关节刚度加权平均的SEA弹簧刚度确定方法；柔顺机械臂采用位置PID（比例－微分－积分）控制，并通过监控末端接触力和关节力矩适时修改指令轨迹．在柔顺机械臂SoftArm II上执行了自由空间中的圆形轨迹跟踪、人机直线对推和碰撞模拟实验，结果显示，SoftArm II在自由空间中具有较好的轨迹跟踪性能，能够实现与操作者的柔顺交互以及对碰撞的安全避让．基于SEA的被动柔顺结构设计以及基于末端力和关节力矩监控的控制策略能够满足人机共存环境对机械臂柔顺性及安全性的要求．

( Zhang

Xiuli

, Gu

Xiaoxu

, Zhao

Hongfu

, et al. Design of a compliant robotic arm based on series elastic actuator
Robot, 2016,38(4):385-394 (in Chinese)).

DOI Magsci [本文引用: 2]

王萌, 孙雷, 尹伟等. 一种面向交互应用的串联弹性驱动器有限时间输出反馈控制方法
机器人, 2016,38(5):513-521

DOI Magsci

串联弹性驱动器（SEA）被广泛地应用于机器人与环境、机器人与人的交互场景中，针对这种交互应用，本文提出了一种新型的有限时间输出反馈控制策略（FTOFC），保证SEA的输出力矩在交互过程中能够快速达到期望值/轨迹．具体而言，首先对SEA的动力学模型进行了分析和变换；其次，基于有限时间控制理论，设计了有限时间扩张状态观测器和2阶滑模控制器，将两者结合实现了一种有限时间输出反馈控制策略，并对闭环系统的稳定性及信号有界性进行了严格的理论分析．相比于已有方法，本文方法有以下3个方面的优势：1)本文的控制方法适用于非线性SEA，更具有通用性；2)本文方法基于有限时间控制理论，具有更优的暂态响应性能；3)本文控制方法充分考虑了交互过程中负载端动力学可能会发生剧烈变化的情况，更适用于交互应用．为了验证以上3点，在自主搭建的单关节SEA交互机器人平台上进行了实验验证并与传统的级联PID方法进行了对比，结果表明本文设计的控制器能取得更好的控制效果，并且对外界干扰具有很强的鲁棒性．

( Wang

Meng

, Sun

Lei

, Yin

Wei

, et al. A finite time output feedback control approach for interaction oriented series elastic actuators
Robot, 2016,38(5):513-521 (in Chinese))

DOI Magsci

Wang

, Pan

, Li

, et al. Robust sliding mode control for robots driven by compliant actuators
IEEE Transactions on Control Systems Technology, 2018, 1-8

[本文引用: 1]

[27]

谢立敏, 陈力 . 漂浮基柔性空间机器人的鲁棒控制及振动抑制
力学学报, 2012,44(6):1057-1065

DOI Magsci [本文引用: 1]

讨论了漂浮基柔性空间机器人系统的动力学建模、运动控制算法设计以及关节、臂双重柔性振动的分级主动抑制问题. 利用系统动量、动量矩守恒关系和拉格朗日-假设模态法对系统进行动力学分析,建立系统动力学方程. 基于奇异摄动法,将系统分解为表示系统刚性运动部分的慢变子系统, 表示由柔性臂引起的系统柔性运动部分的快变子系统1和表示由柔性关节引起的系统柔性运动部分的快变子系统2. 针对慢变子系统提出一种鲁棒控制方法来补偿系统参数的不确定性和柔性关节引起的转动误差,实现系统期望运动轨迹的渐近跟踪;针对快变子系统1采用线性二次型最优控制器来抑制由柔性臂引起的系统柔性振动;针对快变子系统2设计了基于机械臂和电机转子的转角速度差值的反馈控制器来抑制由柔性关节引起的系统柔性振动. 因此,系统的总控制律为以上3个子系统控制律的综合. 最后通过仿真实验证明了所提出的混合控制方法的有效性.

( Xie

Limin

, Chen

. Robust control and vibration suppression of free-floating flexible space robot
Chinese Journal of Theoretical and Applied Mechanics, 2012,44(6):1057-1065 (in Chinese))

DOI Magsci [本文引用: 1]

, Cansever

. Three link robot control with fuzzy sliding mode controller based on rbf neural network
IEEE, 2006: 2719-2724

[本文引用: 1]

[29]

Wang

, Liu

, et al. Neural-based adaptive output-feedback control for a class of nonstrict-feedback stochastic nonlinear systems
IEEE Transactions on Cybernetics, 2017,45(9):1977-1987

[本文引用: 1]

[30]

Zhao

Dongya

, Cao

Qianlei

, Li

Shurong

, et al. Adaptive full-order sliding mode control of rigid robotic manipulators
//Proceedings of the 34th Chinese Control Conference, Hangzhou, China, 2015: 657-662

[本文引用: 2]

[31]

Corradini

, Cristofaro

. Nonsingular terminal sliding mode control of nonlinear planar systems with global fixed-time stability guarantees
Automatica, 2018,95:561-565

DOI URL [本文引用: 1]

[32]

Jin

, Chang

, Jin

, et al. Stability guaranteed time-delay control of manipulators using nonlinear damping and terminal sliding mode
IEEE Transactions on Industrial Electronics, 2013,60(8):3304-3317

[33]

Rath

, Karimi

, Defoort

, et al. Output feedback active suspension control with higher order terminal sliding mode
IEEE Transactions on Industrial Electronics, 2017,64(2):1392-1402

DOI URL [本文引用: 1]