, 叶正寅CIRCULATION CONTROL ON WIND TURBINE AIRFOIL WITH BLUNT TRAILING EDGE1)
QiaoChenliang, YeZhengyin中图分类号:V211.3
文献标识码:A
版权声明:2019力学学报期刊社力学学报期刊社 所有
基金资助:
作者简介:
-->
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (8020KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
为提高发电效率,风力机朝着大型化方向发展. 随着大型水平轴风力机的尺寸不断增大,风力机叶片自身的重量及其受到的气动载荷逐渐增大,叶片根部附近区域的结构强度要求逐渐增高[1]. 为增大叶片的结构强度,同时降低叶片的表面污染敏感度,相关****提出了钝后缘风力机翼型的概念[2]. 钝后缘风力机翼具有结构强度高、对表面污染不敏感、最大升力系数大、失速迎角大、升力曲线斜率大等特点[3 - 5]. 但钝后缘翼型的压差阻力较大,翼型尾迹区有较强的脱体涡产生[6],而且脱体涡会引发一系列诸如气动噪声[7]、涡致振动等问题. 因此,选择合适的流动控制方法来改善钝后缘风力机翼型气动特性,降低翼型后缘脱体涡强度具有重要研究意义.
为改善钝后缘风力机翼型存在的相关问题,起初人们采用在翼型后缘加装隔板的方法对该类翼型后缘附近的流场进行流动控制. Baker等[8]通过在翼型后缘加装隔板来削弱钝后缘翼型尾迹区的脱体涡,加装隔板之后翼型尾迹区的脱体涡变成了两个分别位于隔板两侧的驻涡,翼型的阻力系数有所降低. 宋科等[9]对钝后缘风力机翼型后缘加装隔板的位置进行研究,研究结果表明隔板位于后缘中间位置时控制效果最好. Manolesos等[10]通过风洞实验研究了四种隔板组合对翼型的减阻效果以及尾迹区脱体涡的控制效果. 实验结果表明Flap + Offset Cavity组合的控制效果最好,该组合方式可将部分工况下翼型的升阻比提升至原来的2.38倍.
相对于以上提到的以减阻为目的的流动控制方法,2014年Nikoueeyan等[11]首次通过风洞实验研究了Gurney襟翼对钝后缘翼型的增升效果. 通过对比发现,在翼型后缘加装长度为0.05$c$的Gurney襟翼可以使翼型的升力系数提升38%~41%.
然而,上述几种控制方法均属于被动流动控制方法,在非设计工况下无法达到理想的控制效果. 主动流动控制方法有很多,但目前关于钝后缘风力机翼型主动流动控制方法的相关研究很少. Naghiblahouti等[12]采用基于等离子激励器的流动控制方法对钝后缘翼型进行流动控制,研究结果表明,该方法可以促进翼型后缘附近流动的掺混,但对气动力系数的提升有限.
环量控制(circulation control, CC)方法[13]是一种基于柯恩达效应[14]的主动流动控制方法, 该方法因其显著的增升减阻效果受到诸多****的关注[15-16]. Chen等[17]采用RANS方法对不同射流动量系数($C_{\mu }$)下厚度为弦长($c$)的15%的椭圆型环量控制翼型流场进行了数值模拟,对该方法的增升效果以及$C_{ L}-C_{\mu }$曲线出现的临界点进行了分析.
Forster等[18]、宋彦萍等[19]研究了柯恩达曲面形状对环量控制方法的影响,结果表明在射流强度相同情况下曲率较小的柯恩达曲面有利于射流附着后缘流动,以提升控制方法的增升减阻效果. Tongchitpakdee等[20]将环量控制方法用于尖后缘风力机翼型. 但是尖后缘翼型后缘厚度太小,从而导致射流附着翼型流动的距离很短,射流对后缘附近流场的影响较弱,最终使得控制效果并不理想. 另外,冯立好等[21]、 张艳华等[22]采用等离子体激励器结合环量控制方法对NACA0012翼型进行流动控制,实验结果表明该方法与传统环量控制方法的增升机理相同,但由于目前等离子激励器所激发的射流的流速较低,该方法对翼型升力系数的提升相对有限.
环量控制方法一般需要光滑的后缘曲面或者后缘襟翼[23]来实现,而传统翼型较难通过修形的方式来达到相应的要求. 与传统翼型相比,钝后缘风力机翼型后缘的厚度较大,便于修形,非常适合进行环量控制,并且环量控制方法施加在翼型的后缘附近, 可以对钝后缘翼型后缘脱体涡进行控制. 本文采用环量控制方法对钝后缘风力机翼型进行流动控制,使用RANS方法对相关风力机翼型绕流流场进行数值模拟,研究射流动量系数对环量控制方法的影响,并对环量控制方法进行能效分析,以期为风力机环量控制方法相关研究提供参考数据.
1 风力机翼型的修形
为研究钝后缘风力机翼型的环量控制方法,本文在DU97-flatback翼型[24]的基础上进行修形.首先,将DU97-flatback翼型上下翼面靠近后缘部分向翼型内部平移0.005$c$得到相应的曲线.然后,作与上述两条曲线以及翼型后缘的公切圆,以公切圆与两条曲线的切点为界,取向后缘方向凸起的圆弧作为柯恩达曲面.最后,在翼型内部开设高压气室以及相应的喷口,喷口高度为0.002$c$.修形后得到的环量控制翼型命名为DU97-flatback-CC翼型,其形状如图1所示.
显示原图|下载原图ZIP|生成PPT图1DU97-flatback翼型与DU97-flatback-CC翼型...
-->Fig. 1DU97-flatback airfoil and DU97-flatback-CC airfoil...
-->
该修形方法简单有效地将钝后缘风力机翼型修形为环量控制翼型,并且在修形过程中未改变翼型的后缘厚度,保留了钝后缘风力机翼型的优点.
修形后翼型后缘变成了光滑曲面,当射流从喷口流出时,在柯恩达效应的作用下,射流附着柯恩达曲面流动,从而实现钝后缘风力机翼型的环量控制方法.
2 数值模拟方法与验证
2.1 数值计算方法
本文的数值模拟采用基于S-A模型的可压缩雷诺平均Navier-Stokes方程求解程序,无黏通量项采用Roe格式离散和三阶MUSCL格式插值,黏性项采用二阶中心差分格式离散,拟时间推进采用隐式LU-SGS迭代方法.远场边界采用基于一维Riemann不变量的无反射远场边界条件[25],壁面采用无滑移边界条件.高压气室的入流边界给定总压、总温和入流角,速度由内场插值得到.在环量控制翼型的相关算例中,每隔500个伪时间推进步,计算喷口的射流动量系数,并与预设值进行比较.根据比较的结果调整总压,直至喷口射流动量系数达到预设值.射流动量系数是衡量射流强弱的无量纲参数,其定义如下
\begin{equation}\label{eq1} C_\mu = \frac{\dot {m}_{ jet} V_{ jet} }{0.5\rho_\infty V_\infty ^2 S}\tag{1}\end{equation}
其中, $\dot {m}_{ jet} $为喷口处的质量流量,$V_{jet}$为喷口处的平均速度,$\rho _\infty$为自由来流的密度,$V_\infty$为自由来流的速度,$S$为参考面积,对于翼型而言$S=c(1)=c$.
2.2 DU97-flatback算例验证与网格收敛性分析
为了降低网格划分对流场求解的影响,并兼顾计算效率等因素,本文在进行相应的数值模拟研究之前,对DU97-flatback翼型进行了网格收敛性分析.采用三套不同规模的网格对DU97-flatback翼型的绕流流场进行数值模拟,计算条件为：{AoA} =11.05$^\circ$,{Ma} = 0.168,{Re} = 3.0$\times$10$^{6}$. 为确保计算网格的$y^{ +}$小于1,三套网格的第一层高度均为10$^{ -5}c$量级,网格相关参数见表1.气动力系数的计算结果与风洞实验结果[24]的对比情况见表2.
Table 1
表1
表1DU97-flatback翼型网格参数
Table 1Details of the grids employed for the DU97-flatback airfoil
| Parameters | Coarse grid | Medium grid | Fine grid |
|---|---|---|---|
| wrap-around points | 225 | 450 | 630 |
| normal layers | 100 | 200 | 283 |
| total number of cells | 2.25X104 | 9.0X104 | 17.8X104 |
| first layer spacing (c) | 1.2X10-5 | 0.8X10-5 | 0.6X10-5 |
| spacing increasing ratio | 1.20 | 1.13 | 1.10 |
新窗口打开
Table 1
表2
表2升阻力系数比较结果
Table 1Comparison of lift and drag coefficients
| Parameters | Coarse grid | Medium grid | Fine grid | cfd[24] | Exp[24] |
|---|---|---|---|---|---|
| Cl | 1.7339 | 1.7292 | 1.7248 | 1.769 | 1.736 |
| Cd | 0.050 95 | 0.047 15 | 0.046 30 | 0.046 5 | 0.054 5 |
新窗口打开
网格收敛性主要根据各套网格对应的气动力系数计算结果的变化趋势来判断[26].从三套网格对应$C_{D}$的比较结果来看,从粗网格到中等网格,$C_{D}$降低7.46%;从中等网格到密网格,$C_{ D}$仅降低1.80%.因此,可以看出随着网格量的逐渐增长,网格划分对计算结果的影响逐渐降低,即网格收敛性良好.从中等网格到密网格,翼型的气动力系数相差不大,但网格量却增加近一倍.另外,从表2可以看出,与文献${[24]的计算结果相比,本文升力系数的计算结果更加接近实验值.因此,本文选用如图2所示的中等网格作为DU97-flatback翼型相关数值模拟的计算网格,而且环量控制翼型的计算网格根据相同的网格规模进行划分.
显示原图|下载原图ZIP|生成PPT图2DU97-flatback翼型的计算网格...
-->Fig. 2Computational grid for DU97-flatback airfoil...
-->
2.3 环量控制翼型数值模拟方法验证
由于环量控制方法的实验数据相对有限,为了对环量控制方法进行数值模拟验证,选用GACC翼型[27]对射流流动的相关数值模拟进行方法验证.对喷口高度为0.001$c$的GACC翼型进行数值模拟,计算条件为：{AoA}= 0$^{\circ}$,{Ma} = 0.10,{Re} = 5.33$\times$10$^{5}$, $C_{\mu }$ =0.060,将数值模拟结果与文献${[27]中的实验结果和数值计算结果进行了对比.图3给出了GACC翼型压力系数分布的对比结果.可以看出,压力系数的计算结果与实验结果吻合良好,且与文献${[27]中的计算结果基本重合.图4给出了$C_{\mu }$ = 0.060时GACC翼型的流场图.从流场图来看,在环量控制方法的影响下翼型后缘附近流动方向弯向斜下方,从而使得翼型绕流环量增大,升力系数增大.从压力系数比较结果和流场结构来看,本文采用的数值模拟方法可以较为准确地模拟环量控制方法中的射流流动.
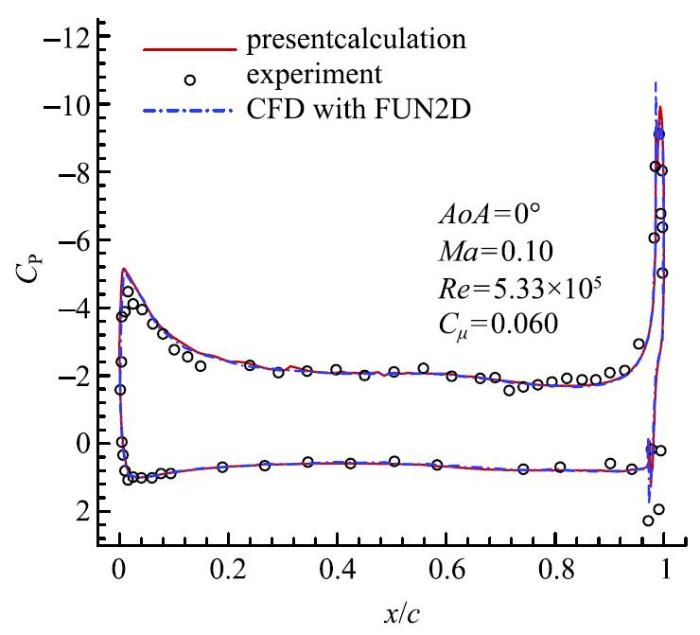显示原图|下载原图ZIP|生成PPT图3GACC翼型压力系数分布的对比结果...
-->Fig. 3Comparison of pressure coefficients of GACC airfoil...
-->
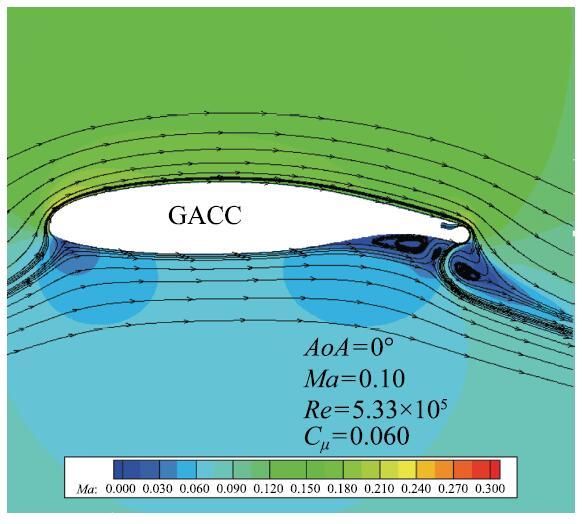显示原图|下载原图ZIP|生成PPT图4GACC翼型流场图...
-->Fig. 4Flow field of GACC airfoil...
-->
3 结果分析
3.1 环量控制方法对翼型气动特性的影响
本文对迎角从$-4^{\circ}$到20$^{\circ}$范围内,DU97-flatback翼型和DU97-flatback-CC翼型的绕流流场进行数值模拟,并将升阻力曲线、压力系数$C_{P}$曲线以及流场信息的计算结果进行比较和分析.计算条件为：{Ma} = 0.10,{Re} = 3.0$\times$10$^{6}$,对于DU97-flatback-CC翼型射流动量系数统一取0.030.其中,DU97-flatback-CC翼型的计算网格如图5所示.
显示原图|下载原图ZIP|生成PPT图5DU97-flatback-CC翼型计算网格...
-->Fig. 5Computational grid for DU97-flatback-CC airfoil...
-->
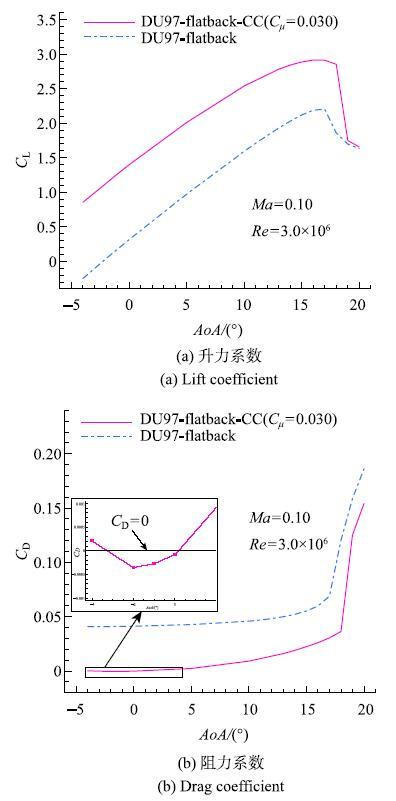
图6给出了两翼型的$C_{ L}$-{AoA}曲线和$C_{D}$-{AoA}曲线的计算结果.从图6(a)可以看出,在失速之前,相同迎角下DU97-flatback-CC翼型的$C_{L}$比DU97-flatback翼型大,而且两翼型$C_{L}$之间的差距与迎角的关系不大.由于环量控制方法施加在翼型的后缘,因此该方法对流动分离的抑制效果较弱,当翼型上翼面发生流动分离时,射流仅仅对分离区有一定的影响.从升力曲线的比较结果来看,两翼型的失速迎角大致相同,失速后DU97-flatback-CC翼型的$C_{L}$迅速下降.
显示原图|下载原图ZIP|生成PPT图6升阻力系数曲线的比较结果...
-->Fig. 6Comparison of lift and drag coefficient curves...
-->
从图6(b)给出的$C_{D}$-{AoA}曲线比较结果来看,由于DU97-flatback翼型后缘厚度较大,翼型的后缘压力较低,压差阻力较大,阻力系数明显较大.在射流的作用下,尾迹区的脱体涡被吹散,射流补充了翼型后缘的低压区,降低了翼型的压差阻力.同时,射流产生的反推力抵消了一部分阻力,从而进一步降低了翼型的阻力系数.甚至迎角在$-2^{\circ}\sim $0$^{\circ}$范围内时,DU97-flatback-CC翼型的阻力系数小于零.但由于此时阻力系数的绝对值很小,再加上RANS方法对阻力系数预测的精度不足,不能排除该情况是由计算误差造成的. 另外,本文还对$C_{\mu } =0.080,{AoA} = -2^\circ,{Ma} =0.1$时对应翼型绕流流场进行了数值模拟,计算得到该状态下的$C_{D}$为$-0.006~24$,此时$C_{ D}$的大小已经超出了误差的量级.所以,小迎角时翼型在环量控制方法的作用下会表现出负阻力现象,这是因为此时射流产生的反推力大于翼型的压差阻力和摩擦阻力之和.从计算结果来看,DU97-flatback-CC翼型的阻力系数比DU97-flatback翼型小很多,这证明了环量控制方法的减阻效果明显.
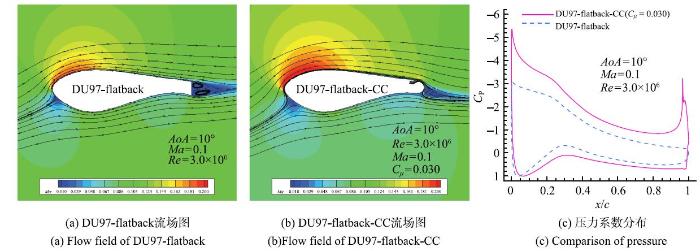
图7给出了10$^{\circ}$迎角下两翼型的马赫数云图和流线分布以及压力系数分布的比较结果.从图7(a)可以看出,由于DU97-flatback翼型后缘厚度较大,自由来流流经上下翼面后无法及时到达翼型后方,因此翼型后缘附近形成一定范围的低压区,并且形成了一定强度的脱体涡.翼型后缘的低压区使翼型压差阻力增大,而且翼型尾迹区产生的脱体涡会引发相应的涡致振动和气动噪声问题.对于DU97-flatback-CC翼型而言,如图7(b)所示,在柯恩达效应的影响下,射流附着柯恩达曲面流动.射流的强剪切作用使得周围的流体随射流向斜下方流动,从而改变了翼型的等效弯度,大幅提高了翼型的升力系数.另外,前缘驻点在射流的作用下向后缘方向移动,前缘吸力峰附近马赫数明显增大.而且在射流的作用下,翼型后方低压区的压强有所增大,尾迹区的脱体涡消失,翼型的压差阻力降低.
显示原图|下载原图ZIP|生成PPT图7{AoA} = 10$^{\circ}$时两翼型流场图和压力系数分布的比较结果...
-->Fig. 7Flow fields of two airfoils and the comparison of pressure coefficients...
-->
从图7(c)所示的两翼型$C_{P}$曲线的比较结果来看,在环量控制方法的作用下,翼型等效弯度增大,对应的$C_{P}$曲线所围成的面积明显增大.DU97-flatback-CC翼型上翼面压力系数明显低于DU97-flatback翼型,尤其是前缘吸力峰和后缘喷口附近;射流在后缘附近产生的阻塞效应使翼型下翼面的压力系数增大;翼型前缘驻点位置明显后移.
综上所述,环量控制方法改变了整个翼型绕流流场,DU97-flatback-CC翼型对应的$C_{P}$曲线所围成的面积明显比DU97-flatback翼型的大.由于射流对翼型后缘附近流场的影响,翼型的等效弯度和绕流环量增大,并且由于下翼面附近压强的增大,自由来流在接近翼型时发生明显的偏转,从而使翼型的等效迎角增大.总体来说,环量控制方法具有显著的增升减阻效果,对后缘脱体涡也起到了良好的抑制作用.
3.2 射流动量系数对环量控制方法影响
射流强度是翼型环量控制方法控制效果的重要影响因素之一.为了研究射流强弱对环量控制方法的影响,本节对$C_{\mu }$ =0.010$\sim $0.080时DU97-flatback-CC翼型的绕流流场进行了数值模拟.通常情况下,风场的实际风速与气候和天气等因素有关.当风场风速在切入风速到额定风速范围内时,大型风力机一般通过变桨距的方式使叶片的迎角保持较大的数值,从而使风轮能够产生较大的输出功率[28].此时,叶片靠近根部区段的实际迎角接近且小于失速迎角.因此,本节相关算例的计算条件为：{Ma} =0.10,{Re} = 3.0$\times$10$^{6}$,{AoA} = 17$^{\circ}$.不同射流动量系数下DU97-flatback-CC翼型升力系数和阻力系数的计算结果如图8所示.
显示原图|下载原图ZIP|生成PPT图8翼型升阻力系数随射流动量系数的变化曲线图...
-->Fig. 8Variation of lift and drag coefficients with jetmomentumcoefficient...
-->
从图8(a)给出的$C_{ L}-C_{\mu}$曲线图可以看出,随着$C_{\mu }$的增大翼型升力系数不断增长.在$C_{\mu }$ = 0.038附近,$C_{ L}-C_{\mu}$曲线的斜率在很小范围内急剧降低. $C_{ L}-C_{\mu}$曲线出现临界点的现象在之前环量控制的相关研究工作[29-30]中有所介绍.临界点前为分离控制阶段(即随着$C_{\mu}$增大射流分离位置逐渐远离喷口),临界点后为超环量控制阶段(即随着$C_{\mu}$增大射流分离位置不再发生变化).相比之下,分离控制阶段的增升效率更高. 随着$C_{\mu}$的增长,射流产生的反推力逐渐增大,但从图8(b)给出的$C_{D}-C_{\mu }$曲线图可以看出翼型的阻力系数并不是单调降低. 在$C_{\mu}$达到临界点附近时,翼型的阻力系数随$C_{\mu}$的增大而小幅回升. 当$C_{\mu}$大于阻力系数极大值对应的值后,$C_{ D}-C_{\mu }$曲线单调下降.
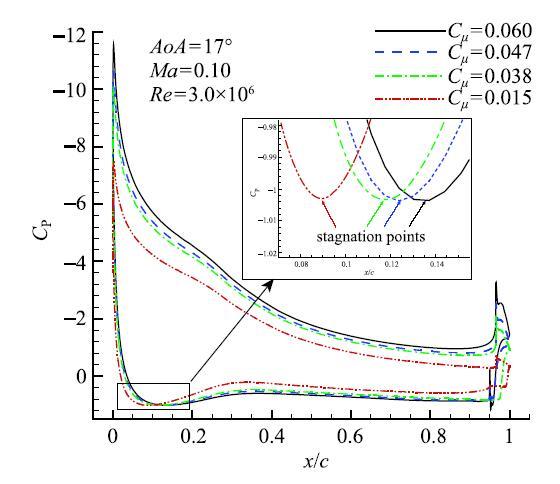
从图9给出了迎角为17$^\circ$时$C_{\mu }$分别为0.015,0.038,0.047和0.060时翼型的$C_{P}$曲线的对比结果来看,随着$C_{\mu}$增大,前缘吸力峰的压强不断减小,翼型前缘驻点后移.翼型前缘驻点位置与翼型绕流环量关系紧密,前缘驻点后移说明翼型绕流环量随$C_{\mu}$增大而增大,进一步说明翼型升力系数随$C_{\mu }$增大而增大.
显示原图|下载原图ZIP|生成PPT图9不同$C_{\mu }$下翼型压力系数分布曲线的比较结果...
-->Fig. 9Comparison of pressure coefficients between different$C_{\mu }$...
-->
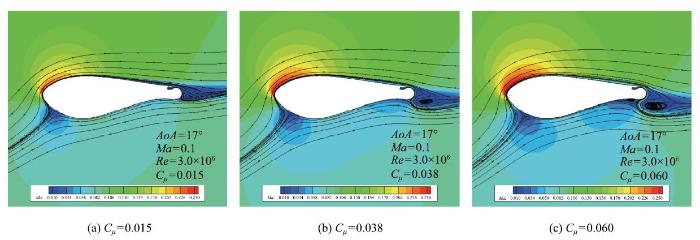
图10给出了不同$C_{\mu }$下DU97-flatback-CC翼型的流场图.从图10(a)所示的$C_{\mu }$ =0.015时翼型的流场图来看,在射流的强剪切作用下翼型尾迹区流线的曲率变大,但没有明显的脱体涡产生,射流的分离位置均在柯恩达曲面上,此时环量控制方法处于分离控制阶段.当$C_{\mu }$ = 0.038时射流的分离点非常靠近柯恩达曲面末端.当$C_{\mu }$ =0.060时,如图10(c)所示,射流的分离点位于柯恩达曲面末端,环量控制方法处于超环量控制阶段.
显示原图|下载原图ZIP|生成PPT图10不同射流动量系数下DU97-flatback-CC翼型的流场图...
-->Fig. 10Flow fields of DU97-flatback-CC airfoil with different $C_{\mu }$...
-->
在图10(a)到图10(b)对应的分离控制阶段中,射流的分离位置由射流动量系数决定,射流越强(射流动量系数越大),射流附着柯恩达曲面流动的距离越远.在图10(b)到图10(c)对应的超环量控制阶段中,射流的分离点均达到柯恩达曲面末端,射流从柯恩达曲面分离后与流经下翼面的来流混合.此时射流在$x$方向上的速度分量小于0,射流与来流之间强烈的相互作用使翼型的相对弯度增大,这种现象与吹气式Gurney襟翼十分相似.因为下翼面绕流无法穿过射流,射流后方便会形成低压区,而当射流动量系数较大时上翼面绕流无法及时填充低压区域,于是在该区域产生脱体涡.
3.3 环量控制方法能效分析
流动控制方法的能量消耗和控制效果的关系对控制方法的可行性和经济性至关重要,尤其是与风力机相关的主动流动控制方法.假设环量控制方法中由气压泵将外界自由流动的气体进行压缩后通过管道送入高压气室,高压气体通过高压气室从喷口喷出形成射流.形成射流的整个过程所消耗的功率系数$P_{c,jet}$的计算公式如下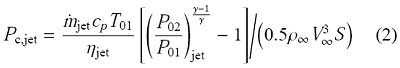
其中,{$\eta $}$_{jet}$为气压泵的工作效率,本文中取0.85;$c_{p}$为气体定压比热容;$P_{01}$为自由来流的总压;$P_{02}$为高压气室入流边界处的总压.$T_{01}$为自由来流的总温.
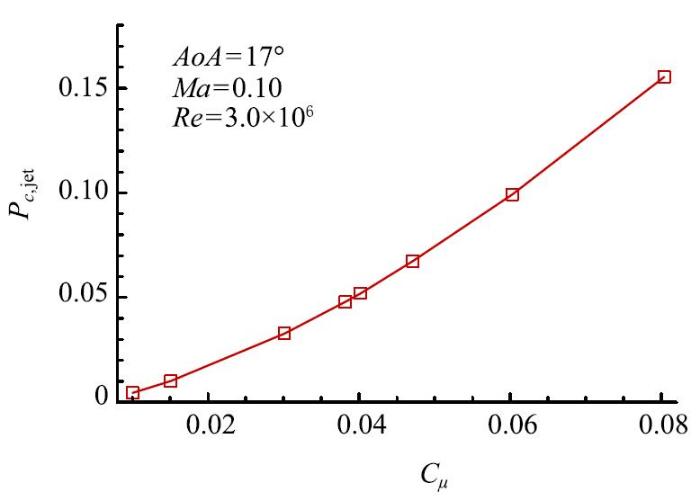
图11给出了DU97-flatback-CC翼型的射流能耗功率系数曲线.从图11可以看出,射流功率系数$P_{ c,jet}$随$C_{\mu}$增大而不断增大,且$P_{ c,jet}-C_{\mu }$曲线的斜率也逐渐增大.
一定的能量输入可以提高翼型的气动特性,对于风力机而言,叶片气动特性的提升将会使风力机的输出功率得到提升.那么,环量控制方法使风力机输出功率提升的部分是否大于环量控制方法本身所消耗的功率是一个至关重要的问题.
显示原图|下载原图ZIP|生成PPT图11射流能耗功率系数...
-->Fig. 11Variation of power coefficient with jet momentum coefficient...
-->
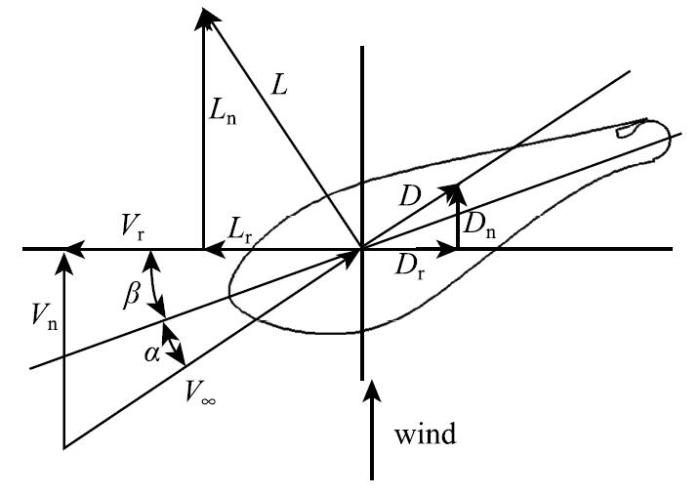
钝后缘风力机翼型一般被用在大型风力机叶片根部到叶片总长的1/2位置之间的部分.为方便分析,图12给出了风力机叶片截面受力分析示意图.
显示原图|下载原图ZIP|生成PPT图12叶片截面受力分析示意图...
-->Fig. 12Illustration of pertinent parameters...
-->
图12中{$\beta $}为叶片当地扭转角,{$\alpha$}为叶片当地迎角,$L_{ r}$和$D_{r}$分别为升力$L$和阻力$D$在旋转平面上的分量.假设风力机的转速为13.7r/min,能耗分析的采样点位于离桨毂距离为叶片长度40%的位置,叶片长度为50m,则采样点当地旋转线速度$V_{ r}$ = 28.7 m/s. 假设来流风速为10m/s,风轮偏航角为零度,可以得到此时叶片尖速比为7.2.当地来流$V_{\infty }$的方向与旋转平面的夹角{$\theta $ }={$\alpha $} + {$\beta $} = 19.210$^{\circ}$.假设叶片当地扭转角{$\beta $} =2.210$^{\circ}$,那么叶片当地的迎角{$\alpha $} =17$^{\circ}$. 这里假设叶片的当地弦长$c$ = 1.44m,则基于当地弦长的雷诺数{Re} = 3.0$\times $10$^{6}$.假设风力机将风轮扭矩转化为输出功率的转化效率{$\eta $}$_{e}$ = 0.85.不考虑叶片旋转效应的影响,在上述工作条件下,单位长度的叶片提供的输出功率系数$P_{c}$的计算公式如下
\begin{equation}\label{eq3} P_{ c} = \frac{\left( {L_{ r}-D_{ r} }\right)V_{ r} }{q_\infty c(\ref{eq1})V_\infty } \cdot \eta_{ e}\tag{3}\end{equation}
由上式可以分别求得DU97-flatback翼型和DU97-flatback-CC翼型能够获得的输出功率系数$P_{c,fb}$和$P_{ c,fb-CC}$.在对环量控制方法的能耗和控制效率进行分析之前,需要建立一个衡量流动控制方法控制效果和效率的相关参数.Seifert[31]在其先前研究[32]的基础上以升阻比为衡量基准分别定义了闭环主动流动控制的气动品质因子AFM1(firstaerodynamic figure of merit)和AFM2(second aerodynamic figure ofmerit),Stalnov等[33]对上述两种气动品质因子进行改进,提出了适用于零质量射流控制方法的气动品质因子AFM3.由于式(3)中$P_{c}$与AFM3计算公式中相应项的表达式非常相似,因此将AFM3中各项替换为对应的功率系数,从而得到本文的适用于环量控制方法的气动品质因子$\eta_1$,其表达式如下
\begin{equation}\label{eq4} \eta_1 = \frac{P_{ c,fb-CC}-P_{ c,jet}}{P_{ c,fb} }\tag{4}\end{equation}
从上式可以看出,$\eta_1$体现了环量控制方法对叶片输出功率的提升效果,也反应了该方法的控制效果.为比较叶片输出功率的增量与射流消耗的功率之间的关系,即能量的投入与回报之间的关系,本文对$\eta_1$的表达式进行修改,得到衡量环量控制方法控制效率的气动品质因子$\eta_2$,其表达式如下
\begin{equation}\label{eq5} \eta_2 = \frac{P_{ c,fb-CC}-P_{ c,flatback}}{P_{ c,jet} }\tag{5}\end{equation}
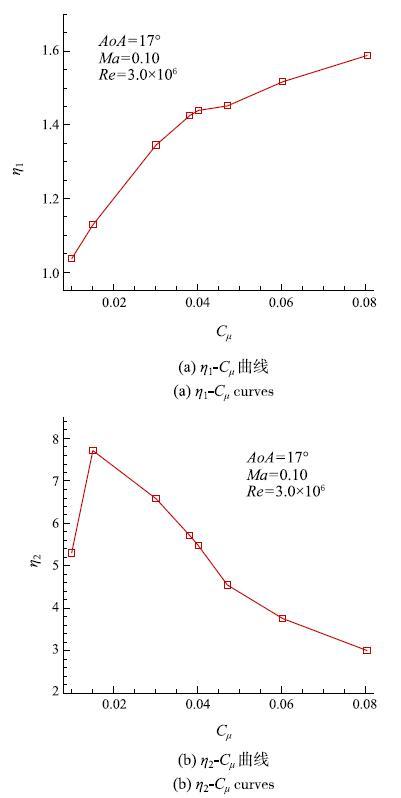
不同射流动量系对应的$\eta_1$和$\eta_2$的计算结果如图13所示.从$\eta_1$-$C_{\mu }$曲线的计算结果来看,$\eta_1$随$C_{\mu}$的变化趋势与图8(a)所示的$C_{ L}-C_{\mu }$曲线的变化趋势相近.这是因为$\eta_1$的计算公式中$P_{c,jet}$的数量级较小,$\eta_1$的大小主要由$P_{ c,fb -CC}$和$P_{ c,fb}$的比值决定. 然而{AoA} =17$^\circ$时,$P_{ c,fb}$为定值,$P_{ c,fb -CC}$的值由$L_{ r}$和$D_{ r}$的线性组合决定,而$D_{r}$的值相对$L_{ r}$要小很多,因此,$\eta_1$的值主要由$L_{r}$决定.
随着$C_{\mu }$增大,翼型升力系数增大,$\eta_1$值随之增大.图13(a)所示的$\eta_1$-$C_{\mu}$曲线同样具有分离控制阶段和超环量控制阶段,临界点位于$C_{\mu }$ =0.038位置附近,临界点前后曲线斜率发生明显变化. 当$C_{\mu}$达到0.080时,$\eta_1$的值大约为1.59,即此时环量控制方法使该段叶片产生的输出功率提升约59%.图13(b)所示的$\eta_2$-$C_{\mu }$曲线可以看出,随着$C_{\mu}$增大,环量控制方法的控制效率呈现先增大减小的趋势. $C_{\mu}$值较小时$\eta_2$随$C_{\mu }$增大快速增长,当$C_{\mu }$ =0.015时达到$\eta_1$最大值7.7. 当$C_{\mu } >0.015$时,$\eta_2$随$C_{\mu}$增大逐渐降低,降低速率逐渐放缓,$C_{\mu }$ =0.080时$\eta_2$降至3.0. 虽然当$C_{\mu}$取0.015时控制效率最高,但此时射流消耗的功率较小,叶片输出功率的提升效果不够明显.综合考虑$\eta_1$和$\eta_2$的计算结果,$C_{\mu}$的值取不应过大或过小.
总体来说,环量控制方法对叶片输出功率的提升效果明显. $C_{\mu}$越大控制段叶片输出功率越大,而射流能耗功率也随之增大.权衡叶片输出功率和射流能量功率之间的关系,$C_{\mu}$的值取在分离控制阶段和超环量控制阶段的临界点附近较优,此时通过环量控制方法所得到的输出功率的增长量是射流消耗功率的5.7倍,该段叶片的输出功率提升近43%
显示原图|下载原图ZIP|生成PPT图13气动品质因子曲线...
-->Fig. 13$\eta_1$-$C_{\mu }$ and $\eta_2$-$C_{\mu }$ curves...
-->
4 结论
本文采用数值模拟方法,对风力机翼型的环量控制方法进行了研究,得出以下结论：(1)通过将计算结果与风洞实验结果进行对比,证明了本文所用数值模拟方法可以较为准确地模拟钝后缘风力机翼型和环量控制翼型的绕流流场.
(2)通过对{Ma} = 0.10,{Re }= 3.0$\times$10$^{6}$时不同迎角下DU97-flatback翼型和DU97-flatback-CC翼型的数值模拟,将计算结果进行对比和分析,结果表明：环量控制方法具有显著的增升效果;在射流的作用下,翼型尾迹区脱体涡的强度大幅减弱,翼型压差阻力降低;射流产生的反推力能够有效地降低翼型的阻力.
(3)随着$C_{\mu }$的增大,环量控制翼型的$C_{L}$不断增大;$C_{ L}-C_{\mu}$曲线的斜率在临界点前后发生明显变化,该点将曲线分成分离控制阶段和超环量控制阶段;分离控制阶段的控制效率较高.
(4)叶片输出功率和射流能耗功率同时随$C_{\mu}$的增大而增大;当$C_{\mu }$ =0.080时,叶片对应区段的输出功率增长59%;权衡输出功率和射流能耗之间的关系,$C_{\mu
}$的值取在$C_{ L}-C_{\mu}$曲线的临界点附近较优,此时叶片输出功率的增长量约为射流消耗功率的5.7倍,输出功率提升近43%.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . |
| [2] | . |
| [3] | . . |
| [4] | . |
| [5] | . |
| [6] | . |
| [7] | . |
| [8] | |
| [9] | . . |
| [10] | . |
| [11] | |
| [12] | . |
| [13] | |
| [14] | |
| [15] | . |
| [16] | . |
| [17] | . |
| [18] | |
| [19] | . . |
| [20] | . |
| [21] | . . |
| [22] | . . |
| [23] | . . |
| [24] | |
| [25] | |
| [26] | . |
| [27] | |
| [28] | . |
| [29] | |
| [30] | . . |
| [31] | |
| [32] | . |
| [33] | . |
