中国计量大学流体检测与仿真研究所,杭州 310018
WIND TUNNEL INVESTIGATION OF THE AERODYNAMIC CHARACTERISTICS OF PURPLE WISTERIA COMPOUND LEAVES1)
YuKejie, ShaoChuanping中图分类号:V211.74
文献标识码:A
版权声明:2019力学学报期刊社力学学报期刊社 所有
基金资助:
作者简介:
-->
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (13384KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
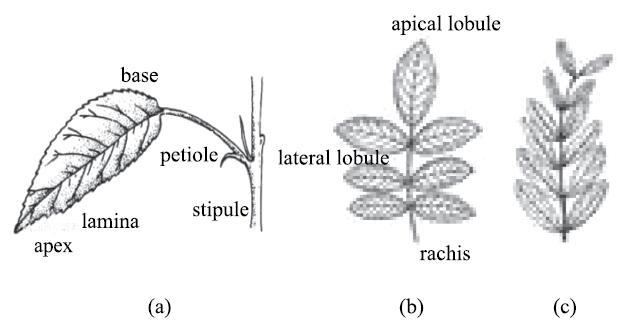
树叶一般由托叶、叶轴(或叶柄)和叶片三部分组成,其中叶柄上端与叶片基部连接,叶柄下端与茎或枝条连接. 树叶可分为单叶和复叶两种,其中一个叶柄上仅有一个叶片的为单叶,而一个叶轴上有多个小叶片的称为复叶. 当复叶的小叶在叶轴两侧对称排列的,称为羽状复叶. 有些羽状复叶在叶轴末端有单个小叶,总叶片为奇数; 有些则在叶轴末端没有单个小叶,总叶片数为偶数.
显示原图|下载原图ZIP|生成PPT图1树叶及其构成：(a)单叶, (b)奇数羽状复叶, (c)偶数羽状复叶...
-->Fig. 1Tree leaves and their components: (a) single leaf, (b) imparipinnate leaf, (c) paripinnate leaf...
-->
风是破坏植物的关键影响因素[1-3],经过千百万年的演化,每种树叶都进化出了其适环境变化的能力[4]. 当风速较大时,阔叶树单叶能够自动卷成流线体,而一些复叶的小叶由分散状态卷成一个流线形整体,以保护自己免受破坏[5]. 而一些阔叶树的树叶在很低风速下就会发生摇摆和振动. 树叶的这些特质在空气动力学和仿生学领域中得到了关注[6],受其启发,工程师们开发了新的风能发电技术[7],设计了新型太阳能帆板[8]、 新型机翼结构[9]和仿生天线[10].
Vogel[11]最早对单叶进行研究,发现当风速达到一定值后,叶片两侧上翻,横截面呈"U"形;风速再增大到一定值,叶片卷成锥形. 形状变化对叶片阻力产生较大影响. Vogel发现树叶阻力系数$C_{ D} = 2D/({\rho _{ a}}V_\infty ^2A)$,其中,$D$为树叶总阻力, $A$为叶片平展面积,$\rho_{ a}$为空气密度,与风速 之间具有关系：$C_{ D}\sim V_\infty ^\alpha$,$\alpha $被称为Vogel指数. 在计算$\alpha $值时,Vogel采用风速10$\sim $20 m/s范围内的实验数据. 对于刚性钝体,$\alpha =0$,因此该系数代表变形后的树叶与钝体之间的差别. 如果特征面积用树叶实际迎风面积,则当风速大于一定值后,阻力系数为常数,指数为0. 因此$\alpha $是衡量树叶迎风面积随风速减小(或增长)的指数,是树叶变形能力的体现.
Vogel[11]对洋槐(black locust)、黑胡桃(black walnut)、光叶山核桃(pignut hickory)、红枫(red maple)、鹅掌楸(tulip tree)和栎树(white oak)等6种树的成熟阔叶进行单叶测试后发现$\alpha $值在$-1.18 \sim -0.52$之间,说明大多数树叶在较高风速下具有收缩变形减阻的能力. Albayrak 等[12]对长条形的水生甜茅浮叶(glyceria fluitans)在水槽中进行了阻力测试,发现$\alpha $在$-0.74 \sim -0.25$之间, 其中,嫩叶平均$\alpha $值为$-0.52$,半成熟叶$\alpha $平均值为$-0.44$,成熟叶为$-0.29$. Speck[13]发现芦竹(arundo donax)阻力随风速线性增长,即系数$\alpha =-1.0$.
树叶形状和刚度[14]对其在风中的变形和减阻能力具有重要影响. Albayrak等[15]采用3种面积相等但形状不同的人造叶片进行测试,发现"椭圆形"与 "矩形"叶片阻力接近,当$Re>1.5\times 10^{4}$时,两者都仅为羽状复叶模型阻力系数的50％$\sim $60％. Miller$^{ [16]研究了杜衡(wild ginger)和野紫罗兰(wild violet) 的真叶和模型叶, 用5 $\mu$m厚透明乙酸胶片,分别做成圆形和矩形模型,其中圆形沿一条径线从边缘剪开至圆心. 在圆形圆心和矩形边的中间位置用弹性或刚性棒固定,以模仿树叶叶片与叶柄的连接. 数值模拟结果显示,当风速较小时,叶片尾流中有大尺度的强旋涡脱落. 随着风速变大,叶片变形,迎风面积减小,旋涡尺度减小. 叶片刚度减小时,旋涡尺度也减小. 叶柄由弹性变为刚性时,旋涡变弱. 风速由小增大时,矩形叶片变为"U"形,圆形叶片变为锥形. "U"形阻力系数较大,锥形阻力系数较小、更稳定,但两者都没有真实叶片的阻力系数低. Schouveiler和Boudaoud[17]也研究了沿半径开缝的圆形胶片树叶模型,发现叶片在水中卷成锥形,锥形的张开角(锥角的补角)随流速增大不断增大,并得到了阻力系数与张角的关系.
上述所有研究中,叶柄和叶片都是顺流向放置.当风速较低时,叶片接近于平铺状态,迎风面积小,树叶主要承受摩擦阻力,$\alpha$指数接近于$-1$.
从物理直观上看,随着风速的提高,树叶阻力系数不可能持续地减小,直至趋于0,Vogel公式不适用于很高风速的情况.
邵传平和朱园园$^{ [18]将单片鹅掌楸叶柄固支、叶片垂直悬挂,进行风洞测试. 随着风速增大,叶柄弯曲,阻力系数呈下降趋势.当风速大于一定值以后,叶片卷成锥体状,锥体轴线接近于水平,阻力系数$C_{ D}$稳定在0.1附近,Vogel指数 $\alpha $近于0. 说明在风速达到一定值以后,叶片基本形状不再有大的变化.
悬铃木[19]和鹅掌楸[18]树叶处于叶柄固支的垂直悬挂状态时,在风速为2$\sim $3 m/s下会出现低频大幅摆动,在10 m/s左右风速下,出现高频振动. 高频振动出现前叶片呈"U"形稳定,高频振动消失后出现锥形稳定. 这些振动现象是叶片顺流向放置时所没有的.
叶片振动分为流向、侧向和扭转振动,其中流向振动指在与来流平行的平面内的振动. 悬铃木、鹅掌楸等叶片在低风速下以侧向和扭转振动为主,高风速时以流向和侧向振动为主[18-19]. Tadrist 等[20]研究了无花果树叶在风中的扭转颤振,通过对扭转振动方程的无量纲化,得到颤振发生的风速判据 $$V >V_{ c}= (40\pi /3) f_{0}h\xi (M/\rho )/\sin\psi$$ 其中$V_{ c}$,$f_{0}$,$h$,$\xi$,$M$,$\rho$,$\psi $分别为临界风速、叶片扭转固有频率、叶片厚度、扭转阻尼、叶片密度、空气密度、叶片扭转角. 从中可以看出,叶面顺流向(扭转角接近0$^\circ$或180$^\circ)$时,难以发生扭转颤振. 临界风速随密度比、固有频率和叶片厚度的增大而增大.
有些植物种类的长条形叶片,会生长出螺旋式扭转的外形,这种扭转外形对其弯曲和气动力具有重要影响[21-22]. Zhao等[23]数值模拟了长宽比为16的香蒲叶在流体中悬挂固支时的流向挠度,发现当叶片刚度为0.067时, 从基部到叶尖按左手性扭转360$^\circ$的叶片比平直叶片的挠度减小20％以上.
树叶在风中的位移与叶柄的长度,横截面惯性矩,及弯曲和扭转弹性模量有关. Niklas[24]发现单叶、羽状复叶和掌状复叶的叶柄(叶轴)弯曲刚度(弹性模量与惯性矩的乘积)与叶柄(叶轴)长度呈统计线性关系,与叶片重量也存在统计线性关系. 这些统计规律保证了叶柄有足够强度支撑大叶片.
对于复叶或树叶串来说,叶片之间如何相互影响,怎样对风环境作协同反应是我们感兴趣的问题.
Vogel[11]研究了洋槐和黑胡桃两种羽状复叶和叶轴两侧交错排列的酸木复叶,发现这3种复叶在风速达到一定值后小叶都相互协同卷成长圆柱(绳)状,且随着风速增大其直径减小. 但当风速大于12.5 m/s后,3种复叶都变得不稳定,随着风速增大,颤振越来越强烈.
Vogel[11]在较高风速(10$\sim $20 m/s)下对比了红枫、鹅掌楸、栎树和光叶山核桃4种树的单叶及其复叶(或叶串),发现复叶阻力系数(基于各小叶平展面积之和) 总小于单叶阻力系数(基于单叶平展面积). Vogel系数方面,红枫、鹅掌楸叶串的$\alpha $值分别为$-0.64$和$-0.91$,单叶对应值分别为$-0.79$和$-1.18$,说明这两种叶串的收缩变形能力没有单叶强,其减阻性能主要靠各叶片相互协同,使叶串的整体形状更接近流线体. 但是,栎树和光叶山核桃叶串的$\alpha $值分别为$-0.44$和$-0.78$,单叶对应值分别为$0.97$和$-0.2$,说明这两种叶串的收缩变形能力比单叶好. 与其他树叶较为柔软不同,栎树单叶的刚度大,顺流向放置时接近于平板流动,在风速达到一定值后树叶才开始弯曲, 形状逐渐变为钝体,迎风面积由小变大,因此其$E$值为正.
树叶在低风速下的阻力与较高风速下有较大差别,阔叶树树叶在横向放置时,阻力系数随着风速增大而减小,针叶树的情况却不同.Grant[25]研究了具有三叉小枝、布满针叶的云杉枝条,每个小枝的外形(针叶外形)为圆柱形.发现风速在0.5$\sim $1.5m/s时,整体阻力系数(所用特征面积不随风速变化)在0.1~0.22之间,风速为4$\sim $5 m/s时整体阻力系数升高到约0.8.研究认为风速较低时流体从针叶之间的空隙流过因而阻力系数较小.当风速变大以后,虽然针叶收缩变形,迎风面积减小,但针叶之间空隙减小,大部分流体不能穿过而只能绕过柱形枝条,因而阻力系数增大.Guan等[26]对人造针叶树模型透气率的影响进行实验,发现阻力系数随透气率的增大而减小.
O'Hare等[27]对针形复叶的溪水毛茛、穗状狐尾草,窄长矩形叶片的黑三菱,阔叶的水马齿苋和眼子菜(杂交种)等沉水植物一根茎上的叶串在水槽中进行实验,发现尽管不同植物的形状和面积相差很大,但其茎叶的$E$值相差不大,在$-1.43\sim -1.62$之间.
Holland等[28]研究了3个品种豌豆植株的阻力系数：普通全叶型、半卷须半叶型和全须无叶型.风洞实验显示[29],在一定生长阶段,全叶型的阻力系数最小,无叶型却最大.他们认为,全叶型株冠的叶片经过变形重构后在风中的迎风面积减小很多,而无叶型的卷须像混乱卷发一样三维分布,无论哪个风向其迎风面积都不会有显著减小.
羽状复叶与多个独立柔性体的串列组合在气动特性方面有些相似.Ristroph和Zhang[30]测试了6个串行放置的旗帜,注重研究其中每一个旗帜的流体阻力与孤立旗帜流体阻力的比值.发现当相邻旗帜间距为零时,领头的前两个旗帜分别有50％和25％的减阻,中间两个的阻力比接近1,最后两个分别有50％和60％的减阻.当旗帜个数减为2时,领头旗帜可减阻50％,后面旗帜阻力则有一定增大.领头旗帜在流体中的横向摆动幅度小,后面的旗帜横摆幅度大,两者的尾迹构成漂亮的旋涡结构.领头者阻力显著低于尾随者的现象是串列柔性体所特有的.作为对比,刚性柱体串列布置时,领头柱体减阻不显著,后面的物体则减阻显著[31].如上所述,对复叶或树叶串已有很多研究,对其气动特性有了一些了解.但是,在树叶串振动及其形成条件与原因,以及叶片个数对气动特性的影响等方面,目前还知之甚少.本文以紫藤萝复叶为研究对象,就这些方面的问题开展研究.
1 实验材料和方法
紫藤萝的奇数羽状复叶由叶轴、顶生小叶和两侧对称排列的侧生小叶组成.小叶叶片通过很短的小叶柄与叶轴连接.叶轴横截面近圆形,轴径由底端到顶端缓慢减小,平均轴径较小.叶片薄,平展形状近似椭圆,中脉为椭圆长轴,叶尖明显,叶片面积较小.自然状态下,叶片与叶轴近似在一个平面内,侧叶中脉与叶轴之间的夹角一般小于45$^\circ$.紫藤萝羽状复叶于6月上旬,采集于中国计量大学校园内10株2m高的紫藤萝植被. 采集的复叶浸泡在常温自来水中保鲜,并在3h内用于实验.
实验在循环风洞内进行. 风洞试验段长2 m,宽和高各0.6 m.风洞实验段能够提供0.5~40 m/s,湍流度小于0.5％的均匀稳定风速.
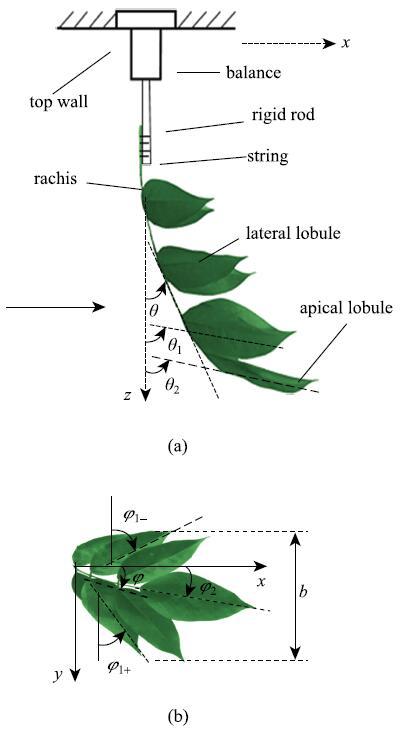
如图2所示,紫藤萝羽状复叶垂直悬挂于风洞实验段内,叶轴端部用细线固定在垂直刚棒上,钢棒穿过风洞顶壁的小孔与固定于顶壁外部的六分力风洞天平连接.天平可测量复叶的瞬时力和力矩,脉动力的保真频率范围为0$\sim $350Hz,采样频率50 kHz,采样时间16 s.
显示原图|下载原图ZIP|生成PPT图2测试中的紫藤萝复叶：(a)侧视, (b)仰视...
-->Fig. 2The purple wisteria compound leaf in test: (a) side view,\\ (b) upward view
-->
复叶的振动过程由摄速为1000 frame/s 的高速相机Photron FASTCAM MiniUX50 从风洞侧面和底部两个方向透过玻璃壁拍摄记录.叶轴和叶片的振动频率通过观察图像中特定点的位置变化周期数和所占图片帧数来确定.在风洞顶壁和侧壁贴有坐标纸,摄像截图后根据投影坐标可得到不同风速下叶轴和叶片的位移和变形量.
自然生长的紫藤萝复叶的小叶一般在5$\sim $9片之间.还有一些复叶有11片小叶,但这种复叶最靠近叶轴根部的一对小叶面积比其他小叶小很多,在空气动力方面所起的作用很小,在本文中将不加考虑.测试的羽状复叶按照小叶多少分为3组,第一组、第二组和第三组中每个复叶拥有的小叶数分别为5片、7片和9片.
每个复叶分别进行正面迎风和反面迎风测试.每次测试的风速从0开始依次递增,增量为1~1.5 m/s,直至22.8 m/s 为止.在每个风速下,先稳定15 s,再用风洞天平配套软件采集数据.整个增速过程中树叶状态及其变化由高速相机全程拍摄.
测试的3组紫藤萝羽状复叶的具体数量分布如表1所示.
Table 1
表1
表1(按小叶数目划分的) 各种复叶的测试数量
Table 1Tested compound leaves in groups divided according to their lobule number
 |
新窗口打开
2 结果与分析
2.1 复叶的稳定和振动状态
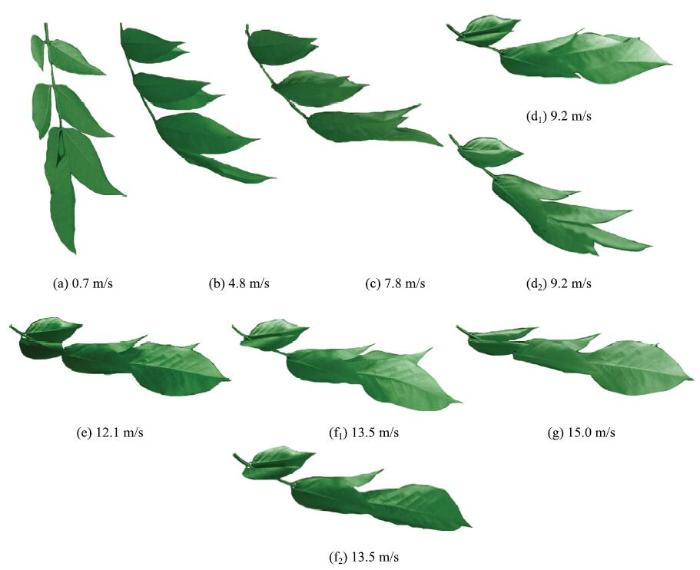
将一个紫藤萝复叶垂挂于风洞实验段正中,然后逐步提高风速,观察复叶的变形情况.图3为有7个小叶的复叶正面迎风的情况.如图3(a)所示, 2.0m/s以下风速时,复叶静止,叶轴向下游弯曲很小,各小叶中脉与$z$轴夹角及迎风面积与零风速时相比变化不大.
如图3(b)所示,当风速超过3m/s时,叶轴弯曲明显增大,小叶分为四层,每层的小叶像飞翔的羽翼一样张开,侧叶倾角$\theta_{1}$(侧叶中脉线与$z$轴夹角)增大到90$^\circ$左右,但固定风速下复叶仍处于静止.我们将此种状态称为分层飞翼稳定状态,这种状态开始出现的最低风速称为第一临界风速,用$V_{1}$表示.
如图3(c)所示,当风速达到7.8m/s时,叶轴弯曲加大,顶叶与其相邻的一对侧叶卷成锥形,其他两层侧叶仍呈飞翼形,形成多层飞翼形-锥形稳定状态.
显示原图|下载原图ZIP|生成PPT图3复叶正面迎风时状态随风速的变化: (a)初始状态,(b)多层飞翼形稳定, (c)翼形-锥形多层稳定,(d$_1$), (d$_2$)叶轴振动中的不同位置,(e)中间稳定, (f1),(f2)叶片振动中的不同位置,(g)锥形稳定...
-->Fig. 3State variation of a compound leaf with itsfront side facing wind: (a) initial state, (b) multi-layer wingsteady, (c) multi-layer wing-cone steady,(d$_1$) and (d$_2$) rachis in vibration, (e) intermediate steady, ($f_1$) and ($f_2$) lobules in vibration, (g) cone steady
-->
如图3(d$_{1})$和图3(d$_{2})$所示,当风速达到9.2m/s时,稳定平衡被打破,叶轴发生上下振动,并带动叶片一起振动.这种叶轴开始振动的最低风速称为第二临界风速,用$V_{2}$表示.
如图3(e)所示,当风速增大到12.1 m/s时,叶轴和叶片停止振动,复叶分为两层,靠近叶轴基部的第一层是飞翼形,另外一层为锥形.这种状态称为中间稳定状态,它出现的最低风速称为第三临界风速$V_{3}$.
如图3(f$_{1})$和图3(f$_{2})$所示,当风速增大到13.5m/s时,稳定平衡再次被打破,顶叶与其相邻的一对侧叶发生振动,振动的频率较高,幅值较小.叶轴和其他叶片则接近于静止.出现部分叶片振动的最低风速称为第四临界风速$V_{4}$.
如图3(g)所示,风速增大到15m/s时,叶片的振动停止,复叶又恢复到稳定状态.此时各层叶片相互连在一起,形成一个近似细锥形的整体.这种从叶片振动到稳定转变的风速称为第五临界风速$V_{5}$.
虽然每个复叶有自己的特点,但经过大量复叶的测试后,发现紫藤萝复叶气动行为根据风速都可分为3个阶段：
(1)前期稳定阶段,从叶轴弯曲快速增大到侧小叶出现振动之前;
(2)中间调整阶段,从叶轴开始振动到叶片振动结束;
(3)后期稳定阶段,叶片振动结束以后的稳定阶段.
复叶在不同阶段具有不同的稳定状态. 每种稳定状态对应一种复叶形态.除了上面提到的多层飞翼形以外,根据复叶横截面形状,还存在U形、楔形、锥形等.
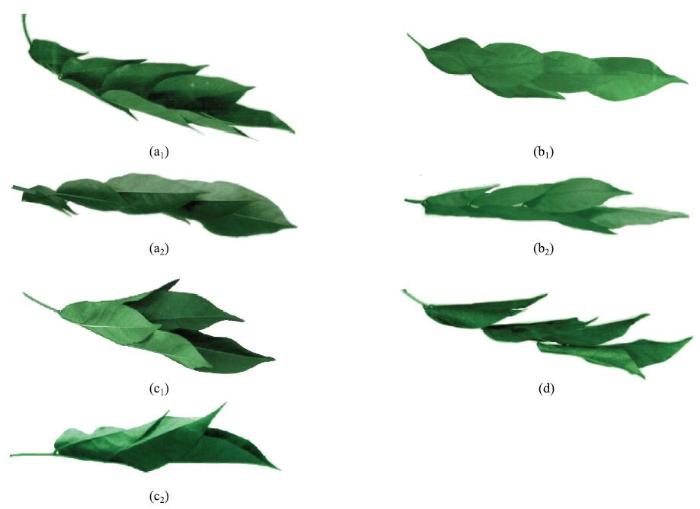
图4(a$_{1})$和图4(a$_{2})$分别为U形稳定状态的侧视和仰视图,每对侧叶半重叠或接近于重叠,并向上卷成U形,从叶轴基部到顶部,后面的叶片搭在前面的叶片上,形成一个U形槽道.
图4(b$_{1})$和图4(b$_{2})$分别为楔形稳定状态的侧视和仰视图.从侧视图看,侧叶都竖起来前后相搭,从仰视图看,两侧叶片中脉之间距离从叶轴基部到顶部由小到大,形成尖劈状.
图4(c$_{1})$和图4(c$_{2})$分别为锥形稳态的侧视和仰视图.从两个视图看,从叶轴基部到顶部,叶片横向尺度基本上都是由小变大,且叶轴同一位置的横向尺度在两个视图中也基本接近,说明横截面近似圆形,复叶整体呈锥形.
显示原图|下载原图ZIP|生成PPT图4复叶的各种稳定状态： (a$_1$) U形, 侧视; (a$_2$) U形,仰视; (b$_1$) 楔形, 侧视; (b$_2$) 楔形, 仰视;(c$_1$) 锥形,侧视;(c$_2$) 锥形, 仰视;(d) 多层结构, 侧视...
-->Fig. 4Various steady states of a compound leaf: (a$_1$)U-shape, side view; (a$_2$) U-shape, upward view;(b$_1$) wedge, side view; (b$_2$) wedge, upward view; (c$_1$) cone, side view; (c$_2$) cone, upward view; (d) multi-layer structure, side view
-->
图4(d)为多层结构稳态的侧视图.靠近叶轴基部的第一排两个侧叶各自卷起呈双锥形稳定,形成第一层.第二排的两个侧叶和第三排的一个侧叶卷在一起成近似锥形,形成第二层.第三排的另一个侧叶和顶叶卷在一起呈近似锥形,形成第三层.
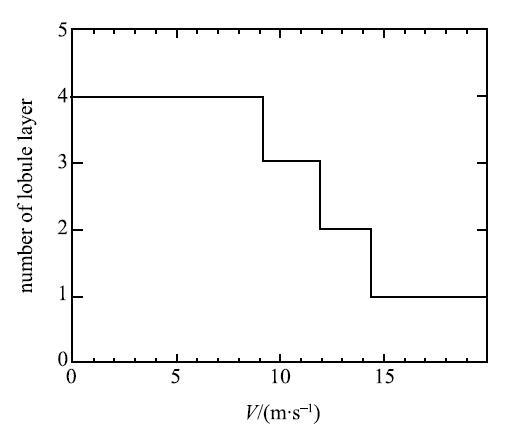
由于紫藤萝小叶较轻,连结叶轴和小叶的小柄很短但较柔软,较小的风就可将叶片由下垂状态吹成中脉近乎水平的状态,而风较小时,叶轴倾斜角$\theta$仍不大,因此叶片形成多层飞翼形. 随着风速的增大,叶片中脉仍处于水平位置附近,而叶轴弯曲增大,且越靠近顶部叶轴越接近水平.因而顶叶和相邻的一对叶片首先处于一个水平线上,形成三叶卷在一起的状态,叶片层数减少一个.风速进一步增大,叶轴接近于水平的部分加长,又一对叶片搭在下游的叶片上,叶片层数进一步减少.图5为有七小叶的复叶层数随风速变化的统计规律.可知叶片层数随风速的增大呈阶梯式下降.
复叶在风速逐步增大过程中并不是每种状态都会出现,一个复叶可能出现几种状态,另一个复叶可能出现另外几种状态.通过多个复叶的测试与统计,可以得到每个状态出现的概率.
表2为每个阶段各个状态出现的概率分布(统计时不分复叶正面迎风和反面迎风).可知在前期阶段,有两种稳定状态出现：(1)多层飞翼形,每层的小叶都像张开翅膀飞翔,这种状态在前期阶段出现概率为60％以上;(2)多层多形状,各层的小叶形状不尽相同,有的是飞翼状,有的是锥状,还有的是U形.第(2)种稳定状态在前期阶段出现的概率大于40％.有5％的情况会是两种稳定状态都在前期阶段出现,先出现状态(1),然后转变为状态(2).
显示原图|下载原图ZIP|生成PPT图5七小叶复叶的叶片层数随风速的变化...
-->Fig. 5The Change of lobule layer number with wind speed, the lobule number of the compound leaf is seven
-->
Table 2
表2
表2复叶状态在各阶段的存在概率
Table 2Existence probability of each state at different stages
| Earlier steady stage | Intermediate stage | Later steady stage | ||||
|---|---|---|---|---|---|---|
| multi-layer wing steady | multi-layer varied shape Steady | multi-layer varied rachis vibration shape steady | lobules vibration | two-layer steady | cone steady U-shape steady wedge steady | |
| 61.2% | 43.8% | 60% 32.5% | 36.2% | 48.8% | 28.2% 11.2% | 5% |
新窗口打开
在中间过渡阶段,仅出现叶片振动的概率小于40％,出现叶轴(叶片也一起)振动的概率约为60％.在该阶段,随着风速增大,也可能出现从一种振动(叶轴振动)到另一种振动(叶片振动)之间的转变.在转变的中间,还可能出现一种过渡稳定状态,为多层、多形状稳定,出现的概率略大于30％.当两种或三种状态先后出现时,每个状态的出现都将计入其出现概率中,因此会出现三者概率之和大于100％的情况.
在后期阶段,有两种主要的稳定状态,即复叶的两层稳定状态和单一整体稳定状态.这个单一整体的形状可分为锥形、楔形和U形3种.这里的两层稳定状态,是指靠近叶轴基部的一对侧叶成为第一层,其他小叶卷在一起成为第二层.在第一层,两个侧叶并排,主叶脉与来流方向接近平行,每个叶片的两侧下卷,呈飞翼状,或卷成锥状.在第二层,卷在一起的小叶形状也分为锥形、楔形和U形3种.在后期阶段,两层稳定状态出现的概率接近50％,单一整体稳定状态中的锥形稳定状态出现的概率接近30％,其他形状出现的概率较小.有一小部分复叶在测试的风速上限,仍处于振动状态,没有达到后期稳定阶段,这部分复叶占6.8％.
2.2 振动及姿态变化
图6为典型复叶在固定风速下叶轴及叶片在半个周期内的振动过程.从侧视图看,$t=0$时叶轴处于最下方,随着时间推移,叶轴开始弯曲上升,在$t=T/4$叶轴接近水平位置,$t=2T/4$时,叶轴到达最高位.
显示原图|下载原图ZIP|生成PPT图6叶轴半个周期的振动过程, 风速9.2 m/s(a$_1$)和(a$_2$), $t=0$侧视和仰视;(b$_1$)和(b$_2$), $t=T/4$侧视和仰视; (c$_1$)和(c$_2$), $t= 2T/4$侧视和仰视...
-->Fig. 6Vibration process of the rachis in aperiod, wind speed 9.2 m/s.(a$_1$) and (a$_2$), $t=0$, side and upward view; (b$_2$) and (b$_2$), $t=T/4$, side and upward view; (c$_1$) and (c$_2$), $t= 2T/4$, side and upward view
-->
从仰视图看,$t=0$时叶轴向左侧偏斜,具有一个较大的正偏航角.随着时间推移,偏航角减小,$t=T/4$时,偏航角变为零,时间再推移,偏航角变为负值,并在$t=2T/4$时,偏航角达到负的极值.此后叶轴回摆,并在$t=4T/6$时,叶片的振动更加复杂,除了跟随叶轴作上下和左右摆动外,还有叶片的扭转振动.一般情况下,叶片扭转的频率大于摆动频率.
为了定量研究叶轴的变形,用叶轴倾角$\theta$代表叶轴的弯曲程度,偏航角$\varphi$代表轴线与来流方向的偏离程度.叶轴各处的弯曲和偏航都不相同,接近顶叶的地方叶轴很软,其他地方则相对刚度较大.取邻近顶叶的一对侧叶叶柄处的叶轴弯角$\theta $和偏航角$\varphi$作为特征角. 测量时不能直接得到$\theta$,只能得到叶轴在$x-z$平面的投影与$z$轴的夹角$\theta _{0}$.两者换算关系是
$$\theta = \arctan(\tan\theta _{0}/\cos\varphi)$$
从实验结果看,在稳定状态下各侧叶的倾角(方位角)之间相差不大.引入侧叶平均倾角$\theta_{1}$(各侧叶中脉线与$z$轴夹角的平均值)和平均方位角$\varphi_{1}$(各侧叶中脉线在$xoy$平面投影与$x$轴夹角的平均值)来描述侧叶的变形量.
引入顶叶倾角$\theta _{2}$和偏航角$\varphi _{2}$来描述顶叶的变形.$\theta _{1}$及$\theta _{2}$实际值与测量值的换算关系与叶轴相似.
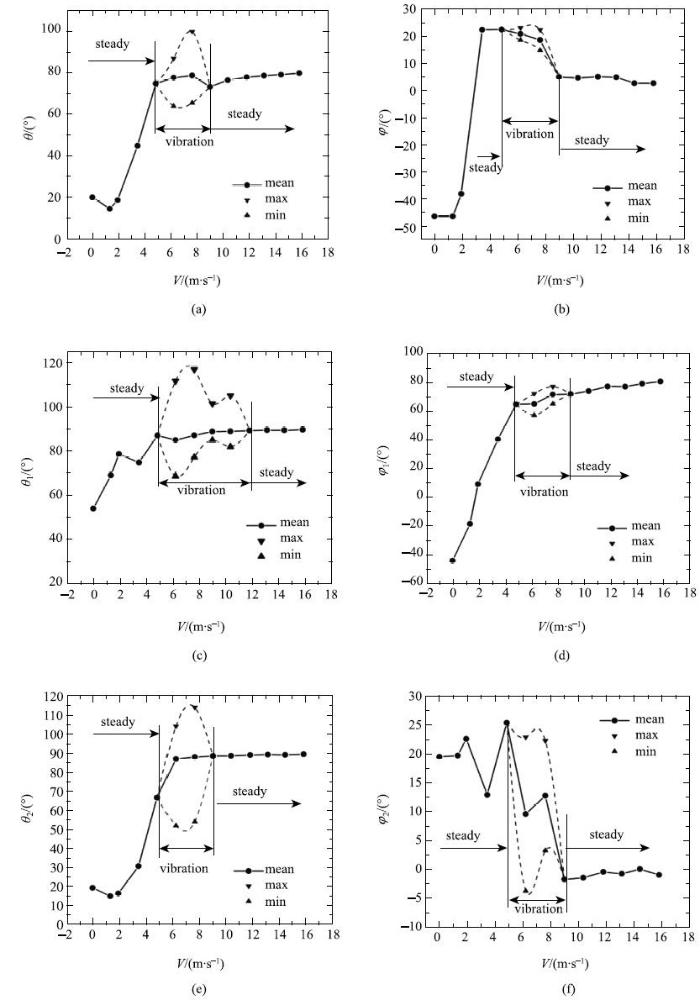
图7(a)和图7(b)分别为某个复叶叶轴倾角$\theta $和偏航角$\varphi$随风速变化的典型情况.当风速为零时,叶轴自然地向上游和右侧弯曲,倾角$\theta=20^\circ$,偏航角$\varphi =-47^\circ$. 当风速$V_{\infty }=1$m/s时,叶轴的弯曲被矫正,$\theta \approx 0$,但偏航角无变化.再增大风速,叶轴向下游弯曲,倾角$\theta $增大. 当$V_{\infty }\leqslant 2$ m/s时,$\theta $增加缓慢,偏航角有所减小. $V_{\infty}=3$ m/s附近倾角$\theta $迅速增大,偏航角$\varphi$由负值迅速改变到正值. 但风速大于4 m/s以后,$\theta $与$\varphi$的变化缓慢.
从$V_{\infty }=4.8$ m/s开始直到9.2 m/s,叶轴发生振动,$\theta$与$\varphi $都在其最小值与最大值之间波动变化,其中$\theta$变化的最大幅值在$\pm $20$^\circ$左右,但$\varphi$变化最大幅值仅在$\pm$5$^\circ$左右,说明叶轴的上下摆动较强,左右摆动较弱.
当$V_{\infty }>4.8$ m/s后,$\theta $平均值变化不大. $V_{\infty}=4.8\sim 9.2$ m/s范围内$\varphi $平均值也变化较小.
在$V_{\infty }=9.2$ m/s附近,$\varphi$值突然由接近20$^\circ$减小到5$^\circ$左右,$V_{\infty }>9.2$m/s以后保持在5$^\circ$水平,直到$V_{\infty }>13$ m/s后,$\varphi$趋近于0.
图7(c)为侧叶的平均倾角随风速的变化. $V_{\infty }=0$m/s时,侧叶自然下垂,倾角$\theta _{1} \approx 53^\circ$.随着风速$V_{\infty }$增大,两侧侧叶像鸟翅膀一样逐渐抬起,$\theta_{1}$增大. 当$V_{\infty }>4.8$ m/s时,$\theta_{1}$或其时均值接近90$^\circ$. 在$V_{\infty }=4.8\sim 9.2$m/s范围内,侧叶随叶轴一起振动. 在$V_{\infty }=9.2\sim 12$m/s范围内,叶轴静止,但部分侧叶仍然振动. 因此$V_{\infty }=4.8 \sim12$m/s范围内,侧叶像鸟翅膀一样上下拍打,平均倾角在最小值与最大值之间
显示原图|下载原图ZIP|生成PPT图7叶轴与叶片姿态角随风速的变化,复叶的小叶数为7片. (a)叶轴倾角,(b)叶轴偏航角, (c)侧叶平均倾角, (d)侧叶平均方位角,\\(e)顶叶倾角,(f)顶叶偏航角...
-->Fig. 7Changes of attitude angles of the rachis and lobuleswith wind speed, the lobule number of the leaf is seven. (a)Rachis inclined angle,(b) rachis yaw angle, (c) averaged laterallobule inclined angle, (d) averaged lateral lobule azimuth angle,(e) apical lobule inclined angle,(f) apical lobule yaw angle
-->
波动变化,最大波动幅值$\pm 25^\circ$左右. $V_{\infty}>12$ m/s以后,侧叶由振动变为稳定,$\theta _{1} \approx 90^\circ$.
图7(d)为侧叶的平均方位角随风速的变化. 由于复叶正面迎风,$V_{\infty}=0$ m/s时,两边的侧叶向上游方向倾斜,方位角$\varphi _{1} \approx-45^\circ$. 当$V_{\infty } \approx 1.5$m/s时,侧叶被矫正,方位角$\varphi _{1}=0^\circ$.随着风速增大,两侧的侧叶迅速向下游顺流方向扭转,到$V_{\infty }\approx 4.8$ m/s时,$\varphi _{1} \approx 65^\circ$. 在$V_{\infty}=4.8\sim 9.2$ m/s范围内,侧叶随叶轴一起振动,$\varphi_{1}$在上下值之间波动,幅值变化$\pm 7^\circ$左右. 在$V_{\infty}=9.2\sim 12$ m/s范围内,方位角$\varphi_{1}$没有变化,说明在此风速范围,侧叶叶片仅有上下摆动,没有左右摆动.风速$V_{\infty }$从9.2 m/s 增大到16m/s过程中,侧叶进一步偏向顺流方向,方位角$\varphi_{1}$从70$^\circ$逐渐增大到80$^\circ$.
图7(e)为顶叶倾角$\theta _{2}$随风速的变化. $V_{\infty }=0$m/s时顶叶稍向下游偏斜.$ V_{\infty }<3$ m/s时$\theta_{2}$变化不大,但是当风速由3 m/s 逐步增大到6m/s时,顶叶由接近竖直位置急速向水平位置转变,$\theta _{2 }$(或其时均值)由20$^\circ$左右增大到85$^\circ$以上. 风速在$V_{\infty}=4.8\sim 9.2$ m/s范围内时,顶叶发生振动,$\theta_{2}$在上下限之间波动变化,最大波动幅值约为$\pm 32^\circ$.当$V_{\infty }>9.2$ m/s,随着风速再增大,$\theta_{2}$趋近于90$^\circ$.
图7(f)为顶叶偏航角$\varphi _{2}$随风速的变化.风速$V=0$时,顶叶中脉向左侧偏20$^\circ$. 风速小于2 m/s时$\varphi_{2}$变化不大. $V_{\infty }$从2 m/s增大到3.4 m/s时,$\varphi_{2}$下降到12$^\circ$. $V_{\infty }$从3.4 m/s增大到4.8m/s时,$\varphi _{2}$又增大到26$^\circ$. 在$V_{\infty }=4.8\sim9.2$ m/s范围内,顶叶发生振动,偏航角$\varphi_{2}$的波动幅值约为$\pm 14^\circ$. 风速由$V_{\infty }=4.8$ m/s增大到$V_{\infty }=9.2$ m/s时,$\psi_{2}$由26$^\circ$减小到$-2^\circ$. 此后再增大风速,$\varphi_{2}$逐渐趋于0$^\circ$.
2.3 复叶投影宽度与雷诺数$Re$的统计关系
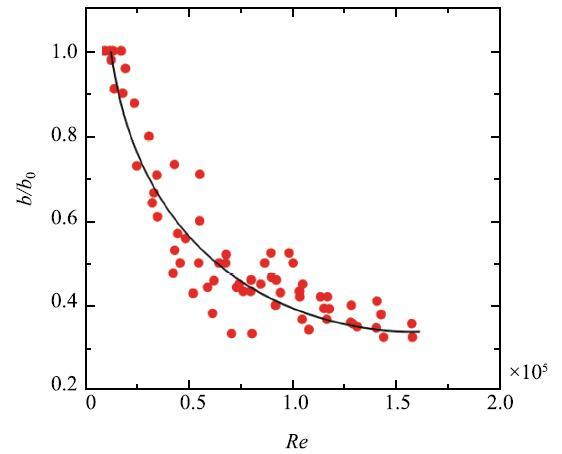
复叶在水平面的投影宽度$b$与在垂直来流平面的投影宽度相同.投影宽度越小,代表复叶在风中的瘦身能力越强.同时,叶轴的倾角越大,复叶在垂直来流平面上的投影长度越小.因此,复叶的迎风面积由投影宽度$b$和叶轴时均倾角$\theta$决定,而迎风面积的大小决定着复叶气动阻力的大小.===图8为复叶投影宽度比$b/b_{0}$与复叶雷诺数之间的统计关系.可知$b/b_{0}$与名义雷诺数$Re$呈近似反比关系,$Re$越高,复叶越收缩,宽度比越小.当$Re$趋近于实验的最大值时,$b/b_{0}$趋近于0.34.
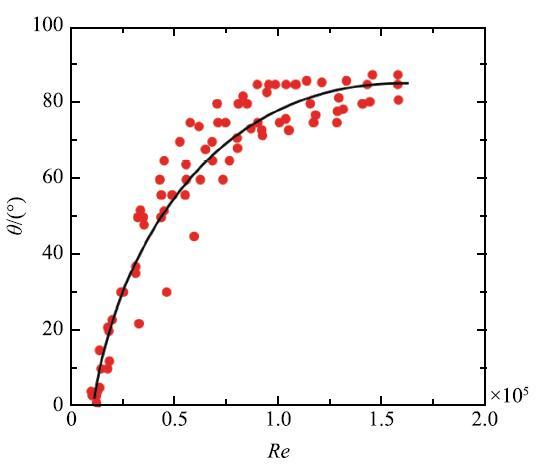
===图9为叶轴倾角$\theta$与名义雷诺数$Re$之间的统计关系.随着雷诺数的增大,叶轴向下游弯曲,倾角$\theta $增大. 当$Re$趋近于实验的最大值时,$\theta$趋近于一个极限值$\theta _{\max} \approx 82.5^\circ$.
显示原图|下载原图ZIP|生成PPT图8复叶投影宽度$b/b_0$与雷诺数$Re=Ub_0/v$之间的统计关系...
-->Fig. 8Statistical relation between projected width $b/b_0$ of the compound leaf and Reynolds number $Re=Ub_0/v$...
-->
显示原图|下载原图ZIP|生成PPT图9叶轴倾角$\theta$与雷诺数$Re=Ub_0/v$之间的统计关系...
-->Fig. 9Statistical relation between rachis inclined angle$\theta$ and Reynolds number $Re=Ub_0/v$
-->
2.4 叶轴和小叶的振动频率
叶轴和叶片的振动频率由视频回放,通过记录在一定帧数图像范围内叶轴或叶片最高位置出现的次数来确定.图10为叶轴和叶片振频$f $随$V_{\infty}/b$的变化,这里$b$是复叶的时均投影宽度.可知小叶振动频率比叶轴振动频率高.叶轴出现明显振动时其振动频率$f$与参量$V_{\infty}/b$呈近似线形关系,即$f$与来流速度呈近似正比,与复叶宽度呈近似反比关系.这使我们想到钝体绕流旋涡脱落频率与来流速度及钝体横向尺度之间的关系.这个关系使我们有理由认为,叶轴的大幅振动是复叶两侧的旋涡脱落频率与叶轴弯曲振动固有频率接近时的共振效应所引起.实验值有一定离散性,说明还有其他影响因素存在.小叶的振动与参数$V_{\infty}/b$之间没有相关性,这是因为一般情况下,只有个别或部分小叶发生振动,小叶振动与来流速度及其自身变形后的尺度有关,而与整个复叶的宽度$b$不相干.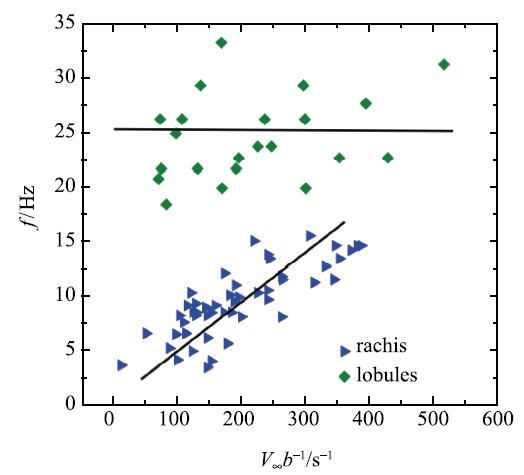
显示原图|下载原图ZIP|生成PPT图10叶轴和叶片振频随参数$V_\infty b^{-1}$的变化...
-->Fig. 10Changes of vibration frequencies of the rachis and lobules with parameter $V_\infty b^{-1}$
-->
2.5 临界风速
在2.1节我们定义了叶轴发生大幅弯曲的第一临界风速,叶轴发生大幅振动的第二临界风速,从叶轴振动到复叶整体静止的第三临界风速,部分小叶发生振动的第四临界风速,及从小叶振动到复叶整体恢复静止的第五临界风速.不同小叶个数的复叶正面迎风42组,反面迎风38组数据统计的临界风速结果如表3所示.可知,除了第二临界风速以外,其他临界风速值随小叶个数增多而减小.小叶数越多,复叶承受的气动阻力越大,复叶会在更低风速下发生大的弯曲,因而第一临界风速越小.小叶数越多,对叶轴振动的阻尼也越大,达到中间稳定的第三临界风速越小.小叶数越多,叶片分层数越多,个别叶片出现振动的可能性越大,因而第四临界风速越小.小叶数越多,叶轴越早接近于水平位置,叶片相互包裹在一起形成单一流线体越提前,因而第五临界风速越小.叶轴发生大幅振动,并带动小叶叶片一起振动对复叶的损伤最大,因此第二临界风速最为重要.第二临界风速值几乎不受小叶个数的影响.这是因为叶轴的固有频率由叶轴密度、弹性模量及自身尺度决定的.另外,复叶投影宽度随风速的变化也与叶片个数关系不大.
Table 3
表3
表3不同小叶数的复叶正面和反面迎风时临界风速统计值
Table 3Critical wind speeds for the leaves of different lobules
| The surface to face wind | Lobules per leaf | V1 | V2 | V3 | V4 | V5 |
|---|---|---|---|---|---|---|
| 5 | 3.7 | 7.1 | 11.3 | 12.8 | 17.1 | |
| front | 7 | 3.6 | 6.9 | 9.3 | 11.0 | 14.4 |
| 9 | 3.5 | 7.0 | 8.1 | 10.0 | 13.4 | |
| 5 | 4.4 | 7.6 | 11.8 | 13.4 | 17.0 | |
| back | 7 | 3.9 | 7.6 | 9.4 | 13.2 | 15.7 |
| 9 | 3.5 | 7.3 | 8.7 | 11.2 | 14.9 | |
| front | weighted average | 3.6 | 7.0 | 9.9 | 11.2 | 15.2 |
| back | 4.1 | 7.5 | 10.0 | 12.7 | 15.9 |
新窗口打开
反面迎风的各临界风速均大于正面迎风的相应值,说明反面迎风时复叶在风中的稳定性更好.这是因为自然状态下复叶呈曲面形状,反面迎风时,复叶接近流线体,较为稳定.当正面迎风时,复叶为钝体,易变形,较不稳定,只有风速增大到一定值以后,复叶变形为流线体,才达到反面迎风时的最初状态.因此正面迎风与反面迎风的临界状态有一定的风 速差.
引入临界风速概率密度分布[18]来反映临界风速统计结果的离散情况.图11(a)和图11(b)分别为正面迎风42个复叶和反面迎风38个复叶统计的各临界风速概率密度分布.从中可以看出,正面迎风时只有第一临界风速概率密度较为集中,其他临界风速数据离散度大.反面迎风时,总体情况稍好,但离散度仍较大.数据离散主要是没有考虑叶片个数变化的影响.
显示原图|下载原图ZIP|生成PPT图11各临界风速的概率密度...
-->Fig. 11Probability density distribution of every critical wind speed
-->
2.6 复叶气动阻力与Vogel 指数
图12是由天平测量得到的复叶阻力系数$C_{D}$与雷诺数之间的统计关系. 在$Re=2.0\times 10^{4}\sim 5.0\times10^{4}$之间,$C_{ D}$迅速下降,当$Re >5.0\times10^{4}$时,$C_{ D}$缓慢减小并趋近于常数0.06.
显示原图|下载原图ZIP|生成PPT图12复叶阻力系数与雷诺数$Re$之间的统计关系...
-->Fig. 12The statistical relation between compound leaf drag coefficient and Reynolds number
-->
Vogel幂次率的对数关系为$$\ln\;C_{ D} = k + \alpha \;\ln V_\infty$$以测量的某个复叶的阻力系数的对数值为纵坐标,以风速的对数值为横坐标,得到两者的关系如图13.其中在一个风速区间内$C_{ D}$与$V_{\infty}$在对数图上为线性关系,这个区间称为Vogel幂率区,直线的斜率即为Vogel指数.
显示原图|下载原图ZIP|生成PPT图13某复叶的阻力系数$C_{ D}$与风速$V_\infty$之间的对数关系...
-->Fig. 13The logarithmic relation between compound leaf drag coefficient $C_{ D}$ and wind speed $V_\infty$
-->
表4为有不同小叶数的复叶在正面迎风和反面迎风时的Vogel指数统计值.从总体上看,小叶数目多的复叶,Vogel指数具有更大的负值.小叶数目的增加,复叶迎风面积收缩能力增强,复叶整体上更易趋于流线体,因而阻力系数随风速增大而下降的趋势更明显.
Table 4
表4
表4不同小叶数^的复叶Vogel系数统计平均值
Table 4Statistical values of Vogel coefficient for the compound leaves of different lobule number n
| n | 5 | 7 | 9 | Average |
|---|---|---|---|---|
| aF | -0.40 | —0.51 | —0.54 | —0.48 |
| aB | —0.50 | —0.60 | —0.54 | —0.55 |
新窗口打开
复叶反面迎风比正面迎风具有更小的钝度[32],变形收缩更容易,因而阻力系数更小,Vogel指数有更大的负值.但是随着小叶数$n$的增大,正面迎风和反面迎风的差别减小,到$n=9$时,两者的统计结果已经没有差别.这是因为随着$n$增大,复叶迎风面积的收缩主要靠叶轴弯曲程度的增大,叶片自身弯曲对迎风面积的影响减弱.
2.7 叶片个数的影响
上文已经对不同小叶数的复叶临界风速和Vogel指数作了统计比较.为了剔除其他因素的作用,更加准确地研究小叶个数对复叶气动特性的影响,取一个9叶复叶先进行测试.然后去掉靠近叶轴基部的一对侧叶,再对这个7叶复叶进行测试.最后去掉靠近叶轴基部的第二对侧叶,对这个5叶复叶进行测试,然后作比较.图14(a)为小叶数$n$不同时复叶阻力系数$C_{ D}$随雷诺数的变化.在这里的阻力系数$C_{D}$定义中,参考面积取$n$个小叶平铺面积之和,不随风速改变.可知当雷诺数$Re$较小时,随着$n$的减少,$C_{ D}$增大.由此可以判断,小叶个数越多,复叶的重构能力越强,相对迎风面积越小,阻力系数越小.
但$Re>8.0\times10^{4}$时,不同叶片数的复叶阻力系数已相差很小,且随$Re$进一步增大都趋近于0.05.
为了研究阻力系数随小叶数$n$增大而减小的原因,测量了复叶宽度、叶轴倾角和顶叶倾角随雷诺数的变化.复叶迎风面积的改变是复叶阻力系数改变的唯一原因,而迎风面积与复叶投影宽度成正比.如图14(b)所示,当叶片个数较少时,复叶宽度比较大,随着叶片个数的增加,宽度比减小,这是原因之一.复叶迎风面积还与复叶在垂直来流平面的投影长度成正比,而这个长度与叶片倾角以及叶片层数有关. 如图14(c),对于不同的$n$,侧叶平均倾角相差不多.如图14(d),$n=5$时,侧叶叶层数最早由三层变为两层,减小了投影长度,从而中和了投影宽度的影响,这可能是随雷诺数增大,三者阻力系数趋于一致的原因.
显示原图|下载原图ZIP|生成PPT图14叶片个数$n$的影响...
-->Fig. 14The influence of lobule number $n$
-->
3 关于第二和第四临界风速的讨论
3.1 叶轴振动第二临界风速的相似关系
由附录中叶轴振动方程(9a)和(9b)以及叶轴两端齐次边界条件可得到叶轴倾角与偏航角$$\theta = \theta \left(Reb,\frac{\bar {b}}{l},\varPi, \varGamma,\bar {\theta}, \bar{\varphi}, \xi, \tau \right) \\ \varphi = \varphi \left(Reb,\frac{\bar {b}}{l}, \varPi,\varGamma, \bar {\theta}, \bar {\varphi}, \xi,\tau\right)$$
将$\theta $和$\varphi $在时间$\tau$和长度$\xi $上进行平均,可解出平均值
$$\bar {\theta } = \bar {\theta }\left(Reb,\frac{\bar{b}}{l},\varPi, \varGamma\right)\\ \bar {\varphi } = \bar {\varphi }\left(Reb,\frac{\bar{b}}{l},\varPi, \varGamma \right)$$
复叶叶轴大幅振动发生在复叶旋涡脱落频率与叶轴固有频率相接近,即产生共振的时候.
复叶旋涡脱落频率$f_{ v}$ 除与来流速度$V_{\infty}$和复叶宽度$b$有关外,还是叶轴时均倾角$\bar{\theta}$和时均偏航角$\bar{\varphi}$,以及复叶宽长比的函数,这里复叶长度近似用叶轴长度$l$代替
$$\frac{f_{ v} \bar {b}}{V_\infty } = St\left(Reb,\bar {\theta },\bar {\phi},\frac{\bar {b}}{l}\right)$$
叶轴振动发生的雷诺数$Reb$一般在10$^{4}$量级,此时复叶受力与涡脱落Strouhal数与雷诺数无关,可得
$$f_{ v} = \frac{V_\infty }{\bar {b}}St\left(\varPi, \varGamma, \frac{\bar{b}}{l}\right)$$
旋涡脱落频率达到叶轴共振频率捕获区下限时,发生共振,有
$$f_{ v} \approx f_n$$
由附录的式(A10b)解出$f_{n}$,再由上述$f_{ v}$ 表达式,得
$$\frac{\varGamma }{4}\sqrt {\dfrac{E}{\rho }} \frac{d}{l^2} \approx\frac{V_2 }{\bar {b}}St\left(\varPi, \varGamma, \frac{\bar{b}}{l}\right)$$
附录中式(A10b)的无量纲量$\varGamma$仅与叶轴自身尺度与材料性质有关,与空气流动情况无关.因此对于固定振动模态来说,$\varGamma$为绝对常数.
因此,由上述等式及附录(A10a)中$\varPi$,求解得到无量纲第二临界速度
$$\frac{V_2 }{\sqrt {E / \rho } } = f\left(\sqrt {\frac{\rho _{ a} }{\rho }},\frac{\bar {b}}{l},\frac{d}{l}\right)$$
实验中测量的叶轴密度$\rho$变化较小,空气密度$\rho _{a}$也基本不变,两者比值可看做常数. 将公式中复叶平均宽度$\bar{b}$简单地用投影宽度$b$代替,得到
$$\frac{V_2 }{\sqrt {E/\rho} } =f\left(\frac{b}{l},\frac{d}{l}\right)$$
$$\frac{V_2 }{\sqrt {E /\rho } } = 0.001~4+ 0.022~9{ e}^{ - \eta}$$
其中
$$\eta = 2.69\frac{b}{l} + 10.01\frac{d}{l}$$
拟合曲线与实验数据得到的$V_2 / \sqrt {E / \rho } $与$\eta $关系的对比如图15所示.可以看出,实验点都在拟合曲线附近,但仍由一定离散度.引起数据离散的原因主要是,按照Strouhal关系估算的复叶旋涡脱落频率与叶轴固有频率之间不完全相同引起的.
显示原图|下载原图ZIP|生成PPT图15第二临界风速相似关系拟合曲线...
-->Fig. 15The second critical wind speed similarity curve
-->
3.2 叶片稳定性与第四临界风速
风速达到第四临界值时,个别小叶发生振动.小叶振动的情况与旗子振动有相似之处.人们对旗子或柔性薄板的失稳问题做了大量研究.Alben[33]在无黏背景流条件下用涡层代替尾流,研究了二维流动中的一维丝线(无限宽旗子简化模型)不稳定性的非线性特征值问题.Alben和Shelley[34](2008)用二维流场中的一维丝线模型研究了旗子的双稳态到混沌的转变.Chen等[35]用实验摄像和振动频谱分析方法研究了旗子在风中的失稳,分叉与混沌现象.Eloy等[36-37]提出旗子由稳定状态,到失稳发生振动,主要由以下无量纲参量决定
$$U^\ast = V_\infty l_1 \sqrt {\dfrac{\rho _l h}{D}} = \frac{2\sqrt3 V_\infty }{\sqrt {E_l / \rho _l } }\frac{l_1 }{h}\\ H^\ast = \frac{b_1 }{l_1 }, \quad M^\ast = \frac{\rho _l h}{\rho_a l_1 }$$
式中,$U^\ast$为折减速度,$H^\ast$为小叶平展宽度与长度的比值,$M^\ast$为空气与叶片质量比.$b_1, l_1, h, E_l, \rho _l$分别为叶片的宽度、长度、厚度、弯曲弹性模量和密度;$\rho _{a}$为空气密度. 由于木质材料泊松比很小,因此叶片弯曲刚度$D$近似为
$$D \approx \frac{E_l h^3}{12}$$
在本文中,如果设小叶叶片发生振动的临界$U^\ast$值为$U_4^\ast $,则它是无量纲量$M^\ast$和$H^\ast$的函数
$$U_4^\ast = f(M^\ast ,H^\ast )$$
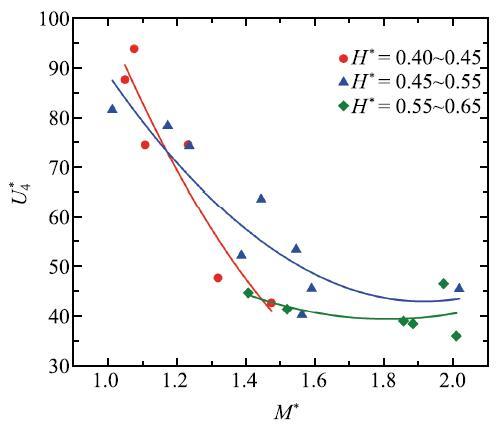
图16为紫藤萝叶片振动的无量纲第四临界风速随密度比$M^\ast$的变化.随机选取的紫藤萝叶片宽长比$H^\ast$变化范围不大,在0.4~0.65之间.由于$H^\ast$在实验中无法精确控制$H^\ast$,根据$H^\ast$的不同粗略地将数据分为三组.图中$U_4^\ast$随$M^\ast$的增大有减小的趋势,与Watanabe等[38-39],Tian等[40]结果的变化趋势相同,但与Eloy等[36-37]结果的变化趋势不同. 本文$U_4^\ast$拟合曲线高于Watanabe等[38 -39]的曲线,但低于Tian等[40]等的曲线.
显示原图|下载原图ZIP|生成PPT图16第四临界风速$U^\ast_4$与密度比$M^\ast$的关系...
-->Fig. 16The 4th critical wind speed $U^\ast_4$ vs. mass ratio $M^\ast$
-->
对于旗子颤振临界风速,各研究者结果相差很大,可能是影响临界风速的无量纲参数选择不尽合理,致使如Yu等[41] 认为影响参数包括雷诺数,密度比$\rho _l / \rho_{ a}$,宽长比,长厚比等.
叶片与旗子或柔性薄板之间有多个方面的不同：(1)叶片非矩形,而旗子为矩形;(2)叶片为单点支撑,支撑的叶柄为弹性杆,而旗子为边线固定,旗杆为刚体;(3)叶片为曲面形状,旗子为平面; (4)叶轴弯曲,叶片与来流之间有夹角,旗子与来流无夹角;(5)各叶片之间相互影响,与单面旗子情况不同.
关于薄板弯曲度的影响,Eloy等[37]}$做了研究,发现当宽长比小于1时,弯曲薄片失稳的风速临界值$U_{c}^\ast $比平面薄片大很多.
关于旗子密度的影响,Tian[42]做了研究.他对旗子时均尾流进行稳定性分析,发现单个旗子尾流是对流不稳定的,旗子密度对旗子稳定性有重要影响,当旗子密度接近零时,旗子不会失稳,只有旗子密度比大于一定值,才会发生失稳和振动.相互靠近的两个旗子,尾流中存在较大的绝对不稳定区,即使两旗子密度都为零,也会发生失稳.叶片弯曲并与来流存在夹角,形成钝体,其尾流中存在一定的绝对不稳定区,受叶片密度的影响变弱.但在本实验中,不同叶片的密度差异不大,$M^\ast$主要受叶片长厚比控制.因此叶片长厚比对临界风速有重要影响.
5 结论
本文用80个羽状复叶,按照每个复叶所含小叶数目分成三组.每个复叶分正面和反面迎风分别进行风洞测试,风速由零逐步增大,直到25m/s为止.用高速摄像机全程记录复叶状态变化,同时用风洞天平测量复叶的气动力.通过图像和数据分析得到如下结论：(1)紫藤萝羽状复叶存在3个阶段：前期稳定阶段,中间过渡阶段和后期稳定阶段.前期阶段存在两种稳定状态,即分层飞翼形稳定和分层多形状稳定.中间阶段存在两种振动状态,即叶轴振动状态和部分小叶振动状态.在这两种振动状态之间,有时会存在中间稳定状态,复叶呈分层多形状稳定.在后期稳定阶段,可分为两层稳定和单一整体稳定,其中单一整体根据其横截面形状分为锥形、U形和楔形.叶片层数随风速逐步减少,直至所有叶片合在一起形成单一的流线形整体.随着复叶雷诺数的增大,复叶宽度减小,叶轴与竖直线倾角增大,叶轴偏航角减小.在前期阶段,存在叶轴迅速弯曲的第一临界风速.在中间阶段,存在叶轴振动、中间稳定、部分叶片振动的第二、三、四临界风速.在后期,存在从叶片振动到整体稳定的第五临界风速.叶轴振动的第二临界风速几乎不随小叶个数而改变,但其他临界风速都随着复叶所含小叶数目的增加而减小.
(2)以$Re=5.0\times10^{4}$为界,复叶阻力系数随雷诺数增大的变化趋势可分为两个区段：在较低$Re$区段,阻力系数呈迅速下降趋势,这与叶轴的迅速弯曲有直接关系.在较高$Re$区段,阻力系数变化缓慢,直至趋近于常数不再改变.复叶阻力系数随着小叶数目的增多而减少.复叶的Vogel指数均为负值,且随着所含小叶数目的增大,指数绝对值增大.阻力系数和Vogel指数的变化趋势说明,小叶数越多,整体更趋近于流线形.复叶反面迎风比正面迎风具有更大的Vogel指数绝对值,但随着小叶数目增多,两者的指数趋于一致.
(3)量纲分析得出,叶轴振动的无量纲第二临界风速$V_2 / \sqrt {E /\rho }$是复叶投影宽度与叶轴长度之比$b/l$,以及叶轴直径与叶轴长度之比$ d/l$的函数.叶片的失稳与振动,与旗子在风中的稳定性类似,叶片振动的无量纲第四临界风速可表达为叶片宽长比和密度比的函数.由实验数据给出了两个临界风速的变化图.
附录：叶轴振动方程的推导
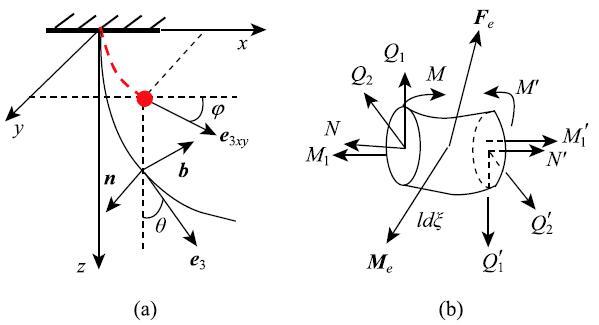
如图A1所示,设叶轴上某点$P$的切线方向单位矢量为$e_3$,它与叶轴在该点的倾角$\theta$ (叶轴切线与$z$轴夹角)和偏航角$\varphi$ (叶轴在$xy$平面投影线的切线与$x$轴夹角)有关$$ e_3= i\sin \theta\cos \varphi+ j\sin\theta\sin\varphi+ k\cos\theta$$ 设与$ e_3$垂直的另外两个单位矢量为
$$ e_1=\dfrac{\partial e_3}{\partial \theta }= i\cos\theta \cos\varphi + j\cos\theta \sin\varphi - k\sin\theta\\ e_2 = \frac{1}{\sin\theta }\frac{\partial e_3}{\partial \phi } = - i\sin\varphi + j\cos\varphi$$
设$P$点的曲率半径,法向单位矢量,次法线单位矢量分别为$R$,$n$和$ b$,则
$$- \frac{ n}{R} = \frac{1}{l}\frac{\partial e_3 }{\partial\xi }\tag {A1a}$$
$$b = n\times e_3\tag {A1b} $$
其中$l$为叶轴长度(从固支点到最末端),$\xi$为叶轴从固支点到$P$点的无量纲曲线长度坐标,则有
$$\frac{l}{R}= \sqrt {\theta _\xi ^2 + \varphi _\xi ^2 \sin^2\theta}\tag {A2a}$$
$$n = - \frac{\theta _\xi e_1 + \varphi _\xi \sin\theta e_2 }{\sqrt {\theta _\xi ^2 + \varphi _\xi ^2\sin^2\theta }}\tag {A2b}$$
$$b = \frac{\theta _\xi e_2 - \varphi _\xi \sin\theta e_1 }{\sqrt {\theta _\xi ^2 + \varphi _\xi ^2 \sin^2\theta }}\tag {A2c}$$
设$P(\xi )$点横截面上$ e_1$,$ e_2$和$ e_3$方向的剪切和拉伸力分别为 $-Q_{1}$,$-Q_{2}$和$-N$,该横截面的弯曲和扭转力矩分别为$M$和$M_{t}$. 设$P'(\xi $+d$\xi )$ 点横截面上3个方向$ e'_1, e'_2, e'_3$的剪切和拉伸力分别为$ Q'_1, Q'_2, N'$,该横截面上的弯曲和扭转力矩分别为${M}',{M}'_t $.将作用于复叶的气动外力近似为沿叶轴长度的分布力,并设该微段上单位长度的外力和外力矩分别为$ F_e, M_e$,则微元段的力和力矩平衡方程分别为
$$ {N}' \cdot e'_3 - N \cdot e_3 + {Q}'_1 \cdot e'_1- Q_1 \cdot e_1 + {Q}'_2 \cdot e'_2 - Q_2 \cdot e_2+\\ \qquad F_e ld\xi = \rho \frac{\pi}{4}d^d\xi\frac{\partial ^2 r}{\partial t^2} \tag {A3a}$$
$${M}'_t e'_3 - M_t e_3 + {M}' b' - M b +\left(\frac{l{ d}\xi }{2} e'_3 \right)\times ({Q}'_1 e'_1 )+ \\ \qquad \left(\frac{- l{ d}\xi }{2} e_3 \right)\times ( - Q_1 e_1 ) +\left(\frac{l{ d}\xi }{2} e'_3 \right)\times ({Q}'_2 e'_2 ) +\\ \qquad \left(\frac{- l{ d}\xi }{2} e_3 \right)\times ( - Q_2 e_2 ) + M_e ld\xi = {\bf 0}\tag {A3b} $$
显示原图|下载原图ZIP|生成PPT图A1第四临界风速$U^\ast_4$与密度比$M^\ast$的关系...
-->Fig. A1 The 4th critical wind speed $U^\ast_4$ vs. mass ratio $M^\ast$
-->
其中,$d$为叶轴直径,$r$为从叶轴固支点(坐标原 点)到微元体中心的矢量. 沿叶轴有
$$ r = \int { d} r = \int_0^\xi e_3 l{ d}\xi= l\int_0^\xi e_3 (\xi ,t){ d}\xi\tag A4$$
引入无量纲时间$\tau = f_{n}t$,其中$f_n$为叶轴固有频率,将式(A3a)和式(A3b)两边分别除以${ d}\xi $,得
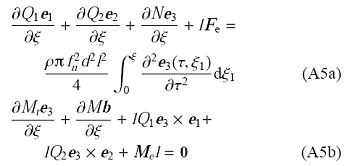
弯矩$M$与弯曲半径$R$的关系
$$\frac{1}{R} = \frac{M}{EI}$$
即
$$M = \frac{EI}{l}\sqrt {\theta _\xi ^2 + \varphi _\xi ^2\sin^2\theta }\tag A5c$$
其中$E$为叶轴弯曲弹性模量,$I$为截面惯性矩
$$I = \frac{\pi d^4}{64}$$
由力矩方程(A5b)解出$Q_{1}$,$ Q_{2}$ 和$M_{t}$
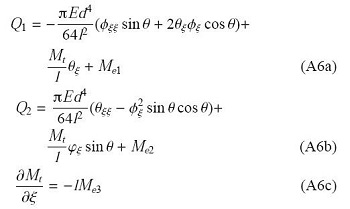
其中$M_{e1}$,$M_{e2}$,$M_{e3}$分别为单位长度的外力矩在$ e_1, e_2, e_3 $方向的分量.如果设$M_{e10}, M_{e20}, M_{e30}$分别为整个复叶所受总力矩的3个分量,则
$$\left\{ {\begin{array}{c} M_{e10} \\ M_{e20} \\ M_{e30} \\ \end{array}} \right\} = \rho _a V_\infty ^2 l^2\bar {b}\left\{{\begin{array}{c} C_{M10} \\ C_{M20} \\ C_{M30} \\ \end{array}} \right\}$$
且3个方向的总外力矩系数$C_{M10}, C_{M20} ,C_{M30}$都是$\left(Reb,\dfrac{\bar {b}}{l},\bar {\theta },\bar {\varphi},\tau \right)$的函数,其中$\bar {b},\bar {\theta },\bar {\varphi}$分别为复叶平均宽度,平均倾角和平均偏航角,复叶雷诺数
$$Reb = \frac{V_\infty \bar {b}}{\nu }$$
而局部外力矩与总外力矩的比值为$\xi$和$\tau $的函数
$$\frac{lM_{ej}}{M_{ej0} } = f_j (\xi ,\tau ), \quad j = 1,2,3$$
因此局部外力矩可表示为
$$\left\{\begin{array}{c} lM_{e1} \\ lM_{e2} \\ lM_{e3} \\ \end{array} \right\} = \rho _{ a} V_\infty ^2 \bar {b}l^2\left\{\begin{array}{c} C_{M1} \left(Reb,\dfrac{\bar {b}}{l},\bar {\theta },\bar {\varphi },\xi ,\tau \right) \\[3mm] C_{M2} \left(Reb,\dfrac{\bar {b}}{l},\bar {\theta },\bar {\varphi },\xi ,\tau \right) \\[3mm] C_{M3} \left(Reb,\dfrac{\bar {b}}{l},\bar {\theta },\bar {\varphi },\xi ,\tau \right)\end{array}\right\}\tag A7$$
同样,外力也可表示为
$$l F_e = \rho _{ a} V_\infty ^2 l\bar {b} C_F \left(Reb,\bar{\theta },\bar {\varphi },\dfrac{\bar {b}}{l},\xi ,\tau\right)\tag A8$$
将方程(A5a)两边乘以${ d}\xi $,然后从$\xi$到1积分,消去未知量$N$,得到关于$\theta$和$\varphi $的两个方程
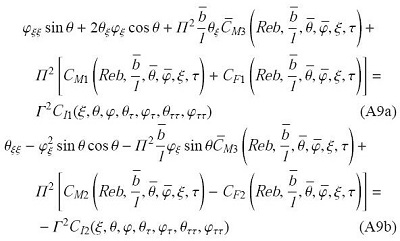
其中
$$\bar {C}_{M3} = \int_\xi^1 C_{M3}\left(Reb,\frac{\bar {b}}{l},\bar {\theta },\bar {\varphi},\xi _1, \tau\right){ d}\xi _1$$
$C_{F1},C_{F2}$为从$\xi$到1所受合力
$$\int_\xi ^1 C_F \left(Reb,\frac{\bar {b}}{l},\bar{\theta },\bar{\varphi}, \xi _1 ,\tau \right){ d}\xi _1$$
在$ e_1, e_2 $方向的投影. $C_{I1} ,C_{I2}$为方程5(a)右侧加速度积分项在$ e_1, e_2 $的投影
$$C_{I1} = J_1 \cos \theta \cos \varphi + J_2 \cos \theta \sin\varphi + J_3 \sin \theta\\ C_{I2} = - J_1 \sin \varphi + J_2 \cos \varphi $$
其中
而无量纲量
从而式(A9a)和式(A9b)为关于$\theta $和$\varphi$的微分-积分方程.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . |
| [2] | . |
| [3] | . |
| [4] | . |
| [5] | . |
| [6] | . |
| [7] | . |
| [8] | . |
| [9] | . . |
| [10] | . . |
| [11] | . |
| [12] | . |
| [13] | . |
| [14] | . |
| [15] | . |
| [16] | . |
| [17] | . |
| [18] | . . |
| [19] | . |
| [20] | . |
| [21] | . |
| [22] | . |
| [23] | . |
| [24] | . |
| [25] | . |
| [26] | . |
| [27] | . |
| [28] | . |
| [29] | . |
| [30] | . |
| [31] | . |
| [32] | . |
| [33] | |
| [34] | . |
| [35] | . |
| [36] | . |
| [37] | . |
| [38] | . |
| [39] | . |
| [40] | . |
| [41] | . |
| [42] | . |
