周春晓^1,2, 汪锐琼^1,2, 聂肇坤¹, 李刚¹, 曾岩^2,*
1大连理工大学 工程力学系工业装备结构分析国家重点实验室,大连 116024
²北京宇航系统工程研究所,北京 100076

PROBABILISTIC MODELLING OF DYNAMIC RESPONSE OF UNDERWATER VEHICLE STRUCTURE VIA MAXIMUM ENTROPY METHOD

ZhouChunxiao^1,2, WangRuiqiong^1,2, NieZhaokun¹, LiGang¹, ZengYan^1,*
1State Key Laboratory of Structural Analysis for Industrial Equipment, Department of Engineering Mechanics, Dalian University of Technology,Dalian 116024,China
²Beijing Institute of Astronautical Systems Engineering,Beijing 100076,China
中图分类号:O324
文献标识码:10.6052/0459-1879-17-022

通讯作者:*通讯作者：曾岩, 讲师,主要研究方向：结构非线性随机动力学. E-mail: zengyan@dlut.edu.cn
版权声明:2018《力学学报》编辑部《力学学报》编辑部 所有
基金资助:国家重点基础研究发展计划 (973 计划)(2014CB046506) 和国家自然科学基金 (11372061, 11302035) 资助项目.

展开

摘要
水下航行体结构承受的水动力外载荷具有显著的时空分布不确定性,其引发的结构动力响应,诸如结构最大内力、最大内力发生时刻、最大内力发生位置等也由此产生了不确定性;同时,水下航行体的动力响应还会因其连接或分离结构的拉压刚度不同而出现非线性特征. 为了在水动力外载荷样本有限的基础上,分析水下航行体结构连接非线性对动力响应统计特性的影响, 利用水下航行体结构的简化动力学模型,计算了水动力横向载荷作用下响应的样本统计矩,采用最大熵方法实现了动力响应的概率建模. 在分别求出结构最大内力、最大内力发生时刻、最大内力发生位置的概率密度函数后,通过与蒙特卡洛模拟结果对比验证了最大熵方法拟合的响应概率密度函数精度;而后,基于这些结构响应概率密度曲线讨论了系统连接非线性参数变化对结构动力响应的影响. 最终得出如下结论：连接非线性会导致结构在只有横向力的作用时产生的轴力响应,并且最大轴力概率密度函数峰值会因连接结构非线性程度增大而逐渐增大;连接非线性对不确定性传播有显著影响,当连接非线性比较强时,输入正态分布的载荷所得到的内力响应不是正态分布的;最大内力响应的发生位置也会受到连接非线性程度的影响. 上述结果可以为结构优化提供技术支持.

关键词：最大熵方法;动力响应;概率建模;时空分布随机外载;蒙特卡洛模拟;水下航行体
Abstract
Hydrodynamic loads of underwater vehicle structure have a high degree of randomness in time and space, which leads to random responses of structure such as maximum internal forces, time and position they taking place, etc. Dynamic response of underwater vehicle will also be nonlinear due to different tension and compression stiffness of its connecting or separated structures. To analyse the influence of nonlinearity of connection on statistics of response of underwater vehicle based on limited sample data of hydrodynamic external load, probabilistic modelling of dynamic response of underwater vehicle is completed by using maximum entropy method in which statistical moments of response samples are obtained from a simplified dynamic model of the structure. Probability density functions of maximum internal forces, time and position they taking place, are proposed separately to predict the most dangerous cases of the underwater vehicle. Accuracy of results proposed here is verified through Monte Carlo simulation. Effects of nonlinear parameters of connections on dynamic response are studied and discussed. Final conclusions are as follows: Nonlinearity of connection leads to axial force response of structures under transverse loads; peak of probabilistic density function of maximum axial force of the structure increases with nonlinear degree of connections which leads to significant effect of propagation of uncertainty; internal force response of structure with nonlinear connections under normal random loads is non-normal; position of maximum internal force response of underwater vehicle structure is influenced by degree of nonlinearity of connections. These findings can provide technical support for structural optimization.

Keywords：maximum entropy method;dynamic response;probabilistic modelling;external loads with randomness in time and space;Monte Carlo simulation;underwater vehicle

-->0
PDF (9261KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
周春晓, 汪锐琼, 聂肇坤, 李刚, 曾岩. 基于最大熵方法的水下航行体结构动力响应概率建模[J]. 力学学报, 2018, 50(1): 114-123 https://doi.org/10.6052/0459-1879-17-022
Zhou Chunxiao, Wang Ruiqiong, Nie Zhaokun, Li Gang, Zeng Yan. PROBABILISTIC MODELLING OF DYNAMIC RESPONSE OF UNDERWATER VEHICLE STRUCTURE VIA MAXIMUM ENTROPY METHOD[J]. Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(1): 114-123 https://doi.org/10.6052/0459-1879-17-022

引言

水下航行体结构的水动力外部载荷具有高度的时空分布不确定性,因此结构动力响应的最大轴力、最大弯矩、最大弯矩发生时刻和位置等都有很大的不确定性;同时水下航行体连接与分离机构还受到拉压刚度不同导致的非线性特性的影响,加之对其进行不确定性分析所需的水动力外载样本的数据有限,因此结构动力响应不确定性的传播更加复杂,这给水下航行体结构设计带来了很大挑战. 为了解决这种载荷不确定性带来的结构动力响应与可靠性问题,许多****进行了各种尝试. 比如,在水下航行体响应分析方面,吕海波等 ^[1] 利用附加质量与细长梁模型相结合的方法解决了水弹性下的流固耦合问题,对带空泡的水下航行体出水过程中的结构动响应问题进行分析;李国良等 ^[2] 使用有限元流固耦合仿真程序对潜射导弹整个出水过程进行数值模拟,计算出各截面最大响应弯矩.
螺栓法兰结构是一种简单、可靠性高的连接形式,因此,在各类航行器设计中被广泛采用 ^[3]. 研究发现,连接结构非线性会对航天器动力学性能产生较大影响 ^[4]. 栾宇等 ^[5] 研究了螺栓 -- 法兰连接结构静刚度非线性特性,发现连接结构拉压不同刚度对整体结构动力特性有重要影响;江召兵等 ^[6] 利用杆单元和梁单元组合成非线性混合单元,较好模拟接头特性和浮桥的动态响应. 冯韶伟等 ^[7] 研究了拉压不同刚度的运载火箭捆绑连接装置的动力学性能;芦旭等 ^[8] 利用等效梁模型结合局部三维有限元精细模型讨论了结构局部刚度变化对惯性部件安装位置振型斜率的影响,还研究了含剪力销螺栓-法兰连接结构在剪力冲击作用下的动力学特性 ^[9]. 同时,在连接结构动响应特性与可靠性分析等方面,文献[10,11,12,13,14,15] 也都分别开展了各种相关的研究工作. 但是,螺栓法兰连接结构非线性特性对航行器结构不确定性传播的影响仍是一个有待解决的问题.
矩方法作为一种研究不确定性传播、求解结构可靠度的有效方法,不需要得到设计验算点,也不需要计算功能函数的导数,因此在近年来受 到广泛关注. 在各类矩方法中,最大熵方法依据最大熵原理可以拟合出比较准确的概率密度函数. 最大熵方法中的信息熵概念源于 1948 年,Shannon^[16] 将热力学熵的概念引入到信息科学中,以便研究信息的不确定性;1957 年, Jaynes^[17] 提出了最大熵原理,即根据部分信息推测未知分布时,应该选择服从所有已知信息同时使熵值最大的分布,而这个分布 是最无偏的分布. 在结构可靠性分析领域,1988 年 Zellner 和 Highfield^[18] 给出了用最大熵法计算概率密度函数的途径,并在 1999 年由 Ormoneit 和 White^[19] 进行了改进;2007 年,韦征等 ^[20] 探讨了基于最大熵法的可靠度理论在工程中的应用;2009 年,李枝军等 ^[21] 提出了用最大熵谱代替传统频率谱来识别运营状态下拉索索力,缩短了测试时间;2010 年,郑俊杰等 ^[22] 利用最大熵 原理研究了极限状态方程中每个随机变量对基桩竖向承载力可靠度分析的影响;2011 年,蒋运华等 ^[23] 采用最大熵方法分析了 超空泡射弹的发射装置及射弹在制造、安装过程中存在的各种不确定性对射弹弹道的影响;2015 年,周云等 ^[24] 使用最大熵方法 对连续梁进行参数敏感位置排序. 在概率建模方面,2014 年,臧红霞等 ^[25] 给出了最大熵方法在三参数对数正态分布中的应用,并与传统参数估计方法进行了比较; 肖东升等 ^[26] 通过最大熵原理实现人员空间分布模型建立;2015 年,赖雄鸣等 ^[27] 提出了首先使用最大熵方法对随机自变量 进行拟合,再对功能函数使用一阶可靠度算法求解的方法;王宇和李洪双 ^[28] 使用最大熵方法对疲劳寿命进行拟合,得到疲劳寿命 的概率密度分布. 此外,2016 年, Giffin 等 ^[29] 应用最大熵方法推断铁磁材料的磁特性; Lawrence 等 ^[30] 使用最大熵方法预测了疾病的传播.
考虑到最大熵方法在结构不确定性传播研究中的优点,本文使用最大熵方法研究时空分布随机外部载荷作用下水下航行体结构动力响应 的统计特性. 针对螺栓法兰结构非线性特征,把水下航行体结构简化为非线性连接的梁模型,并将随机外载荷换算成节点力施加在梁模型上 进行有限元分析. 通过与蒙特卡洛模拟 (Monte Carlo simulation, MCS) 的结果进行对比,验证了最大熵方法概率建模结果的准确性后,计算了给定工况下由最大熵方法得到的最大结构内 力响应概率密度,分析了非线性连接结构参数对动力响应统计特性的影响.

1 最大熵方法的基本原理

由于统计矩通常都是最容易获得的统计信息,从样本矩出发来进行概率建模的方法层出不穷 ^[31]. 但这些方法中,唯有最大熵方法独有其他方法所不具备的优点 ^[32]：其一,数学上已经证明最大熵方法可获得概率分布最佳的无偏估计;其二,指数多项式函数的概率密度形式,有利于待定系数求解;其三,统计矩阶次增大时,指数多项式阶次也会随之增大,使最大熵方法能够不断逼近真实概率分布. 因此,本文采用最大熵方法进行水下航行体结构动力响应概率建模,这里首先给出此方法的分析流程.
若随机事件分布是连续的,且其概率密度函数为$f_{X}(x)$,则其信息熵为
H=-∫-∞+∞?fXxlnfXxdx (1)
根据Jaynes 最大熵原理,如果将随机变量$X$ 的前$m$ 阶几何统计矩 $\mu_{i}$ ($i=0$, 1, 2, $\cdots $,$m$) 作为已知条件,那么在满足 式(2) 条件下使式(1) 取最大值的$f_{X }(x)$ 就是真实概率密度函数的最佳估计
μi=EXi=∫-∞+∞?xifXxdx,i=0,1,2,?,m (2)
具体来说,就是首先引入拉格朗日乘子,利用式 (1) 和式 (2) 构造如下拉格朗日函数
L=H+∑i=0m?λi∫-∞+∞?xifXxdx-μi (3)
式中,$\lambda_{0}$,$\lambda_{1}$,$\cdots$,$\lambda_{m}$ 为待定常数. 在拉格朗日函数稳定点处设偏导数为零,即${\partial L}/ {\partial f_X \left( x \right)} = 0$,得到$\ln f_X \left( x \right) = - 1 + \sum_{i = 0}^m {\lambda _i } x^i$. 假设概率密度函数形式为
$f_X \left( x \right) = \exp \left( { - \sum_{i = 0}^m {a_i x^i} }\right) $ (4)
其中,$a_0 = 1 - \lambda _0$, $a_i = - \lambda _i$ $ \left( {i = 1,2,\cdots,m} \right)$ 为待定参数. 若取$m$=4,即已知前四阶矩的情况下,由式(2) 可知,$a_0 ,a_1 ,a_2, a_3,,a_4 $ 从式(5) 可以求出,
Gja=∫?xjexp-∑i=04?aixidx=μj,j=0,1,2,3,4 (5)
这里采用标准牛顿法迭代求解式 (5),对其在给定的待定参数初值 a0处泰勒级数展开并截取至一阶项,可将式 (5) 简化为线性方程组
Gj(a0)+(a-a0)TgradGj(a)=μj,j=0,1,2,3,4(6)
当求得式 (4) 中的各个待定系数后,就可以从此随机变量的统计矩获得其概率密度函数的近似表达式. 当此随机变量 $X$是结构内力响应 (弯矩或轴力等) 时,如果结构在某一内力取值$Z$时失效 (破坏或失去工作性能),那么可由如下积分计算出此内力响应作用下的结构失效概率
$P(x \le Z)=\int^{Z}_{- \infty} exp(-\sum ^{m}_{i=0} a_{i} x{i}) dx$ (7)
由上述流程可知,最大熵方法的应用受限于以下两点：一是式 (4) 给出的概率密度往往定义在无穷区间,故式 (2) 的积分运算需要人工设定有效的上下界,本文针对实际结构内力响应样本,其上下界可以通过实际情况设定而回避此缺点;二是式 (4) 中的指数多项式阶次受限于统计矩个数,有限的统计矩可能无法提供足够概率信息用于建模,这一点在第 3 节中会有针对性的讨论.

2 水下航行体结构的动力学模型

2.1 水下航行体结构简化动力学模型

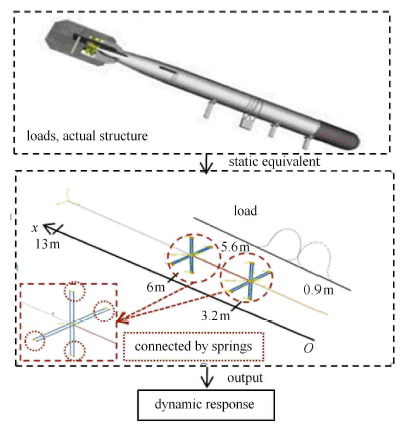
本文采用栾宇等 ^[33] 提出的考虑拉压不同刚度的连接结构简化动力学模型,即基于整体线性梁模型,应用连接结构的简化动力学建模方法对其关键连接部位进行重新建模.
在Abaqus 中建立含有非线性连接的梁模型,如图1 所示(这里模型参数为假设值,并非真实模型). 梁模型总长度为13\,m,梁截面为直径2.11\,m、厚度7.1 mm 的圆环,材料杨氏模量为70GPa,泊松比为0.3;考虑到实际航行体内的非承力结构质量也需要折算到当前梁模型内,换算后的等效材料密度为9.8$\times$10$^4$\,kg/m$^{3}$. 如图1 所示,该结构有两个连接面,分别位于3.2\,m 和6\,m 处,每个连接面由4 个螺栓连接组成,整个螺栓法兰面的等效刚度经由文献[31] 给出的方法,换算为连接两侧梁单元节点的弹簧单元,其轴拉刚度为1.1$\times$10$^6$ kN/m、轴压刚度为3.3$\times$10$^7$ kN/m、弯曲刚度3$\times$10$^8$ kN/rad.
显示原图|下载原图ZIP|生成PPT
图 1水下航行体结构含有非线性连接梁简化模型
-->Fig. 1Three section linear beams with nonlinear connection structures for underwater vehicle structure
-->

2.2 随机时空分布载荷模型

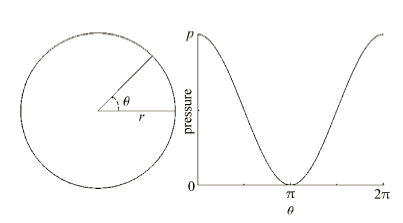
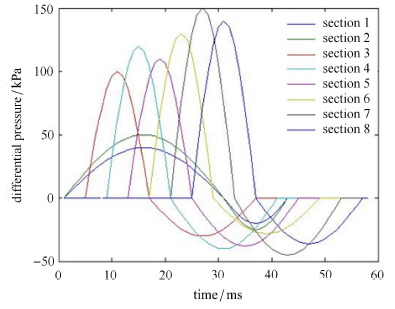
水下航行体出水过程的外载荷可以通过实验获取. 在水下发射的航行体表面布置压力传感器,环向每个象限布置一个,共 4 个;轴向则是每个隔一定距离取一个截面;测量的表面压 力随时间的变化按采样间隔 0.001 s 输出,载荷作用范围如图 1 所示,在 0.9 m 至 5.6 m 之间. 总结发现,结构表面压差的时空变化符合如下规律：航行体表面环向压力分布近似于图 2 所示的余弦分布;任一截面的压差时程曲 线为类正弦冲击波,在结构表面依轴向向下推进,依次发生,扫过如图 3 所示的各个截面 (截面位置见表 1). 因此,将截面压差的峰值作为随机变量进行抽样,获得了基本符合正态分布的随机水动力载荷模型. 由于结构表面压差这类水动力载荷样本是作用在水下航行体的壳体表面的,故无法直接施加在有限元梁模型上,需将抽样获得的 水动力载荷等效为梁模型的节点载荷进行有限元计算. 根据余弦分布形式 (如图 2),某一时刻同一截面上的任一点的压力服从
p(θ)=p(cosθ+1)/2 (8)
其中, p为此截面上的压差峰值. 在环向进行积分,就可以获得截面上的分布力强度
qq=∫02π?pθcosθdθ (9)
显示原图|下载原图ZIP|生成PPT
图 2截面压差分布形式
-->Fig. 2Distribution of pressure difference on surface of a section
-->

显示原图|下载原图ZIP|生成PPT
图 3不同截面载荷时程示意图
-->Fig. 3Schematic diagram of external loads
-->

Table 1
表1
表1截面位置
Table 1Section position

Section	1	2	3	4	5	6	7	8
Position/m	0.9	1.6	2.3	3.0	3.6	4.2	4.9	5.6

新窗口打开
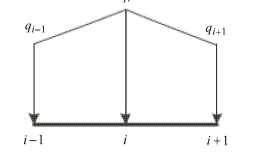
基于式 (9) 给出的不同截面上的分布力强度,假设在结构有限元梁模型上,每个单元上分布力强度为线性变化 (如图 4 所示),可以根据 Timoshenko 梁理论获得梁节点i的横向节点力
Fi=(qi-1+4qi+qi+1)l/6 (10)
其中,$q_{i - 1} $, $q_i $, $q_{i + 1}$ 分别表示对应节点处的横向分布力强度大小;$l$ 为梁单元长度.
显示原图|下载原图ZIP|生成PPT
图 4梁单元节点受力示意图
-->Fig. 4Diagram of force acting on a beam unit
-->

2.3 水下航行体结构内载荷响应样本特征

根据实验数据,我们假设此水下航行体表面压差峰值为随机变量,其分布为均值为 200 kPa、标准差为 40 kPa 的正态分布. 将生成的载荷样本经上一小节中的节点力变换,作用到梁模型上计算结构内力响应,可得到如图 5 和图 6 所示的轴力、弯矩的时空分布图,显然可以分别找到最大轴力和最大弯矩的取值、发生时刻和发生位置,这些内力响应样本都是对水下航行体进行结构可靠性分析与设计时必须考虑的工况. 水动力载荷样本的不确定性,导致结构动力学分析得到的内力响应也具有不确定性,因此本文的概率建模对象正是这些内力响应的最大值,在此同时考虑结构连接的非线性特征对其统计特性的影响.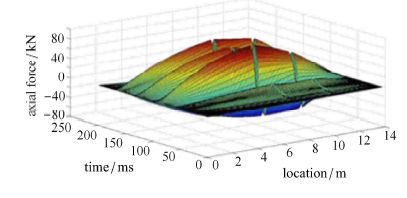
显示原图|下载原图ZIP|生成PPT
图 5轴力时空分布图
-->Fig. 5Figures of space-time distribution of axial force
-->

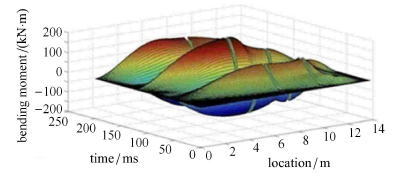显示原图|下载原图ZIP|生成PPT
图 6弯矩时空分布图
-->Fig. 6Figures of space-time distribution of bending moment
-->

3 基于最大熵方法的结构响应概率建模验证

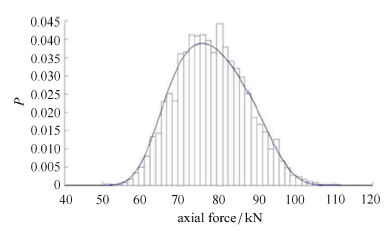
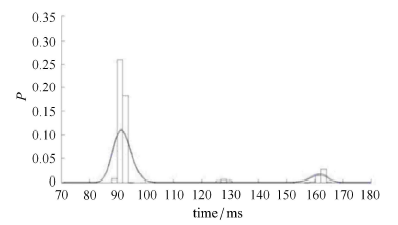
为验证最大熵方法对含连接非线性的水下航行体结构动力响应概率建模的精度,针对上述载荷与结构模型,首先使用 Matlab 调 用 Abaqus 模型进行 500 次抽样计算;再基于 500 次抽样结果来使用最大熵方法进行概率建模;最后,以基于 5 000 次抽样数据的 MCS 结果 进行比对检验.
本文所关注的梁模型内力响应因素为：最大轴力及其发生时刻、产生位置;最大弯矩及其发生时刻、产生位置. 对这六个因素分别 概率建模,500 次抽样计算得到前四阶统计矩如表 2 所示;而后, 根据最大熵方法基本原理,建立这六个结构动力响应随机因素 的概率密度曲线,并与 MCS 结果进行对比 (如图 7 到图 12 所示,其中实线为最大熵方法结果,直方图为各项内力响应的 MCS 结果).
由表 2 可知,最大轴力和最大弯矩 取值及发生时刻的前四阶统计矩中,高阶矩往往取值较小,主要概率信息由低阶矩提供, 因此在图 7、图 8、图 11 和图 12 中,最大熵方法结果与 MCS 结果更加接近. 而最大轴力和最大弯矩 发生位置的第四阶统计矩则较大,意味着尚未考虑的更高阶矩信息也会产生影响,导致了图 9 和图 12 中的 结果偏差稍大.
Table 2
表2
表2含非线性连接的梁最大内力响应前四阶矩
Table 2The first four moments of the maximum internal force of the beam with nonlinear connections

	$E(X^{1})$	$E(X^{2)}$	$E(X^{3)}$	$E(X^{4)}$
$F$/kN&	78.01	9.27	0.13	2.47
$t_{F}$/ms	100.63	23.37	2.17	5.88
$L_{F}$/m	7.27	0.21	-6.57	64.52
$M$/(kN$\cdot$m)	188.52	14.98	-0.16	2.80
$t_{M}$/ms	123.46	2.21	-0.37	2.99
$L_{M}$/m	7.20	0.32	1.03	6.71

新窗口打开
其中,$F$ 为最大轴力;$t_{F}$ 为最大轴力发生时刻;$L_{F}$ 为最大轴力产生位置;$M$ 为最大弯矩;$t_{M}$ 为最大弯矩发生时刻;$L_M$为最大弯矩产生位置.
显示原图|下载原图ZIP|生成PPT
图 7最大轴力概率密度曲线
-->Fig. 7Probability density curve of maximum axial force
-->

显示原图|下载原图ZIP|生成PPT
图 8最大轴力发生时刻概率密度曲线
-->Fig. 8Probability density curve of the time of occurrence of maximum axial force
-->

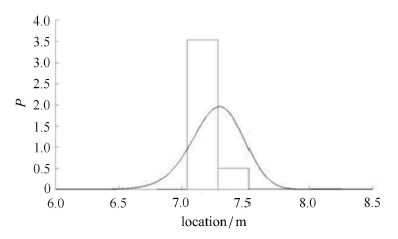
显示原图|下载原图ZIP|生成PPT
图 9最大轴力产生位置概率密度曲线
-->Fig. 9Probability density curve of the location of maximum axial force
-->

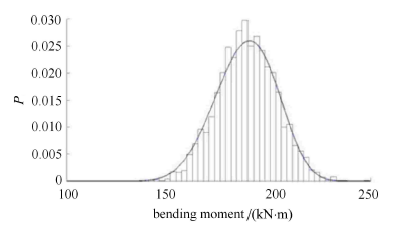
显示原图|下载原图ZIP|生成PPT
图 10最大弯矩概率密度曲线
-->Fig. 10Probability density curve of maximum bending moment
-->

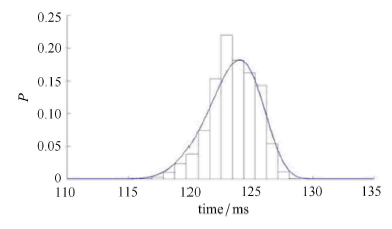
显示原图|下载原图ZIP|生成PPT
图 11最大弯矩发生时刻概率密度曲线
-->Fig. 11Probability density curve of the time of occurrence of maximum bending moment
-->

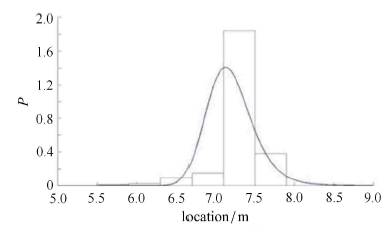
显示原图|下载原图ZIP|生成PPT
图 12最大弯矩产生位置概率密度曲线
-->Fig. 12Probability density curve of the location of maximumbending moment
-->

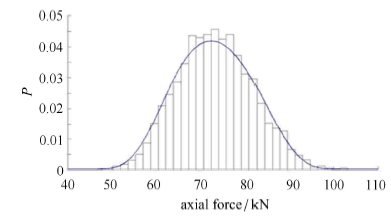
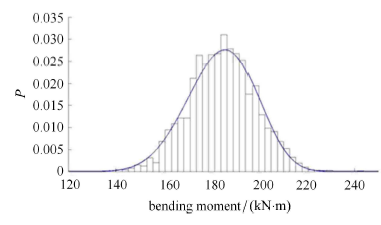
此外,由图 9 可知,最大轴力发生位置为接近模型 7.3 m 处;而由图 12 可知,最大弯矩发生位置为接近模型 7.1 m 处. 考虑到这两个位置是比较危险的位置,故继续对这两个最大内力发生位置的内力响应使用最大熵方法分析,计算出其前四阶矩, 如表 3 所示;再得到这两个位置上的最大轴力、最大弯矩概率密度函数曲线,并与 MCS 结果得到的直方图对比,如图 13 和图 14 所示. 显然,最大熵方法拟合的概率密度曲线与 MCS 结果相差不大,拟合比较准确. 其中,F_7.3m 为 7.3 m 处最大轴力;M_7.1m 为 7.1 m 处最大弯矩.
Table 3
表3
表3含非线性连接的梁危险位置内力响应前四阶矩
Table 3The first four moments of the maximum internal force on dangerous location of the beam with nonlinear connections

	$E(X^{1})$	$E(X^{2})$	$E(X^{3})$	$E(X^{4})$
$F_{7.3m}$/kN	73.12	8.67	0.05	2.52
$M_{7.1m}$/(kN$\cdot$m)	184.15	14.14	-0.18	2.84

新窗口打开
显示原图|下载原图ZIP|生成PPT
图 137.3 m 处最大轴力概率密度曲线
-->Fig. 13Probability density curve of maximum axial force at 7.3 m
-->

显示原图|下载原图ZIP|生成PPT
图 147.1 m 处最大弯矩概率密度曲线
-->Fig.14Probability density curve of maximum bending moment at 7.1 m
-->

因此,对于含非线性连接的梁模型可以使用最大熵方法进行内力响应峰值的概率建模. 由于以往针对水下航行体等结构的内力响应包络设计,都尚未同时考虑到结构连接面非线性特征和载荷随机性的共同影响. 而本文方法给出的结果与 MCS 结果对比后,可以发现：通过引入基于统计矩的最大熵方法,可以有效地对连接非线性和载荷随机性影响下的结构内力响应概率分布进行预估. 从容易获得的内力响应统计矩获得内力响应概率分布,对结构关键截面的内力载荷失效概率估计给出了行之有效的计算手段,这一方法可以为后续开展结构可靠性分析和基于可靠性的结构优化设计提供方便的理论工具.

4 非线性连接结构参数对内力响应峰值概率的影响分析

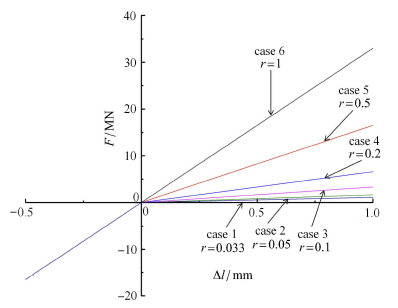
为了在水下航行体结构设计时,有效地控制结构失效概率在可接受的范围,需要在结构设计优化过程中,掌握结构的系统参数对 其内力响应的影响趋势. 由于通过与 MCS 结果比较,验证了可以使用最大熵方法得到比较准确的结构内力响应概率分布,故在本节以最大熵方法拟合水下航行 体结构非线性连接刚度参数取值不同时,结构内力响应概率分布受这些参数的影响.
鉴于螺栓法兰结构的连接面密合后,压缩刚度为上下部段的材料刚度,故后续讨论中可指定连接面的压缩刚度恒定;而连接面的拉伸刚度 会受螺栓预紧力及结构受力状态等因素的影响,且一般情况下拉伸刚度要低于压缩刚度. 虽然栾宇 ^[33] 的研究表明航行器结构螺栓法兰连接的拉压刚度比 (r值) 通常在 5% 到 35% 之间,但本文由于要研究连接非线 性的影响趋势,所以适当放大了拉压刚度的取值范围. 因此,本文考虑的非线性连接结构拉压刚度比参数变化如图 15 所示,此 6 种工况 (case 1 至 case 6) 的连接结构压缩刚度与模型原取值大小相同,而拉伸刚度则按照不同的拉压刚度比来根据压缩刚度换算,其中工况 6 假定拉压刚度 比r=1,即连接结构拉压刚度相同,相当于考虑连接仍为线性的情况.
显示原图|下载原图ZIP|生成PPT
图 15具有不同刚度曲线与拉压刚度比参数的六种非线性连接工况
-->Fig. 156 cases with different stiffness curves and values of ratio of tension and compression for nonlinear connections
-->

对上述 6 种工况的水下航行体结构,使用最大熵方法进行横向外部随机载荷作用下内力响应概率建模,得到概率密度分布如图 16 到图 19 所示.
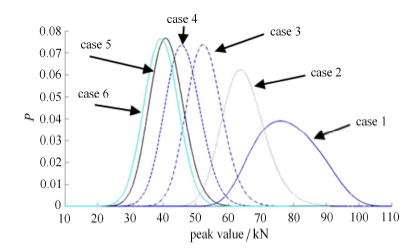
在图 16 中,比较工况 1 到 6,可以发现：随着拉压刚度比增大,最大轴力峰值逐渐减小,同时概率分布逐渐向均值附近集中. 相对而言,工况 1 最大轴力峰值最大并且分布最为离散;工况 2 最大轴力峰值较大并且分布较为离散;而工况 3 到 6 的最大轴力分布较为集中并且离散程度比较接近,峰值逐渐减小. 上述结果表明,非线性连接结构在只有横向力的作用下产生的最大轴力峰值,会因连接结构非线性程度增大而逐渐增大. 其中,工况 6 作为线性连接状态,其轴力大小仍不能忽略,与以往水下航行体线性模型的情况有所差距,这是由于本文简化梁模型连接面用多个弹簧单元来表征螺栓连接,而不是直接用一个线性梁单元来描述的结果.
显示原图|下载原图ZIP|生成PPT
图 16最大轴力概率密度曲线
-->Fig. 16Probability density curve of maximum axial force
-->

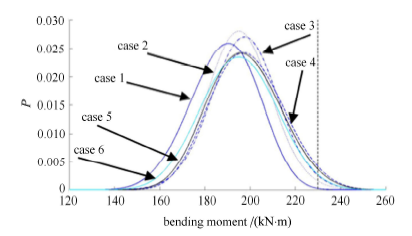
显示原图|下载原图ZIP|生成PPT
图 17最大弯矩概率密度曲线
-->Fig. 17Probability density curve of maximum bending moment
-->

假定结构最大弯矩大于 $230 kN \cdot m$时,认为结构处于危险状态,可由图 17 所示的最大弯矩概率密度计算出上述 6 种工况下危险弯矩发生的概率 (图 17 中的竖直虚线位置即是弯矩大小为$230 kN \cdot m$处),计算结果如表 4 所示.
Table 4
表 6
表 6种工况下危险弯矩发生的概率
Table 4Probabilities of dangerous bending moments for 6 cases

Case	1	2	3	4	5	6
P/%	0.07	0.89	1.59	2.93	2.52	1.68

新窗口打开
由图 17 和表 4 可知,最大弯矩概率密度函数峰值处于 190 到 $200 kN \cdot m$之间;根据工况 1 到 4 的结果比较,可发现在拉压刚度比 小于 1:5 时,随着拉压刚度比增大,最大弯矩概率密度函数峰值右移,这时危险弯矩出现的概率明显增大;而若比较工况 4, 5, 6 的结果,会发现在拉压刚度比大于 1:5 时,随着拉压刚度比的进一步增大,最大弯矩概率密度函数峰值稍向左移,危险弯矩出现的概 率有所减小. 同时,工况 1, 2, 3 的最大弯矩分布较为集中,而工况 4, 5, 6 的最大弯矩分布较为离散,且离散程度相近. 此外,工况 6 的概率分布接近正态分布,这是由于输入的外部载荷是正态分布随机变量,而线性模型对正态分布载荷的响应往往也是正 态分布的;而工况 1 分布具有比较明显的偏度,这说明连接非线性对输入外部载荷的不确定性的传播有显著的影响,当结构连接非线性 比较强时,输入正态分布的载荷所得到的内力响应显然不是正态分布的,必然会产生一定的偏度.
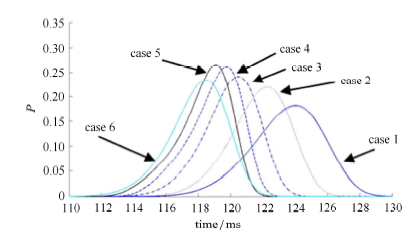
显示原图|下载原图ZIP|生成PPT
图 18最大弯矩发生时刻概率密度曲线
-->Fig. 18Probability density curve of the time of maximum bending moment
-->

进一步研究 6 种工况下,最大弯矩的发生时刻,可由图 18 发现,最大弯矩大多出现在 0.11 s 到 0.13 s 之间. 比较工况 1 到 6 的结果可知,随着拉压刚度比增大,最大弯矩发生时刻的概率密度峰值左移,意味着延时效应逐渐减弱. 其中,工况 1 最大弯矩发生时刻分布最为离散且概率密度峰值最大,有明显的延时现象;而工况 5 最大弯矩发生时刻的概率分布相对最为集中.
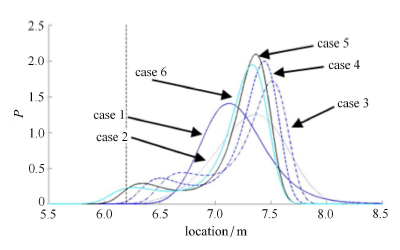
显示原图|下载原图ZIP|生成PPT
图 19最大弯矩产生位置概率密度曲线
-->Fig. 19Probability density curve of the location of maximum bending moment
-->

另一方面,最大弯矩产生位置的概率分布则如图 19 所示,可以发现：最大弯矩产生位置均在含有非线性连接面的梁模型下段,并且在比较靠近整体结构中段的位置. 比较工况 1, 2, 3 的结果,可知在拉压刚度比小于 1:10 时,随着拉压刚度比增大,最大弯矩产生位置的概率密度峰值右移;而比较工况 3 到 6 的结果,会发现在拉压刚度比大于 1:10 时,随拉压刚度比的进一步增大,最大弯矩产生位置的概率密度峰值左移. 此外,最大弯矩产生位置在拉压刚度比较小,即连接结构非线性程度强时,概率分布比较分散;而在拉压刚度比趋近于 1,即连接结构非线性程度弱时,概率分布比较集中.

5 结论

本文使用最大熵方法得到在随机时空分布载荷下,水下航行体结构非线性连接模型的动力响应,并与使用 MCS 结果对比验证了最大熵方法结果的准确性,最后基于最大熵方法的概率建模结果,讨论了非线性连接梁模型参数对结构最大内力响应的影响. 通过对比分析,得到以下结论：
(1) 模型连接处拉压刚度比越小,连接非线性程度越强,其轴力峰值越大且概率分布越离散.
(2) 拉压刚度比小于 1:5 时,随着拉压刚度比增大,最大弯矩概率密度峰值右移,导致危险弯矩出现的概率增大;拉压刚度比大于 1:5 时,随着拉压刚度比的进一步增大,最大弯矩概率密度峰值稍向左移,危险弯矩出现的概率减小. 连接非线性对输入外部载荷的不确定性的传播有显著的影响,当结构连接非线性比较强时,输入正态分布的载荷所得到的内力响应显然不是正态分布的,必然会产生一定的偏度.
(3) 随着拉压刚度比增大,最大弯矩发生时刻的概率密度峰值左移,延时效应逐渐减弱.
(4) 最大弯矩产生位置均在含有非线性连接面的梁模型下段,且比较靠近整体模型中段位置;随拉压刚度比增大,在拉压刚度比小于 1:10 时,最大弯矩产生位置概率密度峰值右移,而当拉压刚度比大于 1:10 时,随着拉压刚度比的进一步增大,最大弯矩产生位置概率密度峰值左移.
从上述结论中可以发现,最大熵方法可以有效的应用于水下航行体内力响应的概率分布建模,并分析连接非线性对内力响应概率分布的影响. 由于外载荷随机特性也对内力响应分布具有影响,在未来可以继续应用最大熵方法实现结构内力响应概率建模,开展结构外载荷随机演化规律作用下结构内力不确定性传播规律的研究.
The authors have declared that no competing interests exist.

---

参考文献文献选项 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]	吕海波,权晓波,尹云玉等. 考虑水弹性影响的水下航行体结构动力响应研究 . 力学学报,2010, 42(3): 351-356 [本文引用: 1] Lü Haibo, Quan Xiaobo, Yin Yunyu, et al.Dynamic response research of underwater vehicle with consideration of hydroelascity . Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(3): 351-356 (in Chinese) [本文引用: 1]
[2]	李国良,袁湘江,敖林. 潜射导弹出水载荷数值算法研究 . 力学与实践,2013, 35(4): 24-30 [本文引用: 1] Li Guoliang, Yuan Xiangjiang, Ao Lin, Simulation of under-water launched missile’s water-exitload . Mechanics in Engineering, 2013, 35(4): 24-30 (in Chinese) [本文引用: 1]
[3]	郑晓亚,徐超,王焘等. 螺栓–法兰连接结构非线性优化设计方法研究综述 . 强度与环境,2008, 3(1): 7-13 [本文引用: 1] Zheng Xiaoya, Xu Chao, Wang Tao, et al.Study on nonlinear optimization design for bolted flanged connection . Structure & Environment Engineering, 2008, 3(1): 7-13 (in Chinese) [本文引用: 1]
[4]	吴志刚,王本利. 在轨航天器连接结构动力学及其参数辨识 . 宇航学报,1998, 19(13): 103-109 [本文引用: 1] Wu Zhigang, Wang Benli.Dynamics and parameters identification of joints in spacecraft . Journal of Astronautics, 1998, 19(13): 103-109 (in Chinese) [本文引用: 1]
[5]	栾宇,刘松,关振群等. 小变形下螺栓法兰连接结构的静刚度非线性特性 . 强度与环境, 2011, 38(3): 29-35 [本文引用: 1] Luan Yu, Liu Song, Guan Zhenqun, et al.The nonlinear character of static stiffness in the structure with bolted flanged connection under small deformation . Structure & Environment Engineering, 2011, 38(3): 29-35(in Chinese) [本文引用: 1]
[6]	江召兵,陈徐均,赵红亮. 浮桥运动响应分析的非线性间隙单元构造与应用 . 工程力学, 2012, 29(10): 335-339 [本文引用: 1] Jiang Zhaobing, Chen Xujun, Zhao Hongliang.Construction and application of nonlinear gap element for dynamic analysis of floating bridge . Engineering Mechanics, 2012, 29(10): 335-339(in Chinese) [本文引用: 1]
[7]	冯韶伟,刘竹生,栾宇等. 基于拉压不同刚度的运载火箭捆绑联接装置力学特性研究 . 导弹与航天运载技术, 2013 (4): 9-13 [本文引用: 1] Feng Shaowei, Liu Zhusheng, Luan Yu, et al.Dynamic analysis of strap-on equipment in launch vehicle based on different tensile and compressive stiffness .Missiles and Space Vehicles, 2013 (4): 9-13 (in Chinese) [本文引用: 1]
[8]	芦旭,王平,关振群等. 航天运载器局部连接刚度对振型斜率的影响 . 强度与环境, 2014, 41(1): 10-16 [本文引用: 1] Lu Xu, Wang Ping, Guan Zhenqun, et al.Mode shape slopes prefigure analysis of aerospace vehicle structure . Structure & Environment Engineering, 2014, 41(1): 10-16(in Chinese) [本文引用: 1]
[9]	芦旭,王平,王建男等. 含剪力销 (锥) 螺栓法兰连接结构非线性特性 . 计算力学学报, 2015, 32(4): 503-511 [本文引用: 1] Lu Xu, Wang Ping, Wang Jiannan, et al.Nonlinear behavior of bolted flange connections containing shear pin(cone) . Chinese Journal of Computational Mechanics, 2015, 32(4): 503-511(in Chinese) [本文引用: 1]
[10]	Muscolino G, Santoro R, Sofi A.Reliability analysis of structures with interval uncertainties under stationary stochastic excitations . Computer Methods in Applied Mechanics and Engineering, 2016, 300: 47-69 [本文引用: 1]
[11]	An YH, Spencer Jr. BF, Ou JP.Real-time fast damage detection of shear structures with random base excitation . Measurement, 2015, 74: 92-102 [本文引用: 1]
[12]	Blachowski B, Gutkowski W.Effect of damaged circular flange-bolted connections on behaviour of tall towers, modelled by multilevel substructuring . Engineering Structures, 2016, 111: 93-103 [本文引用: 1]
[13]	Yapici A, Saracoglu G.Fatigue analysis of bolted flange joints of a rotary dryer . Engineering Failure Analysis, 2016, 63: 182-190 [本文引用: 1]
[14]	Piollet E, Poquillon D, Michon G.Dynamic hysteresis modeling of entangled cross-linked fibres in shear . Journal of Sound and Vibration, 2016, 383: 248-264 [本文引用: 1]
[15]	Scarselli G, Castorini E, Panella FW, et al.Structural behaviour modelling of bolted joints in composite laminates subjected to cyclic loading . Aerospace Science and Technology, 2015, 43: 89-95 [本文引用: 1]
[16]	Shannon CE.A mathematical theory of communication . The Bell System Technical Journal, 1948, 27: 379-423 [本文引用: 1]
[17]	Jaynes ET.Information theory and statistical mechanics . Physical Review, 1957, 106(4): 620-630 [本文引用: 1]
[18]	Zellner A, Highfield RA.Calculation of maximum entropy distributions and approximation of marginal posterior distributions . Journal of Econometrics, 1988, 37(2): 195-209 [本文引用: 1]
[19]	Ormoneit D, White H.An efficient algorithm to compute maximum entropy densities . Econometrics Reviews, 1999, 18(2): 127-140 [本文引用: 1]
[20]	韦征,叶继红,沈世钊. 最大熵法可靠度理论在工程中的应用 . 振动与冲击, 2007, 26(6): 146-151 [本文引用: 1] Wei Zheng, Ye Jihong, Shen Shizhao, Engineering application of the maximum entropy reliability theory . Journal of Vibration and Shock, 2007, 26(6): 146-151(in Chinese) [本文引用: 1]
[21]	李枝军,李爱群,韩晓林等. 基于最大熵谱和模糊聚类分析的斜拉桥拉索索力测试与评估 . 工程力学, 2009, 26(11): 88-94 [本文引用: 1] Li Zhijun, Li Aiqun, Han Xiaolin, et al.Measurement and estimation of the cable tension based on maximum entropy spectral and fuzzy clustering . Engineering Mechanics, 2009, 26(11): 88-94 (in Chinese) [本文引用: 1]
[22]	郑俊杰,徐志军,刘勇等. 基于最大熵原理的基桩竖向承载力的可靠度分析 . 岩土工程学报, 2010, 32(11): 1643-1647 [本文引用: 1] Zheng Junjie, Xu Zhijun, Liu Yong, et al.Reliability analysis for vertical bearing capacity of piles based on the maximum entropy principle . Chinese Journal of Geotechnical Engineering, 2010, 32(11): 1643-1647 (in Chinese) [本文引用: 1]
[23]	蒋运华,安伟光,周凌. 随机参数超空泡射弹弹道随机特性分析 . 计算力学学报, 2011, 28(1): 25-30 [本文引用: 1] Jiang Yunhua, An Weiguang, Zhou Ling.Trajectory stochastic characteristics analysis of supercavitation projectile with stochastic parameters . Chinese Journal of Computational Mechanics, 2011, 28(1): 25-30(in Chinese) [本文引用: 1]
[24]	周云,谢利民,蒋运忠等. 多模型结构识别方法及在混凝土连续梁的应用 . 地震工程与工程振动, 2015, 35(4): 130-138 [本文引用: 1] Zhou Yun, Xie Limin, Jiang Yunzhong, et al.Multi-model structural identification method and its application inconcrete continuous beam . Earthquake Engineering and Engineering Dynamics, 2015. 35(4): 130-138(in Chinese) [本文引用: 1]
[25]	臧红霞,郑华山,陈长茵. 三参数对数正态分布最大熵参数估计方法探讨 . 水利科技与经济, 2014, 20(5): 1-4 [本文引用: 1] Zang Hongxia, Zheng Huashan, Chen Changyin.Maximum entropy estimation methods for ln3 distribution considering . Water Conservancy Science and Technology and Economy, 2014, 20(5): 1-4 (in Chinese) [本文引用: 1]
[26]	肖东升,吴锟,胡启军等. 基于最大熵的人员震时空间分布模型研究 . 世界地震工程, 2014, 30(4): 55-60 [本文引用: 1] Xiao Dongsheng, Wu Kun, Hu Qijun, et al.Study on distribution of staff at time of earthquake based on maximum entropy model . World Earthquake Enginering, 2014, 30(4): 55-60 (in Chinese) [本文引用: 1]
[27]	赖雄鸣,王成,张勇等. 最大熵法在可靠度计算中的应用 . 计算力学学报, 2015, 32(1): 41-47 [本文引用: 1] Lai Xiongming, Wang Cheng, Zhang Yong, et al.Application of maximum entropy method in reliability computation . Chinese Journal of Computational Mechanics, 2015, 32(1): 41-47(in Chinese) [本文引用: 1]
[28]	王宇,李洪双. 最大熵准则识别材料疲劳寿命分布 . 航空工程进展, 2015, 6(3): 297-305 [本文引用: 1] Wang Yu, Li Hongshuang.Maximum entropy principle for identifying the fatigue life distribution of material . Advances in Aeronautical Science and Engineering, 2015, 6(3): 297-305(in Chinese) [本文引用: 1]
[29]	Giffin A, Cafaro C, Ali SA.Application of the maximum relative entropy method to the physics of ferromagnetic materials . Physica A, 2016, 455: 11-26 [本文引用: 1]
[30]	Lawrence KE, Summers SR, Heath ACG, et al.Predicting the potential environmental suitability for Theileriaorientalis transmission in New Zealand cattle using maximum entropy niche modeling . Veterinary Parasitology, 2016, 224: 82-91 [本文引用: 1]
[31]	Xi ZM, Hu C, Youn BD.A comparative study of probability estimation methods for reliability analysis . Structural and Multidisciplinary Optimization, 2012, 45(1): 33-52 [本文引用: 2]
[32]	Li G, Zhang K.A combined reliability analysis approach with dimension reduction method and maximum entropy method . Structural and Multidisciplinary Optimization, 2011, 43(1): 121-134 [本文引用: 1]
[33]	栾宇. 航天器结构中螺栓法兰连接的动力学建模方法研究. [博士论文] . 大连: 大连理工大学, 2011 [本文引用: 2] Luan Yu.Study on dynamic modeling of bolted flange connections in aerospace structures. [PhD Thesis] . Dalian: Dalian University of Technology, 2011 (in Chinese) [本文引用: 2]