 ,3)同济大学航空航天与力学学院,上海200092
,3)同济大学航空航天与力学学院,上海200092THE SIMULATION OF AIRFOIL FLUTTER CHARACTERISTIC BASED ON ACTIVE CONTROL STRATEGY 1)
Liu Chuyuan2), Liu Zesen, Song Hanwen ,3)School of Aerospace Engineering and Applied Mechanics, Tongji University, Shanghai 200092, China
,3)School of Aerospace Engineering and Applied Mechanics, Tongji University, Shanghai 200092, China通讯作者: 3) 宋汉文,教授,主要研究方向:模态分析与主动控制. E-mail:hwsong@tongji.edu.cn
收稿日期:2018-08-8接受日期:2018-10-16网络出版日期:2019-03-18
| 基金资助: |
Received:2018-08-8Accepted:2018-10-16Online:2019-03-18
作者简介 About authors
2)刘楚源,硕士研究生,主要研究方向:模态分析与主动控制.E-mail:1631806@tongji.edu.cn

摘要
航空航天飞行器舵翼类结构的气动颤振是一种灾难性的动力学行为.在基于偶极子理论的气动弹性动力学模型中,气动载荷可表达为基于结构动力学响应的一种状态反馈的闭环控制力,控制律取决于翼型的几何参数、材料参数、结构动力学特性以及来流速度等多种条件,通常需通过实际飞行或风洞实验进行辨识与检验.在实验室条件下,以系统动力学响应的模态特征等效为前提,提出了一种基于人工主动控制的方式进行气动载荷下舵翼类结构自激颤振的特征值跟踪策略.建立并讨论了等效系统的非自伴随动力学微分方程及其特征方程的求解过程,并与通用软件的计算结果进行了对比,二者具有较好的一致性.通过优化搜索分别获得了位移和速度的最优反馈点、最优作动点位置及最优反馈增益系数,经对比计算拟合得到风速-位移增益曲线和风速-速度增益曲线,从而实现了由单点反馈、单点作动的集中力的闭环控制等效系统的真实气动力分布控制.仿真算例表明,由此预示的实验过程无需辨识和重构非定常气动力的时域波形,无需其他干预即可实现地面模拟实验,主动控制的效果满足预期,初步实现了自激颤振的特征值跟踪,为进一步推动主动控制模拟实验及颤振参数辨识提供了基础.
关键词:
Abstract
The aerodynamic flutter of aerospace vehicle Rudder-airfoil structure is a catastrophic dynamic behavior. In the aeroelastic dynamic model that is on the basis of doublet lattice theory, aerodynamic load can be expressed as a closed-loop control force that is a kind of state feedback based on structural dynamic response. In fact, the aerodynamic forces received by each node are derived from the complex coefficient proportional feedback of the displacement response and velocity response of all nodes. The control law of feedback is dependent on the geometric parameters, material parameters, dynamic characteristics of the structure, flight altitude, air density and inflow velocity etc. It usually needs to be identified and validated by actual flight or wind tunnel testing. Under laboratory conditions, with the premise of equivalent modal characteristic in system dynamic responds, a strategy is put forward that is based on active control in order to track the eigenvalues of self-excited flutter in Rudder-airfoil structure under aerodynamic load. The process of solving the non-self-adjoint dynamic differential equation and its characteristic equation of the equivalent system is established and discussed. The comparison between the computed results and those results from the common software shows good consistency. Through optimization search, the optimal feedback point for displacement and velocity, the optimal actuation point, and the optimal feedback-gain factor can be obtained respectively. The fitting of the wind velocity-displacement gain curve and wind velocity-velocity gain curve can help to realize the real contribution control of the aerodynamic force of the equivalent system. Simulation example shows that the first two modal are the main modal of flutter and higher order modals do not participate in flutter, so the active control strategy focuses on the main modal of flutter. The result also shows that the predicted experimental process does not need identification or reconstruction of the unsteady aerodynamic force in time domain. Ground simulation experiment can be achieved without any other meddles. The active control reaches satisfied effects, ensure the variation characteristics of eigenvalue, achieves preliminary eigenvalue tracking of self-excited flutter, and provides a basement to further promote the active control simulation experiment and flutter parameter identification.
Keywords:
PDF (3005KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
刘楚源, 刘泽森, 宋汉文. 基于主动控制策略的机翼颤振特性模拟 1). 力学学报[J], 2019, 51(2): 333-340 DOI:10.6052/0459-1879-18-265
Liu Chuyuan, Liu Zesen, Song Hanwen.
引 言
飞行器舵翼类结构的气动颤振是一种灾难性的动力学行为.1916年英国的Handle Page 0/400双引擎轰炸机因发生剧烈的尾翼颤振而坠毁,这是已知的最早的有记载的飞机颤振事故[1].由于全尺寸风洞试验费用昂贵且实施困难[2-3],研究者一直试图寻找替代的研究方法. 20世纪60年代,Kearns[4]提出了地面颤振模拟(ground flutter simulation)的概念.因实验条件所限,并未对激振器系统实现闭环控制,也未能对这一问题实现进一步深入探索.随着振动控制理论的进一步发展,地面颤振模拟又重新受到了重视.2001年与2011年,俄罗斯中央流体研究院(TsAGI)和美国ZONA公司相继提出了电动机械模拟技术(EMM)[5]和干风洞(dry wind tunnel)思想[6]. 2011年,杨超等[7-8]针对利用激振器模拟非定常气动力加载进行了研究,在实验室内实现了细长体导弹模型的气动伺服弹性半实物模拟试验,并利用最小状态法[9-10]对非定常气动力进行了缩减[11]. 2013年,Daborn等[12-14]通过多个传感器与激振器,以响应谱的一致性为目标,在实验室对火箭结构实现了气动环境的等效再现.经典结构动力学主动控制理论的研究近年来取得了丰富的研究成果.在主动结构的研究过程中,张景绘等[15]针对主动结构的理论研究定义概念和数值计算做出了奠基性的工作;Malas等[16]进行了基于继电反馈的自激振动系统的理论建模与优化控制;欧阳华江等[17]对非对称刚度矩阵的特征根问题进行了研究;刘海标等[18]以主动结构的动力学特征为目标,研究了主动结构的非特定目的主动控制行为,辨识来自环境控制的未知控制律,为自激振动的形成机理及参数辨识等研究提供支持. Ouisse等[19]等为复模态适用于非自伴随系统提供方法,并用于辨识方程的系统矩阵.Warminski等[20]针对非线性梁的主动振动控制进行研究,探索了负阻尼对于结构的影响.胡海岩等[21]对飞机结构气动弹性分析与控制展开了综述,指出今后一个时期值得研究的若干气动弹性分析与控制问题.王在华等[22]对于具有采样反馈的力控制系统的稳定性进行了分析与解释.2016年,冯伟等[23]在实验室以悬臂梁为研究对象,完成了利用速度反馈控制实现响应发散的最优控制律研究.牛江川等[24]针对达芬振子的主共振进行了研究,认定基于速度反馈的分数阶比例-积分-微分控制对达芬振子主共振振幅的控制效果要优于传统整数阶比例-积分-微分控制.Zhao等[25-26]通过一套结合式翼板的主动气动控制系统,并通过风洞试验研究了颤振抑制效果.高逦等[27]提出了一种形状记忆弹簧扭转机翼自适应控制系统,采用反馈控制,通过记忆弹簧驱动控制产生相应的变形以稳定结构抑制颤振.2018年,Bera等[28]使用静态输出反馈实现桥面板的颤振控制.
气动弹性动力学模型中认为临界颤振是弹性结构受到非定常气动力、弹性力和惯性力的耦合作用而发生的振幅不衰减的自激振动.非定常气动载荷表达为基于结构响应的一种分布式状态反馈控制力.由于结构与载荷耦合,在飞行中直接测量气动力是不可能的,以文献[5-11]为代表的地面模拟实验(EMM及DWT技术),其技术路线都是根据事先建立的有限元计算模型、实验获得的结构模态参数、飞行响应实测数据等在颤振参数辨识的基础上进行气动载荷的时域重构,然后利用计算机生成模拟气动力驱动激振器进行开环加载实验.因此,目前多数研究工作集中于控制律的识别方面或颤振预测研究[29-33].
非定常气动力在风速变化时辨识与重构的困难是显而易见的,无法保证模拟实验的精度.本文放弃这种思路,试图构造一种闭环控制的形式,通过寻找结构上最优反馈参考点,直接将实测响应信息经比例控制通过激振器施加到结构的最优作动点上,构成一种人工主动控制,通过调节增益系数实现颤振过程的特征值跟踪,再现颤振行为.
1 气动载荷下机翼结构自激励模型与动力学方程
颤振是一种具有发散性、灾难性的系统动力学响应特征.对于一个$n$自由度线性翼类结构系统而言,其动力学运动微分方程如下式中,M,C,K分别为$n\times n$阶质量、阻尼、刚度矩阵;$ {\ddot {x}\left( t \right)}, {\dot {x}\left( t \right)}, {x\left( t \right)}$分别为$n\times 1$阶加速度、速度、位移向量;$ {f_1 \left( t \right)}$表示由紊流引起的激励力,通常简化为开环的随机激励;$ {f_2 \left( t \right)}$为$n\times 1$阶由均匀流引起的自激力.x为垂直板面方向,y和z为平行板面方向;在偶极子理论[34]中,气动压力即自激力可表示为
式中,$\rho$为当地空气密度,V为均匀流速度,D为气动力影响系数矩阵,其数值与均匀流速度V无关[35],$S$为气动网格面积矩阵,$ {w\left( t \right)}$为下洗控制点处的下洗速度列阵. 将式(2)代入式$\left(1 \right)$式得
令$ \frac{\partial }{\partial z} {x\left( t \right)} \mbox{ = }{\theta \left( t \right)} = G {x\left( t \right)}$,$\theta \left( t \right)$为转角,$G$为转角位移变换矩阵. 将式(3)右端与刚度、阻尼有关项移至式(3)左端并与原系统合并同类项,得到新的动力学方程
令
$$ C-\frac{1}{2}\rho VSD^{-1} = {C_1 }$$
$$K-\frac{1}{2}\rho V^2SD^{-1}G = {K_1 }$$
式(4)简记为
式(5)中,在给定均匀流速度V的情况下,M,$C_1 $和$K_1$是等效的系统矩阵. 由于矩阵D为非对称复数矩阵,且矩阵$ C_1$中所有元素均为均匀流速度V的函数,矩阵$K_1$中所有元素均为$V^2$的函数.因此,该两个矩阵的各元素不再保持为实数、矩阵不再保持对称性,成为"非自伴随动力学系统".仅当均匀流速度V为0时,方程$\left( 5 \right)$退化为方程(1).
2 非自伴随动力学系统求解与特征值分析
2.1 非自伴随动力学系统求解
令由紊流引起的激励力$ {f_1 \left( t \right)}$为$0$,考虑式$\left( 5 \right)$系统的齐次方程取$ {h\left( t \right)} = \left\{ {{\begin{array}{*{20}c} {\dot {x}\left( t \right)} \\ {x\left( t \right)} \\ \end{array} }} \right\}$,$ {\dot {h}\left( t \right)} = \left\{ {{\begin{array}{*{20}c} {\ddot {x}\left( t \right)} \\ {\dot {x}\left( t \right)} \\ \end{array} }} \right\}$为状态向量,表达为状态方程形式
由工程经验可知,随风速增长,式(7)所述系统的稳定性将逐步丧失,当至少有某一阶特征值的实部由负到零并进一步变为正值(即负阻尼)时,响应发散,此时的风速称为"稳定性临界风速Vs". 同时,这类非自伴随系统的另一个特征是,随风速增长,原本相邻的两阶相异特征值将相互接近,当二者重合之后,进一步发展将导致系统亏损,此风速称为"亏损临界风速Vd".系统亏损前后,微分方程及其解的特征是不一样的[36],系统亏损以后,需要重新建立解的结构,本文暂不讨论亏损以后的微分方程及其求解问题.但需要指出,如果系统的稳定性丧失发生在亏损以前,即$V_{\rm s} < V_{\rm d}$,那么系统发散以后的响应计算依然可信,直至系统亏损.反之,若亏损发生在稳定性丧失之前,即$V_{\rm d} < V_{\rm s}$,那么响应计算只能到亏损为止,其后的响应计算需要重新建立.
以模态分析的视角观察,在系统亏损之前,任意确定的常数速度V下,式(7)表述的系统依然符合线性、时不变要求,可以进行模态分解.即在每一个确定的常数风速V下,系统运动都能够分解为一系列模态运动的组合.由此,可以拟合得到每阶模态频率和模态阻尼比随风速变化的曲线,即常用的V-f图(风速-频率图)和V-g图(风速-阻尼比图).需要稍作解释的是,V-g图中的g定义为由气动力造成的附加阻尼比系数,工程中习惯画法的是以式(3)描述的微分方程右端的正负号为准.而式(6)描述的非自伴随动力学系统的等效阻尼比是将该项移至方程左端并与结构固有阻尼比合并后的数值,移项过程将造成符号反转,后文中叙述"负阻尼"发生时的符号与V-g图形恰好相反.
在系统亏损临界速度之前,令速度$V \in [ 0 ~~ {\Delta V}$${2\Delta V} ~~\cdots ~~ {p\Delta V} ]$,逐次代入式(7)中,得到$\left. {\left[ {A\left( V \right)} \right]} \right|_{V = V_i } ,$$i = 0,1,2, \cdots ,p$,可进行特征值与特征向量求解.
2.2 算例
针对一个简单翼型板进行示例计算,分别使用Nastran软件和非自伴随动力学系统理论获取相应的图形,并将二者进行比较.图1
 新窗口打开|下载原图ZIP|生成PPT
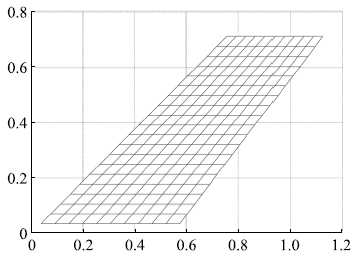
新窗口打开|下载原图ZIP|生成PPT图1模型示意图
Fig.1Model schematic
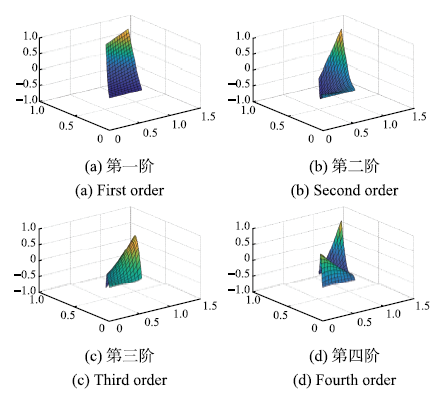
模型及参数如下:半机翼型铝板,铝板半展长0.712 m,根弦弦长0.546~3 m,翼梢弦长0.368~3 m,厚度4 mm,材料密度2820 kg/m3,杨氏模量71 GPa,泊松比0.320~5. 使用Patran软件建模,网格划分采用CQUAD4板单元,$10\times 20$共200个;节点数量为220个,计算获得各阶模态固有频率与振型(见表1).前4阶振型如图2所示. 然后,使用Nastran软件求解颤振特性,计算状态为:空气密度取1.293 kg/m3,参考马赫数Ma = 0,初始阻尼比为0,得到V-f和V-g图如图3所示.
Table 1
表1
表1模态参数
Table 1
| Order | Modal mass | Modal stiffness | Frequency /Hz |
|---|---|---|---|
| 1 | 1.873 | 1620.5 | 4.68 |
| 2 | 0.506 | 8916.7 | 21.13 |
| 3 | 0.197 | 8473.2 | 33.00 |
| 4 | 0.275 | 32 562.9 | 54.77 |
| 5 | 0.000 04 | 12.9 | 90.37 |
新窗口打开|下载CSV
图2
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图2振型图
Fig.2Modal shape diagram
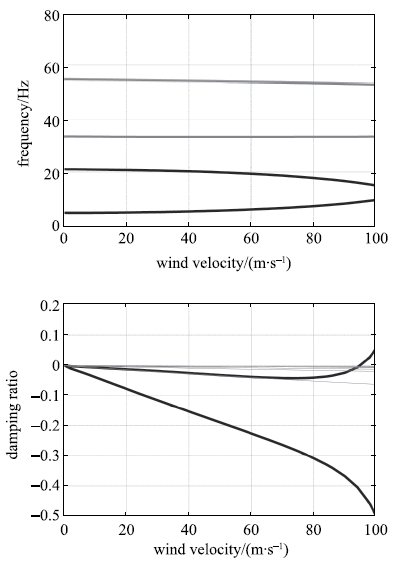
从图3可知,随风速增长,前两阶模态频率逐渐靠近,第一阶模态阻尼比持续增大,第二阶模态阻尼比先升后降,并在94.7 m/s处穿越零点形成负阻尼,此后结构响应将发散.
图3
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图3Nastran的V-f和V-g图
Fig.3V-f and V-g from Nastran
2.3 非自伴随系统特征值求解
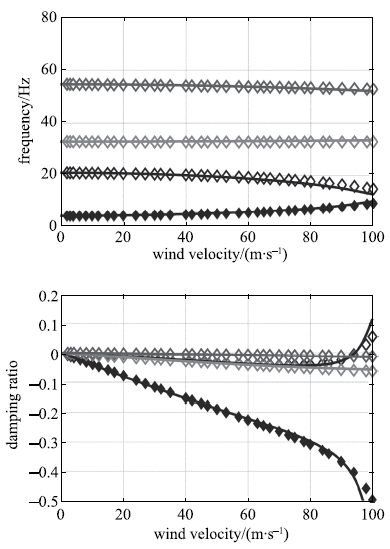
由式(7)求解特征值,计算条件与Nastran相同,并将计算得到的V-f图与V-g图与Nastran的V-f和V-g图进行比较(见图4).下图中实线是非自伴随系统解出的频率与阻尼比,点标记是Nastran软件的计算结果.图4
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图4非自伴随系统与Nastran对比
Fig.4Comparison between non-self-adjoint system and Nastran
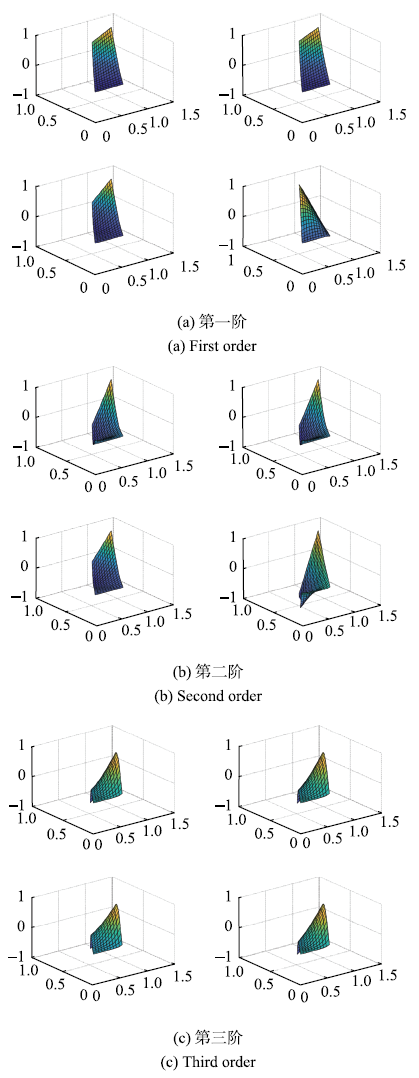
从图4可以看到,两种计算一致性良好.图5为各阶特征向量,由于系统的非自伴随特性,左-右特征向量不再相等且均为复向量(为图示方便,做了实数化处理),文中分别给出并适当对比.每幅图第一行风速为20 m/s,第二行风速为100 m/s;左图为右特征向量,右图为左特征向量.
图5
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图5特征向量图
Fig.5Eigenvector diagram
从图4和图5可以看出,在风速为95.3 m/s时,系统第二阶模态阻尼比穿越零点,响应发散;但直到100 m/s时,频率尚未重合,表明系统尚未亏损.对于第一、二阶模态而言,由于系统矩阵的对称性被破坏,气动载荷使得系统的左右特征向量不再相同,随着风速增大,系统的特征向量变异程度也随之增大.
3 基于主动控制的特征值跟踪
偶极子理论中,机翼在真实飞行时由气动载荷引起自激振动的颤振行为可以描述为一种复杂的闭环控制行为,其每个节点受到的气动力均来自所有节点的位移响应和速度响应的复系数比例反馈.事实上,对于连续系统来说,这是一种分布式的复杂控制行为,其控制律是由翼型的几何参数、材料参数、动力学参数及来流速度等诸多条件联合确定的.另一方面,以模态分析角度考察,上述控制行为的效果主要表现为针对低阶模态参数的连续修正,这是一个普遍特征.就本例来说,控制造成的效果是:随风速单调增长,第一阶模态频率及阻尼比单调上升,第二阶模态频率单调下降,第二阶阻尼比先单调上升,到达最大值后开始单调下降,最终跨越零点出现负阻尼,从而导致第二阶模态响应发散.同时,三阶及以上高阶模态参数基本没有变化.
鉴于上述分析,本文提出一种基于主动控制跟踪系统特征值的技术路线如下.
构造人工主动控制的方式,以第一、二阶模态特征值跟踪误差极小化为目标函数,逼近和等效真实系统不同风速下的系统特征值.约束条件为:以结构上某特定位置d点作为位移反馈的参考点,以v点作为速度反馈的参考点,以$e$点作为作动点,以两组单调的实常数序列分别作为位移和速度的反馈增益系数并与单调增的风速数值一一对应,实现以人工控制的集中力代替真实气动载荷的分布力.在此基础上,进一步要求对三阶及以上模态参数不造成显著变化.控制力可表达如下
其中
$$ {\hat {f}_2 \left( t \right)} = \left\{ {{\begin{array}{*{20}c} 0 \\ \vdots \\ {f_{\rm e} \left( t \right)} \\ \vdots \\ 0 \\ \end{array} }} \right\}, {\dot {x}\left( t \right)} = \left\{ {{\begin{array}{*{20}c} \vdots \\ {\dot {x}_{\rm v} \left( t \right)} \\ \vdots \\ \vdots \\ \vdots \\ \end{array} }} \right\}, {x\left( t \right)} = \left\{ {{\begin{array}{*{20}c} \vdots \\ \vdots \\ \vdots \\ {x_{\rm d} \left( t \right)} \\ \vdots \\ \end{array} }} \right\}$$
$$ P = \left[ {{\begin{array}{*{20}c} 0 & \cdots & 0 & \cdots & 0 \\ \vdots & \ddots & \vdots & \ddots & 0 \\ 0 & {p_{\rm e{v}} } & 0 & \cdots & 0 \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ 0 & \cdots & 0 & \cdots & 0 \\ \end{array} }} \right], Q = \left[ {{\begin{array}{*{20}c} 0 & \cdots & 0 & \cdots & 0 \\ \vdots & \ddots & \vdots & \ddots & 0 \\ 0 & \cdots & 0 & {q_{\rm ed} } & 0 \\ \vdots & \ddots & \vdots & \ddots & \vdots \\ 0 & \cdots & 0 & \cdots & 0 \\ \end{array} }} \right]$$
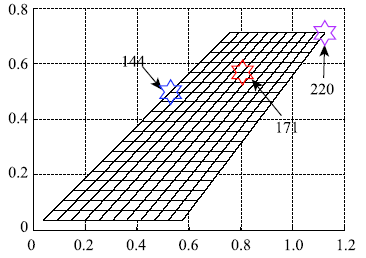
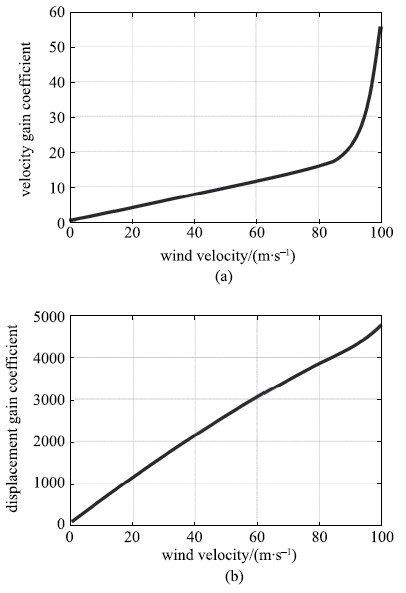
经优化计算,选取第171号节点为速度参考点v,第144号节点为位移参考点d,第220号节点为作动点$e$,如图6所示.由此获得的风速与增益关系曲线如图7所示.
图6
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图6参考点与控制点示意图
Fig.6Reference point and control point schematic
图7
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图7风速-增益曲线
Fig.7Wind velocity-gain coefficient curve
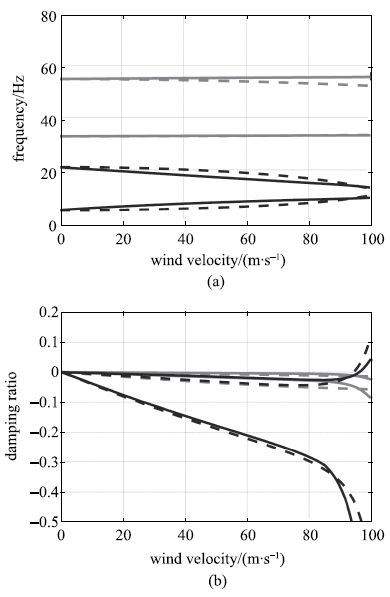
该控制律下得到的V-f与V-g对比图如图8所示.
图8
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图8主动控制与气动载荷对比
Fig.8Comparison between active control and aerodynamic load
图8中,实线表示主动控制曲线,虚线表示气动曲线.黑线表示前两阶模态,灰线表示高阶模态.主动控制基本实现了第一阶频率上升,第二阶频率下降;第一阶阻尼比持续上升,第二阶阻尼比先升后降且穿越零点最终变为负数的特征,两阶频率起始与终了位置及阻尼穿越零点位置基本吻合;高阶模态的频率和阻尼比也与气动载荷下接近,主动控制的效果满足预期,初步实现了气动力模拟.
4 结 论
提出了一种基于人工主动控制的方式进行气动载荷下舵翼类结构自激颤振的特征值跟踪策略,以单点反馈、单点作动的集中力闭环控制等效系统的真实气动力分布控制.由此预示的实验过程无需辨识和重构气动力时域波形,只要通过优化搜索获得v,d,$e$的位置以及图7所示的风速-增益曲线,无需其他干预即可实现地面模拟实验.参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[本文引用: 1]
DOIURL [本文引用: 1]

This paper introduces a new curvature based design parameterization of two-dimensional high pressure compressor blade sections to be used in a multi-criteria aerodynamic design optimization process. The suction side of the airfoil section is represented by its curvature distribution which is described by a B-spline curve. The coordinates are then derived by numerical integration. The camber line as well as pressure side are obtained by adding a thickness distribution perpendicularly to the camber line. The thickness distribution itself is modeled as a B-spline curve as well and varied during optimization. In order to achieve smoothness between leading edge, trailing edge and pressure side, respectively, specific conditions for the control points of the thickness distribution are derived. The resulting compressor blade section is optimized w.r.t. pressure loss and working range using process integration and a genetic algorithm. The results show major improvements over a manually "optimized" datum design regarding both criteria. (C) 2010 Elsevier Masson SAS. All rights reserved.
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]

A half model of a scaled-down aircraft is designed and tested in the wind tunnel to validate the mathematical model of uncertainty for unsteady pressure coefficients in the frequency domain. In the wind-tunnel test a step-swept test was conducted to obtain the frequency response function. Then a time-domain response test was performed with turbulence excitation to identify the aircraft's on-line poles. Based on the tested frequency response function for the on-line poles the structured singular value (mu) method was applied to determine the aerodynamic uncertainty level. Finally, the widely used mu analysis method was employed to compute the worst-case flutter boundary, and the result was compared with the experimental flutter velocity. The experimental flutter velocity (30.5 m/s) is in the range of the predicted robust flutter boundary (28.5 m/s) in which parameter uncertainties were taken into account in the numerical model. Experimental results validate that the uncertainty quantification theoretical frameworks incorporating experimental data can estimate the proper aerodynamic uncertainty level and predict a safe flutter boundary. The present results suggest that the time-response validation theoretical framework is more advantageous in robust stability analysis than the one based upon the frequency response function.
DOIURL [本文引用: 1]

Abstract An analytical design technique for an active flutter-suppression and gust-alleviation control system is presented. It is based on a rational approximation of the unsteady aerodynamic loads in the entire Laplace domain, which yields matrix equations of motion with constant coefficients. Some existing rational approximation schemes are reviewed, and a new technique which yields a minimal number of augmented states for a desired accuracy is presented. The state-space aeroelastic model is used to design a constant gain, partial-feedback control system, which simultaneously assures stability and optimizes any desired combination of gust response parameters throughout the entire flight envelope.
DOIURL [本文引用: 1]

Not Available
URLMagsci [本文引用: 2]

地面颤振模拟试验作为一种颤振研究的新方法,可以有效地弥补传统气动弹性试验的不足。对地面颤振模拟试验的主要难点,即非定常分布式气动力集成减缩加载的方法开展研究:基于亚声速偶极子格网法和活塞理论建立了亚声速以及超声速翼面的非定常气动力模型,通过曲面样条插值以及有理函数拟合获得了试验时域减缩气动力;提出以颤振关键模态的振型为优化目标,使用遗传算法搜寻气动力最优减缩位置的优化方法;建立了闭环系统的时域状态空间模型,使用颤振时域仿真结果与频域理论结果进行对比,对比发现二者误差可控制在3%以内。研究结果表明,该文提出的非定常气动力模拟方法可以很好地表征翼面非定常气动力分布特性,可以作为地面颤振模拟试验研究可靠的理论基础。
URLMagsci [本文引用: 2]

地面颤振模拟试验作为一种颤振研究的新方法,可以有效地弥补传统气动弹性试验的不足。对地面颤振模拟试验的主要难点,即非定常分布式气动力集成减缩加载的方法开展研究:基于亚声速偶极子格网法和活塞理论建立了亚声速以及超声速翼面的非定常气动力模型,通过曲面样条插值以及有理函数拟合获得了试验时域减缩气动力;提出以颤振关键模态的振型为优化目标,使用遗传算法搜寻气动力最优减缩位置的优化方法;建立了闭环系统的时域状态空间模型,使用颤振时域仿真结果与频域理论结果进行对比,对比发现二者误差可控制在3%以内。研究结果表明,该文提出的非定常气动力模拟方法可以很好地表征翼面非定常气动力分布特性,可以作为地面颤振模拟试验研究可靠的理论基础。
//
DOIURL [本文引用: 1]

Abstract Many structures experience random vibration caused by the rapid flow of air over the external surface of the structure. One example of this “aerodynamic excitation” occurs when missiles fly through the atmosphere en-route to target in powered flight, or slung to the undercarriage of an aircraft. In most cases, it is necessary to carry out laboratory testing in order to qualify the design of the structure and to assess the pedigree of the manufacturing and assembly process. The laboratory test should replicate, as closely as possible, the damage potential of the in-flight environment. The traditional method of replicating the aerodynamic induced vibration in the laboratory is to rigidly attach the structure to a large electrodynamic shaker and to subject the structure to random vibration. This testing methodology is inadequate and non-representative for two main reasons: (1) the excitation mechanisms are very different, i.e. through a distinct region when attached to a shaker compared to distributed excitation over the entire outer surface in-flight, (2) The boundary conditions are very dissimilar, i.e. attachment to a very high mechanical impedance shaker compared to “free” flight. There is much evidence to show that this testing methodology often leads to overly severe tests. Furthermore, the test program can be costly and time-consuming as tests are often carried out sequentially in three orthogonal axes. In addition, tests have to be repeated with different response control accelerometers as it is impossible to maintain in-flight responses all over the structure simultaneously due to the two reasons given previously. This paper details research carried out to replace the traditional rigid shaker approach to one with the structure “freely” supported and excited at multiple locations simultaneously using Multi Input Multi Output (MIMO) vibration control. The research focusses on analytical models in Matlab and Ansys to carry out “virtual tests” in order to demonstrate issues with the current testing methodology and to highlight the benefits of a new approach. Results from the analytical models show significant improvements in degree-of-replication and would result in faster and more cost effective laboratory testing.
//
DOIURL

This paper describes a radically new approach to the vibration testing of structures in order to demonstrate their endurance under simulated service conditions. The excitation mechanisms of structures in-service typically fall into one of three configurations; (i) excitation from a parent structure through mechanical connections (e.g. during transportation), (ii) excitation from aerodynamic forces distributed over the outer surface of the structure (e.g. aircraft and rockets in flight), or (iii) A combination of (i) and (ii). In nearly all cases, the in-service excitation is multi-directional, yet it is standard practice to replicate these environments with three orthogonal single-axis vibration tests. In addition, a considerable mismatch of the boundary conditions between the in-service and laboratory configurations is common, especially when replicating aerodynamic environments. This paper presents quantitative evidence of limitations with the status quo and demonstrates a superior method; Impedance Matched Multi-Axis Testing (IMMAT). Three noteworthy improvements of the new method are; (i) enhanced replication of the in-service environment, (ii) much shorter test durations, and (iii) a significant reduction in costs associated with random vibration tests.
DOIURL [本文引用: 1]

61Demonstrates the current limitations of replicating aerodynamic environments.61A new method is proposed which offers considerable improvements.61It utilises free boundary conditions and Multi-Input–Multi-Output vibration control.61Numerous small shakers are used instead of a large single-shaker system.61The new method is more realistic, faster and cost effective.
DOIURL [本文引用: 1]

本文是系列讲座文章的第四篇,介绍了主动结构和智能结构的基本概念,以及目前的研究现状。讨论了线性主动结构的基本概念,给出了模态及其基本属性;重点介绍了有限元的建模方法;考虑建模的不确定性,讨论了不确定性的表示方法及振动鲁棒控制问题;针对航天结构的复杂性,给出了优化问题的一般提法,介绍了遗传算法和模拟退火算法两种优化算法。最后引用了两个桁架结构的实例,说明主动结构或智能结构的有关问题。
DOIURL [本文引用: 1]

本文是系列讲座文章的第四篇,介绍了主动结构和智能结构的基本概念,以及目前的研究现状。讨论了线性主动结构的基本概念,给出了模态及其基本属性;重点介绍了有限元的建模方法;考虑建模的不确定性,讨论了不确定性的表示方法及振动鲁棒控制问题;针对航天结构的复杂性,给出了优化问题的一般提法,介绍了遗传算法和模拟退火算法两种优化算法。最后引用了两个桁架结构的实例,说明主动结构或智能结构的有关问题。
DOIURL [本文引用: 1]

Recently, a few research efforts are made to utilize artificially generated self-excited vibration in several mechanical and micromechanical applications. The present paper considers some important theoretical aspects in connection with the efficacy of the relay-feedback in generating and controlling self-excited oscillation in a class of mechanical systems. The force applied by the relay-feedback is essentially constant and acts in the direction of the measured quantity. Mathematically, an ideal relay-feedback is represented by the signum function of the measured variable. Detailed theoretical analyses, both analytic and numerical, are presented for single, two, and three degrees-of-freedom spring–mass–damper systems under relay-feedback with underactuated, collocated, and noncollocated control configurations. It is shown that relay-feedback, if used in a suitable way, can be effective in selectively generating a particular mode of oscillation in a multi degrees-of-freedom mechanical system. It is also possible to change the mode of oscillation and its amplitude by suitably selecting the control gains.
DOIURL [本文引用: 1]

This paper studies the latent roots of damped asymmetric systems in which the stiffness matrix is asymmetrical. The asymmetric terms are due to ‘external’ loads and are represented by a parameter or parameters. The latent roots of such asymmetric systems are complex and the real parts become positive at some critical values of the parameter(s) (critical points). The work reported in this paper consists of two parts. The first part presents a method for predicting the latent roots of the damped asymmetric system from the receptance of the damped symmetric system. The second part presents an inverse method for assigning latent roots by means of mass, stiffness and damping modifications to the damped asymmetric system again based on the receptance of the unmodified damped symmetric system. The simulated numerical examples of a friction-induced vibration problem show the complexity in assigning stable latent roots for damped asymmetric systems. It is found that it is quite difficult to assign the real parts of latent roots to stabilise the originally unstable asymmetric system and sometimes there is no solution to the modification that is intended to assign certain latent roots.
DOIURLMagsci [本文引用: 1]

<FONT face=Verdana>主动结构主要存在于主动控制以及各种自激颤振场合。对主动结构的动力学特征进行理论分析。从不同的角度对主动结构进行分类,讨论了主动结构的几种具有代表性的范例。进而分析主动结构与非自伴随结构之间的关系。对主动结构的频域特性进行探讨,阐述了主动结构与对应的被动结构的频响函数之间的关系。通过数值算例揭示主动结构的频响函数与被动结构的频响函数之间的差异,进一步展示仿真系统的左右特征向量。通过实验及数据处理,获得一个由自由-自由梁构造的主动结构频响函数,验证主动结构的频域特性。<BR></FONT>
DOIURLMagsci [本文引用: 1]

<FONT face=Verdana>主动结构主要存在于主动控制以及各种自激颤振场合。对主动结构的动力学特征进行理论分析。从不同的角度对主动结构进行分类,讨论了主动结构的几种具有代表性的范例。进而分析主动结构与非自伴随结构之间的关系。对主动结构的频域特性进行探讨,阐述了主动结构与对应的被动结构的频响函数之间的关系。通过数值算例揭示主动结构的频响函数与被动结构的频响函数之间的差异,进一步展示仿真系统的左右特征向量。通过实验及数据处理,获得一个由自由-自由梁构造的主动结构频响函数,验证主动结构的频域特性。<BR></FONT>
DOIURL [本文引用: 1]

Non-symmetric second-order systems can be found in several engineering contexts, including vibroacoustics, rotordynamics, or active control. In this paper, the notion of properness for complex modes is extended to the case of non-self-adjoint problems. The properness condition is related to the ability of a set of complex modes to represent in an exact way the behavior of a physical second-order system, meaning that the modes are the solutions of a quadratic eigenvalue problem whose matrices are those of a physical system. This property can be used to identify the damping matrices which may be difficult to obtain with mathematical modeling techniques. The first part of the paper demonstrates the properness condition for non symmetric systems in general. In the second part, the authors propose a methodology to enforce that condition in order to perform an optimal reconstruction of the losest physical system starting from a given basis complex modes. The last part is dedicated to numerical and experimental illustrations of the proposed methodology. A simulated academic test case is first used to investigate the numerical aspects of the method. A physical application is then considered in the context of rotordynamics. Finally, an experimental test case is presented using a structure with an active control feedback. An extension of the LSCF identification technique is also introduced to identify both left and right complex mode shapes from measured frequency response functions.
DOI [本文引用: 1]

An application of the nonlinear saturation control (NSC) algorithm for a self-excited strongly nonlinear beam structure driven by an external force is presented in the paper. The mathematical model accounts for an Euler-Bernoulli beam with nonlinear curvature, reduced to first mode oscillations. It is assumed that the beam vibrates in the presence of a harmonic excitation close to the first natural frequency of the beam, and additionally the beam is self-excited by fluid flow, which is modelled by a nonlinear Rayleigh term for self-excitation. The self- and externally excited vibrations have been reduced by the application of an active, saturation-based controller. The approximate analytical solutions for a full structure have been found by the multiple time scales method, up to the first-order approximation. The analytical solutions have been compared with numerical results obtained from direct integration of the ordinary differential equations of motion. Finally, the influence of a negative damping term and the controller's parameters for effective vibrations suppression are presented.
DOIURLMagsci [本文引用: 1]

<p>随着主动控制技术的发展,飞机结构设计理念已由提高结构刚度的被动设计转变为随控布局的主动设计.主动设计理念不再刻意回避气动弹性问题,而是采用主动控制技术实时调节结构气动弹性,进而减轻结构重量、优化飞机性能. 在飞机随控布局主动设计中,必须深入分析结构与气流之间的耦合,才能更好发挥气动弹性主动控制技术的作用. 从20 世纪80 年代起,航空科技界对该问题进行了长期研究,对飞机结构-空气动力-主动控制相互耦合后的关键力学问题有了深入理解. 然而,已有研究多基于简化模型,导致研究结果难以直接应用于工程. 本文将针对气动弹性动态问题,综述空气动力非线性、控制面间隙非线性、时滞诱发失稳、颤振主动抑制、突风载荷减缓、风洞实验验证等方面的国内外研究进展,重点介绍近年来作者团队所提出的若干方法及相关算例和风洞实验. 最后,指出今后一个时期值得研究的若干气动弹性分析与控制问题.</p>
DOIURLMagsci [本文引用: 1]

<p>随着主动控制技术的发展,飞机结构设计理念已由提高结构刚度的被动设计转变为随控布局的主动设计.主动设计理念不再刻意回避气动弹性问题,而是采用主动控制技术实时调节结构气动弹性,进而减轻结构重量、优化飞机性能. 在飞机随控布局主动设计中,必须深入分析结构与气流之间的耦合,才能更好发挥气动弹性主动控制技术的作用. 从20 世纪80 年代起,航空科技界对该问题进行了长期研究,对飞机结构-空气动力-主动控制相互耦合后的关键力学问题有了深入理解. 然而,已有研究多基于简化模型,导致研究结果难以直接应用于工程. 本文将针对气动弹性动态问题,综述空气动力非线性、控制面间隙非线性、时滞诱发失稳、颤振主动抑制、突风载荷减缓、风洞实验验证等方面的国内外研究进展,重点介绍近年来作者团队所提出的若干方法及相关算例和风洞实验. 最后,指出今后一个时期值得研究的若干气动弹性分析与控制问题.</p>
DOIURLMagsci [本文引用: 1]

<p>基于计算机的数字采样控制对离散信号进行运算并向作动器提供控制输入,是当前的主流控制技术.数字采样控制系统是这样一类控制系统,其控制对象由微分方程(组)描述,而控制律由离散采样信号给出.以采样PD(proportional-derivative)反馈作用下的单自由度力控制系统为例,基于离散系统的稳定性分析方法,研究采样控制律对控制系统稳定性的影响.为了突出采样反馈的作用,将系统取为无刚度、无阻尼的最简单形式.不同于已有研究假设位移采样信号与速度采样信号相互同步,本文研究当位移采样信号与速度采样信号不同步时受控系统的稳定性,发现位移采样信号与速度采样信号的采样周期不同组合对受控系统在增益平面上的稳定性区域有重要影响.结果表明,对所关心的三种数字采样反馈控制律,当位移采样信号滞后于速度采样信号一个采样周期时,受控系统具有最大的稳定性区域且对相同的增益值可以有最好的稳定效果.论文对这种现象进行分析,给出了一种力学解释.</p>
DOIURLMagsci [本文引用: 1]

<p>基于计算机的数字采样控制对离散信号进行运算并向作动器提供控制输入,是当前的主流控制技术.数字采样控制系统是这样一类控制系统,其控制对象由微分方程(组)描述,而控制律由离散采样信号给出.以采样PD(proportional-derivative)反馈作用下的单自由度力控制系统为例,基于离散系统的稳定性分析方法,研究采样控制律对控制系统稳定性的影响.为了突出采样反馈的作用,将系统取为无刚度、无阻尼的最简单形式.不同于已有研究假设位移采样信号与速度采样信号相互同步,本文研究当位移采样信号与速度采样信号不同步时受控系统的稳定性,发现位移采样信号与速度采样信号的采样周期不同组合对受控系统在增益平面上的稳定性区域有重要影响.结果表明,对所关心的三种数字采样反馈控制律,当位移采样信号滞后于速度采样信号一个采样周期时,受控系统具有最大的稳定性区域且对相同的增益值可以有最好的稳定效果.论文对这种现象进行分析,给出了一种力学解释.</p>
DOIURL [本文引用: 1]

工程中自激振动常被作为不利因素而加以抑制,然而在振动能量捕获等振动利用研究中,自激振动也有振幅响应大、抗干扰能力强等优点,利用自激振动作为振动驱动将具有极大的优势。论文以悬臂梁为研究对象,通过模态参数与测点组合条件,导出了基于速度反馈控制下各阶模态的变化模式,得到了产生自激振动的数值判据,并对单模态进入自激振动以后的非线性极限环现象进行了讨论。通过理论建模、数值仿真和控制实验及数据处理,验证了本文的正确性,并得到了一些有趣的结论。
DOIURL [本文引用: 1]

工程中自激振动常被作为不利因素而加以抑制,然而在振动能量捕获等振动利用研究中,自激振动也有振幅响应大、抗干扰能力强等优点,利用自激振动作为振动驱动将具有极大的优势。论文以悬臂梁为研究对象,通过模态参数与测点组合条件,导出了基于速度反馈控制下各阶模态的变化模式,得到了产生自激振动的数值判据,并对单模态进入自激振动以后的非线性极限环现象进行了讨论。通过理论建模、数值仿真和控制实验及数据处理,验证了本文的正确性,并得到了一些有趣的结论。
DOIURLMagsci [本文引用: 1]

<p>与传统整数阶比例-积分-微分(PID)控制器相比,分数阶比例-积分-微分控制器由于增加了两个控制参数,因此能够更灵活地控制受控对象.研究了基于速度反馈分数阶比例-积分-微分控制的达芬振子的主共振,利用平均法获得了系统的近似解析解.研究发现分数阶比例-积分-微分控制器的比例环节以等效线性阻尼的形式影响系统的共振振幅,积分环节以等效线性阻尼和等效线性刚度的形式影响系统的动力学特性,微分环节以等效线性阻尼和等效质量的形式影响系统的动力学特性.建立了主共振幅频响应方程的解析表达式和稳定性判断准则,并对主共振幅频响应的近似解析解和数值解进行了比较,二者吻合良好,验证了求解过程和近似解析解的正确性.分析了分数阶比例-积分-微分控制器的比例环节系数、积分环节系数、微分环节系数以及分数阶阶次变化时,对系统主共振幅频响应的影响.对分数阶比例-积分-微分控制器与传统整数阶比例-积分-微分控制器的控制效果进行了对比,发现当控制器各个环节的系数相同时,基于速度反馈的分数阶比例-积分-微分控制对达芬振子主共振的控制效果要优于传统整数阶比例-积分-微分控制.</p>
DOIURLMagsci [本文引用: 1]

<p>与传统整数阶比例-积分-微分(PID)控制器相比,分数阶比例-积分-微分控制器由于增加了两个控制参数,因此能够更灵活地控制受控对象.研究了基于速度反馈分数阶比例-积分-微分控制的达芬振子的主共振,利用平均法获得了系统的近似解析解.研究发现分数阶比例-积分-微分控制器的比例环节以等效线性阻尼的形式影响系统的共振振幅,积分环节以等效线性阻尼和等效线性刚度的形式影响系统的动力学特性,微分环节以等效线性阻尼和等效质量的形式影响系统的动力学特性.建立了主共振幅频响应方程的解析表达式和稳定性判断准则,并对主共振幅频响应的近似解析解和数值解进行了比较,二者吻合良好,验证了求解过程和近似解析解的正确性.分析了分数阶比例-积分-微分控制器的比例环节系数、积分环节系数、微分环节系数以及分数阶阶次变化时,对系统主共振幅频响应的影响.对分数阶比例-积分-微分控制器与传统整数阶比例-积分-微分控制器的控制效果进行了对比,发现当控制器各个环节的系数相同时,基于速度反馈的分数阶比例-积分-微分控制对达芬振子主共振的控制效果要优于传统整数阶比例-积分-微分控制.</p>
DOIURL [本文引用: 1]

61Wind tunnel experiment: bridge deck section with leading and trailing edge flaps.61Buffet response to grid-generated turbulence compared to 3D lifting surface theory.61Buffet suppression control system investigated theoretically and experimentally.61Deck position or velocity feedback; controllable leading and trailing edge flaps.61Control reduced buffet response, simultaneously increased critical flutter speed.
DOIURL [本文引用: 1]

We experimentally investigate the suppression of flutter in long-span suspension bridges. A rigid sectional model of a long-span suspension bridge is mounted in a wind tunnel on a suspension system. Control surfaces, which are used to suppress flutter, are movable flaps that are fitted to the bridge section's leading and trailing edges. The flaps are responsive to the deck's heave and pitch motions. In this paper, the aerodynamic force is modeled using a thin aerofoil theory, although other modeling techniques can be used. The controller has a second-order passive transfer function with inputs of a combination of the deck's pitch angle and heave position, and outputs of the flaps' angular positions. The control system design problem is solved as an H optimization problem.
DOIURL [本文引用: 1]

飞行器飞行过程中由于气动弹性效应会引起机翼颤振,并且随着飞行马赫数(速度)的提高,颤振类型会发生改变,对飞机结构的破坏性增大,因此若不能有效抑制机翼颤振将对高超音速飞行器飞行造成严重后果。为此,提出了一种形状记忆弹簧扭转机翼自适应控制系统,该系统采用反馈控制,通过记忆弹簧驱动控制产生相应的变形以稳定结构抑制颤振。根据驱动结构设计、理论推导以及测试实验成功验证了该方案的可行性,采用参数自整定模糊PID控制算法,通过控制实验得到了SMA弹簧驱动器的偏转角度与电流强度的关系,在控制电流为8 A时,偏转角度在6 s内可达到60°,响应速度10°/s。事实表明,采用文中设计的形状记忆弹簧扭转机翼自适应控制系统,可以对机翼翼面受力状态进行自适应监测与控制,使机翼结构吸取的能量等于消耗的能量,保持等幅振动而不发生颤振。
DOIURL [本文引用: 1]

飞行器飞行过程中由于气动弹性效应会引起机翼颤振,并且随着飞行马赫数(速度)的提高,颤振类型会发生改变,对飞机结构的破坏性增大,因此若不能有效抑制机翼颤振将对高超音速飞行器飞行造成严重后果。为此,提出了一种形状记忆弹簧扭转机翼自适应控制系统,该系统采用反馈控制,通过记忆弹簧驱动控制产生相应的变形以稳定结构抑制颤振。根据驱动结构设计、理论推导以及测试实验成功验证了该方案的可行性,采用参数自整定模糊PID控制算法,通过控制实验得到了SMA弹簧驱动器的偏转角度与电流强度的关系,在控制电流为8 A时,偏转角度在6 s内可达到60°,响应速度10°/s。事实表明,采用文中设计的形状记忆弹簧扭转机翼自适应控制系统,可以对机翼翼面受力状态进行自适应监测与控制,使机翼结构吸取的能量等于消耗的能量,保持等幅振动而不发生颤振。
[本文引用: 1]
//
[本文引用: 1]
//
DOIURL

Using an inviscid flow computational-fluid-dynamic model and a harmonic balance flow solver, a parametric investigation of how structural-inertial parameters and freestream Mach number of a transonic flow affect the limit-cycle oscillation characteristics of a typical two-degree-of-freedom transonic airfoil configuration is presented. The computational efficiency of the harmonic balance... [Show full abstract]
DOIURL

Recently, flutter active control using linear parameter varying(LPV) framework has attracted a lot of attention. LPV control synthesis usually generates controllers that are at least of the same order as the aeroelastic models. Therefore, the reduced-order model is required by synthesis for avoidance of large computation cost and high-order controller. This paper proposes a new procedure for generation of accurate reduced-order linear time-invariant(LTI) models by using system identification from flutter testing data. The proposed approach is in two steps. The well-known poly-reference least squares complex frequency(p-LSCF) algorithm is firstly employed for modal parameter identification from frequency response measurement. After parameter identification,the dominant physical modes are determined by clear stabilization diagrams and clustering technique. In the second step, with prior knowledge of physical poles, the improved frequencydomain maximum likelihood(ML) estimator is presented for building accurate reduced-order model. Before ML estimation, an improved subspace identification considering the poles constraint is also proposed for initializing the iterative procedure. Finally, the performance of the proposed procedure is validated by real flight flutter test data.
DOIURL [本文引用: 1]

This paper compares four LPV identification methods: local, global, and glocal, for flutter prediction and modeling. Important properties of the methods are highlighted and simulations are performed to compare the performance, using a bending-torsion flutter model from literature. Results show that a trade-off between bias and variance exists for the local and global method, after which a glocal method can further improve performance.
DOIURL [本文引用: 1]

http://arc.aiaa.org/doi/abs/10.2514/3.44322
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
