航天器噪声试验中结构振动响应预示方法研究 1)

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-01

李青²⁾, 邢立坤, 柏江, 邹元杰北京空间飞行器总体设计部,北京 100094

METHOD STUDY ON RESPONSE PREDICTION OF STRUCTURAL VIBRATIONS IN SPACECRAFT ACOUSTIC TESTS ¹⁾

Li Qing²⁾, Xing Likun, Bai Jiang, Zou YuanjieBeijing Institute of Spacecraft System Engineering, Beijing 100094, China

收稿日期:2018-10-16接受日期:2019-01-23网络出版日期:2019-03-18

基金资助:

国家重大科技专项工程资助.

Received:2018-10-16Accepted:2019-01-23Online:2019-03-18
作者简介 About authors
2)李青,高级工程师,主要研究方向：航天器总体设计与仿真、力学分析与环境试验研究.E-mail:lqcast@163.com

摘要
航天器在随运载火箭发射过程中要承受严酷的噪声环境,需通过噪声试验来检验航天器承受噪声环境并能正常工作的能力.航天器噪声试验中结构振动的响应特性是结构强度设计应该考虑的因素之一,更是制定器上组件随机振动试验条件的重要依据,因此有必要在航天器研制初期对噪声载荷作用下的结构振动进行响应预示.文章应用商用有限元分析软件MSC.Patran和MSC.Nastran建立了某型号航天器结构舱板的有限元模型,将噪声载荷声压谱转换为脉动压力功率谱密度,进而采用模态法分析结构在噪声载荷作用下的随机振动响应,并将仿真预示结果与试验结果进行对比研究,在仿真分析中考虑阻尼参数模型和流场附加质量效应等因素的影响;通过研究表明：采用阻尼比随频率提高而减小的经验阻尼参数模型可以较好地反映中高频响应特性、得到较为准确的总均方根响应分析结果,进一步采用虚拟质量法考虑流场附加质量效应可以得到较为准确的功率谱密度响应分析结果.文章提出的仿真分析方法建模简便、计算成本低,适用于在航天器研制初期对航天器噪声试验中的结构振动进行响应预示.
关键词： 噪声试验;随机振动;模态阻尼;虚拟质量法;响应预示

Abstract
Spacecraft suffer severe acoustic environments in the course of launching along with launch vehicles. Acoustic tests should be done to check up whether the spacecraft work well while suffering acoustic environments. Response properties of structural vibrations during acoustic tests for spacecraft should be considered in the structural strength design. Moreover, they are important foundations for specifying the random vibration test conditions of the spacecraft equipment mounted on the structural boards. Therefore, it is necessary to predict the structural responses due to acoustic loads in the preliminary stage of spacecraft development. In this paper, a finite element model of a spacecraft structure is built using the commercial finite element analysis software MSC.Patran and MSC.Nastran. The sound pressure level spectrum of acoustic loads is transformed to the power spectrum density of fluctuating pressure. And then, the random vibration responses of the spacecraft structure under the acoustic loads are analyzed using the modal method. The simulation results are compared with the acoustic test results. In the simulation analysis, the effects of the damping ratio model and the fluid added mass are studied. The research shows that: using an empirical damping ratio model that the damping ratio decreases with the rising of the frequency can do a better response prediction for the medium-high frequency properties as well as for the total root mean square results; further using the virtual mass method to consider the fluid added mass effect can do a better response prediction for the power spectrum density results. The proposed simulation method in the article is convenient for modeling and efficient for computation, which is appropriate for the response prediction of structural vibrations in spacecraft acoustic tests in the preliminary stage of spacecraft development.
Keywords：acoustic tests;random vibrations;modal damping;virtual mass method;response prediction

PDF (11063KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex 收藏本文
本文引用格式
李青, 邢立坤, 柏江, 邹元杰. 航天器噪声试验中结构振动响应预示方法研究 ¹⁾. 力学学报[J], 2019, 51(2): 569-576 DOI:10.6052/0459-1879-18-337
Li Qing, Xing Likun, Bai Jiang, Zou Yuanjie. METHOD STUDY ON RESPONSE PREDICTION OF STRUCTURAL VIBRATIONS IN SPACECRAFT ACOUSTIC TESTS ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2019, 51(2): 569-576 DOI:10.6052/0459-1879-18-337

引言

在大气层内高速运行的物体都会受到气动效应的影响,如高速列车^[1-2]、高速飞行器^[3]等.航天器受到的噪声载荷主要来自于运载火箭发动机的喷气噪声和大气层内飞行的气动噪声^[4],它对航天器结构产生随机振动激励,其频率范围大致为20~2000 Hz^[5].噪声载荷是航天器结构强度设计的输入条件之一,应根据其产生的结构应力分布开展强度裕度分析;同时,噪声载荷作用下航天器结构振动响应对结构舱板上安装的航天器组件产生随机振动激励,需根据响应情况制定组件随机振动试验条件并作为组件开展抗力学设计和力学环境试验的输入条件之一^[6].因此,在航天器研制初期对噪声载荷作用下航天器结构振动进行响应预示具有重要的工程意义.

前人在噪声载荷作用下结构振动响应预示方面做了一些研究工作.文献[7,8]采用半解析的方法分别给出了薄壁板结构和薄壁柱壳结构在噪声载荷作用下的随机振动响应谱估算公式.对于一般构型的结构,业界普遍采用数值仿真分析方法,主要分为有限元分析(FEA)方法和统计能量分析(SEA)方法两种^[9].前者理论上可以计算出结构任意一点的响应并获得响应分布情况,但随着分析频率的提高,网格密度的增加和结构中不确定性因素影响的增加会大幅提高计算成本并降低分析精度^[10],因此不适用于高频段振动响应预示;后者在高频段振动响应预示方面具有理论优势,在面对结构的连接方式、制造工艺等不确定性因素时,不需要复杂精确的模型就可以高效地计算出振动响应的统计平均结果^[11-14],但也正因如此,不能给出具体位置的响应和响应分布情况,并且中低频段计算精度较差^[15].文献[16]采用MSC.Nastran对某飞行器进行了自由——自由状态下的模态分析和气动噪声作用下的随机振动响应分析,并且与模态试验和噪声试验结果作了比较,验证了使用三维有限元模型进行振动环境预示方法的有效性,但在其方法中没有研究模态阻尼参数和流固耦合作用的影响.文献[17]应用AutoSEA2统计能量分析软件对某喷流噪声产生的结构振动进行计算分析,并与试验结果作比较,发现预示结果与试验结果在趋势上大致相当,预示结果高于试验结果,尤其低频段相差较大. 文献[18]采用VA One软件提供的混合有限元——统计能量分析(FE-SEA)方法建立整星级和系统级航天器(整流罩——卫星——仪器舱——适配器组合体)的混合预示模型,将预示结果与噪声试验数据进行对比,验证了预示方法和模型的有效性.FE-SEA方法是目前研究结构声振力学响应问题的热门方法,它集合了有限元分析和统计能量分析的优点,理论上为结构的宽频振动响应分析提供了一种有效手段^[19-22],但在有限元子系统和统计能量子系统的划分问题上没有确定的方法,且划分方法不同对分析结果影响很大^[23].在实际应用中,一般将航天器结构建成有限元子系统、声场建成统计能量子系统,建立结构与声场双向能量流动的耦合界面,这种方法既保留了航天器结构响应细节又大幅缩减了声场的计算量,实质上是一种考虑流固耦合作用^[24]的方法,对航天器结构模型本身面对的高频段计算成本和精度问题并无改善;如果将航天器结构局部或全部建成统计能量子系统,将丢失结构响应细节,则势必会与结构强度设计和组件力学环境条件设计的工程需求产生矛盾;另外,受到软件工具的限制,将航天器结构有限元模型转换为FE-SEA混合模型的过程繁琐、工作量较大. 由于上述原因,FE-SEA方法在航天器研制初期的应用并不广泛.

从机理上讲,噪声载荷作用下航天器结构振动响应预示的难点在于如何选取阻尼参数模型和考虑流固耦合作用,对高于2000 Hz频段的响应预示意义一般不大;从需求上讲,航天器结构关键部位的响应细节是研究的主要对象,必须采用有限元分析方法建模.本工作基于有限元分析方法开展研究,采用MSC.Patran/Nastran有限元软件建立某型号航天器结构舱板有限元分析模型,将噪声试验条件的声压谱转换为脉动压力功率谱密度并施加在该结构舱板上,计算了一些关键部位的随机振动响应,并将计算结果与噪声试验结果进行了对比和分析,研究了阻尼参数模型和流场附加质量效应等因素的影响,以期为航天器噪声试验中结构振动响应预示方法的选用提供参考.

1 有限元分析模型

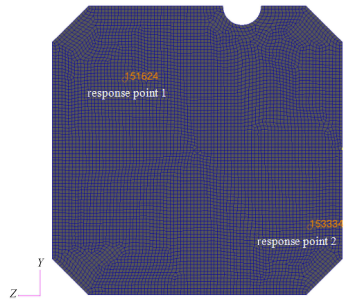
某型号航天器由多个结构舱段组成,首先采用MSC.Patran建立航天器结构的几何模型,然后进行有限元网格划分,主要采用板壳单元和梁单元建模,对于大型组件按其设计状态建成有限元模型、对于小型组件采用集中质量元或非结构质量来模拟,整个有限元模型共有322 604个单元、337 703个结点. 为了减少计算量、便于开展研究,仅针对其中的一块结构舱板进行分析,如图1所示,图中Node 153 334和Node 151 624为关注的两个响应输出点(以下简称为响应点1和响应点2),该舱板与其他舱板的连接边界均处理为固支.

图1

新窗口打开|下载原图ZIP|生成PPT
图1航天器结构舱板有限元模型

Fig.1Finite element model for a spacecraft structure board

采用MSC.Nastran分析程序的模态法(SOL 111)进行频率响应计算,再采用MSC.Patran的Random后处理模块实现随机振动响应计算,计算频率范围为20~2000 Hz,步长为4 Hz,与噪声试验数据的频率范围和步长保持一致.

2 噪声载荷

噪声试验条件按声压谱形式给出,如表1所示.

Table 1
表1
表1噪声试验条件
Table 1Acoustic test conditions

Octave center frequency/	Sound pressure level/	Test tolerance/
Hz	dB	dB
31.5	128	±5.0
63	132	±5.0
125	135	±3.0
250	138	±3.0
500	137	±3.0
1000	136	±3.0
2000	134	±3.0
4000	132	±5.0
8000	130	±5.0
total sound pressure level	144	±1.5

Note： 0 dB reference pressure is 2.0x10^-5Pa.

新窗口打开|下载CSV

为了能采用MSC.Patran/Nastran进行噪声激励下的随机振动响应分析,就必须将声压谱转换为脉动压力功率谱密度,转换公式如下

(1)$ \varphi (f_c) = \frac{P_0^2 }{\Delta f_{\rm c} }10^{0.1 L_{P} }$

式中,$f_{\rm c}$为倍频程带中心频率,$P_{0}$=2.0×10$^{-5}$Pa,$\Delta f_{\rm c}$为倍频程带的带宽,$L_{\rm P}$为倍频程带声压级.

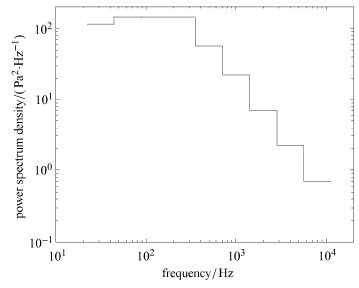
利用转换式(1)将噪声试验条件声压谱的标称值转换为脉动压力功率谱密度曲线,如图2所示. 将其施加在整个结构舱板的表面,计算得到各响应输出点的加速度功率谱密度曲线.

图2

新窗口打开|下载原图ZIP|生成PPT
图2脉动压力功率谱密度曲线

Fig.2Power spectrum density of pulsating pressure

3 阻尼参数模型

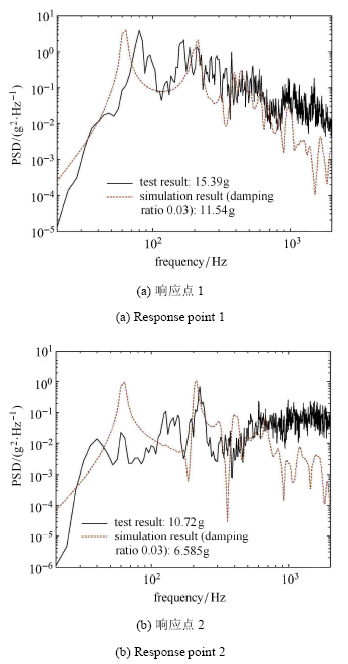
在没有模态试验数据的情况下,频率响应分析中的模态阻尼比一般取常值0.03. 采用该常值阻尼比计算了响应输出点的加速度功率谱密度曲线,并与试验结果进行对比,如图3所示(图中g为重力加速度,本文依照行业习惯用作单位).可见,仿真结果在中高频段明显低于试验结果,并且仿真得到的总均方根加速度也明显低于试验结果.

图3

新窗口打开|下载原图ZIP|生成PPT
图3仿真结果(阻尼比取0.03)与试验结果对比

Fig.3Comparison between simulation results (damping ratio 0.03)-1mm and test results

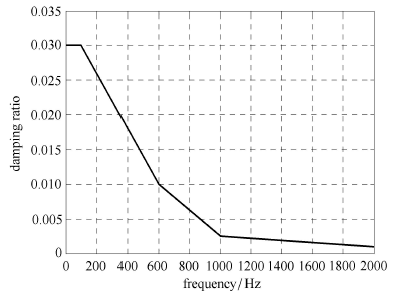
一般来说,结构阻尼会随着振幅的增大而增大^[25-26].而在航天器结构振动中,振幅一般随着振动频率的提高而减小. 因此,采用一个随频率提高而减小的阻尼参数模型是合理的.根据对大量不同型号航天器噪声试验数据的统计分析结果,对于航天器结构的随机振动响应预示建立如图4所示的阻尼参数模型,称为经验阻尼参数模型.

图4

新窗口打开|下载原图ZIP|生成PPT
图4经验阻尼参数模型

Fig.4Empirical damping ratio model

采用该经验阻尼参数模型,重新计算了响应输出点的加速度功率谱密度曲线,并与试验结果进行对比,如图5所示.可见,中高频段的响应曲线符合情况得到明显改善,并且仿真得到的总均方根加速度也与试验结果比较一致,但加速度功率谱密度峰值的预示结果比试验结果高.

图5

新窗口打开|下载原图ZIP|生成PPT
图5仿真结果(使用经验阻尼参数模型)与试验结果对比

Fig.5Comparison between simulation results (using empirical damping ratio model) and test results

4 流场附加质量效应

在上一节的分析中,完全没有考虑流固耦合作用. 本节先从理论上推导流固耦合动力学方程,然后介绍在仿真分析中考虑流固耦合作用的应用方法.

假设流体为无黏、可压缩和小扰动的,固体则考虑为线弹性的,对流固耦合系统的基本方程和边界条件采用加权余量的迦辽金提法,可得到位移——压力格式的有限元方程为^[27]

(2)$$ \left[ \begin{array}{cc} {{\pmb M}_{\rm s} } & 0 {-{\pmb Q}^{\rm T}} & {{\pmb M}_{\rm f} } \end{array} \right]\left[ \begin{array}{c} { \ddot{\pmb u}_{\rm s} } { \ddot{\pmb p}_{\rm f} } \end{array} \right] + \left[ \begin{array}{cc} {{\pmb K }_{\rm s} } & \frac{1}{\rho _{\rm f} }{\pmb Q } 0 & {{\pmb K }_{\rm f} } \end{array} \right]\left[ \begin{array}{c} {{\pmb u }_{\rm s} } {{\pmb p }_{\rm f} } \end{array} \right] = \left[ \begin{array}{c} {{\pmb F}_{\rm s} } 0 \end{array} \right]$$

其中,${\pmb u}_{\rm s}$为固体单元结点位移向量,${\pmb p}_{\rm f}$为流体单元结点压力向量,${\pmb M}_{\rm s}$和${\pmb K}_{\rm s}$分别为固体的质量矩阵和刚度矩阵,${\pmb M}_{\rm f}$和${\pmb K}_{\rm f}$分别为流体的质量矩阵和刚度矩阵,${\pmb Q}$为耦合矩阵,$\rho _{\rm f}$为流体质量密度,${\pmb F}_{\rm s}$为固体外载荷向量.${\pmb M}_{\rm f}$通常由两部分组成,即

(3)$$ {\pmb M}_{\rm f} = {\pmb M}_{{\rm fV}} + {\pmb M}_{{\rm fS}}$$

式中,${\pmb M}_{{\rm fV}}$为由流体可压缩性引起的质量矩阵,${\pmb M}_{{\rm fS}}$为流体自由表面波动引起的质量矩阵.

对于噪声试验所用的混响声场而言,可以假定流体是不可压缩的,同时又不考虑流体自由表面波动的影响,则方程(2)中的${\pmb M}_{\rm f}$项为零,从而可消去流体结点自由度,得到解耦的方程为

(4)$$ ({\pmb M}_{\rm s} + {\pmb M}_{\rm s}^{\rm f} ) \ddot {\pmb u}_{\rm s} + {\pmb K}_{\rm s} {\pmb u}_{\rm s} = {\pmb F}_{\rm s}$$

其中

(5)$$ {\pmb M}_{\rm s}^{\rm f} = \frac{1}{\rho _{\rm f} }{\pmb Q \pmb K}_{\rm f}^{-1} {\pmb Q}^{\rm T}$$

式(5)代表流体对固体的作用,称为附加质量矩阵. 这时流固耦合问题退化为考虑流体附加质量效应的结构动力学问题.

基于上述附加质量理论,MSC.Nastran采用边界元法得到附加质量矩阵,并称之为虚拟质量法(virtual mass method). 下面对虚拟质量法的理论做一个简要介绍^[28].

对于不可压缩、忽略自由表面波动的非黏性流体,流体力学的基本方程可以简化为Laplace方程. 用Helmholtz边界积分法求解Laplace方程,可得到流场边界上任意一点$ {\pmb r}_i$处的速度向量和压力向量分别为

(6)$\dot{\pmb u}_i = \sum_j ∫_{A_j } \frac{\sigma _j {\pmb e}_{ij} }{\left| {{\pmb r}_i-{\pmb r}_j } \right|^2} d A_j$

(7)${\pmb p}_i = \sum_j ∫_{A_j } \frac{\rho \dot {\sigma }_j {\pmb e}_{ij} }{\left| {{\pmb r}_i-{\pmb r}_j } \right|} d A_j$

式中,$\sigma _j$为流场在点${\pmb r}_j$处面元$A_j$上的流体通量,${\pmb e}_{ij}$为从点$j$到点i的单位向量. 将式(6)和式(7)在结构有限元表面进行积分,得到

(8)$ \dot {u } = \chi \sigma$

(9)$F = \varLambda \dot{\sigma}$

式中,矩阵${\pmb \chi }$和${\pmb \varLambda }$为积分系数矩阵,${\pmb F}$为流体作用在结构上的结点力. 联立式(8)和式(9),得到虚拟质量法的附加质量矩阵为

(10)$$ {\pmb M}_{\rm s}^{{\rm vf}} ={\pmb F} \ddot {\pmb u}^{-1} = {\pmb \varLambda }{\pmb \chi }^{-1}$$

虚拟质量法避免了流体单元网格的划分,大大简化了建模过程,有利于工程应用. 该方法已成功用于充液容器液固耦合振动特性的仿真^[29],本节将其用于噪声环境下结构振动特性的仿真.

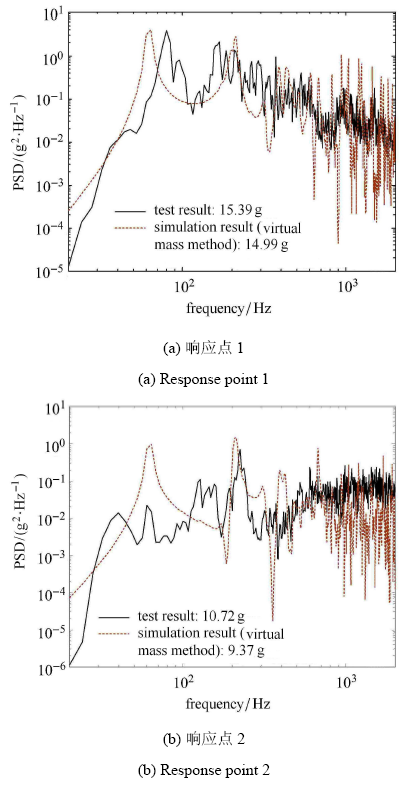
在上节经验阻尼参数模型的基础上,再采用虚拟质量法考虑流场附加质量效应,流体密度取为1.293 kg/m$^{3}$,重新计算响应输出点的加速度功率谱密度曲线,并与试验结果进行对比,如图6所示. 可见,考虑流场附加质量效应后,加速度功率谱密度的预示值有所降低,且与试验结果更为接近.

图6

新窗口打开|下载原图ZIP|生成PPT
图6仿真结果(虚拟质量法)与试验结果对比

Fig.6Comparison between simulation results (virtual mass method) and test results

5 误差分析

为展示响应预示的效果,本文仿真所建立的有限元分析模型并未经过模态试验等数据的修正,毕竟在航天器研制初期这些数据是无法获得的.因此,加速度功率谱密度响应峰频率的预示结果与试验结果存在差异,但这并不影响响应曲线趋势和总均方根值达到较好的一致.将上述仿真结果中的若干关键参数与试验结果的对比分析情况汇总于表2.可见,采用经验阻尼模型后总均方根加速度响应的仿真结果与试验结果的相对误差明显减小;响应点2的总均方根加速度响应的仿真结果普遍小于试验结果,这是因为该点离边界较近,受到固支边界条件的仿真假定影响较大,仿真结果与试验结果的相对误差也较大.另外,不论采用常值阻尼比0.03还是采用经验阻尼参数模型,功率谱密度峰值响应的仿真结果普遍大于试验结果,这是因为所用的模态阻尼无

Table 2
表2
表2仿真结果与试验结果的误差分析
Table 2Error analysis between simulation results and test results

		Simulation results		Test results	Relative error/dB
response point 1	total root mean square acceleration/g	damping ratio 0.03 empirical damping ratio empirical damping ratio & virtual mass method	11.54 16.59 14.99	15.390 15.390 15.390	-2.5010 0.652 2 -0.2287
	peak value of power spectrum density/(g² ? Hz^-1)	damping ratio 0.03 empirical damping ratio empirical damping ratio & virtual mass method	4.77 6.546 4.077	3.890 3.890 3.890	0.203 9 2.260 0 0.203 9
	total root mean square	damping ratio 0.03	6.585	10.72	-4.2330
	acceleration/g	empirical damping ratio	10.37	10.72	-0.2883
response point 2		empirical damping ratio & virtual	9.370	10.72	-1.1690
		mass method
	peak value of power	damping ratio 0.03	1.072	0.7092	1.794 0
	spectrum density/(g² ? Hz^-1)	empirical damping ratio	1.811	0.709 2	4.072 0
		empirical damping ratio & virtual	1.508	0.7092	3.276 0
		mass method

新窗口打开|下载CSV

法反映结构发生模态谐振时随振幅增大阻尼增大的非线性现象.采用虚拟质量法考虑流场附加质量效应后,功率谱密度峰值响应的仿真结果有所下降,仿真结果与试验结果的相对误差有所降低.

6 结论

本文基于MSC.Patran/Nastran软件,建立了噪声载荷作用下航天器结构振动的有限元分析模型,从机理上研究了阻尼参数模型和流场附加质量效应对仿真结果的影响,通过将仿真分析结果与噪声试验结果相比对的方法开展了误差分析和评估. 研究表明：采用随频率升高阻尼比降低的经验阻尼参数模型可以较好地反映中高频响应特性、得到较为准确的总均方根响应分析结果,进一步采用虚拟质量法考虑流场附加质量效应可以得到较为准确的功率谱密度响应分析结果. 文章所提出的仿真分析方法工程适用性强,可用于在航天器研制初期开展噪声环境响应预示,并为结构强度设计和器上组件随机振动试验条件制定提供支持和参考.

The authors have declared that no competing interests exist.

作者已声明无竞争性利益关系。

参考文献原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]

王英学, 高波, 任文强 . 高速铁路隧道缓冲结构气动载荷与结构应力特性分析
力学学报, 2017,49(1):48-54

DOI URL Magsci

高速列车通过隧道时，会引起车隧气动效应.在隧道洞口设置缓冲结构是简便有效的应对措施之一.而缓冲结构一般设置在隧道洞口，列车通过隧道产生气动载荷对该结构的影响也不容忽视.本文采用数值方法，利用Ansys软件的workbench模拟平台，对列车通过隧道产生的气动载荷作用在顶部单开口缓冲结构上的压应力变化进行模拟.研究结果表明：气动载荷所引起的结构附加应力作用明显.当行车速度为350 km/h时，附加应力可以达到80 kPa，而缓冲结构开口周围成为气动载荷附加应力集中区.对于双线隧道，近车壁面与远车壁面的附加压应力规律一致，但近车侧应力值要大于远车侧.与压力波在隧道内的传播特性类似，气动载荷所引起的附加压应力具有往复传播特征.另外，对顶部缓冲结构开口附近出现附加应力集中的原因进行了分析，确定缓冲结构形式是引起应力集中的决定因素.以上结论对隧道洞口缓冲结构的设计及安全巡查具有一定的指导意义.

( Wang

Yingxue

, Gao

, Ren

Wenqiang

. Aerodynamic load and structure stress analysis on hood of high-speed railway tunnel
Chinese Journal of Theoretical and Applied Mechanics, 2017,49(1):48-54 (in Chinese))

DOI URL Magsci

安翼, 莫晃锐, 刘青泉 . 高速列车头型长细比对气动噪声的影响
力学学报, 2017,49(5):985-996

DOI URL

高速列车的头尾车外形对气动噪声具有重要的影响.工程实践中随着车速的增加，车辆头部越来越细长，日本高速磁悬浮列车实践中甚至出现了具有极端长细比的头部形状.本文以讨论头型长细比对列车气动噪声的影响规律为出发点，应用非线性声学求解器(NLAS)和FW–H声学比拟法的混合算法，在3种运行速度下对基于CRH380A高速列车头型概化的4种不同头型长细比的模型车的气动噪声进行了数值模拟.给出了不同头型长细比列车的流场特征、气动阻力和气动噪声.结果表明，列车的气动总阻力随头型长细比的增大而减小，且头型长细比对列车总气动阻力的影响随运行速度的增加而增强.而头型长细比对气动噪声的影响呈现出较为复杂的影响，并不存在单调的影响关系；综合考虑气动阻力和气动噪声，长细比最大的头型综合性能较优，但差异并不显著，因此在不考虑微气压波等因素的条件下，简单增加车头长细比并不一定能带来明显的气动噪声性能提升.

( An

, Mo

Huangrui

, Liu

Qingquan

. Study on the influence of the nose slenderness ratio of high-speed train on the aerodynamic noise
Chinese Journal of Theoretical and Applied Mechanics, 2017,49(5):985-996 (in Chinese))

DOI URL

张子健, 刘云峰, 姜宗林 . 振动激发对高超声速气动力/热影响
力学学报, 2017,49(3):616-626