, 王琪A NUMERICAL METHOD FOR DYNAMICS OF PLANAR MULTI- RIGID-BODY SYSTEM WITH FRICTIONAL TRANSLATIONAL JOINTS BASED ON LUGRE FRICTION MODEL1)
WangXiaojun, WangQi中图分类号:O31
文献标识码:A
收稿日期:2018-07-7
网络出版日期:2019-01-20
版权声明:2019力学学报期刊社力学学报期刊社 所有
基金资助:
作者简介:
-->
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (3665KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
摩擦在机械系统中是普遍存在的,并会影响其动力学特性.人们对摩擦的研究已有几百年的历史,建立了多种摩擦模型,如Coulomb干摩擦模型、修正的Coulomb摩擦模型、Stribeck摩擦模型、Dahl摩擦模型以及LuGre摩擦模型[1- 5].其中,Coulomb干摩擦模型虽然表达形式简单,但该模型描述的摩擦力是接触点相对速度的多值函数,给含摩擦机械系统动力学方程的数值求解带来诸多困难.人们为了避免这些困难,采用了修正的Coulomb摩擦模型描述摩擦力(接触点相对速度的单值函数),但它不能反映摩擦的黏滞状态.LuGre摩擦模型是在Dahl摩擦模型的基础上发展起来,它能有效地揭示摩擦的黏滞-滑移(stick-slip)现象以及Stribeck现象[3-6].
近十年来,人们用多体系统动力学或非光滑动力学的方法研究含摩擦、接触与碰撞等多体系统的动力学特性,在建模方法、数值算法和实验研究等方面取得了一系列成果[7-19],并且在航空航天[20-23]、机械车辆[24 -27]以及土木工程[28-29]等领域得到了广泛应用.最初,研究用修正的Coulomb摩擦模型和多体系统动力学方法,构建含非理想铰(具有间隙与摩擦的转动铰和移动铰)机械多体系统的动力学模型及数值算法,该方法适用于无黏滞状态的机械系统[30].
基于Dahl摩擦模型,PennestrÌ给出了含摩擦转动铰和滑移铰的链状机械系统动力学的建模方法与数值算法[31].在其建模中,将转动铰和滑移铰视为双边约束(忽略铰链的间隙),仅考虑铰链的摩擦;在其数值仿真中,揭示了滑块的黏滞状态,但未揭示滑块在滑道内的多种接触状态.
Flores等[32]用非光滑动力学方法,给出了含非理想(具有间隙与摩擦)滑移铰多体系统动力学的建模方法与数值算法;用Coulomb干摩擦模型描述铰链内的摩擦,基于时间步进法,将非光滑事件(接触与分离,黏滞与滑移)的判断转化为线性互补问题(LCP)的求解;并指出当间隙很小时,数值计算会出现约束的漂移.基于Coulomb干摩擦模型,Zhuang 等[33]给出了含非理想(有摩擦)滑移铰平面多刚体系统动力学的建模方法和数值算法,将滑移铰接触状态的判断以及黏滞与滑移状态的判断转化为水平线性互补问题(HLCP)的求解,并利用Baumgarte约束稳定化方法抑制了约束的漂移;但该方法不能计算滑块对角接触且处于黏滞状态时的摩擦力.
基于LuGre摩擦模型,Muvengei等[34]给出了含非理想(具有间隙与摩擦)转动铰多刚体系统动力学的建模方法与数值算法,并通过数值仿真分析了曲柄滑块机构的动力学行为.Wang等[35]研究含非理想(具有间隙与摩擦)转动铰刚柔耦合多体系统动力学的建模方法与数值算法,运用修正的Coulomb摩擦模型和LuGre摩擦模型描述转动铰内的摩擦,并通过数值仿真分析了曲柄滑块机构的动力学行为.研究结果表明,LuGre摩擦模型与修正的Coulomb摩擦模型相比,能更好地反映摩擦的特性.文献[34,35]的研究内容未涉及含摩擦的滑移铰.
从综述性文献[7,8,9,10,11]可以看出：近年来,关于非理想转动铰的研究成果较多,而关于非理想滑移铰的研究成果较少,一些问题有待作进一步地研究.
本文将给出一种含摩擦滑移铰多体系统动力学的建模方法和数值算法.采用线性互补方法,将滑移铰中的滑块与滑道接触状态的判断及其法向接触力的计算转化为线性互补问题(LCP)的求解,用LuGre摩擦模型描述滑块与滑道间的摩擦;结合约束稳定化方法,应用第一类Lagrange方程建立该多体系统的动力学方程,将线性互补方程与常微分方程的数值算法结合求解其动力学方程,以弥补原有关于含摩擦滑移铰多体系统动力学的建模方法与数值算法中的不足.
1 系统描述及滑移铰模型
设平面多刚体系统由$n$个物体组成,彼此间由理想转动铰和非理想滑移铰连接,设在惯性系中刚体$i$的质心坐标及其转角为${x_{Ci},{y_{Ci},{\theta _i}(i = 1,2, \cdots ,n)$,则 ${{q}}= [x_{C1} ,y_{C1} ,\theta _1 , \cdots ,x_{Cn} ,y_{Cn} ,\theta _n]^{T}$为该系统的位形坐标.滑移铰由滑道和滑块组成,设滑块$j$的长与宽分别为2$a_{j}$和2$b_{j}$,如图1所示.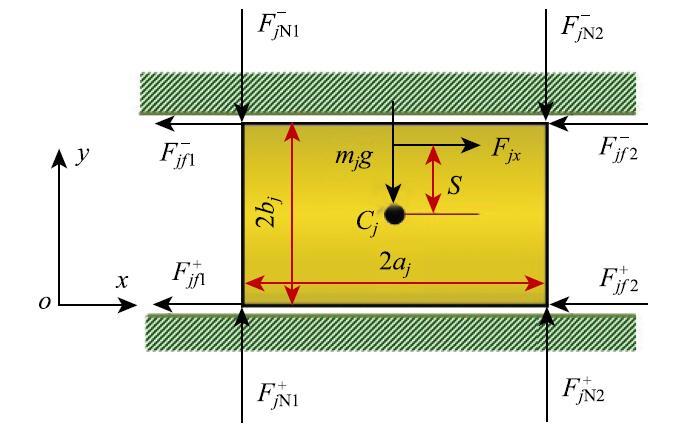
显示原图|下载原图ZIP|生成PPT图 1滑移铰模型...
-->Fig. 1Planar translational joint with tiny clearance...
-->
1.1 法向接触力模型
当间隙充分小,可忽略滑块与轨道间的碰撞,将滑移铰的约束视为双边约束[31];作用在滑块侧边的法向接触力可等效作用在滑块的顶角上[33].设作用在滑块$j$下表面的法向接触力用${F}_{j\,{N1}}^ + ,{{F}}_{j\,{N2}}^ + $表示,作用于上表面的法向接触力用${ {F}}_{j\,{N1}}^-,{{F}}_{j\,{N2}}^ -$表示,如图1和图2所示.当滑块在滑道内运动时,滑道和滑块间可能出现以下几种接触情况[33],如图2所示.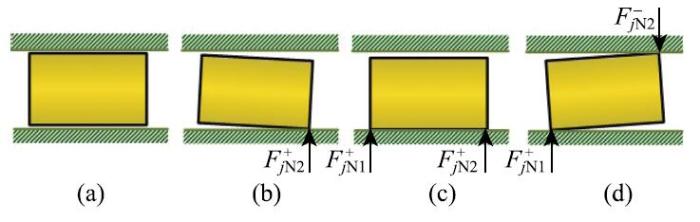
显示原图|下载原图ZIP|生成PPT图 2滑块与滑道间不同的接触状态...
-->Fig.2Different scenarios for the slider and guide interaction...
-->
(a) 无接触状态：滑块上没有法向接触力,即
$$F_{j\,{N}l}^+ = F_{j\,{N}l}^-= 0 ~~(l=1,2)$$
(b) 单点接触状态：滑块上只有一个顶角有法向接触力,即
$$F_{j\,{ N1}}^ + > 0,F_{j\,{N1}}^-= F_{j\,{N2}}^ + = F_{j\,{ N2}}^-= 0$$
or $F_{j\,{N2}}^ + > 0,F_{j\,{N1}}^ + = F_{j\,{ N1}}^-= F_{j\,{N2}}^-= 0$
or $F_{j {N1}}^-> 0$, $F_{j\,{N1}}^ + = F_{j\,{ N2}}^ + = F_{j\,{N2}}^-= 0$
or $F_{j\,{N2}}^-> 0$, $F_{j\,{N1}}^ + = F_{j\,{N2}}^ + = F_{j\,{N1}}^-= 0$
(c) 单面接触状态：滑块的相邻顶角有法向接触力,即$$F_{j\,{ N}l}^ + > 0,F_{j\,{N}l}^-= 0~~~\mbox{or}~~~F_{j\,{N}l}^ + = 0,F_{j\,{N}l}^-> 0~~ (l=1,2)$$
(d) 对角接触状态：滑块对角点上有法向接触力,即
$$ F_{j{\kern 1pt} {N1}}^ + > 0,F_{j {N1}}^-= 0~~{and}~~ F_{j{\kern 1pt} {N2}}^ + = 0,F_{j {N2}}^-> 0$$
or $F_{j {N1}}^ + = 0,F_{j {N1}}^ - > 0$~~ and~~ $F_{j {N2}}^ + > 0,F_{j {N2}}^-= 0$
从图2及上式中可知,无论哪种接触状态,作用于滑块上的法向接触力存在互补关系,即
$$F_{j {N}l}^ + \ge 0,\quad F_{j { N}l}^-\ge 0,\quad F_{j {N}l}^ + \cdot F_{j {N}l}^-= 0\quad (l = 1,2)(1) $$
1.2 切向接触力模型
作用在滑块侧边上的摩擦力可以简化为作用在滑块顶角上,用${F}_{j f{1}}^ + ,{F}_{j f{2}}^ + ,{F}_{j f{1}}^ - ,{F}_{j f{2}}^-$表示,如图1所示.根据LuGre摩擦模型,滑块$j$顶角上受到的摩擦力在滑道上的投影$F_{j{\kern 1pt} f\,l}^ + ,F_{j f\,l}^-$与其法向接触力的大小$F_{j {N}l}^ + ,F_{j {N}l}^-,$有下列关系式[34]$$\left. \begin{array}{lll} {F_{jfl}^ + = \mu _{L} F_{j {N}l}^ +} \\ {F_{jfl}^-= \mu _{L} F_{j {N}l}^ -} \\ \end{array}\quad {(l = 1,2)} \right\}(2) $$
式中,$\mu _{L} = \sigma _0 z + \sigma _1 \dot {z} + \sigma _2 v_{t} $,其中$\sigma _0 $为鬃毛的刚度,$\sigma _1 $为微观阻尼系数,$\sigma _2 $是黏性摩擦系数.鬃毛平均变形量可用下列微分方程表示[34]
$$\dot {z} = \left(1 - \frac{\sigma _0 }{g(v_{t} )}z{sgn}(v_{t})\right)v_{ t}(3) $$
式中, $v_{t} $为接触点的相对速度,$g(v_{t} )$可表达为
$$g(v_{t} ) =\mu + (\mu _0-\mu ){e}^{-\left( {\textstyle{{\left| {v_{t} } \right|} \over {v_{s} }}} \right)^\gamma }(4) $$
式中,$\mu $和$\mu _0 $分别为库伦动摩擦系数和静摩擦系数,$v_{ s} $为Stribeck速度,$\gamma $为依赖速度的摩擦力衰减梯度系数[34].
2 动力学方程及其算法
2.1 动力学方程
设该多体系统具有$s$个理想转动铰和$s^{\ast }$个含摩擦滑移铰, 由局部递推法[33]列写相应的约束方程, 并可表示为下列矩阵形式$${{\tilde {\varPhi }}}({{q}}) = {{\bf 0}}(5)$$
$${{\varPhi }}^\ast ({{q}}) = {{\bf 0}}(6)$$
其中,式(5)为转动铰的约束方程,式(6)为滑移铰的约束方程. 由第一类拉格朗日方程可以得到该系统的动力学方程
$$\left. {\begin{array}{l} {{{{M}\ddot {q}}}} = {{\tilde {\varPhi }}}_q^{T} {{\tilde{\lambda }}} + {{\varPhi }}^{*{T}}_q {{\lambda }}^ * + {{Q}} + {{Q}}_f \\ {{\tilde {\varPhi }}}({{q}}) = {{0}} \\ {{\varPhi }}^ * ({{q}}) = {{0}} \\ \end{array}} \right\}(7) $$
式中,${{M}}$为广义质量矩阵,${{Q}}$, ${{Q}}_f $分别为系统主动力和摩擦力的广义力;${{\tilde {\varPhi }}}_{ { q}}^{T} $, ${{\varPhi }}^{*{T}} _{{ q}} $分别为约束方程(5)和(6)的雅可比矩阵;${{\tilde {\lambda }}} = [\tilde {\lambda }_{1(x)} ,\tilde {\lambda }_{1(y), \cdots ,\tilde {\lambda }_{s(x),\tilde {\lambda }_{s(y)} ]$为拉格朗日乘子列向量,其中$\tilde {\lambda }_{i\,\,(x),\tilde {\lambda }_{i\,\,(y)} (i = 1,2, \cdots ,s)$为约束方程(5)对应的约束力;${{\lambda }}^ * $为对应滑移铰约束方程(6)的拉格朗日乘子列向量：${{\lambda }}^ * = [{{\lambda }}_1^ * ,{{\lambda }}_2^ * , \cdots ,{{ \lambda }}_i^ * , \cdots {{\lambda }}_{s^ * }^ * ]$,其中,${{\lambda }}_i^ * = \left[ {\lambda _{iR_{N} }^ * ,\lambda _{iM_{N} }^ * } \right]^{T}$. $\lambda _{iR_{N} }^ * $和$\lambda _{iM_{N} }^ * $分别为滑块$i$的约束方程${{\varPhi }}_i^ * = \left[ {y_{Ci - b_i ,\;\theta _i } \right]^{T} = {{ 0}}$对应的拉格朗日乘子,其中, $\lambda _{i R_{N} }^ * = F_{i {N}1}^ +-F_{i {N1}}^-+ F_{i {N2}}^ +-F_{i { N2}}^-$为作用在滑块$i$上的法向接触力在$y$轴上投影的代数和. $\lambda _{i M_{N} }^ * =-a_i F_{i {N}1}^ + + a_i F_{i {N}2}^ + \, + a_i F_{i {N}1}^-- a_i F_{i {N}2}^ - $为作用在滑块$i$上的法向接触力对其质心之矩的代数和. 可以将其表达为下列矩阵形式
$${{\lambda }}_i^ * = {{ A}}_{i{\kern 1pt} 1} {{F}}_{i\,\,{N}\,\,}^ + + {{ A}}_{i\,2} {{F}}_{i\, {N}}^ -(8) $$
式中
$${{A}}_{i1} = \left[{\begin{array}{ccc} 1&1 \\ -a_i&a_i \end{array}}\right], {A}_{i2} = \left[{\begin{array}{cc} -1&- 1 \\ a_i &- a_i \\ \end{array}} \right]$$
$$ {{F}}_{i\,\,{N}\,\,}^ + { = }\left[ {{\begin{array}{*{20}c} {F_{i {N}1}^ + } \hfill \\ {F_{i {N}2}^ + } \hfill \\ \end{array} }} \right], {{F}}_{i\,\,{N}\,\,}^-=\left[ {{\begin{array}{*{20}c} {F_{i\,{N}1}^-} \\ {F_{i\,{N}2}^-} \\ \end{array} }} \right] $$
对系统中所有的滑移铰,可以将式(8)写成如下的矩阵形式
$${{ \lambda }}^ * = {{A}}_1 {{F}}_{N}^ + + {{A}}_2 {{F}}_{N}^ -(9) $$
式中
${{A}}_1 = {dig}\left[ {{{A}}_{11} ,{{A}}_{21} , \cdots ,{{A}}_{i1} , \cdots ,{{A}}_{S^ * 1} } \right]$
${{A}}_2 = {dig}\left[ {{{A}}_{12} ,{{A}}_{22} , \cdots ,{{A}}_{i2} , \cdots ,{{A}}_{S^ * 2} } \right]$
${{F}}_{N}^ + = [{{F}}_{{1N1}}^ + ,{{F}}_{{ 1N2}}^ + , \cdots ,{{F}}_{S^ * {N1}}^ + ,{{F}}_{S^ * {N2}}^ + ]^{T}$
${{F}}_{N}^-= [{{F}}_{{1N11}}^-,{{ F}}_{{1N21}}^-, \cdots {{F}}_{S^ * {N1}}^-,{{ F}}_{S^ * {N2}}^-]^{T} $
根据式(2),作用于滑块$i$上的摩擦力可以表达为
$$\left. \begin{array}{lll} {F_{ifl}^ + = \mu _{{L}i} F_{i\,{N}l}^ + } \\ {F_{ifl}^-= \mu _{{L}i} F_{i\,{N}l}^-} \end{array}\quad {(l = 1,2)} \right\}(10) $$
系统中滑移铰摩擦力的广义力可表达为
$${{Q}}_{{f}} = {{ A}}_3 {{F}}_{N}^{{+ }} + {{A}}_4 {{F}}_{ N}^ -(11) $$
其中
${{A}}_{3} = {dig}\left[ {{{ A}}_{{31}} ,{{A}}_{{32}} , \cdots ,{{A}}_{3i} , \cdots ,{{A}}_{3S^ * } } \right]$
${{A}}_4 = {dig}\left[ {{{A}}_{41} ,{{A}}_{42} , \cdots ,{{A}}_{4i} , \cdots ,{{A}}_{4S^ * } } \right] $
$${{A}}_{{3}i} = \left[ {\begin{array}{cccc} -\mu _{{L}i} &-\mu _{{L}i} \\ 0&0 \\ -b_i \mu _{{L}i} &-b_i \mu _{{L}i} \\ 0&0 \\ 0&0 \\ 0&0 \\ \end{array}} \right],\quad {{A}}_{4i} = \left[ {\begin{array}{ccc} -\mu _{{L}i} &-\mu _{{L}i} \\ 0&0 \\ b_i \mu _{{L}i} &b_i \mu _{{L}i} \\ 0&0 \\ 0&0 \\ 0&0 \\ \end{array}} \right](12) $$
2.2 法向接触力的互补方程
应用Baumgarte约束稳定化方法[33,36],方程(7)中的第二式和第三式可分别改写为$${{\ddot {\tilde {\varPhi }} + }}\alpha {{\dot {\tilde {\varPhi }} + }}\beta {{\tilde {\varPhi } = {\bf 0}}}~~~(13) $$
$${{\ddot {\varPhi }}}^ * {{+ }}\alpha {{\dot {\varPhi }}}^ * {{+ }}\beta {{\varPhi }}^ * {{\bf = 0}}(14) $$
其中$\alpha ,\beta $为大于零的常数[36],由上述两式可得
$${{\tilde {\varPhi }}}_{{ q}} {{\ddot {q} + \dot {\tilde {\varPhi }}}}_{{ q}} {{\dot {q} + }}\alpha {{\tilde {\varPhi }}}_{{ q}}^ {{\dot {q} + }}\beta {{\tilde {\varPhi } = {\bf 0}}}~~(15) $$
$${{\varPhi }}_{{ q}}^ * {{\ddot {q} + \dot {\varPhi }}}_{{ q}}^ * {{\dot {q} + }}\alpha {{\varPhi }}_{{ q}}^* {{\dot {q} + }}\beta {{\varPhi }}^ * { {\bf = 0}}(16) $$
其中,${{\tilde {\varPhi }}}_{{ q}} = \partial {{ \tilde {\varPhi }}} / \partial {{q},\;{{\dot {\tilde {\varPhi }}}}_{{ q}} = {d}{{\tilde {\varPhi }}}_{{ q}} / {d}t,\;{{\varPhi }}_{{ q}}^ * = \partial {{\varPhi }}^* / \partial {{q}}$,\ ${{\dot {\varPhi }}}_{{q}}^ * = {d}{{\varPhi }}_{{ q}}^ * / {d}t$.
将动力学方程(7)的第一式改写为
$${{\ddot {q}}} = {{M}}^{ - 1}{{\varPhi }}_q^{ * {T}} {{\lambda }}^ * + {{M}}^{-1}{{ \tilde {\varPhi }}}_q^{T} {{\tilde {\lambda }}} + { { M}}^{-1}{{Q}} + {{M}}^{-1}{{Q}}_f(17) $$
将其代入式(15)可得
$${{\tilde {\lambda }}} =-{{E}}^{ - 1}{{\tilde {\varPhi }}}_{{ q}} {{M}}^{-{1}}{ {Q}}_f-{{E}}^{-1}{{\tilde {\varPhi }}}_{{ q}} {{M}}^{-{1}}{{\varPhi }}_q^{ * {T}} {{\lambda }}^ *-{{E}}^{-1}{ {I}}(18) $$
其中${{I}} = {{\tilde {\varPhi }}}_{{ q}} {{M}}^{ - 1}{{Q}} + {{\dot {\tilde {\varPhi }}}}_{{ q}} { { \dot {q}}} + {{{\alpha} \tilde {\varPhi }}}_{{ q}} { {\dot {q}}} + {{{\beta} \tilde {\varPhi }}}$, ${{ E}} = {{\tilde {\varPhi }}}_{{ q}} {{M}}^{-{ 1}}{{ \tilde {\varPhi }}}_{{ q}}^{T} $, 将式(18)代入动力学方程式(17)后,再代入式(16),可得
$${{B}}_1 {{Q}}_f + {{B}}_1 {{Q}} + {{B}}_2 {{\lambda }}^ * + {{B}}_0 = {{\bf 0}}(19) $$
式中${{B}}_0 = {{\varPhi }}_{{ q}}^ * {{M}}^{ - 1}{{\tilde {\varPhi }}}_q^{T} {{E}}^{-1}(-{{ \dot {\tilde {\varPhi }}}}_{{ q}} {{\dot {q}}}-{{{ \alpha }\tilde {\varPhi }}}_{{ q}} {{\dot {q}}} - {{{\beta} \tilde {\varPhi }}})-{{\dot {\varPhi }}}_{{ q}}^ * {{\dot {q} + {{\beta \varPhi}}}}^ * $,$ {{{{ B}}}_1} = {{\varPhi }}_q^ * {{{M}}^{-1}}(1 - {{\tilde {\varPhi}}}_q^T{{{E}}^{-1}}{{{\tilde {\varPhi} }}_{{ q}}}{{{M}}^{-1}}), {{{B}}_2} = {{\varPhi }}_q^ * {{{M}}^{-1}}(1-{{\tilde {\varPhi} }}_q^{{T}}{{{E}}^{-1}}{{{\tilde {\varPhi} }}_{{ q}}}{{{M}}^{-1}}){{\varPhi }}_q^{ * {{T}}}$.
设${{H}} = {{B}}_1 {{A}}_3 + {{B}}_2 {{ A}}_{1} $,${{H}}_{00} =-{{H}}^{-1}({{B}}_1 {{A}}_4 + {B}_2\cdot \{{A}}_{2} )$,${{B}} =-{{H}}^{-1}({{B}}_1 {{Q}} + {{ B}}_0 )$,将式(9)和式(11)代入式(19),可以得到作用在滑块上法向接触力的互补方程
$${{F}}_{N}^ + = {{H}}_{00} {{F}}_{N}^-+ {{B}} (20) $$
$${{F}}_{N}^ + \ge 0,\quad {{F}}_{N}^-\ge 0,\quad \left( {{{F}}_{N}^ + } \right)^{T}{{F}}_{N}^ - = 0(21) $$
用线性互补的数值计算方法求解上式,可得作用在滑块上的法向接触力,并可得知各个滑块的接触状态.
2.3 动力学方程的算法
步骤1：给定系统的参数、仿真时间$t_{ end}$和系统的初始条件${ {q}}_0 ,{{\dot {q}}}_0 ,z_0 $.步骤2：计算${{M},{{\tilde {\varPhi }},{{\tilde {\varPhi }}}_{{ q}} ,{{\dot {\tilde {\varPhi }}}}_{ { q}} ,{{\varPhi }}^ * ,{{\varPhi }}_{{ q}}^ * ,{{\dot {\varPhi }}}_{{ q}}^ * $,并得到${{H}}_{00} ,{{B}}$.
步骤3：应用线性互补问题的数值算法, 由式(20)和式(21)求解出作用在所有滑块上的法向接触力$F_{i{N}l}^ + ,F_{i{N}l}^-\,(l = 1,2,i= 1, 2,\cdots, s^\ast )$;再由式(10)计算出对应的摩擦力$F_{ifl}^ + ,F_{ifl}^-\,(l = 1,2; i = 1, 2, \cdots ,s\ast )$.
步骤4：由式(9)和式(18)计算${{\lambda }}^ *,{\tilde {\lambda}}$;将计算结果代入式(17),应用常微分方程的数值算法联立求解方程(17)和式(3)得到${ {q},{{\dot {q}, z$.
步骤5：如果$t \le t_{end} $,转到步骤2,将${{ q},{{\dot {q}},z$代入并计算相关矩阵;如果$t > t_{end} $,结束计算.
3 算例
在本文的算例中,LuGre摩擦模型中的相关参数以及Baumgarte违约修正参数的取值参考了文献[34, 36]的相关数据,具体参数取值如下： $\sigma _0 = 1.3\times 10^6\;{N} / {m, \sigma _1 = 350\,{N}\cdot{s / m}, \sigma _2 = 0\,{N}\cdot{s / m, \mu = 0.56, \mu _0 = 0.75, \gamma = 2.0, v_{s} = 0.000~9\,{m / s}; \alpha = 10^6,\beta {= }1.414\times 10^6;$ 数值仿真的计算步长$h = 1.0\times 10^{-6}$.3.1 算例1
===图1所示系统中,均质滑块的质量$m = 2.0~{ kg}$、长为2$a$、宽为2$b$,在水平主动力$F_x $的作用由静止开始沿水平滑道($x$轴方向)运动.情况1：$a = 0.3~{ m}$, $b = 0.1~{ m}$, $S$=0 m, $F_x = 15.5\sin (0.5t)~{N}$.
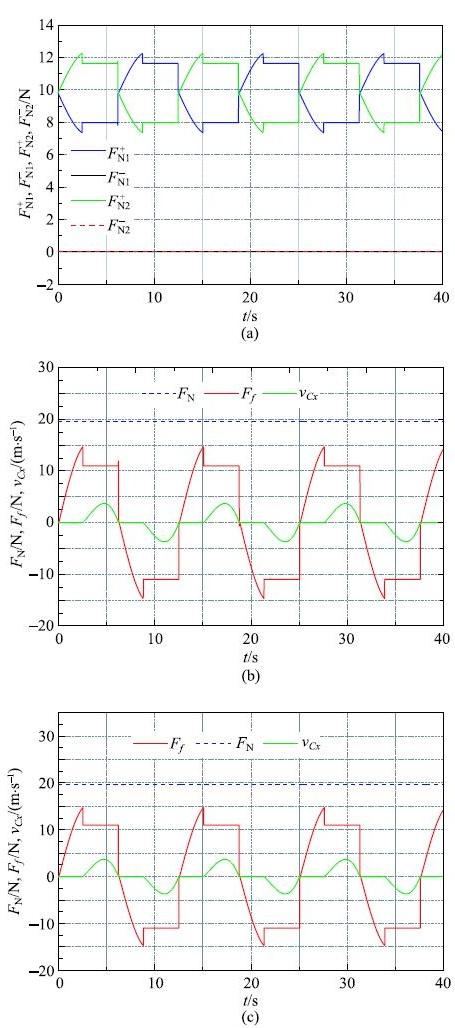
===图3给出了作用于滑块上法向接触力、摩擦力以及滑块沿$x$轴方向运动速度$v_{Cx} $的时间历程. 从图3(a)中可知$F_{{N1}}^-= F_{{N2}}^-= 0$,$F_{{N1}}^{ + } > 0,F_{{N2}}^{ + } > 0$,这表明滑块只有下表面与滑道接触,还进一步表明了法向接触力的互补关系.
显示原图|下载原图ZIP|生成PPT图 3情况1中作用在滑块上法向约束力、摩擦力和滑块移动速度的时间历程...
-->Fig.3Time history of normal and frictional forces on the slider and its translational speed in case 1...
-->
在图3(b)中, 设：$F_{N} = F_{{N1}}^ + + F_{{N2}}^ + - F_{{N1}}^-- F_{{N2}}^-$,$F_f = F_{f{1}}^ + + F_{f{2}}^ + { + }F_{f{1}}^-+ F_{f{2}}^ - $,由该图可知,由于滑块无铅垂方向的运动,即$y \equiv 0$,因此有$F_N = mg$为常值;从图3(b)还可知,滑块出现了stick-slip运动现象,当滑块处于slip状态时,摩擦力是常值;当滑块处于stick状态时,摩擦力的值小于等于最大摩擦力的值. 图3(c)是用Coulomb摩擦模型和试算法计算所得的结果,与图3(b)的结果一致.
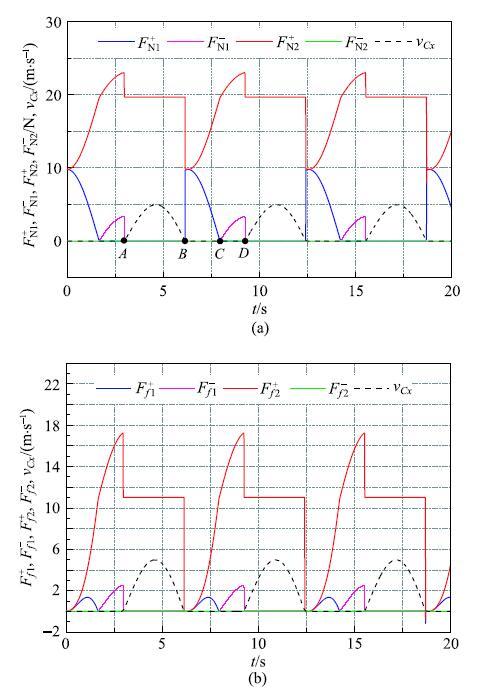
显示原图|下载原图ZIP|生成PPT图 4情况2中作用在滑块上法向约束力、摩擦力和滑块移动速度的时间历程...
-->Fig.4Time history of normal and frictional forces on the slider and its translational speed in case 2...
-->
情况2：$a = 0.3~{ m}$, $b = 0.54~{m}$,$S$=0 m, $F_x = 20\sin ^2(0.5t)~{N}$.
图4给出了滑块的移动速度$v_{Cx}$及其各接触点的法向接触力和摩擦力的时间历程.根据法向接触力是否为零,可以判断滑块的接触状态,从图4(a)可以看出：滑块有3种接触状态出现,并且有stick-slip运动现象.其中：区间 AB对应的是单点接触且处于slip状态;区间BC对应的是单面接触(滑块下表面与滑道接触)且处于stick状态;区间CD对应是滑块上边和下边的两个对角点与滑道接触且处于stick状态.从图4(b)可以看出,本文的方法可以计算各种接触状态时的摩擦力(文献[33]给出的方法无法计算对角接触且处于stick状态时的摩擦力).
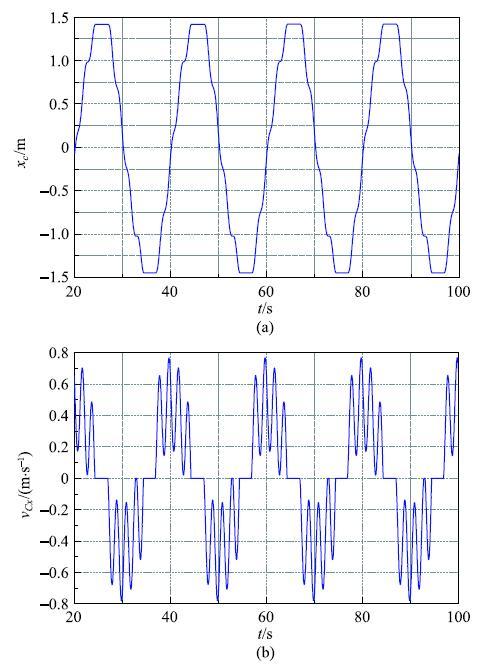
显示原图|下载原图ZIP|生成PPT图 5情况3中滑块$x_{C}$和$v_{Cx}$的时间历程图...
-->Fig.5Time history of $x_{C }$ and $v_{Cx }$of the slider in case 3...
-->
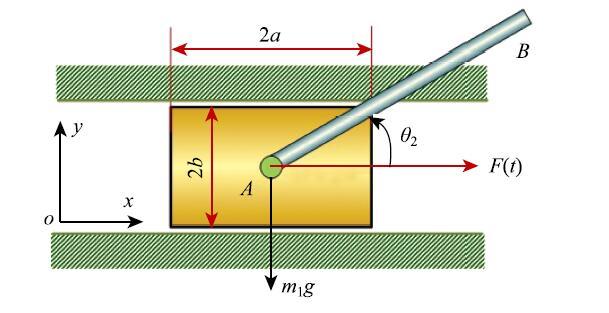
显示原图|下载原图ZIP|生成PPT图 6滑块摆杆机构...
-->Fig.6Slider-pendulum system...
-->
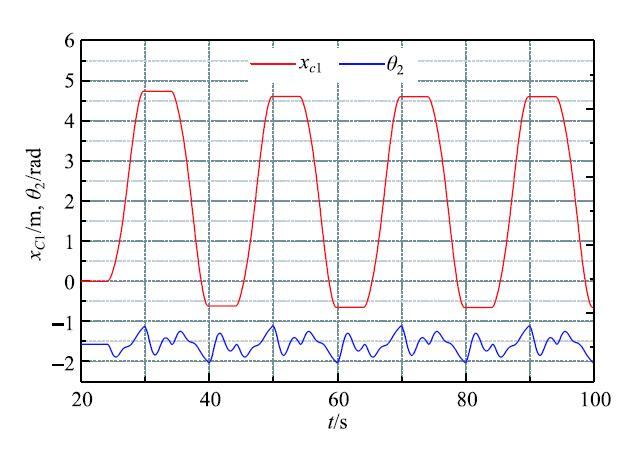
显示原图|下载原图ZIP|生成PPT图 7滑块$x_{C1} $和摆杆$\theta _2 $的时间历程...
-->Fig.7Time history of slider's $x_{C1} $and pendulum's...
-->
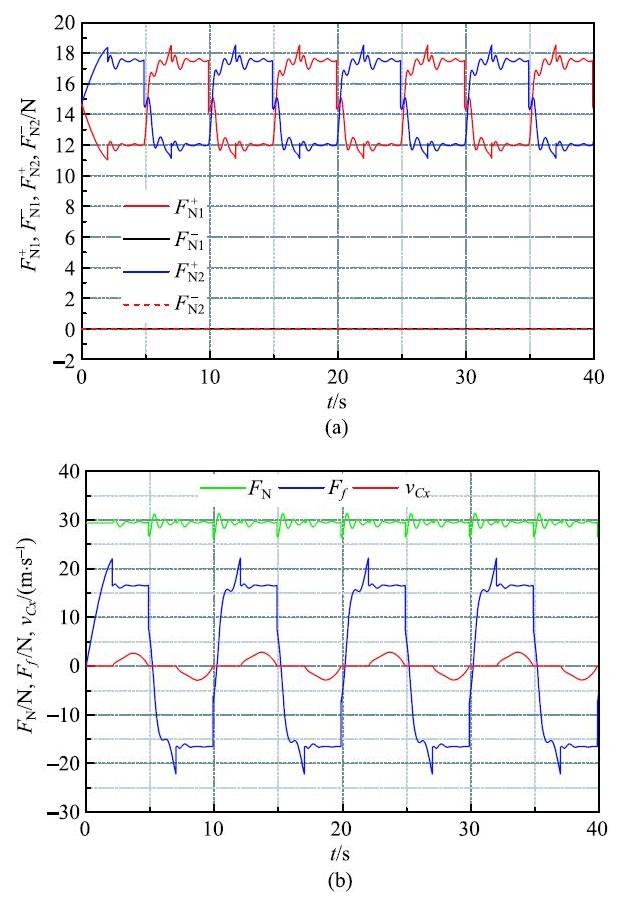
显示原图|下载原图ZIP|生成PPT图 8法向接触力和摩擦力的时间历程...
-->Fig.8Time history of normal and frictional forces on the slider...
-->
情况3：用本文的方法仿真文献[33]中的算例1.
图5给出了滑块质心的水平坐标$x_C $及其滑移速度$v_{Cx} $的时间历程,本文的仿真结果与文献[33]的结果完全相同.
算例2
质量为$m_1 $的均质滑块,其质心作用有水平主动力$F(t) = A_0 \sin (\omega t)$,可在非光滑的水平滑道内移动;质量为$m_2 $、长为2$L$的均质摆杆AB通过理想柱铰链与滑块的质心连接,如图6所示.设摆杆在运动过程中还受到阻力矩$M_{R} =-c_2 \dot {\theta }_2 $的作用.
设系统参数为: $m_1 = 1.0~{kg}$, $m_2 = 2.0~{kg,~ a = 0.3~{ m}$, $b = 0.1~{ m}$, $L = 0.5~{m}$, $A_0 = 23.0~{N}$, $\omega = \pi / 5$, $c_2 = 0.8~{N} \cdot { m} \cdot {s}$;初始条件：$\theta _2 =-0.5\pi $,系统由静止开始运动.
===图7给出了滑块质心坐标$x_{C1} $和摆杆摆角$\theta _2 $的时间历程,由图可知,滑块和摆杆均作周期运动,且滑块出现了stick-slip运动现象.
===图8给出了滑块上下面法向接触力和摩擦力的时间历程. 从图8(a)中可以看出,$F_{{N}1}^ + > 0,F_{{N}2}^ + > 0$, $F_{{N}1}^-= F_{{N}2}^-= 0$;由此可知,滑块只有下表面与滑道接触. 由图8(b)可知,因摆杆的摆动,作用于滑块下表面的法向支撑力不再等于滑块与摆杆重力之和,而在$(m_1 + m_2 )g$附近变动;由于支撑力不是常值,导致摩擦力也随之变化,由该图也可以看出滑块的stick-slip运动现象.
数值仿真结果表明,利用约束稳定化方法,可有效抑制约束的漂移：$\left| {\theta _1 } \right| \le 1.4\times 10^{{-}20}~{ rad}$,$\sqrt {{\tilde {\varPhi }}_1^2 + {\tilde {\varPhi }}_2^2 + {\varPhi }_2^{* 2} } \le 2.1\times 10^{-13}$m.
同样,用Coulomb干摩擦模型和试算法对该算例进行了数值仿真,仿真结果与图示结果完全相同.
4 结 论
针对含摩擦非理想滑移铰,本文基于LuGre摩擦模型(具有单值性和连续性且能反映stick-slip运动),结合线性互补方法,建立了滑移铰中滑块法向接触力的互补关系,将滑移铰接触状态的判断以及法向接触力的计算转换为线性互补问题的求解.本文给出的方法与文献[33]的方法相比,降低了线性互补方程的维数,提高了计算效率(避免了黏滞-滑移状态的判断),并可计算滑块对角接触且处于黏滞状态时接触点的摩擦力(若用Coulomb干摩擦模型,在该状态下摩擦力的解不唯一).本文为含摩擦滑移铰多体系统动力学的研究提供了一个新的建模方法和数值算法.通过数值仿真,揭示了含摩擦滑移铰的动力学特性.用本文方法算得的结果与用Coulomb干摩擦模型及试算法算得的结果进行对比,仿真结果完全吻合,说明了本文方法的有效性.值得指出的是,Coulomb干摩擦模型的特点是形式简单,动、静摩擦系数易于获得,但用该模型描述的摩擦力不是相对速度的单值函数(在相对速度为零时),对于某些含多点摩擦的多体系统动力学数值仿真带来一定困难.LuGre摩擦模型的特点是形式比较复杂(用微分方程的形式给出),但能反映摩擦的stick-slip现象;该模型的参数较多,有些参数不易获得;由于$\sigma_0 $和$\sigma _1$的值较大,须在数值仿真时取较小的计算步长,降低了数值仿真的效率.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . . |
| [2] | . . |
| [3] | . |
| [4] | . |
| [5] | . |
| [6] | . |
| [7] | . . |
| [8] | . . |
| [9] | . . |
| [10] | . . |
| [11] | . |
| [12] | . . |
| [13] | . |
| [14] | . . |
| [15] | . |
| [16] | . |
| [17] | . |
| [18] | . . |
| [19] | . . |
| [20] | . . |
| [21] | . |
| [22] | . . |
| [23] | . . |
| [24] | . . |
| [25] | . |
| [26] | . |
| [27] | . . |
| [28] | . . |
| [29] | . |
| [30] | . |
| [31] | . |
| [32] | . |
| [33] | . |
| [34] | . |
| [35] | . |
