, 崔洋洋, 佟安北方工业大学土木工程学院,北京 100144
STRUCTURAL DYNAMIC AND STABILITY ANALYSIS OF A STRIPPED SOLAR SAIL1)
ZhangJunhui, CuiYangyang, TongAn中图分类号:V414.1
文献标识码:A
版权声明:2019力学学报期刊社力学学报期刊社 所有
基金资助:
作者简介:
-->
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (3770KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
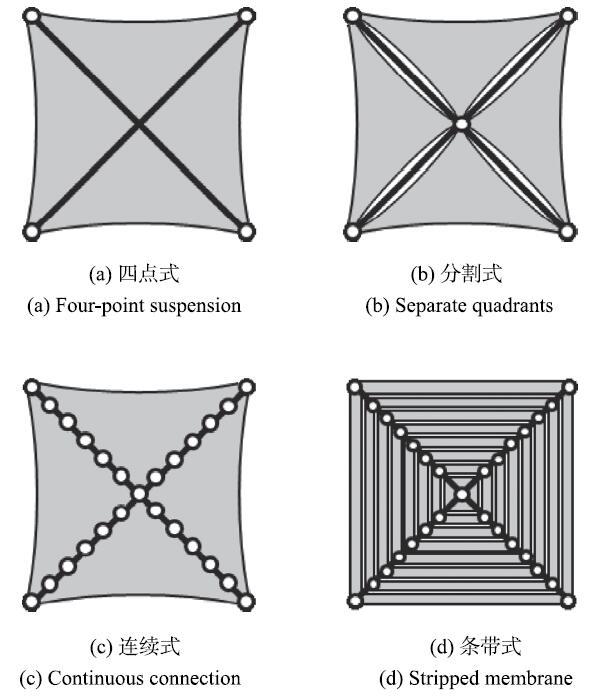
光对被照射物体的压力称为光压.依靠光压推进的太阳帆航天器,无需携带推进剂,具有无穷大的比冲,被认为是最可行的星际探测航天器[1].日本IKAROS号太阳帆[2](2010年)和美国Nanosail-D号太阳帆[3](2011年)的相继成功发射,把人类星际旅行的梦想照进了现实.太阳光压非常微弱,为了获得足够的推进力,太阳帆必须具有面积很大的薄膜帆面.按照展开和维持帆面构型的方式,太阳帆可分为无桅杆式和有桅杆式两种,它们各有利弊,通常认为有桅杆式太阳帆具有展开可靠性高,姿态控制简单和消耗控制能量小等优点[1].按照帆面与桅杆的连接方式,有桅杆式太阳帆方案又有：四点式(图1(a)),分割式(图1(b)),连续式(图1(c))和条带式(图1(d))等[4].与图1(a)$\sim$图1(c)所示的将帆面薄膜整体连接到桅杆上不同,条带式太阳帆(图1(d))将帆面薄膜裁成若干独立的窄条,依次连接在对角桅杆上.条带式太阳帆可以有效减小帆面薄膜褶皱面积、提高帆面反射效率、改善桅杆受力、降低空间碎片危害,被认为是最理想的太阳帆构型,十分具有研究价值[5].
目前,我国在太阳帆总体方案[6-7]、轨道设计[8 -12]、姿态控制[13-16]、帆面薄膜材料制备[17 -18]和帆面展开[19 -21]等方面都进行了不同程度的研究,成果较为丰富,但关于太阳帆结构分析方面的研究还十分薄弱.郭红军等[22]对自主设计的太阳帆在太阳光线平行和垂直两种姿态下进行了模态分析,获得了太阳帆在两种姿态下的固有频率和振型.马鑫等[23]给出了太阳帆支撑桅杆的屈曲模态和临界屈曲载荷,进行了太阳帆结构的无预紧力和有预紧力结构模态分析,为太阳帆姿态控制设计提供了参考数据.李纯等[24]对比分析了膜面应力导入方式对膜面应力分布以及膜面应力大小对帆面形态和结构刚度的影响,获得了膜面应力与桅杆轴压之间的关系.崔乃刚等[25]应用矢量力学基本原理,推导出考虑桅杆弹性振动的基于控制叶片和控制杆的两类太阳帆航天器的姿态动力学方程.张瑾等[26]研究了控制叶片和控制杆两种控制方法下太阳帆柔性结构对太阳帆大角度机动的影响,建立了太阳帆轨道-姿态-弹性振动耦合的动力学降阶模型.
显示原图|下载原图ZIP|生成PPT图1太阳帆构型...
-->Fig. 1Solar sail suspension patterns
-->
在国外,Holland等[27]研究了桅杆轴压对一个边长2m太阳帆整体结构模态的影响,结果表明桅杆轴压明显改变了太阳帆整体结构的前两阶频率.Sleight等[28]采用有限元数值分析方法对分割式和连续式太阳帆结构进行了参数研究,研究了结构尺寸、帆膜预紧力、帆膜厚度和桅杆刚度对结构变形、桅杆载荷和结构频率的影响.Sleight等[29]还对一个边长10m的太阳帆进行了静力加载和动态测试实验,获得了帆面变形的加载曲线和结构整体的模态结果,并分别采用有限元软件Nastran和Abaqus对实验结果进行了分析.Sakamoto等[30]采用非线性有限元方法,研究了帆面变形与太阳帆结构载荷之间的耦合影响.Stanciulescu等[31]对比研究了两种太阳帆桅杆结构的屈曲载荷和动态特性,在分析过程中重点关注了桅杆的后屈曲行为.美国宇航局兰利研究中心进行了比较全面的太阳帆结构实验方面的研究,对太阳帆分别进行了组件级和系统级的地面真空实验和非真空实验,用实验结果验证太阳帆理论模型的正确性[32].
综上,一方面,目前国内外对太阳帆结构的动力学特性方面的研究局限于四点式、分割式和连续式等多点连接式太阳帆构型,而对于具有理想结构效率的条带式太阳帆的结构分析未见报道;另一方面,对太阳帆这种超薄、超大、超轻的非常规结构,现有研究采用的大都是有限元等数值分析方法,存在精度不高,数值稳定性差等问题.因此,本文针对条带式太阳帆结构进行研究,建立考虑薄膜条带与支撑桅杆耦合振动的条带式太阳帆结构动力学理论模型,推导条带式太阳帆结构自由振动和屈曲载荷的求解方法,为条带式太阳帆的结构设计和姿态控制提供理论基础.
1 理论模型
图2所示为一个边长为$L$的正方形条带式太阳帆,相互独立的若干帆面薄膜条带(简称膜带)由4根对角桅杆支撑.总体坐标系$\left( {O,X,Y,Z}\right)$将太阳帆分为4个象限,每个象限有$n$条宽度为$b$的膜带,如图在第$j$象限的第$i$条膜带上建立膜带局部坐标轴$\xi _{i,j} \left( {i = 1,2, \cdots ,n;j =1,2,3,4} \right)$.每根对角桅杆被膜带划分为$n$个长度为$l$的小桅杆段,如图在第$j$根桅杆的第$i$个桅杆段上建立桅杆段局部坐标轴$x_{i,j}\left( {i = 1,2, \cdots ,n;j = 1,2,3,4} \right)$.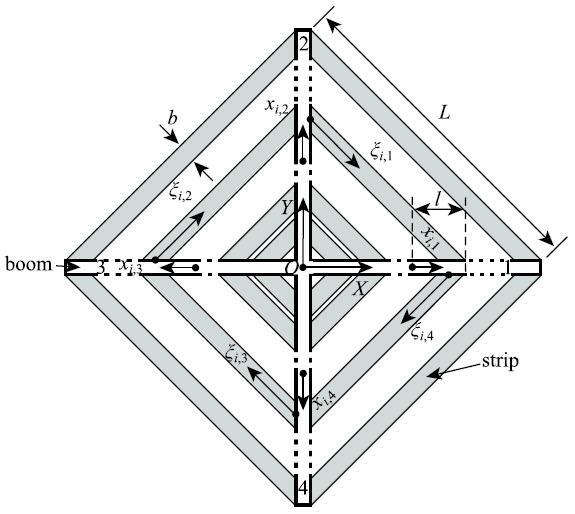
显示原图|下载原图ZIP|生成PPT图2条带式太阳帆...
-->Fig.2Stripped solar sail
-->
为了表述方便,分别用桅杆段局部坐标轴$x_{i,j} $和膜带局部坐标轴$\xi_{i,j}$指代相应的桅杆段和膜带,具有相同$i$下标的4个桅杆段和4条膜带($x_{i,j = 1,2,3,4} $和$\xi _{i,j = 1,2,3,4} )$被合称为第$i$个桅杆-膜带组件,这样,条带式太阳帆可看作是由$n$个桅杆-膜带组件依次连接而成的整体结构.
1.1 桅杆-膜带组件的动力学方程
由于膜带中的预应力,假设单条膜带对桅杆的拉力为$P$,则第$i$个桅杆-膜带组件中桅杆段承受的轴压为$\left({n-i + 1} \right)\sqrt 2P$,根据欧拉-伯努利梁理论,桅杆-膜带组件中四个桅杆段的运动方程为$$ EIw_{i,j}^{\left( 4 \right)} \left( {x_{i,j} ,t} \right) + \left( {n-i +1} \right)\sqrt 2 P{w}"_{i,j} \left( {x_{i,j} ,t} \right) +\\\qquad \rho _{b} \ddot {w}_{i,j} \left( {x_{i,j} ,t} \right)\!=\! 0 \quad {\left( {0 < x_{i,j} < l;j \!=\! 1,2,3,4}\right)}\quad \tag{1}$$
式中,$E$为桅杆的弹性模量,$I$为桅杆的截面惯性矩,$\rho _{b}$为桅杆的密度,$t$为时间,$l$为桅杆段的长度,$w_{i,j}$为桅杆段在垂直太阳帆膜面方向的位移,$w_{i,j}^{\left( 4 \right)}$表示$w_{i,j} $对$x_{i,j} $的四阶偏导数,${w}"_{i,j}$表示$w_{i,j} $对$x_{i,j} $的二阶偏导数,$\ddot {w}_{i,j}$表示$w_{i,j} $对$t$的二阶偏导数.
考虑零初始条件,对(1)式进行Laplace变换
$$EI\tilde {w}_{i,j}^{\left( 4 \right)} \left( {x_{i,j} ,s} \right) + \left({n-i + 1} \right)\sqrt 2 P\tilde {{w}"}_{i,j} \left( {x_{i,j},s} \right)+\\ \qquad s^2\rho _{b} \tilde {w}_{i,j} \left( {x_{i,j} ,s}\right)\! =\! 0\quad {\left( {0 \!<\! x_{i,j} \!<\! l;j \!=\!1,2,3,4} \right)}\quad \tag{2}$$
式中,$s$为复参量,$\tilde {w}_{i,j} $为$w_{i,j} $的Laplace变换.
定义状态向量
\begin{equation}\label{eq3} {\eta}_i = \left[\!\! {{\begin{array}{*{20}c} {\tilde {w}_{i,1} } ~~ {{\tilde {w}}'_{i,1} } ~~ {{\tilde{w}}"_{i,1} } ~~ {{\tilde {w}}"'_{i,1} } ~~ \cdots ~~ {\tilde{w}_{i,4} } ~~ {{\tilde {w}}'_{i,4} } ~~ {{\tilde{w}}"_{i,4} } ~~ {{\tilde {w}}"'_{i,4} } \\\end{array} }}\!\! \right]^{T} \tag{3}\end{equation}
则式(2)可表示为状态方程形式
\begin{equation}\label{eq4} {{\eta }'}_i = {{F}}_i \left( s \right){{\eta }}_i \tag{4}\end{equation}
式中
\begin{equation}\hspace{-15.8mm} {{F}}_i \left( s \right) = \left[{{\begin{array}{*{20}c} {{{f}}_i \left( s \right)} 0 0 0\\ 0 {{{f}}_i \left( s \right)} 0 0\\ 0 0 {{{f}}_i \left( s \right)} 0\\ 0 0 0 {{{f}}_i \left( s \right)}\\\end{array} }} \right] \tag{5{a}}\end{equation}
\begin{equation}\label{eq6} {{f}}_i \left( s \right) = \left[{{\begin{array}{*{20}c} 0 1 0 0 \\ 0 0 1 0 \\ 0 0 0 1 \\ {-\dfrac{\rho _{b} }{EI}s^2} 0 {-\dfrac{\left( {n-i +1} \right)\sqrt 2 P}{EI}} 0 \\\end{array} }} \right] \tag{5{b}}\end{equation}
根据分布参数传递函数法[33-34],式(4)的精确解析解为
\begin{equation}\label{eq7} {\begin{array}{*{20}c} {{{\eta }}_i = {e}^{{{F}}_i \left( s \right)x_i }{{\eta }}_i \left( {0,s} \right)} & {\left( {0 < x_i < l} \right)} \\\end{array} } \tag{6}\end{equation}
由于膜带的截面尺寸远小于其长度,第$i$个桅杆-膜带组件中膜带的振动可看作是张力为$P$的弦振动
$${c^2{u}"_{i,j} \left( {\xi _{i,j} ,t} \right)-\ddot{u}_{i,j} \left({\xi _{i,j} ,t} \right) = 0}\\ \qquad {(0 < \xi _{i,j} < i\sqrt 2 l;j = 1,2,3,4)} \tag{7}$$
式中,$u_{i,j} $为膜带在垂直太阳帆膜面方向的离面位移,$c = \sqrt{P / \rho _{s} } $,$\rho _{s} $为膜带的密度.
考虑到膜带两端与桅杆连接的位移边界条件
\begin{equation}\label{eq9} \begin{array}{l} {u_{i,j} \left( {0,t} \right) = w_{i,j + 1} \left( {l,t} \right)} \\ {u_{i,j} \left( {i\sqrt 2 l,t} \right) = w_{i,j} \left( {l,t} \right)} \\\end{array} \quad {\left( {j\mbox{ = 1,2,3,4}} \right)} \Bigg\} \tag{8}\end{equation}
式中,$w_{i,5} \left( {l,t} \right) = w_{i,1} \left( {l,t}\right)$.
采用分离变量法,膜带振动方程式(7)的解为
$$u_{i,j} \left( {\xi _{i,j} ,t} \right) =w_{i,j} \left( {l,t} \right)\cos \dfrac{\omega \xi _{i,j} }{c} + \\\qquad \left( {\begin{array}{l} w_{i,j} \left( {l,t} \right)\csc \dfrac{\omega i\sqrt 2 l}{c} \\[3mm]-w_{i,j + 1} \left( {l,t} \right)\cot \dfrac{\omega i\sqrt 2 l}{c} \\ \end{array}} \right)\sin \dfrac{\omega \xi _{i,j} }{c} \tag{9}$$
式中,$\omega $为结构振动的固有频率.
1.2 条带式太阳帆的动力学方程}
将桅杆-膜带组件依次连接组成条带式太阳帆整体结构,在相邻的两个桅杆-膜带组件的4个连接点处应满足变形协调条件和力平衡条件,第$i$个桅杆-膜带组件与第$i+ 1$个桅杆-膜带组件在连接点处应满足：(1)位移相等
\begin{equation}\label{eq11} {\begin{array}{*{20}c} {\tilde {w}_{i,j} \left( {l,s} \right) = \tilde {w}_{i + 1,j} \left( {0,s}\right)} & {\left( {j = 1,2,3,4} \right)} \\\end{array} } \tag{10{a}}\end{equation}
(2)转角相等
\begin{equation}\label{eq12} {\begin{array}{*{20}c} {{\tilde {w}}'_{i,j} \left( {l,s} \right) = {\tilde {w}}'_{i + 1,j} \left({0,s} \right)} & {\left( {j = 1,2,3,4} \right)} \\\end{array} } \tag{10{b}}\end{equation}
(3)弯矩平衡
\begin{equation}\label{eq13} {\begin{array}{*{20}c} {EI{\tilde {w}}"_{i,j} \left( {l,s} \right) = EI{\tilde {w}}"_{i + 1,j}\left( {0,s} \right)} & {\left( {j = 1,2,3,4} \right)} \\\end{array} } \tag{10{c}}\end{equation}
(4)剪力平衡
\begin{equation}\label{eq14} {\begin{array}{l} T_{i,j-1} \left( {0,s} \right) + T_{i,j} \left( {i\sqrt 2 l,s} \right) +\\\qquad EI{\tilde {w}}"'_{i,j} \left( {l,s} \right)-EI{\tilde{w}}"'_{i + 1,j}\left( {0,s} \right) = 0 \quad {\left( {j = 1,2,3,4} \right)} \\\end{array} } \tag{10{d}}\end{equation}
式中,$T_{i,0} \left( {0,s} \right) = T_{i,4} \left( {0,s}\right)$;$T_{i,j} \left( {0,s} \right)$和$T_{i,j} \left( {i\sqrt2 l,s}\right)$分别表示因膜带振动在膜带两端引起的剪力,可由式(9)求得
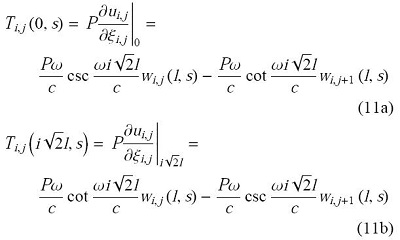
式(10)所列的桅杆-膜带组件连接条件可表示为矩阵形式
\begin{equation}\label{eq17} {{C}}_i {{\eta }}_i \left( {l,s} \right) ={{D}}_i {{\eta }}_{i + 1} \left( {0,s} \right)\tag{12}\end{equation}
式中,${{C}}_i $和${{D}}_i $为转换矩阵.
由式(6)和式(12),有
\begin{equation}\label{eq18} {{\eta }}_{i + 1} \left( {0,s} \right) = {{D}}_i^{-1} {{C}}_i {e}^{{{F}}_i \left( s\right)l}{{\eta }}_i \left( {0,s} \right) \tag{13}\end{equation}
反复利用式(13),可得
\begin{equation}\label{eq19} {{\eta }}_n \left( {0,s} \right) = {{Q}}_n\left( s \right){{\eta }}_1 \left( {0,s} \right)\tag{14}\end{equation}
式中
\begin{equation}\label{eq20} {{Q}}_n \left( s \right) = \prod\limits_{i = n -1}^1 {{{D}}_i^{-1} {{C}}_i {e}^{{{F}}_i \left( s\right)l}} \tag{15}\end{equation}
条带式太阳帆在中心和自由端应满足的固支和自由边界条件可表示为
\begin{equation}\label{eq21} {{L\eta }}_1 \left( {0,s} \right) + {{R\eta}}_n \left( {l,s} \right) ={\bf 0} \tag{16}\end{equation}
式中, ${{L}}$和${{R}}$为转换矩阵.
将式(6)和式(14)代入式(16)
\begin{equation}\label{eq22} \left( {{{L}} + {{R}}{e}^{{{F}}_n\left( s \right)l}{{Q}}_n } \right){{\eta }}_1 \left({0,s} \right) = 0 \tag{17}\end{equation}
根据分布参数传递函数法,条带式太阳帆自由振动的固有频率应满足式(17)的特征方程
\begin{equation}\label{eq23} \det \left[ {{{L}} + {{R}}e^{{{F}}_n\left( s \right)l}{{Q}}_n } \right] = 0 \tag{18}\end{equation}
解得式(18)的根$s_k (k = 1,2, \cdots )$,则$\omega _k = s_k / \sqrt{-1} $,即为条带式太阳帆结构的第$k$阶固有频率.
与第$k$阶固有频率相应的模态为
\begin{equation}\label{eq24} {{\eta }}_i^k \left( {x_i ,s} \right) = {e}^{{{F}}_i \left( {\omega _k } \right)x_i }\prod\limits_{m =i-1}^1 {{e}^{{{F}}_m \left( {\omega _k } \right)l}}{{\psi }}_k \tag{19}\end{equation}
式中,${{\psi }}_k $应满足
\begin{equation}\label{eq25} \left[ {{{L}}\left( {\omega _k } \right) + {{R}}\left( {\omega _k } \right){e}^{{{F}}_n \left( {\omega_k } \right)l}{{Q}}_n \left( {\omega _k } \right)}\right]{{\psi }}_k = 0 \tag{20}\end{equation}
在式(18)中,令$s =0$,即可得条带式太阳帆结构稳定性应满足的特征方程
\begin{equation}\label{eq26} \det \left[ {{{\bar {L}}} + {{\bar {R}}}{e}^{{{F}}_n \left( 0 \right)l}{{\bar {Q}}}_n } \right] =0 \tag{21}\end{equation}
令膜带张力$P$为变量,式(21)的根$P_k (k = 1,2, \cdots)$即为条带式太阳帆的屈曲载荷.
类似地,与第$k$阶屈曲载荷相应的屈曲模态为
\begin{equation}\label{eq27} {{\bar {\eta }}}_i^k \left( {x_i ,s} \right) ={e}^{{{F}}_i \left( {P_k } \right)x_i }\prod\limits_{m = i- 1}^1 {{e}^{{{F}}_m \left( {P_k } \right)l}} {{\bar {\psi }}}_k \tag{22}\end{equation}
式中,${{\bar {\psi }}}_k $应满足
\begin{equation}\label{eq28} \left[ {{{\bar {L}}}\left( {P_k } \right) + {{\bar {R}}}\left( {P_k } \right){e}^{{{F}}_n \left({P_k } \right)l}{{\bar {Q}}}_n \left( {P_k } \right)}\right]{{ \bar {\psi }}}_k = 0 \tag{23}\end{equation}
2 算例分析
以太阳帆特征加速度达到1mm/s$^2$为目标,考虑结构质量、静态变形等因素,文献[4]给出了条带式太阳帆的多个结构设计方案,但没有给出条带式太阳帆结构的模态信息和稳定性分析.利用本文提出的方法,本节对条带式太阳帆进行结构动力学分析,所采用的结构设计参数见表1.表中,$d_{b} $为桅杆截面直径,$t_{b}$为桅杆截面壁厚,$t_{s} $为帆面薄膜厚度,$\sigma _{s}$为帆面薄膜的预应力.Table 1
表1
表1条带式太阳帆结构和材料参数
Table 1Dimensions and material properties of the stripped solar sail
| L/m | E/GPa | db /mm | tb /mm |
|---|---|---|---|
| 100 | 68.95 | 71.10 | 0.15 |
| Pb/(kg.m_3) | ts/"m | Ps/(kg-m_3) | ^s /Pa |
| 1660 | 2.5 | 1660 | 6895 |
新窗口打开
2.1 条带式太阳帆的结构模态分析
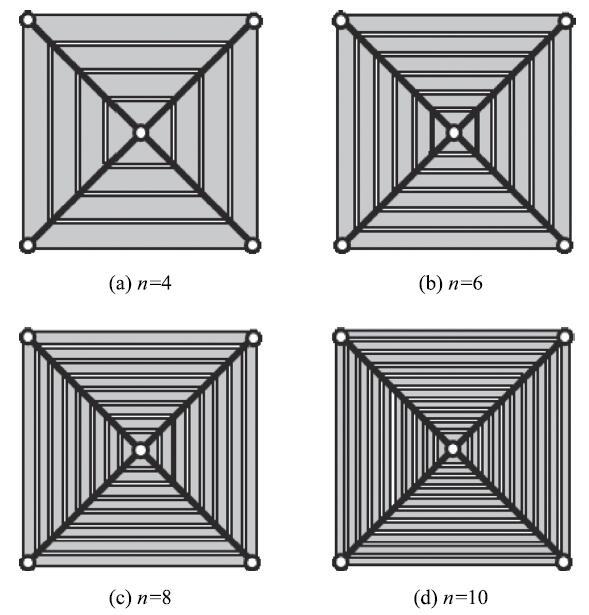
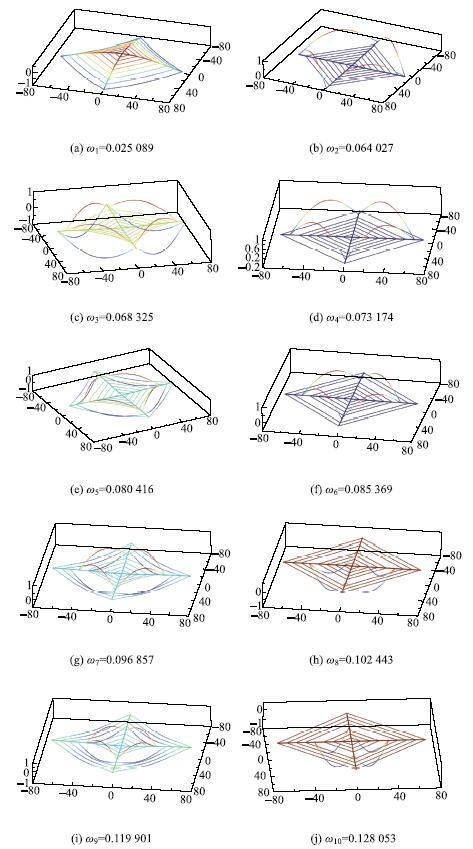
假设太阳帆面薄膜被裁成$n =4,6,8,10$条膜带,如图3所示,这4种工况下的膜带、桅杆段和张力的参数见表2.利用本文提出的方法,表3给出了4种设计工况下条带式太阳帆的前10阶固有频率,图4给出了$n= 8$条膜带时太阳帆的前10阶振型.从图中可以看出太阳帆的低阶频率密集,其中奇数阶模态表现为桅杆和膜带耦合的整体振动,偶数阶模态为膜带的独立振动,边缘至中心的膜带频率依次增大.
显示原图|下载原图ZIP|生成PPT图3不同膜带条数的太阳帆...
-->Fig.3Stripped solar sail with various stripped membranes
-->
Table 2
表2
表2膜带和桅杆段参数
Table 2Parameters of the stripped membranes and boom segments
| n | b/m | l/m | P/N | |
|---|---|---|---|---|
| 4 1 | L2.50 | 11.68 | 0.215 | |
| 6 | 8.33 | 11.19 | 0.144 | |
| 8 | 6.25 | 8.84 | 0.108 | |
| 10 | 5.00 | 1.01 | 0.086 |
新窗口打开
Table 3
表3
表3条带式太阳帆的固有频率
Table 3Natural frequencies of the stripped solar sail
| n | 4 | 6 | 8 | 10 |
|---|---|---|---|---|
| ^1 | 0.018 810 | 0.023 015 | 0.025 089 | 0.026 348 |
| u2 | 0.064 021 | 0.064 021 | 0.064 021 | 0.064 021 |
| ^3 | 0.015 181 | 0.010 411 | 0.068 325 | 0.061 188 |
| ^4 | 0.085 369 | 0.016 832 | 0.013 114 | 0.011 141 |
| ^5 | 0.113 250 | 0.089 061 | 0.080 416 | 0.016 121 |
| ⑴6 | 0.128 054 | 0.096 040 | 0.085 369 | 0.080 034 |
| ⑴1 | 0.139 164 | 0.111513 | 0.096 851 | 0.081336 |
| ^8 | 0.192 081 | 0.128 054 | 0.102 443 | 0.091 461 |
| ^9 | 0.214 331 | 0.139100 | 0.119 901 | 0.102 009 |
| ^10 | 0.251 014 | 0.181196 | 0.128 053 | 0.106112 |
新窗口打开
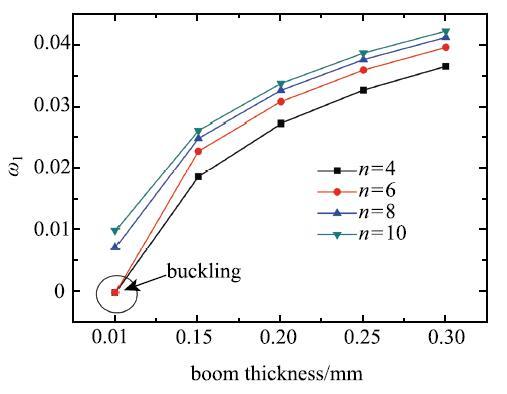
研究桅杆壁厚和膜带条数对太阳帆一阶频率的影响,图5给出了4种工况下($n=4,6,8,10)$太阳帆一阶频率随桅杆壁厚变化的曲线,可以看出,随着壁厚增大,桅杆刚度增大,太阳帆的一阶频率$\omega_1 $升高;另外,壁厚相同的情况下,膜带条数$n$越多,一阶频率$\omega_1 $越大,表明膜带条数的增多有利于条带式太阳帆整体刚度的提高.当桅杆壁厚减小至0.1 mm,膜带条数较少($n =4,6)$的太阳帆发生了整体\ 屈曲.
显示原图|下载原图ZIP|生成PPT图4条带式太阳帆的前十阶振型($n = 8)$ ...
-->Fig.4The first ten modes of the stripped solar sail ($n = 8)$
-->
显示原图|下载原图ZIP|生成PPT图5桅杆壁厚对条带式太阳帆频率的影响...
-->Fig.5Natural frequency of the stripped solar sail varies with thickness of the boom
-->
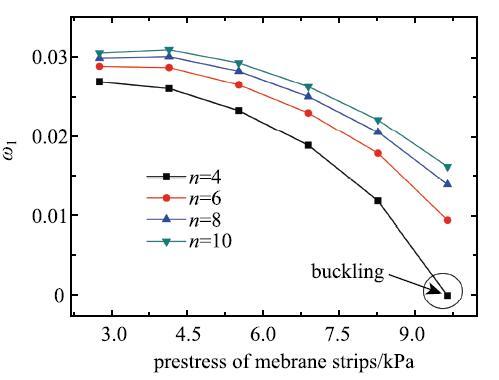
研究太阳帆膜预应力对太阳帆一阶频率的影响,图6给出了4种工况下($n =4,6,8,10)$太阳帆一阶频率随帆面薄膜预应力变化的曲线,可以看出,随着帆面薄膜预应力的增加,太阳帆的一阶频率$\omega_1 $减小,当帆面预应力$\sigma _{s} $增大至9 653Pa时,膜带条数最少($n = 4)$的太阳帆发生了整体屈曲.另外,随着膜带条数的增大,一阶频率$\omega _1$增大,与之前的规律一致.
显示原图|下载原图ZIP|生成PPT图6帆面薄膜预应力对太阳帆频率的影响...
-->Fig.6Natural frequency of the stripped solar sail varies with pre-stress of the membrane
-->
2.2 条带式太阳帆的结构稳定性分析
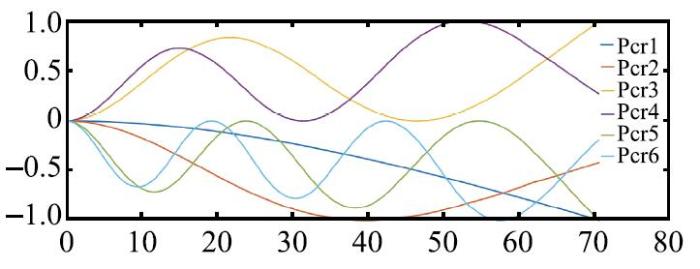
随着薄膜预应力的增大,条带式太阳帆将会发生结构稳定性问题,表4给出了4种设计工况($n= 4,6,8,10)$下条带式太阳帆桅杆的前6阶失稳载荷$P_{cr}$,图7给出了$n = 8$条膜带时太阳帆桅杆的前6阶失稳模态.根据桅杆失稳载荷与帆面薄膜预应力之间的关系
$$ \sigma _{cr} = \frac{\sqrt 2 nP_{cr}}{Lt_{s} } \tag{24}$$
换算得到不同膜带条数时可以施加在帆面薄膜上的最大预应力：9123.6Pa($n = 4)$,10 165.4 Pa($n = 6)$,10 753.8 Pa($n = 8)$,11 131.6Pa($n = 10)$,可见,消除薄膜褶皱所需的预应力$\sigma _{s} =6895.0$Pa均小于这4种工况下结构稳定所需的预应力,因此,4种设计工况下太阳帆的结构稳定性均能满足.
Table 4
表4
表4条带式太阳帆桅杆的失稳载荷
Table 4Buckling loads of the stripped solar sail
| Pcr/N | 4 | 6 | 8 | 10 |
|---|---|---|---|---|
| Pcr1 | 0.285 11 | 0.211 78 | 0.168 03 | 0.13915 |
| Pcr2 | 2.040 34 | 1.514 94 | 1.201 34 | 0.994 52 |
| Pcr3 | 5.382 31 | 4.019 67 | 3.188 46 | 2.639 40 |
| P cr4 | 10.557 50 | 7.709 64 | 6.12813 | 5.073 95 |
| P cr5 | 16.784 29 | 12.58482 | 10.011 34 | 8.296 83 |
| P cr6 | 25.709 64 | 19.242 45 | 14.815 84 | 12.302 77 |
新窗口打开
显示原图|下载原图ZIP|生成PPT图7太阳帆桅杆的前六阶失稳模态($n = 8)$ ...
-->Fig.7The first six buckling modes of the boom ($n = 8)$
-->
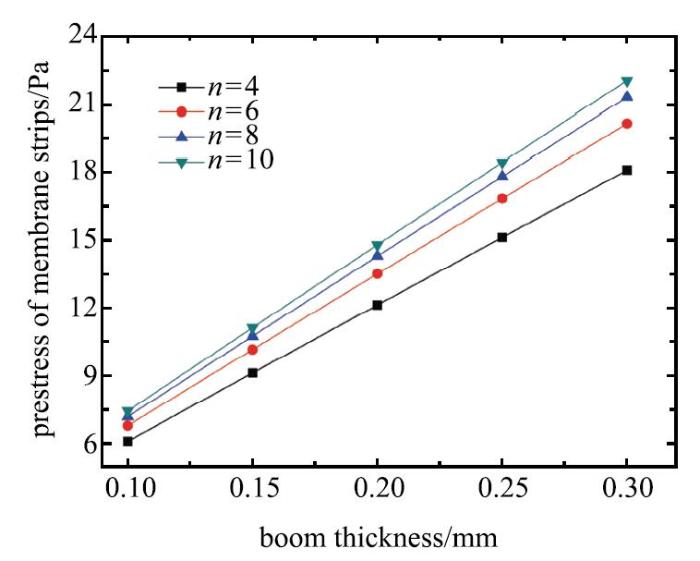
研究桅杆壁厚和膜带条数对太阳帆面薄膜预应力上限的影响,图8给出了4种工况下($n=4,6,8,10)$太阳帆面薄膜预应力上限随桅杆壁厚变化的曲线,可以看出,帆面薄膜预应力上限随着桅杆壁厚线性增大;在壁厚相同的情况下,膜带条数$n$越多,帆面薄膜预应力上限越大,膜带条数的增多有利于条带式太阳帆整体结构稳定性的提高.
显示原图|下载原图ZIP|生成PPT图8桅杆壁厚对帆面薄膜预应力上限的影响...
-->Fig.8The limits on pre-stress of sail membrane varies with thickness of the boom
-->
3 结论
条带式太阳帆具有理想的结构效率,本文对条带式太阳帆的动力特性和结构稳定性进行研究：(1)建立了考虑帆面薄膜条带与支撑桅杆耦合振动的条带式太阳帆结构动力学理论模型,给出了条带式太阳帆结构自由振动和失稳载荷的求解方法;
(2)条带式构型有利于提高太阳帆结构的整体刚度,随着帆面薄膜条带数目的增大,条带式太阳帆结构的一阶频率增大,有利于太阳帆航天器姿态控制和轨道调整;
(3)条带式构型有利于提高太阳帆结构的稳定性,随着帆面薄膜条带数目的增大,条带式太阳帆结构的失稳载荷增大,可以承受更大的帆面薄膜预应力,有利于帆面薄膜褶皱的消除,有利于太阳帆光压推进力的提高;
(4)帆面薄膜预应力增大,条带式太阳帆结构的振动频率减小,当预应力增大到一定程度,条带式太阳帆将发生结构失稳;
(5)支撑桅杆刚度增加,条带式太阳帆结构的整体刚度提高;条带式太阳帆结构的失稳载荷随支撑桅杆壁厚的增加线性增大.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . . |
| [2] | . |
| [3] | . |
| [4] | . |
| [5] | . |
| [6] | . |
| [7] | . |
| [8] | . . |
| [9] | . . |
| [10] | . . |
| [11] | . . |
| [12] | . . |
| [13] | . . |
| [14] | . . |
| [15] | . . |
| [16] | . . |
| [17] | . . |
| [18] | . . |
| [19] | . . |
| [20] | . . |
| [21] | . |
| [22] | . . |
| [23] | . . |
| [24] | . . |
| [25] | . . |
| [26] | . . |
| [27] | . |
| [28] | , |
| [29] | . |
| [30] | . |
| [31] | . |
| [32] | . |
| [33] | . |
| [34] | . |
