, 李明HIGH-ORDER DDG/FV HYBRID METHOD FOR VISCOUS FLOW SIMULATION ON UNSTRUCTURED/HYBRID GRIDS1)
ShaoShuai, LiMing中图分类号:V211.3
文献标识码:A
通讯作者:
版权声明:2018力学学报期刊社力学学报期刊社 所有
基金资助:
作者简介:
-->
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (12855KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引 言
基于非结构/混合网格的高阶精度格式是CFD领域当前和未来的重要研究方向之一[1]. 间断迦辽金有限元方法 (discontinuous Galerkin method, DGM) 作为其中代表性的方法之一, 继承了有限元方法和有限体积方法的优点, 主要包括: (1) 优良的数学特性, 即守恒性、稳定性和收敛性; (2) 通过改变单元分布多项式的阶数, 容易向高阶精度拓展; (3) 能够处理复杂的几何外形、物理边界和不相容网格(悬空节点); (4) 良好的紧致特性, 易于进行超大规模并行计算; (5) 容易实现网格和阶数自适应 (hp-adaptive), 适合处理间断问题. 基于以上优点DGM成为欧洲高精度数值算法工程ADIGMA[2]和IDHOM[3] 的主要研究对象.当前, DGM研究主要集中于两个方面: 一是发展相容、紧致、高效的黏性项处理方法; 二是降低计算量和存储量. 黏性项中界面物理量的导数若直接使用界面两侧导数平均值, 而不考虑界面两侧可能存在的物理量阶跃, 将导致数值解与原方程的解不相容
[4]. 因此DGM对黏性项的处理方法成为诸多****的研究对象. 最早的解决方案是内罚(interior penalty, IP)方法[5], 但其并不对任意$P$阶分布都最优, 同时罚因子需要随着精度阶数提高进行相应的调节. DGM 适合求解一阶方程, 自然的想法是引入辅助变量将二阶方程转化为一阶方程, BR1[6]和LDG[7]方法利用了这种思想, 但紧致性较差, BR2[8]和CDG[9]方法通过相似的手段, 引入局部提升算子, 分别改善了BR1 和LDG的紧致特性. 2005年Hartmann等[10-11]将界面两侧基函数梯度的阶跃考虑在内, 得到对称内罚方法(SIP). 2007年van Leer等[12-13]提出RDG方法, 基于恢复原理恢复了光滑连续解.
2008年Liu和Yan[14]提出了直接间断迦辽金(direct discontinuous Galerkin, DDG)方法, 类比传热方程解的梯度公式, 利用界面两侧物理量和物理量的各阶梯度, 计算扩散通量. 文献[14]通过一系列的数值实验验证了DDG方法在一维和二维对流和扩散问题中的数值精度. DDG方法保持了DGM优良的紧致特性, 同时相对前面提到的黏性项处理方法拥有更简单的计算形式和更高的计算效率. 2010 年Liu和Yan[15]又对DDG方法进行了改进, 加入了界面修正项, 从而避免了计算DDG通量公式中的高阶导数项. 之后张梦萍等[16]通过傅里叶误差分析推导出DDG的理论数值精度, 与数值实验的结果吻合良好. 近两年程剑等[17-18]使用DDG方法求解混合网格上的N-S方程和RANS方程, 比较了基于原始变量和守恒变量的通量公式, 验证了相同精度阶下DDG方法相比BR2方法拥有更高的计算效率.
DGM的另一个研究重点在于降低计算量和存储量. DGM的计算量和存储量巨大, 对于网格规模达到百万甚至数千万的大型实际复杂流动问题, 其计算量和存储量对计算资源的消耗是难以承受的. 相比DG方法, 二阶FV方法计算量和存储量较小, 因此很多****尝试将两种方法的优点结合以达到更高的计算效率. Cockburn等[19]和Ryan 等[20]提出最早的重构方法, 仅仅作为计算结束后的一种后处理过程, 因此这种方法在计算过程中略去的高阶信息无法在最后一步通过重构完全恢复. Dumbser等[21-22]发展出$\text{P}_\text N\text{P}_\text M$方法, 常规的DG方法和高阶FV方法分别是$\text{P}_0\text{P}_\text M$和$\text{P}_\text M\text{P}_\text M$两种特例. $\text{P}_\text N\text{P}_\text M$方法是时空耦合的, 因此实现起来较为复杂, 计算量较大. 基于相似的思想Luo等\textsuperscript{[23,24]}提出了rDG方法, 对应于$\text{P}_1\text{P}_2$格式. 张来平等[25-31]提出了分布多项式"静态重构"、"动态重构"和"混合重构"的概念, 并发展了一类DG/FV混合方法. DG/FV方法基于本单元和相邻单元物理量的低阶分布重构出高阶分布, 要求重构后的高阶分布在相邻单元上的延拓与相邻单元的低阶分布在积分意义上相等. 近几年DG/FV 混合格式已经成功用于求解Euler 方程[30]、N-S 方程[31]和耦合了S-A湍流模型的RANS方程[26], 计算效率相比经典的DGM 有较大提升.
总结当前的研究进展, DDG方法和DG/FV混合格式分别提供了相容、紧致、高效的黏性项处理方法和高效低存储的重构方法. 两个优秀方法的结合将是对DG方法最自然的拓展, 然而目前这方面的研究尚未见报道.
因此, 本文将DDG方法推广应用于DG/FV混合算法, 得到新的DDG/FV混合格式, 利用其求解非结构/混合网格上的N-S方程, 并通过对典型二维算例: Couette流动、层流平板边界层、定常圆柱绕流, 非定常圆柱绕流和层流NACA0012翼型绕流的计算, 验证新格式在定常和非定常问题中的精度和计算效率, 以期待获得更高效的N-S方程高阶精度非结构/混合网格求解方法. 与广泛使用的BR2-DG格式进行精度阶、计算效率和稳定性的比较表明, 新发展的DDG/FV算法达到了设计精度, 并且拥有更高的效率和更好的稳定性, 具有良好的应用前景.
1 数值离散方法
1.1 控制方程
二维可压缩Navier-Stokes方程可以写为\begin{equation*}\dfrac{\partial u}{\partial t}+\nabla \cdot\mathcal{F}_c( u)-\nabla \cdot\mathcal{F}_v( u,\nabla u)= 0\tag*{(1)}\end{equation*}
式中守恒变量$ u=(u_i)$, 无黏通量$\mathcal{F}_c( u)=( F_c, G_c)$ 定义如下
\begin{equation*} u= \left\lgroup \begin{matrix} \rho\\ \rho u\\ \rho v\\ E \end{matrix} \right\rgroup , F_c( u)= \left\lgroup \begin{matrix} \rho u\\ \rho u^2+p\\ \rho uv\\ u(E+p) \end{matrix} \right\rgroup , G_c( u)= \left\lgroup \begin{matrix} \rho v\\ \rho uv\\ \rho v^2+p\\ v(E+p) \end{matrix} \right\rgroup \tag*{(2)} \end{equation*}
黏性通量$\mathcal{F}_v( u,\nabla u)=( F_v, G_v)$定义如下
\begin{equation*} \left. \begin{split} & F_v( u,\nabla u)= \left\lgroup \begin{matrix} 0\\ \tau_{11}\\ \tau_{21}\\ u\tau_{11}+v\tau_{12}+kT_x \end{matrix} \right\rgroup\\ & G_v( u,\nabla u)= \left\lgroup \begin{matrix} 0\\ \tau_{12}\\ \tau_{22}\\ u\tau_{21}+v\tau_{22}+kT_y \end{matrix} \right\rgroup \end{split} \right\} \tag*{(3)} \end{equation*}
1.2 DGM空间离散
利用DG方法对控制方程(1)进行空间离散. 控制方程乘以检验函数$b$, 在计算域$\varOmega$ 上进行分部积分, 得到控制方程等效积分形式的弱形式\begin{equation*} \begin{split} &\int_{\varOmega}\dfrac{\partial u}{\partial t}b\text d\varOmega+\int_{\partial\varOmega}\Big(\mathcal{F}_c\Big( u\Big)-\mathcal{F}_v\Big( u,\nabla u\Big)\Big)\cdot nb\text d\varGamma-\\ &\quad\quad\int_{\varOmega}\Big(\mathcal{F}_c\Big( u\Big)-\mathcal{F}_v\Big( u,\nabla u\Big)\Big)\cdot \nabla b\text d\varOmega= 0 \end{split} \tag*{(4)} \end{equation*}
式中$\partial\varOmega$是计算域$\varOmega$的边界, $ n$是计算域边界的外法矢量. 将计算域划分为互不重叠的单元$\varOmega_e$的集合. 接着将控制方程的弱形式应用于每一个离散后的单元$\varOmega_e$, 得到
\begin{equation*} \begin{split} &\dfrac{\text d}{\text d t}\int_{\varOmega_e} u_hb_h\text d\varOmega+\int_{\partial\varOmega_e}\Big(\mathcal{F}_c\Big( u_h\Big)-\mathcal{F}_v\Big( u_h,\nabla u_h\Big)\Big)\cdot nb_h\text d\varGamma-\\ &\quad\quad\int_{\varOmega_e}\Big(\mathcal{F}_c\Big( u_h\Big)-\mathcal{F}_v\Big( u_h,\nabla u_h\Big)\Big)\cdot\nabla b_h\text d\varOmega= 0 \end{split} \tag*{(5)} \end{equation*}
式中$ u_h$和$b_h$分别代表对解析解$ u$和检验函数$b$的有限元近似, 在单元界面上$ u_h$ 可能出现间断, 因此对单元界面的积分需要构造特殊的数值通量$ H_c$和$ H_v$ 分别代替$\mathcal{F}_c\cdot n$和$\mathcal{F}_v\cdot n$. $b_h$直接取$ u_h$的基函数$b_i$. 式(5)可以改写为
\begin{equation*} \begin{split} &\dfrac{\text d}{\text dt}\int_{\varOmega_e} u_hb_i\text d\varOmega-\int_{\varOmega_e}\Big(\mathcal{F}_c\Big( u_h\Big)-\mathcal{F}_v\Big( u_h,\nabla u_h\Big)\Big)\cdot\\ &\quad\quad\nabla b_i\text d\varOmega+\int_{\partial\varOmega_e}\Big( H_c\Big( u^+_h, u^-_h, n\Big)-\\ &\quad\quad H_v\Big( u^+_h, u^-_h,\nabla u^+_h,\nabla u^-_h, n\Big)\Big)b_i\text d\varGamma= 0 \end{split} \tag*{(6)} \end{equation*}
式中上标$^-$和$^+$分别代表单元界面的左右值(下同). 本文中无黏数值通量$ H_c$ 采用HLLC 格式, 黏性数值通量$ H_v$分别采用DDG和BR2格式.
1.3 DDG黏性项离散
Liu和Yan[14]提出了DDG方法, 并给出二维扩散问题中物理量梯度的数值通量公式\begin{equation*} \left. \begin{split} &\widehat{u}_x=\beta_0\dfrac{[u]}{\varDelta}n_x+\overline{u_x}+\beta_1\varDelta\Big(\Big[u _{xx}\Big]n_x+\Big[u_{xy}\Big]n_y\Big)\\ &\widehat{u}_y=\beta_0\dfrac{[u]}{\varDelta}n_y+\overline{u_y}+\beta_1\varDelta\Big(\Big[u _{yx}\Big]n_x+\Big[u_{yy}\Big]n_y\Big)\\ &\Big[u\Big]=u^+-u^-,\bar{u}=\dfrac{1}{2}\Big(u^++u^-\Big) \end{split} \right\} \tag*{(7)} \end{equation*}
式中, $\varDelta$是跨界面特征长度, 本文取为界面左右单元中心连线在界面法线方向的投影长度. 边界采用虚拟单元的形式, $\varDelta$取单元中心到边界距离的2倍. 从式(7) 可以明显看出, DDG 格式是紧致、守恒和相容的. DDG 格式计算界面当前高斯积分点的数值通量时, 只依赖于当前高斯积分点上物理量和物理量的梯度信息; 而BR2 格式则需要当前界面上所有高斯积分点物理量和物理量的梯度信息. 同时相比BR2 格式, DDG 不必计算并存储提升算子, 体积分中也不需要考虑提升算子的贡献. 因此DDG 格式程序实现更简洁, 计算量和存储量更小.
将式(7)应用到N-S方程黏性数值通量的计算, 可以分为3个步骤:
(1) 根据式(7)计算守恒变量的数值通量$\widehat{\nabla\rho}$, $\widehat{\nabla(\rho u)}$, $\widehat{\nabla(\rho v)}$, $\widehat{\nabla e}$.
不失一般性, 以守恒变量$x$方向的梯度为例
\begin{equation*} \left. \begin{split} &\widehat{\rho_x}=\beta_0\dfrac{[\rho]}{\varDelta}n_x+\overline{\rho_x}+\beta_1\varDelta\Big (\Big[\rho_{xx}\Big]n_x+\Big[\rho_{xy}\Big]n_y\Big)\\ &\widehat{(\rho u)_x}=\beta_0\dfrac{[\rho u]}{\varDelta}n_x+\overline{(\rho u)_x}+\\ &\quad\quad\beta_1\varDelta\Big(\Big[\Big(\rho u\Big)_{xx}\Big]n_x+\Big[\Big(\rho u\Big)_{xy}\Big]n_y\Big)\\ &\widehat{(\rho v)_x}=\beta_0\dfrac{[\rho v]}{\varDelta}n_x+\overline{(\rho v)_x}+\\ &\quad\quad\beta_1\Delta\Big(\Big[\Big(\rho v\Big)_{xx}\Big]n_x+\Big[\Big(\rho v\Big)_{xy}\Big]n_y\Big)\\ &\widehat{e_x}=\beta_0\dfrac{[e]}{\varDelta}n_x+\overline{e_x}+\beta_1\varDelta\Big(\Big [e_{xx}\Big]n_x+\Big[e_{xy}\Big]n_y\Big) \end{split} \right\} \tag*{(8)} \end{equation*}
(2) 通过守恒变量的数值通量计算原始变量的数值通量
\begin{equation*} \left. \begin{split} &\widehat{u_x}=\dfrac{1}{\bar{\rho}}\Big(\widehat{(\rho u)_x}\Big)-\widehat{\rho_x}\bar{u}\Big)\\ &\widehat{v_x}=\dfrac{1}{\bar{\rho}}\Big(\widehat{(\rho v)_x}\Big)-\widehat{\rho_x}\bar{v}\Big)\\ &\dfrac{\widehat{T_x}}{\alpha}=\dfrac{\widehat{e_x}}{\bar{\rho}}-\dfrac{\bar{e} \widehat{\rho_x}}{\bar{\rho}^2}-\Big(\bar{u}\widehat{u_x}+\bar{v}\widehat{v_x} \Big)\\ &\Big(\bar{u},\bar{v}\Big)=\left\lgroup\overline{{\left\lgroup\dfrac{\rho u}{\rho}\right\rgroup}},\overline{{\left\lgroup\dfrac{\rho v}{\rho}\right\rgroup}}\right\rgroup,\alpha=\dfrac{\gamma-1}{R} \end{split} \right\} \tag*{(9)} \end{equation*}
(3) 将$\widehat{\nabla\rho}$, $\widehat{\nabla u}$, $\widehat{\nabla v}$, $\widehat{\nabla T}$代入黏性通量公式$\mathcal{F}_v( u,\nabla u)=( F_v, G_v)$ 中, 即可得到DDG离散的黏性数值通量
\begin{equation*} \left\lgroup \begin{matrix} 0\\ \widehat{\tau_{xx}}n_x+\widehat{\tau_{xy}}n_y\\ \widehat{\tau_{yx}}n_x+\widehat{\tau_{yy}}n_y\\ \Big(\bar{u}\widehat{\tau_{xx}}+\bar{v}\widehat{\tau_{xy}}+\sigma\widehat{T_x} \Big)n_x+\Big(\bar{u}\widehat{\tau_{yx}}+\bar{v}\widehat{\tau_{yy}}+\sigma \widehat{T_y}\Big)n_y \end{matrix} \right\rgroup \tag*{(10)} \end{equation*}
其中$\sigma=\dfrac{\gamma\bar{\mu}}{Pr\alpha}$.
1.4 DG/FV混合重构
DG/FV混合重构借鉴了$\text P_N\text P_M$和$k-\text{exact}$ FV的重构思想. 在DG/FV 混合重构中, 当前单元的高阶分布多项式, 通过相邻单元(重构模板)的低阶多项式重构得到. 当前单元$\varOmega_e$ 内的低阶多项式和重构后的高阶多项式分别记作$u^e_h$和$w^e_h$, 形式如下\begin{equation*} u^e_h=\sum\limits^{Dof\_DG-1}_{i=0}u^e_ib_i( \xi^e),w^e_h=\sum\limits^ {Dof\_FV-1}_{i=0}w^e_i\phi_i( \xi^e) \tag*{(11)} \end{equation*}
式中$ \xi^e$是$\varOmega_e$上的局部坐标, 基函数是使用Gram-Schmidt规范正交化方法对泰勒基函数正交化得到的正交基函数. 重构过程的作用域是单元$\varOmega_e$ 的重构模板$S_e=\lbrace s_j\rbrace,j=0,1,2\cdots,n_e$, $j=0$对应$s_j=e$. 为避免计算域边界三角形单元由于von Neumann 模板(共享边的单元)单元数较少, 重构信息不足, 导致重构失败, 边界三角形单元使用Moore 模板(共享格点的单元), 其他单元均使用von Neumann模板. 对模板$S_e$中的每个单元$\varOmega_j$ 建立如下等式
\begin{equation*} \dfrac{1}{|\varOmega_j|}\int_{\varOmega_j}w^e_hb\text d\varOmega=\dfrac{1}{|\varOmega_j|}\int_{\varOmega_j}u^j_hb\text d\varOmega \tag*{(12)} \end{equation*}
注意到式(12)等式左边是在$\varOmega_j$上对单元$\varOmega_e$上的分布$w^e_h$进行积分. 这意味着, 将单元$\varOmega_e$的重构多项式拓展到其模板中的任意单元上. 重构完成后, 再将重构多项式限制到只应用于本单元物理量和通量计算中. $b$取单元$\varOmega_j$的基函数$b_n( \xi^j)$, 式(12)可重写为
\begin{equation*} \begin{split} &\int_{\varOmega_j}\left\lgroup\sum\limits^{Dof\_DG-1}_{l=0}w^e_l\phi_l(\xi ^e)\right\rgroup b_n( \xi^j)\text d\varOmega=\\ &\int_{\varOmega_j}\left\lgroup\sum\limits^{Dof\_FV-1}_{m=0}u^j_mb_m(\xi ^j)\right\rgroup b_n( \xi^j)\text d\varOmega,\\ &n=0,1,\cdots,Dof\_DG-1 \end{split} \tag*{(13)} \end{equation*}
模板中的每个单元$\varOmega_j$的每个基函数$b_n( \xi^j)$, 都能得到方程(13), 联立得到超定方程组, 使用最小二乘法求解, 即可得到当前单元内的高阶项. 高阶项与原始的低价项(由DGM得到)结合, 可以得到较原DG重构高一阶的DG/FV混合重构, 由此得到更高阶的DG/FV混合格式.
1.5 隐式时间离散
本文对非定常问题使用显式2阶Runge-Kutta(RK)方法进行时间离散; 对定常问题使用隐式LU-SGS方法进行时间离散, 求解过程中使用局部时间步长策略加速收敛, 使用Matrix-Free技术减少计算量[31-32]. 由于篇幅限制, 此处不再赘述.2 典型算例数值实验结果分析
2.1 Couette流动
Couette流动有精确解, 参考式(14), 常被用来测试数值格式的精度阶数. 本文将用其测试DDG 格式的参数选择、新格式的精度阶数以及格式的计算效率. 下面所用精度测试方法可详见文献[33,34].\begin{equation*} \left. \begin{split} &u=\dfrac{U}{H}y, v=0, p=\text{const}, \rho=\dfrac{p}{RT}\\ &T=T_0+\dfrac{y}{H}(T_1-T_0)+\dfrac{Pr(\gamma-1)}{2Ma^2_{\infty}}\dfrac{y}{H}\Bigg(1- \dfrac{y}{H}\Bigg) \end{split} \right\} \tag*{(14)} \end{equation*}
式中上下平板距离$H=2$, 上平板速度$U=1$. 上下平板温度分别为$T_1=0.85$, $T_0=0.8$. 其他来流参数为$Pr=0.72$, $\gamma=1.4$, $Ma_{\infty}=0.1$. 计算域为$x\in[0,4]$, $y\in[0,2]$. 左右边界给定精确解, 上下平板使用无滑移等温壁面条件.
本文Couette算例共使用四套逐次加密的网格Grid1, Grid2, Grid3, Grid4(见图1). 其中Grid1, Grid3, Grid4是自相似加密, Grid2采用非自相似加密. 每套网格的单元数量见表1.
显示原图|下载原图ZIP|生成PPT图1Couette算例所用4套网格
-->Fig.1Four types of grids for Couette flow case
-->
Table 1
表1
表1Couette算例所用4套网格单元数量
Table 1Number of cells of grids for Couette flow case
 |
新窗口打开
2.1.1 DDG格式参数验证
DDG格式中, $\beta_0$足够大时, 式(7)中只使用前两项得到的数值通量对任意阶的多项式都是适应的(admissibility). 即对于$P$阶多项式近似, 当$P$是奇数时, 数值结果具有$P+1$阶精度; 当$P$是偶数时, 数值结果具有$P$阶精度. $P=1$ 时, Liu 和Yan 对$\beta_0=1$和$\beta_0=2$做了测试, 达到2阶精度; $P=2$时$\beta_1$ 取1/12, $\beta_0$取7/6或$6/\pi$都能达到3阶精度.
Arnold等[35]证明了BR2格式在$\eta_e\geqslant n_f$($n_f$ 是单元的边数)时稳定. 利用DDG 离散N-S方程的黏性项时, $\beta_0$ 的选择是否有相似的稳定性要求, 有待验证. 本小节将考察DDG-P1 和DDG-P2 中$\beta_0$ 对精度的影响. 待考察的$\beta_0$列于表2 中, DDG-P2格式中的$\beta_1$取1/12, 分别使用结构网格Grid1(边数为4)和非结构网格Grid2(边数为3)进行数值实验.
Table 2
表 2
表 2DDG-P1和DDG-P2格式中$\beta_0$备选值列表
Table 2Candidate $\beta_0$ for DDG-P1 and DDG-P2
 |
新窗口打开
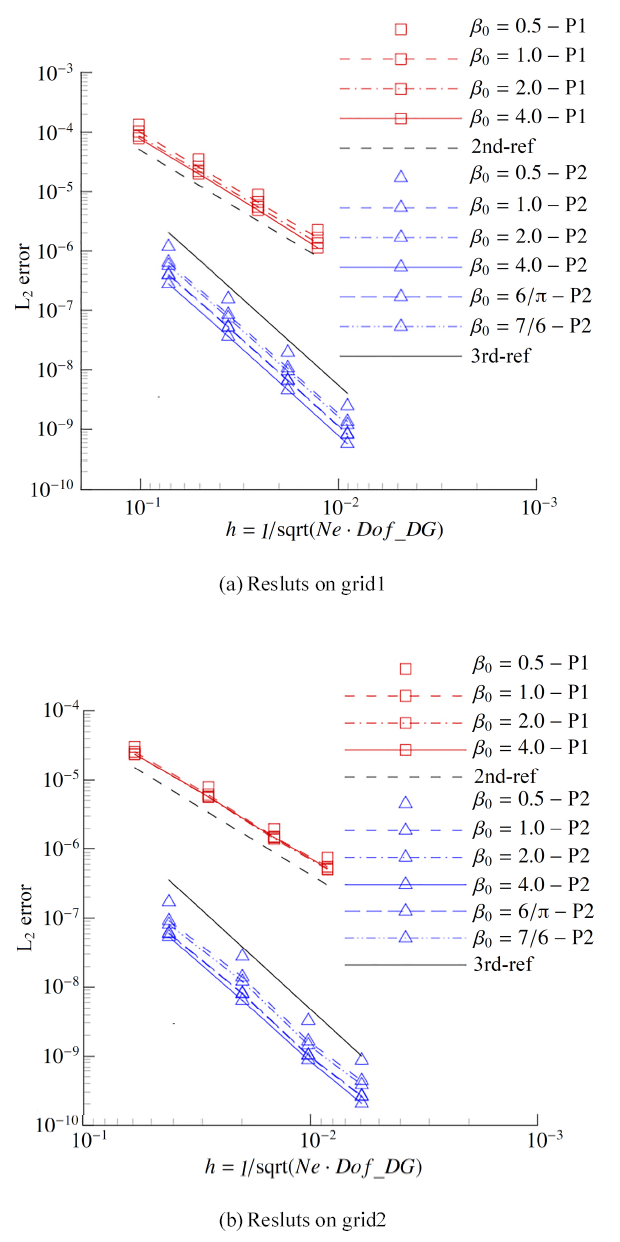
图2给出了不同计算网格, DDG-P1和DDG-P2取不同$\beta_0$时的误差情况. 对于结构网格, 如图2(a)所示, $\beta_0$ 对DDG-P1和DDG-P2的精度阶影响较小. 对于所有$\beta_0$取值, 两种格式都达到了理论数值精度阶. 但在相同计算条件下, $\beta_0$ 越大, 格式的绝对误差越小. 考察非结构网格的情况, 如图2(b)所示, 除$\beta_0=0.5$时, DDG-P2 格式的误差走势稍稍偏离理论值, 其他方面非结构网格与结构网格的表现一致, 即$\beta_0$对精度阶影响较小, $\beta_0$ 越大绝对误差越小.
显示原图|下载原图ZIP|生成PPT图2$\beta_0$对DDG-P1和DDG-P2格式精度的影响
-->Fig.2Impact of $\beta_0$ on the accuracy of DDG-P1 and DDG-P2
-->
计算过程中$\beta_0$无论是否小于单元边数, 残差都能稳定收敛. 并且对比图2(a)和图2(b), $\beta_0$ 无论是否小于单元边数, 精度阶都能达到理论值. 综上, $\beta_0$ 的选择对稳定性和格式精度阶影响很小, 选择较大的$\beta_0$ 能够得到更小的绝对误差. 因此后文中的算例参数默认取值, DDG-P1: $\beta_0=4$; DDG-P2: $\beta_0=4$, $\beta_1=1/12$.
2.1.2 精度验证
本小节验证6种数值格式: DDG-P1, BR2-P1, DDG-P2, BR2-P2, DDG-DG1/FV2, BR2-DG1/FV2 的数值精度, 其中前4 种为纯DG方法, 后2种为DG/FV混合算法. 使用的4 套网格分别为grid1, grid2, grid3, grid4.
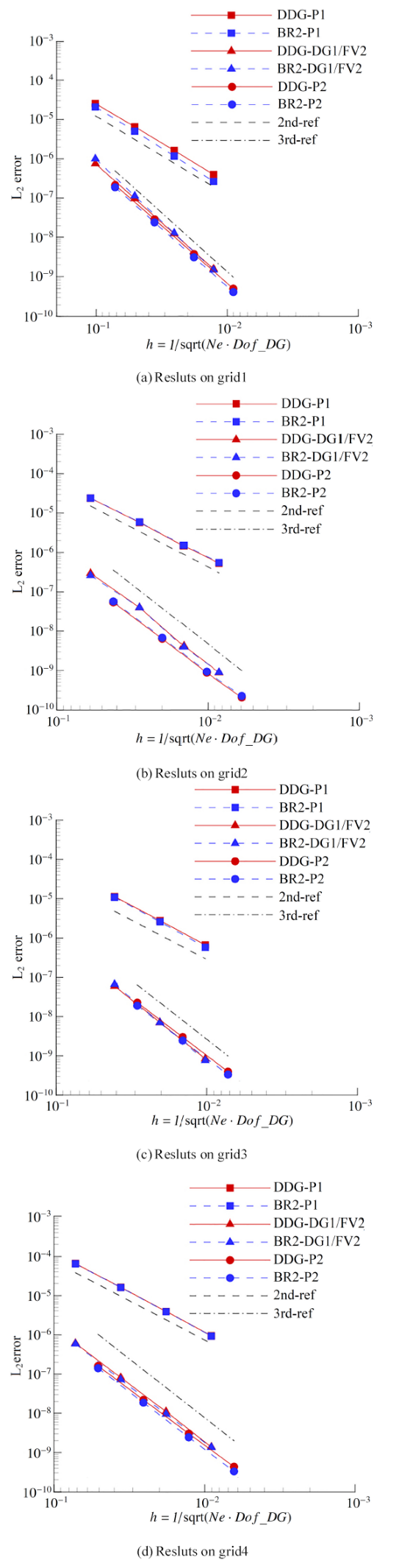
图3显示, 6种格式在4种类型网格中精度阶均达到理论值(前2种为2阶精度, 后4 种为3 阶精度). 自由度相同时, 在网格grid2上DG/FV混合算法比同阶DGM绝对误差稍大(如图 3(b)) 而在其他类型网格中, 绝对误差水平相当. 在网格grid1 上DDG-P1 比BR2-P1 绝对误差稍大(如图 3(a)), 在其他类型网格中, 绝对误差基本一致.
显示原图|下载原图ZIP|生成PPT图36种格式精度验证
-->Fig.3Order of accuracy for 6 different schemes
-->
2.1.3 效率验证
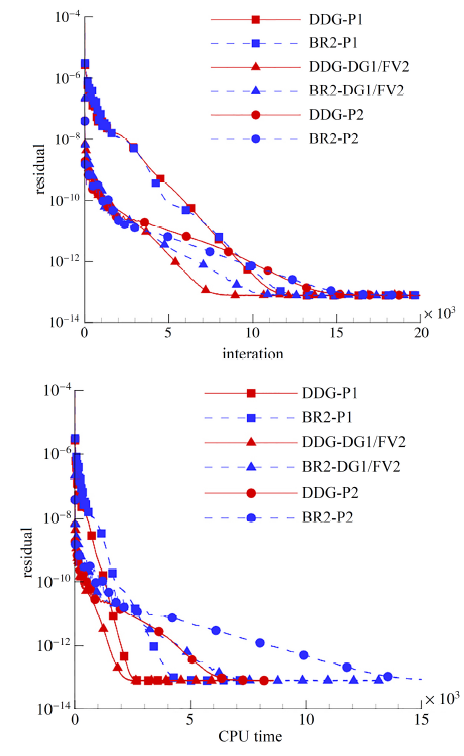
DGM方法主要应用于非结构网格, 因此使用非结构网格grid2中最密的网格, 比较6 种格式的计算效率, 计算使用单个CPU核心. 图4给出了密度残差收敛曲线, 从收敛步数来看DDG-DG1/FV2收敛速度最快; 从总CPU时间来看, 3 阶精度的DDG-DG1/FV2达到收敛花费的时间最少, 甚至少于2阶精度的DDG-P1.
显示原图|下载原图ZIP|生成PPT图4非结构网格Couette流动收敛历程对比
-->Fig.4Comparison of convergence history between 6 different methods for Couette flow in unstructured cell
-->
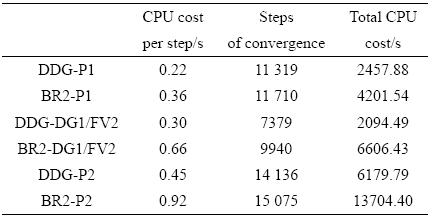
表3列出了6种格式的单步计算时间, 达到收敛的迭代步数和CPU时间, 根据其中的数据分析可知, DDG-DG1/FV2 比BR2-DG1/FV2收敛所需的迭代步数减少了25%. 同时DG/FV 混合格式相比同阶的DG格式, 收敛步数减少了34% 以上. 从单步计算时间来看, DDG-DG1/FV2 效率比BR2-P2提高3倍. 考虑达到收敛的总CPU 时间, DDG-DG1/FV2 混合格式相比BR2-P2格式效率提高6.5倍.
Table 3
表 3
表 3Couette流动计算时间和收敛步数对比
Table 3CPU time and convergence steps for Couette flow
 |
新窗口打开
Table 4
表 4
表 4层流平板计算时间和收敛步数对比
Table 4CPU time and convergence steps for laminar flow over a flat plate
 |
新窗口打开
2.2 层流平板边界层
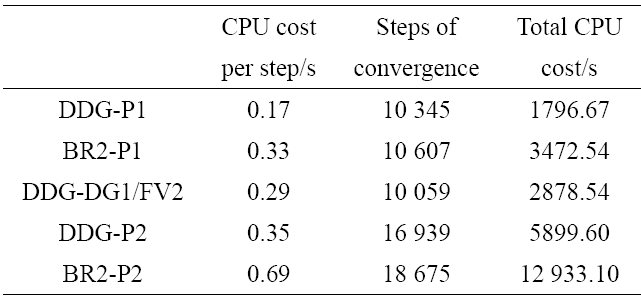
本小节利用层流平板边界层的布拉修斯解验证混合格式计算结果的精度. 来流条件: $Ma=0.1,Re=2\times10^5$, 参考长度为1. 计算域: $x\in[-0.35,2]$, $y\in[0,1]$, 平板从$x=0.0$ 开始, 在$x=2.0$结束. 该算例采用$69\times49$ 的矩形网格, 物面第一层网格高度为$\text dy=2.5\times10^{-4}$.在相同计算参数下, BR2-DG1/FV2格式计算发散, 作为对比DDG/FV具有更好的稳定性. 表 4中的数据显示, DDG-DG1/FV2 混合格式相比同阶的DGM, 收敛步数减少了40\%以上. 从单步计算时间来看, DDG-DG1/FV2效率比BR2-P2 提高2.4倍. 从达到收敛所需要的CPU时间来看, DDG-DG1/FV2混合格式比BR2-P2格式效率提高了4.5倍.
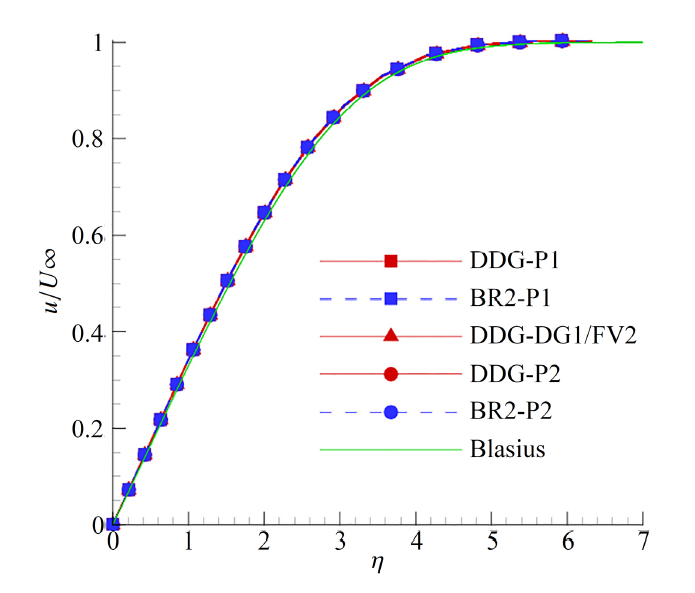
图5和图6分别给出了$x=0.5$站位的速度剖面和壁面摩阻系数曲线. 5种格式的速度剖面与布拉修斯理论解吻合良好. 图6中在$x<0.01$的平板前缘, DDG-P2和BR2-P2仍然与理论解保持一致, DDG-DG1/FV2 混合格式接近同阶DGM 方法的结果, 说明混合格式DDG/FV达到了同阶DGM的计算精度, 同时高阶精度格式较低阶格式在同样的网格上具有更高的计算精度.
显示原图|下载原图ZIP|生成PPT图5$x=0.5$站位的速度剖面
-->Fig.5Profile of $u$ at $x=0.5$
-->
显示原图|下载原图ZIP|生成PPT图6壁面摩阻系数对数曲线
-->Fig.6Distribution of $C_\text f$ on the flat plate
-->
2.3 圆柱绕流
首先将新的DDG/FV混合格式应用于定常圆柱绕流算例, 来流条件: $Ma=0.2$, $Re=40$, 参考长度为1. 壁面采用温度为$288.15~\text K$的无滑移等温壁面边界条件, 外边界给定远场边界条件. 圆柱直径为1, 圆心位于(0.0). 计算域和对称混合网格如图7, 物面第一层单元高度为0.01.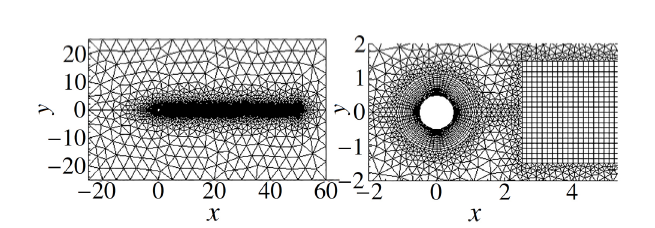
显示原图|下载原图ZIP|生成PPT图7圆柱绕流混合网格
-->Fig.7Hybrid grid for laminar flow over a cylinder
-->
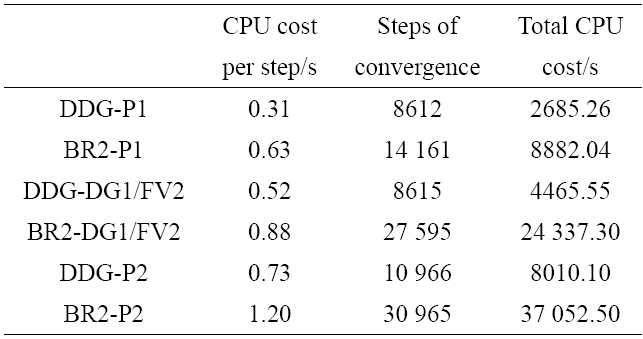
根据表5中的数据可知, DDG-DG1/FV2单步计算效率相比BR2-P2提高2.3倍, 同时收敛所需的迭代步数是BR2-P2的1/3, 最终达到收敛耗费的CPU时间只是BR2-P2 的1/8. DDG/FV 混合算法的高效性再次得到验证.
Table 5
表 5
表 5圆柱绕流计算时间和收敛步数对比
Table 5CPU time and convergence steps for laminar flow over a cylinder
 |
新窗口打开
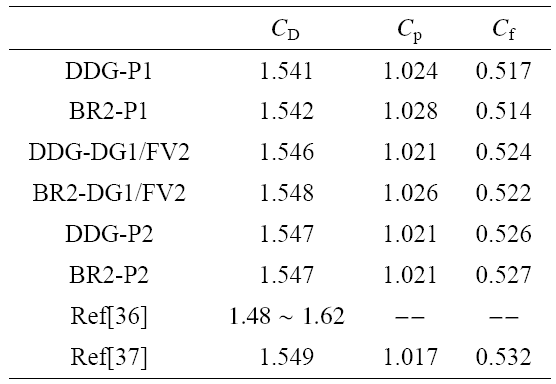
图8展示了DDG-DG1/FV2和BR2-P2格式计算的流场马赫数云图、流线和相应的尾迹涡. 可以看出流场曲线光滑, 尾迹涡分布对称. 对比图8(a)和图8(b), 可以看出两种格式计算的流场分布非常接近. 表6和表7 给出了计算所得分离角度$\theta_\text s$、尾迹涡长度$L_\text w/D$、总阻力系数$C_\text D$、 压差阻力系数$C_\text p$ 和摩阻系数$C_\text f$, 并与文献值进行对比. 6种格式计算的$\theta_\text s$, $L_\text w/D$ 和$C_\text D$均落在文献[36] 给出的范围内. 考察3个气动力参数(见表7), 三阶精度格式(DDG-DG1/FV2、BR2-DG1/FV2、DDG-P2 和BR2-P2) 的计算结果相比二阶精度格式(DDG-P1 和BR2-P1), 更接近文献[37]的值. DDG/FV混合格式的计算结果与同阶DGM 的结果相近, 再次验证了DDG/FV混合格式的计算精度.
Table 6
表 6
表 6圆柱绕流不同格式计算结果比较(分离参数)
Table 6Results of different methods for laminar flow over a cylinder(separation parameters)
 |
新窗口打开
Table 7
表 7
表 7圆柱绕流不同格式计算结果比较(气动力参数)
Table 7Results of different methods for laminar flow over a cylinder(aerodynamic coefficients)
 |
新窗口打开
显示原图|下载原图ZIP|生成PPT图8圆柱绕流马赫数云图
-->Fig.8Mach number contour for laminar flow over a cylinder
-->
为了验证新的混合格式在非定常流动计算中的表现, 我们进一步模拟了非定常圆柱绕流问题. 相对于定常流动条件, 只需将雷诺数提高为100, 其他来流条件、边界条件、计算网格均不变. 计算时, 无量纲全局时间步长$\text dt=2\times10^{-5}$, 使用二阶Runge-Kutta(RK) 时间离散方法. 计算网格被划分为16个区, 使用MPI(message passing interface)方法进行并行计算.
由于非定常流动计算使用全局时间步长的二阶RK方法进行显式时间推进, 因此各种格式的残差发展历程基本一致, 新的混合方法对计算效率的提升主要体现在单步计算时间上.
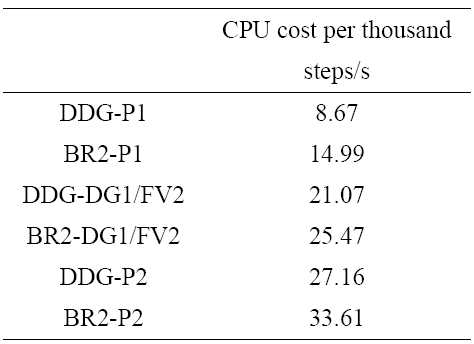
本算例中单步迭代的CPU时间数量级较小, 为了便于比较效率, 表8列出了6种格式的千步CPU 时间. 对于三阶格式, DDG-P2 比BR2-P2效率提高了19%, DG/FV重构又使DDG-DG1/FV2较DDG-P2效率提升22%. 综合DDG和DG/FV的作用, 新的混合格式DDG/FV 的计算效率达到BR2-P2 格式的1.6倍.
Table 8
表 8
表 8非定常圆柱绕流千步CPU时间对比
Table 8CPU time of one thousand time steps for unsteady flow over a cylinder
 |
新窗口打开
混合格式DDG/FV对非定常流动的单步计算效率提升作用弱于对定常流动的效率提升, 主要原因有两点: (1) 定常流动使用隐式LU-SGS方法进行时间离散, 需要额外更新数值通量, DDG格式在计算数值通量时相比BR2格式效率更高. 因此使用LU-SGS 进行时间推进时, DDG 对单步计算效率的提升更大. (2) 本算例中使用了并行计算, 在各个并行分区通信的过程中, DG/FV 重构过程通讯负载较大, 影响其对计算效率的提升. 如果采用双时间步方法模拟非定常问题, 则在每个真实时间步之间的虚拟时间迭代中, DDG/FV 混合格式的效率优势将与定常流的计算一致.
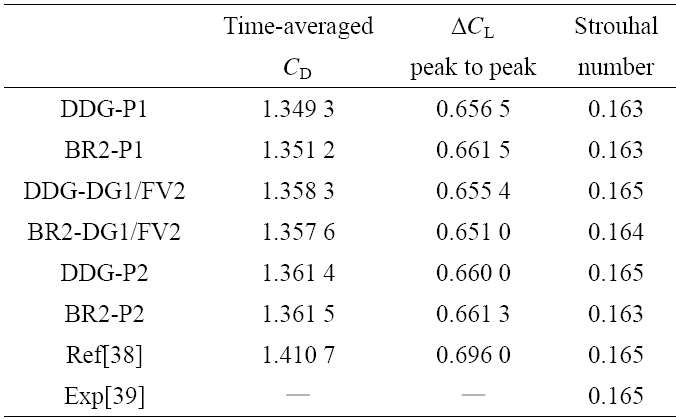
图9给出了$t=200$时, 非定常圆柱绕流的涡量云图. 从图中可以看到明显的卡门涡街, 涡量一正一负的漩涡交替从圆柱表面脱落. 并且在向下游移动的过程中, 由于数值耗散的原因, 涡量绝对值逐步减小. 在$t=200$时, DDG-DG1/FV2 和BR2-P2 的计算结果相位差近似为$\pi$, 前者正涡量漩涡即将脱落, 后者的负涡量漩涡即将脱落. 尽管各格式计算结果的相位有差异, 但升力、阻力系数以及斯特劳哈尔数$St$ 非常接近. 表9列出了各种格式的时均阻力系数, 升力系数峰峰值和$St$ 数值. 可以看到6种格式的时均阻力系数, 升力系数峰峰值结果十分接近, 与文献[38]给出的参考值略有差异. 原因可能是网格密度不足. 但6种格式所计算的$St$数与文献值[38]以及实验值[39]都吻合良好. 验证了混合格式DDG/FV在非定常问题中的计算精度.
Table 9
表 9
表 9时均阻力、升力、$St$数对比
Table 9Comparison of the time-averaged drag coefficient,peak to peak lift coefficient and Strouhal number for unsteady
 |
新窗口打开
显示原图|下载原图ZIP|生成PPT图9非定常圆柱绕流涡量云图, $t=200$
-->Fig.9Vorticity contour for unsteady flow over a cylinder at $t=200$
-->
2.4 NACA0012翼型层流绕流
NACA0012翼型是较为实用的算例, 可以用来考察混合格式的计算效果. 来流条件设定为: $Ma=0.2$, $Re=5000$, 参考长度为1. 壁面采用温度为288.15 K的无滑移等温壁面边界条件, 外边界给定远场边界条件. 计算域和网格分布参考图10, 第一层网格高度0.001.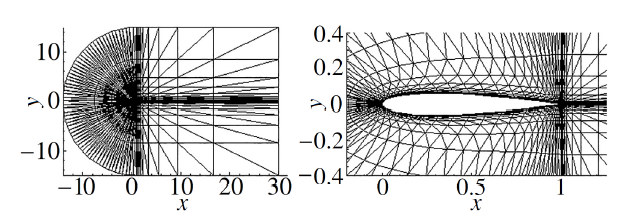
显示原图|下载原图ZIP|生成PPT图10NACA0012翼型非结构网格
-->Fig.10Unstructured grid for laminar flow over a NACA0012 airfoil
-->
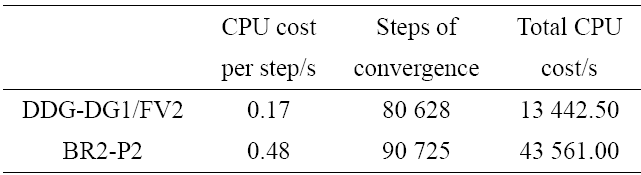
表10列出了DDG-DG1/FV2和BR2-P2格式的单步计算时间, 达到收敛的迭代步数和CPU 时间. 本算例使用全局时间步长$\text dt=2\times10^{-3}~\text s$, 因此DDG-DG1/FV2达到收敛的迭代步数只是比BR2-P2 格式稍少. 因此无论从单步计算时间还是达到收敛的总CPU 时间来看, 混合格式的效率都比BR2-P2 格式提高近3 倍.
Table 10
表 10
表 10NACA0012翼型绕流计算时间和收敛步数对比
Table 10CPU time and convergence steps for laminar flow over a NACA0012 airfoil
 |
新窗口打开
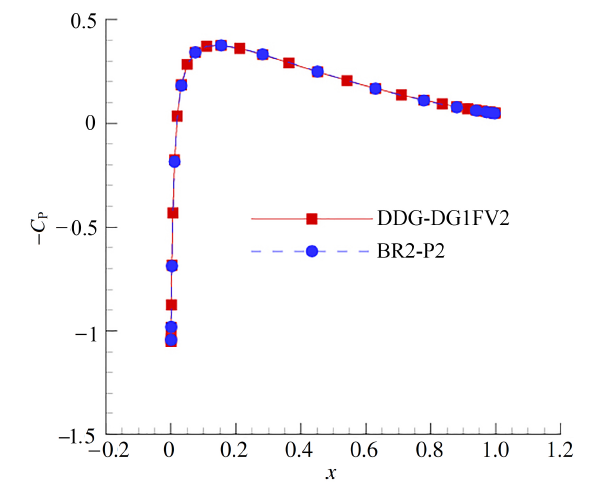
图11给出了两种格式计算得到的马赫数云图. 从图中可以看出, 马赫数分布对称性较好, 两种格式给出的流场分布接近. 图12和图13分别给出了翼型上壁面的摩阻系数和压力系数分布曲线. 两种格式在摩阻系数分布上略有差异, 而压力系数分布曲线则几乎完全重合.
显示原图|下载原图ZIP|生成PPT图11NACA0012翼型绕流马赫数云图
-->Fig.11Mach number contour for laminar flow over a NACA0012 airfoil
-->
显示原图|下载原图ZIP|生成PPT图12NACA0012翼型上壁面摩阻系数分布
-->Fig.12Upper surface friction drag coefficient $C_f$ for laminar flow over a NACA0012 airfoil
-->
显示原图|下载原图ZIP|生成PPT图13NACA0012翼型上壁面压力系数分布
-->Fig.13Upper surface pressure coefficient $C_p$ for laminar flow over a NACA0012 airfoil
-->
3 结 论
本文将DDG黏性项处理方法推广应用于DG/FV混合算法中, 得到了DDG/FV混合格式. 针对新的混合格式通过一系列数值实验, 得出以下结论:(1) DDG数值通量公式中参数$\beta_0$的选择与网格边数无关, 对精度阶和稳定性影响较小. 但在本文测试的取值范围内, $\beta_0$取值越大, 格式的绝对误差越小. 因此在二阶和三阶DDG 方法中, $\beta_0$的推荐值为4.
(2) DDG/FV混合算法在结构和非结构网格上均能达到理论数值精度阶数; 在自由度数相同时, 其绝对误差与同阶DGM相当.
(3) 在定常问题中, 采用隐式LU-SGS时间推进方法, DDG/FV的单步计算效率是同阶BR2-DG的2倍以上; DDG/FV达到收敛所需的计算步数更少; 从达到收敛所需的CPU总时间来看, 新的混合格式相比同阶BR2-DG格式计算效率提升3倍以上. 在非定常问题中, 采用显式Runge-Kutta时间推进方法, DDG/FV的计算效率是同阶BR2-DG的1.6倍. 因此DDG/FV混合格式具有较大效率优势.
(4) 在特定算例中, DDG/FV混合格式相比BR2与DG/FV的混合格式更加稳定.
综上, 本文构造的DDG/FV混合格式对比BR2-DG格式, 在达到相同数值精度的情况下, 计算效率具有明显优势, 并且具有更优良的计算稳定性, 在非结构/混合网格的Navier-Stokes方程求解中具有更好的应用前景. 下一步我们将会拓展DDG/FV混合格式到三维实际外形的计算, 并且将利用新的混合格式离散求解RANS方程, 以期获得更高的计算效率和更好的收敛特性.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . . |
| [2] | . Springer International Publishing, |
| [3] | . Springer International Publishing, |
| [4] | . |
| [5] | . |
| [6] | . |
| [7] | . |
| [8] | |
| [9] | . |
| [10] | |
| [11] | . |
| [12] | |
| [13] | . |
| [14] | . |
| [15] | . |
| [16] | . |
| [17] | . |
| [18] | . |
| [19] | . |
| [20] | . |
| [21] | . |
| [22] | |
| [23] | . |
| [24] | . |
| [25] | . . |
| [26] | . . |
| [27] | . . |
| [28] | . |
| [29] | . |
| [30] | . |
| [31] | . |
| [32] | . |
| [33] | . . |
| [34] | . . |
| [35] | |
| [36] | . |
| [37] | |
| [38] | . |
| [39] |
