, 贺红TRAFFIC FLOW DYNAMIC MODEL CONSIDERING THE INFLUENCES ON DRIVERS BASED ON FIELD FORCE1)
ChenYong, HeHong中图分类号:O39,U491
文献标识码:A
通讯作者:
收稿日期:2018-04-4
接受日期:2018-04-4
网络出版日期:2018-09-18
版权声明:2018力学学报期刊社力学学报期刊社 所有
基金资助:
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (22333KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引言
交通流理论是指运用物理和数学方法描述交通特性的一门交叉学科, 该理论的应用能更好地解析交通现象及其本质, 使道路发挥最大功效. 元胞自动机(cellular automaton, CA) 是一种通过空间局部相互作用的网格动力学模型, 具有时间、空间、状态都离散的特点, 它是一种模拟非线性复杂系统的有效动力学工具[1-6]. CA模型具有规则简单、自组织、易于并行计算的特点, 能够有效模拟交通流中的车辆微观运动, 被广泛应用于微观交通流的研究中[7-9]. Nagel和Schreckenberg[10]提出的NaSch模型就是一种典型的CA 模型, 通过前后车安全距离控制规则及随机慢化来模拟单车道上车辆的行驶行为, 众多****通过对NaSch模型的改进, 模拟了丰富的交通非线性现象, 更好地揭示了交通现象的物理本质[10-14].在道路交通系统中, 驾驶员是道路交通系统中信息的接收者和处理者, 是"人-车-路-环境''中的主导者, 是交通系统的核心部分, 驾驶员的行为是对外部交通环境的认知, 同时其行为直接反馈至交通系统, 驾驶员的行为很大程度上决定了交通系统的运行状态[15-18]. 许多****对驾驶员对交通系统的影响进行了相关研究: 彭莉娟等[19]建立了驾驶员CA模型, 分析了驾驶员不同类型及驾驶方式改变对交通的影响; Wang等[20]建立了考虑交通信号灯对驾驶员影响的CA模型, 研究了驾驶行为与交通延迟的关系; Ding等[21]从驾驶员心理角度, 提出了一种考虑驾驶员学习和遗忘特性扩展NaSch 的交通流模型; 郑亮等[22] 分析了车辆自身速度、安全间距等因素对公路交通的影响; Shi 等[23]研究了驾驶 员使用手机等分心行为对交通安全的影响; 陶鹏飞等[24]采用心理场理论对驾驶员行为进行了建模分析; 华雪东等[25]针对驾驶员在换道时的不同心理, 建立了驾驶员心理换道元胞自动机模型等. 上述研究都是从驾驶员的行为角度出发, 结合驾驶员心理、视觉及行为特性, 模拟了驾驶员在交通过程中的刺激、认知、决策等活动对交通的影响.
目前针对驾驶员对交通流的影响性研究中, 大部分仿真研究模型建立时都是仅考虑前车(速度、距离)对驾驶员的单一影响, 即每个驾驶员仅对来自前方车辆的激励作用做出反应; 驾驶员心理场研究方法虽然借鉴了场强的概念, 但模型建立时也仅考虑了前车速度和距离对驾驶员的影响. 在实际交通过程中, 是一个复杂的人-机-环境系统, 驾驶员不仅受到前车的直接影响, 还受到驾驶员车辆周围交通环境的影响, 以及驾驶员自身的生理和心理也会对驾驶行为产生影响, 然而目前缺少考虑驾驶员复合影响因素的交通流模型. 此外, 现有NaSch模型中随机慢化概率值$P$为固定值, 即默认道路上所有车辆的减速概率都相同, 取固定概率值$P$, 而且该值不随时间而变化, 这显然与实际交通情况不符. 在实际交通系统中, 每辆车的减速概率应该是不同的, 每辆车的驾驶员在每个时刻的减速慢化概率值应该是驾驶员根据道路交通环境而不断实时动态调整变化的.
针对上述驾驶员CA模型的不足, 本文以元胞自动机理论为基础, 结合场力和图论等数学方法, 在NaSch模型的基础上, 提出了一种综合考虑驾驶员影响的动力学交通流模型(influences on drivers celluar automat, IDCA), 利用此模型进行模拟仿真并分析得到了一些复杂的交通现象, 本研究对于研究驾驶员行为对交通的影响有一定的实际意义.
1 考虑驾驶员影响因素CA模型建立
1.1 驾驶员行为影响因素分析
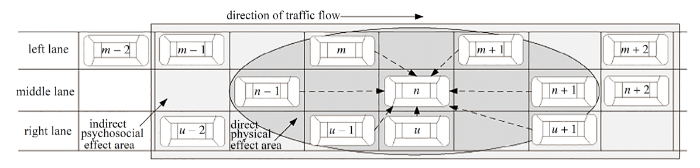
驾驶行为是指在汽车的行驶过程中, 驾驶员通过视觉、听觉和触觉等, 将道路上运行的车辆、车辆本身的工况等外界信息传入大脑, 再根据其知识和经验, 做出判断和决策, 然后通过手、脚操纵机构, 使汽车的速度和方向发生相应的调整. 由此可知, 驾驶员的驾驶行为是由信息感知、判断决策和动作组成的不断反复进行的信息处理过程. 驾驶员的行为会影响车辆活动及车辆之间的相互作用, 从而影响道路交通.目前的NaSch模型中, 默认驾驶员驾驶的车辆仅受前车的影响, 而且NaSch模型中当两车间距非常大的情况下, 后车依然受到前车的影响, 这显然与实际情况不相符. 驾驶员在驾驶车辆过程中, 主要依靠视觉来感知各种交通信息, 受视野约束, 驾驶员驾驶行为会受到前、后及旁道临近其他车辆物理约束的直接影响; 此外驾驶员还受到交通环境的间接心理影响, 例如在驾驶员局部周围车辆越多, 往往驾驶员减速概率越大. 为了便于描述, 本文建立的驾驶员影响因素场景示意如图1 所示, 图中以车辆$n$为例, 对驾驶员受到的直接物理影响、间接心理影响等其他影响因素进行说明.
显示原图|下载原图ZIP|生成PPT图 1驾驶员影响因素交通场景示意图
-->Fig.1Traffic scene sketch of influences on drivers
-->
(1)直接物理影响
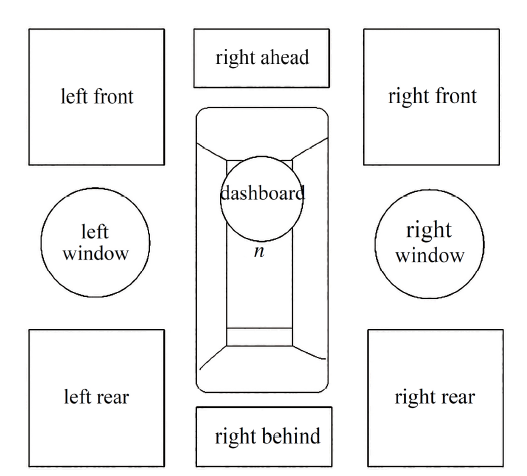
当车辆$n$在中车道行驶时, 驾驶员不断关注不同的视点注视区域, 以获取驾驶所获得的各类区域. 驾驶员注视区域平面分布图如图2所示, 驾驶员都有其特定的视觉搜索规律, 具体包括搜索区域、关注重点等.
显示原图|下载原图ZIP|生成PPT图 2驾驶员注视区域平面分布图
-->Fig.2Plane distribution diagram of driver's gaze area
-->
考虑到实际驾驶员在驾驶车辆时, 由于驾驶员视觉范围约束和其他临近车辆物理制约的因素, 驾驶员的驾驶行为会受到其他车辆的直接物理影响. 如图1中, 车辆$n$在中车道行驶过程中, 其加速、减速、匀速等运行直接受到前车$n+1$的影响,也受到其后方车辆$n-1$ 的影响如鸣笛行为; 此外车辆$n$如果换道到左车道时, 同时也直接受到其左前方车辆$m+1$和左后方车辆$m$的影响, 即车辆$n$如果从中车道换道到左车道时, 取决于换道后车辆$n$与车辆$m+1$ 距离能否满足其驾驶行驶期望以及换道后与左后方车辆$m$的安全间距条件的约束; 同理车辆$n$从中车道换道至右车道时, 也直接受到车辆$u-1$, $u$, $u+1$ 的影响.
(2)间接心理影响
在驾驶员驾驶车辆过程中, 除了受到前方、后方、左侧、右侧等其他车辆直接物理影响外, 还存在这样的现象: 如果车辆$n$所在的车道及旁道上局部车辆越多, 则驾驶员受到的心理压力越大, 驾驶员就会时刻保持警惕的心态, 随机慢化减速的概率就会越大; 如果车辆$n$所在的车道及旁道上局部车辆越少, 则驾驶员就会以相对轻松的心理驾驶车辆, 随机慢化减速概率就会越小, 上述现象说明在实际交通中还存在局部间接心理影响因素.
(3)其他影响
在驾驶员驾驶车辆过程中, 除了直接物理和间接心理影响因素外, 驾驶员的类型、车辆自身的速度、相对速度、车间距对驾驶员的驾驶行为都有影响[19,22].
1.2 驾驶员影响因素IDCA模型建立
在物理学中, 把某个物理量在空间的一个区域内的分布称为场, 如温度场、密度场、引力场、电场、磁场等. 场论是经典物理学的重要组成部分, 分为自然场和社会场. 其中, 自然场有引力场、电磁场等, 自然场具有质量、能量、动量等属性, 是物质存在的基本形式之一[26-28]. 而社会场是把社会当作一个场, 认为任何事物都存在于一定的"场''中[29-30]. 这种"场''即是社会的整体环境, 其也有类似于磁场的一些性质, 具有相互影响的能量[24,30]. 场中的物质不是单一的、孤立的存在, 而是受到场中其他物质和环境的复合影响. 在道路交通系统中, 驾驶员处于道路交通环境中的"社会场''中, 驾驶员不再单一受到驾驶车辆物理条件的影响, 而是会受到交通场的复合影响, 其行为会受到驾驶员的心理、生理及车辆周围物理环境的综合影响, 驾驶员行为随着道路交通情况实时变化而改变, 驾驶员会选择相应的驾驶行为.在场论中, 场力用来描述物质之间的关系, 场力的统一公式为
\begin{align*}F_{a\rightarrow b}=k\dfrac{M_{a}M_{b}}{r^{2}}\end{align*}
式中$M$为物体本身的性质(质量、速度等); $r$为两物质之间的距离、关系等; $k$为作用力系数. 作用力正比于自身物质的场力, 与距离的平方成反比. 本文借鉴场论中场力计算思想, 应用于驾驶员行为建模中, 去描述驾驶员对不同状态下周围车辆直接物理影响和间接心理影响因素、车间距、相对速度等物理环境的行为反应.
NaSch模型中, 随机减速概率$P$为一个常数, 这意味着道路上所有的车辆以相同的减速概率进行, 显然与实际交通情况不符. 在实际交通系统中, 每辆车辆在每个时刻的随机减速概率不仅受到车辆自身速度的影响, 还要受到驾驶员心理、生理(不同性格驾驶员反应时间不同)及道路物理环境的综合影响. 因此, 本文在NaSch模型的基础上, 综合考虑了驾驶员受到心理的直接物理影响、间接心理影响、车辆相对速度、车间距以及车辆自身的速度影响, 并将驾驶员的决策输出通过随机慢化概率$p_{n}(t+1)$体现出来, 以及结合激进型驾驶员驾驶过程中对前导车的变化敏感, 自始至终与前车保持最近距离跟驰的特点, 建立了IDCA交通动力学模型. 本文建立的模型中, 随机慢化概率$p_{n}(t+1)$表达式如下
\begin{equation} p_{n}(t+1)=\left\{ \begin{aligned}&k\dfrac{CCN\cdot(v_{n}(t)-v_{n+1}(t))}{d^{2}_{n}(t)}\cdot\dfrac{1-\text{e}^{-\lambda v_{n}(t)}}{1+\text{e}^{-\lambda v_{n}(t)}}, \\&\qquad\text{if}~v_{n}(t)> v_{n+1}(t)~\text{and}~d_{n}(t)\leqslant d_{\text{safe}} \\&k\cdot CCN\cdot P,~\\&\qquad \text{if}~v_{n}(t)\leqslant v_{n+1}(t)~\text{or}~d_{n}(t)> d_{\text{safe}}\end{aligned} \right.\end{equation}
式(1)中, $p_{n}(t+1)$表示车辆$n$在$t+1$时刻的随机慢化概率值, 其中$k$ 为驾驶员影响场力系数, 参数$CCN$(cybeinetic control number)[31] 表征不同类型驾驶员的人体倾向性行为参数, $k$值和$CCN$的说明和取值下文将具体分析给出.
$p_{n}(t+1)$值的计算分两种情况: 第一种情况为: 当后车速度大于前车速度, 并且两车距离小于等于最小安全间距$d_{\text{safe}}$时, 此时后车跟驰行为明显, 后车受到前车的明显的制约作用, $\dfrac{v_{n}(t)-v_{n+1}(t)}{d^{2}_{n}(t)}$ 为车辆$n$受到的场力值, 其中$v_{n}(t)$ 为车辆$n$的速度, $v_{n+1}(t)$为前车的车速, $d_n(t)$为车辆$n$ 在$t$ 时刻与前车之间的距离. $d_n(t)$值表示当后车与前车之间的速度差异越大, 后车速度越大, 后车越容易受到前车的影响, 此外后车与前车之间的距离越小, 后车跟驰过程中越容易受到前车的影响, 该值越大说明前车对后车形成的场力越大, 后车的驾驶员会谨慎驾驶, 后车随机慢化的概率就越大. 反之, 前车与后车之间距离越大, 后车与前车速度差越小, 此时前车对后车的影响就越小, 说明前车对后车形成的场力越小, 后车的驾驶员也会以一种比较轻松的心情驾驶车辆, 随机慢化的概率就越小. 第二种情况为: 当后车速度小于等于前车速度$v_{n}(t)\leqslant v_{n+1}(t)$ 时, 此时若后车速度$v_{n}(t)$和前车速度$v_{n+1}(t)$ 相等, 说明两车处于匀速行驶状态; 此时若后车速度$v_{n}(t)$小于前车速度$v_{n+1}(t)$, 说明前车速度快, 后车速度慢, 此时后车跟驰行为不明显, 后车基本不受前车的约束, 此时车辆$n$ 与前车之间的场力值将退化为NaSch 模型中的随机慢化概率值$P$, $P$值在NaSch 模型中表示各种不确定性因素造成的减速概率.
式(1)中$\dfrac{1-\text{e}^{-\lambda v_{n}(t)}}{1+\text{e}^{-\lambda v_{n}(t)}}$ 表示当车间距小于安全间距时, 车辆$n$自身速度对随机慢化概率的影响, 其中$\lambda$的最大似然估计值为$N\Big/\sum\limits^{N}_{n=1}v_n(t)$. $\dfrac{1-\text{e}^{-\lambda v_{n}(t)}}{1+\text{e}^{-\lambda v_{n}(t)}}$表示由于后车速度大于前车速度, 跟驰行为明显, 当车辆自身速度比较小时, 驾驶员会以较放松的心情驾驶车辆, 随机慢化概率就越小; 当车辆速度较大时, 驾驶员就会以较紧张的心情驾驶车辆, 考虑到安全问题, 驾驶员通常会选择减速来以便安全行车, 此时随机慢化概率较大[22].
1.3 $k$值和$CNN$
为便于描述, 以图1所示的考虑驾驶员影响因素交通场景为背景, 一共有3个车道, 以车辆$n$ 驾驶员为例进行说明. 车辆$n$在道路上行驶时, 不仅受到直接物理影响(函数$f(n)$表示车辆$n$驾驶员受到的直接物理影响), 还受到间接心理影响(函数$g(n)$表示车辆$n$驾驶员受到的间接心理影响). 综合驾驶员受到的直接物理和间接心理影响因素后, 车辆$n$ 驾驶员受到的影响引力系数$k$通过下式计算\begin{align*}k=f(n)\cdot g(n)\tag*{(2)}\end{align*}
其中, $f(n)$为直接物理影响函数, $g(n)$为间接心理影响函数, 函数定义说明如下.
(1)直接物理影响函数$f(n)$
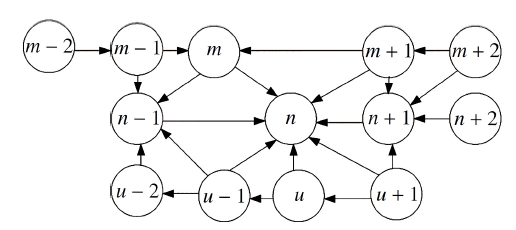
针对驾驶员的直接物理影响, 建立模型时采用图论的方法, 在每个时刻$t$, 从每辆车辆所在的交通场景中, 将每辆车驾驶员受到的直接物理影响车辆抽象为图中的节点, 车辆之间的影响关系抽象为有向弧, 通过对图的计算来实现对驾驶员直接物理影响的量化计算. 如图1所示的交通场景, 以车辆$n$为研究参照点, 抽象为图3所示.
显示原图|下载原图ZIP|生成PPT图 3驾驶员直接物理影响映射图
-->Fig.3Diagram of driver's direct physical influences mapping
-->
通过抽象为图的映射关系, 可以清楚的看到车辆之间的制约关系, 可以弥补NaSch模型只考虑前车影响的不足, 可以真实反映实际交通情况, 结合图2驾驶员注视区域分布特点, 定义车辆$n$的驾驶员受到的直接物理影响函数$f(n)$计算如下
\begin{align*}f(n)=\dfrac{1}{\sum\limits^{s}_{i=1}(d(n,i)\cdot\text{cos}\theta)},i\in \lbrace par(n)\rbrace\tag*{(3)}\end{align*}
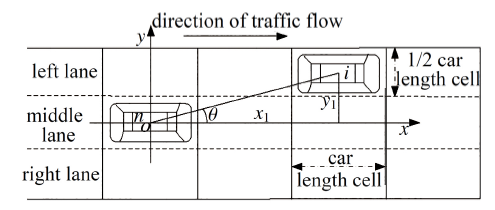
式(3)中$f(n)$用于计算车辆$n$所受的直接物理影响值, $par(n)$为车辆$n$ 在每个时刻$t$从交通场景映射为图后, 图中节点$n$的直接前驱节点集合, 即$f(n)$计算直接物理影响时只考虑对车辆$n$有直接物理影响的车辆制约关系, 而与其他车辆影响无直接因果关系. 如图3 中, 车辆$n$的直接物理影响仅受节点$n$的直接前驱$m, m+1, n+1, n-1, u, u+1, u-1$的影响, 而与其他节点无直接影响关系, 从而反映出驾驶员视觉注视局部关注的特点. 上式中$s$表示节点$n$ 的直接前驱个数之和, 即车辆$n$受到其他车辆直接影响的车辆数. 式(3)中变量$\theta$表示车辆$n$中心原点与直接物理影响车辆中心连线与水平车道的夹角, 车辆直接物理影响下变量$\theta$如图4所示, 一般取车辆$n$的宽度为车辆占据元胞长度的1/2, 通过$\theta=\text{arctan}(y_{1}/x_{1})$求出$\theta$值, 其中变量$x_1$为车辆$n$中心原点与直接影响车辆$i$中心水平距离, 变量$y_1$为直接物理影响车辆$i$中心到水平车道的垂直距离. $\theta$取值范围为$[0,\pi /2]$, 当$\theta$为0时表示对车辆$n$的影响车辆为正前方行驶车辆或为正后方车辆, 当$\theta$为$\pi/2$时表示此时影响车辆位于车辆$n$的左窗或右窗位置.
显示原图|下载原图ZIP|生成PPT图 4车辆直接物理影响下变量$\theta$示意图
-->Fig.4Sketch of variable $\theta$ under the condition of driver's direct physical influences
-->
式(3)中, $d(n,i)\cdot\text{cos}\theta$表示车辆$n$与其直接物理影响车辆$i$的欧式距离通过$\text{cos}\theta$投影映射变换到车辆$n$所在的水平车道, 从而将车辆$i$ 对车辆$n$的直接物理影响定量转换到水平车道上. 式(3)中, $\sum\limits^{s}_{i=1}(d(n,i)\cdot \text{cos}\theta)$ 为所有直接物理影响车辆$n$的车辆复合影响. 从式(3)中$f(n)$计算可以看出, 某车辆所受的综合直接物理影响 $f(n)$ 与$d(n,i)\cdot \text{cos}\theta$成反比, 这是因为在真实交通状况中, 如果车辆$n$与其直接物理影响车辆越近, 即$d(n,i)\cdot \text{cos}\theta$ 越小, 则驾驶员就会时刻保持警惕的心态, 随机慢化的概率就会越大, 如果车间距较大, $d(n,i)\cdot \text{cos}\theta$ 越大, 则驾驶员就会以轻松的心态驾驶, 随机慢化概率就越小.
(2)间接心理影响函数$g(n)$
在NaSch模型中将车道道路划分为若干个离散的格子, NaSch模型中主要考虑前车对后车的影响, 而当车间距比较大时, 模型中两车依然有联系, 显然这与实际情况是不符的. 本文驾驶员行为模型建立时, 对该NaSch模型不足点进行约束改进, 模型建立时, 对于两车的间接心理影响间距为$d_{\text{safe}}$, 当两车间距$d_{n}(t)$大于$d_{\text{safe}}$ 时, 两车不存在间接心理影响; 对于车道车辆及道旁车辆的间接心理影响, 本文建立模型时采用稀疏矩阵进行定量描述, 在该矩阵中, 每一行代表一个车道, 如果对应的车道上元胞位置没有被车辆占据, 则对应的矩阵元素值为0, 如果对应的车道上元胞位置被车辆占据则对应为1. 因为两车的最大影响间距为$d_{\text{safe}}$, 所以车辆$n$所在的车道上, 对车辆$n$影响的车辆元胞位置最大为车辆$n$ 前后方各$d_{\text{safe}}$距离范围内, 因此该稀疏矩阵为$m$行($m$为车道数), $2d_{\text{safe}}+1$列, 形成一个$m\cdot(2d_{\text{safe}}+1)$ 大小的稀疏矩阵. 例如, 对于图1 所示的驾驶员影响因素交通场景示意图中, 则车辆$n$所受的间距影响稀疏矩阵表示如下
\begin{align*}\begin{bmatrix}a_{1,1}\hskip -2mm&a_{1,2}&\cdots&\cdots&\cdots&\cdots&\cdots\hskip -1mm&a_{1,n+d_{\text{safe}}}\\b_{1,n-d_{\text{safe}}}\hskip -2mm&\cdots&\cdots&b_{2,n-1}&b_{2,n}&b_{2,n+1}&\cdots\hskip -1mm &b_{2,n+d_{\text{safe}}}\\c_{3,1}\hskip -2mm&c_{3,2}&\cdots&\cdots&\cdots&\cdots&\cdots \hskip -1mm&c_{3,n+d_{\text{safe}}}\end{bmatrix}\end{align*}
该矩阵中, 第1行表示左车道, 第2行表示车辆$n$所在的中车道, 第3行表示右车道. 例如图1所示的交通场景中, 如果$d_{\text{safe}}=3$, 则车辆$n$受到的间接心理影响稀疏矩阵相应取值为
\begin{align*}\begin{bmatrix}1&0&1&0&1&0&1\\0&1&0&1&0&1&1\\1&0&1&1&0&1&0\end{bmatrix}\end{align*}
在驾驶员间接心理影响稀疏矩阵表示的基础上, 函数$g(n)$进行间接心理影响定量计算. 在实际交通情况中, 驾驶员行驶过程中, 驾驶员影响范围内的车辆越多, 进入视野的信息量也越大, 驾驶员需要注意的信息也很多, 则需要驾驶员注意力高度集中, 从中筛选出有用的信息, 随机慢化的概率就会越大, 从而会导致车速下降. 若驾驶员影响范围内的车辆越少, 信息量较少, 则驾驶员便会处于放松的状态, 随机慢化概率较小, 车速较高[32]. 结合驾驶员这一特点, 本文采用矩阵稠密度来表示驾驶员受到的间接心理影响的大小, 在稀疏矩阵中, 一般定义非零元素的总数比上矩阵所有元素的总数为矩阵的稠密度. 因此本文IDCA模型中, 车辆$n$所受的间接心理影响在稀疏矩阵表示的基础上, 进一步通过计算该稀疏矩阵的稠密度来得出车辆$n$ 驾驶员受到的间接心理影响值, 即统计稀疏矩阵中非零元素(即车道上有车个数)的总和与矩阵所有元素的比值, 来实现对驾驶员间接心理影响的定量计算, 计算公式如下
\begin{align*}g(n)=\dfrac{\sum\limits^{m}_{i=1}\sum\limits^{2d_{\text{sdfe}}+1}_{j=1}a[i,j]-1}{m\cdot(2d_{\text{safe}}+1)}, a[i,j]=1\tag*{(4)}\end{align*}
\noindent 式中$g(n)$表示车辆$n$的驾驶员所受到的间接心理影响值, 分母$m\cdot(2d_{\text{safe}}+1)$为稀疏矩阵中所有元素的个数, 分子$\sum\limits^{m}_{i=1}\sum\limits^{2d_{\text{safe}}+1}_{j=1}a[i,j]-1$ 为所有$m$ 条车道上, 车辆$n$间接心理影响$m\cdot(2d_{\text{safe}}+1)$矩形范围内车辆总数减去车辆$n$自身所占的一个车长元胞长度空间. $g(n)$的值越大, 说明车辆$n$周围的影响车辆越多, 驾驶员受到的间接心理影响越大, 随机慢化的概率就越大, 从而会导致车速下降, 反之则随机慢化概率越小.
在NaSch模型中, 车辆与车辆之间的作用通过局部左右元胞邻居来进行车辆与车辆之间的交互作用, 在本文建立的考虑驾驶员影响因素的IDCA模型中, 元胞邻居选取扩展Moore型, 扩展Moore型由$M\cdot(2d_{\text{safe}}+1)$的矩阵构成, 从而体现出驾驶员间接心理影响的作用范围.
(3)驾驶员生理$CNN$参数
从生理学的角度, 认为人的行为是由人的中枢神经活动与手、足等器官的协调配合而形成的, 通常用表征人体倾向性行为特征的参数$CCN$来表示, $CCN$的值可以通过个体选择反应时间$T_x$和神经滞后时间$T_d$来计算得出: $CCN=\dfrac{3}{T_x}-\dfrac{1}{2T_d}$[31]. 驾驶员的反应判断能力与手足的协调动作能力可以分别用反应速度和动作速度的快慢来表示在道路交通中, 不同性格驾驶员的驾驶行为不同, 其性格、反应能力等都会对交通有不同的影响. 一般情况下, 驾驶员的性格特性可以归纳为3种类型, 分别为激进型、保守型和中立型, 道路中不同类型驾驶员所占比例和为1[19]. 不同类型驾驶员具有不同的特点, 其中: \textcircled{\small{1}} 激进型驾驶员在行车过程中喜欢开快车, 总试图保持最大速度和效率最大化, 其减速的概率较小; \textcircled{\small{2}}保守型驾驶员考虑更多的则是安全, 与前车保持较大的车间距, 会时刻保持警惕进行安全驾驶, 减速概率较大; \textcircled{\small{3}}中立型介于激进型和保守型驾驶员之间, 驾驶员会根据实际情况选择自己的驾驶行为, 当两车间距大于安全间距时, 其驾驶行为与激进型驾驶员相同; 当两车间距小于等于安全间距时, 其驾驶行为与保守型驾驶员保持一致. 对于不同类型驾驶员$CCN$参数取值, 文献[33]通过对不同类型驾驶员多种车型进行多种情况实际驾驶试验得到相应数据集, 然后进行数据分析和参数标识, 得出神经滞后时间$T_d\in [0.175,0.53]$. 在上述参数辨识基础上, 通过$CCN$计算综合分类后得到当$CCN\in[0.1,1.74]$ 时, 驾驶员特征为激进型; 当$CCN\in[1.75,2.99]$时, 驾驶员特征为中立型; 当$CCN\geqslant 3$时, 驾驶员特征为保守型[31].
1.4 考虑驾驶员影响因素IDCA模型演化规则
此外为了能够得到更加丰富的交通流特性, 本文IDCA模型建立时, 还进一步考虑了对"高速跟驰'' 现象的模拟. 国内一些****通过架设的视频采集设备拍摄了上海、北京、西安、郑州等城市的主要快速路段的交通视频, 通过视频处理得到了"车速-车头间距''交通流实测数据集, 发现在数据集中的跟驰交通流中, 道路上存在一些车速较高的车辆, 车速大于它与前车的车头间距. 数据集显示, 间距较小的车辆并非都是低速行驶, 存在部分车辆速度明显高于通常处于该密度时应有的速度, 即"高速跟驰'' 现象[34]. 这种"高速跟驰'' 需要适当的交通模型来描述.NaSch基本模型是无法模拟出高速跟驰现象, 因为在NaSch演化规则第2步: 确定性减速过程中, 为了描述安全防护, 下一单位演化时间内, 车速始终要求小于或等于该车与前车的车头间距, 不会出现车速大于车头间距的情况. 在NaSch模型中在车头间距计算的过程中, 将前车视为静止的粒子, 没有将前车的运动动态特性进行考虑, 而高速跟驰交通流实测文献[34]中也指出不同特征的驾驶员驾驶行为会影响到高速跟驰现象的发生.
本文IDCA模型建立时, 结合激进型驾驶员在驾驶过程中对前导车的变化最为敏感, 自始至终与前车保持最近距离, 其他类型驾驶员保持较大车间距的特点, 结合前车的动态效应, 对激进型驾驶员跟驰的前车赋予一个动态预期速度$v'_{n+1}(t+1)$, 将激进型驾驶员的确定性减速过程修改为
\begin{align*}v_{n}(t+1)\rightarrow \text{min}(v_{n}(t+1),d_{n}(t)+v'_{n+1}(t+1))\tag*{(5)}\end{align*}
其中$v'_{n+1}(t+1)$是车辆$n$的前车$n+1$的动态预期速度, 该预期速度是按NaSch模型的演化规则可以得到的最小的期望速度, 通过下式计算得出
\begin{align*}v'_{n+1}(t+1)\rightarrow \text{min}(v_{\text{max}}-1,v_{n+1}(t),\text{max}(0,d_{n+1}(t)-1))\tag*{(6)}\end{align*}
对于激进型驾驶员的跟驰过程中, 本文提出的IDCA模型考虑了前车的动态运动效应, 前后车辆之间的车间距遵循同步的变化规律, 改变了基本NaSch模型中把当前时刻的车间距作为下一时刻车辆运动极限距离的约束规则, 同时式(5)进行了安全防护, 确保了更新过程中不会发生撞车行为.
综合以上分析后, IDCA模型建立时, 综合考虑了驾驶员受到心理的直接物理影响、间接心理影响、车辆相对速度、车间距、车辆自身的速度影响, 以及激进型驾驶员小间距跟驰的特点, 改进元胞自动机IDCA模型更新演化规则如下.
(1)确定每辆车$t+1$时刻随机慢化概率
\begin{align*}&\text{if}v_{n}(t)>v_{n+1}(t)~\text{and}~d_{n}\leqslant d_{\text{safe}}\\&\qquad p_{n}(t+1)=k\cdot\dfrac{CCN \cdot\left\lbrack v_{n}(t)-v_{n+1}(t)\right\rbrack}{d^{2}_{n}(t)}\cdot\\&\qquad \qquad \dfrac{1-\text{e}^{-\lambda v_{n}(t)}}{1+\text{e}^{-\lambda v_{n}(t)}}\\&\text{else}\\&\qquad p_{n}(t+1)=k\cdot CCN\cdot P\end{align*}
(2)加速过程
\begin{align*}v_{n}(t+1)\rightarrow \text{min}(v_{n}(t)+a,v_{\text{max}})\end{align*}
(3)确定性减速过程
(1)如果是激进型驾驶员, 确定减速过程如下
\begin{align*}v_{n}(t+1)\rightarrow \text{min}(v_{n}(t+1), d_{n}(t)+v'_{n+1}(t+1))\end{align*}
(2)如果是其他类型驾驶员, 确定减速过程如下
\begin{align*}v_{n}(t+1)\rightarrow \text{min}(v_{n}(t+1),d_n(t))\end{align*}
规则(1)和(2)表示不同驾驶员类型的车辆$n$行驶时为了避免和前车发生碰撞而采取的安全减速措施.
(4)车辆$n$在$t+1$时刻, 以概率$p_{n}(t+1)$随机慢化
\begin{align*}v_{n}(t+1)\rightarrow \text{min}(v_{n}(t+1)-b,0)\end{align*}
(5)车辆运动
$x_{n}(t+1)\rightarrow x_{n}(t)+v_{n}(t+1)$; 车辆按照调整后的速度向前行驶.
上式中$a$为车辆加速度, $b$为车辆减速度, $x_{n}(t+1)$表示$t+1$时间车辆$n$在道路中的位置, $d_{n}(t)$表示车辆$n$在$t$时刻与前车之间的距离. $p_{n}(t+1)$为车辆$n$在$t+1$时刻的随机慢化概率值, 通过式(1)计算得到; $k$为车辆$n$的驾驶员影响场力系数, 通过式$(2)\sim$式(4)计算得到; $P$为NaSch模型随机慢化概率值, $d_{\text{safe}}$为两车之间影响距离范围, 一般取$d_{\text{safe}}=v_{\text{max}}$. 在上述规则中$v'_{n+1}(t+1)$ 表示车辆$n$的前车$n+1$ 的动态预期速度, 通过式(6)计算得到.
2 数值模拟与仿真分析
模型建立时, 以图1所示的交通场景为背景, 道路场景由3条单向车道构成, 每条车道视为长度为$L$ 的一维离散格子组成, 每个格子大小相同, 每个格子或者为空, 或者被车辆占据, 车辆速度取0到$v_{\text{max}}$之间的整数, 为了将研究驾驶员影响因素的IDCA模型与NaSch 进行比较, 道路车辆单向行驶无换道行为. 车辆$n$在$t$时刻的状态由列车本身的行驶速度$v_{n}(t)$表示, $v_{n}(t)\in[0,v_{\text{max}}]$ , 其中$v_{\text{max}}$为车辆最大限速. 元胞自动机模型在仿真时, 可以根据实际情况规定元胞自动机迭代时间间隔和元胞长度, 使模拟结果具有实际的物理意义, 为了提高数值模拟的精度, 本文数值模拟时设定每个元胞长度为1.5 m, 车辆长度为7.5 m, 则每辆车占据5 个连续的元胞, 系统刷新时间间隔为1 s, 这就意味着, 当\mbox{$v_{\text{max}}=$1 cell/s} 时, 对应的车辆实际速度为5.4 \mbox{km/h, $v_{\text{max}}=$25 cell/s} 时, 对应的车辆实际速度为135 km/h.在数值模拟仿真时, 取道路长度$L=10~000$, 模型每一次演化时步取演化$5\times10^4$ 步, 为了消除初始状态随机性的影响, 每次记录每次演化达到稳态的后10~000步作为仿真时步, 迭代运行30次后样本数据取平均值. 为了便于对数值模拟结果进行比较分析, 避免左、中、右3条车道采用不同演化规则对相邻车道的车辆不同等影响, 数值模拟时按照3 条车道均采用NaSch规则演化和均采用本文提出的 IDCA模型演化后进行数值模拟结果的分析比较. 车辆加速度$a$和减速度$b$均为$1~\text{cell/s}^{2}$, 仿真元胞自动机模型是采用周期型边界条件, 每个元胞的邻居采用扩展Moore型, Moore型由$3\times(2d_{\text{safe}}+1)$ 的矩阵构成. 初始时, 3 条车道上激进型、中立型、保守型和三种类型的驾驶员驾驶车辆按比例$P_a$, $P_n$, $P_c$随机分布在车道上, 三种类型驾驶员$CCN$值分别取1.5, 2.5, 3.
2.1 不同密度下时空特性分析
仿真时取三种类型驾驶员混合比$P_a=0.2$, $P_n=0.5$, $P_c=0.3$, NaSch模型慢化概率$P=0.2$, 仿真车辆最大车速为25~cell/s即$v_{\text{max}}=$135 km/h, 改变3条车道不同的车辆密度$\rho$, 仿真时3条车道均按照NaSch规则进行演化并记录仿真结果, 然后同等3条车道车辆分布情况下均采用IDCA规则进行演化并记录仿真结果. 通过仿真得到了不同车流密度下不同车道的时空分布图, 取其中不同密度下中车道三组模拟对比结果如图$5\sim$ 图7所示, 图中横向表示道路空间位置, 纵坐标表示时间, 以黑色的点表示有车占据该位置, 白色表示该位置无车. 图5是在交通流密度都在$\rho=0.12$的条件下得到的时空图, 从图5(a)为3条车道均采用NaSch规则演化时得到的中车道时空图, 图5(b)为3条车道均采用IDCA演化规则得到的中车道时空图. 从中车道不同规则下时空图可以看出, 随着车流密度逐渐增加,采用NaSch 的中车道都出现了局部的拥塞情况, 图5(a)左车道空间位置3300 cell 附近出现局部堵塞,大约经过1400 s后才逐步消解; 图5(b)是采用本文建立的IDCA模型演化得到的中车道时空图, 可以看出在较低密度条件下, 与NaSch 模型相比, IDCA 模型局部拥堵能够在较短的时间内进行消解, 并恢复到自由流状态.
显示原图|下载原图ZIP|生成PPT图5$\rho=0.12$中车道时空图
-->Fig.5Space-time diagrams of middle lane under the condition
-->
显示原图|下载原图ZIP|生成PPT图6$\rho=0.15$中车道时空图
-->Fig.6Space-time diagrams of middle lane under the condition of $\rho=0.15$
-->
显示原图|下载原图ZIP|生成PPT图7$\rho=0.25$中车道时空图
-->Fig.7Space-time diagrams of middle lane under the condition of $\rho=0.25$
-->
仿真实验时, 继续增大道路交通流密度, 图6是在左、中、右3条车道都是在道路交通流密度$\rho=0.15$条件下得到的时空图, 图6(a)是3条车道均采用NaSch演化规则的中车道时空图, 可以看出随着车流密度逐渐增大, 在中密度车流情况下, 中车道出现了时走时停的交通波现象, 这是因为在中密度条件下由于车辆之间的相互影响增大, 将发生自挤压过程, 随着车道密度升高而车速下降, 伴随着这种挤压效应, 此时会出现窄运动阻塞相, 并随着时间向车道上游传播, 堵塞带更宽,不能在较短的时间内恢复. 图6(b)是3 条车道均采用IDCA演化规则的中车道时空图, 与采用NaSch模型的中车道相比, 可以看出系统拥堵相明显减少, 大部分区域内车辆都处于畅行状态. 图7 是在3 条车道密度$\rho=0.25$ 的条件下得到的高密度时空图, 可以看出随着密度的增大, NaSch 规则下的中车道由窄运动阻塞相逐渐演变为宽运动阻塞, 出现了畅行相向宽幅运动阻塞相转变和宽幅运动阻塞向畅行相转变的交通交替变化的现象, 不同的是图7(a) 3条车道均采用NaSch规则下中车道与采用3 条车道均采用IDCA演化的中车道相比, 图7(b) 中车道虽然也出现了交通拥堵现象, 但部分区域车辆分布均匀, 处于较为稳定的运动状态. 这是因为在IDCA模型中, 体现了驾驶员能够根据实际交通影响因素, 实时调整相对速度和安全间距来调节自己的驾驶行为的特点.
从上述3组不同密度下3条车道均采用NaSch规则和均采用IDCA规则得到的中车道时空图对比分布可以看出, 与NaSch模型相比, 考虑驾驶员影响因素的IDCA模型仿真结果表明拥堵能在更短的时间内稳定的消退, 这正说明IDCA模型体现了驾驶员能够根据道路实际交通场景, 实时动态调整驾驶行为, 从而使得堵塞消融的效率更高, 交通更能保持畅通状态.
2.2 不同密度下速度波动与车头间距波动性分析}
取3种类型驾驶员混合比$Pa=0.2$, $Pn=0.5$, $Pc=0.3$, NaSch模型慢化概率$P=0.2$, 仿真车辆最大车速为25 cell/s即$v_{\text{max}}=$135 km/h, 改变3条车道不同的车辆密度$\rho$, 通过仿真得到了不同车流密度下速度分布图、速度波动图和车头间距波动图. 当3 条车道密度均为0.08时, 得到了3条车道均采用NaSch规则和均采用IDCA 规则得到的中车道速度分布如图8所示, 速度波动图如图9所示. 图8(a)中, 少部分车辆由于固定随机慢化的影响, 会出现降速的情形. 从图9(a) 3条车道均采用 NaSch规则演化下中车道车辆速度波动图也体现出来这一特点, 大部分车辆车速在24 cell/s 到最大车速\mbox{25 cell/s}之间波动, 小部分车辆速度受随机慢化影响较大. 在同等条件下如图8(b) 所示, 可以看出均采用IDCA规则得到的中车道中大部分车辆车速都维持接近最大车速25 cell/s. 图9(b)为均采用IDCA 规则得到的中车道速度波动图, 与3条车道均采用NaSch 模型演化下9(a)相比, IDCA模型车速大部分接近最大车速, 个别车辆速度动态调整.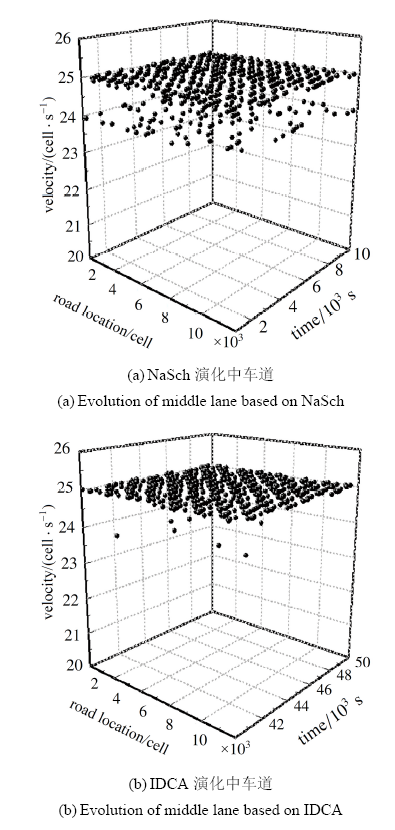
显示原图|下载原图ZIP|生成PPT图8$\rho=0.08$中车道速度分布图
-->Fig.8Velocity distribution diagram of middle lane under the condition of $\rho=0.08$
-->
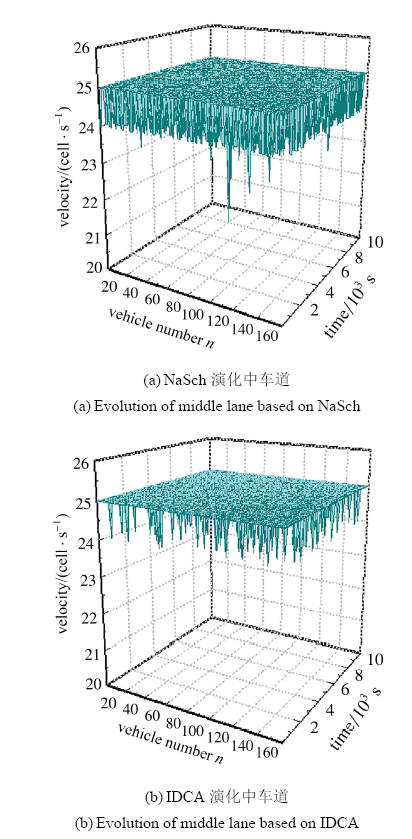显示原图|下载原图ZIP|生成PPT图9$\rho=0.08$中车道速度波动图
-->Fig.9Velocity fluctuation diagram of middle lane under the condition of $\rho=0.08$
-->
图10为$\rho=0.08$下, 3条车道均采用NaSch规则和均采用IDCA规则得到的中车道车辆车头间距波动情况分布, 从图中可以看出在低密度下, 因为密度较低的原因, 无论采用NaSch规则还是采用IDCA规则, 中车道车辆车头间距都可以保持一个相对较大的值. 采用IDCA 规则得到的中车道车头间距波动如图10(b)所示可以看出, 车辆在行驶过程中, 车头间距波动平缓, 未出现陡增陡降的波动, 车辆编号29, 编号107和编号123 等车辆都维持了较大的车头间距; 而采用NaSch规则得到的中车道车头间距波动如10(a) 所示, 可以看出, 车头间距波动更加无序, 且波动幅度更大. 这也正说明了采用了考虑驾驶员影响因素的IDCA模型体现了驾驶员在实际交通状况下, 可以根据车辆受到的其他车辆直接物理影响因素, 和局部交通状态及车辆自身运行特性可以调节自己的驾驶行为, 在低密度下可以保持较高的行驶车速和较大的车头间距, 从而使得交通流保持更加平稳, 与实际情况相符.
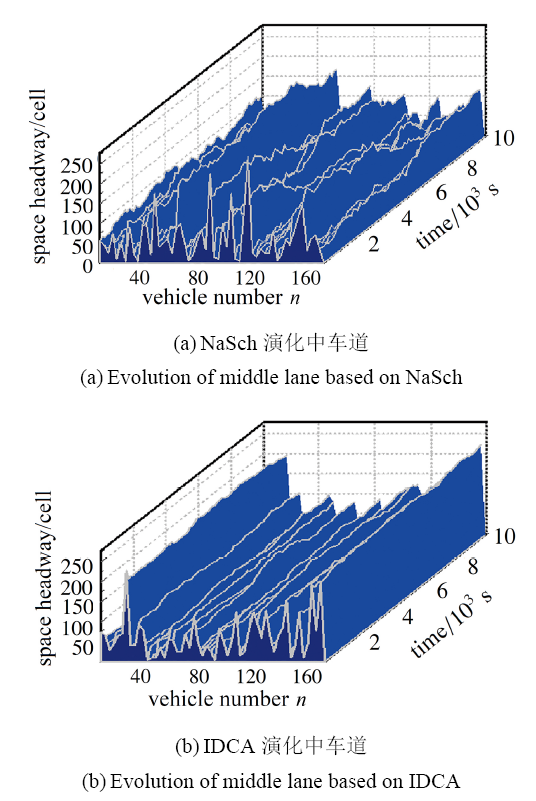显示原图|下载原图ZIP|生成PPT图10$\rho=0.08$中车道车头间距波动图
-->Fig.10Space headway fluctuation diagram of middle lane under the condition of $\rho=0.08$
-->
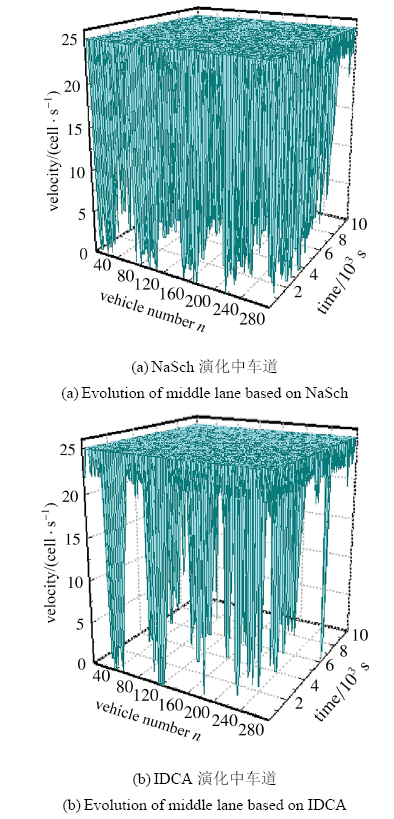
在以上仿真条件下, 增大道路密度, 得到$\rho=0.14$下速度分布和波动图. 此时道路处于中密度条件下, 图11(a)所示为3条车道均采用NaSch规则得到的中车道速度分布图, 可以看出采用基本NaSch规则演化的中车道车辆速度受车间距及慢化影响, 随机涨落, 部分时刻车速为零, 出现短暂拥塞情况. 图12(a)所示为3条车道均采用NaSch规则得到的中车道速度波动图, 更直观地描述出中车道车辆速度变化情况, 可以看出速度振荡变化剧烈, 无法形成稳定的交通流状态. 相比3条车道均采用NaSch规则演化得到的结果, 3条车道均采用IDCA 规则得到的中车道速度分布图11(b)和中车道速度波动图12(b), 可以看出大部分车辆可以保持最大车速$v_{\text{max}}$行驶, 形成局部稳定的畅行交通流.
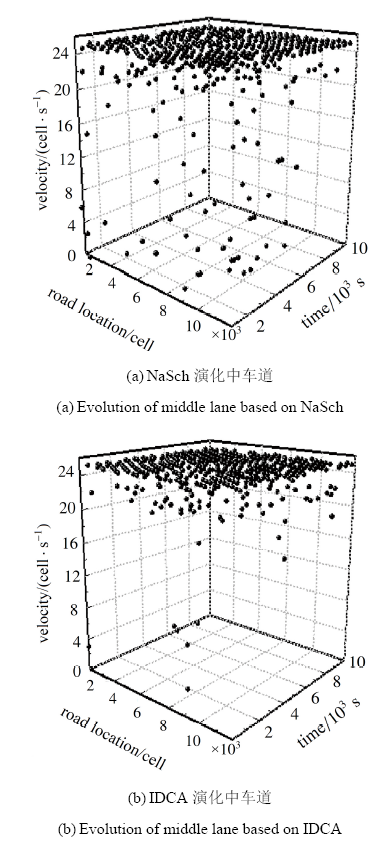显示原图|下载原图ZIP|生成PPT图11$\rho=0.14$中车道速度分布图
-->Fig.11Velocity distribution diagram of middle lane under the condition of $\rho=0.14$
-->
显示原图|下载原图ZIP|生成PPT图12$\rho=0.14$中车道速度波动图
-->Fig.12Velocity fluctuation diagram of middle lane under the condition of $\rho=0.14$
-->
图13所示为道路密度$\rho=0.14$条件下, 3条车道分别采用NaSch规则和均采用IDCA规则得到的中车道车头间距波动分布图. 与低密度中车道车头间距分布图10相比, 随着道路密度的增大, 车辆驾驶员出于安全驾驶的目的, 车辆车头间距减小. 3 条车道均采用NaSch 规则得到的中车道车头间距, 相比于低密度时车头间距, 此时中车道车头间距波动非常剧烈和紊乱; 而3条车道均采用IDCA规则得到的中车道车头间距如图13(b) 所示, 受中车道密度的影响此时车辆车头间距也会呈现一定幅度的波动, 但不会像NaSch 演化规则下中车道那样剧烈, 部分车辆会出现以稳定车头间距行驶的情况, 如编号38的车辆, 随着时间的演化, 稳定在车头间距50 cell左右, 编号213的车辆, 稳定维持在38 cell左右, 编号247的车辆, 稳定维持在\mbox{53 cell}左右等等. IDCA 规则下中车道出现稳定的车头间距, 这是因为相比于NaSch 模型所有车都按固定慢化概率的缺点, 在IDCA 模型中, 驾驶员会实时根据当前车道及旁道车辆直接物理影响、及局部车辆稠密间接心理影响等因素, 实时调整随机慢化概率, 使得驾驶更加平稳, IDCA 模型更能体现出驾驶员在交通系统中的主体作用, 反映出驾驶人对车辆周围环境的识别和判断, 更加符合实际交通情况.
显示原图|下载原图ZIP|生成PPT图13$\rho=0.14$中车道车头间距波动图
-->Fig.13Space headway fluctuation diagram of middle lane under the condition of $\rho=0.08$
-->
2.3 不同驾驶员混合比对交通流的影响
将激进型、中立型、保守型三种类型的驾驶员驾驶车辆取不同的混合比例$Pa$, $Pn$, $Pc$ 进行仿真分析随机分布. 从图14可以看出, 7组不同类型驾驶员混合比下, 车速整体都呈现出随着密度增大而逐步减小的趋势. 这与交通流规律一致, 即交通密度越大, 车辆之间的影响越大, 交通流逐步由自由流状态向阻塞相转变. 在低密度区, 仿真当车道上只有激进型驾驶员$(Pa=1, Pn=0, Pc=0)$ 时, 或只有中立性驾驶员$(Pa=0, Pn=1, Pc=0)$, 或只有保守型驾驶员$(Pa=0, Pn=0, Pc=1)$ 时, 车辆特征都是加速很快并可以维持一段畅行运行状态, 但是3种类型驾驶员维持时间和临界密度点不同, 激进型驾驶员维持时间最长, 在密度为0.22时平均速度从24.15 cell/s下降为14.83 cell/s, 然后开始逐步下降, 密度为0.5 时速度下降为3.83 cell/s, 此后速度下降非常快; 而中立型驾驶员维持最大车速时间较短, 平均速度在密度为0.16时已经有明显下降趋势; 当道路上仅有保守型驾驶员时, 维持最大车速时间最短, 在密度为0.14 时已经开始明显速度下降. 此外其他几条仿真曲线可以看出, 在同一密度下, $Pa$值越大时即激进型驾驶员所占比例越大时, 速度下降相对缓慢; $Pc$ 值越大时即保守型驾驶员所占比例越大时, 速度下降越快; $Pn$值越大时即中立型驾驶员所占比例越大时, 速度下降幅度介于激进型和保守型之间. 这是因为不同类型驾驶员受到道路直接物理和间接心理影响及生理等因素影响, 不同驾驶行为会对交通流产生不同的影响, 激进型驾驶员对道路其他车辆的外界影响变化非常敏感, 较小的车间距下仍有较高车速跟驰的行为, 平均速度相对较大; 保守型驾驶员时刻保持警惕, 受外界环境影响非常大, 车速自身速度及前车相对距离影响非常大, 随机慢化概率较大, 所以平均速度相对较小. 中立型驾驶员对车辆周围直接物理影响和间接心理影响变化比较敏感, 平均速度变化介于激进型和保守型驾驶员之间.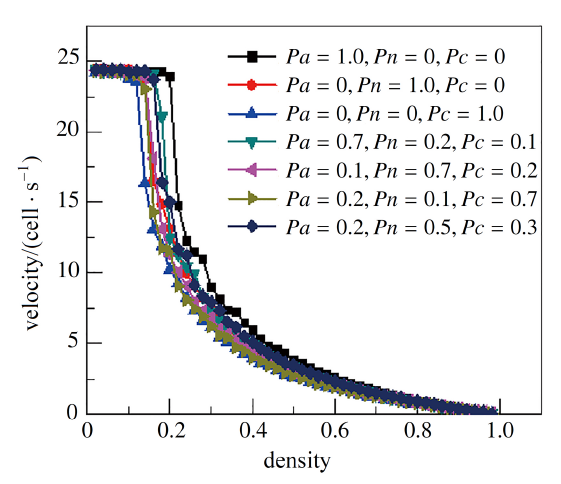
显示原图|下载原图ZIP|生成PPT图14不同驾驶员类型混合比密度与速度关系图
-->Fig.14Density and velocity relationship diagram under the mixing probability of different type drivers
-->
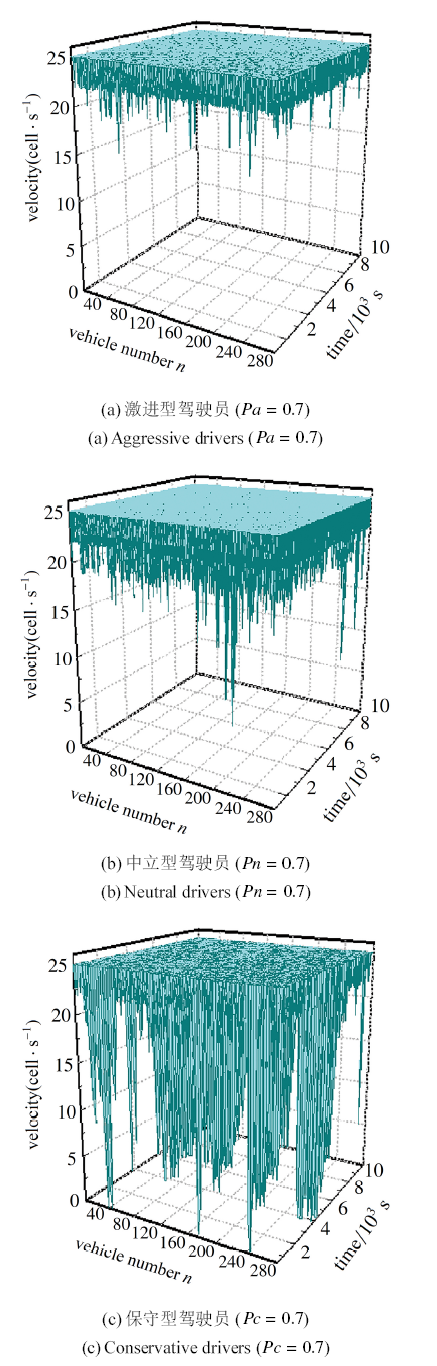
此外不同混合比下驾驶员速度波动图, 也能反映出3种不同类型驾驶员的驾驶行为特点. 图15为道路密度$\rho=0.14$时, 分别将3种类型驾驶员赋予较大的混合比下得到的速度波动图, 图15(a) 为激进型驾驶员比例为$(Pa=0.7, Pn=0.2, Pc=0.1)$条件下的速度波动图, 图15(b)为中立型驾驶员比例为$(Pa=0.1, Pn=0.7, Pc=0.2)$条件下的速度波动图, 图15(c)为保守型驾驶员比例为$(Pa=0.1, Pn=0.2, Pc=0.7)$条件下的速度波动图. 通过对图15对比可以发现, 在同一密度条件下, 当激进型驾驶员比例较大时, 如图15(a)所示, 大部分车辆可以维持较高的行驶速度, 速度波动相对较小; 当保守型驾驶员比例较大时, 从图15(c) 可以看出大量的车辆速度波动非常大, 部分车辆出现时走时停的现象; 当中立型驾驶员比例较大时, 从图15(b)可以看出, 其速度波动介于激进型驾驶员和保守型驾驶员之间.
显示原图|下载原图ZIP|生成PPT图15$\rho=0.14$速度波动图
-->Fig.15Velocity fluctuation diagram under the condition of $\rho=0.14$
-->
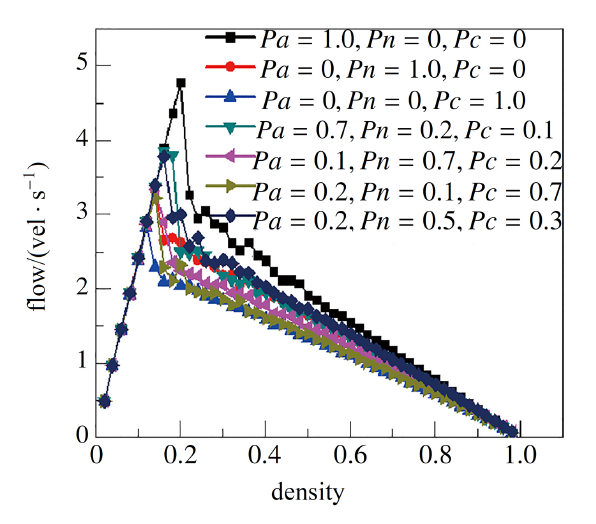
图16为不同驾驶员混合比例下密度与流量的关系图. 从图16可以看出, 在低密度区$\rho <0.12$ 时, 不论3种类型驾驶员比例$Pa, Pn, Pc$以何比例混合, 它们的密度和流量曲线在该低密度区间均会重合, 这是因为在该密度下道路交通流均属于畅行行驶状态, 此时平均流量随密度的变化呈现线形增大关系. 此后不同混合比例仿真曲线可以看出, 密度与流量关系曲线会出现随着密度的变化从自由流向阻塞流相变的过程, 不同混合比相变拐点不同. 当车道上仅有激进型驾驶员$(Pa=1, Pn=0, Pc=0)$时, 拐点密度$\rho=0.22$, 大于该密度后交通流量整体趋势呈现逐渐下降趋势, 但在部分密度区间内密度与流量为非线性的关系; 当道路只有中立性驾驶员$(Pa=0, Pn=1, Pc=0)$ 时, 拐点密度$\rho=0.17$, 以及只有保守型驾驶员$(Pa=0, Pn=0, Pc=1)$ 时, 拐点密度$\rho=0.16$, 其他混合比例下交通流量都随着道路上激进型驾驶员的比例$Pa$ 值下降而下降, 随着保守型驾驶员比例$Pc$ 值增大而下降, 例如当激进型驾驶员占到70\% 时, 拐点密度为0.20, 此时流量最大为3.79; 当激进型驾驶员下降到20% 时, 同等密度下, 此时流量已经下降为2.31. 可以发现整个仿真曲线呈现出: 在道路相同中高密度下, 激进型驾驶员所占的比例越大, 车辆速度与交通流量越大, 交通流量随着保守型驾驶员比例的增大而降低.
显示原图|下载原图ZIP|生成PPT图16不同类型驾驶员混合比密度与流量关系图
-->Fig.16Density and flow relationship diagram under the mixing probability of different type drivers
-->
此外, 与NaSch模型相比, NaSch模型只能模拟出自由流和阻塞交通相, 不能模拟出同步流. 本文提出的IDCA模型, 在激进型驾驶员所占的不同比例下, 在一定的密度区内通过IDCA模型得到的流量值弥散分布在一个二维区域, 在该密度区域内流量和密度数据之间的连线斜率无规律的为正或者为负, 呈现出非线性特点, 此时表现为同步流交通特征, 即通过IDCA模型能够再现NaSch模型无法模拟得到的同步流现象. 如图16所示, 当车道上仅有激进型驾驶员$(Pa=1, Pn=0, Pc=0)$时, 在密度[0.22,0.38]区间内, 此时流量与密度互不相关, 数据点呈无规则散布. 当激进型驾驶员比例为$(Pa=0.7, Pn=0.2, Pc=0.1)$时, 在密度[0.20,0.36]区间内; 以及当激进型驾驶员比例为$(Pa=0.2, Pn=0.5, Pc=0.3)$时, 在密度[0.16,0.32]区间内都呈现弥撒分布. 此时继续减小激进型驾驶员的比例, 当道路上仅有保守型驾驶员时, 即保守型驾驶员$ (Pa=0, Pn=0, Pc=1)$ 时, 此时IDCA模型演化规则中, 激进型驾驶员确定性减速过程规则失效, 此时不会出现同步流现象.
2.4 高速跟驰率分析
文献[34]中通过拍摄上海、北京、西安、郑州等城市的快速路段的交通流, 采集了"车速- 车头间距''的实测交通数据. 通过视频提取整理后得到210 920组交通流实测的大样本数据库. 经过对数据的分析, 发现在实测数据集中, 存在着"高速跟驰''的现象, 在数据集中的小间距车辆并非都是低速行驶, 其速度明显高于通常处于该密度时应有的速度, 即" 高速跟驰''现象. 实测数据得出在小间距跟驰数据中, 发现存在超过7% 的"高速跟驰''车辆. 文献[34]指出传统的交通流模型无法模拟出" 高速跟驰''现象, 需要新的交通模型对此现象进行描述和分析.为了验证本文提出的IDCA模型的有效性, 下面对高速跟驰现象进行模拟和分析. 为了便于与文献实测结果比较, 数值模拟时采用与文献[34]中相同的定义来描述高速跟驰, 即车头间距与车速的比值进行定义, 小间距采用文献参数12.5 m, 通过不同的激进型驾驶员占比进行仿真, 得到6条不同激进型驾驶员占比下的小间距高速跟驰率曲线结果, 如图17所示.
显示原图|下载原图ZIP|生成PPT图17不同激进型驾驶员比例下高速跟驰率
-->Fig.17Rate of high speed car-following and denisty relationship diagram under the different probability of aggressive drivers
-->
从图17可以看出, 在低密度区, 当道路密度$\rho$小于0.12时, 此时由于道路车辆较少, 车辆之间相互制约影响较小, 车辆间车头间距较大, 交通处于自由流状态, 不易出现小间距高速跟驰现象. 在高密度区域, 当密度大于0.9时, 由于道路中车辆密度非常大, 道路进入阻塞相, 此时也不易出现小间距高速跟驰现象. 其余中高密度区均会出现高速跟驰现象, 而且小间距高速跟驰率整体随着道路的密度增大而减小的趋势, 但呈现出非线性的关系. 另外, 从图17可以看出, 在道路同一交通密度下, 小间距高速跟驰率基本上随着激进型驾驶员的比例增加而增大.
当激进型驾驶员比例$Pa=0.2$时, 道路密度$\rho$为0.16时, 小间距高速跟驰率为7.68%; 密度为0.18时, 跟驰率为8.49%; 密度为0.2时, 跟驰率为7.09%, 上述结果符合实测数据中存在的小间距超过7%的规律. 当激进型驾驶员比例$Pa=0.3$时, 密度为0.16 时, 小间距高速跟驰率为10.2%; 密度为0.18时, 跟驰率为8.65%; 密度为0.2时, 跟驰率为10.76%; 密度为0.22时, 跟驰率为9.63%; 密度为0.24时, 跟驰率8.23%, 此外其他激进型驾驶员比例下, 均能得到小间距高速跟驰率超过7%的结果, 上述通过本文提出的IDCA模型数值模拟结果与文献[34]实测统计结果相符合.
3 结束语
在考虑到驾驶行为受到道路物理环境、驾驶员心理和生理、以及车头间距、车辆自身特性等因素的影响, 在NaSch的基础上, 本文建立了一种考虑驾驶员影响因素的元胞自动机交通流动力学模型(IDCA). 模型中, 采用场力将驾驶员受到的直接物理影响通过图论映射方法实现直接影响量化, 采用稀疏矩阵稠密度计算实现间接心理影响对驾驶员影响的量化, 并综合考虑了不同驾驶员类型的生理特征以及车辆自身特性的影响, 结合激进型驾驶员保持较小跟车间距的特点, 建立了相应的交通动力学模型. 通过数值模拟了考虑驾驶员影响因素的时空交通特性、车辆速度波动、车头间距波动、以及不同驾驶混合比例下速度与密度、流量与密度、小间距高速跟驰率等交通流特性. 结果表明: (1)本文IDCA模型能够重现和分析自由流、同步流、阻塞流等复杂的交通现象. (2)时空相图表明, 与传统NaSch模型相比, 考虑驾驶员影响因素的IDCA模型在不同密度区下都具有较大的拥塞消融率, 道路资源利用率更高. (3)不同驾驶员类型混合比条件, 在道路相同中高密度下, 激进型驾驶员所占的比例越大, 车辆速度与交通流量越大, 交通流量随着保守型驾驶员比例的增大而降低. (4) 模拟实现了高速跟驰现象, 得到的小间距高速跟驰率超过7\%的结果与交通实测结果相符合. 与NaSch 模型相比, 本文提出的模型减少了车辆的速度和车头间距波动, 提高了交通系统的稳定性, 对于车流的堵塞有较高的消融率, 再现了丰富的复杂交通现象.The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . |
| [2] | . |
| [3] | . |
| [4] | . |
| [5] | . |
| [6] | . |
| [7] | . |
| [8] | . |
| [9] | . |
| [10] | . |
| [11] | . . |
| [12] | . |
| [13] | |
| [14] | . . |
| [15] | . |
| [16] | . |
| [17] | . |
| [18] | |
| [19] | . . |
| [20] | |
| [21] | . |
| [22] | . . |
| [23] | |
| [24] | . [博士论文]. . [PhD Thesis]. |
| [25] | . . |
| [26] | . . |
| [27] | . . |
| [28] | . . |
| [29] | . |
| [30] | . |
| [31] | |
| [32] | . . |
| [33] | . . |
| [34] | . . |
