, 孙鹏森An evaluation of four threshold selection methods in species occurrence modelling with random forest: Case studies with Davidia involucrata and Cunninghamia lanceolata
ZHANGLei, SUNPeng-Sen通讯作者:
责任编辑:
收稿日期:2016-05-31
接受日期:2017-01-3
网络出版日期:2017-04-10
版权声明:2017植物生态学报编辑部本文是遵循CCAL协议的开放存取期刊，引用请务必标明出处。
基金资助:
展开
摘要
关键词：
Abstract
Methods Here, the RF was used to simulate the current and project the future potential distributions of Davidia involucrata and Cunninghamia lanceolata. Then, four threshold-setting methods (Default 0.5, MaxKappa, MaxTSS and MaxACC) were selected and used to transform modelled probabilities of occurrence into binary predictions of species presence and absence. Lastly, we investigated the difference in model performance among the threshold selection methods by using five model accuracy measures (Kappa, TSS, Overall accuracy, Sensitivity and Specificity). We also used the map similarity measure, Kappa, for a cell-by-cell comparison of similarities and differences of distribution map under current and future climates.
Important findings We found that the choice of threshold method altered estimates of model performance, species habitat suitable area and species range shifts under future climate. The difference in selected threshold cut-offs among the four threshold methods was significant for D. involucrata, but was not significant for C. lanceolata. Species’ geographic ranges changed (area change and shifting distance) in response to climate change, but the projections of the four threshold methods did not differ significantly with respect to how much or in which direction, but they did differ against RF classification predictions. The pairwise similarity analysis of binary maps indicated that spatial correspondence among prediction maps was the highest between the MaxKappa and the MaxTSS, and lowest between RF classification algorism and the four threshold-setting methods. We argue that the MaxTSS and the MaxKappa are promising methods for threshold selection when RF regression algorism is used for the distribution modeling of species. This study also provides promising insights to our understanding of the uncertainty of threshold selection in species distribution modeling.
Keywords：
-->0
PDF (1942KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
物种生境模型对于资源管理、环境评估和生物多样性保护等方面具有重要的价值, 当前物种生境模型已经应用到大量的具有理论和应用目的的研究中(Guisan & Zimmermann, 2000; 王娟和倪健, 2006; 邵慧等, 2009; 金佳鑫等, 2013)。然而物种生境预测结果通常是概率性的(0-1), 如Domain模型(Carpenter et al., 1993)、NeuralEnsembles模型(O’Hanley, 2009)、Biomapper软件(Hirzel et al., 2004)等的预估结果。在具体的保护管理等实践应用过程中通常需要基于二元值(存在/不存在)的物种生境图, 此时就需要把概率性的生境预测结果转化为二元值, 在此转化过程中就涉及阈值选择问题, 大于所设定阈值的地区定义为物种生境适宜区, 否则定义为生境不适宜区。此外, 把物种出现概率预估转换为二元值过程中的阈值选择问题也是物种生境模拟不确定性分析中的一个重要来源, 但它也是不确定性分析过程中最少涉及的领域。
通常, 阈值选择方法分为两种方式: 主观方法和客观方法(Liu et al., 2005)。一些代表性的主观选择的阈值包括默认值0.5 (Bailey et al., 2002; Zhang et al., 2015)以及0.3 (Robertson et al., 2001)等; 由于没有具体设置阈值的指导规则, 它们的选择比较随机, 通常缺乏生态学基础。有时需要一些特定指定的阈值, 如建模者或用户定义模型必须保证物种出现观测记录误分类率低于某一数值(如15%), 因此需要最低敏感度(sensitivity)是0.85 (敏感度指物种出现正确预测比例)。由于敏感度是建模者或用户自定义的, 因此也属于主观方法范畴。
为了避免固定阈值带来的不确定性, 提出了很多阈值最优化选择方法, 这就是客观的阈值选择方法, 这些方法选择的阈值可以最大化地保证观测值和预测值的一致性(Guo & Liu, 2010)。这些客观方法通常都是基于各种各样的模型准确度评价指标。在评估模型预测准确度的时候, 多数评估指标也需要选择一个阈值用于转化概率预测结果。基于准确度方法的目的就是促使特定模型准确度指数(如Kappa)或两个不相容准确度指数之间平衡(如敏感度和特异度)的最优化。如, Kappa最大值方法在生态学研究中就应用得非常普遍(Freeman & Moisen, 2008)。敏感度和特异度之和最大(等同于真实技巧统计法TSS最大)(Liu et al., 2005)、敏感度和特异度之差最小(Jimenez-Valverde & Lobo, 2007)、敏感度等于特异度(Nenzén & Araújo, 2011)等都可以用于确定阈值。此外还有利用物种存在和不存在的平均概率值的中值作为阈值的研究(Fielding & Haworth, 1995)。
虽然目前有很多确定阈值的方法, 但是还缺少关于它们预估结果的比较研究, 导致对它们的表现能力认识不清。此外, 还有一些模型既可以生成生境概率分布图也能生成二元分布图, 如“随机森林” (random forest)的分类和回归算法可以分别生成二元和概率生境分布图(Breiman & Cutler, 2004; 张雷等, 2014)。对于“随机森林”来讲, 采用各种阈值方法把生成的概率预测结果转化为二元值, 是否会比直接生成的二元值结果更可靠, 还未见此方面的报道。为此, 本文以珙桐(Davidia involucrata)和杉木(Cunninghamia lanceolata)生境预测为例, 分别采用“随机森林”的分类和回归算法生成其生境二元值和概率值分布图, 随后采用4个常用的阈值选择方法对概率预测值进行二元值转换, 最后采用5个模型准确度评估指标评价了二元分布图的预测准确度, 并进行了二元分布图的空间相似性以及未来气候条件下生境相对变化的对比分析。
1 材料和方法
1.1 物种分布记录和环境数据
珙桐现实空间分布数据主要来自于中国科学院植被图编辑委员会编制的1:100万植被图(中国科学院植被图编辑委员会, 2001)、中国数字植物标本馆(CVH, http://www.cvh.org.cn)和全球生物多样性数据集(GBIF, http://www.gbif.org)。本文中的1:100万植被图来源于国家自然科学基金委员会“中国西部环境与生态科学数据中心”和“地球系统科学数据共享网”。其中从CVH和GBIF中共计得到88个有效的自然分布点数据; 植被图经转换为1 km分辨率的栅格后再转换为点矢量格式。杉木现实空间分布数据来自于1:100万植被图(中国科学院植被图编辑委员会, 2001), 经同样方法转换后得到点矢量数据。因本研究是在分辨率为8 km × 8 km的全国范围内开展, 为避免单个栅格中落入较多数据点造成重复取样, 对上述分布点数据进行了预处理, 即物种出现的每个栅格中只保留一个数据记录, 最后珙桐和杉木共计分别得到现实分布点记录269和2β756个(图1A)。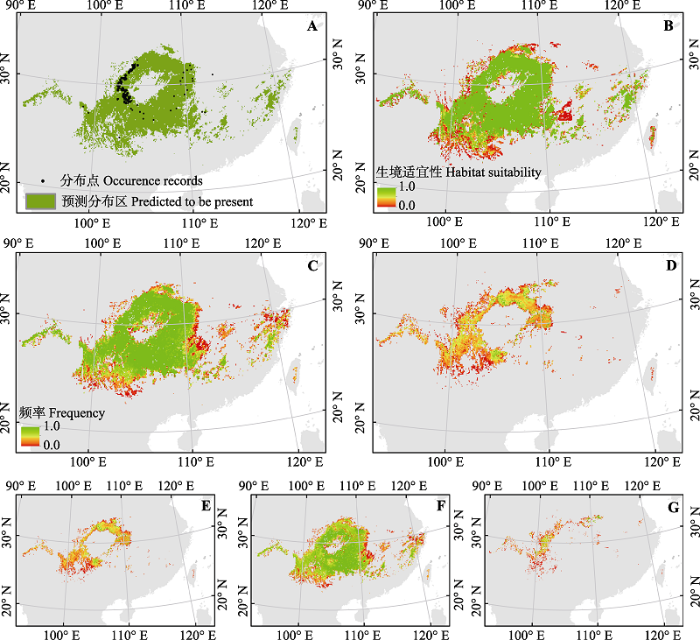
显示原图|下载原图ZIP|生成PPT图1基于同一建模数据的当前气候条件下珙桐生境二元值(A)和概率值(B)预测结果。不同阈值选择法和“随机森林”分类算法所生成的45个生境图中当前(C)和未来(D)气候条件下珙桐出现频率以及未来气候条件下生境不变(E)、生境消失(F)和新生境出现(G)的频率。
-->Fig. 1Binary (A) and probability (B) distribution maps of Davidia involucrata under current climate produced by the same model-building dataset. Frequency of the presence of Davidia involucrata calculated across 45 predictions under current (C) and future (D) climates and the frequency of stable (E), lost (F) and gained (G) habitats under future climate.
-->
选择7个与物种生理特征有关的环境数据进行生境空间预测: 包括年平均气温(℃)、最冷月平均气温(MCMT, ℃)、最暖月平均气温(MWMT, ℃)、气温年较差(MWMT-MCMT, ℃)、年降水量(mm)、夏季降水量(5-9月, mm)及大于5 ℃的积温。这7个气候变量均是1961-1990年连续30年现实观测数据的平均值。未来气候条件下的气候数据来自A2排放情景下加拿大的气候模式CCCMA_ CGCM3 (Coupled Global Climate Model of Canadian Centre for Climate Modelling and Analysis), 为2070-2099年连续30年数据的平均值。模型所采用的当前和未来气候条件下的7个气候变量都是从ClimateChina软件(张雷等, 2011a)中输出。
1.2 模型简介
“随机森林”是一种现代分类与回归技术, 同时也是一种组合式的自学习技术。“随机森林”通过自助法(bootstrap)随机选择(不是全部)变量生长成分类“树”, 每个“树”都会完整生长而不会修剪(pruning)。并且在生成树的时候, 每个节点的变量都仅仅在随机选出的少数几个变量中产生。通过这种随机方式生成的单个、十个、百个或者成千个树被用于分类和回归分析(因此被称为“随机森林”)。最终的决策树是通过对潜在的随机变量树进行“投票”表决(voting system)生成的, 即“随机森林”选择具有最多投票的分类。如果目的是回归分析, 则对这些树的结果进行平均得到因变量预测值。因此, 本文利用“随机森林”分类算法预测珙桐生境时, 输入数据是分类变量(存在/不存在), 输出结果同样也是二元数据(存在/不存在); 当利用其回归算法预测珙桐生境时, 输入数据是数值变量(1代表存在; 0代表不存在), 输出结果是连续变量(0-1)。采用“随机森林”模拟珙桐生境适生区, 这是由于“随机森林”预测准确度通常高于其他模型, 并且具有一定的稳健性(张雷等, 2011a; Zhang et al., 2015)。关于“随机森林”的详细介绍参见张雷等(2014)。本文采用R环境中的“randomForest”软件包(Liaw & Wiener, 2002)进行“随机森林”分析, 参数采用默认设置。1.3 模拟实验设计
由于所采用的模型需要物种存在和物种不存在数据进行建模。采用类似Engler等(2004)和张雷等(2011b)的方法, 把所有没有某一物种记录的地点与有记录地点的环境条件(即7个环境变量)进行对比, 如果某地区与已知点环境条件相同(即此地区的环境变量完全包含在所有已知记录地点的7个环境条件变程范围内), 那么这些地区可以认为适合这一物种分布, 把这些地区从无记录地点中删除, 剩余的地区可以认为是“完全”不适宜这一物种的地区, 这些地区指定为不存在区, 并在其中随机选择了与该物种分布点数量相等的不存在点数据作为模型建模数据。本文之所以选择与物种存在记录数据相等的准不存在数据是基于两个方面的考虑: 一是物种发生率较低时会对阈值选择过度敏感(Freeman & Moisen, 2008), 二是物种存在和不存在数据相等时“随机森林”预测模型最稳定(Barbet-Massin et al., 2012)。为验证模型的预测准确度, 将全部物种分布数据(物种不存在数据+物种存在数据)分为两个数据集: 训练子集和评估子集。通过随机取样, 70%的数据用于建模, 30%的数据用于模型验证。为避免随机选取导致的数据差异影响阈值选择方法的评估, 随机选取物种不存在数据过程重复3次。同时, 针对每次随机选取的物种不存在数据, 数据分割建模重复3次, 总共对数据进行了9次随机分割建模过程, 产生9套训练数据和验证数据, 并且保证训练数据集和验证数据集中物种不存在数据和存在数据之间的比例是恒定的。
1.4 阈值选择及其评估
由于“随机森林”既能进行分类分析也能进行回归分析, 为对比分析分类和回归算法在二元生境分布图预测时的差异, 首先采用回归算法生成珙桐生境概率预测图, 然后采用4个方法(即得到最大总准确度(MaxAcc)、最大Kappa (MaxKappa)和最大TSS (MaxTSS)法时的阈值以及默认值0.5 (Default))把概率预测结果转化为二元值(存在/不存在)结果。同时也采用“随机森林”分类算法直接生成二元值珙桐生境预测图。对于每套建模数据, 4个阈值选择方法各生成一个阈值, 然后把这个阈值应用到建模数据对应的模型评估数据中, 进而评估其对模型预测准确度的影响。本文采用Kappa、TSS、总准确度、敏感度和特异度来评估模型预测准确度(表1)。同时也采用这5个评估指标评价了“随机森林”分类算法的预测结果。Kappa值和TSS的评估标准为: 极好, 1.0-0.85; 很好, 0.7-0.85; 好, 0.55-0.7; 一般, 0.4-0.55; 失败, <0.4。
Table 1
表1
表1模型预测准确度评价指标
Table 1Measures of predictive accuracy
| 精度指标 Accuracy measure | 公式 Formula |
|---|---|
| 总准确度 Overall accuracy | (a +d)/n |
| 敏感度 Sensitivity | a/(a + c) |
| 特异度 Specificity | d/(b + d) |
| Kappa | $\frac{\left( a\text{+}d \right)-\text{ }\!\![\!\!\text{ }\left( a\text{+}c \right)\left( a\text{+}b \right)\text{+}\left( b\text{+}d \right)\left( c\text{+}d \right)\text{ }\!\!]\!\!\text{ /}n}{n-\text{ }\!\![\!\!\text{ }\left( a\text{+}c \right)\left( a\text{+}b \right)\text{+(}b\text{+}d\text{)(}c\text{+}d\text{) }\!\!]\!\!\text{ /}n}$ |
| 真实技巧统计法 True skill statistic (TSS) | Sensitivity + Specificit -1 |
新窗口打开
为了评估不同阈值选择方法对未来气候条件下分布区迁移相对变化预测的影响, 对分布区的面积变化和分布区迁移方向进行了量化。分布区面积变化评价包括: 当前潜在生境分布面积、未来气候条件下的潜在生境分布面积、未来气候条件下生境相对保持不变的比例、生境消失比例、获取新生境的比例、分布区的东向和北向迁移距离以及最适宜海拔分布高度的变化。其中采用分布区质心(centroid)的迁移变化来分析生境分布区东向和西向的迁移距离。最适宜海拔分布高度的变化采用加权平均的方法进行估计(terBraak & Looman, 1986), 以每个海拔高度对应的栅格数量作为权数。
1.5 统计分析
采用Friedman秩和检验方法分析不同阈值选择方法之间模型准确度的差异; 两两之间的比较采用Nemenyi检验法。采用同样的方法也对不同阈值选择方法所生成的当前潜在分布区面积预估之间的差异以及未来气候条件下分布区相对变化之间的差异进行了分析。此外采用Kappa值分别评估了当前和未来气候条件下不同阈值选择方法所生成的生境分布图的两两空间相似性。本文所有统计分析都在R 3.1.2软件(R Core Team, 2014)中进行。2 结果分析
2.1 模型预测准确度
对于珙桐来讲4个阈值选择方法所确立的最佳阈值存在显著差异(表2); 其中默认值方法的阈值0.5显著高于最大Kappa和最大TSS方法, 最大总准确度法选择的阈值低于默认值0.5, 但是它与其他3个阈值选择方法之间没有显著差异。对于杉木而言, 虽然默认值0.5低于最大Kappa和最大总准确度确立的阈值, 并且三者也都低于最大TSS法, 但是四者之间没有显著差异。对于珙桐来讲, “随机森林”分类算法的敏感度高于4个阈值选择方法的敏感度, 但是对于4个模型准确度指标(Kappa、TSS、总准确度和特异度)而言, “随机森林”分类算法低于4个阈值选择方法。对于杉木而言, “随机森林”分类算法的敏感度低于默认值但两者都高于其他3个阈值选择方法; 对于4个模型准确度指标来讲, “随机森林”分类算法高于默认值, 但两者都低于其他3个阈值选择方法。总体来看, 对于两物种而言, 秩和检验分析表明, 不同阈值选择方法之间(包括与“随机森林”分类算法之间), 模型预测准确度评估指标没有显著差异(表2)。Table 2
表2
表2不同阈值选择方法所确立的阈值及其应用于模型评估数据后的模型预测精度
Table 2Thresholds selected by four threshold criteria and model accuracies determined by five measures
| 阈值选择方法 Threshold method | 阈值 Threshold | Kappa | 真实技巧统计法 TSS | 总准确度 Overall accuracy | 敏感度 Sensitivity | 特异度 Specificity | |
|---|---|---|---|---|---|---|---|
| 珙桐 Davidia involucrata | 默认值0.5 Default 0.5 | 0.500 (0.000)a | 0.871 (0.024)a | 0.871 (0.024)a | 0.935 (0.012)a | 0.976 (0.019)a | 0.894 (0.025)a |
| 最大总准确度 Maximizing overall accuracy (MaxAcc) | 0.476 (0.187)ab | 0.872 (0.025)a | 0.872 (0.025)a | 0.936 (0.012)a | 0.975 (0.021)a | 0.897 (0.027)a | |
| 最大Kappa Maximizing Kappa (MaxKappa) | 0.364 (0.185)b | 0.872 (0.025)a | 0.872 (0.025)a | 0.936 (0.012)a | 0.976 (0.020)a | 0.895 (0.027)a | |
| 最大真实技巧统计法 Maximizing true skill statistic (MaxTSS) | 0.364 (0.185)b | 0.872 (0.025)a | 0.872 (0.025)a | 0.936 (0.012)a | 0.976 (0.020)a | 0.895 (0.027)a | |
| 随机森林分类 Random forest classification tree (RFCT) | - | 0.869 (0.030)a | 0.869 (0.030)a | 0.935 (0.015)a | 0.982 (0.022)a | 0.888 (0.031)a | |
| 杉木 Cunninghamia lanceolata | 默认值0.5 Default 0.5 | 0.500 (0.000)a | 0.903 (0.010)a | 0.903 (0.010)a | 0.951 (0.005)a | 0.962 (0.010)a | 0.941 (0.009)a |
| 最大总准确度 Maximizing overall accuracy (MaxAcc) | 0.540 (0.078)a | 0.908 (0.011)a | 0.908 (0.011)a | 0.954 (0.006)a | 0.958 (0.013)a | 0.950 (0.009)a | |
| 最大Kappa Maximizing Kappa (MaxKappa) | 0.540 (0.078)a | 0.908 (0.011)a | 0.908 (0.011)a | 0.954 (0.006)a | 0.958 (0.013)a | 0.950 (0.009)a | |
| 最大TSS Maximizing true skill statistic (MaxTSS) | 0.541 (0.076)a | 0.908 (0.011)a | 0.908 (0.011)a | 0.954 (0.006)a | 0.958 (0.013)a | 0.950 (0.009)a | |
| 随机森林分类 Random forest classification tree (RFCT) | - | 0.905 (0.010)a | 0.905 (0.010)a | 0.952 (0.005)a | 0.961 (0.010)a | 0.943 (0.007)a |
新窗口打开
2.2 当前生境适生区面积及其未来气候条件下的变化
在4个阈值选择方法之间珙桐当前潜在适生区面积没有显著差异; “随机森林”分类算法预测的适生区面积大于4个阈值选择方法, 并且显著高于默认值0.5和最大总准确度法, 但与最大Kappa和最大TSS之间没有显著差异(表3)。对于杉木而言, “随机森林”分类算法和4个阈值选择方法确立的适生区面积之间没有显著差异。Table 3
表3
表3当前潜在适生区面积及未来(2070-2099, 2080s)气候条件下的生境相对变化
Table 3Potential habitat suitable areas and changes in the distribution range of tree species (change in area and shift in distance and direction of mean centers of suitable habitat) for the normal period 2070-2099 (2080s) relative to current baseline (1961-1990).
| 阈值方法 Threshold | 当前适生区 Total habitat area (×103 km2) | 总生境变 化比例 Total range change (%) | 新生境 比例 Habitat gained (%) | 生境消失 比例 Habitat lost (%) | 东向迁移 距离 Eastward shift (km) | 北向迁移 距离 Northward shift (km) | 高程迁移 距离 Uphill shift (m) | |
|---|---|---|---|---|---|---|---|---|
| 珙桐 Davidia involucrata | Default 0.5 | 762.8 (34.6)a | -95.9 (3.8)a | 0.6 (0.9)a | 96.6 (3.0)a | 70.7 (133.2)a | 252.3 (43.5)a | -341 (211)a |
| MaxAcc | 761.1 (69.1)a | -94.8 (6.4)a | 1.0 (1.3)a | 95.8 (5.1)a | 69.3 (164.5)a | 228.4 (80.5)a | -336 (244)a | |
| MaxKappa | 780.1 (69.5)ab | -94.3 (6.6)ab | 1.1 (1.4)ab | 95.4 (5.3)ab | 50.9 (164.4)a | 241.7 (41.7)a | -341 (255)a | |
| MaxTSS | 780.1 (69.5)ab | -94.3 (6.6)ab | 1.1 (1.4)ab | 95.4 (5.3)ab | 50.9 (164.4)a | 241.7 (41.7)a | -341 (255)a | |
| RFCT | 804.3 (27.9)b | -60.1 (1.9)b | 7.9 (1.1)b | 68.0 (1.8)b | -236.0 (33.9)b | 134.5 (9.0)b | 242 (63)b | |
| 杉木 Cunninghamia lanceolata | Default 0.5 | 1β401.5 (14.4)a | -0.3 (0.1)ab | 0.1 (0.0)ab | 0.4 (0.1)ab | -129.1 (22.1)a | 68.5 (14.9)ab | 243.3 (37.5)a |
| MaxAcc | 1β367.4 (67.9)a | -0.4 (0.2)b | 0.1 (0.1)ab | 0.5 (0.1)b | -107.6 (48.2)ab | 57.6 (32.6)b | 238.7 (33.4)ab | |
| MaxKappa | 1β367.4 (67.9)a | -0.4 (0.2)b | 0.1 (0.1)ab | 0.5 (0.1)b | -107.6 (48.2)ab | 57.6 (32.6)b | 238.7 (33.4)ab | |
| MaxTSS | 1β365.7 (65.8)a | -0.4 (0.2)b | 0.1 (0.1)b | 0.5 (0.1)b | -108.0 (48.4)ab | 57.3 (32.5)b | 238.9 (33.5)ab | |
| RFCT | 1β391.2 (11.0)a | -0.3 (0.1)a | 0.1 (0.0)a | 0.4 (0.1)a | -82.0 (26.8)b | 81.5 (12.2)a | 183.0 (38.8)b |
新窗口打开
未来气候条件下, 4个阈值选择方法之间珙桐和杉木生境变化(生境消失、新生境获取、总生境面积变化、最适宜海拔高度变化、北向和东向迁移距离)不存在显著差异(表3)。未来气候条件下, “随机森林”分类算法预测珙桐总生境面积变化比例以及生境消失比例都低于其他4个方法, 但是新生境获取比例高于其他4个方法。总体而言, “随机森林”分类算法预测的生境面积变化(新生境获取比例、生境消失比例、生境总体变化比例)与默认值法和最大总准确度法都存在显著差异, 但是这三者都与最大Kappa法和最大TSS法之间没有显著差异。在4个阈值选择方法之间杉木总生境面积变化及生境消失比例没有显著差异, 但是最大总精确度、最大Kappa和最大TSS三者与“随机森林”分类算法之间存在显著差异。“随机森林”分类算法和最大TSS法预测的杉木获取新生境的比例之间有显著差异, 但是两者与其他3个方法之间没有显著差异。
“随机森林”分类算法预测未来气候条件下珙桐将会向西北方向迁移, 但是其他4个方法预测珙桐将会向东北方向迁移(表3)。同样, “随机森林”分类算法预测未来气候条件下珙桐的最适宜海拔分布高度将会升高, 但是其他4个方法预测最适宜海拔分布高度会下降。就生境适生区迁移(最适宜海拔高度变化, 适生区东西和北向迁移距离)来讲, “随机森林”分类算法与其他4个方法都存在显著差异, 但是这4个方法之间没有显著差异。“随机森林”分类算法预测的杉木东向迁移距离和高程迁移距离与默认值法之间存在显著差异, 但两者与其他3个方法之间没有显著差异。在4个阈值选择方法之间杉木北向迁移距离没有显著差异, 但是最大总精确度、最大Kappa和最大TSS三者与“随机森林”分类算法之间存在显著差异。
2.3 生境适生区估计的空间相关性
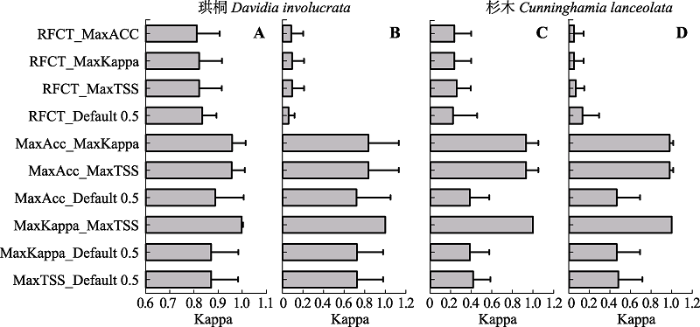
对4个阈值选择法和“随机森林”分类算法所预测的珙桐当前和未来气候条件下的生境分布进行空间叠加分析(图1), 发现当前气候条件下45个生境预测图((4个阈值选择方法+分类算法) × 9套建模数据)出现的不一致区域主要零星分布在分布区的边缘地带, 而分布区中心地区预测结果具有高度一致性。未来气候条件下的生境分布预估的一致性显著下降, 高度预估一致性的区域远远小于低一致性的区域。相对来讲对生境消失区预估具有较高的一致性, 但是生境维持不变区域及新生境区域预估的一致性极低。由于杉木结果与珙桐相似, 本文未显示。对不同阈值选择方法和“随机森林”分类算法所生产的当前和未来气候条件下的生境分布图分别进行两两相似性Kappa分析(图2)。结果发现, 无论是预测当前生境还是未来气候条件下的生境, 不同阈值选择方法所生产的生境相似性可大体分为四组: 第一组, 最大Kappa和最大TSS法具有最高相似性(平均Kappa值：0.998-1.000); 第二组具有第二高的相似性, 是最大总准确度分别与最大Kappa和最大TSS法; 第三组相似性较低, 包括默认值分别与最大总准确度、最大Kappa和最大TSS法的相似性; 第四组具有最低的地图相似性, 集中在“随机森林”分类算法与其他4个方法之间的相似性上, 尤其是在预测未来分布时, 生境分布图相似性更低(平均Kappa值: 0.052-0.260)。
显示原图|下载原图ZIP|生成PPT图2当前(A、C)和未来(B、D)气候条件下不同阈值选择方法生境分布图的两两相似性。误差线代表标准偏差; 阈值方法缩写同
-->Fig. 2Pairwise Kappa correlation of habitat maps of four threshold selection method under current (A, C) and future (B, D) climates. Error bars represent standard errors. The abbreviations of threshold methods are the same as in
-->
3 讨论
不同阈值选择方法所确定的最适宜阈值存在显著差异, 但是其预测准确度之间没有显著差异。默认值0.5是阈值转换过程中经常采用的方法。Liu等(2005)认为默认值0.5方法是一种最差的阈值选择方法, 不建议采用; 但本文却发现它是仅次于具有相同值的最大Kappa、最大TSS和最大总准确度的方法。Freeman和Moisen (2008)也发现默认值0.5对于多数物种而言, 能提供较高的模型预测准确度。这些研究之所以发现默认值0.5是一个较优异的方法, 是因为这些研究采用的建模数据发生率是0.5, 而以往研究表明物种发生率法(即利用物种发生率作为转换阈值)也是一个良好的阈值选择方法(Liu et al., 2005; Freeman & Moisen, 2008)。“随机森林”在分类算法过程中也涉及一个阈值选择问题, 由于采用的是简单多数“投票”的方法, 此处这个阈值为0.5, 但是由于分类树和回归树具体的构建原理有差异, 所以导致分类结果与通过阈值0.5转换后的回归结果之间存在差异(表2)。最大TSS法和最大Kappa法用于阈值选择时, 多数情况下表现出了一定的稳健性。本文发现阈值选择方法最大Kappa和最大TSS法具有最高模型预测准确度, 这与Liu等(2013)的研究结果一致, 他们发现敏感度与特异度之和最大方法(相当于TSS)对于只有存在记录的模型来讲是一个有效的阈值选择方法, 同样Jimenez-Valverde和Lobo (2007)也发现 敏感度与特异度之和最大法具有较高预测准确度; 但是与Norris (2014)的研究结果相反, 他们发现敏感度特异度之和最大法导致最大的遗漏误差并增加了适生区的减少。Liu等(2005)通过对两个物种的研究发现最大Kappa值法并不是一个优秀的确定阈值的方法; 但是Freeman和Moisen (2008)发现最大Kappa方法对于13个物种中的12个物种而言都是优异的阈值选择方法。本文也发现最大Kappa值法具有最大的模型预测准确度, 因此可以基本认定最大Kappa法和最大TSS法选择阈值具有较强的稳健性。本文发现最大总准确度方法与最大Kappa和最大TSS法的模型预测准确度一样都属于最高值, Freeman和Moisen (2008)认为最大总准确度法属于表现中度的阈值选择方法, 而Liu等(2005)通过对两个物种的研究发现最大总准确度法的模型预测准确度较低。
最大Kappa、最大TSS和最大总准确度法确定的最佳转换阈值不同, 但是它们的预测准确度(Kappa、TSS和总准确度)却相同, 这是由于这3个准确度评估指标都是混合式指数, 即它们对遗漏误差和冗余误差给予不同的权重(表1), 导致在敏感度和特异度存在差异时, 这些混合指数取值相等。这与以往的研究结论一致, 即发现在物种发生率为0.5时, 不同的阈值选择方法之间模型预测准确度差异最小(Liu et al., 2005; Freeman & Moisen, 2008)。这也进一步证实了他们的建议, 即在物种生境模拟研究中最好利用发生率为0.5的建模数据。
本研究进一步证实阈值方法的选择将会影响根据生境分布区变化进行的物种受胁迫程度评估(Nenzén & Araújo, 2011)。对于不同的阈值选择方法而言, 当前气候条件下的生境分布预估具有相对较高的一致性, 但未来气候条件下生境预估却具有相对的极大变异性(图1), 尤其是“随机森林”分类算法与回归算法所生成的二元分布图具有最大的差异(图2), 这表明不同阈值选择方法将会显著影响物种生境分布及其相对变化预测。这与Nenzén和Araújo (2011)的观点一致, 即, 即使采用相同的模型, 不同阈值选择方法也会导致生境预估变化的差异。不同的阈值选择方法所生成的二元分布图存在显著差异, 尤其是预估在未来气候条件下的分布时, 这是因为模型预估在新气候条件的分布时具有较大的困难(Thuiller, 2004), 而新气候条件通常出现在分布区的边缘地带, 恰恰就是未来气候条件下空间分布范围的边缘(张雷等, 2011a)。因此本研究进一步表明阈值选择是物种生境模拟预估研究中一个不确定性的重要来源。
4 结论
本文分别采用“随机森林”分类算法和回归算法预测了珙桐和杉木生境二元值分布图和概率分布图, 并采用4个阈值选择方法把概率图转换为二元值图, 并评估了分类算法和二元值转换结果的预测准确度及在预估未来气候条件下生境分布变化时的差异。主要结论如下: 不同的阈值选择方法将会显著影响物种生境预测图, 尤其是在模型外推的时候; 最大Kappa和最大TSS法在用于选择阈值时具有一致的可靠性。在预测物种生境时“随机森林”分类算法和回归算法之间存在显著差异; 考虑到生境概率预测值包含更多信息(如生境适宜性), 建议利用“随机森林”回归算法模拟预测物种生境。本研究有利于加深对物种生境模拟预测中阈值选择不确定性的认识, 同时也为“随机森林”在生境模拟预测中的应用提供了理论支持。为泛化本文研究结果, 需要更多****利用更多的阈值选择方法开展更大量物种的生境模拟预测研究。The authors have declared that no competing interests exist.
作者声明没有竞争性利益冲突.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . |
| [2] | |
| [3] | |
| [4] | . |
| [5] | |
| [6] | . |
| [7] | . |
| [8] | . |
| [9] | . |
| [10] | . |
| [11] | . |
| [12] | |
| [13] | . |
| [14] | . |
| [15] | . |
| [16] | . |
| [17] | . |
| [18] | . |
| [19] | . |
| [20] | . |
| [21] | |
| [22] | . |
| [23] | . . |
| [24] | . |
| [25] | . |
| [26] | . . |
| [27] | . |
| [28] | . . |
| [29] | . . |
| [30] | . . |
1
2002
... 通常, 阈值选择方法分为两种方式: 主观方法和客观方法(
Selecting pseudo-absences for species distribution models: How, where and how many?
1
2012
... 由于所采用的模型需要物种存在和物种不存在数据进行建模.采用类似Engler等(2004)和张雷等(2011b)的方法, 把所有没有某一物种记录的地点与有记录地点的环境条件(即7个环境变量)进行对比, 如果某地区与已知点环境条件相同(即此地区的环境变量完全包含在所有已知记录地点的7个环境条件变程范围内), 那么这些地区可以认为适合这一物种分布, 把这些地区从无记录地点中删除, 剩余的地区可以认为是“完全”不适宜这一物种的地区, 这些地区指定为不存在区, 并在其中随机选择了与该物种分布点数量相等的不存在点数据作为模型建模数据.本文之所以选择与物种存在记录数据相等的准不存在数据是基于两个方面的考虑: 一是物种发生率较低时会对阈值选择过度敏感(
2
... 物种生境模型对于资源管理、环境评估和生物多样性保护等方面具有重要的价值, 当前物种生境模型已经应用到大量的具有理论和应用目的的研究中(
... 虽然目前有很多确定阈值的方法, 但是还缺少关于它们预估结果的比较研究, 导致对它们的表现能力认识不清.此外, 还有一些模型既可以生成生境概率分布图也能生成二元分布图, 如“随机森林” (random forest)的分类和回归算法可以分别生成二元和概率生境分布图(
DOMAIN: A flexible modelling procedure for mapping potential distributions of plants and animals
1993
2
2001
... 珙桐现实空间分布数据主要来自于中国科学院植被图编辑委员会编制的1:100万植被图(
... )、中国数字植物标本馆(CVH, http://www.cvh.org.cn)和全球生物多样性数据集(GBIF, http://www.gbif.org).本文中的1:100万植被图来源于国家自然科学基金委员会“中国西部环境与生态科学数据中心”和“地球系统科学数据共享网”.其中从CVH和GBIF中共计得到88个有效的自然分布点数据; 植被图经转换为1 km分辨率的栅格后再转换为点矢量格式.杉木现实空间分布数据来自于1:100万植被图(
An improved approach for predicting the distribution of rare and endangered species from occurrence and pseudo-absence data
1
2004
... 为了避免固定阈值带来的不确定性, 提出了很多阈值最优化选择方法, 这就是客观的阈值选择方法, 这些方法选择的阈值可以最大化地保证观测值和预测值的一致性(
Testing the generality of bird-habitat models
1995
A review of methods for the assessment of prediction errors in conservation presence/ absence models
4
1997
... 为了避免固定阈值带来的不确定性, 提出了很多阈值最优化选择方法, 这就是客观的阈值选择方法, 这些方法选择的阈值可以最大化地保证观测值和预测值的一致性(
... 由于所采用的模型需要物种存在和物种不存在数据进行建模.采用类似Engler等(2004)和张雷等(2011b)的方法, 把所有没有某一物种记录的地点与有记录地点的环境条件(即7个环境变量)进行对比, 如果某地区与已知点环境条件相同(即此地区的环境变量完全包含在所有已知记录地点的7个环境条件变程范围内), 那么这些地区可以认为适合这一物种分布, 把这些地区从无记录地点中删除, 剩余的地区可以认为是“完全”不适宜这一物种的地区, 这些地区指定为不存在区, 并在其中随机选择了与该物种分布点数量相等的不存在点数据作为模型建模数据.本文之所以选择与物种存在记录数据相等的准不存在数据是基于两个方面的考虑: 一是物种发生率较低时会对阈值选择过度敏感(
... 不同阈值选择方法所确定的最适宜阈值存在显著差异, 但是其预测准确度之间没有显著差异.默认值0.5是阈值转换过程中经常采用的方法.Liu等(2005)认为默认值0.5方法是一种最差的阈值选择方法, 不建议采用; 但本文却发现它是仅次于具有相同值的最大Kappa、最大TSS和最大总准确度的方法.Freeman和Moisen (2008)也发现默认值0.5对于多数物种而言, 能提供较高的模型预测准确度.这些研究之所以发现默认值0.5是一个较优异的方法, 是因为这些研究采用的建模数据发生率是0.5, 而以往研究表明物种发生率法(即利用物种发生率作为转换阈值)也是一个良好的阈值选择方法(
... 最大Kappa、最大TSS和最大总准确度法确定的最佳转换阈值不同, 但是它们的预测准确度(Kappa、TSS和总准确度)却相同, 这是由于这3个准确度评估指标都是混合式指数, 即它们对遗漏误差和冗余误差给予不同的权重(
A comparison of the performance of threshold criteria for binary classification in terms of predicted prevalence and Kappa
3
2008
... 物种生境模型对于资源管理、环境评估和生物多样性保护等方面具有重要的价值, 当前物种生境模型已经应用到大量的具有理论和应用目的的研究中(
... 最大TSS法和最大Kappa法用于阈值选择时, 多数情况下表现出了一定的稳健性.本文发现阈值选择方法最大Kappa和最大TSS法具有最高模型预测准确度, 这与
... 发现最大Kappa方法对于13个物种中的12个物种而言都是优异的阈值选择方法.本文也发现最大Kappa值法具有最大的模型预测准确度, 因此可以基本认定最大Kappa法和最大TSS法选择阈值具有较强的稳健性.本文发现最大总准确度方法与最大Kappa和最大TSS法的模型预测准确度一样都属于最高值,
Predictive habitat distribution models in ecology
1
2000
... 为了避免固定阈值带来的不确定性, 提出了很多阈值最优化选择方法, 这就是客观的阈值选择方法, 这些方法选择的阈值可以最大化地保证观测值和预测值的一致性(
ModEco: An integrated software package for ecological niche modeling
1
2010
... 为了避免固定阈值带来的不确定性, 提出了很多阈值最优化选择方法, 这就是客观的阈值选择方法, 这些方法选择的阈值可以最大化地保证观测值和预测值的一致性(
2
... 物种生境模型对于资源管理、环境评估和生物多样性保护等方面具有重要的价值, 当前物种生境模型已经应用到大量的具有理论和应用目的的研究中(
... )、Biomapper软件(
Threshold criteria for conversion of probability of species presence to either-or presence-absence
1
2007
... “随机森林”是一种现代分类与回归技术, 同时也是一种组合式的自学习技术.“随机森林”通过自助法(bootstrap)随机选择(不是全部)变量生长成分类“树”, 每个“树”都会完整生长而不会修剪(pruning).并且在生成树的时候, 每个节点的变量都仅仅在随机选出的少数几个变量中产生.通过这种随机方式生成的单个、十个、百个或者成千个树被用于分类和回归分析(因此被称为“随机森林”).最终的决策树是通过对潜在的随机变量树进行“投票”表决(voting system)生成的, 即“随机森林”选择具有最多投票的分类.如果目的是回归分析, 则对这些树的结果进行平均得到因变量预测值.因此, 本文利用“随机森林”分类算法预测珙桐生境时, 输入数据是分类变量(存在/不存在), 输出结果同样也是二元数据(存在/不存在); 当利用其回归算法预测珙桐生境时, 输入数据是数值变量(1代表存在; 0代表不存在), 输出结果是连续变量(0-1).采用“随机森林”模拟珙桐生境适生区, 这是由于“随机森林”预测准确度通常高于其他模型, 并且具有一定的稳健性(
基于物种分布模型评价土壤因子对我国毛竹潜在分布的影响
2013
Classification and regression by randomForest
4
2002
... 通常, 阈值选择方法分为两种方式: 主观方法和客观方法(
... 为了避免固定阈值带来的不确定性, 提出了很多阈值最优化选择方法, 这就是客观的阈值选择方法, 这些方法选择的阈值可以最大化地保证观测值和预测值的一致性(
... 不同阈值选择方法所确定的最适宜阈值存在显著差异, 但是其预测准确度之间没有显著差异.默认值0.5是阈值转换过程中经常采用的方法.Liu等(2005)认为默认值0.5方法是一种最差的阈值选择方法, 不建议采用; 但本文却发现它是仅次于具有相同值的最大Kappa、最大TSS和最大总准确度的方法.Freeman和Moisen (2008)也发现默认值0.5对于多数物种而言, 能提供较高的模型预测准确度.这些研究之所以发现默认值0.5是一个较优异的方法, 是因为这些研究采用的建模数据发生率是0.5, 而以往研究表明物种发生率法(即利用物种发生率作为转换阈值)也是一个良好的阈值选择方法(
... 最大Kappa、最大TSS和最大总准确度法确定的最佳转换阈值不同, 但是它们的预测准确度(Kappa、TSS和总准确度)却相同, 这是由于这3个准确度评估指标都是混合式指数, 即它们对遗漏误差和冗余误差给予不同的权重(
Selecting thresholds for the prediction of species occurrence with presence-only data
3
2013
... 为了避免固定阈值带来的不确定性, 提出了很多阈值最优化选择方法, 这就是客观的阈值选择方法, 这些方法选择的阈值可以最大化地保证观测值和预测值的一致性(
... 最大TSS法和最大Kappa法用于阈值选择时, 多数情况下表现出了一定的稳健性.本文发现阈值选择方法最大Kappa和最大TSS法具有最高模型预测准确度, 这与
... 本研究进一步证实阈值方法的选择将会影响根据生境分布区变化进行的物种受胁迫程度评估(
Selecting thresholds of occurrence in the prediction of species distributions
1
2005
... 最大TSS法和最大Kappa法用于阈值选择时, 多数情况下表现出了一定的稳健性.本文发现阈值选择方法最大Kappa和最大TSS法具有最高模型预测准确度, 这与
Choice of threshold alters projections of species range shifts under climate change
1
2011
... 物种生境模型对于资源管理、环境评估和生物多样性保护等方面具有重要的价值, 当前物种生境模型已经应用到大量的具有理论和应用目的的研究中(
Model thresholds are more important than presence location type: Understanding the distribution of lowland tapir (Tapirus terrestris) in a continuous Atlantic forest of southeast Brazil
2
2014
... 通常, 阈值选择方法分为两种方式: 主观方法和客观方法(
... 最大TSS法和最大Kappa法用于阈值选择时, 多数情况下表现出了一定的稳健性.本文发现阈值选择方法最大Kappa和最大TSS法具有最高模型预测准确度, 这与
NeuralEnsembles: A neural network based ensemble forecasting program for habitat and bioclimatic suitability analysis
1
2009
... 物种生境模型对于资源管理、环境评估和生物多样性保护等方面具有重要的价值, 当前物种生境模型已经应用到大量的具有理论和应用目的的研究中(
2
... 为了评估不同阈值选择方法对未来气候条件下分布区迁移相对变化预测的影响, 对分布区的面积变化和分布区迁移方向进行了量化.分布区面积变化评价包括: 当前潜在生境分布面积、未来气候条件下的潜在生境分布面积、未来气候条件下生境相对保持不变的比例、生境消失比例、获取新生境的比例、分布区的东向和北向迁移距离以及最适宜海拔分布高度的变化.其中采用分布区质心(centroid)的迁移变化来分析生境分布区东向和西向的迁移距离.最适宜海拔分布高度的变化采用加权平均的方法进行估计(
... 采用Friedman秩和检验方法分析不同阈值选择方法之间模型准确度的差异; 两两之间的比较采用Nemenyi检验法.采用同样的方法也对不同阈值选择方法所生成的当前潜在分布区面积预估之间的差异以及未来气候条件下分布区相对变化之间的差异进行了分析.此外采用Kappa值分别评估了当前和未来气候条件下不同阈值选择方法所生成的生境分布图的两两空间相似性.本文所有统计分析都在R 3.1.2软件(
A PCA-based modelling technique for predicting environmental suitability for organisms from presence records
1
2001
... 本研究进一步证实阈值方法的选择将会影响根据生境分布区变化进行的物种受胁迫程度评估(
样本容量和物种特征对BIOCLIM模型模拟物种分布准确度的影响——以12个中国特有落叶栎树种为例
1
2009
... 物种生境模型对于资源管理、环境评估和生物多样性保护等方面具有重要的价值, 当前物种生境模型已经应用到大量的具有理论和应用目的的研究中(
Weighted averaging, logistic regression and the Gaussian response model
2
1986
... 通常, 阈值选择方法分为两种方式: 主观方法和客观方法(
... “随机森林”是一种现代分类与回归技术, 同时也是一种组合式的自学习技术.“随机森林”通过自助法(bootstrap)随机选择(不是全部)变量生长成分类“树”, 每个“树”都会完整生长而不会修剪(pruning).并且在生成树的时候, 每个节点的变量都仅仅在随机选出的少数几个变量中产生.通过这种随机方式生成的单个、十个、百个或者成千个树被用于分类和回归分析(因此被称为“随机森林”).最终的决策树是通过对潜在的随机变量树进行“投票”表决(voting system)生成的, 即“随机森林”选择具有最多投票的分类.如果目的是回归分析, 则对这些树的结果进行平均得到因变量预测值.因此, 本文利用“随机森林”分类算法预测珙桐生境时, 输入数据是分类变量(存在/不存在), 输出结果同样也是二元数据(存在/不存在); 当利用其回归算法预测珙桐生境时, 输入数据是数值变量(1代表存在; 0代表不存在), 输出结果是连续变量(0-1).采用“随机森林”模拟珙桐生境适生区, 这是由于“随机森林”预测准确度通常高于其他模型, 并且具有一定的稳健性(
Patterns and uncertainties of species’ range shifts under climate change
2004
植物种分布的模拟研究进展
2006
Consensus forecasting of species distributions: The effects of niche model performance and niche properties
1
2015
... 虽然目前有很多确定阈值的方法, 但是还缺少关于它们预估结果的比较研究, 导致对它们的表现能力认识不清.此外, 还有一些模型既可以生成生境概率分布图也能生成二元分布图, 如“随机森林” (random forest)的分类和回归算法可以分别生成二元和概率生境分布图(
气候变化对马尾松潜在分布影响预估的多模型比较
3
2011
... 选择7个与物种生理特征有关的环境数据进行生境空间预测: 包括年平均气温(℃)、最冷月平均气温(MCMT, ℃)、最暖月平均气温(MWMT, ℃)、气温年较差(MWMT-MCMT, ℃)、年降水量(mm)、夏季降水量(5-9月, mm)及大于5 ℃的积温.这7个气候变量均是1961-1990年连续30年现实观测数据的平均值.未来气候条件下的气候数据来自A2排放情景下加拿大的气候模式CCCMA_ CGCM3 (Coupled Global Climate Model of Canadian Centre for Climate Modelling and Analysis), 为2070-2099年连续30年数据的平均值.模型所采用的当前和未来气候条件下的7个气候变量都是从ClimateChina软件(
... “随机森林”是一种现代分类与回归技术, 同时也是一种组合式的自学习技术.“随机森林”通过自助法(bootstrap)随机选择(不是全部)变量生长成分类“树”, 每个“树”都会完整生长而不会修剪(pruning).并且在生成树的时候, 每个节点的变量都仅仅在随机选出的少数几个变量中产生.通过这种随机方式生成的单个、十个、百个或者成千个树被用于分类和回归分析(因此被称为“随机森林”).最终的决策树是通过对潜在的随机变量树进行“投票”表决(voting system)生成的, 即“随机森林”选择具有最多投票的分类.如果目的是回归分析, 则对这些树的结果进行平均得到因变量预测值.因此, 本文利用“随机森林”分类算法预测珙桐生境时, 输入数据是分类变量(存在/不存在), 输出结果同样也是二元数据(存在/不存在); 当利用其回归算法预测珙桐生境时, 输入数据是数值变量(1代表存在; 0代表不存在), 输出结果是连续变量(0-1).采用“随机森林”模拟珙桐生境适生区, 这是由于“随机森林”预测准确度通常高于其他模型, 并且具有一定的稳健性(
... 本研究进一步证实阈值方法的选择将会影响根据生境分布区变化进行的物种受胁迫程度评估(
基于DOMAIN和NeuralEnsembles模型预估中国毛竹潜在分布
2011
随机森林算法基本思想及其在生态学中的应用——以云南松分布模拟为例
2014
