
 , 吴远远1, 郝晓地2, 王保国3, 徐龙飞3, 刘杰1, 林甲1, 江瀚1
, 吴远远1, 郝晓地2, 王保国3, 徐龙飞3, 刘杰1, 林甲1, 江瀚11. 北京首创生态环保集团股份有限公司, 技术中心/中-荷未来污水技术研发中心, 北京 100044;
2. 北京建筑大学, 北京未来城市设计高精尖中心/中-荷未来污水技术研发中心, 北京 100044;
3. 北京龙庆首创水务有限责任公司, 北京 102101
收稿日期: 2021-03-18; 修回日期: 2021-05-11; 录用日期: 2021-05-11
基金项目: 国家自然科学基金(No.51878022);国家水体污染控制与治理科技重大专项(No.2017ZX07102-003)
作者简介: 李天宇(1992—), 男, E-mail: litianyu@capitalwater.cn
通讯作者(责任作者): 李天宇
摘要:为进一步提高国内基础建模数据质量,降低建模实践中的数据清洗难度,本研究以北京龙庆再生水厂生物建模过程中的实际数据问题为例,基于数理统计理论及国内污水水质特征分别构建误差来源分析方法与误差影响评价方法.通过设计补充采样与实验排查方案,成功识别数据误差来源并实现不同类型误差对数据准确性的影响量化评价.研究结果表明,污水处理厂日常的取样与化验过程中产生的随机误差不可忽视,特别是当大量随机误差存在时,对数据总体造成的波动影响无法通过数据量的积累而消除;而不同的采样位置与不当的样品保存方式则会引起水质发生变化,由此产生的系统误差将导致测量结果长期偏高/偏低.因此,在依赖人工测量数据进行建模的国内实践中,应首先对历史数据进行误差检验,再进行必要的建模补充采样,以避免补充数据质量受相同误差影响,减少非必要的人力、物力浪费.
关键词:污水生物处理生物建模数据清洗误差分析影响评价
Error source detection and effect evaluation of water quality data for modeling biological wastewater treatment
LI Tianyu1

 , WU Yuanyuan1, HAO Xiaodi2, WANG Baoguo3, XU Longfei3, LIU Jie1, LIN Jia1, JIANG Han1
, WU Yuanyuan1, HAO Xiaodi2, WANG Baoguo3, XU Longfei3, LIU Jie1, LIN Jia1, JIANG Han11. Technical Center/Sino-Dutch R&D Centre for Future Wastewater Treatment Technologies, Beijing Capital Eco-Environment Protection Group Co., Ltd, Beijing 100044;
2. Beijing Advanced Innovation Center of Future Urban Design/Sino-Dutch R&D Centre for Future Wastewater Treatment Technologies, Beijing University of Civil Engineering and Architecture, Beijing 100044;
3. Beijing Capital Longqing Water Co., Ltd, Beijing 102101
Received 18 March 2021; received in revised from 11 May 2021; accepted 11 May 2021
Abstract: To improve the original data quality of modeling biological wastewater treatment and to reduce the difficulty of data cleaning in modeling, the study applied a practical data (from Beijing Longqing wastewater treatment plant) problem as an example in modeling, and established both error source detection and error effect evaluation based on the mathematical statistical theory and the domestic wastewater characteristics. With the help of the supplementary sampling and experimental investigation, the data errors from different sources were successfully identified, and the effects on the data accuracy by different error were quantitatively analyzed. The results indicate that random errors in the daily sampling and lab testing process cannot be neglected, and the effect of fluctuations caused by the whole data cannot be eliminated by the data accumulation, particularly when a large number of random errors exist. However, different sampling locations and improper samples' storage methods would cause some changes of water quality, which could result in a systematic error that would further lead to long-term high/low measurement results. Therefore, the historical data should be first checked for their errors, and then necessary supplementary sampling is carried out when manual measurement is used for model application, to avoid the quality of supplementary sampling data affected by the same errors and to reduce unnecessary labors and materials.
Keywords: biological wastewater treatmentmodelingdata cleaningerror detectioneffect evaluation
1 引言(Introduction)随着“碳中和”正式编入十四五规划, 我国未来30年生态文明建设的整体布局和思路已经明确.为了更高效地实现碳中和目标, 责任重大的环保行业应积极探索, 力争走上绿色低碳乃至转型蓝色经济的可持续发展道路(郝晓地等, 2017).其中, 作为碳排放大户的污水处理厂迫切需求“提技术、降成本”的碳中和生产方式.在此方面, 荷兰、奥地利、德国等国家已先后拥有多座污水处理厂逼近碳中和运行的成功经验(van Nieuwenhuijzen et al., 2009;Nowak et al., 2011;Marner et al., 2016;Macintosh et al., 2019).在国内, 以开源/节流措施实现碳中和目标的可持续污水处理技术业已研发多年(郝晓地, 2006), 并陆续开展工程研究实践(宋新新等, 2021).然而, 国内污水处理厂总体上仍处于被动执行标准阶段, 因此, 在满足达标排放的基础上实现节能降耗、提高污水处理综合效能不仅是既有污水处理厂普遍存在的技术需求, 更是其迈向碳中和运行的重要前提(王洪臣, 2017).
基于生物建模技术为污水处理厂制定合理的节能降耗与运行优化方案, 已逐步成为国内应用实践的必要技术手段(孙培德等, 2018;郝二成等, 2020;柳萌萌等, 2020).然而, 数据质量是影响模型可靠性的关键因素, 基于错误数据进行建模将大大增加模型的不确定性, 甚至产生错误结论(Puig et al., 2008;Meijer et al., 2012).研究表明, 利用系统性三步数据清洗方法, 可显著提高基础建模数据质量、简化模型校正过程并大幅提高生物模型可靠性(李天宇等, 2020).但在国内实践中, 系统误差、偶然误差大量存在于日常的取样、运输、保存及化验过程中, 极大地增加数据清洗难度并延长建模周期.
在误差数据处理方面, 虽然国外已有研究对污水厂典型数据误差来源进行了梳理(Rieger et al., 2010), 并可通过标准偏差(SD)分析识别异常数据(Thomann, 2008), 利用冗余物料平衡计算恢复数据一致性(Meijer et al., 2002).但其局限性在于:相关统计结论为针对在线数据的研究结果, 且物料平衡计算仅能消除系统误差对数据总体的影响, 在国内仪表普遍缺乏维护、有效数据量不足且依赖人工测量的情况下, 尚无法在国内直接应用.有鉴于此, 本研究以北京龙庆再生水厂生物建模过程中的实际数据问题为例, 基于数理统计理论及国内污水水质特征构建误差来源分析方法及影响评价方法, 通过设计补充采样与实验方案, 识别误差来源并分析不同类型误差对数据准确性的影响.
2 材料和方法(Materials and methods)2.1 研究水厂概况案例厂位于北京市延庆区, 采用AAO+MBR+臭氧活性炭吸附工艺, 设计规模为60000 t·d-1.该厂服务范围主要为延庆城区、附近村镇及大学城区域的生活污水, 因此, 进水不含工业废水.预处理单元在常规粗格栅、转鼓格栅(细格栅)和平流曝气沉砂池后增加膜格栅以进一步降低进水SS, 污水经预处理后由改良回流的AAO工艺进入MBR池, 因出水COD稳定达标, 臭氧活性炭深度处理装置长期关闭, MBR池出水经超越管线直接入清水池, 全厂工艺流程见图 1.
图 1(Fig. 1)
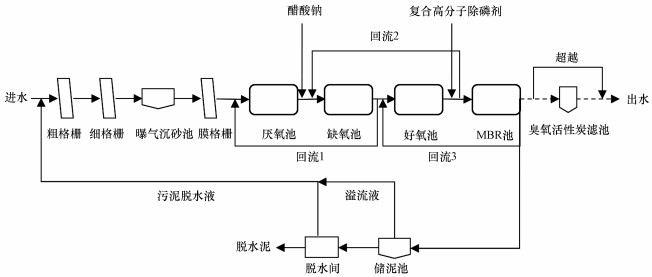 |
| 图 1 北京龙庆城西污水处理厂工艺流程图 Fig. 1Process flow diagram of Beijing Longqing WWTP |
2.2 数据来源生物建模期间, 首先收集该厂近一年(2018年11月-2019年11月)实验室化验数据, 统计结果显示该厂日平均进水水质为:CODCr≈268.9 mg·L-1, SS≈122.8 mg·L-1, TN≈44.5 mg·L-1, NH4+-N≈37.9 mg·L-1, TP≈5.18 mg·L-1.为进一步划分进水组成, 分别于2019年12月9-12日及2020年4月23-24日期间在膜格栅后补充24 h进水采样(采样间隔2 h).24 h补充采样结果显示日平均进水水质为:CODCr≈479.8 mg·L-1, SS≈212.5 mg·L-1, TN≈53.7 mg·L-1, NH4+-N≈36.3 mg·L-1, TP≈3.79 mg·L-1.然而, 对比发现两组样本水质数据存在较大差异, 特别是进水C/N、C/P差异显著.
考虑到污水厂进水水质波动对数据结果的影响, 根据三步数据清洗法中对国内进水水质波动情况是否正常的判断依据(李天宇等, 2020), 分别计算两组数据源(近一年历史化验数据、24 h补充检测数据)的相对标准偏差.结果表明, 在近一年历史数据中, COD、TP的RSD值显著>20%;在24 h补充检测数据中, COD、TP、TN的RSD值亦全部>20%.说明两组水质数据的波动已超过国内市政污水正常波动特征, 特别是COD、TP、TN数据中可能存在大误差.因此, 两组数据源均无法满足生物建模需求.
2.3 方案设计基于Rieger对污水处理厂典型数据误差来源分析结果(Rieger et al., 2010), 通过跟踪该厂日常水样取样、保存及化验过程, 发现以下4种潜在误差来源:①近一年内进水采样点分别位于细格栅后与膜格栅后, 每日由专人在其中一处完成采样, 但无详细记录;②采样时间为上午8:00-9:00, 每次采样约500 mL, 无平行样;③水样采集完毕送至实验室后未置于4 ℃条件下冷藏, 当样品较多时, 水样经常温保存24 h后于次日完成检测;④实验员每月轮换检测项目, 当样品较多时, 无法保证各项指标专人专测, 且手法操作无法保证全部一致.
有鉴于此, 根据上述4种潜在误差来源设计排查方案:(1)采样点:设2组采样点, 分别位于转鼓格栅后与膜格栅后;(2)采样频率:按日常习惯, 每日上午9:00采瞬时水样, 同一采样点每次采样2瓶, 每瓶500 mL;(3)检测项目:4瓶水样在当日完成COD、TN、TP、PO43-共4项指标检测, 同一采样点的2瓶水样互为对照组;(4)样品保存:按日常习惯, 将4瓶水样继续常温保存24 h后, 重复对4项指标进行复检;(5)注意事项:采样方案宜连续执行7 d, 并参考表 1安排实验员轮岗与负责项目记录.
表 1(Table 1)
| 表 1 误差来源排查结果原始数据表 Table 1 Original data table of error source investigation results | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 1 误差来源排查结果原始数据表 Table 1 Original data table of error source investigation results
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2.4 误差来源分析方法理论上, 测量误差主要分为随机误差与系统误差.上述4种潜在误差来源中:①是不同采样点水质真实变化导致的误差;②是瞬时采样不均匀导致的误差;③是常温保存条件水样变质造成的误差;④是实验员不确定性手法操作引起的误差.其中, ①和③属于系统误差;②和④为随机误差.
实践中, 系统误差与随机误差并非相互独立的, 因此, 如何区分主要影响因素是问题关键.已知在样本数量有限时, 相对标准偏差(RSD)计算已被证明是一种既简便又可量化判断数据可靠性的分析方法(Meijer et al., 2015;李天宇等, 2020), 其基本计算公式为:
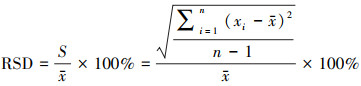 | (1) |
本研究中, 互为对照的一组平行样品是采样点、采样时间、保存方法均相同的两瓶瞬时水样.因样本总体确定, 因此, 公式(1)可改写为:
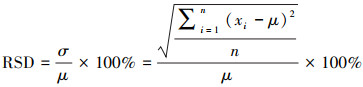 | (2) |
2.5 误差影响评价方法对于随机误差, 因其大小和符号均呈现随机性, 因此, 从数学意义上无法准确测量或表征;然而, 由于污水水质本身具有一定的变化规律与边界约束, 因此, 从现实意义上能够实现对此类误差影响的量化评价.在统计学领域, 标准偏差(SD)常用于衡量数据值偏离算数平均值的程度, 对于已知测量总体求其标准偏差的计算公式见式(3).
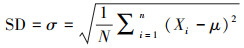 | (3) |
对于系统误差, 由于其特点是测量结果向一个方向偏离, 因此, 需确定大小及符号才可实现对该类误差的准确量化.统计学中, 示值误差(EI)常用于指示测量值与被测量值的实际值之差, 由于真值往往不能确定, 因此, 实际使用的是约定真值, 其基本计算公式见式(4).
 | (4) |
3 结果与讨论(Results and discussion)3.1 随机误差的判别与影响表 1为根据排查方案获取的原始数据记录表, 共计224条.表中, “首检”表示样品于采集当天完成检测, “复检”表示样品经常温保存24 h后的重复检测;采样点后缀数字1、2表示该采样点的2个平行样品.首先, 基于表 1分别计算平行样品检测结果的平均值及相对标准偏差(RSD), 结果列于表 2.根据判定标准(1), 首先筛选表 2中RSD>5%的项目并加粗显示, 表明该组平行样品的结果误差偏大;然后在加粗项目中统计某日首检与复检的4个检测项目中均出现2次及以上(出现概率≥50%)的大误差样品.统计结果表明, 2020-5-21膜格栅与2020-5-25转鼓格栅的两组平行样品存在随机误差.
表 2(Table 2)
| 表 2 平行样品检测结果数据分析 Table 2 Data analysis of the parallel sample test results | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 2 平行样品检测结果数据分析 Table 2 Data analysis of the parallel sample test results
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
然后, 基于表 2各组平均值计算首检与复检结果差异的相对标准偏差(RSD), 结果列于表 3.根据判定标准(2), 首先在表 2中筛选同一天两个采样点的同一检测项目RSD值均>5%的项目, 满足该条件的检测项目及化验员姓名已在表 2中阴影标注;同时, 在表 3中筛选同一检测项目不同采样点的结果差异RSD均>20%的项目, 满足该条件的检测项目及实验员姓名已在表 3中阴影标注.统计结果表明, 同时满足以上两个筛选条件的化验员为段丹波、闫祎含, 分别在2020-5-21首检TN、2020-5-25首检COD、2020-5-26复检TP、2020-5-27复检TN共4组检测项目中存在随机误差.
表 3(Table 3)
| 表 3 平行样品检测结果RSD分析 Table 3 RSD analysis of parallel samples | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 3 平行样品检测结果RSD分析 Table 3 RSD analysis of parallel samples
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
根据标准偏差公式(3)及误差判定结果, 分别提取表 1、表 2中与随机误差②和④相关的误差数据并计算其标准偏差(SD), 结果列于表 4.表 4统计结果表明:(1)瞬时样品误差对溶解性及非溶解性水质指标均造成不同程度影响, 其中以COD影响最为显著而对TP、TN及PO43-的影响相对较小, 说明误差主要来源于取样点有机颗粒的不均匀分布, 通过优化采样点流态、增加重复取样次数可有效减少此类误差;(2)因化验员不当操作引起的误差主要对非溶解性水质指标造成影响, 且影响幅度较瞬时采样误差更大, 说明该厂化验员段丹波、闫祎含在操作手法上存在不规范问题, 通过培训、学习、奖惩等形式或手段强化实验员基础操作能力可有效减小此类误差.
表 4(Table 4)
| 表 4 随机误差SD分析与统计 Table 4 SD analysis and statistics of Random error | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 4 随机误差SD分析与统计 Table 4 SD analysis and statistics of Random error
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.2 系统误差的判别与影响根据随机误差判定结果, 首先剔除表 1中共计44条误差数据, 包括2020-5-21膜格栅与2020-5-25转鼓格栅的两组平行样品首检及复检全部数据、2020-5-21首检TN、2020-5-25首检COD、2020-5-26复检TP、2020-5-27复检TN数据, 最终剩余180条有效数据, 数据剔除率约19.6%.然后根据示值误差公式(4), 分别以膜格栅水样数据和首检数据作为约定真值, 计算有效数据中与系统误差①和③相关水质数据的示值误差(EI), 计算结果分别绘制于图 2、图 3, 统计结果列于表 5.
图 2(Fig. 2)
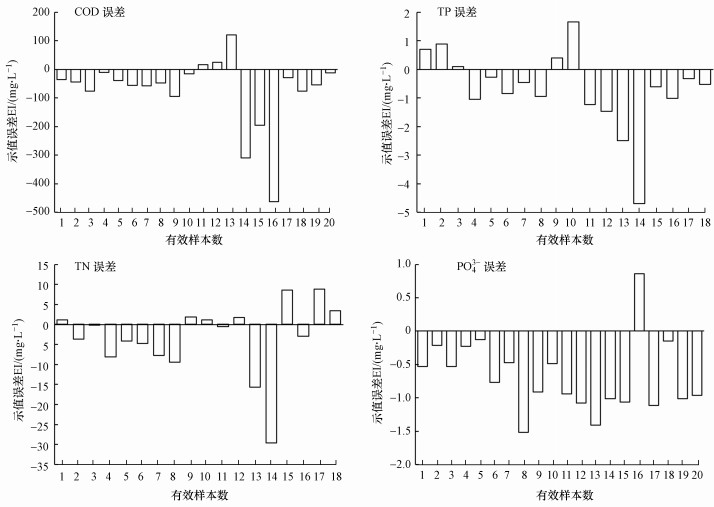 |
| 图 2 采样位置对测量结果误差分布的影响 Fig. 2Influence of sampling position on error distribution of measurement results |
图 3(Fig. 3)
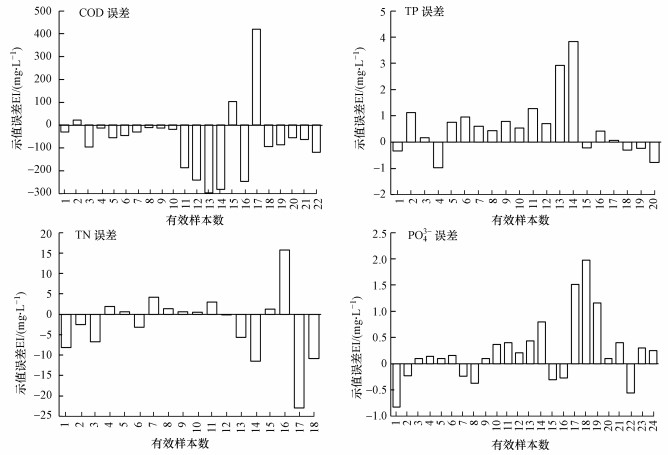 |
| 图 3 常温保存对测量结果误差分布的影响 Fig. 3Influence of normal temperature storage on error distribution of measurement results |
表 5(Table 5)
| 表 5 系统误差EI分析与统计 Table 5 EI analysis and statistics of systematic error | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 5 系统误差EI分析与统计 Table 5 EI analysis and statistics of systematic error
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
通过图 2采样位置误差分布及表 5统计结果发现, 转鼓格栅后水样在曝气沉砂池与膜格栅的物理作用下水质发生了变化, 因此, 造成两组采样点测量结果的误差, 具体表现为:转鼓格栅后COD、TN、TP、PO43-水质指标均低于膜格栅后水样, 且TP的变化几乎全部来源于PO43-.这是由于在曝气沉砂池的气泡与水力剪切作用下, 大量吸附于原水无机颗粒表面的有机絮体脱落, 无机颗粒经沉砂池、膜格栅被大量去除后, 脱落的絮状有机物则分散于原水中.表 5统计结果显示, 污水经曝气沉砂池与膜格栅后增加的COD∶TN (TKN)∶PO43-(TP)之比接近100∶5∶1, 为良好的生物质碳源, 该现象与前期研究发现一致(郝晓地等, 2017).
通过图 3常温保存误差分布及表 5统计结果表明, 常温保存24 h后在微生物作用下出现了水样变质, 因此, 造成首检与复检结果的误差, 具体表现为:复检结果COD下降明显, TN小幅降低, TP、PO43-小幅增加.这是由于贮泥池回流液与脱水回流液的回流点均位于粗格栅前, 且案例厂MBR工艺系统污泥浓度高, 回流液流量大, 因此, 位于粗格栅后的水样中均含有数量可观的回流活性污泥.一方面, 在采样水温18.5 ℃、室内温度23 ℃条件下, 异养微生物代谢速率快, 消耗水中COD、N、P营养物质;另一方面, 因案例厂存在生物除磷现象, 模型拟合结果显示PAOs菌丰度约占活性污泥的30%, 因此, 推测TP和PO43-的增加主要与厌氧释磷现象有关(郝晓地等, 2020).
3.3 误差来源分析结果已知在生物建模期间, 案例厂24 h补充检测数据的采样点均设置于膜格栅后, 各检测项目均于采样当日完成化验, 因此, 该组数据总体中不存在①和③两类系统误差, 理论上仅受偶然误差影响.相反, 对于近一年历史数据, 由于总体数据量大, 因此, 理论上该组数据总体不受②和④两类随机误差影响, 但由于无法提供准确采样点及检测时间记录, 因此, 不能排除系统误差对测量结果的影响.
为深入分析两组水质数据误差来源, 首先根据公式(1)、(2)分别计算近一年历史数据与24 h补充检测数据两组数据源的RSD值并列于表 6, 然后根据公式(3)分别计算近一年历史数据(各检测项目数据量均≥360个)及24 h补充检测数据(各检测项目数据量均为48个)的标准偏差, 结果见表 6.将表 6中SD值统计结果与表 4两类随机误差SD值特征范围对比可知:(1)两组数据源中COD、TP、TN标准偏差均与随机误差④特征范围相符;(2)随机误差的影响并未因数据量的积累而消除.最后, 以24 h补充检测数据均值为约定真值, 根据公式(3)计算近一年历史数据的示值误差, 结果见表 6.将表 6中EI统计结果与表 5两类系统误差EI特征值对比可知:(1)近一年历史数据相关示值误差与系统误差③特征规律一致;(2)在未剔除随机误差数据的情况下, COD、TP、TN的示值误差均高于系统误差影响范围.
表 6(Table 6)
| 表 6 历史数据及24 h补充数据统计表 Table 6 Statistical table of historical data and 24 h supplementary data | ||||||||||||||||||||||||||||||||||||||||||||||||||
表 6 历史数据及24 h补充数据统计表 Table 6 Statistical table of historical data and 24 h supplementary data
| ||||||||||||||||||||||||||||||||||||||||||||||||||
综上分析, 两组数据源均存在不同来源的测量误差, 这是导致两组数据质量较差的主要原因.其中, 近一年历史数据中存在相当数量的随机误差, 该误差主要来源于实验员的不当操作;并且测量结果长期受系统误差影响导致COD与TN偏低、TP偏高, 该误差主要来源于样品保存不规范导致水样变质.在24h补充检测结果中, 随机误差导致测量结果出现不确定性错误, 该误差亦主要来源于实验员的不当操作.
4 结论(Conclusions)1) 结合国内污水处理厂实际水质数据问题, 基于数理统计理论及国内污水水质特征构建的误差来源分析方法与影响评价方法切实可行.通过设计连续一周的补充采样与化验方案, 可完成对不同来源误差数据的识别, 并实现不同类型误差对数据准确性影响的量化评价.
2) 因瞬时采样不均匀及实验员不当操作引起的随机误差不可忽视, 大量随机误差对水质数据的影响难以通过数据的单向积累而消除;不同的采样位置与不当的样品保存方式均会引起水质发生变化, 由此产生的系统误差将导致测量结果长期偏高/偏低.本研究中案例厂实验室方面的不规范操作是导致数据异常的首要原因, 因此, 应强化实验员基础操作能力、增加平行对照组等方法以消除误差影响.
3) 在依赖人工测量数据进行建模的国内实践中, 应首先设计误差排查方案, 识别历史数据中的主要误差来源并完成误差数据影响检查后, 再进行必要的建模补充采样.否则, 相同来源的误差会同步出现于后续测量结果中, 不仅影响数据质量还造成人力、物力的浪费.
参考文献
| 郝晓地. 2006. 可持续污水-废物处理技术[M]. 北京: 中国建筑工业出版社. |
| 郝晓地, 李天宇, van Loosdrecht M C M, 等. 2017. 蓝色经济下的水技术变革[J]. 中国给水排水, 33(2): 5-12. |
| 郝晓地, 李天宇, 吴远远, 等. 2017. A2/O工艺用于污水处理厂升级改造的适宜性探讨[J]. 中国给水排水, 33(21): 18-24. |
| 郝晓地, 陈峤, 刘然彬. 2020. Tetrasphaera聚磷菌研究进展及其除磷能力辨析[J]. 环境科学学报, 40(3): 741-753. |
| 郝二成, 郭毅, 刘伟岩, 等. 2020. 基于数学模拟的污水厂运行分析-控制与优化[J]. 中国给水排水, 36(17): 23-29. |
| Hulsbeek J J, Kruit J, Roeleveld P, et al. 2002. A practical protocol for dynamic modelling of activated sludge systems[J]. Water Science & Technology, 45(6): 127-136. |
| 李天宇, 吴远远, 郝晓地, 等. 2020. 数据清洗对污水处理厂生物建模可靠性影响研究[J]. 环境科学学报, 40(9): 3298-3310. |
| 柳蒙蒙, 陈梅雪, 齐嵘, 等. 2020. 面向寒冷地区城镇污水处理厂提标改造的ASM模拟优化及其应用[J]. 环境工程学报, 14(4): 1119-1128. |
| Macintosh C, Astals S, Sembera C, et al. 2019. Successful strategies for increasing energy self-sufficiency at Grüneck wastewater treatment plant in Germany by food waste co-digestion and improved aeration[J]. Applied Energy, 242: 797-808. DOI:10.1016/j.apenergy.2019.03.126 |
| Marner S T, Schrter D, Jardin N. 2016. Towards energy neutrality by optimising the activated sludge process of the WWTP Bochum-?lbachtal[J]. Water Science & Technology, 73(12): 3057-3063. |
| Meijer S C F, van der Spoel H, Susanti S, et al. 2002. Error diagnostics and data reconciliation for activated sludge modelling using mass balance[J]. Water Science & Technology, 45: 145-156. |
| Meijer S C F, Brdjanovic D. 2012. A Practical Guide to Activated Sludge Modelling[M]. UNESCO-IHE. |
| Meijer S C F, van Kempen R N A, Appeldoorn K J, et al. 2015. Applications of Activited Sludge Models[M]. IWA Publishing. |
| Nowak O, Keil S, Fimml C. 2011. Examples of energy self-sufficient municipal nutrient removal plants[J]. Water Science & Technology, 64(1): 1-6. |
| Puig S, van Loosdrecht M C M, Colprim J, et al. 2008. Data evaluation of full-scale wastewater treatment plants by mass balance[J]. Water Research, 42: 4645-4655. DOI:10.1016/j.watres.2008.08.009 |
| Reiger L, Takacs I, Villez K, et al. 2010. Data reconciliation for wastewater treatment plant simulation studies planning for high-quality data and typical sources of errors[J]. Water Environmental Research, 82: 426-433. DOI:10.2175/106143009X12529484815511 |
| 宋新新, 林甲, 刘杰, 等. 2021. 面向未来污水处理技术应用研究现状及工程实践[J]. 环境科学学报, 41(1): 39-53. |
| 孙培德, 杨朋飞, 楼菊青, 等. 2018. 全耦合活性污泥模型(FCASM3)在A+A2/O工艺污水处理厂中的数值模拟应用[J]. 环境科学学报, 38(9): 3561-3572. |
| Thomann M. 2008. Quality evaluation methods for wastewater treatment plant data[J]. Water Science & Technology, 57(10): 1601-1610. |
| van Nieuwenhuijzen A F, Havekes M, Reitsma B A, et al. 2009. Wastewater treatment plant amsterdam west: New, large, high-tech and sustainable[J]. Water Practice & Technology, 4(1). DOI:10.2166/wpt.2009.006 |
| 王洪臣. 2017. 我国城镇污水处理行业碳减排路径及潜力[J]. 给水排水, 53(3): 1-3+73. |
