A SMOOTHED MESHFREE GALERKIN METHOD FOR 2D ELASTICITY PROBLEM1)
MaWentao中图分类号:O241,O343
文献标识码:A
通讯作者:
收稿日期:2018-04-25
网络出版日期:2018-09-18
版权声明:2018力学学报期刊社力学学报期刊社 所有
基金资助:
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (7984KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引 言
为了克服有限元法面临的网格生成、重构以及其他与网格有关的困难, Belytschko等[1]于1994年提出了无网格Galerkin 法(element-free Galerkin method, EFGM). 基于散乱数据的灵活插值、任意阶的光滑形函数、超收敛的数值结果以及在断裂力学问题中的成功表现, 使EFGM很快成为了计算力学和工程领域众多研究者关注的热点, 同时也掀起了无网格方法研究的热潮. 到目前为止, 已提出几十种无网格方法, 并在偏微分方程数值解、金属冲压成形、高速冲击、裂纹动态扩展、流固耦合和局部化等诸多领域取得令人满意的成果[2-7]. 尽管无网格法种类繁多, 但极少有数值方法能同时兼顾EFGM 的灵活性、高精度和稳定性. 因此, EFGM仍然具有十分重要的研究价值和地位.然而, 历经二十多年的发展, EFGM还仅仅是实验室高精度结果的生成者, 并没有像有限元那样真正成为解决复杂工程问题的参与者. 阻挠EFGM深入发展的根本原因是EFGM的计算效率非常低, 严重影响了其处理实际问题的能力. 其他类型的无网格法, 如重构核质点法(reproducing kernel particle method, RKPM)[3], 无网格局部Petrove-Galerkin法(meshless local Petrove-Galerkin method, MLPG)[4, 8]、径向点插值无网格法(radial point interpolation meshless method, RPIM)[9]和一些结合式的无网格法[10]等, 也存在着同样的问题. 众所周知, EFGM 采用滑动最小二乘法(moving least square method, MLS)建立近似函数及其导数, 涉及矩阵求逆, 计算量很大. 其次, EFGM的形函数不具有Kronecher delta性质, 导致本质边界条件施加困难. 虽然Lagrange乘子法、耦合法和罚函数等[2, 5]都能解决EFGM边界条件施加的问题, 但同时也会带来诸如引入附加变量、改变系统矩阵性质等一系列新的问题, 导致计算复杂度和计算时间的增加. 另外, EFGM 生成的是非多项式形式的近似解, 要想获得稳定和高精度的弱形式数值解需要在每个背景网格中采用高阶高斯积分. Duan 等[11]研究表明对于弹性力学问题, 每个三角形背景积分网格中至少需要16 个积分点才能使EFGM达到2阶精度. 相比有限元法, EFGM的计算量要大得多. 如何提高EFGM的计算效率成为近年来无网格法研究的热点和难点问题.
为了提高EFGM的计算效率, Bessel等[12]提出了节点积分方案, 也就是仅在近似节点上计算积分. 该方法是不稳定的, 在一些问题中会出现虚假的近奇异模态. Chen等[13-14]利用应变光滑技术, 根据线性分片实验推导出Galerkin无网格法对应的积分约束, 提出了稳定一致节点积分(stabilized conforming nodal integration, SCNI). SCNI很好地继承了节点积分的优势, 同时完全避免了形成整体刚度矩阵时复杂形函数导数的计算过程. 另外, SCNI能保证线性精度, 而与无网格离散模式无关. 为了弱化场函数近似的一致性要求, Liu及其团队[15-16]推广了应变光滑技术, 提出了G空间理论和广义光滑Galerkin (GS-Galerkin)弱形式, 建立了两类光滑数值方法的(weakened weak, W$^2$)理论基础. 这两类方法分别称为光滑有限元法(smoothed finite element method, S-FEM)和光滑点插值法(smoothed point interpolation method, S-PIM). S-FEM[17-20]的基本思想是: 在有限元网格上创建的光滑区域内光滑化场函数导数, 进而获得比传统有限元"更软"的光滑刚度矩阵, 提高解的精度和收敛性. 由于不需要计算形函数导数, 避免了等参映射过程, 因此S-FEM对畸形网格具有极强的适应性. S-PIM与S-FEM的基本原理相同, 不同之处在于S-PIM使用多项式或径向基函数建立节点形函数. Liu[21]指出, S-FEM 仅仅是S-PIM的特殊形式. Cui等[22]将MLS与GS-Galerkin弱形式结合, 提出了光滑伽辽金法. 但与Galerkin无网格法相比, 其计算精度较低. 杜超凡等[23]采用S-PIM分析了旋转柔性梁的频率, 得到固有频率的下界值. Liu 等[24]在传统数值流形方法中引入光滑应变, 改善其计算精度. Duan等[25-27]将SCNI中的线性积分约束推广到二阶情况, 提出了二阶一致节点积分(quadratially consistent nodal integration, QCI). QCI满足二阶精度, 但为了求解形函数导数, 必须在每个光滑区域内额外求解2个$3\times3$的代数方程, 计算代价并不小. Wang等[28] 将三角形背景网格划分为两水平嵌套光滑区域, 利用梯度光滑技术和Richardson外推法, 提出了嵌套子域梯度光滑积分(NSGSI)算法. NSGSI 算法将SCNI 的精度提高到二阶. 与高斯积分相比, NSGSI仅需要6 个积分点, 极大地提高了计算效率. 为了得到二阶精度的数值算法, NSGSI必须使边界积分、外力项积分与刚度积分保持一致. 显然, NSGSI 的一致性要求大大降低了方法的灵活性.
本文目的是提出一种能精确、高效地求解弹性力学问题的光滑无网格Galerkin法. 基本思想是利用MLS 近似位移场函数, 在两层嵌套光滑子域上计算最优光滑应变, 基于GS-Galerkin弱形式推导系统方程. 两层嵌套网格由三角形背景积分网格以及连接三角形网格的三条边中点组成的4个三角形子网格构成. 利用Richardson外推法, 得到两层网格下对应的最优光滑应变. 另外, 为了通过线性分片试验条件, GS-Galerkin弱式要求在所有的边界上(包括自然边界和本质边界上)采用线性插值建立近似函数. 因此, 边界条件可以像有限元方法那样直接施加.
1 MLS形函数
在EFGM中, MLS方法被用于建立无网格形函数, 具体形式为\begin{equation*}u^{h}(\textbf{x})=\sum\limits^n_{I=1}N_I(\textbf{x})\textbf{u}_I= N(x) u\tag*{(1)}\end{equation*}
其中$ N( x)= p^\text T( x) A^{-1}( x) B( x)$是MLS形函数; $n$ 是支持域内的节点数目; $ u=[u_1~u_2~L~u_n]^\text T$为名义节点值向量, $\textbf{p}^{{T}}(\textbf{x})$ 为基函数向量, 通常对于连续问题
\begin{equation*}\textbf{p}^{{T}}=[1xy]\tag*{(2)}\end{equation*}
对于线弹性断裂问题
\begin{equation*}\begin{split}&\textbf{p}^{{T}}=\Big[1,x,y,\sqrt{r}~{cos}\dfrac{\theta}{2},\sqrt{r}~{sin}\dfrac{\theta}{2}, \\&\quad\quad\sqrt{r}~{sin}\dfrac{\theta}{2}{sin}\theta,\sqrt{r}~{cos}\dfrac{\theta}{2}{sin}\theta \Big]\end{split}\tag*{(3)}\end{equation*}
其中$(r,\theta)$为裂尖极坐标系下定义的位置参数. 其他矩阵的定义分别为
\begin{align*}&\textbf{A}(\textbf{x})=\sum\limits^n_{I=1}w_I(\textbf{x}_I)\textbf{p}(\textbf{x}_I)\textbf{p}^{{T}}(\textbf{x}_I)\tag*{(4)}\\&\textbf{B}(\textbf{x})=\big[w_1(\textbf{x})\textbf{p}(\textbf{x}_1),w_2(\textbf{x})\textbf{p}(\textbf{x}_2),L,\\& w_n(\textbf{x})\textbf{p}(\textbf{x}_n)\big]\tag*{(5)}\\&N_I(\textbf{x})=\textbf{p}^{{T}}(\textbf{x})\Big[\textbf{A}^{-1}(\textbf{x})\textbf{B}(\textbf{x})\Big]_I\tag*{(6)}\\\end{align*}
其中$w_I(\textbf{x})=w(\textbf{x}-\textbf{x}_I)$为权函数, 本文中使用3次样条权函数.
2 系统离散方程
2.1 光滑应变
广义梯度光滑算子[13]作用于协调应变$\textbf{ε}(\textbf{x})$\begin{equation*}\bar{\textbf{ε}}(\textbf{x}_c)=\int_\Omega\textbf{ε}(\textbf{x})\varPhi(\textbf{x};\textbf{x}-\textbf{x}_c){d}\varOmega\tag*{(7)}\end{equation*}
其中$\bar{\textbf{ε}}$为节点$\textbf{x}_c$处的光滑应变, $\varPhi$为光滑函数, 满足$\int_{\varOmega_c}\varPhi(\textbf{x};\textbf{x}-\textbf{x}_c){d}\varOmega=1$. 简单起见, 取
\begin{equation*}\begin{split}\varPhi(\textbf{x};\textbf{x}-\textbf{x}_c)=\begin{cases}1/A_c,\quad&\textbf{x}\in\varOmega_c\\0,&\textbf{x}\notin\varOmega_c\end{cases}\end{split}\tag*{(8)}\end{equation*}
其中$A_c=\int_{\varOmega_c}{d}\varOmega$为光滑区域$\varOmega_c$的面积.
将式(8)代入式(7), 有
\begin{equation*}\begin{split}&\bar{\textbf{ε}}(\textbf{x}_c)=\dfrac{1}{A_c}\int_{\varOmega_c}\textbf{ε}(\textbf{x}){d}\varOmega=\\&\quad\quad~\dfrac{1}{A_c}\int_{\varGamma_c}\Big[u(\textbf{x})n_x,v(\textbf{x})n_y,v(\textbf{x})n_x+u(\textbf{x})n_y\Big]^{T}{d}\varGamma\end{split}\tag*{(9)}\end{equation*}
其中$n_x$和$n_y$分别为光滑区域边界$\varGamma_c$上的单位外法线沿坐标轴方向的分量; $u$和$v$分别为沿坐标轴方向的位移分量.
将方程(1)代入方程(9), 则光滑应变为
\begin{equation*}\begin{split}\bar{\textbf{ε}}(\textbf{x}_c)=\Big[\bar{\varepsilon}_{xx}\quad\bar{\varepsilon}_{yy}\quad\bar{\varepsilon}_{xy}\Big]^{{T}}=\sum\limits^n_{I=1}\bar{\textbf{B}}_I(\textbf{x}_c)\textbf{u}_I\end{split}\tag*{(10)}\end{equation*}
其中$\bar{\textbf{B}}_I$称为光滑应变矩阵, 具体形式为
\begin{equation*}\begin{split}\bar{\textbf{B}}_I(\textbf{x}_c)=\begin{bmatrix}\bar{b}_{Ix}(\textbf{x}_c)\quad&0\\0&\bar{b}_{Iy}(\textbf{x}_c) \bar{b}_{Iy}(\textbf{x}_c)&\bar{b}_{Ix}(\textbf{x}_c)\end{bmatrix}\end{split}\tag*{(11)}\end{equation*}
其中
\begin{equation*}\bar{b}_{Ik}(\textbf{x}_c)=\dfrac{1}{A_c}\int_{\varGamma_c}N_I(\textbf{x})n_k{d}\varGamma\quad(k=x,y)\tag*{(12)}\end{equation*}
2.2 系统离散方程
考虑二维线弹性固体力学问题, 问题区域$\varOmega$内受体力$\textbf{b}$作用, 边界$\varGamma_t$上受给定外力$\textbf{t}$作用, 边界$\varGamma_u$上满足$\textbf{u}=\bar{\textbf{u}}$. 用光滑应变$\bar{\textbf{ε}}$代替协调应变$\textbf{ε}$, 得到GS-Galerkin弱式为\begin{equation*}\begin{split}\int_\varOmega&\delta (\bar{ \varepsilon}(\textbf{u}))^{{T}}\textbf{D}(\bar{ \varepsilon}(\textbf{u})){d}\varOmega-\int_\varOmega\delta\textbf{u}^{{T}}\textbf{b}{d}\varOmega-\\&\int_{\varGamma_t}\delta\textbf{u}^{{T}}\textbf{t}{d}\varGamma=0\end{split}\tag*{(13)}\end{equation*}
将方程(1)和(10)代入方程(13)得
\begin{equation*}\bar{\textbf{K}}\textbf{u}=\textbf{f}\tag*{(14)}\end{equation*}
其中$\bar{\textbf{K}}$为光滑刚度矩阵, 由所有光滑区域组装得到. 具体形式为
\begin{align*}&\bar{\textbf{K}}=\sum\limits^{nsc}_{c=1}\bar{\textbf{B}}^{{T}}(\textbf{x}_c)\textbf{D}\bar{\textbf{B}}(\textbf{x}_c)A_c\tag*{(15)}\\&\textbf{f}=\int_{\varOmega}\textbf{N}^{{T}}\textbf{b}{d}\varOmega+\int_{\varGamma_t}\textbf{N}^{{T}}\textbf{t}{d}\varGamma\tag*{(16)}\end{align*}
式中, $nsc$为光滑区域总数.
2.3 施加边界条件
由以上推导可以看出, 光滑应变运算不涉及任何形函数导数计算. 因此, 问题域内近似函数的不连续性并不会给光滑应变的计算带来任何困难. 与标准Galerkin弱形式相比, 形函数的一致性要求大大降低了. 因此, 在光滑无网格Galerkin法中, 问题域内的点和边界上的点往往可以采用不同的近似形式. 对于任何在问题域内的计算点均采用无网格近似函数; 而对于任何在问题域边界上的计算点则采用线性插值函数. 在边界上引入线性插值函数的目的是使光滑无网格法能够顺利通过线性分片试验, 同时也使边界条件的施加变得和在有限元中一样容易.3 两层嵌套光滑积分网格
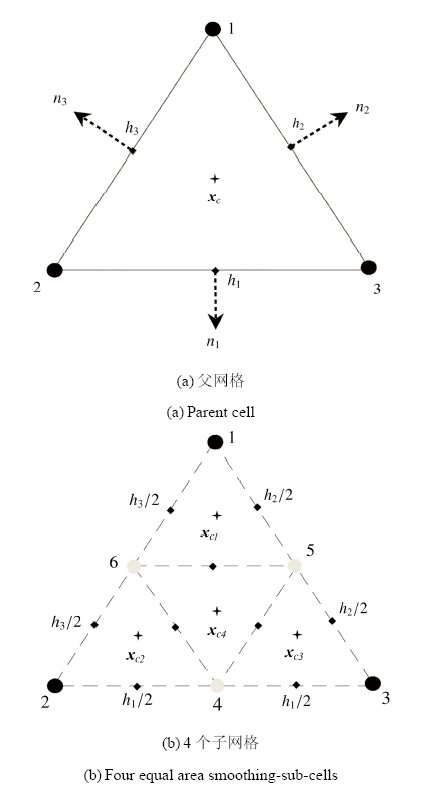
为了计算光滑应变, 光滑区域的选择至关重要. Liu等[21]基于背景积分网格本身、网格边界和网格顶点依次建立了不同类型的S-PIM. 很显然, 将背景三角形积分网格作为光滑区域是最简单、最直接的, 不需要任何的附加工作. 根据式(12)和Liu等[21]的研究结论, 光滑区域内的光滑应变是个常数, 导致了网格型光滑无网格法仅能达到线性精度, 也就是说与传统三角形有限元法的精度相当. 为了提高计算精度, 进一步细分三角网格是非常有必要的. 然而, 细分过多的光滑子网格又会大大降低光滑无网格法计算效率. 因此, 寻找到最优的光滑网格细分方案是发展高效和高精度光滑无网格法的关键. 本文提出两层嵌套光滑区域解决背景网格细分的问题.首先将问题域$\varOmega$离散为三角形背景积分网格. 每个三角形网格称为父网格(见图1(a)). 然后依次连结父网格的3条边的中点, 形成4个等面积的子网格, 如图1(b)所示.
显示原图|下载原图ZIP|生成PPT图1两层嵌套三角形光滑网格($\bullet$场节点,
积分点,
高斯点-->Fig.1Two-level nesting triangular smoothing cells($\bullet$node,
grade point,Gauss point) -->
在每个光滑子网格边界上取一个高斯积分点, 则根据方程(12), 图1(a)所示的父网格对应的光滑应变矩阵为
\begin{equation*}\begin{split}\bar{\textbf{B}}^{[1]}_I(\textbf{x}_c)=\sum\limits^3_{J=1}\dfrac{N_I(\textbf{x}_J)l_J}{A_c}\begin{bmatrix}n_{xJ}\quad&0\\0&n_{yJ}\\n_{yJ}&n_{xJ}\end{bmatrix}\end{split}\tag*{(17)}\end{equation*}
其中$l_J$和$\textbf{x}_J$分别是第$J$条边的边长和高斯积分点(即边界中点), $n_{xJ}$和$n_{yJ}$分别是第$J$ 条边单位外法线分别沿$x$, $y$方向的分量. 组装所有父网格的光滑刚度矩阵可得
\begin{equation*}\bar{\textbf{K}}^{[1]}=\sum\limits^{nsc}_{c=1}\bar{\textbf{B}}^{[1]{T}}(\textbf{x}_c)\textbf{D}\bar{\textbf{B}}^{[1]}(\textbf{x}_c)A_c\tag*{(18)}\end{equation*}
由方程(17), 可以很容易计算第$m$个子网格对应的光滑应变矩阵为
\begin{equation*}\begin{split}\bar{\textbf{B}}^{[2]}_I(\textbf{x}_{cm})=\sum\limits^3_{J=1}\dfrac{l^{[m]}_JN_I(\textbf{x}^{[m]}_J)}{A_{cm}}\begin{bmatrix}n^{[m]}_{xJ}&0\\0&n^{[m]}_{yJ}\\n^{[m]}_{yJ}&n^{[m]}_{xJ}\end{bmatrix}\end{split}\tag*{(19)}\end{equation*}
其中$A_{cm}=A_c/4$. 组装所有子网格的光滑刚度矩阵为
\begin{equation*}\bar{ {K}}^{[2]}=\sum_{c=1}^{nsc}\sum_{m=1}^4\bar{ {B}}^{[2]{\rm T}}( {x}_{cm}) {D}\bar{ {B}}^{[2]}({x}_{cm})A_{cm}\tag*{(20)}\end{equation*}
由图1可知每个光滑子网格的特征长度减小为父网格特征长度的一半, 根据经典的Richardson外推法理论[28-29], 方程(18)和(20)的最优线性组合可以生成更高精度的解. 方程(21)是在同时考虑粗和细两种网格的基础上建立的, 因此称为二层嵌套光滑区域.
在编程计算式(18)和式(20)的过程中, 由于每个光滑积分区域的边界上采用1个积分点(线段中点)时, 该点处的形函数值正好可以用线段两端点的形函数值的平均值表达. 这样的话, 每个三角形背景网格中需要3个顶点和3个线段中点, 总共6个积分点即可.
4 数值算例
为了研究本文方法的精度, ${L}^2$范数下的位移误差和能量误差分别定义为\begin{align}&e_\text d=\Bigg[\int_\varOmega({u}^\text e-{u}^\text n)^{\rm T}({u}^\text e-{u}^\text n){d}\varOmega\Bigg]^{\frac{1}{2}}\tag*{(22)}\\&e_\text e=\Bigg[\int_\varOmega\dfrac{1}{2}({\varepsilon}^\text e-{\varepsilon}^\text n)^{\rm T}{D}({\varepsilon}^\text e-{\varepsilon}^\text n){d}\varOmega\Bigg]^\frac{1}{2}\tag*{(23)}\end{align}
式(22)、式(23)中, ${u}^\text e$, ${u}^\text n$分别代表位移精确解和数值解; $\textbf{ε}^\text e$, $\textbf{ε}^\text n$ 分别代表应变精确解和数值解. 为了书写的方便, 使用父网格(1 个网格)、4 个子网格以及嵌套网格(1个网格及其4 个子网格)的3种光滑Galerkin无网格法分别简记为FSMM, SSMM 和NSMM. EFGM采用拉格朗日乘子法施加位移边界条件. 笔者根据Duan等[11]的研究结论, 在EFGM的每个三角形背景积分网格中采用16个高斯积分点. 上述4 种方法, 在悬臂梁、无限大开孔平板和双连拱隧道算例中均使用线性基函数(见式(2)), 在含中心裂纹的无限大板算例中则使用内部扩展基函数(见式(3)). 4种方法都在同一台电脑(处理器: Intel(R) Core(TM) i7-8550U CPU @1.80 GHz)上采用matlab语言编程实现.
4.1 悬臂梁
如图2所示, 悬臂梁左侧固定, 右侧受剪切作用. 在平面应力条件下, 解析解[30] 为\begin{align*}&u_{x}(x,y)=-\dfrac{Py}{6EI}\left\lbrack(6L-3x)x+(2+v)\Bigg(y^{2}-\dfrac{D^{2}}{2}\Bigg)\right\rbrack\tag*{(24)}\\&u_{y}(x,y)=\dfrac{P}{6EI}\Bigg\lbrack3vy^{2}(L-x)+(4+5v)\dfrac{D^{2}x}{4}+\\&\quad\quad\quad\quad(3L-x)x^{2}\Bigg\rbrack\tag*{(25)}\\&\sigma_{x}(x,y)=-\dfrac{P(L-x)y}{I}\tag*{(26)}\\&\sigma_{xy}(x,y)=-\dfrac{P}{2I}\left\lgroup\dfrac{D^{2}}{4}-y^{2}\right\rgroup\tag*{(27)}\\&\sigma_{y}(x,y)=0\tag*{(28)}\end{align*}
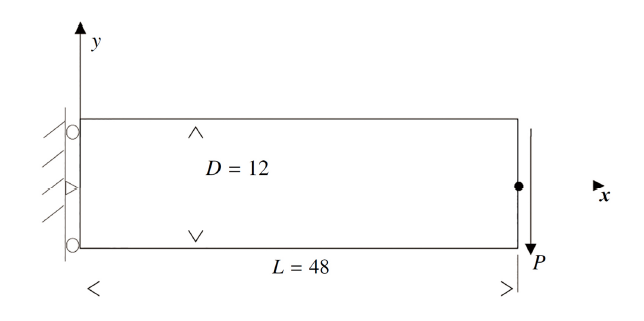显示原图|下载原图ZIP|生成PPT图2悬臂梁
-->Fig.2The cantilever beam
-->
其中$I=D^3/12$. 梁的材料参数取为$E=3\times10^7~{MPa}$, $v=0.3$, $P=1000~{N}$. 在梁上分别布置$17\times5$, $33\times9$和$65\times17$个节点.
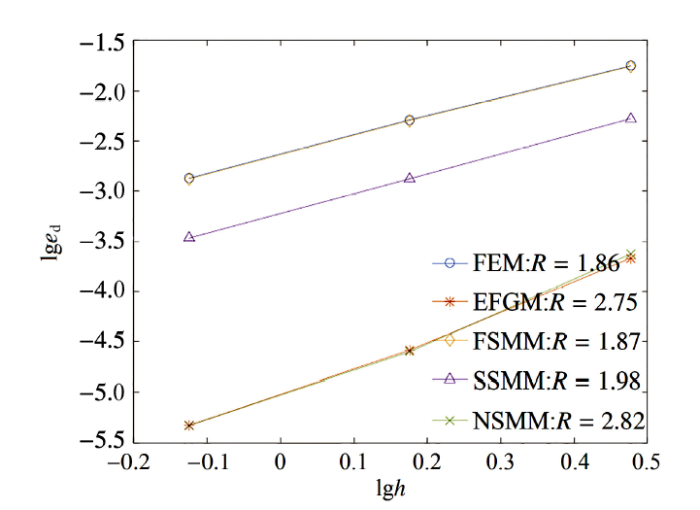
图3比较了3种节点分布下5种方法求解悬臂梁问题时的位移误差. 可以看出, FSMM与传统三角形FEM的精度几乎一致; SSMM的精度要高于FSMM的; 而NSMM 与EFGM的计算精度几乎一致, 且远远高于其他3种方法.
显示原图|下载原图ZIP|生成PPT图3悬臂梁问题的位移误差比较
-->Fig.3Displacement error comparison for the cantilever beam problem
-->
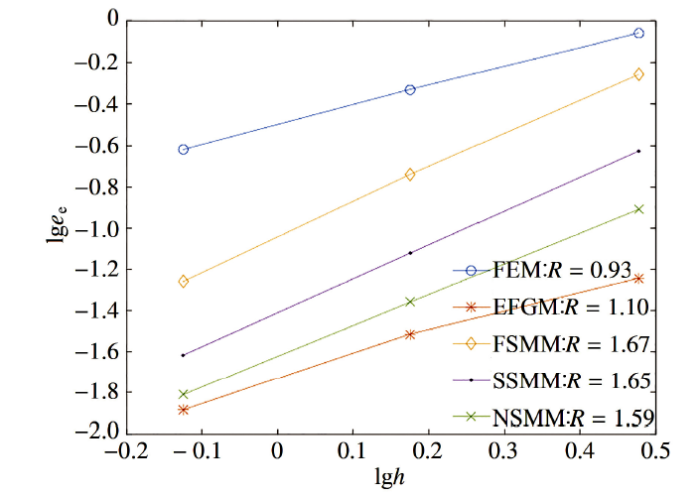
图4则给出了5种方法的能量误差比较. 从图4可以看出, 无网格法的精度都要高于FEM的, NSMM比FSMM 和TSMM的精度高; 虽然EFGM的精度高于3种光滑无网格Galerkin法的, 但其收敛率却最低. 这些结论很好地证明了随着光滑区域的增加, 积分点的个数也随之增加, 光滑无网格Galerkin 法的计算精度会逐步升高.
显示原图|下载原图ZIP|生成PPT图4悬臂梁问题的能量误差比较
-->Fig.4Energy error comparison for the cantilever beam problem
-->
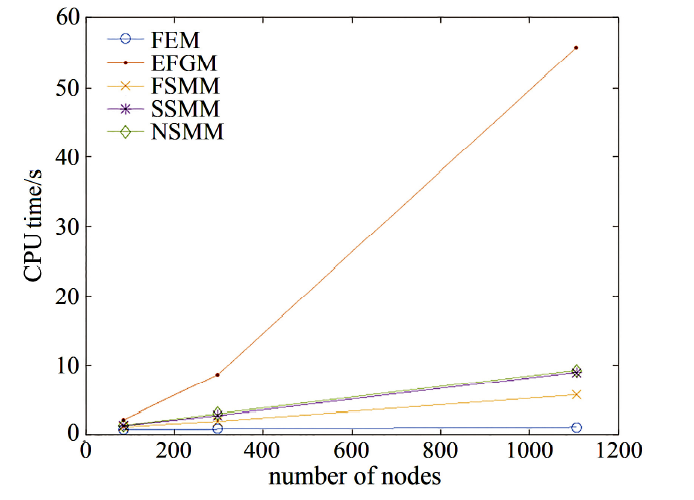
图5给出了5种方法的CPU时间比较. 可以看出, 在节点分布相同时, FSMM的计算耗时比FEM 略长; NSMM 与SSMM 的计算耗时相当, 比FSMM的要长, 但要远远短于EFGM的. 从精度和效率两个方面综合考虑, NSMM 是5 种方法中表现最好的.
显示原图|下载原图ZIP|生成PPT图5悬臂梁问题的CPU时间比较
-->Fig.5CPU time comparison for the cantilever beam problem
-->
4.2 无限大开孔平板
设一无限大平板, 中心开有半径为$a$的圆孔, 在远离孔心的位置沿水平方向受$\sigma_0=1$ Pa的轴向拉伸作用. 该问题的解析解[30]为\begin{align*}&u_{r}=\dfrac{1}{4G}\Bigg\lbrace r\left\lgroup\dfrac{\kappa +1}{2}+\text{cos}~2\theta \right\rgroup+\\&\quad\quad\dfrac{a^{2}}{r}[1+(\kappa+1)\text{cos}~2\theta]-\dfrac{a^{4}}{r^{4}}\text{cos}~2\theta\Bigg\rbrace\tag*{(29)}\\&u_\theta=-\dfrac{1}{4G}\Bigg\lbrack r-(1-\kappa)\dfrac{a^2}{r}+\dfrac{a^4}{r^4} \bigg\rbrack \text{sin}~2\theta\tag*{(30)}\\&\sigma_{xx}=1-\dfrac{a^2}{r^2}\Bigg(\dfrac{3}{2}\text{cos}~2\theta+\text{cos}~4\theta\Bigg)+\dfrac{3}{2}\dfrac{a^4}{r^4}\text{cos}~4\theta\tag*{(31)}\\&\sigma_{yy}=-\dfrac{a^2}{r^2}\Bigg(\dfrac{1}{2}\text{cos}~2\theta-\text{cos}~4\theta\Bigg)-\dfrac{3}{2}\dfrac{a^4}{r^4}\text{cos}~4\theta\tag*{(32)}\\&\sigma_{xy}=-\dfrac{a^2}{r^2}\Bigg(\dfrac{1}{2}\text{sin}~2\theta-\text{sin}~4\theta\Bigg)+\dfrac{3}{2}\dfrac{a^4}{r^4}\text{sin}~4\theta\tag*{(33)}\end{align*}
其中, $r$, $\theta$为以孔心为原点的极坐标
\begin{equation*}G=\dfrac{E}{2(1+v)}, \kappa=\begin{cases}3-4v,\quad\text{for plane stress}\\\dfrac{v}{1-v},\quad\quad~\text{for plane strain}\end{cases}\end{equation*}
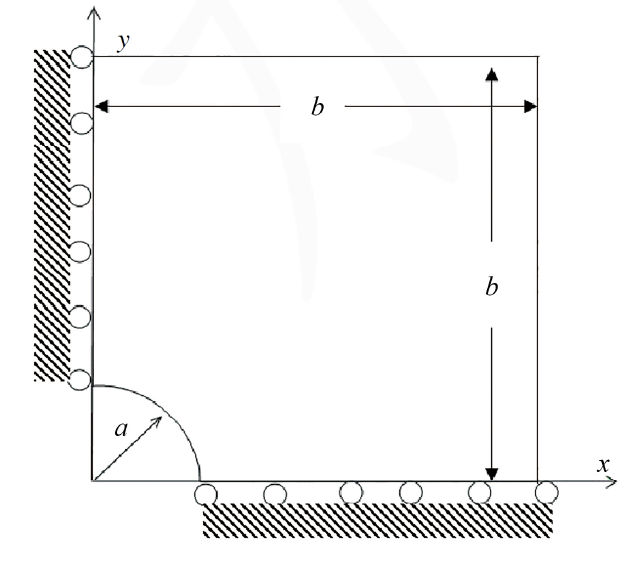
考虑对称性, 仅取平板右上角四分之一进行数值计算, 见图6. 设板长、宽均为$b=5$ cm, 圆孔半径$a=1$ cm, 弹性模量$E=30$ MPa, 泊松比$v=0.3$. 在底部和左侧边界上分别给定位移边界条件$u_y(x,0)=0$和$u_x(0, y)=0$; 在板右端$(x=b)$和上部$(y=b)$边界按精确解施加自然边界条件.
显示原图|下载原图ZIP|生成PPT图6无限大开孔平板模型
-->Fig.6Model of the infinite plate with a circle hole
-->
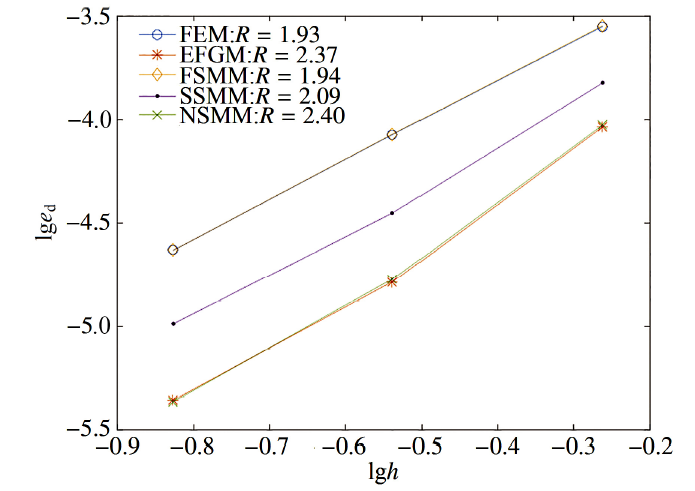
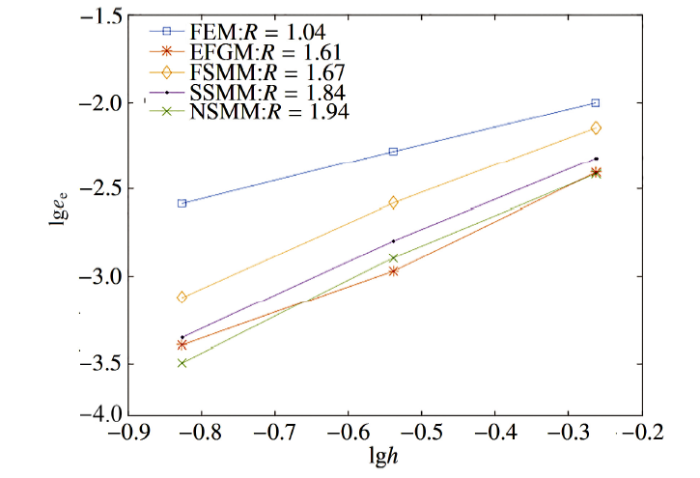
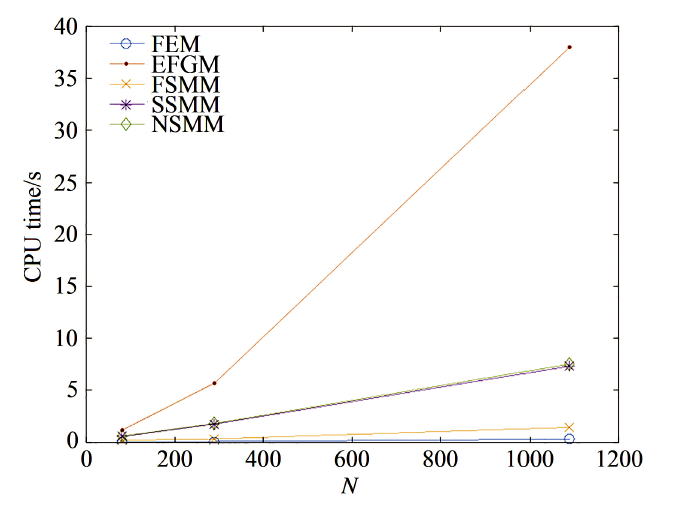
在平板模型上分别布置$9\times9$, $17\times17$和$33×\times33$个节点. 图7 $\sim$ 图9分别给出了3种节点分布下不同方法对应的位移误差、能量误差和花费的CPU时间. 从图7 $\sim$图8可以看出, 本文提出的NSMM的精度与EFGM 的基本相同的, 要高于其他几种方法. 图9再次证明了NSMM的效率要远远高于EFGM.
显示原图|下载原图ZIP|生成PPT图7无限大开孔平板问题的位移误差比较
-->Fig.7Displacement error comparison for the problem of the infinite plate with a circle hole
-->
显示原图|下载原图ZIP|生成PPT图8无限大开孔平板问题的能量误差比较
-->Fig.8Energy error comparison for the problem of the infinite plate with a circle hole
-->
显示原图|下载原图ZIP|生成PPT图9开孔平板问题的CPU时间比较
-->Fig.9CPU time comparison for the problem of the infinite plate with a circle hole
-->
4.3 含中心裂纹的无限大板
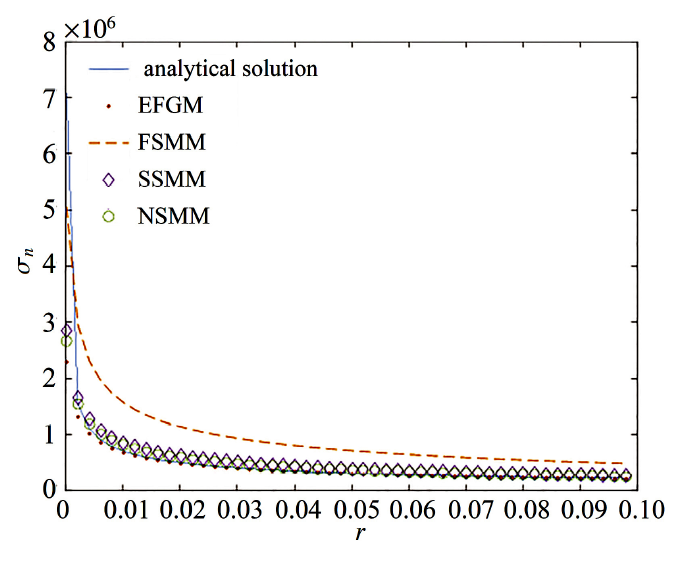
考虑一无限大板, 中心包含一长度为$2a$的直裂纹, 在远端受单向拉应力$\sigma$作用, 见图10. 计算过程中, 计算区域ABCD取为$10~{mm}\times10~{mm}$, $a=100~{mm}$; $E=300~{MPa}$, $v=0.3$, $\sigma=1~{MPa}$; 在计算区域内均匀分布$20\times20$个节点. 分别采用\mbox{EFGM, FSMM}, SSMM和NSSM求解该问题. 图11为4种方法计算得到的裂纹前端应力与精确解[31]的比较. 可以看出, FSMM, SSMM和NSSM的应力曲线呈现依次逼近解析解的特征, 说明随着光滑区域数量的增加, 光滑Galerkin无网格法的精度也随之提高; NSMM 和EFGM 的计算结果与解析解吻合得非常好.
显示原图|下载原图ZIP|生成PPT图10含中心裂纹的无限大板的几何结构和载荷
-->Fig.10Geometry and loads of infinite plate with a center crack
-->
显示原图|下载原图ZIP|生成PPT图11裂纹前端$(r>0,\theta=0)$应力比较
-->Fig.11Stresses comparison ahead of the crack tip$(r>0,\theta=0)$ for the near-tip crack
-->
4.4 双连拱隧道
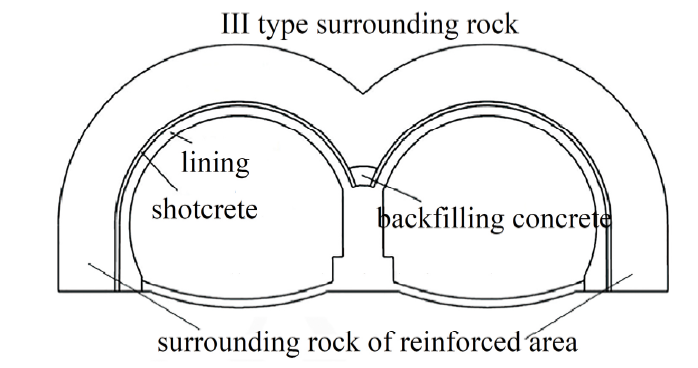
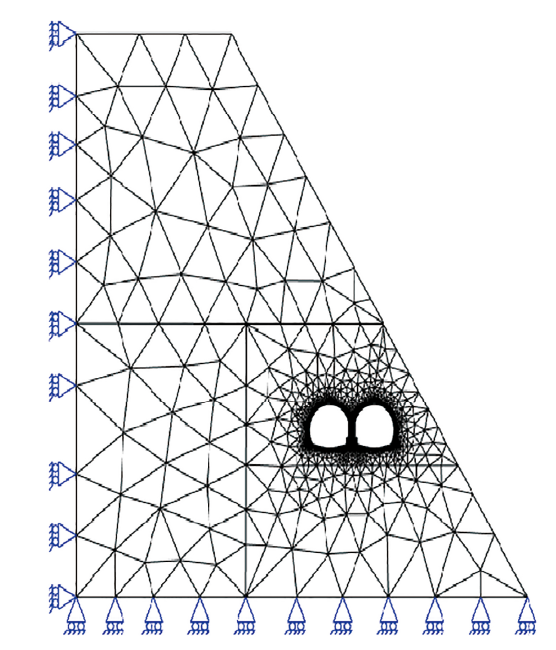
设有一双连拱形隧道, 基本结构如图12所示. 分别采用本文方法(NSMM)和EFGM, 按照平面应变假设分析隧道围岩和衬砌在自重作用下的变形和应力分布. 计算过程中, 围岩及混凝土力学参数见表1; 三角形背景网格划分见图13. 将单元角点作为节点, 共5145个背景单元, 2729个节点. 根据对称性, 模型左侧边界上各点处$x$方向固定, $y$方向自由, 而在下边界上各点$x$方向自由, $y$方向固定.Table 1
表 1
表 1材料参数性能
Table 1Parameters of material property
| Material type | E /GPa | V | Bulk density/ (kN • m-3) |
|---|---|---|---|
| III type surrounding rock | 2 | 0.25 | 22 |
| surrounding rock of reinforced area | 2.6 | 0.2 | 23 |
| lining(C25) | 28.5 | 0.2 | 25 |
| shotcrete(C25) | 28.5 | 0.2 | 23 |
| backfilling concrete(C10) | 18.5 | 0.2 | 22 |
新窗口打开
显示原图|下载原图ZIP|生成PPT图12双连拱隧道结构
-->Fig.12The structure sketch of twin-arched tunnel
-->
显示原图|下载原图ZIP|生成PPT图13三角形背景网格和边界条件
-->Fig.13Triangular background mesh and boundary conditions
-->
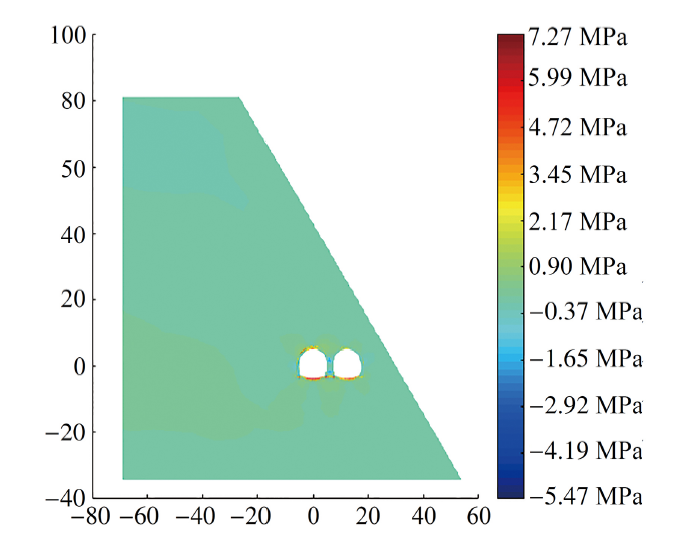
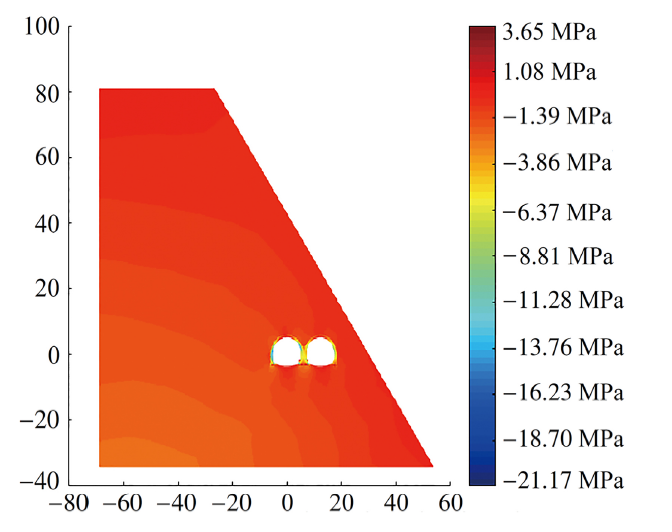
果绘制的第一、第二主应力云图. 由图14可以看出, 拱圈顶部附近、仰拱拱底附近、边墙和中墙基础底部都出现了较大的拉应力. 从图15可以看出, 几个形状突变较为明显的区域, 由于应力集中导致了较大压应力的出现. 图14和图15的结论与文献[32]的结论是一致的. NSMM与EFGM的计算结果十分接近, 但EFGM的CPU用时为197.48 s, 而本文方法仅为35.44 s, 进一步说明本文方法具有极高的计算效率.
显示原图|下载原图ZIP|生成PPT图14第一主应力图
-->Fig.14The first principal stress
-->
显示原图|下载原图ZIP|生成PPT图15第二主应力
-->Fig.15The second principal stress
-->
5 结 论
EFGM是一种十分重要的无网格数值方法, 但其计算效率低的问题长期困扰着研究工作者. 本文基于广义梯度光滑技术, 提出了光滑无网格Galerkin法, 试图解决这一难题. 本文方法的基本思想是利用MLS近似位移场函数, 在两层嵌套光滑子域上计算最优光滑应变, 基于GS-Galerkin弱形式推导了系统方程. 两层嵌套网格由三角形背景积分网格以及连接三角形网格的3条边中点组成的4个三角形子网格构成. 利用Richardson外推法, 得到两层网格下对应的最优光滑应变. 几个数值算例验证了本文方法的精度和计算效率. 从这些数值结果可以看出, 本文方法具有以下优势:(1)计算效率高. 本文方法充分利用了光滑梯度技术, 将区域积分转化为区域边界积分, 完全避免了形成整体刚度矩阵时复杂形函数导数计算. 因此, 极大地提高了的计算效率. 数值结果表明, 在节点分布相同的情况下, NSMM比EFGM花费的计算时间要少的多.
(2)计算精度高. FSMM类似SCNI, 仅有线性精度: SSMM将FSMM的光滑区域细分为4个子区域, 相当于引入了更多的积分取样点, 因此SSMM比FSMM的精度更高: Richardson外推法又从理论上保证NSMM比FSMM 和SSMM二者的精度更高. 4个数值算例证明了NSMM具有几乎和EFGM相同的计算精度.
(3)易于施加边界条件. 本文方法在实现过程中, 域内计算点采用MLS近似, 而在域边界上的计算点则采用线性插值. 一方面, 本文方法可以自然满足线性分片试验; 另一方面, 边界条件的施加过程就和FEM一样了. 这样, 无网格边界条件施加困难的问题也就迎刃而解了.
综上所述, 本文提出的光滑Galerkin无网格法, 既保持了无网格法的精度高的优势, 又极大地减少了计算用时, 同时也解决了施加边界条件的难题, 具有十分广阔的发展空间. 将本文方法进一步推广到结构动力学分析、大变形分析以及裂纹动态扩展等问题将是未来的研究方向.
6 结论
采用理论分析方法研究了阶跃载荷作用下润滑油黏度、油膜厚度和油腔面积对轴承动态特性的影响, 揭示了油膜动态响应规律, 探究了正弦载荷作用双矩形腔静压推力轴承油膜稳定性, 并进行了动态稳定性的实验验证.当润滑油黏度与油腔面积一定时, 随着油膜厚度的降低, 系统响应时间变短, 油膜越薄, 油膜刚度越大, 油膜变形量越小. 当油膜厚度与油腔面积一定时, 随着润滑油黏度降低, 系统响应时间随之增长, 油膜位移量也随之增大. 当油膜厚度与润滑油黏度一定时, 油腔面积增大, 润滑油膜承载能力提高, 油膜刚性增加, 在承受阶跃载荷作用下, 旋转台能在较短时间到达新的平衡位置. 正弦载荷作用双矩形腔静压推力轴承具有超强稳定性能, 较大阻尼系数, 较大阻尼率, 保证油膜较大动刚度, 其承受不同频率正弦载荷都保持较小振幅, 轴承稳定运行.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . |
| [2] | . |
| [3] | . |
| [4] | . |
| [5] | . |
| [6] | . |
| [7] | . . |
| [8] | . |
| [9] | . |
| [10] | . . |
| [11] | . |
| [12] | . |
| [13] | . |
| [14] | . |
| [15] | . |
| [16] | . |
| [17] | |
| [18] | . |
| [19] | . |
| [20] | . |
| [21] | . |
| [22] | . |
| [23] | . . |
| [24] | . |
| [25] | . |
| [26] | . |
| [27] | . . |
| [28] | . |
| [29] | |
| [30] | |
| [31] | . |
| [32] |
