, 彭淼NON-SMOOTH BURSTING OSCILLATION MECHANISMS IN A FILIPPOV-TYPE SYSTEM WITH MULTIPLE PERIODIC EXCITATIONS1)
QuZifang, PengMiao中图分类号:O322
文献标识码:A
通讯作者:
收稿日期:2018-04-25
网络出版日期:2018-09-18
版权声明:2018力学学报期刊社力学学报期刊社 所有
基金资助:
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (5447KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引言
非光滑动力系统因其在模拟各种物理和工程技术系统方面表现出强大的功能而备受关注. 带有摩擦的机械系统、步行机器人系统、基因调控网络系统、电子变换器系统等皆因非光滑因素的存在而表现出不同的动力学行为[1-3]. 通常, 系统相空间可被划分为若干个与系统向量场的不同功能形式相关联的区域. 当系统的部分轨线在相空间的不同区域之间的边界相切时, 系统的轨迹会发生一系列奇特的变化[4]. 由于轨线与分界面接触点的不同特性和系统向量场的特点, 当系统参数变化时轨线可能发生的滑动、转迁、穿越、黏滞等多种非线性现象会频繁出现[5-9]. 在分段光滑系统中同样有非光滑特性体现, 如系统在转换边界平衡点发生的分岔行为, 极限环经历的擦边和滑动分岔等[10]及线性碰振系统周期解的擦边分岔[11].在自然科学和工程实践中, 非线性系统的动力学行为不仅仅是各子系统行为的简单叠加, 而是一定数量的子系统耦合而成, 即由子系统层面的动力学行为到整个系统层面的动力学行为的演变, 于是多尺度耦合现象应运而生[12-15]. 通常所讲的两尺度耦合, 指的是由于含不同时间尺度的对象, 导致在无量纲数学模型中, 状态变量或其不同形式的组合可以分为两个不同的组, 而各组之间随时间变化的速率存在着明显量级上的差异[16-20]. 在对两个或多个单向的或双向振荡器的耦合现象的研究基础上, 可深入地了解系统中的相互同步、准周期振荡、混沌等现象的产生机制[21-24].
目前, 针对多尺度耦合系统的研究, 国内外****大都遵循着耦合系统的模型分析、近似求解、数值模拟和实验分析等环节进行[25-27], 研究方法缺乏针对性, 而直到Izhikevich[28]快慢分析法的提出, 才使研究方法得以丰富, 并能深入地分析各种动力学行为的演化机制, 其主旨是将不同尺度耦合系统分解为相互耦合的快慢两子系统, 通过对快子系统的平衡态及其分岔分析, 得到沉寂态和激发态之间相互转化的分岔机制, 从而揭示相应簇发振荡的产生机理.
虽然含一个慢变周期参数的系统的周期簇发振荡分析已有诸多成果[29-30], 但由于实际系统中往往存在着多种激励共存的现象, 因此含多频激励的系统的动力学行为分析也激起了****们浓厚的兴趣, 特别是含参数激励和外部激励共同作用的系统表现出了更为丰富和神奇的周期簇发振荡等动力学行为[31].
尽管分别关于非光滑系统, 多尺度耦合系统, 含多频激励的系统都有各自针对性的研究成果, 但对于含两个慢变周期参数的非光滑耦合系统的簇发振荡分析却仍有进一步的研究空间.
本文以Duffing和Van der Pol耦合振子为例, 研究了含两慢变激励的具有非光滑向量场的Filippov系统的簇发振荡模式及非光滑行为演化机制. 给出了平衡曲线和分岔图及在非光滑边界产生非光滑行为的演化行为分析; 结合转换相图, 得到了在外部激励频率不变的情况下, 参数激励频率改变引起的系统簇发振荡模式及非光滑演化行为机理; 通过数值模拟, 分析了平衡曲线在不同参数激励频率下发生的曲折变化情况.
1 计算模型
以Duffing和Van der Pol耦合振子为例, 引入一个双边二极管作为调和开关, 考虑含双频激励的具非光滑向量场的Filippov系统, 无量纲化后的数学模型为\begin{equation*}\left.\begin{split}&\dot{x}_1=y_1+w_1+\delta {\rm{sgn}}(x_1) &\dot{y}_1=-w_2x_1-\alpha_1x^3_1-\alpha_2x^5_1-2\mu y_1+\xi(x_1-x_2) &\dot{x}_2=y_2\\&\dot{y}_2=-\alpha_3x_2+(1-x_2^2)y_2-\xi(x_1-x_2)\end{split}\right\}\tag*{(1)}\end{equation*}
其中$w_1\!=\!A_1{\rm{cos}}(\varOmega_1\tau)$\mbox{为外部激励项, $w_2\!=\!A_2{\rm{cos}}(\varOmega_2\tau)$为参数激励项, $A_1,A_2$表示振幅, $\varOmega_1,\varOmega_2$表示频率, $\alpha_1,\alpha_2,\alpha_3,\mu$是常系数, $\xi$代表两子系统的耦合强度.以$\delta{\rm{sgn}}x_1$定义的非光滑分界面$\sum=(x_1,y_1,x_2,y_2) |x_1=0$按照两个非自治光滑子系统$F_+$和$F_-$将向量场分为两个光滑区域, 分别以$D_+$和$D_-$表示在应用快慢分析法分析含双频激励的系统的簇发振荡时, 考虑各激励间并非相互独立, 往往以一个激励项作为慢变参数, 其他激励项表示为该慢变参数的函数表达式的方法进行分析讨论. 这里保持$\varOmega_1=0.000\,5$不变, 改变$\varOmega_2$的值, 其他参数取常规量, 此时两激励频率与系统的固有频率之间存在了量级差, 于是产生了尺度效应, 即不同频域尺度之间的耦合, 导致簇发等特殊的振荡模式.
2 分岔分析
系统(1)中各状态变量振荡行为主要由系统的固有频率$\omega$决定, 然而, $\omega$同时又受到外部激励项$w_1$和参数激励项$w_2$的调制. 就外部激励项$w_1$而言, 对一任意周期$T_{\rm N}$, 定义$T_{\rm N}=2\pi/\omega$, 有$t\in[t_0,t_0+T_N]$, 外部激励项$w_1$ 将在$w_A=A{\rm{cos}}(\varOmega t_0)$和$w_{\rm B}=A{\rm{cos}}(\varOmega t_0+2\pi\varOmega/\omega)$之间变化. 而$\varOmega_1\ll\varpi$意味着$0<\varOmega_1/\omega=1$, 因此有$w_A\approx w_B$. 这意味着在一相应周期内, 外部激励项几乎为一常数. 同理可得: 参数激励项也几乎为一常数.根据上述分析, 相对于状态变量而言, 由于整个外部激励项$w_1$和参数激励项$w_2$在更慢的时间尺度上变化, 因此可以视$w_1$和$w_2$为慢变参数, 而又因为外激频率$\varOmega_1$和参激频率$\varOmega_2$存在共振关系, 这里假设$W={\rm{cos}}(\varOmega_1\tau)={\rm{cos}}(0.000\,5\tau)$, 外部激励可表示为$w_1=A_1{\rm{cos}}(\varOmega_1\tau)=A_1W$, 参数激励表示为$w_2=A_2{\rm{cos}}(\varOmega_2\tau)=A_2f_i(W)(i=1,2)$. 于是实际上可以将$W$看作一个慢变参数, 此时这里的$w_1$和$w_2$仅是普通参数, 而不再具有$w_1=A_1{\rm{cos}}(\varOmega_1\tau)$和$w_2=A_2{\rm{cos}}(\varOmega_2\tau)$的形式. 此时称含慢变参数$W$的系统(1)为广义自治系统. 即整个系统(1)可视为快慢两个系统的耦合.
快子系统为
\begin{equation*}\left.\begin{split}&\dot{x}_1=y_1+A_1W+\delta{\rm{sgn}}x_1\\&\dot{y}_1=-A_2f_i(W)x_1-\alpha_1x_1^3-\alpha_2x_1^5-2\mu y_1+\\&\quad\quad\xi(x_1-x_2) &\dot{x}_2=y_2\\&\dot{y}_2=-\alpha_3x_2+(1-x_2^2)y_2-\xi(x_1-x_2),i=1,2\end{split}\right\}\tag*{(2)}\end{equation*}
其中, 当$\varOmega_1=0.000\,5,\varOmega_2=0.002$时,
\begin{equation*}f_1(W)=8W^4-8W^2+1\tag*{(3)}\end{equation*}
当$\varOmega_1=0.000\,5,\varOmega_2=0.003$时,
\begin{equation*}f_2(W)=(-1+2W^2)(16W^4-16W^2+1)\tag*{(4)}\end{equation*}
慢子系统为$W={\rm{cos}}(0.000\,5\tau)$.
为揭示快慢耦合系统复杂行为的产生机制, 首先分析快子系统(2)的分岔行为. 由于系统(1)为广义自治系统, 其中的参数$w_1$和$w_2$此时已是普通参数, 于是可以看作是一个自治系统[30]. 根据快慢分析法[28], 系统(1) 由快子系统(2)和慢子系统耦合而成, 所以系统(2)也是一个自治系统. 于是可以求出平衡点为:
当$x_0>0$时, 平衡点可表示为
\begin{equation*}EQ_+:=(x_1,y_1,x_2,y_2)=(x_0,-A_1W-\delta,\dfrac{\xi x_0}{\xi-\alpha_3},0)\end{equation*}
其中$x_0$满足
\begin{equation*}\begin{split}&-\alpha_2x_0^5-\alpha_1x_0^3-A_2f_i(W)x_0-\dfrac{\alpha_3\xi}{-\alpha_3+\xi}x_0-\\&\quad\quad\quad2\mu(-A_1W-\delta)=0\quad(i=1,2)\end{split}\tag*{(5)}\end{equation*}
当$x_0<0$时, 平衡点为
\begin{equation*}EQ_-:=(x_1,y_1,x_2,y_2)=(x_0,-A_1W+\delta,\dfrac{\xi x_0}{\xi-\alpha_3},0)\end{equation*}
其中$x_0$满足
\begin{equation*}\begin{split}&-\alpha_2x_0^5-\alpha_1x_0^3-A_2f_i(W)x_0-\dfrac{\alpha_3\xi}{-\alpha_3+\xi}x_0-\\&\quad\quad\quad2\mu(-A_1W+\delta)=0\quad(i=1,2)\end{split}\tag*{(6)}\end{equation*}
平衡点的稳定性可通过其特征方程表征, 表示为
\begin{equation*}\lambda^4+\alpha_1\lambda^3+\alpha_2\lambda^2+\alpha_3\lambda+\alpha_4=0\tag*{(7)}\end{equation*}
其中
$\alpha_1=2\mu-v, \alpha_2=\alpha_3-\xi-2\mu v-k$
$\alpha_3=2\mu(\alpha_3-\xi)+kv, a_4=-k(\alpha_3-\xi)-\xi^2$\\
$k=-5\alpha_2x_0^4-3\alpha_1x_0^2-A_2f_i(W)+\xi, v=1-\Bigg(\dfrac{\xi x_0}{\xi-\alpha_3}\Bigg)^2$
当参数满足$a_1>0,a_1a_2-a_3>0,a_1a_2a_3-a_1^2a_4-a_3^2>0,a_4>0$时, 平衡点$EQ_\pm$是稳定的.
当参数满足$a_4=0(a_1>0,a_1a_2-a_3>0,a_3>0)$, 即
\begin{equation*}\left.\begin{split}&\Big(5\alpha_2x_0^4+3\alpha_1x_0^2+A_2f_i(W)+\xi\Big)(\alpha_3-\xi)-\xi^2=0\\&-\alpha_2x_0^5-\alpha_1x_0^3-A_2f_i(W)x_0-\dfrac{\alpha_3\xi}{-\alpha_3+\xi}x_0-\\&\quad\quad2\mu(-A_1W{m}\delta)=0, i=1,2\end{split}\right\}\tag*{(8)}\end{equation*}
系统可能会发生fold分岔, 导致不同平衡点之间的跳跃现象.
根据系统可能会发生Hopf分岔的判定条件, 具体到系统(2), 三个判定条件列举如下:
(I)分岔条件
$a_1a_2a_3-a_1^2a_4-a_3^2=0~(a_1>0,a_4>0,a_1a_2-a_3>0)$\\其中$a_1=2\mu-v,a_2=a_3-\xi-2\mu v-k$, $a_3=2\mu(a_3-\xi)+kv,a_4=-k(a_3-\xi)-\xi^2$, $k=-5\alpha_2x_0^4-3\alpha_1x_0^2-A_2f_i(W)+\xi,v=1-\Bigg(\dfrac{\xi x_0}{\xi -\alpha_3}\Bigg)^2$.
(II)非退化条件
快子系统(2)可以改写为$\dot{x}_1= Jx+F(x),x\in R^4$,
其中, $ J$是雅可比矩阵, 可以表示为
\begin{equation*}\begin{split}& J=\begin{pmatrix}0 & 1 & 0 & 0\\-w_2+\xi & -2\mu & -\xi & 0\\0 & 0 & 0 & 1\\-\xi & 0 & -\alpha_3+\xi & 1\\\end{pmatrix}\\& J q=\text i\omega q, J^{\rm T} p=-\text i\omega p,\,\langle p, q\rangle =\sum^4_{i=1}\bar{p}_iq_i=1\\\end{split}\end{equation*}
其中, $ J^{\rm T}$是雅可比矩阵$ J$的转置矩阵, $\langle\cdot,\cdot\rangle$ 是$\rm R_4$中的标准内积. $F(x)=O(\|x\Arrowvert^2)$是一个光滑函数, 在$x=0$附近, 其Taylor展开为
\begin{equation*}F(x)=\dfrac{1}{2}B(x,x)+\dfrac{1}{6}C(x,x,x)+O(\|x\Arrowvert^4)\end{equation*}
式中$B(x,y)$和$C(x,y,z)$是多重线性函数, 在坐标下的分量为
\begin{equation*}\begin{split}&B_i(x,y)=\sum_{j,k=1}^4\dfrac{\partial^2F_i(\xi,0)}{\partial\xi_j\partial\xi_k}\bigg|_{\xi=0}x_jy_k, i=1,2,3,4\\&C_i(x,y,z)=\sum_{j,k,l=1}^4\dfrac{\partial^3F_i(\xi,0)}{\partial\xi_j\partial\xi_k\partial\xi_l}\bigg|_{\xi=0}x_jy_kz_l, i=1,2,3,4\end{split}\end{equation*}
通过matcont软件可以验证
\begin{equation*}l_1(0)\neq 0\end{equation*}
其中
\begin{equation*}\begin{split}&l_1(0)=\dfrac{{\rm{Re}}\Big[\Big\langle p,C(q,q,\bar{q})\Big\rangle-2\Big\langle p,B(q,J^{-1}B(q,\bar{q}))\Big\rangle\Big]}{2\omega_0}+\\&\quad\quad\quad\dfrac{{\rm{Re}}\Big[\Big\langle p,B(\bar{q},(2\text i\omega E-J)^{-1}B(q,q))\Big\rangle\Big]}{2\omega_0}\end{split}\end{equation*}
(III)横截性条件
讨论当$\varOmega_1=0.000\,5,\varOmega_2=0.002$时的情形, 当$\varOmega_1=0.000\,5,\varOmega_2=0.003$时可类似讨论.
对特征方程(7)两边关于$W$求偏导, 得
\begin{equation*}\dfrac{{\rm d}\lambda}{{\rm d}W}=\dfrac{-\lambda^2\dfrac{{\rm d}\,a_2}{{\rm d}\,W}-\lambda\dfrac{{\rm d}\,a_3}{{\rm d}\,W}-\dfrac{{\rm d}\,a_4}{{\rm d}\,W}}{4\lambda^3+3a_1\lambda^2+2a_2\lambda+a_3}\tag*{(9)}\end{equation*}
将
\begin{equation*}\begin{split}&\dfrac{{\rm d}a_2}{{\rm d}W}=A_2(32W^3-16W)\\&\dfrac{{\rm d}a_3}{{\rm d}W}=-A_2{\rm v}(32W^3-16W)\\&\dfrac{{\rm d}a_4}{{\rm d}W}=A_2(\alpha_3-\xi)(32W^3-16W)\end{split}\end{equation*}
代入式(9)并令$\lambda=\text i\omega$, 得
\begin{equation*}\dfrac{{\rm d}\lambda}{{\rm d}W}=\dfrac{A_2(32W^3-16W)(\omega^2+\text i\omega v-\alpha_3+\xi)}{-4\text i\omega^3-3\alpha_1\omega^2+2\alpha_2\text i\omega+\alpha_3}\tag*{(10)}\end{equation*}
整理式(10)并分离$\dfrac{{\rm d}\,\lambda}{{\rm d}\,W}$的实部, 得
\begin{equation*}\begin{split}{\rm Re}&\Bigg(\dfrac{{\rm d}~\lambda}{{\rm d}~W}\Bigg)=A_2(32W^3-16W)[(\omega^2-a_3+\xi) &(-3a_1\omega^2+a_3)+\omega v(-4\omega^3+2a_2\omega)]~/~\\&[(-3a_1\omega^2+a_3)^2+(-4\omega^3+2a_2\omega)^2]\\&\end{split}\end{equation*}
将参数赋值后可以判定得出
\begin{equation*}{\rm{Re}}\Bigg(\dfrac{{\rm d}\lambda}{{\rm d}W}\Bigg)\neq 0\end{equation*}
证明系统会出现Hopf分岔, 平衡点可能会因Hopf分岔而失稳.
3 数值模拟
固定参数$\alpha_1=8$, $\alpha_2=1$, $\alpha_3=1$, $\xi=0.7$, $\mu=0.2$, $\delta=-1$, 讨论当双频激励振幅及外激频率不变, 参激频率改变的情况下, 系统出现的不同周期簇发振荡模式和轨线与非光滑分界面接触后发生的特殊非光滑动力学行为. 主要阐述: (1) $\varOmega_1=0.000\,5,\varOmega_2=0.002$; (2) $\varOmega_1=0.000\,5,\varOmega_2=0.003$. 两种情形下系统周期簇发振荡的产生机制与非光滑行为演化分析.3.1 $\varOmega_1=0.000\,5,\varOmega_2=0.002$时簇发振荡机理分析
固定振幅$A_1=7,A_2=3,$取$\varOmega_1=0.000\,5$, $\varOmega_2=0.002$. 通过数值模拟研究系统所可能发生的各种簇发振荡模式和非光滑演变行为. 图1和图2分别给出了系统在$(x_1,y_1)$平面上的相图和$x_1$的时间历程图.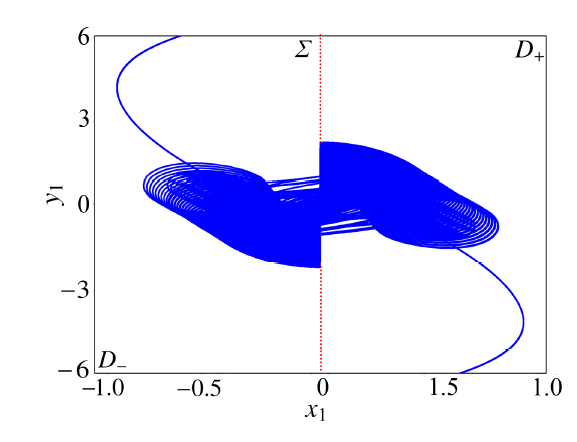
显示原图|下载原图ZIP|生成PPT图1$\varOmega_1=0.000\,5,\varOmega_2=0.002$时$(x_1,y_1)$平面上相图
-->Fig.1Phase portrait on the $(x_1,y_1)$ plane for $\varOmega_1=0.000\,5,\varOmega_2=0.002$
-->
显示原图|下载原图ZIP|生成PPT图2$\varOmega_1=0.000\,5,\varOmega_2=0.002$时$x_1$的时间历程图
-->Fig.2Time history of $x_1$ for $\varOmega_1=0.000\,5,\varOmega_2=0.002$
-->
如图1所示, 根据非光滑分界面$Σ$, 系统向量场被划分为两个光滑的子区域$D_+$和$D_-$, 轨线在分界面$Σ$和子区域$D_+$, $D_-$中都表现出了丰富的非光滑动力学行为. 轨线或在分界面发生滑动, 或穿过分界面在两子区域$D_+$和$D_-$ 间来回往返, 表现为大幅振荡和微幅振荡的交替出现, 即系统在沉寂态和激发态之间来回转化, 呈现为簇发振荡.
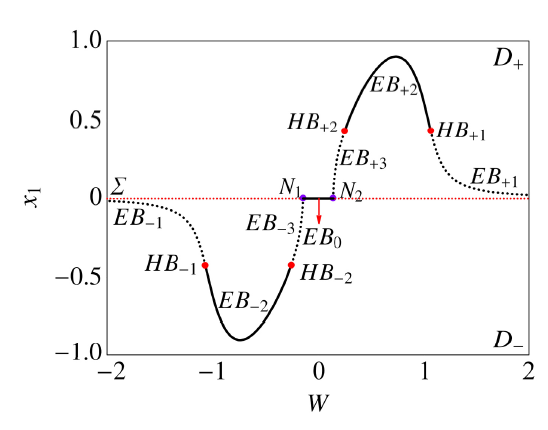
为揭示系统周期簇发振荡的演化机制, 我们给出了系统随慢变参数$W$变化的平衡曲线及分岔图, 如图3所示.
显示原图|下载原图ZIP|生成PPT图3$\varOmega_1=0.000\,5,\varOmega_2=0.002$时平衡曲线及分岔图
-->Fig.3Equilibrium branches as well as the bifurcations for $\varOmega_1=0.000\,5,\varOmega_2=0.002$
-->
如平衡曲线及分岔图$\!$3$\!$中所示,$\!$系统的平衡曲线被4个超临界Hopf分岔点$HB_{\pm1}(W,x_1)\!=(\pm1.068\,6,$$\pm$$0.428\,2)$, $HB_{\pm2}(W,\!x_1)\!=\!(\pm0.252\,9,\pm0.427\,0)$ 及曲线与分界面的2个交点$N_1(W,x_1)=(-0.146\,7,0)$和$N_2(W,x_1)=(-0.146\,7,0)$分成7部分. 实线代表稳定的平衡曲线, 虚线代表不稳定的平衡曲线. 运用微分包含理论, 引入辅助参数$q$, 以$F$ 表示系统(1), 于是系统(1)可改写为
\begin{equation*}F:=qF_++(1-q)F_-\tag*{(10)}\end{equation*}
其中辅助参数$q$可表示为
\begin{equation*}q=\dfrac{-y_s-A_1W_s+\delta}{2\delta}\tag*{(11)}\end{equation*}
式中, $y_s$, $W_s$分别表示当轨线接触到非光滑分界面时状态变量$y$和慢变参数$W$ 的值. 由于非光滑分界面的非线性动力学特性, 结合微分包含理论, 系统的平衡曲线中出现了一段$Σ$-平衡点曲线$EB_0$, 如图3所示.
在$(W,x_1)$平面上的转换相图与平衡曲线及相关分岔图的叠加能更好地诠释系统周期簇发振荡机制, 如图4和图5所示.
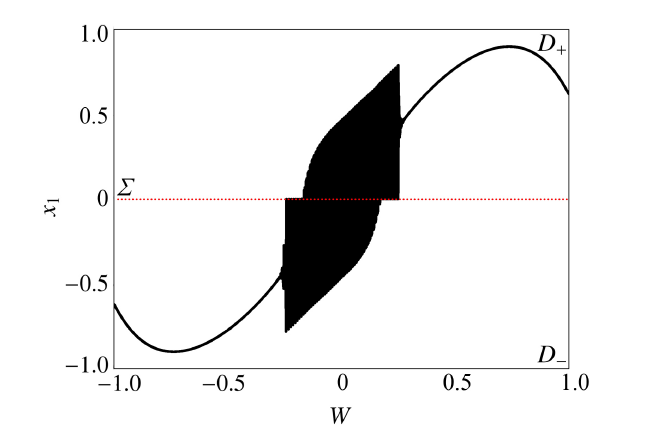显示原图|下载原图ZIP|生成PPT图4$\varOmega_1=0.000\,5,\varOmega_2=0.002$时$(W,x_1)$平面转换相图
-->Fig.4Transformed phase portrait on the $(W,x_1)$ plane for $\varOmega_1=0.000\,5,\varOmega_2=0.002$
-->
显示原图|下载原图ZIP|生成PPT图5$\varOmega_1=0.000\,5,\varOmega_2=0.002$时转换相图与平衡曲线的叠加图
-->Fig.5Overlap of equilibrium branches and transformed phase portrait on the $(W,x_1)$ for $\varOmega_1=0.000\,5,\varOmega_2=0.002$
-->
可以发现, 在一个周期的簇发振荡中, 轨线出现了多个激发态和沉寂态, 且轨线在不同激发态之间转迁时多次接触分界面, 或发生滑动行为, 或进入另一子区域, 如此在两子区域$D_+$和$D_-$中多次往返并表现出特殊的振荡模式.
通过转换相图与平衡曲线及相关分岔图的叠加图5阐述系统周期簇发振荡机制. 不失一般性, 假设轨线从子区域$D_-$中$W$取最小值$W=-1$处出发, 之后轨线几乎严格沿焦点型稳定平衡曲线$EB_{-2}$运动, 表现为沉寂态$QS_1$, 当轨线穿越Hopf分岔点$HB_{-2}(W,x_1)=(-0.252\,9,-0.427\,0)$时, Hopf分岔出现, 平衡点失稳, 产生稳定的极限环$LC$. 由于极限环$LC$在随着慢变参数$W$变化的过程中会与非光滑分界面有接触, 因而受到非光滑因素的影响, 轨线的振荡结构会发生明显的变化.
为更好地展现轨线在光滑区域的振荡形式及接触到分界面后发生的簇发振荡行为. 图$6\sim$图9给出了因Hopf分岔产生的不同慢变参数情形下的稳定极限环的演变过程. 当$W=-0.252\,9$时, 超临界Hopf分岔点$HB_{-2}(W,x_1)=(-0.252\,9,-0.427\,0)$出现, 产生了围绕位于平衡线$EB_{-3}$的不稳定焦点振荡的极限环$LC$. 图6给出了对应于慢变参数$W=-0.252\,9$的极限环, 可以发现, 其在围绕平衡曲线$HB_{-3}$逆时针振荡的过程中完全处于光滑区域$D_-$, 并未接触非光滑分界面$\varSigma$.
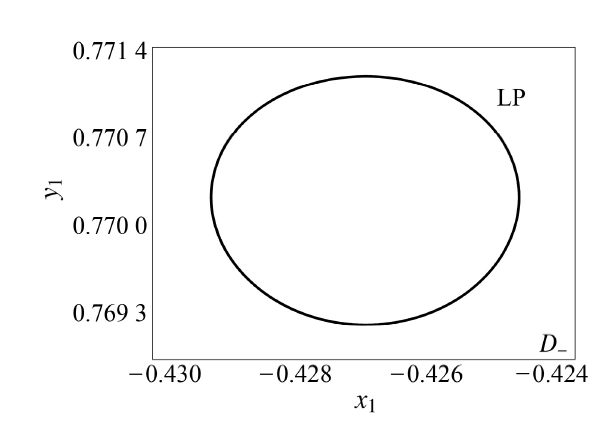显示原图|下载原图ZIP|生成PPT图6$W=-0.252\,9$时的稳定极限环
-->Fig.6Stable limit cycle with $W=-0.252\,9$
-->
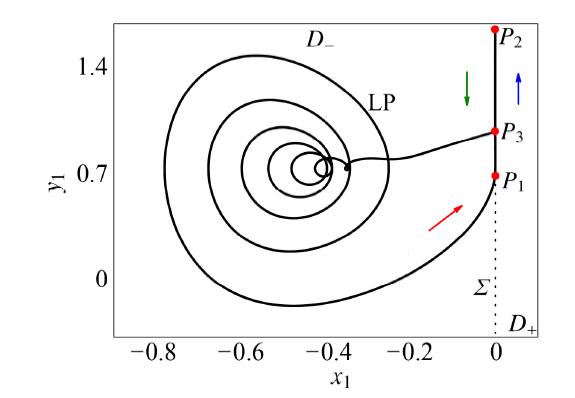显示原图|下载原图ZIP|生成PPT图7$W=-0.247\,6$时的稳定极限环
-->Fig.7Stable limit cycle with $W=-0.247\,6$
-->
显示原图|下载原图ZIP|生成PPT图8$W=-0.165\,0$时的稳定极限环
-->Fig.8Stable limit cycle with $W=-0.165\,0$
-->
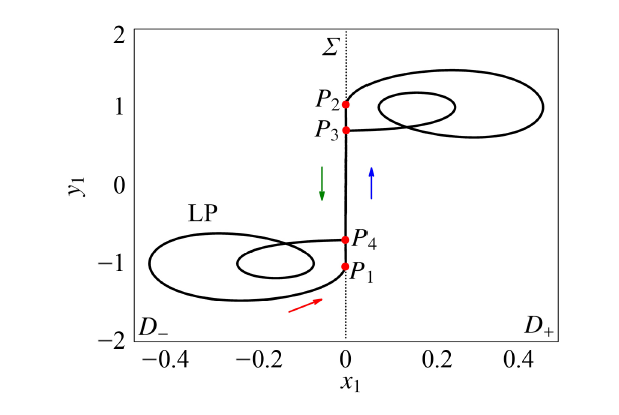显示原图|下载原图ZIP|生成PPT图9$W=0$时的稳定极限环
-->Fig.9Stable limit cycle with $W=0$
-->
随着慢变参数$W$的增大, 极限环$LC$的振幅在光滑区域$D_-$内逐渐增加. 当慢变参数$W$增大到$W=-0.247\,6$时, 极限环在$P_1(x_1,y_1)=(0,0.684\,7)$点接触到非光滑分界面, 然后沿向上箭头方向在分界面上开始滑动, 经过一段时间滑动到点$P_2(x_1,y_1)=(0,0.985\,7)$后, 又沿向下箭头方向运动到点$P_3(x_1,y_1)=(0,1.660\,1)$, 之后离开分界面$\varSigma$, 即表现为从光滑区域$D_-$进入分界面滑动一段时间之后, 然后脱离分界面, 后又再次返回光滑区域$D_-$继续运行. 所以, 慢变参数$W=-0.247\,6$对应着Filippov型广义自治系统的同宿分岔.
当慢变参数增加至$W=-0.165\,0$时, 极限环$LC$从位于分界面上的$P_1(x_1,y_1)=(0,0.106\,6)$点进入分界面后沿向上箭头方向滑动到$P_2(x_1,y_1)=(0,1.994\,3)$点, 之后立刻穿过分界面$Σ$进入光滑区域$D_+$, 然后继续在区域$D_+$短暂运动后又于$P_3(x_1,y_1)=(0,2.156\,0)$点返回到分界面, 沿分界面按向下箭头方向继续滑动到位于分界面上的$P_4(x_1,y_1)=(0,0.577\,5)$ 点, 继而返回到区域$D_-$继续运动. 所以, 慢变参数$W=-0.165\,0$对应着Filippov型广义自治系统的非常规分岔——多滑分岔[32].
图9给出的是$W=0$时轨线呈现的一种对称的振荡模式. 极限环仍然是在$P_1(x_1,y_1)=(0,-1.033\,6)$点接触到分界面后沿向上箭头方向滑动到$P_2(x_1,y_1)=(0,1.033\,6)$点, 然后立刻穿过分界面$Σ$进入光滑区域$D_+$, 在区域$D_+$内进行大幅振荡后于$P_3(x_1,y_1)=(0,0.699\,0)$点再次进入分界面, 继续按向下箭头方向滑动到$P_4(x_1,y_1)=(0,-0.699\,0)$点, 之后进入区域$D_-$ 开始大幅振荡. 在区域$D_+$和$D_-$内轨线表现为对称的簇发振荡.
$W$值随时间继续增大, 轨线振荡幅值逐渐减小, 当$W$增大到最大值$W=1$时, 轨线收敛到平衡曲线$EB_{+2}$.之后, $W$的值将开始逐渐减小, 轨线几乎严格沿稳定的平衡曲线$EB_{+2}$ 运动, 表现为沉寂态$QS_2$, 直到遇到Hopf分岔点$HB_{+2}(W,x_1)=(0.252\,9,0.427\,0)$, 再次出现Hopf分岔, 仍然产生稳定的极限环, 呈现出与由$HB_{-2}(W,x_1)=(0.252\,9,0.427\,0)$ 产生的极限环$LC$在不同参数下的相似且对称的演化状态, 此时轨线处于激发态. 随着$W$值继续减小, 轨线振荡幅值逐渐减小, 当$W$减小到最小值$W=-1$ 时, 轨线收敛到平衡曲线$EB_{-2}$. 至此, 轨线完成一个周期的簇发振荡.
3.2 $\varOmega_1=0.000\,5,\varOmega_2=0.003$时簇发振荡机理分析
固定振幅$A_1=7, A_2=3$, 取$\varOmega_1=0.000\,5,\varOmega_2=0.003$. 通过数值模拟研究系统所可能发生的各种簇发振荡模式以及非光滑演变行为. 图10和图11分别给出了系统在$(x_1,y_1)$ 平面的相图和$x_1$的时间历程图.
显示原图|下载原图ZIP|生成PPT图10$\varOmega_1=0.000\,5,\varOmega_2=0.003$时$(x_1,y_1)$平面上相图
-->Fig.10Phase portrait on the $(x_1,y_1)$ plane for $\varOmega_1=0.000\,5,\varOmega_2=0.003$
-->
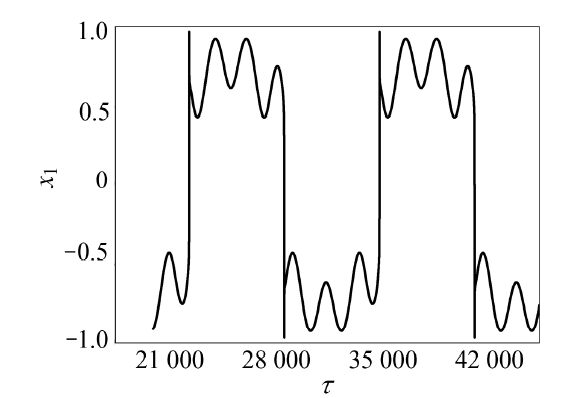显示原图|下载原图ZIP|生成PPT图11$\varOmega_1=0.000\,5,\varOmega_2=0.003$时$x_1$的时间历程图
-->Fig.11Time history of $x_1$ for $\varOmega_1=0.000\,5,\varOmega_2=0.003$
-->
为揭示系统周期簇发振荡的演化机制, 我们仍然给出了系统随慢变参数$W$变化的平衡曲线及分岔图, 在$(W,x_1)$平面上的转换相图, 在$(W,x_1)$平面上的转换相图与平衡曲线的叠加图, 如图$12\sim$图14所示. 同时图$15\sim$图18给出了在$(W,x_1)$平面上转换相图的局部放大图.
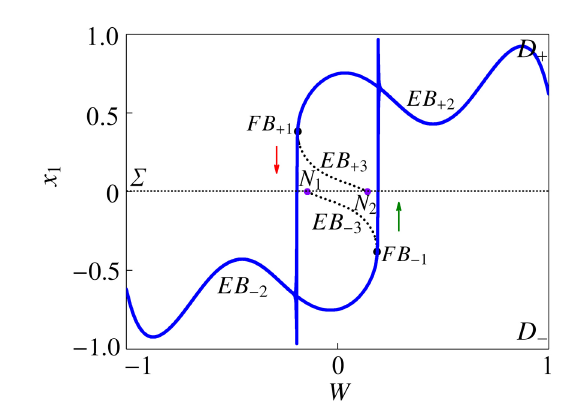显示原图|下载原图ZIP|生成PPT图14$\varOmega_1=0.000\,5,\varOmega_2=0.003$时转换相图与平衡曲线的叠加图
-->Fig.14Overlap of equilibrium branches and transformed phase portrait on the $(W,x_1)$ for $\varOmega_1=0.000\,5,\varOmega_2=0.003$
-->
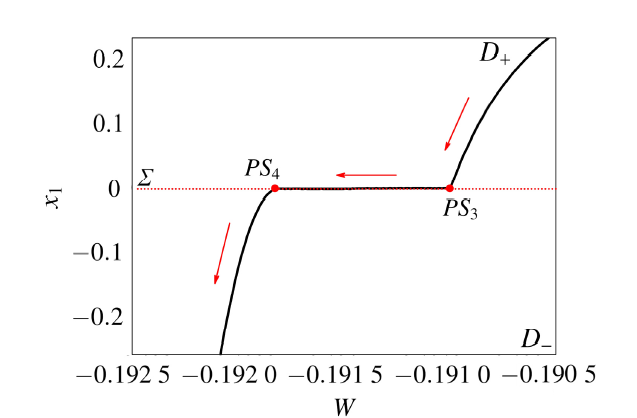显示原图|下载原图ZIP|生成PPT图15$\varOmega_1=0.000\,5,\varOmega_2=0.003$时$(W,x_1)$平面上的转换相图的局部放大
-->Fig.15Locally enlarged part one of the transformed phase portrait on the $(W,x_1)$ for $\varOmega_1=0.000\,5,\varOmega_2=0.003$
-->
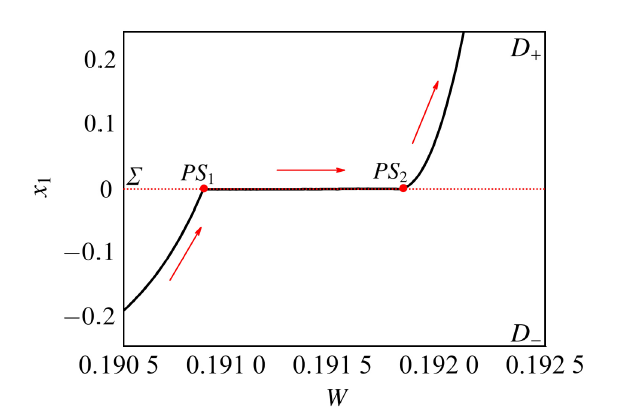显示原图|下载原图ZIP|生成PPT图16$\varOmega_1=0.000\,5,\varOmega_2=0.003$时$(W,x_1)$平面上的转换相图的局部放大
-->Fig.16Locally enlarged part two of the transformed phase portrait on the $(W,x_1)$ for $\varOmega_1=0.000\,5,\varOmega_2=0.003$
-->
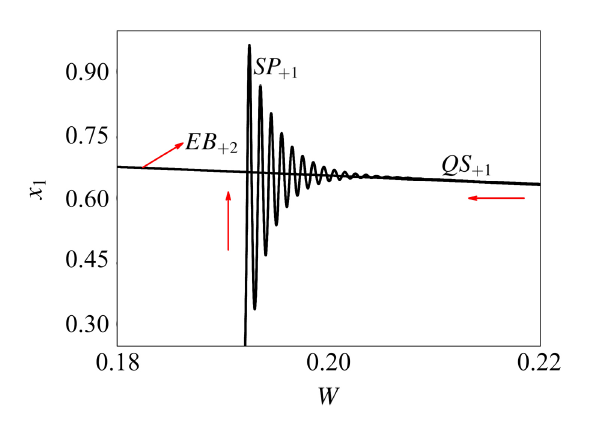显示原图|下载原图ZIP|生成PPT图17$\varOmega_1=0.000\,5,\varOmega_2=0.003$时$(W,x_1)$平面上的转换相图的局部放大
-->Fig.17Locally enlarged part three of the transformed phase portrait on the $(W,x_1)$ for $\varOmega_1=0.000\,5,\varOmega_2=0.003$
-->
显示原图|下载原图ZIP|生成PPT图18$\varOmega_1=0.000\,5,\varOmega_2=0.003$时$(W,x_1)$平面上的转换相图的局部放大
-->Fig.18Locally enlarged part four of the transformed phase portrait on the $(W,x_1)$ for $\varOmega_1=0.000\,5,\varOmega_2=0.003$
-->
如平衡曲线及分岔图12中所示, 系统的平衡曲线被2个超临界Hopf分岔点$HB_{\pm1}(W,x_1)=(\pm1.028\,5,\pm0.428\,2)$, 2个fold分岔点$FB_{\pm1}(W,x_1)=(\pm0.187\,4,\pm0.382\,1)$ 和曲线与分界面的2个交点$N_1(W,x_1)=(-0.146\,7,0)$和$N_2(W,x_1)=(0.146\,7,0)$分成7部分. 实线代表稳定的平衡曲线, 虚线代表不稳定的平衡曲线. 对比$\varOmega_1:\varOmega_2=1:4$时, 平衡曲线发生了多次曲折, 对应极值点的个数也由2个变为6个.
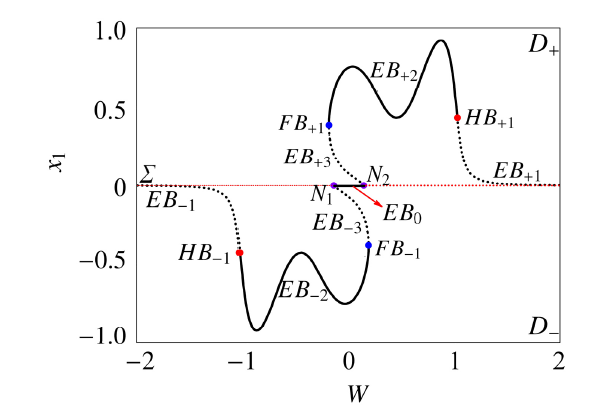显示原图|下载原图ZIP|生成PPT图12$\varOmega_1=0.000\,5,\varOmega_2=0.003$时平衡曲线及分岔图
-->Fig.12Equilibrium branches as well as the bifurcations for\\\vskip -2mm $\varOmega_1=0.000\,5,\varOmega_2=0.003$
-->
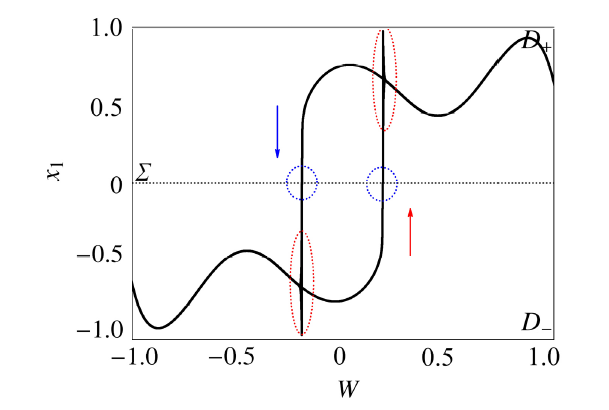显示原图|下载原图ZIP|生成PPT图13$\varOmega_1=0.000\,5,\varOmega_2=0.003$时$(W,x_1)$平面上转换相图
-->Fig.13Transformed phase portrait on the $(W,x_1)$ plane for $\varOmega_1=0.000\,5,\varOmega_2=0.003$
-->
从$(W,x_1)$平面上的转换相图与平衡曲线的叠加图14看出, 在一个周期的簇发振荡中, 轨线出现了2个激发态$SP_{\pm i}(i=1,2)$和2个沉寂态$QS_{\pm i}(i=1,2)$. 轨线在不同激发态之间转迁时会接触到分界面, 沿分界面滑动之后, 进入另一区域发生簇发振荡现象, 并经一段时间之后又返回分界面, 回到之前所在区域, 如此在两子区域$D_+$和$D_-$中往返并表现为簇发振荡.
不失一般性, 假设轨线从子区域$D_-$中$W$取最小值$W=-1$处出发, 之后轨线几乎严格沿焦点型稳定平衡曲线$EB_{-2}$运动, 表现为沉寂态$QS_{-1}$, 直到轨线抵达fold分岔点$FB_{-1}(W,x_1)=(0.187\,4,-0.382\,1)$, fold分岔出现导致轨线开始跳跃, 使得轨线表现为激发态$SP_{-1}$, 在$PS_1(W,x_1)=(0.190\,9,0)$点(如图10)到达分界面, 滑动至点$PS_2(W,x_1)=(0.191\,8,0)$后穿过分界面, 到达区域$D_+$后轨线继续大幅振荡, 表现为激发态$SP_{+1}$. 随着$W$值的增大, 振荡幅值逐渐减小, 当$W$增大到最大值$W=1$时,轨线收敛到平衡曲线$EB_{+2}$. 随着时间的延长, $W$ 值将逐渐减小,轨线几乎严格沿稳定的平衡曲线$EB_{+2}$运动, 表现为沉寂态$QS_{+1}$, 直到轨线抵达$FB_{+1}(W,x_1)=(-0.187\,4,0.382\,1)$, fold分岔再次发生, 轨线开始跳跃, 表现为激发态$SP_{+2}$, 在$PS_3(W,x_1)=(-0.190\,9,0)$点到达分界面, 滑动至点$PS_4(W,x_1)=(-0.191\,8,0)$ 后穿过分界面. 当轨线到达区域$D_-$ 后, 继续大幅振荡, 表现为激发态$SP_{-2}$. 随着$W$取值的减小, 振荡幅值也逐渐减小, 当$W$ 减小到最小值$W=-1$ 时, 轨线稳定到平衡曲线$EB_{-2}$,表现为沉寂态$QS_{-2}$. 至此, 轨线完成一个周期的非光滑簇发振荡.
4 两种情形下平衡曲线的演化趋势
观察两种情形下的平衡曲线图3和图12可以发现, 虽然平衡曲线具有相似的结构, 但随着参数激励频率的改变, 平衡曲线发生曲折的次数有所增加, 致使极值点个数也随之增多, 相应簇发振荡的转换相图也变得复杂, 而导致这一现象产生的原因是两激励的频率存在明显的量级差. 以$\varOmega_1=0.000\,5,\varOmega_2=0.002$为例, 当频率小的变量运动一个周期时, 频率大的变量却已经运动了4个周期, 而此两者的耦合恰好形成一个新周期.为描述平衡曲线极值点个数的变化, 图19和图20给出了两种情形下极值点个数的变化趋势, 其中, 图19和图20中的黑色标识点分别对应图3和图12中的平衡曲线中的极值点. 图19中的曲线对应的函数表达式分别为$y_1=32W^3-16W$和$y_2=\dfrac{14}{15W}$. 图20中的曲线对应的函数表达式分别为$y_1=192W^5-192W^3+36W$和$y_2=\dfrac{14}{15W}$.
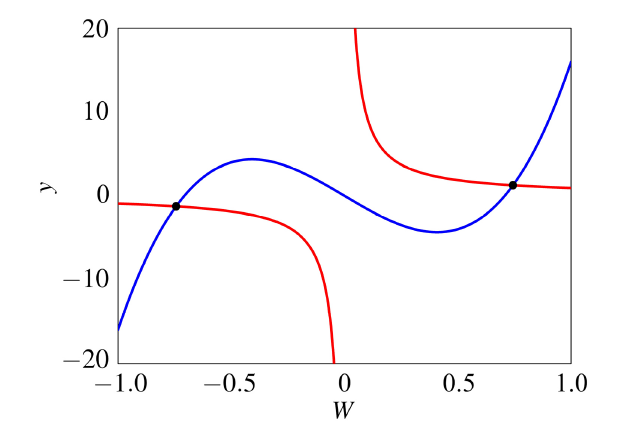显示原图|下载原图ZIP|生成PPT图19$\varOmega_1=0.000\,5,\varOmega_2=0.002$时极值点个数情况
-->Fig.19Variation of extreme points with $\varOmega_1=0.000\,5,\varOmega_2=0.002$
-->
显示原图|下载原图ZIP|生成PPT图20$\varOmega_1=0.000\,5,\varOmega_2=0.003$时极值点个数情况
-->Fig.20Variation of extreme points with $\varOmega_1=0.000\,5,\varOmega_2=0.003$
-->
如图19和图20所示, 当$\varOmega_1=0.000\,5,\varOmega_2=0.002$时, 平衡曲线的极值点个数为2, 当$\varOmega_1=0.000\,5$, $\varOmega_2=0.003$时, 极值点增加为6个. 将图19和图20分别与图3和图12进行对比, 发现图19和图20中黑色标识的极值点的个数分别与图3 和图12所示的平衡曲线中的极值点个数相一致, 并且各极值点坐标也与平衡曲线所示的相吻合. 当$\varOmega_1=0.000\,5,\varOmega_2=0.002$时, 对应极值点的$W$ 的坐标是$W=\pm0.743\,5$, 当$\varOmega_1=0.000\,5,\varOmega_2=0.003$ 时, 对应极值点的$W$的坐标是$W_{\pm1}=\pm0.175\,6$, $W_{\pm2}=\pm0.454\,7$.
5 结论
对于含双频激励的Filippov系统进行非光滑簇发振荡机理分析时, 引入周期变化的双频激励项, 当两激励频率之间存在共振关系, 且周期激励频率远小于系统的固有频率时, 将两周期激励项转换为单一周期激励项的函数表达式, 并将该单一周期激励项视为慢变参数, 利用快慢分析法, 在固定两激励振幅的取值, 保持外激频率不变, 改变参激频率的情形下, 得到了快子系统随慢变参数变化的平衡曲线及其分岔行为的演化机制. 结合转换相图和不同慢变参数情形下的稳定极限环的演变过程, 发现随着慢变参数的改变, 轨线会出现同宿分岔、多滑分岔及多种复杂振荡模式, 而参激频率的改变, 使得系统的分岔模式增加, 系统的簇发振荡机制变得复杂, 从而非光滑动力学行为特性也更明显. 通过对比两种不同参激频率下的平衡曲线及分岔图, 发现虽然系统有相似的平衡曲线结构, 却因参激频率取值的不同, 致使平衡曲线发生曲折的次数增加, 极值点个数也由$\varOmega_1=0.000\,5,\varOmega_2=0.002$时的2个变为$\varOmega_1=0.000\,5,\varOmega_2=0.003$时的6个, 数值模拟也很好地验证了这一结果.必须指出的是, 本文讨论的是保持外激频率$\varOmega_1=0.000\,5$不变, 改变参激频率$\varOmega_2$的值时系统产生的簇发振荡及非光滑行为特性. 若固定$\varOmega_2$ 不变, 改变$\varOmega_1$的值, 系统可能会有不同的非线性动力学行为, 我们将另外讨论这种情形.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . . |
| [2] | . . |
| [3] | . . |
| [4] | . |
| [5] | . |
| [6] | . |
| [7] | . |
| [8] | . |
| [9] | . . |
| [10] | . |
| [11] | . . |
| [12] | . . |
| [13] | . |
| [14] | . |
| [15] | . |
| [16] | . |
| [17] | . . |
| [18] | . |
| [19] | . . |
| [20] | . |
| [21] | . |
| [22] | . |
| [23] | . |
| [24] | . |
| [25] | . |
| [26] | . |
| [27] | . |
| [28] | . |
| [29] | . |
| [30] | . |
| [31] | . |
| [32] | . |
