郑健康, 张晓芳²⁾, 毕勤胜江苏大学土木工程与力学学院,江苏镇江 212013

BURSTING OSCILLATIONS AS WELL AS THE DELAYED PITCHFORK BIFURCATION BEHAVIORS IN A CLASS OF CHAOTIC SYSTEM ¹⁾

Zheng Jiankang, Zhang Xiaofang²⁾, Bi QinshengFaculty of Civil Engineering and Mechanics, Jiangsu University, Zhenjiang 212013, Jiangsu, China

收稿日期:2018-07-20接受日期:2018-10-18网络出版日期:2019-03-18

基金资助:

国家自然科学基金资助项目.11632008 国家自然科学基金资助项目.11872188

Received:2018-07-20Accepted:2018-10-18Online:2019-03-18
作者简介 About authors
2)张晓芳,副教授,主要研究方向：动力学与控制.E-mail：xfzhang@ujs.edu.cn



摘要
由于多时间尺度问题在实际工程系统中广泛存在,关于其复杂动力学行为及其产生机制的研究已成为当前国内外的热点课题之一.簇发振荡是多时间尺度系统复杂动力学行为的典型代表,而分岔延迟又是簇发振荡中的常见现象.本文为探讨非线性系统中分岔延迟所引发的簇发振荡的分岔机制,在一个三维混沌系统中引入参数激励,当激励频率远小于系统的固有频率时,系统产生了两时间尺度簇发振荡.将整个激励项看做慢变参数,激励系统转化为广义自治系统也即快子系统,分析快子系统平衡点的稳定性以及分岔条件,并运用快慢分析法和转换相图揭示了簇发振荡的动力学机理.文中考察了4组参数条件下系统的动力学行为,研究发现当慢变激励项周期性地通过分岔点时,系统产生了明显的超临界叉形分岔延迟行为,随着参数激励振幅的增大,分岔延迟的时间也逐渐延长,当这种延迟的动态行为终止于不同的参数区域时,导致系统轨线围绕不同稳定吸引子(平衡点,极限环)运动,从而得到了不同的簇发振荡行为.
关键词： 叉形分岔;慢变激励;簇发;吸引域;延迟

Abstract
Due to wide existence of multiple-time-scale problems in practical engineering, the complicated dynamic behaviors and their generation mechanism have become one of the hot topics at home and abroad. The systems with multiple time scales can often exhibit bursting oscillations with the bifurcation delay phenomenon. In order to investigate the bifurcation mechanism of bursting oscillations caused by bifurcation delay in a nonlinear system, a parametric excitation is introduced in a novel three-dimensional chaotic system. When the exciting frequency is far less than the natural frequency, the coupling of two time scales involves the vector field, which leads to the bursting oscillations. By considering the whole exciting term as a slow-varying parameter, the original system can be considered as a generalized autonomous system, which can be regarded as the fast subsystem. Upon the analysis of equilibrium points and bifurcation conditions of the fast subsystem, combining with the transformed phase portraits, the bifurcation mechanisms of bursting oscillations is presented. Four typical cases with different parameter conditions are discussed to reveal the evolution of the bursting oscillations. It is found that when the slow-varying exciting term passes across the bifurcation points, the delayed behaviors of super-critical pitchfork bifurcation can be observed. With the increase of the exciting amplitude, the occurring needed for the bifurcation delay is increased gradually. When the delayed behaviors end in different parameter regions, different types of bursting oscillations which may surround different attractors such as equilibrium points and limit cycles appear.
Keywords：pitchfork bifurcation;slow-varying excitation;bursting oscillation;domain of attraction;delay


PDF (7520KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
郑健康, 张晓芳, 毕勤胜. 一类混沌系统中的簇发振荡及其延迟叉形分岔行为 ¹⁾. 力学学报[J], 2019, 51(2): 540-549 DOI:10.6052/0459-1879-18-241
Zheng Jiankang, Zhang Xiaofang, Bi Qinsheng. BURSTING OSCILLATIONS AS WELL AS THE DELAYED PITCHFORK BIFURCATION BEHAVIORS IN A CLASS OF CHAOTIC SYSTEM ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2019, 51(2): 540-549 DOI:10.6052/0459-1879-18-241

引 言

多时间尺度耦合动力系统涉及力学、化学以及生物学等多个不同学科领域^[1-5],具有广泛的工程背景.如输电塔线体系中塔线之间的耦合^[6]、化学反应中存在着不同量级的反应速率^[7-8]、生物代谢过程中的变构效应^[9]、神经元的簇发放电活动^[10-11]等.显然,能够导致多时间尺度耦合的因素是多种多样的,但是这类系统的数学模型及其振荡特性仍具有一定的相似性,都可以用含慢变参数或慢变量的非线性动力系统来刻画.与一般的非线性系统相比,多时间尺度耦合会导致系统产生复杂的动力学行为,主要表现为各个状态变量在真实时间上的快慢效应,通常表现为大幅振荡与微幅振荡之间的耦合.当状态变量处在微幅振荡或几乎不变时,称为沉寂态或静息态(quiescent state,QS),而大幅振荡则称为激发态(spiking state,SP)^[12-13],当系统在沉寂态和激发态之间来回变化时,会呈现为簇发振荡^[14-15].在过去的研究中由于缺乏有效的分析方法,相关工作主要围绕耦合系统的近似求解^[16]、数值仿真^[17]和实验分析^[18],直到2000年,Izhikevich^[19]引入了Rinzel的快慢分析法,才将相关研究提升到机理分析的层次,其中心思想是：将不同尺度耦合系统分解为相互耦合的快慢两子系统,通过对快子系统的平衡态及其分岔分析,得到沉寂态和激发态之间相互转化的分岔机制,从而揭示相应簇发振荡的产生机理^[20-23].近年来,基于快慢分析法,国内外****围绕两时间尺度耦合动力系统开展了大量的研究,如Freire和Gallas^[24]搭建了两快一慢三维BVP振子电路并给出了相应的簇发演化机理;Chumakov等^[25]构建了金属催化氧化系统模型,分析了化学反应过程中的簇发振荡现象;韩修静等^[26]探究了洛伦兹系统由快慢尺度效应导致的簇发现象并分析了其相应的分岔机制.

而分岔延迟现象^[27-31]在簇发振荡中广泛存在,并且通常出现在具有缓慢变化的控制参数的动力系统中,其一般形式为

(1)$ \dot {x} = f(x,\gamma (\varepsilon t)) $

其中,$x \in R^n$,$\gamma (\varepsilon t)(\varepsilon \ll 1)$是缓慢变化的控制参数,当控制参数通过分岔点后,由于稳定性发生变化,系统状态没有立即发生变化,而保持当前状态一段时间,这种现象就是分岔延迟现象.在分岔延迟现象的研究中,叉形分岔的延迟^[32-33]行为可以产生非常丰富的动力学现象.当轨线通过叉形分岔点时,系统的稳定性发生变化,在不同的参数区域可能出现一个或者多个吸引域,由于延迟的原因,系统轨线可能跳到不同的吸引域^[34-35],从而产生不同的动力学行为.

针对以上情况,本文基于一个三维混沌系统,并引入周期参数激励,同时调节参数使得激励频率和系统的固有频率之间产生量级差异,建立一个参数激励下的两时间尺度系统.以此模型为例,给出了由于分岔延迟导致不同的簇发振荡行为,结合快子系统平衡点稳定性及分岔分析,运用经典快慢分析法揭示不同类型簇发模式的诱发机理,进一步丰富了非线性动力学理论.

1 数学模型

与经典的Lorenz等系统不同,通过引入偶次非线性项,Abooee等^[36]建立了一个新的三维混沌系统,进而基于电路仿真,证实了一类新型混沌吸引子的存在,并探讨了不同参数控制下各类吸引子的演化.文中拟考察该系统在参数周期激励控制下的行为,其相应的动力学模型可以表示为

(2)$$\left. \begin{array}{l} \dot {x} = a(y-x) + byz^2 \\ \dot {y} = (\beta + w)x-xz^2 \\ \dot {z} = cz + dx^2 \\ \end{array}\right\}$$

其中,$w = A\cos (\omega t)$,A为激励幅值,$\omega$为相应的激励频率,$\beta$为恒定的控制增益项.对于系统(2),做变换$(x,y,z) \to (-x,-y,z)$后,系统保持不变,可见,系统关于z轴对称.

当激励项的频率与系统的固有频率$\Omega _N$存在量级差异时,系统存在频域上的两时间尺度,表现出明显的快慢效应.从而产生诸如簇发等类型的特殊振荡模式.

2 快子系统的分岔分析

当激励频率远小于系统自身的固有频率时,即$\omega \ll \Omega _N$,在固有频率的任意一个周期$t$内,$t \in [t_0 ,t_0 + 2π / \Omega _N ]$,激励项将在$w_A = A\cos (\omega t_0 )$和$w_B = A\cos (\omega t_0 + 2π \omega / \Omega _N )$之间变化.虽然在一个激励频率对应的周期内,激励项会在$\pm A$之间变化,但在任一固有频率所对应的周期内,w变化是非常小的.因此,激励项w可视为系统(2)的一个慢变参数,系统(2)可看作广义自治系统.

在快慢分析法中,认为快子系统的分岔模式决定了沉寂态和激发态之间相互转化机制,而慢变量则对系统行为起着调节作用.所以,可以将系统(2)中慢变参数w定义为慢变量,而相应的广义自治系统(2)定义为快子系统,进一步分析w变化下快子系统的分岔行为.

对于系统参数$a > 0,c < 0,d < 0$时,当$w \le-\beta$时,快子系统有唯一平衡点${E}_{0} = (0,0,0)$,稳定性由其特征方程决定

(3)$$ (\lambda-c)(\lambda ^2 + a\lambda-aw-a\beta ) = 0$$

可以得到$\lambda _1 = c$,其他两个根$\lambda _2$,$\lambda _3$可由以下方程求得

(4)$$ \lambda ^2 + a\lambda-aw-a\beta = 0$$

根据Routh-Hurwitz准则,可知方程(4)的一切特征根实部为负数的条件为

(5)$$ w + \beta < 0$$

即,当$w <-\beta$时,${E}_0$为稳定平衡点,当$w >-\beta$时,${E}_0$为不稳定平衡点. 显然,${E}_0$发生简单分岔的条件为

(6)$$ w + \beta = 0$$

由平衡点${E}_0$处的特征方程易知,随着参数$a,w,\beta$的变化,特征方程只会出现零根,而始终无纯虚根,故平衡点${E}_0$不会发生Hopf分岔.

当$w >-\beta$时,系统中除了存在不稳定的平衡点${E}_0$外,还存在一对对称的平衡点${E}_\pm =\Big(x_0 ,$$ \frac{a}{a + b(w + \beta )}x_0,-\sqrt {w + \beta } \Big)$,其中$x_0 = \pm \sqrt {\frac{c\sqrt {w + \beta } }{d}}$,${E}_\pm$稳定性由相同的特征方程决定

(7)$$ \lambda ^3 + a_2 \lambda ^2 + a_1 \lambda + a_0 = 0$$

其中

$$\begin{array}{l} a_2 = \frac{ab\beta + abw-bc\beta-bcw + a^2-ac}{a + b(w + \beta )}\\[3mm] a_{^1} = \frac{-2abc\sqrt {\beta + w}-abc\beta-abcw-a^2c}{a + b(w + \beta )}\\[3mm] a_0 =-4c(w + \beta )(a-b\sqrt {\beta + w} )\end{array}$$

根据Routh-Hurwitz准则,可知方程(7)的一切特征根实部为负数的条件为

(8)$$\left.\begin{array}{l} a_1 a_2-a_0 > 0\\ a_0 a_1 a_2-a_0^2 > 0\end{array}\right\}$$

否则平衡点${E}_\pm$失稳变成不稳定平衡点.

由特征方程(7)可知,${E}_\pm$发生简单分岔的条件为

(9)$$ w + \beta = 0\quad \mbox{or}\quad a-b\sqrt {w + \beta } = 0$$

对于平衡点${E}_\pm$,当其特征根穿过虚轴时,可能发生Hopf分岔,根据Hopf分岔条件,将$\lambda = {\rm i}\omega _0$代入特征方程,可以得到Hopf分岔所满足的条件

(10)$$ a_1 a_2-a_0 = 0\quad (a_0 / a_2 > 0, a_1 > 0)$$

且分岔参数w需满足横截性条件

(11)$$ \frac{{\rm{dRe}}(\lambda )}{{\rm d}w}\left|_{{w = w} _{0 } } \right. \ne 0$$

此时,由Hopf分岔产生的频率为$\Omega _H = \sqrt {a_0 / a_2 }$.

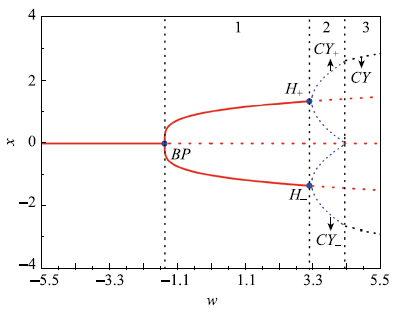
为了进一步讨论平衡点稳定性及其分岔条件,将参数取定$a = 35$,$b = 1$,$c =-5$,$d =-6$,$\beta = 1.5$,由以上分析可知${E}_0$在$w <-1.5$时为稳定结点,当w穿过$w =-1.5$时,系统发生超临界叉形分岔,${E}_0$变为不稳定结点,同时产生对称的稳定焦点${E}_\pm$.对于平衡点${E}_\pm$,当其满足Hopf分岔条件时,此时分岔参数$w =3.169~09$,将其值代入式(11)可得$\frac{{\rm{dRe}}(\lambda )}{{\rm d}w}\left| {_{w_0 = 3.169~09} } \right. = 0.445~91 \ne 0$,且其第一Lyapunov系数$l_1 =-0.317~4 < 0$,所以当w穿过$w_0 = 3.169~09$时,${E}_\pm$发生Hopf分岔,稳定焦点变为不稳定焦点的同时产生稳定极限环.图1给出了快子系统随慢变参数$w = A\cos (\omega t)$变化的分岔图.红色实线为稳定平衡点,红色虚线表示平衡点不稳定,蓝色虚线表示经过超临界Hopf分岔点所产生的独立极限环${CY}_\pm$,以及极限环${CY}_\pm$碰撞产生大的极限环${CY}$(黑色虚线表示).根据吸引域存在范围的不同,可以分为三个区域,区域1：有稳定平衡点${E}_\pm$和不稳定平衡点${E}_{0}$,即点的吸引域,存在区间为[$-$1.500,3.170);区域2：有稳定极限环${CY}_\pm$,即环的吸引域,存在区间为[3.170, 4.342);区域3：由稳定极限环${CY}_\pm$相碰产生更大的稳定极限环${CY}$,也是环的吸引域,区间为[4.342, 6.424].下面将分析叉形分岔延迟终止于不同区域导致的簇发振荡的动力学行为.

图1

新窗口打开|下载原图ZIP|生成PPT
图1快子系统平衡曲线及分岔图

Fig.1The equilibrium branches as well as bifurcation points of fast subsystem

3 簇发振荡现象分析

首先分析动力系统的频域两尺度效应,在此取$\omega = 0.05$,其他参数不变,则有$\omega \ll \Omega _N$.为了揭示这些平衡点分支及其相关的分岔对两尺度耦合系统的动力学行为的影响机理,这里引入了转换相图(transformed phase portrait,TPP)的概念,前面提出将慢变激励项$w=A{\rm{cos}}(\omega t)$视为慢变量,则原先的三维系统(2)延拓为具有变量$(x,y,z,w) = (x,y,z,A\cos (\omega t))$的四维系统,而系统(2)则是延拓后的四维系统在$(x,y,z)$空间上的投影,当延拓后的四维系统向含有慢变量w子平面(如子平面$(x,w))$或者子空间(如子空间$(x,y,w))$投影时,便得到了所谓的转换相图.在转换相图上利用快慢分析法可以分析系统随慢变激励变化的分岔行为.接下来根据叉行分岔延迟终止的3个不同区域,分析其产生不同簇发振荡的机制.

3.1 点-点簇发

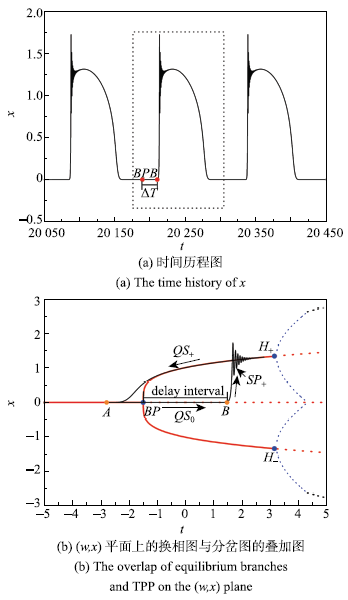
首先分析叉行分岔延迟终止于区域1时的动力学行为,固定其他参数,取振幅$A = 2.8$,即慢变参数$w = 2.8\cos (0.05t)$.图2给出了在此参数下的时间历程图以及$(w\mbox{,}x)$平面上的转换相图与分岔图的叠加图.

图2

新窗口打开|下载原图ZIP|生成PPT
图2$A = 2.8$时的簇发振荡

Fig.2Bursting oscillations for $A = 2.8$



假设轨线从A点出发(图2(b)),可以判断轨线将沿着稳定平衡点${E}_0$向右运动进入沉寂态$QS_{0}$,当轨线经过$BP(w =-1.50)$点时,${E}_{0}$变成不稳定的平衡点,并产生两个稳定平衡点${E}_\pm$,即超临界叉形分岔.当轨线穿过$BP$点时,并没有立即跳跃,而是沿着不稳定的平衡点${E}_0$走了一段时间(即分岔延迟现象),当分岔延迟终止在区域1时,即$B$点$(1.484,0)$后轨线向${E}_ +$跳跃,产生大幅振荡进入激发态$SP_{ + }$,随着慢变参数w的增大,振荡轨迹逐渐趋于${E}_ +$进入沉寂态$QS_{ +}$,当w到达最大值2.80时,随着时间的延长,w将逐渐减小,轨线严格沿着${E}_+$向左运动,且随着w的减小并经过$BP$点时,${E}_ +$消失,轨线最终收敛到稳定平衡点${E}_0$,回到A点完成一个周期的簇发振荡.由于系统轨线是围绕两个平衡点周期振荡,因此该簇发振荡可以称为点-点簇发.

为了得到分岔延迟的时间,文中选取一个周期的时间历程图,如图2(a)所示,在其中的一个周期内$BP$点和$B$点所对应的时间分别为20~189.13 s和20 210.13 s,可以得到分岔延迟时间$\Delta T = 21~\mbox{s}$,即当$A = 2.8$时,产生了明显的分岔延迟现象.

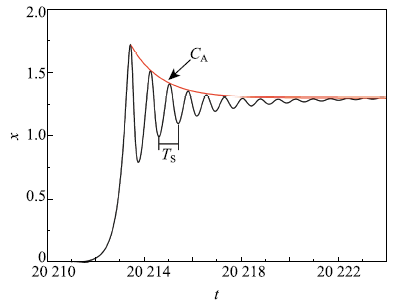
为讨论激发态的振荡特性,图3给出了状态变量x的时间历程处于激发态时的局部放大图,由于激发态是从平衡曲线${E}_0$跳跃趋于平衡曲线${E}_ +$,因此跳跃过程可近似视为以$B$点为初值趋于平衡曲线${E}_ +$的渐进过程. 首先计算${E}_ +$上与$B$点具有相同w值的平衡点的特征值分别为$\lambda _1 = -38.412$,$\lambda _{2,3} =-0.794\pm 7.64{\rm i}$,由于$\lambda _1$所对应的特征分量会很快收敛到${E}_ +$,因此从$B$到${E}_ +$的激发态特征主要由$\lambda _{2,3}$决定. 虽然在平衡曲线${E}_ +$上平衡点位置的不同,其相应特征值会发生变化,但是其变化相对较小,因此可以由$\lambda _{2,3}$近似给出激发态的振动特性.

图3

新窗口打开|下载原图ZIP|生成PPT
图3时间历程处于激发态时的局部放大图

Fig.3Locally enlarged parts of time history in the spiking state



簇发振荡中激发态的振荡幅值的变化主要受该对共轭复根的实部影响,其在x方向上的变化可以用曲线$C_A= A_B \exp [-0.794(t-t_0 )]$近似描述,其中$A_B$为$B$点与${E}_+$之间在x方向上的距离,$t_0$为轨迹到达$B$时的时间,图3给出了其随时间$t$的变化曲线,可以发现其与激发态时的振动符合良好.

激发态的频率特性同样可以通过$\lambda _{2,3}$的虚部近似确定,即$\Omega _{SP} = 7.641$.从图3中的时间历程可以计算得其振荡的频率为$\Omega _P = 2π / T_S = 7.837$,与理论结果符合良好.

值得注意的是,由于分岔延迟终止于区域1,而区域1有两个对称的稳定平衡点吸引子${E}_\pm$,这种情况下,轨线可能趋于平衡点${E}_ +$或${E}_-$,这取决于对初值的选取,事实上,在图2相同参数的情况下,取初值$(0,-0.1,0)$可以得到与图2(初始值$(0,0.1,0))$对称的簇发振荡模式,如图4所示,其中粉色线表示初始值为$(0,-0.1,0)$相图和转换相图与分岔图的叠加图.

图4

新窗口打开|下载原图ZIP|生成PPT
图4初始值分别取$(0,0.1,0)$和$(0,-0.1,0)$的簇发振荡

Fig.4The bursting oscillations with different initial values of\\$(0,0.1,0)$ and$(0,-0.1,0)$

3.2 点-环簇发

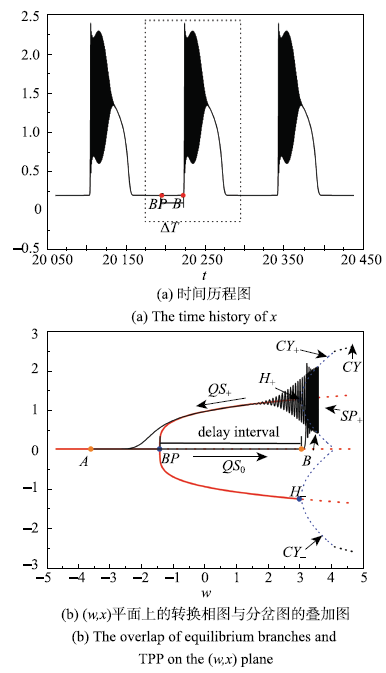
当叉形分岔延迟相对较长并终止于区域2时,其簇发振荡模式发生了明显的变化,针对这种情况下,文中给出了在$A=3.8$的这组参数下的时间历程图以及$(w,x)$平面上的转换相图与分岔图的叠加图,如图5所示.

图5

新窗口打开|下载原图ZIP|生成PPT
图5$A = 3.8$时的簇发振荡

Fig.5Bursting oscillations for $A = 3.8$



还是假设轨线从A点出发(图5(b)),可以判断轨线沿着稳定平衡点${E}_0$向右运动进入沉寂态$QS_{0}$,当经过$BP(w =-1.50)$点时,${E}_0$变成不稳定的平衡点,由于分岔延迟现象的存在,轨线并没有立即跳跃,而是沿着不稳定的平衡点${E}_0$走了一段时间,当分岔延迟终止在区域2时,即$B$点$(3.245, 0)$,由于区域2存在由超临界Hopf点${H}_\pm$产生的稳定极限环${CY}_\pm$,并且3个平衡点都处于失稳状态,受到${CY}_ +$的吸引,轨线的振荡幅值迅速增大,系统进入激发态$SP_{ +}$,随着慢变参数w的增大,轨迹逐渐趋于${CY}_ +$,当w到达最大值3.80时,随着时间的延长,w将逐渐减小,轨线围绕着${CY}_+$振荡并向左运动,由于极限环的逐渐缩小,振荡幅值也逐渐缩小,直到穿过分岔点${H}_+$,极限环${CY}_ +$消失,轨线退出激发态并逐渐收敛于${E}_ +$进入沉寂态$QS_{ + }$,且随着w的减小并经过$BP$点时,${E}_ +$消失,轨线最终收敛到稳定平衡点${E}_{0}$,回到A点完成一个周期的簇发振荡.由于系统轨迹是围绕平衡点和极限环${CY}_ +$周期振荡,因此该簇发振荡可以称为点-环簇发.

同样的,为了得到这组参数下的分岔延迟时间,文中选取一个周期的时间历程图,如图5(a)所示：

在其中的一个周期内$BP$点和$B$点所对应的时间分别为20~192.32 s和20~220.87 s,即分岔迟时间$\Delta T = 28.55~\mbox{s}$,可以看出当$A = 3.8$时,分岔延迟时间增加.

与上面类似,当文中取初始值为$(0,-0.1,0)$时系统的簇发振荡模式与初始值$(0,0.1,0)$对称,如图6所示.

图6

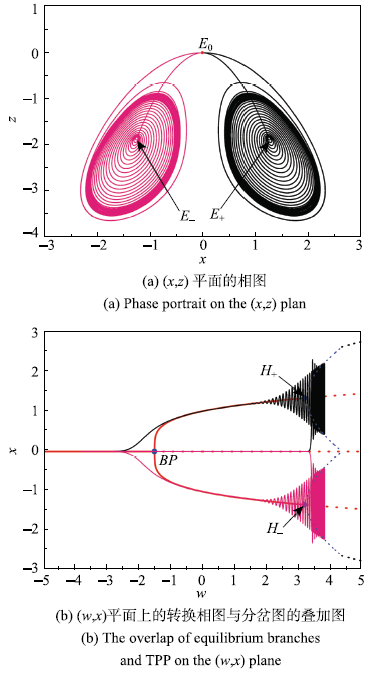新窗口打开|下载原图ZIP|生成PPT
图6初始值分别取$(0,0.1,0)$和$(0,-0.1,0)$的簇发振荡

Fig.6The bursting oscillations with different initial values of $(0,0.1,0)$ and $(0,-0.1,0)$

3.3 点-环-环簇发

当叉形分岔延迟终止于区域3时,其簇发振荡模式发生了明显的变化,在区域3中存在由${CY}_\pm$相碰产生更大的稳定极限环${CY}$,针对上述情况,将分为两种情况进行讨论.

3.3.1 非对称式点-环-环簇发

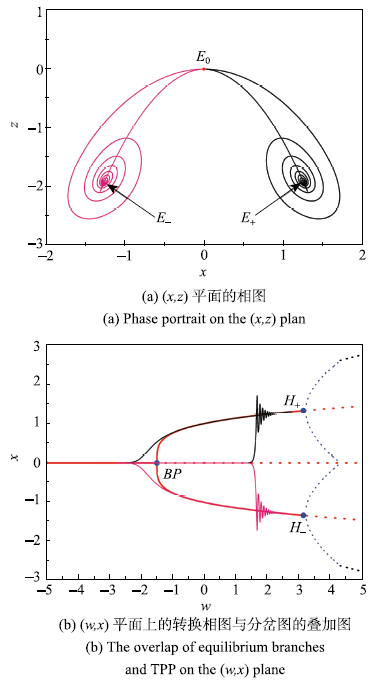
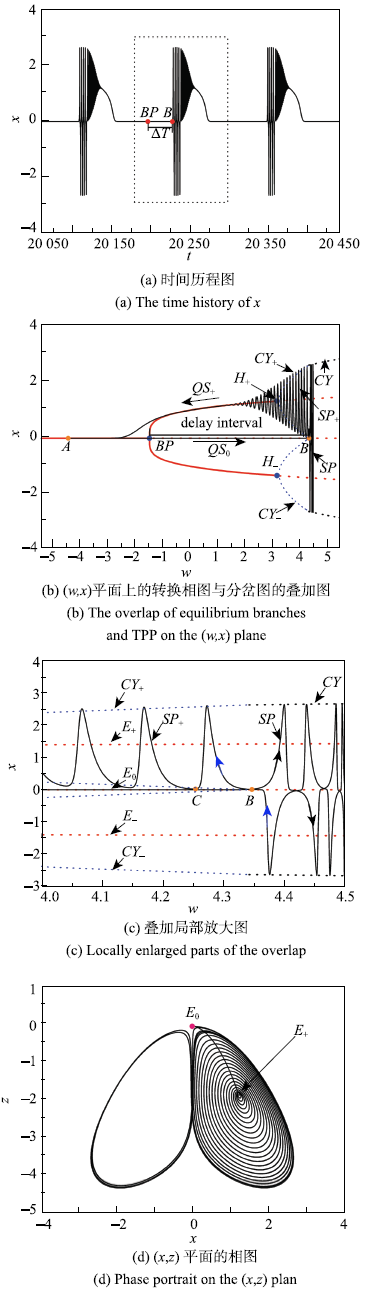
文中给出了在$A =4.5$的这组参数下的时间历程图,$(w\mbox{,}x)$平面上的转换相图与分岔图的叠加图,叠加图的局部放大以及$(x,z)$平面的相图,如图7所示.

图7

新窗口打开|下载原图ZIP|生成PPT
图7$A = 4.5$时的簇发振荡

Fig.7Bursting oscillations for $A = 4.5$



与上面类似,然而当延迟终止于$B$点(4.347,0)时(图7(b)),轨线受到${CY}$的吸引,振荡幅值迅速增大进入激发态$SP$并迅速趋于${CY}$,且随着w的增加(参见图7(c)),轨线将沿着${CY}$向右运动,当w到达最大值4.5时,随着时间的延长,w将逐渐减小,轨线沿着${CY}$向左运动,在C(4.254,0)点时,${CY}$消失,轨线已经进入${CY}_+$的吸引域,所以轨线逐渐趋于极限环${CY}_ +$,当w穿过Hopf分岔点时,极限环${CY}_ +$消失,轨线退出激发态并趋于稳定的平衡点${E}_ +$进入沉寂态$QS_{ +}$. 且随着w的减小并经过$BP$点时,${E}_ +$消失,轨线最终收敛到稳定平衡点${E}_{0}$,回到A点完成一个周期的簇发振荡.由于系统轨迹是围绕平衡点和极限环${CY}_ +$及${CY}$周期振荡,因此该簇发振荡称为非对称式点-环-环簇发.

下面计算当振幅$A = 4.5$时的分岔延迟时间,文中选取一个周期的时间历程图,如图7(a)所示：在其中的一个周期内$BP$点和$B$点所对应的时间分别为20~193.64 s和20~226.47 s,所以对应分岔延迟时间$\varDelta T=32.83$~s,可以看出当$A = 4.5$时,分岔延迟时间持续增加.

与上面类似,当文中取初始值为$(0,-0.1,0)$时系统的簇发振荡模式与取初始值$(0,0.1,0)$对称,如图8所示.

图8

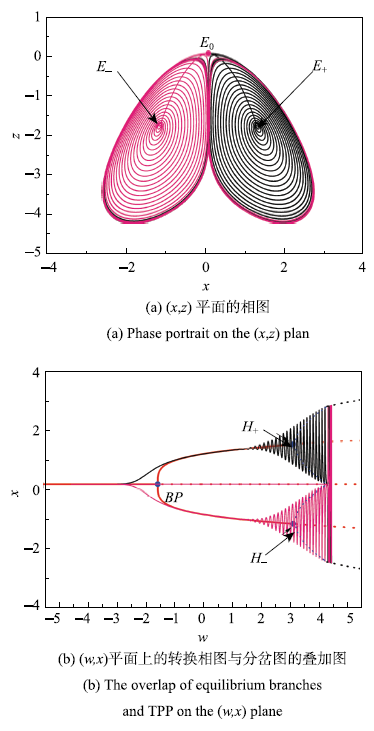新窗口打开|下载原图ZIP|生成PPT
图8初始值分别取$(0,0.1,0)$和$(0,-0.1,0)$的振荡

Fig.8The bursting oscillations with different initial values of$(0,0.1,0)$ and$(0,-0.1,0)$



3.3.2 对称式点-环-环簇发

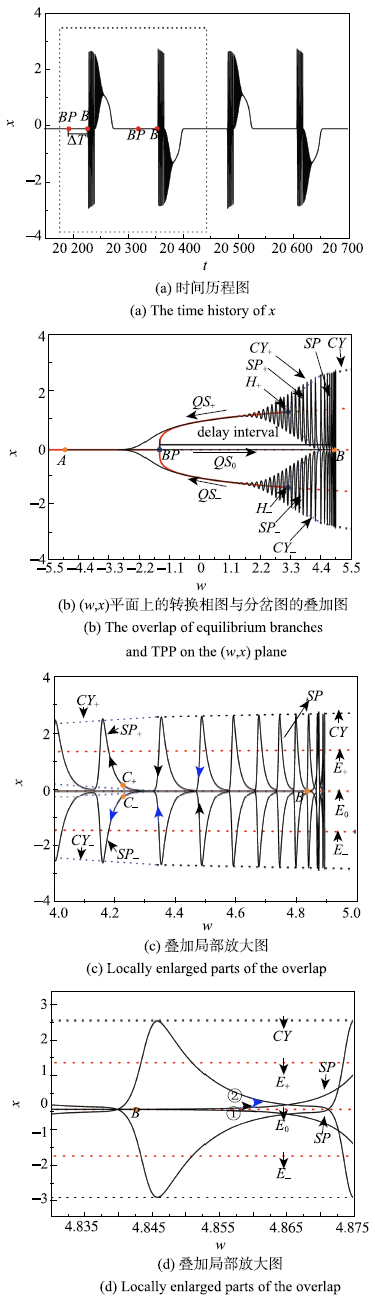
取定振幅$A = 4.9$时,虽然分岔延迟终止在区域3,但是其簇发振荡模式发生了明显地变化,图9给出了这组参数下的时间历程图,$(w\mbox{,}~x)$平面上的转换相图与分岔图的叠加图以及叠加局部放大图.

图9

新窗口打开|下载原图ZIP|生成PPT
图9${A} = 4.9$时的簇发振荡

Fig.9Bursting oscillations for$A = 4.9$



从图9(b)可以看出,假设轨线从A点出发,当分岔延迟终止于$B$点时,此时所对应w的值为4.842,由于受到稳定极限环${CY}$的吸引,轨线的振荡幅值迅速增大进入激发态$SP$,轨线首先向着${CY}$的下半部运动(参见9(d)),随着w的增大,轨线沿着整个极限环${CY}$运动(参见图9(c)),当w增大到最大值4.90时,随着时间的继续延长,w将逐渐减小,轨线沿着极限环${CY}$向左运动,当轨线运动到${C}_ +$(4.228,0.207)点后系统的极限环${CY}$消失,且轨线已经运动到${CY}_ +$的吸引域中,因此围绕着${CY}_ +$继续向左运动,从图9(b)可以看出,随着极限环的逐渐减小,振荡幅值也逐渐减小,直到轨线穿过Hopf点${H}_+$,极限环${CY}_ +$消失,轨线退出激发态逐渐收敛于稳定平衡点${E}_+$进入沉寂态$QS_{ + }$,且随着w的减小并经过$BP$点时,$E_ +$消失,轨线最终收敛到稳定平衡点${E}_0$,直到运动到A点,完成半个周期的簇发振荡.由于对称性,系统的下半个周期和上半个周期运动机理相同,直到再次回到A点,完成一个周期的簇发振荡.这里,在一个完整的簇发周期内,系统共经历了4个沉寂态和4个激发态,且系统轨迹是围绕平衡点和极限环${CY}_+$及${CY}$周期振荡,因此该簇发振荡称为对称式点-环-环簇发.

下面计算当振幅$A = 4.9$时的分岔延迟时间,文中选取一个周期的时间历程图,如图9(a)所示：在其中的一个周期内$BP$点和$B$点所对应的时间分别为20~194.21~s和20~228.02~s,所以分岔延迟时间$\Delta T = 33.81~\mbox{s}$,可以看出当$A = 4.9$时,分岔延迟时间继续延长.

4 结 论

在一个混沌系统中引入慢变周期激励,在一定的参数条件下,调节激励振幅A,系统产生了不同的簇发振荡.结合转换相图,通过对广义自治系统平衡点的分岔分析,发现广义自治系统产生了超临界叉形分岔,并且轨线经过超临界叉形分岔点时产生了明显的延迟现象.随着慢变激励振幅A的变化,延迟现象终止于不同的吸引域,系统轨线受到不同吸引域的影响,从而产生了点-点簇发,点-环簇发,点-环-环簇发等不同的动力学行为.而随着周期激励的振幅A增加,分岔延迟的时间也会持续增加,加之激励频率相同,导致激励项速度增加,使得转换相图上分岔延迟的情况也更加明显.

The authors have declared that no competing interests exist.

作者已声明无竞争性利益关系。

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] Li XH, Hou JY, Chen JF . An analytical method for Mathieu oscillator based on method of variation of parameter
Communications in Nonlinear Science & Numerical Simulation, 2016,37:326-353
DOIURL [本文引用: 1]
A simple, but very accurate analytical method for forced Mathieu oscillator is proposed, the idea of which is based on the method of variation of parameter. Assuming that the time-varying parameter in Mathieu oscillator is constant, one could easily obtain its accurately analytical solution. Then the approximately analytical solution for Mathieu oscillator could be established after substituting periodical time-varying parameter for the constant one in the obtained accurate analytical solution. In order to certify the correctness and precision of the proposed analytical method, the first-order and ninth-order approximation solutions by harmonic balance method (HBM) are also presented. The comparisons between the results by the proposed method with those by the numerical simulation and HBM verify that the results by the proposed analytical method agree very well with those by the numerical simulation. Moreover, the precision of the proposed new analytical method is not only higher than the approximation solution by first-order HBM, but also better than the approximation solution by the ninth-order HBM in large ranges of system parameters.

[2] Dai HH, Yue XK, Liu C . A multiple scale time domain collocation method for solving nonlinear dynamical system
International Journal of Nonlinear Mechanics, 2014,67:342-351
DOIURL
61We proposed a novel multiple scale time domain collocation (MSTDC) method to solve the Duffing equation.61The MSTDC method is simpler than the harmonic balance method.61The MSTDC method has a comparable accuracy as the harmonic balance method.61A multiple scale differential transformation method is also developed based on the multi-scaling technique.

[3] 张洪武, 张盛, 毕金英 . 周期性结构热动力时间-空间多尺度分析
力学学报, 2006,38(2):226-235
DOIURLMagsci
研究一种时间-空间多尺度渐近均匀化分析方法，模拟不同的极端热和动力载荷下微尺度多相周期性结构中热动力响应问题，并建立一个广义的波动函数场控制方程描述热动力响应.通过引入一个放大空间尺度和两个缩小时间尺度，在不同时间尺度上获得由空间非均匀性引起的波动效应和非局部效应. 根据高阶均匀化理论在空间和时间上进行均匀化，获得高阶非局部函数场波动方程. 并进一步用C0连续修正了高阶非局部函数场波动方程的有限元近似解，使问题的求解避免了对有限元离散的C1连续性要求. 并与经典的空间均匀化方法相比较，指出了经典的空间均匀化方法的局限性，进一步以一维非傅立叶热传导和热动力问题为例，讨论了各种情况下方法的正确性与有效性.
( Zhang Hongwu, Zhang Sheng, Bi Jinying . Thermodynamic analysis of multiphase periodic structures based on a spatial and temporal multiple scale method
Chinese Journal of Theoretical and Applied Mechanics, 2006,38(2):226-235 (in Chinese))
DOIURLMagsci
研究一种时间-空间多尺度渐近均匀化分析方法，模拟不同的极端热和动力载荷下微尺度多相周期性结构中热动力响应问题，并建立一个广义的波动函数场控制方程描述热动力响应.通过引入一个放大空间尺度和两个缩小时间尺度，在不同时间尺度上获得由空间非均匀性引起的波动效应和非局部效应. 根据高阶均匀化理论在空间和时间上进行均匀化，获得高阶非局部函数场波动方程. 并进一步用C0连续修正了高阶非局部函数场波动方程的有限元近似解，使问题的求解避免了对有限元离散的C1连续性要求. 并与经典的空间均匀化方法相比较，指出了经典的空间均匀化方法的局限性，进一步以一维非傅立叶热传导和热动力问题为例，讨论了各种情况下方法的正确性与有效性.

[4] Br?ns M, Kaasen R . Canards and mixed-mode oscillations in a forest pest model
Theoretical Population Biology, 2010,77(4):238-242
DOIURLPMID
We consider a three-variable forest pest model, proposed by Rinaldi & Muratori (1992) [Rinaldi, S., Muratori, S., 1992. Limit cycles in slow–fast forest–pest models. Theor. Popul. Biol. 41, 26–43]. The model allows relaxation oscillations where long pest-free periods are interspersed with outbreaks of high pest concentration. For small values of the timescale of the young trees, the model can be reduced to a two-dimensional model. By a geometrical analysis we identify a canard explosion in the reduced model, that is, a change over a narrow parameter interval from outbreak dynamics to small oscillations around an endemic state. For larger values of the timescale of the young trees the two-dimensional approximation breaks down, and a broader parameter interval with mixed-mode oscillations appear, replacing the simple canard explosion. The analysis only relies on simple and generic properties of the model, and is expected to be applicable in a larger class of multiple timescale dynamical models.

[5] 古华光 . 神经系统信息处理和异常功能的复杂动力学
力学学报, 2017,49(2):410-420
DOIURL [本文引用: 1]
神经系统通过电活动实现信息处理及生物功能,电活动的节律和时空行为是功能的动力学表征.神经电生理实验结合理论模型,借助于分岔揭示了外界激励、参数和噪声调控下的周期、混沌和随机等多样性的节律模式及其节律的复杂转迁规律,揭示了感觉神经对信息(如血压压力信号和痛觉信息)的节律编码机制,揭示了突触噪声扩大脑神经元的信息传递能力并对能力强弱进行了分类,结果可用于提高信息检测能力和指导镇痛;借助于单神经元节律的动力学——如分岔和簇放电节律的快慢动力学——解释了网络功能异常的时空行为,如药物调控脑皮层的螺旋波/癫痫和慢抑制耦合调控的运动网络的同步转迁/运动模式异常,结果给出了调控系统功能的途径;通过大数据分析获得自闭症患者的脑功能网络的时空行为特征——症状相关脑区的同步活动降低,给出了用于诊断的潜在指标.通过新实验发现、新建理论模型、新分析方法和新观点阐释,揭示了神经系统的复杂动力学,认识和解释了神经系统的信息处理机制和异常生物功能/疾病,具有重要科学意义和潜在应用价值.
( Gu Guaguang . Complex dynamics of the nervous system for information processing and abnormal functions
Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(2):410-420 (in Chinese))
DOIURL [本文引用: 1]
神经系统通过电活动实现信息处理及生物功能,电活动的节律和时空行为是功能的动力学表征.神经电生理实验结合理论模型,借助于分岔揭示了外界激励、参数和噪声调控下的周期、混沌和随机等多样性的节律模式及其节律的复杂转迁规律,揭示了感觉神经对信息(如血压压力信号和痛觉信息)的节律编码机制,揭示了突触噪声扩大脑神经元的信息传递能力并对能力强弱进行了分类,结果可用于提高信息检测能力和指导镇痛;借助于单神经元节律的动力学——如分岔和簇放电节律的快慢动力学——解释了网络功能异常的时空行为,如药物调控脑皮层的螺旋波/癫痫和慢抑制耦合调控的运动网络的同步转迁/运动模式异常,结果给出了调控系统功能的途径;通过大数据分析获得自闭症患者的脑功能网络的时空行为特征——症状相关脑区的同步活动降低,给出了用于诊断的潜在指标.通过新实验发现、新建理论模型、新分析方法和新观点阐释,揭示了神经系统的复杂动力学,认识和解释了神经系统的信息处理机制和异常生物功能/疾病,具有重要科学意义和潜在应用价值.

[6] Liu X, Huo B . Nonlinear vibration and multimodal interaction analysis of transmission line with thin ice accretions
International Journal of Applied Mechanics, 2015,7(1):1540007
DOIURL [本文引用: 1]
A study of multimodal galloping is carried out on an iced transmission line with thin ice accretions. The partial differential governing equations of iced transmission line are established to describe the nonlinear interactions between the in-plane, out-of-plane and torsional vibration, in which geometrical and aerodynamic nonlinearities are considered. The transformation of modal galloping with the continuous variations of parameters and modal interactions are analyzed based on the reduced model obtained by employing Galerkin spatial discretization. Eigenvalue analysis is applied on linear system to determine the switch of different modal galloping in plane U -l, where Hopf bifurcation occurs and mono-modal, bi-modal and multi-modal galloping are observed. Various numerical procedures are implemented to capture the outstanding nonlinear dynamic features of every regional galloping in plane U -l. Internal resonance is observed and investigated to interpret the phenomenon of modal transition which is also ...

[7] Li XH, Bi QS . Single-Hopf bursting in periodic perturbed Belousov-Zhab-otinsky reaction with two time scales
Chin. phys. lett, 2013,30(1):10503-10506
[本文引用: 1]

[8] 李向红, 毕勤胜 . 铂族金属氧化过程中的簇发振荡及其诱发机理
物理学报, 2012,61(2):88-96
DOIURL [本文引用: 1]
铂族金属表面氧化过程是典型的多相催化反应之一,具有广泛的应用背景及丰富的振荡行为,因此深入研究铂族金属的氧化中的物理及化学过程具有重要的理论意义及工程应用前景.通过对铂族金属CO的氧化过程中实测数据的回归分析,建立了不同尺度耦合解析动力学理论模型.通过对平衡态的稳定性分析,指出在一定条件下稳态解会由鞍-结同宿轨道分岔导致周期振荡.当快子系统产生Hopf分岔时,该周期振荡会进一步演化为两尺度耦合的周期簇发振荡,即N~k振荡,并由加周期分岔使得系统处于激发态的时间显著增加.在此基础上,利用分岔理论进一步分析了周期簇发及加周期分岔的产生机理,揭示了周期簇发中沉寂态和激发态相互转化时的不同分岔模式.
( Li Xianghong, Bi Qinsheng . Bursting oscillations and the bifurcation mechanism in oxidation on platinum group metals
Acta Phys Sin, 2012,61(2):88-96(in Chinese))
DOIURL [本文引用: 1]
铂族金属表面氧化过程是典型的多相催化反应之一,具有广泛的应用背景及丰富的振荡行为,因此深入研究铂族金属的氧化中的物理及化学过程具有重要的理论意义及工程应用前景.通过对铂族金属CO的氧化过程中实测数据的回归分析,建立了不同尺度耦合解析动力学理论模型.通过对平衡态的稳定性分析,指出在一定条件下稳态解会由鞍-结同宿轨道分岔导致周期振荡.当快子系统产生Hopf分岔时,该周期振荡会进一步演化为两尺度耦合的周期簇发振荡,即N~k振荡,并由加周期分岔使得系统处于激发态的时间显著增加.在此基础上,利用分岔理论进一步分析了周期簇发及加周期分岔的产生机理,揭示了周期簇发中沉寂态和激发态相互转化时的不同分岔模式.

[9] Courbage M, Nekorkin VI, Vdovin LV . Chaotic oscillations in a map-based model of neural activity
Chaos, 2007,17(4):043109
DOIURLPMID [本文引用: 1]
We propose a discrete time dynamical system (a map) as phenomenological model of excitable and spiking-bursting neurons. The model is a discontinuous two-dimensional map. We find condition under which this map has an invariant region on the phase plane, containing chaotic attractor. This attractor creates chaotic spiking-bursting oscillations of the model. We also show various regimes of other neural activities (subthreshold oscillations, phasic spiking etc.) derived from the proposed model.

[10] Izhikevich EM . Resonance and selective communication via bursts in neurons having subthreshold oscillations
Bio Systems, 2002,67(1-3):95-102
DOIURLPMID [本文引用: 1]
Revealing the role of bursts of action potentials is an important step toward understanding how the neurons communicate. The dominant point of view is that bursts are needed to increase the reliability of communication between neurons [Trends Neurosci. 20 (1997) 38]. In this paper we present an alternative but complementary hypothesis. We consider the effect of a short burst on a model postsynaptic cell having damped oscillation of its membrane potential. The oscillation frequency (eigenfrequency) plays a crucial role. Due to the subthreshold membrane resonance and frequency preference, the responses (i.e. voltage oscillations) of such a cell are amplified when the intra-burst frequency equals the cell's eigenfrequency. Responses are negligible, however, if the intra-burst frequency is twice the eigenfrequency. Thus, the same burst could be effective for one cell and ineffective for another depending on their eigenfrequencies. This theoretical observation suggests that, in addition to coping with unreliable synapses, bursts of action potentials may provide effective mechanisms for selective communication between neurons.

[11] Ferrari FAS, Viana RL, Lopes SR , et al. Phase synchronization of coupled bursting neurons and the generalized Kuramoto model
Neural Networks , 2015,66:107-118
DOIURLPMID [本文引用: 1]
Bursting neurons fire rapid sequences of action potential spikes followed by a quiescent period. The basic dynamical mechanism of bursting is the slow currents that modulate a fast spiking activity caused by rapid ionic currents. Minimal models of bursting neurons must include both effects. We considered one of these models and its relation with a generalized Kuramoto model, thanks to the definition of a geometrical phase for bursting and a corresponding frequency. We considered neuronal networks with different connection topologies and investigated the transition from a non-synchronized to a partially phase-synchronized state as the coupling strength is varied. The numerically determined critical coupling strength value for this transition to occur is compared with theoretical results valid for the generalized Kuramoto model.

[12] Bi QS . The mechanism of bursting phenomena in BZ chemical reaction with multiple time scales
Science in China, 2012,10:2820-2830
DOIURL [本文引用: 1]
The dynamics of a typical Belousov-Zhabotinsky (BZ) reaction with multiple time scales is investigated in this paper. Different forms of periodic bursting phenomena, and specially, three types of chaotic bursters with different structures can be obtained, which are in common with the behaviors observed in experiments. The bifurcations connecting the quiescent state and the repetitive spikes are presented to account for the occurrence of the NK oscillations as well as the different forms of chaotic bursters. The mechanism of the period-adding bifurcation sequences is explored to reveal why the length of the periods in the sequences does not change continuously with the continuous variation of the parameters.

[13] 陈章耀, 张晓芳, 毕勤胜 . 周期激励下Hartley模型的簇发及分岔机
力学学报, 2010,42(4):765-773
DOIURLMagsci [本文引用: 1]
通过在Hartley电路模型中引入周期变化的电流源, 选取适当的参数, 使得周期激励的频率与系统的固有频率之间存在量级上的差距, 从而建立了具有快慢效应的非线性电路. 引入广义自治系统的概念, 分析了其相应的平衡点及各种分岔行为, 给出了不同参数下广义自治系统存在fold分岔以及同时存在fold分岔与Hopf分岔下的两种不同的簇发现象, 即fold/fold簇发现象和fold/subHopf/supHopf簇发现象. 利用广义自治系统的分岔分析方法和转换相图, 揭示了不同簇发现象的产生机制.
( Chen Zhangyao, Zhang Xiaofang, Bi Qinsheng . Bursting phenomena as well as the bifurcation mechanism in periodically excited Hartley model
Chinese Journal of Theoretical and Applied Mechanics, 2010,42(4):765-773(in Chinese))
DOIURLMagsci [本文引用: 1]
通过在Hartley电路模型中引入周期变化的电流源, 选取适当的参数, 使得周期激励的频率与系统的固有频率之间存在量级上的差距, 从而建立了具有快慢效应的非线性电路. 引入广义自治系统的概念, 分析了其相应的平衡点及各种分岔行为, 给出了不同参数下广义自治系统存在fold分岔以及同时存在fold分岔与Hopf分岔下的两种不同的簇发现象, 即fold/fold簇发现象和fold/subHopf/supHopf簇发现象. 利用广义自治系统的分岔分析方法和转换相图, 揭示了不同簇发现象的产生机制.

[14] Farazmand M, Sapsis T . Dynamical indicators for the prediction of bursting phenomena in high-dimensional systems
Physical Review E, 2016,94(3):032212
DOIURL [本文引用: 1]
Drawing upon the bursting mechanism in slow-fast systems, we propose indicators for the prediction of such rare extreme events which do not require a priori known slow and fast coordinates. The indicators are associated with functionals defined in terms of Optimally Time Dependent (OTD) modes. One such functional has the form of the largest eigenvalue of the symmetric part of the linearized dynamics reduced to these modes. In contrast to other choices of subspaces, the proposed modes are flow invariant and therefore a projection onto them is dynamically meaningful. We illustrate the application of these indicators on three examples: a prototype low-dimensional model, a body forced turbulent fluid flow, and a unidirectional model of nonlinear water waves. We use Bayesian statistics to quantify the predictive power of the proposed indicators.Farazmand, Mohammad; Sapsis, Themistoklis

[15] Wu H, Bao BC, Liu Z , et al. Chaotic and periodic bursting phenomena in a memristive Wien-bridge oscillator
Nonlinear Dynamics, 2016,83(1-2):893-903
DOIURL [本文引用: 1]
Abstract Bursting, an important communication activity in biological neurons and endocrine cells, has been widely found in fast-slow dynamical systems. In this paper, a modified second-order generalized memristor, memristive diode bridge cascaded with LC network, is presented and its fingerprints of the pinched hysteresis loops are analyzed. By replacing the parallel resistor with the modified generalized memristor, a novel memristive Wien-bridge oscillator is constructed and its mathematical model is established, from which the dynamical behaviors of symmetric chaotic and periodic bursting oscillations are observed and the corresponding bifurcation mechanisms are explained. Based on a hardware realization circuit, experimental observations are performed, which verify the numerical simulations.

[16] Fujimoto K, Kaneko K . How fast elements can affect slow dynamics
Physica D , 2003,180(1):1-16
DOIURL [本文引用: 1]
A chain of coupled chaotic elements with different time scales is studied. In contrast with the adiabatic approximation, we find that correlations between elements are transferred from faster to slower elements when the differences in the time scales of the elements lie within a certain range. For such correlations to occur, three features are essential: strong correlations among the elements, a bifurcation in the dynamics of the fastest element by changing its control parameter, and cascade propagation of the bifurcation. By studying coupled R ssler equations, we demonstrate that fast elements can affect the dynamics of slow elements when these conditions are satisfied. The relevance of our results to biological memory is briefly discussed.

[17] Egghea L, Rousseaub R . Lorenz theory of symmetric relative concentration and similarity, incorporating variable array length
Mathematical & Computer Modelling, 2006,44(7):628-639
DOIURL [本文引用: 1]
This paper extends the Lorenz theory, developed in [L. Egghe, R. Rousseau, Symmetric and asymmetric theory of relative concentration and applications, Scientometrics 52 (2) (2001) 261 290], so that it can deal with comparing arrays of variable length. We show that in this case we need to divide the Lorenz curves by certain types of increasing functions of the array length N. We then prove that, in this theory, adding zeros to two arrays increases their similarity, a property that is not satisfied by the Pearson correlation coefficient. Among the many good similarity measures satisfying the developed Lorenz theory, we deduce the correlation coefficient of Spearman, hence showing that this measure can be used as a good measure of symmetric relative concentration (or similarity).

[18] Stork W . Subharmonic response and synchronisation for the forced van der Pol equation via Cesari's method
Journal of Mathematical Analysis & Applications, 1984,102(1):134-148
DOIURL [本文引用: 1]

[19] Izhikevich EM . Neural excitability, spiking and bursting
International Journal of Bifurcation and Chaos, 2000,10(6):1171-1266
[本文引用: 1]

[20] Bi QS, Li SL, Kurths J , et al. The mechanism of bursting oscillations with different codimensional bifurcations and nonlinear structures
Nonlinear Dynamics, 2016,85(2):1-13
DOIURL [本文引用: 1]
Abstract The main purpose of this article is to demonstrate that bursting oscillations can be observed not only in the slow ast autonomous dynamical systems with multiple scales associated with time domain, but also in the non-autonomous dynamical systems with periodic excitations when an order gap exists between the exciting frequency and the natural frequency, implying multiple scales in frequency domain. Furthermore, we try to investigate the influence of different codimensional bifurcations between the quiescent states (QS) and repetitive spiking states (SP) and the nonlinear structures with different equilibrium branches on the bursting oscillations. By introducing an inductor as well as a periodically changed electrical current source in a traditional Chua circuit and taking suitable parameter values, a modified four-dimensional periodically excited oscillator with multiple scales in frequency domain is established. Bursting oscillations for two cases with nonlinear terms up to third and fifth order with codimension-1 and codimension-2 bifurcations have been explored, respectively. It is found that more equilibrium states may exist when higher order nonlinear terms are introduced in the vector field, which may cause multiple quiescent states, and accordingly, multiple forms of repetitive spiking oscillations in one bursting attractor, leading to more complicated bursting phenomena. Furthermore, instead of jumping from one stable equilibrium branch to settle down to another stable equilibrium branch when codimension-1 bifurcations (fold bifurcations) exist between QSs and SPs, codimension-2 bifurcation (fold-Hopf bifurcation) may cause QS approximately located on one stable equilibrium branch to jump to repetitive spiking oscillations surrounding another stable equilibrium branch of the generalized autonomous system.

[21] Han XJ, Bi QS, Ji P , et al. Fast-slow analysis for parametrically and externally excited systems with two slow rationally related excitation frequencies
Physical Review E, 2015,92(1):012911
DOIURLPMID
We present a general method for analyzing mixed-mode oscillations (MMOs) in parametrically and externally excited systems with two low excitation frequencies (PEESTLEFs) for the case of arbitrary m:n relation between the slow frequencies of excitations. The validity of the approach has been demonstrated using the equations of Duffing and van der Pol, separately. Our study shows that, by introducing a slow variable and finding the relation between the slow variable and the slow excitations, PEESTLEFs can be transformed into a fast-slow form with a single slow variable and therefore MMOs observed in PEESTLEFs can be understood by the classical machinery of fast subsystem analysis of the transformed fast-slow system.

[22] Yu Y, Tang HJ, Han XJ , et al. Bursting mechanism in a time-delayed oscillator with slowly varying external forcing
Communications in Nonlinear Science & Numerical Simulation, 2014,19(4):1175-1184
DOIURL
This paper investigates the generation of complex bursting patterns in the Duffing oscillator with time-delayed feedback. We present the bursting patterns, including symmetric fold–fold bursting and symmetric Hopf–Hopf bursting when periodic forcing changes slowly. We make an analysis of the system bifurcations and dynamics as a function of the delayed feedback and the periodic forcing. We calculate the conditions of fold bifurcation and Hopf bifurcation as well as its stability related to external forcing and delay. We also identify two regimes of bursting depending on the magnitude of the delay itself and the strength of time delayed coupling in the model. Our results show that the dynamics of bursters in delayed system are quite different from those in systems without any delay. In particular, delay can be used as a tuning parameter to modulate dynamics of bursting corresponding to the different type. Furthermore, we use transformed phase space analysis to explore the evolution details of the delayed bursting behavior. Also some numerical simulations are included to illustrate the validity of our study.

[23] 张晓芳, 陈小可, 毕勤胜 . 快慢耦合振子的张驰簇发及其非光滑分岔机制
力学学报, 2012,44(3):576-583
DOIURL [本文引用: 1]
通过引入适当的参数值,得到了两时间尺度下的快慢耦合振子,分析了耦合系统及子系统的平衡点及其性质,进而利用微分包含理论,探讨了非光滑分界面上的奇异性,指出在适当的参数条件下,系统轨迹在穿越分界面时会产生由Hopf分岔和Fold分岔组合的非常规分岔.给出了不同参数条件下的周期簇发行为,分析了簇发过程的振荡特性,指出激发态的频率取决于快子系统在非光滑分界面上的Hopf分岔频率,而慢子系统的固有频率影响了簇发行为的振荡周期,并进一步揭示了由非光滑分岔引起的不同周期簇发的分岔机制.
( Zhang Xiaofang, Chen Xiaoke, Bi Qinsheng . Relaxation bursting of a fast-slow coupled oscillation as well as the mechanism of non-smooth bifurcation
Chinese Journal of Theoretical and Applied Mechanics, 2012,44(3):576-583(in Chinese))
DOIURL [本文引用: 1]
通过引入适当的参数值,得到了两时间尺度下的快慢耦合振子,分析了耦合系统及子系统的平衡点及其性质,进而利用微分包含理论,探讨了非光滑分界面上的奇异性,指出在适当的参数条件下,系统轨迹在穿越分界面时会产生由Hopf分岔和Fold分岔组合的非常规分岔.给出了不同参数条件下的周期簇发行为,分析了簇发过程的振荡特性,指出激发态的频率取决于快子系统在非光滑分界面上的Hopf分岔频率,而慢子系统的固有频率影响了簇发行为的振荡周期,并进一步揭示了由非光滑分岔引起的不同周期簇发的分岔机制.

[24] Freire JG, Gallas JAC . Stern-Brocot trees in cascades of mixed-mode oscillations and canards in the extended Bonhoeffer-van der Pol and the FitzHugh-Nagumo models of excitable systems
Phys Lett A, 2011,375(7):1097-1103
[本文引用: 1]

[25] Chumakov GA, Chumakova NA . Relaxation oscillations in a kinetic model of catalytic hydrogen oxidation involving a chase on canards
Chemical Engineering Journal, 2003,91(2):151-158
DOIURL [本文引用: 1]
A detailed study of two- and three-variable mathematical models of a heterogeneous catalytic system is presented with special attention to weakly stable dynamics, a type of complex irregular behavior frequently encountered in oscillating chemical reactions. One of the most important properties of the weakly stable dynamics is “a sensitive dependence on the initial conditions”. Our analysis of a global error in long-term numerical integration shows that a high sensitive dependence on the initial conditions appears in the three-variable system with fast, intermediate and slow variables due to existence of the canard cycles which occur close to Hopf bifurcation in the one-parameter family of two-variable subsystems.

[26] 韩修静, 江波, 毕勤胜 . 快慢型超混沌Lorenz系统分析
物理学报, 2009,58(9):6006-6015
DOIURLMagsci [本文引用: 1]
讨论了快慢两时间尺度下超混沌Lorenz系统原点的稳定性问题，分析了原点的Hopf分岔，包括Hopf分岔的存在性，分岔方向以及分岔周期解的稳定性等问题，并用数值例子对所得到的结果加以验证.在一定的参数条件下，快慢系统会产生对称簇发并能达到超混沌状态.基于快慢分析法，揭示了对称簇发中沉寂态与激发态相互转迁的不同分岔模式，并进一步分析了耦合强度对慢过效应的影响.
( Han Xiujing, Jiang Bo, Bi Qinsheng . Analysis of the fast-slow hyperchaotic Lorenz system
Acta Phys Sin, 2009,58(9):6006-6015(in Chinese))
DOIURLMagsci [本文引用: 1]
讨论了快慢两时间尺度下超混沌Lorenz系统原点的稳定性问题，分析了原点的Hopf分岔，包括Hopf分岔的存在性，分岔方向以及分岔周期解的稳定性等问题，并用数值例子对所得到的结果加以验证.在一定的参数条件下，快慢系统会产生对称簇发并能达到超混沌状态.基于快慢分析法，揭示了对称簇发中沉寂态与激发态相互转迁的不同分岔模式，并进一步分析了耦合强度对慢过效应的影响.

[27] Hou JY, Li XH, Zuo DW , et al. Bursting and delay behavior in the Belousov-Zhabotinsky reaction with external excitation
European Physical Journal Plus, 2017,132(6):283
DOIURL [本文引用: 1]
The dynamics of a typical Belousov-Zhabotinsky (BZ) reaction with two time scales and low perturbation frequency is investigated in this paper. For specific parameters, the typical phenomenon called as double-Hopf bursting is observed, and the corresponding generation mechanism is presented based on the slow-fast dynamical analysis method. With the decrease of the amplitude of external excitation, the double-Hopf bursting evolves into a single-Hopf one. Furthermore, periodic bifurcation delay behaviors are found when the time-varying parameter slowly passes through the critical point of Hopf bifurcation, which results into spiking state (SP) delay behaviors. The detailed delay phenomena as well as their mechanisms are exhibited by theoretical analysis and numerical simulation.

[28] Baer SM, Erneux T, Rinzel J . The slow passage through a Hopf bifurcation: Delay, memory effects, and resonance
Siam Journal on Applied Mathematics, 1989,49(1):55-71
DOIURL
This paper explores analytically and numerically, in the context of the FitzHugh-Nagumo model of nerve membrane excitability, an interesting phenomenon that has been described as a delay or memory effect. It can occur when a parameter passes slowly through a Hopf bifurcation point and the system's response changes from a slowly varying steady state to slowly varying oscillations. On quantitative observation it is found that the transition is realized when the parameter is considerably beyond the value predicted from a straightforward bifurcation analysis which neglects the dynamic aspect of the parameter variation. This delay and its dependence on the speed of the parameter variation are described. The model involves several parameters and particular singular limits are investigated. One in particular is the slow passage through a low frequency Hopf bifurcation where the system's response changes from a slowly varying steady state to slowly varying relaxation oscillations. We find in this case the onset of oscillations exhibits an advance rather than a delay. This paper shows that in general delays in the onset of oscillations may be expected but that small amplitude noise and periodic environmental perturbations of near resonant frequency may decrease the delay and destroy the memory effect. This paper suggests that both deterministic and stochastic approaches will be important for comparing theoretical and experimental results in systems where slow passage through a Hopf bifurcation is the underlying mechanism for the onset of oscillations.

[29] Hao LJ, Yang ZQ, Lei JZ . Bifurcation analysis of a delay differential equation model associated with the induction of long-term memory
Chaos Solitons & Fractals, 2015,81:162-171
DOIURL
The ability to form long-term memories is an important function for the nervous system, and the formation process is dynamically regulated through various transcription factors, including CREB proteins. In this paper, we investigate the dynamics of a delay differential equation model for CREB protein activities, which involves two positive and two negative feedbacks in the regulatory network. We discuss the dynamical mechanisms underlying the induction of long-term memory, in which bistability is essential for the formation of long-term memory, while long time delay can destabilize the high level steady state to inhibit the long-term memory formation. The model displays rich dynamical response to stimuli, including monostability, bistability, and oscillations, and can transit between different states by varying the negative feedback strength. Introduction of a time delay to the model can generate various bifurcations such as Hopf bifurcation, fold limit cycle bifurcation, Neimark acker bifurcation of cycles, and period-doubling bifurcation,etc.Increasing the time delay can induce chaos by two routes: quasi-periodic route and period-doubling cascade.

[30] Mahmoud GM, Arafa AA, Mahmoud EE . Bifurcations and chaos of time delay Lorenz system with dimension 2$n$+1
European Physical Journal Plus, 2017,132(1):461
DOIURL
The aim of this paper is to introduce a generalized form of the Lorenz system with time delay. Instead of considering each state variable of the Lorenz system belonging to \(\mathbb{R}\) , the paper considers two of them belonging to \(\mathbb{R}^{n}\) . Hence the Lorenz system has (2 n +1) dimension. This system appears in several applied sciences such as engineering, physics and networks. The stability of the trivial and nontrivial fixed points and the existence of Hopf bifurcations are studied analytically. Using the normal form theory and center manifold argument, the direction and the stability of the bifurcating periodic solutions are determined. Finally, numerical simulations are calculated to confirm our theoretical results. The paper concludes that the dynamics of this system are rich. Additionally, the values of the delay parameter at which chaotic and hyperchaotic solutions exist for different values of n using Lyapunov exponents and Kolmogorov-Sinai entropy are calculated numerically.

[31] 陈振阳, 韩修静, 毕勤胜 . 一类二维非自治离散系统中的复杂簇发振荡结构
力学学报, 2017,49(1):165-174
DOIURLMagsci [本文引用: 1]
<p>簇发振荡是多时间尺度系统复杂动力学行为的典型代表，簇发振荡的动力学机制与分类问题是簇发研究的重要问题之一，但当前****们所揭示的簇发振荡的结构大多较为简单.研究以非自治离散Duffing系统为例，探讨具有复杂分岔结构的新型簇发振荡模式，并将其分为两大类，一类经由Fold分岔所诱发的对称式簇发，另一类经由延迟倍周期分岔所诱发的非对称式簇发.快子系统的分岔表现为典型的含有两个Fold分岔点的S形不动点曲线，其上、下稳定支可经由倍周期（即Flip）分岔通向混沌.当非自治项（即慢变量）穿越Fold分岔点时，系统的轨线可以向上、下稳定支的各种吸引子（例如，周期轨道和混沌）进行转迁，因此得到了经由Fold分岔所诱发的各种对称式簇发；而当非自治项无法穿越Fold分岔点，但可以穿越Flip分岔点时，系统产生了延迟Flip分岔现象.基于此，得到了经由延迟Flip分岔所诱发的各种非对称簇发.特别地，文中所报道的簇发振荡模式展现出复杂的反向Flip分岔结构.研究结果表明，这与非自治项缓慢地反向穿越快子系统的Flip分岔点有关.研究结果丰富了离散系统簇发的动力学机理和分类.</p>
( Chen Zhenyang, Han Xiujing, Bi Qinsheng . Complex bursting oscillation structures in a two-dimensional non-autonomous discrete system
Chinese Journal of Theoretical and Applied Mechanics, 2017,49(1):165-174(in Chinese))
DOIURLMagsci [本文引用: 1]
<p>簇发振荡是多时间尺度系统复杂动力学行为的典型代表，簇发振荡的动力学机制与分类问题是簇发研究的重要问题之一，但当前****们所揭示的簇发振荡的结构大多较为简单.研究以非自治离散Duffing系统为例，探讨具有复杂分岔结构的新型簇发振荡模式，并将其分为两大类，一类经由Fold分岔所诱发的对称式簇发，另一类经由延迟倍周期分岔所诱发的非对称式簇发.快子系统的分岔表现为典型的含有两个Fold分岔点的S形不动点曲线，其上、下稳定支可经由倍周期（即Flip）分岔通向混沌.当非自治项（即慢变量）穿越Fold分岔点时，系统的轨线可以向上、下稳定支的各种吸引子（例如，周期轨道和混沌）进行转迁，因此得到了经由Fold分岔所诱发的各种对称式簇发；而当非自治项无法穿越Fold分岔点，但可以穿越Flip分岔点时，系统产生了延迟Flip分岔现象.基于此，得到了经由延迟Flip分岔所诱发的各种非对称簇发.特别地，文中所报道的簇发振荡模式展现出复杂的反向Flip分岔结构.研究结果表明，这与非自治项缓慢地反向穿越快子系统的Flip分岔点有关.研究结果丰富了离散系统簇发的动力学机理和分类.</p>

[32] Maree GJM . Slow passage through a pitchfork bifurcation
SIAM Journal on Applied Mathematics, 1996,56(3):889-918
DOIURL [本文引用: 1]
This paper deals with a class of second-order differential equations with a slowly varying bifurcation parameter. The parameter slowly varies through a critical value corresponding to a transition from a stable equilibrium to one of the two stable branches of an intersecting parabolic curve. The local transition behavior is described by the second Painleve transcendent. In this study we predict which branch will be followed after passage of the bifurcation point given the initial state. For that purpose, use is made of averaging methods and of asymptotic matching techniques connecting local solutions valid before, during, and after the transition.

[33] Premraj D, Suresh K, Banerjee T , et al. An experimental study of slow passage through Hopf and pitchfork bifurcations in a parametrically driven nonlinear oscillator
Communications in Nonlinear Science & Numerical Simulation, 2016,37:212-221
DOIURL [本文引用: 1]
Understanding the effect of slowly varying control parameters in dynamical systems is important in many fields such as mechanics, biology, ecology and social sciences, where normally changes in parameters take place very slowly. When a control parameter becomes time varying, the system dynamics exhibits a delay in bifurcation, i.e., the system responds to the bifurcation scenario with a lag in real time. In this paper, we experimentally explore the delay associated with Hopf and pitchfork bifurcations in a parametrically driven nonlinear oscillator. For this study we choose a generic nonlinear oscillator, namely the parametrically driven Murali akshmanan hua (PDMLC) oscillator. We identify and characterize the occurrence of delay in bifurcations in both the rising and falling edges of the external force and measure the delay associated with these bifurcations in both the edges. We show that the delay in Hopf and pitchfork bifurcations increase when the rate of change of control parameter decreases. We further show that the delay obeys a power law as a function of the external frequency. All the numerical simulation results are corroborated with the real-time electronic circuit experiment and we find a good qualitative agreement between the numerical and experimental results.

[34] Yu Y, Han XJ, Zhang C , et al. Mixed-mode oscillations in a nonlinear time delay oscillator with time varying parameters
Communications in Nonlinear Science & Numerical Simulation, 2017,47:23-34
DOIURL [本文引用: 1]
In this study, the mechanism for the action of time-invariant delay on a non-autonomous system with slow parametric excitation is investigated. The complex mix-mode oscillations (MMOs) are presented when the parametric excitation item slowly passes through critical bifurcation values of this nonlinear time delay oscillator. We use bifurcation theory to clarify certain generation mechanism related to three complex spiking formations, i.e., “symmetric sup-pitchfork bifurcation”, “symmetric sup-pitchfork/sup-Hopf bifurcation”, and “symmetric sup-pitchfork/sup-Hopf/homoclinic orbit bifurcation”. Such bifurcation behaviors result in various hysteresis loops between the spiking attractor and the quasi-stationary process, which are responsible for the generation of MMOs. We further identify that the occurrence and evolution of such complex MMOs depend on the magnitude of the delay. Specifically, with the increase of time delay, the two limit cycles bifurcated from Hopf bifurcations may merge into an enlarged cycle, which is caused by a saddle homoclinic orbit bifurcation. We can conclude that time delay plays a vital role in the generation of MMOs. Our findings enrich the routes to spiking process and deepen the understanding of MMOs in time delay systems.

[35] 陈章耀, 王亚茗, 张春 等. 双状态切换下 BVP振子的复杂行为分析
力学学报, 2016,48(4):953-962
DOIURLMagsci [本文引用: 1]
<p>非线性切换系统具有广泛的工程背景，而传统的非线性理论不能直接用来解决其中的问题，因而成为当前国内外热点和前沿课题之一. 目前相关工作大都是围绕固定时间或单状态切换开展的，而实际工程系统大都属于多状态切换问题，同时多状态切换涉及到更为丰富的动力学行为. 本文基于两广义BVP 振子，通过引入双向切换开关，构建了双状态切换下的非线性动力学模型，进而研究状态切换导致的各种运动模式及其相应的产生机制. 应用非光滑系统的Poincar&eacute;映射理论，推导了双状态切换下的Lyapunov 指数的计算公式，结合子系统的分岔分析，得到了切换系统随分岔参数变化的动力学演化过程及其相应的最大Lyapunov 指数的变化情况. 得到了双状态切换条件下系统存在着各种形式的振荡行为，分析了诸如周期突变等现象及通往混沌的倍周期分岔道路，揭示了不同运动模式的产生机制及倍周期序列的本质. 与固定时间切换和单状态切换系统不同，双临界状态切换系统存在着更为丰富的非线性现象，其主要原因在于双状态切换会产生更多的切换点，且切换点的位置更加多变. 同时切换系统的倍周期分岔序列与光滑系统中的倍周期分岔序列不同，切换系统的倍周期分岔序列只对应于切换点数目的成倍增加，而其相应的周期一般不对应于严格的周期倍化过程.</p>
( Chen Zhangyao, Wang Yaming, Zhang Chun , et al. Complicated behaviors as well as the mechanism in BVP oscillator with switches related to two states
Chinese Journal of Theoretical and Applied Mechanics, 2016,48(4):953-962(in Chinese))
DOIURLMagsci [本文引用: 1]
<p>非线性切换系统具有广泛的工程背景，而传统的非线性理论不能直接用来解决其中的问题，因而成为当前国内外热点和前沿课题之一. 目前相关工作大都是围绕固定时间或单状态切换开展的，而实际工程系统大都属于多状态切换问题，同时多状态切换涉及到更为丰富的动力学行为. 本文基于两广义BVP 振子，通过引入双向切换开关，构建了双状态切换下的非线性动力学模型，进而研究状态切换导致的各种运动模式及其相应的产生机制. 应用非光滑系统的Poincar&eacute;映射理论，推导了双状态切换下的Lyapunov 指数的计算公式，结合子系统的分岔分析，得到了切换系统随分岔参数变化的动力学演化过程及其相应的最大Lyapunov 指数的变化情况. 得到了双状态切换条件下系统存在着各种形式的振荡行为，分析了诸如周期突变等现象及通往混沌的倍周期分岔道路，揭示了不同运动模式的产生机制及倍周期序列的本质. 与固定时间切换和单状态切换系统不同，双临界状态切换系统存在着更为丰富的非线性现象，其主要原因在于双状态切换会产生更多的切换点，且切换点的位置更加多变. 同时切换系统的倍周期分岔序列与光滑系统中的倍周期分岔序列不同，切换系统的倍周期分岔序列只对应于切换点数目的成倍增加，而其相应的周期一般不对应于严格的周期倍化过程.</p>

[36] Abooee A, Yaghini-Bonabi HA, Jahed-Motlagh MR . Analysis and circuitry realization of a novel three-dimensional chaotic system
Communications in Nonlinear Science & Numerical Simulation, 2013,18(5):1235-1245
DOIURL [本文引用: 1]
In this paper a new three-dimensional chaotic system is introduced. Some basic dynamical properties are analyzed to show chaotic behavior of the presented system. These properties are covered by dissipation of system, instability of equilibria, strange attractor, Lyapunov exponents, fractal dimension and sensitivity to initial conditions. Through altering one of the system parameters, various dynamical behaviors are observed which included chaos, periodic and convergence to an equilibrium point. Eventually, an analog circuit is designed and implemented experimentally to realize the chaotic system.