基于指数准则在莫尔空间对岩石剪切强度的研究

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-01

尤明庆¹⁾河南理工大学能源科学与工程学院,河南焦作 454010

STUDY ON SHEAR STRENGTH OF ROCKS USING THE EXPONENTIAL CRITERION IN MOHR'S STRESS SPACE

You Mingqing¹⁾School of Energy Science and Engineering, Henan Polytechnic University, Jiaozuo 454010, Henan, China

收稿日期:2018-09-5接受日期:2018-12-18网络出版日期:2019-03-18

Received:2018-09-5Accepted:2018-12-18Online:2019-03-18
作者简介 About authors
1)尤明庆,教授,主要研究方向：岩石的力学性质及强度准则.E-mail:youmq@hpu.edu.cn

摘要
岩石是多种矿物颗粒构成的天然材料,内部存在不同尺度的孔隙、裂隙等损伤;岩体工程设计及灾害防治所使用的强度准则仍在研究之中.材料的黏结和摩擦在局部不能同时存在,线性的Coulomb准则仅在小范围内近似描述圆柱试样的常规三轴强度,众多非线性强度准则只是经验公式而缺乏物理背景. 作者提出的指数准则可描述岩石剪切破坏时强度与围压的关系;基于对11组试验数据的拟合结果在莫尔应力空间分析黏结力和摩擦力的变化特征：岩石承载的剪切力存在上限即材料的真实黏结力c₀;在试验范围内莫尔概念的内摩擦力达到约为0.38 c₀的峰值,且黏结力在其附近相交. 材料真实黏结力与正应力无关,因而名义黏结力表征了完好材料剪切破裂的面积;基于裂隙面积计算的等效摩擦因子随正应力降低,意味着裂隙滑移的爬坡角减小,而后者取决于正应力与真实黏结力的比值. 等效摩擦因子与指数准则的材料参数具有确定关系,体现了岩石在压应力作用下剪切破裂的物理背景.
关键词： 岩石力学;指数准则;莫尔应力空间;物理背景;真实黏结力;内摩擦力;等效摩擦因子

Abstract
Rocks are natural materials composed of various mineral particles within fissures and pores in different sizes, those result in complicate mechanical properties. Strength criteria for rocks in engineering design and disaster prevention are still an open question. As cohesion and friction in rock do not work simultaneously, the linear Coulomb criterion proposed in 1773 is only reliable to describe pseudo-triaxial compression strength of cylindrical specimen in a small range of confining pressure. Many nonlinear criteria are merely empirical formulas but lack of physical background. The exponential criterion proposed by the author is applicable to fit the relationship between strength and confining pressure of rocks in shear failure; therefore, the cohesion and friction are analyzed in Mohr's stress space on the fitting solutions for eleven rocks. Shear stresses in rock have an upper limit, i.e. the genuine cohesion c₀ of rock; and the internal friction has a peak of about 0.38 c₀, by which intersection of the cohesion and internal friction is. The genuine cohesion is independent to normal stress, so the nominal cohesion of rock specimen represents the shear fracture area of intact material when rock specimen reaches its strength. The equivalent friction factor of slipping fissure decreases with the normal stress, so as the climbing angle that depends on ratio of normal stress to the genuine cohesion. Relationship between the equivalent friction factor and parameters in the exponential criterion reflects the physical background of shear fracture for rock under compressive stresses.
Keywords：rock mechanics;exponential criterion;Mohr's stress space;physical background;genuine cohesion;internal friction;equivalent friction factor

PDF (1128KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex 收藏本文
本文引用格式
尤明庆. 基于指数准则在莫尔空间对岩石剪切强度的研究. 力学学报[J], 2019, 51(2): 607-619 DOI:10.6052/0459-1879-18-291
You Mingqing. STUDY ON SHEAR STRENGTH OF ROCKS USING THE EXPONENTIAL CRITERION IN MOHR'S STRESS SPACE. Chinese Journal of Theoretical and Applied Mechanics[J], 2019, 51(2): 607-619 DOI:10.6052/0459-1879-18-291

引言

岩石是矿物颗粒构成的天然材料,存在各种尺度的孔隙、裂隙等损伤,在细观乃至宏观具有非均质性和各向异性;种类繁多,力学性质复杂^[1-3].若以压应力为正,岩石承载的主应力$\sigma _{1} \ge$ $\sigma _{2} \ge$ $\sigma _{3}$ 之界限或曲面$\sigma _{1}=S$($\sigma$₂, $\sigma _{3})$称为强度准则;对长方体试样加载可以确定给定$\sigma$₂和$\sigma _{3}$时$\sigma$₁的最大值即强度,近来已有大量试验结果,并提出多种真三轴强度准则^[3-8].不过,在两个方向即试样的4个侧面以刚性压板加载,应力较高时会产生显著摩擦而使强度失真,对相关结论需持谨慎态度^[9-10].

中间主应力有助于提高岩石强度. 仅考虑最小主应力$\sigma _{3}$,即基于$\sigma$₂=$\sigma _{3}$的强度进行设计是偏于安全的,因而为岩体工程广泛采用^[11-12];另一方面,真三轴强度准则首先需经过$\sigma$₂=$\sigma _{3}$的试验结果确认,能够退化为可靠的常规三轴强度准则.后者在岩石力学领域具有特别重要的价值.

1911年von Karman^[13]报道了大理岩圆柱试样在围压$\sigma$₂=$\sigma _{3}$下轴向压缩试验后,在世界范围内进行了大量试验.不过,岩石试样围压下压缩的变形和破坏特征仍在研究之中,其承载的最大轴向应力$\sigma _{\rm S}$与围压的关系即常规三轴强度准则,多是具有较好拟合精度的经验公式^{[2,6-8, 14-16]},但缺乏确切的物理背景,并不能作为力学模型而具有广泛的适用性,如含有3个参数的广义Hoek-Brown准则不能描述大理岩延性变形的强度特征^[16].

就材料分离而言,岩石破坏只有拉伸和剪切两种形式.试验表明,圆柱试样单轴或低围压下轴向压缩可能产生沿轴向的拉伸劈裂,但围压稍高则转为剪切破坏;高围压时试样进入延性变形状态,产生多个剪切屈服面而不出现宏观的滑移破裂面^{[1-3,12, 17]}. 1887年Mohr 将描述土体破坏的Coulomb准则(1773年)用于描述岩石的压剪破坏,即剪切强度$\tau _{\rm S}$由黏结力c和内摩擦力f构成,后者是内摩擦因子 $\mu$与正应力$\sigma$的乘积,其等价于最大主应力 $\sigma$₁与最小主应力 $\sigma _{3}$成线性关系^[11-12].不过,岩石局部并不能同时黏结和摩擦：裂隙没有黏结力,而完好材料断裂前并无摩擦^[18-21]. Mogi^[3,19]基于Coulomb准则估计花岗岩中黏结部分仅占破裂断面的1/8;Savage 等^[20]基于Mohr准则分析花岗岩黏结和裂隙面积的变化.不过,岩石的黏结和摩擦可以相互转化,如围压增高引起破裂面上正应力增大,若裂隙摩擦承载能力超过了材料的黏结力则不会滑移,而是其附近的材料剪切破坏^[21].与此相应,圆柱试样的强度随围压增大速率而逐步降低,承载的主应力差并不会随围压而无限增大^[16,21-23].

摩擦是岩石的基本性质之一,事关地震、滑坡等地质灾害发生的临界点^[3,11,24-25],有岩块直接剪切、常规三轴压缩以及光面和毛面岩板的静摩擦或滑动摩擦等试验方法^{[3,8, 26-27]}. Byerlee定律已得到广泛认可：正应力200 MPa以上摩擦因子为0.6,与岩石及断面粗糙程度无关,除非充填有蒙脱石、伊利石等断层泥^{[1, 3, 28-29]},但相关机理尚缺乏明确解释. 此外文献[29]收集了19组光面摩擦试验结果而将30$^{\circ}$作为基本摩擦角;不过,所称"该值源于岩石屈服流动机制,根据Mises准则可确定摩擦角为30$^{\circ}$"或许有所误解：$J_{2}$常数假设下的纯剪强度与单向拉伸或压缩强度之比值并非摩擦因子,而Mises准则实际上并不能适用于岩石.

本文说明指数准则能够准确描述多种岩石的常规三轴压缩强度与围压的关系,基于对11组试验数据的拟合结果在Mohr应力空间解释其物理背景,分析岩石的黏结、摩擦特性,进而理解岩石的变形、承载以及应力状态之间的关系.

1 指数准则对试验数据的拟合

目前已公开发表的强度准则有20种以上^{[2, 6-8, 14-16]},You^[22]提出的真三轴强度准则中以指数形式描述最小主应力$\sigma _{3}$或围压$\sigma$₂=$\sigma _{3}$对强度的影响

(1)$$\sigma _{\rm S}-\sigma _3 = Q_\infty-(Q_\infty-Q_0 )\exp \left(-\frac{K_0-1}{Q_\infty-Q_0 }\sigma _3 \right)$$

式中,参数$K_{0}$ 为围压0时强度随围压的增加速率,$Q_{0}$为单轴强度,$Q_{\infty }$ 为主应力差 $\sigma _{\rm D}$=$\sigma _{\rm S}-$$\sigma _{3 }$的极限值,即岩石承载的剪切应力上限为$c_{0}$=0.5$Q_{\infty }$.记岩石材料参数为

(2)$$R = \frac{Q_\infty-Q_0 }{K_0-1}$$

并对式(1) 求导,有

(3)$$k = \frac{{\rm d}\sigma _{\rm D} }{{\rm d}\sigma _{\rm 3} } = \frac{Q_\infty-\sigma _{\rm D} }{R}$$

即主应力差与参数k 为线性关系

(4)$$\sigma _{\rm D} = Q_\infty-kR$$

指数准则可准确描述岩石剪切破坏时强度随围压的变化特征-主应力差$\sigma _{\rm D}$随围压增大的速率k逐步降低而趋于常数,已得到大量试验结果支持,并据其构造真三轴强度准则^{[2,16, 22-23, 30-31]}.

指数强度准则对11种岩石强度的拟合结果在图1~图3 给出.以绝对偏差最小得到的拟合曲线,简记为Exp($Q_{0}$,$Q_{\infty}$,$K_{0})$,将试验数据等量分为两半,其靠近多数正常数据,而使少数异常数据具有较大偏差^[32],但拟合结果可能并不唯一;不过,试验数据较多或离散较小时,拟合曲线的变动范围较小,并不影响实际使用.

图1

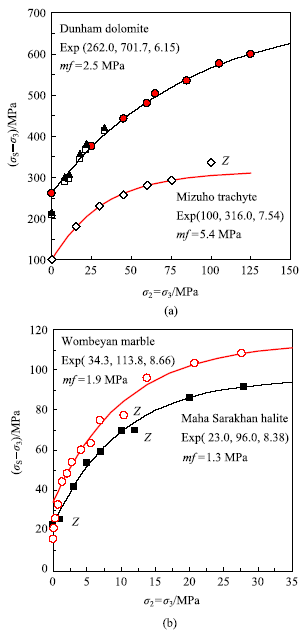
新窗口打开|下载原图ZIP|生成PPT
图1四种岩石的强度及指数准则的拟合^{[3, 35, 37]}

Fig.1Fitting curves using the exponential criterion for strengths of four rocks cited from Refs. [3, 35, 37]

图2

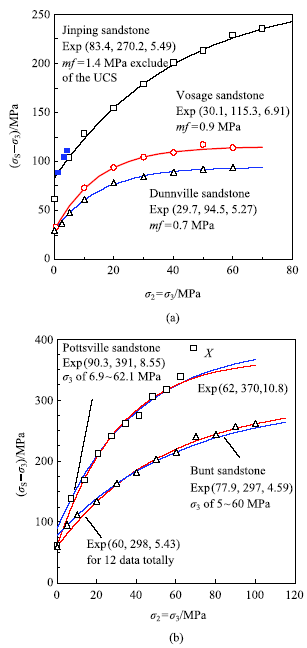
新窗口打开|下载原图ZIP|生成PPT
图2五种砂岩的强度及指数准则的拟合^{[8, 38, 40-42]}

Fig.2Fitting curves using the exponential criterion for strengths of sandstones cited from Refs. [8, 38, 40-42]

图3

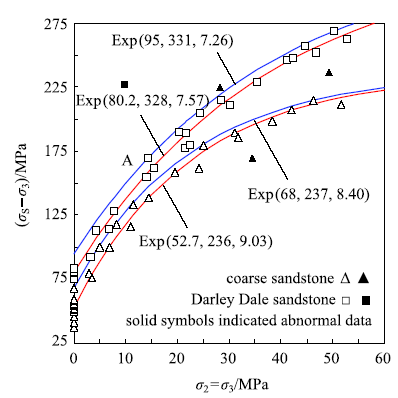
新窗口打开|下载原图ZIP|生成PPT
图3砂岩强度的离散性及指数准则的拟合^[43]

Fig.3Fitting curves using the exponential criterion for scattering strengths of sandstones cited from Ref. [43]

图1所示为4种岩石的强度及指数准则的似合.粗面岩^[3]单轴强度为100 MPa,围压为100 MPa时,试样达到承载峰值所需变形较大,引起压头端部摩擦效应而使强度偏高^[33];不考虑该数据,指数准则对6个数据的平均拟合偏差仅mf1.1 MPa.

Dunham 白云岩的强度来自3个岩块^[3]. 以指数准则拟合围压0~125 MPa 的一组数据,参数$Q_{0 }$= 262 MPa与单轴强度试验值 258 MPa 和265 MPa 的平均值相同.另两组单轴强度为209 MPa和217 MPa明显偏低,均来自多个试验的平均值,如后者是210~226 MPa的6组数据^[3];围压下强度则与前述一组数据相近.显然,三组试样的材料性质相同,只是后两者存在特定倾角的弱面使单轴强度偏低,而围压增高后弱面摩擦承载就不再影响试样强度^[34].}

Wombeyan大理岩试样加热至600${^\circ}$C保持恒定,待晶粒破裂声完全消失后室温冷却;其晶粒可以手指剥离而裂面平整^[35].对围压1.4 MPa 以上的10组数据进行指数准则拟合,$Q_{0}$=34.3 MPa远高于实际单轴强度 15.9 MPa,表明试样单轴压缩时并非单一断面的剪切破坏(图1).该大理岩完整试样及另一组热损伤的强度分析参见文献[36].

Maha Sarakham岩盐强度总计9组数据^[37],指数准则拟合曲线下方有两个试验点的偏差皆达到4.5 MPa,源于试样间差异而引起的数据离散.

若不考虑图1中标为Z的4组数据,指数准则的平均拟合偏差仅为单轴强度的1%.

图2所示为5种砂岩的强度及指数准则的拟合. Vosage砂岩^[38-39]的压缩试验以摩擦因子0.02的 Stearic acid-Vaseline进行压头与试样端面间的减摩,因而围压高达2倍单轴强度亦未出现端部摩擦效应.Dunnville砂岩的试验均重复两次,此处仅选用强度较高的一组^[8].这两种砂岩的主应力差已趋于常数,因而不能采用Hoek-Brown准则等描述.

锦屏砂岩^[40]围压下的8个强度($\Box$)可以用指数准则描述,但参数$Q_{0}$=83.4 MPa明显高于单轴强度的试验值61.6 MPa (图2).不过,3个卸围压破坏的强度($\blacksquare$)与指数准则拟合曲线相近,表明实际单轴强度属于"异常数据"：试样存在缺陷,或并非单一断面的剪切破坏.若不考虑单轴强度,指数准则的平均拟合偏差mf从3.6 MPa下降到1.4 MPa.

Bunt 砂岩在围压100 MPa时峰后应力保持恒定,更高围压时轴向应力持续增大^[41].}指数准则拟合结果为Exp (60, 298, 5.43),参数$Q_{0}$与实际单轴强度 60 MPa 相同,但拟合曲线(图2中细线)低于围压强度 5 MPa 和10 MPa,偏差显得奇特达到 25.4 MPa.若仅对围压范围为5~60 MPa的7组数据进行拟合,得到的$Q_{0}$=77.9 MPa则远高于实际单轴强度;不过,平均拟合偏差1.6 MPa表明拟合曲线(图2中粗线)体现了Bunt 砂岩相应围压范围的强度特性,而围压为70 MPa以上的强度稍许偏高,缘于端部摩擦效应^[33].

Pottsville砂岩未风化且质地均匀,石英颗粒接触处有少量硅质胶结;剪切破裂面粗燥且不规则,清除粉末后断面形态与压缩试验前相同,显示颗粒或材料具有较高的黏结力.试验重复3次,图2中的强度数据为平均值^[42].与前述粗面岩类似,围压强度为69 MPa的强度$X$异常偏高,未用于强度准则拟合.此外,试样单轴压缩时可能出现局部拉伸劈裂而使强度偏低,因而不考虑单轴强度的拟合结果Exp(90.3, 391, 8.55) 更能体现岩石剪切破坏时的强度特性.

砂岩类沉积岩的颗粒尺度、孔隙以及胶结物质随位置变化,试样之间可能存在差异而引起强度离散.低围压尤其是单轴强度离散较大,而高围压时离散较小.基于单轴压缩强度的范围可以利用指数准则给出其常规三轴强度的界限^[34,36]. 基于文献[43] 的两组数据予以说明(图3).

粗砂岩的13个单轴强度在37.2~67.7 MPa范围内;围压增大,强度的离散性有所降低.单轴强度以均值计算且不考虑3个异常数据($\blacktriangle$),指数准则的拟合结果为Exp(52.7, 236.0, 9.03),mf=4.3 MPa.不过,强度准则原本的含义是围压对相同试样的强度影响.若粗砂岩单轴强度的最高值为 68 MPa,该试样进行围压下压缩时强度也应达到实际试验数据的上限;如图3所示,强度上限可以指数准则Exp(68, 237, 8.40) 描述,其参数$Q_{\infty }$仅比原拟合值提高 1 MPa.

Darley Dale砂岩的5个单轴强度在74.9~ 83.2 MPa范围内. 基于所有试验结果的指数准则的拟合结果为Exp(80.2, 328, 7.57),{\ziju{-0.03}即图中红色细线;不过,三轴强度始终维持一定的差异,并未随围压增大而减小,如围压为14.3 MPa时的三轴强度为183.5 MPa} (数据$A)$,其值高于拟合曲线10.8 MPa. 该组试样中真实黏结力或许存在差异;若参数$Q_{\infty }$的最大值比拟合值大 3 MPa,则该岩石的强度上限可用Exp (95, 331, 7.26)来描述.前述试样A若单轴压缩且单一断面剪切破坏,则其强度将达到 95 MPa.基于指数准则可以估算岩石单轴强度的分布范围^{[34, 36]}.

试样的承载能力即强度试验数值是试样质量、试验参数以及试验装置的综合体现,并不完全取决于围压.含有多个参数的复杂公式或分段表示的公式,尽管可以降低对试验数据的拟合偏差,但并不是体现岩石力学性质的强度准则.图1~图3表明指数准则能够描述岩石试样剪切破坏时强度随围压的变化特征,能够以较大拟合偏差揭示少数异常数据.当然,实际围岩承受复杂的应力状态,可能产生拉伸破坏,相应强度需要另作研究^[44-45].

表1列出上述11组岩石(其中7组为砂岩SS)强度的拟合结果,将据此讨论岩石的黏结摩擦特性.

Table 1
表1
表1岩石常规三轴压缩试验参数及指数强度准则的分析
Table 1Test results of conventional triaxial compression and analyses with the exponential strength criterion

references cited		Q0 /MPa	/MPa	K0	CP/MPa	c*/c0	fM/C0		TS /C0	T/C0	^3/Q0
Mizuho^[3]	100.0	100.0	316.0	7.54	0 ?75.0	0.111	0.376	0.795	0.738	0.742	0.455
Dolomite^[3]	262.0	262.0	701.7	6.15	0 ?125.0	0.144	0.364	0.754	0.744	0.778	0.408
Marble^[35]	15.9	34.3	113.8	8.66	1.4 ?27.6	0.099	0.378	0.838	0.735	0.703	0.437
Halite^[37]	23.0	23.0	96.0	8.38	0 ?28.0	0.080	0.388	0.791	0.732	0.747	0.630
Vosage SS^[38]	33.5*	30.1	115.3	6.91	0.5 ?60.0	0.096	0.383	0.735	0.729	0.797	0.648
Dunn. SS^[8]	29.7	29.7	94.5	5.27	0 ?60.0	0.132	0.369	0.662	0.735	0.880	0.623
Jinping SS^[40]	61.6	83.4	270.2	5.49	1.2 ?70.0	0.127	0.371	0.674	0.735	0.865	0.618
Bunt SS^[41]	60.0	77.9	297.0	4.59	5.0 ?60.0	0.119	0.374	0.581	0.727	0.995	0.937
Potts. SS^[42]	62.1	90.3	391.0	8.55	6.9 ?62.1	0.077	0.388	0.796	0.729	0.740	0.648
Coarse SS^[43]	37.2 ?67.7	52.7	236.0	9.03	0 ?51.7	0.072	0.389	0.814	0.726	0.721	0.645
		68.0	237.0	8.40	upper	0.095	0.381	0.817	0.736	0.723	0.485
Darley Dale	74.9 ?83.2	80.2	328.0	7.57	0 ?52.8	0.086	0.386	0.759	0.729	0.774	0.661
_SS[43]		95.0	331.0	7.26	upper	0.103	0.379	0.766	0.733	0.766	0.542

^* Strength at confining pressure of 0.5 MPa. Test data are cited from Ref. [39], to which the author of Ref. [38] provided in personal communication.

新窗口打开|下载CSV

2 Mohr应力空间的指数强度准则

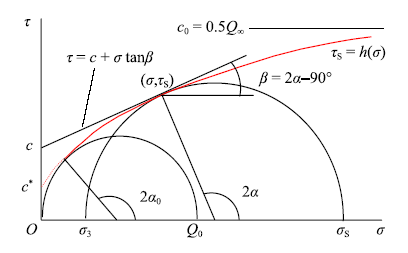
基于不同围压$\sigma$₂=$\sigma$₃的强度$\sigma_{\rm S}$可作出Mohr 应力圆,其包络线即给定正应力$\sigma$下岩石所能承受的最大剪切力$\tau _{\rm S}=h$($\sigma$),即Mohr 强度准则(图4). 破坏断面的倾角$\alpha$及相应的正应力和剪应力为

(5)$${\rm tan}^2\alpha = \frac{{\rm d}\sigma _{\rm S} }{{\rm d}\sigma _{\rm 3} } = k + 1$$

(6)$$\sigma = \sigma _{\rm S} \cos ^2\alpha + \sigma _3 {\rm sin}^{\rm 2}\alpha = \sigma _{\rm D} \cos ^2\alpha + \sigma _3$$

(7)$$\tau _{\rm S} = (\sigma _{\rm S}-\sigma _3 )\sin \alpha \cos \alpha = \sigma _{\rm D} \sin \alpha \cos \alpha$$

图4

新窗口打开|下载原图ZIP|生成PPT
图4岩石的剪切强度准则和Mohr 应力圆

Fig.4Shear strength criterion for rock and Mohr stress circles

利用式(5)~式(7)将指数准则Exp($Q_{0}$,$Q_{\infty}$,$K_{0})$ 转换为剪应力和正应力的关系$\tau _{\rm S}=h$($\sigma$).图4中虚线所示部分对应的最小主应力为负值即拉应力,岩石可能发生拉伸破坏而非剪切破坏;至于正应力为零的纯剪强度$c^{\ast }$ 则肯定不是真实发生的试验值.

某些岩石单轴压缩,如图1中Wombeyan 大理岩以及图2中锦屏、Pottsville 和 Bunt砂岩,试样内可以出现沿轴向的拉伸劈裂,并非沿倾角$\alpha$₀的截面剪切破坏而使实际强度偏低,即拟合参数$Q_{0}$只是假想试样单轴压缩时发生剪切破坏的轴向承载能力.不过,围压达到 5 MPa 前述岩石的强度均符合剪切破坏特征.此外,花岗岩和二长岩等在围压20 MPa 以上轴向压缩将是剪切破坏^[33,36].

围压微小变化时,剪切强度与正应力的关系可以近似表示为切线,即局部成立的Coulomb强度准则(图4),由式(5)可以得到内摩擦系数

(8)$$\mu {\rm = tan}\beta {\rm = tan(2}\alpha-90^ \circ ) = \frac{k}{2\sqrt {k + 1} }$$

据此可确定不同围压下岩石剪切承载能力$\tau _{\rm S}$中的摩擦力f=$\mu \sigma$ 和黏结力c=$\tau _{\rm S}-$$\mu \sigma$. 图5~图7具体绘出7种岩石的计算结果;空心圆点之间是所用的试验数据范围,相应的围压在表1给出.

图5

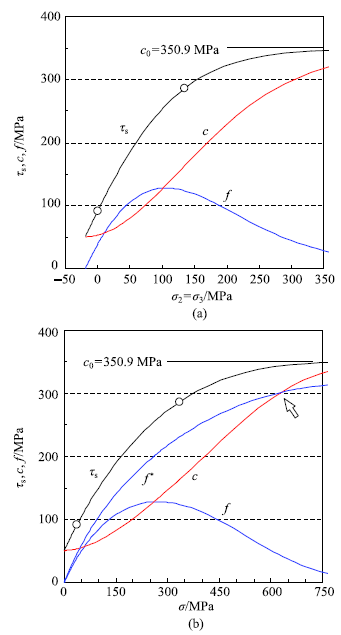
新窗口打开|下载原图ZIP|生成PPT
图5白云岩的内摩擦力和黏结力随应力状态的变化

Fig.5Internal friction and cohesion of Dunham dolomite

图6

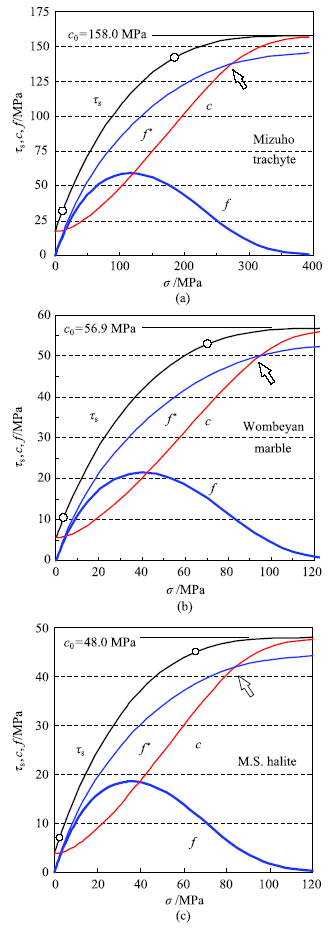
新窗口打开|下载原图ZIP|生成PPT
图6基于指数准则三种岩石在莫尔空间的剪切强度特征

Fig.6Shear strength property of three rocks in Mohr's stress space based on the exponential criterion

图7

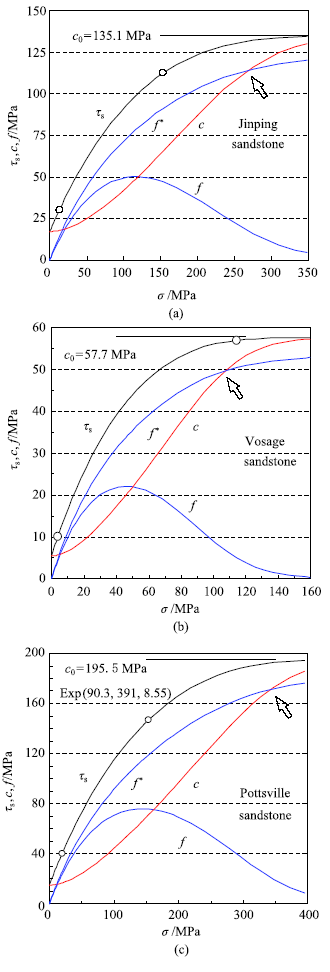
新窗口打开|下载原图ZIP|生成PPT
图7基于指数准则三种砂岩在莫尔空间的剪切强度特征

Fig.7Shear strength property of three sandstones in Mohr's stress space based on the exponential criterion

2.1 岩石的剪切承载特性

白云岩的剪切强度以及Mohr概念下的黏结力和内摩擦力随围压、正应力的变化特征在图5分别给出.试验围压的范围是0~125 MPa.

正应力较低时内摩擦力f相对较低,岩石的剪切强度主要取决于黏结力;内摩擦力随正应力增大的速率逐步降低,在围压107.0 MPa时f达到峰值127.7 MPa,而围压在90~125 MPa之间时,f仅低于峰值1.8 MPa;摩擦力在峰值附近变化较缓,峰后正应力增大引起摩擦对剪切强度的贡献份额减少.

图5和图6中可以看到,粗面岩和大理岩的黏结力c在内摩擦力f峰值点附近相交,白云岩稍许偏前而岩盐则稍许偏后.其后随着正应力增大,黏结力近乎直线增大而内摩擦力单调降低.

Mohr概念下的岩石黏结力c随正应力增大而趋于常数$c_{0}$,即材料的真实黏结力.其真实的物理背景是：随着正应力增大,部分裂隙的摩擦承载能力超过材料的真实黏结力$c_{0}$,裂隙不会产生滑移而是其附近材料剪切破裂,宏观表现为剪切强度中内摩擦力f减小而黏结力c增大(图4).

内摩擦力总是存在峰值,且峰值附近变化较缓：围压变动范围为单轴强度的10%时,内摩擦力与其峰值的差异小于1%.如图6中粗面岩在围压为 45.5 MPa时,f达到峰值59.4 MPa,围压在41~50 MPa之间时,f都大于59 MPa,而单轴强度为 100 MPa.

指数准则对锦屏砂岩强度与围压关系拟合偏差较低,且试验围压80 MPa 与其单轴强度相当,因而其在莫尔应力空间的计算结果是可信的(图7).黏结力c正好在内摩擦力f峰值点50.2 MPa通过,相应的围压为51.5 MPa.

Vosage砂岩试验围压达到2倍单轴压缩强度,但剪切强度仍含有少许摩擦力,源于其内部22%的孔隙难以完全闭合.Pottsville砂岩高围压强度不够准确(图2),因而黏结力与内摩擦力交点偏离峰值点最多,但两者数值仍大致相同.其余4种砂岩的剪切强度具有类似的变化特征,不再具体讨论.

2.2 原始黏结面积

莫尔概念下的内摩擦力f达到峰值时,黏结力c正好与其相当(图5~图7). 这是一个普遍性现象,如Yamaguchi 大理岩^[3]、Tyndall 石灰岩^[46]等岩石的强度同样具有这一特征. 内摩擦力f的峰值之前,原黏结的材料在剪断之前可能产生部分屈服;而峰值之后c近乎线性增大,表明原有裂隙的承载能力逐步达到材料的真实黏结力$c_{0}$而不再产生滑移.黏结力c的增大源于完好材料产生破裂的面积增大,或原始裂隙达到承载极限而发生滑移的面积减小.

从图5~图7看出,正应力较低时名义黏结力$c$变化较小：单轴压缩时的数值比纯剪强度$c^{\ast }$仅增大2.6%~4.9%,即岩石黏结部分的面积大致为原始状态.白云岩的原始黏结部分所占面积的比例$c^{\ast }$/$c_{0}$为0.144,是11种岩石中最大的.

岩石中具有大量的微观损伤,砂岩的孔隙所占体积已达到15%左右,非黏结的面积则更大,而岩石破裂总是沿着最弱承载截面.基于指数准则拟合结果确定的岩石原始黏结面积在10%左右(表1),据此也可以理解岩石抗拉强度远低于抗压强度.

Pottsville 砂岩的$c^{\ast }$/$c_{0}$为0.077,这与其22%的孔隙率相关.粗砂岩^[43]的孔隙率为16.1%,但试样差异较大(图3),$c^{\ast }$/$c_{0}$为最低值0.072;但基于强度上限确定的$c^{\ast }$/$c_{0}$则提高到0.095. 与此类似,Darley Dale砂岩^[43]的孔隙率为12.6%但强度离散较小,基于强度上限确定的$c^{\ast }$/$c_{0}$提高幅度稍小 (表1).

Dunnville 砂岩的孔隙率高达29%~30%,但孔隙之外黏结较好而裂隙较少^[8,47],因此$ c^{\ast }$/$c_{0}$具有较高数值 0.132.不过,石英颗粒之间胶结物的质量较差,其试样强度是11种岩石中最低的(图3).

文献[3]基于线性的库仑准则以及内外摩擦因子之比估计Westerly花岗岩黏结面积为1/8,其孔隙率仅在1%量级而单轴强度达到 250 MPa左右;不过,所用摩擦因子的准确性需要确认,且实际剪断的黏结部分面积随围压的增大而增大,并非常数.

2.3 内摩擦力的峰值

内摩擦力f的峰值出现在试验范围之内,是岩石强度特性的表现;其与名义黏结力c的主导位置转变意味着脆延性转换的开始.表1给出内摩擦力峰值及相关参数.

Bunt 砂岩内摩擦力达到峰值55.54 MP时,围压约为 73.0 MPa即0.937$Q_{0}$,与单轴强度77.9 MPa大致相当. 这与Bunt砂岩的矿物结构相关：其亚圆-圆形颗粒嵌于黏土基体中,缺少颗粒之间的咬合摩擦.其余10种岩石的内摩擦力达到峰值时,围压在(0.408~0.661)$Q_{0}$之间、正应力在(0.703~0.865)$c_{0 }$之间,而相应的剪切强度为(0.726~0.744)$c_{0}$,差别仅为均值0.735$ c_{0 }$的2.4%.内摩擦力的峰值则变化不大：白云岩为0.364$c_{0}$,其余在0.369$c_{0 }\sim$0.389$c_{0}$之间,差别约4.5%.

倘若黏结力正好在内摩擦力的峰值点通过,则基于该点的参数k并利用式(5)~式(8),可确定破裂面倾角$\alpha$和名义摩擦因子$\mu$以及主应力差$\sigma _{\rm D}=Q_{\infty }-$kR,再写出相应的正应力$\sigma$、剪切强度$\tau _{\rm S}$以及黏结力c和内摩擦力f=$\mu \sigma$,作极值分析可得到峰值点的参数k与强度准则参数的关系

(9)$$Y = \frac{R}{Q_\infty } = \frac{4k + 4-k^2}{4k(k + 1)(k + 3)-k^3}$$

给定参数k之后,可逐步求出$\sigma _{\rm D}$等各应力量以及$Q_{\infty }$归一化的数值,最终求出$K_{0}$和$Q_{0}$/$Q_{\infty }$,图8给出k在0.7~2.0 之间的计算结果以及实际拟合参数.显然,黏结力并非精确地从内摩擦力峰值点通过.

图8

新窗口打开|下载原图ZIP|生成PPT
图8黏结力通过内摩擦力峰值的参数关系及实际数据

Fig.8Relationship of criterion parameters as cohesion and internal friction intersect at the latter peak

图8中空心符号是Bunt 砂岩、Darley Dale砂岩以及粗砂岩基于所有强度确定的指数准则参数,Pottsville砂岩考虑单轴强度的拟合参数$K_{0}$=10.8和$Q_{0}$/$Q_{\infty }$=0.168,已在图8 幅面外的右下方. Bunt 砂岩和Pottsville砂岩不考虑单轴强度的拟合曲线也更接近理想的剪切破坏状态;基于Darley Dale砂岩以及粗砂岩强度上限的指数准则确定的黏结力与内摩擦力的交点更靠近内摩擦力的峰值点.此外,Dunham白云岩的黏结力与内摩擦力曲线的交点稍偏前于后者的峰值点(图8),是仅有的一例.

文献[22]提出指数强度准则时已说明,不考虑单轴强度而得到的拟合曲线更能体现岩石的剪切破坏特征,所确定的黏结力在内摩擦力相交处更加靠近后者的峰值.当然,黏结力几乎但并不是绝对从内摩擦力的峰值点通过,而参数变化对两者交点的影响并不敏感.就此而言,文献[23]称"确定岩石的强度特征需要3个独立的参数"仍是成立的.由于岩石的黏结力与内摩擦的变化曲线交点尽管略有偏后,但内摩擦力在峰值附近变化较少,与黏结力的数值没有差别,因此两者都是剪切强度之半.

3 岩石的等效摩擦因子

黏结力与内摩擦力只是破裂面承载能力达到临界状时的平均值-该截面实际处于部分摩擦、部分黏结的状态,因而真实的黏结力和摩擦力都要高于Mohr准则概念下的名义值c和f.

3.1 剪切破坏的力学模型

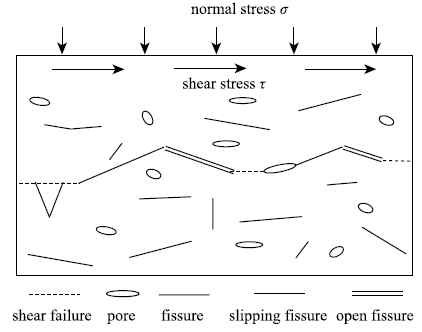
材料的真实黏结力$c_{0}$与正应力无关,张开部分并不承载正应力,摩擦滑移部分实际承载的正应力并不等于破裂断面的名义值$\sigma$.但真实黏结力$c_{0}$较高,即剪断颗粒所需应力较大,因而摩擦滑移断面并不是平面,总会略有起伏而"爬坡"(图9).

图9

新窗口打开|下载原图ZIP|生成PPT
图9剪切破裂面局部结构示意图

Fig.9Diagram of local structure of shear fracture surface

试样达到轴向承载的峰值应力即强度$\sigma _{\rm S}$时,其剪切破裂面可分为黏结材料被剪断的部分$\lambda$₁、裂隙部分$\lambda$₂ 以及未闭合孔隙部分$\lambda _{3}$,三者之和为1,且材料的真实黏结力$c_{0}$与正应力无关,Mohr概念下的黏结力c实际上表示了剪断或屈服的面积,即

(10)$$\lambda _{\rm 1} = c / c_0 = 2c / Q_\infty$$

基于纯剪强度$c^{\ast }$估计的岩石原始黏结部分所占比值在0.072~0.144 之间(表1).

剪切破裂面产生时,裂隙部分闭合滑移而部分张开引起剪胀^[48].基于图9的模型,若不考虑孔隙所占面积$\lambda _{3}$引起的正应力变化,且将非黏结部分作为整体考虑,则摩擦承载的剪应力满足

(11)$$\tau = \sigma \tan (\varphi _0 + i) = \mu ^\ast \sigma$$

式中,$\mu ^{\ast }$为裂隙的等效摩擦因子,$\varphi$₀为岩石材料的基本摩擦角,i为爬坡角. 于是,前述内摩擦力

(12)$$f = \mu \sigma = \lambda _2 (\mu ^\ast \sigma )$$

不考虑孔隙所占面积$\lambda _{3}$,则等效摩擦因子

(13)$$\mu ^\ast \approx \frac{\mu }{1-\lambda _1 } = \frac{\mu }{1-(\tau _{\rm S}-\mu \sigma ) / c_0 }$$

整个断面的平均摩擦力即内摩擦力为f,并不是作用于整个断面,参数$\mu$并不具有真实的物理含义;而单位面积裂隙以摩擦承载的有效摩擦力为

(14)$$f^\ast = f / (1-\lambda _1 )$$

3.2 黏结和摩擦

有效摩擦力$f^{\ast }$已在图5~图7给出,随正应力增大而趋近真实黏结力$c_{0}$;在名义黏结力c偏离直线处相交(图中箭头处),此前$f^{\ast }$低于c.显然,在实际试验范围内试样达到承载极限仍以材料的剪断作为标志.另一方面,正应力较高使多数裂隙承载达到真实黏结力$c_{0}$后即保持恒定,少量没有闭合的孔隙影响程度增加,计算的$f^{\ast }$以及$\mu ^{\ast }$可靠性降低.

白云岩、粗面岩以及2种砂岩的名义摩擦因子$\mu$、等效摩擦因子$\mu ^{\ast }$及参数$\lambda$₁随正应力的变化在图10和图11给出;横坐标正应力以真实黏结力$c_{0}$归一化.剪切强度$\tau _{S}$也归一化给出,而黏结材料被剪断比例$\lambda _{1 }$就是黏结力c的归一化;两者与图5~图7所示变化完全相同. 有效摩擦力$f^{\ast }$与此类似,不再给出.

图10

新窗口打开|下载原图ZIP|生成PPT
图10白云岩和粗面岩的黏结和摩擦特性

Fig.10Cohesion and friction of the dolomite and trachyte

图11

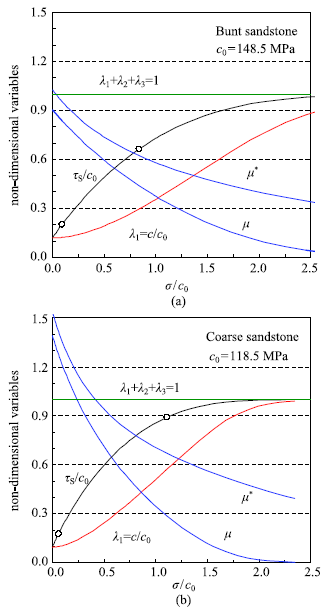新窗口打开|下载原图ZIP|生成PPT
图11砂岩的黏结和摩擦特性

Fig.11Cohesion and friction of sandstones

内摩擦因子$\mu$随着正应力增大而趋于零;对粗面岩、锦屏砂岩等,在试验围压最高时$\mu$已低于0.3.就此而言,内摩擦因子与材料的摩擦特性并不相符,并不能据此讨论岩石在高应力下的承载和破坏.

白云岩$\mu ^{\ast }$从单轴压缩时1.222 单调下降至围压125 MPa时的0.711：正应力增大引起的等效摩擦因子下降意味着爬坡角i的减小,裂隙滑移分量降低而剪断部分增大.

正应力较低时砂岩的摩擦因子差别显著(图11). Bunt砂岩孔隙率15%,次圆到圆形的中等粒径石英颗粒嵌在粘粒基质中^[41],因正应力较低时颗粒之间相对滑移或"爬坡",其摩擦因子较低;而真实黏结力$c_{0}$较高,使得裂隙承载能力达到$c_{0}$所需正应力增大,或摩擦力影响剪切强度的范围较大.

正应力接近2$c_{0}$ 即主应力差的极限$Q_{\infty}$时,黏结部分面积$\lambda$₁大于0.9,其后$\lambda$₁增大偏离直线而变缓;等效摩擦因子$\mu ^{\ast }$已小于0.5.这意味着许多裂隙承载达到真实黏结力而不再摩擦滑移;少量滑移裂隙爬坡角近乎消失,其等效摩擦因子趋于光面摩擦的数值.具体情形将在后面予以讨论.

等效摩擦因子随归一化正应力的变化取决于无量纲参数$Q_{0}$/$Q_{\infty }$和$R$/$Q_{\infty }$;由式(2)~式(4)可得参数

(15)$$Y = \frac{R}{Q_\infty } = \frac{1-Q_0 / Q_\infty }{K_0-1} = \frac{1-\sigma _{\rm D} / Q_\infty }{k}$$

表明了主应力差随围压增大的程度. 由式(6)、式(7)和式(15) 可以得到

(16)$$\frac{\sigma }{c_0 } = 2Y\left[\ln \left(1-\frac{Q_0 }{Q_\infty }\right)-\ln (kY)\right] + \frac{2(1-kY)}{k + 2}$$

(17)$$\frac{\tau _{\rm S} }{c_0 } = \frac{2(1-kY)\sqrt {k + 1} }{k + 2}$$

以$k$作为参变量,在给定$Q_{0}$/$Q_{\infty }$和$Y=R$/$Q_{\infty }$后以式(16)和式(17)计算正应力和剪切强度,再代入式(13)即得到等效摩擦因子$\mu ^{\ast }$. 实际计算表明,参数$Y$恒定时,$Q_{0}$/$Q_{\infty }$在0.2~0.4范围内的变动对$\mu ^{\ast }$与正应力$\sigma$/$c_{0}$的关系几乎没有影响,即由参数$Y$所决定.

图12给出所有11种岩石的等效摩擦因子$\mu ^{\ast }$随正应力的变化,对局部区域放大2倍. 在正应力$\sigma$以真实黏结力$c_{0}$归一化之后,所有岩石的变化特征相似.正应力较高时孔隙也会逐渐闭合,岩石之间的差异会减小.岩石名称依据曲线顺序给出,岩盐、粗面岩的数据用"$\circ$"标出,与Pottsville砂岩几乎相同.

图12

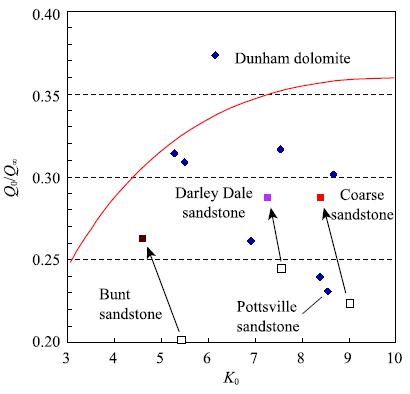
新窗口打开|下载原图ZIP|生成PPT
图12岩石的等效摩擦系数随正应力的变化关系

Fig.12Effect of the normal stress on the equivalent friction actors of eleven rocks

等效摩擦因子$\mu ^{\ast }$与参数$Y$是负相关.热损伤的Wombeyan 大理岩$Y$=0.0912是最小值,最大值是Bunt砂岩的$Y$=0.205 5;而Pottsville 砂岩、M. S. 盐岩和Mizuho粗面岩的参数$Y$在0.101 9~0.104 5 之间,差别仅 2.5%.基于表1中指数强度准则的13组拟合结果,Dunham白云岩的$Q_{0}$/$Q_{\infty }$为0.373,其余在0.223~ 0.316,对$\mu ^{\ast }$没有明显影响.

3.3 讨论

岩石断裂面的真实摩擦取决于颗粒爬坡角,而爬坡角取决于摩擦与剪断的平衡点.摩擦与正应力相关,而剪断与真实黏结力相关;于是,不同岩石的等效摩擦因子$\mu ^{\ast }$随正应力与真实黏结力之比值的变化特征大致相同.

砂岩(SS)的孔隙率对$\mu ^{\ast }$没有直接影响.基于非黏结部分面积计算的$\mu ^{\ast }$随正应力降低,意味着裂隙滑移的爬坡角减小,裂隙滑移分量降低而剪断部分增加.粗砂岩具有最高而Bunt 砂岩最低的$\mu ^{\ast }$,与"剪切爬坡"机理相协调.爬坡角取决于正应力与真实黏结力的比值,这是图12所体现的物理背景.

文献[49]对抛光岩块进行无外加正应力试验,4种岩石表面轮廓最大峰高大于10μm、最大谷深大于20μm,静摩擦因子大于0.8;4种岩石峰高小于 6μm且谷深小于16μm,静摩擦因子为0.38~0.47. 后者相当于正应力达到$Q_{\infty }$=2$c_{0}$时11种岩石的等效摩擦因子(图12).据此可以确定岩石的基本摩擦因子在0.4 左右,低于Byerlee 定律中的0.6.

岩石是非均质材料,黏结力随位置而变化,前述参数$c_{0}$只是基于圆柱试样常规三轴强度确定的平均值.试样围压下轴向压缩达到峰值承载能力之前,黏结力较低的材料将剪切屈服或破裂,转变为裂隙而摩擦承载.若围压较高破裂面的摩擦承载极限可以超过原来的黏结力,即材料发生屈服强化;具有更高黏结力的材料在持续轴向压缩下也将破裂,岩石内可能产生多组平行的断裂面,如X型节理.

岩石的实际摩擦因子具有确定的下限$\mu$₀,正应力达到$c_{0}$/$\mu$₀则破裂面不再摩擦滑移,随着压缩变形增大而产生大量屈服面,表现为延性特征.岩石在极高应力状态下摩擦属性将会完全消失,受控于最大剪切力而屈服破坏.

4 结论

Coulomb准则以及广义Hoek-Brown准则等没有给出主应力差的极限值或材料的真实黏结力,不能得到图12的等效摩擦因子以揭示岩石的剪切承载特征.指数准则具有力学性质明确的3个参数,能够拟合岩石常规三轴压缩强度与围压的关系,且以较大偏差凸现异常数据;据此在莫尔应力空间分析岩石的剪切承载特征,得到如下认识.

(1)岩石的黏结力和摩擦力在局部不能同时存在;材料的真实黏结力与正应力无关,而裂隙的摩擦承载能力因正应力增加达到真实黏结力后不会滑移,只是其邻近材料发生剪断.

(2)无量纲参数$Y$控制了岩石的真实摩擦特性;基于非黏结部分面积计算的等效摩擦因子随正应力降低,意味着裂隙滑移的爬坡角减小.爬坡角取决于正应力与真实黏结力的比值.

(3)名义黏结力随正应力单调增大,表明原有裂隙承载能力逐步达到真实黏结力而不再滑移,引起完好材料剪断面积的增大;内摩擦力在围压达到单轴强度50%左右出现峰值,且与黏结力正好相等,意味着脆延性转换的开始.

(4)正应力达到岩石的主应力差极限值时,等效摩擦因子与光面岩块的静摩擦因子相当;岩石的基本摩擦因子大约为0.4.

The authors have declared that no competing interests exist.

作者已声明无竞争性利益关系。

参考文献原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]

陈颙, 黄庭芳, 刘恩儒 . 岩石物理学.合肥: 中国科学技术大学出版社,2009:1- 17, 160-162

( Chen

Yong

, Wong

Tengfong

, Liu

Enru

. Rock Physics. Hefei: Press of University of Science and Technology of China, 2009: 1- 17, 160-162(in Chinese))

[2]

尤明庆 . 完整岩石的强度和强度准则
复旦大学学报(自然科学版), 2013,52(5):569-582

URL

岩石是天然材料，种类繁多，力学性质复杂．给出岩石反复加载强化、材料损伤对承载能力影响、软弱岩石强度与杨氏模量的关系以及孔道试样拉应力下破坏的试验结果，分析材料非均质性对岩石剪切破坏和拉伸破坏的影响．岩石内粘结和摩擦在同一点不能同时存在，应力状态达到承载极限时黏结力随变形降低，同时引起摩擦力变化；该变化与应力状态相关，就此讨论岩石变形、载荷与破坏的关系．总结常规三轴和真三轴强度准则的构造方式，讨论指数强度准则的适用性，并说明强度准则参数应以偏差绝对值之和最小为目标拟合试验数据来确定．

( You

Mingqing

. Strength and strength criteria for intact rocks
Journal of Fudan University (Natural Science), 2013,52(5):569-582 (in Chinese))

URL

Mogi

. Experimental Rock Mechanics. London: Taylor & Francis, 2007: 36-37, 83- 110, 307-320

[本文引用: 10]

[4]

Haimson

. Consistent trends in the true triaxial strength and deformability of cores extracted from ICDP deep scientific holes on three continents
Tectonophysics, 2011,503(1-2):45-51

DOI URL

78Intermediate principal stress s 2 affects mechanical behavior in all rock types. 78 Mohr-Coulomb criterion is only a conservative estimate of rock strength. 78 For constant minimum stress, fault angle rises with σ 2. 78 The onset of dilatancy rises with σ 2. 78 3D testing of ICDP cores reveals consistent σ 2 effects on strength and deformation.

[5]

, Shi

, Bai

, et al. True-triaxial testing techniques of rocks-state of the art and future perspectives
//Kwasniewski M, Li X, Takahashi M (eds). True Triaxial Testing of Rocks. London: CRC Press, 2012: 3-18

[6]

万征, 秋仁东, 郭金雪 . 岩土的一种强度准则及其变换应力法
力学学报, 2017,49(3):726-740

DOI URL

基于岩土摩擦性，假设岩土破坏是由其物理空间内特征面上的应力比决定，提出了等效应力比的概念，即物理空间特征面上的剪应力合力与正应力合力的比值。在二维条件下，等效应力比可表示为σ-τ坐标系下与摩尔圆相切的直线扣除截距正切值；在三维条件下，假设在XYZ空间内存在一三维物理空间平面，此三维空间特征平面的等效应力比为影响材料强度特性的决定性因素，基于上述三维空间特征面建立了强度准则并称之为a准则。SMP准则以及广义Mises准则都是a准则的特例，当二维坐标中的截距为零时，则强度准则退化为SMP（spatially mobilized plane）强度准则，而当正切角为零时，则强度准则退化为广义Mises准则。而当截距与外切角均不为零时，则强度准则为介于上述两者之间的一种强度准则，在偏平面上为介于SMP曲边三角形与广义Mises圆形之间的曲边三角形。在子午面上，采用考虑岩土压剪耦合的屈服准则，破坏准则采用幂函数表达式。在偏平面上提出了基于a准则的形状函数，并采用真三维应力状态表示的破坏强度准则表示在三轴压缩路径下以p，q二维应力变量表达的准则公式，推导得到了基于a准则的变换应力公式，可简单地将一般以p，q为基本变量的二维模型转变为三维应力模型。通过强度以及多种应力路径的测试对比，验证了a准则及基于该准则的变换应力公式的合理性。

( Wan

Zheng

, Qiu

Rendong

, Guo

Jinxue

. A kind of strength and yield criterion for geomaterials and its transformation stress method
Chinese Journal of Theoretical and Applied Mechanics, 2017,49(3):726-740 (in Chinese))

DOI URL

, Chen

. A failure criterion for isotropic materials based on Mohr's failure plane theory
Mechanics Research Communications, 2018,87(1):1-6

DOI URL

A failure criterion for isotropic materials is developed in the present study. The fundamental hypotheses of the Mohr-Coulomb criterion are re-examined and re-evaluated. The failure function of Mohr’s envelope is firstly expanded into a polynomial in terms of the stress components ( σ n , τ n ) on the failure plane, then truncated at the second order due to the fine curve-fitting results of quadratic functions with experimental data. The parameters of the nonlinear failure functions are calibrated by the three basic mechanical properties—the uniaxial tensile and compressive strengths, T and C , as well as the pure shear strength, S . Theoretical and experimental evaluation for various isotropic materials demonstrates that the present failure criterion provides no worse results for ductile materials and far better results for brittle materials compared with the linear Mohr-Coulomb criterion. The strength theory shows good agreement with physical reality and has a wide range of applicability.

[8]

Labuz

, Zeng

, Makhnenko

, et al. Brittle failure of rock: A review and general linear criterion
Journal of Structural Geology, 2018,112:7-28

DOI URL [本文引用: 4]

A failure criterion typically is phenomenological since few models exist to theoretically derive the mathematical function. Indeed, a successful failure criterion is a generalization of experimental data obtained from strength tests on specimens subjected to known stress states. For isotropic rock that exhibits a pressure dependence on strength, the simplest failure criterion is a linear equation in major and minor principal stresses, independent of the intermediate principal stress. A general linear failure criterion called Paul-Mohr-Coulomb (PMC) contains all three principal stresses with three material constants: friction angles for axisymmetric compressionand extensionand isotropic tensile strength. PMC provides a framework to describe a nonlinear failure surface by a set of planes “hugging” the curved surface. Brittle failure of rock is reviewed and multiaxial test methods are summarized. Equations are presented to implement PMC for fitting strength data and determining the three material parameters. A piecewise linear approximation to a nonlinear failure surface is illustrated by fitting two planes with six material parameters to form either a 6- to 12-sided pyramid or a 6- to 12- to 6-sided pyramid. The particular nature of the failure surface is dictated by the experimental data.

[9]

尤明庆 . 端部效应对岩石真三轴压缩强度的影响
岩石力学与工程学报, 2016,35(S1):2 603-2 607

URL

真三轴强度准则已提出很多,而真三轴试验结果却很少,且可靠性需要确认。如茂木清夫所做Orikabe二长岩和Yamaguchi大理岩,在真三轴应力下的强度及变形较为特别:中间主应力?2恒定时强度不随最小主应力?3增加而增加,在延性变形阶段?2对强度的影响大于?3。拉西瓦花岗岩强度也存在类似的奇异。合理的解释是,在?3较高时试样轴向变形较大,引起加载?2压板产生摩擦而提高强度。修正摩擦效应意味着增大?3而减小?1,?2对强度的真实影响将不再随?3显著增加。

( You

Mingqing

. End effects on strengths of rocks under true triaxial compression
Chinese Journal of Rock Mechanics and Engineering, 2016,35(S1):2603-2607 (in Chinese))

URL

范鹏贤, 李颖, 赵跃堂等. 茂木式真三轴试验机的端部摩擦效应
岩石力学与工程学报, 2017,36(11):2720-2730

DOI URL

茂木式真三轴试验中需要在加载装置和试件之间至少设置两对刚性接触的垫块,由于加载过程中端部摩擦限制了试件的自由变形,因而提高了试样的测试强度。为定量评估端部摩擦效应,采用同一批红砂岩试样开展不同端部摩擦因数和中间主应力条件下的双向压缩试验,试验结果表明,不同端部摩擦因数条件下的试件强度测试值存在显著差异,相同中间主应力条件下摩擦因数从0.12提高到0.28时,最大主应力极限值提高5.5%~43%。基于试验数据分析采用不同破坏准则时摩擦效应的合理性,结果表明应变能准则对双向受压工况适用性最好。基于试验数据和应变能准则,建立摩擦效应的定量表达式,绘制考虑摩擦效应的中间主应力效应曲线,分析摩擦效应对1 2?-?曲线形状的影响,分析结果与试验数据吻合良好。通过试验揭示摩擦效应的重要影响,建立定量分析模型,对于评价真三轴试验数据的可靠性具有重要参考意义。

( Fan Peng-

xian

, Li

Ying

, Zhao

Yuetang

, et al. End friction effect of Mogi type of true-triaxial test apparatus
Chinese Journal of Rock Mechanics and Engineering, 2017,36(11):2720-2730 (in Chinese))

DOI URL

Brady

BHG

, Brown

. Rock Mechanics for Underground Mining. Netherlands: Springer, 2004: 105-107

[本文引用: 1]

[12]

Jaeger

, Cook

NGW

, Zimmerman

. Fundamentals of Rock Mechanics. New York: Wiley-Blackwell, 2007: 90-95

[本文引用: 1]

[13]

von Karman

. Festigkeitsversuche unter allseitigem Druck
Zeitschrift des Vereines Deutscher Ingenieure, 1911,55(42):1749-1757

URL [本文引用: 1]

[14]

Sinha

, Walton

. A progressive S-shaped yield criterion and its application to rock pillar behavior
International Journal of Rock Mechanics and Mining Sciences, 2018,105:98-109

DOI URL

Yielding of hard rock pillars under moderate to high stresses involves the formation of excavation-parallel extensile fractures. In recent decades, researchers have found that this behavior can be best replicated by a Cohesion-Weakening-Frictional-Strengthening (CWFS) model which captures the non-simultaneous mobilization of cohesion and friction; this is a mechanism that has been experimentally proved to occur in rocks undergoing brittle failure. In the context of rock pillars, the extensile fracturing process is limited only to the surficial portions. The inner core of rock pillars, on the other hand, fails through a shear mechanism. A realistic rock strength criterion must therefore account for the two different failure behaviors. To this end, this study introduces an improved yield criterion that represents small-scale damage processes (extensile cracking under low confinement and semi-brittle shear under higher confinement) while exhibiting an emergent pillar behavior consistent with what has been observed in the field. The failure criterion was implemented in the finite difference software FLAC 3D which was then used to investigate the effect of width to height and length to width ratios on the strength of pillars.

[15]

Bineshian

, Ghainian

, Bineshian

. Comprehensive compressive-tensile strength criterion for intact rock
Journal of Rock Mechanics and Geotechnical, 2012,4(2):140-148

DOI URL

This paper presents a strength criterion for intact rock, which can well describe triaxial test data under compressive or tensile stress state. The proposed criterion is defined in terms of three parameters. One parameter expresses the apparent unconfined compressive strength (AUCS), obtained from the Coulomb-Mohr criterion, as a regulated unconfined compressive strength (RUCS). Two other parameters, and , are material-dependent that can be determined by regression analysis. The proposed criterion is compared with selected applicable strength criteria separately for compressive and tensile strengths. Coefficient of determination and accordance coefficient are considered in comparisons between the proposed and selected strength criteria.

[16]

You

. Comparison of the accuracy of some conventional triaxial strength criteria for intact rock
International Journal of Rock Mechanics and Mining Sciences, 2011,48(5):852-863

DOI URL [本文引用: 1]

? Sixteen criteria are evaluated using test data of ten rocks. ? Different solutions are obtained using various methods to fit test data. ? The author suggests searching criterion parameters on the least absolute deviation. ? The exponential criterion is feasible for brittle rocks and ductile rocks as well.

[17]

Paterson

, Wong

. Experimental Rock Deformation-the Brittle Field. Netherlands: Springer, 2004: 211-232

[18]

Handin

. On the Coulomb-Mohr failure criterion
Journal of Geophysical Research, 1969,74(22):5343-5350

DOI URL

Coulomb's criterion for the shear fracture of a brittle material is that total shearing resistance is the sum of the cohesive shear strength (independent of direction) and the product of the effective normal stress and the coefficient of internal friction (a constant independent of normal stress). Mohr generalized this criterion by extending it to a three-dimensional state of stress, and by allowing for a variable coefficient. The coefficients of internal and external (sliding) friction are not the same in general. Both tend to decrease with increasing normal stress, and their relative magnitudes may determine if failure occurs by new shear fracturing or by slip on pre-existing cohesionless surfaces like joints in rocks.

[19]

Mogi

. On the pressure dependence of strength of rocks and the Coulomb fracture criterion
Tectonophysics, 1974,21(3):273-285

DOI URL [本文引用: 1]

The observed microfracturing before faulting in rocks provides a basis for a physical model for the internal friction and the cohesive stress of the Coulomb criterion. Based on recent experimental results in the literature, the applicability of the Coulomb criterion is reexamined. The pressure dependence of strength of brittle rocks can be predicted approximately by the Coulomb criterion using measured values of sliding friction, except for a low-pressure region for certain rocks and near the brittle-ductile transition pressure. Deviation at low pressure seems to be explained either by the effect of cracked state or by different fracture mechanisms at low confining pressures, and deviation near the transition pressure is attributed to the increase of local yielding or fracturing before faulting.

[20]

Savage

, Byerlee

, Lockner

. Is internal friction friction?
Geophysical Research Letter, 1996,23(5):487-490

[本文引用: 1]

[21]

尤明庆 . 基于粘结和摩擦特性的岩石变形与破坏的研究
地质力学学报, 2005,11(3):286-292

DOI URL [本文引用: 1]

In terms of microscopic textures, mineral particles are either cohesive or separated, and the cohesive force and intemal frictional force of the Coulomb criterion cannot exit together locally. Cracks are produced and increase gradually with deformation, and the cohesion between particles in material loses with the deformation. The new cracks will produce friction and the shear stress of the material is supported by friction. If the loss of cohesive forces reduces the supporting capacity, then yield and failure will occur in localized fracture surfaces of a specimen and show the brittle character, otherwise the yield and failure will be distributed and show the ductile character. With increasing confining pressures, the frictional force of fissures will exceed the cohesive force of rock material. Then when the axial stress increases to the value of the cohesive force, shear yield will occur in material, producing plastic deformation. The frictional force will not increase to its maximum but keep the value of cohesive forces and the fissures will not slide either. Knowledge of the concept of friction is the key to understanding the deformation, strength and failure of various kinds of rock with changes in confining pressure.

( You

Mingqing

. Study of deformation and failure of rock based on properties of cohesion and friction
Journal of Geomechanics, 2005,11(3):286-292 (in Chinese))

DOI URL [本文引用: 1]

You

. True-triaxial strength criteria for rock
International Journal of Rock Mechanics and Mining Sciences, 2009,46(1):115-127

DOI URL [本文引用: 2]

This paper reviews some strength criteria which include the role of the intermediate principal stress, and proposes a new criterion. Strength criteria of the form =(), such as Drucker–Prager, represent a rotation surface in the principal stress space, symmetric to the line == in the meridian plane. Because =() must fit the pseudo-triaxial compressive strength, it will have a non-physical outcome for triaxial extension. Mogi's criteria, =(=(β) are able to fit experimental data reasonably well, but the prediction of strength is not good and sometimes problematic. Strength criterion with the form (,02,02)=[(,02,02)], or a curve of two variables which can be decided by fitting pseudo-triaxial experimental data, is not expected to describe the strength under various stress states, no matter how high the correlation coefficient of and is, or how low the misfit of the equation =() is, as these seemingly good correlations usually result from the dominant influence of the maximum principal stress in the metrics of and . The intermediate principal stress may improve the strength of rock specimen, but its influence will be restricted by . Also when is high enough to cause failure in the – direction, the strength will decrease with the increasing . The new strength criterion with exponent form has just such a character, and gives much lower misfits than do all seven criteria discussed by Colmenares and Zoback [Colmenares LB, Zoback MD. A statistical evaluation of intact rock failure criteria constrained by polyaxial test data for five different rocks. Int J Rock Mech Min Sci 2002;39:695–729].

[23]

You

. Three independent parameters to describe conventional triaxial compression strength of intact rocks
Journal of Rock Mechanics and Geotechnical Engineering, 2010,2(4):350-356

DOI URL [本文引用: 1]

The strengths of 12 rocks cited from literatures increase in a nonlinear way with increasing confining pressure against the Coulomb criterion. The criteria with power forms like the generalized Hoek-Brown criterion are not available for describing the strength properties in the whole test range for Indiana limestone, Yamaguchi marble and Vosges sandstone, of which the differential stresses are approximately constant at high confining pressures. The exponential criterion with three parameters fits the test data of those 12 rocks well with a low misfit. The three parameters are independent of the uniaxial compressive strength (UCS), the initial increasing rate of strength with confining pressure, and the limitation of differential stress.

[24]

关成尧, 赵国春, 白相东等. 断层力学科学范畴、发展脉络评论及未来发展思考
地质力学学报, 2018,24(4):555-586

URL

为了看清断层力学的理论全貌,文章研究了断层力学的发展脉络、应有体系、框架性缺失,总结了学术各界关注点及研究内容差异。结果表明断层力学关联领域存在尺度差异和目标差异,断层力学是多学科纽带,却是"三不管"地带。岩石裂纹和含内部构造的断层之间存在尺度差异和变形速度差异。断层力学的百年发展经历了从外力研究断层—构造应力场—滑移线场研究断层三个阶段,这三个阶段总的发展方向就是逐渐简化、实用化,阻碍了定量理论的发展。"Mohr范式"是支撑,带有实用化、简单化特点,也阻碍了断层力学向机理化和定量化方向发展。断层研究存在正演和反演两类方法,正演主要包括实验断层力学和理论断层力学两类途径,正演和反演结合是未来发展方向。"地质力学"秉承"力学统一律",体现断层空间联系和力学联系,属于"广义断层力学"范畴。"广义断层力学"体系适用"统一发展,关注联系"发展途径,"狭义断层力学"体系适用"分散发展,各自攻克"发展途径。先存断层或薄弱带控制后生断层,并影响应力展布,"应力制约论"是重要方向。未来将产生"流变摩擦学"和"断层岩组构摩擦学"两个方向,"断层岩组构摩擦学"应整合显微构造学成就,研究岩石组构稳定特征、流变特征、广义摩擦特征等,需要将显微构造学唯象理论上升到大尺度断层力学理论中,将岩石组构引入到岩石力学实验中。不同尺度关注点不同、理论不同、取用参数不同,加剧了研究群体的隔离。断层内泥粒是可以迁移的,由此产生"断层泥粒迁移学"。断层闭锁的概念需要重新考虑,未来研究应立足"慢应变"和"大尺度"的断层摩擦延展力学。

( Guan

Chengyao

, Zhao

Guochun

, Bai

Xiangdong

, et al. Review of category and development context of fault mechanics
Journal of Geomechanics, 2018,24(4):555-586 (in Chinese))

URL

Iba?ez

, Hatzor

. Rapid sliding and friction degradation: Lessons from the catastrophic Vajont landslide
Engineering Geology, 2018,244:96-106

[26]

Byerlee

. The frictional characteristics of Westerly granite. [PhD Thesis]. USA: Massachusetts Institute of Technology, 1966

[27]

, Fukuyama

, Yamashita

, et al. Strain rate effect on fault slip and rupture evolution: Insight from meter-scale rock friction experiments
Tectonophysics, 2018,733:209-231

[28]

Byerlee

. Friction of rock
Pure and Applied Geophysics, 1978,116:615-626

[29]

陶振宇, 陈铁民 . 岩石的基本摩擦角及高压摩擦特性
科学通报, 1991 ( 20):1567-1569

URL [本文引用: 1]

正岩石的摩擦特性直接影响到岩石的强度特征,目前岩石力学中几乎所有的强度理沦都通过C,φ值不同程度地考虑了摩擦的影响,甚至Griffith理论也需考虑裂纹面上的摩擦效应作适当修正才能很好地适用于岩石,此外,岩石摩擦还与地壳断层的稳定及粘滑等问题有密切的关系。

( Tao

Zhenyu

, Chen

Tiemin

. Basic friction angle of rock and friction property under high pressure
Science Bulletin of China, 1991(20):1567-1569 (in Chinese))

URL [本文引用: 1]

正岩石的摩擦特性直接影响到岩石的强度特征,目前岩石力学中几乎所有的强度理沦都通过C,φ值不同程度地考虑了摩擦的影响,甚至Griffith理论也需考虑裂纹面上的摩擦效应作适当修正才能很好地适用于岩石,此外,岩石摩擦还与地壳断层的稳定及粘滑等问题有密切的关系。

[30]

张磊, 刘保国 . 考虑抗拉强度的岩石强度准则对比分析
工程力学, 2016,33(11):201-207

DOI URL

岩石强度准则的研究一般着重于抗压强度而忽略抗拉强度,抗拉强度是岩石的一个重要力学性质,在工程设计中是一个重要的力学参数。该论文采用五种岩石的室内岩石力学试验数据对四种强度准则进行拟合,以对抗拉强度的描述精度、最小平均标准拟合差和拟合的主应力间关系曲线综合评价强度准则与试验值的吻合性,探究不同的强度准则对抗拉强度的预测效果。分析表明:指数强度准则拟合值与试验值最接近,描述精度最好,评价不同应力状态下岩石的强度特征优先考虑指数强度准则。

( Zhang

Lei

, Liu

Baoguo

. A comparison study of rock strength criteria considering tensile strength
Engineering Mechanics, 2016,33(11):201-207 (in Chinese))

DOI URL

Zhang

, Li

, Quan

, et al. New true-triaxial rock strength criteria considering intrinsic material characteristics
Acta Mechanica Sinica, 2018,34(1):130-142

DOI URL

A reasonable strength criterion should reflect the hydrostatic pressure effect, minimum principal stress effect,and intermediate principal stress effect. The former two effects can be described by the meridian curves, and the last one mainly depends on the Lode angle dependence function. Among three conventional strength criteria, i.e.Mohr oulomb(MC), Hoek rown(HB), and Exponent(EP) criteria, the difference between generalized compression and extension strength of EP criterion experience a firstly increase then decrease process, and tends to be zero when hydrostatic pressure is big enough. This is in accordance with intrinsic rock strength characterization. Moreover, the critical hydrostatic pressure I_c corresponding to the maximum difference of between generalized compression and extension strength can be easily adjusted by minimum principal stress influence parameter K. So, the exponent function is a more reasonable meridian curves, which well reflects the hydrostatic pressure effect and is employed to describe the generalized compression and extension strength.Meanwhile, three Lode angle dependence functions of L_(MN),L_(WW), and L_(YMH), which unconditionally satisfy the convexity and differential requirements, are employed to represent the intermediate principal stress effect. Realizing the actual strength surface should be located between the generalized compression and extension surface, new true-triaxial criteria are proposed by combining the two states of EP criterion by Lode angle dependence function with a same lode angle. The proposed new true-triaxial criteria have the same strength parameters as EP criterion. Finally, 14 groups of triaxial test data are employed to validate the proposed criteria. The results show that the three new true-triaxial exponent criteria,especially the Exponent Willam-Warnke criterion(EPWW)criterion, give much lower misfits, which illustrates that the EP criterion and L_(WW) have more reasonable meridian and deviatoric function form, respectively. The proposed new true-triaxial strength criteria can provide theoretical foundation for stability analysis and optimization of support design of rock engineering.

[32]

You

. Comparison of two true-triaxial strength criteria
International Journal of Rock Mechanics and Mining Sciences, 2012,54:114-124

DOI URL [本文引用: 1]

Publication » Comparison of two true-triaxial strength criteria.

[33]

尤明庆 . 常规三轴压缩的端部效应及花岗岩强度的研究
岩石力学与工程学报, 2018,37(S1):3160-3168

URL [本文引用: 3]

圆柱试样的轴向压缩因压头刚性而存在端部摩擦效应使强度偏高;K.Mogi进行白云岩和花岗岩的不同长度试样在低围压下压缩试验,发现端部效应对强度的影响随着围压增大而消失。基于以往对砂岩、粗面岩、大理岩和白云岩以及众多花岗岩的试验结果,围压较高时试样达到峰值强度时变形较大,经试样断面修正后的强度仍会因端部摩擦效应而偏高。花岗岩由力学性质差异显著的多种晶粒组成,试样尺度较小时端部摩擦可通过晶粒传递而引起高围压下强度的极端离散。讨论了不同围压下端部效应以及尺度效应对花岗岩强度的影响程度,评价指数强度准则的适用性,并预测高围压下花岗岩的破裂强度。

( You

Mingqing

. Study on ends effect in conventional triaxial compression test and the strengths property of granites
Chinese Journal of Rock Mechanics and Engineering, 2018,37(S1):3160-3168 (in Chinese))

URL [本文引用: 3]

尤明庆 . 围压对岩石试样强度的影响及离散性
岩石力学与工程学报, 2014,33(5):929-937

DOI URL Magsci [本文引用: 3]

岩石是非均质性材料，试样差异引起试验结果离散，强度准则的拟合曲线仅表示围压对岩石强度影响的平均特性。围压100 MPa 以内的试验结果表明，试样内部裂隙引起的强度差异随围压增大而减小，指数强度准则表示围压对强度影响的2个参数与试样无关，而依据围压下强度可以确定试样应有的单轴压缩强度，并以其分布描述岩石的总体强度特征，从而应用于工程设计。花岗岩中石英、长石、云母的力学性质差异显著，小尺度试样内矿物的含量不同，将引起高围压下强度的显著离散；而较大压缩变形引起的端部摩擦效应也会影响试样的强度。

( You

Mingqing

. Study on effect of confining pressure on strength and the scatter of rock specimens
Chinese Journal of Rock Mechanics and Engineering, 2014,33(5):929-937 (in Chinese))

DOI URL Magsci [本文引用: 3]

Rosengren

, Jaeger

. The mechanical properties of an interlocked low-porosity aggregate
Geotechnique, 1968,18(3):317-326

[本文引用: 4]

[36]

尤明庆 . 岩石损伤、黏结和摩擦特性的研究
岩土工程学报, 2019,41(3):554-560

[本文引用: 4]

( You

Mingqing

. Study on the properties of damage, cohesion and friction for rocks
Chinese Journal of Geotechnical Engineering, 2019,41(3):554-560 (in Chinese))

[本文引用: 4]

[37]

Sriapai

. True triaxial compressive strengths of Maha Sarakham rock salt. [Master Thesis]. Thailand: Suranaree University of Technology, 2010: 33-36

[本文引用: 4]

[38]

Bésuelle

, Desrues

, Raynaud

. Experimental characterisation of the localization phenomenon inside a Vosges sandstone in a triaxial cell
International Journal of Rock Mechanics and Mining Sciences, 2000,37(8):1223-1237

DOI URL [本文引用: 3]

The behaviour of a Vosges sandstone is studied, including quasi-homogeneous deformation, incipient strain localisation and localised rupture. The homogeneous behaviour is first presented from about 60 experiments in triaxial compression with two slenderness ratios ( H/ D=1 and 2), in triaxial extension, and in isotropic compression. A large range of confining pressures (0 60 MPa) is investigated, showing a significant evolution of material response. A strong positive dilatancy is observed at lower pressure, decreasing to become negative (contractancy) at higher pressure. Simultaneously, the strength decreases with increasing confining pressure. The localisation is described in terms of onset of localisation, shear band orientation and patterning. The volumetric strain is analysed inside the band with computed X-ray tomography and electron microscopy. We observed the formation of a gouge layer, and around it, a dilating shear band at lower confining pressure and a compacting shear band at higher pressure. This compacting shear band seems to be the transition mechanism between the brittle and semi-brittle regime.

[39]

Fang

, Harrison

. A mechanical degradation index for rock
International Journal of Rock Mechanics and Mining Sciences, 2001,38(8):1193-1199

DOI URL [本文引用: 1]

http://linkinghub.elsevier.com/retrieve/pii/S1365160901000703

[40]

汪斌, 朱杰兵, 邬爱清等. 高应力下岩石非线性强度特性的试验验证
岩石力学与工程学报, 2010,29(3):542-548

URL Magsci [本文引用: 3]

<FONT face=Verdana>深埋工程岩体开挖后围岩的强度特性表现出明显的非线性特征。基于室内岩石三轴加载及卸荷力学试验成果，对高应力下岩石的非线性强度特性予以验证，并开展高应力下应力路径对强度参数影响规律研究。采用已有的二次抛物线型、双曲线型、幂函数型等型式的包络线来研究强度特征的非线性，结果表明，幂函数型Mohr准则能够作为在高应力加载和卸荷应力路径下的岩石破坏的强度判据。在低围压下(＜10 MPa)，三轴卸围压破坏强度要小于常规三轴强度；而在高围压下，前者略高于后者。内摩擦角的正切值与等效法向应力的函数关系表明岩样的实际内摩擦角并不是一个不变值，具有幂函数关系的非线性特征，在低应力下卸载破坏内摩擦角要比常规三轴压缩剪切内摩擦角略大，在高应力下则相反；根据Mohr准则中内摩擦角与理论破裂角之间的关系，随着应力增加它们的破裂角均呈非线性衰减并趋向π/4。</FONT>

( Wang

Bin

, Zhu

Jiebing

, Wu

Aiqing

, et al. Experimental validation of nonlinear strength property of rock under high geostress
Chinese Journal of Rock Mechanics and Engineering, 2010,29(3):542-548 (in Chinese))

URL Magsci [本文引用: 3]

Gowd

, Rummel

. Effect of confining pressure on the fracture behavior of a porous rock
International Journal of Rock Mechanics and Mining Sciences, 1980, 17(2):225-229

DOI URL [本文引用: 3]

Triaxial compression tests were carried out on a porous sandstone from SW-Germany. The confining pressures ranged up to 200 MPa. Direct volumetric strain measurements indicated that pre-peak microfracturing is a precursory deformation process to the development of macroscopic shear faults in intact porous rock at low confining pressures. Post-peak dilation at low pressures is due to fault dilation. At high pressures multiple shear fractures develop with progressively less dilation. Transition from brittle to ductile deformation takes place at a confining pressure of 100 MPa. Ductile shear at high pressure occurs without any dilation, and leads to progressive compaction and homogeneous shear throughout the rock specimen. Applied to earthquake precursory phenomena this implies that dilatancy effects in low porosity fault zones may only exist at shallow depths. At greater depth compaction will dominate over dilation.

[42]

Schwartz

. Failure of rock in the triaxial shear test
//Proceedings of the 6th US Symposium on Rock Mechanics. Rolla, Missouri, 1964: 109-151

[本文引用: 3]

[43]

Franklin

, Hoek

. Development in triaxial testing technique
Rock Mechanics, 1970,2(4):223-228

DOI URL [本文引用: 7]

A simple triaxial cell is described together with details of the technique employed for triaxial testing. Triaxial strength results for 254 specimens of eight rock types are tabulated.

[44]

张顶立 . 隧道及地下工程的基本问题及其研究进展
力学学报, 2017,49(1):3-21

DOI URL Magsci

<p>作为隧道及地下工程学科的3个基本问题，隧道围岩稳定性、支护——围岩相互作用和结构体系的动力响应一直都是本学科研究的核心问题，本文围绕上述问题重点分析了隧道围岩力学特性及其载荷效应，建立了深浅层围岩结构力学模型，并通过分析深层围岩中结构层稳定性得到了围岩特性曲线的解析公式，提出了围岩结构性特点及载荷效应的计算方法；通过对隧道支护与围岩作用关系的分析，将支护与围岩的动态作用分为4个阶段：即自由变形、超前支护、初期支护和二次衬砌阶段.由此提出了动态作用全过程的描述方法；基于广义与狭义载荷的理念，提出隧道支护具有调动和协助围岩承载基本功能的观点，明确了两种功能的实现方式，即通过围岩加固、超前加固及锚杆支护实现调动围岩承载，通过支护结构协助围岩承载；针对复杂的隧道支护结构体系，提出了多目标、分阶段协同作用动态优化概念，可使各种支护结构的施作实现时间和空间上的协调，提高可靠性；针对极不稳定的复杂隧道围岩的安全性特点，建立了3种模式的安全事故机理模型，基于工程响应特点提出了安全性分级的新理念，并形成了分级指标体系和分级方法；针对水下隧道及富水围岩条件，建立了3种模式的隧道突涌水机理模型，提出了基于围岩变形控制的安全性控制理论和方法.最后，对本学科发展的热点和核心问题进行了分析和展望.</p>

( Zhang

Dingli

. Essential issues and their research progress in tunnel and underground engineering
Chinese Journal of Theoretical and Applied Mechanics, 2017,49(1):3-21 (in Chinese))

DOI URL Magsci

王启智, 李炼, 吴礼舟等. 改进巴西试验:从平台巴西圆盘到切口巴西圆盘
力学学报, 2017,49(4):793-801

( Wang

Qizhi

, Li

Lian

, Wu

Lizhou

, et al. Improvement of Brazilian test: From flattened Brazilian disc to grooved Brazilian disc
Chinese Journal of Theoretical and Applied Mechanics, 2017,49(4):793-801 (in Chinese))

[46]

Carter

, Duncan

SEJ

, Lajtai

. Fitting strength criteria to intact rock
Geotechnical and Geological Engineering, 1991,9(1):73-81

DOI URL [本文引用: 1]

Rock strength data covering the full range of possible stress conditions are presented for three rocks: a granite, a limestone and a salt rock. The Hoek and Brown square root parabola and the Johnston criteria are fitted to the strength data coming from around 500 laboratory tests. The fitting procedure is facilitated by a specially built PC code, ROCKER, which is available to anyone on request.The Hoek and Brown criterion is modified through the inclusion of a third parameter to account for the low tensile strength of the salt rock. A new criterion, the Rocker function is formulated to follow strength data closely in the tension-low confining pressure region.

[47]

Folta

. Strength testing under multi-axial stress states. [Master Thesis]. USA: The University of Minnesota, 2016: 42-43

[本文引用: 1]

[48]

Mas

, Chemenda

. An experimentally constrained constitutive model for geomaterials with simple friction-dilatancy relation in brittle to ductile domains
International Journal of Rock Mechanics and Mining Sciences, 2015,77:257-264

DOI URL [本文引用: 1]

61Yield functions F are constrained from the experimental data for 3 geomaterials.61F are defined for wide range of pressure and are similar for different materials.61Plastic potential function G is related to and can be obtained from F.61Both F and G are strongly dependent on the mean stress and inelastic deformation.61Relation of F and failure envelopes is discussed in view of practical applications.

[49]

韩文梅, 康天合 . 微凸体对抛光岩石表面静摩擦系数影响试验研究
岩土力学, 2013,34(3):674-578

URL [本文引用: 1]

对典型岩石摩擦滑动试验装置进行了改进,以8种硅酸盐岩作为研究对象,在低正应力条件下对岩石摩擦滑动过程中的静摩擦系数进行了试验研究。对滑动表面形貌进行了表征,从统计学角度分析了粗糙度对静摩擦系数的影响,并基于滑动表面微凸体(凹凸体、微观粗糙度)对这一影响作进一步分析。研究表明:滑动面为抛光面时,千枚岩、石英岩、岩屑砂岩和石英砂岩的静摩擦系数为0.38～0.47,砾岩、含砾粗粒石英砂岩、中粒岩屑砂岩和中粒石英砂岩的静摩擦系数为0.83～1.07;在粗糙度中,轮廓最大谷深Rm和轮廓最大峰高Rp两个参数导致摩擦滑动中产生不同静摩擦系数,且随着这两个参数的增加,静摩擦系数呈指数规律增加;千枚岩、石英岩、岩屑砂岩和石英砂岩滑动表面的微凸体数量较少,砾岩、含砾粗粒石英砂岩、中粒岩屑砂岩和中粒石英砂岩滑动表面的微凸体数量较多,随着微凸体数量的增加岩石摩擦滑动过程中的静摩擦系数增加。

( Han

Wenmei

, Kang

Tianhe

. Experimental study of influence of asperity on static friction coefficient for polished rock surface
Rock and Soil Mechanics, 2013,34(3):674-578 (in Chinese))

URL [本文引用: 1]