, 洪广洋, 李红影东北大学理学院, 沈阳 110819
THE COMPOSITE-MAPPING HYBRID ALGORITHM AND ITS APPLICATIONS OF VIBRATION PLATE BURIED IN PARTICLES1)
PanJingwu, LiJian, HongGuangyang, LiHongying中图分类号:O322
文献标识码:A
版权声明:2019力学学报期刊社力学学报期刊社 所有
基金资助:
作者简介:
-->
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (6580KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
连续体与散体颗粒材料的相互作用广泛存在于工程及生产实践中,散体颗粒材料的类固、类液等物理力学特性给连续体与颗粒材料的耦合研究带来了诸多挑战.埋入颗粒材料中的弹性板振动是工程领域中典型的连续-离散耦合动力学问题,如地基梁[1-3]、物料搅拌[4-5]等.
有限单元法已经是当今工程分析中应用最为有效且广泛的计算方法,离散单元法与有限单元法的耦合计算发展迅速,并成为连续-离散耦合计算的主要实现方式[6-9].在有限元与离散元耦合计算中,接触判断是耦合过程的主要难点,一些****提出利用过渡层[10-11]的方式解决相互接触问题.在过渡层中同时利用有限元和离散元进行计算,将离散元的位置信息与有限元节点相对应,这为连续-离散耦合体系的计算提供了一种新的思路. 尽管这样,目前有限元和离散元耦合计算仍然存在接触判断过于复杂且算法不连续,难以进行结构破碎过程[12]研究等诸多问题.连续体与离散介质的动态耦合作用仍需更加高效和完善的耦合计算方法.
随着离散单元法的逐渐发展以及连续-离散耦合研究的需要,离散单元法也开始应用于连续体介质的模拟和计算[13-15].通过弹簧连接质点构造连续介质的方法已经应用于块体岩石模拟[15]和脆性材料破碎[16-17]研究.相对于有限元方式,离散单元法在计算弹性体时更易于进行破碎相关扩展.但该方法在确定质点间弹簧相关系数、阻尼等方面存在一定难度,平行键[6,8]、弹簧元[14-15]、刚度矩阵映射[18]是目前离散单元法实现对连续介质计算的几种主要方式,其中刚度矩阵映射方式在参数的选取和模拟准确性上具有一定优势.
对连续体的边界构造,球形颗粒组合粘接[19-21]、扩展多面体[22]、超二次曲面[23-24]等方式不断发展和完善.其中球形颗粒组合粘接具有易于接触判断和可构造形状复杂等特点,其模型构造的精细程度与粘接颗粒数目和大小有关.利用球形组合粘接算法可以实现连续体与散体颗粒的相互作用,但粘接算法本身的局限性使数值模拟过程无法反映粘接体的变形和内力等信息.作为固体力学范畴模拟方法的质点弹簧法[18,24-25]与离散元有着类似的计算结构,这使得两种算法具有很强的兼容性.
一直以来,离散单元法存在计算量大、效率低等亟待解决的难点,并行计算作为提升计算效率的有效途径已广泛应用于离散元数值模拟[27].集群和图形处理器(graphics processing unit,GPU)作为两种主要的并行计算方式可改善程序计算结构,显著缩短计算时长.
本文将粘接算法与质点弹簧法相结合,通过有限元映射方式获得连续体中相关系数,形成粘接-映射混合算法. 利用信息传递接口(message passinginterface,MPI)和统一计算设备架构(compute unified devicearchitecture,CUDA)接口设计集群和GPU两个层级的并行算法.针对颗粒材料中的振动板问题,采用粘接-映射混合算法对离散-连续耦合下板的动力学行为和颗粒材料的耗能特性进行研究.
1 连续体映射算法
1.1 质点弹簧法
质点弹簧方法可以用于模拟弹性连续体的运动和变形[24].在质点弹簧模型中,连续体被离散为有限个质点和相连弹簧组成的网状结构.质点间以弹簧和阻尼器连接,质点携带质量、位移、速度、加速度等信息,弹簧结构反映物质的刚度、泊松比等属性.通过质点间位移可以获得结构体的运动和变形.对于连续体内矢径为${{r}}\left( {x,y,z}\right)$的任意质点($x,y,z$分别表示质点在笛卡尔坐标系下的3个直角坐标),当连续体发生移动和变形时,${{r}}$移动至${{r}}'$,质点位移可表示为${{u}} = {{r}}'-{{r}}$.对于一个弹簧连接的两个质点$i$和$j$,弹簧变形可表示为
\begin{equation}\label{eq1} \Delta {{u}} = {{u}}_i-{{u}}_j\tag{1}\end{equation}
弹簧产生的弹性力${{F}}_{ij} $可表示为
\begin{equation}\label{eq2} {{F}}_{ij} = {{k}}^{s}\Delta {{u}}\tag{2}\end{equation}
其中,${{k}}^{s}$是弹簧的连接刚度. 这样,非边界上内部质点$i$的受力${{f}}_i$为质点所连接的所有弹簧弹性力累加值
\begin{equation}\label{eq3} {{f}}_i = \sum\limits_{q = 1}^n {{{F}}_{iq}}\tag{3}\end{equation}
采用Verlet算法[24]可计算由某时刻$t$经过一个微小的时间增量到达时刻$t+ \deltaup t$时,质量为$m_i $的质点$i$的加速度${{a}}_i$、速度${{v}}_i $ 和矢径${{r}}_i $,即
$${{v}}_i \left(t + \frac{1}{2}\delta t\right) ={{v}}_i (t) + \frac{1}{2}{{a}}_i (t)\delta t\tag{4}$$
$${{a}}_i (t + \delta t) = \frac{{{f}}_i (t +\delta t)-c{{v}}_i (t +\delta t/2)}{m_i }\tag{5}$$
$${{v}}_i (t + \delta t) = {{v}}_i \left(t +\frac{1}{2}\delta t\right) + \frac{1}{2}{{a}}_i (t + \delta t)\delta t\tag{6}$$
$${{r}}_i (t + \delta t) = {{r}}_i (t) + {{ v}}_i(t)\delta t + \frac{1}{2}{{a}}_i (t)\delta t^2\tag{7}$$
式中$c$为介质阻尼系数.
在质点弹簧模型中,弹簧分布结构和刚度系数是真实反映连续体力学特性的决定因素.采用Gusev[28]提出的映射方法可以基于有限元矩阵获得质点弹簧结构中弹簧的刚度系数并与有限元节点具有相同的排布形式.本文在刚度矩阵映射的基础上,
提出了集中质量矩阵映射和Rayleigh阻尼映射方法.
1.2 弹簧刚度映射方法
对于一个有$n$个节点,单节点自由度为$m$的有限元系统,单元应变能$U^{e}$ 可表示为\begin{equation}\label{eq8} U^{e} = \frac{1}{2}{{u}}^{{e}^{T}}{{K}}^{e}{{u}}^{e}\tag{8}\end{equation}
其中,${{u}}^{e}$是单元位移向量,${{K}}^{e}$是单元刚度矩阵. 整个系统的应变能$U$为各单元应变能的累加
\begin{equation}\label{eq9} U = \sum\limits_e {U^e} = \frac{1}{2}{{ u}}^{T}{{Ku}}\tag{9}\end{equation}
式中,${{u}}$是整体位移向量,${{K}}$是总体刚度矩阵.通过最小位能原理可以得到节点载荷${{\widehat {F}}}$和位移向量${{u}}$ 之间关系为
\begin{equation}\label{eq10} {{\widehat{F}}} = {{Ku}}\tag{10}\end{equation}
以节点自由度$m$为单位将式(10)展开得
\begin{equation}\label{eq11} \left( {{\begin{array}{*{20}c} {{{\widehat {F}}}_1 } \\ \vdots \\ {{{\widehat {F}}}_i } \\ \vdots \\ {{{\widehat{F}}}_j } \\ \vdots \\ {{{\widehat{F}}}_n } \\\end{array} }} \right) = \left[ {{\begin{array}{*{20}c} {{{K}}_{11} } & \cdots & {{{K}}_{1i} }& \cdots & {{{K}}_{1j} } & \cdots & {{{K}}_{1n} } \\ \vdots & \ddots & \vdots & & \vdots & & \vdots \\ {{{K}}_{i1} } & \cdots & {{{K}}_{ii} }& \cdots & {{{K}}_{ij} } & \cdots & {{ {K}}_{in} } \\ \vdots & & \vdots & \ddots & \vdots & & \vdots \\ {{{K}}_{j1} } & \cdots & {{{K}}_{ji} }& \cdots & {{{K}}_{jj} } & \cdots & {{{K}}_{jn} } \\ \vdots & & \vdots & & \vdots & \ddots & \vdots \\ {{{K}}_{n1} } & \cdots & {{{K}}_{ni} }& \cdots & {{{K}}_{nj} } & \cdots & {{{K}}_{nn} } \\\end{array} }} \right]\left( {{\begin{array}{*{20}c} {{{u}}_1 } \\ \vdots \\ {{{u}}_i } \\ \vdots \\ {{{u}}_j } \\ \vdots \\ {{{u}}_n } \\\end{array} }} \right)\tag{11}\end{equation}
其中,${{\widehat {F}}}_i $和${{u}}_i$是节点$i$的载荷向量和位移向量,${{K}}_{ij} $为$m\times m$矩阵.当连续体无载荷下做刚体平动时系统应变能不变,依据此条件(即${{\widehat{F}}} = {\bf 0})$,可得刚度矩阵同一行元素中,主对角线元素等于非对角线元素之和的相反数,即
\begin{equation}\label{eq12} {{K}}_{ii} =-\sum\limits_{ q = 1 \atop q \ne i \\}^n {{{K}}_{iq} }\tag{12}\end{equation}
同时,节点$i$的受力可由式(11)对节点$i$展开得到
$$\label{eq13} {{f}}_i =-{{\widehat{F}}}_i = -({{K}}_{i1} {{u}}_1 + \cdots + {{K}}_{ii} {{u}}_i + \cdots +\\ \qquad {{K}}_{ij} {{u}}_j + \cdots + {{K}}_{in}{{u}}_n ) \tag{13} $$
将式(12)代入式(13)可得
\begin{equation}\label{eq14}\begin{array}{l} {{f}}_i =- \bigg[ {{{K}}_{i1} {{u}}_1 + \cdots } {-\sum\limits_{ q = 1 \atop q \ne i }^n {{{K}}_{iq} {{u}}_i } } + \cdots + \\\qquad { {{K}}_{ij} {{u}}_j + \cdots + {{ K}}_{in}{{u}}_n } \bigg] ={{K}}_{i1} ({{u}}_i-{{u}}_1 ) +\cdots+ \\\qquad {{K}}_{ij} ({{u}}_i-{{u}}_j ) + \cdots + {{K}}_{in} ({{u}}_i-{{u}}_n ) = \sum\limits_{ q = 1 \atop q \ne i }^n {{{K}}_{iq} ({{u}}_i-{{u}}_q )} \\ \end{array}\tag{14}\end{equation}
类比式(1)、式(2)、式(3)可得:在与有限元具有相同节点分布形式的质点弹簧系统中,弹簧刚度系数可由刚度矩阵中的元素表示.对于质点$i$和$j$之间连接的弹簧有
\begin{equation}\label{eq15} \left( {{\begin{array}{*{20}c} {{{F}}_{ij} } \\ {{{F}}_{ji} } \\\end{array} }} \right) = \left[ {{\begin{array}{*{20}c} {{{K}}_{ij} } & {-{{K}}_{ij} } \\ {-{{K}}_{ij} ^{T}} & {{{K}}_{ij} ^{T}} \\\end{array} }} \right]\left( {{\begin{array}{*{20}c} {{{u}}_i } \\ {{{u}}_j } \\\end{array} }} \right)\tag{15}\end{equation}
映射得到弹簧刚度${{\overline{k}}}^{s}$可表示为
\begin{equation}\label{eq16}{\overline{k}}^{s}=\bigg[\begin{array}{*{20}c}{{K}}_{ij} & {-{{K}}_{ij} } \\{-{{K}}_{ij} ^{T}} & {{{K}}_{ij} ^{T}} \\\end{array} \bigg]\tag{16}\end{equation}
由此通过有限元刚度矩阵映射得到了对应质点弹簧结构中的弹簧刚度系数.以图1为例,左图为由8个六面体8节点实体单元组成的有限元系统,通过有限元映射后,获得与中心位置处质点$i$相连的弹簧结构如右图所示.
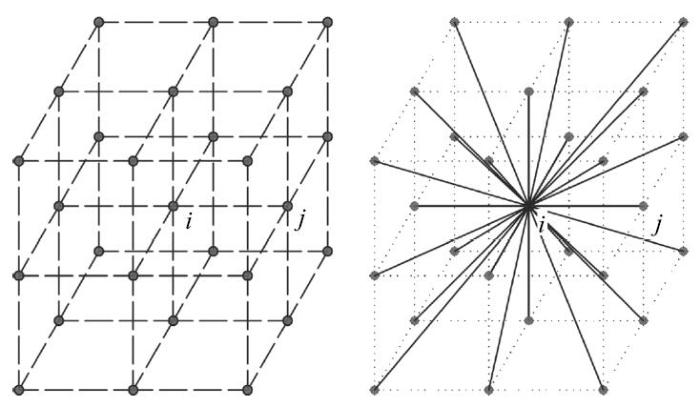显示原图|下载原图ZIP|生成PPT图1有限元映射弹簧结构...
-->Fig. 1Configuration of the lattice spring model by finite element mapping method
-->
1.3 质量和阻尼映射方法
质量矩阵${{M}}$由单元质量矩阵${{M}}^e$集成,即\begin{equation}\label{eq17}\left.\begin{array}{l} {{M}}^e = \int_{V_e } {\rho {{N}}^{T}} {{N}}\mbox{d}V \\[5mm] {{M}} = \sum\limits_e {{{M}}^e} \\ \end{array}\right\}\tag{17}\end{equation}
式中,$V_e$是单元体积,$\rho$是材料密度,${{ N}}$是插值函数.通过对单元质量矩阵中的元素$({{ M}}^e)_{\lambda \zeta }$进行对角化获得单元集中质量矩阵${{ M}}_l^e $,即
式中缩放因子$a$根据质量守恒原则确定. 集中质量矩阵是对角阵,质点弹簧算法中的质点质量$m_i$可由质量矩阵以节点自由度$m$为单位展开中对应项系数得到
\begin{equation}\label{eq19} {{M}}_{ii} = m_i {{I}}\tag{19}\end{equation}
式中${{I}}$是$ m\times m$的单位矩阵.
将质点弹簧中质点受到的阻尼力${{f}}^c$构造为正比于质点运动速度的介质阻尼和正比于弹簧连接质点间相对速度的结构阻尼两个部分.
\begin{equation}\label{eq20} {{f}}^c = c_1 {{\dot {u}}} + {{c}}_2 \Delta{{\dot {u}}}\tag{20}\end{equation}
其阻尼系数$c_1 $和${{c}}_2 $可通过有限元中的Rayleigh阻尼映射得到.Rayleigh阻尼可写为质量矩阵${{M}}$和刚度矩阵${{K}}$的线性组合,即
\begin{equation}\label{eq21} {{C}} =\alpha {{M}} + \beta {{ K}}\tag{21}\end{equation}
式中$\alpha $和$\beta $是比例系数. 则运动方程中阻尼力项可表示为
\begin{equation}\label{eq22} {{C\dot {u}}}\mbox{ = }\alpha {{M\dot{u}}} + \beta {{K\dot {u}}}\tag{22}\end{equation}
其中,$\alpha {{M\dot {u}}}$和$\beta {{K\dot {u}}}$两项可分别通过映射质量$\overline{m}$和映射刚度${{\overline{k}}}^s$的方法得到阻尼系数
\begin{equation}\label{eq23}\left.\begin{array}{l} c_1 = \alpha \bar {m} \\ {{c}}_2 = \beta {{\bar {k}}}^s \\ \end{array}\right\}\tag{23}\end{equation}
质点$i$受到的阻尼力${{f}}_i^c$ 可表示为
\begin{equation}\label{eq24} {{f}}_i ^c = \alpha m_i {{\dot {u}}}_i \mbox{+ }\beta \sum\limits_{ q = 1 \atop q \ne i }^n {{{K}}_{iq} ({{\dot {u}}}_i-{{\dot{u}}}_q )}\tag{24}\end{equation}
由此通过有限元质量和阻尼矩阵获得了对应结构的质点弹簧系统中的质量和阻尼系数.
2 粘接-映射算法及并行计算
2.1 离散元接触模型
颗粒接触模型是离散单元法的核心,本文采用软球模型.颗粒间的相互作用可分解为法向、切向、滚动方向.法向接触力$f_n $ 基于Hertz理论[29-30],即
\begin{equation}\label{eq25} f_n = k_n \delta ^{\frac{3}{2}} + c_n \Delta \dot{u}\tag{25}\end{equation}
式中,$\delta $是接触重叠量,$c_n $是法向非线性阻尼系数,$k_n$是法向接触刚度,其计算式为
\begin{equation}\label{eq26} k_n = \frac{4}{3}\left( {\frac{1-\nu _1^2 }{E_1 } +\frac{1-\nu _2^2 }{E_2 }} \right)^{-1}\sqrt {\frac{R_1 R_2}{R_1 + R_2 }}\tag{26}\end{equation}
式中,$\nu _1 $,$E_1 $,$R_1 $和$\nu _2 $,$E_2 $,$R_2$分别为两接触颗粒的泊松比、弹性模量和半径.
切向接触力$f_{t} $基于Mindlin-Deresiewicz理论和Mohr-Coulomb摩擦定律[31],即
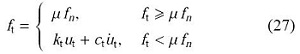
式中,$\mu $是摩擦系数,$u_{t} $,$\dot {u}_{t}$是接触点的滑移量和滑动速度,$c_{t}$是切向阻尼系数,$k_{t}$是切向接触刚度,其表达式为
\begin{equation}\label{eq28} k_{t} = \frac{16}{3}\left( {\frac{1-\nu _1^2}{G_1 } + \frac{1-\nu _2^2 }{G_2 }} \right)^{-1}\sqrt{\frac{R_1 R_2 }{R_1 + R_2 }\delta }\tag{28}\end{equation}
式中,$G_1 $和$G_2 $分别为两接触颗粒的剪切模量.
滚动方向力矩$f_{r} $ 可写为
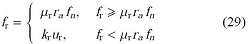
式中,$\mu _{r} $是滚动摩阻,$r_a $是接触半宽,$u_{r}$是转动角度,$k_{r} $是弹性转动刚度,其计算式为[32]
\begin{equation}\label{eq30} k_{r} = \left( {\frac{2R_1 R_2 }{R_1 + R_2 }}\right)^2k_{t}\tag{30}\end{equation}
2.2 粘接-映射混合算法的实现
质点弹簧法可以计算连续体受力后的变形及运动,但质点间的相互作用力计算基于相对位移,没有接触判断过程.因此在连续体与离散体相互作用的数值模拟中,质点弹簧算法无法通过接触判断这一过程完成与散体颗粒系统的相互作用.本文将质点弹簧系统与粘接系统耦合形成粘接-映射混合算法,实现质点弹簧系统与散体颗粒的耦合计算.在粘接-映射混合算法中,对连续体进行有限元网格划分并获得对应质点弹簧系统的质点分布结构.同时,基于有限元整体刚度矩阵${{K}}$、质量矩阵${{M}}$、阻尼矩阵${{C}}$,通过映射方法获得质点弹簧系统中弹簧网格分布,以及各弹簧刚度${ {\overline{k}}}^{s}$、质点质量$\overline{m}$、阻尼系数$c_1$和${{c}}_2 $.在质点弹簧系统外边界包络粘接颗粒,形成粘接-映射结构.在结构与散体颗粒相互作用时,通过外包络粘接系统获得颗粒对结构的作用力大小及位置并将其加载至内部质点弹簧系统中的对应质点,通过质点弹簧系统计算各质点位移,反馈至外部粘接系统中粘接颗粒的运动(如图2所示).由此可快速实现连续体与散体颗粒的直接力交互,在精细计算连续-离散系统耦合运动的同时,获得连续体内部动态力场及形变.
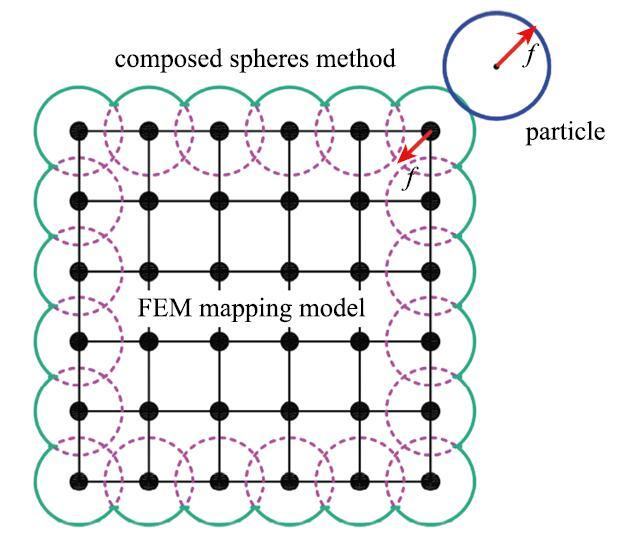显示原图|下载原图ZIP|生成PPT图2粘接-映射混合算法示例...
-->Fig.2The sample of composite-mapping hybrid algorithm
-->
2.3 并行计算
在散体颗粒和连续体耦合计算的数值模拟中,颗粒之间的接触搜索耗费大量计算费用.这主要是由于数目众多的颗粒需要在计算过程的每一个时间步中重新搜索颗粒接触状态.本文利用空间网格法[27]进行颗粒接触搜索.将数值模拟所需计算空间划分为有限个相等的方形网格(如图3所示).通过颗粒A球心坐标确定其所在网格编号,搜索相邻网格即可获得A所有接触对.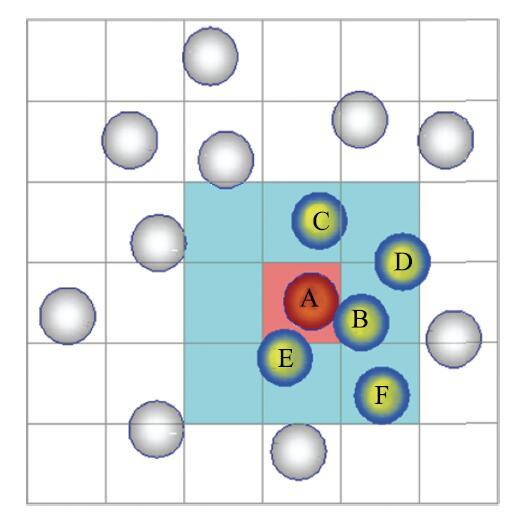
显示原图|下载原图ZIP|生成PPT图3空间网格法搜索示意...
-->Fig.3Schematic of spatial hashing algorithm
-->
利用该搜索算法的特性,可通过MPI+CUDA进行计算机集群和GPU两个层级的并行计算.计算机集群层级,利用分块切分数据方式实现并行. 以图4为例,长方形的数值模拟区域切分为4个相对独立的计算区,MPI中单个计算进程负责一个计算区域的任务处理.在单个计算区域内同时包含该区域及扩展区域的颗粒和网格信息,其中扩展区域为相邻计算区域部分重叠信息,以此保障数据的准确和连贯.通过数据切分减少计算机集群系统信息交互数据量. 在单个计算区域内,通过GPU并行进行颗粒搜索以及颗粒间、颗粒和连续体间的接触力和运动计算.
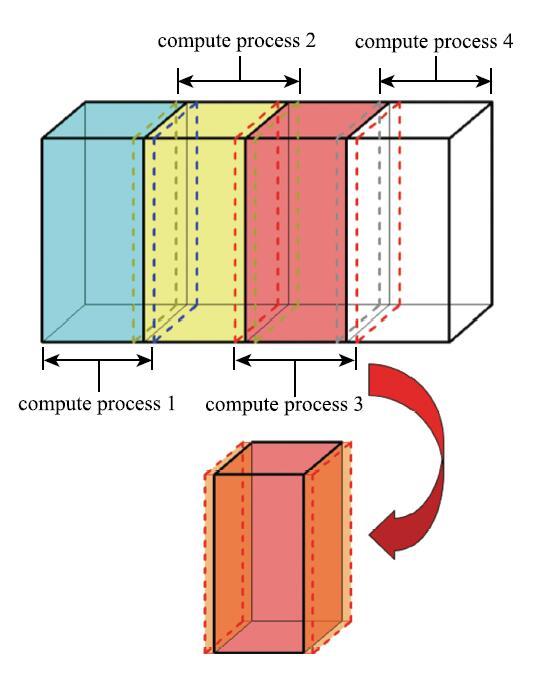显示原图|下载原图ZIP|生成PPT图4分块数据切分...
-->Fig.4Data segmentation by block
-->
质点弹簧算法拥有和离散元一样分布形式的数据结构. 与有限元算法相比,基于映射的质点弹簧算法无需获得荷载后进行整体的矩阵运算求解,而直接将质点作为动力学方程求解的基本单位. 因此,映射后的质点弹簧算法可通过上述并行方式获得和离散元一致的数据切分和并行计算结构.这使得粘接-映射混合算法便于集群和GPU双层级并行优化
3 颗粒材料中方板振动的数值分析
3.1 颗粒-振动板耦合系统模型
颗粒材料中的振动方板是典型的连续-离散耦合动力计算问题.采用粘接-映射混合算法可实现对振动方板和散体颗粒相关力学特性研究.数值仿真模型如图5所示,采用粘接-映射方式形成的四边固支方板位于箱体中(图5左),生成5982个颗粒埋没方板(图5右),板中心施加垂直于板面简谐激励$F(t)\mbox{ = }F_0 \sin (2{\pi}\theta t)$,其中$F_0 $和$\theta $分别是激振力幅值和频率.由8节点实体单元映射得到质点弹簧结构,相关模拟参数列于表1中.
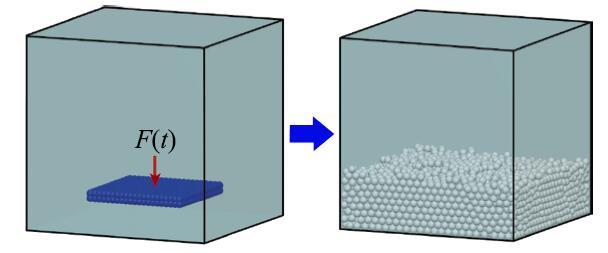显示原图|下载原图ZIP|生成PPT图5板在颗粒材料中振动的数值实验模型...
-->Fig.5The numerical simulation model of square plate vibration in granular media
-->
Table 1
表1
表1颗粒材料中方板振动模拟主要计算参数
Table 1Physical parameters used in numerical simulation of square plate vibration in granular media
 |
新窗口打开
3.2 激振力频率对耦合系统动态特性影响
为验证模型和算法可靠性,对未浸没颗粒的方板进行扫频激励.使用ANSYS软件建立相同网格的有限元模型进行对比. 激振力幅值$F_0 = 50~{N}$,扫频间隔10 Hz,获得激振点板厚方向位移响应$u$,采用快速傅里叶变换(FFT)得到各频率下位移响应幅值.图6是软件ANSYS的计算结果与粘接-映射混合算法计算结果对比,二者吻合良好,验证了算法的准确性. 从图中可知,板的一阶固有频率为300 Hz.
显示原图|下载原图ZIP|生成PPT图6未埋入颗粒时方板幅频响应曲线...
-->Fig.6Amplitude-frequency curve without particles
-->
将方板埋入颗粒中并进行扫频激励,扫频间隔10 Hz,激振力幅值分别为50N和100 N时得到激振点的幅频响应如图7所示. 由图中可知,由于颗粒的附加质量、刚度和阻尼效应,两种激励幅值下方板共振频率均大幅减小,振幅明显下降. 二者相比,相同频率下,振幅随激振力幅值增加而增大但一阶共振频率相同,均在90Hz处达到峰值,这表明颗粒的附加质量和刚度效应主要依赖于激振力频率,而不是激振力幅值.
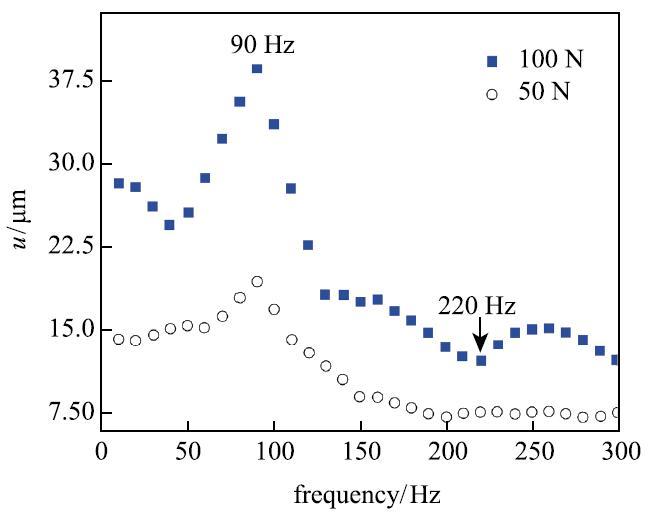显示原图|下载原图ZIP|生成PPT图7埋入颗粒后方板幅频响应曲线...
-->Fig.7Amplitude-frequency curve with particles
-->
为进一步探究颗粒-振动板耦合过程中颗粒材料能量耗散特性,考虑方板为无阻尼板,即在颗粒-振动板耦合系统中,只有颗粒产生能量损耗.通过计算系统输入有功功率$P$得到颗粒材料耗能情况[33].有功功率为
\begin{equation}\label{eq31} P = \frac{1}{T}\int_0^T {p(t)\mbox{d}} t =\frac{1}{T}\int_0^T {F(t)\dot {u}(t)\mbox{d}} t\tag{31}\end{equation}
其中,$T$为振动周期,$p(t)$为瞬时功率.对于简谐信号有功功率可表示为
\begin{equation}\label{eq32} P\mbox{ = }F_{\mbox{rms}} \dot{u}_{\mbox{rms}} \cos\varphi\tag{32}\end{equation}
其中,$F_{\mbox{rms}} $和$\dot {u}_{\mbox{rms}}$分别是激振力和速度的均方根,$\varphi $为二者相位差.
图8是激振力幅值为100 N时,方板埋入颗粒前后系统输入的有功功率随频率的变化图.对于未埋入颗粒的无阻尼板,系统稳定后各频率下有功功率均接近0值.埋入颗粒的简谐激励下振动板,有功功率分别在100 Hz,160 Hz,270Hz处出现波峰,130 Hz,220 Hz处出现波谷. 结合图7分析,有功功率与位移幅值随频率的波动形式具有一定对应关系(图7曲线在90 Hz,140 Hz,260 Hz处出现波峰在130 Hz,220 Hz处出现波谷). 由此可见,颗粒材料对于振动板的附加阻尼效应随着频率的增大而不断增大,虽然在振幅峰值附近均出现了颗粒材料耗能局部极值,但在最大振幅处未出现耗能最大值,这表明耦合系统中的颗粒耗能不完全取决于板的振动幅值,而是与振动频率高度相关并进一步受到板振动形态的影响.
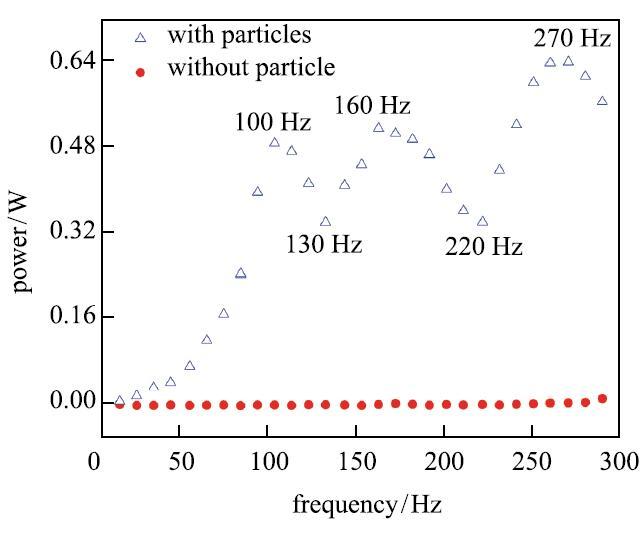显示原图|下载原图ZIP|生成PPT图8振动板埋入颗粒前后有功功率-频率曲线...
-->Fig.8Power-frequency curves for plate with and without particles
-->
3.3 激振力幅值对颗粒中方板振动行为影响
保持激振力频率不变,分别使用20$\sim$200N的激振力幅值对埋入颗粒中的方板进行定频变幅激振. 在激频150 Hz时,位移幅值和有功功率随激振力幅值变化如图9所示. 由图可知,位移幅值随激振力幅值单调增大,在力幅达到140 N后呈线性变化.有功功率在140 N之前随力幅增大不断递增,这表明当激振力频率保持不变时,力幅增大将使振幅增大,由于颗粒材料的非线性耗散特性,振幅随力幅变化也呈非线性. 在达到140N后有功功率基本保持不变.为进一步研究方板振动特性,图10给出了150Hz激励时不同力幅下的方板振动相轨迹、庞加莱映射和功率谱密度图.由图中可以看到,随着激振力幅值增加,方板振动发生二倍周期分岔,并在180 N功率谱密度中出现四倍周期迹象. 结合图9进行分析,在力幅增大到140 N产生二倍周期运动后,功率不再增加且位移幅值与激振力幅值呈线性关系递增. 这些现象表明,倍周期分岔使颗粒材料耗能存在临界值,这也验证了本文上一节观察到的"颗粒耗能不完全取决于板的振动幅值"现象.倍周期分岔后,颗粒材料耗能不再随振幅增大而发生改变,主频振幅随力幅呈线性变化. 图11给出了产生二倍周期振动的参数分布图,主要考虑激励频率和力幅两个参数的影响. 图中二倍周期区域呈片状分布,表明二倍周期产生于特定频率范围内并需要激振力达到一定水平.
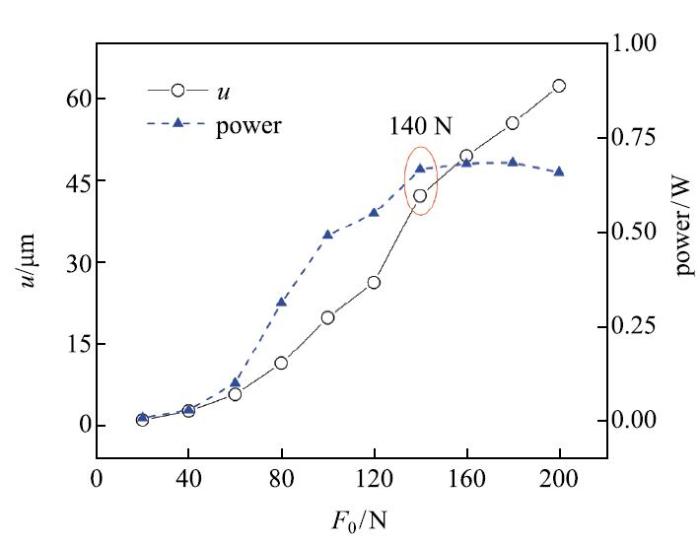显示原图|下载原图ZIP|生成PPT图9激振力幅值对位移幅值和有功功率的影响...
-->Fig.9Displacement-excitation and power-excitation curves of plate
-->
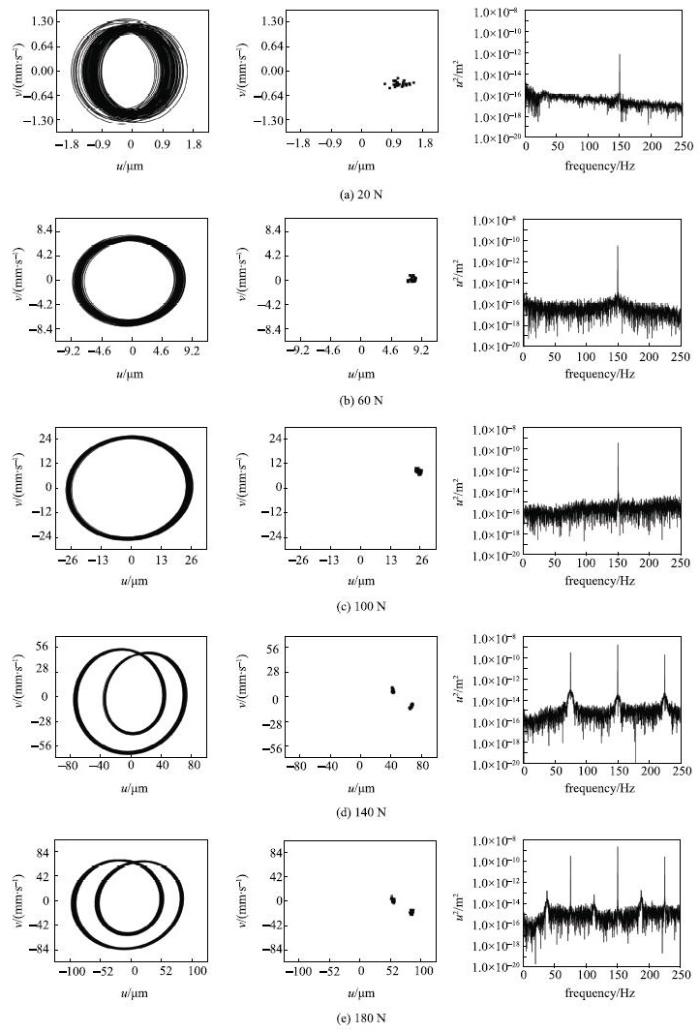显示原图|下载原图ZIP|生成PPT图10激频150 Hz时不同力幅下方板振动相轨迹、庞加莱映射和功率谱密度图...
-->Fig.10Phase diagram, poincare map and power spectrum of the plate under excitation with 150 Hz
-->
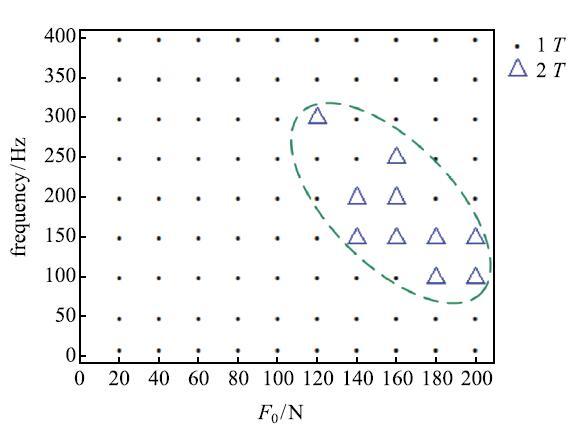显示原图|下载原图ZIP|生成PPT图11产生二倍周期振动的频率和力幅分布图...
-->Fig.11The vibrational configuration of the plate for various frequency and amplitude of excitation force
-->
4 结论
本文提出了基于并行技术的粘接-映射混合算法并将其应用于连续-离散耦合动力学问题研究.将粘接算法中的易于模型构造、接触判断快速便捷与质点弹簧算法中的力学参数便于考察、计算精度较高等特点相结合,实现了连续体与离散介质的动态耦合计算.给出了有限元映射至质点弹簧体系过程中弹簧刚度、质点质量和阻尼的完整映射方法.利用混合算法中的计算特性引入并行技术,实现了集群和GPU双层级并行计算. 通过在颗粒材料振动板问题中的应用,验证了算法的有效性.对颗粒材料中的方板进行简谐激励时,由于颗粒的附加刚度、质量和阻尼效应,系统共振频率大幅前移,振动幅值显著减小.在特定频率范围和激振力幅值达到一定水平时出现二倍周期分叉.颗粒材料阻尼耗能不完全取决于振动幅值并与振动频率密切相关,在定频变幅激振时颗粒材料耗能在二倍周期分叉后趋于稳定.
粘接精细程度对连续-离散界面力的交互影响有待研究.在瑞利波速较高的材料中,需选取较小计算时间步长,使得模拟效率存在限制,粘接映射算法计算效率仍需进一步优化. 此外,粘接-映射混合算法便于进行连续到离散的扩展,结构破碎等典型相关应用有待进一步展开.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . |
| [2] | . |
| [3] | . |
| [4] | . |
| [5] | . |
| [6] | |
| [7] | . |
| [8] | . |
| [9] | . |
| [10] | . . |
| [11] | . |
| [12] | . . |
| [13] | . |
| [14] | . . |
| [15] | . . |
| [16] | . |
| [17] | . |
| [18] | |
| [19] | . |
| [20] | . . |
| [21] | . |
| [22] | . . |
| [23] | . |
| [24] | . . |
| [25] | . |
| [26] | . |
| [27] | . |
| [28] | . |
| [29] | . |
| [30] | |
| [31] | . |
| [32] | . |
| [33] | . |
