,2), 王曙光, 李威威南京工业大学土木工程学院,南京211816NON-UNIFORM TIME STEP TVD SCHEME FOR PROBABILITY DENSITY EVOLUTION FUNCTION WITH IMPROVEMENT OF INITIAL CONDITION 1)
Shi Sheng, Du Dongsheng,2), Wang Shuguang, Li WeiweiColleye of Civil Engineering, Nanjing Tech University, Nanjing 211816, China通讯作者: 2) 杜东升,副教授,主要研究方向：工程抗震及振动控制.E-mail：ddshy@163.com
收稿日期:2018-12-24接受日期:2019-05-5网络出版日期:2019-07-18
| 基金资助: |
Received:2018-12-24Accepted:2019-05-5Online:2019-07-18
作者简介 About authors
摘要
随机性普遍存在于实际工程问题中,而复杂结构的非线性随机响应分析是其中的一个难点,近年发展的概率密度演化方法为此类问题的求解提供了新的途径.由于实际问题的复杂性,概率密度演化方程通常采用数值方法求解,因此提高计算效率和求解精度对实际应用具有重要意义.本文基于变网格技术,推导了概率密度演化方程在非均匀时间步长上的总变差减小(total variation diminishing,TVD)差分格式,算例结果表明通过自适应插值可将迭代次数减少为原来的43.4%,当随机过程样本持续时间增大时均值估计的平均误差基本不变,而标准差估计的平均误差不断增大,但增大幅度不断减小;计算耗时随样本持续时间的增大也呈增大趋势,而由于使用了时间步长自适应插值算法导致有些情况下长持时样本的计算耗时反而比短持时样本的计算耗时短;在传统的脉冲函数型初值条件基础上,提出了一种高阶导数更稳定的余弦函数型初值条件形式.结果表明,脉冲函数型的初值条件是余弦函数型初值条件的一个特例,当参数取值适当时,余弦函数型初值条件的数值求解结果具有更高的精度.本文的工作进一步完善了概率密度演化方程的求解方法,为其在实际工程中的应用提供了基础.
关键词：
Abstract
Randomness appears widely in practical engineering problems, and nonlinear stochastic response analysis of complex structures is one of the major difficulties. Fortunately, the probability density evolution method proposed in recent years has provided a feasible way to solve this kind of problem. Due to the complexity of practical engineering problems, however, the probability density evolution function is commonly solved by time-consuming numerical methods. Hence, it is crucial to improve the computational efficiency and accuracy of these numerical algorithms. Base on the non-uniform mesh partitioning technique, a new kind of non-uniform time step TVD (total variation diminishing) scheme for probability density evolution function was derived, which improves the computational efficiency by reducing the number of iterations to 43.4%. With the increase of sample duration, the error of estimated mean value remained almost constant, while the error of estimated standard deviation increased accordingly, but the increase rate tended to diminish. The computing time also increased as the sample duration increased, but unusual cases appeared due to the adaptive time step mesh partitioning of the randomly generated samples. In addition, a new kind of initial condition with cosine function form is proposed based on the conventional initial condition with pulse-like function form. The result revealed that the initial condition with pulse-like function form is a special case of the proposed cosine function form initial condition, and the initial condition with cosine function form possesses better accuracy than the initial condition with pulse-like function form when a proper parameter is selected. The improved TVD scheme for probability density evolution equation on non-uniform time step grids with improved initial condition is illustrated with several numerical examples provided in the last section. The work accomplished in this paper is a supplement for the solving method of probability density evolution equation, and provides a basis for engineering application.
Keywords：
PDF (9149KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
石晟, 杜东升, 王曙光, 李威威. 概率密度演化方程TVD格式的自适应时间步长技术及其初值条件改进 1). 力学学报[J], 2019, 51(4): 1223-1234 DOI:10.6052/0459-1879-18-446
Shi Sheng, Du Dongsheng, Wang Shuguang, Li Weiwei.
引言
随机性普遍存在于实际工程问题中,这些随机性包括激励的随机性(如海浪、风载荷、 地震地面运动等)和系统本身的随机性(如强度、刚度、几何尺寸等). 由这些随机源激起的机械或结构系统的振动称为随机振动,当随机源是外加激励时的随机振动是一种强迫振动, 由系统参数发生随机变化引发的随机振动称为参激随机振动[1].在工程抗震领域,Housner [2]首先指出地震动加速度是一个随机过程, 并建议将基底加速度模型化为白噪声. 经过多年的研究,已经发展出了一系列随机地震动模型. 如Kanai-Tajimi谱、Clough-Penzien谱等功率谱密度模型,经过时间调制的演变功率谱密度模型[3-5],考虑震源、传播途径、场地作用的物理随机函数模型[6]等.
结构的随机响应分析方面,线性结构的随机响应分析方法已经发展成熟. 采用经典的振型分解方法,可以由输入功率谱密度和频响函数计算输出功率谱密度[7]. 非线性系统的随机响应分析方法主要有FPK (Fokker Planck Kolmogorov)方程法[8-9]、随机响应面法[10-11]、蒙特卡洛模拟等. 另外,对于强非线性的滞迟系统,刘俊等[12]运用等效线性化法结合加权残值法得到了高斯白噪声激励下滞迟系统的稳态概率密度函数近似闭合解. 值得指出的是,目前虽然有许多预测非线性系统随机响应的方法,但没有一个是十分令人满意的,尤其是对多自由度非线性系统[1].
近年来,由李杰和陈建兵[13-17]发展的概率密度演化方法为复杂非线性结构的随机响应预测及其可靠度分析提供了新的途径,该方法也被越来越多地应用于解决实际工程问题. 宋鹏彦等[18]对结构参数具有随机性的混凝土框架进行了非线性随机地震反应概率密度演化分析,实现从材料随机性到整体结构可靠度的精细化分析. 余志武等[19]基于概率密度演化理论发展了多动力作用下轨道、桥梁系统随机振动分析方法和桥上行车安全评定方法. 刘章军等[20]运用概率密度演化理论对重庆石板坡长江第三大桥在随机地震作用下的可靠度进行分析,对比了一致激励与非一致激励下可靠度的差异. 郭弘原和顾祥林等[21]使用概率密度演化方法计算了钢筋在非均匀锈蚀情况下的时变可靠度,并与蒙特卡洛法的结果对比,验证了概率密度演化方法预测时变可靠度的准确性. 李杰和徐军[22]运用概率密度演化方法,提出了一种定量求解结构动力稳定概率的新方法,并通过和蒙特卡洛模拟结果对比验证了该方法的有效性.
概率密度演化方程是一种非线性平流方程,虽然对于几类典型的随机动力系统也发展了一些解析求解方法[23],但由于实际工程问题的随机性和复杂性,该方程一般通过数值方法求解.概率密度演化方程的数值求解主要包括概率空间剖分和差分求解两个步骤.在概率密度空间剖分方面,对于均布随机参数的概率空间剖分可以使用陈建兵和李杰提出的数论选点方法[24-25]和切球选点方法[26-27].对于非均布随机参数的概率空间剖分,陈建兵和张圣涵[28]提出了广义F偏差的概念,建议了以广义F偏差最小化为原则的概率空间最优剖分策略.在概率密度演化方程的求解方面,李杰和陈建兵[29]建议了一种带通量限制器的总变差减小(totalvariation diminishing, TVD)差分格式,并获得了较好的求解效果.Papadopoulos等[30]发展了一类基于伽辽金方法的有限差分格式,并对求解效果进行了验证.然而,文献中对算法的验证局限于较为平缓的演变速度,实际应用中演变速度通常是剧烈变化的,如结构受地震动、海浪和风载荷作用的动力响应.概率密度演化方程的求解精度会直接影响后续的可靠度分析结果,因此,方程的求解精度也需要得到重视.本文基于TVD格式的差分求解方法,推导了其在非均匀时间步长网格上的迭代方法,并提出一种余弦函数型的初值条件形式.数值验算表明,非均匀时间步长网格可以在保证精度的前提下减少迭代次数,结合余弦函数型的初值条件形式有利于提高概率密度演化方程数值求解的精度.值得指出的是,通常使用的脉冲函数型初值条件形式是余弦函数型初值条件的一个特例.
1 概率密度演化方程及其求解
概率密度演化方法是由李杰和陈建兵[13]提出的随机结构动力反应分析方法.该方法可以同时考虑输入随机性和结构随机性,适用于线性结构和非线性结构的随机动力响应分析.通过选点对概率空间剖分,将随机动力分析问题转化为多次确定性分析.对每一组选定的随机参数,求解一个概率密度演化方程,可以得到输出的演化概率密度.根据文献[16]的推导,对每一组选定的随机参数,概率密度演化方程具有如下的一般形式\begin{equation} \label{eq1} \frac{\partial p_{X\theta } \left( { x, \theta , t} \right)}{\partial t} + \sum\limits_{j = 1}^n {g_j \left( { \theta , t} \right)\frac{\partial p_{X\theta } \left( { x, \theta , t} \right)}{\partial x_j }} = 0 (1) \end{equation}其中,$p_{X,\theta }({x}, \theta,t)$为$t$时刻的响应$x$和随机参数$\theta$的联合概率密度函数;$g_{j}(\theta $,t)$为选定一组随机参数$\theta $时,响应量$x$的演变速度.
当考察系统响应第$l$个分量的概率信息时,可以得到如下的一维偏微分方程 \begin{equation} \label{eq2} \frac{\partial p_{X\theta } \left( {x_l , \theta , t} \right)}{\partial t} + g_l \left( { \theta , t} \right)\frac{\partial p_{X_l \theta } \left( {x_l , \theta , t} \right)}{\partial x_l } = 0 (2) \end{equation} 概率密度演化方程的解析求解非常困难,实际应用时通常采用数值求解方法,如李杰和陈建兵[15]推荐的Lax-Wendroff差分方法.
用$p_{i,j}$表示$p(i\Delta x,j\Delta t)$,$g_{j}$表示$g(j\Delta t)$,并令$h=$ $\Delta x,k=\Delta t$. 将$p$在$t=j\Delta t$处对时间$t$泰勒展开,并忽略高阶无穷小量可以得到 \begin{equation} \label{eq3} p_{i,j + 1} = p_{i,j} + k\frac{\partial p_{i,j} }{\partial t} + \frac{k^2}{2}\frac{\partial ^2p_{i,j} }{\partial t^2} (3) \end{equation} 利用概率密度演化方程的等量关系 \begin{equation} \label{eq4} \frac{\partial p_{i,j} }{\partial t} + g_j \frac{\partial p_{i,j} }{\partial x} = 0 (4) \end{equation} 通过恒等变换并在等式两边分别对$t$求导,可得到
$$ \frac{\partial p_{i,j} }{\partial t} =-g_j \frac{\partial p_{i,j} }{\partial x} (5)\\ \frac{\partial ^2p_{i,j} }{\partial t^2} = g_j \frac{\partial ^2p_{i,j} }{\partial x^2} (6) $$
将式(5)和式(6)代入$p_{i,j + 1}$的泰勒展开式(3)可得到 \begin{equation} \label{eq7} p_{i,j + 1} = p_{i,j}-kg_j \frac{\partial p_{i,j} }{\partial x} + \frac{k^2}{2}g_j^2 \frac{\partial ^2p_{i,j} }{\partial x^2} (7) \end{equation}
将$p$对$x$的一阶和二阶偏导数用中心差分公式表示为
$$ \label{eq8} \frac{\partial p_{i,j} }{\partial x} = \frac{p_{i + 1,j}-p_{i-1,j} }{2h} (8)\\ \frac{\partial ^2p_{i,j} }{\partial x^2} = \frac{p_{i + 1,j}-2p_{i,j} + p_{i-1,j} }{h^2} (9) $$
通过化简,可以得到$p$的Lax-Wendroff差分格式的递推表达式
$$ p_{i,j + 1} = p_{i,j}-r_L g_j p_{i-{1}/{2}} -\\ \qquad \frac{r_L g_j }{2}\left( {1-r_L g_j } \right)\left( {p_{i + {1}/{2}}-p_{i-{1}/{2}} } \right) (10) $$
其中
$$ \left.\begin{array}{l} p_{i + {1}/{2}} = p_{i + 1,j}-p_{i,j} \\ p_{i-{1}/{2}} = p_{i,j}-p_{i-1,j} \\ r_{L} = \dfrac{\Delta t}{\Delta x} \end{array}\right\} (11) $$
Lax-Wendroff差分格式是一种显示的差分格式,需要满足CFL条件$\vert r_{L}g_{j}\vert \le $1. 由于泰勒展开时忽略了高阶量,导致Lax-Wendroff格式计算得到的结果产生振荡,甚至出现负值. 因此,李杰和陈建兵[29]又发展了一种加入通量限制器的差分格式
$$ \begin{equation} p_{i,j + 1} = p_{i,j}-r_{L}[\frac{1}{2}(g_j + |g_j|)(p_{i,j}-p_{i-1,j}) + \\ \qquad \frac{1}{2}(g_j-| {g_j} |)(p_{i + 1,j}-p_{i,j})] - \\ \qquad \frac{|r_{L} g_j}{2}(1-|r_{L}g_j|)[\psi(r_{i + 1 / 2}^ + ,r_{i + 1 / 2}^-)(p_{i + 1,j}-p_{i,j})-\\ \qquad \psi(r_{i-1 / 2}^ + ,r_{i-1 / 2}^-)(p_{i,j}-p_{i-1,j})] (12) \end{equation} $$
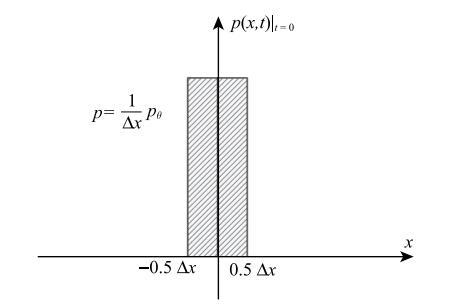
式中,$p_{i,j} $表示在网格点$\left( {i,j} \right)$处的概率密度值; $r_{i + 1 / 2}^ + = \left( {p_{i + 2,j}-p_{i + 1,j} } \right) / {\left( {p_{i + 1,j}-p_{i,j} } \right)} $; $r_{i + 1 / 2}^-= \left( p_{i,j} - p_{i-1,j} \right) / {\left( {p_{i + 1,j}-p_{i,j} } \right)} $; $r_{i-1/ 2}^ + = {\left( {p_{i + 1,j}-p_{i,j} } \right)} / {\left( {p_{i,j}-p_{i-1,j} } \right)} $; $r_{i-1/2}^-= {\left( {p_{i-1,j}-p_{i-2,j} } \right)} / {\left( {p_{i,j}-p_{i-1,j} } \right)} $; $\psi \left( {r^ + ,r^-} \right) = u\left( {-g_j } \right)\psi _{sb} \left( {r^ + } \right) + u\left( {g_j } \right)\psi _{sb} \left( {r^-} \right) $是Roe-Sweby通量限制 器;$ u\left( x \right)$为Heaviside函数;$\psi_{sb} \left( {r^ + } \right) = max \left[0,min \left( 2r^ + , 1 \right), min \left( {r^ + ,2} \right) \right]$; 一般,初始赋得概率可以通过下式计算 \begin{equation} \label{eq13} p_\theta \left( {x_i ,t} \right)\left| {_{t = 0} } \right. = \left\{ {\begin{array}{ll} \dfrac{1}{\Delta x}p_\theta , & x_i \in \left[ {x_0 - \frac{1}{2}\Delta x,x_0 + \frac{1}{2}\Delta x} \right] \\ 0 , &\mbox{otherwise} \end{array}} \right. (13) \end{equation} 其函数图像如图1所示
图1
新窗口打开|下载原图ZIP|生成PPT图1脉冲函数型初值条件
Fig. 1Initial condition with pulse-like function form
为了便于编程实现,本文推导了更加简洁的矩阵形式的迭代表达式.首先,对TVD差分迭代式(12)稍做变换,可以得到
$$p_{i,j + 1} = p_{i,j}-A_j \left( {p_{i,j}-p_{i-1,j} } \right) + B_j \left( {p_{i + 1,j}-p_{i,j} } \right) -\\ \qquad C_j \left( {p_{i + 1,j}-p_{i,j} } \right)-D_i \left( {p_{i,j}-p_{i-1,j} } \right) =\\ \qquad \left( {A_j-D_i } \right)p_{i-1,j} + \left( {1 - A_j + B_j + C_i + D_i } \right)p_{i,j} +\\ \qquad \left( {-B_j-C_i } \right)p_{i + 1,j} (14)$$
其中
$$ A_j = \frac{1}{2}\left( {g_j + \left| {g_j } \right|} \right) (15)\\ B_j = \frac{1}{2}\left( {g_j-\left| {g_j } \right|} \right) (16)\\ C_{i,j} = \frac{\left| {r_{L} g_j } \right|}{2}\left( {1-\left| {r_{L} g_j } \right|} \right)\psi \left( {r_{i + 1 / 2}^ + ,r_{i + 1 / 2}^-} \right) (17)\\ D_{i,j} = \frac{\left| {r_{L} g_j } \right|}{2}\left( {1-\left| {r_{L} g_j } \right|} \right)\psi \left( {r_{i-1 / 2}^ + ,r_{i-1 / 2}^-} \right) (18) $$
因此,迭代式可以用矩阵表示为 \begin{equation} \label{eq19} P_{j + 1} = M_j P_j (19) \end{equation}
其中
\begin{equation} \label{eq20} P_j =\left( {p_{1,j} }\quad {p_{2,j} }\quad {p_{3,j} } \quad \cdots \quad {p_{n-2,j} } \quad {p_{n-1,j} }\quad {p_{n,j} } \right)^{T} (20) \end{equation}
矩阵\textbf{M}$_{j}$可以分解为两个矩阵\textbf{M}$_{j1}$与\textbf{M}$_{j2}$之和. 可以发现,矩阵\textbf{M}$_{j1}$与\textbf{M}$_{j2}$均是稀疏带状矩阵. 当时间确定后,\textbf{M}$_{j1}$中的$A_{j}$和$B_{j}$在每个时刻的值是常数,而\textbf{M}$_{j2}$中的$C_{i,j}$和$D_{i,j}$会随矩阵的行数$i$发生变化.
$$ \begin{align*} &{ M_{j1} = \left( {{\begin{array}{*{20}c} 0 & {A_j } & {1-A_j + B_j } & {-B_j } & 0 & 0 & \cdots & 0 & 0 & 0 & 0 \\ 0 & 0 & {A_j } & {1-A_j + B_j } & {-B_j } & 0 & \cdots & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {A_j } & {1-A_j + B_j } & {-B_j } & \cdots & 0 & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \cdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & 0 & 0 & \cdots & {A_j } & {1-A_j + B_j } & {-B_j } & 0 \\ \end{array} }} \right)} (21)\\ &{ M_{j2} = \left( {{\begin{array}{*{20}c} 0 & {-D_{3,j} } & {C_{3,j} + D_{3,j} } & {-C_{3,j} } & 0 & 0 & \cdots & 0 & 0 & 0 & 0 \\ 0 & 0 & {-D_{4,j} } & {C_{4,j} + D_{4,j} } & {-C_{4,j} } & 0 & \cdots & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {-D_{5,j} } & {C_{5,j} + D_{5,j} } & {-C_{5,j} } & \cdots & 0 & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \cdots & \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & 0 & 0 & \cdots & {-D_{n-2,j} } & {C_{n-2,j} + D_{n-2,j} } & {-C_{n-2,j} } & 0 \\ \end{array} }} \right) }\qquad (22) \end{align*} $$
2 余弦函数型初值条件
概率密度演化方程在差分求解时,首先将空间$x$和时间$t$离散化,因此考虑初值条件时需要采取离散近似.由式(13)可知,公式将落在范围[$x_{0}-0.5\Delta x$, $x_{0}+0.5\Delta x$]内的赋得概率近似地累积在网格点$x_{i}$上.并且,由于TVD差分格式中使用了泰勒二阶展开,使初值条件的可导性对数值结果产生影响.因此,初值条件的处理方法是一个值得研究的问题.根据Lax-Wendroff格式的差分递推表达式(7),有$$ \left.\begin{array}{l} p_{i,j + 1} = p_{i,j}-kg_j \dfrac{\partial p_{i,j} }{\partial x} + \dfrac{k^2}{2}g_j^2 \dfrac{\partial ^2p_{i,j} }{\partial x^2} \\ p_{i,j + 2} = p_{i,j + 1}-kg_{j + 1} \dfrac{\partial p_{i,j + 1} }{\partial x} + \dfrac{k^2}{2}g_{j + 1}^2 \dfrac{\partial ^2p_{i,j + 1} }{\partial x^2} = \\ \qquad p_{i,j}-k\left( {g_j + g_{j + 1} } \right)\dfrac{\partial p_{i,j} }{\partial x} + \dfrac{k^2}{2}\left( {g_j + g_{j + 1} } \right)^2\dfrac{\partial ^2p_{i,j} }{\partial x^2} - \\ \qquad \dfrac{k^3}{2}g_j g_{j + 1} \left( {g_j + g_{j + 1} } \right)\dfrac{\partial ^3p_{i,j} }{\partial x^3}+ \dfrac{k^4}{4}g_j^2 g_{j + 1}^2 \dfrac{\partial ^4p_{i,j} }{\partial x^4} \\ \quad\qquad\qquad\qquad \qquad \qquad \vdots \\ p_{i,j + n} = {L}\left( {\dfrac{\partial p_{i,j} }{\partial x},\dfrac{\partial ^2p_{i,j} }{\partial x^2},\dfrac{\partial ^3p_{i,j} }{\partial x^3}, \cdots ,\dfrac{\partial ^{2n}p_{i,j} }{\partial x^{2n}}} \right) \end{array} \right\} (23) $$
其中,${L}( \cdot )$表示括号中表达式的线性组合. 从迭代式中可以发现,$p_{i,j + n}$总是可以由$p_{i,j}$各阶导数的线性组合得到. 因此,数值计算结果很大程度上受到初值条件可导性的影响,某个时刻的概率密度计算值可以由初值条件对$x$的各阶导数来表示. 本文基于余弦函数提出一种各阶导数更为光滑的初值条件形式,如图2所示,并推导了通用的构造公式.
图2
新窗口打开|下载原图ZIP|生成PPT图2余弦函数型初值条件
Fig. 2Initial condition with cosine function form
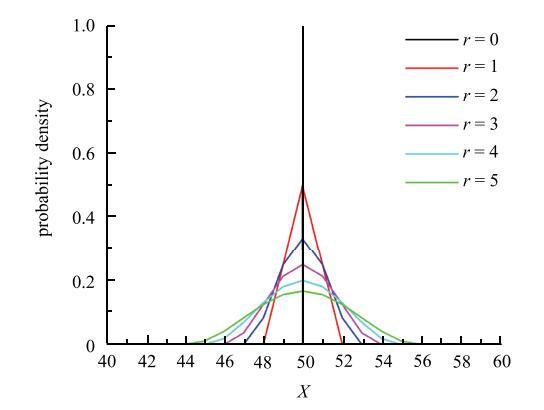
用$\Delta x$表示差分网格对$x$的差分步距,在初值条件函数$p(x,t)\vert _{t = 0}$的支集上均匀选取2$r+$1个点,则有如下等式 \begin{equation} \label{eq23} \frac{\pi }{k\left( {r + 1} \right)} = \Delta x (24) \end{equation} 那么,$x$轴上各个点的坐标值为 \begin{equation} \label{eq24} x \!=\! i\Delta x \!=\! \frac{{\pi i}}{{k\left( {r + 1} \right)}}, \quad i \!=\! -r,1-r,2-r, \cdots ,0,1,2, \cdots ,r (25) \end{equation} 将$x_{n}$代入函数表达式$p$中,并使所有点的函数值之和为1,有 \begin{equation} \label{eq25} \left. \begin{array}{l} p_i = \cos \dfrac{\pi i}{r + 1} + 1 \\ \sum\limits_{i =-r}^r {p_i = 1} \\ i=-r,1-r,2-r, \cdots ,0,1,2, \cdots ,r\end{array} \right\} (26) \end{equation} 联立方程组(26),可以得到如下的初值条件生成公式 \begin{equation} \label{eq26} p_\theta \left( {x_i ,t} \right)\left| {_{t = 0} } \right. = \left\{ {\begin{array}{ll} p_\theta \dfrac{\cos \dfrac{\pi }{\left( {r + 1} \right)\Delta x}x_i + 1}{\sum\limits_{n =-r}^r {\left( {\cos \frac{\pi n}{r + 1} + 1} \right)} }, \\ \qquad x_i \in \left[ {x_0-r\Delta x,x_0 + r\Delta x} \right] \\ 0 ,\quad {otherwise } \\ \end{array}} \right. (27) \end{equation} 因此,基于余弦函数的初值条件比原本的初值条件多了一个参数$r$. 参数$r$会决定初值条件的支集大小,并影响数值结果的精度. 如图3所示,$r$值越大对应的初值条件越平缓. 特别地,当$r=0$时,余弦函数型初值条件退化为脉冲函数型初值条件.
图3
新窗口打开|下载原图ZIP|生成PPT图3不同$r$值下的初值条件
Fig. 3Initial condition with differen values of $r$
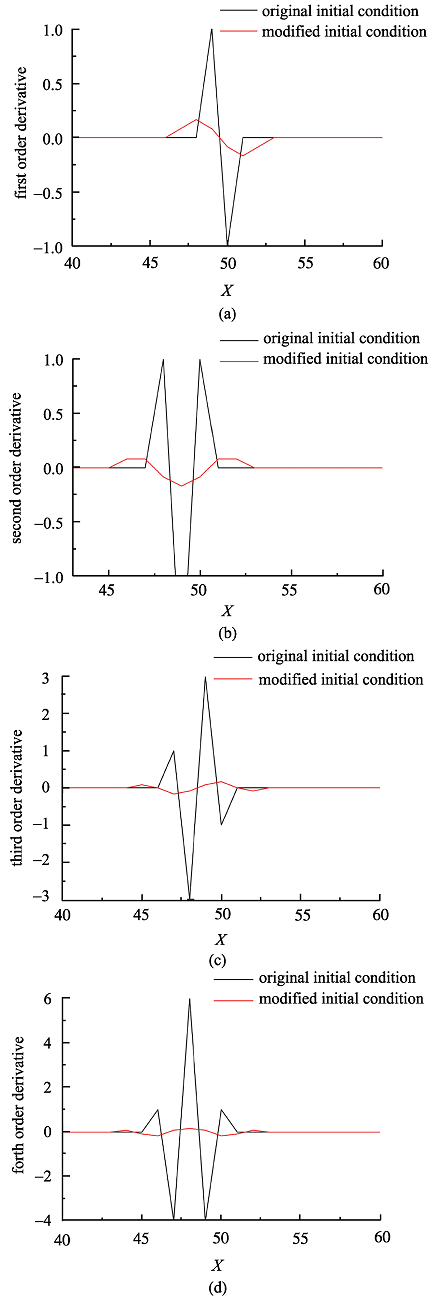
当$r=2$时,计算两种初值条件的前四阶导数如图4所示.可以发现,脉冲函数型的初值条件振荡越来越大,而余弦函数型的初值条件较为平稳.由于TVD差分格式下,任意节点处的解可以由初值条件各阶导数的线性组合得到,因此初值条件的可导性会影响数值结果的精度.
图4
新窗口打开|下载原图ZIP|生成PPT图4两种初值条件的各阶导数对比图
Fig. 4Derivatives of two types of initial conditions
3 非均匀时间步长网格
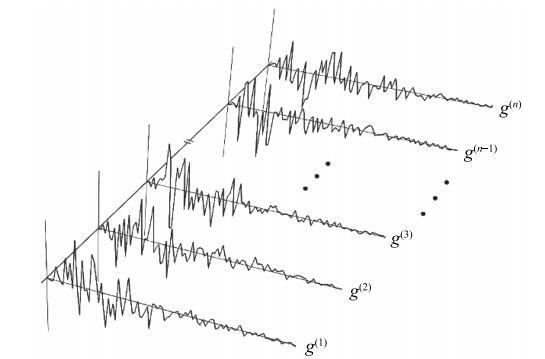
TVD格式是一种显式差分格式,需要满足CFL条件(Courant-Friedrichs-Lewy condition)才能保证收敛,即 \begin{equation} \label{eq27} \frac{\Delta t}{\Delta x}\left| {g_j } \right| \le 1 (28) \end{equation}一般情况下,PDEM的求解对象是地震载荷和风载荷等剧烈变化的随机过程,其导数过程{$g^{n}$}往往很大.因此,满足式(28)需要更小的时间步长和更大的空间步长.为了保证空间上的精度不能采取放大空间步长的方法,因此实际求解中采取对随机过程序列插值加密,以减小$\Delta t$的方式来满足收敛条件.然而,由于导数值在各个时间点处不同,满足收敛条件的插值密度也不同.若全局采用相同的插值密度,必然会增加不必要的计算量,因此,必须寻找一种更加科学的插值方法,使差分网格可以在需要的时刻局部加密.本文基于这个事实,提出了一种根据各个时刻的演变速度值$g_{j}$,在相邻网格点间自适应插值的方法,使TVD迭代求解在非均匀时间步长网格上进行.图5为演变速度样本.图5
新窗口打开|下载原图ZIP|生成PPT图5演变速度样本
Fig. 5Samples of evolution speed
考察图6中任意两个点($t_{j}, g_{j})$和($t_{j + 1}$, $g_{j + 1})$,假设每个时间点对应的值呈线性变化,则两点间某一个插值点($t_{j,k}$, $g_{j,k})$的CFL数为 \begin{equation} \label{eq28} CFL_{j,k} = \frac{t_{j,k + 1}-t_{j,k} }{\Delta x}\left| {g_{j,k}^n } \right| (29) \end{equation} 其中,$g^{n}_{j,k}$表示第$n$条响应量在第$j$和$j+$1个时刻之间第$k$个插值点的演变速度. 自适应插值后的$\Delta $t$_{j,k}$值需要使每一条响应在该时刻都满足CFL条件,因此,$t_{j}$和$t_{j + 1}$时刻之间的第$k$个插值点可以根据$g^{n}_{j,k}$值按以下迭代式取得 \begin{equation} \label{eq29} t_{j,k + 1} = \min \left\{ {\frac{C\Delta x}{\mathop {\max }\limits_n \left| {g_{j,k}^n } \right|} + t_{j,k} ,t_{j + 1} } \right\} (30) \end{equation} 其中,$C$是确定插值密度的常数,称为自适应插值系数,取值范围为$(0,1]$,$C$值越小插值密度越大.
图6
新窗口打开|下载原图ZIP|生成PPT图6演变速度的自适应插值
Fig. 6Adaptive interpolation of time points
4 数值算例
4.1 问题描述
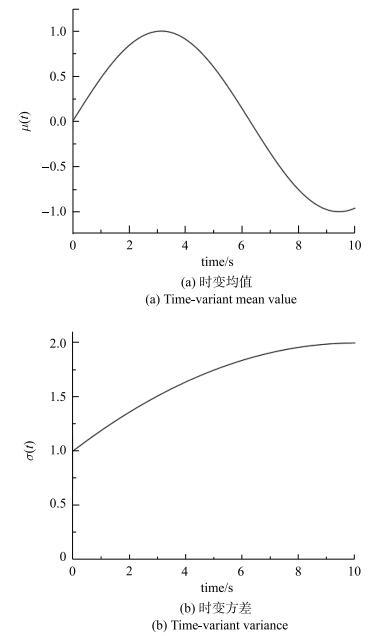
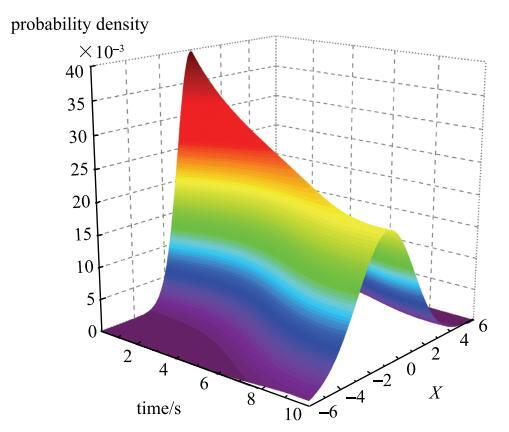
将一个均值和方差均为时变的正态分布概率密度函数为目标演变概率密度,生成100条随机过程样本.使用提出的改进算法计算其演变概率密度,再将改进前后的计算值与理论值对比.首先,定义一个演变概率密度函数作为随机过程生成的依据 \begin{equation} \label{eq30} p\left( {x,t} \right) = \frac{1}{\sqrt {2\pi } \sigma \left( t \right)}{\exp}\left[{-\frac{\left( {x-\mu \left( t \right)} \right)^2}{2\sigma ^2\left( t \right)}}\right] (31) \end{equation} 其中,概率密度函数的均值和方差随时间发生变化(图7), 变化规律为 $$ \sigma \left( t \right) = \frac{t\left( {20-t} \right)}{100} + 1, t \in \left[ {0,10} \right] (32)\\ \mu \left( t \right) = \sin \frac{t}{2}, t \in \left[ {0,10} \right] (33) $$ 由式(32)和式(33)生成的目标演变概率密度如图8所示.
图7
新窗口打开|下载原图ZIP|生成PPT图7正态分布时变参数
Fig. 7Time-variant parameters for normal distribution
图8
新窗口打开|下载原图ZIP|生成PPT图8目标演变概率密度
Fig. 8Target evolutionary PDF
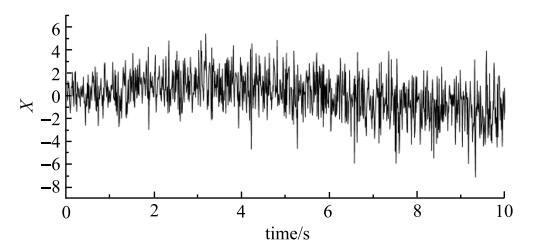
在每一个固定的时刻目标概率密度函数$p(x,t=t_{0})$是一个关于$x$的正态分布函数,本例在每一时刻以$p(x,t=t_{0})$为目标概率密度函数生成100个随机点.最后,可以得到100条形如图9所示的随机时程样本.
图9
新窗口打开|下载原图ZIP|生成PPT图9某一条随机过程响应
Fig. 9A typical sample of stochastic response process
4.2 余弦函数型初值条件
使用$r$值不同的余弦函数型初值条件结合TVD差分格式,分别求解以上100条随机过程的PDEM方程.需要注意的是,随机过程的方差越大其导数也越大,为了满足CFL条件需要对演变速度序列插值加密.以概率密度函数的均值和标准差作为算法精度验证的依据.当$r=4$时,TVD差分格式得到的演变概率密度图如图10所示.对比图8中的目标演变概率密度图可以发现,计算结果较为满意.值得指出的是,算法的误差一方面来自于数值方法本身,另一方面来源于生成的随机过程样本不能完全精确地反映概率信息.
图10
新窗口打开|下载原图ZIP|生成PPT图10估计演变概率密度($r=4$)
Fig. 10Estimated evolutionary PDF with $r=4$
由于差分格式计算得到的概率密度函数是一个二维矩阵,因此按式(34)和式(35)估计指定时刻的均值和标准差
$$ \widehat{\mu }\left( t \right) = \sum\limits_{i = 1}^{i_{\max } } {x_i p\left( {x_i ,t} \right)\Delta x} (34)\\ \widehat{\sigma }\left( t \right) = \sqrt {\sum\limits_{i = 1}^{i_{\max } } {x_i^2 p\left( {x_i ,t} \right)\Delta x-\hat{{\mu}}^2\left( t \right) } } (35) $$
理论值和估计值的误差定义为两者误差绝对值的均值
$$ error\left( \mu \right) = \frac{\sum\limits_{i = 1}^{i_{\max } } {\left| {\mu \left( {i\Delta t} \right)-\widehat{\mu }\left( {i\Delta t} \right)} \right|} }{i_{\max } \Delta t} \\ error\left( \sigma \right) = \frac{\sum\limits_{i = 1}^{i_{\max } } {\left| {\sigma \left( {i\Delta t} \right)-\widehat{\sigma }\left( {i\Delta t} \right)} \right|} }{i_{\max } \Delta t} (36) $$
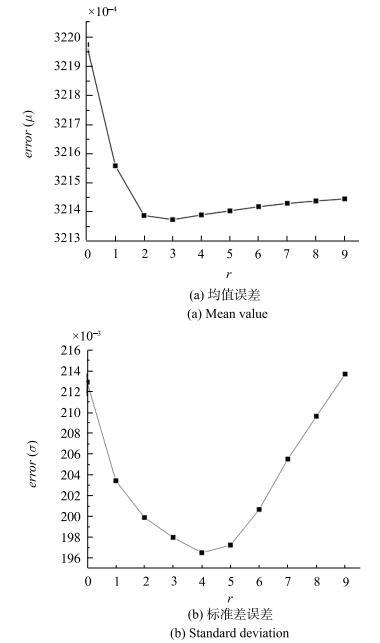
当$r$取值为0~9时,计算100条随机过程实现在各个情况下数字特征的平均绝对误差如图11所示. 值得注意的是,当$r=0$时,初值条件形式退化为最初的脉冲函数型.
图11
新窗口打开|下载原图ZIP|生成PPT图11数字特征的平均误差
Fig. 11Mean error of numerical characteristics
从图11可以发现,均值和方差的平均误差都有随着$r$先减小后变大的趋势.均值在$r$取3时平均误差最小,而标准差在$r$取4时达到最小.
4.3 非均匀时间步长
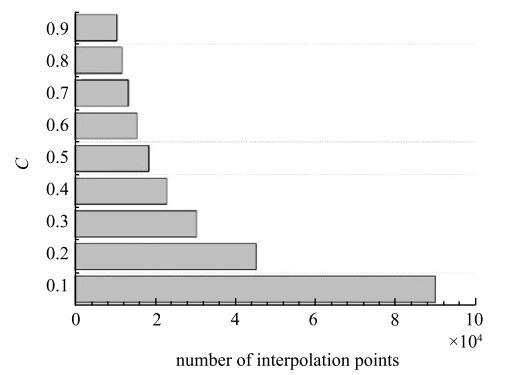
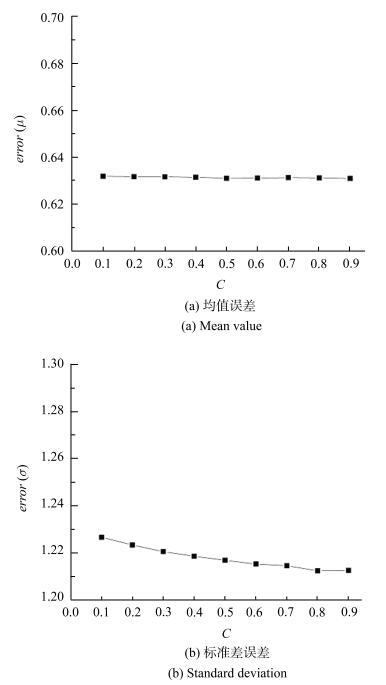
本例研究了自适应插值系数$C$对迭代次数和迭代精度的影响.对上例中生成的随机过程自适应插值,插值系数从0.1取到0.9,统计相应的迭代次数和精度的变化趋势.图12中显示了插值点数随插值系数$C$的变化规律,实际上在本例中,当取$C$值大于等于0.4时,自适应插值方法的插值点数已经小于全局插值方法.图13中记录了每个$C$值对应的绝对误差平均值,结果表明插值系数$C$的选取对均值和标准差计算精度的影响非常小.均值的误差随插值系数的变化较小,标准差的误差随插值系数的增大有所减小但变化也不明显.图12
新窗口打开|下载原图ZIP|生成PPT图12插值系数对插值点数目的影响
Fig. 12Variation of number of interpolation points with $C$
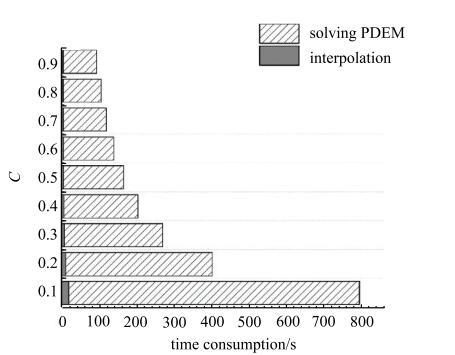
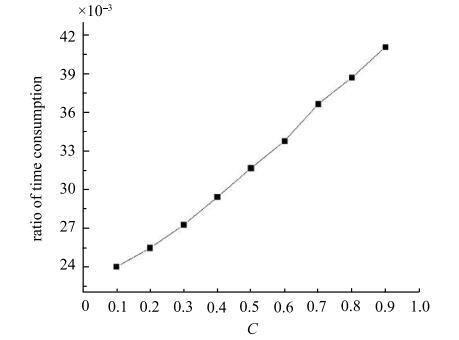
AAA图14展示了求解PDEM的计算时间分布,主要包括两个部分：演变速度的插值和PDEM方程的数值求解.可以发现,总计算时间和插值点数目的变化趋势一致.图15中绘制了插值时间和求解PDEM方程时间的比值,发现该比值随着插值系数的增大而增大,说明演变速度插值所花的时间占总时间的比率越来越大,算法在非均匀时间步长网格上的求解效率随插值系数$C$的增大而提高.
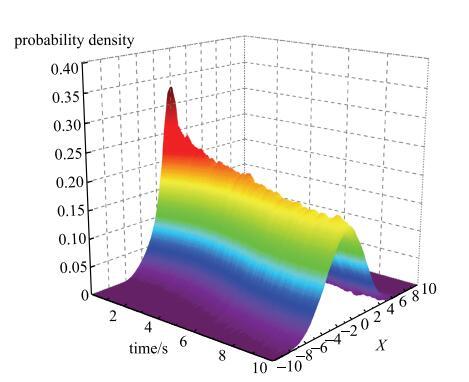
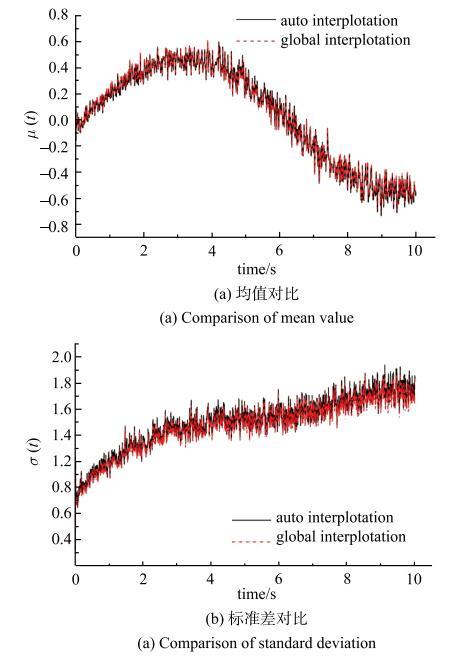
将自适应插值系数$C$设为0.9,得到图16所示的演变概率密度,图17中将自适应插值计算结果和常规的全局插值TVD格式对比.结果显示,在满足收敛条件的前提下,本例中常规TVD格式插值加密后需要24~000次迭代计算,而自适应插值算法仅需10~418次迭代计算.并且,自适应插值算法使用了较少计算量得到的结果和常规TVD格式具有相当的精度.
图13
新窗口打开|下载原图ZIP|生成PPT图13插值系数对精度的影响
Fig. 13Effects of $C$ on accuracy
图14
新窗口打开|下载原图ZIP|生成PPT图14插值和求解PDEM的计算时间
Fig. 14Time consumed by interpolation and solving PDEM
图15
新窗口打开|下载原图ZIP|生成PPT图15插值时间和求解PDEM时间的比值
Fig. 15Ratio of time consumed by interpolation and solving PDEM
图16
新窗口打开|下载原图ZIP|生成PPT图16估计演变概率密度($C=0.9$)
Fig. 16Estimated evolutionary probability density function ($C=0.9$)
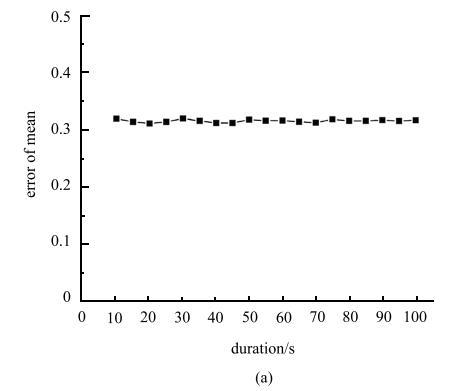
通常,工程实际中遇到的随机激励持续时间是任意的,显式的TVD算法会在迭代过程中使计算误差累积.为研究样本持续时间对算法精度的影响,本例中考察了样本持续时间分别为10s, 15 s, 20 s, $ \cdots $, 95 s, 100s的19种情况,从计算耗时、均值估计的平均误差、标准差估计的平均误差三个方面对比算法的性能,如图18所示.
从图18(a)和图18(b)可以发现,当样本持续时间从10 s增加到100s的过程中,均值的平均误差基本没有发生变化,而方差的平均误差有不断增大的趋势,但是误差的增幅不断趋于平缓.由于TVD格式是一种显式的差分格式,因此每次迭代求解都会将微小的误差不断累积;另外,由于加入了通量限制器限制了总变差不增,导致标准差的估计精度受到影响,但均值的估计精度基本不受影响.
图17
新窗口打开|下载原图ZIP|生成PPT图17自适应插值和全局插值精度对比($C=0.9$)
Fig. 17Results obtained by auto interpolation and global interpolation
AAA图18(c)中绘制了计算耗时随样本持续时间的变化曲线图.可以发现,随着样本持续时间的增大,计算耗时呈不断增大的趋势,但其中也有计算耗时随样本持续时间增大而减小的反常现象出现.出现这种现象的原因一方面有计算机性能波动的因素;另一方面是因为使用了时间步长自适应插值的算法,由于每次计算中使用的随机过程样本都是随机生成的,其演变速度也是随机的,因此会出现持时更长的样本自适应插值后计算量反而小于持时更短的样本.
图18
新窗口打开|下载原图ZIP|生成PPT图18样本持续时间对算法性能影响
Fig. 18Influence of sample duration on algorithm performance
图18
新窗口打开|下载原图ZIP|生成PPT图18样本持续时间对算法性能影响(续)
Fig. 18Influence of sample duration on algorithm performance (continued)
5 结论
概率密度演化方法是对复杂结构非线性随机响应分析的一种有效途径,但由于实际问题的复杂性,概率密度方程往往只能通过数值方法求解.传统的TVD差分格式中,通过对时间的二阶泰勒展开推导出了Lax-Wendroff差分迭代式.正是由于忽略了高阶泰勒展开项,导致数值结果出现振荡甚至出现负值.另外,为了满足CFL条件需要对演变速率序列加密插值,显式的差分格式会将误差在每个迭代步累积.总结本文的工作得到如下结论：(1)TVD格式是一种五点的显示差分格式,演变速度的高密度插值导致迭代计算量巨大.本文采用变网格技术,推导了概率密度演化方程在非均匀时间步长网格上的TVD差分迭代格式,通过自适应插值极大地减少了迭代次数,提高了求解效率.
(2)重新考察了TVD差分迭代式,发现任意时间格点的解可以表示为初值条件空间导数的线性组合.基于这个事实,在传统的脉冲函数型初值条件基础上提出了一种高阶导数更稳定的余弦函数型初值条件形式.结果表明,脉冲函数型的初值条件是余弦函数型初值条件的一个特例;当参数$r$取值适当时,余弦函数型初值条件的数值求解结果具有更高的精度.
(3)分别考察样本持续时间为10 s, 15 s, 20 s, $ \cdots $,95 s, 100s的19种情况,从计算耗时、均值估计的平均误差、标准差估计的平均误差三个方面对比时间步长自适应TVD算法性能.结果表明估计均值估计的平均误差随样本持续时间的增大变化不大,而标准差估计的误差随样本持续时间的增大不断增大,但增大的幅度越来越小;计算耗时随样本持续时间的增大也呈增大趋势,而由于使用了时间步长自适应插值算法导致有些情况下长持时样本的计算耗时反而比短持时样本的计算耗时短.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
DOIURL [本文引用: 1]
DOIURL
DOIURL [本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 2]
Magsci
从概率密度演化的基本思想出发,阐述了概率密度演化方程的历史、进展与应用.文中首先剖析和澄清了概率守恒原理的物理意义,论述了概率守恒原理的随机事件描述和状态空间描述,并由此阐明了概率密度演化与系统物理演化的内在联系, 即:系统的物理状态演化构成了概率密度演化的内在机制. 在此基础上,结合概率守恒原理的两类描述以及系统状态的物理演化方程,以与历史上不同的方式,重新推导了经典概率密度演化方程,包括Liouville方程、FPK方程和Dostupov-Pugachev方程,进一步阐明了这些方程的物理意义, 以及它们不能降阶的原因.结合概率守恒原理的随机事件描述和解耦的系统物理方程,导出了广义概率密度演化方程. 分析了广义概率密度演化方程的物理意义.以非线性结构随机反应的概率密度演化分析为例,展示了概率密度演化理论的应用前景. 最后,指出了需要进一步研究的问题.
Magsci
从概率密度演化的基本思想出发,阐述了概率密度演化方程的历史、进展与应用.文中首先剖析和澄清了概率守恒原理的物理意义,论述了概率守恒原理的随机事件描述和状态空间描述,并由此阐明了概率密度演化与系统物理演化的内在联系, 即:系统的物理状态演化构成了概率密度演化的内在机制. 在此基础上,结合概率守恒原理的两类描述以及系统状态的物理演化方程,以与历史上不同的方式,重新推导了经典概率密度演化方程,包括Liouville方程、FPK方程和Dostupov-Pugachev方程,进一步阐明了这些方程的物理意义, 以及它们不能降阶的原因.结合概率守恒原理的随机事件描述和解耦的系统物理方程,导出了广义概率密度演化方程. 分析了广义概率密度演化方程的物理意义.以非线性结构随机反应的概率密度演化分析为例,展示了概率密度演化理论的应用前景. 最后,指出了需要进一步研究的问题.
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIMagsci [本文引用: 1]
地震动无论是时间分布还是空间分布都具有很强的随机性，对于长大桥梁结构的随机地震反应与抗震可靠度分析，需要考虑地震动的时间和空间特性，才能较全面地反映桥梁结构的动力反应性态.采用非平稳地震动随机过程的正交展开模型，结合概率密度演化理论，对某连续刚构桥在一致激励和非一致激励下的随机地震反应与抗震可靠度进行了分析.研究结果表明，长大桥梁结构在一致激励与非一致激励下的抗震可靠度存在明显差异，按墩顶位移控制失效准则的抗震可靠度的相对误差可达50%，而按墩顶弯矩控制失效准则的抗震可靠度的相对误差则高达200%.
DOIMagsci [本文引用: 1]
地震动无论是时间分布还是空间分布都具有很强的随机性，对于长大桥梁结构的随机地震反应与抗震可靠度分析，需要考虑地震动的时间和空间特性，才能较全面地反映桥梁结构的动力反应性态.采用非平稳地震动随机过程的正交展开模型，结合概率密度演化理论，对某连续刚构桥在一致激励和非一致激励下的随机地震反应与抗震可靠度进行了分析.研究结果表明，长大桥梁结构在一致激励与非一致激励下的抗震可靠度存在明显差异，按墩顶位移控制失效准则的抗震可靠度的相对误差可达50%，而按墩顶弯矩控制失效准则的抗震可靠度的相对误差则高达200%.
[本文引用: 1]
[本文引用: 1]
DOIMagsci [本文引用: 1]
<p>提出了结构随机动力稳定性的定量分析方法,讨论了经典的随机动力稳定性概念,指出结构动力稳定性不仅与结构参数有关,也与作用在结构上的外部载荷密切相关,据此引入了一种判定结构动力稳定性的新准则,明确了结构随机动力稳定性的基本涵义.在概率守恒原理基础上,推导了概率耗散系统的广义概率密度演化方程.引入结构动力失稳的物理机制作为引起概率耗散的驱动力,利用概率耗散系统概率密度演化方程、可以方便获得结构响应的概率密度演化过程,从而定量求解结构的动力稳定概率.据此,可以定量评价结构系统依概率为1或依给定概率意义上的结构随机动力稳定性.采用本文所建议方法对典型结构动力系统进行了随机动力稳定性分析,并与蒙特卡洛方法计算结果进行对比.数值结果表明了所建议方法的有效性.</p>
DOIMagsci [本文引用: 1]
<p>提出了结构随机动力稳定性的定量分析方法,讨论了经典的随机动力稳定性概念,指出结构动力稳定性不仅与结构参数有关,也与作用在结构上的外部载荷密切相关,据此引入了一种判定结构动力稳定性的新准则,明确了结构随机动力稳定性的基本涵义.在概率守恒原理基础上,推导了概率耗散系统的广义概率密度演化方程.引入结构动力失稳的物理机制作为引起概率耗散的驱动力,利用概率耗散系统概率密度演化方程、可以方便获得结构响应的概率密度演化过程,从而定量求解结构的动力稳定概率.据此,可以定量评价结构系统依概率为1或依给定概率意义上的结构随机动力稳定性.采用本文所建议方法对典型结构动力系统进行了随机动力稳定性分析,并与蒙特卡洛方法计算结果进行对比.数值结果表明了所建议方法的有效性.</p>
DOIMagsci [本文引用: 1]
<p>近年来逐步发展的概率密度演化方法理论为随机动力系统的分析与控制研究提供了新的途径.过去若干年来,已经发展了一系列数值方法如有限差分法、无网格法用于求解广义概率密度演化方程.但是,针对典型随机系统,关于这一方程解析解尚比较缺乏.本文以李群方法为工具,研究给出了Van der Pol振子、Riccati方程和Helmholtz振子3类典型随机非线性系统的广义概率密度演化方程解析解.这些结果,不仅可以作为检验求解广义概率密度演化方程的数值方法结果正确性的判别依据,也为概率密度演化理论的进一步深入研究提供了若干分析实例.</p>
DOIMagsci [本文引用: 1]
<p>近年来逐步发展的概率密度演化方法理论为随机动力系统的分析与控制研究提供了新的途径.过去若干年来,已经发展了一系列数值方法如有限差分法、无网格法用于求解广义概率密度演化方程.但是,针对典型随机系统,关于这一方程解析解尚比较缺乏.本文以李群方法为工具,研究给出了Van der Pol振子、Riccati方程和Helmholtz振子3类典型随机非线性系统的广义概率密度演化方程解析解.这些结果,不仅可以作为检验求解广义概率密度演化方程的数值方法结果正确性的判别依据,也为概率密度演化理论的进一步深入研究提供了若干分析实例.</p>
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
DOIMagsci [本文引用: 1]
<p>首先考察了概率密度演化理论中的点演化和群演化与概率空间剖分的关系. 继而，讨论了点集筛选的基本准则. 在此基础上推广了点集偏差的概念，对非均匀、非正态的一般多维分布，提出了广义F 偏差（GF 偏差）的概念，避免了偏差计算的NP 难解问题. 探索了GF 偏差与EF 偏差的关系. 以GF 偏差最小化为准则，建议了概率空间最优剖分与点集重整的新策略. 结果表明，上述方法能够处理包含多达数10 个随机变量的结构动力响应概率密度演化分析问题. 最后，指出了需要进一步研究的问题.</p>
DOIMagsci [本文引用: 1]
<p>首先考察了概率密度演化理论中的点演化和群演化与概率空间剖分的关系. 继而，讨论了点集筛选的基本准则. 在此基础上推广了点集偏差的概念，对非均匀、非正态的一般多维分布，提出了广义F 偏差（GF 偏差）的概念，避免了偏差计算的NP 难解问题. 探索了GF 偏差与EF 偏差的关系. 以GF 偏差最小化为准则，建议了概率空间最优剖分与点集重整的新策略. 结果表明，上述方法能够处理包含多达数10 个随机变量的结构动力响应概率密度演化分析问题. 最后，指出了需要进一步研究的问题.</p>
[本文引用: 2]
[本文引用: 1]
