同济大学 土木工程防灾国家重点实验室, 土木工程学院,上海 200092
DIMENSION REDUCTION OF FPK EQUATION FOR VELOCITY RESPONSE ANALYSIS OF STRUCTURES SUBJECTED TO ADDITIVE NONSTATIONARY EXCITATIONS1)
RuiZhenmei, ChenJianbing中图分类号:U260.17
文献标识码:A
通讯作者:
收稿日期:2018-12-5
网络出版日期:2019-05-18
版权声明:2019力学学报期刊社 所有
基金资助:
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (8144KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引 言
工程结构所受的灾害性动力作用, 如地震和风荷载等都是非平稳随机过程,结构在其作用下的非线性响应分析迄今依然是具有高度挑战性的困难问题. 经过长期研究,已经发展了等价线性化法、矩截断方法、Monte Carlo方法和FPK方程法等[1-4]. 其中,等价线性化法得到了广泛的应用[5]. 但遗憾的是,该方法仅适用于弱非线性结构[6],且不能获得概率密度函数解答, 因而难以应用于结构可靠度分析[7]. 矩截断方法[3,8]的推导过程复杂,且精度难以得到保证. 而Monte Carlo方法的计算工作量巨大,且是随机收敛的,因而几乎无法用于实际工程分析之中. 对于白噪声或滤过白噪声激励,求解FPK方程理论上能够获得非线性结构概率密度精确解,因此得到了国内外****的高度关注[9],在其近似或精确平稳解答方面取得了重要的进展[10-13]. 同时,研究了多种数值求解方法,如有限差分法[13]、有限单元法[15]、特征函数展开[2]和路径积分法[16-17]等. 值得指出,对于低维问题,路径积分法是一种精度较高、结果较为稳健的方法[18-21],因而得到不少****的青睐. 然而,迄今为止,高维系统的非平稳响应分析问题依然面临巨大的困难.进行高维随机系统的降维是解决上述难题的可行途径之一. 例如通过随机平均法可将FPK方程的维数降低一半[12, 22-23]. Er[24]则结合等价线性化方法提出了一类降维近似方法,但其可求解的维度仍有较大限制. 近年来,李杰和陈建兵[4,25]发展的概率密度演化理论实现了系统的非线性和随机性的解耦,得到了不受制于系统维度的广义概率密度演化方程,并系统研究和发展了数值求解方法[26-27]. 在此基础上,将概率密度演化理论和FPK方程相结合,导出了降维的等价通量概率密度演化方程[28-29],进而通过引入等价漂移系数[30],提出了降维FPK型方程的形式[31].
基于上述研究,针对幅值调制的加性白噪声激励多自由度结构非平稳响应分析问题,本文导出了相应的降维FPK型方程,建议了构造等价漂移系数的条件均值函数方法. 通过单自由度Rayleigh振子、10层剪切型线性框架结构与非线性框架结构的非平稳速度响应概率密度函数的求解,讨论了本文建议方法的精度和效率,验证了该方法的有效性.
1 高维FPK方程降维
1.1 幅值调制的白噪声激励系统及其非平稳响应的FPK方程
工程中的随机动力过程、例如地震动过程[32],一般都是非平稳过程. 对白噪声过程进行幅值调制可以获得一个非平稳过程$$\tilde {\xi }(t) = g(t)\xi (t) (1)$$
其中,$g(t)$是进行幅值调制的确定性时间包络函数,$\xi (t)$是白噪声过程,满足
$$E[\xi (t)] = 0,\;\;E[\xi (t)\xi ({t}')] = D\delta (t - {t}') (2)$$
考虑一个多自由度体系在非平稳激励下的响应. 例如,设地震动加速度过程可以采用式(1)的模型简化表示,则结构地震响应动力方程为
$${\pmb M}\ddot{\pmb X} + {\pmb f} ({\pmb X}, \dot{\pmb X} ) = -{\pmb M} {\pmb 1}\tilde {\xi }(t) (3)$$
其中,${\pmb X} = (X_1 ,X_2 , \cdots ,X_n )^{\rm T}$表示$n$自由度系统相对地面的位移,${\pmb M} = [M_{ij}]_{n\times n} $是质量矩阵,${\pmb f}({\pmb X}, \dot {\pmb X}) = (f_1 ,f_2 , \cdots ,f_n )^{\rm T}\left({{\pmb X}, \dot{\pmb X}} \right)$表示阻尼力和恢复力向量,${\pmb 1} = (1,1, \cdots ,1)^{\rm T}$是分量均为1的列向量.
将式(1)代入式(3),并引入状态向量${\pmb Y} = \left( { {\pmb X}^{\rm T},\dot{\pmb X}^{\rm T}} \right)^{\rm T} = \left( {{\pmb X}^{\rm T},{\pmb V}^{\rm T}} \right)^{\rm T}$,则动力方程(3)可写成如下状态方程
$$\dot{\pmb Y} = {\pmb A}\left( {{\pmb Y},t} \right) +{\pmb B}g(t)\xi (t) (4)$$
其中
$${\pmb A}\left( {{\pmb Y},t} \right) = \left\{ \!\!\begin{array}{l} {\pmb V} -{\pmb M}{\pmb f}^{ - 1}\left( {{\pmb X},{\pmb V}} \right) \end{array} \right\},, \ {\pmb B} = - \left\{ \!\!\begin{array}{l} {\bf 0}_{n\times 1} {\pmb I} \end{array} \right\} (5)$$
从物理上看,式(4)可理解为Stratonovich随机微分方程. 由于其扩散系数与状态向量无关,即白噪声$\xi (t)$在式(4)中是加性的,因此与之相应的It\^{o}随机微分方程是
$$ {\pmb Y}(t) = {\pmb A}({\pmb Y},t) t + {\pmb B}g(t) W(t) (6)$$
其中,$W(t)$是维纳过程,满足$E[ W(t)] = 0$, $E\{[ W(t)]^2\} = D t$. 初始条件为${\pmb Y}(0) = {\pmb Y}_0 $, ${\pmb Y}_0 $是确定性或随机的初始向量.
记响应${\pmb Y}(t)$的联合概率密度为$p_{ Y} ({\pmb y},t)$,其中${\pmb y} = (y_1 ,y_2 , \cdots ,y_{2n})^{\rm T}$,则与It\^{o}随机微分方程(6)相对应,可得$p_{ Y} ( {\pmb y},t)$满足的FPK方程[33]
$$ \dfrac{\partial p_{ Y} ({\pmb y},t)}{\partial t} = - \sum_{j = 1}^{2n} \dfrac{\partial [{\pmb A}_j ({\pmb y},t)p({\pmb y},t)]}{\partial y_j }+ \dfrac{g^2(t)}{2}\sum_{i = 1}^{2n} \sum_{j = 1}^{2n} \sigma _{ij} \dfrac{\partial ^2p({\pmb y},t)}{\partial y_i \partial y_j } (7) $$
其中,漂移系数$A_j ({\pmb y},t)$是${\pmb A}({\pmb y},t)$的第$j$个分量,扩散系数$\sigma _{ij} $是扩散矩阵${\pmb \sigma }$的分量,且
$${\pmb \sigma } = {\pmb B}{\pmb B}^{\rm T}D (8)$$
FPK方程(7)的边界条件一般为
$$\left. {p_{ Y} ({\pmb y},t)} \right|_{y_j \to \infty } = 0 (9)$$
若初始条件是确定性的,则方程(7)的初始条件为
$$p_{ Y} ({\pmb y},t) = \delta ({\pmb y} - {\pmb y}_0 ) (10)$$
其中,${\pmb y}_0 $是确定性初始向量,$\delta ( \cdot )$为Dirac函数.
1.2 FPK方程的降维
上述FPK方程是一个$ {2}n$维偏微分方程. 如前所述,直接求解高维FPK方程十分困难. 事实上,在工程实际中,往往并不需要所有状态量的联合概率密度函数,而仅需要其中的一个或少数分量的概率分布信息. 本文中考虑仅关心一个物理量时的FPK方程降维问题.假设待求的是分量$Y_l (t)$的概率密度函数$p_{Y_l } (y_l ,t)$,则将方程(7)两边关于除$y_l $以外的所有其他分量积分,并注意边界条件(9),可得如下通量方程$^{[28\hbox{-}29]}$
$$ \dfrac{\partial p_{Y_l } (y_l ,t)}{\partial t} = - \dfrac{\partial J_l (y_l,t)}{\partial y_l } + \dfrac{\sigma _{ll} g^2(t)}{2}\dfrac{\partial^2 p_{Y_l } (y_l ,t)} {\partial y_l^2 } (11) $$
其中,边缘概率密度函数
$p_{Y_l } (y_l ,t) = \int_{ - \infty }^\infty { \cdots \int_{ - \infty }^\infty {p_{ Y} ({\pmb y},t)} } y_1 \cdots y_{l - 1} y_{l + 1} \cdots y_{2n} $
$J_l (y_l ,t)$为$y_l $方向的概率通量
$$J_l (y_l ,t) = \int_{ - \infty }^\infty { \cdots \int_{ - \infty }^\infty {A_l ({\pmb y},t)} } \cdot p_{ Y} ( {\pmb y},t ) \qquad y_1 \cdots y_{l - 1} y_{l + 1} \cdots y_{2n} (12) $$
进而,引入等价漂移系数[30]
$$a^{\rm eq}(y_l ,t) = \dfrac{J_l (y_l ,t)}{p_{Y_l } (y_l ,t)} (13)$$
式(11)可进一步改写为
$$ \dfrac{\partial p_{Y_l } (y_l ,t)}{\partial t} = - \dfrac{\partial a^{eq}(y_l ,t)p^2_{Y_l } (y_l ,t)}{\partial y_l } + \qquad \dfrac{\sigma _{ll} g^2(t)}{2}\dfrac{\partial^2 p_{Y_l } (y_l ,t)}{\partial y_l^2 } (14) $$
这一方程与一维FPK方程的形式相同,可称为降维FPK型方程. 由扩散系数$\sigma _{ij} $的形式知,只有当$n + 1 \leqslant l \leqslant 2n$时,$\sigma _{ll} \ne 0$,也即当$Y_l $是${\pmb Y}$的速度分量时,式(14)是FPK型方程. 在本文中,仅研究这种情形.
1.3 等价漂移系数的意义
为了求解降维FPK型方程(14),需要首先获得等价漂移系数. 而根据式(12)和式(13),为了获取等价漂移系数,则需要首先知道联合概率密度函数$p_{ Y} ({\pmb y},t)$和边缘概率密度函数$p_{Y_l } (y_l ,t)$,而这两个函数是未知的. 因此,初看起来降维FPK型方程(14)是不封闭的. 在Chen 和 Yuan$^{ [28\hbox{-}29]}$的研究中,针对白噪声激励(其中$g(t) \equiv 1$),通过首先求解广义概率密度演化方程构造数值通量,实现了方程(11)的闭合.本文将从另一个角度解决这一问题. 为此,首先进一步考察等价漂移系数的意义. 将式(12)代入式(13),有
$ a^{\rm eq}(y_l ,t) = $
$\quad \dfrac{\int_{ - \infty }^\infty { \cdots \int_{ - \infty }^\infty {A_l ({\pmb y},t)} } p_{ Y} ( {\pmb y},t ) y_1 \cdots y_{l - 1} y_{l + 1} \cdots y_{2n} }{p_{Y_l } (y_l ,t)} =$
$\quad \int_{ - \infty }^\infty { \!\cdots\! \int_{ - \infty }^\infty \!{A_l ( {\pmb y},t)} } \dfrac{p_{ Y} ( {\pmb y},t ) }{p_{Y_l } (y_l ,t)} y_1 \cdots y_{l - 1} y_{l + 1} \cdots y_{2n} =$
$\quad \int_{ - \infty }^\infty { \cdots \int_{ - \infty }^\infty A_l ( {\pmb y},t) } p_{{ Y}\vert Y_l } ( {\pmb y},t\vert Y_l = y_l )$
$\quad y_1 \cdots y_{l - 1} y_{l + 1} \cdots y_{2n} = E[A_l ( {\pmb Y},t\vert Y_l = y_l ) ] (15)$
由此可见,等价漂移系数$a^{\rm eq}(y_l ,t)$是原方程漂移系数$A_l ({\pmb Y},t)$在$Y_l = y_l $条件下的期望,即等价漂移系数本质上是条件均值函数[31].
2 降维FPK型方程求解的数值方法
2.1 等价漂移系数的确定
可以采用不同的途径确定降维FPK型方程(14)中的等价漂移系数. 本文中建议一类数值估计方法,具体步骤是：(1) 通过数值模拟生成若干(例如$m$个)白噪声样本$\{\xi ^{(k)}(t)\}_{k = 1}^m $,将其进行幅值调制、即代入式(4)中,进行确定性系统分析,获得一系列响应$\{{\pmb Y}^{(k)}(t)\}_{k = 1}^m $及其分量$\{Y_l^{(k)} (t)\}_{k = 1}^m $,同时可以获得相应的漂移系数样本值$\{A_l^{(k)} (t) = A_l ({\pmb Y}^{(k)}(t),t)\}_{k = 1}^m $.
(2) 对于时刻$t$,可以获得$m$个数据对$\{(y_l^{(k)} ,A_l^{(k)} )\}_{k = 1}^m $,其中$y_l^{(k)} = Y_l^{(k)} (t)$.
(3) 根据二维数据对$\{(y_l^{(k)} , A_l^{(k)} )\}_{k = 1}^m $,估计条件均值函数,由此给出等价漂移系数$a^{\rm eq}(y_l ,t)$. 一般情况下,可以采用数理统计中的诸多方法进行条件均值估计. 例如,当数据较多、而对条件均值函数的数学形式信息较少时,可采用局域平均法;当对条件均值函数的数学形式有清楚的认识时,则可采用最小二乘法获得条件均值函数估计的满意结果.
2.2 降维FPK型方程的路径积分求解
降维FPK型方程的求解可采用多种不同数值方法. 这里将采用路径积分法[16,20]. 这时,将时间离散为$t_j = j\tau$, $j = 0,1,2, \cdots $,则路径积分的数值解答可通过如下递推公式获得(注意在本小节中为方便计以$y$代替$y_l $)$$ p_{Y_l } (y,t_{j + 1} ) = \int_{ - \infty }^\infty {p_{Y_l } (y,t_{j + 1} \vert {y}',t_j ) \cdot p_{Y_l } ({y}',t_j ) {y}'} (16) $$
其中转移概率密度函数$p_{Y_l } (y,t_{j + 1} \vert {y}',t_j )$可近似用短时高斯分布代替
$$ p_{Y_l } (y,t_{j + 1} \vert {y}',t_j ) = \dfrac{1}{\sqrt {2\pi \sigma _{ll} \tau } g(t_j )} \cdot \qquad \exp \left\{ { - \dfrac{(y - {y}' - \tau a^{\rm eq}({y}',t_j ))^2}{2\sigma _{ll} \tau g^2(t_j )}} \right\} (17) $$
初始条件为
$$p_{Y_l } (y,0) = \delta (y - y_{l0} ) (18)$$
其中,$y_{l0} $为确定性初始向量${\pmb y}_0 $的第$l$个分量.
3 典型实例分析
一般情况下,在地震动加速度过程的持续时间$[0,T]$内,幅值调制函数具有初始增长段、强震段和衰减段,且$\mathop{\max }\limits_{0 \leqslant t \leqslant T} g(t) = 1$. 本文中取[34]$$g(t) = C \cdot \left( { {\rm e}^{ - B_1 t} - {\rm e}^{ - B_2 t} + \dfrac{1}{3}} \right) (19)$$
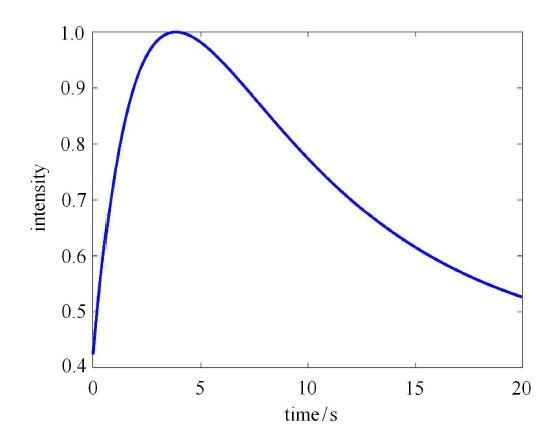
其中$B_1 = 0.04\pi $,$B_2 = 0.15\pi $,$C$是归一化常数,调制函数在20,s内的形状如图1所示.
显示原图|下载原图ZIP|生成PPT图1时间调制函数
-->Fig. 1Modulation function versus time
-->
在本文中,用谱表达方法生成白噪声,频率范围取为[0,100],rad/s,间隔为0.1,rad/s,共1001项谐和分量,随机相位用Sobol'点列模拟,时间步长取0.001,s. 以下给出的单自由度和多自由度体系实例分析均采用上述基本参数,仅白噪声强度不同.
3.1 单自由度Rayleigh振子的非平稳速度响应概率密度函数
Rayleigh振子系统具有非线性阻尼,在具有幅值调制的白噪声激励下其运动方程为[35]$$ \ddot {X} + 2\zeta _0 \omega _0 ( - 1 + \varepsilon \dot {X}^2)\dot {X} + \omega _0^2 X = g(t)\xi (t) (20)$$
其中,参数取值为$\omega _{0} = 1.1$, $\zeta _0 = 0.1$, $\varepsilon = 0.4$,峰值强度为1.
通过采用数值方法求解二维FPK方程,可以获得上述Rayleigh振子速度$\!$-$\!$-$\!$位移响应的时变联合概率密度函数.进而,可以获得速度响应的瞬态边缘概率密度函数. 求解的时间步长为$\tau = 0.01$,s,空间步长为$\Delta x = 0.05$,m,$\Delta \dot {x} = 0.05$,m/s. 本文中将以这一结果作为与降维FPK型方程解答对比的基准.
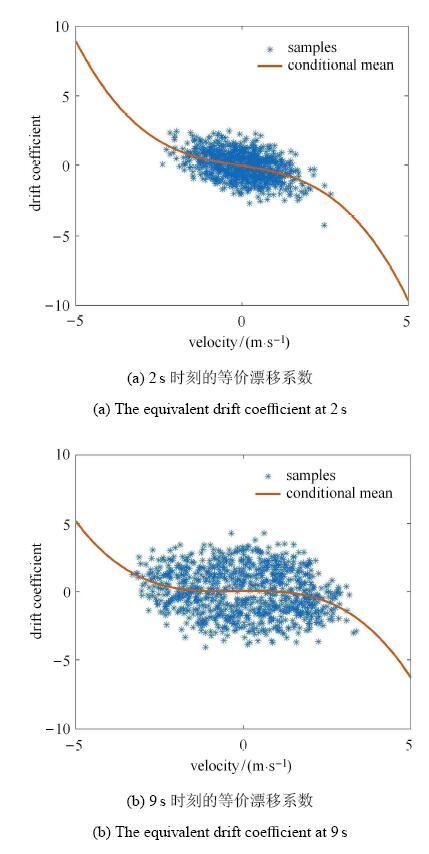
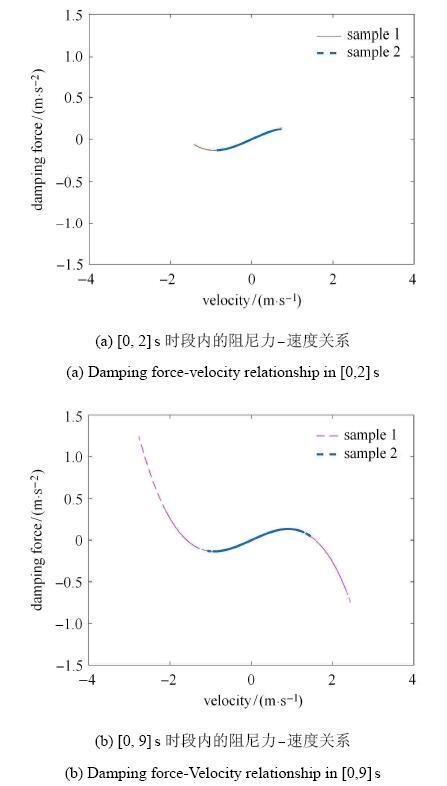
为了估计以速度概率密度函数为未知函数的降维FPK型方程的等价漂移系数,根据2.1节的方法,进行了1000次确定性分析,并在每个时刻估计条件期望. 在2,s和9,s时刻的二维点集图和估计的等价漂移系数函数如图2.值得指出的是,这里估计的条件均值函数,并非一般曲线拟合中的趋势拟合.换言之,其根本目的,不是通过估计曲线进行因变量的某种最优估计,而是获取随机变量的条件均值.因此,即便两个变量之间的相关系数为零(此时进行"线性"拟合是没有意义的),其条件均值函数依然是有意义的.因而,尽管表面上看起来图2中的点集具有较大的离散性,但对条件均值的估计依然是合理的.图3分别是对应时间区段内的阻尼力-速度关系,可见漂移系数的曲线形式与之具有某种内在的关系.换句话说,等价漂移系数本质上决定于物理系统的性质,因之,概率密度函数的变化本质上决定于物理状态的变化.而进行一系列确定性分析的根本目的,则是揭示上述内在物理机制. 这正是概率密度演化理论的物理本质[4, 27].如何进一步建立物理系统非线性形式与等价漂移系数数学形式之间的关系,是一个值得进一步研究的重要问题.
显示原图|下载原图ZIP|生成PPT图2典型时刻的等价漂移系数(条件均值函数)
-->Fig. 2The equivalent drift coefficient at typical time instants (conditional mean function)
-->
显示原图|下载原图ZIP|生成PPT图3典型时间区段内的阻尼力$\!$-$\!$-$\!$速度曲线
-->Fig. 3Damping force-Velocity curve in typical time periods
-->
在此基础上,求解速度响应概率密度函数的一维降维FPK型方程. 本文采用路径积分法求解,时间步长和空间步长分别取为$\tau = 0.001$,s和$\Delta \dot {x} = 0.015$,m/s.
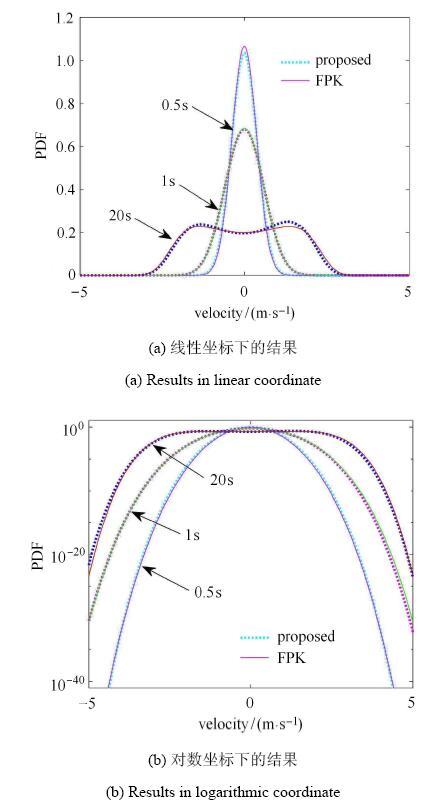
采用直接求解二维FPK方程和降维FPK型方程两种方法获得的0.5,s,1,s和20,s三个时刻的速度响应概率密度函数结果如图4. 从图4(a)中可见,二者在总体形状上相当一致.特别是,由于阻尼力的非线性,随着时间的发展速度响应的概率密度函数逐渐偏离正态分布而发展到双峰曲线形状.而从图4(b)可见,本文建议方法在概率密度函数尾部也具有很高的精度.
显示原图|下载原图ZIP|生成PPT图4典型时刻的速度响应概率密度函数解答
-->Fig. 4Probability density function solution of velocity response at typical time instants
-->
3.2 十层线性剪切型框架结构
考虑一个十层剪切型线性框架结构,其运动方程如式(3),但具有线性阻尼力和线性恢复力.结构的各层集中质量均为9.78$\times $10$^{4}$,kg,结构的层间剪切刚度从底层到顶层分别为3$\times $[3.3, 3.3,2.96, 2.96, 2.96, 2.96, 2.96, 2.96, 2.96, 2.96]$\times$10$^{7}$,N/m,阻尼采用Rayleigh阻尼,第一、二阶振型阻尼比均取为5%. 通过分析可知,各阶振型周期分别为1.368,4,0.461,1,0.282,2,0.206,9,0.165,9,0.140,8,0.124,7,0.114,3,0.108,1和0.105,0,s.结构受到的地震作用简化为幅值调制的基底白噪声,幅值标准差取0.2,g,即谱密度为0.120,7,调制函数同上.这里将求解结构在白噪声作用下的顶层速度非平稳响应.对于该10层线性结构,相应的FPK方程是关于位移$\!$-$\!$-$\!$速度联合向量概率密度函数的20维偏微分方程. 但因为结构响应服从联合正态分布,可以通过Duhamel积分获得其非平稳响应概率密度函数的解答[3-4].以下将以这一解答作为本文方法对比的基准(图标为"analytical"). 另一方面,采用本文方法,将20维原FPK方程降维,可以获得顶层速度响应概率密度函数满足的一维FPK型方程.为了构造等价漂移系数,进行了1000次确定性分析. 对此方程,采用路径积分法求解,时间步长和空间步长分别取为$\Delta T = 0.001$,s, $\Delta v = 0.005$,m/s.
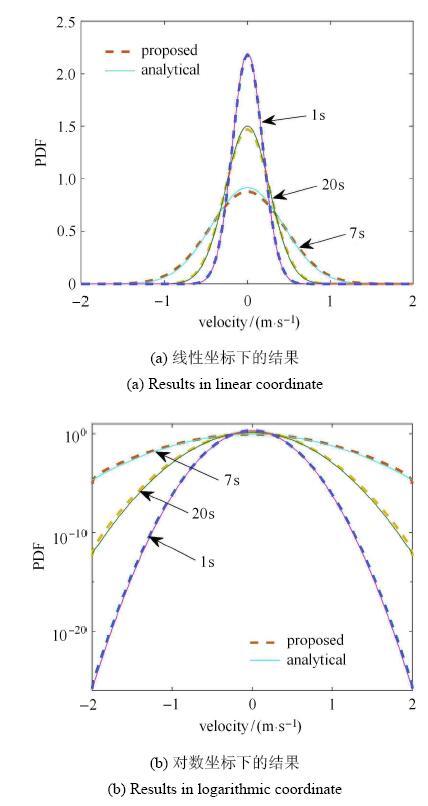
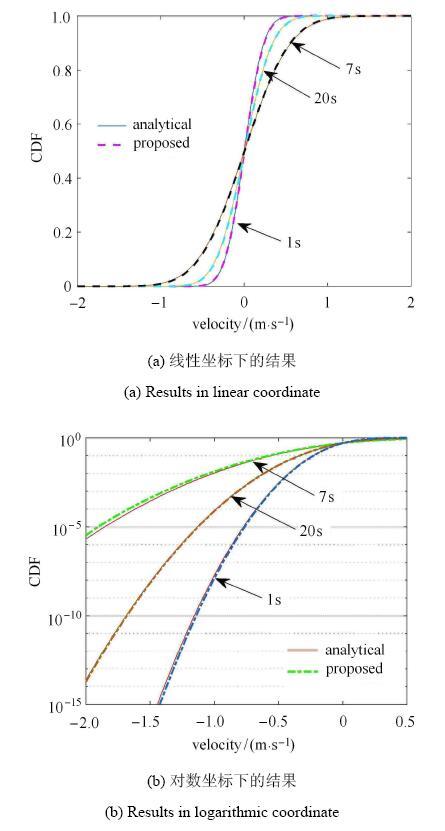
图5给出了典型时刻速度概率密度函数(PDF)解答及其与理论解的对比.图中可见,无论从总体形状(图5(a))还是尾部(图5(b))来看, 二者均具有高度的一致性.图6进一步给出典型时刻概率分布函数(CDF)与精确解的对比,同样可见二者不仅具有全局一致性(图6(a))、而且在尾部也具有 很高的精度(可达10$^{-15}$以上).这表明上述方法有望应用于失效概率很低的结构动力可靠度分析问题之中.值得指出的是,这里仅采用了10$^{3}$次确定性分析,在此基础上进行一维FPK方程求解(其求解时间与确定性分析相比很小),因而与Monte Carlo方法相比,其效率提高了数个数量级.
显示原图|下载原图ZIP|生成PPT图5典型时刻的概率密度函数解答
-->Fig. 5Probability density function solutions at typical instants
-->
显示原图|下载原图ZIP|生成PPT图6典型时刻线性结构速度响应的概率分布函数解答
-->Fig. 6Cumulative distribution function solutions at typical instants
-->
3.3 具有非线性恢复力的十层剪切型框架结构
在本例中,十层剪切型框架结构各层集中质量为3.73$\times $10$^{6}$,kg,层间剪切刚度从底层到顶层分别为5.5, 5.5,5.0, 5.0, 5.0, 5.0, 5.0, 5.0, 5.0和5.0($\times $10$^{9}$,N/m). 质量和刚度均处理为确定性变量.采用Rayleigh阻尼,即${\pmb C} = a{\pmb M} + b{\pmb K}$,其中$a = 0.416,4$,$b = 0.004,5$.用Bouc-Wen模型[36]模拟结构的非线性层间恢复力,模型中的13个基本参数均取为确定性变量[4],分别取值：$\alpha = 0.04 $, $A = 1 $, $n = 1 $, $\beta = 150 $, $\gamma = 20 $, $q = 0.25 $, $p = 1000$, $\varphi = 0.05 $, $d_\varphi = 5 $, $\lambda = 0.5 $, $d_\nu = 1 $, $d_\eta = 1 $,$\zeta _s =0.99 $. 结构的层间位移$\!$-$\!$-$\!$恢复力的关系的典型样本如图7.可以看到,此时结构已经进入了很强的非线性状态. 基底受到幅值调制的白噪声激励,峰值强度为$D =0.1$,m$^{2}$/s$^{4}$,调制函数同上. 结构的初始位移和初始速度均为零. 这里求解顶层速度随机响应的概率密度函数.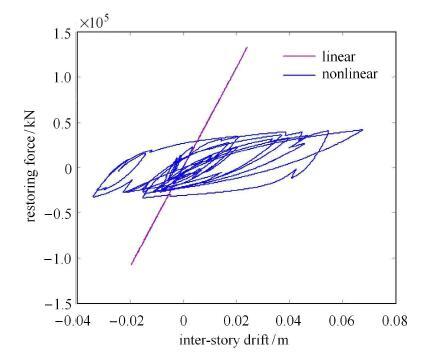
显示原图|下载原图ZIP|生成PPT图7层间位移$\!$-$\!$-$\!$恢复力曲线典型样本
-->Fig. 7Typical sample of Inter-story drift-Restoring force curve
-->
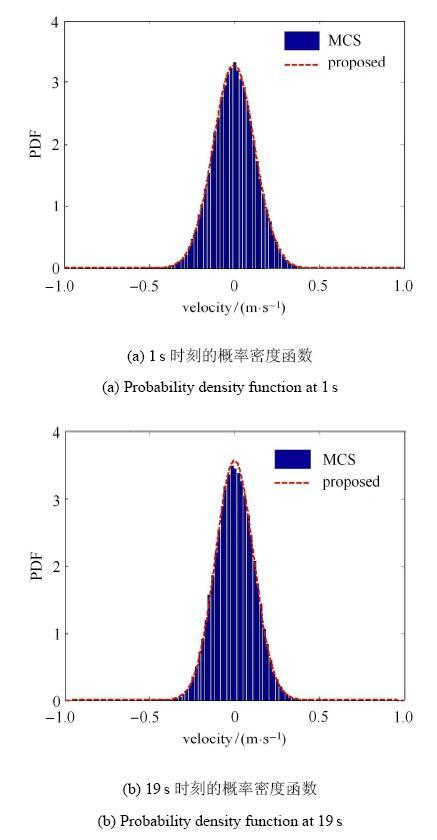
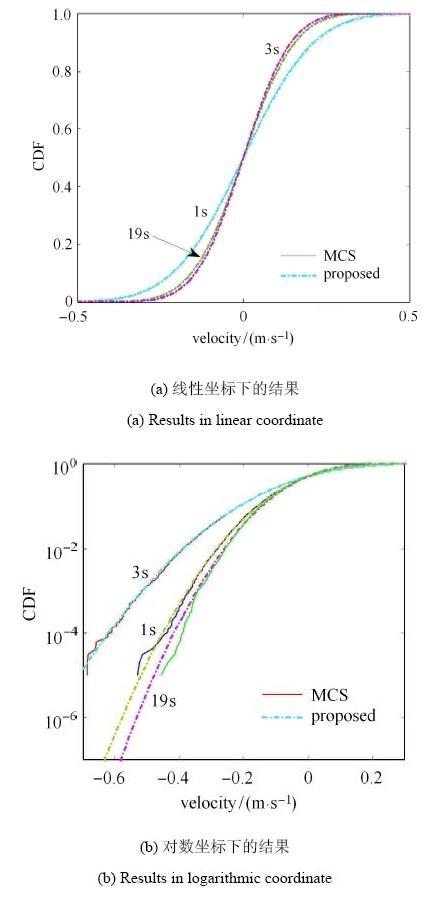
由于结构具有非线性恢复力[37],无法获得其速度概率密度函数的精确解答.事实上,由于引入Bouc-Wen模型描述层间非线性恢复力,其中含有新的辅助变量[29],因此,这时系统状态量的FPK方程是30维. 这里将以10$^{5}$次Monte Carlo模拟的结果作为对比的基准.采用本文建议方法,得到一维的FPK型方程,首先进行2000次确定性分析以估计顶层速度的等价漂移系数.进而,采用路径积分法求解速度概率密度函数满足的降维FPK型方程. 图8是典型时刻速度响应概率密度函数与Monte Carlo结果的对比,可见二者在总体上具有很好的一致性. 图9给出其概率分布函数解答的对比,可见与Monte Carlo模拟相比,不仅在总体上二者具有高度的一致性,在尾部亦可达到10$^{ - 3}$$\sim$10$^{ -4}$量级的精度.值得注意的是,这里仅包含了2000次确定性分析,而通常采用Monte Carlo方法时,若需要达到10$^{ - 3}$$\sim$10$^{ -4}$ 量级的精度,需要10$^{5}$$\sim$10$^{6}$次随机模拟分析. 且由于求解降维FPK型方程的成本很小,所以,与Monte Carlo相比,在同等精度情况下本文建议的方法其效率提高了两个数量级以上.
显示原图|下载原图ZIP|生成PPT图8典型时刻非线性结构速度响应的概率密度函数解答
-->Fig. 8Probability density function solutions of velocity response of the nonlinear structure at typical instants
-->
显示原图|下载原图ZIP|生成PPT图9典型时刻非线性结构速度响应的概率分布函数解答
-->Fig. 9Cumulative distribution function solutions of velocity response of the nonlinear structure at typical time instants
-->
顺便指出,在本文中,仅考虑了速度响应概率密度信息的求解. 对于位移响应概率密度信息的求解,可以采用类似的思想.这时,一般需要构造二维FPK方程[31]. 对于具体的实施,尚需专门研究.
4 结 论
针对幅值调制的加性白噪声激励非线性结构的非平稳响应分析,通过引入等价漂移系数,本文将关于联合概率密度函数的高维PFK方程转化为降维FPK型方程. 进而,采用路径积分方法求解该方程,获取速度响应瞬态概率密度函数的解答. 通过含有非线性阻尼的单自由度Rayleigh振子、多自由度线性结构和多自由度非线性结构在幅值调制的加性白噪声激励下非平稳速度响应概率密度函数的求解,验证了本文建议方法的精度. 具体结论如下：(1)等价漂移系数就是原高维系统漂移系数的条件均值函数. 等价漂移系数的形式与物理系统中的非线性形式有关. 为了构造数值稳健的等价漂移系数,一般需要10$^{2}$~10$^{3}$量级的确定性分析.
(2)对幅值调制的加性白噪声激励下线性系统的非平稳速度响应,采用本文建议方法可以获得几乎精确的概率密度函数,其概率分布函数的尾部精度可达10$^{-15}$甚至更高的量级.
(3)对非线性系统在幅值调制的加性白噪声激励下的速度响应,采用本文建议方法亦可获得很高的精度. 与Monte Carlo相比,其效率提高2个数量级以上.
本文方法有望推广到一般非平稳、非白噪声激励的非线性结构随机响应分析中去,对于位移响应概率密度函数的求解算法、条件均值函数的理性构造准则等问题尚需进一步深入研究.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | supports all the CNKI file formats; |
| [2] | . We have tabulated the form of the coefficientsg1(x) andg2(x) as well as the boundary values [a, b] of the Fokker-Planck equation \frac09P(x, t)09t = - \frac0909x[g1 (x)P(x, t)] + \frac09209x2 [g2 (x)P(x, t)],a \leqslant x \leqslant b for which the solution can be written as an eigenfunction expansion in the classical orthogonal polynomials. We also discuss the problem of finding solutions in terms of the discrete classical polynomials for the differential difference equations of stochastic processes. |
| [3] | . |
| [4] | . |
| [5] | . |
| [6] | |
| [7] | |
| [8] | . The probability density function (PDF) and the mean up-crossing rate (MCR) of the stationary responses of nonlinear stochastic systems excited by white noise is analyzed based on the assumption that the PDF of the responses is approximated with an exponential function of a polynomial in the state variables. Based upon the approximate PDF, a new technique is developed for the approximate PDF solution of Fokker–Planck–Kolmogorov equation, and consequently, the MCR of the system responses is analyzed. Numerical results showed that the approximate PDFs and MCRs approach to the exact ones as the degree of the polynomial increases. |
| [9] | One of the central problems synergetics is concerned with consists in the study of macroscopic qualitative changes of systems belonging to various disciplines such as physics, chemistry, or electrical engineering. When such transitions from one state to another take place, fluctuations, i.e., random processes, may play an im portant role. Over the past decades it has turned out that the Fokker-Planck equation pro vides a powerful tool with which the effects of fluctuations close to transition points can be adequately treated and that the approaches based on the Fokker Planck equation are superior to other approaches, e.g., based on Langevin equa tions. Quite generally, the Fokker-Planck equation plays an important role in problems which involve noise, e.g., in electrical circuits. For these reasons I am sure that this book will find a broad audience. It pro vides the reader with a sound basis for the study of the Fokker-Planck equation and gives an excellent survey of the methods of its solution. The author of this book, Hannes Risken, has made substantial contributions to the development and application of such methods, e.g., to laser physics, diffusion in periodic potentials, and other problems. Therefore this book is written by an experienced practitioner, who has had in mind explicit applications to important problems in the natural sciences and electrical engineering. |
| [10] | In this paper exact steady state solutions are constructed for a class of non-linear systems subjected to stochastic excitation. The results are then applied to both classical and non-classical oscillator problems. |
| [11] | . This is an analysis of multidimensional nonlinear dissipative Hamiltonian dynamical systems subjected to parametric and external stochastic excitations by the Fokker-Planck equation method.The author answers three types of questions concerning this area. First, what probabilistic tools are necessary for constructing a stochastic model and deriving the FKP equation for nonlinear stochastic dynamical systems? Secondly, what are the main results concerning the existence and uniqueness of an invariant measure and its associated stationary response? Finally, what is the class of multidimensional dySoize, Christian |
| [12] | |
| [13] | . 滞迟系统属于一类典型的强非线性系统,滞迟力不仅取决于系统的瞬时变形,还与变形历程有关.虽然滞迟系统的随机振动问题已被广泛研究,但至今尚未得到滞迟系统随机响应概率密度函数的精确闭合解.本文运用迭代加权残值法获得了高斯白噪声激励下Bouc-Wen滞迟系统稳态响应概率密度函数的近似闭合解.首先,运用等效线性化法求出系统的稳态高斯概率密度函数;然后以此构造权函数,应用加权残值法求得了系统指数多项式形式的非高斯概率密度函数;最后引入迭代的过程,逐步优化权函数,提高计算所得结果的精度.以随机地震激励下钢纤维陶粒混凝土结构的稳态响应作为算例,其中Bouc-Wen模型的参数是基于拟静力学试验数据,并应用最小二乘法辨识获得.与Monte Carlo模拟结果相比,等效线性化法得到的结果精度较差;由加权残值法得到的结果能够表现出非线性特征,但其精度依然无法令人满意;采用迭代加权残值法得到的近似闭合解与Monte Carlo模拟的结果吻合非常好;对于较强随机激励情形,采用渐进迭代加权残值法具有较高的求解效率,所获得的理论解析解具有较高的精度.结果表明,所获得的近似闭合解不仅对于土木工程领域具有重要的实际应用价值,而且还可作为检验其他非线性系统随机响应预测方法的精度的标准. . 滞迟系统属于一类典型的强非线性系统,滞迟力不仅取决于系统的瞬时变形,还与变形历程有关.虽然滞迟系统的随机振动问题已被广泛研究,但至今尚未得到滞迟系统随机响应概率密度函数的精确闭合解.本文运用迭代加权残值法获得了高斯白噪声激励下Bouc-Wen滞迟系统稳态响应概率密度函数的近似闭合解.首先,运用等效线性化法求出系统的稳态高斯概率密度函数;然后以此构造权函数,应用加权残值法求得了系统指数多项式形式的非高斯概率密度函数;最后引入迭代的过程,逐步优化权函数,提高计算所得结果的精度.以随机地震激励下钢纤维陶粒混凝土结构的稳态响应作为算例,其中Bouc-Wen模型的参数是基于拟静力学试验数据,并应用最小二乘法辨识获得.与Monte Carlo模拟结果相比,等效线性化法得到的结果精度较差;由加权残值法得到的结果能够表现出非线性特征,但其精度依然无法令人满意;采用迭代加权残值法得到的近似闭合解与Monte Carlo模拟的结果吻合非常好;对于较强随机激励情形,采用渐进迭代加权残值法具有较高的求解效率,所获得的理论解析解具有较高的精度.结果表明,所获得的近似闭合解不仅对于土木工程领域具有重要的实际应用价值,而且还可作为检验其他非线性系统随机响应预测方法的精度的标准. |
| [14] | . Stochastic wave-particle acceleration may be responsible for producing suprathermal particles in many astrophysical situations. The process can be described as a diffusion process through the Fokker-Planck equation. If the acceleration region is homogeneous and the scattering mean free path is much smaller than both the energy change mean free path and the size of the acceleration region, then the Fokker-Planck equation reduces to a simple form involving only the time and energy variables. in an earlier paper (Park & Petrosian 1995, hereafter Paper 1), we studied the analytic properties of the Fokker-Planck equation and found analytic solutions for some simple cases. In this paper, we study the numerical methods which must be used to solve more general forms of the equation. Two classes of numerical methods are finite difference methods and Monte Carlo simulations. We examine six finite difference methods, three fully implicit and three semi-implicit, and a stochastic simulation method which uses the exact correspondence between the Fokker-Planck equation and the it5 stochastic differential equation. As discussed in Paper I, Fokker-Planck equations derived under the above approximations are singular, causing problems with boundary conditions and numerical overflow and underflow. We evaluate each method using three sample equations to test its stability, accuracy, efficiency, and robustness for both time-dependent and steady state solutions. We conclude that the most robust finite difference method is the fully implicit Chang-Cooper method, with minor extensions to account for the escape and injection terms. Other methods suffer from stability and accuracy problems when dealing with some Fokker-Planck equations. The stochastic simulation method, although simple to implement, is susceptible to Poisson noise when insufficient test particles are used and is computationally very expensive compared to the finite difference method. |
| [15] | . The finite element method is applied to the solution of the transient Fokker-Planck equation for several often cited nonlinear stochastic systems accurately giving, for the first time, the joint probability density function of the response for a given initial distribution. The method accommodates nonlinearity in both stiffness and damping as well as both additive and multiplicative excitation, although only the former is considered herein. In contrast to the usual approach of directly solving the backward Kolmogorov equation, when appropriate boundary conditions are prescribed, the probability density function associated with the first passage problem can be directly obtained. Standard numerical methods are employed, and results are shown to be highly accurate. Several systems are examined, including linear, Duffing, and Van der Pol oscillators. |
| [16] | . The joint probability density function of the state space vector of a white noise exoited van der Pol oscillator satisfics a Fokker-Planck-Kolmogorov (FPK) equation. The paper describes a numerical procedure for solving the transient FPK equation based on the path integral solution (PIS) technique. It is shown that by combining the PIS with a cubic B-spline interpolation method, numerical solution algorithms can be implemented giving solutions of the FPK equation that can be made accurate down to very low probability levels. The method is illustrated by application to two specific examples of a van der Pol oscillator. |
| [17] | A new path integration scheme based on the Gauss-Legendre quadrature integration rule is proposed for calculating the probability density of the response of a dynamical system under Gaussian white-noise excitation. The new scheme is capable of producing accurate results of probability density as it evolves with time, including the tail region where the probability level is very low. This low probability region is important for the system reliability estimation. |
| [18] | . New approaches for numerical implementation of the path integration (PI) method are described. In essence the PI method is a stepwise calculation of the joint probability density function (PDF) of a set of state space variables describing a white noise excited nonlinear dynamic system. The basic idea behind the proposed procedure is to apply a splines interpolation method to the logarithm of the calculated PDF to obtain an accurate representation of the PDF over the whole domain and not only at the chosen grid points. This exploits the fact that the logarithm of the PDF shows a more polynomial behaviour than the PDF itself, and therefore is better adapted to a splines representation. It is demonstrated that the proposed techniques may lead to significantly improved performance in calculating the response statistics of large classes of nonlinear oscillators excited by white or coloured noise when compared to other available implementations of the PI method. An advantage of the new approaches is that they allow time-variant dynamic systems to be analysed without significant increase in computer time. Numerical results for both 2D and 3D problems are presented. |
| [19] | . 78 A novel analytical Wiener path integral technique is developed. 78 The non-stationary response PDF of a class of nonlinear oscillators is determined. 78 The technique is based on statistical linearization and on stochastic averaging. 78 A variational formulation is used for determining the most probable path. 78 No need to advance the solution in short time steps. |
| [20] | |
| [21] | . Abstract The recently developed approximate Wiener path integral (WPI) technique for determining the stochastic response of nonlinear/hysteretic multi-degree-of-freedom (MDOF) systems has proven to be reliable and significantly more efficient than a Monte Carlo simulation (MCS) treatment of the problem for low-dimensional systems. Nevertheless, the standard implementation of the WPI technique can be computationally cumbersome for relatively high-dimensional MDOF systems. In this paper, a novel WPI technique formulation/ implementation is developed by combining the “localization” capabilities of the WPI solution framework with an appropriately chosen expansion for approximating the system response PDF. It is shown that, for the case of relatively high-dimensional systems, the herein proposed implementation can drastically decrease the associated computational cost by several orders of magnitude, as compared to both the standard WPI technique and an MCS approach. Several numerical examples are included, whereas comparisons with pertinent MCS data demonstrate the efficiency and reliability of the technique. |
| [22] | Results obtained by applying the method of stochastic averaging to random vibration problems are discussed. This method is applicable to a variety of problems involving the response of lightly damped systems to broad-band random excitations. Solutions pertaining to both linear and non-linear vibrations are reviewed, and it is shown that the technique enables, in the case of parametric excitation, stability criteria to be established. Some results which have been obtained relating to the first-passage reliability problems are also surveyed. Various applications of the theory to engineering problems are outlined. |
| [23] | . A stochastic averaging method is proposed to predict approximately the response of quasi-integrable Hamiltonian systems to bounded noise excitations. Two cases of external resonance only and both internal and external resonances are considered separately. The reduced averaged Fokker–Planck–Kolmogorov equation is solved by using the combination of the finite difference method and the successive over relaxation method. An example of two coupled Duffing oscillators under bounded noise excitations is given to illustrate the application of the proposed procedure. It is shown that the analytical results agree well with those from digital simulation of original system. |
| [24] | . In this paper, a new methodology is formulated for solving the reduced Fokker-Planck (FP) equations in high dimensions based on the idea that the state space of large-scale nonlinear stochastic dynamic system is split into two subspaces. The FP equation relevant to the nonlinear stochastic dynamic system is then integrated over one of the subspaces. The FP equation for the joint probability density function of the state variables in another subspace is formulated with some techniques. Therefore, the FP equation in high-dimensional state space is reduced to some FP equations in low-dimensional state spaces, which are solvable with exponential polynomial closure method. Numerical results are presented and compared with the results from Monte Carlo simulation and those from equivalent linearization to show the effectiveness of the presented solution procedure. It attempts to provide an analytical tool for the probabilistic solutions of the nonlinear stochastic dynamics systems arising from statistical mechanics and other areas of science and engineering. |
| [25] | . 结构随机动力反应与可靠度分析对保障工程结构在灾害性动力作用下的安全性至关重要。数十年来,国内外****进行了大量的研究,取得了丰硕的成果,但在多自由度非线性系统随机动力反应与可靠度分析方面遇到了巨大的困难。概率密度演化理论提供了全新的处理方法。该文在评述已有研究方法的基础上,着重讨论了概率密度演化理论及其在结构随机地震反应与整体可靠性分析应用方面的新进展。 . 结构随机动力反应与可靠度分析对保障工程结构在灾害性动力作用下的安全性至关重要。数十年来,国内外****进行了大量的研究,取得了丰硕的成果,但在多自由度非线性系统随机动力反应与可靠度分析方面遇到了巨大的困难。概率密度演化理论提供了全新的处理方法。该文在评述已有研究方法的基础上,着重讨论了概率密度演化理论及其在结构随机地震反应与整体可靠性分析应用方面的新进展。 |
| [26] | . The present paper aims to provide a uniform and rigorous theoretical basis for the family of newly developed probability density evolution method. Conservation laws are among the most important features of continuum systems, so is the principle of preservation of probability for stochastic dynamical systems. The classical Liouville equation together with its Dostupov鈥揚ugachev extension is firstly discussed. They could be reasonably thought to hold for stochastic systems where the randomness could be characterized by finite random variables but unfortunately they are unfeasible for practical applications because of analytical and numerical intractability. The generalized density evolution equation in conjunction with its numerical implementation procedure is then discussed with assistance of the formal solution. Comparing the Liouville equation and the generalized density evolution equation finds that the former is essentially based on the state space while the latter is on the ground of substantial particle description. The principle of preservation of probability is accordingly revisited from the two descriptions: the state space description and the random event description. On the clear basis, the generalized density evolution equation is derived once again in a more natural way. Underlying problems open for investigations and practical applications and possible extensions are outlined. |
| [27] | . 介绍了随机动力系统中概率密度演化理论的基本方程与求解方法〖CX4〗．〖CX〗在此基础上，论述了广义概率密度演化方程求解的若干新进展，包括群演化方程及其求解、概率空间剖分的理性准则、点集加密技术与信息拓展方法等. . 介绍了随机动力系统中概率密度演化理论的基本方程与求解方法〖CX4〗．〖CX〗在此基础上，论述了广义概率密度演化方程求解的若干新进展，包括群演化方程及其求解、概率空间剖分的理性准则、点集加密技术与信息拓展方法等. |
| [28] | . |
| [29] | . Engineering structures usually exhibit hysteretic property when they are subjected to disastrous loadings such as earthquakes, strong wind and huge waves. The solution of FPK equation related to such complex systems are of great significance but is still an extremely challenging problem. In the present paper, the FPK equation for hysteretic systems is studied and the dimension is reduced to render an efficient numerical solution. The equivalence of probability flux in two different treatments, i.e., in the FPK equation which is based on the state space description and in the generalized density evolution equation which is mainly based on the random event description, are first examined. Then the FPK equation for additively excited multi-degree-of-freedom structures exhibiting nonlinear behaviors, including hysteresis together with strength degradation and stiffness degradation, is discussed. By invoking the basic idea of equivalence of probability flux, an equivalent probability flux due to drift could be constructed by the probability density evolution method (PDEM) instead of the direct coupled high-dimensional integral. Numerical implementation procedure is outlined. Two numerical examples are illustrated. Problems to be further studied are discussed. |
| [30] | . The Fokker—Planck—Kolmogorov (FPK) equation plays an essential role in nonlinear stochastic dynamics. However, neither analytical nor numerical solution is available as yet to FPK equations for high-dimensional systems. In the present paper, the dimension reduction of FPK equation for systems excited by additive white noise is studied. In the proposed method, probability density evolution method (PDEM), in which a decoupled generalized density evolution equation is solved, is employed to reproduce the equivalent flux of probability for the marginalized FPK equation. A further step of constructing an equivalent coefficient finally completes the dimension-reduction of FPK equation. Examples are illustrated to verify the proposed method. |
| [31] | . The joint probability density function (PDF) of response of a system subjected to Gaussian white noise satisfies the Fokker–Planck–Kolmogorov (FPK) equation, to which neither analytical nor numerical solution is readily available for high-dimensional nonlinear stochastic systems. In the present paper, for the systems excited by additive white noise, by invoking the concept of equivalent drift coefficient, a high-dimensional FPK equation is reduced to a one- or two-dimensional partial differential equation. The equivalent drift coefficient in the new lower-dimensional equation is proved to be the conditional mean function of the drift coefficient in the original high-dimensional FPK equation. The path integral solution is then employed to solve the dimension-reduced FPK-like equation. The response analyses for several systems excited by white noise are exemplified to illustrate the proposed method. The idea proposed in the present paper can be extended to multiplicative white noise and colored noise. |
| [32] | . 数值模拟是解决土–结构动力相互作用问题的重要手段,而合理地实现地震波动输入直接影响地震作用下土–结构动力相互作用问题数值模拟的精度.波动法是目前常用的地震动输入方法之一,该方法将输入地震动转化为人工边界上的等效载荷,相较于其他地震动输入方法,波动法模拟精度高,但实施上相对复杂.从有限元模型入手,推导了采用波动法确定等效输入地震载荷的另一种形式,以此为基础,提出了一种在人工边界上实现地震动输入的新方法.新方法通过对土–结构有限元模型中由包含人工边界节点的单元组成的子结构施加自由场位移时程并进行动力分析,直接获得可实现地震波动有效输入的等效载荷,然后将等效输入地震载荷施加在土–结构模型的人工边界节点上,从而完成土–结构动力相互作用问题分析中地震动输入和地震反应计算.与原有波动法相比,新方法避免了需分别计算人工边界上自由场应力和由引入人工边界条件带来的附加力,以及需要根据不同人工边界面确定载荷的作用方向等较为复杂的处理过程,具有等效地震载荷计算简便、地震动输入过程更易于实施的特点.采用竖直入射和斜入射地震波动作用下的弹性半空间和成层半空间地震反应算例验证了新方法的有效性. . 数值模拟是解决土–结构动力相互作用问题的重要手段,而合理地实现地震波动输入直接影响地震作用下土–结构动力相互作用问题数值模拟的精度.波动法是目前常用的地震动输入方法之一,该方法将输入地震动转化为人工边界上的等效载荷,相较于其他地震动输入方法,波动法模拟精度高,但实施上相对复杂.从有限元模型入手,推导了采用波动法确定等效输入地震载荷的另一种形式,以此为基础,提出了一种在人工边界上实现地震动输入的新方法.新方法通过对土–结构有限元模型中由包含人工边界节点的单元组成的子结构施加自由场位移时程并进行动力分析,直接获得可实现地震波动有效输入的等效载荷,然后将等效输入地震载荷施加在土–结构模型的人工边界节点上,从而完成土–结构动力相互作用问题分析中地震动输入和地震反应计算.与原有波动法相比,新方法避免了需分别计算人工边界上自由场应力和由引入人工边界条件带来的附加力,以及需要根据不同人工边界面确定载荷的作用方向等较为复杂的处理过程,具有等效地震载荷计算简便、地震动输入过程更易于实施的特点.采用竖直入射和斜入射地震波动作用下的弹性半空间和成层半空间地震反应算例验证了新方法的有效性. |
| [33] | |
| [34] | . |
| [35] | . 78 Melnikov theorem it applied with an active control strategy. 78 The Rayleigh oscillator with fractional order deflection is considered. 78 The horseshoes structure of chaos in analyzed. 78 The parameter order α influence considerably the control strategy. 78 The periodic perturbation from the controller enhances the performance of the active control strategy. |
| [36] | . |
| [37] | . . |
