ELECTROHYDRODYNAMIC CHARACTERISTICS OF LIQUID BRIDGE FORMATION AT THE DRIPPING MODE OF ELECTROSPRAYS 1)
Huo Yuanping, Wang Junfeng2), Zuo Ziwen, Liu HailongSchool of Energy and Power Engineering, Jiangsu University, Zhenjiang 212013, Jiangsu, China收稿日期:2018-08-4接受日期:2018-10-16网络出版日期:2019-03-18
| 基金资助: |
Received:2018-08-4Accepted:2018-10-16Online:2019-03-18
作者简介 About authors
2)王军锋,教授,主要研究方向：荷电多相流理论及工程应用.E-mail：wangjunfeng@ujs.edu.cn
摘要
对电场作用下微通道荷电液滴脱落过程中液桥形成及断裂的显微演变特征进行了可视化实验研究.借助时空分辨率较高的高速摄像技术精确捕捉了电场作用下液桥形成及断裂的界面演化过程,研究了液桥的界面结构变化及其断裂的动力学显微演变行为,获得了时间特征数、电邦德数及半月面形成角对液桥长度及断裂顺序的作用规律.实验结果显示,液桥断裂长度取决于黏度与表面张力之比,而受荷电弛豫时间的影响甚微,低电压工况下各实验介质液桥相对长度的变化并不明显,而在较高电压工况下相对液桥长度的增长速度加快.随着电邦德数的不断增加,液桥长度的变化在较高邦德数下更为明显且存在突变区,此时伴随着雾化模式的转变,表明液桥的突变恰恰是雾化模式过渡的信号.不同物性介质的射流过渡行为由于液桥上下游形成角的变化而存在较大差异.对于无水乙醇介质,电邦德数的增加使滴状模式首先过渡到纺锤模式,而对于生物柴油,滴状模式后会首先出现脉动模式而非纺锤模式.
关键词：
Abstract
A detailed visualization study on the evolution of Liquid bridge formation and fracture from a capillary is reported. By means of high-speed microscopy with high time-space resolution, special attention has been paid to the formation dynamics of the liquid bridge in the dripping mode, the change of interface structure and the fracture dynamics behavior of hydraulic bridge are studied, and the action rule of time characteristic number, electric Bond number and half-moon angle on liquid length and fracture order of liquid bridge is obtained. The results show that the fracture length of liquid bridge depends on the ratio of viscosity to surface tension, but is little affected by the relaxation time of charge. Under low voltage condition, the change of liquid bridge relative length for each experiment medium is not obvious, while the relative length of liquid bridge grows rapidly during high voltage condition. With the continuous increase of electric Bond number, the change of liquid bridge length is more obvious under the higher Bond number, and a mutation zone occur which shows the transition of the atomization model, this means the mutation of liquid bridge is a transition signal of atomization modes. With the changes of the formation angle of liquid bridge upstream and downstream, the transition behavior of jet flow in different physical media varies greatly. In the case of ethyl alcohol, the increase in the number of electric bonds causes the dropping mode to first transition to the spindle mode, while in the case of biodiesel, the pulsation mode rather than the spindle mode will first appear after the dropping mode. It is of great significance to reveal the transition law of charged micro fluidic atomization model and enrich the theory of electrostatic atomization.
Keywords：
PDF (2874KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
霍元平, 王军锋, 左子文, 刘海龙. 滴状模式下液桥形成及断裂的电流体动力学特性研究 1). 力学学报[J], 2019, 51(2): 425-431 DOI:10.6052/0459-1879-18-256
Huo Yuanping, Wang Junfeng, Zuo Ziwen, Liu Hailong.
引 言
作为电流体动力学的一个重要分支,微通道静电雾化是区别于传统机械雾化的一种新型喷雾技术,带电液滴在库仑斥力的作用下削弱了液滴的表面张力,从而促使液滴易于破碎成更细小的微液滴[1].这种雾化技术凭借低能耗(毫瓦级)可获得大量粒径小、单分散性好、可控性强、沉积率高的荷电微液滴,在微/纳薄膜及颗粒制备、微型燃烧、空间微动力推进等领域应用潜能巨大[2-4].静电雾化理论的发展涉及到荷电液滴的变形及其破碎机理、静电雾化模式及其雾化特性、荷电射流不稳定性等各个方面[5-8],如1882年Rayleigh[9]首次通过理论分析预测了球形荷电液滴的临界破碎条件(瑞利极限),1915年Zeleny[10]通过较为系统的实验研究最早对静电雾化进行了观察与分析,确立了高电压作用下从毛细管尖端喷射出液锥的分裂破碎机制,Taylor等[11-14]理论分析结合实验测量对电场中无黏射流的稳定性进行了开拓性的研究,在小扰动近似下计算了Varicose模态和Kink模态的增长率.这一系列的研究为静电雾化机理的研究奠定了理论及数值模拟基础,建立在此基础上的研究工作使静电雾化理论的发展取得了长足的进步.值得一提的是,滴状模式下液桥的形成及演化行为是荷电微射流雾化模式研究中经常容易被忽视的一个科学问题,对液桥形成及断裂的动力学行为的深入分析是揭示射流雾化模式过渡演变规律的关键,其电流体动力学特性直接影响着静电雾化模式显微形貌的发展.Jaworek等[15]对蒸馏水、乙二醇和乙醇不同雾化模式下的射流状态进行高速摄影,单一地描述了滴状模式、微滴落模式、纺锤模式、多股射流模式等的液滴及射流形成过程,未涉及滴落机制及射流模式过渡演变的分析.文献[16]在不综合考虑液滴物性的前提下,围绕滴状模式下液滴形成过程对液线断裂及卫星液滴运动规律开展实验研究,结果表明注射流量及电场强度影响下液滴尺寸与液线形貌的变化存在映射关系,而对液桥自身的演变特征未过多关注.Lee等[17]重点研究了交流电场中液滴的形成机理及动力学问题,分析了液滴拉长和破碎两阶段的机理,并提及了电极距离和绝缘材料等影响液滴形成过程的一些关键参数.Mariano等[18]报道了高邦德数下毛细管脱落液滴形成的动力学特性及射流过渡行为,定量分析了在定流量时黏度及毛细管径对卫星液滴形成及射流演变的影响,并描述了高黏液滴液桥形貌随韦伯数的变化规律.Moloud等[19]针对牛顿与非牛顿流体,定义液滴拉伸长度、最小液桥宽度及当前接触角分析了非荷电液滴的形成过程,结果表明在液体浓度及流量的影响下非牛顿流体与牛顿流体的液桥变化存在明显差异.综上所述,液桥的形成及演变是滴状模式下液滴脱落所孪生的流体动力学行为,相关研究****从多角度直接或间接的描述了液桥的动力学行为,然而针对静电雾化过程中滴状模式的液桥演变特征却仍存在较多的研究盲点,尤其是在综合考虑表面张力、黏度及电导率等参数情况下对液桥长度及液桥破碎顺序的探讨还缺乏相关报道.本文基于时空分辨率较高的高速摄像技术,通过精确捕捉静电雾化滴状模式下液桥形成及断裂过程的显微形貌特征,研究了不同电压下液体电导率、表面张力及黏度对液桥电流体动力学演变行为的影响,并从液桥断裂长度及断裂顺序的角度分析了滴状模式的变化及过渡演变机制,对揭示荷电微射流雾化模式演变规律及丰富静电雾化基础理论具有十分重要的意义.
1 实验装置及方法
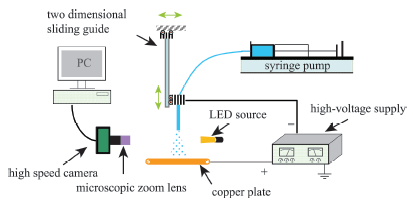
图1为实验的装置示意图. 实验所采用的毛细微通道内径为0.47 mm,外径0.7 mm. 微流量注射泵精确控制液体流量在50μL/min,使单液滴形成稳定的发生频率;负高压静电发生器(0~20 kV)的负极与毛细微通道尖端连接,正极接板状电极(紫铜材质)并接地,构成负高压静电发生系统.板状电极放置在距毛细微通道尖端正下方1.3 cm处,组成针-板荷电形式的电场区域;关键结合部位用聚四氟乙烯材料绝缘;二维滑动导轨可以精确调节微射流在相机拍摄区域的位置,为射流捕捉区域的选取与定位提供便利.为获得亚毫秒至微秒级时间内的微射流演变过程,借助奥林巴斯公司i-SPEED 3高速摄像机(拍摄频率为2000帧/秒时图像分辨率为1280×1024),配合型号为NAVITAR 12X的显微变焦镜头对射流雾化区域内从滴状模式到多股射流模式的射流演变行为进行显微拍摄从而进行可视化研究.拍摄光源为LED冷光源,放置在相机正对面.实验中为了防止静电累积,测量设备均应作接地处理进行保护.图1
新窗口打开|下载原图ZIP|生成PPT图1荷电液滴形成的可视化实验装置
Fig.1Experimental device for charged droplet formation
本实验工况均在(25$\pm$ 0.5)\textcelsius恒温环境中进行,室内湿度控制在30％.实验选取了生物柴油、不同浓度的氯化钠水溶液及无水乙醇等几种实验介质,如表1所示.无水乙醇和去离子水的物性方面差异性较大的是它们的表面张力,而生物柴油的黏性较大;对于不同浓度的NaCl去离子水溶液,其包括密度、表面张力、黏度等的物性参数基本相似,但电导率存在较大差异外(彼此至少存在一个数量级的差异),因此可以通过对比分析这三种液体的射流雾化特征获取黏度、表面张力及电导率对其射流雾化界面演变及射流雾化区间的影响及作用规律.
Table 1
表1
表1试验介质的相关物性参数
Table 1
| Experimental medium | Density/(kgm- | 3) Viscosity/(mm2 s-1) | Conductivity/(^Scm-1) | Surface tension/(mN m-1) | Relative dielectric constant |
|---|---|---|---|---|---|
| biodiesel | 880 | 6.95 | 4.0 x 10-6 | 26 | 1.90 |
| ethyl alcohol | 790 | 1.3 | 0.5 | 21 | 25.7 |
| deionized water | 999 | 1.07 | 1.3 | 72 | 77.5 |
| 0.5%NaCl | 1012 | 1.04 | 9.2 x 103 | 72 | 73.2 |
| 10% NaCl | 1071 | 1.02 | 1.42 x 105 | 75 | 70.3 |
新窗口打开|下载CSV
2 结果与讨论
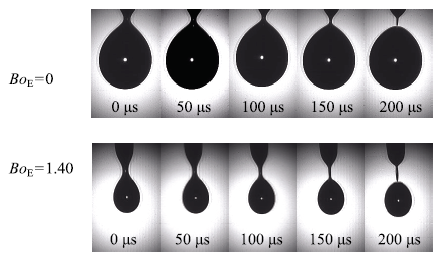
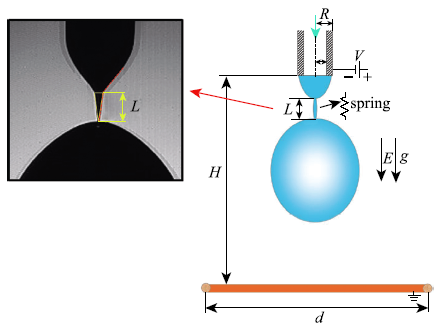
对于单液滴发生器来说,液滴从毛细管口脱落过程中会与管口半月面之间形成液桥,无水乙醇的液桥形成过程如图2所示.$L$代表临界液桥长度,它表示液桥任意一端脱落瞬间的端点到液桥边界与半月面边界的交点的垂直距离(见图3),即图中液桥所形成锥体的高度.这个长度不仅与液体的物性如表面张力、黏度、密度等有密切关系,同时还受液体流量、毛细管径等的重要影响,这里引入相对液桥长度$L_{\rm R}$ (临界液桥长度与毛细管半径之比).当液滴发生器周围存在电场时,即把负高压静电发生器的高压端与毛细微通道相连,板状电极接地,形成一个负高压荷电区域,此时在液桥的拉升过程中电场力将扮演着非常重要的角色.图2
新窗口打开|下载原图ZIP|生成PPT图2无水乙醇的液桥形成过程图像
Fig.2Formation process of liquid bridge for ethyl alcohol
图3
新窗口打开|下载原图ZIP|生成PPT图3液桥的形成示意图
Fig.3Schematic of liquid bridge formation process
毛细微通道静电雾化过程中,管口半月面形貌的过渡演变是静电力与毛细管力共同作用的结果,可以通过电邦德数加以描述[20]
其中,$\varepsilon$和$\sigma$分别代表空气的介电常数与液体的表面张力,$R$是毛细管半径,$E(0)$表示毛细管口的电场强度.对于实验中采用的针-板极形式的电场形态,毛细管口电场强度为[21]
其中V为毛细管口的荷电电压,H表示板电极表面到毛细管口端面的距离.结合方程(1)和(2)可知
电邦德数$Bo_{\rm E}$与电压的平方成正比,且受毛细管尺寸、极间距及液体表面张力的影响,较单一的电压参数能更准确地鉴别射流模式的过渡行为,对于研究荷电液滴形成及射流转变的动力学行为特征有重要的指导意义.
2.1 液桥的断裂长度
不可压缩流体黏性的增强会导致临界液桥长度的显著增大,因为黏性力的增大使作用于液桥界面的阻尼干扰增强.与此同时,因液体相对表面张力的减小而导致收缩性下降,液桥长度也会有一定程度的增大.众所周知,弹簧系统中弹性系数与位移是成反比的,如果用液桥弹簧模型进行分析,黏性的增大或表面张力的减小会导致弹性系数的下降,此时类比于弹簧位移的临界液桥长度$L$将会增大.外加电场存在的情况下,直径为D、荷电量为$q$的荷电液滴,其相对表面张力将被削弱[22]
其中,$\sigma$和$\sigma _0$分别代表液体的相对表面张力和固有表面张力,而$q$是此时液滴的荷电量.当相对表面张力减小时,液滴抵抗变形的能力减弱,液滴不稳定性增强从而更容易发生变形.值得注意的是,方程(4)成立的假设条件是电荷在液滴表面是均匀分布的,实际上由于液桥的非球形特征,其表面电荷密度是非均一的,电荷主要聚集在液桥上下游两个曲率较大的断裂点处,这导致轴向(电场力方向)断裂点处的相对表面张力比液桥其余位置处削弱的更明显,意味着液桥沿轴向更容易变形,因此滴状模式下临界液桥长度$L$对外加电场的变化十分敏感.
2.1.1 时间特征数对临界相对液桥长度的影响
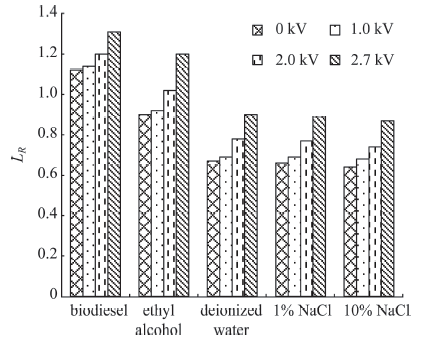
图4给出了不同电压下各种试验介质的相对液桥长度.这里引入流体动力学弛豫时间[23]$\tau _{\rm H} = \eta R / \sigma $及荷电弛豫时间[24]$\tau _{\rm c} = \varepsilon ' / 4π \gamma$来分析黏度和电导率对液桥长度的影响规律.其中$\varepsilon'$和$\gamma$分别表示液体的介电常数及电导率,$\eta$代表液体的黏度,$\tau _{\rm c}$能够直接反应表面电荷沿电场力方向迁移速度的大小,而$\tau _{\rm H}$能够直观地反应毛细波(表面张力波)的机械变形速度. 根据表1计算出5种实验介质的相关时间常数,其对应的相对液桥长度如表2所示.从表中可以看出,生物柴油、无水乙醇、去离子水、1％NaCl及10％NaCl的$\tau _{\rm H}$分别为80.8,13.2,5.2,5.0及4.7μs,此时对应$Bo_{\rm E} = 0$时的相对液桥长度分别为1.12,0.9,0.67,0.66及0.64,这表明相对液桥长度对流体动力学弛豫时间的变化十分敏感.去离子水、1％NaCl及10％NaCl三种介质的荷电弛豫时间至少存在一个数量级的差别,然而在荷电情况下他们之间的相对液桥长度基本一致,这意味着相对液桥长度与荷电弛豫时间的变化关系不大.根据表2可以进一步发现,不同浓度的NaCl水溶液除了电导率和去离子水有较大差异之外,其他物性参数处于同一数量级.这意味着液体的电导率对相对液桥长度的变化影响微弱.此外需要注意的是,低电压工况下各实验介质液桥相对长度的变化并不明显,而在较高电压工况下相对液桥长度的增长速度加快.生物柴油和无水乙醇之间除了黏度差别较大外其他物性参数相似,而生物柴油的液桥长度总是比同等实验工况下的无水乙醇要大,这表明在液桥拉伸的过程中黏度是影响相对液桥长度的一个非常重要的参数;同时与无水乙醇相比,去离子水在其他物性参数与之相似的前提下表面张力是无水乙醇的3倍,而其相对液桥长度总比同工况的无水乙醇要小,这意味着表面张力同样对液桥拉伸的形貌特征影响显著.
Table 2
表2
表2不同物性液体的相关时间常数及相对液桥长度
Table 2
| Medium | TH/^s | Tc/呷 | lr | |||
|---|---|---|---|---|---|---|
| 0kV | 1.0 kV | 2.0 kV | 2.7 kV | |||
| biodiesel | 80.00 | 3.5 x 103 | 1.12 | 1.14 | 1.20 | 1.31 |
| ethyl alcohol | 13.2 | 0.36 | 0.90 | 0.92 | 1.02 | 1.20 |
| deionized water | 5.20 | 0.40 | 0.67 | 0.69 | 0.78 | 0.90 |
| 1 % NaCl | 5.00 | 6.0 x 10-5 | 0.66 | 0.69 | 0.77 | 0.89 |
| 10%NaCl | 4.70 | 3.7 x 10-6 | 0.64 | 0.68 | 0.74 | 0.87 |
新窗口打开|下载CSV
图4
新窗口打开|下载原图ZIP|生成PPT图4不同实验介质的临界相对液桥长度
Fig.4Relative lengths of different experimental media。
2.1.2 电邦德数对相对液桥长度的影响
滴状模式下随着$Bo_{\rm E}$的不断增大,母液滴脱落过程中液桥的长度及母液滴的半径r也都在发生相应的变化,图5给出了其高速数码拍摄的液桥形成过程的显微形貌.两种实验介质的液桥长度均会随着电邦德数的增大而增大,而母液滴的尺寸却都在电邦德数的增大过程中不断减小.从图中不难发现,两种实验介质的液滴脱落模式均存在突变区,当$Bo_{\rm E} > 1.51$时无水乙醇由滴状模式过渡到纺锤模式,而当$Bo_{\rm E} > 1.82$时生物乙醇由滴状模式过渡到脉动模式.不同的是,两者突变区来临前的液桥长度存在较大差异,生物柴油突变区的液桥长度成倍增大.图6给出了两种实验介质相对液桥长度及相对母液滴尺寸随电邦德数的变化.当$Bo_{\rm E}$较小时,两种实验介质的液桥相对长度对电场强度的变化并不明显,均表现为略微增大,此时无水乙醇液桥相对长度始终小于生物柴油,此时相对于静电力,液体的毛细管力占主导地位.当$Bo_{\rm E}$较大时,生物柴油和无水乙醇的相对液桥长度随着$Bo_{\rm E}$的增大均有明显提升,这说明相对液桥长度仅对较高的电场强度变化敏感,由方程(4)可知,这是由于液滴荷电削弱了相对表面张力而导致的,此时无水乙醇的相对液桥长度要大于生物柴油的值.从图中可以看出,无论是无水乙醇还是生物柴油介质,相对液桥长度均存在突变区.对于无水乙醇,当$Bo_{\rm E}$从1.41增大到1.51时,相对液桥长度从1.5陡然升至2.25,此后从液桥形貌可以发现,滴状模式过渡到纺锤模式.同样对于生物柴油,当$Bo_{\rm E}$从1.82增大到1.88时,相对液桥长度从2.25陡然升至4.25,此后从液桥形貌可以发现,滴状模式过渡到脉动模式.这表明液桥的突变恰恰就是雾化模式过渡的信号.此外从母液滴的尺寸变化来看,随着$Bo_{\rm E}$的增大,母液滴的相对大小均在不断下降,在液桥长度微增大区间,两种介质的$r/R$近似线性递减,而在在液桥长度明显增大区间$,$两种介质的$r/R$呈现非线性递减特点.同时对比两种实验介质,无水乙醇母液滴的大小始终比同$Bo_{\rm E}$下的生物柴油要小.
图5
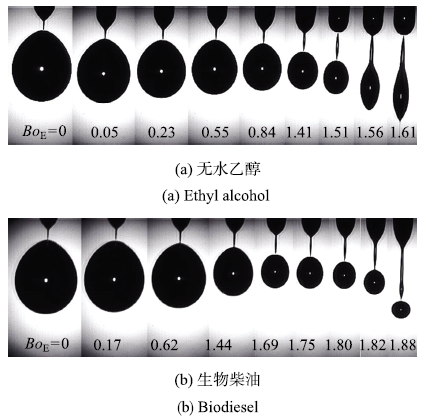新窗口打开|下载原图ZIP|生成PPT图5不同$Bo_{\rm E}$下液桥形成过程的显微演变形貌
Fig.5Micro morphology of the liquid bridge formation process at different$Bo_{\rm E}$
图6
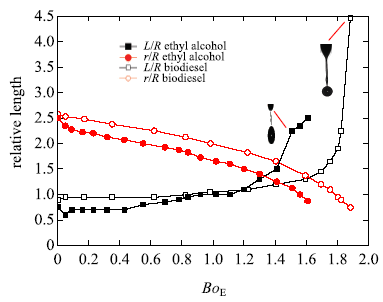新窗口打开|下载原图ZIP|生成PPT图6不同$Bo_{\rm E}$下相对液桥长度及母液滴相对大小
Fig.6Relative lengths of the liquid bridge and droplet radius at different$Bo_{\rm E}$
相对液桥长度是反映卫星液滴形成过程的一个非常重要的因素.在外加电场存在的情况下,液桥的表面张力随着电压的不断增大被削弱的程度也在不断增大,这导致相对液桥长度会持续增大.相对表面张力的减小会引起弹性系数的降低,使得液桥收缩形成卫星液滴后其向上的初始动量减小,最终带来的影响将是卫星液滴沿微通道轴向空间上下振幅的缩小.
2.2 液桥的断裂顺序
当液桥达到一个临界长度时便会从上下游末端依次断裂,而此时液桥的断裂顺序将直接影响到射流模式过渡演变的形貌特征.液桥断裂后管口半月面及母液滴可以近似为球形曲面,此时基于球形半径的曲率半径可以通过测量直接获得.这里我们引入相对曲率$Z_{\rm R}$(曲率半径与毛细管半径之比)使得曲率半径具有可参照性,液桥的破碎顺序取决于上游管口半月面及下游母液滴的相对曲率值的大小.图7给出了不同$Bo_{\rm E}$下无水乙醇的液桥上下游相对曲率值的变化情况. 图中发现,当$Bo_{\rm E}$范围在0~1.40范围内时,母液滴的相对曲率半径值$Z_{\rm R2}$的测量值一直大于半月面的相对曲率半径值$Z_{\rm R1}$.由于界面的曲率更大,此时半月面管口毛细压力较母液滴的大,这导致液桥始终会在下游先断裂而后是上游与半月面夹断.然而,随着$Bo_{\rm E}$的不断增大,从微通道管口脱落的初始液滴的尺寸在不断减小.当$Bo_{\rm E}$达到1.51时,$ Z_{\rm R2}$近似于$Z_{\rm R1}$,此时液桥的上下游两端几乎同时夹断;继续增大$Bo_{\rm E}$至1.56时,母液滴的$Z_{\rm R2}$值开始小于管口半月面的$Z_{\rm R1}$值,这导致液桥从上游末端先断裂而后才是下游末端断裂.这也就意味着如果$Z_{\rm R2} > Z_{\rm R1}$,液桥总是从下游先断裂,这种破碎顺序的发生是基于非荷电或荷电电压较低的实验工况.当电场强度足够高时,从微通道管口脱落的母液滴尺寸开始逐渐小于管口半月面从而导致$Z_{\rm R2} < Z_{\rm R1}$,此时液桥将从上游末端先发生断裂.图7
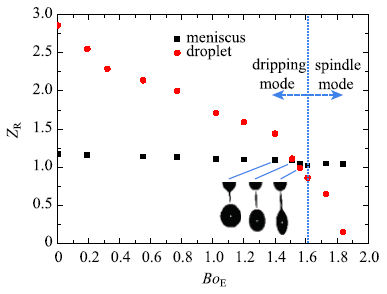新窗口打开|下载原图ZIP|生成PPT图7不同$Bo_{\rm E}$下液桥的上下游相对曲率半径. 介质为无水乙醇
Fig.7Relative curvature radius of the liquid bridge at different$Bo_{\rm E}$. Liquid is ethyl alcohol
后处理过程中我们把液桥上游末端瞬间断裂后的管口半月面锥与水平线的形成角记为$\alpha$,同时把液桥下游末端瞬间断裂后的母液滴上游锥面与水平线的形成角记为$\beta$,通过图片后处理获得不同$Bo_{\rm E}$工况下的$\alpha$和$\beta$值并类比$Z_{\rm R1}$和$Z_{\rm R2}$,如图8所示.对于无水乙醇,随着$Bo_{\rm E}$不断增大,$\alpha$值从$Bo_{\rm E} = 0$工况下的50.2$^\circ$缓慢增长到$Bo_{\rm E} = 1.61$时的55$^\circ$;然后大不相同的是,$\beta$值却从$Bo_{\rm E} = 0$工况下的17.4$^\circ$迅速增长到$Bo_{\rm E} = 1.61$时的62$^\circ$.这期间$\alpha$和$\beta$值在$Bo_{\rm E} = 1.51$时有一个交叉点,$\alpha \approx \beta = 53.8^{\circ}$.与图5对比可以发现,$\alpha$和$\beta$的数值关系直接反映着管口半月面和母液滴曲率的变化,表明形成角数值与曲率半径成反比关系. 当$\beta<53.8^\circ$时,液桥将始终从下游末端先断裂,而一旦$\beta > 53.8^\circ$时,液桥的断裂顺序发生突变,开始从上游末端先破裂.这与曲率比$\varphi$表达的思想是一致的, 如果$\alpha > \beta$,$Z_{\rm R2} > Z_{\rm R1}$; 同样,$Z_{\rm R2} < Z_{\rm R1}$如果$\alpha < \beta$. 因此$\alpha$和$\beta$值是用来评估液桥破碎顺序的一个非常重要的参数.实际上,随着$Bo_{\rm E}$的不断增大,不同物性的液体其形成角变化存在较大差异.图中对于生物柴油,当$Bo_{\rm E}$从0逐渐增大到1.69时,$\alpha$值从52$^\circ$缓慢增长到57$^\circ$,$\beta$值从32$^\circ$较快增长到46$^\circ$;然而当$Bo_{\rm E}$增大到1.86时,$\alpha$值将迅速增长到66\r{ }而$\beta$值依旧维持在46$^\circ$附近. 此时从图中可以发现,整个过程中$\alpha$值均大于$\beta$值,这导致整个滴状模式区间内液桥将始终从下游末端先断裂.因此随着$Bo_{\rm E}$的不断增大,不同物性液体的射流过渡行为由于形成角变化的不确定性而存在较大差异.当前实验研究发现,对于无水乙醇液体,$Bo_{\rm E}$的增大使滴状模式首先过渡到纺锤模式,而对于生物柴油液体,滴状模式后会首先出现脉动模式而非纺锤模式,这在一定程度上映射了不同物性液体的静电雾化模式存在着差异性.
图8
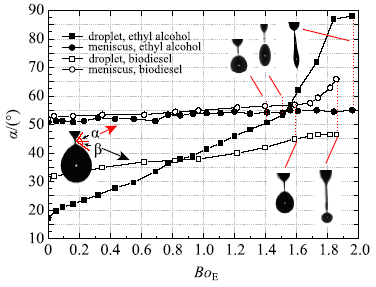新窗口打开|下载原图ZIP|生成PPT图8不同$Bo_{\rm E}$下形成角的变化
Fig.8Angle changes with the increase of$Bo_{\rm E}$
3 结 论
(1)流体动力学弛豫时间是影响相对液桥长度一个非常重要的无量纲数,表明黏度与表面张力之比决定着液桥的断裂长度,而通过荷电弛豫时间的对比发现液体电导率对液桥长度的变化影响甚微.(2)当$Bo_{\rm E}$较小时,液桥相对长度变化并不明显,当$Bo_{\rm E}$较大时,相对液桥长度随着$Bo_{\rm E}$的增大均有明显提升.两种介质的相对液桥长度均存在突变区并伴随着雾化模式的转变,表明液桥的突变恰恰是雾化模式过渡的信号.
(3)$\alpha$和$\beta$值是用来评估液桥破碎顺序的重要参数,随着$Bo_{\rm E}$的不断增大,无水乙醇存在液桥断裂顺序转变的临界形成角值,进而过渡到纺锤模式;对于生物柴油,由于$\beta$值始终小于$\alpha$值,液桥无法从上游半月面率先脱落,这导致当$Bo_{\rm E}$增大到某一临界值时滴状模式会过渡到脉动模式而非纺锤模式.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
DOIURL [本文引用: 1]
Three spray systems with multiple nozzles arranged linearly, of different geometrical configurations were tested experimentally: (1) spray nozzles without induction electrodes facing a distant plate, (2) spray nozzles with two parallel bar induction electrodes, and (3) spray nozzles with individual ring induction electrodes. The systems were set to operate at the precession mode of spraying. In all the systems, except that of individual induction electrodes, the precession mode of spraying was first set at peripheral nozzles, and next, for higher voltages, at central nozzles. In the system with ring induction electrodes, the precession mode of spraying was generated for all nozzles at the same voltage level. The size and charge distributions of the droplets were measured for each spray system. The charge distribution of the droplets was measured with a ring induction probe, and it was compared with the charge distribution determined numerically from the size distribution of the droplets, based on the Rayleigh limit formula. It was shown that both these distributions correlate quite well. Free droplets suspended and moving irregularly within the centre of the charged spray plume were observed in the system with individual rings.
[本文引用: 1]
DOIURL
纳米流体液滴撞击固体壁面的铺展动力学特性是基于液滴沉积实现高效传热传质过程的关键因素,然而由于纳米流体的非牛顿流变特性及液滴内微流动与纳米颗粒的耦合作用,目前对纳米流体液滴撞击固体壁面的铺展动力学行为缺乏足够的认识.本研究利用了两步法分别配制了分散有3种纳米颗粒的均匀稳定纳米流体(碳纳米管、石墨烯、纳米石墨粉),并对流体的流变特性进行了测量分析.利用显微高速数码摄像技术捕捉了液滴撞击固体壁面的动态过程,通过图像处理技术分析铺展过程中液滴的无量纲高度、铺展因子及动态接触角,探究了液滴在韦伯数约为200及800时撞击壁面后铺展沉积形态的演变规律.研究表明,3种不同纳米颗粒的加入均使基液表现出明显的剪切变稀特性,在液滴撞击壁面的铺展过程中,流体的剪切黏度起重要作用,液滴的无量纲高度和铺展因子的变化幅度随着纳米流体剪切黏度的增大而减小.纳米流体液滴撞击疏水表面时能更快的达到平衡状态,液滴的惯性力主导着液滴的初始铺展阶段,液滴的铺展范围和速度随撞击速度的增大而增大.开展该研究能够为基于液滴沉积的增益冷却技术以及微型高导热及导电材料的制造提供理论依据和技术指导.
DOIURL
纳米流体液滴撞击固体壁面的铺展动力学特性是基于液滴沉积实现高效传热传质过程的关键因素,然而由于纳米流体的非牛顿流变特性及液滴内微流动与纳米颗粒的耦合作用,目前对纳米流体液滴撞击固体壁面的铺展动力学行为缺乏足够的认识.本研究利用了两步法分别配制了分散有3种纳米颗粒的均匀稳定纳米流体(碳纳米管、石墨烯、纳米石墨粉),并对流体的流变特性进行了测量分析.利用显微高速数码摄像技术捕捉了液滴撞击固体壁面的动态过程,通过图像处理技术分析铺展过程中液滴的无量纲高度、铺展因子及动态接触角,探究了液滴在韦伯数约为200及800时撞击壁面后铺展沉积形态的演变规律.研究表明,3种不同纳米颗粒的加入均使基液表现出明显的剪切变稀特性,在液滴撞击壁面的铺展过程中,流体的剪切黏度起重要作用,液滴的无量纲高度和铺展因子的变化幅度随着纳米流体剪切黏度的增大而减小.纳米流体液滴撞击疏水表面时能更快的达到平衡状态,液滴的惯性力主导着液滴的初始铺展阶段,液滴的铺展范围和速度随撞击速度的增大而增大.开展该研究能够为基于液滴沉积的增益冷却技术以及微型高导热及导电材料的制造提供理论依据和技术指导.
DOIURL [本文引用: 1]
为解决制冷系统除霜技术存在的问题,介绍了利用高压静电场技术及扫频高压交流电场技术在制冷系统中除霜的机理及研究进展,基于电流体动力学理论分析了霜晶分别在自然生长以及受高压静电场影响两种情况下不同的生长特性、机理和高压静电场中影响霜沉积量的主要电场参数,以及影响扫频高压交流电场技术除霜效率和能耗的主要参数。研究表明:电压及电场极性对高压静电场除霜的效率影响显著,频宽及交流电场持续施加的时间则是影响扫频高压交流电场除霜效率及能耗的主要电场参数;扫频高压交流电场除霜技术相比于静电场除霜技术,在除霜效率上更高,但能耗上处于劣势。最后,从除霜效率及能耗角度出发,提出了进一步深入研究的方向。
DOIURL [本文引用: 1]
为解决制冷系统除霜技术存在的问题,介绍了利用高压静电场技术及扫频高压交流电场技术在制冷系统中除霜的机理及研究进展,基于电流体动力学理论分析了霜晶分别在自然生长以及受高压静电场影响两种情况下不同的生长特性、机理和高压静电场中影响霜沉积量的主要电场参数,以及影响扫频高压交流电场技术除霜效率和能耗的主要参数。研究表明:电压及电场极性对高压静电场除霜的效率影响显著,频宽及交流电场持续施加的时间则是影响扫频高压交流电场除霜效率及能耗的主要电场参数;扫频高压交流电场除霜技术相比于静电场除霜技术,在除霜效率上更高,但能耗上处于劣势。最后,从除霜效率及能耗角度出发,提出了进一步深入研究的方向。
DOIURL [本文引用: 1]
研究液滴在静电喷雾下的速度特性是理解喷雾形态的形成及演化的关键.结合锥射流模式下乙醇静电喷雾实验数据,建立了静电喷雾二维轴对称模型.基于离散相液滴运动方程、连续相空气运动方程、电场方程以及用户自定义函数,进行了数值求解,获得了锥射流模式下的乙醇静电喷雾形态、空间电场分布以及液滴速度场分布.考虑了不同空气入口流速的影响,得到了乙醇/空气同轴射流静电喷雾形态的变化规律.结果表明,喷雾外围液滴与空气流场有较强的相互作用,导致喷雾中轴线附近的液滴速度分布变化较小,而在喷雾外围处的液滴速度分布沿径向剧烈变化;随着空气入口速度的增大,乙醇/空气同轴射流静电喷雾形态先趋于发散,当空气入口速度大于喷雾外围液滴轴向速度时,喷雾形态则趋于聚拢.因此,除改变施加电压、液体流量和电极结构外,通过控制空气入口速度来影响喷雾液滴速度场,也可获得不同的静电喷雾效果.
DOIURL [本文引用: 1]
研究液滴在静电喷雾下的速度特性是理解喷雾形态的形成及演化的关键.结合锥射流模式下乙醇静电喷雾实验数据,建立了静电喷雾二维轴对称模型.基于离散相液滴运动方程、连续相空气运动方程、电场方程以及用户自定义函数,进行了数值求解,获得了锥射流模式下的乙醇静电喷雾形态、空间电场分布以及液滴速度场分布.考虑了不同空气入口流速的影响,得到了乙醇/空气同轴射流静电喷雾形态的变化规律.结果表明,喷雾外围液滴与空气流场有较强的相互作用,导致喷雾中轴线附近的液滴速度分布变化较小,而在喷雾外围处的液滴速度分布沿径向剧烈变化;随着空气入口速度的增大,乙醇/空气同轴射流静电喷雾形态先趋于发散,当空气入口速度大于喷雾外围液滴轴向速度时,喷雾形态则趋于聚拢.因此,除改变施加电压、液体流量和电极结构外,通过控制空气入口速度来影响喷雾液滴速度场,也可获得不同的静电喷雾效果.
DOIURLPMID
The axisymmetric stability of an electrified jet is analyzed under electrospinning conditions using the linear stability theory. The fluid is considered Newtonian with a finite electrical conductivity, modeled as a leaky dielectric medium. While the previous studies impose axisymmetric disturbances on a cylindrical jet of uniform radius, referred to as the base state, in the present study the actual thinning jet profile, obtained as the steady-state solution of the one-dimensional slender filament model, is treated as the base state. The analysis takes into account the role of variation in the jet variables like radius, velocity, electric field, and surface charge density along the thinning jet in the stability behavior. The eigenspectrum of the axisymmetric disturbance growth rate is constructed from the linearized disturbance equations discretized using the Chebyshev collocation method. The most unstable growth rate for the thinning jet is significantly different from that for the uniform radius jet. For the same electrospinning conditions, while the uniform radius jet is predicted to be highly unstable, the thinning jet profile is found to be unstable but with a relatively very low growth rate. The stabilizing role of the thinning jet is attributed to the variation in the surface charge density as well as the extensional deformation rate in the fluid ignored in the uniform radius jet analysis. The dominant mode for the thinning jet is an oscillatory conducting mode driven by the field-charge coupling. The disturbance energy balance finds the electric force to be the dominant force responsible for the disturbance growth, potentially leading to bead formation along the fiber. The role of various material and process parameters in the stability behavior is also investigated.
DOIURL
通过对气体驱动同轴电流动聚焦的实验模型进行简化,开展了电场力和惯性力共同作用下同轴带电射流的不稳定性理论研究.在流动为无黏、不可压缩、无旋的假设下,建立了三层流体带电射流物理模型并得到了扰动在时间域内发展演化的解析形式色散关系,利用正则模方法求解色散方程发现了流动的不稳定模态,进而分析了主要控制参数对不稳定模态的影响.结果表明,在参考状态下轴对称模态的最不稳定增长率最大,因此轴对称扰动控制整个流场.外层气流速度越高,气体惯性力越大,射流的界面越容易失稳.内外层液-液同轴射流之间的速度差越大,射流越不稳定.表面张力对射流不稳定性起到促进作用.轴向电场对射流不稳定性具有双重影响:当加载电场强度较小时,射流不稳定性被抑制;当施加电压大于某一临界值时,轴向电场会促进射流失稳.临界电压的大小与界面上自由电荷密度和射流表面扰动发展关系密切.这些结果与已有的实验现象吻合,能够对实验的过程控制提供理论指导.
DOIURL
通过对气体驱动同轴电流动聚焦的实验模型进行简化,开展了电场力和惯性力共同作用下同轴带电射流的不稳定性理论研究.在流动为无黏、不可压缩、无旋的假设下,建立了三层流体带电射流物理模型并得到了扰动在时间域内发展演化的解析形式色散关系,利用正则模方法求解色散方程发现了流动的不稳定模态,进而分析了主要控制参数对不稳定模态的影响.结果表明,在参考状态下轴对称模态的最不稳定增长率最大,因此轴对称扰动控制整个流场.外层气流速度越高,气体惯性力越大,射流的界面越容易失稳.内外层液-液同轴射流之间的速度差越大,射流越不稳定.表面张力对射流不稳定性起到促进作用.轴向电场对射流不稳定性具有双重影响:当加载电场强度较小时,射流不稳定性被抑制;当施加电压大于某一临界值时,轴向电场会促进射流失稳.临界电压的大小与界面上自由电荷密度和射流表面扰动发展关系密切.这些结果与已有的实验现象吻合,能够对实验的过程控制提供理论指导.
URL [本文引用: 1]
液体射流热稳定性研究是对射流稳定性问题的更深层次的探讨,可以进一步加深对液体射流分裂与雾化机理的认识,具有重要的学术意义和工程应用价值.基于射流稳定性理论,在同时考虑射流周围气体旋转、射流和周围气体可压缩性以及射流液体中含空化气泡的条件下,建立了描述可压缩旋转气体中超空化射流热稳定性的数学模型,并对数学模型及其求解方法进行了验证分析；在此基础上,分析了液体射流表面与周围气体间温差及射流内部温度梯度同时作用下对射流稳定性的影响；并进一步探讨了超空化射流的热稳定性.结果表明,射流表面扰动波的最大扰动增长率、最不稳定频率以及最大扰动波数皆随气液温差的增大呈近似线性增大趋势；射流内部温度梯度的存在使得气液温差对射流的失稳作用更加显著；射流内部温度梯度会抑制超空化对射流稳定性的影响,但气液温差会在一定程度上促进超空化对射流的失稳作用.
URL [本文引用: 1]
液体射流热稳定性研究是对射流稳定性问题的更深层次的探讨,可以进一步加深对液体射流分裂与雾化机理的认识,具有重要的学术意义和工程应用价值.基于射流稳定性理论,在同时考虑射流周围气体旋转、射流和周围气体可压缩性以及射流液体中含空化气泡的条件下,建立了描述可压缩旋转气体中超空化射流热稳定性的数学模型,并对数学模型及其求解方法进行了验证分析；在此基础上,分析了液体射流表面与周围气体间温差及射流内部温度梯度同时作用下对射流稳定性的影响；并进一步探讨了超空化射流的热稳定性.结果表明,射流表面扰动波的最大扰动增长率、最不稳定频率以及最大扰动波数皆随气液温差的增大呈近似线性增大趋势；射流内部温度梯度的存在使得气液温差对射流的失稳作用更加显著；射流内部温度梯度会抑制超空化对射流稳定性的影响,但气液温差会在一定程度上促进超空化对射流的失稳作用.
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
ABSTRACT The stability of the horizontal interface between conducting and non-conducting fluids under the influence of an initially uniform vertical electric field is discussed. To produce such a field when the conducting fluid is the heavier it is imagined that a large horizontal electrode is immersed in the non-conducting fluid. As the field increases the part of the interface below the electrode rises till at a voltage V, which depends on the interfacial tension, the height of the electrode above the interface and the density difference, the interface becomes unstable for vertical displacements Z which satisfy the equation $({\frac{\delta^2}{\delta x^2}} + {\frac{\delta^2}{\delta y^2}}+k^2) Z=0.$ The value of k consistent with the lowest value of V is found. When the electrode is situated above the interface at less than a certain distance the lowest value of V is attained when k = 0 so that the horizontal extent of an unstable crest is likely to be great. As the electrode height increases above this critical value k increases and the unstable crests become more closely spaced till an upper limiting value of k is obtained.
DOIURL
The elongation of a drop of one dielectric fluid in another owing to the imposition of an electric field has previously been studied assuming that the interface is uncharged and the fluids at rest. For a steady field this is unrealistic, because however small the conductivity of either fluid the charge associated with steady currents must accumulate at the interface till the steady state is established. It is shown that equilibrium can only be established in a drop when circulations are set up both in the drop and its surroundings. A relation is found between the ratios of the conductivity, viscosity and dielectric constant for the drop and surrounding fluid which permits the drop to remain spherical when subjected to a uniform field. The streamlines of the circulation for this case are shown and criteria are given for distinguishing between circulations which carry the surface of the drop towards or away from the poles and for predicting whether the drop will become prolate or oblate. Experiments by S. G. Mason and his co-workers are compared with the theoretical predictions and agreement is found in all cases for which the necessary data are given.
DOIURL [本文引用: 1]
ABSTRACT Electrohydrodynamics of fluids having uniform electrical properties, emphasizing shear effects for interfacially confined electromechanical coupling
DOIURL [本文引用: 1]
The surface of the liquid issuing from a capillary subjected to the electric stresses deforms to an elongated jet which disrupts to a series of droplets. In the paper the detailed experimental studies of jet and drop formation from liquid issuing from a capillary maintained at high voltage of positive or negative polarity have been reported. The forms of the jet and the way it disrupts into droplets have been classified into the modes of spraying. A definition of the mode of spraying and the criteria for the mode classification, based on the geometrical form of the meniscus, jet or drop formation are given.
DOIURL [本文引用: 1]
This paper reports an experimental study of the effects of an externally applied electric field on the dynamics of drop formation in the dripping mode from a vertical metal capillary. The fluid issuing out of the capillary is a viscous liquid, the surrounding ambient fluid is air, and the electric field is generated by establishing a potential difference between the capillary and a horizontal, circular electrode of large radius placed downstream of the capillary outlet. By means of an ultra-high-speed video system that is capable of recording up to 12000 frames per second, special attention is paid to the dynamics of the liquid thread that connects the primary drop that is about to detach and fall from the capillary to the rest of the conical liquid mass that is hanging from it. The experiments show that as the strength of the electric field increases, the volume of the primary drop decreases whereas the maximum length attained by the thread increases. The reduction in the volume of primary drops and the increase in the length of threads occur because the effective electromechanical surface tension of the fluid interface falls as the field strength rises. For the highly conducting drops of aqueous NaCl solutions studied in this work, the increase in thread length is due solely to the rising importance of normal electric stress relative to the falling importance of surface tension. However, as the conductivity of the drop liquid decreases, the thread length is further increased on account of the stabilizing influence exerted by the increasing electric shear stress that acts on the charged liquid as interface. Two new phenomena are also reported that have profound implications for electrohydrodynamics and practical applications. First, it is shown that whereas the liquid thread always ruptures at its downstream end in the absence of an applied electric field or when the field strength is low, it ruptures at its upstream end when the field strength is sufficiently high. Since satellite drops are produced directly from the thread once both of its ends have ruptured, the change in the mechanism of breakup with field strength influences the dynamics and fate of satellite drops. Second, it is demonstrated that the generation of satellites, which are often undesirable in applications, can be suppressed by the judicious application of an electric field. This is accomplished by using a field of moderate strength to induce charges of the opposite sign on the nearby surfaces of the satellite drop and the liquid that remains pendant from the tube following thread rupture. At high field strengths, induced charge effects are too weak to compete with net charge effects: the satellite is repelled by the pendant drop and falls under gravity as a distinct entity.
DOIURLPMID [本文引用: 1]
Mechanism in a newly proposed EHD method of drop formation in an AC electric field is studied and it is divided into two stages, such as drop elongation and breakup of a liquid bridge.
DOIURL [本文引用: 1]
We report experiments on the dripping dynamics and jetting transitions that take place when a liquid is injected vertically downwards at a constant flow rate, for wide ranges of the liquid viscosity and injector radius. We explore values of the Bond number significantly larger than in previous works, revealing the existence of period-2 dripping regimes with satellite formation that do not exist at small Bond numbers. In addition, we quantify the influence of liquid viscosity on the hysteresis associated with the dripping-jetting transition, that had previously been studied only for the particular case of water.
DOIURL [本文引用: 1]
The presence of small amount of polymer in Newtonian liquids affects the fluid behavior significantly and creates superficial differences between Newtonian and non-Newtonian drop formation. In the present study, Newtonian and non-Newtonian shear-thinning drop formation in air is examined experimentally and the geometrical parameters, such as drop elongation length, minimum neck diameter and current contact angle are studied for water, glycerin solutions (79, 89 and 94% w/w) and Carboxymethyl cellulose (CMC) solutions (0.5 to 1.5% w/w) drops. The results indicate that at initial stages of the drop growth, Newtonian and non-Newtonian liquids behave similarly. However, at the start of the necking process in which the deformation rate increases, clear differences can be seen between Newtonian and shear-thinning fluids. The most important effects of an increase in the glycerin and CMC concentration, which enlarges the viscosity, are an increase in the time span of the necking process, a decrease in the elongation rate, an increase in the length of the liquid filament and an increase in the probability of the satellite drop formation. On the other hand, due to the shear-thinning properties of CMC solutions, their viscosity decreases in the necking region and as a result, the length of the Newtonian drop at the moment of separation is longer than that of the shear-thinning drop with equal viscosity. The variation of minimum neck thickness with the time remaining until the detachment for the investigated liquids is presented by h min ∝(t d -t) α h min ∝ ( t d - t ) α mathContainer Loading Mathjax , 02 in which α α mathContainer Loading Mathjax is 2/3 for water, 1 for viscous Newtonian fluids, and for non-Newtonian shear-thinning fluids it is equal to the index of fluid in the power-law relation.
DOIURL [本文引用: 1]
ABSTRACT The shape evolution of small droplets attached to a conducting surface and subjected to relatively strong electric fields is studied both experimentally and numerically. The problem is motivated by the phenomena characteristic of the electrospinning of nanofibres. Three different scenarios of droplet shape evolution are distinguished, based on numerical solution of the Stokes equations for perfectly conducting droplets. (i) In sufficiently weak (subcritical) electric fields the droplets are stretched by the electric Maxwell stresses and acquire steady-state shapes where equilibrium is achieved by means of the surface tension. (ii) In stronger (supercritical) electric fields the Maxwell stresses overcome the surface tension, and jetting is initiated from the droplet tip if the static (initial) contact angle of the droplet with the conducting electrode is $\alpha_{s} {<} 0.8\pi $; in this case the jet base acquires a quasi-steady, nearly conical shape with vertical semi-angle $\beta {\leq} 30^{\circ}$, which is significantly smaller than that of the Taylor cone ($\beta_{T} {=} 49.3^{\circ}$). (iii) In supercritical electric fields acting on droplets with contact angle in the range $0.8\pi {<} \alpha_{s} {<} \pi $ there is no jetting and almost the whole droplet jumps off, similar to the gravity or drop-on-demand dripping. The droplet et transitional region and the jet region proper are studied in detail for the second case, using the quasi-one-dimensional equations with inertial effects and such additional features as the dielectric properties of the liquid (leaky dielectrics) taken into account. The flow in the transitional and jet region is matched to that in the droplet. By this means, the current oltage characteristic $I {=} I(U)$ and the volumetric flow rate $Q$ in electrospun viscous jets are predicted, given the potential difference applied. The predicted dependence $I {=} I(U)$ is nonlinear due to the convective mechanism of charge redistribution superimposed on the conductive (ohmic) one. For $U {=} O(10kV)$ and fluid conductivity $\sigma {=} 10^{-4}$ S m$^{-1}$, realistic current values $I {=} O(10^{2}nA)$ were predicted.
[本文引用: 1]
URLMagsci [本文引用: 1]
为探讨荷电液滴的变形机理，对滴状模式下荷电液滴的脉动变形特征进行了实验研究。综合考虑毛细管经、荷电电压及液滴的物性参数，采用带有显微变焦镜头的高速数码相机对荷电液滴进行了微距拍摄，并结合图像处理技术研究了荷电液滴的脉动变形问题。实验结果表明：随着电压的增加，液滴的最大变形率逐渐增大，但其脉动变形周期却逐步减小。对于导电性液体，电导率对荷电液滴的变形率及脉动周期影响微弱。表面张力与荷电液滴的最大变形率呈反比，与其脉动变形周期呈正比。
URLMagsci [本文引用: 1]
为探讨荷电液滴的变形机理，对滴状模式下荷电液滴的脉动变形特征进行了实验研究。综合考虑毛细管经、荷电电压及液滴的物性参数，采用带有显微变焦镜头的高速数码相机对荷电液滴进行了微距拍摄，并结合图像处理技术研究了荷电液滴的脉动变形问题。实验结果表明：随着电压的增加，液滴的最大变形率逐渐增大，但其脉动变形周期却逐步减小。对于导电性液体，电导率对荷电液滴的变形率及脉动周期影响微弱。表面张力与荷电液滴的最大变形率呈反比，与其脉动变形周期呈正比。
[本文引用: 1]
DOIURL [本文引用: 1]
Nonlinear breakup of charged liquid jets is numerically analyzed in this work in the limit of a very small electrical Strouhal number T-e/T-b much less than 1 (i.e. negligible charge relaxation effects, applicable to highly conducting liquids), where T-e is the electric relaxation time of charges, and T, is the breakup time in a Lagrangian framework following the liquid jet at its average axial velocity. The influence of the electrical Bond＇s number and viscosity on (i) the capillary Rayleigh＇s most probable breakup length, (ii) the breakup time, (iii) the volume of the satellite, and (iv) the charge of both main drop and satellite, are analyzed. The model is related to the microjet break-up phenomena in the electrospraying of liquids in steady cone-jet mode, and its range of applicability to those particular problems discussed. Previous experimental results [Mutoh et al., 1979, Convergence and disintegration of liquid jets induced by an electrostatic field. J. Appl. Phys. 50, 3174-3179; Clopeau and Prunet-Foch, 1989, Electrostatic spraying of liquids in cone-jet mode. J. Electrostatics 22, 135-159] support our numerical finding that the influence of the electrical Bond＇s number on Rayleigh＇s length is small within the usual parametrical limits of stability of a steady Taylor cone-jet at atmospheric pressure.
