, 黄彪, 刘影北京理工大学机械与车辆学院,北京 100081
NUMERICAL INVESTIGATION ON CAVITY STRUCTURES AND HYRODYNAMICS OF THE VEHICLE DURING VERTICAL WATER-ENTRY1)
ZhangJiayue, LiDaqin, WuQin, HuangBiao, LiuYing中图分类号:O352
文献标识码:A
通讯作者:
收稿日期:2018-11-1
网络出版日期:2019-05-18
版权声明:2019力学学报期刊社 所有
基金资助:
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (17227KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引 言
无动力运载体、导弹空中点火失败下落入水的过程中,会受到巨大的抨击作用,可能会导致其结构受损,传感器等内部组织被破坏等问题.这一过程中航行体周围流场会发生一系列十分复杂的物理变化,具有强烈的非定常特性,并对航行体运动过程有显著的影响.因此,航行体以尾部向下姿态入水过程的流场特性研究,对射弹等武器的优化以及回收[1],降低发射成本[2]等具有重要意义.对于固体的入水过程,国内外****通过实验、理论方法和数值模拟等多种途径进行了大量的研究工作[3-6].Worthington等[7-8]最早使用闪光照相机技术得到的球体垂直方向入水过程图像,定性地分析了入水空泡的发展过程以及早期闭合. 较为早期的入水空泡的理论方法是Logvinovich[9]提出的,他利用了能量守恒对空泡截面的扩张或者收缩运动过程进行求解.基于这一理论,Karman[10]假设在入水初期时能量守恒,提出了附加质量法理论,并且基于该理论对飞机迫降水面的冲击载荷进行了研究,推导出了入水载荷的公式.Aristoff等[11-12]对球体垂直入水过程进行了实验和理论研究,将闭合形式分为：表面闭合,深闭合,浅闭合和准静态闭合,在此基础上提出了一种理论模型,求解了产生夹断时间和深度的表达式,结果表明,无量纲夹断时间与深度为常值.Abraham等[13]通过数学建模并结合数值模拟研究了球体入水过程所受阻力.结果表明,改变球体速度、表面张力、流动状态和雷诺数,阻力系数结果没有明显变化,阻力主要由球体到相邻液体的动量传递造成.Alaoui等[14]对头部为不同锥角的锥形进行了入水实验,讨论了不同轴对称形状对冲击载荷的影响.结果表明,阻力系数与入水速度的平方成正比;恒定速度下,锥形轴对称体的阻力系数只取决于锥角,且锥角越小,冲击载荷系数越大.顾懋祥等[15]将鱼雷作为主要研究对象,开展了1:1模型实验研究,并且用截锥头段代替了头部球状段,利用传感器获得了入水过程的压力、加速度及应变等多组实验数据,重点分析了入水撞击阶段的压力变化.实验结果表明,轴对称平头运动体入水的压力最大值与初始的入水速度成正比关系.
随着计算机技术和计算流体力学的发展,国内外****采用数值模拟方法[16-23],并以多样的实验方法为依托,扩大了入水问题的研究范围以及研究内容的多样化.Gaudet[24]对低弗劳德数下,质量一定的圆盘垂直入水过程进行了数值模拟研究.结果表明入水空泡闭合深度以及圆盘阻力系数均与圆盘质量有关. Shi等[25-26]对弹体入水后的弹道、空泡发展,以及压力场进行了研究.结果表明,弹体高速入水是一个强烈的三维混沌过程,并且在弹体撞击自由液面以及形成的空泡拉脱发生溃灭时,均形成了冲击波.Erfanian等[27]利用数值方法和实验研究了球形弹丸的入水问题,建立了具有六自由度刚体运动的射弹的三维模型.数值计算结果与实验结果的良好一致性揭示了所提出的数值算法的准确性和能力. Areti等[28]建立了一种mSPH数值计算方法适用于模拟不同速度和密度下二维圆柱体自由下落过程.Iranmanesh等[29]对低速下不可压缩流体VOF方法对小球和水平圆柱体入水进行数值计算,与实验结果进行对比,研究了圆柱体直径,长度,冲击速度等对无量纲深度的影响.季斌等[30]提出了考虑气$\!$-$\!$-$\!$汽$\!$-$\!$-$\!$液三相的空化模型,对水下航行体的空化流动进行了数值模拟,并且与实验吻合较好.何春涛等[31]对球体和圆锥匀速垂直入水进行了数值模拟,并与May等[32]提出的垂直匀速入水理想空泡模型取得较好一致性.结果表明,空泡面闭合时间随入水速度增大而减小,无量纲闭合时间为常值.王易君等[33]对平底结构自由入水的砰击载荷和入水空泡进行了模拟.结果表明,砰击载荷最大值出现在入水瞬间并且随入水速度的增大而增大.
目前,很多****针对航行体以头部向下姿态的入水问题进行了大量的研究,但弹体发射失败下落回收时往往以尾部向下姿态入水,并且对于回收射弹的下落速度也会低于用于军事打击的高速航行射弹,对于航行体以尾部向下姿态的入水依然值得进一步研究.本文针对航行体以尾部向下姿态垂直入水过程进行数值模拟研究,分析航行体入水过程中的流体动力特性,入水空泡的形成机理以及流入水空泡发展对阻力系数影响;分析航行体入水速度对流体动力特性和入水空泡发展的影响规律,对航行体入水过程流场特性变化规律开展较为全面的研究.
1 数值计算方法
1.1 基本控制方程
假设气液两相是均相流动且相间无速度滑移,其基本控制方程为$\dfrac{\partial \rho _{\rm m} }{\partial t} + \dfrac{\partial }{\partial x_j } \left( {\rho _{\rm m} u_j } \right) = 0 (1)$
$ \dfrac{\partial (\rho _{\rm m} u_i )}{\partial t} + \dfrac{\partial (\rho _{\rm m} u_i u_j )}{\partial x_j } = $
$\qquad \rho _{\rm m} g - \dfrac{\partial p}{\partial x_i }+ \dfrac{\partial }{\partial x_j } \Bigg [\big (\mu _{\rm m} + \mu _{\rm T} \big) \Big (\dfrac{\partial u_i }{\partial x_j } + \dfrac{\partial u_j }{\partial x_i } \Big) \Bigg ] (2)$
式中,$u$为速度;$p$为静压; $\rho_{\rm m}$为混合介质的密度; $\tau _{ij}$为应力张量; $\mu _{\rm m}$为混合相动力黏性系数,是汽、液两相体积分数与两相动力黏性系数的加权平均; $\mu _{\rm T}$为动力黏性系数.
对于$\rho_{\rm m}$和$\mu_{\rm m}$,其表达式分别为
$ \rho _{\rm m} = \rho _{\rm v} \alpha _{\rm v} + \rho _{\rm g} \alpha _{\rm g}+\rho_{\rm l}(1-\alpha_{\rm v}-\alpha_{\rm g}) (3)$
$\mu _{\rm m}= \mu _{\rm v} \alpha _{\rm v} + \mu _{\rm g} \alpha _{\rm g} + \mu_{\rm l}(1-\alpha_{\rm v}-\alpha_{\rm g}) (4)$
式中, $\alpha $ 表示蒸汽体积率,表征了水$\!$-$\!$-$\!$汽两相之间的相变, $\rho $为介质的密度;下标v, l, g分别表示蒸汽、气相和水.
1.2 湍流模型
本文采用由Menter[34]提出的剪切应力输运$k$-$\!$-$\omega $模型,即SST$ k$-$\!$-$\omega $模型. SST模型既利用了$k$-$\!$-$\omega $模型近壁面处的稳定性,以捕捉黏性底层的流动;又在主流区结合了$k$-$\!$-$\omega $模型边界层外部独立性的优点.$k$-$\!$-$\omega $模型中,$k$方程和$\omega $方程表示如下
$\dfrac{\partial }{\partial t}\left( {\rho k} \right) + \dfrac{\partial }{\partial x_i }\left( {\rho ku_i } \right) = \dfrac{\partial }{\partial x_j }\left( { \varGamma_k \dfrac{\partial _k }{\partial x_j }} \right) + G_k-Y_k + S_k (5)$
$\dfrac{\partial }{\partial t}\left( {\rho \omega } \right) + \dfrac{\partial }{\partial x_i }\left( {\rho \omega u_i } \right) = $
$\dfrac{\partial }{\partial x_j }\left( { \varGamma_\omega \dfrac{\partial _\omega }{\partial x_j }} \right) + G_\omega - Y_\omega + D_\omega + S_\omega (6)$
其中,$k$为湍流动能, $\omega $湍流频率,$\varGamma _{k}$, $\varGamma _{\omega }$为湍流扩散系数,$G_{k}$, $G_{\omega }$为湍流生成项,$Y_{k}$, $Y_{\omega }$为湍流动能耗散项,$S_{k}$, $S_{\omega }$为自定义项.
1.3 空化模型
当前常用基于质量传输的空化模型中,忽略热传输和非平衡相变效应,采用组分传输方程来描述液相体积含量的输运方程为$$ \dot {m} = \dfrac{\partial \rho _{\rm l} \alpha _{\rm l} }{\partial t} + \dfrac{\partial (\rho _{\rm l} \alpha _{\rm l} u_j )}{\partial x_j } = \dot {m}^ + + \dot {m}^ - (7) $$
Zwart-Gerber-Belamri空化模型[35]结合泡间两相流动理论,认为空穴为一密度剧烈变化的可压缩性黏性流体,空穴内外是连续体,重点考虑了空穴生长和溃灭时气泡体积变化的影响,适于模拟空化的非定常过程. 在该模型中,单位体积内的相间传输速率为
$\dot {m}^{ + } = F_{\rm vap} \dfrac{3\alpha _{\rm nuc} (1 - \alpha _v )\rho _v }{R_{\rm B} }\left( {\dfrac{2}{3}\dfrac{p_v - p}{\rho _{\rm l} }} \right)^{1 / 2}\,, \ p < p_v (8)$
$\dot {m}^ - = - F_{\rm cond} \dfrac{3\alpha _v \rho _v }{R_{\rm B} }\left( {\dfrac{2}{3}\dfrac{p_ - p_v }{\rho _{\rm l} }} \right)^{1 / 2}\,, \ p > p_v (9)$
式中, $\alpha_{\rm nuc}$为汽核体积分数,$R_{\rm B}$为汽泡半径,$p_{v}$为汽化压强. $F_{\rm vap}$和$F_{\rm cond}$分别为蒸发和凝结经验系数.
1.4 网格及边界条件
本文采用航行体的尺寸及计算域截面示意图如图1所示. 航行体采用半圆头形,实心圆柱体结构,航行体总长为$L$,直径为$D_{0}$.计算域中$XY$平面为对称平面,计算域长为$5L$,高5.8$L$,宽6$D_{0}$,其中,空气域高为1.3$L$,水域高为4.5$L$.航行体尾部最低点距自由液面0.13$D_{0}$.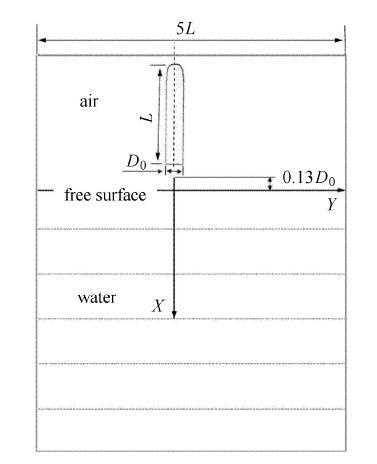
显示原图|下载原图ZIP|生成PPT图1计算域示意图
-->Fig. 1The computational domain diagram
-->
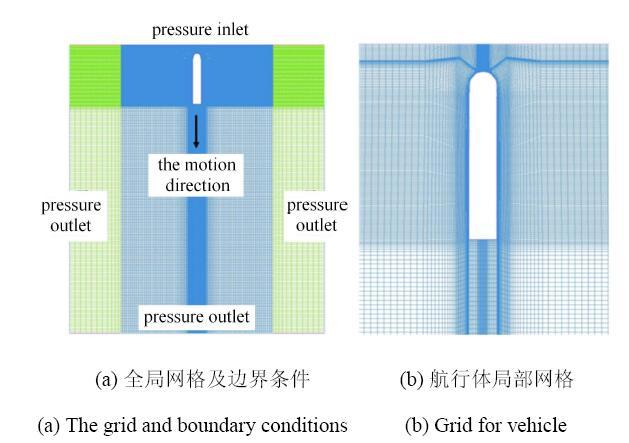
采用运动网格动态铺层法实现航行体入水过程数值计算,图2给出了航行体入水计算域网格分布和边界条件设置示意图.计算域分为两部分,蓝色网格位置为动网格区域,大小为3$L\times $4$D_{0}\times$5.8$L$,外部嵌套静网格区域,即绿色网格部分,大小为5$L\times $9.3$D_{0}\times $5.8$L$.利用界面将两个域连接起来. 动网格与静网格的流域边界条件均为压力出/入口.为保证计算精度,航行体周围及自由液面处网格进行加密,水域网格沿入水方向渐疏.分离求解算法采用SIMPLE算法,压力项采用PRESTO!,空间与时间离散采用一阶迎风模式.
显示原图|下载原图ZIP|生成PPT图2计算域网格及边界条件示意图
-->Fig. 2The grid distribution and boundary conditions
-->
2 结果分析与讨论
2.1 数值计算方法验证
为了验证本文所采用的数值计算方法,对入水速度为2.17,m/s垂直下落的球体进行数值计算,并与实验结果[12]进行对比.图3给出了实验测量与数值计算的球体入水深度随入水时间的变化对比,图4给出了典型时刻实验观测和数值计算的空泡形态图.从图中可以看出,实验与数值计算结果吻合较好.随着入水深度的增大,入水空泡沿轴向方向不断拉长,沿径向方向不断扩张,入水空泡始终与大气相连,随着入水空泡的进一步发展,动能不断转化为排开水的势能,空泡壁面扩张速度逐渐降低最后开始向轴线方向收缩,空泡闭合在沿轴线一点,发生深闭合.从图中可以看出,对于入水空泡形态,无论是在开空泡航行阶段还是空泡闭合阶段,实验与数值计算结果吻合度较好,验证了本文所采用数值方法的准确性与可行性.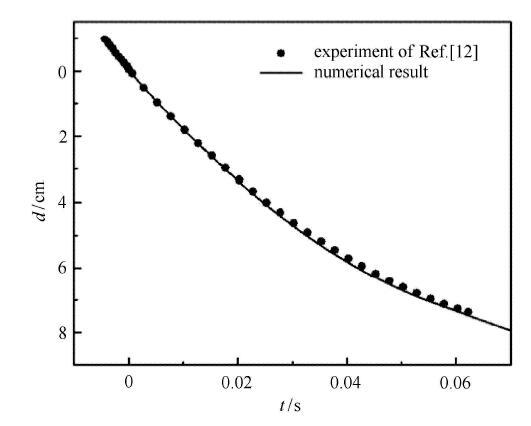
显示原图|下载原图ZIP|生成PPT图3球体入水深度随时间变化对比图
-->Fig. 3Comparing numerical results for the sphere depth as a function of time with the experimental data of Aristoff[
-->
显示原图|下载原图ZIP|生成PPT图4实验[
-->Fig. 4Comparing numerical results with experimental photographs[
-->
2.2 航行体垂直入水过程流场特性研究
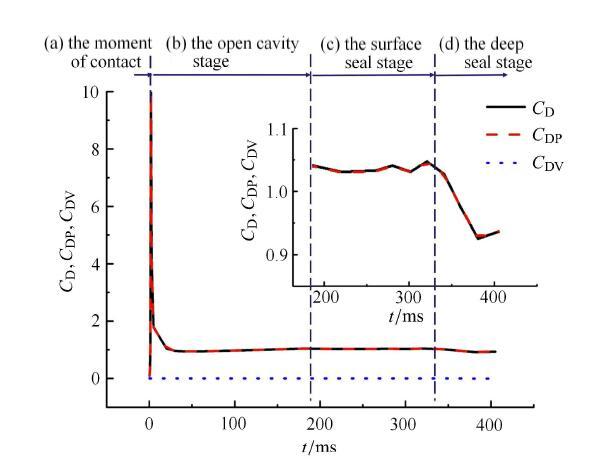
图5给出了射弹以35,m/s的入水速度垂直入水过程中,航行体所受到的阻力系数随时间的变化,其中横坐标为航行体入水航行时间,零时刻对应航行体尾部最低点触水时刻,纵坐标为总阻力系数$C_{\rm D}$、压差阻力系数$C_{\rm DP}$和黏性力系数$C_{\rm DV}$,分别定义为$$ C_{\rm D} = \dfrac{F_{\rm D} }{0.5\rho v^2S} \,, \quad C_{\rm DP} = \dfrac{F_{\rm DP} }{0.5\rho v^2S} \,, \quad C_{\rm DV} = \dfrac{F_{\rm DV} }{0.5\rho v^2S} (10) $$
式中,$C_{\rm D}$, $C_{\rm DP}$, $C_{\rm DV}$分别为航行体所受总阻力、压差阻力和黏性力, 且$F_{\rm D}=F_{\rm DP}+F_{\rm DV}$, $\rho $ 为水的密度, $v$为航行体速度,$S$为 航行体尾部横截面积.
显示原图|下载原图ZIP|生成PPT图5航行体垂直入水阻力系数随时间变化曲线
-->Fig. 5Effect of water-entry process on force coefficient
-->
由图5可以发现,航行体压差阻力系数和总阻力系数变化趋势一致,且峰值差别不大,而黏性力系数约为8.0$\times $10$^{-4}$,与压差阻力系数数量级差别较大,因此,航行体垂直入水过程中总阻力主要由压差阻力构成,黏性力系数对航行体入水过程阻力特性影响很小.
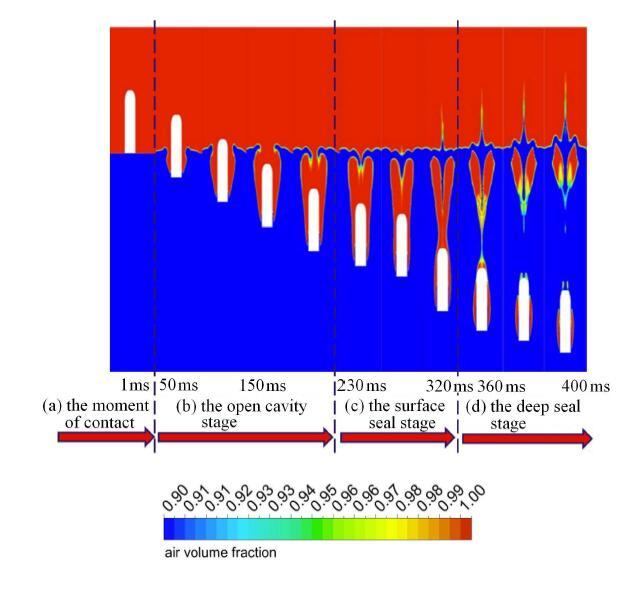
为了进一步分析航行体入水过程的流场特性,图6给出了航行体入水过程空泡形态随时间的演变情况.结合图5和图6,将航行体 入水过程分为4个阶段：入水冲击阶段、空泡敞开阶段、面闭合阶段和深闭合阶段.在入水冲击阶段,弹体撞击自由液面,总阻力系数在极短时间内迅速增大,达到一个峰值,如图5(a)所示;在空泡敞开阶段,如图6(b)所示,随着入水深度的增大,液体与弹体壁面产生分离,部分空气灌入,弹体开始携带空泡航行,入水空泡始终与大气相连,入水空泡长度不断拉长,宽度逐渐不断增大,此时总阻力系数逐渐降低,最终趋于平缓,如图5(b)所示;在空泡面闭合阶段,如图6(c)所示,随着入水空泡的进一步增长,空泡排开水的体积逐渐增大,在液面处空泡壁面开始出现收缩趋势,逐渐发生面闭合,外界空气不再灌入,空泡体积不再增大,此时阻力系数趋于稳定;在空泡深闭合阶段,如图6(d)所示,航行体携带空泡继续向下运动,在压力作用下空泡壁面向轴向收缩最终闭合于轴线上一点,发生深闭合($t=360$\,ms),形成上下两股射流,由于航行体仍被部分空泡包裹,且入水空泡体积的减小航行体在水中航行所受浮力,总阻力系数产生了微小的波动,略有下降.
显示原图|下载原图ZIP|生成PPT图6航行体垂直入水含气量云图分布
-->Fig. 6Air volume fraction contours of vehicle vertical water-entry
-->
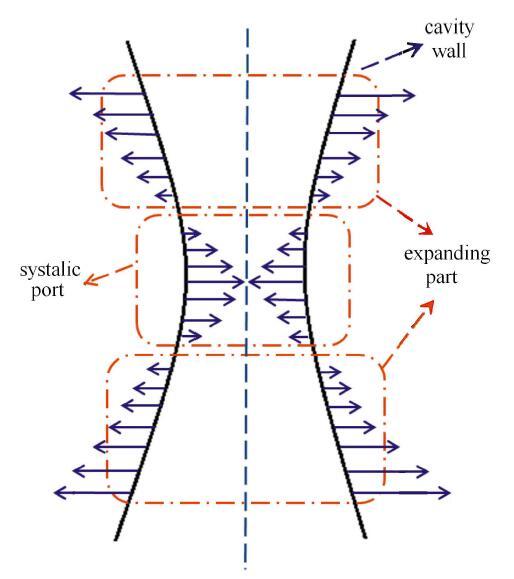
为了进一步分析航行体入水空泡形态的演变规律,图7提取了空泡敞开阶段和面闭合阶段典型时刻航行体的入水空泡轮廓演变情况.在入水空泡发展的过程中,在惯性力与内外压差的共同作用下,空泡壁面会同时存在扩张与收缩两种阶段,如图8所示.根据能量守恒定律,航行体撞击自由液面后,航行体将动能传递给周围的流体,流体质点获得一定的速度向径向运动,在内外压差的作用下,流体质点的动能逐渐转换为周围水域的压力势能以及因为流体黏性力所产生的热扩散等.当流体质点的径向扩张速度降低为零,在压力势能的作用下,流场质点会开始做反向运动.
显示原图|下载原图ZIP|生成PPT图7航行体垂直入水入水空泡随时间形态变化图
-->Fig. 7Developent of vertical water-entry cavity of vehicle
-->
显示原图|下载原图ZIP|生成PPT图8航行体垂直入水过程入水空泡壁面运动示意图
-->Fig. 8Cavity wall motion diagram at vertical water-entry process
-->
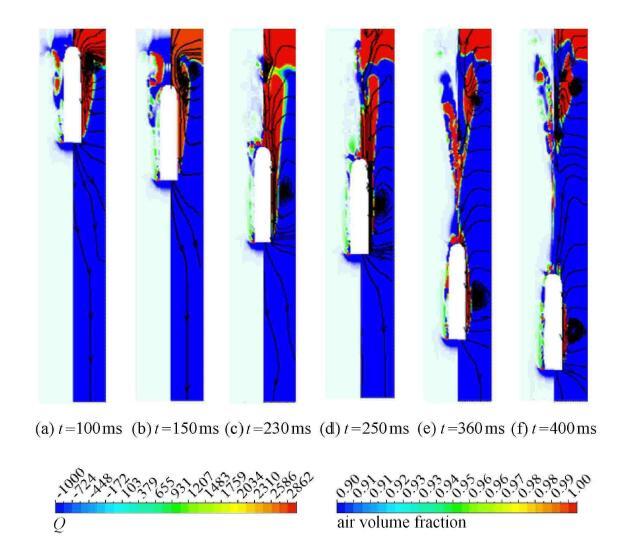
图9给出了航行体不同入水时刻的Q分布云图,涡量云图与流线分布. 其中,Q准则[36]定义为
$Q = \dfrac{\left| { \varOmega_{ij} } \right|^2 - \left| {S_{ij} } \right|^2}{2} (11)$
${\pmb\varOmega}_{ij} = 0.5\left( {\dfrac{\partial {\pmb u}_i }{\partial x_j } - \dfrac{\partial {\pmb u}_j }{\partial x_i }} \right) (12)$
${\pmb S}_{ij} = 0.5\left( {\dfrac{\partial {\pmb u}_i }{\partial x_j } + \dfrac{\partial {\pmb u}_j }{\partial x_i }} \right) (13)$
其中,${\pmb\varOmega} $为涡度张量, ${\pmb S}$为应变率张量.
显示原图|下载原图ZIP|生成PPT图9航行体垂直入水过程涡量图(左)和流线图(右)
-->Fig. 9Vortex(left) and streamline(right) contours of vehicle vertical water-entry
-->
从图9中可以看出,航行体在水中航行,入水空泡打开与空气联通,自由液面位置处涡量值较大,如图9(a)所示,这是由于入水表面喷溅及空泡口低压区的共同作用,产生明显的涡旋现象.入水空泡在发生面闭合过程中,如图9(b)所示,空泡壁处和自由液面处产生了对称涡旋,高速气流的迅速涌入造成了入水空泡壁处涡旋的产生,空泡内部湍流强度增大.在空泡发生表面闭合后,两侧涡旋逐渐向轴线靠拢,并在自由液面上方与射流汇合为一体,如图9(c)所示.入水空泡颈缩过程中,如图9(e)所示,空泡内部涡流强度以及尺度大大增强,空泡内部气压进一步降低,加速了空泡壁面的收缩趋势,空泡壁面逐渐向轴对称处聚拢,气液混合相运动加剧,内部流场较为复杂;从图中可看到流线从颈缩处分为上下两部分延伸,空泡内上方气液混合相无法再向下方流动,空泡内部流动被隔断,说明此时空泡壁面并未完全接触发生深闭合,但泡内流动上下表明深闭合现象已经发生.空泡发生深闭合后,分割为独立的两个空泡,如图9(f)所示,夹断后上方产生的空泡在内部流体交汇处形成多个涡旋,附近流体与泡内混合相作用剧烈,以及面闭合时产生向下的射流击穿上方空泡,加剧了空泡的溃灭.
2.2 入水速度对流场特性的影响
为了研究入水速度对航行体垂直入水过程流场特性的影响,图10给出了不同入水速度下,总阻力系数随时间的变化曲线.从图中可以看出,航行体垂直入水不同速度下总阻力系数随入水时间呈现出相同的变化规律,在入水冲击阶段总阻力系数迅速增加,达到峰值,随后空泡敞开阶段,总阻力系数逐渐下降趋于稳定.其中,在入水冲击阶段,如图10(b)所示,在35,m/s的入水速度下. 航行体受到总阻力系数的峰值在9$\sim$10之间,随着入水速度的减小,总阻力系数峰值随之减小;如图10(c)所示,在随后面闭合阶段,总阻力系数趋于平稳,此时阻力系数相差不大,在深闭合阶段,总阻力系数出现微小波动,随着速度的增大有所下降.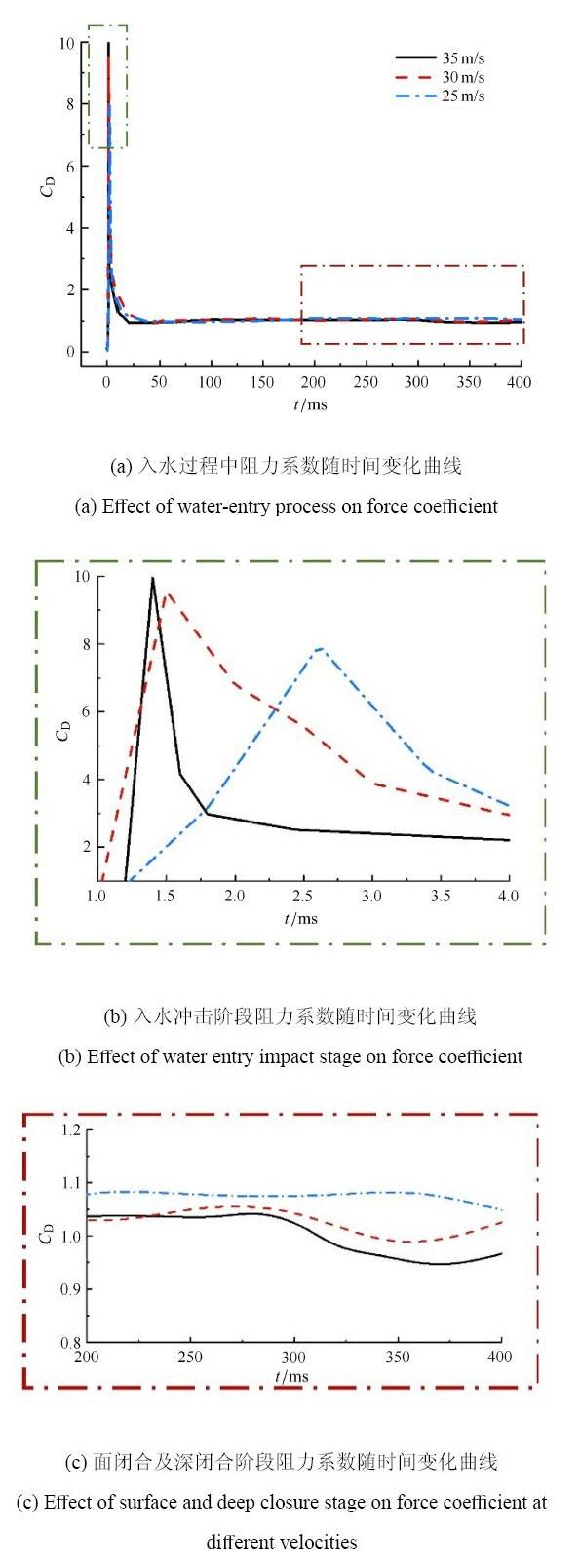
显示原图|下载原图ZIP|生成PPT图10不同入水速度下航行体所受阻力系数随时间变化曲线
-->Fig.10Effect of water-entry process on force coefficient at different velocities
-->
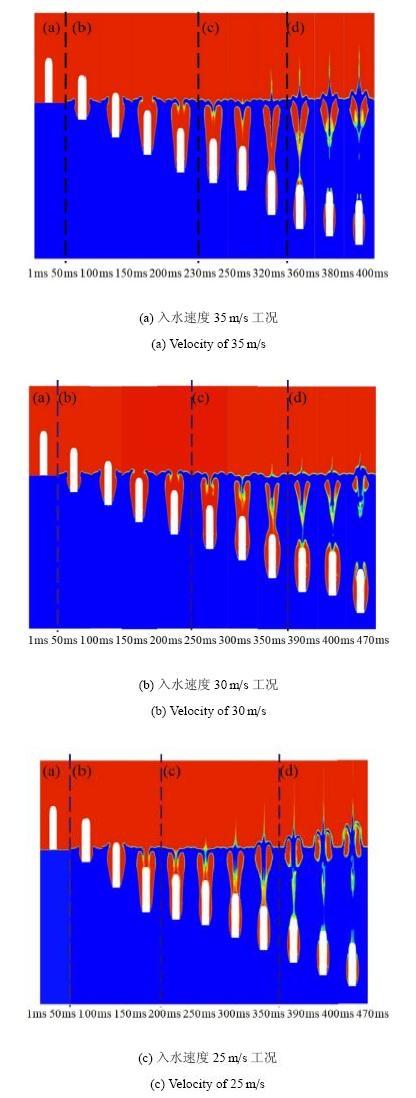
图11给出了航行体不同速度垂直入水过程的空泡形态随时间的变化曲线.可以看出,在冲击阶段和空泡敞开阶段,如图11(a)和 图11 (b)阶段所示,航行体接触水面后,流体质点迅速与航行体发生分离,随后形成的入水空泡随时间沿轴线方向不断拉长,沿径向不断扩张,空泡发展形态基本一致;在面闭合阶段,如图11(c)阶段所示,随着入水速度的增大,伴随面闭合产生的射流更加细长,在对称轴线处空泡的凹陷深度增大;在随后的深闭合阶段,如图11(d)阶段所示,入水空泡发生夹断后形成上下两个独立的空泡,航行体继续携带下方空泡航行,而上方夹断所形成的空泡尺度随入水速度的增大而增大.
显示原图|下载原图ZIP|生成PPT图11航行体垂直入水不同入水速度下气相分布图
-->Fig. 11Air volume fraction contours of vehicle water-entry at different velocities
-->
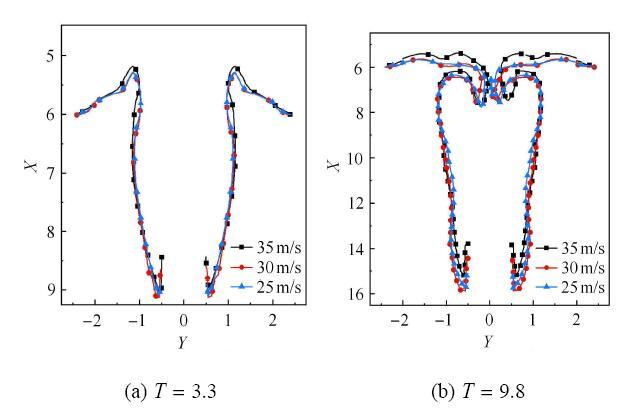
图12给出了航行体不同入水速度垂直入水过程典型时刻的空泡轮廓图,其中无量纲时间$T=tv/D_{0}$,$t$代表航行体航行时间,$v$代表航行体航行速度,$D_{0}$表示航行体弹身直径.提取气相体积分数为0.1的曲线为空泡轮廓线,横纵坐标分别为$x$,$y$方向无量纲长度,$X=x/D_{0}$,$Y=y/D_{0}$.从图12(a)中可以看出,在空泡敞开阶段($T=3.3$),不同入水速度条件下,同一无量纲时刻的空泡形态近似一致.从图12(b)中可以看出,在空泡面闭合阶段($T=9.8$),不同入水速度条件下,空泡轮廓线逐渐发生差异,随着速度的增大,液面位置逐渐上移,空泡口以及颈缩位置出现了一定的差异.在相同无量纲速度下,在颈缩位置处入水空泡无量纲直径随着入水速度的增大而减小,在自由液面处空泡开口随着速度增大而不对称性加剧,并且飞溅的水冠高度增大.
显示原图|下载原图ZIP|生成PPT图12航行体不同入水速度下空泡轮廓比较
-->Fig. 12Comparison of cavity features with different velocities
-->
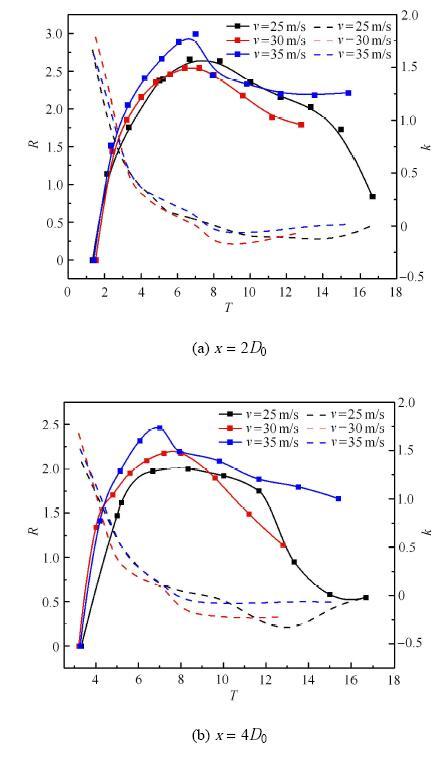
为了进一步分析不同入水速度对航行体空泡演变的影响,图13给出了不同入水速度下,$x=2D_{0}$和$x=4D_{0}$水深下入水空泡无量纲半径和扩张速率随时间的变化曲线,空泡无量纲半径$R=r/(d/2)$,在图13中用实线表示,其中$r$为空泡半径,$D_{0}$为射弹直径,$k$为空泡半径无量纲变化速率,图中用点划线表示,$k=v_{\rm r}/v$,其中$v_{r}$代表空泡半径变化速率,$v$代表航行体入水速度.从图中可以看出,随着时间的推移,不同入水速度航行体无量纲空泡半径、半径变化速率基本一致,入水空泡的无量纲半径随无量纲时间先增大后减小,$k$随无量纲时间推移基本呈现衰减趋势.初始时刻半径变化速率随速度的增大而增大;同一时刻,不同速度下空泡无量纲半径和半径的变化速率近似.结合图11可以看出,不同入水速度下,面闭合阶段空泡半径变化速率随时间的推移逐渐趋于平缓,其中在25,m/s入水速度下,在深度为4$D_{0}$,速率曲线在$T =12$后出现明显降低,这是由于入水空泡逐渐发生深闭合($T=13.3$发生深闭合),空泡壁面向轴线收缩速度明显增大,而相同无量纲时刻30,m/s,35,m/s入水速度工况下均处于面闭合阶段,此时,空泡收缩速率随深度的增大而加大;同一深度下,收缩位置空泡直径随着速度的增大而增大,速率也随着速度的增大而加大.
显示原图|下载原图ZIP|生成PPT图13航行体垂直入水过程入水空泡无量纲半径和扩张速率随时间变化曲线
-->Fig. 13Dimensionless radius and expansion rate of cavity at vertical water-entry process
-->
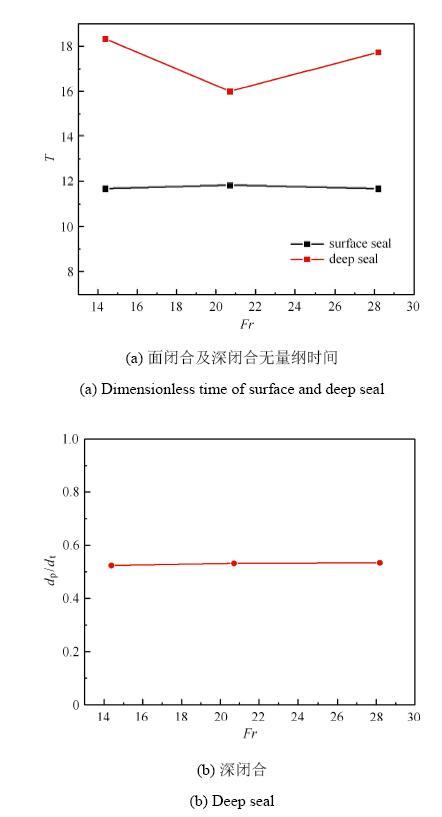
图14给出了面闭合以及深闭合无量纲时间随${Fr}$变化的发展规律,其中${Fr}=v^{2}/gL$. 从图14(a)中可以看出,入水空泡面封闭的无量纲时间随着弗劳德数增大基本不变,深闭合发生的无量纲时间有较大波动;从图14(b)中可以看出,不同入水速度下,入水空泡夹断深度($d_{\rm p})$与该夹断时间下航行体入水深度($d_{\rm l})$的比值随弗劳德数的变化近似一致,其中,夹断深度表示自由液面到颈缩断裂的距离.
显示原图|下载原图ZIP|生成PPT图14航行体垂直入水过程中面/深闭合发展规律
-->Fig. 14Developent of surface and deep seal at vertical water-entry process
-->
3 结 论
本文基于VOF多相流模型,结合动网格技术,建立了针对航行体入水过程的数值计算模型,开展了航行体以尾部向下姿态垂直入水过程的数值模拟研究,分析了航行体垂直入水过程中流体动力特性、入水空泡及流场结构的演变,并且进一步讨论了入水速度对流体动力特性和入水空泡发展的影响. 研究结论如下：(1)垂直入水过程中,航行体总阻力系数在撞击自由液面之时迅速增大,达到一个峰值;随着入水时间的推移,总阻力系数缓慢降低,最终趋于稳定,空泡发生溃灭时产生微小波动.
(2)在入水空泡发展的过程中,在惯性力与内外压差的共同作用下,空泡壁面会同时存在扩张与收缩两种阶段. 空泡发生面闭合以及深闭合时,泡内涡流强度大大增强,湍流强度增大;在空泡尚未完全发生夹断时,空泡上下两部分内部流动已被阻断此时深闭合现象已经发生.
(3)随着速度的增大,总阻力系数峰值加大,面闭合阶段总阻力系数有所下降;空泡的最大直径增大,空泡扩张阶段半径变化速率近似,空泡半径收缩速率随速度增加而增大. 入水空泡面闭合的无量纲时间随弗劳德数的变化趋于定值;深闭合时,颈缩分割点随入水速度的增加而加深,不同速度下空泡夹断深度与入水深度的比值一致.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . 首先从伞降回收、垂直返回、带翼飞回和升力体式等类型分析了国外典型重复使用运载器的发展现状；然后从技术难度、对总体设计体系的影响、运载能力损失、对主发动机的技术要求、回收过程复杂性等方面对各技术途径进行全面的对比分析，并概述了重复使用运载火箭的关键技术，开展了重复使用运载火箭经济性分析；最后对未来重复使用运载火箭技术发展进行展望。重复使用是运载火箭发展的必然途径，中国还需大力发展重复使用运载火箭技术，未来还将走向天地往返+重复使用空间运输的模式。 . 首先从伞降回收、垂直返回、带翼飞回和升力体式等类型分析了国外典型重复使用运载器的发展现状；然后从技术难度、对总体设计体系的影响、运载能力损失、对主发动机的技术要求、回收过程复杂性等方面对各技术途径进行全面的对比分析，并概述了重复使用运载火箭的关键技术，开展了重复使用运载火箭经济性分析；最后对未来重复使用运载火箭技术发展进行展望。重复使用是运载火箭发展的必然途径，中国还需大力发展重复使用运载火箭技术，未来还将走向天地往返+重复使用空间运输的模式。 |
| [2] | . 为全面分析SpaceX公司垂直起降重复使用"猎鹰9"火箭技术水平和发展潜力,系统概括了SpaceX公司特点和"猎鹰9"火箭相关飞行试验,采用经验总结法剖析了SpaceX公司取得成功的深层次原因,研究了海上平台垂直回收的优缺点和重复使用关键技术。通过模型假定和仿真计算表明,"猎鹰9"重复使用火箭运载能力损失约30%以上、发射费用可降低30%;在此基础上提出"猎鹰9"火箭后续跟踪研究的主要问题,我国低成本运载火箭发展策略以及我国运载火箭技术发展差距等。 . 为全面分析SpaceX公司垂直起降重复使用"猎鹰9"火箭技术水平和发展潜力,系统概括了SpaceX公司特点和"猎鹰9"火箭相关飞行试验,采用经验总结法剖析了SpaceX公司取得成功的深层次原因,研究了海上平台垂直回收的优缺点和重复使用关键技术。通过模型假定和仿真计算表明,"猎鹰9"重复使用火箭运载能力损失约30%以上、发射费用可降低30%;在此基础上提出"猎鹰9"火箭后续跟踪研究的主要问题,我国低成本运载火箭发展策略以及我国运载火箭技术发展差距等。 |
| [3] | . 无论在理论分析还是数值模拟方面，入水冲击和砰击都是比较复杂的瞬态物理问题。按照时间历程分三个阶段综述了入水冲击理论、试验和数值仿真的发展概况，阐述了入水冲击和砰击现象现阶段研究的内容和热点，特别针对数值建模技术发展的研究状况进行重点叙述。为航天和航海领域进一步开展入水研究提供参考。 . 无论在理论分析还是数值模拟方面，入水冲击和砰击都是比较复杂的瞬态物理问题。按照时间历程分三个阶段综述了入水冲击理论、试验和数值仿真的发展概况，阐述了入水冲击和砰击现象现阶段研究的内容和热点，特别针对数值建模技术发展的研究状况进行重点叙述。为航天和航海领域进一步开展入水研究提供参考。 |
| [4] | . 本文归纳了入水冲击问题的简化模型并对各种研究方法进行了概述.从前提假设出发,对入水冲击问题的理论模型进行了分类.总结归纳出入水冲击问题的难点,针对各个难点,概述了入水冲击问题的研究方法,同时讨论了不同解决方案的优点及缺点.最后对下一步的研究方向给出了建议. . 本文归纳了入水冲击问题的简化模型并对各种研究方法进行了概述.从前提假设出发,对入水冲击问题的理论模型进行了分类.总结归纳出入水冲击问题的难点,针对各个难点,概述了入水冲击问题的研究方法,同时讨论了不同解决方案的优点及缺点.最后对下一步的研究方向给出了建议. |
| [5] | . 高速射弹入水稳定性研究是世界范围内的一大难题.详细地介绍了高速射弹入水稳定性在理论研究、实验研究方面的研究历程及成果,并对入水空泡的发展过程、入水冲击载荷与入水过程水动力、入水稳定性影响因素3个方面的研究现状逐一解读.此外,结合当前理论基础与实验、数值计算条件对高速射弹入水过程的研究难点进行了总结与分析. . 高速射弹入水稳定性研究是世界范围内的一大难题.详细地介绍了高速射弹入水稳定性在理论研究、实验研究方面的研究历程及成果,并对入水空泡的发展过程、入水冲击载荷与入水过程水动力、入水稳定性影响因素3个方面的研究现状逐一解读.此外,结合当前理论基础与实验、数值计算条件对高速射弹入水过程的研究难点进行了总结与分析. |
| [6] | . |
| [7] | . Not Available |
| [8] | . |
| [9] | . |
| [10] | |
| [11] | . We present the results of a combined experimental and theoretical investigation of the normal impact of hydrophobic spheres on a water surface. Particular attention is given to characterizing the shape of the resulting air cavity in the low Bond number limit, where cavity collapse is driven principally by surface tension rather than gravity. A parameter study reveals the dependence of the cavity structure on the governing dimensionless groups. A theoretical description based on the solution to the Rayleigh鈥揃esant problem is developed to describe the evolution of the cavity shape and yields an analytical solution for the pinch-off time in the zero Bond number limit. The sphere's depth at cavity pinch-off is also computed in the low Weber number, quasi-static limit. Theoretical predictions compare favourably with our experimental observations in the low Bond number regime, and also yield new insight into the high Bond number regime considered by previous investigators. Discrepancies are rationalized in terms of the assumed form of the velocity field and neglect of the longitudinal component of curvature, which together preclude an accurate description of the cavity for depths less than the capillary length. Finally, we present a theoretical model for the evolution of the splash curtain formed at high Weber number and couple it with the underlying cavity dynamics. |
| [12] | . We present the results of a combined experimental and theoretical investigation of the vertical impact of low-density spheres on a water surface. Particular attention is given to characterizing the sphere dynamics and the influence of its deceleration on the shape of the resulting air cavity. A theoretical model is developed which yields simple expressions for the pinch-off time and depth, as well as the volume of air entrained by the sphere. Theoretical predictions compare favorably with our experimental observations, and allow us to rationalize the form of water-entry cavities resulting from the impact of buoyant and nearly buoyant spheres. |
| [13] | . Mathematical modeling, absent simplifying assumptions and coupled with numerical simulation, has been implemented to determine the motions and forces experienced by a sphere penetrating a water surface from an air space above the surface. The model and simulation are validated by comparisons with extensive experimental data and with trends from approximate analyses. Although the present work adds to the understanding and quantification of the sphere as an entry object, its major contribution is model development and validation to enable investigation of water entry of objects of practical utility such as the expendable bathythermograph (XBT). The XBT device is widely used in the determination of temperature distributions in large water bodies such as oceans. The measured temperature distributions are, in turn, used to determine the thermal energy content of oceans. During the course of the numerical simulations, parametric variations were made of the sphere velocity, surface tension, flow regime (laminar or turbulent), and Reynolds number. The drag-coefficient results were found to be independent of these quantities. This outcome indicates that momentum transfer from the sphere to the adjacent liquid is responsible for the drag force and that friction is a secondary issue. (C) 2013 Elsevier Ltd. All rights reserved. |
| [14] | . This paper presents an original experimental approach of three-dimensional water impact at constant speed. The hydrodynamic force acting on axisymmetric rigid bodies striking a horizontal liquid surface at constant vertical speed is investigated using a hydraulic shock machine. The different aspects of the experimental device allowing to carry out impacts at high-speeds with small deviation of the velocity are initially detailed. Then, results of observations on several axisymmetric shapes are presented and discussed. Good agreements between theoretical model, numerical results and available experimental measurements have been obtained. |
| [15] | . . |
| [16] | . 基于高速摄像试验方法,研究了开放空腔壳体的倾斜入水运动特性,重点分析了开放空腔结构引起的空泡流动特征和壳体运动规律.通过试验数据分析了开放空腔内气体运动将引起独特的空泡流动和阶段性的运动规律,探讨了初始入水速度、入水姿态对入水弹道和空泡形态等运动特征的影响.结果表明:开放空腔壳体入水空泡出现阶段波动演化现象,并先后经历两次闭合;入水空泡演化改变流体动力分布,直接影响壳体运动方式,进而改变水下弹道特征;空腔内部形成相对独立流场环境和开放端周期性流动,在重力作用下液体对空腔内下侧壁面作用力较大,加剧壳体偏转,从而改变入水运动过程的稳定性;随着入水速度的增大,空泡波动特征逐渐明显,闭合时间延迟,非对称深闭合引起的横向位移减小,但偏转角度与入水速度无关;随着初始姿态倾角减小,空泡波动程度减弱、闭合时间延迟,偏转角速度增大,闭合引起的横向位移增大. . 基于高速摄像试验方法,研究了开放空腔壳体的倾斜入水运动特性,重点分析了开放空腔结构引起的空泡流动特征和壳体运动规律.通过试验数据分析了开放空腔内气体运动将引起独特的空泡流动和阶段性的运动规律,探讨了初始入水速度、入水姿态对入水弹道和空泡形态等运动特征的影响.结果表明:开放空腔壳体入水空泡出现阶段波动演化现象,并先后经历两次闭合;入水空泡演化改变流体动力分布,直接影响壳体运动方式,进而改变水下弹道特征;空腔内部形成相对独立流场环境和开放端周期性流动,在重力作用下液体对空腔内下侧壁面作用力较大,加剧壳体偏转,从而改变入水运动过程的稳定性;随着入水速度的增大,空泡波动特征逐渐明显,闭合时间延迟,非对称深闭合引起的横向位移减小,但偏转角度与入水速度无关;随着初始姿态倾角减小,空泡波动程度减弱、闭合时间延迟,偏转角速度增大,闭合引起的横向位移增大. |
| [17] | . 对于水下发射过程来说，掌握水动力载荷形成机理与结构响应特征是一个亟待解决的问题.研究该问题需要考虑含相变的复杂多相流动，变约束的结构运动以及这二者之间的耦合效应.本文采用松耦合的方法，以流体求解器为主体，将自编的固体结构程序接入流体求解器中，在每个时间步长内分别对流体动力学方程和固体结构动力学方程进行求解，通过流固界面之间的数据交换实现耦合计算.其中，流体求解器基于雷诺平均纳维斯托克斯方程，采用单流体模型处理多相流问题，引入空化模型描述空化相变，采用修正的湍流模型模拟混合物的湍流效应，并采用动网格技术处理移动边界问题.航行体的刚体运动和结构振动分开求解.结构求解器采用等效梁模型描述结构的振动，通过坐标变换给出了随体坐标系下的结构振动方程，求解方法采用时域积分法.所建立的流固耦合方法不仅能够捕捉到自然空化的演化情况，还可获得航行体所受水动力、结构振动响应以及截面的弯矩，获得了实验的验证.基于该方法研究了结构刚度、发射速度对空泡溃灭与结构振动耦合效应的影响规律.结果表明，同步溃灭是影响结构载荷的主要因素，包括溃灭压力幅值，溃灭压力作用位置，以及溃灭压力与结构振动的相位关系. . 对于水下发射过程来说，掌握水动力载荷形成机理与结构响应特征是一个亟待解决的问题.研究该问题需要考虑含相变的复杂多相流动，变约束的结构运动以及这二者之间的耦合效应.本文采用松耦合的方法，以流体求解器为主体，将自编的固体结构程序接入流体求解器中，在每个时间步长内分别对流体动力学方程和固体结构动力学方程进行求解，通过流固界面之间的数据交换实现耦合计算.其中，流体求解器基于雷诺平均纳维斯托克斯方程，采用单流体模型处理多相流问题，引入空化模型描述空化相变，采用修正的湍流模型模拟混合物的湍流效应，并采用动网格技术处理移动边界问题.航行体的刚体运动和结构振动分开求解.结构求解器采用等效梁模型描述结构的振动，通过坐标变换给出了随体坐标系下的结构振动方程，求解方法采用时域积分法.所建立的流固耦合方法不仅能够捕捉到自然空化的演化情况，还可获得航行体所受水动力、结构振动响应以及截面的弯矩，获得了实验的验证.基于该方法研究了结构刚度、发射速度对空泡溃灭与结构振动耦合效应的影响规律.结果表明，同步溃灭是影响结构载荷的主要因素，包括溃灭压力幅值，溃灭压力作用位置，以及溃灭压力与结构振动的相位关系. |
| [18] | . 基于多物质的任意拉格朗日-欧拉-拉格朗日流体与固体耦合算法,考虑水的可压缩性,建立了低亚声速射弹垂直入水的流体与固体耦合计算模型.对低亚声速射弹入水时空泡、流场与弹道间的多介质耦合问题进行了数值计算,得到了不同入水条件下入水深度、速度变化曲线和空泡面闭合、空泡深闭合时间.模拟了高速射弹入水后的空泡演化过程,得到了射弹初始入水速度对空泡面、空泡深闭合时间的影响规律以及射弹加速度、应力、应变响应.将阻力系数数值计算结果与经验公式计算结果进行了比较,二者吻合良好,表明该数值计算方法是可行的. . 基于多物质的任意拉格朗日-欧拉-拉格朗日流体与固体耦合算法,考虑水的可压缩性,建立了低亚声速射弹垂直入水的流体与固体耦合计算模型.对低亚声速射弹入水时空泡、流场与弹道间的多介质耦合问题进行了数值计算,得到了不同入水条件下入水深度、速度变化曲线和空泡面闭合、空泡深闭合时间.模拟了高速射弹入水后的空泡演化过程,得到了射弹初始入水速度对空泡面、空泡深闭合时间的影响规律以及射弹加速度、应力、应变响应.将阻力系数数值计算结果与经验公式计算结果进行了比较,二者吻合良好,表明该数值计算方法是可行的. |
| [19] | . <p>通过对比标准<em>k</em>-<em>ω</em> SST 湍流模型和基于标准<em>k</em>-<em>ω</em> SST 湍流模型修正的<em>γ</em>-<em>Re</em><sub><em>θ</em></sub> 转捩湍流模型对绕振荡NACA66 水翼流动的数值计算结果与实验结果，对水翼振荡过程的水动力特性和流场结构变化进行了分析研究. 结果表明：与标准<em>k</em>-<em>ω</em> SST 湍流模型的数值计算结果相比，基于标准<em>k</em>-<em>ω</em> SST 湍流模型修正的<em>γ</em>-<em>Re</em><sub><em>θ</em></sub> 转捩湍流模型能有效预测绕振荡翼型流场结构和水动力特性，捕捉流场边界层发生的流动分离和转捩现象；绕振荡水翼的流动过程可分为5 个特征阶段，当来流攻角较小时，在水翼前缘发生层流向湍流的转捩现象，水翼动力特征曲线出现变化拐点；随着来流攻角的增大，顺时针尾缘涡逐渐形成并向水翼前缘发展；当攻角较大时，前缘涡分离导致动力失速，水翼的动力特征曲线出现大幅波动；水翼处于顺时针向下旋转阶段，绕水翼的流动状态逐渐由湍流过渡为层流.</p> . <p>通过对比标准<em>k</em>-<em>ω</em> SST 湍流模型和基于标准<em>k</em>-<em>ω</em> SST 湍流模型修正的<em>γ</em>-<em>Re</em><sub><em>θ</em></sub> 转捩湍流模型对绕振荡NACA66 水翼流动的数值计算结果与实验结果，对水翼振荡过程的水动力特性和流场结构变化进行了分析研究. 结果表明：与标准<em>k</em>-<em>ω</em> SST 湍流模型的数值计算结果相比，基于标准<em>k</em>-<em>ω</em> SST 湍流模型修正的<em>γ</em>-<em>Re</em><sub><em>θ</em></sub> 转捩湍流模型能有效预测绕振荡翼型流场结构和水动力特性，捕捉流场边界层发生的流动分离和转捩现象；绕振荡水翼的流动过程可分为5 个特征阶段，当来流攻角较小时，在水翼前缘发生层流向湍流的转捩现象，水翼动力特征曲线出现变化拐点；随着来流攻角的增大，顺时针尾缘涡逐渐形成并向水翼前缘发展；当攻角较大时，前缘涡分离导致动力失速，水翼的动力特征曲线出现大幅波动；水翼处于顺时针向下旋转阶段，绕水翼的流动状态逐渐由湍流过渡为层流.</p> |
| [20] | . Cavity formation during water entry of a solid corresponds to the deceleration experienced by the solid. Several experimental studies in the past have facilitated qualitative understanding of the rela |
| [21] | . Hydroelastic phenomena play a critical role on the dynamics of lightweight marine vessels, but a comprehensive understanding of their potential benefits and drawbacks in water impact remains elusive. In contrast with the literature on hydroelastic impact that focuses on plane strain deformations and two-dimensional fluid flows, we address the water entry of compliant slender bodies. We propose a mathematically-tractable framework to predict the rigid body motion and elastic deformation of a beam impacting the water surface in free fall. At each location on the beam, the hydrodynamic loading is determined from the level of submersion of the cross-section and its local velocity and acceleration. Slamming, added mass, and drag are all included in the model and cogently weighted based on the level of submersion of the cross-section. Edge effects are incorporated in the model through a shape function that modulates the hydrodynamic loading as a function of the distance from the edges. Model predictions are validated through experiments on compliant beams of circular cross-section, which detail both the structural response and the resulting flow physics, through the integration of high-speed imaging, direct acceleration measurement, and particle image velocimetry. Results of this study are expected to aid in the design of lightweight ship hulls, experiencing dynamic bending deformations during sailing and maneuvering. |
| [22] | . 基于完全耦合算法对绕二维NACA0009水翼流固耦合特性进行了数值模拟研究.采用Theodorsen模型和Munch模型对刚性和弹性水翼的水弹性响应进行了数值计算,分析了流体与结构的相互作用关系,研究了影响结构水弹性响应和流固耦合特性的因素.研究结果表明:考虑了流体黏性的Munch模型与基于势流理论的Theodorsen模型对气动弹性响应的数值计算结果基本一致,而Theodorsen模型由于没有考虑流体黏性在一定程度上低估了结构的水弹性响应.结构的惯性、阻尼和刚度力矩与流体的相应附加载荷均处于同一数量级,故流体与结构的相互作用不可忽略,尤其对于弹性水翼,流体的惯性、附加阻尼作用增大,流固耦合算法的数值稳定性对流固耦合特性的计算结果影响将更大.外部激励频率为非共振频率时,结构的刚度作用是影响水弹性响应的主要因素,外部激励频率为共振频率时,流体的附加阻尼和附加刚度作用减弱,除结构的刚度作用外,流体与结构的惯性作用对水弹性响应和流固耦合特性的影响也较大. . 基于完全耦合算法对绕二维NACA0009水翼流固耦合特性进行了数值模拟研究.采用Theodorsen模型和Munch模型对刚性和弹性水翼的水弹性响应进行了数值计算,分析了流体与结构的相互作用关系,研究了影响结构水弹性响应和流固耦合特性的因素.研究结果表明:考虑了流体黏性的Munch模型与基于势流理论的Theodorsen模型对气动弹性响应的数值计算结果基本一致,而Theodorsen模型由于没有考虑流体黏性在一定程度上低估了结构的水弹性响应.结构的惯性、阻尼和刚度力矩与流体的相应附加载荷均处于同一数量级,故流体与结构的相互作用不可忽略,尤其对于弹性水翼,流体的惯性、附加阻尼作用增大,流固耦合算法的数值稳定性对流固耦合特性的计算结果影响将更大.外部激励频率为非共振频率时,结构的刚度作用是影响水弹性响应的主要因素,外部激励频率为共振频率时,流体的附加阻尼和附加刚度作用减弱,除结构的刚度作用外,流体与结构的惯性作用对水弹性响应和流固耦合特性的影响也较大. |
| [23] | . <p>超疏水壁面由于具有减阻和自清洁功能而成为国内外减阻和海洋防污等研究领域的热点之一，而20世纪湍流中相干结构的发现为湍流的控制指出新的方向，尤其近壁区涡结构对摩擦阻力贡献很大.利用高时间分辨率粒子图像测速技术，研究了超疏水壁面（SH）以及亲水壁面（PH）湍流边界层中正负展向涡的空间分布特征，研究逆向涡对超疏水壁面近壁区流动结构的影响和超疏水壁面的减阻机理.首先利用空间多尺度局部平均涡量的概念提取壁湍流发卡涡展向涡头（顺向涡）和逆向涡，实现了准确识别涡心并排除小尺度涡的干扰；然后根据检测到的顺向涡和逆向涡流线分布图，发现逆向涡始终处于正向涡的上游和下方，并且对正向涡的进一步发展起抑制作用；最后对两种壁面边界层中逆向涡数量以及出现概率进行对比，发现具有减阻效果的超疏水壁面边界层中出现更多逆向涡.说明逆向涡可抑制上方顺向涡与壁面的强烈剪切，并使靠近壁面的流体加速，从而产生减阻效果；超疏水壁面中涡结构具有更大的角，使其更好地阻碍了发卡涡头附近强烈的喷射和扫略；超疏水壁面逆向涡出现概率明显大于亲水壁面.这些结果表明：超疏水壁面表现出的减阻特性（<em>Re</em><sub><em>δ</em></sub>≈13 500，减阻5.8%）与两板产生逆向涡的差异有关.</p> . <p>超疏水壁面由于具有减阻和自清洁功能而成为国内外减阻和海洋防污等研究领域的热点之一，而20世纪湍流中相干结构的发现为湍流的控制指出新的方向，尤其近壁区涡结构对摩擦阻力贡献很大.利用高时间分辨率粒子图像测速技术，研究了超疏水壁面（SH）以及亲水壁面（PH）湍流边界层中正负展向涡的空间分布特征，研究逆向涡对超疏水壁面近壁区流动结构的影响和超疏水壁面的减阻机理.首先利用空间多尺度局部平均涡量的概念提取壁湍流发卡涡展向涡头（顺向涡）和逆向涡，实现了准确识别涡心并排除小尺度涡的干扰；然后根据检测到的顺向涡和逆向涡流线分布图，发现逆向涡始终处于正向涡的上游和下方，并且对正向涡的进一步发展起抑制作用；最后对两种壁面边界层中逆向涡数量以及出现概率进行对比，发现具有减阻效果的超疏水壁面边界层中出现更多逆向涡.说明逆向涡可抑制上方顺向涡与壁面的强烈剪切，并使靠近壁面的流体加速，从而产生减阻效果；超疏水壁面中涡结构具有更大的角，使其更好地阻碍了发卡涡头附近强烈的喷射和扫略；超疏水壁面逆向涡出现概率明显大于亲水壁面.这些结果表明：超疏水壁面表现出的减阻特性（<em>Re</em><sub><em>δ</em></sub>≈13 500，减阻5.8%）与两板产生逆向涡的差异有关.</p> |
| [24] | . In this paper numerical simulations of the irrotational fluid flow associated with the entry of circular disks of a given mass into a semi-infinite fluid domain in the limits of very low to moderate Froude numbers are reported. This work is motivated by an experimental study performed by Glasheen and McMahon who investigated the low-Froude-number water entry of circular disks and found a linear relationship between the cavity seal depth and the Froude number and also showed that a single value of a modified drag coefficient is sufficient to predict the drag force on the disk. The numerical calculations performed in this paper confirm these experimental findings for steady cavity regimes and identify the ranges of Froude number and dimensionless mass values for which these results hold. Excellent agreement between the numerical computations and analytical velocity predictions, as well as the experimental cavity seal depth measurements, are obtained although the agreement between the measured and the computed drag coefficient values is not as good. The cavity seal depth and the drag coefficient are also found to depend on the disk mass and the numerical results in this paper show that for any disk of dimensionless massMthere exists a value of the Froude number for which the cavity dynamics are steady. Also, a very low-Froude-number regime in which gravitational forces are dominant and for which the cavity dynamics are qualitatively different than for low-to-moderate-Froude-number cases is also numerically explored in this paper. Finally, a bifurcation in the cavity seal mechanism from deep seal to surface seal was found at a Froude numberF=105. |
| [25] | . An experimental study was conducted to investigate the water entry phenomenon. A facility was designed to carry out the tests with the entry velocities of around 352 m/s. Visualization, pressure measurement, velocity measurement and underwater impact test were performed to investigate the hydroballistic behavior of the underwater moving body, the underwater flow field, the supercavitation, etc.. This study shows that the motion of a high-speed underwater body is strongly three-dimensional and chaotic. Furthermore, it is found that the distribution of the trajectory deflection of the underwater projectile depends on the depth of water. It is also found by measuring the deformation on a witness plate submerged in water, that the impact energy of an underwater projectile is reduced as it penetrates deeper into water. |
| [26] | . The fluid mechanics of water entry is studied through investigating the underwater acoustics and the supercavitation. Underwater acoustic signals in water entry are extensively measured at about 30 different positions by using a PVDF needle hydrophone. From the measurements we obtain (1) the primary shock wave caused by the impact of the blunt body on free surface; (2) the vapor pressure inside the cavity; (3) the secondary shock wave caused by pulling away of the cavity from free surface; and so on. The supercavitation induced by the blunt body is observed by using a digital high-speed video camera as well as the single shot photography. The periodic and 3 dimensional motion of the supercavitation is revealed. The experiment is carried out at room temperature. |
| [27] | . 61A Coupled Eulerian–Lagrangian (CEL) method is employed for the water entry problem.61Experiments are performed for the water entry of a spherical-nose projectile.61A three dimensional model of the projectile is simulated with the proposed method.61The numerical results for the air cavity and the projectile trajectory are well compared with the experimental results.61Good agreement observed between the numerical results and those of the experiments. |
| [28] | . We consider the water entry of horizontal cylinders with vertical impact velocity, either kept constant or freely falling, without and with spin, into quiescent water under the effect of gravity. We focus on the flow and cavity forming stages with non-dimensional submergence time , Froude numbers , spin ratios and mass ratios , all of . We develop numerical simulations using a modified smoothed particle hydrodynamics method to obtain predictions for the impact kinematics and dynamics. These are in detailed agreement with available experiments. We elucidate the evolutions of the free surface, contact point positions, flow field, forces and trajectories and their dependence on , and . We define and quantify the contact point location as a function of , clarifying the qualitative difference between sub- and supercritical and the observed absence of air-entrained trailing cavities at low . By subtracting the buoyancy associated with , we show that, unlike the total drag, the remaining dynamic components are qualitatively similar for all . For a freely falling cylinder, we show that the total drag can be predicted from the constant velocity case with the same instantaneous velocity, providing a simple way to predict its trajectory based on the latter. The presence of spin results in lift, even when the asymmetry in is small. For fixed , lift increases with subcritical . For a freely falling cylinder, the lateral motion causes an appreciable asymmetry in and a reduction in lift. |
| [29] | . 61A 3D numerical approach is presented to simulate the solid-liquid interaction.61The free surface interface is tracked using the VOF method.61The no slip boundary condition is exerted by increasing the viscosity.61The effect of diameter on the cylinder motion is studied numerically. |
| [30] | . |
| [31] | . 基于VOF(Volume of Fluid)方法和有限体积法求解气、水两相流动的RANS方程,并结合动网格技术,对物体垂直入水空泡流动进行了数值计算研究。通过对球体垂直入水早期空泡形态进行数值计算,并将计算结果与May A 理想空泡模型拟合结果进行对比分析,二者具有较好的一致性,验证了数值计算方法的有效性。在此基础之上,进一步研究了150°锥角回转体垂直入水空泡生成过程,空泡壁面运动特性和空泡表面闭合特性,给出了垂直匀速入水空泡形态随时间变化规律,空泡壁面随入水过程时间变化运动规律,以及空泡表面闭合时间与入水速度之间的关系。 . 基于VOF(Volume of Fluid)方法和有限体积法求解气、水两相流动的RANS方程,并结合动网格技术,对物体垂直入水空泡流动进行了数值计算研究。通过对球体垂直入水早期空泡形态进行数值计算,并将计算结果与May A 理想空泡模型拟合结果进行对比分析,二者具有较好的一致性,验证了数值计算方法的有效性。在此基础之上,进一步研究了150°锥角回转体垂直入水空泡生成过程,空泡壁面运动特性和空泡表面闭合特性,给出了垂直匀速入水空泡形态随时间变化规律,空泡壁面随入水过程时间变化运动规律,以及空泡表面闭合时间与入水速度之间的关系。 |
| [32] | . Drag coefficients have been determined from high speed motion pictures for 04‐inch to 105‐inch steel spheres shot into water vertically with speeds from 25 to 208 ft./sec. These drag coefficients correspond to the entrance cavity phase and to thev‐squared‐law drag forces only, the immediate effects on the spheres of other forces being eliminated in the calculations. It is found thatCDis a function of both the Reynolds and Froude Numbers. Within the range investigated, the dependence may be expressed byCD=0.0174 ln(RF05). |
| [33] | . 应用动网格技术和VOF方法模拟了平底结构的自由落体入水过程和气-液两相流，得到了平底物体自由落体入水过程的运动特性、砰击载荷特性以及入水空泡演化过程。结果表明：整个入水过程中，平底物体在入水瞬间受到来自液面的砰击载荷最大，砰击面的载荷压力分布中间高两端低；砰击载荷随入水初速的增加而增大；平底物体入水空泡破裂后对上表面造成冲击压力。数值计算方法和结果对入水结构安全性和适应性评估具有实际意义。<br> . 应用动网格技术和VOF方法模拟了平底结构的自由落体入水过程和气-液两相流，得到了平底物体自由落体入水过程的运动特性、砰击载荷特性以及入水空泡演化过程。结果表明：整个入水过程中，平底物体在入水瞬间受到来自液面的砰击载荷最大，砰击面的载荷压力分布中间高两端低；砰击载荷随入水初速的增加而增大；平底物体入水空泡破裂后对上表面造成冲击压力。数值计算方法和结果对入水结构安全性和适应性评估具有实际意义。<br> |
| [34] | . |
| [35] | |
| [36] | . Recent studies of turbulent shear flows have shown that many of their important kinematical and dynamical properties can be more clearly understood by describing the flows in terms of individual events or streamline patterns. These events or flow regions are studied because they are associated with relatively large contributions to certain average properties of the flow, for example kinetic energy, Reynolds stress, or to particular processes in the flow, such as mixing and chemical reactions, which may be concentrated at locations where streamlines converge for fast chemical reactions (referred to as convergence or C regions), or in recirculating eddying regions for slow chemical reactions. The aim of this project was to use the numerical simulations to develop suitable criteria for defining these eddying or vortical zones. The C and streaming (S) zones were defined in order to define the whole flow field. It is concluded that homogeneous and sheared turbulent flow fields are made up of characteristic flow zones: eddy, C, and S zones. A set of objective criteria were found which describe regions in which the streamlines circulate, converge or diverge, and form high streams of high velocity flow. |
