, 常兴华VERIFICATION AND VALIDATION OF HYPERFLOW SOLVER FOR SUBSONIC AND TRANSONIC TURBULENT FLOW SIMULATIONS ON UNSTRUCTURED/HYBRID GRIDS1)
WangNianhua, ChangXinghua中图分类号:V211.3
文献标识码:A
通讯作者:
收稿日期:2018-11-9
网络出版日期:2019-05-18
版权声明:2019力学学报期刊社 所有
基金资助:
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (2725KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引 言
随着计算机技术和数值方法的飞速发展,计算流体力学(computationalfluid dynamics,CFD)数值模拟在航空航天等领域发挥着越来越重要的作用.经过几十年的发展,基于二阶有限体积法的CFD软件的成熟度逐渐提高,各国的研究机构和商业软件公司均已开发出自己的内部解算器或商业软件,如美国宇航局兰利研究中心开发的结构解算器CFL3D[1-3]和非结构解算器FUN3D[1-3]、法国宇航局开发的结构解算器elsA[4-5]、德国宇航院开发的非结构解算器TAU[6]、ANSYS公司的Fluent软件[7]和CFX软件[8]等等.国内相关机构也开发了一些具有特色的CFD软件,如中国空气动力研究与发展中心(以下简称气动中心)开发的结构解算器TRIP[9]、非结构解算器MFlow[10]和结构/非结构混合解算器HyperFLOW[11-12]等等.这些内部解算器和商业软件的开发极大地提高了CFD数值模拟对复杂流动机理的研究能力和实际工程问题的应用能力.然而,CFD数值模拟的可信度却很难明确给出,这就导致CFD工作者在应用CFD软件工具时处于一种矛盾状态：他们既想利用CFD的经济性和高效性等优点,又无法避免CFD结果可信度不确定的疑虑[13].CFD的重要地位决定了CFD可信度研究的必要性和紧迫性.
验证与确认是CFD可信度研究的重要内容,早在二十世纪八九十年代,国外就开始对验证与确认的研究给予高度重视,并逐步开展相关研究工作.1998年,美国航空航天学会在总结之前工作的基础上发布了第一部系统阐述CFD验证与确认的指南[14].从2001年起,美国航空航天学会成功组织了6届阻力预测会议(DragPrediction Workshop, DPW)[15-16],主要针对运输机标模巡航状态进行阻力预测的验证与确认.从2010年起,美国航空航天学会又成功组织了3届高升力预测会议(HighLift Prediction Workshop, HiLiftPW)[17-18],主要针对运输机起降状态高升力构型进行升力预测的验证与确认.除此之外,针对CFD的验证,从2004年到2008年,在里斯本还举办了3届CFD不确定度分析研讨会[19].这些研讨会吸引了全世界各地的CFD研究者参与,形成了一系列经验和结论,对CFD验证与确认的发展起到极大的推动作用.
国内在验证与确认方面起步稍晚,2003年,气动中心联合中航工业航空计算所举办了一次统一算例的验证与确认活动[20],采用了DLR-F4翼身组合体、NLR7301两段翼型、高超声速钝锥等3个算例.2004年又举办了一届针对飞行器大攻角状态的验证与确认研讨会[20].2007年,国内****建议在国内广泛开展验证与确认研究,进而推动国内CFD可信度研究[13].参照DPW的经验,针对国内自主设计的运输机标模CHN-T1,气动中心在2018年举办了第一届航空CFD可信度研讨会[21],吸引了国内多家单位参与,有力地推动了国内CFD验证与确认的发展,但是相对于国外的系列研讨会,国内在验证与确认活动组织方面还存在不够系统、持续性不强的问题,还没有形成比较规范的流程.
在验证与确认方法方面,针对CFD数值模拟精度的验证,主要有两种手段：第一种即通过采用精确解方法[22-23]或制造解方法[24-31],结合网格收敛性测试研究微分方程的求解精度及数值精度阶,以验证算法或者代码的正确性.第二种则是通过Richardson外插法结合网格收敛性研究进行复杂问题的CFD数值模拟精度验证[32-39].而计算结果的确认,一般采用与高可信度的风洞实验或飞行试验结果进行对比,确认计算模型的合理性和准确性,如前述的DPW会议、HiLiftPW会议等系列验证与确认活动.
国外在验证与确认方法的研究和应用上也相对领先.除了举办多届DPW和HiLiftPW研讨会之外,在制造解方法、Richardson插值法等方面也取得明显成果,比如将制造解方法应用到数值方法精度测试、代码验证、边界条件验证等方面,这方面可以参考文献[31]的综述,相较于国外的蓬勃发展,国内在制造解方法的研究和应用上与国外相比还有较大差距.余云龙等[29-30]较早开展了这方面的研究,但是要在国内真正推广使用制造解方法进行CFD验证还需要更多工作.
基于Richardson外插法的网格收敛性精度测试是另一类有效的CFD验证方法.如前述的DPW、HiLiftPW等研讨会中就广泛采用这一方法进行计算结果的分析.与此同时,一些****对Richardson外插法进行了较为基础的研究,如Roache[33]在标准Richardson外插方法的基础上提出了适用于任意网格加密比例和任意阶精度的广义Richardson外插方法;Roy[34]又在Richardson标准外插、广义外插方法的基础上提出混合一阶/二阶的外插方法,并将其应用于含有强激波流动的数值模拟验证;Roache[35]还提出了利用网格收敛指数(grid convergence index,GCI)将离散误差的估计转换为不确定度估计;赵训友等[36]在GCI的基础上,用加权平均的数值解代替细网格数值解来估计离散误差及不确定度.
基于Richardson外插法的复杂外形流动CFD数值模拟验证和确认方法在国内已有较多应用.如陈坚强和张益荣[37]针对典型高超声速流动问题,利用Richardson外插法研究了多套连续变化结构网格下数值解的空间离散误差和收敛性.李钊等[38]采用广义Richardson外插方法分别对二维简单构型的压差阻力、摩阻和三维复杂构型的总阻力CFD预测精度进行了分析.作者所在课题组[39]在结构/非结构混合CFD数值模拟软件HyperFLOW验证与确认工作中应用了Richardson外插方法,验证了该软件流场解算器具有较好的网格收敛性.
从上述的综述可见,CFD软件的验证与确认是一项系统工程,验证和确认是两类不同的问题,需要分别采用不同的方法进行实践,只有经过全面系统的验证与确认,才能掌握CFD软件模拟该类问题的可信度.同时,国内在验证与确认研究与应用方面与国外还存在一定差距,主要体现在验证与确认活动还不够系统,方法研究还不够基础、广泛.为此,本文在上述验证与确认工作的基础上,提出一种比较完整的对CFD软件湍流模拟能力进行验证与确认的思路：即首先通过严格的制造解精度测试,验证CFD数值方法和实现代码能否达到所设计的精度阶;在此基础上通过简单湍流算例的网格收敛性研究,如美国宇航局湍流模型验证与确认数据库(NASA Turbulence ModelingResource, TMR)[40-42]中的湍流平板、二维翼型近尾迹流动、二维Bump等,采用观测精度阶和网格收敛性指数[43-44]量化分析CFD数值结果的网格收敛性和不确定度;最后在实际复杂工程外形算例中,如DPWVI的通用研究模型(common research model,CRM)标模算例,考核CFD软件的网格收敛性、计算精度和不确定度,从而实现对CFD解算器的全面验证与确认,提高CFD数值结果的可信度.
基于以上思路,对自主研发的二阶精度有限体积CFD软件------HyperFLOW在非结构网格上模拟亚跨声速复杂湍流流动的能力进行了比较全面的验证与确认,计算结果表明HyperFLOW在复杂外形的亚跨声速湍流流动模拟中具有较好的网格收敛性和计算结果可信度.
1 HyperFLOW软件及数值方法简介
1.1 HyperFLOW软件平台简介
HyperFLOW软件平台[11-12]是中国空气动力研究与发展中心自主发展的结构和非结构混合解算器.其可以进行结构解算器和非结构解算器的独立求解,也可实现两种解算器在空间上的耦合求解.下文的工作仅针对非结构解算器.解算器的空间离散采用了二阶精度的格心型有限体积方法. 集成了Roe, van Leer, AUSM, Steger-Warming等通量计算格式以及Barth,Venkatakrishnan等多种限制器函数.湍流模拟方法有SA一方程湍流模型、SST两方程湍流模型以及DES方法等.时间离散格式有Runge-Kutta、隐式BLU-SGS等方法.为了适应大规模工程计算的需求,两种解算器均发展了基于网格分区的大规模并行计算技术.关于该软件的设计思想和研究进展,请参见文献[11,12].
1.2 RANS方程有限体积离散方法
本文所采用的流动控制方程为积分形式的控制方程\begin{equation} \label{eq1} \frac{\partial }{\partial t}\int\limits_\varOmega { { W}} {\rm d}\varOmega + \oint\limits_{\partial \varOmega} {\left( {{{ F}}_{{\bf c}} - {{ F}}_{{\bf v}} } \right)} {\rm d}S = {{ 0}} \tag{1} \end{equation}
式中,${{ W}}$为守恒变量,${{ F}}_{{\bf c}}$为无黏通量矢量,${ { F}}_{{\bf v}} $为黏性通量矢量.
方程采用格心型非结构二阶精度有限体积法进行离散.本文无黏通量离散默认采用Roe格式、GG-Cell梯度重构[45],黏性项采用法向导数法[46],时间推进采用LU-SGS隐式格式,湍流模型采用SA一方程模型,湍流对流项采用一阶迎风离散,因为本文所计算的算例属于亚跨声速,即便有激波出现,其强度也较弱,因此采用的迎风格式隐含合适的数值耗散能有效抑制激波处的非物理波动,为排除限制器对计算精度的影响,本文所有算例均不采用限制器.如无特殊说明,下文均采用本节所述的数值格式.
1.3 制造解精度测试方法
为了严格测试CFD数值结果的精度(阶),通常需要一个精确解.但是大多数的可压缩黏性流动的精确解都过于简单,不能完整地体现控制方程的所有项.为了解决这个问题,Roache和Steinberg[47]提出了人为构造精确解的制造解方法.制造解方法的基本思路是将人为构造的制造解代入原始的控制方程,如Navier-Stokes方程、Euler方程或者标量方程等,一般来说,制造解不能满足原始的控制方程,代入控制方程后,右端项不为零,可以把引入的右端项设为源项.因此,制造解可以理解为带源项的修正方程(如式(2)所示)的精确解.
\begin{equation} \label{eq2} \frac{\partial {{ Q}}}{\partial t} + \nabla \cdot {{ F}} - \nabla \cdot {{ F}}_v = {{ S}} \tag{2} \end{equation}
文献[31]对制造解方法进行了详细的介绍,并将分量制造解方法和标量制造解方法应用于非结构网格二阶精度有限体积离散格式的精度测试与验证,具体细节在此不再详述.
2 制造解精度测试
CFD数值算法和代码实现过程能否达到设计的精度阶对数值模拟结果的精度有直接影响.本节分别通过基于Euler方程和基于标量扩散方程的制造解精度阶测试,验证HyperFLOW非结构解算器能否在任意非结构网格上达到设计的二阶精度.为了确定数值结果的精度阶,需要在一系列加密的网格上进行网格收敛性研究.本节网格收敛性测试选取5套依次加密的网格,边界条件为Dirichlet边界,以消除边界条件离散的误差.测试离散误差的$L_1 $模随网格尺度减小时的收敛情况.随着网格加密,误差的下降速率,即所谓的精度阶.方法的具体细节可以参考文献[31].
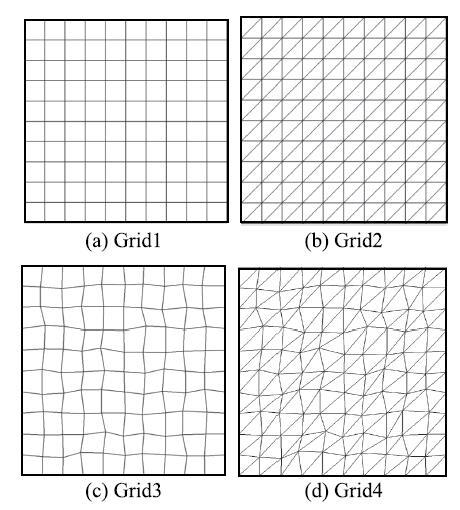
测试网格包括如图1所示的4种类型的网格：grid1为规则矩形网格,grid2为规则三角形网格,grid3为节点扰动四边形网格,grid4为节点扰动三角形网格.这4类网格既包括不同类型(四边形和三角形),又包括不同质量(规则和不规则)的网格,具有一定的代表性.对于四边形网格,将其数据结构转化为非结构形式进行求解.后面的测试均采用这种方式进行,后续不再重述.
显示原图|下载原图ZIP|生成PPT图1制造解精度测试网格
-->Fig. 1Grids for MMS accuracy tests
-->
2.1 Euler方程精度测试
图2给出了4种常用迎风型无黏通量格式：AUSM+格式、Roe格式、Steger-Warming格式和van Leer格式在图1所示的4种网格上的精度测试结果. 图中"1st order ref."和"2nd order ref."分别为一阶精度和二阶精度参考曲线.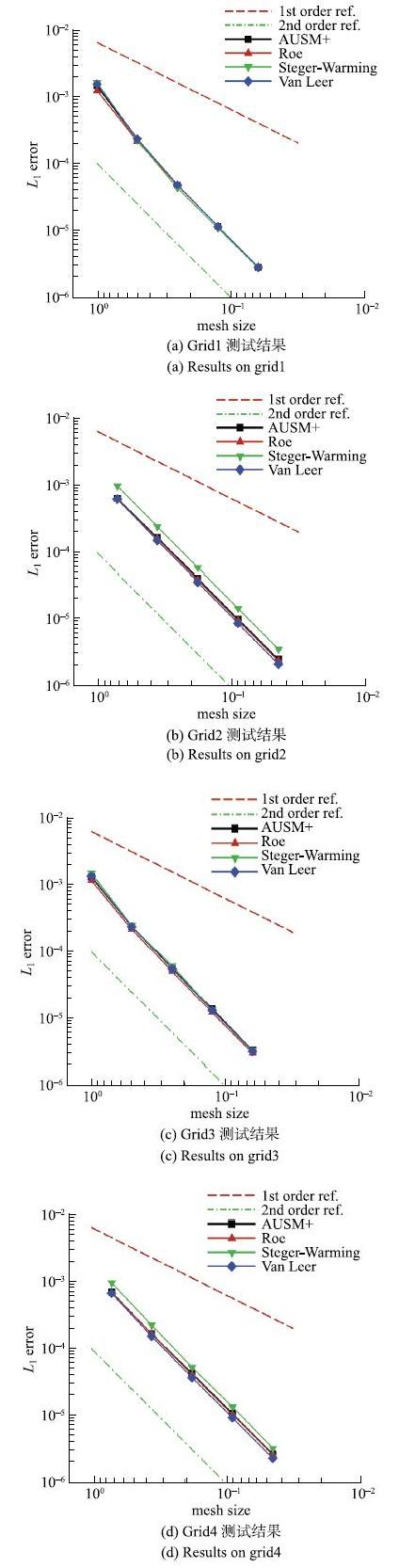
显示原图|下载原图ZIP|生成PPT图2Euler制造解精度测试结果
-->Fig. 2Euler MMS accuracy tests results
-->
本算例选择的单元梯度重构方法为采用面相邻单元模板的最小二乘法(LSQ-basic).该重构方法能够在任意非结构网格上保证单元梯度重构达到一阶精度,具有较高的精度优势[45].结果显示,Hyper-FLOW中常用的4种迎风型通量格式在4种不同类型和不同质量的非结构网格上均能达到设计的二阶精度.
2.2 标量扩散方程精度测试
图3给出了黏性项中界面梯度计算常用的差分修正法[46](edge correction method)和法向导数法[46](face normal difference method)在4种网格上的精度测试结果.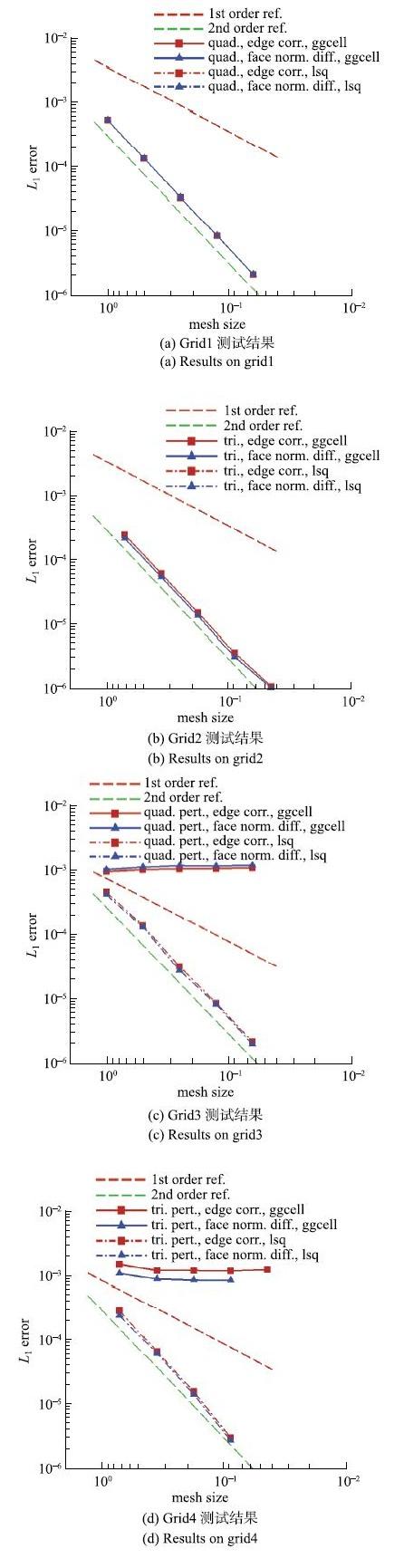
显示原图|下载原图ZIP|生成PPT图3扩散方程制造解精度测试结果
-->Fig. 3MMS accuracy tests results of diffusion equation
-->
结果显示,在单元梯度重构达到一阶精度时,HyperFLOW中黏性项处理的差分修正法和法向导数法能够在所测试的非结构网格上达到保持二阶精度.图3(c)和图3(d)中精度下降到零阶的曲线是由于GG-Cell梯度重构方法(图中标记为ggcell)在扰动网格上单元梯度重构下降到零阶精度[46],导致黏性项计算精度也下降到零阶,采用LSQ-basic单元梯度重构(图中标记为lsq)可以避免这一问题.
在此要说明的是,由于界面梯度的平均梯度法(average method)在笛卡尔网格上会发生奇偶失联,无法保证二阶精度,本节不采用这一黏性项处理方法.具体分析可以参考文献[46].
在4种具有代表性的非结构网格上的制造解精度测试结果表明：在选择合适的方法时,HyperFLOW中的4种无黏通量格式和2种黏性项格式均达到了设计的二阶精度.
3 简单算例的验证
本节采用美国宇航局湍流模型验证与确认算例库(NASA TMR)[40-42]中的二维湍流平板、二维Bump流动、二维翼型近尾迹流动等3个简单亚声速湍流算例对HyperFLOW进行验证与确认.其中,二维Bump流动算例被DPW V和HiLiftPW-2采用作为湍流模型基础验证算例;说明这些简单算例在代码和算法验证方面具有重要的作用.这3个算例的计算网格均采用TMR官方提供的用于网格收敛性测试的一系列依次稀疏化的各向异性四边形网格(采用非结构数据结构存储),网格信息可以参考TMR官网[40],以下不再赘述.
3.1 二维湍流平板
二维湍流平板计算工况为：$Ma = 0.2$,$Re _{\rm c} = 5.0 \times 10^6$,$c=1$. 计算网格示意图如图4所示.
显示原图|下载原图ZIP|生成PPT图4平板算例各向异性矩形网格示意图
-->Fig. 4Anisotropic quadrilateral grids of a flate plate
-->
图5给出了各向异性矩形网格上的网格收敛性测试结果,图中同时给出了CFL3D和FUN3D的测试结果[41-42],CFL3D和FUN3D均采用了Roe格式、UMUSCL重构(CFL3D中$\kappa = 0.333~3$,FUN3D中$\kappa =0.5)$、SA湍流模型对流项采用一阶迎风离散.本文所采用的算法与CFL3D和FUN3D基本相同.
显示原图|下载原图ZIP|生成PPT图5矩形网格平板湍流网格收敛性测试结果
-->Fig. 5Grid convergence tests of turbulent flat plate
-->
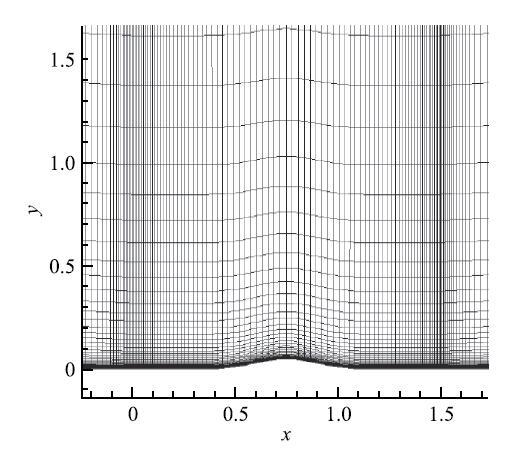
显示原图|下载原图ZIP|生成PPT图 62D Bump 算例各向异性网格示意图
-->Fig. 6Anisotropic quadrilateral grids of 2D Bump
-->
结果显示,随着网格加密,HyperFLOW的收敛趋势与CFL3D相同,与FUN3D相反.粗网格上HyperFLOW计算精度略高于CFL3D和FUN3D;在最密网格上,HyperFLOW能够收敛到与非结构解算器FUN3D相同的结果.
根据文献[43,44]给出的分析方法,在最密的三套网格上计算阻力系数的观测精度阶(observed order of accuracy, $p)$和网格收敛性指数GCI.
观测精度阶$p$表征的是最密的三套网格上数值结果的实际数值精度阶, 而网格收敛性指数GCI表征的是数值结果的相对不确定度的大小. 表1给出数据还包括最密的两套网格结果之间的相对误差$e_{\rm a}^{21}$,以及外插结果与最密网格结果之间的相对误差$e_{\rm ext}^{21}$,这两个相对误差表征的是数值结果的网格无关性程度. 以上4个量在网格收敛性研究中具有重要的作用,其具体算法比较成熟, 读者可以参考文献[43,44],本文不再赘述.
Table 1
表1
表1平板湍流算例观测精度阶和 GCI
Table 1Observed order and GCI of 2D flat plate case
 |
新窗口打开
表1结果显示：HyperFLOW数值结果的网格收敛性与CFL3D接近,观测精度阶$p$接近二阶,与设计精度阶非常接近, 而相对误差$e_{\rm a}^{21}$和$e_{ext}^{21}$也非常小,证明HyperFLOW数值结果在密网格上已经具有较好的网格无关性,网格收敛性指数GCI为0.028%,最密网格的数值结果的不确定度较小.
3.2 二维 Bump 算例
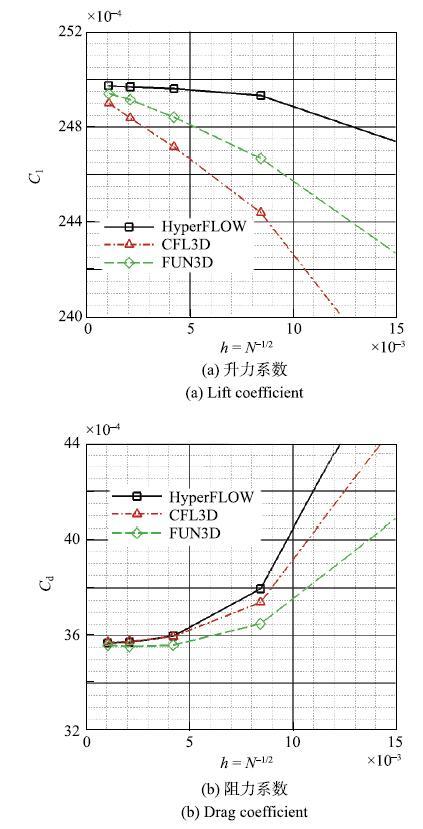
二维~Bump 算例计算工况为：$Ma=0.2$,$Re_{\rm L}=3.0\times 10^{6}$,$L=1$,攻角为~$0^ \circ $,$T_{\rm ref}=300$ K. Bump局部网格如图 6 所示.图7给出了Bump的升、阻力系数的网格收敛性曲线以及与CFL3D、FUN3D结果的对比.结果显示,HyperFLOW在粗网格上升力的计算精度略高,阻力的计算精度与CFL3D相当.HyperFLOW在最密网格上的数值结果与CFL3D和FUN3D的数值结果十分接近,几款求解器能够达到相当的计算精度.
显示原图|下载原图ZIP|生成PPT图 72D Bump 网格收敛性测试结果
-->Fig. 7Grid convergence tests of 2D Bump
-->
显示原图|下载原图ZIP|生成PPT图 82D ANW 算例各向异性四边形网格示意
-->Fig. 8Anisotropic quadrilateral grids of the 2D ANW case
-->
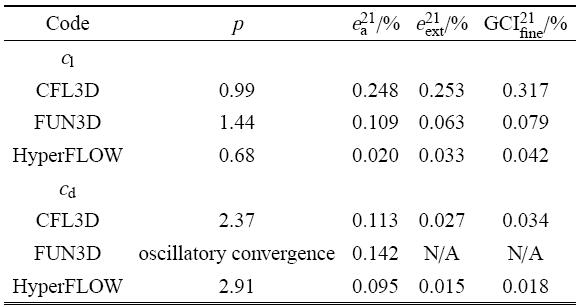
表2给出了最密的三套网格上升阻力系数的观测精度阶$p$和网格收敛性指数GCI. 结果显示,HyperFLOW计算结果的相对误差$e_{\rm a}^{21}$和$e_{\rm ext}^{21}$较小,显示出密网格结果和外插结果较好的网格无关性. 同时,计算结果的网格收敛性指数GCI较小,结果的相对不确定度较小. HyperFLOW升力系数的观测精度阶只有0.68阶,略低于CFL3D和FUN3D的观测精度阶,可能是由于各向异性网格加密非自相似导致, 这也可能导致了FUN3D的阻力系数在最密的3套网格上不单调收敛,而CFL3D和HyperFLOW的升力系数观测精度阶均超过二阶.
Table 2
表2
表22D Bump 算例观测精度阶和 GCI
Table 2Observed order and GCI of 2D Bump case
 |
新窗口打开
3.3 二维翼型近尾迹流动
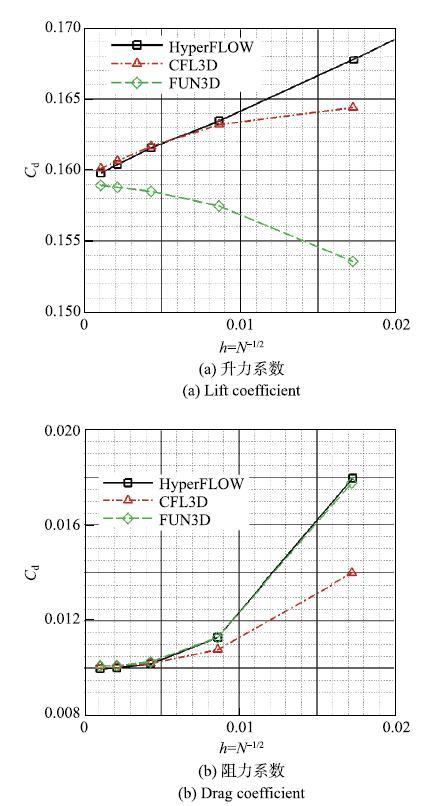
二维翼型近尾迹流动 (2D airfoil near wake, ANW)的计算条件为：$Ma=0.088$,$Re_{\rm c}=1.2\times 10^{6}$,$c=1$,攻角为$0^\circ$,$T_{\rm ref}=300$K,网格示意如图~8 所示.图9给出了翼型升力系数、阻力系数的网格收敛性测试结果.结果显示：HyperFLOW具有较好的网格收敛性,计算精度与FUN3D相当,且在最密的网格上,HyperFLOW的数值结果与CFL3D和FUN3D的数值结果几乎相同.
显示原图|下载原图ZIP|生成PPT图 92D ANW 网格收敛性测试结果
-->Fig. 9Grid convergence tests of 2D airfoil near wake
-->
同样,表3给出了升力系数、阻力系数的观测精度阶和网格收敛性指数.结果显示,升力系数的观测精度阶均接近一阶,而阻力系数的观测精度阶均接近二阶,HyperFLOW升力系数的相对误差$e_{\rm a}^{21}$和$e_{\rm ext}^{21}$及GCI与CFL3D的结果相近,阻力的GCI不确定度与FUN3D接近.证实HyperFLOW数值结果与CFL3D和FUN3D具有相当的计算精度阶和不确定度.
Table 3
表3
表32D ANW 算例观测精度阶和 GCI
Table 3Observed order and GCI of 2D ANW case
 |
新窗口打开
在此需要说明的是,与本文第2节中制造解精度测试得到严格的二阶精度不同,上述3个简单算例的阻力观测精度阶接近二阶,而升力观测精度阶均接近一阶.部分结果降阶的原因主要有：(1)在网格加密过程中,各向异性拉伸网格的加密无法做到完全自相似,导致精度测试无法准确得到严格的精度阶;(2)由于二阶精度的有限体积离散方法在实际流动数值模拟中容易发散,为了保证计算稳定性,在单元梯度重构过程中,采用了GG-Cell方法,这类方法在实际流动模拟中往往会发生精度降阶,也导致无法达到设计的精度阶.
此外,通过上述3个算例,初步验证了HyperFLOW对简单亚声速湍流问题的模拟精度和可信度,但是HyperFLOW与其他两款基于二阶有限体积法的求解器的结果仍然存在一定差异,这可能是由于格式本身存在差异导致的.如CFL3D是二阶格心型结构解算器[1-3],FUN3D是二阶格点型非结构解算器[1-3],而本文的HyperFLOW则是二阶格心型非结构解算器,因此难以保证算法完全相同,也难以保证计算精度完全相同.本文仅仅在二阶有限体积法的框架内,验证解算器是否满足二阶精度要求,是否能够与其他主流二阶CFD解算器达到相当的计算精度和可信度.
4 DPW VI CRM 标模验证与确认
4.1 CRM 标模算例介绍
CRM标模是跨声速运输机典型构型,该模型是第4届到第6届DPW会议使用的基准研究模型.DPW VI的研究内容和结论可以参考文献[14,15],本文选取DPW VI的定升力系数的网格收敛性研究(case2)和气动力极曲线预测(case3)两个算例.
计算工况为：$Ma = 0.85$,$Re = 5.0\times 10^6$,$T_{\rm ref} = 100^ \circ$F. 其中case2固定升力系数$C_{\rm L} = 0.5\pm 0.000~1$,\linebreak DPW VI官方提供了Wing/Body(WB)构型和Wing/Body/Nacelle/Pylon (WBNP)两种构型,由于计算量较大,本文仅仅选择WB构型对HyperFLOW软件平台进行验证与确认.
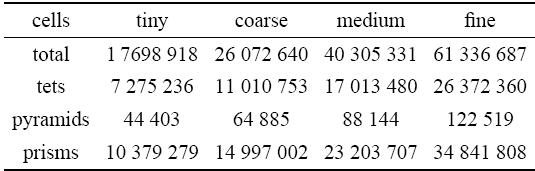
网格收敛性研究在tiny,coarse,medium,fine四套依次加密的网格上进行,四套网格的网格量如表4所示.
Table 4
表4
表4CRM算例网格信息
Table 4Grid information of CRM case
 |
新窗口打开
4.2 CRM标模算例结果分析
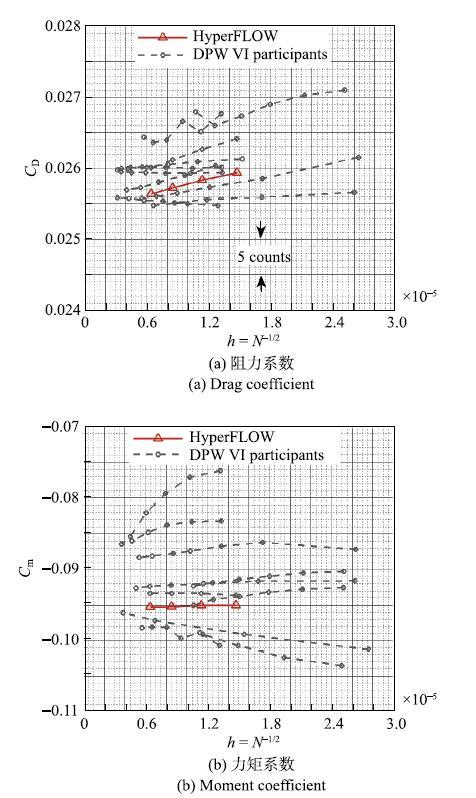
根据DPW的经验,原始SA湍流模型无法准确模拟CRM翼身结合部的分离泡,可以引入Quadratic Constitutive Relation(QCR)修正提高模拟精度,因此本算例主要采用SA-QCR2000湍流模型[48].图10分别给出了HyperFLOW计算得到的阻力系数、力矩系数网格收敛性结果,同时给出了部分其他DPW VI参会者提交的结果[16](图中标记为DPW VI Participants).结果显示,HyperFLOW的计算结果落在参会者提交的结果之间.
显示原图|下载原图ZIP|生成PPT图 10CRM定升力系数网格收敛性测试结果
-->Fig. 10Grid convergence tests of CRM
-->
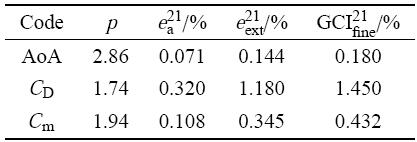
同样,在粗、中、细三套网格上计算攻角、阻力系数和力矩系数的观测精度阶和网格收敛性指数,如表5所示.
Table 5
表5
表5CRM算例观测精度阶和GCI
Table 5Observed order and GCI of CRM case
 |
新窗口打开
表5的结果显示：HyperFLOW计算结果攻角的观测精度阶保持在二阶以上,且密网格收敛解的相对误差$e_{\rm a}^{21}$和外插结果相对误差$e_{\rm ext}^{21}$也较小,显示出密网格上计算结果已经达到较好的网格无关性.
阻力和力矩的观测精度阶均接近二阶,此外,阻力相对误差也相较攻角的相对误差稍大,密网格结果的不确定度也明显大于本文第3节中的几个简单算例,说明对于如CRM标模这样的复杂算例来说,阻力预测的不确定度比简单算例要大得多,阻力的精确预测仍然存在一定挑战性.
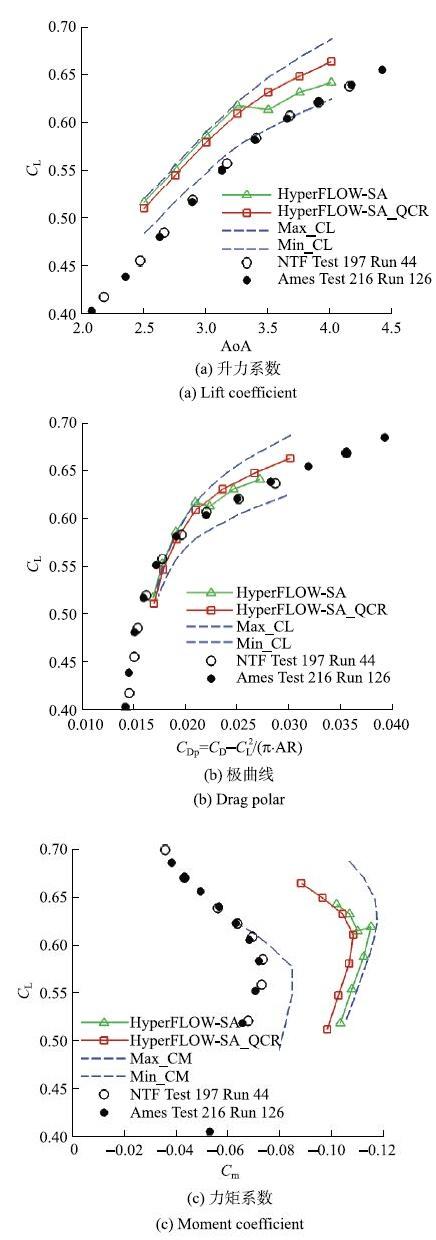
图11给出了WB构型的升力系数曲线、阻力系数曲线、力矩系数曲线及升阻极曲线,同时给出了DPW VI参会者结果的上下限值曲线[16].结果显示,HyperFLOW的计算结果均落在DPW其他参会者的计算结果的上下限之间,证明HyperFLOW的数值结果具有较好的可信度.
显示原图|下载原图ZIP|生成PPT图11CRM气动性能计算结果
-->Fig. 11Aerodynamic forces and moments of CRM
-->
不过由于风洞试验没有修正支撑干扰,而数值计算均未考虑模型支撑,因此数值计算结果与风洞实验结果有一定的差异,图中的两组风洞试验结果均仅供参考.文献[49]考察了支撑装置对CRM-WB构型气动力的影响,证实包含支撑装置有助于减小数值结果与试验结果之间的差异.
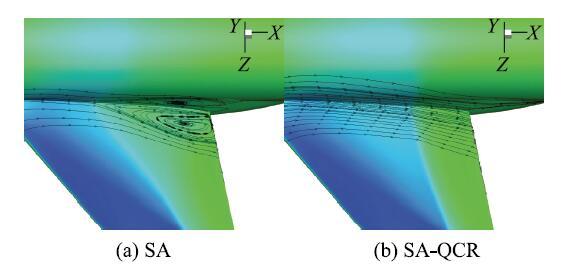
同时,由图11可以看到,在大攻角时(3.5$^\circ$)利用原始SA模型计算得到气动力曲线发生拐折,文献[16]认为这是由于采用SA模型无法准确模拟大攻角时翼身结合部的分离泡,导致分离泡明显比实际流动偏大,而采用SA-QCR模型则可以减弱甚至消除分离泡(如图12所示),更加符合风洞试验结果.
显示原图|下载原图ZIP|生成PPT图 12翼身结合部流线(SA和SA-QCR对比)
-->Fig. 12Side of body streamlines by SA and SA-QCR
-->
5 结 论
本文从制造解精度测试、简单和复杂湍流算例的网格收敛性研究等三个方面,给出了一种比较完整地研究CFD软件验证与确认的方法和思路.制造解精度测试能够严格地测试计算方法和软件的数值精度阶,典型Benchmark算例可以定量测试软件对实际流动问题的观测精度阶和网格收敛性指数.而针对复杂飞行器构型,通过计算结果与精细风洞试验结果的比较,则可以对CFD方法和软件进行确认.本文利用上述方法,对自主研发的CFD软件平台HyperFLOW进行了验证与确认,得到如下结论：(1) 在选择合适的方法时,HyperFLOW软件平台中无黏通量格式和黏性通量格式均能在任意非结构网格上达到设计的二阶精度.
(2) HyperFLOW软件平台对于简单湍流问题的模拟能力达到了与FUN3D相当的水平,具有较好的网格收敛性、计算精度和不确定度.
(3) HyperFLOW软件平台具备实际复杂外形非结构网格亚跨声速湍流的模拟能力,同时具备良好的可信度.
本文只给出了几个简单亚音速和跨音速流动算例的验证与确认结果,未来可以采用更多实际算例考察软件的计算精度和鲁棒性,形成从简单到复杂的验证与确认算例数据库[20],并且将算例集成到自动化验证与确认平台中去[50-51],实现CFD软件完全自动化的、全面系统的验证与确认.此外,不确定度量化[52]、大规模计算的并行效率测试与优化[53]也是未来的研究方向.
致 谢
感谢中国空气动力研究与发展中心的张耀冰博士、陈江涛博士提供了DPW VI CRM模型的非结构计算网格及相关指导.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . ABSTRACT Two Reynolds-averaged Navier-Stokes codes were used to compute flow over the NASA Trapezoidal Wing at high lift conditions for the 1 st AIAA CFD High Lift Prediction Workshop, held in Chicago in June 2010. The unstructured-grid code FUN3D and the structured-grid code CFL3D were applied to several different grid systems. The effects of code, grid system, turbulence model, viscous term treatment, and brackets were studied. The SST model on this configuration predicted lower lift than the Spalart-Allmaras model at high angles of attack; the Spalart-Allmaras model agreed better with experiment. Neglecting viscous cross-derivative terms caused poorer prediction in the wing tip vortex region. Output-based grid adaptation was applied to the unstructured-grid solutions. The adapted grids better resolved wake structures and reduced flap flow separation, which was also observed in uniform grid refinement studies. Limitations of the adaptation method as well as areas for future improvement were identified. |
| [2] | . 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition 07 - 10 January 2013, Grapevine (Dallas/Ft. Worth Region), Texas AIAA 2013-0050 CFL3D, FUN3D, and NSU3D Contributions to the Fifth Drag Prediction Workshop Michael A. Park65 NASA Langley Research Center, Hampton, VA 23681 Kelly R. Laflin69 and Mark S. Chaffin60 Cessna Aircraft Company, Wichita, KS, 67218 Nicholas Powell § Gulfstream Aerospace Corporation, Savannah, GA 31402 David W. Levy09 Cessna Aircraft Company, Wichita, KS, 67218 Results presented at the Fifth Drag Prediction Workshop using CFL3D, FUN3D, and NSU3D are described. These are calculations on the workshop provided grids and drag adapted grids. The NSU3D results have been updated to reflect an improvement to skin friction calculation on skewed grids. FUN3D results generated after the workshop are included for custom participant generated grids and a grid from a previous workshop. Uni- form grid refinement at the design condition shows a tight grouping in calculated drag, where the variation in the pressure component of drag is larger than the skin friction com- ponent. At this design condition, A fine-grid drag value was predicted with a smaller drag adjoint adapted grid via tetrahedral adaption to a metric and mixed-element subdivision. The buffet study produced larger variation than the design case, which is attributed to large differences in the predicted side-of-body separation extent. Various modeling and discretization approaches had a strong impact on predicted side-of-body separation. This large wing root separation bubble was not observed in wind tunnel tests indicating that more work is necessary in modeling wing root juncture flows to predict experiments. I. Introduction The AIAA Drag Prediction Workshop (DPW) series has been an invaluable forum to evaluate Computa- tional Fluid Dynamics (CFD) tools. A detailed history of the DPW series and its objective are available from Vassberg et al.1 and Morrison.2 An abbreviated history and summary of key results are provided here to provide context for this DPW-V contribution. The objectives for these workshops include the assessment of the the state-of-the-art computational methods as practical aerodynamic tools for aircraft force and moment prediction of industry relevant geometries, the provision of an impartial forum for evaluating the effectiveness of existing computer codes and modeling techniques using Reynolds averaged Navier-Stokes (RANS) solvers, and identification of areas needing additional research and development. DPW-I3 solicited CFD predictions of the lift, drag, and pitching moment for a subsonic transport wing body, the DLR-F4. The conclusions of Levy et al.3 set the tone for the subsequent workshops, "The overall level of scatter is too high and needs to be reduced to determine overall accuracy and trends with grid type, turbulence model, etc. Future work should try to identify sources of the scatter, for example, grid quality." DPW-II4 focused on grid refinement studies and the prediction of installed pylon-nacelle drag increments for 65Research Scientist, Computational AeroSciences Branch, AIAA Senior Member. 69Senior Specialist Engineer, AeroSciences, AIAA Associate Fellow. 60Specialist Engineer, AeroSciences, AIAA Senior Member. §Engineer II, Applied Aerodynamics, AIAA Member. 09Principal Engineer, AeroSciences, AIAA Associate Fellow. 1 of 22 This material is declared a work of the U.S. Government and is not subject to copyright protection in the United States. American Institute of Aeronautics and Astronautics the DLR-F6 wing-body and wing-body-nacelle-pylon configurations. The DLR-F6 has substantial areas of separation at the wing-body juncture and at the wing-pylon juncture. These regions of flow separation were considered a likely culprit for the observed lack of grid convergence.4, 5 DPW-III6 introduced two wing only configurations and retained the DLR-F6 wing-body with the addition of a new wing-body fairing designed to eliminate the side-of-body separation. Details of the FX2B fairing design are documented by Vassberg, Sclafani, and DeHann7 and verified in a wind tunnel test.8 A higher Reynolds number was specified in DPW-III to reduce the wing upper-surface trailing-edge flow separation. DPW-III was held between the design and test of the fairing, so this workshop was truly a prediction. After the workshop was complete, the test data was compared9 to the results submitted to DPW-III. The DPW-III cases showed a reduction in variation with grid refinement.10 However, the configuration including the FX2B fairing without wing-root separation had a similar level of variation as the the DLR- F6 configuration with wing-root separation. Eliminating the wing root separation region did not reduce variation. Morrison and Hemsch10 conclude, "After three workshops, it is still clear that grids remain a first order effect and obtaining high quality grids is the first step t |
| [3] | . |
| [4] | . Abstract This paper gives an overview of the elsA Onera software for complex external and internal flow simulations and multidisciplinary applications. The objectives of the elsA software co-operative project are presented. The paper outlines capabilities of the software. A first set of recent applications illustrates some important features: fundamental applications for RSM turbulence modeling, wing/fuselage and tilt-rotor configurations for advanced multi-block techniques, transport aircraft for fluid/structure coupling, power-plant integration for calculation of sensitivities, wing buffet prediction for Detached Eddy Simulation. Then, a second set of applications shows the diversity of configurations which are today addressed by elsA: optimisation of a supersonic transport aircraft, high lift aircraft configuration, helicopter rotor-fuselage interaction, compressor and turbine stages, heat transfer analysis in a nozzle guide vane, space vehicle configuration. The paper finally outlines the perspectives of development of the elsA software. |
| [5] | . Abstract The development of the new generation software package elsA was initiated in 1997 at ONERA. The aim is to group a very broad range of CFD capabilities together in an interoperable and evolving software package, designed both as a tool to tackle industrial problems and as a platform for further innovative CFD developments. To meet this challenge, the project team has chosen an Object Oriented (oo) design method as well as an oo implementation. The paper describes the main features of the oo design, some key points in managing the software development project, an outline of the solver capabilities and real-world application results dealing with external and internal aerodynamics (aircrafts, helicopters, turbomachinery). The broadness of the examples given here, together with good CPU efficiency, clearly demonstrates the benefits of a full oo approach. 漏 2002 by the American Institute of Aeronautics and Astronautics, Inc. All rights reserved. |
| [6] | . The only implicit smoothing method implemented in the DLR Flow Solver TAU is the LU-SGS method. It was chosen several years ago because of its low memory requirements and low operation counts. Since in the past for many examples a severe restriction of the CFL number and loss of robustness was observed, it is the goal of this paper to revisit the LU-SGS implementation and to discuss several alternative implicit smoothing strategies used within an agglomeration multigrid for unstructured meshes. Starting point is a full implicit multistage Runge-Kutta method. Based on this method we develop and suggest several additional features and simplifications such that the implicit method is applicable to high Reynolds number viscous flows, that is the required matrices fit into the fast memory of our cluster hardware and the arising linear systems can be approximately solved efficiently. To this end we focus on simplifications of the Jacobian as well as efficient iterative approximate solution methods. To significantly improve the approximate linear solution methods we take care of grid anisotropy for both approximately solving the linear systems and agglomeration strategy. The procedure creating coarse grid meshes is extended by strategies identifying structured parts of the mesh. This seems to improve the quality of coarse grid meshes in the way that an overall better reliability of multigrid can be observed. Furthermore we exploit grid information within the iterative solution methods for the linear systems. Numerical examples demonstrate the gain with respect to reliability and efficiency. |
| [7] | |
| [8] | |
| [9] | . 采用“亚跨超声速计算流体力学软件平台”（TRIP2.0）数值模拟了阻力预测小组（AIAA CFD Drag Prediction Workshop Ⅱ,DPWⅡ）翼/身/架/舱复杂组合体运输机构型，数值模拟采用的多块对接网格、测压和测力的试验结果均来自DPWⅡ，对比计算采用了CFL3D的结果。重点针对DLR-F6翼/身/架/舱复杂组合体构型，详细研究了网格密度和湍流模型对总体气动特性和压力分布的影响，计算结果与相应的试验结果取得了较好的一致。采用SA一方程和SST两方程模型均得到了网格收敛结果；不同的湍流模型对压差阻力影响较小，对摩擦阻力影响较大；不同的网格密度和湍流模型对压力分布有一定的影响。 . 采用“亚跨超声速计算流体力学软件平台”（TRIP2.0）数值模拟了阻力预测小组（AIAA CFD Drag Prediction Workshop Ⅱ,DPWⅡ）翼/身/架/舱复杂组合体运输机构型，数值模拟采用的多块对接网格、测压和测力的试验结果均来自DPWⅡ，对比计算采用了CFL3D的结果。重点针对DLR-F6翼/身/架/舱复杂组合体构型，详细研究了网格密度和湍流模型对总体气动特性和压力分布的影响，计算结果与相应的试验结果取得了较好的一致。采用SA一方程和SST两方程模型均得到了网格收敛结果；不同的湍流模型对压差阻力影响较小，对摩擦阻力影响较大；不同的网格密度和湍流模型对压力分布有一定的影响。 |
| [10] | . Flip-chip technology has been widely accepted as a solution for electronic packaging of high-pin-count devices. Due to the demand for smaller and thinner package dimensions, coreless build-up substrat |
| [11] | . HyperFLOW,a structured/unstructured hybrid CFD software,is introduced in this paper.For HyperFLOW,the structured solver runs on structured grids,while the unstructured solver runs on unstructured grids,in order to fully take advantages of both grids and solvers.The architecture of HyperFLOW is briefly introduced firstly.Then,some typical cases are tested to validate both the structured and unstructured solver,including the Trap-Wing configuration from HiLiftPW-I and the DLR-F6wing-body configuration from DPW-II.The performance of grid convergence is studied for both solvers.The numerical results demonstrate that HyperFLOW has good grid convergence property on both structured and unstructured grids.The computational results match well with the reference and experimental data,indicating acceptable credibility. |
| [12] | . HyperFLOW is a structured/unstructured hybrid integrated computational environment for multi-purpose fluid simulation. In this paper, the objectives, frame structure of HyperFLOW are introduced briefly. And then, a number of test cases are simulated to demonstrate the capability of HyperFLOW, including compressible RANS simulations, time-accurate simulations with dynamic meshes, chemical non-equilibrium simulations and so on. All those test cases demonstrate that HyperFLOW has a good performance as an integrated platform. |
| [13] | . 计算流体力学(CFD)在航空航天等诸多领域的应用越来越广泛.特别是近年来, CFD在实际飞行器的设计中扮演着越来越重要的角色, 许多设计参数直接来源于CFD的计算结果.由此, 飞行器设计师对CFD提供结果的可信度提出了更高的要求.验证(verification)与确认(validation)是评价数值解精度和可信度的主要手段.本文综述了国内外开展CFD验证与确认研究的进展.在引言中论述了开展CFD验证与确认的重要性和必要性, 简述了国内外CFD验证与确认研究的历史和发展现状.第2节中讨论了CFD验证与确认的一些基本概念,以及这些概念定义的形成过程, 并指出了进行CFD验证与确认的基本步骤.第3节和第4节分别讨论了CFD验证与确认的方法, 如CFD验证中的精确解比较方法, 制造解比较方法, 网格收敛性研究;CFD确认中的层次结构, 流动分类法, 确认实验指南.在第5节中我们列举了几个CFD验证与确认的应用实例.最后, 对我国开展CFD验证与确认研究工作提出了若干建议, 包括:(1)开展流动分类法研究,(2)推行软件质量工程方法,(3)开展规范精细的实验, 建立国内的网络数据库. . 计算流体力学(CFD)在航空航天等诸多领域的应用越来越广泛.特别是近年来, CFD在实际飞行器的设计中扮演着越来越重要的角色, 许多设计参数直接来源于CFD的计算结果.由此, 飞行器设计师对CFD提供结果的可信度提出了更高的要求.验证(verification)与确认(validation)是评价数值解精度和可信度的主要手段.本文综述了国内外开展CFD验证与确认研究的进展.在引言中论述了开展CFD验证与确认的重要性和必要性, 简述了国内外CFD验证与确认研究的历史和发展现状.第2节中讨论了CFD验证与确认的一些基本概念,以及这些概念定义的形成过程, 并指出了进行CFD验证与确认的基本步骤.第3节和第4节分别讨论了CFD验证与确认的方法, 如CFD验证中的精确解比较方法, 制造解比较方法, 网格收敛性研究;CFD确认中的层次结构, 流动分类法, 确认实验指南.在第5节中我们列举了几个CFD验证与确认的应用实例.最后, 对我国开展CFD验证与确认研究工作提出了若干建议, 包括:(1)开展流动分类法研究,(2)推行软件质量工程方法,(3)开展规范精细的实验, 建立国内的网络数据库. |
| [14] | . |
| [15] | . |
| [16] | , |
| [17] | . Abstract The second AIAA CFD High-Lift Prediction Workshop was held in San Diego, California, in June 2013. The goals of the workshop continued in the tradition of the first high-lift workshop: to assess the numerical prediction capability of current-generation computational fluid dynamics (CFD) technology for swept, medium/high-aspect-ratio wings in landing/takeoff (high-lift) configurations. This workshop analyzed the flow over the DLR-F11 model in landing configuration at two different Reynolds numbers. Twenty-six participants submitted a total of 48 data sets of CFD results. A variety of grid systems (both structured and unstructured) were used. Trends due to grid density and Reynolds number were analyzed, and effects of support brackets were also included. This paper analyzes the combined results from all workshop participants. Comparisons with experimental data are made. A statistical summary of the CFD results is also included. |
| [18] | . |
| [19] | |
| [20] | . CFD验证和确认是气动计算可信度分析的基本活动。通过这类活动将产生大量数据资源。如何有效管理和利用这些数据资源是基准数据库要解决的主要问题。研究并提出了一种可行的共享基准数据库设计方案,重点强调数据库的管理、数据库的可用性、数据的可靠性评估、数据标准和开放的系统架构,目的是提供建立用于CFD验证和确认的气动共享基准数据库的一种示范,解决现有气动数据库普遍存在的缺乏协调性、连贯性和必要的交流等诸多问题。此外,简要介绍了近年来中国在气动计算可信度分析方面所做的努力。 . CFD验证和确认是气动计算可信度分析的基本活动。通过这类活动将产生大量数据资源。如何有效管理和利用这些数据资源是基准数据库要解决的主要问题。研究并提出了一种可行的共享基准数据库设计方案,重点强调数据库的管理、数据库的可用性、数据的可靠性评估、数据标准和开放的系统架构,目的是提供建立用于CFD验证和确认的气动共享基准数据库的一种示范,解决现有气动数据库普遍存在的缺乏协调性、连贯性和必要的交流等诸多问题。此外,简要介绍了近年来中国在气动计算可信度分析方面所做的努力。 |
| [21] | . . |
| [22] | . An exact similarity solution of the compressible-flow NavierStokes equations is presented, which embeds supersonic, transonic, and subsonic regions. Describing the viscous and heat-conducting high-gradient flow in a shock wave, the solution accommodates non-linear temperature-dependent viscosity as well as heat-conduction coefficients and provides the variation of all the flow variables and their derivatives. Also presented are methods to obtain time-dependent and/or multi-dimensional solutions as well as verification benchmarks of increasing severity. Comparisons between the developed analytical solution and CFD solutions of the NavierStokes equations, with determination of convergence rates and orders of accuracy of these solutions, illustrate the utility of the developed exact solution for verification purposes. Copyright (c) 2012 John Wiley & Sons, Ltd. |
| [23] | . This paper presents a collection of fluid mechanics problems with exact solutions which can be used to verify the numerical accuracy of solutions obtained by CFD codes. This document is a product of the AIAA Committee On Standards (COS). It is intended to serve as the start of a catalog of exact solutions for fluid mechanics problems, and as a complement to the Verification and Validation Guide prepared by the AIAA. While the solutions presented in this paper do not necessarily test all aspects of a code or all terms of the governing equations, they constitute fundamentals tests for identifying coding errors. Hence, documenting these solutions is an important step towards consolidating significant verification cases. A. |
| [24] | . The modified Laplacian has been used to move unstructured grids in response to changes in the surface grid for a variety of grid movement applications including store separation, aero-elastic wing deformation and free surface flow simulations. However, the use of the modified Laplacian can result in elements with negative areas/volumes, because it has no inherent mechanism to prevent inversion... [Show full abstract] |
| [25] | . This article discusses Code Verification of Reynolds-Averaged Navier Stokes (RANS) solvers that rely on face based finite volume discretizations for volumes of arbitrary shape. The study includes test cases with known analytical solutions (generated with the method of manufactured solutions) corresponding to laminar and turbulent flow, with the latter using eddy-viscosity turbulence models. The procedure to perform Code Verification based on grid refinement studies is discussed and the requirements for its correct application are illustrated in a simple one-dimensional problem. It is shown that geometrically similar grids are recommended for proper Code Verification and so the data should not have scatter making the use of least square fits unnecessary. Results show that it may be advantageous to determine the extrapolated error to cell size/time step zero instead of assuming that it is zero, especially when it is hard to determine the asymptotic order of grid convergence. In the RANS examples, several of the features of the ReFRESCO solver are checked including the effects of the available turbulence models in the convergence properties of the code. It is shown that it is required to account for non-orthogonality effects in the discretization of the diffusion terms and that the turbulence quantities transport equations can deteriorate the order of grid convergence of mean flow quantities. |
| [26] | . 61Verification of a boundary layer numerical code by the Method of Manufactured Solutions.61Convergence order analysis of a boundary layer numerical code.61Validation of a boundary layer numerical code through comparison with experimental data.61Agreement between boundary layer numerical code and Linear Stability Theory results.61Use of high-order approximations. |
| [27] | . Abstract Loci CHEM is a Computational Fluid Dynamics (CFD) code developed using the Loci Framework that can simulate three-dimensional flows of chemically reacting mixtures of thermally perfect gases. It is a library of Loci rules that consists of reusable rules that can be dynamically reconfigured to solve a variety of problems. The present study involves the verification of Euler and Navier-Stokes equations and their associated sub-models in Loci- CHEM on different mesh types using the Method of Manufactured Solutions (MMS). MMS is the most general approach for ensuring that there are no mistakes (i.e. bugs) in the computer code and that the algorithms are consistent and convergent. The different meshes include both 2D and 3D meshes. The observed order of accuracy is calculated and compared with the formal order of accuracy of the chosen numerical method. The code is verified when the observed order of accuracy matches the formal order in the limit as the mesh is refined. |
| [28] | . A detailed code verification study of an unstructured finite volume CFD code is presented. The Method of Manufactured Solutions is used to generate exact solutions to the Euler and Navier-Stokes equations to verify the order of accuracy of the code. Testing is performed on different grid types including triangular and quadrilateral elements in 2D and tetrahedral, prismatic and hexahedral elements in 3D. The requirements for systematic mesh refinement are discussed, particularly in regards to unstructured meshes. Different code options verified include the baseline steady-state governing equations, transport models, turbulence models, boundary conditions and unsteady flows. |
| [29] | . 针对一维Lagrange辐射流体力学方程组,基于物理量在Euler空间和Lagrange空间的微分关系,提出了一种人为解构造方法,并构造了一类一维Lagrange辐射流体力学方程组人为解.构造的人为解在整个计算区域光滑可微,质量方程无源项.将构造的人为解应用至二维辐射流体力学Lagrange程序中,从数值误差、收敛阶方面验证了程序的正确性,展示了人为解的可行性和适用性. . 针对一维Lagrange辐射流体力学方程组,基于物理量在Euler空间和Lagrange空间的微分关系,提出了一种人为解构造方法,并构造了一类一维Lagrange辐射流体力学方程组人为解.构造的人为解在整个计算区域光滑可微,质量方程无源项.将构造的人为解应用至二维辐射流体力学Lagrange程序中,从数值误差、收敛阶方面验证了程序的正确性,展示了人为解的可行性和适用性. |
| [30] | . 针对科学计算中工程应用程序的研制和预测能力的评估，基于应用程序研制的过程与软件开发的生命周期，提出了一种科学计算程序验证与确认（V8LV）模型．论述了物理建模、数值模拟与科学计算程序验证与确认的关系，以及科学计算程序验证与确认的方法，为科学计算程序验证与确认提供一种置信度评估方法． . 针对科学计算中工程应用程序的研制和预测能力的评估，基于应用程序研制的过程与软件开发的生命周期，提出了一种科学计算程序验证与确认（V8LV）模型．论述了物理建模、数值模拟与科学计算程序验证与确认的关系，以及科学计算程序验证与确认的方法，为科学计算程序验证与确认提供一种置信度评估方法． |
| [31] | . 随着计算机技术的飞速进步,计算流体力学得到迅猛发展,数值计算虽能够快速得到离散结果,但是数值结果的正确性与精度则需要通过严谨的方法来进行验证和确认.制造解方法和网格收敛性研究作为验证与确认的重要手段已经广泛应用于计算流体力学代码验证、精度分析、边界条件验证等方面.本文在实现标量制造解和分量制造解方法的基础上,通过将制造解方法精度测试结果与经典精确解(二维无黏等熵涡)精度测试结果进行对比,进一步证实了制造解精度测试方法的有效性,并将两种制造解方法应用于非结构网格二阶精度有限体积离散格式的精度测试与验证,对各种常用的梯度重构方法、对流通量格式、扩散通量格式进行了网格收敛性精度测试.结果显示,基于Green-Gauss公式的梯度重构方法在不规则网格上会出现精度降阶的情况,导致流动模拟精度严重下降,而基于最小二乘(least squares)的梯度重构方法对网格是否规则并不敏感.对流通量格式的精度测试显示,所测试的各种对流通量格式均能达到二阶精度,且各方法精度几乎相同;而扩散通量离散中界面梯度求解方法的选择对流动模拟精度有显著影响. . 随着计算机技术的飞速进步,计算流体力学得到迅猛发展,数值计算虽能够快速得到离散结果,但是数值结果的正确性与精度则需要通过严谨的方法来进行验证和确认.制造解方法和网格收敛性研究作为验证与确认的重要手段已经广泛应用于计算流体力学代码验证、精度分析、边界条件验证等方面.本文在实现标量制造解和分量制造解方法的基础上,通过将制造解方法精度测试结果与经典精确解(二维无黏等熵涡)精度测试结果进行对比,进一步证实了制造解精度测试方法的有效性,并将两种制造解方法应用于非结构网格二阶精度有限体积离散格式的精度测试与验证,对各种常用的梯度重构方法、对流通量格式、扩散通量格式进行了网格收敛性精度测试.结果显示,基于Green-Gauss公式的梯度重构方法在不规则网格上会出现精度降阶的情况,导致流动模拟精度严重下降,而基于最小二乘(least squares)的梯度重构方法对网格是否规则并不敏感.对流通量格式的精度测试显示,所测试的各种对流通量格式均能达到二阶精度,且各方法精度几乎相同;而扩散通量离散中界面梯度求解方法的选择对流动模拟精度有显著影响. |
| [32] | |
| [33] | |
| [34] | . New developments are presented in the area of grid convergence error analysis for mixed-order numerical schemes. A mixed-order scheme is defined as a numerical method where the formal order of the truncation error varies either spatially, for example, at a shock wave, or for different terms in the governing equations, for example, third-order convection with second-order diffusion. The case examined is the Mach 8 inviscid flow of a calorically perfect gas over a spherically blunted cone. This flowfield contains a strong bow shock wave, where the formally second-order numerical scheme is reduced to first order via a flux-limiting procedure. The proposed mixed-order error analysis method allows for nonmonotonic behavior in the solution variables as the mesh is refined |
| [35] | . |
| [36] | . 在CFD离散误差和不确定度估计问题中,为研究计算得到的观测精度对仿真计算结果的影响,消除GCI离散不确定度估计法中当观测精度大于格式精度时出现的不合理的小不确定度,提出了1种改进的CFD离散不确定度估计方法,即用加权平均的数值解代替细网格数值解来估计离散误差及不确定度。针对低雷诺数二维非轴对称圆柱绕流模型进行数值计算,划分5套网格,用二阶迎风格式计算圆柱绕流的阻力系数和升力系数,分别给出了GCI和改进方法的离散不确定度估计结果,并与文献参考值进行比较,结果表明改进的方法对离散不确定估计要优于GCI方法,且置信度更高。 . 在CFD离散误差和不确定度估计问题中,为研究计算得到的观测精度对仿真计算结果的影响,消除GCI离散不确定度估计法中当观测精度大于格式精度时出现的不合理的小不确定度,提出了1种改进的CFD离散不确定度估计方法,即用加权平均的数值解代替细网格数值解来估计离散误差及不确定度。针对低雷诺数二维非轴对称圆柱绕流模型进行数值计算,划分5套网格,用二阶迎风格式计算圆柱绕流的阻力系数和升力系数,分别给出了GCI和改进方法的离散不确定度估计结果,并与文献参考值进行比较,结果表明改进的方法对离散不确定估计要优于GCI方法,且置信度更高。 |
| [37] | . 针对典型高超声速流动问题(T2-97模型)，利用Richardson插值法，研究了多套连续变化网格下数值解的空间离散误差、收敛性。通过网格收敛性研究，完成了CFD的验证过程。利用不确定度分析方法，结合实验数据，开展了该问题的确认。研究表明：针对所选问题，在现有实验数据及计算条件下，该问题的CFD得到了验证与确认。 . 针对典型高超声速流动问题(T2-97模型)，利用Richardson插值法，研究了多套连续变化网格下数值解的空间离散误差、收敛性。通过网格收敛性研究，完成了CFD的验证过程。利用不确定度分析方法，结合实验数据，开展了该问题的确认。研究表明：针对所选问题，在现有实验数据及计算条件下，该问题的CFD得到了验证与确认。 |
| [38] | . <p>利用计算流体力学(CFD)方法预测阻力是飞行器气动设计中的关键环节。采用广义Richardson外插方法分别对数值方法预测二维简单构型的压差阻力、摩擦阻力和三维复杂构型的总阻力的精度进行了分析。在NACA 0012翼型无黏绕流和平板湍流边界层两个算例中验证了NSAWET程序和广义Richardson外插方法,分别得到数值算法预测压差阻力和摩擦阻力能达到的名义精度。进而模拟三维通用研究模型(CRM)翼身组合体绕流,得到的阻力名义精确值在DPW 5的统计误差带范围之内;综合DPW 5的计算结果来看,不同CFD解算器的结果之间存在一定差别,阻力预测精度总体上不符合二阶。可见,标准Richardson方法采用的二阶精度假设难以普遍适用,有必要采用广义Richardson外插方法得到名义精度。针对不合理的名义精度,采用Roache建议的方法加以限制。广义Richardson外插方法有助于提高误差分析的合理性,可以进一步降低网格对阻力预测的影响。</p> . <p>利用计算流体力学(CFD)方法预测阻力是飞行器气动设计中的关键环节。采用广义Richardson外插方法分别对数值方法预测二维简单构型的压差阻力、摩擦阻力和三维复杂构型的总阻力的精度进行了分析。在NACA 0012翼型无黏绕流和平板湍流边界层两个算例中验证了NSAWET程序和广义Richardson外插方法,分别得到数值算法预测压差阻力和摩擦阻力能达到的名义精度。进而模拟三维通用研究模型(CRM)翼身组合体绕流,得到的阻力名义精确值在DPW 5的统计误差带范围之内;综合DPW 5的计算结果来看,不同CFD解算器的结果之间存在一定差别,阻力预测精度总体上不符合二阶。可见,标准Richardson方法采用的二阶精度假设难以普遍适用,有必要采用广义Richardson外插方法得到名义精度。针对不合理的名义精度,采用Roache建议的方法加以限制。广义Richardson外插方法有助于提高误差分析的合理性,可以进一步降低网格对阻力预测的影响。</p> |
| [39] | . 采用High-Lift研讨会提供的梯形翼外形(TrapWing),利用自主研发的基于结构、非结构网格的通用CFD软件HyperFLOW进行了数值计算,以评估其对复杂外形低速流的模拟能力。分别采用了三套不同拓扑结构的计算网格,包括两套非结构/混合网格和一套多块结构网格,每套网格又分为粗、中、细三种密度不同的网格数量以考察其网格收敛性。利用Richardson插值法,对计算结果开展了可信度分析。结果表明,不管是结构网格还是非结构网格,HyperFLOW均建立了可接受的可信度;对于高升力外形数值模拟,SA湍流模型要比SST湍流模型模拟的更准确;在失速迎角附近,现有的二阶精度解算器仍需持续改进。 . 采用High-Lift研讨会提供的梯形翼外形(TrapWing),利用自主研发的基于结构、非结构网格的通用CFD软件HyperFLOW进行了数值计算,以评估其对复杂外形低速流的模拟能力。分别采用了三套不同拓扑结构的计算网格,包括两套非结构/混合网格和一套多块结构网格,每套网格又分为粗、中、细三种密度不同的网格数量以考察其网格收敛性。利用Richardson插值法,对计算结果开展了可信度分析。结果表明,不管是结构网格还是非结构网格,HyperFLOW均建立了可接受的可信度;对于高升力外形数值模拟,SA湍流模型要比SST湍流模型模拟的更准确;在失速迎角附近,现有的二阶精度解算器仍需持续改进。 |
| [40] | |
| [41] | |
| [42] | . summary papers written near the time that the site was initiated.13,14 In the next section, the website's main features are described. These main features include new aspects that may be unfamiliar to some readers. Then, in the summary, future plans for the website and open questions are discussed. |
| [43] | . Since 1990, the Fluids Engineering Division of ASME has pursued activities concerning the detection, estimation and control of numerical uncertainty and/or error in computational fluid dynamics (CFD) studies. The first quality-control measures in this area were issued in 1986 (1986, ldquoEditorial Policy Statement on Control of Numerical Accuracyrdquo, ASME J. Fluids Eng., 108, p. 2) and revised in 1993 (1993, ldquoJournal of Fluids Engineering Editorial Policy Statement on the Control of Numerical Accuracyrdquo, ASME J. Fluids Eng., 115, pp. 339-340). Given the continued increase in CFD related publications, and the many significant advancements in computational techniques and computer technology, it has become necessary to revisit the issue and formulate a more detailed policy to further improve the quality of publications in this area. This brief note provides specific guidelines for prospective authors for calculation and reporting of discretization error estimates in CFD simulations where experimental data may or may not be available for comparison. The underlying perspective is that CFD-related studies will eventually aim to predict the outcome of a physical event for which experimental data is not available. It should be emphasized that the requirements outlined in this note do not preclude those already published in the previous two policy statements. It is also important to keep in mind that the procedure recommended in this note cannot possibly encompass all possible scenarios or applications. |
| [44] | |
| [45] | . 综合利用理论分析和数值测试手段,研究了非结构格心型有限体积离散中梯度重构算法的计算精度,分别给出了非结构算法中常用的基于Green-Gauss公式(GG方法)和基于Least squares方法(LSQ方法)的梯度重构方法达到至少一阶精度的条件.其中,GG方法在面积分低阶项不能互相抵消的情况下,要求面心插值精度达到至少二阶;而LSQ方法对于任意网格均能实现梯度重构一阶精度.在各向同性网格上的梯度重构精度数值测试验证了数学推导结论;进一步通过制造解方法量化无粘流动数值离散误差,结合网格收敛性测试研究了网格质量(网格点随机扰动、网格弯曲度和网格倾斜度等因素)以及网格类型(三角形和四边形)对无粘流动模拟精度的影响,验证了理论分析结论. . 综合利用理论分析和数值测试手段,研究了非结构格心型有限体积离散中梯度重构算法的计算精度,分别给出了非结构算法中常用的基于Green-Gauss公式(GG方法)和基于Least squares方法(LSQ方法)的梯度重构方法达到至少一阶精度的条件.其中,GG方法在面积分低阶项不能互相抵消的情况下,要求面心插值精度达到至少二阶;而LSQ方法对于任意网格均能实现梯度重构一阶精度.在各向同性网格上的梯度重构精度数值测试验证了数学推导结论;进一步通过制造解方法量化无粘流动数值离散误差,结合网格收敛性测试研究了网格质量(网格点随机扰动、网格弯曲度和网格倾斜度等因素)以及网格类型(三角形和四边形)对无粘流动模拟精度的影响,验证了理论分析结论. |
| [46] | . 非结构网格二阶有限体积离散方法广泛应用于计算流体力学工程实践中,研究非结构网格二阶精度有限体积离散方法的计算精度具有现实意义.计算精度主要受到网格和计算方法的影响,本文从单元梯度重构方法、黏性通量中的界面梯度计算方法两个方面考察黏性流动模拟精度的影响因素.首先从理论上分析了黏性通量离散中的"奇偶失联"问题,并通过基于标量扩散方程的制造解方法验证了"奇偶失联"导致的精度下降现象,进一步通过引入差分修正项消除了"奇偶失联"并提高了扩散方程计算精度;其次,在不同类型、不同质量的网格上进行基于扩散方程的制造解精度测试,考察单元梯度重构方法、界面梯度计算方法对扩散方程计算精度的影响,结果显示,单元梯度重构精度和界面梯度计算方法均对扩散方程计算精度起重要作用;最后对三个黏性流动算例(二维层流平板、二维湍流平板和二维翼型近尾迹流动)进行网格收敛性研究,初步验证了本文的结论,得到了计算精度和网格收敛性均较好的黏性通量计算格式. . 非结构网格二阶有限体积离散方法广泛应用于计算流体力学工程实践中,研究非结构网格二阶精度有限体积离散方法的计算精度具有现实意义.计算精度主要受到网格和计算方法的影响,本文从单元梯度重构方法、黏性通量中的界面梯度计算方法两个方面考察黏性流动模拟精度的影响因素.首先从理论上分析了黏性通量离散中的"奇偶失联"问题,并通过基于标量扩散方程的制造解方法验证了"奇偶失联"导致的精度下降现象,进一步通过引入差分修正项消除了"奇偶失联"并提高了扩散方程计算精度;其次,在不同类型、不同质量的网格上进行基于扩散方程的制造解精度测试,考察单元梯度重构方法、界面梯度计算方法对扩散方程计算精度的影响,结果显示,单元梯度重构精度和界面梯度计算方法均对扩散方程计算精度起重要作用;最后对三个黏性流动算例(二维层流平板、二维湍流平板和二维翼型近尾迹流动)进行网格收敛性研究,初步验证了本文的结论,得到了计算精度和网格收敛性均较好的黏性通量计算格式. |
| [47] | . |
| [48] | . In this paper we have confirmed that eddy viscosity turbulence models are inadequate to predict secondary vortical flows developed from corners in internal flows. To remedy this shortcoming, we have added the quadratic constitutive relation (QCR) of Spalart to the one-and two-equation SA and SST turbulence models, respectively. The results of QCR with the SA and SST turbulence models have been validated against experimental data of Davis and Gessner for supersonic flow through a square duct. The approach is shown to be simple to implement and overall agreement is seen to improve with the use of QCR. |
| [49] | . CRM（Common Research Model）是第四届～第六届AIAA阻力预测研讨会（DPW）选择的参考外形。第四届和第五届DPW会议气动特性数值模拟结果的统计分析表明试验与计算之间存在明显差异。采用CFD方法和流固耦合（FSC）方法数值模拟了带支撑装置的CRM翼身组合体（CRM-WBS）构型的气动特性,以评估模型支撑装置和静气动弹性变形对CRM翼身组合体（CRM-WB）构型气动特性数值模拟结果的影响。通过与不包含支撑装置的CRM-WB构型的数值模拟结果和NASA Langley NTF风洞试验结果的对比分析,CRM-WBS构型的CFD计算结果表明,支撑装置导致机翼上翼面激波位置前移,升力系数、阻力系数、低头力矩系数下降。CRM-WBS构型的流固耦合计算结果表明,静气动弹性变形主要影响机翼上表面激波位置并显著降低外侧机翼激波位置前的负压值,进一步导致升力系数、阻力系数、低头力矩系数下降。包含支撑装置和静气动弹性变形的CRM-WB构型气动特性数值模拟结果更加接近试验结果。 . CRM（Common Research Model）是第四届～第六届AIAA阻力预测研讨会（DPW）选择的参考外形。第四届和第五届DPW会议气动特性数值模拟结果的统计分析表明试验与计算之间存在明显差异。采用CFD方法和流固耦合（FSC）方法数值模拟了带支撑装置的CRM翼身组合体（CRM-WBS）构型的气动特性,以评估模型支撑装置和静气动弹性变形对CRM翼身组合体（CRM-WB）构型气动特性数值模拟结果的影响。通过与不包含支撑装置的CRM-WB构型的数值模拟结果和NASA Langley NTF风洞试验结果的对比分析,CRM-WBS构型的CFD计算结果表明,支撑装置导致机翼上翼面激波位置前移,升力系数、阻力系数、低头力矩系数下降。CRM-WBS构型的流固耦合计算结果表明,静气动弹性变形主要影响机翼上表面激波位置并显著降低外侧机翼激波位置前的负压值,进一步导致升力系数、阻力系数、低头力矩系数下降。包含支撑装置和静气动弹性变形的CRM-WB构型气动特性数值模拟结果更加接近试验结果。 |
| [50] | . 针对大型计算流体力学(CFD)软件的验证与确认,为了减少人工成本,提高软件质量和开发效率,并适应于未来高性能计算发展的要求,基于云计算思想,提出了自动化测试云平台的解决方案.该方案采用模块化的浏览器/服务器(B/S)网络架构;利用LAMP(Linux+ Apache+ MySQL+ PHP/Python)开发工具;建立了持续集成的专业数据库;构建了涵盖可靠集群监控、复杂作业调度及大规模并行计算功能的云端环境;实现了通过便捷的网络访问,自动加载测试算例、提交集群计算、监测实时进度、自动化后处理、输出分析结果,并提供丰富的实验对比图、误差分析报表和汇总报告等;完成了对大型CFD软件的自动化验证与确认.将该方案应用于某大规模并行计算的CFD软件,验证了该解决方案的可行性与实用性. . 针对大型计算流体力学(CFD)软件的验证与确认,为了减少人工成本,提高软件质量和开发效率,并适应于未来高性能计算发展的要求,基于云计算思想,提出了自动化测试云平台的解决方案.该方案采用模块化的浏览器/服务器(B/S)网络架构;利用LAMP(Linux+ Apache+ MySQL+ PHP/Python)开发工具;建立了持续集成的专业数据库;构建了涵盖可靠集群监控、复杂作业调度及大规模并行计算功能的云端环境;实现了通过便捷的网络访问,自动加载测试算例、提交集群计算、监测实时进度、自动化后处理、输出分析结果,并提供丰富的实验对比图、误差分析报表和汇总报告等;完成了对大型CFD软件的自动化验证与确认.将该方案应用于某大规模并行计算的CFD软件,验证了该解决方案的可行性与实用性. |
| [51] | . 针对大型通用CFD软件研制的需求,为了提升CFD软件的开发效率,初步设计与开发了一个CFD软件自动化测试平台。该平台基于MySQL数据库,通过前台界面和远程集群后台管理程序的网络信息交互,实现了自主研发的通用CFD软件平台(HyperFLOW)的自动测试及验证与确认。根据需要适当修改前置处理接口,该平台亦可推广应用于其他CFD软件的自动测试。本文重点介绍了平台的基本框架和总体设计思路、平台的数据库和前台管理GUI设计、网络交互和后台管理等,并利用典型算例对计算结果的验证与确认过程进行了简要介绍,最后对平台构建的后续工作进行了展望。 . 针对大型通用CFD软件研制的需求,为了提升CFD软件的开发效率,初步设计与开发了一个CFD软件自动化测试平台。该平台基于MySQL数据库,通过前台界面和远程集群后台管理程序的网络信息交互,实现了自主研发的通用CFD软件平台(HyperFLOW)的自动测试及验证与确认。根据需要适当修改前置处理接口,该平台亦可推广应用于其他CFD软件的自动测试。本文重点介绍了平台的基本框架和总体设计思路、平台的数据库和前台管理GUI设计、网络交互和后台管理等,并利用典型算例对计算结果的验证与确认过程进行了简要介绍,最后对平台构建的后续工作进行了展望。 |
| [52] | . 本文回顾了CFD验证、确认中不确定度的概念和研究方法,CFD的不确定度尚无表达式可以使用.本文也讨论了现在正在进行的实验验证,对各个参加验证的软件,如何作出定量的精度评价也缺乏原则.针对这些情况,我们在不改变不确定度定义的前提下,对不确定度作了新的解读,即不确定度可解读为计算值或实验值与真值准确到前n位,从而可给出不确定度的表达式和真值估算的原则.并根据大样本数据的统计理论,对真值认为接近数学期望,从而给出准确到n位真值的计算方法.这个方法,可用于计算结果的检验,例如当模型一定时,可用此法寻求计算方法的真 . 本文回顾了CFD验证、确认中不确定度的概念和研究方法,CFD的不确定度尚无表达式可以使用.本文也讨论了现在正在进行的实验验证,对各个参加验证的软件,如何作出定量的精度评价也缺乏原则.针对这些情况,我们在不改变不确定度定义的前提下,对不确定度作了新的解读,即不确定度可解读为计算值或实验值与真值准确到前n位,从而可给出不确定度的表达式和真值估算的原则.并根据大样本数据的统计理论,对真值认为接近数学期望,从而给出准确到n位真值的计算方法.这个方法,可用于计算结果的检验,例如当模型一定时,可用此法寻求计算方法的真 |
| [53] | . , |
