, 邢海军, 杨绍普石家庄铁道大学机械工程学院,石家庄 050043
PARAMETERS OPTIMIZATION OF A DYNAMIC VIBRATION ABSORBER WITH AMPLIFYING MECHANISM AND NEGATIVE STIFFNESS1)
XingZhaoyang, ShenYongjun, XingHaijun, YangShaopu中图分类号:O328,TH113.1
文献标识码:A
通讯作者:
收稿日期:2018-11-9
网络出版日期:2019-05-18
版权声明:2019力学学报期刊社 所有
基金资助:
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (1543KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引 言
动力吸振器(dynamic vibration absorber,DVA)又称调谐质量阻尼器(tuned massdamper,TMD),是一种利用具有不同形式及参数的附加系统以减小主系统振动的设备. Frahm[1]发明了第一个无阻尼DVA,但是该吸振器只有在主振系固有频率附近很窄的范围内才能发挥作用. Ormondroyd和Den Hartog[2]在无阻尼DVA中加入阻尼,得到了减振效果更好的Voigt型DVA,并首次提出了固定点理论. 很多****[3-4]根据该理论对Voigt型DVA进行了参数优化. Den Hartog[5]在专著中总结了DVA系统参数的设计方法. Nishihara和Asami[6-8]研究并提出了主系统存在阻尼时DVA的设计方法,推导了Voigt型DVA的精确最优解,发现由固定点理论推导的结果与精确解极为接近,验证了固定点理论得到的结果在实际工程中的应用价值. 为进一步改善DVA的减振效果,Ren[9]提出了一种接地式DVA,可以通过改变接地阻尼来提高振动控制效果. Liu等[10]采用了一种近似方法也得到了与文献[9]相近的结果,这种方法对于较难求解的微分方程效果显著. 基于黏弹性器件的优良特性,Asami等[11-12]提出了减振性能更好的三要素型DVA并对其进行了优化设计. 为了提高DVA对精密仪器的减振效果,赵艳影等[13-15]研究发现采用时滞反馈控制能有效抑制主系统的振动,理论上几乎能够完全消除主系统的振动. 申永军等[16-18]研究了4种半主动DVA的近似解析解及其参数优化,提出了一种与主动隔振系统性能相同的单自由度被动隔振系统. 为了提高时滞DVA对随机激励系统的减振性能,李帅等[19]提出了一种新的时变参数时滞减振控制方法,获得了良好的减振效果.随着高精密领域对振动控制技术的要求逐渐提高,很多****尝试把负刚度装置运用到隔振领域中并取得了显著效果. Alabuzhev等[20]在专著中介绍了含负刚度元件隔振系统的理论和应用. 彭献等[21]从能量角度验证了正负刚度系统并联使用的理论可行性. Trimboli[22]提出了正负刚度元件并联隔振系统,并研究了该系统的减振效果. 彭解华等[23]推导了判定弹性系统静态稳定性的刚度准则,解决了正负刚度并联结构的稳定性问题. 文献[24]提出并研究了将正负刚度元件串联而成的零功率磁悬浮主动减振器,大幅降低生产成本的同时兼顾了抗干扰性能[25-28]. Park等[29]推导了正负刚度并联系统的最优设计参数,并通过实验验证了优异的隔振性能. 纪晗等[30]将负刚度装置附加到隔振层中,有效改善了结构减振性能. 文献[31]研究了向两级隔振器中引入负刚度装置的有效性,发现第一级负刚度装置能明显提高系统的减振效果,随后又对该装置进行了改进,使两级负刚度装置均能有效改善系统的减振性能,并通过实验进行了验证[32]. 文献[33]研究发现对于非线性隔振系统,使用激励响应的均方根值来定义系统的传递率更为准确. 文献[34]提出了附加负刚度的无阻尼自适应DVA,发现该模型能够有效降低主系统振幅. 申永军等[35-36]提出了将负刚度元件应用在Voigt型DVA与三要素型DVA中,从理论上证明了负刚度元件能够提高DVA的隔振性能. 文献[37]提出将时滞引入正负刚度并联系统并讨论了时滞参数的取值范围. 文献[38]提出了一种附加非线性负刚度元件的DVA,研究发现比线性负刚度DVA具有更好的鲁棒稳定性. 近些年来,许多****对非线性系统进行了一系列研究[39-41],但是在一般情况下很难获得非线性系统在随机激励下的频域解析解,对含非线性负刚度的隔振系统的随机动力学行为研究较少[42].
杠杆与惯容器等放大机构已被应用到隔振领域,表现出了良好的隔振性能. 李春翔等[43]研究了杠杆式TMD的动力特性,验证了该机构的有效性,发现比传统的TMD具有更大的最优调谐频率比和更小的最优阻尼比. 文献[44]在常规非线性DVA中引入了杠杆机构,分析了主要参数对隔振性能的影响,从理论上证明了杠杆机构能够提高系统的减振性能,具有良好的工程应用前景. 张孝良等[45]在车体悬架模型中将天棚阻尼器与惯容器并联,为理想天棚阻尼的被动实现提供了理论支持. 文献[46]提出了一种将惯容器和拟零刚度结合的复合式超低频隔振器,发现该装置可以有效降低系统的谐振频率,进而获得超低频隔振性能.
基于负刚度元件与放大机构在振动控制领域中的良好性能,本文在经典的Voigt型动力吸振器中附加放大机构与接地负刚度弹簧元件,得到了一种新的动力吸振器模型. 利用固定点理论对该模型的刚度和阻尼项进行了参数优化,并在保证系统稳定性的前提下得到了负刚度项的最优值. 通过与其他动力吸振器模型进行对比,证明了含放大机构的负刚度模型在减振方面具有很大优势,能够大幅降低共振振幅、拓宽减振频带并降低系统的谐振频率,为新型动力吸振器的设计提供了一种选择.
1 动力吸振器模型及参数优化
图1所示为本文所提出的含有放大机构(图中以杠杆机构为例)与负刚度弹簧元件的动力吸振器模型. 该模型的主系统和动力吸振器之间有一固定支撑的杠杆,杠杆的两端分别有一滑块,主系统与动力吸振器各自与滑块铰接形成一个完整的系统.其中$m_1 $和$m_2 $分别代表主系统质量和动力吸振器质量;$k_1 $和$k_2$分别代表主系统和动力吸振器的刚度;$c$代表动力吸振器的阻尼;$k_3 $代表接地负刚度元件的刚度;$r_1 $和$r_2$分别代表杠杆支撑点$O$到两滑块铰接点$M$, $N$的距离;$F_0 $和$\omega $分别代表激振力的振幅和频率;$x_1 $和$x_2 $分别代表主系统和动力吸振器的位移.由三角形相似定理与杠杆定理可设$L$为放大比,$M$点受力为$N$点受力的$L = {r_2 } / {r_1}$倍,$M$点位移为$N$点位移的$1 /L$.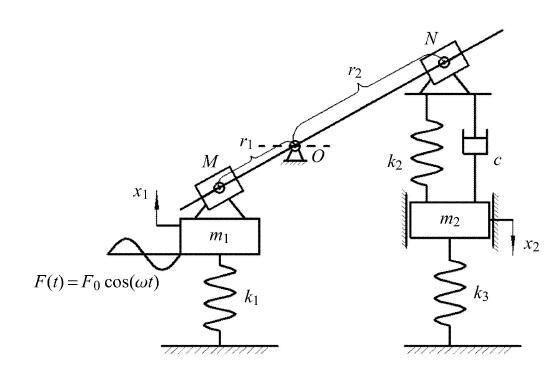
显示原图|下载原图ZIP|生成PPT图1动力吸振器模型
-->Fig. 1Mechanical model of dynamic vibration absorber
-->
忽略放大机构的质量和运动过程中的摩擦,根据牛顿第二定律可以建立该系统的动力学方程为
$$ \left.\!\!\begin{array}{l} m_1 \ddot {x}_1 + k_2 L(Lx{ }_1 - x_2 ) + k_1 x_1 + \\ cL(L\dot {x}_1 - \dot {x}_2 ) = F_0 \cos (\omega t) \\ m_2 \ddot {x}_2 + k_2 (x_2 - Lx_1 ) + c(\dot {x}_2 - L\dot {x}_1 ) + k_3 x_2 = 0 \end{array} \!\!\right \} (1) $$
引入以下参数
$$ \mu = \dfrac{m_2 }{m_1 }\,, \quad \omega _1 = \sqrt {\dfrac{k_1 }{m_1 }} \,,\quad \omega _2 = \sqrt {\dfrac{k_2 }{m_2 }} \xi = \dfrac{c}{2m_2 \omega _2 }\,, \quad f = \dfrac{F_0 }{m_1 }\,, \quad n = \dfrac{k_3 }{k_2 } $$
式(1)可以化为
$$ \left. \!\!\begin{array}{l} \ddot {x}_1 + L\mu \omega _2^2 (Lx{ }_1 - x_2 ) + \omega _1^2 x_1 + \\ 2L\mu \xi \omega _2 (L\dot {x}_1 - \dot {x}_2 ) = f\cos (\omega t) \ddot {x}_2 + \omega _2^2 (x_2 - Lx_1 ) + \\ 2\xi \omega _2 (\dot {x}_2 - L\dot {x}_1 ) + n\omega _2^2 x_2 = 0 \end{array} \!\! \right \} (2) $$
1.1 解析解
设式(1)解的形式为$$x_1 = X_1 {\rm e}^{{\rm j}\omega t}\,,\quad x_2 = X_2 {\rm e}^{{\rm j}\omega t} (3)$$
其中j为虚数单位. 将式(3)代入式(2)解得
$$ X_1 = \dfrac{f({\rm j} A_1 + B_1 )}{ {\rm j} C_1 + D_1 }\,, \quad X_2 = \dfrac{f({\rm j} A_2 + B_2 )}{ {\rm j} C_1 + D_1 } (4) $$
式中参数如下
$$ \left.\!\!\begin{array}{l} A_1 = 2\omega \omega _2 \xi \\ B_1 = - \omega ^2 + (1 + n)\omega _2^2 \\ C_1 = - 2\omega ^3\omega _2 \xi + 2\omega \omega _1^2 \omega _2 \xi - \\ 2L^2\omega ^3\omega _2 \xi \mu + 2L^2n\omega \omega _2^3 \xi \mu \\ D_1 = \omega ^4 + \omega _2^2 [(1 + n)\omega _1^2 + L^2n\omega _2^2 \mu ] - \\ \omega ^2[\omega _1^2 + \omega _2^2 (1 + n + L^2\mu )] \\ A_2 = 2L\omega \omega _2 \xi \\ B_2 = L\omega _2^2 \end{array} \right \} (5) $$
引入参数
$$ \lambda = \dfrac{\omega }{\omega _1 }\,, \quad \beta = \dfrac{\omega _2 }{\omega _1 }\,, \quad X_{st} = \dfrac{F_0 }{k_1 } $$
定义主系统振幅放大因子$A$
$$A^2 = \left| {\left. {\dfrac{X_1 }{X_{st} }} \right|} \right.^2 = \dfrac{\xi ^2A_3^2 + B_3^2 }{\xi ^2C_2^2 + D_2^2 } (6)$$
其中
$$ \left.\begin{array}{l} A_3 = 2\beta \lambda \\ B_3 = [-(1 + n)\beta ^2 + \lambda ^2] \\ C_2 = 2\beta \lambda [1 + L^2n\beta ^2\mu - \lambda ^2(1 + L^2\mu )] \\ D_2 = ( - 1 + \lambda ^2)[ - (1 + n)\beta ^2 + \lambda ^2] + \\ \mu L^2\beta ^2(n\beta ^2 - \lambda ^2) \end{array} \right \} (7) $$
系统的固有频率可以通过令式(6)的分母为零得到
$$\omega '^2_{1,2} = \dfrac{1}{2}\big [\omega _1^2 + \omega _2^2 (1 + n + \mu L^2)\pm \sqrt \gamma \big ] (8)$$
其中
$$ \begin{array}{l} \gamma = - 4\omega _2^2 [(1 + n)\omega _1^2 + n\mu L^2\omega _2^2 ] + \qquad [\omega _1^2 + \omega _2^2 (1 + n + \mu L^2)]^2 \end{array} $$
1.2 最优参数
基于固定点理论,易证明归一化的幅频曲线均通过2个独立于阻尼比的点,也就是该模型主系统幅频曲线的固定点. 图2中给出了阻尼比分别为0.2,0.4和0.6时的归一化幅频曲线,从图中可以看出对于不同的阻尼比,曲线均通过$P$, $Q$两点.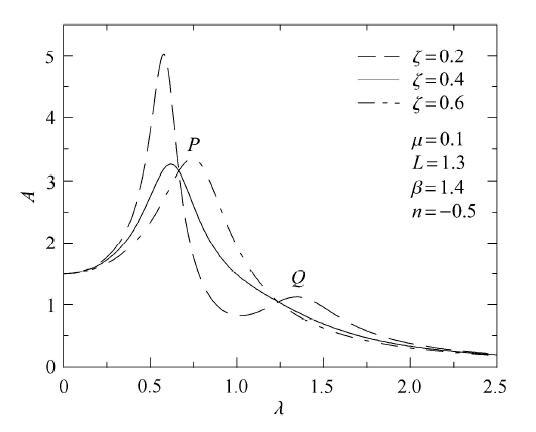
显示原图|下载原图ZIP|生成PPT图2不同阻尼比下的归一化幅频响应曲线
-->Fig. 2The normalized amplitude-frequency curves for different damping ratios
-->
由于固定点与阻尼比无关,因此当阻尼比趋于零和趋于无穷时的响应值相等,即
$$\left| {\dfrac{A_3 }{C_2 }} \right| = \left| {\dfrac{B_3 }{D_2 }} \right| (9)$$
进而得到
$$ \dfrac{ - (1 + n)\beta ^2 + \lambda ^2}{( - 1 + \lambda ^2)[ - (1 + n)\beta ^2 + \lambda ^2] + \mu L^2\beta ^2(n\beta ^2 - \lambda ^2)} = \qquad \dfrac{1}{1 - \lambda ^2 - \mu L^2( - n\beta ^2 + \lambda ^2)} (10) $$
化简得
$$ \lambda ^4(2 + \mu L^2) + \lambda ^2[ - 2 - 2\beta ^2(1 + n)(1 + \mu L^2)] + \qquad 2(1 + n)\beta ^2 + n\mu L^2(2 + n)\beta ^4 = 0 (11) $$
假设式(11)存在2个实根$\lambda _P $和$\lambda _Q $,由韦达定理可得
$$ \lambda _P^2 + \lambda _Q^2 = \dfrac{2[1 + \beta ^2(1 + n)(1 + \mu L^2)]}{2 + \mu L^2} (12) $$
优化的最终目的是使得幅频曲线的最大值最小,因此可以通过使固定点等高并且幅频曲线的峰值正好落在这两个固定点处以达到要求.
由$\lambda _P $和$\lambda _Q $处的响应值相等可以得到
$$ \dfrac{1}{1 - \lambda _P^2 - \mu L^2( - n\beta ^2 + \lambda _P^2 )} = \qquad - \dfrac{1}{1 - \lambda _Q^2 - \mu L^2( - n\beta ^2 + \lambda _Q^2 )} (13) $$
进一步整理可得
$$\lambda _P^2 + \lambda _Q^2 = \dfrac{2 + 2\mu nL^2\beta ^2}{1 + \mu L^2} (14)$$
联立式(12)和式(14)并化简得到
$$[n + (1 + \mu L^2)^2]\beta ^2 - 1 = 0 (15)$$
从而解得最优频率比为
$$\beta _{\rm opt} = \sqrt {\dfrac{1}{n + (1 + \mu L^2)^2}} (16)$$
将最优频率比代入式(10)可得两个固定点处的横坐标
$ \lambda _P^2 =\Big \{n(2 + \mu L^2) + (1 + \mu L^2)\Big[2 + \mu L^2 - $
$ \qquad L\sqrt {\mu (2 + \mu L^2)} \Big ]\Big\} \Big / $
$ \qquad \Big \{(2 + \mu L^2)[n + (1 + \mu L^2)^2]\Big \} $ (17a)
$\lambda _Q^2 = \Big \{n(2 + \mu L^2) + (1 + \mu L^2) \Big [2 + \mu L^2 + $
$ \qquad L\sqrt {\mu (2 + \mu L^2)} \Big] \Big \} \Big / $
$ \qquad \Big \{(2 + \mu L^2)[n + (1 + \mu L^2)^2] \Big \} $ (17b)
当频率比取最优值时,$P$, $Q$两个固定点处响应的纵坐标为
$$\left. A \right|_{(\lambda _P ,\lambda _Q )} = \dfrac{n + (1 + \mu L^2)^2}{(1+ \mu L^2)^2}\sqrt {1 + \dfrac{2}{\mu L^2}} (18)$$
由式(18)可知,固定点处的响应与质量比$\mu $和放大比$L$有关. 在质量比$\mu$一定时,可以通过增大放大比$L$,使固定点处的响应减小.
由于本文模型中含有负刚度项,根据负刚度的特性,当元件承受预加荷载时,才能表现出负刚度性质,不恰当的负刚度值将会使得系统出现不稳定现象,因此必须对负刚度项进行优化.研究发现当预加载荷使系统产生位移等于固定点处响应值时,系统将处于稳定状态,于是令
$$\left. {A^2} \right|_{\lambda = 0} = \left. {A^2} \right|_{(\lambda _P,\lambda _Q )} (19)$$
即
$$ \dfrac{(1 + n)^2[n + (1 + \mu L^2)^2]^2}{[(1 + n)^2 + \mu L^2(2 + 3n) + \mu ^2L^4(1 + n)]^2} = \qquad \dfrac{(2 + \mu L^2)[n + (1 + \mu L^2)^2]^2}{\mu L^2(1 + \mu L^2)^4} (20) $$
求解式(20)得到所有可能的最优负刚度比值
$ n_1 = - (1 + \mu L^2)^2 $ (21a)
$n_{2,3} = - 1 - \mu L^2\pm \dfrac{(1 + \mu L^3)\sqrt {\mu (2 + \mu L^2)} }{2 + \mu L^2} $ (21b)
$n_{4,5} = - (1 + \mu L^2) \Big [1 + \mu L^2\pm L\sqrt {\mu (2 + \mu L^2)} \Big ] $ (21c)
将上述求得的负刚度比值分别代入式(8)中,发现只有$n_5 $能保证系统的固有频率均为正值,所以取最优负刚度比为$n_5$,即
$$n_{\rm opt} = n_5 = - (1 + \mu L^2) \Big [1 + \mu L^2 - L\sqrt {\mu (2 + \mu L^2)} \,\Big] (22)$$
至此已经得到了最优频率比与最优负刚度比,固定点$P$和$Q$已经被调整到同一高度. 由于$P$, $Q$两固定点的坐标与阻尼比$\xi$的取值无关,为了达到最优的减振效果,可以使两固定点成为或者近似成为幅频曲线的最高点. 由极值条件知,幅频曲线在两固定点处的导数应该为零,即
$$\dfrac{\partial A^2}{\partial \lambda _P ^2} = 0\,,\qquad\dfrac{\partial A^2}{\partial \lambda _Q ^2} = 0 (23)$$
由式(23)可以得到使$P$, $Q$两固定点成为或者近似成为幅频曲线最高点时$\xi _1 $和$\xi _2$的值,进而得到最优阻尼比$\xi _{\rm opt} = {(\xi _1 + \xi _2 )} /2$,但是这种方法有时难以得到解析结果.Liu[10]使用了一种非常简单的方法,可以不用微分而直接求出阻尼比的近似值.
为了使幅频曲线水平通过$P$点,先假设其通过邻近点$P'$,$P'$点的坐标为$(\lambda_{P'},A_{P'})$. 令
$$ \left.\begin{array}{l} \lambda _{P'}^2 = \lambda _P^2 + \delta \\ A_{P'} = A = \dfrac{n + (L + \mu L^2)^2}{L(1 + \mu L^2)^2}\sqrt {L^2 + \dfrac{2}{\mu }} \end{array} \!\! \right \} (24) $$
其中
$$\delta \to 0$$
将式(24)代入式(6)中可以得到关于$\xi _1^2 $的等式
$$\xi _1^2 = - \dfrac{(ab + c)(ad + c)}{e} (25)$$
其中
$$ \left.\begin{array}{l} a = - (1 + n)\beta ^2 + \lambda _{P'}^2 \\ b = - 1 + A_{P'} ( - 1 + \lambda _{P'}^2 ) \\ c = \mu \beta ^2A_{P'} L^2(n\beta ^2 - \lambda _{P'}^2 ) \\ d = 1 + A_{P'} ( - 1 + \lambda _{P'}^2 ) \\ e = 4\beta ^2\lambda _{P'}^2 \Big \{ - 1 + A_{P'}^2 \Big [ - 1 + \lambda _{P'}^2 + \\ \mu L^2( - n\beta ^2 + \lambda _{P'}^2 ) \Big]^2 \Big \} \end{array} \!\! \right \} (26) $$
将式(25)展开后,可以得到下列形式的等式
$$ \xi _1^2 = \dfrac{a_0 + a_1 \delta + a_2 \delta ^2 + a_3 \delta ^3 + \cdots }{b_0 + b_1 \delta + b_2 \delta ^2 + b_3 \delta ^3 + \cdots } (27) $$
如果$\delta = 0$, 式(25)为$0 / 0$形式的不定式,结合式(27)可以得到$a_0 = b_0 = 0$. 由于$\delta $是一个非常小的量,在式(27)中可以忽略其高次项,此时的阻尼比为
$$\xi _1^2 = \dfrac{a_1 }{b_1 } (28)$$
我们只需要找到式(27)的分子与分母中所有$\delta $的一次项系数
$$ \left.\!\!\begin{array}{l} a_1 = - 4A_P^2 \lambda _P^6 + 6A_P^2 \lambda _P^4 [1 + \beta ^2(1 + n + \\ \mu L^2)] + 2\beta ^2[ - 1 - n + A_P^2 (1 + n + \\ n\mu L^2\beta ^2)(1 + \beta ^2 + n\beta ^2 + \mu \beta ^2L^2)] + \\ 2\lambda _P^2 - 2\lambda _P^2 A_P^2 \{1 + 2\beta ^2(2 + 2n + \mu L^2) - \\ 2\beta ^4[n^2 + (1 + \mu L^2)^2 + n(2 + 4\mu L^2)]\} \\ b_1 = 4\beta ^2\{ - 1 + A_P^2 [ - 1 + \lambda _P^2 + \mu L^2(\lambda _P^2 - \\ n\beta ^2)][ - 1 - n\mu L^2\beta ^2 + 3\lambda _P^2 (1 + \mu L^2)]\} \end{array} \!\! \right \} (29) $$
将式(16)、式(17a)、式(18)及式(22)代入式(28),得到使幅频曲线水平通过$P$点时的阻尼比
$$\xi _1^2 = \dfrac{\mu L^2(2 + \mu L^2) + (3L + \mu L^3)\sqrt {\mu (2 + \mu L^2)} }{4(1 + \mu L^2)(2 + \mu L^2)} (30)$$
同理可得到使幅频曲线水平通过$Q$点时的阻尼比
$$\xi _2^2 = \dfrac{\mu L^2(2 + \mu L^2) + (L + \mu L^3)\sqrt {\mu (2 + \mu L^2)} }{4(1 + \mu L^2)(2 + \mu L^2)} (31)$$
通过上述推导,最终求得本模型的近似最优阻尼比为
$$\xi _{\rm opt}^2 \cong \dfrac{\xi _1^2 + \xi _2^2 }{2} = \dfrac{L[\mu L + \sqrt {\mu (2 + \mu L^2)} ]}{4(1 + \mu L^2)} (32)$$
至此已经得到了本模型所有最优参数. 将所求得的最优频率比、最优负刚度比、近似最优阻尼比代入式(8)可以得到系统的固有频率
$\omega '^2_1 = \dfrac{1}{2}\omega _1^2 \Bigg [2 - \dfrac{\mu L}{\sqrt {\mu (2 + \mu L^2)} } -\sqrt {1 + \dfrac{2}{2 + \mu L^2}}\,\Bigg ] $ (33a)
$\omega '^2_2 = \dfrac{1}{2}\omega _1^2 \Bigg [2 - \dfrac{\mu L}{\sqrt {\mu (2 + \mu L^2)} } +\sqrt {1 + \dfrac{2}{2 + \mu L^2}} \,\Bigg] $ (33b)
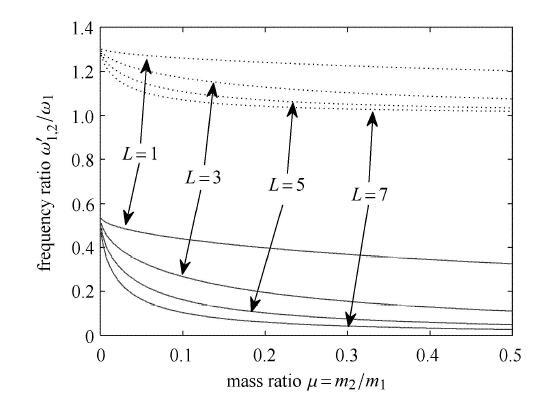
图3给出了安装动力吸振器之后系统的固有频率之间的关系,当放大比为1时表示系统中不引入放大机构. 由图可见,系统具有两个固有频率,随着质量比$\mu $的增大,两固有频率均逐渐减小. 在区间$ [0,0.1]$上,固有频率减小更剧烈,且放大比$L$越大,变化率越大,减小幅度越大. 随着放大比$L$的增大,两固有频率的差值逐渐增大但始终小于系统主振系频率$\omega _1 $. 因此通过加入放大机构可以拓宽动力吸振器的减振频率.
显示原图|下载原图ZIP|生成PPT图3不同放大比下系统固有频率与质量比的关系曲线
-->Fig. 3The relation curves between the natural frequencies and mass ratio under different amplifying ratios
-->
2.1 数值仿真
为了验证前文结果的正确性,选取质量比$\mu = 0.1$,激励幅值$F_0 = 1000$,N,放大比$L =2.5$,根据前述优化结果得到的最优参数为$\beta = 0.693\,1$,$\xi = 0.541\,5$,$n = - 0.559\,2$.利用四阶龙格库塔法,选取计算时间为500,s,可以得到在给定简谐激励下的数值解.略去瞬态响应,选取稳态解的最大值为响应幅值并进行归一化处理,从而可以得到归一化的幅频曲线.图4给出了系统的数值解与解析解曲线,圆圈绘制的曲线为系统的数值解,实线为系统的解析解.从图中可以看出,数值解与解析解所得结果完全吻合,验证了本文求解过程的正确性.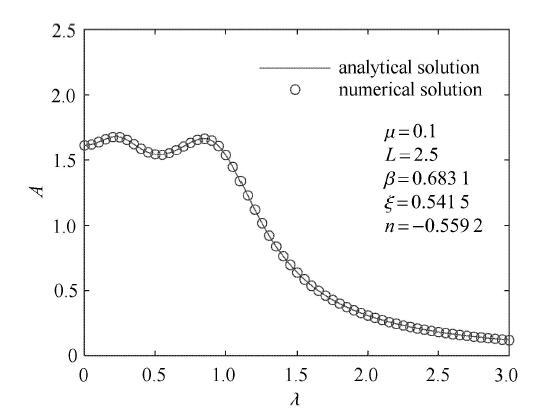
显示原图|下载原图ZIP|生成PPT图4$\mu = 0.1$时数值解与解析解对比
-->Fig. 4Comparison between numerical simulation and analytical solution when $\mu = 0.1$
-->
2.2 与其他形式动力吸振器模型的对比
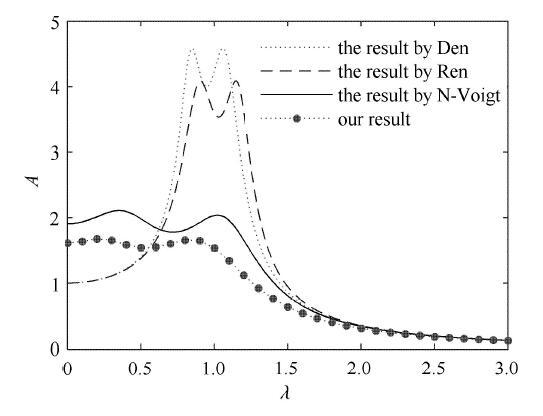
2.2.1 简谐激励下的响应对比为验证本文提出的动力吸振器模型的减振效果,取放大比$L = 2.5$,将该模型与传统的Voigt型动力吸振器、接地式动力吸振器及文献[32]中附加负刚度元件的Voigt型动力吸振器模型(后文中简称N-Voigt模型)进行了对比. 对比过程中均选取质量比为$\mu = 0.1$,并按照已有的结果计算得到各模型的相应最优参数,在最优参数下的归一化幅频曲线如图5所示.
显示原图|下载原图ZIP|生成PPT图5$\mu = 0.1$时与其他形式动力吸振器模型对比
-->Fig. 5Comparison with other DVAs when $\mu = 0.1$
-->
从图中可以看出,在质量比相同的情况下,本文模型与N-Voigt模型相对于传统的动力吸振器,均能够大幅度降低系统共振区的振幅,同时拓宽减振频率;相对于N-Voigt模型,在加入放大机构后本文模型的共振振幅更低,虽然减振频带宽度相差不大,但是明显降低了系统的谐振频率.
2.2.2 随机激励下的响应对比
由于在实际工程中系统所受的激励多为随机激励,因此本文进一步研究了在随机激励下的主系统响应. 设该系统受均值为零、功率谱密度为$S(\omega ) = S_0 $的白噪声激励,则两种传统动力吸振器、N-Voigt模型和本文模型主系统位移响应的功率谱密度函数分别为
$$ \left.\begin{matrix} S_{\rm V} (\omega ) = \left| {X_{\rm V_1 } } \right|^2S_0 \,, \quad S_{\rm R} (\omega ) = \left| {X_{\rm R_1 } } \right|^2S_0 \\ S_{\rm N} (\omega ) = \left| {X_{\rm N_1 } } \right|^2S_0 \,, \quad S_{\rm LN} (\omega ) = \left| {X_{\rm LN_1 } } \right|^2S_0 \\\end{matrix} \right\} (34) $$
其中下角标 V, R, N, LN 分别代表Voigt模型、Ren提出的接地式动力吸振器模型、N-Voigt模型以及本文模型.这4种动力吸振器模型的主系统位移均方值为
$$ \left. \!\!\begin{array}{l} \sigma _{\rm V}^2 = \int_{ - \infty }^\infty S_{\rm V} (\omega ) \omega = S_0 \int_{- \infty }^\infty \left| {X_{{\rm V}_1 } } \right|^2 \omega = \\ \dfrac{\pi S_0 Y_1 }{2\mu \xi \beta \omega _1^3 } \\ \sigma _{\rm R}^2 = \int_{ - \infty }^\infty {S_{\rm R} (\omega )} \omega = S_0 \int_{- \infty }^\infty {\left| {X_{\rm R_1 } } \right|^2 \omega } = \\ \dfrac{\pi S_0 Y_2 }{2\mu \xi \omega _1^3 \beta ^5} \\ \sigma _{\rm N}^2 = \int_{ - \infty }^\infty {S_{\rm N} (\omega )} \omega = S_0 \int_{ - \infty }^\infty {\left| {X_{\rm N_1 } } \right|^2 \omega } = \\ \dfrac{\pi S_0 Y_3 }{2\mu \xi \beta \omega _1^3 (1 + n + n\mu \beta ^2)(n\beta ^2 - 1)^2} \\ \sigma _{\rm LN}^2 = \int_{ - \infty }^\infty {S_{\rm LN} (\omega )} \omega = S_0 \int_{ - \infty }^\infty {\left| {X_{\rm LN_1 } } \right|^2 \omega } = \\ \dfrac{\pi S_0 Y_4 }{2\mu \xi \beta L^2\omega _1^3 (1 + n + n\mu \beta ^2L^2)(n\beta ^2 - 1)^2} \end{array} \!\!\right \} (35) $$
其中
$$ \left.\!\!\begin{array}{l} Y_1 = 1 + \beta ^4(1 + \mu )^2 + \beta ^2(4\mu \xi ^2 + 4\xi ^2 - \mu - 2) \\ Y_2 = 1 + \beta ^4 + \beta ^2(\mu + 4\xi ^2 - 2) \\ Y_3 = (1 + n)\{[\beta ^2(1 + n) - 1]^2 + 4\beta ^2\xi ^2\} + \\ \mu \beta ^2[4\xi ^2(1 + n) + 2\beta ^2(1 + n + 2n\xi ^2) - 1] + \\ \mu ^2\beta ^4(1 + 4n\xi ^2) \\ Y_4 = (1 + n)\{[\beta ^2(1 + n) - 1]^2 + 4\beta ^2\xi ^2\} + \\ \mu \beta ^2L^2[4\xi ^2(1 + n) + 2\beta ^2(1 + n + 2n\xi ^2) - 1] + \\ \mu ^2\beta ^4L^4(1 + 4n\xi ^2) \end{array} \right \} (36) $$
选取四类系统中动力吸振器与主系统的质量比为$\mu =0.1$,根据文献[3,4,5,6,7,8,9]、文献[32]及本文中的最优参数结果得到均方值分别为
$$ \left.\begin{matrix} \sigma _{\rm V}^2 = \dfrac{6.401\pi S_0 }{\omega _1^3 }\,, \quad \sigma _{\rm R}^2 = \dfrac{5.780\pi S_0 }{\omega _1^3 } \\ \sigma _{\rm N}^2 = \dfrac{3.302\pi S_0 }{\omega _1^3 }\,, \quad \sigma _{\rm LN}^2 = \dfrac{2.139\pi S_0 }{\omega _1^3 } \\\end{matrix} \right\} (37) $$
结果表明,当主系统参数相同时,在随机激励情况下本文模型仍然具有良好的减振效果.
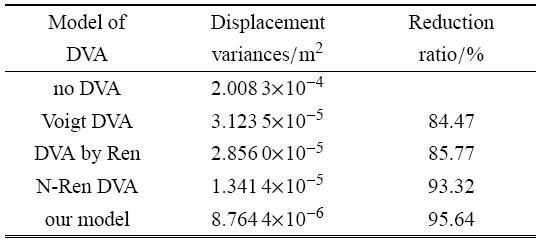
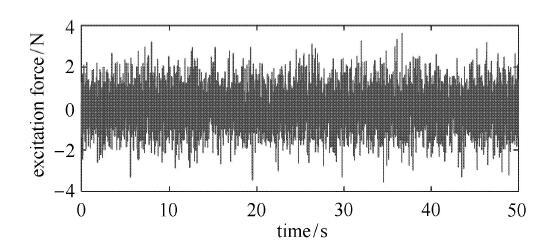
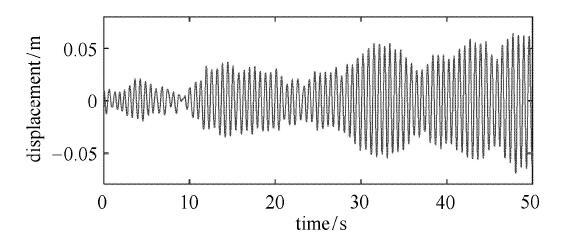
为了更真实地模拟工程实际,本文构建了50\,s均值为0方差为1的随机激励,其时间历程如图6所示. 选取主系统质量为$m_1= 1$\,kg、主系统刚度为 $k_1 = 100$\,N/m,并根据文献[3,4,5,6,7,8,9]及本文推导得到其他最优参数.主系统不附加DVA时的位移响应如图7所示,主系统附加4种不同的DVA时的位移响应分别如图8 $\sim $图11所示.由于系统振动能量可由主系统位移方差衡量,在表1中总结了主系统位移方差及其衰减比.
Table 1
表1
表1主系统位移方差及衰减比
Table 1The variances and reduction ratios of the primary system
 |
新窗口打开
显示原图|下载原图ZIP|生成PPT图6随机激励时间历程
-->Fig. 6The time history of the random excitation
-->
显示原图|下载原图ZIP|生成PPT图7无吸振器的主系统时间历程
-->Fig. 7The time history of the primary system without DVA
-->
从图7 $\sim $图11以及表1可以看出,本文模型比其他3种模型具有更优良的隔振性能,能够在整个频率范围内大幅降低主系统的振动能量.
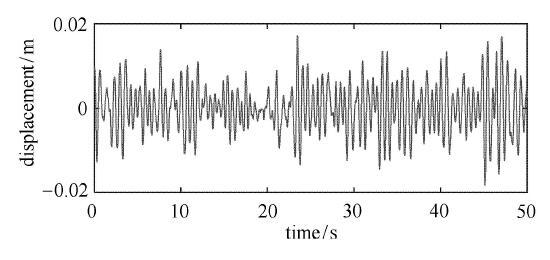显示原图|下载原图ZIP|生成PPT图8附加Voigt型动力吸振器的主系统时间历程
-->Fig. 8The time history of the primary system with DVA by Den Hartog
-->
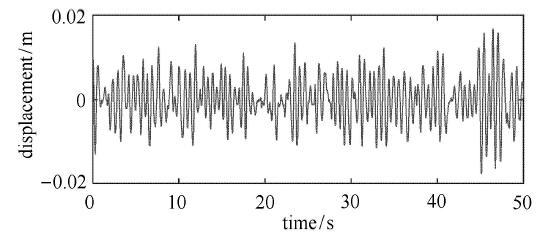显示原图|下载原图ZIP|生成PPT图9附加接地式动力吸振器的主系统时间历程
-->Fig. 9The time history of the primary system with DVA by Ren
-->
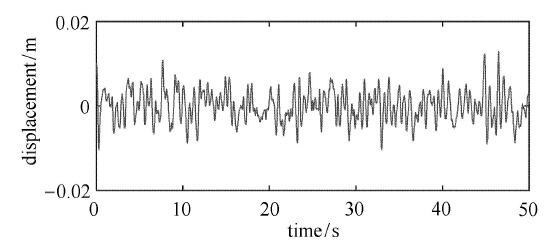显示原图|下载原图ZIP|生成PPT图10附加N-Voigt动力吸振器的主系统时间历程
-->Fig. 10The time history of the primary system with DVA by N-Voigt
-->
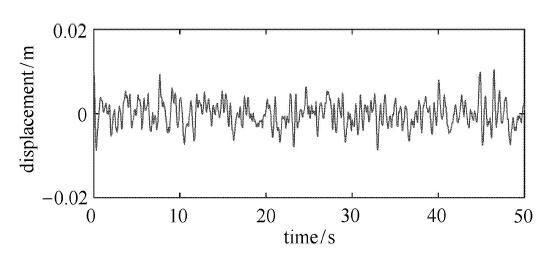显示原图|下载原图ZIP|生成PPT图11附加放大机构与负刚度动力吸振器的主系统时间历程
-->Fig. 11The time history of the primary system with DVA using amplifying mechanism and negative stiffness
-->
3 结 论
提出了一种含有放大机构与负刚度元件的动力吸振器模型,对该模型进行了参数优化,得到了最优频率比、近似最优阻尼比和最优负刚度比. 通过与其它形式的动力吸振器模型对比,说明本文模型能够大幅降低共振振幅、拓宽减振频带并且降低系统的谐振频率;在随机激励情况下,本文模型也体现出较大优势,具有良好的减振效果. 进一步的研究表明,放大比越大,动力吸振器模型的减振性能越好;通过适当增大放大比,可以达到降低系统总质量以提高减振效果的目的;对于变质量的主系统,可以加入合适的控制策略,通过对放大比进行适当调整,从而得到稳定的减振效果.The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | , |
| [2] | . |
| [3] | . |
| [4] | . |
| [5] | |
| [6] | . |
| [7] | . |
| [8] | . |
| [9] | . A different design of a dynamic vibration absorber (DVA) was investigated. The damping element in this design was connected to the earth (a base structure) and not to the structure to be controlled. The proposed design of DVA provided a more effective control over an ordinary design, for a same mass ratio. |
| [10] | . The free vibrational response of clamped homogeneous or symmetrically laminated orthotropic annular plates with edge damage on the outer circumference has been studied for the first time, using the finite difference method. The edge damage is modeled via the application of a non-uniform boundary condition. The sensitivity of vibrational frequencies to the extent of the edge damage is investigated and shown to be strongly influenced by the material properties and the relative thicknesses of the materials comprising the laminated plates. It is shown that the orthotropy ratio for the plate (defined here by D-rr/D-theta theta) is a convenient compact parameter for indicating the sensitivity to edge damage. Mode shapes are also computed and found to be profoundly affected by the orthotropy ratio. The behavior of higher modes of vibration is also discussed and the phenomenon of cross over, whereby two modes exist having the same frequency, is observed. (c) 2004 Elsevier Ltd. All rights reserved. |
| [11] | . |
| [12] | . |
| [13] | . The delayed feedback control is applied to suppress the vibration of vertical displacement in a two-degree-of-freedom nonlinear system with external excitation. Effects of both positive and negative feedback control are observed when the primary resonance and 1:1 internal resonance occur in the system simultaneously. The method of multiple scales is employed to obtain analytical solutions of the system under consideration. With the time delay varying for a fixed gain, it is seen that the vibration can be suppressed at some values of the delay. These values form a called “vibration suppression region”, where one can easily observe the “maximum vibration suppression point”. At this point, the vertical vibration could be suppressed about 65% for the positive feedback and 86% for the negative one by comparing with the nonlinear vibration absorber without delayed feedback control. However, the vibration suppression is invalid at some values of the delay. Effects of the gain on the vibration suppression are also investigated. The dynamical behaviors became complex with the gain increasing at some values of the delay, but the vibration can be suppressed more efficiently at other values. It implies that one can always choose a suitable delay and gain to achieve a vibration suppression. All analytical predictions of this paper are in good agreement with the numerical simulation. |
| [14] | . 对一个带有时滞非线性动力吸振器的两自由度结构，采用多尺度法研究了时滞非线性动力吸振器对主系统的减振性能，得到了主系统的振幅-时滞响应曲线.研究结果表明，对时滞非线性动力吸振器，可以通过调节反馈增益系数和时滞控制主系统的振动. 研究还发现，对确定的反馈增益系数，可以存在时滞的一些调节区域，时滞非线性动力吸振器可以减小主系统的振动. 并且在时滞的这些可调区域里，存在一个``最大减振点''对应这一反馈增益系数下主系统振幅的最小值.对不同的反馈增益系数，``最大减振点''对应的主系统的振幅也不同.因此能够找到一组反馈增益系数和时滞量的最佳值，最大程度地减小主系统的振动.研究结果表明，当反馈增益系数和时滞量调到最佳值时，主系统的振动较无时滞非线性动力吸振器可以减少90{\%}左右, 数值模拟也证实了解析结果的正确性. 对一个带有时滞非线性动力吸振器的两自由度结构，采用多尺度法研究了时滞非线性动力吸振器对主系统的减振性能，得到了主系统的振幅-时滞响应曲线.研究结果表明，对时滞非线性动力吸振器，可以通过调节反馈增益系数和时滞控制主系统的振动. 研究还发现，对确定的反馈增益系数，可以存在时滞的一些调节区域，时滞非线性动力吸振器可以减小主系统的振动. 并且在时滞的这些可调区域里，存在一个``最大减振点''对应这一反馈增益系数下主系统振幅的最小值.对不同的反馈增益系数，``最大减振点''对应的主系统的振幅也不同.因此能够找到一组反馈增益系数和时滞量的最佳值，最大程度地减小主系统的振动.研究结果表明，当反馈增益系数和时滞量调到最佳值时，主系统的振动较无时滞非线性动力吸振器可以减少90{\%}左右, 数值模拟也证实了解析结果的正确性. |
| [15] | . 主要研究采用时滞状态反馈控制自参数动力吸振器减振系统中主系统的振动问题.系统在简谐激励作用下,采用多尺度方法得到了自参数动力吸振器减振系统中饱和控制的范围.当系统处于饱和控制时,引入时滞状态反馈控制主系统的振动.主要分析了反馈增益系数和时滞两控制参数对主系统振动的影响.结果表明,存在反馈增益系数和时滞的调节区域能够减小主系统的振动.对某一反馈增益系数,可以在某段区间内调节时滞以减小主系统的振动.在时滞的调节区间内存在一个时滞的``最大减振点'',能够在该反馈增益系数下最大程度地减小主系统的振动.研究还表明,随着反馈增益系数的不断增大,时滞在``最大减振点''时系统的减振能力也不断提高.通过合理的选择反馈增益系数和时滞两参数,主系统的振动几乎可以完全消除. 主要研究采用时滞状态反馈控制自参数动力吸振器减振系统中主系统的振动问题.系统在简谐激励作用下,采用多尺度方法得到了自参数动力吸振器减振系统中饱和控制的范围.当系统处于饱和控制时,引入时滞状态反馈控制主系统的振动.主要分析了反馈增益系数和时滞两控制参数对主系统振动的影响.结果表明,存在反馈增益系数和时滞的调节区域能够减小主系统的振动.对某一反馈增益系数,可以在某段区间内调节时滞以减小主系统的振动.在时滞的调节区间内存在一个时滞的``最大减振点'',能够在该反馈增益系数下最大程度地减小主系统的振动.研究还表明,随着反馈增益系数的不断增大,时滞在``最大减振点''时系统的减振能力也不断提高.通过合理的选择反馈增益系数和时滞两参数,主系统的振动几乎可以完全消除. |
| [16] | . |
| [17] | . In this paper four semi-active dynamic vibration absorbers (DVAs) are analytically studied, where the time delay induced by measurement and execution in control procedure is included in the system. The first-order approximate analytical solutions of the four semi-active DVAs are established by the averaging method, based on the illustrated phase difference of the motion parameters. The comparisons between the analytical and the numerical solutions are carried out, which verify the correctness and satisfactory precision of the approximate analytical solutions. Then the effects of the time delay on the dynamical responses are analyzed, and it is found that the stability conditions for the steady-state responses of the primary systems are all periodic functions of time delay, with the same period as the excitation one. At last the effects of time delay on control performance are discussed. |
| [18] | . |
| [19] | . 时滞动力吸振器对谐波激励有着良好的减振控制效果,但对随机激励的减振控制效果却并不明显,具体表现为时滞动力吸振器对随机激励的减振控制效果与被动吸振器几乎相同.针对上述问题,提出了一种新的时变参数时滞减振控制方法.在原有时滞减振控制方法的基础上,首先将时滞增益系数由定值形式变为时间函数形式,然后通过时变优化得到多组时滞控制参数并使其以一定时间周期循环作用于减振控制过程,通过这种方法进一步改善了时滞动力吸振器减振性能.最后以二自由度时滞动力吸振器减振模型为例,以主系统的振动响应为仿真对象,运用精细积分法求解了具有时变时滞参数的时滞动力学方程,以此得到了在谐波激励和随机激励作用下主系统振动的时域仿真结果.研究结果表明,在时变参数时滞动力吸振器的控制下,主系统无论是受谐波激励作用还是受随机激励作用,其振动位移、振动速度和振动加速度均比在定值参数时滞动力吸振器控制下时有大幅的减小,时滞动力吸振器的减振性能有了明显的改善. . 时滞动力吸振器对谐波激励有着良好的减振控制效果,但对随机激励的减振控制效果却并不明显,具体表现为时滞动力吸振器对随机激励的减振控制效果与被动吸振器几乎相同.针对上述问题,提出了一种新的时变参数时滞减振控制方法.在原有时滞减振控制方法的基础上,首先将时滞增益系数由定值形式变为时间函数形式,然后通过时变优化得到多组时滞控制参数并使其以一定时间周期循环作用于减振控制过程,通过这种方法进一步改善了时滞动力吸振器减振性能.最后以二自由度时滞动力吸振器减振模型为例,以主系统的振动响应为仿真对象,运用精细积分法求解了具有时变时滞参数的时滞动力学方程,以此得到了在谐波激励和随机激励作用下主系统振动的时域仿真结果.研究结果表明,在时变参数时滞动力吸振器的控制下,主系统无论是受谐波激励作用还是受随机激励作用,其振动位移、振动速度和振动加速度均比在定值参数时滞动力吸振器控制下时有大幅的减小,时滞动力吸振器的减振性能有了明显的改善. |
| [20] | |
| [21] | . 本文讨论含负刚度弹簧系统的隔振原理,并对这样的系统进行了能量分析.作为该方法的应用,最后给出了等频隔振系统的设计实例.结果表明,含负刚度弹簧的振动系统具有固有频率低、承载能力大、隔振效果好等优点. . 本文讨论含负刚度弹簧系统的隔振原理,并对这样的系统进行了能量分析.作为该方法的应用,最后给出了等频隔振系统的设计实例.结果表明,含负刚度弹簧的振动系统具有固有频率低、承载能力大、隔振效果好等优点. |
| [22] | . |
| [23] | . 从判定系统静态稳定性的能量准则出发，推导了判定弹性系统静态稳定性的刚度准则，从而十分方便地解决了正、负刚度并联结构的稳定性问题．文中还对此结构在振动控制中的应用进行了研究。 从判定系统静态稳定性的能量准则出发，推导了判定弹性系统静态稳定性的刚度准则，从而十分方便地解决了正、负刚度并联结构的稳定性问题．文中还对此结构在振动控制中的应用进行了研究。 |
| [24] | A new vibration isolation system is proposed which ischaracterized by using zero-power magnetic suspension.Since the zero-power magnetic suspension systembehaves as if it has a negative stiffness, infinite stiffnessagainst disturbances on the isolation table can beachieved by combining it with a normal spring. It enablesthe system to have good characteristics in both theperformances of isolation from ground and suppression ofdirect vibration. The fundamental properties of the systemare analytically studied based on a basic model. It isshown that the proposed system has an infinite stiffnessagainst disturbance on the isolation table. |
| [25] | A new vibration isolation system is proposed which uses zero-power magnetic suspension. Since a zero-power system behaves as if it has a negative stiffness, combining it with a normal spring can generate infinite stiffness against disturbances on the isolation table. It enables the system to have good performance both in reducing vibration transmitted from ground and in suppressing direct vibration. The basic characteristics of the proposed system are studied both analytically and experimentally. |
| [26] | . |
| [27] | . An active vibration isolation system using zero-power magnetic suspension was studied analytically and experimentally. Since a zero-power magnetic suspension system behaves as if it has negative stiffness, connecting it in series with a normal spring can generate infinite stiffness against disturbances acting on an isolation table. This property is maintained even when a suspension that supports the weight of the isolation table is introduced in parallel with the serial combination. Analysis of a simple model involving a single-axis apparatus clarified the fundamental characteristics of the system. The force-displacement characteristics of the zero-power magnetic suspension were measured to estimate the negative stiffness properties. It was experimentally confirmed that combining a zero-power magnetic suspension with a normal spring generates high stiffness against static direct disturbances acting on an isolation table. [All rights reserved Elsevier] |
| [28] | . A new vibration isolation system using negative stiffness realized by active control technique is proposed in this paper. The serial connection of a normal spring and a suspension system with negative stiffness enables the isolation system to have low stiffness for vibration from the ground and high (theoretically infinite) stiffness against direct disturbance acting on the isolation table. A control method of realizing negative stiffness with a linear actuator is presented in an analytical form. The validity of this method is confirmed experimentally with an apparatus equipped with a voice coil motor. It is also confirmed experimentally that high stiffness against direct disturbance on the isolation table can be achieved in the proposed vibration isolation system. |
| [29] | |
| [30] | . 针对长周期结构隔震效果较差的问题,提出了在普通隔震层附加负刚度阻尼装置（NSD）的新型隔震系统,并讨论了NSD对隔震体系性能的影响.首先,通过推导和讨论NSD隔震体系的自振频率、阻尼比和动力放大系数,指出该隔震系统可以显著延长结构自振周期和增加结构阻尼比,较适合长周期结构隔震.然后,采用ANSYS有限元软件分析了铅芯橡胶支座（LRB）隔震体系、隔震橡胶支座（LNR）与NSD并联隔震体系的地震反应,结果表明后者的各种反应均比前者要小,对层间位移和柱底剪力降低更明显,并且LNR隔震层附加负刚度比不超过-0.30的NSD可以获得较好的隔震效果,更易实现长周期结构的隔震目标. . 针对长周期结构隔震效果较差的问题,提出了在普通隔震层附加负刚度阻尼装置（NSD）的新型隔震系统,并讨论了NSD对隔震体系性能的影响.首先,通过推导和讨论NSD隔震体系的自振频率、阻尼比和动力放大系数,指出该隔震系统可以显著延长结构自振周期和增加结构阻尼比,较适合长周期结构隔震.然后,采用ANSYS有限元软件分析了铅芯橡胶支座（LRB）隔震体系、隔震橡胶支座（LNR）与NSD并联隔震体系的地震反应,结果表明后者的各种反应均比前者要小,对层间位移和柱底剪力降低更明显,并且LNR隔震层附加负刚度比不超过-0.30的NSD可以获得较好的隔震效果,更易实现长周期结构的隔震目标. |
| [31] | . 78 A two-stage nonlinear vibration isolation system is modeled. 78 Force transmissibility is used as the measure of the isolation performance. 78 Nonlinearity in the lower stage can improve the effectiveness of the isolator. 78 High damping in the upper stage and low damping in the lower stage are preferable. |
| [32] | . |
| [33] | . 61Two definitions of nonlinear transmissibility are compared.61Two definitions are slightly different for both force and displacement transmission.61Force and displacement transmissibility with modified definition are more agreement.61Transmissibility for aperiodic response is evaluated by the modified definition. |
| [34] | . 78 We introduce a new adaptive dynamic vibration absorber (DVA) design. 78 The DVA consists of a string under variable tension with a central mass attachment. 78 A negative stiffness mechanism is utilized to minimize tuning actuator effort. 78 Analytically, numerically and experimentally obtained frequency responses match. 78 Experimental results show that the DVA can adapt to varying excitation conditions. |
| [35] | . 提出了一种含有负刚度弹簧元件的新型动力吸振器模型,对该模型的最优参数进行了详细研究. 通过拉氏变换得到了系统的解析解,发现该系统存在着两个固定点,利用固定点理论得到了动力吸振器的最优阻尼比和最优频率比. 进一步研究发现接地刚度取负值时能够得到更好的减振效果,根据负刚度的特性得到了在保证系统稳定情况下的最优负刚度比. 通过数值解与解析解的对比证明了解析解的正确性. 通过与两种已有的典型动力吸振器模型在简谐激励和随机激励情况下的对比,说明了负刚度模型在主系统减振方面具有很大的优势,减振效果远优于两种已有动力吸振器模型,从而为设计新型动力吸振器模型提出了理论上的依据. . 提出了一种含有负刚度弹簧元件的新型动力吸振器模型,对该模型的最优参数进行了详细研究. 通过拉氏变换得到了系统的解析解,发现该系统存在着两个固定点,利用固定点理论得到了动力吸振器的最优阻尼比和最优频率比. 进一步研究发现接地刚度取负值时能够得到更好的减振效果,根据负刚度的特性得到了在保证系统稳定情况下的最优负刚度比. 通过数值解与解析解的对比证明了解析解的正确性. 通过与两种已有的典型动力吸振器模型在简谐激励和随机激励情况下的对比,说明了负刚度模型在主系统减振方面具有很大的优势,减振效果远优于两种已有动力吸振器模型,从而为设计新型动力吸振器模型提出了理论上的依据. |
| [36] | . 提出了一种含有负刚度弹簧元件的三要素型动力吸振器模型，对该模型最优参数进行了研究。首先，建立了系统的运动微分方程，得到了系统的解析解，发现该系统存在着3个固定点。利用固定点理论将3个固定点调到同一高度得到了动力吸振器的最优调谐比和最优刚度比设计公式，根据负刚度的特性得到了在保证系统稳定情况下的最优负刚度比，通过最小化幅频曲线的最大值得到了系统最优阻尼比设计公式。最后，通过数值解与解析解的对比说明了解析解的正确性。并通过与3种典型动力吸振器模型在简谐激励和随机激励情况下的对比，说明了此模型在主系统减振方面具有很大的优势，减振效果远优于3种已有动力吸振器模型，为设计新型动力吸振器模型提出了理论上的参考。 . 提出了一种含有负刚度弹簧元件的三要素型动力吸振器模型，对该模型最优参数进行了研究。首先，建立了系统的运动微分方程，得到了系统的解析解，发现该系统存在着3个固定点。利用固定点理论将3个固定点调到同一高度得到了动力吸振器的最优调谐比和最优刚度比设计公式，根据负刚度的特性得到了在保证系统稳定情况下的最优负刚度比，通过最小化幅频曲线的最大值得到了系统最优阻尼比设计公式。最后，通过数值解与解析解的对比说明了解析解的正确性。并通过与3种典型动力吸振器模型在简谐激励和随机激励情况下的对比，说明了此模型在主系统减振方面具有很大的优势，减振效果远优于3种已有动力吸振器模型，为设计新型动力吸振器模型提出了理论上的参考。 |
| [37] | . 准零刚度隔振器可以通过正负刚度并联来实现.研究了一种由三弹簧系统并联而成的准零刚度隔振器在简谐力激励下的动力学特性,并引入线性位移时滞控制策略.通过平均法分析得到系统在简谐力激励下的响应特性,并利用一阶李亚普洛夫近似稳定理论和劳斯-赫尔维茨准则分析了受控系统的稳定性和跳跃现象以及Hopf分叉现象.研究结果表明,时滞控制可以有效地改善准零刚度系统的稳定性,并且能够抑制系统跳跃现象的发生;通过选择合适的控制参数,可以避免系统发生Hopf分叉现象. . 准零刚度隔振器可以通过正负刚度并联来实现.研究了一种由三弹簧系统并联而成的准零刚度隔振器在简谐力激励下的动力学特性,并引入线性位移时滞控制策略.通过平均法分析得到系统在简谐力激励下的响应特性,并利用一阶李亚普洛夫近似稳定理论和劳斯-赫尔维茨准则分析了受控系统的稳定性和跳跃现象以及Hopf分叉现象.研究结果表明,时滞控制可以有效地改善准零刚度系统的稳定性,并且能够抑制系统跳跃现象的发生;通过选择合适的控制参数,可以避免系统发生Hopf分叉现象. |
| [38] | . 为有效抑制航天设备中由干扰源诱发的低频/超低频振动,提出了一种新型可调动力吸振器(NDVA)。该动力吸振器主要由柔性螺旋弹簧(SFS)及磁性负刚度弹簧(MNSS)组成。将所设计动力吸振器应用于振动控制时,采用平均法推导出系统在简谐激励下的稳态频响方程组及稳定性判据。基于稳定性分析,提出一种优化方法,通过简单迭代获得吸振器最优参数。最后,对提出吸振器的鲁棒稳定性进行分析。结果表明,除可实现低频振动有效抑制外,提出吸振器优越的鲁棒稳定性使得其在实际应用中能取得比线性吸振器更佳的振动控制效果。 . 为有效抑制航天设备中由干扰源诱发的低频/超低频振动,提出了一种新型可调动力吸振器(NDVA)。该动力吸振器主要由柔性螺旋弹簧(SFS)及磁性负刚度弹簧(MNSS)组成。将所设计动力吸振器应用于振动控制时,采用平均法推导出系统在简谐激励下的稳态频响方程组及稳定性判据。基于稳定性分析,提出一种优化方法,通过简单迭代获得吸振器最优参数。最后,对提出吸振器的鲁棒稳定性进行分析。结果表明,除可实现低频振动有效抑制外,提出吸振器优越的鲁棒稳定性使得其在实际应用中能取得比线性吸振器更佳的振动控制效果。 |
| [39] | . <p>分段光滑隔振系统是一类具备分段刚度或阻尼的非线性动力学系统,在振动控制领域中具有广泛代表性,诸如限位隔振系统、分级汽车悬挂等. 分段光滑的刚度或阻尼特性能够实现隔振系统的特定动力学性能及提升隔振性能,如抑制共振响应、提升共振区隔振性能等,但是亦会给隔振系统的动力学行为带来诸多不利影响. 以分段双线性分段光滑隔振系统为理论模型,系统研究了摒除不利于隔振的非线性动力学现象设计方法,包括幅值跳跃、周期运动的倍周期分岔等. 首先,利用平均法与奇异性理论给出了主共振频响曲线拓扑特征的完整拼图. 研究结果表明,参数空间分为4 个区域,其中2 个区域存在幅值跳跃,而其产生跳跃原因分别由鞍结分岔与擦边分岔所导致;基于此提出避免主共振跳跃的设计方法. 其次,建立了隔振有效区内周期运动的庞加莱映射,通过特征值分析给出了避免倍周期分岔发生的条件,证实增大阻尼可以抑制倍周期分岔的发生. 最后通过数值仿真分析了噪声对多稳态运动的影响. 研究结果发现在噪声影响下,分段光滑隔振系统的响应会在不同稳态间跃迁,非常不利于隔振. 因此,在完成跳跃与倍周期分岔的防治设计后,应采用数值仿真校验系统是否存在多稳态运动.</p> . <p>分段光滑隔振系统是一类具备分段刚度或阻尼的非线性动力学系统,在振动控制领域中具有广泛代表性,诸如限位隔振系统、分级汽车悬挂等. 分段光滑的刚度或阻尼特性能够实现隔振系统的特定动力学性能及提升隔振性能,如抑制共振响应、提升共振区隔振性能等,但是亦会给隔振系统的动力学行为带来诸多不利影响. 以分段双线性分段光滑隔振系统为理论模型,系统研究了摒除不利于隔振的非线性动力学现象设计方法,包括幅值跳跃、周期运动的倍周期分岔等. 首先,利用平均法与奇异性理论给出了主共振频响曲线拓扑特征的完整拼图. 研究结果表明,参数空间分为4 个区域,其中2 个区域存在幅值跳跃,而其产生跳跃原因分别由鞍结分岔与擦边分岔所导致;基于此提出避免主共振跳跃的设计方法. 其次,建立了隔振有效区内周期运动的庞加莱映射,通过特征值分析给出了避免倍周期分岔发生的条件,证实增大阻尼可以抑制倍周期分岔的发生. 最后通过数值仿真分析了噪声对多稳态运动的影响. 研究结果发现在噪声影响下,分段光滑隔振系统的响应会在不同稳态间跃迁,非常不利于隔振. 因此,在完成跳跃与倍周期分岔的防治设计后,应采用数值仿真校验系统是否存在多稳态运动.</p> |
| [40] | . 随着对自然界客观规律的深入认识，工程系统设计的精细化和复杂性要求也与日剧增。在许多耦合的动态系统设计过程中要考虑由耦合过程的时滞所引发的动力学行为，该时滞来自于与传感系统、作动系统和控制系统耦合的过程。耦合时滞也广泛存在于交通、系统生物学、电子通讯、神经和信息网络等技术中。本文首先从耦合时滞出发，在以时滞为中心的耦合系统复杂动力学机制、时滞镇定耦合系统的实验基础和实现、快慢变时滞耦合系统动力学和时滞神经网络同步和去同步4个方面，对耦合时滞诱发的动力学研究进展进行综述。着重介绍了时滞耦合系统中耦合时滞诱发的高余维分岔奇异性及新的定量分析方法、中立型时滞微分方程的规范型计算、具有耦合时滞的非线性系统中耦合时滞和非线性参数的辨识方法与实验实现、快慢变时滞耦合系统的张弛振荡、耦合时滞诱发的网络系统的同步模式切换等问题的研究进展；然后在应用方面重点介绍了车床磨削加工过程中耦合时滞诱发的颤振及其机理、具有惯性项和耦合时滞的神经网络系统中耦合时滞诱发的高余维分岔和复杂动力学、时滞动力吸振器与隔振装置的设计与实验实现。最后，从耦合时滞系统的一般性理论和工程应用两个方面展望了近期值得关注的一些问题。 . 随着对自然界客观规律的深入认识，工程系统设计的精细化和复杂性要求也与日剧增。在许多耦合的动态系统设计过程中要考虑由耦合过程的时滞所引发的动力学行为，该时滞来自于与传感系统、作动系统和控制系统耦合的过程。耦合时滞也广泛存在于交通、系统生物学、电子通讯、神经和信息网络等技术中。本文首先从耦合时滞出发，在以时滞为中心的耦合系统复杂动力学机制、时滞镇定耦合系统的实验基础和实现、快慢变时滞耦合系统动力学和时滞神经网络同步和去同步4个方面，对耦合时滞诱发的动力学研究进展进行综述。着重介绍了时滞耦合系统中耦合时滞诱发的高余维分岔奇异性及新的定量分析方法、中立型时滞微分方程的规范型计算、具有耦合时滞的非线性系统中耦合时滞和非线性参数的辨识方法与实验实现、快慢变时滞耦合系统的张弛振荡、耦合时滞诱发的网络系统的同步模式切换等问题的研究进展；然后在应用方面重点介绍了车床磨削加工过程中耦合时滞诱发的颤振及其机理、具有惯性项和耦合时滞的神经网络系统中耦合时滞诱发的高余维分岔和复杂动力学、时滞动力吸振器与隔振装置的设计与实验实现。最后，从耦合时滞系统的一般性理论和工程应用两个方面展望了近期值得关注的一些问题。 |
| [41] | . 随着航天重大工程的逐步实施,航天器正朝着超高速、超大尺度、多功能的方向发展,其面临的发射和运行环境也更加恶劣.航天器发射过程中的振动及其主/被动控制、在轨运行中大型柔性航天器动力学建模与动态响应分析、结构振动与飞行器姿态的混合控制等问题越来越复杂且难于处理;航天器结构的大型化和柔性化(如大阵面天线和太阳翼等)也对其地面试验和半实物仿真提出了挑战.本文着重介绍大型柔性航天器涉及到的动力学与振动控制问题,包括航天器发射过程中的整星隔振,大型柔性结构动力学建模与振动响应分析,大型柔性航天器的结构振动与姿轨控耦合动力学及其混合控制等.提炼出航天动力学与控制领域中亟待解决的若干基础科学问题,包括:多刚柔体系统动力学建模与模型降阶(涉及大变形柔性体动力学建模、多求解器合作仿真、模型降阶、组合结构动力学建模的解析方法等);复杂结构状态空间模型构建方法与能控性(涉及状态空间模型构建的理论与实验方法、复杂结构振动控制系统的能观性与能控性等);航天器姿态运动与大型柔性结构振动的混合控制律设计(涉及姿态机动与结构振动的鲁棒混合控制、执行机构与压电控制器的协同控制等). . 随着航天重大工程的逐步实施,航天器正朝着超高速、超大尺度、多功能的方向发展,其面临的发射和运行环境也更加恶劣.航天器发射过程中的振动及其主/被动控制、在轨运行中大型柔性航天器动力学建模与动态响应分析、结构振动与飞行器姿态的混合控制等问题越来越复杂且难于处理;航天器结构的大型化和柔性化(如大阵面天线和太阳翼等)也对其地面试验和半实物仿真提出了挑战.本文着重介绍大型柔性航天器涉及到的动力学与振动控制问题,包括航天器发射过程中的整星隔振,大型柔性结构动力学建模与振动响应分析,大型柔性航天器的结构振动与姿轨控耦合动力学及其混合控制等.提炼出航天动力学与控制领域中亟待解决的若干基础科学问题,包括:多刚柔体系统动力学建模与模型降阶(涉及大变形柔性体动力学建模、多求解器合作仿真、模型降阶、组合结构动力学建模的解析方法等);复杂结构状态空间模型构建方法与能控性(涉及状态空间模型构建的理论与实验方法、复杂结构振动控制系统的能观性与能控性等);航天器姿态运动与大型柔性结构振动的混合控制律设计(涉及姿态机动与结构振动的鲁棒混合控制、执行机构与压电控制器的协同控制等). |
| [42] | . 工程中航空航天、船舶与海洋结构物及其上装备和精密仪器易受极端环境干扰和破坏,使得非线性隔振理论在近十年来迅猛发展;针对日益严峻的隔振和抗冲击等要求,工程师和科学家们已发展出各种不同的非线性隔振系统,包括主动、半主动、被动和复合隔振.利用非线性改善的被动隔振兼具传统被动隔振的鲁棒性和主动隔振的高效性成为振动控制领域的先进技术.本文主要综述了非线性隔振理论和应用的近十年进展,包括非线性隔振设计、建模、分析、仿真和实验.在隔振系统的构建中,既考虑了刚度非线性又考虑了阻尼非线性;动力学响应的研究中,既有确定性分析又有随机分析.首先提出了适用于非线性隔振系统改进的评价方式;其次综述了高静态低动态刚度隔振及其加强形式非线性阻尼加强和双层非线性隔振,混沌反控制技术、内共振影响、非线性能量阱应用等振动机制利用型隔振和非线性隔振功能材料.最后,对非线性隔振研究发展的热点和关键性问题进行了分析和展望. . 工程中航空航天、船舶与海洋结构物及其上装备和精密仪器易受极端环境干扰和破坏,使得非线性隔振理论在近十年来迅猛发展;针对日益严峻的隔振和抗冲击等要求,工程师和科学家们已发展出各种不同的非线性隔振系统,包括主动、半主动、被动和复合隔振.利用非线性改善的被动隔振兼具传统被动隔振的鲁棒性和主动隔振的高效性成为振动控制领域的先进技术.本文主要综述了非线性隔振理论和应用的近十年进展,包括非线性隔振设计、建模、分析、仿真和实验.在隔振系统的构建中,既考虑了刚度非线性又考虑了阻尼非线性;动力学响应的研究中,既有确定性分析又有随机分析.首先提出了适用于非线性隔振系统改进的评价方式;其次综述了高静态低动态刚度隔振及其加强形式非线性阻尼加强和双层非线性隔振,混沌反控制技术、内共振影响、非线性能量阱应用等振动机制利用型隔振和非线性隔振功能材料.最后,对非线性隔振研究发展的热点和关键性问题进行了分析和展望. |
| [43] | . 根据建立的LT-TMD结构系统的动力放大系数解析式,讨论了LT-TMD的动力特性(包括冲程).数值结果表明,LT-TMD和传统的TMD具有相等的控制有效性和冲程.然而,LT-TMD比传统的TMD具有更大的最优调谐频率比和更小的最优阻尼比.LT-TMD的关键优点是,通过移动支撑的位置,可以限制弹簧的静力和动力伸长而保持其控制有效性和冲程不变. . 根据建立的LT-TMD结构系统的动力放大系数解析式,讨论了LT-TMD的动力特性(包括冲程).数值结果表明,LT-TMD和传统的TMD具有相等的控制有效性和冲程.然而,LT-TMD比传统的TMD具有更大的最优调谐频率比和更小的最优阻尼比.LT-TMD的关键优点是,通过移动支撑的位置,可以限制弹簧的静力和动力伸长而保持其控制有效性和冲程不变. |
| [44] | |
| [45] | . 为解决理想天棚阻尼要求阻尼元件与惯性参考系相连的技术问题，利用“惯容-弹簧-质量”系统的反共振现象，提出一种理想天棚阻尼的被动实现方法．将这种方法应用于车辆悬架，建立悬架的半车模型，分析悬架系统的频响特性，从理论上检验理想天棚阻尼被动实现方法的正确性与有效性．结果表明，被动天棚阻尼悬架改善了车辆的低频频响特性，有效抑制了车身垂直和俯仰振动，提高了车辆的乘坐舒适性，实现了理想天棚阻尼悬架的主要功能． . 为解决理想天棚阻尼要求阻尼元件与惯性参考系相连的技术问题，利用“惯容-弹簧-质量”系统的反共振现象，提出一种理想天棚阻尼的被动实现方法．将这种方法应用于车辆悬架，建立悬架的半车模型，分析悬架系统的频响特性，从理论上检验理想天棚阻尼被动实现方法的正确性与有效性．结果表明，被动天棚阻尼悬架改善了车辆的低频频响特性，有效抑制了车身垂直和俯仰振动，提高了车辆的乘坐舒适性，实现了理想天棚阻尼悬架的主要功能． |
| [46] | . 抑制低频振动是当前振动领域的一个热点问题,将惯容器与液压蓄能器结合在一起,同时利用形状记忆合金弹簧的超弹性,设计了一种将惯容器和拟零刚度隔振结合的复合式超低频隔振器。说明了超低频隔振的原理,分析了隔振器的力传递比,研究了惯容器惯容值以及弹簧刚度对系统谐振频率的影响。计算结果表明,所设计的超低频隔振器的谐振频率可以降低至1 Hz以内。 . 抑制低频振动是当前振动领域的一个热点问题,将惯容器与液压蓄能器结合在一起,同时利用形状记忆合金弹簧的超弹性,设计了一种将惯容器和拟零刚度隔振结合的复合式超低频隔振器。说明了超低频隔振的原理,分析了隔振器的力传递比,研究了惯容器惯容值以及弹簧刚度对系统谐振频率的影响。计算结果表明,所设计的超低频隔振器的谐振频率可以降低至1 Hz以内。 |
