,2), 徐元迪, 逄燕, 任彦霖, 高山山, 钟希祥北京工业大学先进制造技术北京市重点实验室,北京 100124STUDY OF PROCESS CONTROL ON PIEZOELECTRIC DROP-ON-DEMAND EJECTION 1)
Liu Zhaomiao,2), Xu Yuandi, Pang Yan, Ren Yanlin, Gao Shanshan, Zhong XixiangBeijing Key Laboratory of Advanced Manufacturing Technology,Beijing University of Technology,Beijing 100124, China通讯作者: 2) 刘赵淼,教授,主要研究方向：微尺度流体力学、血流动力学、流固耦合理论及工程应用.E-mail:lzm@bjut.edu.cn
收稿日期:2019-01-29接受日期:2019-04-13网络出版日期:2019-07-18
| 基金资助: |
Received:2019-01-29Accepted:2019-04-13Online:2019-07-18
作者简介 About authors
摘要
微滴喷射增材制造技术中沉积微滴的大小与均匀性是影响成型件质量的关键因素.本文设计了一种用于生成均匀微滴的压电驱动式微滴喷射装置,通过压电材料带动柔性膜片振动,将液体从喷嘴中喷出生成微滴,采用数值模拟和实验相结合的方法,研究了不同控制参数下膜片振幅及其对生成微滴尺寸和均匀性的影响.研究结果表明：膜片振幅大小受到驱动电压和压电频率的共同影响,压电频率是导致膜片中心点振幅实验测量值小于理论计算值的主要原因,膜片振动会导致喷嘴内部压力发生变化从而影响微滴生成尺寸.在相同驱动电压条件下,压电频率为10 Hz时存在压电膜片振幅最大值.随着膜片振幅的增大,喷孔处液体速度和液柱长度增大到临界值时可以生成微滴,当喷孔处的液柱长度超过临界值时,会形成卫星液滴. 当膜片振幅区间在30 $\mu$m$\sim $42 $\mu $m可以稳定生成微滴,生成最小微滴尺寸为339.8$\mu$m,直径最大变化率为0.29%,相邻两微滴间距最大变化率为2.67%,生成微滴的尺寸及均匀性较好.研究结果有助于提高压电式微滴喷射装置的液滴生成质量.
关键词：
Abstract
The size and uniformity of micro-droplets are key factors influencing the quality of the molded part by micro-droplet ejecting additive manufacturing technology. In this paper, a piezo-actuated micro-droplet ejection device for generating uniform micro-droplets is studied. The piezoelectric material drives the flexible diaphragm to vibrate and pushes the liquid out of the nozzle and produces micro-droplets. The amplitude of the diaphragm under different control parameters and its influence on the size and uniformity of the generated micro-droplets are investigated by numerical simulation and experiment. The results indicate that the amplitude of the diaphragm is affected by the driving voltage and the piezoelectric frequency and the experimental value of the diaphragm's center point amplitude is less than that of the theoretical calculation value which is mainly influenced by the piezoelectric frequency. The amplitude of the diaphragm will change the pressure inside the nozzle, which leads to the varied sizes of the micro-droplet. When the driving voltage is constant, the diaphragm has the maximum amplitude for the piezoelectric frequency at 10 Hz. As the amplitude of the diaphragm increases, droplets can be generated when the liquid velocity at the orifice and the length of the liquid column increase to a critical value. As the amplitude of the diaphragm continues to increase and the length of the liquid column at the orifice is beyond to a critical value, a satellite micro-droplet is formed. When the amplitude range of the membrane is between 30 $\mu $m and 42 $\mu $m, micro-droplets can be stably formed whose uniformity and size meet the demand well, and the minimum generating micro-droplets size is 339.8 $\mu $m. The maximum change rate of droplet diameter and adjacent two droplets are 0.29% and 2.67% respectively. Results are benefit to promote the uniformity of micro-droplets and will provide a reference for the development of piezoelectric droplet ejection devices.
Keywords：
PDF (12321KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
刘赵淼, 徐元迪, 逄燕, 任彦霖, 高山山, 钟希祥. 压电式微滴按需喷射的过程控制和规律 1). 力学学报[J], 2019, 51(4): 1031-1042 DOI:10.6052/0459-1879-19-035
Liu Zhaomiao, Xu Yuandi, Pang Yan, Ren Yanlin, Gao Shanshan, Zhong Xixiang.
微滴喷射增材制造技术(freeform fabrication with micro-dropletjetting)是一种利用计算机辅助设计(computer aideddesign)并结合驱动控制系统的非接触式增材制造技术,通过驱动控制按需生成尺寸均匀的微米级微滴,并依据零件形状特点直接打印出满足使用要求的功能性零件[1-4],具有工艺流程简单、生产成本低和成形速度快等优势,在微机械和微器件制造、生物组织工程3D打印、微透镜阵列模具制造等领域具有广阔的发展前景[5-12].
目前,微滴按需喷射驱动装置主要采用压电式、气压式和机械式[13-18].压电驱动式微滴按需喷射装置主要通过压电晶片振动带动金属膜片产生形变,挤压喷嘴实现材料的喷射.因其结构简单且工作稳定性好,得到了较为广泛的研究.魏大忠等[19]分析了腔体内部流体运动状态,发现喷腔内流体体积的变化是由压电片振动引起的.Sadeghian等[20]对膜片振动导致喷腔体积扩张和压缩时间对液滴喷射过程的影响进行了研究,认为压缩时间与抽吸时间比值的增加会导致生成微滴尺寸增大.Fan等[21]得到了压电脉冲宽度的下限值和上限值之间液滴稳定喷射的驱动参数控制范围.除了电压、脉宽等影响因素外,压电信号的波形同样会对微滴喷射过程产生影响,Wang等[22]研究发现驱动波形的变化会改变喷出液体的体积.
除了实验研究外,数值仿真同样是研究微滴喷射过程的有效手段.Wu等[23]建立了驱动电压与喷嘴入口压力之间的关系,并对仿真系统施加压力,得到了入口压力对微滴喷射过程的影响规律.Luo等[24]分析了不同喷嘴直径对生成微滴尺寸的影响,当喷嘴直径减小到100$\mu$m时,生成微滴尺寸与喷嘴直径的比率迅速增加,通过施加高频扰动加速射流破碎,可以进一步降低生成微滴尺寸. Zhong等[25]基于流体体积方法分析了供给压力对微滴喷射过程的影响,发现随着供给压力的增大,液滴喷射速度和极限长度增大,可以产生单液滴.于永泽等[26]使用参数渐进法Phan-Thien-Tanner(PTT)分析了黏度与压力对微滴喷射过程的影响,当供给压力恒定时,凝胶材料的挤出胀大率随着黏度的增大而减小;黏度恒定时,凝胶材料的挤出胀大率随着供给压力的上升而增大.郑大龙等[27]利用限点集法(FPM)对微滴喷射过程进行分析,发现驱动频率越大生成微滴尺寸越小,液体黏度越大生成的微滴尺寸越小,但是随着液体黏度增大喷射更加困难.
现有研究多集中在压电信号和喷嘴内压力对液滴喷射过程的影响,忽略了驱动电压和压电频率等控制参数的改变会使膜片振幅发生变化、进而引起喷嘴体积及喷嘴内部压力发生变化,并影响生成微滴的尺寸及均匀性.因此,在研究控制参数对微滴喷射过程的影响时,需要考虑膜片振幅的变化以及不同振幅所对应的喷腔内部压力变化.本文采用数值模拟与实验相结合的方法研究压电驱动式微滴按需喷射过程中膜片振幅和喷嘴内部压力变化对微滴喷射过程的影响规律,分析不同控制参数下膜片的振幅及其对生成微滴尺寸、液柱伸长长度和卫星液滴数量的影响.研究结果有助于提高压电式液滴喷射装置的微滴生成质量,为促进微滴喷射增材制造技术的发展提供技术参考.
1 压电式喷头结构模型及实验系统
1.1 压电式喷头结构模型
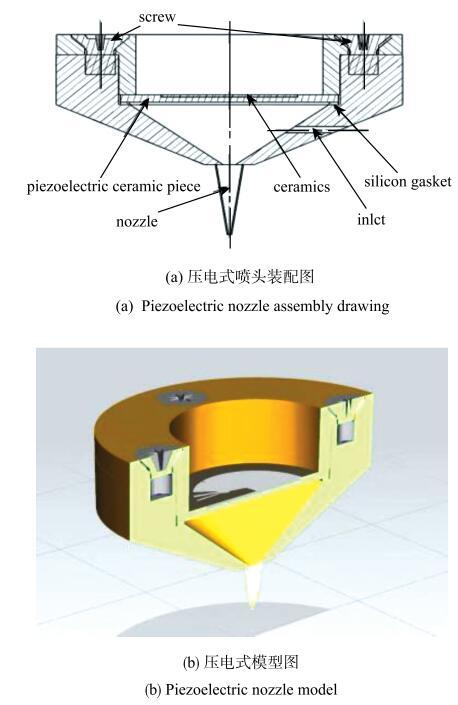
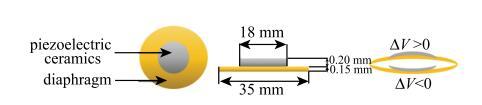
本文在Fan等[21]研究的基础上对压电式喷头进行了改进.改进后的压电式喷头主要由五个部分组成：上端盖,压电片,密封垫圈,喷腔,喷嘴,如图1所示.其中压电片是由一层厚度0.20 mm、直径18 mm的压电陶瓷以及一个厚度0.15mm、直径35 mm的薄铜膜片构成,如图2所示.压电片放置在上端盖与喷腔之间,使用螺栓连接并用硅胶垫圈密封.将喷腔改进为锥形结构,有助于减小喷腔体积并避免内部液体在进入喷嘴前产生旋涡区.将喷头改进为内径200 $\mu$m的移液枪的枪头,可以减小液体因界面突然缩小而产生的局部能量损失[28].图1
新窗口打开|下载原图ZIP|生成PPT图1压电式喷头
Fig. 1Sketch of Piezoelectric nozzle
图2
新窗口打开|下载原图ZIP|生成PPT图2压电片结构示意图
Fig. 2Sketch of piezoelectric structure
1.2 实验系统
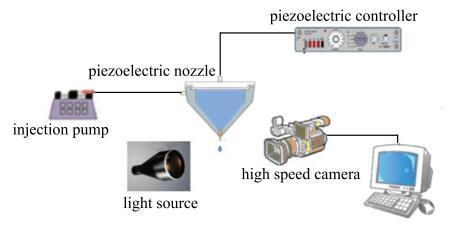
本文使用数字型双极性压电陶瓷驱动控制器(RH34-DS)控制输入的驱动电压和压电频率,使用流量泵(Pump11 Elite, Harvard Apparatus)和5 mL玻璃注射器(HarvardApparatus)组成流量供给系统为压电式喷头提供稳定流量,并通过CCD高速摄像机(HiSenseMKII, Dantec Dynamics)记录微滴喷射过程. 实验系统如图3所示.图3
新窗口打开|下载原图ZIP|生成PPT图3微滴按需喷射系统
Fig. 3Droplet-on-demand ejection system
实验选取的驱动电压范围为10~200 V,压电频率范围为1~150Hz. 供给流量为1000 $\mu $L/min.记录微滴喷射过程时CCD高速摄像机快门时间为1/3000 s,帧率为1000 幅每秒,分辨率为640$\times$480像素.
1.3 数值模拟方法
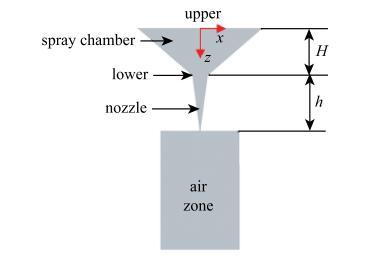
按照喷嘴的实际尺寸建立了二维简化模型,为了确保能够模拟生成微滴的下落过程,喷嘴下方的空气区域应该足够长,使生成的液滴在表面张力的作用下形成圆球状[29-30].仿真模型如图4所示,模型尺寸参数如表1所示.图4
新窗口打开|下载原图ZIP|生成PPT图4喷嘴仿真模型
Fig. 4Nozzle simulation model
Table 1
表1
表1仿真模型尺寸(mm)
Table 1
 |
新窗口打开|下载CSV
微滴喷射仿真的控制方程是连续性方程和Navier-Stokes方程
$$\begin{align*} &\label{eq1} \frac{{d}}{{d}t}\int_{V} {\rho } {{d}V + }\frac{{d}}{{d}t}\int_{S} \rho (v \cdot n)\mbox{d}S = 0(1) \\ &\label{eq2} \frac{{d}}{{d}t}\int_{V} \rho v{{d}V + }\frac{{d}}{{d}t}\int_S {\rho v} (v \cdot n)\mbox{d}S =\\ &\qquad \oint_S {(F \cdot n)} \mbox{d}S + \int_{V} \rho {b}_\phi \mbox{d}V(2) \end{align*}$$
式中,${V}$为流体单元的体积,由带有法向指向外侧矢量$n$的封闭曲面${S}$确定; $v$为流体的流速;$\rho $为流体密度;${t}$为时间;${F}$为作用在${S}$面上的外加作用力;${b}_\phi $为标量函数$\phi $的源项.
喷嘴中流体流速较高且喷孔尺寸微小,可将喷嘴中的流体流动简化为细管道中的Hagen-Poiseuille流,此时满足连续方程,动量方程中的对流项为零,Navier-Stokes方程在$z$方向的运动可以简化 为[29] \begin{equation} \label{eq3} \frac{\mbox{d}\rho }{\mbox{d}z} = u\left[ {\frac{\mbox{1}}{r}\frac{\mbox{d}}{\mbox{d}r}\left( {r\frac{\mbox{d}w}{\mbox{d}r}} \right)} \right](3) \end{equation} 式中,$u$为流体的黏度,$r$为径向距离,$w$为$z$方向 速度.
根据喷嘴管壁的边界条件$v_r = \dfrac{{d}}{\mbox{2}} = 0$,可以得出喷嘴处流体喷射的体积流量 \begin{equation} \label{eq4} \mbox{q}_v = \int_0^{{d_1 }/{2}} {{2\pi }} wr\mbox{d}r = \frac{\pi d^4}{128\mu \Delta h}\Delta p(4) \end{equation} 式中,$\Delta h$为喷嘴孔深度,$\Delta p = p-p_1 $, 其中$p$为喷腔内压力,$p_1 $为喷孔外压力,压力值等于大气压.
对微滴按需喷射过程中做如下假设[30] (1)喷射材料为不可压缩牛顿流体; (2)流体特性稳定不随时间改变; (3)喷嘴和喷孔内壁面光滑,接触角恒定不变. 使用包含空气区域的二维模型进行数值模拟,如图4所示. 采用疏水边界条件,壁面与待喷射液体的接触角为130$^\circ$,壁面均为无滑移壁面,入口速度为0.025 m/s,出口压力为0 Pa. 液体腔内待喷射液体为去离子水(密度1.0 g/cm$^{3}$、黏度1.003 mPa$\cdot$s、表面张力0.073 N/m). 液体腔的上表面定义为可动边界用以表示膜片振动过程,膜片中心点振幅$z$随电压$U$的变化为 \begin{equation} \label{eq5} z = 0.309~3U(5) \end{equation}
方程(5)作为入口振动边界的输入函数,通过用户定义程序(UDF)加载到模型的入口边界上. 为了求出自由表面的形状和位置,跟踪微滴的生成过程,本文使用FLUENT 软件(Ansys Inc. USA),采用多相流中模型的流体体积模型对微滴按需喷射过程进行仿真.
为了验证数值模拟的准确性,不同网格量仿真结果如表2所示,三种网格划分情况下,最小网格尺寸分别为50 $\mu $m$\times $50 $\mu $m,25 $\mu $m$\times $25 $\mu $m,20 $\mu $m$\times $20 $\mu $m. 数值模拟与高速运动分析系统拍摄的微滴尺寸结果对比表明,相对误差$\dfrac{d_{{ n}}-d_{{e}} }{d_{{e}} }$均小于0.5%,证明本文采用的数值分析方法可以对微滴喷射过程进行准确的表征. 为了提高计算效率,采用第二种方案的网格尺寸25 $\mu $m$\times $25 $\mu $m对喷嘴进行划分.
Table 2
表2
表2网格独立性验证
Table 2
 |
新窗口打开|下载CSV
2 膜片振幅计算与实验验证
通过理论公式对膜片振幅进行计算,并使用红外线位移采集系统对计算结果进行了实验验证,得到了不同控制参数下膜片振幅的变化规律.
2.1 膜片振幅的理论推导
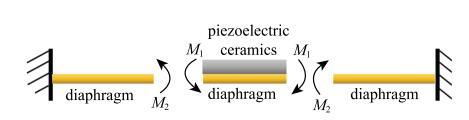
为了获得控制参数对膜片振幅影响的解析解,将压电片分为压电陶瓷与铜膜片和膜片剩余部分,其受力情况及应力应变分布情况如图5和图6所示.图5
新窗口打开|下载原图ZIP|生成PPT图5压电膜片受力图
Fig. 5Moment balance for piezoelectric diaphragm
图6
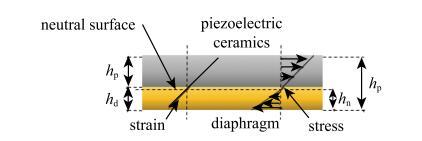新窗口打开|下载原图ZIP|生成PPT图6压电膜片应力应变分布图
Fig. 6Distribution of strain and stress in piezoelectric diaphragm
当膜片随压电陶瓷发生形变时,存在一个无应变和最小势能的中性面$h_{ n}$ \begin{equation} \label{eq6} h_{n} =\frac{ \frac{E_{d} h_{d} ^2}{1-\gamma _{d} ^2} + \frac{E_{p} \left( {H_{p} ^2-h_{d} ^2} \right)}{1-\gamma _{p} ^2}}{2\left( \frac{E_{d} h_{d} }{1-\gamma _{d} ^2} + \frac{E_{ p} h_{p} }{1-\gamma _{p} ^2}\right)}(6) \end{equation} 式中,$h_{n}$ 为中性面厚度,$h_{d}$ 为膜片厚度,$h_{ p}$ 为压电陶瓷厚度,$H_{p}$ 为压电片厚度,$E_{d}$ 为膜片杨氏模量,$E_{p}$ 为压电陶瓷杨氏模量,$\gamma_{d}$ 为膜片的泊松比,$\gamma_{p}$ 为压电陶瓷的泊松比.
力矩$M_1$ 可以根据压电陶瓷和膜片的平衡方程求出[31]
$$\begin{align*} &M_1 = \int_{-h_{n} }^{h_{d}-h_{n} } {\sigma _{ p} z{d}z} =\\ &\qquad \frac{E_{p} }{1-\gamma _{p} }Vd_{31} \frac{E_{d} }{1-\gamma _{d} }\left[ {h_{p} + 2\left( {h_{d}-h_{n} } \right)} \right]\big[ \left( {h_{d}-h_{n} } \right)^3 + \\ &\qquad h_{n} ^3 \big]\bigg/2\bigg\{ \frac{E_{d} }{1-\gamma _{d} }\left[ {h_{n} ^3 + \left( {h_{d}-h_{n} } \right)^3} \right] +\\ &\qquad \frac{E_{p} }{1-\gamma _{p} }\left[ {\left( {h_{d}-h_{n} + h_{p} } \right)^3-\left( {h_{d}-h_{n} } \right)^3} \right] \bigg\}(7) \end{align*}$$
式中,$\sigma _{p} $是膜片的应力,$V$是驱动电压,$d_{31} $是压电常数.
根据理论公式[32],求解得到膜片挠度以及压电陶瓷和膜片的复合板挠度解分别为
$$\begin{align*} & \label{eq8} W_1 \left( d \right) = \frac{ M_2 r^2\left( {-d^2 + 2R^2\lg \frac{r}{R} + R^2} \right)}{ \frac{E_{d} h_{n} ^3}{6\left( {1-\gamma _{d} ^2} \right)}\left[ {\left( {1-\gamma _{d} } \right)R^2 + \left( {1 + \gamma _{d} } \right)r^2} \right]},\;0 < d < r (8)\\ &\label{eq9} W_2 \left( d \right) =\\ &\qquad \frac{ M_2 r^2\left( {-d^2 + 2R^2\lg \frac{r}{R} + R^2} \right) + \frac{\dfrac{M_1 }{E'h_{n} ^3}}{6\left( {1-\gamma '^2} \right)}\left( {r^2-d^2} \right)}{ \frac{E_{d} h_{n} ^3}{6\left( {1-\gamma _{d} ^2} \right)}\left[ {\left( {1-\gamma _{d} } \right)R^2 + \left( {1 + \gamma _{d} } \right)r^2} \right]}\;,\\ &\qquad r \le d < R(9) \end{align*}$$
式中,$r$为压电陶瓷半径,$R$为膜片半径,$E'$为等效杨氏模量,$\gamma '$为等效泊松比.
由于材料的连续性,在$d=r$ 时,式(8)和式(9)具有相同的斜率. \begin{equation} \label{eq10} \frac{{d}W_1 }{d_{d} }\bigg|_{d = r} = \frac{{d}W_2 }{d_{d} }\bigg| _{d = r} (10) \end{equation}由此可以求得力矩$M_2$
$$\begin{align*} &\label{eq11} M_2 =-{M_1 \frac{E_{d} h_{n} ^3}{6\left( {1-\gamma _{d} ^2} \right)}\left[ {\left( {1-\gamma _{ d} } \right)R^2 + \left( {1 + \gamma _{d} } \right)r^2} \right]}\bigg/\\ &\qquad{\left[\frac{E'h_{n} ^3}{6\left( {1-\gamma '^2} \right)}\left( {1 + \gamma '} \right)\left( {R^2-r^2} \right)\right]}(11) \end{align*}$$
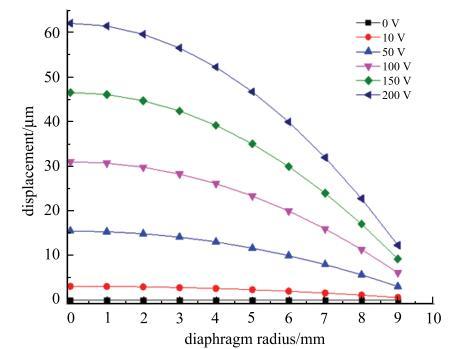
得到不同驱动电压下膜片振动幅度如图7所示. 在驱动电压一定时,膜片中心点振动幅度最大,振幅从中心点向外逐渐降低. 在驱动电压为10~200 V时,膜片中心点振幅依次为3.10 $\mu $m,15.50 $\mu $m,31.01 $\mu $m, 46.51 $\mu $m和62.02 $\mu $m.
图7
新窗口打开|下载原图ZIP|生成PPT图7不同驱动电压下的膜片振幅
Fig. 7Amplitude of diaphragm in different voltages
2.2 控制参数对膜片振幅的影响
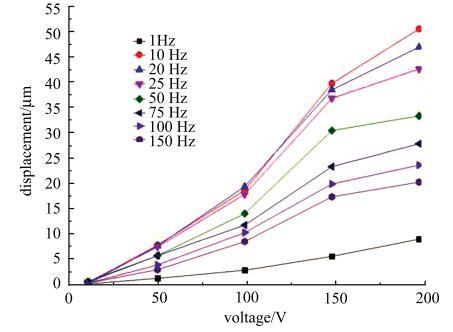
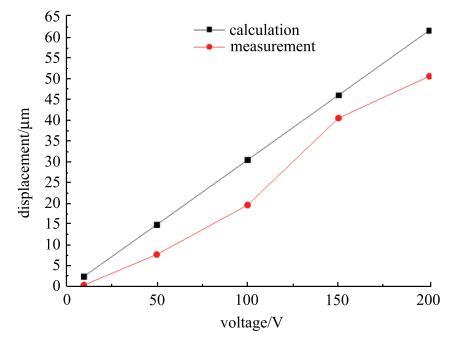
压电驱动式微滴按需喷射装置基于压电陶瓷的逆压电效应,其工作电压为控制微滴按需喷射过程的主要控制参数[33].通过红外线位移采集系统,对不同驱动电压下膜片中心点的振幅进行了测量,建立了驱动电压与膜片振幅之间的关系并与理论计算值进行对比,如图8和图9所示.由图8可知,当驱动电压为10 V,压电频率为 1$\sim $150 Hz时,膜片振幅变化幅度为0.48 $\mu $m,膜片振动幅度变化不明显;随着驱动电压的增大,在压电频率为1~150 Hz时,膜片振幅变化幅度由 50 V对应的6.63 $\mu $m依次增大至200 V对应的41.55 $\mu $m. 由图9可知,膜片中心点振幅理论计算值与驱动电压呈线性关系,其振幅随着驱动电压的增大而增大. 而实验测量值显示膜片振幅随着驱动电压的增大而增大,实验得到的振幅均小于理论计算值. 理论计算模型中没有考虑到压电频率对振幅的影响,会导致实验测量值低于理论计算值,因此有必要测试压电频率对膜片振幅的影响.
图8
新窗口打开|下载原图ZIP|生成PPT图8驱动电压与膜片振幅的关系
Fig. 8Relationship between voltage and diaphragm amplitude
图9
新窗口打开|下载原图ZIP|生成PPT图9膜片振幅理论值与测量值对比图
Fig. 9Comparison of theoretical and measured values of diaphragm amplitude
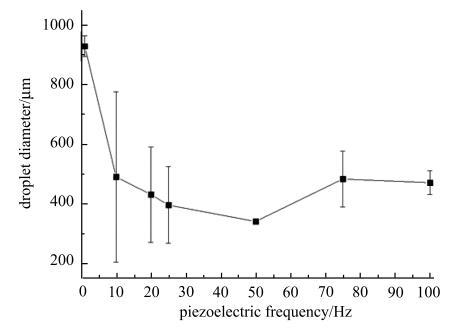
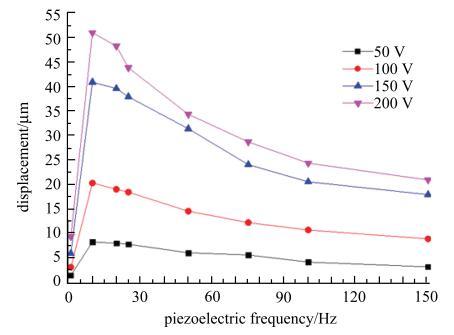
压电频率是指单位时间内压电陶瓷片由于逆压电效应实现机械振动与交流电的转换次数,在微滴喷射过程中压电频率同样会对微滴喷射效果产生一定影响. 通过红外线位移采集系统,对不同压电频率下膜片的振幅进行了测量,建立了微滴直径与压电频率之间的关系,如图10所示. 以及压电频率与膜片振幅之间的关系,如图11所示.
由图10所示,随着压电频率的增大,生成的微滴直径先减小后增大. 实验中压电频率由1 Hz增长到10 Hz时微滴直径下降速度最快,由926 $\mu $m下降至489 $\mu $m,但是生成微滴均匀性较差. 由图11可知随着压电频率的增大,膜片振幅先增大后减小,在压电频率为10 Hz时,膜片振幅达到峰值. 随着驱动电压的增大,压电频率对膜片振幅的影响效果更加明显,当压电频率为1 Hz时,驱动电压从50 V增大到200 V,膜片振幅由1.67 $\mu $m增大至9.55 $\mu $m,振幅变化幅度为7.88 $\mu $m,增大4.7倍;当压电频率为10 Hz时,驱动电压从10 V增大到200 V,膜片振幅峰值由对应的8.36 $\mu $m增大到51.05 $\mu $m, 振幅变化幅度42.69 $\mu $m,增大5.1倍;随着压电频率继续增大,在驱动电压为10 V$\sim $200 V时,膜片振幅变化幅度由25 Hz对应的35.91 $\mu $m,依次减小至150 Hz对应的17.68 $\mu $m. 由此可见,膜片振幅受驱动电压和压电频率的共同作用.
图10
新窗口打开|下载原图ZIP|生成PPT图10压电频率与微滴直径的关系
Fig. 10Relationship between piezoelectric frequency and droplet diameter
图11
新窗口打开|下载原图ZIP|生成PPT图11压电频率与膜片振幅的关系
Fig. 11Relationship between piezoelectric frequency and diaphragm amplitude
3 结果分析与讨论
3.1 微滴生成过程
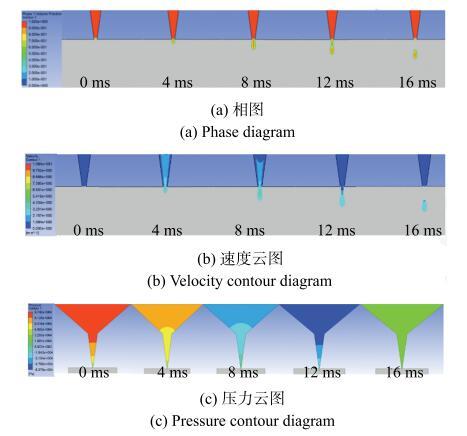
为研究压电驱动式微滴按需喷射中微滴的生成过程,以去离子水(密度1.0 g/cm$^{3}$、黏度1.003 cP、表面张力73 dyn/cm)为喷射材料,喷嘴直径$d_{1}$= 0.2 mm,接触角为130$^\circ$. 根据实验数据,将液体入口速度设置为0.025 m/s,取微滴生成初始为$t_{0}$时刻(令$t_{0}$=0),得到压电片振幅为35 $\mu $m时微滴喷射过程的液相图、速度云图和压力云图,如图12所示.图12
新窗口打开|下载原图ZIP|生成PPT图12微滴生成过程仿真
Fig. 12Simulation of micro-droplet generation process
模拟结果表明,微滴的生成过程主要经历液柱伸长、颈缩、断裂、微滴下落及剩余液柱回缩这四个阶段. 0 ms$\sim $8 ms为液柱伸长阶段,此时膜片先向下运动挤压喷腔,喷腔体积减小,内部压力增大至92 674 Pa,使液面向外凸出形成液柱并逐渐伸长,喷嘴口处液体运动速度从0.8 m/s迅速增大至3.05 m/s,之后膜片向上运动喷腔体积增大,内部压力逐渐减小,液柱在惯性力作用下继续伸长. 8 ms$\sim $12 ms进入颈缩阶段,膜片复位并继续向上运动,喷腔体积继续增大,内部压力逐渐减小为负值,液柱头部速度从3.05 m/s缓慢减小至2.95 m/s,喷嘴口处液柱的速度为0.6 m/s,液柱前后两部分出现速度极小值域. 随着液柱上下两部分速度差扩大,同时在惯性力和喷嘴口处黏性阻力的作用下,12 ms时液柱在速度场接近零的区间发生断裂. 12 ms$\sim $16 ms为微滴振荡下落及剩余液柱回缩阶段,此时喷腔内的负压力使喷嘴口处液体获得向上的速度,喷嘴口处剩余液柱回缩至喷嘴内部,同时膜片由最高点向下运动复位, 喷腔内部压力逐渐增加为正值,准备进行下一个喷射周期,已生成的微滴在下落一定距离后会在表面张力作用下逐渐稳定成为圆球状.
选择微滴喷射过程中的几个代表性位置,讨论振动幅值对微滴喷射过程的影响,如图13所示. 点a1~a3表示微滴,与喷嘴口的轴向距离分别为$x$(a1)~$x$(a3). 点a1表示液柱的前端,后来成为主液滴的头部. 点a2在液柱断裂时出现,表示主液滴的尾部. 均匀生成单颗微滴时a3代表剩余液柱的 尖端.
图13
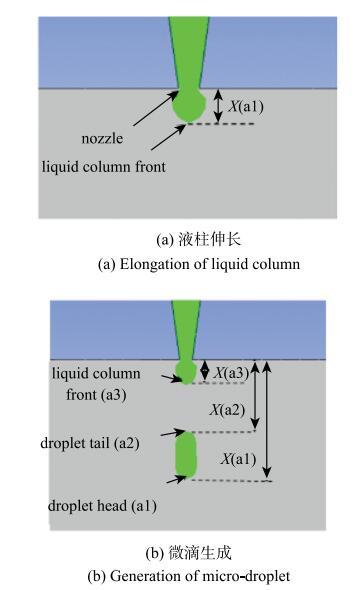新窗口打开|下载原图ZIP|生成PPT图13微滴生成过程中的代表点
Fig. 13Representative points in the process of micro-droplet generation
生成微滴轴向距离变化如图14所示,随着膜片振动,膜片中心点位移先增大后减小(如图14中虚线所示). 喷嘴内部压力随之增大,喷腔内液体被加速挤出喷嘴孔. 随着被挤出液体体积的增大,在喷嘴孔处形成一个前端为圆形的液柱,在膜片振幅达到最大值时液柱断裂,剩余液柱短暂停顿后回缩入喷嘴孔, 微滴头部和微滴尾部在极短时间内振动,然后达到近似相同的速度,此时微滴保持稳定下落 状态[25].
图14
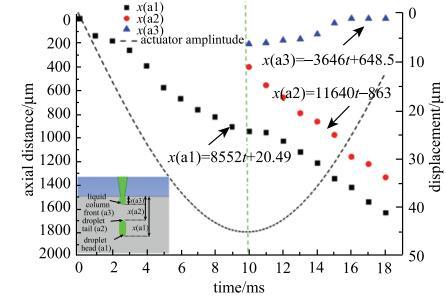新窗口打开|下载原图ZIP|生成PPT图14生成微滴轴向距离变化
Fig. 14Curve of the generated micro-droplet versus axial distance
3.2 膜片振幅对生成微滴尺寸的影响
通过调整控制参数得到不同膜片振动幅值对微滴生成尺寸的影响,如图15所示.图15
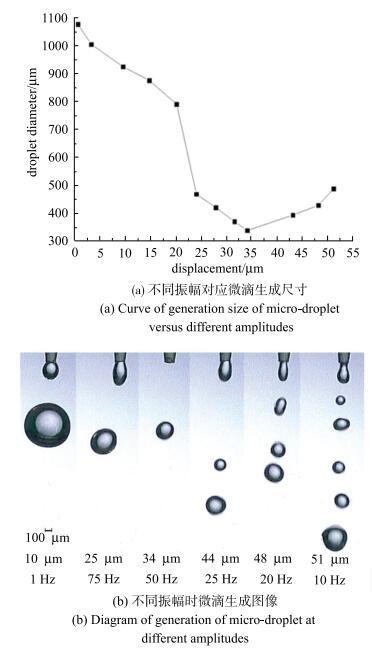新窗口打开|下载原图ZIP|生成PPT图15膜片振动幅值对生成微滴尺寸的影响
Fig. 15Effect of vibration amplitude on sizes of micro-droplets
通过研究膜片振幅对生成微滴尺寸的影响发现：当膜片振动幅值小于16 $\mu $m时,实验中可以观察到微滴生成时存在振荡现象,但是由于振幅太小不足以使液滴产生颈缩并断裂,此时微滴主要依靠重力去克服表面张力产生颈缩断裂,生成的微滴直径大于1 mm. 随着膜片振幅增大至16 $\mu $m$\sim $28 $\mu $m,实验中观察到微滴在喷嘴口处多次伸长后产生颈缩并断裂,此时膜片的振动幅度不足以一次将喷腔内的液体挤出,微滴在喷嘴口处反复伸长回缩导致微滴生成不稳定,微滴下落时会发生偏斜,此时生成的微滴直径在480 $\mu $m $\sim $910 $\mu $m之间. 当膜片振幅增大至29 $\mu $m$\sim $42 $\mu $m时,生成微滴尺寸较小且较稳定,微滴直径在339 $\mu $m $\sim $495 $\mu $m之间. 当膜片振幅超过42 $\mu $m时,生成的微滴会伴随一颗至多颗卫星液滴,主液滴直径在400 $\mu $m $\sim $500 $\mu $m之间,同时微滴在下落过程中还伴随着液滴间的融合现象,令液滴生成更加不稳定. 结果表明,存在微滴均匀稳定生成的振幅区间,通过控制膜片振动幅值可以实现微滴尺寸的按需喷射.
进一步研究膜片振幅对生成微滴尺寸的影响,定义膜片振幅为$z$,微滴直径系数为$k_{ d} = d / d_0 $,其中$d$为生成微滴直径,$d_0 = 200~{\mu m}$为喷嘴直径. 通过对图15(a)中振幅数据进行拟合,可以得到微滴均匀生成区间的微滴直径系数$k_{ d} $与膜片振幅$z$的关 系式 \begin{equation} \label{eq12} k_{d} = 0.006z^2-0.435z + 9.576,\quad {29 < z < 42} (12) \end{equation}
可以看出,在微滴稳定按需喷射的参数条件下,微滴直径系数随着膜片振幅的增大先减小后增大.
取微滴生成初始时刻为$t_{0}$(令$t_{0}$=0),得到在膜片振幅为34 $\mu $m时微滴喷射过程,如图16所示.
图16
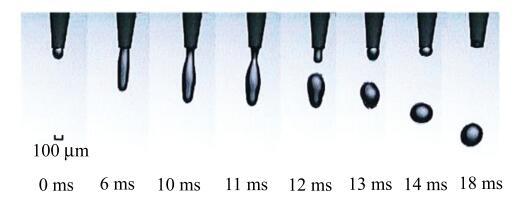新窗口打开|下载原图ZIP|生成PPT图16膜片振幅为34 $\mu $m时微滴生成过程
Fig. 16Generation process of micro-droplet at the diaphragm amplitude of 34 $\mu $m
通过实验结果得到的微滴生成过程与数值模拟结果比较吻合,微滴生成主要经历液柱伸长、液柱颈缩、液柱断裂、微滴下落及剩余液柱回缩这4个阶段. 其中0$\sim $8 ms为液柱伸长阶段,此阶段液柱的平均伸长长度为930 $\mu $m;8$\sim $11 ms为液柱颈缩阶段;11$\sim $12 ms为液柱断裂阶段;12$\sim $16 ms为微滴下落及剩余液柱回缩阶段. 对15组实验生成的微滴直径及微滴间距进行测量,结果如图17所示,微滴最大直径是340 $\mu $m,最小直径是339 $\mu $m,平均值为339.8 $\mu $m,所测量微滴的直径最大变化率为0.29%,相邻两微滴最大间距为3.05 mm,最小间距为2.92 mm,平均值为3.00 mm,所测得的间距最大变化率为2.67%,此时生成微滴的尺寸及均匀性 较好.
图17
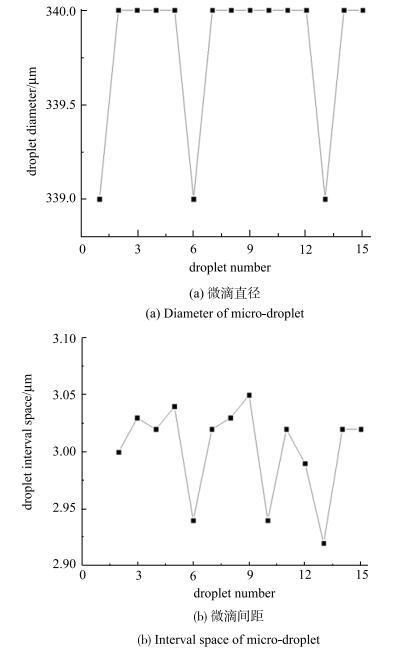新窗口打开|下载原图ZIP|生成PPT图17生成微滴尺寸与均匀性
Fig. 17Size and uniformity of the generated micro-droplet
3.3 膜片振幅对喷嘴内压力的影响
在微滴喷射过程中膜片振动产生形变,膜片由初始的平面圆形经历了向下凹陷、复位、向上凸起再复位四个变化过程[18]. 由式(4)可知,喷嘴内部压力$\Delta p$ 增加使流体速度$q_v$ 增大,液体更容易从喷口喷出并断裂形成微滴,在微滴喷射过程中膜片振动对喷腔的挤压作用导致喷腔体积发生变化,喷嘴内部压力发生显著变化并影响微滴生成. 取喷嘴中轴线上13个点(取点距膜片0.2 mm至喷嘴孔处,间距$L$=0.2 mm),得到微滴喷射过程中不同阶段喷嘴内部压力变化,如图18所示.图18
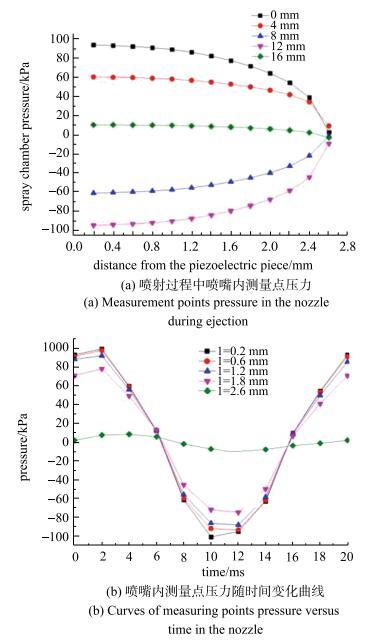新窗口打开|下载原图ZIP|生成PPT图18膜片振幅为34 $\mu $m时喷嘴内部压力变化
Fig. 18Pressure change inside the nozzle at the diaphragm amplitude of 34 $\mu $m
由图18可看出,在液柱伸长阶段(0 ms$\sim $8 ms)喷腔内部压力先小幅增大后减小,压力最大值为98 310.2 Pa,达到峰值后压力逐渐下降为负值. 在8 ms$\sim $12 ms喷腔内压力为负并存在最小值-100 196 Pa,在此阶段液柱发生颈缩并在12 ms时发生断裂,随着微滴下落喷腔内压力由负向正变化,准备下一次喷射. 微滴喷射过程中喷腔内部压力近似余弦变化,喷腔内压力变化由上到下变化幅度依次递减,喷嘴口处压力变化幅度最小.
当膜片振幅为35 $\mu $m,45 $\mu $m,55 $\mu $m时,不同时刻膜片中轴线下方$L$ = 0.2 mm位置处喷嘴内部压力随时间变化曲线,如图19所示.
图19
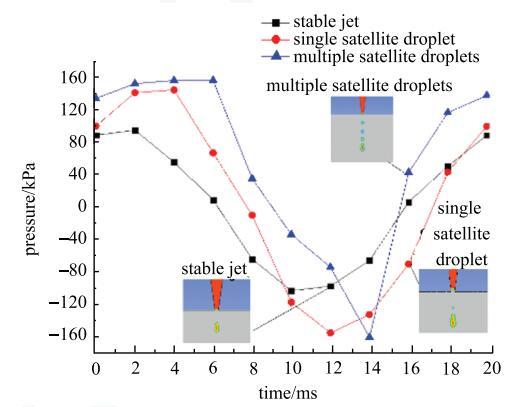新窗口打开|下载原图ZIP|生成PPT图19不同喷射状态时喷嘴内部压力变化
Fig. 19Pressure change inside the nozzle under different ejection conditions
膜片振幅为35 $\mu $m时,在2 ms时刻喷嘴内压力达到最大值,压力为99 915 Pa,在10 ms时刻喷嘴内压力出现最小值,压力为-100 196 Pa,此时稳定生成一滴微滴. 膜片振幅为45 $\mu $m时,在4 ms时刻喷嘴内压力达到最大值,压力为150 065 Pa,在12 ms时刻喷嘴内压力出现最小值,压力为-152 724 Pa,此时生成的微滴伴随一颗卫星液滴. 膜片振幅为55 $\mu $m时,在6 ms时刻喷嘴内压力达到最大值,压力为 161 877.6 Pa,在14 ms时刻喷嘴内压力出现最小值,压力为-158 288 Pa,此时生成的微滴伴随多颗卫星液滴. 随着膜片振动幅度增大,喷嘴内峰值压力增大,压力峰值出现时间随着膜片振幅增大向后 推移[34].
图20显示了三种膜片振幅下微滴的轮廓和轴向速度扰动. 在膜片振幅为35 $\mu $m和45 $\mu $m时,液柱在e1和e2位置发生颈缩,液柱的断裂位置和剩余液柱头部出现速度差异最大值. 在膜片振幅为55 $\mu $m时,喷嘴内压力进一步增大,液柱长度继续增大,在距离液柱末端较远的e3位置发生第一次颈缩. 三种膜片振幅情况下对应的液柱伸长长度分别为940 $\mu $m,952 $\mu $m和1040 $\mu $m. 结果表明,喷嘴内部压力随着振动幅度的增大而增大,同时液柱伸长长度增大. 当膜片振幅增大至55 $\mu $m时,生成的微滴直径显著增大.
图20
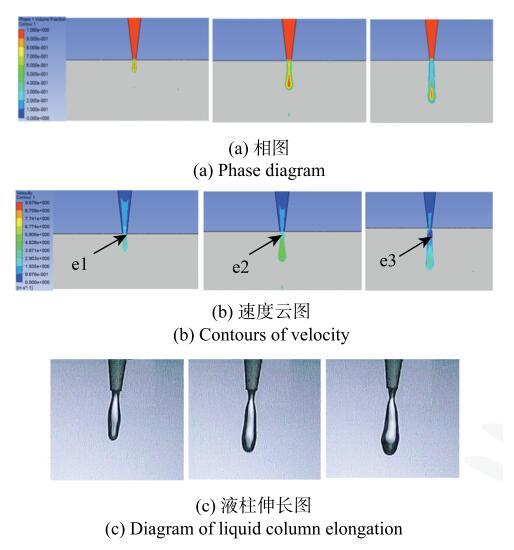新窗口打开|下载原图ZIP|生成PPT图20液柱颈缩前轮廓及轴向速度
Fig. 20Liquid column profile and axial speed before necking
4 结论
(1)膜片振幅受驱动电压和压电频率的共同作用,压电频率是导致膜片中心点振幅测量值小于理论计算值的主要原因.(2)膜片中心点振幅在29 $\mu $m$\sim $42 $\mu $m区间可以稳定生成单颗微滴,生成微滴最小直径为339.8 $\mu $m,直径最大变化率为0.29%,相邻两微滴间距最大变化率为2.67%,生成微滴的尺寸及均匀性较好.
(3)喷嘴内峰值压力随着膜片振幅的增大而升高,压力峰值出现时间随着膜片振幅增大向后推移. 在生成单颗微滴的振幅区间,喷嘴内部的峰值压力越小,生成微滴的稳定性越好.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
DOIURL [本文引用: 1]
DOIURL
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL
DOIURL
DOI
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
DOIURL
DOIURL [本文引用: 2]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 2]
[本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 2]
[本文引用: 1]
[本文引用: 1]
DOIMagsci [本文引用: 1]
设计了一种电-液混合驱动的机械撞针式液滴喷射成型系统，研究了该成型系统的各个组成部分及其作用，利用无网格模拟技术模拟了机械撞针式液滴喷射的全过程，通过实验研究了操作工艺参数对液滴喷射的影响规律。实验选用直径为0.25 mm的钨钢喷嘴，实现了高温下黏度为12 Pa·s高黏度聚丙烯（PP）中的喷射成型。
DOIMagsci [本文引用: 1]
设计了一种电-液混合驱动的机械撞针式液滴喷射成型系统，研究了该成型系统的各个组成部分及其作用，利用无网格模拟技术模拟了机械撞针式液滴喷射的全过程，通过实验研究了操作工艺参数对液滴喷射的影响规律。实验选用直径为0.25 mm的钨钢喷嘴，实现了高温下黏度为12 Pa·s高黏度聚丙烯（PP）中的喷射成型。
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 2]
Magsci [本文引用: 2]
<p>为使气压驱动式微滴喷射装置能产生均匀的微滴和稳定的喷射过程，使用FLUENT建立了二维轴对称计算模型并对微喷过程进行了模拟仿真。研究了气压驱动式微滴按需产生过程及腔体内压力峰值对单颗微滴成形的影响规律，利用构建的喷射系统对水进行喷射试验，并对产生微滴的均匀性进行了研究。仿真获得了单颗微滴的成形过程并得到了腔体内较低压力峰值有利于提高微喷稳定性的结论。实验结果表明，产生的微滴附着直径最大变化率为1.82%，均匀性较好。</p>
Magsci [本文引用: 2]
<p>为使气压驱动式微滴喷射装置能产生均匀的微滴和稳定的喷射过程，使用FLUENT建立了二维轴对称计算模型并对微喷过程进行了模拟仿真。研究了气压驱动式微滴按需产生过程及腔体内压力峰值对单颗微滴成形的影响规律，利用构建的喷射系统对水进行喷射试验，并对产生微滴的均匀性进行了研究。仿真获得了单颗微滴的成形过程并得到了腔体内较低压力峰值有利于提高微喷稳定性的结论。实验结果表明，产生的微滴附着直径最大变化率为1.82%，均匀性较好。</p>
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
[本文引用: 1]
[本文引用: 1]
