基于微米力学实验的页岩I型断裂韧度表征 1)

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-01

韩强^,^*^,^?^,^**^,²⁾, 屈展^*^,^?^,^**, 叶正寅^**, 董广建^??

* 西安石油大学石油工程学院/博士后创新基地,西安 710065

? 西安石油大学陕西省油气井及储层渗流与岩石力学重点实验室,西安 710065

** 西北工业大学航空学院/博士后科研流动站,西安 710072

?? 西南石油大学石油与天然气工程学院,成都 610500

STUDY ON FRACTURE TOUGHNESS OF MODE I OF SHALE BASED ON MICRO-MECHANICAL TEST ¹⁾

Han Qiang^,^*^,^?^,^**^,²⁾, Qu zhan^*^,^?^,^**, Ye Zhengyin^**, Dong Guangjian^??

* College of Petroleum Engineering/Postdoctoral Innovation Base, Xi'an Shiyou University, Xi'an 710065 China

? Shaanxi Key Laboratory of Well Stability and Fluid & Rock Mechanics in Oil and Gas Reservoirs, Xi'an Shiyou University, Xi'an 710065 China;

** School of Aeronautics/Center for Postdoctoral Studies, Northwestern Polytechnical University, Xi'an 710072, China

?? Petroleum Engineering School, Southwest Petroleum University, Chengdu 610500 China

通讯作者: 2) 韩强, 讲师, 主要研究方向: 岩石力学与随钻测量. E-mail：hqcampus@163.com

收稿日期:2018-08-29接受日期:2018-10-18网络出版日期:2019-07-18

基金资助:

1) 国家自然科学基金.51704233
国家自然科学基金.51674200
中国博士后科学基金.2017M613207
陕西省自然科学基础研究计划.2018JQ5068

Received:2018-08-29Accepted:2018-10-18Online:2019-07-18
作者简介 About authors

摘要
页岩断裂韧度($K_{IC})$是页岩气储层水力压裂设计的基础参数之一,由于组成的非均质性,常规宏观力学测量方法存在制样困难、力学解释参数不连续、精度偏低等问题. 如何及时获取页岩的断裂特性,确保安全高效的工程施工,是当前面临的一大问题. 因此,提出了基于微米力学实验的页岩Ⅰ型断裂韧度分析方法,可用于页岩微裂纹起裂、发育直至形成宏观裂纹的机理研究,进行页岩宏观Ⅰ型断裂韧度预测. 基于页岩多尺度组成分析,开展了维氏压头和玻氏压头的页岩微米力学实验,分析了页岩残余压痕与压头间的相似关系、有效测试载荷以及压头参数的优化与选择. 分析了不同压入载荷下的页岩细观断裂韧度分布特征,开展了宏观巴西圆盘实验,验证页岩微米力学测试方法的适用性. 研究结果表明,在有效载荷范围内的页岩细观Ⅰ型断裂韧度波动性较小,当压入载荷过大时,由于岩样压痕区域出现局部剥落导致断裂韧度测量值偏小. 与宏观实验的比对分析显示,微米力学实验的$K_{IC}$平均值为0.86 MPa$\cdot \sqrt{m}$,直槽切缝巴西圆盘实验得到的$K_{IC}$平均值为0.92 MPa$\cdot \sqrt{m}$,两类方法的统计平均值较为接近,页岩局部组成的非均质性使得微米力学测量结果较宏观测试更为分散. 研究结果可用于页岩宏观Ⅰ型断裂韧度预测,为有效解决页岩气储层水力压裂参数评价提供新的思路和方法.
关键词： 页岩;微米力学测试;影响因素;Ⅰ型断裂韧度;

Abstract
Fracture toughness of mode I ($K_{IC})$ is one of the important mechanical parameters for hydraulic fracturing of shale gas reservoir. Due to the heterogeneity of shale composition, the conventional mechanical measurement has some problems such as large sample volume, discontinuous mechanical interpretation parameters, and low interpretation accuracy. One of the challenges is to obtain the fracture characteristics of shale in time to ensure the safety and efficiency of engineering construction. In this paper, research on fracture toughness of mode I of shale is performed based on micro-indentation. It can be used to study the mechanism of shale micro-crack initiation, development and formation of macro-crack, and to predict the macro-parameters of shale. Based on the analysis of multi-scale composition of shale, the fracture toughness tests with pyramid indenter (Vickers indenter and Berkovich indenter) were performed by micro-indentation. The relationship between residual indentation and indenter was evaluated, and the effect of experimental load on shale micro-fracture was analyzed. The optimization of indenter parameter also was discussed. The fracture toughness of shale is evaluated at meso-scale. The applicability of the micro-indentation test was evaluated, based on a comparative analysis with the results of the Brazil disc test. The results show that t the fluctuation of fracture toughness obtained by micro-indentation is slight when load is within the effective range. When load is too large, the fracture toughness of meso-scale is gradually reduced due to local drop-cuts on the indentation area. The average value of $K_{IC}$ obtained by micro-indentation is 0.86 MPa$\cdot \sqrt{m}$,and the average value obtained by Brazilian disc test is 0.92 MPa$\cdot\sqrt{m}$. The heterogeneity of shale composition results in more dispersed meso-mechancial measurement than macroscopic measurement. Micro-indentation test can be used to characterize shale fracture toughness of mode I and perform macroscopic prediction. It provides a new method for effectively solving shale gas hydraulic fracturing.
Keywords：shale;micro-indentation test;influencing factor;fracture toughness of

PDF (23418KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex 收藏本文
本文引用格式
韩强, 屈展, 叶正寅, 董广建. 基于微米力学实验的页岩I型断裂韧度表征 ¹⁾. 力学学报[J], 2019, 51(4): 1245-1254 DOI:10.6052/0459-1879-18-283
Han Qiang, Qu zhan, Ye Zhengyin, Dong Guangjian. STUDY ON FRACTURE TOUGHNESS OF MODE I OF SHALE BASED ON MICRO-MECHANICAL TEST ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2019, 51(4): 1245-1254 DOI:10.6052/0459-1879-18-283

mode I

引言

岩气储层岩石具有低渗透、天然裂缝发育等特征,页岩气井水平段由于水力压裂施工的岩石裂纹发育,裂纹扩展的模式主要为Ⅰ型、Ⅱ型断裂或复合型断裂^{[1- 6]}. 通过页岩断裂韧度、脆性指数等参数的综合分析,可以为页岩气储层水力压裂设计及支撑剂选型提供科学依据^[7-8]. 作为准脆性材料,页岩内部会存在裂缝、空隙、夹杂等天然微缺陷,其破坏特征表现为断裂的突发性,在裂缝扩展前不存在明显的裂尖塑性区,通过微裂隙的扩展最终连通形成宏观裂缝.如何在钻井、开采发生早期,超前或及时获取页岩断裂行为并准确做出异常情况预警,确保工程施工的安全和高效,是当前岩石力学面临的一大难题.

目前对岩石起裂的室内研究主要参照岩石物理与力学特性关系,通过宏观实验获取力学属性^[9-10]. 陈勉等^[11-12]围绕砂岩储层进行了大量宏观实验研究,分析了砂岩断裂韧度受单轴抗拉、抗压强度等的影响规律.陈建国等^[13]通过巴西圆盘实验分析了页岩Ⅰ型和Ⅱ型断裂韧度,并结合测井资料拟合了断裂韧度预测模型.该类方法虽然可以得到页岩的基本力学特征,但可能会存在制样困难、力学解释参数不连续、精度偏低等问题^[14].测井仪器因井下空间制约或测试范围受限,常会导致测井解释资料品质不高、测量误差较大^[15].在基础理论方面,通过开展裂纹尖端应力与裂纹扩展规律分析,描述裂纹扩展的有效判据和裂纹对自身结构的影响因素,分析裂缝的形成、发育、扩展等特征,建立了宏观损伤演化本构关系^[16].但是,传统的宏观唯象模型没有考虑页岩内部的非均质性对宏观破坏的响应特征.页岩是典型的非均匀材料,由纳米级的多孔黏土、微米级非黏土夹杂和裂纹、孔洞、位错等组成复杂的微结构,页岩的弹性、硬度和变形破坏等都与组成有关^[17].唐春安等^[18-19]根据Weibull分布假设提出了岩石显微尺度分析,认为细观非均匀性是造成材料宏观非线性的内在原因.王士民等^[20]通过非均匀性对宏观破坏形式的研究,指出材料坡度参数越小,其破坏形式越具有随机性.页岩的断裂破损本质上是微裂纹的产生、发育、扩展、直到贯通为宏观裂纹,使其失稳破坏的过程.该过程可分为3个阶段：某些孤立点产生应力集中,开裂后可以达到平衡态的起裂过程;随着载荷的增大介质沿开裂面产生相对滑移,裂纹扩展稳定阶段;当微裂纹相互贯通形成控制强度的宏观裂纹时,进入不稳定扩展阶段,逐渐失去承载能力.

现代力学按研究内容、尺度大小,将研究范畴划分为微观力学、细观力学和宏观力学.其中细观力学分析作为连接微观和宏观的桥梁,不仅可以研究料力学属性的形成机理,还可以评价和预测宏观尺度的有效性能^[21-23]. 张泰华等^[24-25]通过纳米力学测试技术,分析了金属、薄膜等材料的显微力学特性.近些年来,该技术逐渐被用于生物材料、晶体硅、水泥石等材料的微观力学评价^[26-28].根据Ulm对页岩组成的尺度划分方法,可以将页岩按尺寸属性划分为单晶黏土矿物,微观多孔黏土介质(尺度为10$^{-8}\sim$10$^{ - 6}$ m),细观多孔黏土夹杂复合介质(尺度为10$^{-5}\sim$10$^{ - 4}$ m)和尺寸大于10$^{ - 3}$ m的宏观岩样^[29].基于页岩多尺度组成分布,本文通过微米力学实验讨论页岩细观断裂特性,研究一种适用于测量页岩细观Ⅰ型断裂韧度参数的新方法,开展测试参数影响因素评价,并与宏观巴西圆盘实验进行比对分析,为页岩显微断裂评价提供新的思路.

1 分析方法

微米力学测试仅需要满足测试表面的平整性,对样品形状和尺寸几乎无限制,实验压入深度在微米级,对材料属于微损测试.

测试区域的应力场分布受压头几何形状的影响,在实际测量过程中会根据不同目的选用合适类型的压头,常用的棱锥压头有维氏压头和玻氏压头.

1.1 维氏压头

维氏压头为正四棱锥状,相对棱面夹角136$^\circ$、等效半锥角70.3$^\circ$,底面棱长与深度之比为4.95,投影面积为24.5$h^{2}$,压痕形状产生的径向裂纹如图1所示.图中$a$为压痕半径,$c$是径向裂纹长度,$l$是压痕点尖端距裂纹尖端的长度.

图1

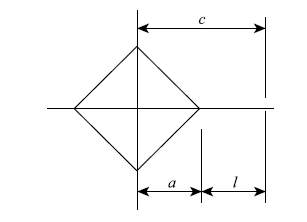新窗口打开|下载原图ZIP|生成PPT
图1维氏压头产生径向裂纹示意图

Fig. 1Schematic diagram of radial crack with Vickers indenter

维氏压头与材料通过接触作用产生的裂纹可分为两类,一种是贯穿样品内部呈轴对称的半饼状裂纹,另一类是在试样表面产生的径向裂纹(图2).

基于实验结果分析和量纲函数的拟合,给出适用维氏压头的材料裂纹沿径向充分扩展经验模型^[30]

(1)$$ \frac{K_{IC} \phi }{H_{IT} \sqrt a }\infty \left({\frac{1}{\phi }\frac{H_{IT} }{E_{IT} }} \right)^{2/5}\left( {\frac{c}{a}} \right)^{-3/2} $$

式中, $K_{IC}$为断裂韧度,MPa$\cdot \sqrt{m}$;$H_{IT}$为压入硬度,MPa; $E_{IT}$为弹性模量,MPa; $c$为样品表面压痕中心点到裂纹端部的距离,mm; $a$为压痕半对角线长度,mm; {$\phi $}为约束因子,取值3.

图2

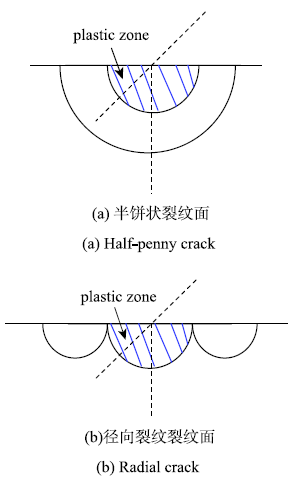新窗口打开|下载原图ZIP|生成PPT
图2韦氏压头产生裂纹面类型

Fig. 2Crack type produced by Vickers indenter

式(1)虽然给出了材料断裂韧度与弹性模量、硬度等参数的定性关系,但是半饼状裂纹的形成机理并不明确.将加载过程中的弹性应力场分解为卸载阶段的弹性可恢复功和因塑性变形的不可逆功进行讨论,Lawn等^[31]提出了弹/塑性压入断裂模型.根据该模型,维氏压头在材料表面的应力场被简化为弹性应力场和塑性残余应力场的叠加问题.对核心塑性区的应力场作如下假设：初始状态为无应力弹性半空间,材料由于压入作用产生的塑性变形量可以通过单位体积的变化来表征.将裂纹充分扩展条件下的塑性区对弹性区的作用,简化为垂直作用于裂纹面中并使其张开的一对集中力$F_{r}$

(2)$$ F_{r} \infty F_{m} \left( {\frac{a}{b}} \right)\left( {\frac{E_{IT} }{H_{IT} }} \right)\cot \psi $$

(3)$$ F_{r} \infty F_{m} \left( {\frac{E_{IT} }{H_{IT} }} \right)^{1 /2}\left( {\cot \psi } \right)^{2/3} $$

式中,$b$为塑性区半径,mm; {$\varPsi$}为压头的相对棱边半夹角,($^\circ$); $F_{m}$为压入载荷,N.

根据内嵌圆盘裂纹应力强度因子的解析解^[32],并考虑半空间自由表面的影响,压头卸载后半饼状裂纹前段的应力强度因子可表示为

(4)$$ K_{r} = f\left( \phi \right)\left( {\frac{E_{IT} }{H_{IT} }}\right)^{1 /2}\left( {\cot \psi } \right)^{3 /2}\frac{F_{m}}{c^{3/2}} $$

式中, $f$($\phi$)为应力强度因子修正系数,无因次.

当$\phi $取90$^\circ$时为1. 半饼状裂纹径向扩展的平衡条件为

(5)$$ K_{IC} = \left. {K_r} \right|_{\phi = \pi /2} $$

将式(4)代入式(5)可得到断裂韧度的表达式为

(6)$$K_{IC} = \delta \left( {\frac{E_{IT} }{H_{IT} }} \right)^{1/2}\frac{F_m }{c^{3 /2}} $$

式中, $\delta $为与压头几何形状有关的系数,通过实验确定.

对于一些脆性材料,在维氏压头的作用下并不出现半饼状裂纹,而是在材料表面产生径向裂纹.根据不规则裂缝应力强度因子判据^[33],径向裂纹尖端与半饼状裂纹尖端的应力强度因子满足关系

(7)$$ K^{R} = 2\left( {\frac{{\pi}}{{\pi} + 2}} \right)^{1/2}\left( {\frac{a}{l}} \right)^{1/2}K^{RP} $$

式中, $K^{R}$为径向裂纹尖端的应力强度因子;$K^{RP}$为半圆状裂纹尖端的应力强度因子.

在此基础上通过满足边界条件的模型推导^[34],得到径向裂纹断裂韧度表达式为

(8)$$ K_{IC} = \delta ^L\left( {\frac{a}{l}} \right)^{1 /2}\left({\frac{E_{IT} }{H_{IT} }} \right)^{1 /2}\frac{F_m }{c^{3/2}} $$

式中,$\delta $$^{L}$为待定系数,取值范围在0.014 6~0.015 4.在裂纹扩展充分的条件下,两种裂纹形态下的断裂韧度的计算值接近,这说明裂纹充分扩展时,其具体形态变化对断裂韧度的影响不大.

1.2 玻氏压头

玻氏压头为三棱锥形状,侧面棱边与中心线夹角77.05$^\circ$、棱面与中心线夹角65.3$^\circ$、等效半锥角与维氏压头相同,为70.3$^\circ$,底面棱边与深度比值为7.5315,投影面积24.56$h^{2}$,产生的径向裂纹参数如图3所示.

图3

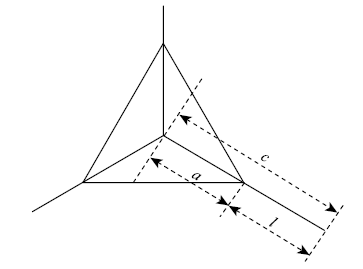新窗口打开|下载原图ZIP|生成PPT
图3玻氏压头产生径向裂纹示意图

Fig. 3Schematic diagram of radial crack with Berkovich indenter

星型裂纹应力强度因子分析表明,对于一次出现任意不多于9条裂纹的断裂问题,维氏压头与玻氏压头的断裂韧度满足一次函数的关系,且维氏压头大约是玻氏压头的1.073倍^[35].给出玻氏压头的断裂韧度表达式为

(9)$$ K_{IC} =1.073\delta ^{L}\left( {\frac{a}{l}} \right)^{1 /2}\left({\frac{E_{IT} }{H_{IT} }} \right)^{2 /3}\frac{F_{m}}{c^{3 /2}} $$

值得注意的是,当满足径向裂纹充分扩展条件时,式(6)同样可适用于玻氏压头,对应的玻氏压头$\delta $值约为0.016.

2 页岩细观断裂测试

2.1 测试设备

页岩细观断裂力学测试选用集成声发射检测技术、摩擦力检测微米位移测量技术及微机自控技术的MFT-4000型多功能表面性能测试仪.该仪器的主要技术参数：加载范围0.5~300 N、加载精度0.5N、加载速率5~100 N/min、位移测量范围0.5~ 200$\mu$m.通过控制最大载荷与加载速度,获取载荷、位移数据,具有载荷、位移和仪器的自校准功能.

2.2 测试样品

页岩样品选自四川盆地龙马溪组地层,质地坚硬,颜色以灰、黑色为主,部分层理发育;X衍射结果显示,页岩中石英含量20%~65%,方解石含量15%~35%,少见正长石和斜长石,黏土矿物含量16%~60%,属于一种典型的硬脆性页岩^[36]. 试样尺寸为50 mm$\times$25 mm$\times $15mm,上下表面的平行度小于0.3$^\circ$、侧面与压入表面垂度小于0.3$^\circ$.为了消除试样表面粗糙度对压入深度的影响,对试样进行二次精心细抛光处理,然后进行烘干、密封待用.

2.3 测试流程

单次测试主要包括3个阶段：加载阶段、保持阶段和卸载阶段(见图4).首先将压头与岩样表面接触,按确定的最大载荷和加载速率压入岩样表面;当达到最大载荷达后保持一定时间,消除测量误差;然后按照一定的卸载速率在规定时间内卸载至0,最后将压头从岩样表面提升移至下一个待测试点.

图4

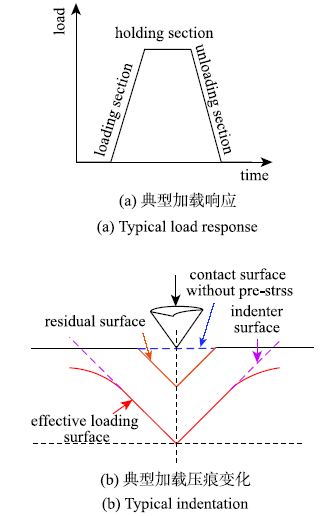新窗口打开|下载原图ZIP|生成PPT
图4典型压痕加载响应与压痕变化

Fig. 4Typical load response and indentation

根据Delesse准则,非均质材料各相介质表面分布百分数可等效为体积百分数,对目标岩样表面的显微力学实验分析可以近似表征块体样的力学属性.同时,由于页岩组成的非均质性,使得单次压入测试不足以表征表面的宏观断裂韧度特征.本文采用网格化压入测试并进行统计分析,减小因压入区域某一组分集中产生的局部效应.根据ISO 14577的标准^[37],确定页岩的相邻压入点间距不小于2mm、压入点距岩样边界7mm,排除相邻测试点的应力场干扰和页岩边界效应的影响.对于微/纳米范围的压入力学实验,压入测试数量应不小于15次,以便提高测量平均值的可靠性和重复性.

3 测试影响因素分析

3.1 压头选型

针对龙马溪组页岩试样,分别选用维氏压头和玻氏压头开展显微断裂测试.图5给出了维氏压头在不同压入载荷(40 N,50 N,60 N,80N)条件下的典型细观压痕.不难看出,维氏压头在页岩压痕表面会产生微小的凹点和局部剥落,且压头与压痕间的自相似性较差.此外,载荷、深度曲线表现出明显的不规则凸起.因此,由维氏压头较难得到径向裂纹和半对角压痕的长度参数.造成这种现象的主要原因是维氏压头尖端加工横刃结构和页岩非均质组成共同作用的结果.

图5

新窗口打开|下载原图ZIP|生成PPT
图5维氏压头在页岩表面的残余压痕

Fig. 5The residual indentation of shale surface produced by Vickers indenter

图6(a)和图6(b)给出了玻氏压头在不同最大载荷(60 N,80 N)条件下的典型细观压痕结果. 不难看出,玻氏压头与压痕点的相似性较好,当压入载荷达到页岩细观破裂阈值60N时,实验压入深度介于55~75 $\mu$m,在岩样表面产生微裂纹.当压入载荷达到80 N,压入深度会达到78~90 $\mu$m,裂纹发育较为明显.通过比对分析,常规的维氏压头不能满足页岩细观Ⅰ型断裂韧度的测量要求,建议采用玻氏压头开展页岩评价.实验中还发现,页岩与金属、陶瓷、薄膜等材料一样,存在有效裂纹产出率较低的问题,需要通过大量的压入实验获取.

图6

新窗口打开|下载原图ZIP|生成PPT
图6玻氏压头在页岩表面的残余压痕

Fig. 6The residual indentation of shale surface produced by Berkovich indenter

3.2 有效载荷与加载速率

压入断裂韧度测试的有效载荷分析,目前仅见于陶瓷、金属等复合材料,对于组成的非均匀页岩尚无名明确的确定方法.通过对页岩弹性模量和硬度参数的细观力学测试分析,已知最大载荷在50N时多数压入点与玻氏压头的自相似性较好,未出现破裂^[38].当加载速率为10 N/min,压入载荷为60N的压入点表面沿压头棱锥端部裂纹开始发育. 载荷为90N的部分压痕点沿棱面出现不规则剥落,当载荷达到100N时,压痕点周边出现明显剥落(图6(c)和图6(d)).因此,岩样断裂韧度测试的有效载荷最好小于90 N.

在加载速率为100N/min时,上述载荷的压痕点周边区域都会出现不同程度的剥落,这是由于过快加载会使压头向页岩表面产生一个冲击力,引起压痕点表面应力场的复杂变化.考虑到MFT-4000型测试仪的加载精度,建议选取10 N/min开展测试.

3.3 压头参数

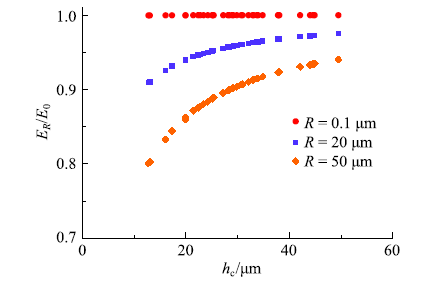
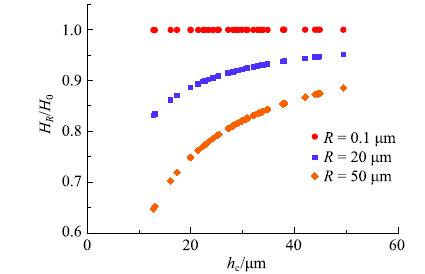
应用微米力学测试方法求解中间参量(弹性模量和硬度)过程中,假设了压头为理想尖端,即不存在曲率半径.然而,由于加工水平、使用磨损等影响,真实压头尖端曲率半径有可能会对弹性模量和硬度产生的影响.通过对式(9)中自变量参数弹性模量和硬度测量的影响,压头参数进而影响到断裂韧度求解的精确度.在相同条件下,通过理想压头和存在曲率半径压头的弹性模量比值和硬度的分析发现,当压头尖端真实曲率半径为20$\mu$m时,弹性模量和压入硬度随压入位移的减小,测量误差开始逐渐增大;当曲率半径达到50$\mu$m,此时的压头已不适用于页岩细观力学测试(图7、图8).因此测试前,需要检测压头曲率半径是否在有效范围.

图7

新窗口打开|下载原图ZIP|生成PPT
图7不同曲率半径下岩样弹性模量关系($E_{R}$为是压头曲率半径$R$下岩样的弹性模量,$E_{0}$为理想压头下的岩样弹性模量, $h_{c}$为压入深度

Fig. 7The relationship between the radius of indenter and the test results of elastic modulus ($E_{R}$ is the elastic modulus of sample when the radius of indenter is $R$, $E_{0}$ is the elastic modulus under ideal condition, $h_{c}$ is indentation depth

图8

新窗口打开|下载原图ZIP|生成PPT
图8不同曲率半径下岩样硬度关系($H_{R}$为是压头曲率半径$R$下岩样的弹性模量,$H_{0}$为理想压头下的岩样弹性模量))

Fig. 8The relationship between the radius of indenter and the test results of hardness ($H_{R}$ is the hardness of sample when the radius of indenter is $R$, $H_{0}$ is the hardness under ideal condition)

4 结果与讨论

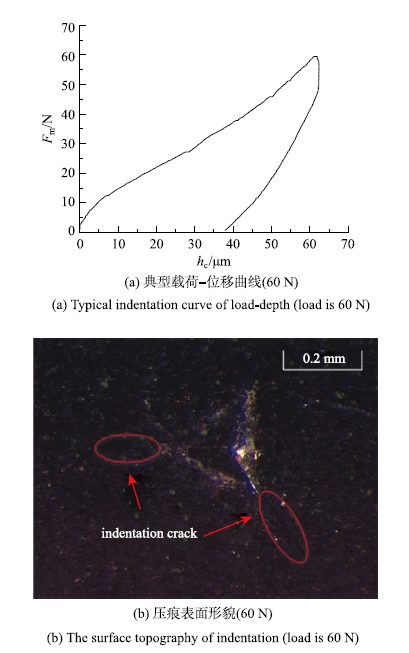
图9给出了采用玻氏压头的页岩典型载荷、位移曲线和残余压痕表面形貌特征,结果显示裂纹面沿压痕角点扩展.表1给出了由微米力学实验,得到的$K_{IC}$随不同压入载荷的变化关系. 在有效载荷范围内,$K_{IC}$随载荷的增加波动较小.当载荷过大导致压入表面出现局部剥落,$K_{IC}$会随之缓慢降低.对于玻氏压头,有效载荷范围内测量得到的页岩试样表面径向裂纹长度介于1~3mm,该小尺寸裂纹的测量准确与否,直接会导致断裂韧度的测量精度.与维氏压头相比,玻氏压头的尖端更为锋利,对页岩微断裂开启具有关键作用.需要注意的是,在对中间参数——弹性模量和硬度,需要在试样表面未发生破裂的情况下另行开展实验和分析计算,保证参数获取的准确性,参数的求解采用Oliver-Pharr方法.

图9

新窗口打开|下载原图ZIP|生成PPT
图9页岩微米力学测试曲线和压痕表面形貌

Fig. 9Typical micro-indentation load-depth curve of shale and the surface topography of indentation

Table 1
表1
表1玻氏压头的页岩细观Ⅰ型断裂韧度与压入载荷关系
Table 1The relationship between fracture toughness typeⅠand load at meso-scale by Berkovich indenter

新窗口打开|下载CSV

由于页岩细观Ⅰ型断裂韧度求解是基于微米力学测试理论,需要与常规宏观测试结果进行比对分析,才能确定该方法对页岩的适用性.这里,通过将巴西圆盘实验测定的页岩宏观Ⅰ型断裂韧度作为约定真值,对细观测试结果进行分析评价.巴西圆盘实验选用WDW-D200型微机控制电子万能实验机,岩样加工为半圆柱状并进行切片处理,采用水力刀切割成预制缝(图10).实验载荷与预制缝的夹角为0度,岩样出现明显的拉伸破坏.巴西圆盘试件测试I型断裂韧度的计算公式为^[39]

(10)$$ K_{IC} =\frac{Fa_{c}^{0.5} }{R_{c} B\pi^{0.5}}N $$

式中, $F$为径向加载载荷,N; $R_{c}$为圆盘半径,mm;$B$为圆盘厚度,mm; $a_{c}$为预制裂缝长度,mm;$N$为无因次强度因子. 当$a_{c}$/$R \le$0.3时,无因次强度因子近似满足

(11)$$ N = 1 - 4\sin ^2\theta + 4\sin ^2\theta \left( {1 - 4\cos ^2\theta } \right)\left( {\frac{a_{ c} }{R}} \right)^2 $$

图10

新窗口打开|下载原图ZIP|生成PPT
图10页岩巴西圆盘测试试件

Fig. 10Test sample of Brazilian disc test

图11给出了页岩微米力学实验和巴西圆盘实验的断裂韧度测试结果.玻氏压头实验方法的$K_{IC}$介于0.65$\sim $1.14 MPa$\cdot\sqrt{m}$,平均值为 0.86 MPa$\cdot\sqrt{m}$,25%~75%的分布偏差小于0.27. 巴西

图11

新窗口打开|下载原图ZIP|生成PPT
图11页岩Ⅰ型断裂韧度的实验对比结果

Fig. 11Comparison of experimental results of fracture toughness

圆盘实验得到的$K_{IC}$介于0.76$\sim $1.21 MPa$\cdot\sqrt{m}$,平均值为0.92 MPa$\cdot \sqrt{m}$,25%~75%的分布偏差小于0.18.不难看出,微米压入测量法和宏观常规实验的统计平均值较为接近,可以进行页岩宏观Ⅰ型断裂韧度的预测.同时,微米压入的$K_{IC}$分布较常规测量更为分散,这主要是由页岩局部矿物组分的异所产生的.

5 结论

本文在页岩多尺度组成分析的基础上,开展了维氏压头和玻氏压头的细观断裂实验,进行了实验参数的影响因素评价,分析了页岩细观Ⅰ型断裂韧度的基本特征,并与宏观实验结果进行比对分析,验证了方法的合理性. 得出以下结论：

(1) 维氏压头由于自身构型和页岩的非均匀组成,导致压痕与压头的自相似性不理想,多数压痕表面出现剥落;对于玻氏压头,当载荷达到破裂阈值60N后,沿棱锥的径向裂纹逐渐发育.在实验开始前,需要明确有效压入载荷和加载速率参数,减小因载荷加载过大、过快导致岩样表面崩落,对弹性模量、硬度等测量参数的影响.

(2) 在有效测试条件下,页岩细观I型断裂韧度受压入载荷增加的影响较小.当载荷过大时,因岩样表面崩落或重复压入导致应力场复杂化,页岩细观I型断裂韧度随压入载荷的增加而逐渐减小.通过对比宏观巴西圆盘实验和微米力学测试结果,分析宏观、细观页岩性断裂韧度.不难看出,通过微米力学测试可以有效表征岩样的Ⅰ型断裂韧度,当获取宏观实验岩样困难时,该技术可作为快速获取页岩断裂属性的一种新方法.

参考文献原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]

陈勉, 葛洪魁, 赵金洲等. 页岩油气高效开发的关键基础理论与挑战
石油钻探技术, 2015,43(5):7-14

[本文引用: 1]

( Chen

Mian

, Ge

Hongkui

, Zhao

Jinzhou

, et al. The key fundamentals for the efficient exploitation of shale oil and gas and its related challenges
Petroleum Drilling Techniques, 2015,43(5):7-14 (in Chinese))

[本文引用: 1]

[2]

李庆辉, 陈勉, 金衍等. 页岩脆性的室内评价方法及改进
岩石力学与工程学报, 2012,31(8):1680-1685

Magsci

页岩气储层脆性对页岩的脆性进行测试、评价具有重要的意义。鉴于此，通过文献调研和室内测试，总结脆性测试的20种基本方法，包括基于强度、硬度和坚固性的评价方法，并重点讨论基于全应力–应变特征的页岩脆性测试原理和试验方法。针对页岩脆性破裂机制结合断裂特征定义脆性，认为页岩的脆性是材料的综合特性，受自身非均质性和外在测试环境共同影响；峰后与峰前应力–应变特征均是表征脆性的关键，模拟地下环境的全应力–应变测试能够提高脆性评价的准确度；试样破坏前抵抗非弹性变形的能力和破坏后承载力丧失速度的快慢是脆性强弱的主要力学表现。为提高脆性评价的准确性，对已有的力学测试方法提出改进方案。开展室内真三轴岩石力学实验，对我国南方黑色页岩的脆性特征进行评价。

( Li

Qinghui

, Chen

Mian

, Jin

Yan

, et al. Indoor evaluation method for shale brittleness and improvement
Chinese Journal of Rock Mechanics and Engineering, 2012,31(8):1680-1685 (in Chinese))

Magsci

Lyu

, Long

, Ranjith

, et al. Experimental investigation on the mechanical properties of a low-clay shale with different absorption times in sub-/super-critical CO$_2$
Energy, 2018,147:1288-1298

DOI URL

[4]

Lyu

, Long

, Ranjith

, et al. Experimental investigation on the mechanical behaviours of a low-clay shale under water-based fluids
Engineering Geology, 2018,233:124-138

DOI URL

[5]

孙可明, 张树翠 . 含层理页岩气藏水力压裂裂纹扩展规律解析分析
力学学报, 2016,48(5):1229-1237

DOI Magsci

页岩气蕴藏在页岩层中，页岩层的层理性构造使其水力压裂裂纹扩展与常规均质储层不同.为研究页岩储层水力压裂的裂纹扩展规律，基于复变函数保角变换，得出裂纹尖端应力集中解，考虑页岩非均质、强度各向异性特点，通过比较裂纹沿各方向扩展所需的裂缝尖端水压力，推导出水力压裂裂纹垂直于最小地应力方向稳定扩展过程中在斜交层理后的扩展判据.分别定义了水力压裂裂纹在层理处起裂和沿层理扩展的弱层和岩石基体临界强度比，根据两个临界强度比确定水力压裂裂纹遇层理时在层理处起裂和沿层理扩展的层理弱面强度范围，以此表示水力压裂裂纹转向层理扩展的难易程度.通过对裂纹扩展判据的分析得出：层理起裂弱层和岩石基体临界强度比随层理走向线与第一主应力夹角和层理倾角的减小以及第三主应力和岩石基体强度的增大而增大；层理走向角小于35.26°时，层理起裂弱层和岩石基体临界强度比随第一主应力的减小以及第二主应力的增大而增大；反之，层理起裂弱层和岩石基体临界强度比随第一主应力的减小以及第二主应力的增大而减小；层理扩展弱层和岩石基体临界强度比随层理走向线与第一主应力夹角、层理倾角和地应力差的减小以及岩石基体抗拉强度的增大而增大.层理起裂条件与层理扩展条件同时满足时，水力压裂裂纹转向层理方向扩展.

( Sun

Keming

, Zhang

Shucui

. Hydraulic fracture propagation in shale gas bedding reservoir analytical analysis
Chinese Journal of Theoretical and Applied Mechancis, 2016,48(5):1299-1237 (in Chinese))

DOI Magsci

张财贵, 曹富, 李炼等. 采用压缩单裂纹圆孔板确定岩石动态起裂、扩展和止裂韧度
力学学报, 2016,48(3):624-635

DOI Magsci [本文引用: 1]

爆炸、冲击、地震等人为或自然灾害不可避免,经常造成大量土木工程设施的破坏,因此岩石在动态载荷作用下的行为受到特别关注.岩石动态断裂韧度是评价岩石抵抗裂纹动态起裂、扩展和止裂性能的材料参数,开展岩石动态断裂韧度测试方法的研究对相关理论基础和实验技术的要求较高.岩石动态断裂韧度分为动态起裂、动态扩展、动态止裂三种,虽然关于动态起裂和动态扩展的研究已有一些成果,对岩石动态止裂的研究仍是一个难题,至今几乎无人问津.研究表明,在分离式霍普金森压杆撞击压缩单裂纹圆孔板岩石试样的I型动态断裂试验中,动态起裂、扩展、止裂的全过程可以由黏贴在压缩单裂纹圆孔板试样上的裂纹扩展计监测,岩石的动态起裂、扩展、止裂韧度可以用实验-数值-解析法确定.特别值得一提的是首次测出了岩石的动态止裂韧度.裂纹扩展计信号还显示,压缩单裂纹圆孔板在止裂后,停止的裂纹还会再次动态起裂、扩展并超出裂纹扩展计的检测范围.从能量的角度分析了动态止裂的过程,指出测试动态止裂韧度时要注意的一些问题.结果显示,岩石动态起裂韧度和动态扩展韧度分别随动态加载率和裂纹扩展速度的增大而增大,岩石动态起裂韧度略大于动态止裂韧度.

( Zhang

Caigui

, Cao

, Li

Lian

, et al. Determination of dynamic fracture initiation, propagation, and arrest toughness of rock using SCDC specimen
Chinese Journal of Theoretical and Applied Mechanics, 2016,48(3):624-635 (in Chinese))

DOI Magsci [本文引用: 1]

郑哲敏 . 关于中国页岩气持续开发工程科学研究的一点认识
科学通报, 2016,61(1):34-35

[本文引用: 1]

( Zheng

Zhemin

. A little understanding of the scientific research on the continuous development of shale gas in China
Science Bulletin, 2016,61(1):34-35 (in Chinese))

[本文引用: 1]

[8]

谢和平, 高峰, 鞠杨等. 页岩气储层改造的体破裂理论与技术构想
科学通报, 2016,61(1):36-46

[本文引用: 1]

( Xie

Heping

, Gao

Feng

, Ju

Yang

, et al. Volume fracture theory and technical conception of reforming shale gas reservoir
Science Bulletin, 2016,61(1):36-46 (in Chinese))

[本文引用: 1]

[9]

Farrokhrouz

, Asef

, Kharrat

. Empirical estimation of uniaxial compressive strength of shale formations
Geophysics, 2014,79(4):227-233

DOI URL [本文引用: 1]

[10]

韩铁林, 师俊平, 陈蕴生等. 轴、侧向同卸荷下砂岩力学特性影响的试验研究
力学学报, 2016,48(4):936-943

DOI Magsci [本文引用: 1]

本文以实际岩体工程为背景，利用WDT-1500 仪器开展了轴向、侧向同时卸荷条件下砂岩的三轴试验. 结果表明：轴、侧向同卸荷这种卸荷路径下，砂岩试样破坏时并没有出现应力峰值，为了定义试样的破坏强度，将最大与最小主应力差随最小主应力的变化关系曲线上应力跌落的拐点处的应力值定义为破坏强度. 砂岩变形初始段发生应力跌落和轴向应变回弹，破坏前无明显的弹性和屈服阶段；试验的过程中，砂岩的侧向变形明显大于轴向变形，其体积应变一直处于膨胀状态；相对于砂岩的常规三轴试验结果，试样破坏时的强度在轴向、侧向同时卸荷条件下有所降低. 初始轴压和初始围压对试样的力学特征有十分显著的影响，但围压的卸荷速率却并不显著. 砂岩的破坏特征主要是以张-拉为主的混合张剪的破坏.

( Han

Tielin

, Shi

Junping

, Chen

Yunsheng

, et al. Experimental study on mechanics characteristics of sandstone under axial unloading and radial unloading path
Chinese Journal of Theoretical and Applied Mechanics, 2016,48(3):936-943 (in Chinese))

DOI Magsci [本文引用: 1]

陈勉, 金衍, 袁长友 . 围压条件下岩石断裂韧性的实验研究
力学与实践, 2001,23(4):32-35

[本文引用: 1]

( Chen

Mian

, Jin

Yan

, Yuan

Changyou

. Study on the experiment for fracture toughness under confining pressure
Mechanics in Engineering, 2001,23(4):32-35 (in Chinese))

[本文引用: 1]

[12]

陈治喜, 陈勉 . 岩石断裂韧性与声波速度相关性的试验研究
石油钻采工艺, 1997,19(5):56-60

[本文引用: 1]

( Chen

Zhixi

, Chen

Mian

. Experimental study on the relationship between rock fracture toughness and acoustic velocity
Oil Drilling and Production Technology, 1997,19(5):56-60 (in Chinese))

[本文引用: 1]

[13]

陈建国, 邓金根, 袁俊亮等. 页岩储层I型和II型断裂韧性评价方法研究
岩石力学与工程学报, 2015,34(6):1101-1105

[本文引用: 1]

( Chen

Jianguo

, Deng

Jinggen

, Yuan

Junliang

, et al. Determination of fracture toughness of modes I and II of shale formation
Chinese Journal of Rock Mechanics and Engineering, 2015,34(6):1101-110 (in Chinese))

[本文引用: 1]

[14]

陈勉, 金衍, 张广清 . 石油工程岩石力学. 北京: 科学出版社, 2008

[本文引用: 1]

( Chen

Mian

, Jin

Yan

, Zhang

Guangqing

. Petroleum Engineering Rock Mechanics. Beijing: Science Press, 2008 (in Chinese))

[本文引用: 1]

[15]

Heng

, Guo

, Yang

, et al. Experimental and theoretical study of the anisotropic properties of shale
International Journal of Rock Mechanics and Mining Sciences, 2015,74(1):58-68

DOI URL [本文引用: 1]

[16]

Liang

, Xiong

, Liu

. Experimental study on crack propagation in shale formations considering hydration and wettability
Journal of Natural Gas Science and Engineering, 2015,23:492-499

DOI URL [本文引用: 1]

[17]

何金钢, 康毅力, 游利军等. 矿物成分和微结构对泥质岩储层应力敏感性的影响
天然气地球科学, 2012,23(1):129-134

Magsci [本文引用: 1]

富含粘土的页岩、泥质粉砂岩和粉砂岩等泥质岩的储层矿物成分、微组构和微孔结构复杂，使得泥质岩储层的应力敏感性存在较大差别。以鄂尔多斯盆地延长组泥质岩为研究对象，开展应力敏感性实验评价研究，并与典型致密砂岩储层进行对比。结果表明，页岩的应力敏感程度强，泥质粉砂岩中等—偏强，致密砂岩弱；在30MPa有效应力作用下，岩石呈现塑性变形。分析指出，岩石的变形主要受到岩石的组分、胶结物类型和含量\,微裂缝系统、孔隙结构参数、骨架颗粒形态、接触方式\,粒度分布、粘土微结构等参数的影响。针对3类岩石的应力敏感性差异，应区别对待，尽力控制储层应力敏感性损害的发生。

( He

Jingang

, Kang

Yili

, You

Lijun

, et al. Effects of mineral composition and microstructure on stress-sensitivity of mudrocks
Natural Gas Geoscience, 2012,23(1):129-134 (in Chinese))

Magsci [本文引用: 1]

夏英杰, 李连崇, 唐春安等. 储层砂岩破坏特征与脆性指数相关性影响的试验及数值研究
岩石力学与工程学报, 2017,36(1):10-28

[本文引用: 1]

( Xia

Yingjie

, Li

Lianchong

, Tang

Chunan

, et al. Experiment and numerical research on failure characteristic and brittleness index for reservoir sandstone
Chinese Journal of Rock Mechanics and Engineering, 2017,36(1):10-28 (in Chinese))

[本文引用: 1]

[19]

唐春安, 刘红元, 秦四清等. 非均匀性对岩石介质中裂纹扩展模式的影响
地球物理学报, 2000,43(1):116-121

Magsci [本文引用: 1]

运用岩石破裂过程分析ＲＦＰＡ２Ｄ系统，通过对岩石试样中预置的倾斜裂纹扩展过程的数值模拟，研究了材料非均匀性对岩石介质中裂纹扩展模式的影响．数值模拟再现了受压试样在裂纹扩展过程中逐步演变的应力场和应变场，以及与岩石非均匀性有关的声发射和断裂扩展模式的“岩桥”现象．模拟结果说明，岩石的非均匀性对含裂纹试样的变形、破裂过程及其破坏模式有很大的影响．

( Tang

Chunan

, Liu

Hongyuan

, Qin

Siqing

, et al. Influence of heterogeneity on crack propagation modes in brittle rock
Chinese Journal of Geophysics, 2000,43(1):116-121 (in Chinese))

Magsci [本文引用: 1]

王士民, 朱合华, 冯夏庭等. 细观非均匀性对脆性岩石材料宏观破坏形式的影响
岩土力学, 2006,27(2):224-227

[本文引用: 1]

( Wang

Shimin

, Zhu

Hehua

, Feng

Xiating

, et al. Influence of heterogeneity on macroscopical crack from the brittle rock
Rock and Soil Mechancis, 2006,27(2):224-227 (in Chinese))

[本文引用: 1]

[21]

罗荣, 曾亚武, 杜欣 . 非均质岩石材料宏细观力学参数的关系研究
岩土工程学报, 2012,34(12):2331-2336

Magsci [本文引用: 1]

利用基于岩石矿物种类及其含量提出的岩石矿物细胞元随机性参数赋值方法，针对两矿物细胞元混合的非均质岩石模型进行参数赋值，通过数值试验研究了非均质岩石材料矿物细胞元含量及其力学参数对岩石宏观力学参数的影响；根据数值试验结果，探讨了岩石材料矿物细胞元弹性模量与宏观模量之间的函数关系。研究结果表明，岩石宏观弹性模量与矿物细胞元弹性模量、矿物细胞元含量都具有十分显著的线性相关关系，即基于岩石矿物种类及其含量的矿物细胞元随机性参数赋值方法建立的岩石有限元模型宏细观力学参数之间呈显著的线性关系；宏观力学参数可用细观力学参数的数学期望值即加权平均值来表示。

( Luo

Rong

, Zeng

Yawu

, Du

Xin

. Relationship between macroscopic and mesoscopic mechanical parameters of inhomogenous rock material
Journal of Geotechnical Engineering, 2012,34(12):2331-2336 (in Chinese))

Magsci [本文引用: 1]

宋仲康, 马德军, 郭俊宏等. 一种改进的纳米压入测试方法
中国有色金属学报, 2012,22(2):520-525

( Song

Zhongkang

, Ma

Dejun

, Guo

Junhong

, et al. A modified method of nanoindentation
The Chinese Journal of Nonferrous Metals, 2012,22(2):520-52 (in Chinese))

[23]

Gianpetro

, Owen

. Multiscaling in Molecular and Continuum Mechanics: Interaction of Time and Size from Macro to Nano
Netherlands: Springer, 2007

[本文引用: 1]

[24]

Zhang

, Feng

, Yang

, et al. A method to determine fracture toughness using cube-corner indentation
Scripta Materialia, 2010,62(4):199-201

DOI URL [本文引用: 1]

[25]

张海霞, 张泰华, 郇勇 . 纳米压痕和划痕法测定氧化硅薄膜材料的力学特性
微纳电子技术, 2003,40(8):245-248

[本文引用: 1]

( Zhang

Haixia

, Zhang

Taihua

, Xun

Yong

. Nanoindentation and nanoscratch measurements on the mechanical properties of SiO$_2$ film. Micro/
Nano Electronic Technology, 2003,40(8):245-248 (in Chinese))

[本文引用: 1]

[26]

Zhu

, Hughes

, Bicanic

, et al. Nanoindentation mapping of mechanical properties of cement paste and natural rocks
Materials Characterization, 2007,58(11):1189-1198

DOI URL [本文引用: 1]

[27]

Bobko

, Ulm

. The nano-mechanical morphology of shale
Mechanics of Materials, 2008,40(4):318-337

DOI URL

[28]

Sebastiani

, Johanns

, Herbert

, et al. Measurement of fracture toughness by nanoindentation methods: Recent advances and future challenges
Current Opinion in Solid State and Materials Science, 2015,19(6):324-333

DOI URL [本文引用: 1]

[29]

韩强, 屈展, 叶正寅 . 页岩多尺度力学特性研究现状
应用力学学报, 2018,35(3):564-570

[本文引用: 1]

( Han

Qiang

, Qu

Zhan

, Ye

Zhengyin

. Research status of shale multi-scale mechanical properties
Chinese Journal of Applied Mechanics, 2018,35(3):564-570 (in Chinese))

[本文引用: 1]

[30]

Evans

, Charles

. Fracture toughness determinations by indentation
Journal of the American Ceramic Society, 2010,59(7-8):371-372

[本文引用: 1]

[31]

Marshall

, Evans

. Reply to "Comment on Elastic/Plastic Indentation Damage in Ceramics: The Median/ Radial Crack System"
Journal of the American Ceramic Society, 2010,64(12):C182-C183

[本文引用: 1]

[32]

Anderson

. Fracture Mechanics-Fundamentals and Applications. CRC Press, 2015

[本文引用: 1]

[33]

Oore

, Burns

. Estimation of stress intensity factors for embedded irregular cracks subjected to arbitrary normal stress fields
Journal of Pressure Vessel Technology, 1980,102(102):202-211

DOI URL [本文引用: 1]

[34]

Laugier

. New formula for indentation toughness in ceramics
Journal of Materials Science Letters, 1987,6(3):355-356

DOI URL [本文引用: 1]

[35]

Ouchterlony

. Stress intensity factors for the expansion loaded star crack
Engineering Fracture Mechanics, 1976,8(2):447-448

DOI URL [本文引用: 1]

[36]

刘向君, 熊健, 梁利喜 . 龙马溪组硬脆性页岩水化实验研究
西南石油大学学报(自然科学版), 2016,38(3):178-186

[本文引用: 1]

( Liu

Xiangjun

, Xiong

Jian

, Liang

Lixi

. Hydration experiment of hard brittle shale of the longmaxi formation
Journal of Southwest Petroleum University, 2016,38(3):178-186 (in Chinese))

[本文引用: 1]

[37]

Zolotnikova

, Solovyev

, Gogolinskiy

, et al. Study of the effect of different sources on the combined error of;hardness measurements by the instrumented indentation method
Measurement Techniques, 2013,56(2):158-163

DOI URL [本文引用: 1]

[38]

Chen

, Han

, Tianshou

, et al. The mechanical properties of shale based on micro-indentation test
Petroleum Exploration and Development, 2015,42(5):723-732

DOI URL [本文引用: 1]

[39]

Atkinson

, Smelser

, Sanchez

. Combined mode fracture via the cracked Brazilian disk test
International Journal of Fracture, 1982,18(4):279-291

[本文引用: 1]