北京工业大学机械结构非线性振动与强度北京市重点实验室,北京 100124
NONLINEAR VIBRATIONS OF COMPOSITE CANTILEVER PLATE IN SUBSONIC AIR FLOW1)
LiuGen, ZhangWei中图分类号:O322
文献标识码:A
通讯作者:
收稿日期:2018-10-15
网络出版日期:2019-05-18
版权声明:2019力学学报期刊社 所有
基金资助:
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (1182KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
引 言
随着材料科学的发展,越来越多的新型材料在工程领域得到了应用.板壳结构在航空航天工程中使用广泛,复合材料层合板以其优良的力学性能在飞行器结构设计中有着重要的应用.飞行器的翼面为整机提供着升力,单位面积上承受着载荷较大,在气流的作用下,翼面极易产生复杂的非线性振动现象[1-3],对由复合材料层合结构所构成的翼面的非线性动力学问题仍是众多****研究的热点.对于复合材料层合结构振动特性[4]的相关研究,国内外****做出了大量的工作.在二十世纪九十年代, 板壳结构的研究已经达到了一个较高的水平.在层合板结构的非线性研究中,Noor等[5-6]、Abe等[7-9]以及Nayfeh等[10-12]做了多方面的探讨.在板结构的高阶理论的研究中,Librescu和Reddy[13]提出了三阶剪切变形板理论.
最近十年间,板壳结构的非线性动力学问题仍是****们关注的热点.Zhang[14]通过引入冯$\cdot$卡门几何非线性,研究了简支矩形薄板在参数激励下的全局分岔和混沌动力学.Kitipornchai等[15]分析了由功能梯度材料组成的考虑剪切变形且含有缺陷的层合板的非线性振动特性.在不规则形状层合板的研究中,Park等[16]对斜形层合板在动态载荷作用下的非线性强迫振动进行了分析.不同的边界也是****们研究的关注点,Chien和Chen[17]研究了初应力和不同参数对复合材料层合板在弹性基础上的非线性振动的影响.Singh等[18]引入几何非线性,考虑高阶剪切变形板理论,研究了不同弹性基础上的复合材料层合板的振动响应.在功能梯度材料结构的非线性振动问题的研究中,Amabili等[19-20]研究了功能梯度材料平板和扁壳的非线性振动,分析了系统的分岔和非线性动力学行为.同时,采用高阶剪切变形理论研究了角层叠合圆柱壳的非线性振动.Zhang等[21-24]以航天工程中星载大型空间可展环形桁架星载天线为背景,将周边环形桁架等效为复合材料圆柱壳结构,研究了结构在热激励下的非线性动力学,利用解析方法和数值模拟研究了系统的分岔和混沌行为.
同时,板壳结构在流体激励下的非线性振动问题也是****们关注的热点.20世纪60年代,Dowell[25-26]对平板的颤振问题做了系统研究.在Amabili和Paidoussis[27]的综述中,对流体中的板壳结构的振动问题进行了较为全面的总结.在现有文献中,气流激励的速度往往都处在超音速阶段,研究的内容也都关注于板壳结构的气动弹性问题.Singha和Ganapathi[28]研究了系统参数对斜形层合板超音速颤振行为的影响.Haddadpour等[29]研究了功能梯度平板的非线性气动弹性行为.Kuo[30]研究了不同层铺间距对矩形平板的超音速颤振的影响.Zhao和Zhang[31]对在超音速气体和平面激励作用下复合材料悬臂矩形板的非线性动力学问题进行了分析.Hao等[32]研究了功能梯度平板在高超音速气流中受外激励及温度载荷下的非线性动力学.
本文工作对复合材料层合矩形悬臂板在亚音速气流中的非线性振动问题进行了研究.利用涡格法计算了有限长平板翼面上的亚音速气动升力.基于三阶剪切变形板理论,利用哈密顿原理建立了在亚声速气动载荷的复合材料层合悬臂板运动的非线性偏微分控制方程.考虑了1:2 的内部共振.研究了多个参数下结构的幅频特性关系,以期为工程对象提供理论上的依据.
1 平板绕流的亚音速气动力计算
翼型是无限长直机翼上的一个剖面,无限长机翼上任何一个剖面的绕流都是一样的,此类翼面上下表面压强差所产生的升力沿翼展是不变的.但是,对于有限翼展翼面来说,翼面下方的高压空气会在翼尖处向上方的低压空气翻转,其结果是翼尖附近上表面处的压强趋向于和下表面的压强相等,因而单位展长的升力是向翼尖递减的.悬臂结构在航空航天工程中有着广泛的应用,飞行器的升力面就是典型的悬臂结构.本节利用涡格法求解平板亚音速绕流的气动载荷.图1给出一个三维翼面的布涡情况.
显示原图|下载原图ZIP|生成PPT图1翼面的布涡情况
-->Fig. 1Lifting surface discretized by a Vortex Lattice of horseshoe vortices
-->
利用毕奥{--}萨瓦尔定律[33]计算控制点的诱导速度,得到涡系的涡流强度,进而推导出上下表面的压力差.由毕奥{--}萨瓦尔定律,单位长度${\rm d} l$和涡强$\varGamma _n$所诱导的速度为
\begin{equation}\label{eq1} {\rm d} V = \frac{\varGamma _n ( l\times r)}{4\pi r^3}\tag{1}\end{equation}
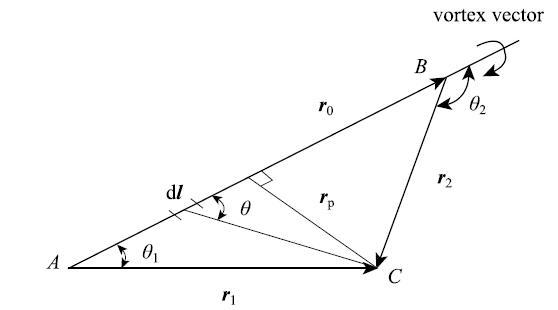
如图2所示,给出了涡段$ {AB}$对于点$C$诱导速度的示意.
显示原图|下载原图ZIP|生成PPT图2有限长涡段所诱导的速度
-->Fig. 2Velocity induced by finite length vortex segments
-->
诱导速度为
\begin{equation}\label{eq2} {\rm d} V = \frac{\varGamma _n \sin \theta {\rm d} l}{4\pi r^2}\tag{2}\end{equation}
令$ {AB}$代表从$A$到$B$的涡段,$C$为一个空间点,到$ {AB}$的距离为$r_{\rm p}$. $ r_0 $,$ r_1 $ 和$ r_2 $分别代表$ {AB}$,$ {AC}$和$ {BC}$涡段矢量,有如下关系
\begin{equation}\label{eq3} r_{\rm p} = \frac{\left| r_1 \times r_2\right|}{ r_{\bf 0}}, \quad \cos \theta_1 = \frac{ r_0 \cdot r_1}{ r_0 r_1 }, \quad \cos \theta_2 = \frac{ r_0\cdot r_2 }{ r_0 r_2 }\tag{3}\end{equation}
在涡段$ {AB}$上进行积分,得到诱导速度
\begin{equation}\label{eq4} V = \frac{\varGamma _n }{4\pi r_{\rm p}}\int_{\theta_1 }^{\theta _2 } \sin \theta {\rm d}\theta = \frac{\varGamma _n}{4\pi r_{\rm p}}(\cos \theta_1 - \cos \theta _2)\tag{4}\end{equation}
通过涡段矢量表达式,可以得到诱导速度的表达式
\begin{equation}\label{eq5} V = \frac{\varGamma _n }{4\pi}\frac{ r_1\times r_2 }{\left| { r_1 \times r_2 }\right|}\left[ r_0 \cdot \left(\frac{ r_1 }{r_1 } -\frac{ r_2 }{r_2 }\right)\right]\tag{5}\end{equation}
利用式(5),涡段$ {AB}$在任意点$(x,y,z)$所产生的诱导速度为
$$ V_{AB} = \frac{\varGamma _n }{4\pi}\{Fac1_{AB} \} \cdot \{Fac2_{AB} \}\tag6a$$
$$ V_{A\infty } = \frac{\varGamma _n }{4\pi}\frac{(z - z_{1n} ) j + (y - y_{1n} ) k}{(z - z_{1n} )^2 + (y - y_{1n} )^2}\bigg[ 1.0 +\\ \frac{x - x_{1n} }{(x - x_{1n} )^2 + (y - y_{1n} )^2 + (z-z_{1n} )^2} \bigg]\tag{6b}$$
$$ V_{B\infty } = - \frac{\varGamma _n }{4\pi}\frac{(z - z_{2n} ) j + (y_{1n} - y) k}{(z - z_{1n} )^2 + (y_{2n} - y)^2}\bigg[1.0 + \\ \frac{x - x_{2n} }{(x - x_{2n} )^2 + (y - y_{2n} )^2 + (z-z_{2n} )^2} \bigg]\tag{6c} $$
其中,$Fac1_{AB} $和$Fac2_{AB}$为根据式(5)得到的涡段$ {AB}$到空间点$C$的矢量关系
$$\{Fac1_{AB} \} = \frac{ r_1 \times r_2 }{\left| { r_1\times r_2 } \right|}, \{Fac2_{AB} \} = \left( r_0 \cdot\frac{ r_1 }{r_1 } - r_0 \cdot \frac{ r_2 }{r_2}\right)$$
其中,$ V_{A\infty}$为沿着$x$轴涡线从$A$点到无穷远处所诱导的速度,$ V_{B\infty }$为沿着$x$轴涡线从$B$点到无穷远处所诱导的速度.
通过式(6)可以计算马蹄涡在任意空间点$\left( {x,y,z}\right)$所诱导出的速度.那么,由$2N$个涡构成的翼面在第$m$控制点处诱导出的速度为
\begin{equation}\label{eq9} V_m = \sum\limits_{n = 1}^{2N} { C_{m,n}\varGamma _n }\tag{7}\end{equation}
在计算得到第$m$控制点的诱导速度后,把所有的涡对第$m$面元控制点处的下洗的贡献累加,得到
\begin{equation}\label{eq10} w_m = \sum\limits_{n = 1}^{2N} {w_{m,n}}\tag{8}\end{equation}
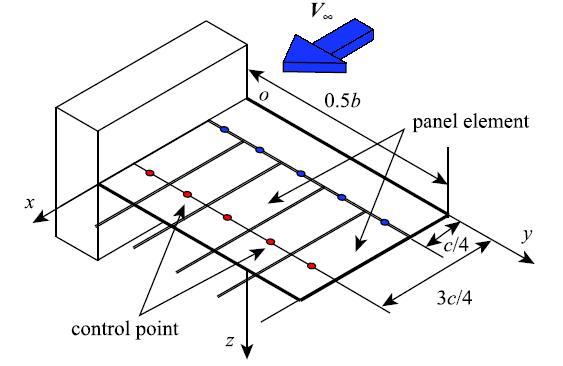
其中,$w_{m,n} $为$n$个面元对第$m$控制点的下洗.根据上面的推导,利用涡格法计算悬臂板的亚音速气流下的绕流.悬臂板上涡的布置如图3所示.
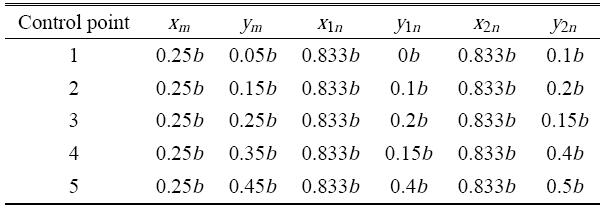
在图3中,$A$为翼展长度的2倍,$c$为弦长,翼面的根梢比为1,后掠角为0℃.考虑$Ma<0.3$时的来流速度$V_\infty $,利用涡格法计算平面上的升力.将涡布置于翼面四分之一弦线处,控制点布置于翼面四分之三弦线处.对于此平板翼面,布置5个马蹄涡,相关点的几何位置如表1所示.
显示原图|下载原图ZIP|生成PPT图3悬臂板上涡格的布置
-->Fig. 3Layout of the vortex lattice on the flat wing surface
-->
Table 1
表1
表1马蹄涡各点的位置
Table 1The coordinates of the attachment vortex and the control point in the wing surface
 |
新窗口打开
通过不穿透条件[33]
\begin{equation}\label{eq11} w_m = - V_\infty \alpha\tag{9}\end{equation}
得到5个涡强的代数方程
$$ \varGamma _1 = 0.10082\left( {4\pi bV_\infty \alpha } \right)\tag{10a}$$
$$\varGamma _2 = 0.13180\left( {4\pi bV_\infty \alpha } \right)\tag{10b}$$
$$\varGamma _3 = 0.13901\left( {4\pi bV_\infty \alpha } \right)\tag{10c}$$
$$\varGamma _4 = 0.12496\left( {4\pi bV_\infty \alpha } \right)\tag{10d}$$
$$\varGamma _5 = 0.09887\left( {4\pi bV_\infty \alpha } \right)\tag{10e} $$
气流在每个控制点处与物面相切,且此平板翼面没有上反角,因此得到
\begin{equation}\label{eq17} L_0 = \rho _\infty V_\infty \sum\limits_{n = 1}^5{\varGamma _n \Delta y_n }\tag{11}\end{equation}
代入相关几何关系,得到
\begin{equation}\label{eq18} L_0 = \rho _\infty V_\infty ^2 \pi b^2\alpha(0.238184)\tag{12}\end{equation}
这里,为了得到翼面上的周期激励,假设翼面的攻角存在一个周期的扰动$\alpha= \alpha _0 + \alpha _1 \cos \varOmega _2t$代入式(12),则气动力的表达式变为
\begin{equation}\label{eq19} L = L_0 + L_1 \cos \varOmega _2 t\tag{13}\end{equation}
其中,$L_0 = \rho _\infty V_\infty ^2 \pi b^2\alpha _0 $,$L_1 =\rho _\infty V_\infty ^2 \pi b^2\alpha $.
2 悬臂复合材料层合板非线性动力学方程
接下来,建立亚音速气流中的复合材料层合悬臂板的非线性振动微分方程.如图4所示,给出了亚音速气流中复合材料层合悬臂板的力学模型.其中,$x$为展向,$y$为弦向,$z$为翼面的法向. $x =0$处复合材料层合板固定端,构成悬臂结构.$b$为展长,$c$为弦长,根梢比为1. 采用$[0^\circ/90^\circ ]_{\rm NS}$的层铺结构. 考虑弦向的面内激励$F = F_0 + F_1 \cos \varOmega _1t$以及法向的气动载荷$L$共同作用下的动力学模型.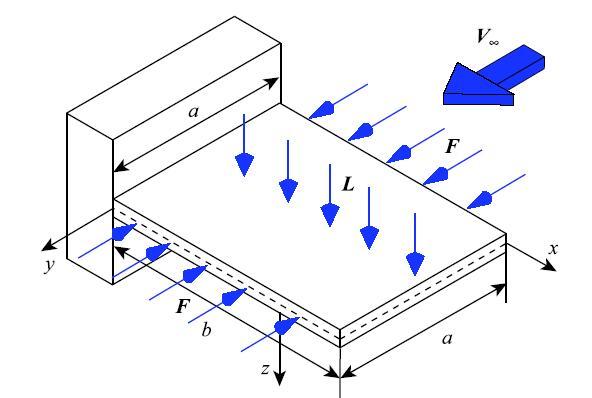
显示原图|下载原图ZIP|生成PPT图4气流中复合材料层合悬臂板的力学模型
-->Fig. 4Mechanical model of cantilever laminated composite plate
-->
考虑Reddy三阶剪切变形理论,引入冯$\cdot$卡门非线性应变位移关系,首先得到位移关系如下
$$ u(x,y,z,t) = u_0 + z\phi _x - z^3\frac{4}{3h^2}\left( {\phi _x + \frac{\partial w_0 }{\partial x}} \right)\tag{14a}$$
$$v(x,y,z,t) = v_0 + z\phi _y - z^3\frac{4}{3h^2}\left( {\phi _y + \frac{\partial w_0 }{\partial y}} \right)\tag{14b}$$
$$w(x,y,z,t) = w_0\tag{14c}$$
应变关系如下
$$\varepsilon _{xx} = \frac{\partial u_0 }{\partial x} + \frac{1}{2}\left( {\frac{\partial w_0 }{\partial x}} \right)^2\tag{15a}$$
$$\varepsilon _{yy} = \frac{\partial v_0 }{\partial y} + \frac{1}{2}\left( {\frac{\partial w_0 }{\partial y}} \right)^2\tag{15b}$$
$$\gamma _{xy} = \frac{1}{2}\left( {\frac{\partial u_0 }{\partial y} + \frac{\partial v_0 }{\partial x} + \frac{\partial w_0 }{\partial x}\frac{\partial w_0 }{\partial y}} \right)\tag{15c}$$
$$\gamma _{yz} = \frac{1}{2}\left( {\frac{\partial v_0 }{\partial z} + \frac{\partial w_0 }{\partial y}} \right)\tag{15d}$$
$$\gamma _{zx} = \frac{1}{2}\left( {\frac{\partial u_0 }{\partial z} + \frac{\partial w_0 }{\partial x}} \right)\tag{15e}$$
将应变表达式代入位移表达式中,得到
$$\left\{ {{\begin{array}{*{20}c} {\varepsilon _{xx} } \\ {\varepsilon _{yy} } \\ {\gamma _{xy} } \\ \end{array} }} \right\} = \left\{ {{\begin{array}{*{20}c} {\varepsilon _x^{\left( 0 \right)} } \\ {\varepsilon _y^{\left( 0 \right)} } \\ {\gamma _{xy}^{\left( 0 \right)} } \\ \end{array} }} \right\} + z\left\{ {{\begin{array}{*{20}c} {\varepsilon _x^{\left( 1 \right)} } \\ {\varepsilon _y^{\left( 1 \right)} } \\ {\gamma _{xy}^{\left( 1 \right)} } \\ \end{array} }} \right\} + z^3\left\{ {{\begin{array}{*{20}c} {\varepsilon _x^{\left( 2 \right)} } \\ {\varepsilon _y^{\left( 2 \right)} } \\ {\gamma _{xy}^{\left( 2 \right)} } \\ \end{array} }} \right\}\qquad\quad\tag{16a}$$
$$\left\{ {{\begin{array}{*{20}c} {\gamma _{yz} } \\ {\gamma _{zx} } \\ \end{array} }} \right\} = \left\{ {{\begin{array}{*{20}c} {\gamma _{yz}^{\left( 0 \right)} } \\ {\gamma _{zx}^{\left( 0 \right)} } \\ \end{array} }} \right\} + z^2\left\{ {{\begin{array}{*{20}c} {\gamma _{yz}^{\left( 2 \right)} } \\ {\gamma _{zx}^{\left( 2 \right)} } \\ \end{array} }} \right\}\qquad\quad\tag{16b}$$
其中
$$\left\{ {{\begin{array}{*{20}c} {\varepsilon _x^{(0)} } \\ {\varepsilon _y^{(0)} } \\ {\gamma _{xy}^{(0)} } \\ \end{array} }} \right\} = \left\{ {{\begin{array}{*{20}c} {\dfrac{\partial u_0 }{\partial x} + \dfrac{1}{2}\left( {\dfrac{\partial w_0 }{\partial x}} \right)^2} \\[3mm] {\dfrac{\partial v_0 }{\partial y} + \dfrac{1}{2}\left( {\dfrac{\partial w_0 }{\partial y}} \right)^2} \\[3mm] {\dfrac{\partial u_0 }{\partial y} + \dfrac{\partial v_0 }{\partial x} + \dfrac{\partial w_0 }{\partial x}\dfrac{\partial w_0 }{\partial y}} \\ \end{array} }} \right\}\tag{17a}$$
$$\left\{ {{\begin{array}{*{20}c} {\varepsilon _x^{(1)} } \\ {\varepsilon _y^{(1)} } \\ {\gamma _{xy}^{(1)} } \\ \end{array} }} \right\} = \left\{ {{\begin{array}{*{20}c} {\dfrac{\partial \phi _x }{\partial x}} \\[3mm] {\dfrac{\partial \phi _y }{\partial y}} \\[3mm] {\dfrac{\partial \phi _x }{\partial y} + \dfrac{\partial \phi _y }{\partial x}} \\ \end{array} }} \right\}\tag{17b}$$
$$\left\{ {{\begin{array}{*{20}c} {\varepsilon _x^{(2)} } \\ {\varepsilon _y^{(2)} } \\ {\gamma _{xy}^{(2)} } \\ \end{array} }} \right\} = - c_1 \left\{ {{\begin{array}{*{20}c} {\dfrac{\partial \phi _x }{\partial x} + \dfrac{\partial ^2w_0 }{\partial x^2}} \\[3mm] {\dfrac{\partial \phi _y }{\partial y} + \dfrac{\partial ^2w_0 }{\partial y^2}} \\[3mm] {\dfrac{\partial \phi _x }{\partial y} + \dfrac{\partial \phi _y }{\partial x} + 2\dfrac{\partial ^2w_0 }{\partial x\partial y}} \\ \end{array} }} \right\}\tag{17c}$$
$$\left\{ {{\begin{array}{*{20}c} {\gamma _{yz}^{(0)} } \\ {\gamma _{zx}^{(0)} } \\ \end{array} }} \right\} = \left\{ {{\begin{array}{*{20}c} {\phi _y + \dfrac{\partial w_0 }{\partial y}} \\[3mm] {\phi _x + \dfrac{\partial w_0 }{\partial x}} \\ \end{array} }} \right\}\tag{17d}$$
$$\left\{ {{\begin{array}{*{20}c} {\gamma _{yz}^{(2)} } \\ {\gamma _{zx}^{(2)} } \\ \end{array} }} \right\} = - c_2 \left\{ {{\begin{array}{*{20}c} {\phi _y + \dfrac{\partial w_0 }{\partial y}} \\[3mm] {\phi _x + \dfrac{\partial w_0 }{\partial x}} \\ \end{array} }} \right\}\tag{17e}$$
根据正交对称铺设方式的层合板得到
\begin{equation} \label{eq35} \left\{ {{\begin{array}{*{20}c} {\sigma _{xx} } \\ {\sigma _{yy} } \\ {\sigma _{yz} } \\ {\sigma _{zx} } \\ {\sigma _{xy} } \\ \end{array} }} \right\} = \left\{ {{\begin{array}{*{20}c} {\bar {Q}_{11} } & {\bar {Q}_{12} } & 0 & 0 & 0 \\ {\bar {Q}_{21} } & {\bar {Q}_{22} } & 0 & 0 & 0 \\ 0 & 0 & {\bar {Q}_{44} } & 0 & 0 \\ 0 & 0 & 0 & {\bar {Q}_{55} } & 0 \\ 0 & 0 & 0 & 0 & {\bar {Q}_{66} } \\ \end{array} }} \right\}\left\{ {{\begin{array}{*{20}c} {\varepsilon _{xx}} \\ {\varepsilon _{yy} } \\ {\gamma _{yz} } \\ {\gamma _{zx} } \\ {\gamma _{xy} } \\ \end{array} }} \right\}\tag{18} \end{equation}
这里$\theta $是层间的铺设角度. 每层的刚度为
$$Q_{11} = \frac{E_1 }{1 - \nu _{12} \nu _{21} }\tag{19a}$$
$$Q_{12} = \frac{\nu _{12} E_2 }{1 - \nu _{12} \nu _{21} }\tag{19b}$$
$$Q_{22} = \frac{E_2 }{1 - \nu _{12} \nu _{21} }\tag{19c}$$
$$Q_{44} = Q_{55} = Q_{66} = G_{12}\tag{19d}$$
其中,$E_i $为材料的杨氏模量,$G_{12} $为材料的剪切模量,$\upsilon_{12} $为材料的泊松比.
根据Hamilton原理
\begin{equation}\label{eq40} \int_{0}^{T} {\left( {\delta K - \delta U + \delta W}\right){\rm d}t = 0}\tag{20}\end{equation}
得到非线性控制微分方程
$$N_{xx,x} + N_{xy,y} = I_0 \ddot {u}_0 + \left( {I_1 - c_1 I_3 } \right)\ddot {\phi }_x - c_1 I_3 \frac{\partial \ddot {w}_0 }{\partial x}\tag{21a}$$
$$N_{yy,y} + N_{xy,x} = I_0 \ddot {v}_0 + \left( {I_1 - c_1 I_3 } \right)\ddot {\phi }_y - c{ }_1I_3 \frac{\partial \ddot {w}_0 }{\partial y}\tag{21b}$$
$$N_{yy,y} \frac{\partial w_0 }{\partial y} + N_{yy} \frac{\partial ^2w_0}{\partial y^2} + N_{xy,x} \frac{\partial w_0 }{\partial y} + N_{xy,y} \frac{\partial w_0 }{\partial x} + \\2N_{xy} \frac{\partial ^2w_0 }{\partial x\partial y} + N_{xx,x} \frac{\partial w_0 }{\partial x} + N_{xx} \frac{\partial ^2w_0 }{\partial x^2} +\\ c_1 \left( {P_{xx,xx} + 2P_{xy,xy} + P_{yy,yy} } \right) + \left( {Q_{x,x} - c_2 R_{x,x} } \right) + \\ \left( {Q_{y,y} - c_2 R_{y,y} } \right) + L - \gamma \dot {w}_0 = c_1 I_3 \left( {\frac{\partial \ddot {u}_0 }{\partial x} + \frac{\partial \ddot {v}}{\partial y}} \right) + \\ c_1\left( {I_4 - c_1 I_6 } \right)\left( {\frac{\partial \ddot {\phi }_x }{\partial x} + \frac{\partial \ddot {\phi }_y }{\partial y}} \right)+ \\ I_0 \ddot {w}_0 - c_1^2 I_6 \left( {\frac{\partial ^2\ddot {w}_0 }{\partial x^2} + \frac{\partial ^2\ddot {w}_0 }{\partial y^2}} \right)\tag{21c}$$
$$M_{xx,x} + M_{xy,y} - c_1 P_{xx,x} - c_1 P_{xy,y} - \left( {Q_x^-c_2 R_x } \right)=\\ \left( {I_1 - c_1 I_3 } \right)\ddot {u}_0 + \left( {I_2-2c_1 I_4 + c_1^2 I_6 } \right)\ddot {\phi }_x -\\ c_1 \left( {I_4 - c_1 I_6 } \right)\frac{\partial \ddot {w}_0 }{\partial x}\tag{21d}$$
$$M_{yy,y} + M_{xy,x} - c_1 P_{yy,y} - c_1 P_{xy,x} - \left( {Q_y-c_2 R_y } \right)=\\ \left( {I_1 - c_1 I_3 } \right)\ddot {v}_0 + \left( {I_2-2c_1 I_4 + c_1^2 I_6 } \right)\ddot {\phi }_y -\\ c_1 \left( {I_4 - c_1 I_6 } \right)\frac{\partial \ddot {w}_0}{\partial y}\tag{21e}$$
式中,$\gamma $为阻尼系数.
内力表达式为
$$\left\{ {{\begin{array}{*{20}c} {N_{\alpha \beta } } \\ {M_{\alpha \beta } } \\ {P_{\alpha \beta } } \\ \end{array} }} \right\} = \int_{ - h / 2}^{h / 2} {\sigma _{\alpha \beta } \left\{ {{\begin{array}{*{20}c} 1 \\ z \\ {z^3} \\ \end{array} }} \right\}} {\rm d}z\tag{22a}$$
$$\left\{ {{\begin{array}{*{20}c} {Q_\alpha } \\ {R_\alpha } \\ \end{array} }} \right\} = \int_{ - h / 2}^{h / 2} { \sigma _{\alpha z} } \left\{ {{\begin{array}{*{20}c} 1 \\ {z^2} \\ \end{array} }} \right\}{\rm d}z\tag{22b}$$
将内力表达式代入微分方程中,得到由位移表达的动力学微分方程
$$A_{11} \frac{\partial ^2u{ }_0}{\partial x^2} + A_{66} \frac{\partial ^2u_0 }{\partial y^2} + \left( {A_{12} + A_{66} } \right)\frac{\partial ^2v_0 }{\partial x\partial y} + \\ A_{11} \frac{\partial w_0 }{\partial x}\frac{\partial ^2w_0 }{\partial x^2}A_{66} \frac{\partial w_0 }{\partial x}\frac{\partial ^2w_0 }{\partial y^2} + \left( {A_{12} + A_{66} } \right) \\ \frac{\partial w_0 }{\partial y}\frac{\partial ^2w_0 }{\partial x\partial y} = I_0 \ddot {u}_0 + J\ddot {\phi }_x - c_1 I_3 \frac{\partial \ddot {w}_0 }{\partial x}\tag{23a}$$
$$A_{66} \frac{\partial ^2v_0 }{\partial x^2} + A_{22} \frac{\partial ^2v_0 }{\partial y^2} + \left( {A_{21} + A_{66} } \right)\frac{\partial ^2u_0 }{\partial x\partial y} + \\ A_{66} \frac{\partial w_0 }{\partial y}\frac{\partial ^2w_0 }{\partial x^2} + A_{22} \frac{\partial w_0 }{\partial y}\frac{\partial ^2w_0 }{\partial y^2} + \\ (A_{21} + A_{66} )\frac{\partial w_0 }{\partial x}\frac{\partial ^2w_0 }{\partial x\partial y} = \\ I_0 \ddot {v}_0 + J_1 \ddot {\phi }_y - c_1 I_3 \frac{\partial \ddot {w}_0 }{\partial y}\tag{23b}$$
$$A_{11} \frac{\partial u_0 }{\partial x}\frac{\partial ^2w_0 }{\partial x^2} + A_{21} \frac{\partial u_0 }{\partial x}\frac{\partial ^2w_0 }{\partial y^2} + 2A_{66} \frac{\partial u_0 }{\partial y}\frac{\partial ^2w_0 }{\partial x\partial y} + \\ A_{11} \frac{\partial ^2u_0 }{\partial x^2}\frac{\partial w_0 }{\partial x} + \left( {A_{21} + A_{66} } \right)\frac{\partial ^2u_0 }{\partial x\partial y}\frac{\partial w_0 }{\partial y} + \\ \left( {A_{12} + A_{66} } \right)\frac{\partial ^2v_0 }{\partial x\partial y}\frac{\partial w_0 }{\partial x} + A_{22} \frac{\partial ^2v_0 }{\partial y^2}\cdot \\ \frac{\partial w_0 }{\partial y} +\frac{3}{2}A_{11} \left( {\frac{\partial w_0 }{\partial x}} \right)^2\frac{\partial ^2w_0 }{\partial x^2} + \left( {\frac{1}{2}A_{21} + A_{66} } \right)\cdot\\ \left( {\frac{\partial w_0 }{\partial x}} \right)^2\frac{\partial ^2w_0 }{\partial y^2} +\left( {A_{12} + A_{21} + 4A_{66} } \right)\cdot \\ \frac{\partial w_0 }{\partial x}\frac{\partial w_0 }{\partial y}\frac{\partial ^2w_0 }{\partial x\partial y} +\frac{3}{2}A_{22} \left( {\frac{\partial w_0 }{\partial y}} \right)^2\frac{\partial ^2w_0 }{\partial y^2} + \\ \left( {\frac{1}{2}A_{12} + A_{66} } \right)\left( {\frac{\partial w_0 }{\partial y}} \right)^2\frac{\partial ^2w_0 }{\partial x^2} + \\ \left( {A_{55} - 2c_2 D_{55} + c_2^2 F_{55} } \right)\frac{\partial ^2w_0 }{\partial x^2} + \\ \left( {F_0 + F_1 \cos \varOmega _1 t} \right)\frac{\partial ^2w_0 }{\partial y^2} + \\ A_{22} \frac{\partial v_0 }{\partial y}\frac{\partial ^2w_0 }{\partial y^2} + A_{66} \frac{\partial w_0 }{\partial x}\frac{\partial ^2u_0 }{\partial y^2} + 2A_{66} \frac{\partial v_0 }{\partial x}\frac{\partial ^2w_0 }{\partial x\partial y} + \\ A_{12} \frac{\partial v_0 }{\partial y}\frac{\partial ^2w_0 }{\partial x^2} + \left( {A_{44} - 2c_2 D_{44} + c_2^2 F_{44} } \right)\frac{\partial ^2w_0 }{\partial y^2} + \\ c_1^2 H_{11} \frac{\partial ^4w_0 }{\partial x^4} - c_1^2 \left( {H_{12} + H_{21} + 4H_{66} } \right)\frac{\partial ^4w_0 }{\partial x^2\partial y^2} + \\ \left( {A_{55} - 2c_2 D_{55} + c_2^2 F_{55} } \right)\frac{\partial \phi _x }{\partial x} - c_1^2 H_{22} \frac{\partial ^4w_0 }{\partial y_4 } + \\ c_1 \left( {F_{11} - c_1 H_{11} } \right)\frac{\partial ^3\phi _x }{\partial x^3} + \\ c_1 \left( {F_{21} + 2F_{66} - c_1 H_{21} - 2c_1 H_{66} } \right)\frac{\partial ^3\phi _x }{\partial x\partial y^2} +\\\left( {A_{44} - 2c_2 D_{44} + c_2^2 F_{44} } \right)\frac{\partial \phi _y }{\partial y} + \\ c_1 \left( {F_{12} + 2F_{66} - c_1 H_{12} - 2c_1 H_{66} } \right)\frac{\partial ^3\phi _x }{\partial x^2\partial y} + \\ A_{66} \frac{\partial ^2v_0 }{\partial x^2}\frac{\partial w_0 }{\partial y} + c_1 \left( {F_{22} - c_1 H_{22} } \right)\frac{\partial ^3\phi _y }{\partial y^3} + L - \gamma \dot {w}_0 = \\ I_0 \ddot {w}_0 - c_1^2 I_6 \left( {\frac{\partial ^2\ddot {w}_0 }{\partial x^2} + \frac{\partial ^2\ddot {w}_0 }{\partial y^2}} \right) + \\ c_1 I_3 \left( \frac{\partial \ddot{u}_0 }{\partial x} + \frac{\partial \ddot{v}_0}{\partial y}\right) + c_1 J_4 \left( \frac{\partial \ddot{\phi }_x }{\partial x} + \frac{\partial \ddot{\phi }_y }{\partial y}\right)\tag{23c}$$
$$\left( {D_{11} - 2c_1 F_{11} + c_1^2 H_{11} } \right)\frac{\partial ^2\phi _x }{\partial x^2} + \\ \left( {D_{66} - 2c_1 F_{66} + c_1^2 H_{66} } \right)\frac{\partial ^2\phi _x }{\partial y^2} + c_1 \left( {F_{11} - c_1 H_{11} } \right)\cdot \\ \frac{\partial ^3w_0 }{\partial x^3}- \left( {A_{55} - 2c_2 D_{55} + c_2^2 F_{55} } \right)\frac{\partial w_0 }{\partial x} + \big( D_{12} + \\ D_{66} + c_1^2 H_{66} - 2c_1 F_{66} + c_1^2 H_{12} - 2c_1 F_{12} \big)\cdot\\\frac{\partial ^2\phi _y }{\partial x\partial y} c_1 \left( {F_{12} + 2F_{66} - c_1 H_{12} - 2c_1 H_{66} } \right)\frac{\partial ^3w_0 }{\partial x\partial y^2} + \\ \left( {2c_2 D_{55} - A_{55} - c_2^2 F_{55} } \right)\phi _x = \\ J_1 \ddot {u}_0 + K_2 \ddot {\phi }_x - c_1 J_4 \frac{\partial \ddot {w}_0 }{\partial x}\tag{23d}$$
$$\left( {D_{66} - 2c_1 F_{66} + c_1^2 H_{66} } \right)\frac{\partial ^2\phi _y }{\partial x^2} - \\ c_1 \left( {F_{21} + 2F_{66} - c_1 H_{21} - 2c_1 H_{66} } \right)\frac{\partial ^3w_0}{\partial x^2\partial y} - \\ c_1 \left( {F_{22} - c_1 H_{22} } \right)\frac{\partial ^3w_0 }{\partial y^3} +\big( D_{21} + D_{66} + c_1^2 H_{21} - \\2c_1 F_{21} + c_1^2 H_{66} - 2c_1 F_{66} \big)\frac{\partial ^2\phi _x }{\partial x\partial y} +\big( c_1^2 H_{22} + D_{22} - \\ 2c_1 F_{22} \big)\frac{\partial ^2\phi _y }{\partial x^2} - \left( {F_{44} c_2^2 - 2c_2 D_{44} + A_{44} } \right)\frac{\partial w_0 }{\partial y} + \\ \left( {2c_2 D_{44} - A_{44} - c_2^2 F_{44} } \right)\phi _y= \\ J_1 \ddot {v}_0 + K_2 \ddot {\phi }_y - c_1 J_4 \frac{\partial \ddot {w}_0 }{\partial y}\tag{23e}$$
悬臂板的边界条件为
$$x = 0:w = v = u = \phi_y = \phi _x = 0\tag{24a}$$
$$x = a:N_{xx} = N_{xy} = M_{xx} = M_{xy} - c{ }_1P_{xy} = \bar {Q}_x = 0\qquad\quad\tag{24b}$$
$$y = 0:N_{xy} = N_{yy} = M_{yy} = M{ }_{xy} - c_1 P_{xy} = \bar {Q}_y = 0\qquad\quad\tag{24c}$$
$$y = b:N_{xy} = N_{yy} = M_{yy} = M_{xy} - c_1 P_{xy} = \bar {Q}_y = 0\qquad\quad\tag{24d}$$
$$\bar {Q}_x = Q_x + \frac{\partial M_{xy} }{\partial y} - c{ }_2R_x + c_1 \left( {\frac{\partial P_{xx} }{\partial x} + \frac{\partial P_{xy} }{\partial y}} \right)\qquad\quad\tag{25a}$$
$$\bar {Q}_y = Q_y + \frac{\partial M_{xy} }{\partial x} - c_2 R_y + c_1 \left( {\frac{\partial P_{yy} }{\partial y} + \frac{\partial P_{xy} }{\partial x}} \right)\qquad\quad\tag{25b}$$
引入无量纲的参数,进行无量纲处理
$$ \left.\begin{array}{l} \bar {w} = \dfrac{w_0 }{h}, \bar {t} = t\pi ^2\left( {\dfrac{E}{ab\rho }} \right)^{\frac{1}{2}}, \bar {A}_{ij} = \dfrac{A_{ij} \left( {ab} \right)^{\frac{1}{2}}}{Eh^2}\\ \bar {B}_{ij} = \dfrac{\left( {ab} \right)^{\frac{1}{2}}}{Eh^3}B_{ij}, \bar {D}_{ij} = \dfrac{\left( {ab} \right)^{\frac{1}{2}}}{Eh^4}D_{ij}, \bar {E}_{ij} = \dfrac{\left( {ab} \right)^{\frac{1}{2}}}{Eh^5}E_{ij}\\ \bar {F}_{ij} = \dfrac{\left( {ab} \right)^{\frac{1}{2}}}{Eh^6}F_{ij}, \bar {H}_{ij} = \dfrac{\left( {ab} \right)^{\frac{1}{2}}}{Eh^8}H_{ij}m \bar {I}_i = \dfrac{1}{\left( {ab} \right)^{\frac{i + 1}{2}}\rho }I_i\\ \bar {\gamma } = \dfrac{\left( {ab} \right)^2}{\pi ^2h^4\left( {\rho E} \right)^{\frac{1}{2}}}\gamma , \quad \bar {x} = \dfrac{x}{a}, \quad \bar {y} = \dfrac{b}{y}\\ \bar {\varOmega }_i = \dfrac{1}{\pi ^2}\left( {\dfrac{E}{ab\rho }} \right)^{\frac{1}{2}}\varOmega _i, \quad \bar {F} = \dfrac{b^2}{Eh^3}F\end{array}\right\}\tag{26} $$
利用Galerkin方法对系统微分方程进行离散
$$w_0 = w_1 \left( t \right)X_1 \left( x \right)Y_1 \left( y \right) + w_2 \left( t \right)X_2 \left( x \right)Y_2 \left( y \right)\tag{27}$$
其中
$$ X_i \left( x \right) = \sin \frac{\lambda _i }{a}x - \sinh \frac{\lambda _i }{a}x + \\ \alpha _i \left( {\cosh \frac{\lambda _i }{a}x - \cos \frac{\lambda _i }{a}x} \right)\tag{28a}$$
$$Y_j \left( y \right) = \sin \frac{\beta _m }{b}y + \sinh \frac{\beta _m }{b}y -\\ \alpha _m \left( {\cosh \frac{\beta _m }{b}y + \cos \frac{\beta _m }{b}y} \right)\tag{28b}$$
这里
$$\cos \lambda _i a\cosh \lambda _i a - 1 = 0\tag{29a}$$
$$\cos \beta _m b\cosh \beta _m b - 1 = 0\tag{29b}$$
$$\alpha _i = \frac{\cosh \lambda _i - \cos \lambda _i }{\sinh \lambda _i + \sin \lambda _i }\tag{29c}$$
$$\alpha _m = - \frac{\cosh \beta _m - \cos \beta _m }{\sinh \beta _m - \sin \beta _m }\tag{29d}$$
同样,对平板所受到法向的气动载荷进行离散
\begin{equation}\label{eq65} L = l_1 X_1 \left( x \right)Y_1 \left( y \right) +l_2 X_2 \left( x \right)Y_2 \left( y \right)\tag{30}\end{equation}
得到两自由度横向振动微分方程
$$\ddot {w}_1 + \gamma _{11} \dot {w}_1 + \omega _1^2 w_1 + \gamma _{12} f_1 \cos \varOmega _1 tw_1 + \gamma _{13} w_2 - \gamma _{14} w -\\ \gamma _{15} w_1^2 w_2 - \gamma _{16} w_1 w_2^2 - \gamma _{17} w_2^3 = \gamma _{18} l_1 \cos \varOmega _2 t\tag{31a}$$
$$\ddot {w}_2 + \gamma _{21} \dot {w}_2 + \omega _2^2 w_2 + \gamma _{22} f_1 \cos \varOmega _1 tw_2 + \gamma _{23} w_1 - \gamma _{24} w_2^3 -\\ \gamma _{25} w_2^2 w_1 - \gamma _{26} w_2 w_1^2 - \gamma _{27} w_1^3 = \gamma _{28} l_2 \cos \varOmega _2 t\tag{31b}$$
3 悬臂复合材料层合板的固有特性
为了研究复合材料层合板不同模态间的内共振关系,建立了悬臂层合板的有限元模型,计算不同展弦比及厚度条件下悬臂层合板的固有频率.层合板的铺设形式采用$[0^ \circ/90^ \circ ]_{\rm 3s}$铺设,材料参数T300/QY8911的$E_{11}=135$ GPa,$E_{22}=88$GPa,$S_{12}=45$ GPa,$\upsilon=0.33$. 其中,单层厚度为$h_i~(i =1,2,\cdots ,6)$. 考虑了不同展弦比$c$的矩形层合板,$c = 1,2,3\cdots,4$.计算了不同展弦比和不同层厚的复合材料层合悬臂板弯曲振动的固有频率,图5$\sim$\!图8给出了不同模态间的比较结果.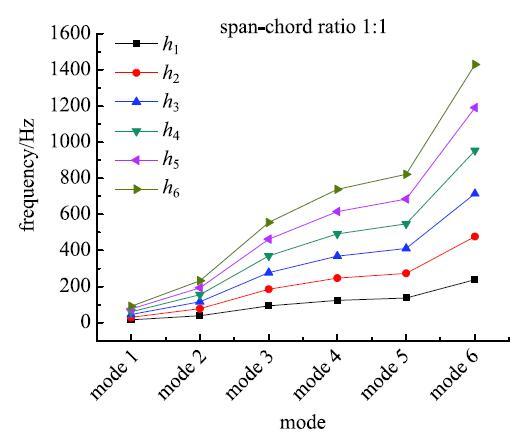
显示原图|下载原图ZIP|生成PPT图5展弦比1:1时前六阶固有频率
-->Fig. 5Natural frequencies with different thickness under the span-chord ratio 1:1
-->
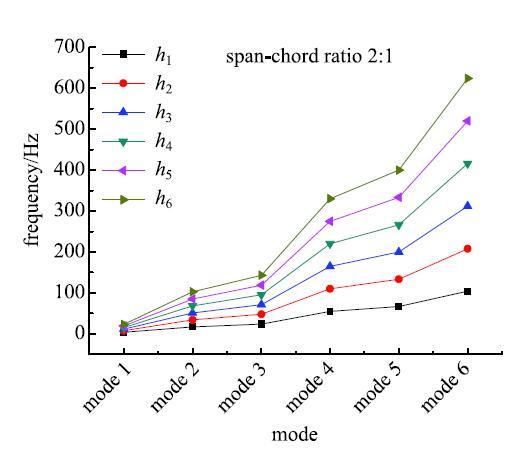显示原图|下载原图ZIP|生成PPT图6展弦比2:1时前六阶固有频率
-->Fig. 6Natural frequencies with different thickness under the span-chord ratio 2:1
-->
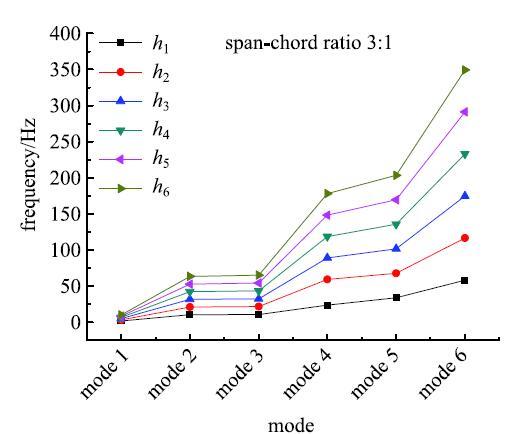显示原图|下载原图ZIP|生成PPT图7展弦比3:1时前六阶固有频率
-->Fig. 7Natural frequencies with different thickness under the span-chord ratio 3:1
-->
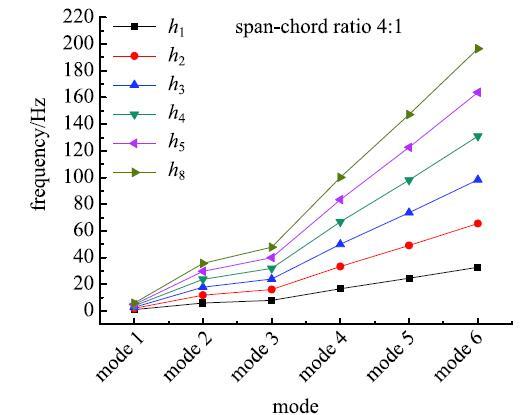显示原图|下载原图ZIP|生成PPT图8展弦比4:1时前六阶固有频率
-->Fig. 8Natural frequencies with different thickness under the span-chord ratio 4:1
-->
从图5$\sim$图8给出的复合材料层合悬臂板的频率中可以看到,在不同材料参数及结构几何参数下,悬臂复合材料层合板横向弯曲模态存着1:1,1:2及1:3等比例关系,这里我们考虑两阶弯曲模态的1:2内共振关系去研究悬臂复合材料层合板在气动载荷及面内激励共同作用下的非线性动力学响应.
4 非线性振动响应分析
通过多尺度方法[33]得到系统的平均方程,考虑1:2内共振关系$$\omega _1^2 = \frac{1}{4}\varOmega _1^2 + \varepsilon \sigma _1\tag{32a}$$
$$\omega _2^2 = \varOmega _2^2 + \varepsilon \sigma _2\tag{32b}$$
$$\varOmega _1 = \varOmega _2 = 1\tag{32c}$$
其中,$\omega _1 $和$\omega _2$为悬臂复合材料层合板的两阶模态频率,$\sigma _1 $和$\sigma _2$为调谐参数.
对方程中的参数进行尺度变换
\begin{equation}\label{eq71} \gamma _{ij} \to \varepsilon \gamma _{ij}, \quad i =1,2;j = 1,2\cdots,8\tag{33}\end{equation}
将式(38)中参数代入式(36),得到
$$\ddot {w}_1 + \varepsilon \gamma _{11} \dot {w}_1 + \omega _1^2 w_1 + \varepsilon \gamma _{12} f_1 \cos \varOmega _1 tw_1 + \varepsilon \gamma _{13} w_2 -\\ \varepsilon \gamma _{14} w_1^3 - \varepsilon \gamma _{15} w_1^2 w_2 - \varepsilon \gamma _{16} w_1 w_2^2 - \varepsilon \gamma _{17} w_2^3 = \\ \varepsilon \gamma _{18} l_1 \cos \varOmega _2 t\tag{34a}$$
$$\ddot {w}_2 + \varepsilon \gamma _{21} \dot {w}_2 + \omega _2^2 w_2 + \varepsilon \gamma _{22} f_1 \cos \varOmega _1 tw_2 + \varepsilon \gamma _{23} w_1 -\\ \varepsilon \gamma _{24} w_2^3 - \varepsilon \gamma _{25} w_2^2 w_1 - \varepsilon \gamma _{26} w_2 w_1^2 - \varepsilon \gamma _{27} w_1^3 = \\ \varepsilon \gamma _{28} l_2 \cos \varOmega _2 t\tag{34b}$$
对横向位移进行一次近似
\begin{equation}\label{eq73} w\left( {x,t,\varepsilon } \right) = w_0 \left({x,T_0 ,T_1 } \right) + \varepsilon w_1 \left( {x,T_0 ,T_1 }\right)\tag{35}\end{equation}
其中,$T_0 = t$,$T_1 = \varepsilon t$.
定义微分算子
$$\frac{{\rm d}}{{\rm d}t} = \frac{\partial }{\partial T_0 }\frac{{\rm d}T_0 }{{\rm d}t} + \frac{\partial }{\partial T_1 }\frac{{\rm d}T_1 }{{\rm d}t} + \cdots = {\rm D}_0 + \varepsilon {\rm D}_1 + \cdots\qquad\quad\tag{36a}$$
$$\frac{{\rm d}^2}{{\rm d}t^2} = \left( {{\rm D}_0 + \varepsilon {\rm D}_1 + \cdots } \right)^2 = {\rm D}_0^2 + 2\varepsilon {\rm D}_0 {\rm D}_1 + \cdots\qquad\quad\tag{36b}$$
其中,${\rm D}_n = \dfrac{\partial }{\partial T_n }$, $n = 0,\;1,\;2,\; \cdots $.
将微分算子式(36)和横向位移展开式(35)代入式(34)中,相处长期项后,得到如下平均方程
$${\rm D}_1 A_1 = - \frac{1}{2}\gamma _{11} A_1 + {\rm i}\sigma _1 A_1 + \frac{1}{2}{\rm i}\gamma _{12} f_1 \bar {A}_1 -\\ 3{\rm i}A_1^2 \bar {A}_1 \gamma _{13} - 2{\rm i}\gamma _{16} A_1 A_2 \bar {A}_2\tag{37a}$$
$${\rm D}_1 A_2 = - \frac{1}{2}\gamma _{21} A_2 + \frac{1}{2}{\rm i}\sigma _2 A_2 - \frac{3}{2}{\rm i}\gamma _{23} A_2^2 \bar {A}_2 -\\ {\rm i}\gamma _{26} A_1 A_2 \bar {A}_1 - \frac{1}{4}{\rm i}\gamma _{28} L_2\tag{37b}$$
令
\begin{equation} \label{eq78} A_1 \left( {T_1 } \right) = \frac{1}{2}a_1 \left( {T_1 } \right){\rm e}^{{\rm i}\varphi \left( {T_1 } \right)}, \quad A_2 \left( {T_2 } \right) = \frac{1}{2}a_2 \left( {T_2 } \right){\rm e}^{{\rm i}\varphi \left( {T_2 } \right)}\tag{38} \end{equation}
将式(38)代入式(37)中,将实部与虚部分离,得到极坐标形式的四维平均方程
$$\dot {a}_1 = - \frac{1}{4}\bigg( {\gamma _{11} a_1 \sin \varphi _1 - 2\sigma _1 a_1 \cos \varphi _1 - \gamma _{12} a_1 f_1 \cos \varphi _1 } +\\ {\frac{3}{2}\gamma _{14} a_1^3 \cos \varphi _1 + \gamma _{16} a_1 a_2^2 \sin \varphi _1 } \bigg)\tag{39a}$$
$$ a_1 \dot {\varphi }_1 = - \frac{1}{4}\bigg( {\gamma _{11} a_1 \cos \varphi _1 + 2\sigma _1 a_1 \sin \varphi _1 + \gamma _{12} a_1 f_1 \sin \varphi _1 } -\\ {\frac{3}{2}\gamma _{14} a_1^3 \sin \varphi _1 + \gamma _{16} a_1 a_2^2 \cos \varphi _1 } \bigg)\tag{39b}$$
$$ \dot {a}_2 = - \frac{1}{4}\bigg( {\gamma _{21} a_2 \sin \varphi _2 - \sigma _2 a_2 \cos \varphi _2 + \frac{3}{4}\gamma _{24} a_2^3 \cos \varphi _2 } +\\ {\frac{1}{2}\gamma _{26} a_2 a_1^2 \sin \varphi _2 + \gamma _{28} l_2 } \bigg)\tag{39c}$$
$$ a_2 \dot {\varphi }_2 = - \frac{1}{4}\bigg( {\gamma _{21} a_2 \cos \varphi _2 + \sigma _2 a_2 \sin \varphi _2 + \frac{3}{4}\gamma _{24} a_2^3 \sin \varphi _2 } +\\ d{\frac{1}{2}\gamma _{26} a_2 a_1^2 \cos \varphi _2 } \bigg)\tag{39d}$$
为了研究悬臂复合材料层合板的非线性振动特性,基于式(39),推导系统的幅频特性关系.令$\dot {a}_1 = \dot {a}_2 = \dot {\varphi }_1 = \dot {\varphi }_2= 0$,$\varphi _1 = \dfrac{\pi }{4}$以及$\varphi _2 =\dfrac{3\pi}{4}$,频响函数如下
$$0 = \gamma _{11} a_1 - 2\sigma _1 a_1 - \gamma _{12} a_1 f_1 + \frac{3}{2}\gamma _{14} a_1^3 + \gamma _{16} a_1 a_2^2\qquad\quad\tag{40a}$$
$$ 0 = \gamma _{21} a_2 + \sigma _2 a_2 - \frac{3}{4}\gamma _{24} a_2^3 + \frac{1}{2}\gamma _{26} a_2 a_1^2 + \sqrt 2 \gamma _{28} l_2\qquad\quad\tag{40b} $$
在方程(40)中幅值$a_1 $和幅值$a_2$是耦合的,这里引入一个比例系数$\varepsilon $,即 $\dfrac{a_1}{a_2 } = \varepsilon $,分析幅值随着调谐参数变化情况.基于结构的几何及材料属性选取系数$\gamma _{11} = 0.2$,$\gamma_{12} = - 6$,$\gamma _{14} = 5$,$\gamma _{16} = - 5$,$\gamma_{21} = 0.6$,$\gamma _{24} = 9$,$\gamma _{28} = - 2$.得到了系统幅值随着调谐参数变化的关系. 图10给出了幅值$a_1$随着调谐参数$\sigma _1 $在不同内力幅值$f_1$时的变化情况,图11给出了幅值$a_2 $ 随着调谐参数$\sigma _2$在不同横向气动载荷幅值$l_2 $时的变化情况.从图9和图10中可以看到,在幅值随着调谐参数的变化中,存在着刚度硬化的现象.在$A^*$点和$B^*$点,幅值存在着跳跃现象,随着外激励幅值加大,幅值的频响范围也随之加大.
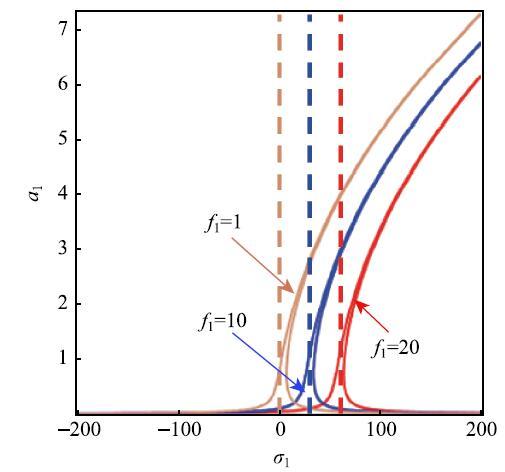显示原图|下载原图ZIP|生成PPT图9选取不同内力幅值$f_1 $时,幅值$a_1$随着调谐参数$\sigma _1$的\linebreak 变化情况
-->Fig. 9The relationship between amplitude $a_1 $ and tuning parameter $\sigma _1 $ in different internal force amplitude $f_1 $
-->
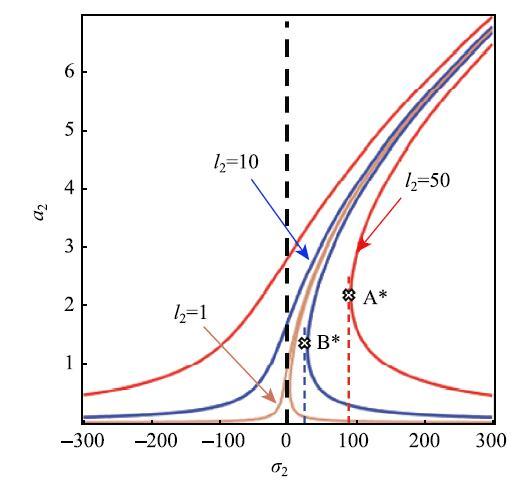显示原图|下载原图ZIP|生成PPT图10选取不同内力幅值$l_2 $时,幅值$a_2$随着调谐参数$\sigma _2$的\linebreak 变化情况
-->Fig. 10The relationship between amplitude $a_2 $ and tuning parameter $\sigma _2 $ in different internal force amplitude $l_2$
-->
5 总 结
本文分析了复合材料层合矩形悬臂板在亚音速气动力作用和面内激励作用下的非线性振动响应.以飞行器翼面为背景,将亚音速气流中的翼面简化为复合材料层合板悬臂板.与二维无限长翼面不同,有限长翼面受到的气动载荷是沿着展向逐渐减小的.根据理想不可压缩流体的流动条件和 Kutta--Joukowski升力定理,利用涡格法计算了有限长平板翼面上的亚音速气动升力.然后,引入冯$\cdot$卡门几何非线性,基于三阶剪切变形板理论,利用哈密顿原理建立了在亚声速气动载荷下的复合材料层合悬臂板运动的非线性偏微分控制方程.通过有限元方法计算了不同几何参数下复合材料层合矩形悬臂板的固有特性,找到了不同模态间的频率比.利用Galerkin方法将偏微分方程进行截断,考虑两阶弯曲模态,得到两自由度的非线性常微分方程,通过比较不同材料和几何参数的线性系统的固有频率,在这里考虑了1:2的内部共振. 对应多个选取参数,对结构的幅频特性关系进行了分析.随着面内参数以及横向气动参数的变化,结构存在着硬弹簧特性及幅值跳跃现象.The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . 对于大长细比导弹，需要在设计阶段准确计算气动弹性/气动伺服弹性，但其复杂的气动力给计算带来困难，因此气动力降阶模型是突破大长细比导弹跨音速气动弹性分析与控制瓶颈的关键技术.虽然气动力模型降阶方法已在预测二维机翼结构的气动弹性方面取得重要进展，但几乎未见关于全机模型的气动力降阶模型研究报道.本文基于递归Wiener模型的气动力降阶方法，利用CFD计算的气动力作为模型辨识数据，用鲁棒子空间和Levenberg-Marquardt算法辨识降阶模型参数，建立了大长细比导弹气动力降阶模型.在此基础上与大长细比导弹有限元模型相结合，构造出气动弹性降阶模型，并在数值仿真中测试气动弹性降阶模型在不同马赫数下的适用性.数值仿真结果表明，该气动弹性降阶模型能够精确预测导弹模型在不同飞行条件下的非定常气动力和导弹模型的气动弹性频率响应特性. . 对于大长细比导弹，需要在设计阶段准确计算气动弹性/气动伺服弹性，但其复杂的气动力给计算带来困难，因此气动力降阶模型是突破大长细比导弹跨音速气动弹性分析与控制瓶颈的关键技术.虽然气动力模型降阶方法已在预测二维机翼结构的气动弹性方面取得重要进展，但几乎未见关于全机模型的气动力降阶模型研究报道.本文基于递归Wiener模型的气动力降阶方法，利用CFD计算的气动力作为模型辨识数据，用鲁棒子空间和Levenberg-Marquardt算法辨识降阶模型参数，建立了大长细比导弹气动力降阶模型.在此基础上与大长细比导弹有限元模型相结合，构造出气动弹性降阶模型，并在数值仿真中测试气动弹性降阶模型在不同马赫数下的适用性.数值仿真结果表明，该气动弹性降阶模型能够精确预测导弹模型在不同飞行条件下的非定常气动力和导弹模型的气动弹性频率响应特性. |
| [2] | . <p>功能梯度材料的宏观物理性能随空间位置连续变化,能充分减少不同组份材料结合部位界面性能的不匹配因素.功能梯度壁板用作高速飞行器的热防护结构,能有效消除气动加热带来的壁板内部热应力集中.本文考虑热过屈曲变形引入的结构几何非线性,分析功能梯度壁板的气动弹性颤振边界.基于幂函数材料分布假设,采用混合定律计算功能梯度材料的等效力学性能.根据一阶剪切变形板理论、冯·卡门应变-位移关系和一阶活塞理论,基于虚功原理建立超声速气流中受热功能梯度壁板的非线性气动弹性有限元方程.采用牛顿-拉弗森迭代法数值求解壁板的热屈曲变形,分析超声速气流对热屈曲变形的影响机理.在壁板热过屈曲的静力平衡位置分析动态稳定性,确定了壁板的颤振边界.研究表明,当陶瓷-金属功能梯度壁板的组份材料沿厚度方向梯度分布时,会破坏结构的对称性导致壁板在面内热应力作用下发生指向金属侧的热屈曲变形.超声速气流中壁板热屈曲变形最大的位置随气流速压增大向下游推移,并伴随屈曲变形量的减小.热过屈曲壁板的几何非线性效应会提高壁板的颤振边界,这种影响在高温、低无量纲速压且壁板发生大挠度热屈曲变形时表现显著.较高无量纲气流速压下由于壁板的热屈曲变形被气动力限定在小挠度范围,几何非线性效应不明显.</p> . <p>功能梯度材料的宏观物理性能随空间位置连续变化,能充分减少不同组份材料结合部位界面性能的不匹配因素.功能梯度壁板用作高速飞行器的热防护结构,能有效消除气动加热带来的壁板内部热应力集中.本文考虑热过屈曲变形引入的结构几何非线性,分析功能梯度壁板的气动弹性颤振边界.基于幂函数材料分布假设,采用混合定律计算功能梯度材料的等效力学性能.根据一阶剪切变形板理论、冯·卡门应变-位移关系和一阶活塞理论,基于虚功原理建立超声速气流中受热功能梯度壁板的非线性气动弹性有限元方程.采用牛顿-拉弗森迭代法数值求解壁板的热屈曲变形,分析超声速气流对热屈曲变形的影响机理.在壁板热过屈曲的静力平衡位置分析动态稳定性,确定了壁板的颤振边界.研究表明,当陶瓷-金属功能梯度壁板的组份材料沿厚度方向梯度分布时,会破坏结构的对称性导致壁板在面内热应力作用下发生指向金属侧的热屈曲变形.超声速气流中壁板热屈曲变形最大的位置随气流速压增大向下游推移,并伴随屈曲变形量的减小.热过屈曲壁板的几何非线性效应会提高壁板的颤振边界,这种影响在高温、低无量纲速压且壁板发生大挠度热屈曲变形时表现显著.较高无量纲气流速压下由于壁板的热屈曲变形被气动力限定在小挠度范围,几何非线性效应不明显.</p> |
| [3] | . 针对激波主导流动下弹性壁板的热气动弹性稳定性分析问题,建立了基于当地活塞流理论的分析模型,并用数值仿真方法来验证其正确性.首先基于Hamilton原理和Von-Karman大变形理论,建立壁板的热气动弹性运动方程,其中假设壁板受热后温度均匀分布,激波前后区域的气动力模型采用当地一阶活塞流理论;利用Galerkin方法将具有连续参数系统的偏微分颤振方程离散为有限个自由度的常微分方程;基于李雅普诺夫间接法将非线性颤振方程组在平衡位置处进行线化,再用Routh-Hurwits判据来判断线性系统的稳定性,从而来推论出非线性颤振系统的气动弹性稳定性.在时域中采用龙格--库塔法对非线性颤振方程进行数值积分,得到壁板非线性颤振响应的时间历程,与理论分析结果进行对比.研究结果表明,壁板受到斜激波冲击时,更容易发生颤振失稳,并且激波强度越大,极限环幅值和频率越大;激波主导流场中的壁板失稳边界不同于传统单纯超声速气流中壁板颤振的失稳边界;只有在斜激波前后不同的动压值都满足颤振稳定性边界的条件下,壁板才可能保持其气动弹性稳定性. . 针对激波主导流动下弹性壁板的热气动弹性稳定性分析问题,建立了基于当地活塞流理论的分析模型,并用数值仿真方法来验证其正确性.首先基于Hamilton原理和Von-Karman大变形理论,建立壁板的热气动弹性运动方程,其中假设壁板受热后温度均匀分布,激波前后区域的气动力模型采用当地一阶活塞流理论;利用Galerkin方法将具有连续参数系统的偏微分颤振方程离散为有限个自由度的常微分方程;基于李雅普诺夫间接法将非线性颤振方程组在平衡位置处进行线化,再用Routh-Hurwits判据来判断线性系统的稳定性,从而来推论出非线性颤振系统的气动弹性稳定性.在时域中采用龙格--库塔法对非线性颤振方程进行数值积分,得到壁板非线性颤振响应的时间历程,与理论分析结果进行对比.研究结果表明,壁板受到斜激波冲击时,更容易发生颤振失稳,并且激波强度越大,极限环幅值和频率越大;激波主导流场中的壁板失稳边界不同于传统单纯超声速气流中壁板颤振的失稳边界;只有在斜激波前后不同的动压值都满足颤振稳定性边界的条件下,壁板才可能保持其气动弹性稳定性. |
| [4] | . 复合材料层合板壳是由多种组分材料组合而成.与单一材料的板壳结构相比,它无明确的材料主方向,各层间材料间断和不连续,具有明显的几何非线性和材料非线性等新的特点.其失效模式也远比单一材料的情况复杂,具有如基体开裂、脱胶、分层、分层裂纹偏转、多分层以及分层传播等多种模式.各国****基于不同的考虑,提出了多种方法研究复合材料层合板壳的失效.首先,在简要介绍了层合板壳线性力学基本理论的基础上,重点回顾了层合板壳结构非线性力学几种基本理论发展的过程,主要阐述了经典大挠度非线性理论、一阶剪切变形理论、高阶剪切变形理论、锯齿理论、广义分层理论的理论体系及基本公式,并对几种理论之间的联系和差异进行了总结;其次,介绍了当前层合结构非线性领域的研究进展,综述了典型复合材料板壳结构的失效机理及优化设计、复合材料板壳结构在复杂环境下的破坏机理、复合材料板壳结构的物理非线性、含脱层纤维增强复合材料板壳结构的破坏机理等各研究热点的最新研究成果;最后,对该领域未来的研究方向进行了展望. . 复合材料层合板壳是由多种组分材料组合而成.与单一材料的板壳结构相比,它无明确的材料主方向,各层间材料间断和不连续,具有明显的几何非线性和材料非线性等新的特点.其失效模式也远比单一材料的情况复杂,具有如基体开裂、脱胶、分层、分层裂纹偏转、多分层以及分层传播等多种模式.各国****基于不同的考虑,提出了多种方法研究复合材料层合板壳的失效.首先,在简要介绍了层合板壳线性力学基本理论的基础上,重点回顾了层合板壳结构非线性力学几种基本理论发展的过程,主要阐述了经典大挠度非线性理论、一阶剪切变形理论、高阶剪切变形理论、锯齿理论、广义分层理论的理论体系及基本公式,并对几种理论之间的联系和差异进行了总结;其次,介绍了当前层合结构非线性领域的研究进展,综述了典型复合材料板壳结构的失效机理及优化设计、复合材料板壳结构在复杂环境下的破坏机理、复合材料板壳结构的物理非线性、含脱层纤维增强复合材料板壳结构的破坏机理等各研究热点的最新研究成果;最后,对该领域未来的研究方向进行了展望. |
| [5] | . ABSTRACT A review is made of the different approaches used for modeling multilayered composite plates. Discussion focuses on different approaches for developing two-dimensional shear deformation theories; classification of two-dimensional theories based on introducing plausible displacement, strain and/or stress assumptions in the thickness direction; and first-order shear deformation theories based on linear displacement assumptions in the thickness coordinate. Extensive numerical results are presented showing the effects of variation in the lamination and geometric parameters of simply supported composite plates on the accuracy of the static and vibrational responses predicted by six different modeling approaches (based on two-dimensional shear deformation theories). The standard of comparison is taken to be the exact three-dimensional elasticity solutions. Some of the future directions for research on the modeling of multilayered composite plates are outlined. |
| [6] | . http://linkinghub.elsevier.com/retrieve/pii/0263822389900585 |
| [7] | |
| [8] | Two-mode responses of thin rectangular laminated plates subjected to a harmonic excitation are studied by using the method of multiple scales (MMS). The plates are assumed to be simply supported along all edges, and internal resonances between two symmetric modes of vibration are analysed. In order to use MMS properly, we introduce new detuning parameters which indicate the relationship of natural frequencies of each mode. It is found analytically that two-mode responses can occur at each primary resonance. The accuracy of analytical results is confirmed in comparison with results of numerical integration of the equation of motion. Furthermore, it is detected that the two-mode response near the primary resonance of the second mode loses its stability via a Hopf bifurcation, giving rise to quasi-periodic response. |
| [9] | . The subharmonic resonance of simply supported, rectangular laminated plates is investigated by the method of multiple scales. The governing equations for the plate, which is based on the first order shear deformation and the von K谩rm谩n-type geometric non-linear theories, are derived by Hamilton's principle. The application of Galerkin's procedure to the governing equations yields the Duffing-type equation in terms of the transverse displacement. In order to use the method of multiple scales properly, we introduce new detuning parameters for the analysis of the subharmonic resonance. The influence of the lamination sequence, thickness ratio, number of layers and in-plane boundary condition is examined on the subharmonic resonance. The analytical result are compared with those obtained by the Runge-Kutta method, and the validity of the present analysis is clearly shown. |
| [10] | . We experimentally investigated nonlinear combination resonances in two graphite-epoxy cantilever plates having the configurations (90/30/-30/-30/30/90) s and (-75/75/75/-75/75/-75) s . As a first step, we compared the natural frequencies and modes shapes obtained from the finite-element and experimental-modal analyses. The largest difference in the obtained frequencies for both plates was 6%. Then, we transversely excited the plates and obtained force-response and frequency-response curves, which were used to characterize the plate dynamics. We acquired time-domain data for specific input conditions using an A/D card and used them to generate time traces, power spectra, pseudo-state portraits, and Poincar茅 maps. The data were obtained with an accelerometer monitoring the excitation and a laser vibrometer monitoring the plate response. We observed the external combination resonance % MathType!MTEF!2!1!+-% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn% hiov2DGi1BTfMBaeXafv3ySLgzGmvETj2BSbqefm0B1jxALjhiov2D% aebbfv3ySLgzGueE0jxyaibaiGc9yrFr0xXdbba91rFfpec8Eeeu0x% Xdbba9frFj0-OqFfea0dXdd9vqaq-JfrVkFHe9pgea0dXdar-Jb9hs% 0dXdbPYxe9vr0-vr0-vqpWqaaeaabiGaciaacaqabeaadaqaaqGaaO% qaaiabfM6axjabgIKi7kabeM8a3naaBaaaleaacaaIYaaabeaakiab% gUcaRiabeM8a3naaBaaaleaacaaI3aaabeaaaaa!45C9!\[\Omega \approx \omega _2 + \omega _7 \] in the quasi-isotropic plate and the external combination resonance % MathType!MTEF!2!1!+-% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn% hiov2DGi1BTfMBaeXafv3ySLgzGmvETj2BSbqefm0B1jxALjhiov2D% aebbfv3ySLgzGueE0jxyaibaiGc9yrFr0xXdbba91rFfpec8Eeeu0x% Xdbba9frFj0-OqFfea0dXdd9vqaq-JfrVkFHe9pgea0dXdar-Jb9hs% 0dXdbPYxe9vr0-vr0-vqpWqaaeaabiGaciaacaqabeaadaqaaqGaaO% qaaiabfM6axjabgIKi7kaacIcacaaIXaGaai4laiaaikdacaGGPaGa% aiikaiabeM8a3naaBaaaleaacaaIYaaabeaakiabgUcaRiabeM8a3n% aaBaaaleaacaaI1aaabeaakiaacMcaaaa!4AAD!\[\Omega \approx (1/2)(\omega _2 + \omega _5 )\] and the internal combination resonance % MathType!MTEF!2!1!+-% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn% hiov2DGi1BTfMBaeXafv3ySLgzGmvETj2BSbqefm0B1jxALjhiov2D% aebbfv3ySLgzGueE0jxyaibaiGc9yrFr0xXdbba91rFfpec8Eeeu0x% Xdbba9frFj0-OqFfea0dXdd9vqaq-JfrVkFHe9pgea0dXdar-Jb9hs% 0dXdbPYxe9vr0-vr0-vqpWqaaeaabiGaciaacaqabeaadaqaaqGaaO% qaaiabfM6axjabgIKi7kabeM8a3naaBaaaleaacaaI4aaabeaakiab% gIKi7kaacIcacaaIXaGaai4laiaaikdacaGGPaGaaiikaiabeM8a3n% aaBaaaleaacaaIYaaabeaakiabgUcaRiabeM8a3naaBaaaleaacaaI% XaGaaG4maaqabaGccaGGPaaaaa!4FDC!\[\Omega \approx \omega _8 \approx (1/2)(\omega _2 + \omega _{13} )\] in the 卤75 plate, where the % MathType!MTEF!2!1!+-% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn% hiov2DGi1BTfMBaeXafv3ySLgzGmvETj2BSbqefm0B1jxALjhiov2D% aebbfv3ySLgzGueE0jxyaibaiGc9yrFr0xXdbba91rFfpec8Eeeu0x% Xdbba9frFj0-OqFfea0dXdd9vqaq-JfrVkFHe9pgea0dXdar-Jb9hs% 0dXdbPYxe9vr0-vr0-vqpWqaaeaabiGaciaacaqabeaadaqaaqGaaO% qaaiabeM8a3naaBaaaleaacaWGPbaabeaaaaa!3F16!\[\omega _i \] are the natural frequencies of the plate and 惟 is the excitation frequency. The results show that a low-amplitude high-frequency excitation can produce a high-amplitude low-frequency motion. |
| [11] | . A general nonlinear theory for the dynamics of elastic anisotropic plates undergoing moderate-rotation vibrations is presented. The theory fully accounts for geometric nonlinearities (moderate rotations and displacements) by using local stress and strain measures and an exact coordinate transformation, which result in nonlinear curvatures and strain-displacement expressions that contain the von Karman strains as a special case. The theory accounts for transverse shear deformations by using a third-order theory and for extensionality and changes in the configuration due to in-plane and transverse deformations. Five third-order nonlinear partial-differential equations of motion describing the extension-extension-bending-shear-shear vibrations of plates are obtained by an asymptotic analysis, which reveals that laminated plates display linear elastic and nonlinear geometric couplings among all motions. |
| [12] | . A general geometrically exact nonlinear theory for the dynamics of laminated plates and shells under-going large-rotation and small-strain vibrations in three-dimensional space is presented. The theory fully accounts for geometric nonlinearities by using the new concepts of local displacements and local engineering stress and strain measures, a new interpretation and manipulation of the virtual local rotations, an exact coordinate transformation, and the extended Hamilton principle. Moreover, the model accounts for shear coupling effects, continuity of interlaminar shear stresses, free shear-stress conditions on the bonding surfaces, and extensionality. Because the only differences among different plates and shells are the initial curvatures of the coordinates used in the modeling and all possible initial curvatures are included in the formulation, the theory is valid for any plate or shell geometry and contains most of the existing nonlinear and shear-deformable plate and shell theories as special cases. Five fully nonlinear partial-differential equations and corresponding boundary and corner conditions are obtained, which describe the extension-extension-bending-shear-shear vibrations of general laminated two-dimensional structures and display linear elastic and nonlinear geometric coupling among all motions. Moreover, the energy and Newtonian formulations are completely correlated in the theory. |
| [13] | . An analysis and comparison of several shear deformable bending theories of composite laminated anisotropic plates currently encountered in the field literature are given in this paper. Although apparently different, it is shown in a unitary way, that these theories constitute in fact only different formulations of a single theory, generically designated to as the moderately thick plate theory. Their connection with the first order transverse shear deformation theory is also emphasized and some conclusions concerning its shortcomings and field applicability are presented. |
| [14] | . The global bifurcations and chaotic dynamics of a parametrically excited, simply supported rectangular thin plate are analyzed. The formulas of the thin plate are derived by von Karman-type equation and Galerkin's approach. The method of multiple scales is used to obtain the averaged equations. Based on the averaged equations, theory of normal form is used to give the explicit expressions of normal form associated with a double zero and a pair of pure imaginary eigenvalues by Maple program. On the basis of the normal form, global bifurcation analysis of the parametrically excited rectangular thin plate is given by a global perturbation method developed by Kovacic and Wiggins. The chaotic motion of thin plate is found by numerical simulation. |
| [15] | . This paper investigates the nonlinear vibration of imperfect shear deformable laminated rectangular plates comprising a homogeneous substrate and two layers of functionally graded materials (FGMs). A theoretical formulation based on Reddy's higher-order shear deformation plate theory is presented in terms of deflection, mid-plane rotations, and the stress function. A semi-analytical method, which makes use of the one-dimensional differential quadrature method, the Galerkin technique, and an iteration process, is used to obtain the vibration frequencies for plates with various boundary conditions. Material properties are assumed to be temperature-dependent. Special attention is given to the effects of sine type imperfection, localized imperfection, and global imperfection on linear and nonlinear vibration behavior. Numerical results are presented in both dimensionless tabular and graphical forms for laminated plates with graded silicon nitride/stainless steel layers. It is shown that the vibration frequencies are very much dependent on the vibration amplitude and the imperfection mode and its magnitude. While most of the imperfect laminated plates show the well-known hard-spring vibration, those with free edges can display soft-spring vibration behavior at certain imperfection levels. The influences of material composition, temperature-dependence of material properties and side-to-thickness ratio are also discussed. |
| [16] | We performed a structural dynamic analysis of skew sandwich plate with laminated composite faces based on the high-order shear deformation plate theory (HSDT). The effects of skew angles and layup sequences on the dynamic response for various parameters are studied using a nonlinear high-order finite element program developed for this study. The numerical results were in good agreement with those reported by other investigators for square composite and skew plates, and the new results reported in this paper show the interactions between the skew angle and layup sequence in the sandwich laminate. Key observation points are discussed and a brief design guideline is given. |
| [17] | . This paper studies the effects of initial stresses on the nonlinear vibrations of laminated plates on elastic foundations. The nonlinear partial differential equations based on Mindlin plate theory are derived for the nonlinear vibration of laminated plates in a general state of nonuniform initial stress. Both rotary inertia and transverse stress are considered. Using the derived governing equations, the nonlinear vibration behavior of an initially stressed cross-ply plate on a Pasternak or Winkler elastic foundation is studied. The Galerkin's approximate method is applied to the governing partial differential equations to yield ordinary differential equations. The ordinary differential equations are solved by Runge鈥揔utta method to obtain the ratio of nonlinear frequency to linear frequency. The initial stress is taken to be a combination of a pure bending stress and an extensional stress in the plane of the plate. It is found that the foundation stiffness and initial stresses may result in a drastic change of the nonlinear vibration behavior. The frequency responses of nonlinear vibration are sensitive to the initial stress, vibration amplitude, modulus ratio and foundation stiffness. The effects of various parameters on the nonlinear vibration are discussed. |
| [18] | . This paper presents an investigation of the stochastic nonlinear bending response of a laminated composite plate resting on a two parameter Pasternak elastic foundation with Winkler cubic nonlinearity with uncertain system properties subjected to transverse distributed static load. The system properties such as material properties and foundation stiffness parameters are modelled as independent basic random variables. A C0 nonlinear finite element formulation of the random nonlinear problem based on higher order shear deformation theory in the von Karman sense is presented. A direct iterative method in conjunction with a stochastic nonlinear finite element method is proposed to analyze the effect of uncertainty in the material properties and foundation stiffness parameters on the nonlinear static response of the composite plates. Numerical results for mean as well as standard deviation of nonlinear transverse central deflection of the laminated composite plates resting on linear and nonlinear elastic foundations have been obtained for various combinations of geometric parameters, foundation parameters, stacking sequences and boundary conditions. The results have been compared with those available in the literature and from an independent Monte Carlo simulation. |
| [19] | . Nonlinear forced vibrations of FGM doubly curved shallow shells with a rectangular base are investigated. Donnell’s nonlinear shallow-shell theory is used and the shell is assumed to be simply supported with movable edges. The equations of motion are reduced using the Galerkin method to a system of infinite nonlinear ordinary differential equations with quadratic and cubic nonlinearities. Using the multiple scales method, primary and subharmonic resonance responses of FGM shells are fully discussed and the effect of volume fraction exponent on the internal resonance conditions, softening/hardening behavior and bifurcations of the shallow shell when the excitation frequency is (i) near the fundamental frequency and (ii) near two times the fundamental frequency is shown. Moreover, using a code based on arclength continuation method, a bifurcation analysis is carried out for a special case with two-to-one internal resonance between the first and second doubly symmetric modes with respect to the panel’s center ( ω 13≈2 ω 11). Bifurcation diagrams and Poincaré maps are obtained through direct time integration of the equations of motion and chaotic regions are shown by calculating Lyapunov exponents and Lyapunov dimension. |
| [20] | . Geometrically nonlinear vibrations of FGM rectangular plates in thermal environments are investigated via multi-modal energy approach. Both nonlinear first-order shear deformation theory and von Karman theory are used to model simply supported FGM plates with movable edges. Using Lagrange equations of motion, the energy functional is reduced to a system of infinite nonlinear ordinary differential equations with quadratic and cubic nonlinearities. A pseudo-arclength continuation and collocation scheme is used and it is revealed that, in order to obtain the accurate natural frequency in thermal environments, an analysis based on the full nonlinear model is unavoidable since the plate loses its original flat configuration due to thermal loads. The effect of temperature variations as well as volume fraction exponent is discussed and it is illustrated that thermally deformed FGM plates have stronger hardening behaviour; on the other hand, the effect of volume fraction exponent is not significant, but modal interactions may rise in thermally deformed FGM plates that could not be seen in their undeformed isotropic counterparts. Moreover, a bifurcation analysis is carried out using Gear鈥檚 backward differentiation formula (BDF); bifurcation diagrams of Poincar茅 maps and maximum Lyapunov exponents are obtained in order to detect and classify bifurcations and complex nonlinear dynamics. |
| [21] | . |
| [22] | . In this paper, the nonlinear oscillations of a composite laminated circular cylindrical shell clamped along a generatrix and with the radial pre-stretched membranes at both ends are studied for the... |
| [23] | . The multi-pulse homoclinic orbits and chaotic dynamics of an equivalent circular cylindrical shell for the circular mesh antenna are investigated in the case of 1:2 internal resonance in this paper for the first time. Applying the method of averaging, the four-dimensional averaged equation in the Cartesian form is obtained. The theory of normal form is used to reduce the averaged equation to a simpler form. Based on the simplified system, the energy phase method is employed to investigate the homoclinic bifurcations and the Shilnikov type multi-pulse chaotic dynamics. First, the energy difference function and the zeroes of the energy difference function are obtained. Then, the existence of the Shilnikov type multi-pulse orbits is determined. The homoclinic trees are depicted to describe the relationship among the layers diameter, the pulse numbers and the phase shift. Finally, we need to verify the condition which makes sure that any multi-pulse orbit departing from a slow sink comes back to the domain of... |
| [24] | . This paper is focused on the resonant responses and chaotic dynamics of a composite laminated circular cylindrical shell with radially pre-stretched membranes at both ends and clamped along a generatrix. Based on the two-degree-of-freedom non-autonomous nonlinear equations of this system, the method of multiple scales is employed to obtain the four-dimensional nonlinear averaged equation. The resonant case considered here is the primary parametric resonance-1/2 subharmonic resonance and 1:1 internal resonance. Corresponding to several selected parameters, the frequency-response curves are obtained. From the numerical results, we find that the hardening-spring-type behaviors and jump phenomena are exhibited. The jump phenomena also occur in the amplitude curves of the temperature parameter excitation. Moreover, it is found that the temperature parameter excitation, the coupling degree of two order modes and the detuning parameters can effect the nonlinear oscillations of this system. The periodic and chaotic motions of the composite laminated circular cylindrical shell clamped along a generatrix are demonstrated by the bifurcation diagrams, the maximum Lyapunov exponents, the phase portraits, the waveforms, the power spectrums and the Poincar茅 map. The temperature parameter excitation shows that the Pomeau-Manneville type intermittent chaos occur under the certain initial conditions. It is also found that there exist the twin phenomena between the Pomeau-Manneville type intermittent chaos and the period-doubling bifurcation. |
| [25] | . An efficient finite element procedure is developed to predict large amplitude nonlinear flutter response of shape memory alloy hybrid composite (SMAHC) plates at an arbitrary supersonic yawed angle and an elevated temperature. The temperature-dependent material properties of shape memory alloy (SMA) and traditional composites, and the von Karman large deflections are considered in the... [Show full abstract] |
| [26] | . Not Available |
| [27] | . Abstract This literature review focuses mainly on geometrically nonlinear (finite amplitude) free and forced vibrations of circular cylindrical shells and panels, with and without fluid-structure interaction. Work on shells and curved panels of different geometries is but briefly discussed. In addition, studies dealing with particular dynamical problems involving finite deformations, eg, dynamic buckling, stability, and flutter of shells coupled to flowing fluids, are also discussed. This review is structured as follows: after a short introduction on some of the fundamentals of geometrically nonlinear theory of shells, vibrations of shells and panels in vacuo are discussed. Free and forced vibrations under radial harmonic excitation (Section 2.2), parametric excitation (axial tension or compression and pressure-induced excitations) (Section 2.3), and response to radial transient loads (Section 2.4) are reviewed separately. Studies on shells and panels in contact with dense fluids (liquids) follow; some of these studies present very interesting results using methods also suitable for shells and panels in vacuo. Then, in Section 4, shells and panels in contact with light fluids (gases) are treated, including the problem of stability (divergence and flutter) of circular cylindrical panels and shells coupled to flowing fluid. For shells coupled to flowing fluid, only the case of axial flow is reviewed in this paper. Finally, papers dealing with experiments are reviewed in Section 5. There are 356 references cited in this article. |
| [28] | . Here, the system parameters effects on supersonic panel flutter behavior of laminated composite skew plates are investigated using a shear deformable finite element approach. The first-order high Mach number approximation to linear potential flow theory is employed for evaluating the aerodynamic pressure. The solutions of complex eigenvalue problem, formulated based on Lagrange's equation of motion are obtained using the standard method for finding eigenvalues. The variation of critical aerodynamic pressure is evaluated considering different parameters such as skew angle, fiber orientation, and boundary conditions. The influence of aerodynamic and structural damping, and thermo-mechanical loads on the critical aerodynamic speed is also examined. |
| [29] | . In this paper, the nonlinear aeroelastic behavior of functionally graded plates is studied in supersonic flow. For this purpose, the von Karman strains and piston theory have been employed to model structural nonlinearity and quasi-steady aerodynamic panel loading, respectively. The material properties of the plate are assumed to be graded continuously in the direction of thickness. The variation of the properties follows a simple power-law distribution in terms of the volume fractions of constituents. The Hamilton鈥檚 principle is used to construct the coupled nonlinear partial differential equations of motion. The derived equations are transformed into a set of coupled ordinary differential equations using the Galerkin method and then solved by numerical time integration. It is found that the use of functionally graded materials greatly changes the flutter behavior of the plate especially in post-flutter region. |
| [30] | . The effect of variable fiber spacing on the supersonic flutter of rectangular composite plates has been investigated using the finite element method and quasi-steady aerodynamic theory. The formulation of the location dependent stiffness and mass matrices due to nonhomogeneous material properties was derived. This study first demonstrates the flutter analysis of composite plates with variable fiber spacing. Numerical results show that the sequence of the natural mode may be altered and the two natural frequencies may be close to each other due to the fiber distribution may change the distributed stiffness and mass of the plate. Therefore, it may change the flutter coalescent modes. It is seen that the flutter boundary may be increased or decreased due to variable fiber spacing. The punch phenomenon on the flutter boundary is obvious in the absence of aerodynamic damping. |
| [31] | . This paper presents the analysis of the nonlinear dynamics for a composite laminated cantilever rectangular plate subjected to the supersonic gas flows and the in-plane excitations. The aerodynamic pressure is modeled by using the third-order piston theory. Based on Reddy’s third-order plate theory and the von Kármán-type equation for the geometric nonlinearity, the nonlinear partial differential equations of motion for the composite laminated cantilever rectangular plate under combined aerodynamic pressure and in-plane excitation are derived by using Hamilton’s principle. The Galerkin’s approach is used to transform the nonlinear partial differential equations of motion for the composite laminated cantilever rectangular plate to a two-degree-of-freedom nonlinear system under combined external and parametric excitations. The method of multiple scales is employed to obtain the four-dimensional averaged equation of the non-automatic nonlinear system. The case of 1:2 internal resonance and primary parametric resonance is taken into account. A numerical method is utilized to study the bifurcations and chaotic dynamics of the composite laminated cantilever rectangular plate. The frequency–response curves, bifurcation diagram, phase portrait and frequency spectra are obtained to analyze the nonlinear dynamic behavior of the composite laminated cantilever rectangular plate, which includes the periodic and chaotic motions. |
| [32] | . An analysis on the nonlinear dynamics of an FGM plate in hypersonic flow subjected to an external excitation and uniform temperature change is presented in this article. Material properties of the constituents are assumed to be temperature-dependent and the effective properties of FGM plate are graded in thickness direction according to a simple power law function in terms of the volume fractions. Based on vonKarman type nonlinear strain-displacement relationship, the nonlinear governing equations of motion are derived by using Hamilton's principle. Galerkin's method is then utilized to discretize the governing partial equations to a two-degree-of-freedom nonlinear system, including the quadratic and cubic nonlinear terms. A third-order piston theory is applied for the hypersonic aerodynamic load. The Mach number and in-plane loading are used as bifurcation parameters. Numerical results including the bifurcations, waveform, phase plots, and Poincare maps are presented, for an FGM plate to show the influences of material gradient index, Mach number, and in-plane load on the nonlinear dynamics. |
| [33] | |
| [34] |
