含孔隙变厚度FG圆板的湿热力学响应 1)

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-01

戴婷, 戴宏亮²⁾, 李军剑, 贺其湖南大学机械与运载工程学院,长沙 410082

HYGROTHERMAL MECHANICAL BEHAVIOR OF A FG CIRCULAR PLATE WITH VARIABLE THICKNESS ¹⁾

Dai Ting, Dai Hongliang²⁾, Li Junjian, He QiCollege of Mechanical and Vehicle Engineering, Hunan University, Changsha 410082, China

收稿日期:2018-10-22接受日期:2018-12-20网络出版日期:2019-03-18

基金资助:

湖南省自然科学基金项目.2017JJ2044
长沙市科技局项目.Kq1701030

Received:2018-10-22Accepted:2018-12-20Online:2019-03-18
作者简介 About authors
2)戴宏亮,教授,主要研究方向：智能材料与结构力学.E-mail:hldai520@sina.com

摘要
功能梯度材料(functionally graded materials, FGM)是组份含量按特定方向连续变化的非均匀复合材料,可有效解决传统复合材料组份之间结合能力弱和不同组份性能难以协调等问题,达到诸如缓和应力集中和优化应力分布等效果,使整体材料在保持细观结构完整性的同时充分发挥各组份材料的性能优势.由于制备技术等原因或出于特殊功能的需要,微孔或孔隙是各类型FGM中的常见缺陷.从细观结构上看,多孔FGM中的孔隙包含了单一组份内的材料孔隙和组份微粒间的结构间隙,这些孔隙将对FGM的力学性能,尤其是在湿热环境下的力学行为产生影响.本文考虑FGM中的两类细观孔隙(材料孔隙和结构孔隙),提出了令各类孔隙依赖于各自组份变化,再线性叠加得到的整体孔隙计算式.考虑组份材料和孔隙填充物(液相水和水蒸气)性质的温度相关性,建立了湿热相关FGM材料模型.针对厚度沿径向变化的旋转圆板结构,应用该FGM材料模型,推导了圆板的非线性稳态湿热控制方程及考虑湿热弹性本构的位移控制方程,采用微分求积法(differential quadrature method,DQM),获得了圆板的湿热场、位移场和应力分布.在数值算例中,利用退化模型的解析解对本文的数值计算方法进行了验证,继而通过改变各关键参数,讨论了两类孔隙率、梯度指数和圆板厚度变化对含孔隙FGM变厚度旋转圆板湿热力学响应的影响规律.
关键词： 湿热环境;孔隙率;功能梯度;变厚度;圆板;微分求积法

Abstract
Functionally graded materials (FGMs) are composed of two or more discrete constituent phases with continuous and smoothly varying components. Due to the distinctive merit comparing with usual composite materials that they can reduce the stress concentration and optimize the stress distribution to make good use of each component, utilizing of FGMs helps to resolve some problems in composite materials such as low bond strength and inharmonious of properties effectively. Because of the preparation technology or for the need of special structures, micropores or pores are commonly found in various types of FGM and play an important role in the influence factors on mechanical properties of FGMs. In addition, the application conditions of FGMs are usually complex or extreme with multiple physical fields, and the mechanical responses of various FGMs under coupling multi-fields will be more complex. On micro scale, the pores in porous FGM include material pores of each components and structural gaps between different particles. These pores will affect the properties of FGM, especially under hygrothermal environments. In this paper, two kinds of micro pores (material pores and structural gaps) in FGM are both considered. An expression to characterize porosity of the whole FGM is proposed, where the porosity of each component is related to its volume fraction and the global porosity is a linear superposition. Considering temperature dependency of the component properties as well as the material properties of pore fillers (liquid water or vapor), a prediction model of the porous FGM is established. Focusing on a rotating circular plate with its thickness varying along the radial direction, and applying the current porous FGM model, governing equations of the nonlinear steady-state temperature and moisture fields as well as displacement field are derived. Solving the governing equations by the differential quadrature method (DQM), distributions of temperature, moisture, displacement and stress of the FG circular plate are obtained. In the numerical examples, analytic solution of a simplified mechanical model is carried out to verify the numerical calculation process of the current study. By changing the key parameters, influences of each porosity, gradient index and thickness change rule on the hygrothermal mechanical responses of the porous FG circular plate with variable thickness are discussed in detail.
Keywords：hygrothermal environment;porosity;FGM;variable thickness;circular plate;DQM

PDF (10368KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex 收藏本文
本文引用格式
戴婷, 戴宏亮, 李军剑, 贺其. 含孔隙变厚度FG圆板的湿热力学响应 ¹⁾. 力学学报[J], 2019, 51(2): 512-523 DOI:10.6052/0459-1879-18-280
Dai Ting, Dai Hongliang, Li Junjian, He Qi. HYGROTHERMAL MECHANICAL BEHAVIOR OF A FG CIRCULAR PLATE WITH VARIABLE THICKNESS ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2019, 51(2): 512-523 DOI:10.6052/0459-1879-18-280

引言

功能梯度材料(functionally graded material, FGM)作为组份和性质连续变化的复合材料,常被设计用于具多物理场或环境条件变化剧烈的结构.含孔隙FGM的性能,不仅与组份材料及其变化规律相关,还受到孔隙率的影响,尤其是在会引起孔隙填充物变化的湿热环境中.因此,建立有效的力学模型进行含孔隙FGM性质预测,并据此研究湿热环境下多孔功能梯度(functionally graded,FG)结构的力学响应,对FGM的设计和工程推广应用具有重要的意义.

国内外对FG结构静、动力学行为的分析已很丰富.基于高阶剪切变形方法及里兹法,Heydari等^[1]研究了Pasternak弹性基础上FG圆板在均匀径向压缩作用下的屈曲行为.通过不同的加载方式,Moita等^[2]研究了FG板在不同载荷作用下的屈曲行为和几何非线性行为.基于一阶剪切理论及有限元分析,Yu等^[3]研究了FG板在温度和机械载荷作用下的屈曲行为.应用改进的无网格法,Nguyen等^[4]研究了FG板的非线性静动态力学行为.借助牛顿-拉夫逊方法以及里兹法,Ashoori和Vanini^[5]分析了FG压电板的非线性弯曲和后屈曲响应.基于Kirchhoff-Love理论的无旋度等几何公式,Yin等^[6]分析了FG薄板的自由振动和屈曲行为.考虑尺度效应和剪切变形,Thai等^[7]采用应变梯度理论和等几何法分析了FG微板的力学行为.基于von Kármán几何非线性理论,张靖华等^[8]研究了热冲击作用下具缺陷FG圆板的动态屈曲及后屈曲问题.应用一阶剪切理论及最小势能原理,Dai等^[9-10]研究了FG圆板的非线性动态行为和低速冲击作用下的动态响应.基于经典板壳理论,Lal和Ahlawat^[11]得到了FG圆板在流体静力学平面力下的屈曲力学行为及圆板的振动特性.应用一阶剪切变形理论,Yousefzadeh等^[12]考虑了旋转惯性效应和横向剪切应力,解决了FG圆板与不可压缩流体接触时的自由振动问题.使用微分求积法,Mahinzare等^[13]分析了旋转双向FG压电圆板的自由振动,得到了FGM压电圆板的振动特性.考虑热屈曲变形引入的结构几何非线性,夏巍和冯浩成^[14]分析了FG壁板的气动弹性颤振.基于单向耦合的热传导理论,许新和李世荣^[15]研究了FG微梁的热弹性阻尼.应用有限元法,高晨彤等^[16]研究了FGM梁在大范围转动下的刚柔耦合动力学问题.

复合材料在湿热环境下的力学响应及含孔隙复合材料的力学性能也已受到国内外****的关注.基于湿热环境下的力学实验,许良等^[17]分析了碳纤维环氧复合材料的力学性能及提高力学性能的方法.利用一阶剪切变形理论和模态叠加法,赵天等^[18]研究了复合材料层合板在湿热环境下受简谐激励作用的振动和声辐射特性.运用近场动力学及有限元法,苏伯阳等^[19]研究了复合材料湿热环境下的冲击损伤特性.吴振和刘子茗^[20]研究了复合材料层合板在湿热环境下的力学行为,探讨了湿热膨胀系数对湿热行为的影响.利用实验的方法,王柏臣等^[21]研究了湿热环境对聚甲基丙烯酸甲酯混杂纳米复合材料性能的影响.基于FG构件动力分析的细观元法,曹志远和程红梅^[22]研究了材料的宏观性能与微观结构之间的关系,尤其是微观孔隙对宏观性能的影响.根据三维剪切变形理论,Zenkour^[23]研究了多孔FG单层板和夹层板的弯曲响应,并且分析了孔隙率对材料性能的影响.应用修正后的混合法则,Boutahar等^[24]研究了不同孔隙度下各向同性矩形板的力学性能.应用有限元法,Kiran和Kattimani^[25]分析了多孔FG磁弹性板的自由振动特性和静态特性,具体分析了孔隙率对自由振动以及静态性能的影响.利用哈密顿原理和变分法,Rezaei等^[26]分析了孔隙率对FG矩形板振动特性的影响.利用修正后的幂律计算公式,Kiran等^[27]分析了孔隙度对FG板自由振动以及静力性能的影响.Wang和Zu^[28]分析了多孔FG板在热环境中的振动.为快速分析功能梯度材料结构在复杂载荷作用下的动态响应,郑保敬等^[29]提出了一种模型降阶方法,并且验证了其准确性和适用性.基于Euler-Bernoulli梁理论和单向耦合的热传导理论,许新和李世荣^[15]分析了功能梯度梁的热弹性阻尼的变化.

FGM细观尺度上的孔隙,包括了组份材料本身带有的材料孔隙和不同微粒之间无法充分接触而形成的界面结构孔隙.以往的多孔FGM模型,仅采用了整体孔隙表达式,而并未对不同类型的孔隙进行表征.因此,本文将从细观结构出发,建立各类孔隙与相应组份含量的关系,并考虑组份和孔隙填充物性质的湿热相关性,提出多孔FGM的材料模型,并将所建立的材料模型应用于旋转变厚度圆板结构,分析其在湿热环境下的力学响应.

1 材料模型和几何模型

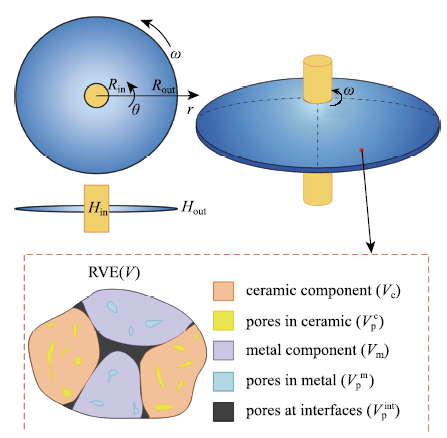
考虑绕中心轴旋转的空心变厚度圆板,其内外半径分别为$R_{{\rm in}}$和$R_{{\rm out}}$,内外边缘厚度分别为$H_{{\rm in}}$和$H_{{\rm out}}$.构成该圆板的FGM包含陶瓷和金属组份,并具有沿环向均匀分布的孔隙.圆板的材料性质参数$P$满足如下关系^[30]

(1)$P = P_{\rm c} V_{\rm c} + P_{\rm m} V_{\rm m} + P_{\rm p} V_{\rm p} $

且各组份材料的体积分数满足

(2)$ V_{\rm c} + V_{\rm m} + V_{\rm p} = 1$

其中,$P_{\rm c}$和$P_{\rm m}$分别表示陶瓷(ceramic)和金属(metal)组份的材料性质,$P_{\rm p}$表示孔隙(pore)或孔隙填充物的材料性质,$V_{\rm c}$,$V_{\rm m}$和$V_{\rm p}$分别表示三者的体积分数,并且$V_{\rm m}$随圆板半径呈如下幂函数变化^[30]

(3)$ V_{\rm m} (r) = \frac{1}{1 + \eta_{\rm m}}\left(\frac{r-R_{{\rm in}}} {R_{{\rm out}}-R_{{\rm in}} }\right)^n$

式中,$\eta _{\rm m}$为金属组份的孔隙参数,$n(0 \le n \le \infty)$为FG指数. 当$n = 0$时,材料成分全部为金属;当$n \to + \infty$时,材料成分全部为陶瓷. 圆板几何形状、所用柱坐标系$(r,\theta,z)$及多孔FGM的代表性体积单元(RVE)示意图如图1所示

图1

新窗口打开|下载原图ZIP|生成PPT
图1变厚度FG圆板材料和几何模型示意图

Fig.1Material and geometrical model of the FG circular plate with variable thickness

本文分别考虑FGM各组份本身带有的孔隙及不同组份结合时产生的界面和结构间隙,上述各类孔隙与各组份含量相关,故假设FG圆板的孔隙体积分数满足

(4)$$V_{\rm p} (r) = V_{\rm p}^{\rm c} (r) + V_{\rm p}^{\rm m} (r) + V_{\rm p}^{{\rm int}} (r)= \\ \frac{\eta _{\rm c} }{1-\eta _{\rm c} }V_{\rm c} (r) + \frac{\eta _{\rm m} }{1-\eta _{\rm m} }V_{\rm m} (r) + \eta _{{\rm int}} V_{\rm c} (r)V_{\rm m} (r)\quad$$

其中,$V_{\rm p}$,$V_{\rm p}^{\rm c}$,$V_{\rm p}^{\rm m}$和$V_{\rm p}^{{\rm int}}$分别为FGM、陶瓷组份、金属组份和结合界面中孔隙所占体积分数;$\eta _{\rm c}$为陶瓷组份的孔隙参数;$\eta _{{\rm int}}$为界面孔隙参数. 显然,当$V_{\rm c} (r) = 0$或$V_{\rm m} (r) = 0$时,为单一材料,无界面孔隙,只有单一材料孔隙;当$V_{\rm c} (r) = V_{\rm m} (r)$时,界面孔隙率达到最大.将(4)式代入(2)式,可得$V_{\rm c} (r)$和$V_{\rm p} (r)$.

考虑到组份材料和孔隙的部分物性参数受温度的影响,本文采用如下与温度相关的材料参数表达式^[23]

(5)$ P(r,T) = P_{\rm c} (T)V_{\rm c} (r) + P_{\rm m} (T)V_{\rm m} (r) + P_{\rm p} (T)V_{\rm p} (r)$

其中

(6)$ P_j (T) = P_{0j} (1 + P_{1j} T + P_{2j} T^2 + P_{3j} T^3) \quad (j = {\rm c},{\rm m},{\rm p})$

式中,$T$表示温度,$P_{ij} (i = 0,1,2,3)$为常数.

湿度的变化是材料中水或水蒸气含量的变化,将对材料的质量和密度产生影响.由于陶瓷和金属组份吸湿能力弱,故仅考虑孔隙的吸湿.忽略孔隙内压强的变化,考虑吸湿孔隙中同时存在气相水和液相水,孔隙的物性参数满足如下关系

(7)$ P_{\rm p} (r,T,S) = S(r)P_{\rm w} (T) + [1-S(r)]P_{\rm v} (T)$

其中,$S(r)$表示液相水饱和度(或称填充率),在此处为孔隙吸湿后液相水占据孔隙的体积分数,即$S(r)= {V_{\rm w} (r)}/{V_{\rm p} (r)}$,显然有$0 \le S(r) \le 1$.

考虑FG圆板厚度沿径向变化,采用如下规律

(8)$ h(r) = H_{{\rm in}} + (H_{{\rm out}}-H_{{\rm in}} )\left( {\frac{r-R_{{\rm in}} }{R_{{\rm out}}-R_{{\rm in}} }} \right)^\lambda$

其中$\lambda (\lambda \ge 0)$是控制厚度变化规律的几何参数.

2 控制方程及求解

2.1 湿热控制方程及其DQM求解

当FG圆板仅有沿径向变化的温度和湿度场时,不计湿热传导过程,采用无源一维稳态温度和湿度方程如下

(9)$$\frac{{\rm d}}{{\rm d}r}\left[ {rh(r)\kappa (r,T)\frac{{\rm d}T}{{\rm d}r}} \right] = 0$$

(10)$$\frac{{\rm d}}{{\rm d}r}\left[ {rh(r)D(r,T,S)\frac{{\rm d}C}{{\rm d}r}} \right] = 0$$

式中,$T = T(r)$,$C = C(r)$.仅考虑固体组份的传热,热传导系数$\kappa (r,T)$满足式(5),且$\kappa _{\rm p} (T) = 0$;仅考虑孔隙传湿,而忽略金属和陶瓷材料的吸湿性时,扩散系数$D(r,T,S) = D_{\rm p} (r,T,S)$满足式(7).

由于吸湿后材料的湿度$C = {(m_{\rm w} + m_{\rm v} )}/ {m_{{\rm dry}} }$,则液相水饱和度和材料湿度之间有如下线性关系

(11)$ C = \frac{(\rho _{\rm w}-\rho _{\rm v} )V_{\rm p} }{\rho _{\rm c} V_{\rm c} + \rho _{\rm m} V_{\rm m} }S + \frac{\rho _{\rm v} V_{\rm p} }{\rho _{\rm c} V_{\rm c} + \rho _{\rm m} V_{\rm m} }$

注意到,由于忽略了孔隙中的空气,即采用了$V_{\rm p} = V_{\rm w} + V_{\rm v}$,故仅当$V_{\rm p} = 0$(无孔隙)时有$C = 0$.总湿度中液相水分量$C_{\rm w}$和水蒸气分量$C_{\rm v}$分别为

(12)$ C_{\rm w} = \frac{\rho _{\rm w} V_{\rm p} }{\rho _{\rm c} V_{\rm c} + \rho _{\rm m} V_{\rm m} }S,~ C_{\rm v} = C-C_{\rm w}$

当$S = 0$时,材料中无液相水;当$S = 1$时,材料达到吸水饱和.利用式(11),则湿度方程式(10)可用液相水填充率$S$表示为

(13)$ \frac{{\rm d}}{{\rm d}r}\left\{ {rh(r)D(r,T,S)\left[ {\frac{{\rm d}\left( {f_{{\rm S1}} S} \right)}{{\rm d}r} + \frac{{\rm d}f_{{\rm S2}} }{{\rm d}r}} \right]} \right\} = 0$

其中

$$ S = S(r)\\ f_{{\rm S1}} = \frac{(\rho _{\rm w}-\rho _{\rm v} )V_{\rm p} (r)}{\rho _{\rm c} V_{\rm c} (r) + \rho _{\rm m} V_{\rm m} (r)}\\ f_{{\rm S2}} = \frac{\rho _{\rm v} V_{\rm p} (r)}{\rho _{\rm c} V_{\rm c} (r) + \rho _{\rm m} V_{\rm m} (r)} $$

不计材料表面与外界的温度和物质交换,给定FG圆板内外边界湿热条件如下

(14)$$T(R_{{\rm in}} ) = T_{{\rm in}} , T(R_{{\rm out}} ) = T_{{\rm out}}$$

(15)$$S(R_{{\rm in}} ) = S_{{\rm in}} , S(R_{{\rm out}} ) = S_{{\rm out}} $$

采用DQM对上述湿热传导方程进行求解.DQM中某个采样点上的微分是由所有采样点上的函数值求加权和所得,故取少量采样点就可以得到光滑曲线.$r = r_i$处$f(r)$的k阶导数表达式为^[31-32]

(16)$ \left. {\frac{{\rm d}^kf(r)}{{\rm d}r^k}} \right|_{r = r_i } = \sum\limits_{j = 1}^q {c_{ij}^{(k)} } f(r_j ) {\kern 1pt}~(i = 1,2,\cdots ,q)$

式中,$q$为沿径向离散采样点总数,c为权系数,其表达式为

(17)$ \begin{array}{ll} c_{ij}^{(1)} = \frac{ \prod {(r_i )} }{(r_i-r_j ) \prod {(r_j )} }& ( i,j = 1,2,\cdots ,q; j \ne i) \\ c_{ij}^{(k)} = k\left[ {c_{ii}^{(k-1)} \cdot c_{ij}^{(1)}-\frac{c_{ij}^{(k-1)} }{r_i-r_j }} \right]&\hspace{-3mm} ~{\begin{array}{*{20}l} {( i,j = 1,2,\cdots ,q;}\\ {j \ne i;k = 2,3,\cdots ,q)}\\ \end{array} } \\ c_{ii}^{(k)} =-\sum\limits_{j = 1,j \ne i}^q {c_{ij}^{(k)} }& ( i,k = 1,2,\cdots ,q) \\ \end{array}$

其中$\prod {(r_i )} = \prod\limits_{j = 1,j \ne i}^q {(r_i-r_j )}$.

为提高计算精度,采用如下非均匀的Chebyshev-Gauss-Lobatto采样网格点^[31]沿径向离散

(18)$ r_i = \frac{R_{{\rm out}}-R_{{\rm in}} }{2}\left[ {1-\cos \left( {\frac{(i-1)π }{q-1}} \right)} \right] + R_{{\rm in}}~(i = 1,2,\cdots ,q)$

基于此,离散后的温度控制方程可写为

(19)$ (r_i h_i \kappa _i )\sum\limits_{j = 1}^q {c_{ij}^{(2)} } T_j + [\kappa _i \mbox{(}rh)'_{r_i } + r_i h_i \mbox{(}\kappa )'_{r_i } ]\sum\limits_{j = 1}^q {c_{ij}^{(1)} } T_j = 0$

其中$i = 1,2,\cdots ,q$;$h_i = h(r_i )$,$\kappa _i = \kappa (r_i ,T_i )$,$T_i = T(r_i )$,$(\quad )'_{r_i } = \left. {\frac{{{\rm d}(}\quad )}{{\rm d}r}} \right|_{r = r_i }$.离散以后,式(14)表示的温度边界条件为

(20)$ T_1 = T_{{\rm in}} , T_q = T_{{\rm out}}$

式(19)和式(20)构成一组高阶代数方程,利用牛顿迭代法可以求解,获得温度场的数值解.

用牛顿迭代法解非线性代数方程$f(x) = 0$,是将$f(x)$在$x_0$点的某领域内展开成泰勒级数,取其线性部分(即泰勒展开的前两项),并令其等于0,以此作为非线性方程的近似方程,即具有迭代关系式$x_{\rm n+1} =x_n-{f(x_n )} / {{f}'(x_n )}$.

将湿度控制方程式(13)进行离散,并将温度场数值结果代入,得到

(21)$$[r_i h_i f_{{\rm S1}}^{(i)} D_i ]\sum\limits_{j = 1}^q {c_{ij}^{(2)} } S_j+ \big\{ [(rhf_{{\rm S1}} )'_{r_i } + \\ r_i h_i (f_{{\rm S1}} )'_{r_i } ]D_i { + r_i h_i f_{{\rm S1}}^{(i)} (D)'_{r_i } } \big\} \sum\limits_{j = 1}^q {c_{ij}^{(1)}} S_j +\\ \left\{ {[rh(f_{{\rm S1}} )'_r ]'_{r_i} D_i + r_i h_i (f_{{\rm S1}} )'_{r_i } (D)'_{r_i } } \right\}S_i+ \\ [rh(f_{{\rm S2}} )'_r ]'_{r_i } D_i + r_i h_i (f_{{\rm S2}} )'_{r_i } (D)'_{r_i } = 0 $$

其中,$f^{(i)} = f(r_i )$,$C_i = C(r_i )$,$D_i = D(r_i ,T_i ,S_i)$. 离散以后,液相水填充率边界条件为

(22)$ S_1 = S_{{\rm in}} , S_q = S_{{\rm out}}$

式(21)和式(22)构成一组高阶代数方程,利用牛顿迭代法可以求解.将求得的液相水填充率数值结果代入式(11)和式(12),即可获得圆板的湿度场及所含液相水和水蒸气分量.

2.2 位移控制方程及其DQM求解

忽略自重,旋转FG圆板受径向体力$f_r (r) = \rho (r)\omega ^2r$.考虑到结构和载荷的对称性,FG圆板内位移和应力与$\theta$无关.于是,圆板的应力平衡方程可写为

(23)$ \frac{{\rm d} [h(r)\sigma _r ]}{{\rm d}r} + \frac{h(r)(\sigma _r-\sigma _\theta )}{r} + rh(r)\rho (r)\omega ^2 = 0$

其中,$\sigma _r =\sigma _r (r)$和$\sigma _\theta =\sigma _\theta(r)$分别表示径向和环向应力,密度$\rho (r)$满足式(1).由于湿度扩散是传质过程,孔隙的质量密度将与湿度相关.

考虑到平面应力问题,且应变和位移分量只与径向相关,FG圆板中面的小变形几何方程为

(24)$ \varepsilon _r = \frac{{\rm d}u}{{\rm d}r},~ \varepsilon _\theta = \frac{u}{r}$

其中,$\varepsilon _r =\varepsilon _r (r)$和$\varepsilon _\theta =\varepsilon _\theta (r)$分别表示径向和环向应变,$u\mbox{ = }u(r)$表示径向位移.

采用如下湿热弹性本构方程

(25)

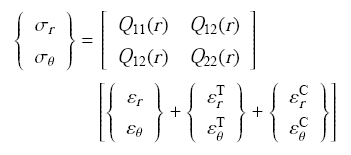
其中

(26)

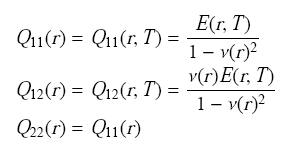
$E(r,T)$是弹性模量,满足式(5)且$E_{\rm p} = 0$;$\nu (r)$为泊松比,满足式(1)且$\nu _{\rm p} = 0$. 上式中湿热应力分量为

(27)$$\left. \begin{array}{l} \varepsilon _r^{\rm T} = \varepsilon _\theta ^{\rm T} =-\alpha (r)\Delta T(r)\\ \varepsilon _r^{\rm C} = \varepsilon _\theta ^{\rm C} =-\beta (r)\Delta C(r) \end{array}\right\} $$

其中,$\Delta T(r) = T(r)-T_0$,$\Delta C(r) = C(r)-C_0$,$T_0$和$C_0$分别为圆板的初始温度和湿度;$\alpha (r) = \alpha (r,T)$是热膨胀系数,$\beta (r) = \beta (r,T)$是湿膨胀系数且$\beta _{\rm c} = \beta _{\rm m} = 0$,则圆板中的湿应变$\varepsilon _r^{\rm C} = \varepsilon _\theta ^{\rm C} = 0$.

将式(24)和式(25)代入式(23),获得旋转FG圆板的位移控制方程如下

(28)$ f_1 \frac{{\rm d}^2u}{{\rm d}r^2} + f_2 \frac{{\rm d}u}{{\rm d}r} + f_3 u + f_4 = 0$

其中

$$ f_1 = h(r)Q_{11} (r) \\ f_2 = Q_{11} (r)\left[ {\frac{h(r)}{r} + \frac{{\rm d}h(r)}{{\rm d}r}} \right] + h(r)\frac{{\rm d}Q_{{\rm 11}} (r)}{{\rm d}r} \\ f_3 = \frac{Q_{12} (r)}{r}\frac{{\rm d}h(r)}{{\rm d}r} + \frac{h(r)}{r}\frac{{\rm d}Q_{{12}} (r)}{{\rm d}r}-\frac{h(r)}{r^2}Q_{{11}} (r)\\ f_4 = rh(r)\rho (r)\omega ^2-\frac{{\rm d}\{[Q_{{11}} (r) + Q_{{12}} (r)]h(r)\alpha (r)\Delta T(r)\}}{{\rm d}r}$$

FG圆板内边与转轴连接,视为固定端,外边自由,则其边界条件可写为

(29)$ u(R_{{\rm in}} ) = 0,~ \sigma _r (R_{{\rm out}} ) = 0$

将式(24)~式(26)代入式(29),可得到用位移描述的边界条件.

同样采用DQM对上述位移控制方程进行求解,离散后的位移控制方程为

(30)$ f_{1}^{(i)} \sum\limits_{j = 1}^q {c_{ij}^{(2)} } u_j + f_2^{(i)} \sum\limits_{j = 1}^q {c_{ij}^{(1)} } u_j + f_3^{(i)} u_j + f_4^{(i)} = 0$

其中,$i = 1,2,\cdots ,q$;$f^{(i)} = f(r_i )$,$u_i = u(r_i )$.用位移表达的离散边界条件为

(31)$$u_1 =0~Q_{11} (r_q ) \sum\limits_{j = 1}^q {c_{qj}^{(1)} } u_j + Q_{12} (r_q )\frac{u_q }{r_q }-\\ \qquad [Q_{11} (r_q ) + Q_{12} (r_q )]\alpha (r_q )\Delta T(r_q ) = 0 $$

将获得的位移场数值解代入式(24)和式(25)即可获得应力场的数值解.

3 算例和讨论

为验证本文数值计算过程的可靠性和正确性,首先考虑一忽略湿热效应的等厚度旋转均质圆板,令该均质圆板由金属材料组成,即取参数$E = 201.04~ {\rm GPa}$,$\nu = 0.326$,$\rho = 8166~{{\rm kg}}/{{\rm m}^3}$和$\omega = 1000~{\rm r}/{{\rm min}}$.事实上,该均质等厚度圆板力学模型是本文变厚度旋转FGM圆板的一种特殊简化形式,具体表现为,梯度指数$n = 0$表示FGM圆板仅含金属组份.该均质等厚度圆板的位移控制方程为

$$ \frac{{\rm d}}{{\rm d}r}\left\{ {\frac{1}{r}\frac{{\rm d}[ru(r)]}{{\rm d}r}} \right\} =-\frac{(1-\nu ^2)\rho \omega ^2r}{E}$$

其中,$\rho$,$\omega$,E和$\nu$均为常数.通过两次求积分运算,可以得到上式的通解

$$ u(r) =-\frac{(1-\nu ^2)\rho \omega ^2}{8E}r^3 + \frac{Y_1 }{2}r + \frac{Y_2 }{r}$$

其中,$Y_1$和$Y_2$是待定常数,应用式(29)的边界条件可以求得,进而可获得该等厚度均质圆板的位移和应力场解析解.

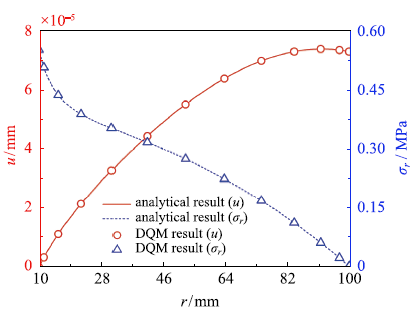
然后,在本文的数值求解模型中,取FG指数$n = 0$,圆板厚度$h(r)\equiv 1$及厚度变化指数$\lambda = 0$,各组份孔隙参数$\eta _{\rm c} = \eta _{\rm m} = \eta _{{\rm int}} \to 0$,湿热场$T(r) = C(r) \equiv 0$,转速$\omega = 1000 ~{\rm r}/{{\rm min}}$,则本文模型退化为与上述均质等厚度圆板一致,将DQM计算结果与解析结果进行对比.

由图2可知,两种结果十分吻合,表明了本文数值计算过程的正确性.

图2

新窗口打开|下载原图ZIP|生成PPT
图2验证算例

Fig.2Validation example

后续的算例中考虑湿热环境下的变厚度旋转FG圆板,其部分常量材料参为：$ \rho _{\rm c} = 2370~{\rm kg / m}^3, \nu _{\rm c} = 0.240$;$\rho _{\rm m} = 8166~{\rm kg / m}^3, \nu _{\rm m} = 0.326$;$ \rho _{\rm v} = 0.017~{\rm kg / m}^3, \rho _{\rm w} = 1000~{\rm kg / m}^3$ 温度相关材料参数见表1.

Table 1
表1
表1FGM温度相关材料参数^[30,^33]
Table 1Temperature dependent material parameters of FGM^[30,33]

	P0	P1	P2	P3
k_c/(W ? (m ? K)^-1)	13.723	-1.032 x 10^-3	5.466 x 10^-7	-7.876 x 10^-11
ac/K^-1	5.872 x 10^-6	9.095 x 10^-4	0	0
E_c/GPa	348.43	-3.070 x 10^-4	2.160 x 10^-7	-8.946 x 10^-11
Km/(W ? (m ? K)^-1)	15.379	-1.264 x 10^-3	2.092 x 10^-6	-7.223 x 10^-10
am /K^-1	1.233 x 10^-5	8.086 x 10^-4	0	0
E_m/GPa	201.04	3.079 x 10^-4	-6.534 x 10^-7	0
Dv/(m² ? s^-1)	2.176 x 10^-5	9.619 x 10^-3	-1.091 x 10^-4	1.523 x 10^-6
Dw/(m² ? s^-1)	1.819 x 10^-9	-1.401 x 10^-2	1.290 x 10^-3	-7.874 x 10^-6

新窗口打开|下载CSV

3.1 材料参数对FG圆板湿热力学行为的影响

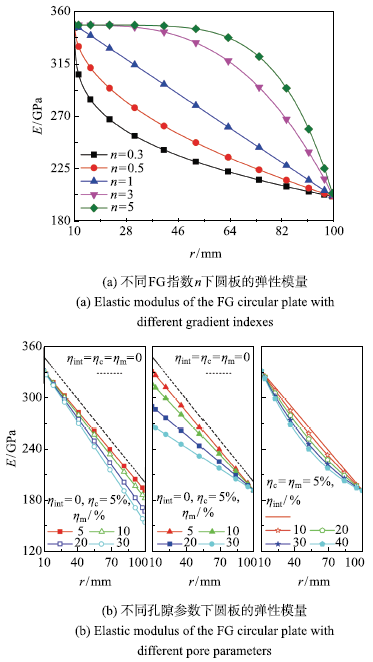
取旋转FG圆板的几何参数$R_{{\rm in}} = 10~\mbox{mm}$,$R_{{\rm out}} = 100~\mbox{mm}$,$H_{{\rm in}} = 1~\mbox{mm}$,$H_{{\rm out}} = 5~\mbox{mm}$,$\lambda = 1$;圆板转速$\omega = 1000~ {\rm r} /{\mbox{min}}$.

常温干燥条件下,材料参数对圆板弹性模量的影响如图3所示.图3(a)给出了不同FG指数$n$下无孔隙($\eta _{\rm c} = \eta _{\rm m} = \eta _{{\rm int}} = 0)$圆板的弹性模量. 可知,当$n = 1$时,FG圆板材料属性沿径向线性变化;当$\mbox{0} < n < 1$时,$n$值越小,材料整体性质越向金属靠拢;当$n > 1$时,$n$值越大,材料整体性质越向陶瓷靠拢. 取FG指数$n = 1$,图3(b)给出了常温干燥条件下不同孔隙参数对圆板弹性模量的影响.易知,孔隙的存在使材料的弹性模量整体降低,且孔隙率越大,降低幅度越大.进一步分析发现,组份孔隙率$\eta _{\rm c}$和$\eta _{\rm m}$的变化并不影响弹性模量曲线的基本形状,其影响程度由各组份含量决定;而界面孔隙率$\eta _{{\rm int}}$使弹性模量曲线下凹,影响程度由$V_{\rm c} \cdot V_{\rm m}$决定,且影响幅度最大处发生在沿圆板径向的中部.

图3

新窗口打开|下载原图ZIP|生成PPT
图3材料参数对弹性模量的影响

Fig.3Influences of material parameters to the elastic modulus

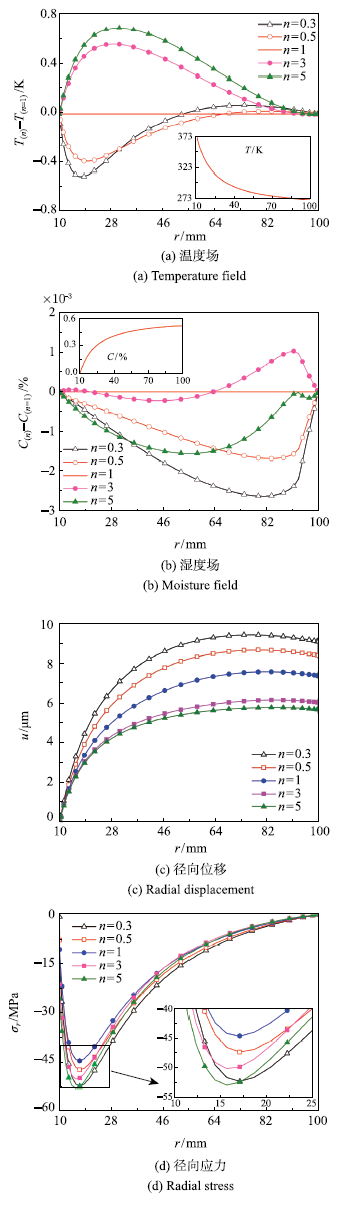
取孔隙参数$\eta _{\rm c} = \eta _{\rm m} = \eta _{{\rm int}} = 10\mbox{％}$,温度边界条件$T_{{\rm in}} = 373~\mbox{K}$和$T_{{\rm out}}=273~{\rm K}$,湿度边界条件$S_{{\rm in}} = 0$和$S_{\rm out}=0.5$,FG指数$n$对变厚度含孔隙FG圆板湿热力学响应的影响如图4所示.从式(9)可知,$n$对温度场的影响来源于其对热传导系数$\kappa$的影响,由表可知本文选取的两种组份材料$\kappa$值相近,故$n$对温度场整体影响较小. 因此图4(a)给出了$n = 1$时的温度场,及$n$取其他值时的温度与$n = 1$温度的差值,简记为$T_{(n)}-T_{(n = 1)}$,以清晰表达$n$对温度场的影响.由图可见,$n$对温度场的影响主要出现在靠近边界温度较高的一侧,并大致呈现随着$n$增大,同一半径处温度增大的趋势.同样地,由于$n$对湿度场整体影响较小,图4(b)给出了$n = 1$时的湿度场和湿度场差值$C_{(n)}-C_{(n = 1)}$.因本文不考虑组份材料的吸湿性,$n$对湿度的影响来源于其对孔隙体积分数$V_{\rm p}$的影响. 由图可知,影响较大处出现在靠近边界湿度较高的一侧,并且$n = 1\sim 3$时整体湿度值最大,$0 < n < 1$时整体湿度随$n$减小而降低,$n > 3$时整体湿度随$n$增大而降低.图4(c)和图4(d)给出了取不同$n$值时圆板的径向位移和径向应力,发现在同一半径处,径向位移随$n$值的增大而减小,结合图3(a)可知这是由于$n$值的增大使圆板整体刚度增加;$\left| {\sigma _r } \right|$的峰值在$0 < n < 1$时随$n$的增大而减小,在$n>1$时随$n$的增大而增大,结合图3(a)可知,组份均匀变化将有利于缓和FG圆板内的应力.

图4

新窗口打开|下载原图ZIP|生成PPT
图4FG指数$n$对圆板湿热力学响应的影响

Fig.4Effect of gradient index$n$ to the hygrothermal mechanical responses of the FG circular plate

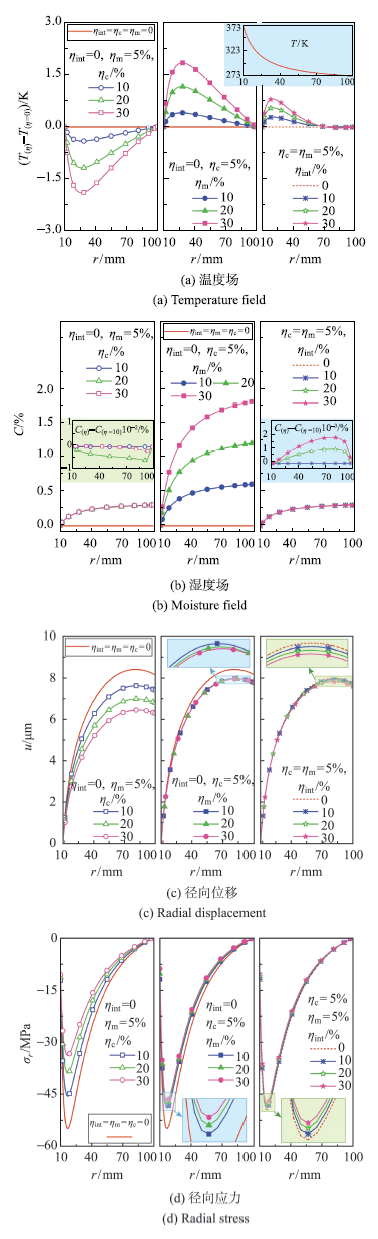
取FG指数$n = 1$,温度边界条件$T_{{\rm in}} = 373~\mbox{K}$和$T_{{\rm out}} = 273~\mbox{K}$,湿度边界条件$S_{{\rm in}} = 0$和$S_{{\rm out}} = 0.5$,孔隙参数对变厚度FG圆板湿热力学响应的影响如图5所示.由于孔隙参数对温度场整体影响较小, 图5(a)给出了$\eta _{\rm c} = \eta _{\rm m} = \eta _{{\rm int}} = 0$时的温度场及温度差$T_{(\eta )}-T_{(\eta = 0)}$,其中$T_{(\eta = 0)}$表示$\eta _{\rm c} = \eta _{\rm m} = \eta _{{\rm int}} = 0$时的温度场.由图易知,各孔隙参数对温度场影响最大处出现在靠近边界温度较高一侧;且在同一半径处,圆板温度随$\eta _{\rm c}$的增大而略微减小,随$\eta _{\rm m}$或$\eta _{{\rm int}}$的增大而略微增大,而$\eta _{\rm c}$和$\eta _{\rm m}$对温度的影响相比于$\eta _{{\rm int}}$稍大.图5(b)显示各孔隙参数对湿度场影响最大处出现在靠近边界湿度较高一侧,但由于本文考虑的热传导主要产生于陶瓷和金属组份材料,湿度扩散主要产生于孔隙,故孔隙参数对湿度场的影响规律与对温度的影响明显不同.由于设定了圆板内侧陶瓷组份占多,外侧金属组份占多,且$S_{{\rm in}}= 0$,$S_{\rm out}=0.5$,图中$\eta _{\rm m}$对湿度场的影响程度明显大于$\eta _{\rm c}$和$\eta _{{\rm int}}$,且在同一半径处湿度随$\eta _{\rm m}$增大而增大. 至于$\eta _{\rm c}$和$\eta _{{\rm int}}$对湿度的影响,图5(b)给出了湿度差$C_{(\eta )}-C_{(\eta = 10)}$,其中$C_{(\eta = 10)}$表示$(\eta _{\rm c} ,\eta _{\rm m} ,\eta _{{\rm int}} ) = (10\mbox{％} ,5\mbox{％} ,0)$或$(\eta _{\rm c} ,\eta _{\rm m} ,\eta _{{\rm int}} ) = (5\mbox{％} ,5\mbox{％} ,10\mbox{％} )$时的湿度场,发现在同一半径处,$\eta _{\rm c}$和$\eta _{{\rm int}}$的增大均会使湿度略微增大.图5(c)和图5(d)给出了取不同孔隙参数时圆板的径向位移和径向应力,孔隙参数对位移和应力的影响是其对刚度和对湿热场影响的综合结果.在同一半径处,径向位移和$\left| {\sigma _r } \right|$分别随$\eta _{\rm c}$,$\eta _{\rm m}$和$\eta _{{\rm int}}$的增大而减小,其中$\eta _{\rm c}$的影响最为明显,这是由于本文设定了FG圆板陶瓷组份占多的一侧为固定端.

图5

新窗口打开|下载原图ZIP|生成PPT
图5孔隙参数对FG圆板湿热力学响应的影响

Fig.5Effect of pore parameters to the hygrothermal mechanical responses of the FG circular plate

3.2 FG圆板厚度参数的影响

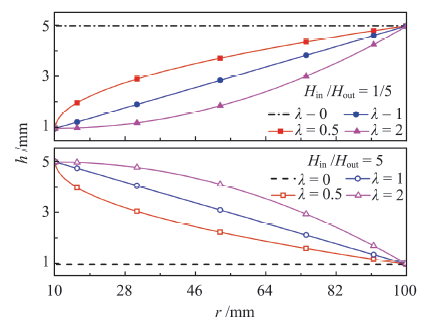
取圆板孔隙参数$\eta _{\rm c} = \eta _{\rm m} = \eta _{{\rm int}} = 10\mbox{％}$,FG指数$n = 1$,温度和湿度边界条件$T_{{\rm in}} = 373~\mbox{K}$,$T_{{\rm out}} = 273~\mbox{K}$,$S_{{\rm in}} = 0$,$S_{{\rm out}} = 0.5$,圆板转速$\omega = 1000~ {\rm r} /{\mbox{min}}$. 图6为不同厚度参数下圆板厚度沿径向的变化.

图6

新窗口打开|下载原图ZIP|生成PPT
图6FG圆板厚度沿径向的变化

Fig.6Thickness variation of the FG circular plate along its radius

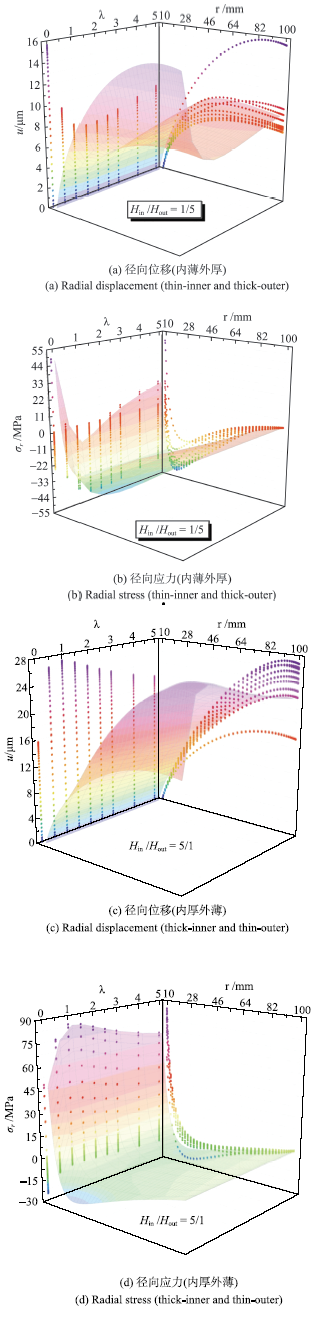
由于圆板厚度参数对材料组份和性质无影响,从而厚度参数的变化不改变其温度和湿度分布,故图7仅给出了不同厚度参数下圆板的径向位移和径向应力.$\lambda =0$(等厚度)时圆板厚度对位移和应力场无影响;$\lambda \ne 0$时,内薄外厚(${H_{{\rm in}} } / {H_{{\rm out}} } = 1/5)$圆板比内厚外薄(${H_{{\rm in}} } / {H_{{\rm out}} } = 5)$圆板的整体位移和应力更小;在同一半径处,内薄外厚圆板的位移和应力随$\lambda$的增大先减小后增大,而内厚外薄圆板的位移和应力随$\lambda$的增大先增大后减小,且上述$\lambda$影响的最大处均出现在$\lambda = 1$附近.结果表明,对于内边固定外边自由的FG旋转圆板,内薄外厚且厚度线性变化的几何结构将有利于缓和其形变和应力分布.

图7

新窗口打开|下载原图ZIP|生成PPT
图7厚度参数对FG圆板湿热力学响应的影响

Fig.7Effect of thickness parameters to hygrothermal mechanical responses of the FG circular plate

4 结论

本文提出了用组份本身孔隙及结合界面孔隙线性叠加得到的孔隙体积分数计算式,考虑组份材料和孔隙填充物(液相水和水蒸气)性质的温度相关性,及圆板整体湿度扩散系数和密度的湿度相关性,建立了湿热环境下旋转变厚度FG圆板的力学模型.采用DQM对控制方程进行求解,获得了圆板的湿热力学响应.通过具体算例,得到了如下结论.

(1)FG指数的变化对圆板湿热场影响较小,而对径向位移和应力影响明显.孔隙参数对圆板湿热力学响应的影响主要来源于组份体积分数的变化,其对温度场影响较小,对湿度场的影响程度取决于组份孔隙参数和湿度边界条件的设定;孔隙参数对位移和应力的影响取决于对整体弹性模量的影响.

(2)在稳态湿热场下,内厚外薄的圆板比内薄外厚的圆板具有更大的整体位移和应力,厚度指数$\lambda$对位移和应力影响最大处出现在$\lambda = 1$附近.对于内边固定外边自由的FG旋转圆板,内薄外厚且厚度线性变化的几何结构有利于缓和形变和应力分布.

The authors have declared that no competing interests exist.

作者已声明无竞争性利益关系。

参考文献原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]

Heydari

, Jalali

, Nemati

. Buckling analysis of circular functionally graded plate under uniform radial compression including shear deformation with linear and quadratic thickness variation on the Pasternak elastic foundation
Applied Mathematical Modelling, 2017,41:494-507