, 龙凯MULTIPHASE MATERIAL LAYOUT OPTIMIZATION CONSIDERING EMBEDDING MOVABLE HOLES1)
WangXuan, LongKai中图分类号:O342
文献标识码:A
通讯作者:
收稿日期:2018-10-8
网络出版日期:2019-05-18
版权声明:2019力学学报期刊社 所有
基金资助:
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (10063KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
topology optimization
引 言
工程结构设计问题经常包含特定的几何限制条件.一个常见的限制是在设计过程中需要事先在设计域内嵌入固定形状的对象(组件或孔洞)以满足某些功能性或者制造性设计要求[1].例如,在航空航天结构中,一些功能设备(通常也用作承载结构),需要被嵌入到主体结构中以充分利用可用空间.比较典型的例子还有嵌入可移动压电驱动器的柔性智能结构设计问题[2],面向压电智能结构精确变形的协同优化设计问题[3],内嵌离散热导体的传热系统布局优化[4]等.此外,在结构设计过程中,通常还需要保留足够的预留空间以使得其他的组件能够顺利通过结构,或者准许嵌入预定的对象,或者单纯出于美学、设备维护的角度考虑预设孔洞.在这些应用中,不仅需要在允许的设计区域中寻找这些已知几何形状的预定对象的最佳位置和摆放方向,还需要设计连接这些嵌入对象的支撑结构以改善结构的整体性能[5-10].对于考虑嵌入组件的连续体结构布局优化问题,研究文献较多,许多研究者提出了非常有效的求解策略[11-16],关于这方面的研究综述可参阅文献[1,10]. 本文主要考虑嵌入移动孔洞的连续体结构布局优化问题.在处理固定位置上带有不可设计孔洞的优化问题中,通常采用被动单元方法(passive elementsapproach),即通过在设计域中定义被动区域(即具有规定密度的区域)来包括具有固定形状和位置的孔洞.在优化的过程中,被动区域内部的单元将从设计变量集合中排除,但包含在结构响应的计算中.这种被动单元方法很容易实施,但是存在一定限制,如孔洞的位置强烈影响优化结构的刚度,在过程中过早进行的设计选择通常基于经验而非优化,存在选择次优配置的风险,而这些配置以后无法更改.因此,对于嵌入可变位置的移动孔洞的优化问题来说,这种被动单元方法并不合适.
目前处理这种带有可移动孔洞的布局优化问题的文献相对较少. Kang和Wang[17]提出了一种新颖的处理嵌入可移动孔洞的拓扑优化方法,该方法结合了水平集方法对规定几何形状孔洞的精确几何描述的能力,以及基于节点变量的材料密度方法的高效率. 与上述"嵌入问题"一样,每个嵌入孔洞的位置和旋转角度由3个设计变量(2D)确定,即表征孔洞上某个参考点平移运动的两个变量,和旋转运动的一个变量. 此外,为了避免嵌入孔洞之间以及每个孔洞与设计域边界之间的重叠,他们提出了一种基于材料体积的单个的显式积分约束,这种非重叠约束是准确且可微分的,有利于设计灵敏度分析. 尽管他们所提方法在处理嵌入可移动孔洞的布局优化问题十分有效,但是通过水平集方法来驱动孔洞的移动、半解析灵敏度计算策略计算量较大.
Clausen等[18]提出一种有效处理具有灵活空隙区域的拓扑优化方法. 与在设计领域内严格指定空隙区域的被动单元方法不同的是,所建议的方法允许这些区域被灵活地重新定形和重新定位,其中使用惯性矩来控制孔洞的变形程度,使用孔洞区域的质心控制平移运动的自由度. 与文献[17]中的方法的主要区别在于空白定义,允许孔洞空间的完全灵活性. 空隙区域不是使用水平集函数描述,而是通过第二个离散设计变量场引入. 尽管该方法可应用于带有可移动孔洞的布局优化问题,但是该方法在处理带有多个移动孔洞的问题中还存在困难,考虑嵌入$n$个移动孔洞则需要引入$n$个离散的设计变量场,而且还缺少有效避免多个移动孔洞之间的重叠的策略. 另外,文献[17,18]均只涉及单相均质材料的优化问题. 在实际工程应用中,结构通常由多种非均匀材料组成,以满足不同的设计要求,如文献[19]指出多相材料组合有利于减轻结构重量.
为了克服以上方法的局限性,本文提出一种有效处理嵌入多个移动孔洞的多相材料布局优化问题的求解方法. Xia等[7]使用参数化水平集函数和$R$函数描述嵌入组件的几何形状,这样确保在整个优化过程中都在固定的Eulerian网格下优化,有利于提高计算效率. 本文受文献[7]启示,也使用参数化水平集函数描述嵌入孔洞的几何形状. 将定义多相材料结构拓扑的材料密度以及用于描述嵌入孔洞的位置和方向的几何参数被看作优化问题的设计变量. 为了将这两个看似不同的变量形式结合到一个统一的计算框架中,首先使用平滑化的Heaviside函数将所有嵌入孔洞映射到固定网格上的密度场,然后将文献[17]中的材料插值格式推广到考虑嵌入孔洞的多相材料布局优化问题当中,用于优化问题的材料参数化. 多个数值算例验证了本文方法的有效性.
1 考虑嵌入孔洞的拓扑优化列式
1.1 嵌入孔洞的拓扑描述
受文献[7, 17]启示,使用水平集函数来描述嵌入孔洞的形状和拓扑,表达式为$$ \left.\begin{array}{ll} {\phi \left( x \right) > 0} \,, & {\rm if} \ {\pmb x} \in \left( {D/ \varOmega } \right) {\phi \left( x \right) = 0} \,, & {\rm if} \ {\pmb x} \in \left( {\partial \varOmega \cap D} \right) {\phi \left( x \right) < 0} \,, & {\rm if} \ {\pmb x} \in \left( {\varOmega / \partial \varOmega } \right) \end{array} \!\! \right \} (1) $$
其中, $D$代表给定的设计域,$\varOmega $和$\partial \varOmega $分别为嵌入孔洞所占据的子区域及其边界.式(1)表明,如果点${\pmb x}$位于嵌入孔洞的里面,则其对应的水平集函数值小于零.
对于常规形状的孔洞(如圆,椭圆,超椭圆等),其对应的水平集函数可表示
$$\phi \left( {{\pmb x}, x_0 ,y_0 ,\theta } \right) = \phi \left( {\bar {x},\bar {y}} \right) (2)$$
其中
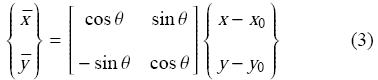
这里$\left( {\bar {x},\bar {y}} \right)$为嵌入孔洞上的局部坐标. $\theta$为嵌入孔洞相对于水平方向的旋转角. $x_0 $和$y_0$为孔洞上特殊参考点的横纵坐标. 为了便于说明,式(4)给出一个圆角方形孔洞的水平集函数
$$\phi _1 = \left( {\dfrac{\bar {x}}{a}} \right)^4 + \left( {\dfrac{\bar{y}}{b}} \right)^4-1 (4)$$
其中, $a$和$b$分别表示圆角方形孔洞的半长轴和半短轴长度.
对于形状不能由式(2)描述的复杂形状孔洞,可以像文献[7,9,20]一样,借助于R函数理论来描述其拓扑.为了简单起见,本文 只考虑了圆形和圆角方形孔洞作为嵌入对象.
为了避免由于孔洞移动导致重新划分网格的繁琐,使用光滑化的Heaviside函数将嵌入孔洞映射为固定分析网格上的密度场[21]
$$\eta _e = \prod\limits_{k = 1}^{N_k } \dfrac{1}{1 + \exp \left( { - \beta \phi _k } \right)} (5)$$
其中, $\phi _k $为第$k$个嵌入孔洞所对应的水平集函数,$N_{k}$为嵌入孔洞的个数. 参数$\beta$控制着密度变化的斜率, 较大的$\beta $给出较窄的中间密度带宽. 数值实验表明参数$\beta$随着迭代步数逐渐增大,优化效果表现更好,与文献[21]一样,本文所有算例均设置$\beta $从2逐渐增大到4.
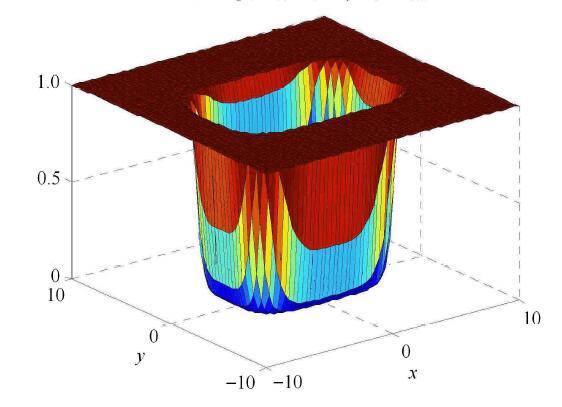
图1显示了中心在原点处的单个圆角方形孔洞在式(5)映射下的单元$e$的密度分布,其中$\beta =8$,这里圆角方形孔洞的半 长轴和半短轴长度分别为6和4.从图1可知,当单元$e$位于圆角方形孔洞内部,其对应的单元密度$\eta _e =0$,当单元$e$位于孔洞外部,其对应的单元密度$\eta _e = 1$.
显示原图|下载原图ZIP|生成PPT图1单个移动孔洞映射下的单元$e$的密度
-->Fig. 1Density of element $e$ mapped from a single moving hole
-->
1.2 考虑嵌入孔洞的材料插值格式
与其他优化问题[22-28]不同,在设计考虑多个嵌入孔洞的结构系统时,需要同步优化嵌入孔洞的位置和方向及每种材料相的拓扑构型,以使得结构总体刚度最大化. 受文献[17]的启发,引入一种在有限元网格上调用的类SIMP材料插值格式$$E_e = \rho _e^p \eta _e^q E_0 (6)$$
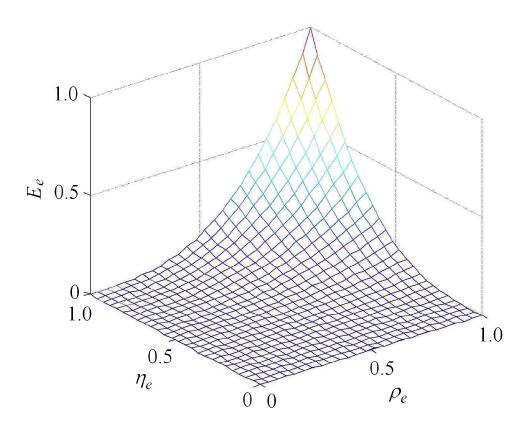
其中,单元密度$\rho _e $与传统的最小柔顺性问题中的密度变量角色一样. $p$,$q$为惩罚参数,本文所有算例中均取$p=q= 3$. $\eta _e$是由嵌入孔洞映射得到的密度场,可通过式(5)计算得到. $E_{0}$为实体材料的杨氏模量,$E_{e}$为插值后的杨氏模量. 图2显示了$E_{0} =1$时类SIMP材料插值格式的示意图. 从 式(6)和图2可知,当且仅当$\rho_e $和$\eta _e $均等于1时,插值后的杨氏模量才等于实体材料的杨氏模量,即$E_e= E_0 $.
显示原图|下载原图ZIP|生成PPT图2类SIMP材料插值格式示意图
-->Fig. 2Schematic illustration of SIMP-liked interpolation scheme
-->
对于多相材料结构,本文将文献[29]中材料插值格式拓展至带有嵌入孔洞的结构布局优化问题中.以两相材料为例,其插值格式可表示为
$ E_e \left( {\rho _1^e ,\rho _2^e } \right) = \left( {\rho _1^e } \right)^{p_1 }\left[{E_1 + \left( {\rho _2^e } \right)^{p_2 }\left( {E_2 - E_1 } \right)} \right]\eta _e^q (7)$
其中,$E_{1}$,$E_{2}$分别为材料1和材料2的杨氏模量;$p_{1}$, $p_{2}$, $q$为惩罚参数. $\rho _1$和$\rho _2 $为定义材料相的密度变量. $\rho _1 = 1$或0表示单元是实体材料或孔洞;$\rho _2 =1$或0分别表示单元选用材料2或材料1.
1.3 考虑嵌入孔洞的拓扑优化模型
结构拓扑优化的目的是寻找一个满足某些约束条件的最优的材料分布,以使结构获得某种最优的结构性能,如结构的重量最轻或刚度最大化. 本文旨在寻找嵌入孔洞的最优位置和每种材料相的最优布局,以最大化结构的整体刚度(即最小化结构的柔顺性). 因此,考虑嵌入孔洞的两相材料布局优化问题的数学列式可表示如下$ \left. \begin{matrix} {\rm find}: {\pmb\rho}_1 = \left\{ {\rho _1^1 , \rho _1^2 , \cdots ,\rho _1^{N_e } } \right\} \\ {\pmb\rho}_2 = \left\{ {\rho _2^1 ,\rho _2^2 , \cdots ,\rho _2^{N_e } } \right\} \\ {\pmb s} = \left\{ {s_1 ,s_2 , \cdots ,s_{N_m } } \right\} \\ {\rm min}: \ J = \sum_{e = 1}^{N_e } E_e {\pmb u}_e^T {\pmb k}_0 {\pmb u}_e \\ {\rm s.t.} {\pmb K}{\pmb U} = {\pmb F} \\ g_1 = \sum _{e = 1}^{N_e } \rho _1^e V_e - f_1 V_0 \leqslant 0 \\ g_2 = \sum_{e = 1}^{N_e } \rho _1^e \rho _2^e V_e - f_2 V_0 \leqslant 0 \\ g_3 = \sum_{e = 1}^{N_e } \eta _e V_e - \left( {V_0 - \sum_{k = 1}^{N_m } V_k } \right) \leqslant 0 \\ 0 ＜ \rho _{\min } \leqslant \rho _1^e \leqslant 1 \\ 0 ＜ \rho _{\min } \leqslant \rho _2^e \leqslant 1 \\ s_{\min } \leqslant s \leqslant s_{\max } \end{matrix} \right\} (8)$
其中,${\pmb K}$, ${\pmb F}$和${\pmb U}$分别为全局的刚度阵,载荷向量和位移向量, ${\pmb u}_{e}$为单元位移向量, $N_{e}$为用来离散设计域的单元个数, $E_{e}$为由 式(6)或式(7)定义的插值后的杨氏模量. 在上述优化模型的约束中,$g_{1}$为限制材料用量的体积约束,其中$V_{e}$和$V_{0}$分别为单元$e$和整个设计域的体积,$f_{1}$为设计领域中可用实体材料的体积分数比;$g_{2}$为限制刚性材料(材料2)用量的体积约束,$f_{2}$是刚性材料在实体材料中的体积分数比;$g_{3}$为非重叠约束[17],用于避免嵌入的孔洞之间,以及嵌入孔洞与设计域边界之间的重叠. $V_{k}$为第$k$个孔洞的体积.
在优化模型(8)中,有两类设计变量,一是用来定义材料1和材料2拓扑构型的单元密度变量${\pmb \rho}_1 $和${\pmb \rho}_2 $,另外一个是用来定义嵌入孔洞位置和方向的几何设计变量${\pmb s}$. 几何设计变量${\pmb s}$由$N_{m}$个嵌入孔洞上参考点的横纵坐标,及嵌入孔洞相当于水平方向的倾斜角组成,即$ {\pmb s}_k= \left\{ {x_k , y_k ,\theta _k } \right\}$ $\left( {k = 1,2, \cdots ,N_m }\right)$. ${\pmb s}_{\min}$和${\pmb s}_{\max}$为几何设计变量的下限和上限,其中$x_k,y_k $坐标变量的上下限根据设计域的几何尺寸确定,$\theta _k \in \left[ { -2\pi , 2\pi } \right]$. $\rho _{\min }$取很小的正数,作为密度设计变量的下限以防止刚度矩阵奇异,这里取$\rho _{\min} = 10^{ - 3}$. 对于单相材料设计问题,可以通过移除第2个相对密度向量${\pmb\rho} _2 $来简化优化模型.
2 灵敏度分析
由于采用基于梯度的优化算法来解决上述优化问题,因此这里需要推导目标函数的灵敏度.为简便起见,这里以内嵌移动孔洞的两相材料设计问题为例,即插值后的杨性模量$E_{e}$由 式(7)确定.2.1 目标函数对单元密度变量的灵敏度
目标函数关于单元密度变量${\pmb\rho}_1 $和${\pmb\rho}_2$的设计灵敏度可以通过伴随方法获得$$ \dfrac{\partial J}{\partial \rho _i^e } = - \dfrac{\partial E_e }{\partial \rho _i^e }{\pmb u}_e^{\rm T} {\pmb k}_0 {\pmb u}_e \,, \ \ \ i = 1,2 (9)$$
式 (9)中${\partial E_e } / {\partial \rho _i^e }$项可以通过对 式(7)中插值后的杨氏模量关于单元密度变量求导得到
$$ \left.\begin{matrix} \dfrac{\partial E_e }{\partial \rho _1^e } = p_1 \left( {\rho _1^e } \right)^{p_1 - 1}\left[ {E_1 + \left( {\rho _2^e } \right)^{p_2 }\left( {E_2 - E_1 } \right)} \right] \eta _e^q \\ \dfrac{\partial E_e }{\partial \rho _2^e } = p_2 \left( {\rho _1^e } \right)^{p_1 }\left( {\rho _2^e } \right)^{p_2 - 1}\left( {E_2 - E_1 } \right) \eta _e^q \\\end{matrix} \right\} (10) $$
2.2 目标函数对几何变量的灵敏度
设$z_{k}$代表第$k$个嵌入孔洞的3个几何设计变量$s_k = \left\{ {x_k ,y_k ,\theta _k }\right\}$中的一个,则目标函数关于$z_{k}$的灵敏度可通过链式法则得到$$\dfrac{\partial J}{\partial z_k } = \sum_{e = 1}^{N_e } \dfrac{\partial J}{\partial \eta _e }\dfrac{\partial \eta _e }{\partial \phi _k }\dfrac{\partial \phi _k }{\partial z_k } (11)$$
式中,${\partial J} / {\partial \eta _e}$可通过伴随法得到
$$ \dfrac{\partial J}{\partial \eta _e } = - \dfrac{\partial E_e }{\partial\eta _e }{\pmb u}_e^{\rm T} {\pmb k}_0{\pmb u}_e (12)$$
其中,${\partial E_e } /{\partial \eta _e}$项可以通过对 式(7)中插值后的杨氏模量关于$\eta _e $求导得到
$$\dfrac{\partial E_e }{\partial \eta _e } = q\left( {\rho _1^e } \right)^{p_1 }\left[ {E_1 + \left( {\rho _2^e} \right)^{p_2 }\left( {E_2 - E_1 } \right)} \right]\eta _e^{q - 1} (13)$$
式(11)中,${\partial \eta _e } /{\partial\phi _k }$可通过式(5)推导得到
$$\dfrac{\partial \eta _e }{\partial \phi _k } = \eta _e \dfrac{\beta \exp\left( { - \beta \phi _k } \right)}{1 + \exp \left( { - \beta \phi _k} \right)} (14)$$
对于式(11)中导数项${\partial \phi _k } / {\partial z_k}$,为了简化推导过程,假设这里考虑的嵌入孔洞的水平集函数可 以由式(2)表示,以式(4)定义的圆角方形孔洞为例,当$z_k = x_0 $时,导数项${\partial \phi _k }/{\partial z_k }$可表示为
$$\dfrac{\partial \phi _k }{\partial z_k } = 4\left( {\dfrac{\bar{x}}{a}} \right)^3\left( {\dfrac{ - \cos \theta }{a}} \right) + 4\left({\dfrac{\bar {y}}{b}} \right)^3\left( {\dfrac{\sin \theta }{b}} \right) (15)$$
当$z_k = y_0 $时,导数项${\partial \phi _k } / {\partial z_k }$可表示为
$$\dfrac{\partial \phi _k }{\partial z_k } = 4\left( {\dfrac{\bar{x}}{a}} \right)^3\left( {\dfrac{ - \sin \theta }{a}} \right) + 4\left({\dfrac{\bar {y}}{b}} \right)^3\left( {\dfrac{ - \cos \theta }{b}} \right) (16)$$
当$z_k = \theta $时,导数项${\partial \phi _k } /{\partial z_k }$可表示为
$ \dfrac{\partial \phi _k }{\partial z_k } = 4\left( {\dfrac{\bar {x}}{a}} \right)^3\dfrac{ -\sin \theta \cdot \left( {x - x_0 } \right) + \cos \theta \cdot \left( {y - y_0 } \right)}{a} +$
$\qquad 4\left( {\dfrac{\bar {y}}{b}} \right)^3\dfrac{ - \cos \theta \cdot \left( {x - x_0 } \right) -\sin \theta \cdot \left( {y - y_0 } \right)}{b} (17)$
关于体积约束$g_{1}$,$g_{2}$和非重叠约束$g_{3}$对设计变量的敏度可直接求导获得,这里省略其细节推导.
3 数值处理
众所周知,由于有限元网格离散的影响,基于单元密度的拓扑优化方法经常遭受棋盘格和网格依赖性等数值不稳定性问题. 为了获得清晰的黑白设计、避免网格依赖性问题,这里使用Sigmund[30]提出的灵敏度过滤技术来修改式(9)中的敏度$$\dfrac{\partial J}{\partial \rho _i } = \dfrac{\sum_{j = 1}^{N_i }{w\left( {{\pmb x}_j } \right)\rho _j \dfrac{\partial J}{\partial \rho _j }} }{\rho_i \sum_{j = 1}^{N_i } {w\left( {{\pmb x}_j } \right)} } (18)$$
其中,权重函数$w\left( {{\pmb x}_j } \right)$定义为
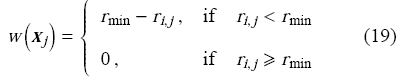
式中,$r_{i,j} $为单元$i$和单元$j$之间的距离,$N_i$是以单元$i$为中心、半径为$r_{\min} $的圆形邻域内的单元个数.
上述优化问题可以用不同的优化算法来求解,如系列二次规划算法(SQP),[31],移动渐近线算法(MMA)[32]等.本文采用MMA算法求解上述优化问题. 对于单相材料设计,当满足以下收敛条件时,优化过程停止迭代
$$\dfrac{\left\| {{\pmb\rho}_k - {\pmb\rho}_{k - 1} } \right\|_2 }{\left\| {{\pmb\rho}_k } \right\|_2 } \leqslant \varepsilon (20)$$
式中,$k $为当前的迭代步数,$\varepsilon $为容许的收敛误差.
由于过滤引起的平均效应会导致结构边界存在一些以灰度呈现的中间密度,对此可以采用文献[33,34]描述的两阶段优化策略来抑制,即在第一阶段采用式(18)定义的灵敏度过滤技术,目的在于消除棋盘格现象和网格依赖性问题. 第二阶段不采用过滤技术直至优化收敛,得到清晰的拓扑优化构型. 两个阶段的收敛精度分别设定为$0.25%$和$0.1% $.
4 数值算例与讨论
本节通过多个算例阐释本文方法的有效性,包括单相材料设计和多相材料设计算例. 不失一般性,本文只考虑二维优化问题.除非特 殊声明,所有算例中变量和几何参数均使用无量纲参数.对于单相材料优化问题,弹性模量和泊松比分别设置为1和0.3.对于多相材料优化问题,材料1和2的弹性模量分别设置为$E_{1} = 1$和$E_{2} = 3$,两种材料的泊松比均设为0.3.为了便于计算,所有角度坐标均以弧度表示. 所有的孔洞只准许在设计域内移动或旋转.4.1 悬臂梁：非重叠约束有效性验证
第一个悬臂梁优化算例验证非重叠约束的有效性. 几何区域和边界条件如图3所示,其中还包括两个半径为10的圆形孔洞.设计 域左边固支,右边中点处受单位集中载荷$F = 1$作用.由于本算例中考虑的嵌入孔洞是圆形的,因此只有圆心的坐标被视为设计变量. 两个圆形孔洞的中心最初位置为 (30.00,30.00)和(90.00, 30.00). 设计域用120$\times $60平面应力单元来离散. 材料准许的体积分数设定为0.4.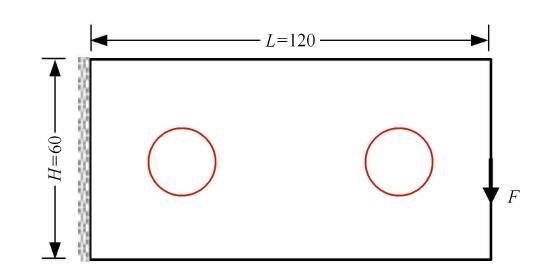
显示原图|下载原图ZIP|生成PPT图3悬臂梁的设计域和边界条件
-->Fig. 3Design domain and boundary condition of cantilever beam problem
-->
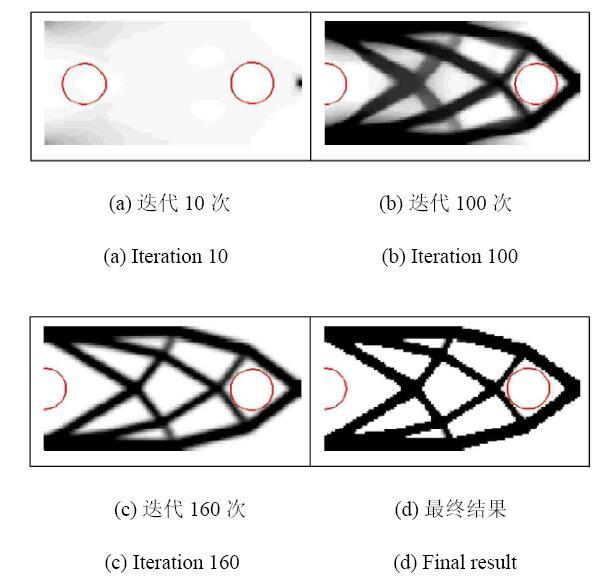
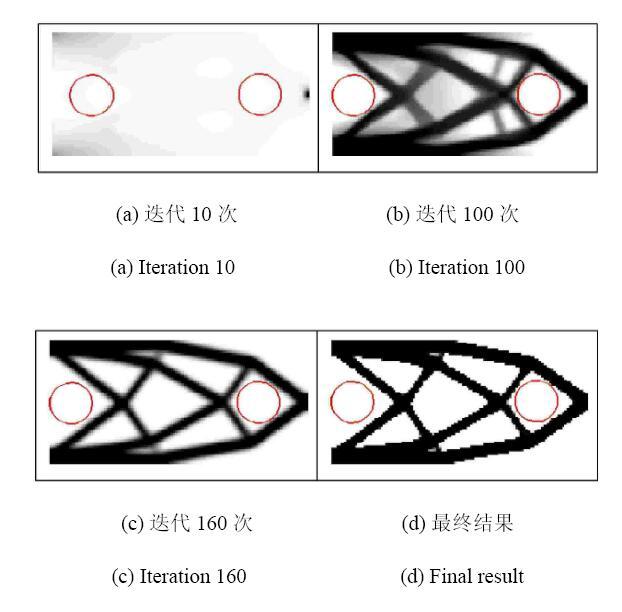
图4和图5分别显示了不考虑非重叠约束和考虑非重叠约束下的拓扑优化结果,分别标记为Case 1和Case 2.由图4可知,在不考虑非重叠约束的测试算例(Case 1)中,两个圆孔的中心最终位于(0.15, 29.66)和(95.99,30.05)处,很明显第一个孔洞(即左侧的孔洞)与预定义的设计 域边界重叠了.由图5可知,在考虑非重叠约束的测试算例(Case 2)中,第一个孔洞完全被设计领域边界所限制.两个圆形孔洞的中心最终分别位于(10.02, 30.05)和(95.99, 30.52).这证明了非重叠约束可以有效地避免嵌入孔洞和设计域边界之间的重叠.
显示原图|下载原图ZIP|生成PPT图4不考虑非重叠约束的悬臂梁优化结果
-->Fig. 4Optimization results of cantilever beam without considering the non-overlap constraint
-->
显示原图|下载原图ZIP|生成PPT图5考虑非重叠约束的悬臂梁优化结果
-->Fig. 5Optimization results of cantilever beam with considering the non-overlap constraint
-->
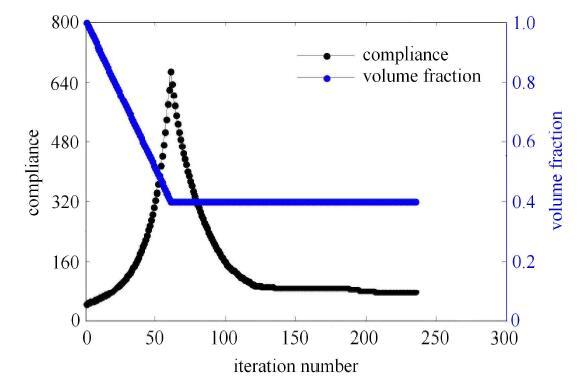
图4给出了考虑非重叠约束下目标函数和体积分数的迭代历史.从图6可知,本文方法优化迭代过程实现了稳定的收敛. 目标函数值从开始到第62个迭代步是不断增加的,这是由于体积分数的减小导致的.当体积分数达到预定的阈值,目标函数值开始稳步下降,最终收敛到75.57的最优值.
显示原图|下载原图ZIP|生成PPT图6目标函数和体积分数的收敛历史
-->Fig. 6Convergence histories of the objective function and volume fraction
-->
4.2 MBB梁：讨论孔洞位置、大小、方向的影响
第二个MBB梁优化算例讨论嵌入孔洞的位置、大小、方向对拓扑构型的影响. 几何区域和边界条件如图 7(a)所示,结构在顶部中心 位置处受单位集中载荷$F = 1$作用. 充分利用对称性,考虑一半的设计域,如图 7(b) 所示. 图7(b)显示的一半的设计域由180$\times $60平面应力单元来离散. 材料准许的体积分数设定为0.4.此算例中考虑将一个圆形孔洞和两个圆角方形孔洞嵌入到设计域中.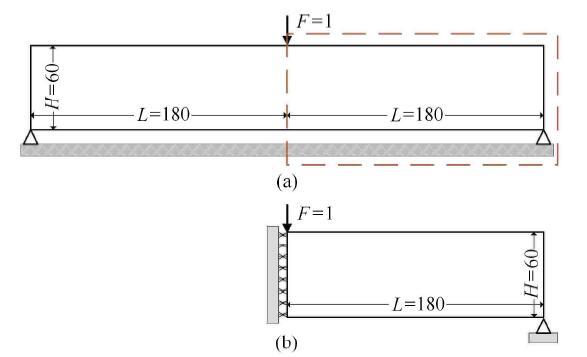
显示原图|下载原图ZIP|生成PPT图7MBB梁的设计域和边界条件
-->Fig. 7Design domain and boundary condition of MBB beam problem
-->
表1显示了5种不同初始布局下的拓扑优化结果,分别标记为Case 3,Case 4,Case 5,Case 6和Case 7. Case 3和Case 4的圆形孔洞半径为10,圆角方形孔洞的边长为20. Case 3和Case 4之间的区别在于嵌入孔洞 的初始位置不同.Case 5和Case 6的圆形孔洞半径为14,圆角方形孔洞的边长为28. Case 7的圆形孔洞半径为16,圆角方形孔洞的边长为32.Case 5和Case 6之间的区别在于嵌入孔洞的初始方向不同. Case 4和Case 5之间的区别在于嵌入孔洞的尺寸不同. Case 6和Case 7之间的区别也在于嵌入孔洞的尺寸不同.
Table 1
表1
表1嵌入孔洞不同初始布局下的优化结果
Table 1Optimization results for different initial layouts of the embedded holes
 |
新窗口打开
表2中列出了5种不同初始布局下3个嵌入孔洞的初始位置、优化后的位置及对应的目标函数值. 比较表1和2中的优化结果,可以发现,嵌入孔洞的位置、大小、方向对拓扑构型和目标函数值均有影响. 对比Case 4和Case 5,Case 6和Case 7的目标函数可知,嵌入孔洞的尺寸越大,结构的柔顺度值也变大,对应的结构刚度变小,也就是说结构性能变差.因此,在实际工程优化问题中需要根据需求做合适的选择.
Table 2
表2
表2嵌入孔洞不同初始布局下的优化结果
Table 2Optimization results for different initial layouts of the embedded holes
 |
新窗口打开
4.3 L型梁：多相材料布局优化问题
本算例考虑带有3个嵌入孔洞的多相材料L型梁设计问题.设计域和边界条件如图8所示,其中还包括3个半长轴为10、半短轴为8 的圆角方形孔洞.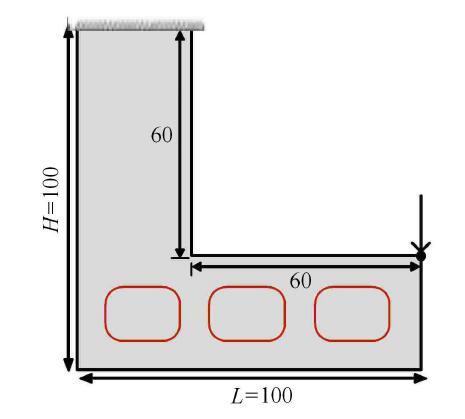
显示原图|下载原图ZIP|生成PPT图8L型梁的设计域和边界条件
-->Fig. 8Design domain and boundary condition of L-shaped beam problem
-->
3个孔洞中心的初始位置分别为(20,20),(50,20)和(80,20). 结构顶部边界固支,右边界顶部受单位集中载荷$F = 1$作用.对于两种固体材料,体积分数约束均设置为$20% $,即整个设计域的$60% $为空洞.设计域由6,400个四边形平面应力单元来离散.为了简单起见,我们采用第3节介绍的第一阶段收敛策略,即在整个多相材料设计过程中始终使用由式(18)定义的过滤技术.两个密度变量$\rho _1 $和$\rho _2 $的容许收敛误差均设置为$0.1% $.
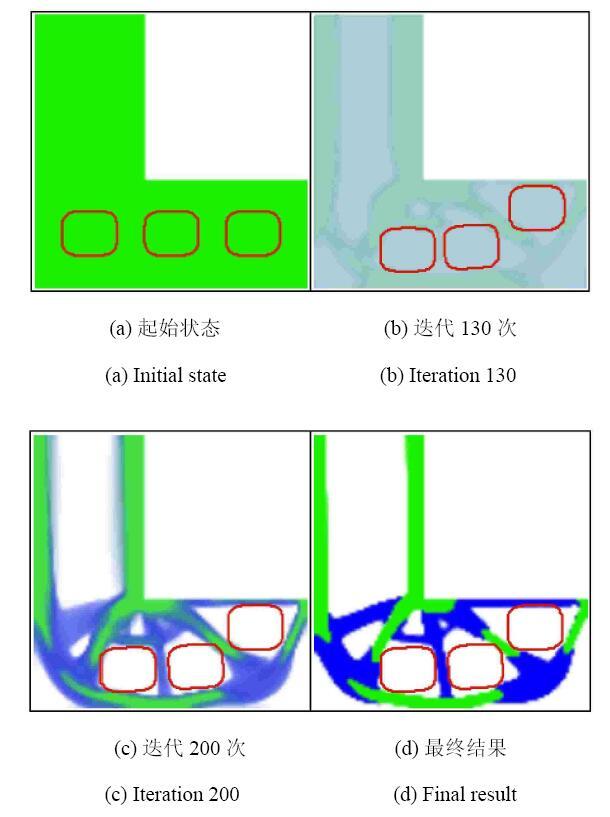
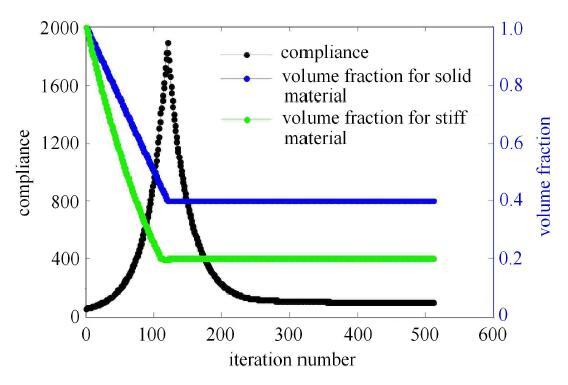
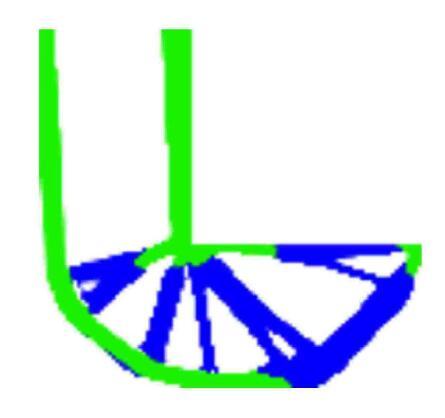
图9给出了拓扑优化结果,其中强材料2和弱材料1分别用绿色和蓝色表示. 图10显示了目标函数和体积分数的收敛历史.从优化结果可以看出,与单相材料设计一样,目标函数先随着体积分数的减小而逐渐增大,当达到目标体积时,体积分数保持不变,目标函数又逐渐减小,最终收敛到102.13的最优值. 对于多相材料设计,这些嵌入孔洞也可以找到合适的位置来保持结构的完整性.强材料主要分布在设计域的负载端和固定端,而弱材料主要分布于刚性的材料之间.另外,还可以观察到,在前160次迭代中,3个圆角方形孔洞的位置变化较大. 相反,嵌入孔洞的位置在随后的迭代中仅略微改变,并且最终位于(34.38,14.00),(59.09,15.00) 和 (81.00,29.33).3个嵌入孔洞相对于水平面的旋转角度(弧度)分别为0.028,2, 0.062,8和0.0314.
显示原图|下载原图ZIP|生成PPT图9考虑3个嵌入孔洞的L型梁的优化结果
-->Fig. 9Optimization results of L-shaped beam with three embedded holes
-->
显示原图|下载原图ZIP|生成PPT图10目标函数和体积分数的收敛历史
-->Fig. 10Convergence histories of the objective function and volume fraction
-->
为了比较,图11显示了没有考虑嵌入孔洞情况下L型梁的多相材料拓扑优化结果,对应的目标函数值为99.01.对比图9和图11的优化结果,可以看出考虑嵌入孔洞的拓扑构型与不考虑嵌入孔洞的拓扑构型明显不同,这也说明在连续体结构设计中考虑孔洞的必要性.对比两种情况下目标函数值可知,考虑嵌入孔洞的结构虽然满足设计要求,但是其对应的柔顺度相对变大,对应的结构刚度变小,说明考虑嵌入孔洞对结构的力学性能也有影响.
显示原图|下载原图ZIP|生成PPT图11未嵌入孔洞的L型梁的优化结果
-->Fig. 11Optimization results of L-shaped beam without embedded holes
-->
为了进一步说明所提方法的有效性,将 式(7)定义的两相材料插值格式进一步推广到内嵌移动孔洞的三相材料拓扑优化问题中,其表达式为
$ E_e = \left( {\rho _1^e } \right)^{p_1 }\Big \{ \left( {\rho _2^e } \right)^{p_2 }\Big[ \left( {\rho _3^e } \right)^{p_3 }E_3 + \left( {1 - \left( {\rho _3^e } \right)^{p_3 }} \right)E_2 \Big ]+$
$ \qquad \left( {1 - \left( {\rho _2^e } \right)^{p_2 }} \right)E_1 \Big \} \eta _e^q (21)$
其中,$E_{1}$,$E_{2}$和$E_{3}$分别为材料1、材料2和材料3的杨氏模量. $p_{1}$, $p_{2}$, $ p_{3}$,$q$为惩罚参数. $\rho _1 $, $\rho _2 $和$\rho _3 $为定义材料相的密度变量. $\rho _1 =1$或0表示单元是实体材料或空洞;$\rho _2 $和$\rho _3 $取值1或0控制着实体结构中不同材料相的选择.
仍然考虑上面内嵌3个移动孔洞的L型梁优化算例.设计域与边界条件以及嵌入孔洞的初始布局均与上面算例相同,不同的是此 算例考虑三相材料优化问题.材料1、材料2和材料3的弹性模量分别设置为$E_{1}= 1$, $E_{2} = 3$和$E_{2} = 5$,3种材料的泊松比均设为0.3.对于3种固体材料,体积分数分别设置为$20% $,$10% $和$10% $,即保留整个设计域的$60% $为空洞.为了方便,此算例设置最大的迭代次数为400.
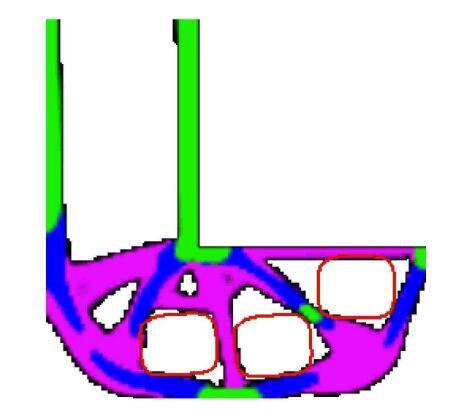
图12给出了拓扑优化结果,其中材料1、材料2和材料3分别用粉色、蓝色和绿色表示. 目标函数最终收敛到80.05的最优值.3个嵌入 孔洞的中心最终分别位于(35.03, 14.28),(60.15, 14.00)和(82.00, 29.25).从优化结果可知,对于内嵌孔洞的三相材料拓扑优化问题,本文方法也能够得到清晰的拓扑构型,这进一步说明本文方法的有效性.
显示原图|下载原图ZIP|生成PPT图12考虑3个嵌入孔洞的L型梁的优化结果
-->Fig. 12Optimization results of L-shaped beam with three embedded holes
-->
5 结 论
本文提出一种有效求解内嵌多个移动孔洞的多相材料布局优化问题的拓扑优化方法. 在当前的优化问题中,需要同时确定嵌入孔洞的最佳位置和方向,以及多相材料的拓扑构型,以最大化整个结构系统的刚度. 为此,使用水平集函数描述嵌入孔洞的几何形状. 将定义多相材料结构拓扑的材料密度以及描述嵌入孔洞的位置和方向的几何参数作为设计变量. 使用平滑化的 Heaviside 函数将嵌入的孔洞投影到固定网格上的密度场,可以有效地避免重新划分网格的繁琐并改善计算效率. 引入一种在有限元水平上调用的类 SIMP 材料插值格式将这两个看似不同的设计变量形式结合到一个统一的计算框架中,实现嵌入孔洞位置、方向和多相材料结构拓扑的同步优化. 算例表明所提方法可以有效处理带有多个嵌入孔洞的多相材料布局优化问题.The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . We provide an introduction and state of the art overview of integrated layout design of multi component systems. We review several packing optimization and overlap detection strategies, some tree-based methods, such as octrees and spheretrees, and a finite circle method (FCM) proposed to favor gradient-based optimization algorithms. Integrated layout design techniques for simultaneous packing and structure topology optimization of multicomponent systems are reviewed; two typical approachs for system stiffness maximization are reviewed and compared in detail. Design of multicomponent systems under inertia forces is presented using polynomial interpolation models; constraints to the centroid position, moment of inertia, and volume fraction are included. Applications to piezoelectric multi-actuated microtools and integrated layout design of bridge systems are presented. Finally, the effectiveness of the FCM. applications to 3D problems, and local optimum phenomena are discussed. |
| [2] | . In the optimal configuration design of piezoelectric smart structures, it is favorable to use actuation elements with certain predefined geometries from the viewpoint of manufacturability of fragile piezoelectric ceramics in practical applications. However, preserving the exact shape of these embedded actuators and tracking their dynamic motions presents a more challenging research task than merely allowing them to take arbitrary shapes. This paper proposes an integrated topology optimization method for the systematic design of compliant smart structures with embedded movable PZT (lead zirconate titanate) actuators. Compared with most existing studies, which either optimize positions/sizes of the actuators in a given host structure or design the host structure with pre-determined actuator locations, the proposed method simultaneously optimizes the positions of the movable PZT actuators and the topology of the host structure, typically a compliant mechanism for amplifying the small strain stroke. A combined topological description model is employed in the optimization, where the level set model is used to track the movements of the PZT actuators and the independent point-wise density interpolation (iPDI) approach is utilized to search for the optimal topology of the host structure. Furthermore, we define an integral-type constraint function to prevent overlaps between the PZT actuators and between the actuators and the external boundaries of the design domain. Such a constraint provides a unified and explicit mathematical statement of the non-overlap condition for any number of arbitrarily shaped embedded actuators. Several numerical examples are used to demonstrate the effectiveness of the proposed optimization method. |
| [3] | . 智能结构集智能材料与传统材料于一体,能够实现结构的主动控制,在航空航天等领域具有巨大的应用潜力.由于其系统复杂且具有多场耦合效应,智能结构的整体式优化设计方法成为结构控制技术研究的关键之一.为了提高压电智能结构的整体性能和变形精度,提出了同时考虑压电驱动器布局(分布位置及角度)和基体结构拓扑构型的协同优化设计新方法.采用多点约束方法(multi-point constraints,MPC)建立压电驱动器和基体结构的连接,定义一种与测量点目标位移相关的权重函数,以实现结构的精确变形控制.通过协同优化设计,压电驱动器可以获得最优的分布位置及角度,同时基体结构获得最优的拓扑构型,从而提升了压电智能结构系统的整体驱动性能和变形精度.通过进一步分析,研究了精确变形、体分比约束与结构优化构型和整体刚度的关系,以及优化结果中可能存在的传力路径畸变现象.数值算例的设计结果表明,采用协同优化设计方法,能够扩大结构的寻优空间,有效减小变形误差,实现压电智能结构的精确变形控制. . 智能结构集智能材料与传统材料于一体,能够实现结构的主动控制,在航空航天等领域具有巨大的应用潜力.由于其系统复杂且具有多场耦合效应,智能结构的整体式优化设计方法成为结构控制技术研究的关键之一.为了提高压电智能结构的整体性能和变形精度,提出了同时考虑压电驱动器布局(分布位置及角度)和基体结构拓扑构型的协同优化设计新方法.采用多点约束方法(multi-point constraints,MPC)建立压电驱动器和基体结构的连接,定义一种与测量点目标位移相关的权重函数,以实现结构的精确变形控制.通过协同优化设计,压电驱动器可以获得最优的分布位置及角度,同时基体结构获得最优的拓扑构型,从而提升了压电智能结构系统的整体驱动性能和变形精度.通过进一步分析,研究了精确变形、体分比约束与结构优化构型和整体刚度的关系,以及优化结果中可能存在的传力路径畸变现象.数值算例的设计结果表明,采用协同优化设计方法,能够扩大结构的寻优空间,有效减小变形误差,实现压电智能结构的精确变形控制. |
| [4] | . |
| [5] | . Extensive published research results exist on the topology design of single-component structures, while multicomponent structural systems have received much less attention. In this article, we present a technique for optimizing the topology of a structure that should be connected to one or more predesigned polygon-shaped components to maximize the stiffness of the overall ensemble. We call it an embedding problem in topology design because predesigned components are to be optimally positioned and oriented within a design region while the connecting structure's topology is optimized simultaneously. Continuous design variables are used to vary the locations of the embedded objects smoothly along with the topology of the connecting structure to apply gradient-based continuous optimization algorithms. A new material interpolation function on the basis of normal distribution function was used for this purpose. An optimality criteria method combined with the steepest descent method was used to minimize the mean compliance to obtain the stiffest structure for a given volume of material for the connecting structure. As a special case of this method, topology optimization of multicomponent structural systems connected with fasteners was also considered. Illustrative examples are presented. |
| [6] | . Based on the previously proposed techniques for the integrated layout optimization of multi-component system, this paper is to demonstrate further developments and applications of the related techniques in the integrated layout design of supports and structures. The design procedure mainly consists of two parts. Firstly, the layout of the supports is described with the positions of movable... [Show full abstract] |
| [7] | . Integrated design of the structure topology and involved component layout is a challenging design issue when compared with traditional topology optimization. In this paper, we propose an implicit modeling approach that works completely on an Eulerian finite element mesh throughout the whole optimization process. To this aim, implicit level-set functions and R-functions are employed to describe geometrical shapes of movable components. In particular, a modified arctan function is adopted to depict the material discontinuity along the interface between the structure domain and each component domain. They are then used for material interpolations and analytical sensitivity analysis w.r.t. both pseudo-density design variables and location design variables related to the host structure and components, respectively. Based on a variety of numerical tests, it is demonstrated that considered design problems with movable components can easily be solved by extending the SIMP material model based topology optimization approach using an Eulerian mesh and the gradient-based optimization algorithm. (C) 2013 Elsevier B.V. All rights reserved. |
| [8] | . 61We present topology optimization with distance control of embedded components.61Both structural topology and multi-component layout are represented by level set.61Specified geometries of component can be well preserved thanks to level set model.61A unified level set-based distance constraint for arbitrary components is proposed.61Explicit integral form of the distance constraint facilitates sensitivity analysis. |
| [9] | . In this paper, two novel methods are proposed for optimizing the layout of structural systems with embedding components considering the minimum/maximum distance constraints between the components. The key ideas are using level set functions to describe the shapes of arbitrary irregular embedding components and resorting to the concept of structural skeleton to formulate the distance control constraints explicitly. Numerical examples presented demonstrate that the proposed approaches can give a complete control of the layout of embedding components in an explicit and local way. |
| [10] | . |
| [11] | . The purpose of this paper is to present an extended integrated layout and topology optimization method dealing with the multi-frame and multi-component fuselage structure systems design. Considering a |
| [12] | . AbstractIn view of the prohibited computing time and the complexity of design procedure, a superelement formulation (SEF) is proposed to deal with the simultaneous optimization of component placement and the framework topology. In the iterative design process, each component is modelled as a movable superelement so that the sensitivity analysis with respect to the location design variables can be largely simplified by the SEF. Moreover, based on the Kuhn鈥揟ucker optimality condition, two decomposition strategies are developed as variant approaches for the simultaneous design of multi-component system. By means of numerical examples, these approaches are compared to show their capability and efficiency for the system compliance minimization. |
| [13] | . |
| [14] | . <p>基于多组件结构系统整体式拓扑布局优化设计方法,研究了同时含有部件布局、组件布局、主结构框架构型和部件结构构型4类设计变量的复杂系统协同优化设计问题,是整体式拓扑布局优化设计面向复杂飞行器结构系统设计的拓展。采用多点约束(MPC)模拟组件、部件及支撑结构之间的刚性连接,采用有限包络圆方法(FCM)解决组件之间、组件与设计域边界之间的几何干涉问题。通过整体式拓扑布局的刚度优化设计,部件和组件均可以获得优化的布局位置,同时主结构框架构型和部件结构构型获得优化的结构样式,充分体现了整体式拓扑布局优化设计方法应用于复杂结构系统设计的能力。</p> . <p>基于多组件结构系统整体式拓扑布局优化设计方法,研究了同时含有部件布局、组件布局、主结构框架构型和部件结构构型4类设计变量的复杂系统协同优化设计问题,是整体式拓扑布局优化设计面向复杂飞行器结构系统设计的拓展。采用多点约束(MPC)模拟组件、部件及支撑结构之间的刚性连接,采用有限包络圆方法(FCM)解决组件之间、组件与设计域边界之间的几何干涉问题。通过整体式拓扑布局的刚度优化设计,部件和组件均可以获得优化的布局位置,同时主结构框架构型和部件结构构型获得优化的结构样式,充分体现了整体式拓扑布局优化设计方法应用于复杂结构系统设计的能力。</p> |
| [15] | . Finally, to validate the proposed design procedure, a variety of multi-component system layout design problems are tested and solved on account of inertia loads and gravity center position constraint. Solutions are compared with traditional topology designs without component. Copyright 漏 2008 John Wiley & Sons, Ltd. |
| [16] | . 多组件结构系统整体优化设计通过协同优化支撑结构拓扑构型和组件布局来使结构系统的位移响应最小。本文提出通过模态加速度法（MAM）求解多组件结构系统的位移响应,并以位移响应值最小作为优化目标;引入多点约束（MPC）方法模拟组件与设计域间的铆钉或螺栓连接形式;采用有限包络圆法（FCM）来避免组件之间及组件与设计域边界产生干涉。建立了多组件结构系统整体优化问题的数学模型,并对动响应目标函数关于设计变量的灵敏度进行了推导。最后,通过几个算例验证了整体优化方法在简谐力激励下求解问题的可行性及其在实际问题中的有效性。 . 多组件结构系统整体优化设计通过协同优化支撑结构拓扑构型和组件布局来使结构系统的位移响应最小。本文提出通过模态加速度法（MAM）求解多组件结构系统的位移响应,并以位移响应值最小作为优化目标;引入多点约束（MPC）方法模拟组件与设计域间的铆钉或螺栓连接形式;采用有限包络圆法（FCM）来避免组件之间及组件与设计域边界产生干涉。建立了多组件结构系统整体优化问题的数学模型,并对动响应目标函数关于设计变量的灵敏度进行了推导。最后,通过几个算例验证了整体优化方法在简谐力激励下求解问题的可行性及其在实际问题中的有效性。 |
| [17] | . This paper presents a novel topology description model for topology optimization problems with embedded movable holes, combining the ability of the level set model for accurate geometrical description of the prescribed hole shapes, and the high efficiency of the material density-based method. By this means, any arbitrary hole shapes can be represented accurately and smoothly, while the topological changes can be easily handled by the material distribution model. An explicit mathematical expression is defined to obtain the actual structural layout by combing both models. Moreover, an effective model for the non-overlap constraint is proposed in a unified and systematic manner to avoid the overlaps between the holes and between each hole and the design domain boundary. Therein, the non-overlap constraint for all the embedded holes is imposed as a single explicit integral constraint over the design domain, thus avoiding the difficulties in the overlap detection of multiple arbitrary-shaped geometries. Such a non-overlap constraint is accurate and differentiable, facilitating an analytical design sensitivity analysis. Numerical examples are given to demonstrate the effectiveness and efficiency of the present method. |
| [18] | . This paper presents a methodology for including fixed-area flexible void domains into the minimum compliance topology optimization problem. As opposed to the standard passive elements approach of rigidly specifying void areas within the design domain, the suggested approach allows these areas to be flexibly reshaped and repositioned subject to penalization on their moments of inertia, the positions of their centers of mass, and their shapes. The flexible void areas are introduced through a second, discrete design variable field, using the same discretization as the standard field of continuous density variables. The formulation is based on a combined approach: The primary sub-problem is to minimize compliance, subject to a volume constraint, with a secondary sub-problem of minimizing the disturbance from the flexible void areas. The design update is performed iteratively between the two sub-problems based on an optimality criterion and a discrete update scheme, respectively. The method is characterized by a high flexibility, while keeping the formulation very simple. The robustness and applicability of the method are demonstrated through a range of numerical examples. The flexibility of the method is demonstrated through several extensions, including a shape measure requiring the flexible void area to fit a given reference geometry. |
| [19] | . 在多相材料的结构拓扑优化问题中,通常给定各相材料体积约束或材料总重量约束作为材料的控制用量.在结构轻量化设计的实际工程背景下,以结构总重量最小化为目标的优化模型具有明确的工程意义.针对含多相材料的稳态传热结构拓扑优化问题,提出了以结构总重量最小化为目标和给定热柔顺度为约束的多工况连续体结构拓扑优化建模方法.遵循独立连续映射建模方式,采用两类独立拓扑变量分别表征单元热传导矩阵和单元重量状态.推导了热柔顺度和总重量对设计变量的敏度,基于一阶和二阶泰勒展开得到各自的近似表达式.通过求解偏微分方程,实现了约束函数一次项过滤,消除了棋盘格现象和网格依赖性问题,并保证了约束方程在过滤后严格成立.建立的近似优化模型具有二次函数形式的目标函数和一次函数形式的约束函数.基于对偶序列二次规划方法对优化模型进行求解直至收敛.通过四个三维结构数值算例分析对比了热柔顺度约束限值、不同材料混合及多工况、多约束条件对优化结果的影响.数值算例结果表明,本文提出的优化方法在基于多相材料的多工况稳态热传导结构轻量化设计中具有可行性和有效性. . 在多相材料的结构拓扑优化问题中,通常给定各相材料体积约束或材料总重量约束作为材料的控制用量.在结构轻量化设计的实际工程背景下,以结构总重量最小化为目标的优化模型具有明确的工程意义.针对含多相材料的稳态传热结构拓扑优化问题,提出了以结构总重量最小化为目标和给定热柔顺度为约束的多工况连续体结构拓扑优化建模方法.遵循独立连续映射建模方式,采用两类独立拓扑变量分别表征单元热传导矩阵和单元重量状态.推导了热柔顺度和总重量对设计变量的敏度,基于一阶和二阶泰勒展开得到各自的近似表达式.通过求解偏微分方程,实现了约束函数一次项过滤,消除了棋盘格现象和网格依赖性问题,并保证了约束方程在过滤后严格成立.建立的近似优化模型具有二次函数形式的目标函数和一次函数形式的约束函数.基于对偶序列二次规划方法对优化模型进行求解直至收敛.通过四个三维结构数值算例分析对比了热柔顺度约束限值、不同材料混合及多工况、多约束条件对优化结果的影响.数值算例结果表明,本文提出的优化方法在基于多相材料的多工况稳态热传导结构轻量化设计中具有可行性和有效性. |
| [20] | . Our approach to shape design and optimization offers great flexibility because it provides explicit parametric control of geometry and topology within a large space of free-form shapes. The resulting method is also general in that it subsumes most other types of shape optimization as special cases. We describe an implementation of the proposed technique with attractive numerical properties. The explicit construction of an implicit representation supports straightforward sensitivity analysis that can be used with most gradient-based optimization methods. Furthermore, our implementation does not require any error-prone polygonization or approximation of level sets (isocurves and isosurfaces). The effectiveness of the method is demonstrated by several numerical examples. Copyright 漏 2006 John Wiley & Sons, Ltd. |
| [21] | . Topology optimization for minimum and maximum thickness control, uniform thickness control, and multiple thickness control is provided by using moving morphable bars formed of rectangles with semicircular ends. By employing the center coordinates of the semicircular ends and the thickness of a moving bar as design variables, the bar can float around the design domain while its shape morphs according to the design sensitivities. The overlapping of moving bars is allowed, and the element density is determined by the approximation of the Heaviside function by measuring the shortest distance from the boundaries of the bars. The minimum thickness of the members of an optimized structure is controlled by simply setting the lower bound of the thickness variables for the moving bars. No constraints or filtering techniques are required for the minimum thickness control. The maximum thickness is controlled for each moving bar through its corresponding constraint, which prevents an over-sized member due to the overlapping of moving bars. By solving benchmark problems, the validity of the method proposed for versatile thickness control is shown. It is also shown that the proposed method alleviates numerical difficulties for hinges when it is applied for compliant mechanism problems. |
| [22] | . For complicated structures assembled by several parts, like launch vehicle, external load in the form of concentrated load exerted on several points is transmitted to a given section of the structure. Therefore, some measures should be taken in the structural design to diffuse the concentrated force. In order to optimize the structure for diffusing the concentrated force, a theoretical model based on the continuum topology optimization is presented in this paper. The minimum structural compliance is taken as the object function subject to structural materials' volume constraint. Constraints on uniformity of the internal force are also considered in this model. Two-dimensional and three-dimensional examples are presented to illustrate the effectiveness of the formulation and algorithm. Finally, based on the actual forces and displacement constraints, a feasible conceptual design is presented for the short shell of a rocket's storage trunk. . For complicated structures assembled by several parts, like launch vehicle, external load in the form of concentrated load exerted on several points is transmitted to a given section of the structure. Therefore, some measures should be taken in the structural design to diffuse the concentrated force. In order to optimize the structure for diffusing the concentrated force, a theoretical model based on the continuum topology optimization is presented in this paper. The minimum structural compliance is taken as the object function subject to structural materials' volume constraint. Constraints on uniformity of the internal force are also considered in this model. Two-dimensional and three-dimensional examples are presented to illustrate the effectiveness of the formulation and algorithm. Finally, based on the actual forces and displacement constraints, a feasible conceptual design is presented for the short shell of a rocket's storage trunk. |
| [23] | . 提出了一种利用拓扑描述函数(TDF)作为拓扑设计变量求解连续体结构拓扑优化问题的新方法. 优化问题的目标函数是结构的整体柔顺性，约束条件为对于可利用材料的体积限制. 这种方法不仅可以消除拓扑优化中经常出现的棋盘格式等数值不稳定现象，而且能够有效地抑制传统算法处理此类优化问题时所引发的边界扩散效应. 与其它的基于水平集描述函数的拓扑优化方法相比，所提出的算法不仅无需求解控制水平集函数演化的双曲守恒方程，而且合理地考虑了目标函数的拓扑导数信息，因而使得算法的计算效率有了显著的提高. . 提出了一种利用拓扑描述函数(TDF)作为拓扑设计变量求解连续体结构拓扑优化问题的新方法. 优化问题的目标函数是结构的整体柔顺性，约束条件为对于可利用材料的体积限制. 这种方法不仅可以消除拓扑优化中经常出现的棋盘格式等数值不稳定现象，而且能够有效地抑制传统算法处理此类优化问题时所引发的边界扩散效应. 与其它的基于水平集描述函数的拓扑优化方法相比，所提出的算法不仅无需求解控制水平集函数演化的双曲守恒方程，而且合理地考虑了目标函数的拓扑导数信息，因而使得算法的计算效率有了显著的提高. |
| [24] | . It is necessary to limit maximum nominal stress for engineering structural design generally, so as to avoid that the failure of fracture or fatigue occurs. Topology optimization approach is a feasible strategy. The conventional bi-evolutionary structural optimization (BESO) method cannot effectively address the topology optimization problem with stress constraint. To overcome this limitation, this paper suggests an improved BESO method for stress-constrained topology optimization, in which the minimum compliance design problem with volume and stress constraints is considered. A global stress measure based on the K-S function is introduced to reduce the computational cost associated with the local stress constraint. Meanwhile, the stress constraint function is added to the objective function by using the Lagrange multiplier method. Moreover, the appropriate value of the Lagrangian multiplier is then determined by a bisection method so that the stress constraint is satisfied. The model of BESO method for solving stress-constrained topology optimization and its sensitivity analysis are detailed. Finally, three typical topology optimization examples are performed to demonstrate the validity of the present method, in which the stress constrained designs are compared with the traditional stiffness based designs to illustrate the merit of considering stress constraint. The optimized results indicate that the improved BESO method, as a robust algorithm with stable iterative history, achieves an ambiguous topology with clearly defined boundaries, and realizes a design that effectively reduces stress concentration effect at the critical stress areas. . It is necessary to limit maximum nominal stress for engineering structural design generally, so as to avoid that the failure of fracture or fatigue occurs. Topology optimization approach is a feasible strategy. The conventional bi-evolutionary structural optimization (BESO) method cannot effectively address the topology optimization problem with stress constraint. To overcome this limitation, this paper suggests an improved BESO method for stress-constrained topology optimization, in which the minimum compliance design problem with volume and stress constraints is considered. A global stress measure based on the K-S function is introduced to reduce the computational cost associated with the local stress constraint. Meanwhile, the stress constraint function is added to the objective function by using the Lagrange multiplier method. Moreover, the appropriate value of the Lagrangian multiplier is then determined by a bisection method so that the stress constraint is satisfied. The model of BESO method for solving stress-constrained topology optimization and its sensitivity analysis are detailed. Finally, three typical topology optimization examples are performed to demonstrate the validity of the present method, in which the stress constrained designs are compared with the traditional stiffness based designs to illustrate the merit of considering stress constraint. The optimized results indicate that the improved BESO method, as a robust algorithm with stable iterative history, achieves an ambiguous topology with clearly defined boundaries, and realizes a design that effectively reduces stress concentration effect at the critical stress areas. |
| [25] | . <p>在许多如大坝、桥梁等大型土木工程结构中，结构的自重是初始设计阶段必须考虑的重要载荷之一，因此研究自重载荷作用下的结构拓扑优化设计问题具有十分重要的意义.针对考虑自重载荷作用的拓扑优化问题所面临的主要困难，总结了现有处理考虑自重载荷的拓扑优化问题的三类主要方法；提出一种基于非均匀有理B样条（non-uniform rational B-splines，NURBS）基函数插值的拓扑描述函数方法，基于此方法研究了考虑设计依赖自重载荷作用的2D/3D结构优化设计问题.在列式下，高阶NURBS基函数被同时用于三维NURBS实体片中的几何场、位移场及设计变量场插值，实现了几何模型、分析模型和优化模型的有效统一，确保了位移场及设计变量场的高阶连续性；详细推导了基于NURBS基函数插值的考虑自重载荷作用的三维结构拓扑优化模型及其灵敏度列式，并采用移动渐进线方法（method of moving asymptotes，MMA）进行了优化求解；多个算例验证了方法的有效性和稳定性，结果表明，优化迭代过程稳健，收敛快，能够有效地克服自重载荷作用下连续体结构拓扑优化中经常遇到的低密度区域材料的寄生效应及目标函数的非单调性等问题.</p> . <p>在许多如大坝、桥梁等大型土木工程结构中，结构的自重是初始设计阶段必须考虑的重要载荷之一，因此研究自重载荷作用下的结构拓扑优化设计问题具有十分重要的意义.针对考虑自重载荷作用的拓扑优化问题所面临的主要困难，总结了现有处理考虑自重载荷的拓扑优化问题的三类主要方法；提出一种基于非均匀有理B样条（non-uniform rational B-splines，NURBS）基函数插值的拓扑描述函数方法，基于此方法研究了考虑设计依赖自重载荷作用的2D/3D结构优化设计问题.在列式下，高阶NURBS基函数被同时用于三维NURBS实体片中的几何场、位移场及设计变量场插值，实现了几何模型、分析模型和优化模型的有效统一，确保了位移场及设计变量场的高阶连续性；详细推导了基于NURBS基函数插值的考虑自重载荷作用的三维结构拓扑优化模型及其灵敏度列式，并采用移动渐进线方法（method of moving asymptotes，MMA）进行了优化求解；多个算例验证了方法的有效性和稳定性，结果表明，优化迭代过程稳健，收敛快，能够有效地克服自重载荷作用下连续体结构拓扑优化中经常遇到的低密度区域材料的寄生效应及目标函数的非单调性等问题.</p> |
| [26] | . More and more stringent structural performance requirements are imposed in advanced engineering application, only a limited number of works have been devoted to the topology optimization of the structures with random vibration response requirements. In this study, the topology optimization problem with the objective function being the structural weight and the constraint functions being structural random vibration responses is investigated. An approximate topological optimization model for suppressing 'localized modes' of vibrating Cauchy solids is established in this paper. Based on moving asymptotes approximate functions, approximated-approximations expressions of the dynamic responses are constructed. In order to control the change' quantity of topologic design variables, new dynamic response constraint limits are formed and introduced into the optimization model at the beginning of each sub-loop iteration. Then, an optimization sequential quadratic programming is introduced, and a set of iteration formulas for Lagrange multipliers is developed. Two examples are provided to demonstrate that the proposed method is feasible and effective for obtaining optimal topology. Crown Copyright (C) 2013 Published by Elsevier Ltd. All rights reserved. |
| [27] | . The topology optimization problem with pressure load is solved by using a level set method. The free boundary and the pressure boundary of a structure are represented separately as two zero-level sets of two level set functions, and they are independently propagated during the optimization by solving two Hamilton鈥揓acobi equations. In order to prevent the two boundaries from touching or crossing each other, the design velocities of the two boundaries that amount to the steepest descent directions are modified. The optimization problem of minimum compliance with perimeter regularization is considered. The shape derivatives of the two boundaries are derived by using the material derivative approach and the adjoint method. The finite element analysis is done through an Eulerian method by employing a fixed mesh and an artificial weak material that represents void. Numerical examples in two dimensions are investigated. |
| [28] | . |
| [29] | . This work is focused on the topology optimization of lightweight structures consisting of multiphase materials. Instead of adopting the common idea of using volume constraint, a new problem formulation with mass constraint is proposed. Meanwhile, recursive multiphase materials interpolation (RMMI) and uniform multiphase materials interpolation (UMMI) schemes are discussed and compared based on numerical tests and theoretical analysis. It is indicated that the nonlinearity of the mass constraint introduced by RMMI brings numerical difficulties to attain the global optimum of the optimization problem. On the contrary, the UMMI-2 scheme makes it possible to formulate the mass constraint in a linear form with separable design variables. One such formulation favors very much the problem resolution by means of mathematical programming approaches, especially the convex programming methods. Moreover, numerical analysis indicates that fully uniform initial weighting is beneficial to seek the global optimum when UMMI-2 scheme is used. Besides, the relationship between the volume constraint and mass constraint is theoretically revealed. The filtering technique is adapted to avoid the checkerboard pattern related to the problem with multiphase materials. Numerical examples show that the UMMI-2 scheme with fully uniform initial weighting is reliable and efficient to deal with the structural topology optimization with multiphase materials and mass constraint. Meanwhile, the mass constraint formulation is evidently more significant than the volume constraint formulation. Copyright 漏 2011 John Wiley & Sons, Ltd. |
| [30] | . |
| [31] | . This article presents a Sequential Quadratic Programming (SQP) solver for structural topology optimization problems named TopSQP. The implementation is based on the general SQP method proposed in Morales et al. J Numer Anal 32(2):553鈥579 ( 2010 ) called SQP+. The topology optimization problem is modelled using a density approach and thus, is classified as a nonconvex problem. More specifically, the SQP method is designed for the classical minimum compliance problem with a constraint on the volume of the structure. The sub-problems are defined using second-order information. They are reformulated using the specific mathematical properties of the problem to significantly improve the efficiency of the solver. The performance of the TopSQP solver is compared to the special-purpose structural optimization method, the Globally Convergent Method of Moving Asymptotes (GCMMA) and the two general nonlinear solvers IPOPT and SNOPT. Numerical experiments on a large set of benchmark problems show good performance of TopSQP in terms of number of function evaluations. In addition, the use of second-order information helps to decrease the objective function value. |
| [32] | . |
| [33] | . Optimal analytical Michell frame structures have been extensively used as benchmark examples in topology optimization, including truss, frame, homogenization, density and level-set based approaches. However, as we will point out, partly the interpretation of Michell鈥檚 structural continua as discrete frame structures is not accurate and partly, it turns out that limiting structural topology to frame-like structures is a rather severe design restriction and results in structures that are quite far from being stiffness optimal. The paper discusses the interpretation of Michell鈥檚 theory in the context of numerical topology optimization and compares various topology optimization results obtained with the frame restriction to cases with no design restrictions. For all examples considered, the true stiffness optimal structures are composed of sheets (2D) or closed-walled shell structures (3D) with variable thickness. For optimization problems with one load case, numerical results in two and three dimensions indicate that stiffness can be increased by up to 80 % when dropping the frame restriction. For simple loading situations, studies based on optimal microstructures reveal theoretical gains of +200 %. It is also demonstrated how too coarse design discretizations in 3D can result in unintended restrictions on the design freedom and achievable compliance. |
| [34] | . |
