朴敏楠^*, 王颖^?, 周亚靖^*, 孙明玮^,*,2), 张新华^**, 陈增强^**南开大学人工智能学院, 天津 300350
^?空间物理重点实验室, 北京 100076
^**北京自动化控制设备研究所, 北京 100074

ANALYSIS OF FRICTION INDUCED VIBRATION UNDER THE ACTIVE DISTURBANCE REJECTION CONTROL FRAMEWORK ¹⁾

Piao Minnan^*, Wang Ying^?, Zhou Yajing^*, Sun Mingwei^,*,2), Zhang Xinhua^**, Chen Zengqiang^**College of Artificial Intelligence, Nankai University, Tianjin 300350, China
^?Science and Technology on Space Physics Laboratory, Beijing 100076, China
^**Beijing Institute of Automatic Control Equipment, Beijing 100074, China

通讯作者: 2)孙明玮, 教授, 主要研究方向: 飞行器制导与控制、自抗扰控制等. E-mail:smw_sunmingwei@163.com

收稿日期:2020-05-6接受日期:2020-05-6网络出版日期:2020-09-18

基金资助:

1)国家自然科学基金资助项目.61573197 国家自然科学基金资助项目.61973175 国家自然科学基金资助项目.51777013

Received:2020-05-6Accepted:2020-05-6Online:2020-09-18
作者简介 About authors


摘要
自抗扰控制(active disturbance rejection control, ADRC)是一种具有两自由度控制结构的工程化方法, 由于其能够直观有效地处理多种扰动, 近些年来在许多机电系统上得到了成功应用. 当采用ADRC对带有摩擦力的机电系统进行调节时, 可能会产生极限环振动. 目前, 还没有ADRC框架下摩擦力振动精确分析的相关工作. 因此, 本文采用非线性动力学系统的分析工具对这一问题进行研究. 首先, 考虑两种典型摩擦力模型, 静态切换模型和动态LuGre 模型, 对一类二阶运动系统设计不同阶次的ADRC, 得到控制器的等效形式, 并揭示出与比例积分微分(proportional-integral-derivative, PID)控制之间的联系. 然后, 采用打靶法结合拟弧长延拓方法求解系统中的极限环, 并根据Floquet理论判断极限环的稳定性、可能出现的分岔以及分岔类型. 此外, 通过雅克比矩阵和近似数值方法对系统平衡点集的局部稳定性进行了分析. 最后, 通过数值计算研究了摩擦力模型和参数、ADRC阶次和参数对极限环和平衡点集的影响. 计算结果表明, 决定摩擦力Stribeck效应负斜率的参数$\beta$作用较大. 当$\beta>1$时, 两种摩擦力模型下的闭环系统呈现出相同的特性, 极限环会出现环面折叠分岔(cyclic fold bifurcation, CFB)且平衡点集是局部稳定的. 然而当$\beta<1$时, 两种闭环系统呈现出完全不同的特性. 此外, 不同阶次的ADRC在极限环的存在性和稳定性、平衡点集的稳定性上面的结论是相同的, 而低阶次的ADRC能够更好地解决摩擦力补偿和稳定鲁棒性之间的矛盾问题. 这些结论对实际现象的理解、ADRC阶次的选择以及参数整定提供了一定指导.
关键词： 静态切换模型;LuGre模型;自抗扰控制;摩擦力振动;拟弧长延拓;动态分岔

Abstract
Active disturbance rejection control(ADRC) is a practical control method with a two-degree-of-freedom structure. Due to its capability of handling multifarious disturbances in a straightforward and effective manner, ADRC has been successfully applied to many mechanical systems. However, the limit cycle vibration may be induced when employing the ADRC for mechanical systems with friction. At present, there is no precise analysis work about the friction induced vibration under the ADRC framework. Therefore, this paper investigates this problem by using the analysis tools of nonlinear dynamic systems. First, two representative friction models, static switch model and dynamic LuGre model, respectively, are considered, and active disturbance rejection controllers of different orders are designed for a class of second-order motion systems. Equivalent forms of the controllers are obtained and their relationships with the proportional-integral-derivative(PID) controller are revealed. Then, the limit cycle is calculated by using the shooting method combined with the pseudo arc-length continuation approach. Based on the Floquet theory, the stability, occurrence and type of bifurcation of the limit cycle can be determined. In addition, the local stability of the equilibrium points is analyzed based on the Jacobian matrix and approximate numerical method. Finally, the effects of the model and parameter of friction, the order and parameters of the ADRC on the limit cycle are investigated by numerical calculations. As shown by the calculation results, the parameter $\beta$, which determines the negative slope of the Stribeck effect, has a significant effect. When $\beta>1$, closed-loop systems with these two friction models have the same characteristics. Cyclic fold bifurcation(CFB) of the limit cycle occurs and the set of equilibrium points is locally stable. However, characteristics of these two closed-loop systems are totally different when $\beta<1$. As for the ADRC order, it is found that the order does not affect the conclusions in terms of the existence and stability of the limit cycle, and the stability of the set of equilibrium points. Moreover, low-order ADRC has superior performance in tackling the conflict between the friction compensation and stability robustness. These results can provide some guidelines on the understanding of practical phenomena, selection of the ADRC order, and parameter tuning.
Keywords：static switch model;LuGre model;ADRC;friction induced vibration;pseudo arc-length continuation;dynamic bifurcation


PDF (419KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
朴敏楠, 王颖, 周亚靖, 孙明玮, 张新华, 陈增强. 自抗扰控制框架下的摩擦力振动分析 ¹⁾. 力学学报[J], 2020, 52(5): 1485-1497 DOI:10.6052/0459-1879-20-149
Piao Minnan, Wang Ying, Zhou Yajing, Sun Mingwei, Zhang Xinhua, Chen Zengqiang. ANALYSIS OF FRICTION INDUCED VIBRATION UNDER THE ACTIVE DISTURBANCE REJECTION CONTROL FRAMEWORK ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2020, 52(5): 1485-1497 DOI:10.6052/0459-1879-20-149

引言

摩擦力广泛存在于各种机电系统, 是影响控制性能的关键因素^[1-3]. 在低速运动时, 摩擦力会诱发极限环振动. 对于给定的控制器, 准确地分析极限环振动对控制参数选取以及决定是否更改控制策略有重要的指导意义.

尽管PID控制及其各种改进形式是运动控制中最常用的算法, 其单自由度控制结构下固有的抗扰和跟踪性能矛盾问题一直是寻求性能更佳控制器的动力. 为改进传统PID 控制, 中科院系统科学研究所韩京清研究员提出了一种新的工程化控制方法—ADRC^[4]. 该方法将串联积分器视为系统标准型并采用扩张状态观测器(extended state observer, ESO)对总扰动进行实时估计. 具有两自由度控制结构的ADRC通过ESO和误差反馈控制律可以实现抗扰和跟踪性能的分开设计. 近些年来, ADRC 在运动控制平台上得到了越来越多的成功应用^[4-10]. 由于ADRC的等效控制律中存在积分作用, 在低速运动时容易产生极限环或者黏滑振动. 目前, ADRC框架下的摩擦力振动研究甚少, 仅有的工作也是基于描述函数法^[8-9], 得出的分析结果在只有库伦摩擦力时精度尚可, 但是当考虑静摩擦力时却存在较大的误差^[11].

在已有文献中, 摩擦力振动分析基本都是针对PID控制或者PD控制, 主要采用描述函数法、代数方法、相平面法和非线性动力学系统分析方法^[11-20]. 描述函数法是一种近似方法, 仅适用于分析在有限时刻速度为零的极限环, 因此具有一定的局限性. 针对一类仅包括静摩擦力和库仑摩擦力的单自由度运动系统, 文献^[14]采用精确的代数方法证明了任何可以使系统稳定的PID控制参数组合都会产生极限环. 代数方法虽然能够提供准确的分析结果, 但是由于需要计算解析解, 其仅适用于低阶控制系统(三阶及以下)和特定的静态摩擦力模型. 针对静态摩擦力模型, 文献^[15,16,17]采用相平面法将三维控制系统降为一维, 并通过事件对映(event map) 分析了不同摩擦力模型以及参数对平衡点集和极限环的影响. 对于带有Stribeck效应(零速度附近的摩擦力骤降)的指数摩擦力模型, 文献^[17]中结果表明Stribeck 负斜率参数会直接影响极限环解的个数、稳定性以及能否通过参数整定消除极限环. 该结论可视为文献^[14]中结论的拓展, 对现实中能够通过PID 参数调节消除极限环的一些情形进行解释. 尽管事件对映是一种直观有效的分析方法, 但是由于需要将系统用一维对映来表示, 其仅适用于静态摩擦力模型, 无法对包括更为复杂的动态摩擦力模型的运动控制系统进行分析. 随着计算能力的增强, 针对一般非线性动力学系统的分析工具如打靶法、轨迹跟踪(path following)、 分岔图、Floquet理论等被引入到闭环的摩擦力振动分析中^[18-27]. 该方法能够对包含一般摩擦力模型的系统进行分析. 针对静态切换摩擦力模型^[21] 和动态LuGre模型^[28], 文献^[18] 采用简单打靶法结合轨迹跟踪得到关于控制增益的极限环解枝轨迹. 结果表明包含这两种摩擦力模型的系统呈现出非常相似的特性, 当控制增益大于某一临界值时, 极限环会消失. 文献^[19,20]联合解析方法和数值方法, 针对三阶控制系统采用打靶法结合二分法在理论参数范围内计算令极限环消失的最小积分泄漏值. 文献^[22]采用分岔图对设计状态观测器和摩擦力前馈补偿策略的闭环系统进行极限环分析.

基于上述分析, 本文研究{ADRC}下的极限环振动. 首先, 考虑两种典型的静态和动态摩擦力模型, 设计不同阶次的ADRC, 并得到其等效形式以沿用PID控制下的结论以及与PID控制进行比较. 为了准确计算高阶控制系统的极限环, 采用非线性动力学系统的分析工具^[29-32], 使用打靶法结合拟弧长延拓跟踪关于ESO带宽的极限环解枝. 通过计算Floquet乘子(floquet multiplier, FM)判断极限环的稳定性、分岔点的出现以及类型. 拟弧长延拓方法能够克服传统局部延拓方法不能顺利通过折叠点的缺点. 此外, 通过雅可比矩阵和近似数值方法对两种系统平衡点集的局部稳定性进行了分析. 最后, 通过仿真研究了Stribeck负斜率参数、控制器阶次、误差反馈调节带宽以及观测器带宽对极限环以及平衡点集的影响, 并对比两种摩擦力模型下的结果. 所得结论可以解释一些现实情形并对参数整定提供一定指导.

1 模型介绍与控制器设计

考虑一类二阶运动系统

(1) $ \begin{eqnarray} J\ddot \theta = c_{\rm m}u-F_{\rm f} \label{1} \end{eqnarray}$
其中, $J$是转动惯量, $\theta$是转动角度, $u$是控制电压, $c_{\rm m}$是输入增益, $F_{\rm f}$ 是摩擦力. 现实中的摩擦力特性多种多样, 为了描述这些特性, 不同复杂程度的摩擦力模型相继被提出, 主要分为静态摩擦力模型和动态摩擦力模型. 文中选用两种经典模型, 静态切换模型^[21]和动态LuGre模型^[28]. 切换模型可表示为

(2) $ \begin{eqnarray} {F_{\rm f}} = \left\{ \begin{array}{l@{\ \ }l} g\left( {\dot \theta }\right){\mathop{\rm sgn}} \left( {\dot \theta }\right) + {\sigma _2}\dot \theta , & \left| {\dot \theta } \right| > \eta \\[1mm] {F_{\rm s}}{\mathop{\rm sgn}} \left( {{c_{\rm m}}u} \right)+ {\sigma _2}\dot \theta, & \left| {\dot \theta } \right| \leqslant \eta {\rm{and}} \left| {{c_{\rm m}}u} \right| > {F_{\rm s}}\\[1mm] {c_{\rm m}}u + \alpha J\dot \theta , & \left| {\dot \theta } \right| \leqslant \eta {\rm{and}} \left| {{c_{\rm m}}u} \right| \leqslant {F_{\rm s}} \end{array} \right. \label{2} \end{eqnarray}$
其中, $\eta$是角速度阈值, $\sigma_2$是滑动摩擦力系数, $F_{\rm s}$是最大静摩擦力, $\alpha$是自定义的停滞阶段的加速度, $g \left( {\dot \theta } \right )$的形式为

(3) $ \begin{eqnarray} g \left( {\dot \theta } \right ) = {F_{\rm c}} + \left( {{F_{\rm s}}-{F_{\rm c}}} \right){{\mathop{\rm e} limits} ^{-{{\left( \frac{{\dot \theta }}{{{\omega _{\rm s}}}} \right)}^\beta }}} \end{eqnarray}$
其中, $F_{\rm c}$是库伦摩擦力, $\omega_{\rm s}$是Stribeck角速度. 该模型包括三部分, 即滑动阶段、由停滞切换到滑动的过渡阶段以及停滞阶段. 通过引入$\alpha$定义停滞状态可以避免传统Karnopp模型^[33]的数值不稳定问题, 并且使得控制系统微分方程组变为非刚性, 提高数值积分效率. Stribeck效应指的是克服最大静摩擦力之后摩擦力绝对值的迅速减小, 是产生极限环振动的主要原因^[34]. $\beta$ 决定了Stribeck效应的负斜率, 即摩擦力在低速时的变化速度, 是影响极限环振动的关键参数. 为了描述预滑动、滞后回线、可变最大摩擦力等现象, 文献^[28]提出了LuGre模型. 该模型假设接触面在微观上是不规则且粗糙的, 两个刚体通过一些弹性鬃毛接触. 鬃毛的平均变形用$z$表示, 其动态为

(4) $ \begin{eqnarray} \dot z = \dot \theta -{\sigma _0}\frac{{\left| {\dot \theta }\right|}}{{g(\dot \theta)}}z \label{3} \end{eqnarray}$
摩擦力可由鬃毛的挠曲产生, 可表示为

(5) $ \begin{eqnarray} {F_{\rm f}} = {\sigma _0}z + {\sigma _1}\dot z + {\sigma _2}\dot \theta \label{4} \end{eqnarray}$
其中, $\sigma _0$是鬃毛刚度, $\sigma _1$是微观阻尼系数.

现基于式(1)设计角度控制器. 首先将式(1)改写为

(6) $ \begin{eqnarray} \ddot \theta = {b_0}u + d \label{6} \end{eqnarray}$
其中, ${b_0} = {c_{\rm m}}/J$, $d = -{F_{\rm f}}/J$. 下面设计降阶扩张状态观测器(reduced-order extended state observer, RESO)^[36] 对摩擦力进行估计. 假设角度和角速度信号同时可测, 则分别可以设计一阶或者二阶RESO. 当采用角速度作为输入时, 可设计一阶RESO

(7) $ \begin{eqnarray} \left.\begin{array}{l} {{\dot w}} =-{\omega_{\rm o}}{b_0}u-{\omega_{\rm o}}w-{\omega_{\rm o}}^2\dot{\theta}\\ \hat d = {w} + {\omega_{\rm o}}\dot{\theta} \end{array} \right\} \label{add6} \end{eqnarray}$
其中, $w$为中间状态, $\omega_{\rm o}$为观测器带宽, $\hat d$为摩擦力估计. 得到摩擦力估计后, 控制律可设计为

(8) $ \begin{eqnarray} u = \frac{{{k_{\rm p}}\left( {{\theta _{\rm d}}-\theta } \right) + {k_{\rm d}}\left( {{{\dot \theta }_{\rm d}}-\dot \theta } \right)-\hat d}}{{{b_0}}} \label{8} \end{eqnarray}$
其中, $\theta _{\rm d}$为参考指令, ${k_{\rm p}}$和${k_{\rm d}}$分别为比例和微分增益, 为了便于分析, 这里根据参数化带宽${\omega_{\rm c}}$ 将其设计为

(9) $ \begin{eqnarray} k_{\rm p}=\omega_{\rm c}^2,\ \ {k_{\rm d}}=2\omega_{\rm c} \end{eqnarray} $
由文献^[35,36]可知, 式(7)和式(8)下的等效控制律就是PID 控制, 因此已有文献中关于PID控制在极限环振动上的结论同样适用于针对二阶对象设计一阶RESO的情形. 基于文献^{[14, 17-18]}中PID控制下的结果, 可以得到ADRC 下的几个关键结论:

(1) 针对只包含静摩擦力和库伦摩擦力的静态模型, 任何可以使系统稳定的ADRC 参数组合都会产生极限环^[14].

(2) 针对切换模型(2), 当$\beta<1$时, 平衡点集是不稳定的, 稳定极限环一直存在且不能通过调节ADRC参数消除(与结论(1)吻合); 当$\beta>1$时, 平衡点集是局部稳定的, 在一定ADRC参数范围内, 稳定和不稳定极限环同时存在且能够通过调节ADRC 参数消除^[17].

(3) 针对LuGre模型(5), 当$\beta=2$时, 极限环振动特性和切换模型下$\beta=2$ 时基本一致^[18].

当采用角度作为输入时, 可设计二阶RESO

(10) $ \begin{eqnarray} \left. \begin{array}{l} {{\dot w}_1} = -{l_1}{w_1} + {w_2} + \left( {{l_2}-{l_1}^2} \right)\theta + {b_0}u\\[1mm] {{\dot w}_2} = -{l_2}{w_1}-{l_1}{l_2}\theta\\[1mm] \hat d = {w_2} + {l_2}\theta \end{array} \right\} \end{eqnarray}$
其中, $w_1$和$w_2$为中间状态, $l_1$和$l_2$为观测器增益, 为了便于分析, 这里根据参数化带宽${\omega_{\rm o}}$将其设计为

(11) $ \begin{eqnarray} l_1=2\omega_{\rm o},\ \ l_2={\omega_{\rm o}}^2 \end{eqnarray}$
基于式(10)可以得到RESO对扰动估计的传递函数为

(12) $ \begin{eqnarray} {\cal L}\left( \hat d \right)= \frac{{\omega _{\rm o}^2}}{{{{\left( {s + {\omega _{\rm o}}} \right)}^2}}}{\cal L}\left( d \right) \label{7} \end{eqnarray}$
其中, ${\cal L}$表示拉氏变换运算符号. 可以看出扰动估计的本质为扰动的低通滤波输出. 显然, ${\omega_{\rm o}}$越高, 越能够快速地跟踪和补偿摩擦力. 因此, ${\omega_{\rm o}}$是影响极限环振动的关键参数. 此外, ${\omega_{\rm o}}$的取值会受到测量噪声、未建模高阶动态等因素的限制. 结合式(6)、式(8)和式(12) 可以得到控制量在零初始条件时的拉氏变换为

(13) $ \begin{eqnarray} {\cal L}\left( u \right) = \left[{\cal L}\left( e \right)\left( {{k_{\rm p}} + {k_{\rm d}}s + \frac{{{k_{\rm p}}\omega _{\rm o}^2}}{{s + 2{\omega _{\rm o}}}}\frac{1}{s} + \frac{{{k_{\rm d}}\omega _{\rm o}^2}}{{s + 2{\omega _{\rm o}}}}} \right)- \\ \qquad {\cal L}\left( \theta \right)\frac{{\omega _{\rm o}^2}}{{s + 2{\omega _{\rm o}}}}s \right]\bigg/b_0 \end{eqnarray}$
其中, $e = {\theta _{\rm d}}-\theta$. 可以看出ADRC的等效控制律包括PD控制、误差积分滤波输出、误差滤波输出和角速度滤波输出. 基于式(13), 定义新的闭环系统状态

(14) $ \begin{eqnarray} \left. \begin{array}{l} {x_1} = \theta -{\theta _{\rm d}}\\[1mm] {x_2} = \dot \theta -{{\dot \theta }_{\rm d}}\\[1mm] {x_3} = \int_0^t {\left( {\theta \left( \tau \right)-{\theta _{\rm d}}} \right){\rm{d}}\tau } \\[2mm] {x_4} = \dfrac{{-{{\dot x}_4}}}{{2{\omega _{\rm o}}}} + \theta -{\theta _{\rm d}} \end{array} \right\} \label{add14} \end{eqnarray}$
其中, ${x_1}$, ${x_2}$, ${x_3}$分别是误差、误差导数和误差积分, ${x_4}$ 是误差的低通滤波输出. 相比于PID控制, 闭环系统增加了误差滤波状态${x_4}$, 上述结论(1)$\sim$(3) 可能不再适用, 因此是本文的研究重点. 将系统状态重构为式(14)是为了揭示出控制器的本质以及便于将后面得到的结果与PID控制的结果进行比较. 在研究极限环振动时, 不失一般性, 令${\theta }_{\rm d}={\dot \theta }_{\rm d}={\ddot \theta }_{\rm d}=0$. 对于切换模型, 闭环系统可表示为

(15) $ \begin{eqnarray} \left. \begin{array}{l} {{\dot x}_1} = {x_2}\\ {{\dot x}_2} = f_{\rm s}\\ {{\dot x}_3} = {x_1}\\ {{\dot x}_4} = a_{41}{x_1}-a_{41}{x_4} \end{array} \right\} \label{11} \end{eqnarray}$
其中, 切换函数$f_{\rm s}$为

(16) $ \begin{eqnarray} f_{\rm s}=\left\{ \begin{array}{l} a_{21}{x_1}+a_{22}{x_2}+a_{23}{x_3} +a_{24}{x_4}-\dfrac{g\left( {x_2}\right){\rm sgn}\left( {x_2}\right)}{J},\\\qquad\quad\quad\ \ \left| {x_2 } \right| > \eta \\ a_{21}{x_1}+a_{22}{x_2}+a_{23}{x_3} + a_{24}{x_4}-\dfrac{F_{\rm s}{\rm sgn}{\left({c_{\rm m}}u\right)}}{J},\\\qquad\quad\quad\ \ \left| {x_2} \right| \leqslant \eta {\rm{and}} \left| {{c_{\rm m}}u} \right| > {F_{\rm s}}\\ -\alpha x_2,\qquad \left| {x_2} \right| \leqslant \eta {\rm{and}} \left| {{c_{\rm m}}u} \right| \leqslant {F_{\rm s}} \end{array} \right. \label{add16} \end{eqnarray}$
其中

(17) $ \begin{eqnarray} &&\left. \begin{array}{l} {a_{21}} = - \left( {{k_{\rm p}} + \omega _{\rm o}^2} \right)\\ a_{22}=-\left({k_{\rm d}+\frac{\sigma _2}{J}}\right) \\[1mm] {a_{23}} = - \dfrac{{{k_{\rm p}}{\omega _{\rm o}}}}{2}\\[1mm]{a_{24}} = \omega _{\rm o}^2 + \dfrac{{{k_{\rm p}}}}{4} - \dfrac{{{k_{\rm d}}{\omega _{\rm o}}}}{2}\\{{a_{41}}}={2{\omega _{\rm o}}}\\ \end{array} \right\} \end{eqnarray}$
(18) $ c_{\rm m}u={J}\left({a_{21}{x_1}-k_{\rm d}{x_2}+a_{23}{x_3} +a_{24}{x_4}}\right)$
对于LuGre模型, 闭环系统可表示为

(19) $ \begin{eqnarray} &&\left. \begin{array}{llll} {{\dot x}_1} = & {x_2}\\ {{\dot x}_2} = &a_{21}x_1+\bar{a}_{22}x_2+a_{23}x_3+a_{24}x_4+a_{25}x_5\\ {{\dot x}_3} = & {x_1}\\ {{\dot x}_4} = &a_{41}x_1-a_{41}x_4\\ {{\dot x}_5}=&x_2-a_{55}{{x}_5} \end{array} \right\} \end{eqnarray} $
(20) $ \begin{eqnarray} \left. \begin{array}{l} {\bar{a}_{22}} = - \left( {{k_{\rm d}} + \dfrac{{{\sigma _1} + {\sigma _2}}}{J}} \right)\\[2mm] {a_{25}} = - \dfrac{1}{J}\left( {{\sigma _0} - \dfrac{{{\sigma _0}{\sigma _1}\left| {{x_2}} \right|}}{{g\left( {{x_2}} \right)}}} \right)\\[2mm] {a_{55}} = - \dfrac{{{\sigma _0}\left| {{x_2}} \right|}}{{g\left( {{x_2}} \right)}} \end{array} \right\} \end{eqnarray}$
其中, ${x}_5=z$. 针对系统(15)和(19), 本文研究控制参数$\omega_{\rm c}$, $\omega_{\rm o}$ 以及摩擦力参数$\beta$ 对极限环存在性以及稳定性的影响. 对于给定的控制和摩擦力参数, 问题的关键即为准确地求解出自治系统(15)和(19)的全部周期解.

2 系统周期解计算与分析

对于系统(15)和(19), 极限环的计算和分析方法相同, 该部分仅针对系统(15)进行介绍. 系统(15) 是自治系统, 即等式右端的向量场不与时间$t$ 显式有关, 不失一般性, 起始时间可设为0. 假设${ {\phi} _t}\left( {{{ {x}_0}}, \lambda} \right)$为系统(15)在初始条件 ${ {x}_0} = \left[ {{x_1}\left( 0 \right)} {{x_2}\left( 0 \right)} {{x_3}\left( 0 \right)} {{x_4}\left( 0 \right)}\right]^{\rm T}$ 下的解, 其中, $\lambda$为某个参数变量. 求解极限环即为求解一个两点边值问题

(21) $ \begin{eqnarray} {H}\left( {{ {x}_0}, T, \lambda} \right) = { {\phi} _T}\left( {{ {x}_0}, \lambda} \right)-{ {x}_0} = {0} \label{13} \end{eqnarray}$
其中, $T$为极限环周期. 打靶法结合拟弧长延拓是计算随参数$\lambda$变化系统周期解的有效方法. 令$ {y}=[ {x}_0^{\rm T} T]^{\rm T}$表示待求解向量. 引入弧长参数$\chi$, 假设$\left( {y}_i, \lambda_i\right)$ $\left(i=1, 2, \cdots\right)$是解枝$\varGamma\left(\chi\right)$上的第$i$个点, 并将$ {y}_i$和$\lambda_i$视为$\chi$ 的函数. 定义如下平面

(22) $ \begin{eqnarray} N_{i}\left({ {y}}, {\lambda}, \Delta \chi \right) =& \left( {y}- {y}_{i}\right)^{\rm T}\dot{ {y}_i}+\left({\lambda}-{\lambda}_{i}\right){\dot{\lambda}_i}-\Delta \chi=0\quad \end{eqnarray}$
其中

(23) $ \begin{eqnarray} \dot{ {y}}_i=\left. {\frac{{\rm d} {y}}{{\rm d}\chi}} \right|_{ {y}= {y}_{i}, {\lambda}={\lambda}_{i}},\ \ \dot{\lambda}_i=\left. {\frac{{\rm d}\lambda}{{\rm d}\chi}} \right|_{ {y}= {y}_{i}, {\lambda}={\lambda}_{i}} \end{eqnarray}$
$\Delta \chi$表示沿单位切向量$\left(\dot{ {y}}_i, \dot{{\lambda}}_i\right)$ 与$\left( {y}_i, \lambda_i\right)$ 之间的距离. 定义

(24) $ \begin{eqnarray} \left({ {y}_{i+1}}^{\rm p}, {{\lambda}_{i+1}}^{\rm p}\right)=\left({ {y}_{i}}, {{\lambda}_{i}}\right)+\Delta \chi\left(\dot{ {y}}_i, \dot{{\lambda}}_i\right) \end{eqnarray}$
则可知平面$N_{i}$经过点$\left({ {y}_{i+1}}^{\rm p}, {{\lambda}_{i+1}}^{\rm p}\right)$且垂直于切线$\left(\dot{ {y}_i}, {{\dot\lambda}_i}\right)$. $N_{i}$与解枝$\varGamma\left(\chi\right)$的交点即为下一个待求点$\left({ {y}_{i+1}}, {{\lambda}_{i+1}}\right)$. 因此, 求解解枝上下一个轨迹点即为求解方程组

(25) $ \begin{eqnarray} \left. \begin{array}{l} {H}\left({ {y}}, {\lambda}\right) = {0}\\ N_{i} \left({ {y}}, {\lambda}, \Delta \chi \right)= 0 \end{array} \right\} \label{14} \end{eqnarray}$
式(25)中有5个方程、6个待求解变量, 因此需要增加额外的约束条件. 对于增加约束条件, 文献中有很多种方法, 例如正交条件法、固定初值状态法等^[37]. 本文根据角速度为零的点一定在极限环轨迹上的特性, 将初始状态中的角速度固定为零, 从而减少一个待求解变量. 此时, $ {x}_0=[x_1(0) 0 x_3(0) x_4(0)]^{\rm T}$, $ {x}_0^{r}=[x_1(0) x_3(0) x_4(0)]^{\rm T}$, $ {y}=[{ {x}_0^{r{\rm T}}} T]^{\rm T}$. 为计算式(25), 首先需要计算$ {c}_i=\left[\dot{ {y}}_i^{\rm T} \dot{{\lambda}}_{i}\right]^{\rm T}$. 定义

(26) $ \begin{eqnarray} \left. \begin{array}{l} {H}_{ {y}_{i}}=\left. {\dfrac{{\partial {H}\left({ {y}}, {\lambda}\right)}}{{\partial { {y}}}}} \right|_{ {y}= {y}_{i}, {\lambda}={\lambda}_{i}}\\[4mm] {H}_{{\lambda_{i}}}=\left. {\dfrac{{\partial {H}\left({ {y}}, {\lambda}\right)}}{{\partial {\lambda}}}} \right|_{ {y}= {y}_{i}, {\lambda}={\lambda}_{i}} \end{array} \right\} \end{eqnarray}$
则$ {c}_i$可由下式解出

(27) $ \begin{eqnarray} \left. \begin{array}{l} \left[ {H}_{ {y}_{i}}, {H}_{{\lambda_{i}}}\right] {c}_i= {0}\\ \left\| { {c}_i} \right\|=1 \end{array} \right\} \label{16} \end{eqnarray}$
基于式(21)可得

(28) $ \begin{eqnarray} {H}_{ {y}_{i}}=\left[ \begin{array}{*{20}{c}} \dfrac{{\partial {\phi} _T}\left( {{ {x}_{0i}}, \lambda_i} \right)}{{\partial { {x}_{0i}^r}}}- {C} {f}_T\left( {\phi} _t\left( {{ {x}_{0i}}, \lambda_i} \right) \right) \end{array} \right] \end{eqnarray}$
其中, 带下标$i$的变量表示解枝上第$i$个点对应的值,

(29) $ \begin{eqnarray} {C} = \left[ {\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} 1&0&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right]^{\rm T} \end{eqnarray}$
$ {f}_T\left( {\phi} _t\left( {{ {x}_{0i}}, \lambda_i} \right)\right)$ 为闭环系统(15)的向量场在$T$时刻的值. 为计算${{\partial {\phi} _T}\left( {{ {x}_{0i}}, \lambda_i} \right)}/{{\partial { {x}_{0i}^r}}}$ 以及FM, 定义基解矩阵${\varPhi _t}\left({ {x}_0}\right) ={{\partial {\phi} _t}\left( {{ {x}_0}, \lambda} \right)}/{{\partial { {x}_0}}}$, 则单值矩阵(monodromy matrix) 为${\varPhi _T}\left({ {x}_0}\right)$. 对于光滑系统, ${\varPhi _T}\left({ {x}_0}\right)$可通过对

(30) $ \begin{eqnarray} \left. \begin{array}{l} \dot{\varPhi}_t\left({ {x}_0}\right)=\dfrac{{\partial {f}}\left( {\phi}_t\left( {{ {x}_{0}}, \lambda} \right) \right)}{{\partial { {x}}}}{\varPhi _t}\left({ {x}_0}\right) \\{\varPhi_0}\left({ {x}_0}\right)= {I}_{4\times4} \end{array} \right\} \label{addadd33} \end{eqnarray}$
进行积分得到, 其中$ {I}_{4\times4}$为四阶单位矩阵. 因为切换模型是不连续的, LuGre模型是非光滑的, 所以${{\partial {f}}\left( {\phi} _t\left( {{ {x}_{0}}, \lambda} \right) \right)}/{{\partial { {x}}}}$在$x_2=0$处不存在且发生跳跃, 不能通过式(30)求解. 本文采用灵敏度分析方法计算单值矩阵^[21]. 令${ {x}_0}$的第$j$ ($j=1, 2, 3, 4$)个状态摄动$\xi$ 其他状态保持不变得到新的初始状态${ {x}_0^j}$, 并以${ {x}_0^j}$为初值计算$ {\phi} _T\left( { {x}_0^j}, \lambda\right)$. 则可得到${\varPhi_{T}}\left({ {x}_0}\right)$的第$j$列元素${\varPhi_{T_{j}}}\left({ {x}_0}\right)$ 为

(31) $ \begin{eqnarray} {\varPhi_{T_{j}}}\left({ {x}_0}\right)=\left({ {\phi} _T\left( { {x}_0^j}, \lambda\right)- {\phi} _T\left( { {x}_0}, \lambda\right)}\right)/{\xi} \end{eqnarray}$
$ {H}_{{\lambda_{i}}}$同样采用灵敏度分析计算求得. 令$ {H}_k$ ($k=1, 2, \cdots, 5$)表示$\left[ {H}_{ {y}_{i}} {H}_{{\lambda_{i}}}\right]$的第$k$ 列, 定义

(32) $ \begin{eqnarray} J_k=(-1)^{k+1}{\rm det}[ {H}_1 \cdots \hat{ {H}}_k \cdots {H}_5] \end{eqnarray}$
其中, $\hat{ {H}}_k$表示从矩阵中去掉第$k$列. 则可以得到

(33) $ \begin{eqnarray} {c}_i=\frac{\left[J_1 J_2 J_3 J_4 J_5\right]^{\rm T}}{\left\| {\left[J_1 J_2 J_3 J_4 J_5\right]} \right\|} \end{eqnarray}$
现采用牛顿迭代法对式(25)进行求解

(34) $ \begin{eqnarray} \left[\begin{array}{*{20}{l}} &{{ {H}_{ {y}_{ik}}}}&{{ {H}_{\lambda_{{ik}}}}}\\ &{{\dot{ {y}}_{i-1}^{\rm T}}}&{{{\dot \lambda }_{i-1}}}\end{array} \right]\left[ {\begin{array}{*{20}{lll}} &{\Delta { {y}_{ik}}}\\ &{\Delta {\lambda _{ik}}} \end{array}} \right] =-\left[ {\begin{array}{*{20}{l}} & {H}_{ik}\\ &N_{ik} \end{array}} \right] \end{eqnarray}$
其中, 下标$k$ $(k=1, 2, \cdots)$表示迭代次数

(35) $ \begin{eqnarray} \left. \begin{array}{lll} {H}_{ik}=&\left. {{ {H}\left( {{ {y}}, {\lambda}} \right)}} \right|_{_{ {y}= {y}_{ik}, {\lambda}={\lambda}_{ik}}}\\ N_{ik}=&\left. {N_{i}\left( {{ {y}}, {\lambda}, \Delta \chi} \right)} \right|_{_{ {y}= {y}_{ik}, {\lambda}={\lambda}_{ik}}} \end{array} \right\} \end{eqnarray}$
则待求解变量的迭代公式为

(36) $ \begin{eqnarray} \left. \begin{array}{l} { {y}_{i\left( {k + 1} \right)}} = { {y}_{ik}} + \Delta { {y}_{ik}}\\ {\lambda _{i\left( {k + 1} \right)}} = {\lambda _{ik}} + \Delta {\lambda _{ik}}\\ { {y}_{i1}}={ {y}_{i-1}}, {\lambda_{i1}}={\lambda_{i-1}} \end{array}\right\} \end{eqnarray}$
在每次迭代中, 都需要多次在不同初始状态和控制参数下进行仿真, 即将一个两点边值问题转化为多次的初值问题求解, 这就是打靶法的思想. 重复上述迭代过程直至满足终止条件

(37) $ \begin{eqnarray} \left. \begin{array}{l}\left\| {H}_{ik}^{\rm T}, {N_{ik}}\right\| \leqslant \varepsilon_1\\ \left| \dfrac{{\Delta {T_{ik}}}}{{{T_{ik}}}} \right|\leqslant \varepsilon_2 \end{array}\right\} \end{eqnarray}$
其中, $\varepsilon_1>0$和$\varepsilon_2>0$为充分小的值以保证求解精度. 传统局部延拓法在折叠点处存在奇异问题, 无法通过折叠点继续跟踪解枝. 拟弧长延拓法通过引入拟弧长变量, 可以避免奇异问题从而顺利通过折叠点. 当$ {y}$为一维时, 该方法的简化原理图如图1所示.

图 1

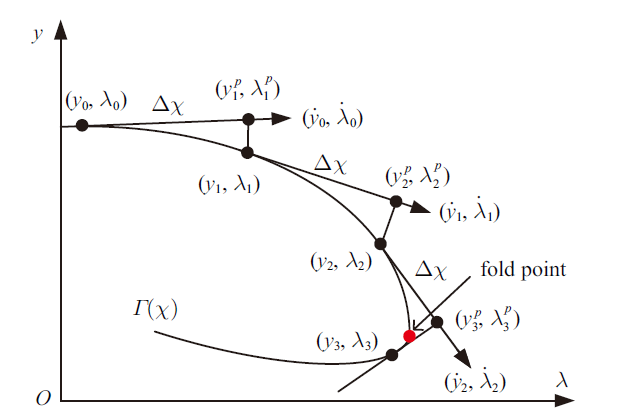新窗口打开|下载原图ZIP|生成PPT
图 1拟弧长延拓方法原理

Fig. 1Principle of pseudo arc-length continuation method



极限环的稳定性以及解枝可能出现的分岔由单值矩阵的特征值FM判断. 当所有FM 位于单位圆内时, 极限环是稳定的. 随着控制参数连续变化, 当某个FM的模变为大于1 时, 系统将出现动态分岔, 稳定周期解被破坏^[38-40]. 根据FM 变化情况的不同, 可能出现3种分岔: 环面折叠分岔(cyclic fold bifurcation, CFB)、倍周期分岔(period doubling bifurcation, PDB)和环面分岔(torus bifurcation, TB). 具体来说, 当有一个FM沿着实轴从$(1, 0)$穿出单位圆时, 将出现CFB; 当有一个FM沿着实轴从$(-1, 0)$ 穿出单位圆时, 将出现PDB; 当有一对共轭的FM穿出单位圆时, 将出现TB.

3 平衡点集与局部稳定性

该部分首先介绍LuGre模型下的平衡点集以及稳定性判定. 由LuGre模型性质可知^[16], $|z(t)|\leqslant F_{\rm s}/\sigma_0$. 因此, 系统(19) 的平衡点集为

(38) $ \begin{eqnarray} {x}_{{\rm LuGre}}^*=\gamma_L\lt[0 0 -\frac{2\sigma_0}{k_{\rm p} \omega_{\rm o} J} 0 1 ]^{\rm T} \end{eqnarray}$
其中, $|\gamma_L|\leqslant F_{\rm s}/\sigma_0$. 误差、误差导数以及误差滤波输出在平衡点处都为零, 鬃毛变形产生的摩擦力由积分作用产生的控制力完全补偿. 平衡点集的局部稳定性可通过计算雅克比矩阵的特征值确定. 由于LuGre模型是非光滑的, 在求解雅可比矩阵时需要使用广义微分^[41]. 向量场$ {f}( {x})$在点$ {x}$处的广义微分定义为包含左导数${{ {f}'}_-}$和右导数${{ {f}'}_+}$的最小闭凸包

(39) $ \begin{eqnarray} &&\partial {f}=\overline {{\rm{co}}} \left\{ {{{ {f}'}_-}, {{ {f}'}_+}} \right\} = \left( {1 - q} \right){{ {f}'}_ - } + q{{ {f}'}_ + }, \\&&\qquad \forall 0 \leqslant q \leqslant 1 \label{addadd39} \end{eqnarray}$
根据式(39)可以得到系统(19)在$ {x}_{{\rm LuGre}}^*$ 处的雅可比矩阵为

(40) $ \begin{eqnarray} {J}\left( {x}_{{\rm LuGre}}^*\right)= \left[ {\begin{array}{*{20}{l}} 0&1&0&0&0\\ {{a_{21}}}&{{{a}_{22}^*}}&{{a_{23}}}&{{a_{24}}}&{{a_{25}^*}}\\ 1&0&0&0&0\\ {{a_{41}}}&0&0&-{{a_{41}}}&0\\ 0&a_{52}^*&0&0&0 \end{array}} \right] \end{eqnarray}$
其中

(41) $ \begin{eqnarray} \left. \begin{array}{l} a_{22}^*=\bar{a}_{22}+\dfrac{\sigma_0\sigma_1\gamma_L\left(2q-1\right)}{F_{\rm s}J} \\a_{25}^*=-\dfrac{\sigma_0}{J}, a_{52}^*=1-\dfrac{\sigma_0\gamma_L\left(2q-1\right)}{F_{\rm s}} \end{array} \right\} \end{eqnarray}$
显然, $ {J}\left( {x}_{{\rm LuGre}}^*\right)$有一个特征值为零, 对应的特征向量为$ {x}_{{\rm LuGre}}^*$. 如果平衡点集是局部稳定的, 则$ {J}\left( {x}_{{\rm LuGre}}^*\right)$的余下四个特征值对于任意的$|\gamma_L|\leqslant F_{\rm s}/\sigma_0$ 和$0 \leqslant q \leqslant 1$都应在开左半平面. 令$\rho=\sigma_0\gamma_L(2q-1)/F_{\rm s}$($|\rho|\leqslant 1$), 则可得特征方程为

(42) $ \begin{eqnarray} &&{\rm det}\left| {J}\left( {x}_{{\rm LuGre}}^*\right)-s {I}_{{5\times5}}\right|= \\&&\qquad s\left(s^4+p_3s^3+p_2s^2+p_1s+p_0\right)=0 \end{eqnarray}$
其中, $ {I}_{{5\times5}}$为五阶单位矩阵, 各系数为

(43) $ \begin{eqnarray} \left. \begin{array}{l} p_3=-\bar{a}_{22}+a_{41}-\dfrac{\sigma_1}{J}\rho\\ p_2=-\left(a_{21}+\bar{a}_{22}a_{41}+a_{25}^*\right)+\left(a_{25}^*-\dfrac{\sigma_1 {a_{41}}}{J}\right)\rho\\ p_1=-\left[a_{23}+a_{41}\left(a_{21}+a_{24}+a_{25}^*\right)\right]+a_{41}a_{25}^*\rho\\ p_0=-a_{23}a_{41}\\ \end{array}\right\} \end{eqnarray}$
当$\omega_{\rm c}>0$且$\omega_{\rm o}>0$时, 可以得到全部系数为正. 根据Hurwitz判据, 平衡点集稳定的充要条件为

(44) $ \begin{eqnarray} && P(\rho)=p_1\left(p_2p_3-p_1\right)-p_0{p_3}^2>0, \\&&\qquad \forall -1 \leqslant \rho \leqslant 1 \label{add39} \end{eqnarray}$
其中, $P(\rho)$是关于$\rho$的三次多项式, 因此, 只需要计算$P(\rho=-1)$、$P(\rho=1)$和极小值就可以判断式(44) 是否成立.

按照切换模型的定义, 系统(15)的平衡点集为

(45) $ \begin{eqnarray} {x}_{{\rm Switch}}^*=\gamma_S\lt[0 0 -\frac{2}{k_{\rm p} \omega_{\rm o} J} 0 ]^{\rm T} \end{eqnarray}$
其中, $|\gamma_S|\leqslant F_{\rm s}$. 由于系统(15)是Filippov型不连续的, 无法采用雅可比矩阵判断平衡点集的稳定性. 和连续微分方程组相比, 判断不连续微分方程组平衡点集稳定性的理论和方法尚不完善, 已有方法大多是通过构建非常复杂的非光滑Lyapunov函数^[42-43]. 考虑到不是本文的研究重点, 这里采用一种近似的数值方法. 通过大量仿真, 发现$x_1$对解轨迹影响最为显著. 因此, 对某个平衡点进行$x_1$ 方向的摄动, 在$\left(0, x_{\rm s}\right)$($x_{\rm s}$ 为相应参数下稳定极限环的幅值)区间内选择$n$ 个值作为摄动值, 在每个摄动值下进行仿真并观察状态能否最终收敛到平衡点集. 对于存在摄动值使得仿真结果收敛到平衡点集的情况, 即可判断此时平衡点集是局部稳定的, 而且这个分析结果是准确的. 对于所有摄动值下仿真结果都不会收敛到平衡点集的情况, 即可判断此时平衡点集是不稳定的, 但是这个分析结果是近似的, 因为初始条件没有遍历整个状态空间.

4 计算结果

仿真模型参数为^[18]

(46) $ \begin{eqnarray} \left. \begin{array}{l} J = 0.026 {\rm{kg}} \cdot {{\rm{m}}^{\rm{2}}}, {c_{\rm m}} = 16 {\rm{N}} \cdot {\rm{m/V}}\\ {F_{\rm s}} = 0.53 {\rm{N}} \cdot {\rm{m}}, {F_{\rm c}} = 0.44 {\rm{N}} \cdot {\rm{m}}\\{v_{\rm s}} = 0.02 {\rm{rad/s}}, {\sigma _2} = 0.1 {\rm{N}} \cdot {\rm{m}} \cdot {\rm{s/rad}}\\ \eta = 10^{-6} {\rm{rad/s}}, \alpha = 10 1{\rm{/s}} \\{\sigma _0} = 2.2\times10^4 {\rm{N}} \cdot {\rm{m/rad}}\\{\sigma _1} = 7.58 {\rm{N}} \cdot {\rm{m}} \cdot {\rm{s/rad}} \end{array} \right\} \end{eqnarray}$
求解器选用ode45算法, 相对和绝对容许误差限设置为$10^{-10}$(需小于切换模型的角速度阈值$\eta$). 参数摄动量${\xi}$ 取为初始状态或控制参数的$1\%$, 且绝对值不小于$10^{-8}$以避免数值敏感问题. $\Delta \chi$分段进行取值, 当跟踪稳定解枝时, 取为2, 当某个FM的模接近1时, 减小$\Delta \chi$至0.01 以顺利经过比较尖锐的折叠点. 迭代精度参数设计为$\varepsilon_1=10^{-6}$, $\varepsilon_2=10^{-4}$.

4.1 基于二阶ESO和切换模型的计算结果

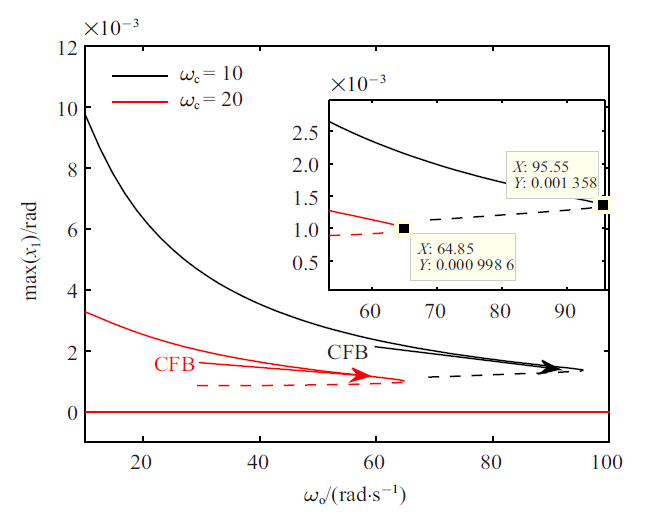
首先令$\beta=2$. $\omega_{\rm c}=10$ rad/s和$\omega_{\rm c}=20$ rad/s时的分岔图、FMs、极限环周期如图2~图4所示. 在以下分岔图中, 同时描述了周期解和平衡点集($x_1=0$), 实线表示周期解或者平衡点集是局部稳定的, 而虚线则表示周期解或者平衡点集是不稳定的. 由于极限环可能是非对称的, 在图2 中, max($x_1$)表示一个极限环周期内角度的最大值(以下简称为极限环幅值). 在解枝起始点, $\omega_{\rm o}=10$ rad/s, 相应的极限环是稳定的. 随着$\omega_{\rm o}$的增大, 极限环幅值不断减小. 当$\omega_{\rm o}$增大到某个临界值时, 有FM沿实轴从$(1, 0)$ 穿出单位圆, 出现CFB, 并通过CFB产生不稳定解枝, 此时对应的$\omega_{\rm o}$称为$\omega_{\rm o}^{\rm CFB}$. 需要说明的是, 任意微小的扰动都会使得不稳定极限环的轨迹不能够保持, 不稳定极限环在现实情形中几乎不可能出现. 因此, 其求解只具有理论意义, 不具有实际意义. 由于不稳定极限环求解计算量很大, 这里只计算出了不稳定解枝的一部分, 但不影响结论. 当$\omega_{\rm o}<\omega_{\rm o}^{\rm CFB}$ 时, 系统中存在两个相近的稳定和不稳定周期解; 当$\omega_{\rm o}=\omega_{\rm o}^{\rm CFB}$时, 两个周期解汇聚一起; 当$\omega_{\rm o}>\omega_{\rm o}^{\rm CFB}$时, 系统中极限环消失. 对平衡点进行$x_1$方向上的摄动, 摄动值为$\left(0, x_{\rm s}\right)$区间内均匀选取的1000个点. 通过大量仿真发现, 当$|x_1(0)|<|x_u|$ ($x_u$为相应参数下不稳定极限环的幅值)时, 轨迹会趋于系统平衡点集; 当$|x_u|<|x_1(0)|<|x_{\rm s}|$时, 轨迹会趋于稳定极限环. 所以平衡点集在所选参数范围内是局部稳定的, 且在$x_1$方向的吸引域近似为$|x_1|<|x_u|$. 此外, 从图2 可以看出, $\omega_{\rm c}$越大, 相同$\omega_{\rm o}$ 下的极限环幅值越小, 对应的$\omega_{\rm o}^{\rm CFB}$也越小. FMs如图3 所示, 其中${\rm FM}_1$随$\omega_{\rm o}$变化明显, ${\rm FM}_2$始终接近于1, ${\rm FM}_3$和${\rm FM}_4$ 一直接近于0. ${\rm FM}_1$在CFB附近先是骤减然后突然穿越1. ${\rm FM}_2$在1附近的波动可认为是由数值计算误差造成的, 不能够用于判断是否出现分岔, 因为其变化范围很小且趋势性不明显. 上述结果和文献^[18]中PID 控制器下的结果很相似, 只是多了一个始终接近于0 的FM. 稳定极限环的周期如图4所示, 可见周期变化非单调, 呈现先减后增的趋势, 且$\omega_{\rm c}$越大, 周期越小.

图 2

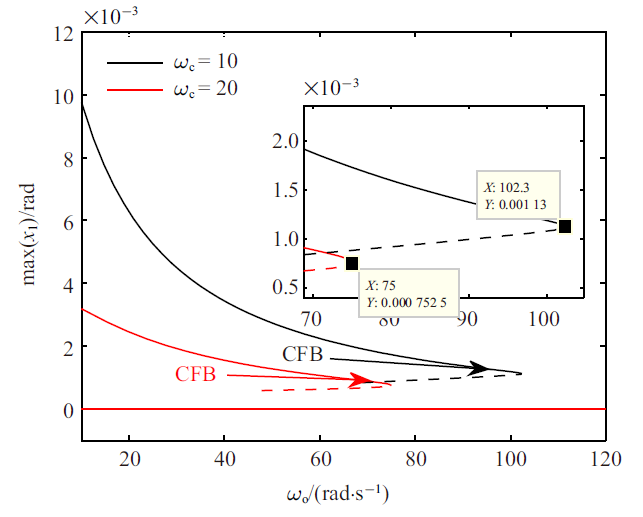新窗口打开|下载原图ZIP|生成PPT
图 2$\beta=2$时切换模型系统分岔图(实线:稳定解枝, 虚线:不稳定解枝)

Fig. 2Bifurcation diagram for the switch model system with $\beta=2$ (solid line: stable branch, dashed line: unstable branch)

图 3

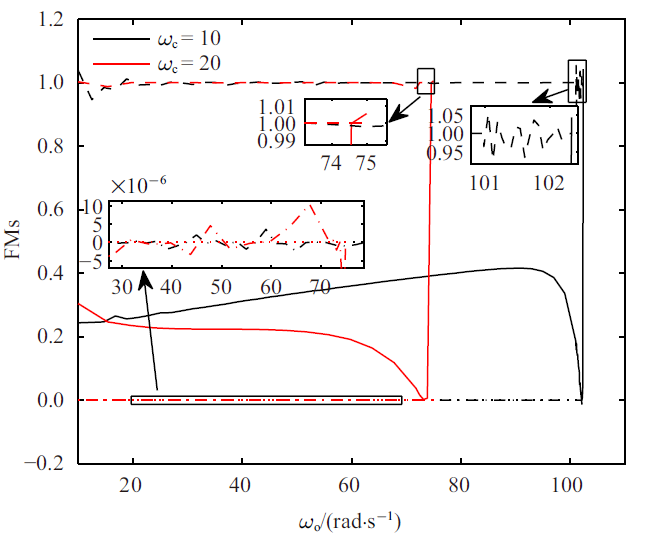新窗口打开|下载原图ZIP|生成PPT
图 3$\beta=2$时切换模型系统稳定解枝的FMs(实线:${\rm FM}_1$, 虚线:${\rm FM}_2$, 点线:${\rm FM}_3$, 点划线:${\rm FM}_4$)

Fig. 3FMs of stable branch for the switch model system with $\beta=2$ (solid line: ${\rm FM}_1$, dashed line: ${\rm FM}_2$, dotted line: ${\rm FM}_3$,dot dash line: ${\rm FM}_4$)

图 4

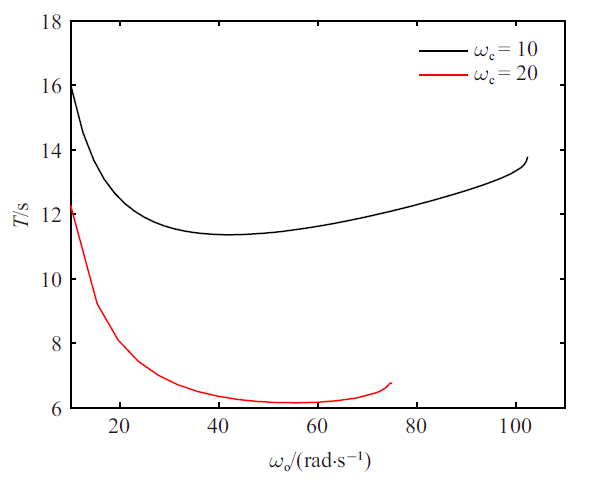新窗口打开|下载原图ZIP|生成PPT
图 4$\beta=2$时切换模型系统的稳定极限环周期

Fig. 4Period of stable limit cycle for the switch model system with $\beta=2$



为研究摩擦力参数对极限环的影响, 令$\beta=0.9$. 对于切换模型, $\beta$越小, 由停滞切换到滑动状态时, 在$|x_2|<\omega_{\rm s}$速度范围内获得的角加速度就越大, 越容易产生超调, 从而越容易诱发极限环. $\beta=0.9$时的分岔图和周期图如图5和图6所示. 当极限环幅值接近于零时, 由于计算量过大终止计算. 同样, 从$\omega_{\rm o}=10$ rad/s开始跟踪稳定的极限环解枝. 随着$\omega_{\rm o}$增大, 极限环幅值不断减小, 周期呈现先减后增趋势. 在计算的参数范围内没有出现动态分岔. 相比于$\beta=2$时结果, $\beta=0.9$时的极限环幅值更大且更加难以消除, 即使观测器带宽很高时, 仍不能够彻底消除极限环. 需要说明的是, 当极限环幅值非常小且周期非常长时, 极限环解虽然存在但是在某些实际应用背景下不会影响控制性能. 对平衡点进行$x_1$ 方向上的摄动, ${\omega _{\rm o}} = 10$, $n = 1000$时, ${\omega _{\rm c}} = 10$和${\omega _{\rm c}} = 20$条件下能够仿真到的最小初始角度${x_{\rm m}}$分别是$1.06 \times {10^{ - 5}}$ (${x_{\rm m}} = {x_{\rm s}}/1000, {x_{\rm s}} = 1.06 \times {10^{ - 2}}$)和$3.36 \times {10^{ - 6}}$ (${x_{\rm m}} = {x_{\rm s}}/1000, {x_{\rm s}} = 3.36 \times {10^{ - 3}}$), 此时仍有极限环产生, 可近似地认为平衡点集是不稳定的. 令$n$取为更小值也是可以的, 这样能够使得初始角度进一步在小于$1.06 \times {10^{ - 5}}$和$3.36 \times {10^{ - 6}}$范围内进行尝试, 但是会存在以下几个问题. 首先, 当初始角度非常小时, 仿真时间会非常长, 计算结果也会受到数值计算精度的影响. 其次, 即使角度间隔取得非常小, 稳定性分析结果仍然可能不是准确的, 因为初始状态摄动还是只考虑了第一个状态, 没有遍历整个状态空间. 所以, 文中令$n = 1000$即可满足要求. 在每个$\omega_{\rm o}$ 下, 最小初始角度摄动下的轨迹都会趋于稳定极限环, 所以可以近似判断平衡点集在所选参数范围内是不稳定的. 当$\omega_{\rm c}=10$ rad/s 和$\omega_{\rm o}=30$ rad/s 时, $\beta=2$和$\beta=0.9$ 下的时域仿真结果如图7所示. 可以看出, $\beta=2$ 时的周期解满足$x_1(t)=-x_1(t+T/2)$, 而当$\beta=0.9$时, 这种对称性被破坏. 因此, 可以推断随着$\beta$的减小周期解会出现对称破缺性分岔(symmetry breaking bifurcation, SBB)^[23].

图 5

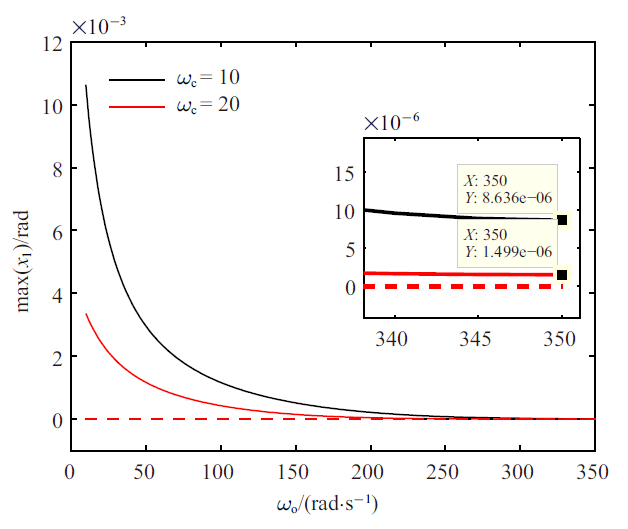新窗口打开|下载原图ZIP|生成PPT
图 5$\beta=0.9$时切换模型系统分岔图(实线:稳定解枝, 虚线:不稳定解枝)

Fig. 5Bifurcation diagram for the switch model system with $\beta=0.9$ (solid line: stable branch, dashed line: unstable branch)

图 6

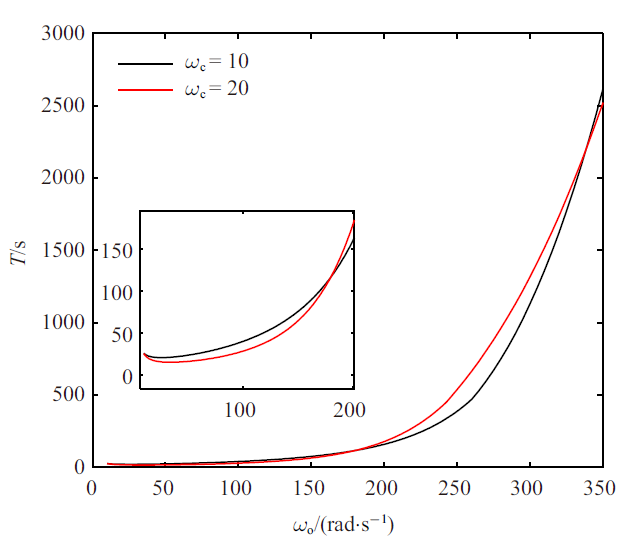新窗口打开|下载原图ZIP|生成PPT
图 6$\beta=0.9$时切换模型系统的稳定极限环周期

Fig. 6Period of stable limit cycle for the switch model system with $\beta=0.9$

图 7

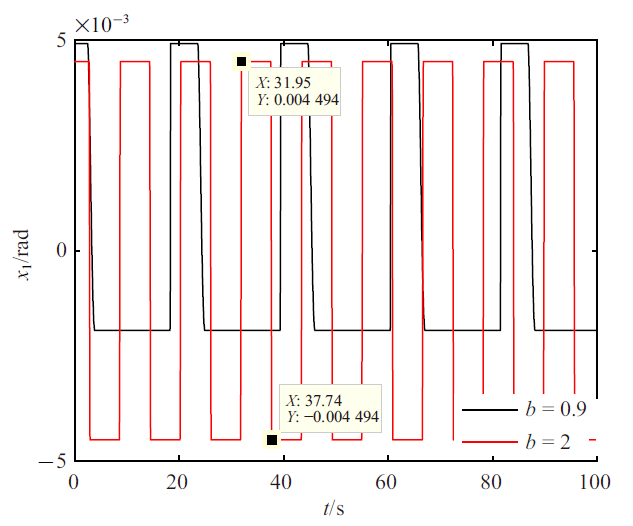新窗口打开|下载原图ZIP|生成PPT
图 7$\beta=0.9, 2$时切换模型系统的角度极限环

Fig. 7Angular position limit cycle for the switch model system with $\beta=0.9, 2$

4.2 基于二阶ESO和LuGre模型的计算结果

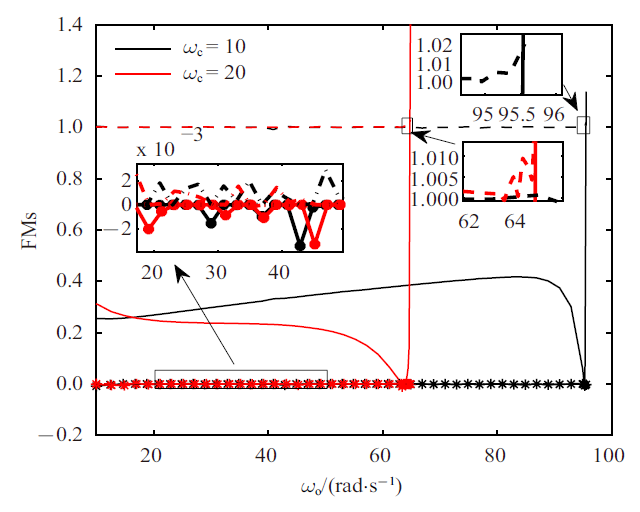
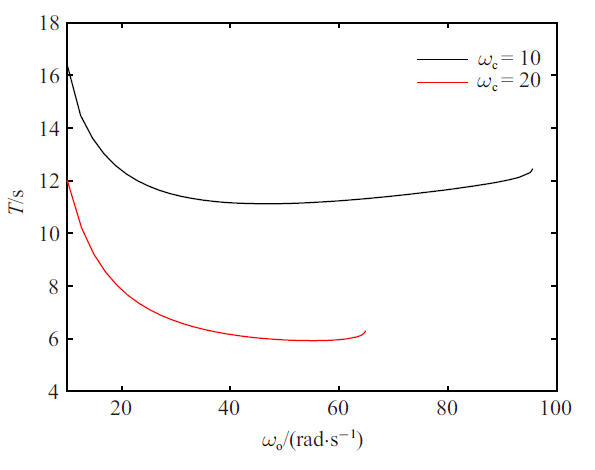
为研究动态和静态摩擦力模型对极限环振动的影响, 采用LuGre模型重复上述过程. 当$\beta=2$时, 仿真结果如图8~图10所示. 和切换模型在$\beta=2$时的结果相似, 随着$\omega_{\rm o}$的增大, 有FM沿实轴从$(1, 0)$穿出单位圆, 出现CFB, 并通过CFB 产生不稳定解枝. 极限环幅值和周期与切换模型下的结果比较接近, $\omega_{\rm o}^{\rm CFB}$稍小于切换模型对应的$\omega_{\rm o}^{\rm CFB}$, 新增加的一个FM在0 附近波动. $\beta=0.9$时的分岔图如图11所示. 可见系统中依然出现了CFB, 且$\omega_{\rm o}^{\rm CFB}$ 比$\beta=2$时的$\omega_{\rm o}^{\rm CFB}$更小, 这一点和切换模型正好是相反的. 对于切换模型, $\beta$ 的减小增大了摩擦力的补偿难度, 即使$\omega_{\rm o}$取值非常大也不能够消除极限环. 然而对于LuGre模型, $\beta$ 的减小反而降低了摩擦力的补偿难度. 可以看出$\beta$ 在静态和动态摩擦力模型中有着不同的影响. 按照前述方法验证平衡点集的稳定性, 可以得到所有考虑参数范围内的平衡点集都是局部稳定的.

图 8

新窗口打开|下载原图ZIP|生成PPT
图 8$\beta=2$时LuGre模型系统分岔图 (实线:稳定解枝, 虚线:不稳定解枝)

Fig. 8Bifurcation diagram for the LuGre model system with $\beta=2$ (solid line: stable branch, dashed line: unstable branch)

图 9

新窗口打开|下载原图ZIP|生成PPT
图 9$\beta=2$时LuGre 模型系统稳定解枝的FMs(实线: ${\rm FM}_1$, 虚线: ${\rm FM}_2$, 点线: ${\rm FM}_3$, 点划线: ${\rm FM}_4$, 星实线: ${\rm FM}_5$)

Fig. 9FMs of stable branch for the LuGre model system with $\beta=2$ (solid line: ${\rm FM}_1$, dashed line: ${\rm FM}_2$, dotted line: ${\rm FM}_3$,dot dash line: ${\rm FM}_4$, solid line with star: ${\rm FM}_5$)

图 10

新窗口打开|下载原图ZIP|生成PPT
图 10$\beta=2$时LuGre模型系统的稳定极限环周期

Fig. 10Period of stable limit cycle for the LuGre model system with $\beta=2$

图 11

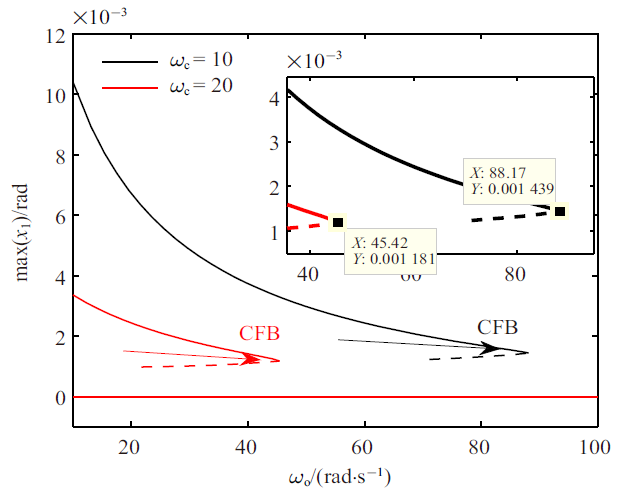新窗口打开|下载原图ZIP|生成PPT
图 11$\beta=0.9$时LuGre模型系统分岔图(实线: 稳定解枝, 虚线:不稳定解枝)

Fig. 11Bifurcation diagram for the LuGre model system with $\beta=0.9$(solid line: stable branch, dashed line: unstable branch)

4.3 基于三阶ESO的计算结果

上述计算结果是针对二阶ESO的, 本文同样针对全阶ESO (三阶ESO)重复进行了4.1 和4.2 小节中的所有计算. 计算结果表明, 上述所得结论(摩擦力模型、参数、ADRC参数对平衡点集以及周期解影响)对于三阶ESO仍然是成立的. 由于闭环系统阶次升高一阶, 切换模型系统和LuGre 模型系统分别多了乘子${\rm FM}_5$和${\rm FM}_6$, 这两个乘子对应的是新增系统状态位置滤波的一阶导数, 且都为接近于零的数. 由于篇幅限制且所得结论是相同的, 该部分结果没有在文中具体呈现.

4.4 二阶三阶ESO性能对比

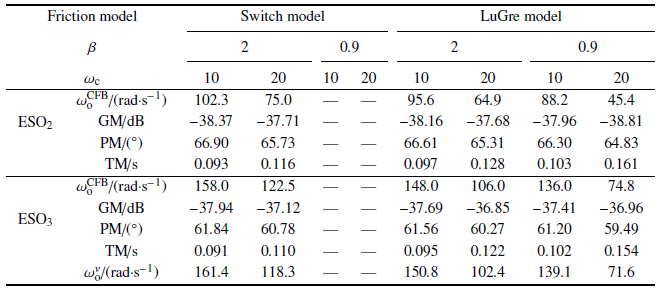
对于给定的摩擦力模型, 降阶和全阶ESO在极限环的存在性和稳定性、平衡点集的稳定性上面的结论是相同的. 但是, 二者在使用时效果还是存在一些区别. 例如, 在相同的${\omega _{\rm c}}$和${\omega _{\rm o}}$下, 全阶ESO相比于降阶ESO的相位延迟更大, 摩擦力补偿效果更差, 极限环的幅值更大. 为了取得和降阶ESO相似的性能, 全阶ESO的${\omega _{\rm o}}$应该更大以补偿高阶次带来的延迟. 因此, 在相同的${\omega _{\rm c}}$下, 全阶ESO对应的$\omega _{\rm o}^{{\rm{CFB}}}$更大. 为了公平地对两者进行性能对比, 我们考虑两种闭环系统在其对应的$\omega _{\rm o}^{{\rm{CFB}}}$下的鲁棒性能, 即令摩擦力补偿效果相同, 比较闭环鲁棒性能, 研究哪一种阶次的观测器能够更好地解决抗扰性能和鲁棒性能之间的矛盾问题. 我们将各种情形下的稳定裕度指标列在表1中. 其中, ${\rm{ES}}{{\rm{O}}_{\rm{2}}}$和${\rm{ES}}{{\rm{O}}_3}$ 分别表示降阶和全阶ESO, GM, PM, TM分别代表幅值裕度、相位裕度和时延裕度. 由于摩擦力模型是非线性的, 在计算稳定裕度时仅考虑了滑动摩擦力, 没有考虑零速附近的摩擦力非线性. 由表1可以看出, 两个闭环系统的鲁棒性能比较相近, 但是${\rm{ES}}{{\rm{O}}_{\rm{2}}}$下的稳定裕度尤其是相位裕度指标更好一些. 因此, 在设计ESO时可以优先选择降阶ESO.

Table 1
表1
表1全降阶ESO下的计算结果对比
Table 1Comparisons of calculation results for full- and reduced-order ESOs

新窗口打开|下载CSV

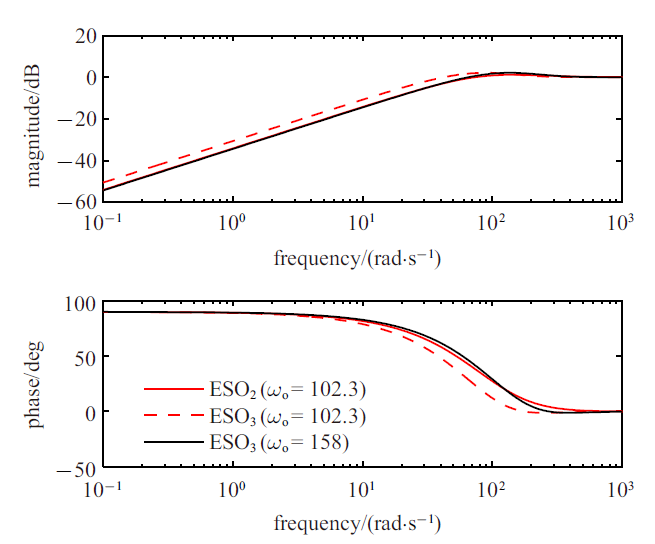
对于切换模型, 当$\beta = 2$ , ${\omega _{\rm c}} = 10$时, ${\rm{ES}}{{\rm{O}}_{\rm{2}}}$和${\rm{ES}}{{\rm{O}}_3}$的$\omega _{\rm o}^{{\rm{CFB}}}$分别为102.3 rad/s和158.0 rad/s, 此时两个ESO的估计误差传函(${\cal L}( {d - \hat d})/{\cal L}( d )$)的频率响应如图12所示. 可见, 两个ESO的频率响应十分接近, 因此, 其相应的极限环特性和稳定鲁棒性能也都是相近的. 那么可以自然地引申出一个问题, 即在怎样的观测器参数化带宽关系下降阶和全阶ESO之间的性能最为接近. 首先考虑传统的$-$3 dB定义的物理带宽, 当两者的物理带宽相同时, 降阶和全阶ESO的参数化带宽${\omega _{\rm or}}$和${\omega _{\rm of}}$之间满足${\omega _{\rm of}} = 1.26{\omega _{\rm or}}$, 显然此时不满足性能相似要求(表1中的带宽关系). 这里我们尝试用衡量线性系统相似性的$\nu $间隙度量^[44]来计算两个ESO参数化带宽之间的关系. 两个线性系统${P_1}$ 和${P_2}$ 之间的$\nu $间隙度量定义为

$$\begin{eqnarray} {\delta _\nu }\left( {{P_1},{P_2}} \right) = \mathop {\sup }\limits_{\omega \in R} \frac{{\left| {{P_1}\left( {j\omega } \right) - {P_2}\left( {j\omega } \right)} \right|}}{{\sqrt {1 + {{\left| {{P_1}\left( {j\omega } \right)} \right|}^2}} \sqrt {1 + {{\left| {{P_2}\left( {j\omega } \right)} \right|}^2}} }}\quad \end{eqnarray}$$

图 12

新窗口打开|下载原图ZIP|生成PPT
图 12全降阶ESO的扰动估计误差的频率响应

Fig. 12Frequency responses of disturbance estimation errors forfull- and reduced-order ESOs



其中, $0 \leqslant {\delta _\nu }\left( {{P_1},{P_2}} \right) \leqslant 1$. ${\delta _\nu }\left( {{P_1},{P_2}} \right)$越小, 相同控制参数下的两个闭环系统性能越相似. 令${P_1}$ 和${P_2}$分别表示降阶和全阶ESO扰动估计的传递函数, 当${\rm{ES}}{{\rm{O}}_{\rm{2}}}$的参数化带宽为$\omega _{\rm o}^{{\rm{CFB}}}$时, ${\rm{ES}}{{\rm{O}}_3}$在最小$\nu $间隙度量下与之对应的参数化带宽如表1中的$\omega _{\rm o}^\nu $所示. 可见$\omega _{\rm o}^\nu $和${\rm{ES}}{{\rm{O}}_3}$的$\omega _{\rm o}^{{\rm{CFB}}}$非常相近, 这说明了$\nu $间隙度量在这个应用上是合理的且精度满足要求. 这也提供了一种思路, 即可以用已知的${\rm{ES}}{{\rm{O}}_{\rm{2}}}$的$\omega _{\rm o}^{{\rm{CFB}}}$推测出${\rm{ES}}{{\rm{O}}_3}$或者${\rm{ES}}{{\rm{O}}_1}$下的$\omega _{\rm o}^{{\rm{CFB}}}$.

5 结论

本文得到以下四个主要结论. 其中, 结论(1)和结论(2)总结了ADRC阶次的影响, 结论(3)和结论(4)总结了摩擦力模型和参数以及控制参数的影响.

(1) 当设计一阶RESO时, 由于等效控制律即为PID控制, 已有的PID 控制下极限环振动结论直接适用. 当设计二阶RESO时, 等效闭环系统增加误差滤波状态. 当设计全阶ESO时, 等效闭环系统增加误差滤波状态及其导数. 在这两种情况下, 虽然阶次分别升高一阶和两阶, 对于给定的摩擦力模型, 闭环系统极限环的存在性和稳定性、平衡点集的稳定性的结论和PID控制下的结论仍然相同, 反映了ADRC阶次对定性结论没有影响.

(2) 在相同的${\omega _{\rm c}}$和${\omega _{\rm o}}$下, 全阶ESO相比于RESO的相位延迟更大, 摩擦力补偿效果更差, 极限环的幅值更大. 因此, 在相同的${\omega _{\rm c}}$下, 全阶ESO对应的$\omega _{\rm o}^{{\rm{CFB}}}$更大. 对比设计有全降ESO的闭环系统在其对应的$\omega _{\rm o}^{{\rm{CFB}}}$下的鲁棒性能, 结果显示RESO下的稳定裕度尤其是相位裕度指标更好一些. 因此, 在设计ESO时可以优先选择RESO.

(3) 对于静态切换模型, $\beta=2$时, $\omega_{\rm o}$增大到某一临界值$\omega_{\rm o}^{\rm CFB}$时极限环出现CFB. 即当$\omega_{\rm o}<\omega_{\rm o}^{\rm CFB}$ 时, 系统中存在两个相近的稳定和不稳定周期解; 当$\omega_{\rm o}=\omega_{\rm o}^{\rm CFB}$ 时, 两个周期解汇聚一起; 当$\omega_{\rm o}>\omega_{\rm o}^{\rm CFB}$时, 系统中极限环消失. $\beta=0.9$时, 在可行的观测器带宽范围内系统没有出现动态分岔且极限环都不会消失, 摩擦力补偿难度增加. 此外, 当$\beta$由2减小到0.9 时, 周期解的对称性被破坏, 出现了SBB.

(4) 对于连续的LuGre模型, 当$\beta=2$和$\beta=0.9$时, 系统都会出现CFB, 即极限环可以通过增大观测器带宽消除. 当$\beta=2$时, 结果和切换模型$\beta=2$ 时结果十分相近. 然而当$\beta=0.9$时, 结果和切换模型$\beta=0.9$时结果正好相反.

下一步将对低速斜坡指令跟踪任务下的黏滑(stick slip)振动展开研究. 跟踪低速斜坡指令时, 系统变为非自治系统, 文中方法不再适用, 其周期解求解将会更加困难, 这也是未来的研究重点.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] 郑鹏, 王琪, 吕敬 等. 摩擦与滚阻对被动行走器步态影响的研究
力学学报, 2020,52(1):162-170
[本文引用: 1]

( Zheng Peng, Wang Qi, Lü Jing, et al. Study on the influence of friction and rolling resistance on the gait of passive dynamic walker
Chinese Journal of Theoretical and Applied Mechanics, 2020,52(1):162-170 (in Chinese))
[本文引用: 1]

[2] 刘兴天, 陈树海, 王嘉登 等. 几何非线性摩擦阻尼隔振系统动力学行为研究
力学学报, 2019,51(2):371-379


( Liu Xingtian, Chen Shuhai, Wang Jiadeng, et al. Anlysis of the dynamic behavior and performance of a vibration isolation system with geometric nonlinear friction damping
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(2):371-379 (in Chinese))


[3] 王晓军, 吕敬, 王琪. 含摩擦滑移铰平面多刚体系统动力学的数值算法
力学学报, 2019,51(1):209-217
[本文引用: 1]

( Wang Xiaojun, Lü Jing, Wang Qi. A numerical method for dynamics of planar multi-rigid-body system with frictional translational joints based on LuGre friction model
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(1):209-217 (in Chinese))
[本文引用: 1]

[4] Han J. From PID to active disturbance rejection control
IEEE Transactions on Industrial Electronics, 2009,56(3):900-906
DOIURL [本文引用: 2]

[5] Tian G, Gao Z. Benchmark tests of active disturbance rejection control on an industrial motion control platform
// Proceedings of the American Control Conference. New York: IEEE, 2009: 5552-5557


[6] Goforth FJ. On motion control design and tuning techniques
// Proceedings of the American Control Conference, New York: IEEE, 2004: 716-721


[7] Xue W, Madonski R, Lakomy K, et al. Add-on module of active disturbance rejection for set-point tracking of motion control systems
IEEE Transactions on Industry Applications, 2017,53(4):4028-4040


[8] Sun M, Wang Z, Wang Y, et al. On low-velocity compensation of brushless DC servo in the absence of friction model
IEEE Transactions on Industrial Electronics, 2013,60(9):3897-3905
DOIURL [本文引用: 1]

[9] Piao M, Wang Y, Sun M, et al. Friction compensation and limit cycle suppression at low velocities based on extended state observer
// 21st IFAC World Congress in Berlin, Germany, July 12-17, 2020, Accepted
[本文引用: 1]

[10] 陈增强, 王永帅, 孙明玮 等. 二阶非线性系统自抗扰控制的全局渐近稳定性
控制理论与应用, 2018,35(11):1687-1696
[本文引用: 1]

( Chen Zengqiang, Wang Yongshuai, Sun Mingwei, et al. Global and asymptotical stability of active disturbance rejection control for second-order nonlinear systems
Control Theory and Technology, 2018,35(11):1687-1696 (in Chinese))
[本文引用: 1]

[11] Armstrong-Hélouvry B, Dupont P, Canudas de wit C. A survey of models, analysis tools and compensation methods for the control of machines with friction
Automatica, 1994,30(7):1083-1138
DOIURL [本文引用: 2]

[12] Kesarkar AA, Selvaganesan N, Priyadarshan H. A novel framework to design and compare limit cycle minimizing controllers: demonstration with integer and fractional-order controllers
Nonlinear Dynamics, 2014,78(4):2871-2882
DOIURL
In this paper, a constrained optimization problem is formulated to tune the limit cycle minimizing controllers meeting additional loop-shaping performances such as phase margin and gain crossover frequency. A graphical approach is proposed so as to determine the superior controller in terms of better limit-cycle suppression. The framework is illustrated with a suitable case of elementary servo plant which has separable static backlash nonlinearity in its model. For this plant, integer-order controllers and their fractional counterparts (PI and ; PID and ) are designed and compared. Interestingly, it is found that the fractional controllers produce better limit-cycle responses than their integer counterparts while both meeting the rest of the specifications. Correspondingly, the better sustained oscillations in the plant output response are obtained with fractional controllers. Such a 'fractional superiority' is further verified with the closed-loop nonlinear simulation.

[13] Kim M, Chung S. Friction identification of ball-screw driven servomechanisms through the limit cycle analysis
Mechatronics, 2006,16(2):131-140
DOIURL

[14] Armstrong-Hélouvry B, Amin B. PID control in the presence of static friction: A comparison of algebraic and describing function analysis
Automatica, 1996,32(5):679-692
[本文引用: 4]

[15] Radcliffe CJ, Southward SC. A property of stick-slip friction models which promotes limit cycle generation
// Proceedings of the American Control Conference, New York: IEEE, 1990: 1198-1203
[本文引用: 1]

[16] Galvanetto U, Knudsen C. Events maps in a stick-slip system
Nonlinear Dynamics, 1997,13:99-115
DOIURL [本文引用: 2]

[17] Hensen RHA. Controlled mechanical systems with friction
Eindhoven: Eindhoven University of Technology, 2002
[本文引用: 4]

[18] Hensen RHA, Molengraft MJGVD, Steinbuch M. Friction induced hunting limit cycles: A comparison between the LuGre and switch friction model
Automatica, 2003,39(12):2131-2137
DOIURL [本文引用: 6]

Abstract

In this paper, friction induced limit cycles are predicted for a simple motion system consisting of a motor-driven inertia subjected to friction and a PID-controlled regulator task. The two friction models used, i.e., (i) the dynamic LuGre friction model and (ii) the static switch friction model, are compared with respect to the so-called hunting phenomenon. Analysis tools originating from the field of nonlinear dynamics will be used to investigate the friction induced limit cycles. For a varying controller gain, stable and unstable periodic solutions are computed numerically which, together with the stability analysis of the closed-loop equilibrium points, result in a bifurcation diagram. Bifurcation analysis for both friction models indicates the disappearance of the hunting behavior for controller gains larger than the gain corresponding to the cyclic fold bifurcation point.

[19] Jeon S. Integrator leakage for limit cycle suppression in servo mechanisms with stiction
Journal of Dynamic Systems, Measurement, and Control, 2012,134(3):034502
DOIURL [本文引用: 1]

[20] 朴敏楠, 王科磊, 孙明玮 等. 基于积分泄漏的机电伺服系统摩擦力补偿
中南大学学报 (自然科学版), 2020,51(3):668-677
[本文引用: 2]

( Piao Minnan, Wang Kelei, Sun Mingwei, et al. Friction compensation of electromechanical servo systems based on integrator leakage
Journal of Central South University (Science and Technology), 2020,51(3):668-677 (in Chinese))
[本文引用: 2]

[21] Leine RI, Campen DHV, Kraker AD, et al. Stick-slip vibrations induced by alternate friction models
Nonlinear Dynamics, 1998,16(1):41-54
DOIURL [本文引用: 3]

[22] Putra D, Nijmeijer HH. Limit cycling in an observer-based controlled system with friction: Numerical analysis and experimental validation
International Journal of Bifurcation and Chaos, 2004,14(9):3083-3093
DOIURL [本文引用: 1]

[23] Leine RI, Campen DHV, Vrande BLVD. Bifurcations in nonlinear discontinuous systems
Nonlinear Dynamics, 2000,23(2):105-164
DOIURL [本文引用: 1]
This paper treats bifurcations of periodic solutions indiscontinuous systems of the Filippov type. Furthermore, bifurcations offixed points in non-smooth continuous systems are addressed. Filippov''stheory for the definition of solutions of discontinuous systems issurveyed and jumps in fundamental solution matrices are discussed. It isshown how jumps in the fundamental solution matrix lead to jumps of theFloquet multipliers of periodic solutions. The Floquet multipliers canjump through the unit circle causing discontinuous bifurcations.Numerical examples are treated which show various discontinuousbifurcations. Also infinitely unstable periodic solutions are addressed.

[24] Vrande BLVD, Campen DHV, Kraker AD. An approximate analysis of dry-friction-induced stick-slip vibrations by a smoothing procedure
Nonlinear Dynamics, 1999,19(2):159-171
DOIURL

[25] Brindley J, Kaas-Petersen C, Spence A. Path-following methods in bifurcation problems
Physica D Nonlinear Phenomena, 1989,34(3):456-461
DOIURL

[26] 易中贵, 戈新生. 自由下落猫姿态最优控制的混合优化策略
力学学报, 2016,48(6):1390-1397
DOIURL
研究猫自由下落时的转体运动对探索宇航员在太空失重状态下的空间运动规律具有重要的参考价值.针对猫自由下落时四肢先着地现象的姿态最优控制问题，提出一种由Gauss伪谱法求解可行解与直接打靶法求解最优精确解相结合的混合优化策略.首先，根据猫在自由下落过程中的角动量守恒原理，推导出简化后的两对称刚体系统的非完整姿态运动方程；然后基于Gauss伪谱法将此无漂移系统的姿态非完整运动规划问题离散为非线性规划问题，并在不考虑实际性能指标函数的条件下利用序列二次规划算法求解此非线性规划问题在较少节点时对应的控制变量可行解，再通过三次样条插值获取较多节点时的控制变量值；最后基于直接打靶法将插值得到的控制值作为序列二次规划算法的初始猜测值，从而求解得到最优的控制输入，再代入系统姿态运动方程，通过数值积分得到落体猫的转体姿态运动曲线.通过数值仿真，求解得到的姿态运动曲线是光滑的，能以较高的精度到达预定的目标姿态；最优控制输入也能满足预先设计的零边界控制要求以及最大控制要求；结果表明了此混合优化策略具有较强的鲁棒性和有效性.
( Yi Zhonggui, Ge Xinsheng. The attitude optimal control with a hybrid optimal strategy for a free-falling cat
Chinese Journal of Theoretical and Applied Mechanics, 2016,48(6):1390-1397 (in Chinese))
DOIURL
研究猫自由下落时的转体运动对探索宇航员在太空失重状态下的空间运动规律具有重要的参考价值.针对猫自由下落时四肢先着地现象的姿态最优控制问题，提出一种由Gauss伪谱法求解可行解与直接打靶法求解最优精确解相结合的混合优化策略.首先，根据猫在自由下落过程中的角动量守恒原理，推导出简化后的两对称刚体系统的非完整姿态运动方程；然后基于Gauss伪谱法将此无漂移系统的姿态非完整运动规划问题离散为非线性规划问题，并在不考虑实际性能指标函数的条件下利用序列二次规划算法求解此非线性规划问题在较少节点时对应的控制变量可行解，再通过三次样条插值获取较多节点时的控制变量值；最后基于直接打靶法将插值得到的控制值作为序列二次规划算法的初始猜测值，从而求解得到最优的控制输入，再代入系统姿态运动方程，通过数值积分得到落体猫的转体姿态运动曲线.通过数值仿真，求解得到的姿态运动曲线是光滑的，能以较高的精度到达预定的目标姿态；最优控制输入也能满足预先设计的零边界控制要求以及最大控制要求；结果表明了此混合优化策略具有较强的鲁棒性和有效性.

[27] Charroyer L, Chiello O, Sinou JJ. Self-excited vibrations of a non-smooth contact dynamical system with planar friction based on the shooting method
International Journal of Mechanical Sciences, 2018,144:90-101
DOIURL [本文引用: 1]

[28] Canudas de wit C, Olsson H, Astrom KJ, et al. A new model for control of systems with friction
IEEE Transactions on Automatic Control, 1995,40:419-425
DOIURL [本文引用: 3]

[29] 曲子芳, 张正娣, 彭淼 等. 双频激励下Filippov系统的非光滑簇发振荡机理
力学学报, 2018,50(5):1145-1155
[本文引用: 1]

( Qu Zifang, Zhang Zhengdi, Peng Miao, et al. Non-smooth bursting oscillation mechanisms in a Filippov-type system with multiple periodic excitations
Chinese Journal of Theoretical and Applied Mechanics, 2018,50(5):1145-1155 (in Chinese))
[本文引用: 1]

[30] 张毅, 韩修静, 毕勤胜. 串联式叉型滞后簇发振荡及其动力学机制
力学学报, 2019,51(1):228-236


( Zhang Yi, Han Xiujing, Bi Qinsheng. Series-mode pitchfork-hysteresis bursting oscillations and their dynamical mechanisms
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(1):228-236 (in Chinese))


[31] 石建飞, 苟向锋, 朱凌云. 两空间耦合下齿轮传动系统多稳态特性研究
力学学报, 2019,51(5):1489-1499


( Shi Jianfei, Gou Xiangfeng, Zhu Lingyun. Research on multi-stability characteristics of gear transmission system with two-space coupling
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(5):1489-1499 (in Chinese))


[32] 郑健康, 张晓芳, 毕勤胜. 一类混沌系统中的簇发振荡及其延迟叉形分岔行为
力学学报, 2019,51(2):540-549
[本文引用: 1]

( Zheng Jiankang, Zhang Xiaofang, Bi Qinsheng. Bursting oscillations as well as the delayed pitchfork bifurcation behaviors in a class of chaos system
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(2):540-549 (in Chinese))
[本文引用: 1]

[33] Karnopp D. Computer simulation of stick-slip friction in mechanical dynamic systems
Journal of Dynamic, Systems, Measurement, and Control, 1985,107(1):100-103
DOIURL [本文引用: 1]

[34] Marton L. On analysis of limit cycles in positioning systems near Striebeck velocities
Mechatronics, 2008,18(1):46-52
DOIURL [本文引用: 1]

Abstract

The paper deals with the analysis of friction induced oscillatory behavior in mechanical control systems at non-zero velocities. It is considered that in the positioning system under investigation the mechanical plant is controlled by linear control algorithm and the reference position trajectory is time varying. To perform the limit cycle analysis near the Striebeck velocity, a novel linearly parameterized friction model is introduced for the separation of high and low velocity regimes (under and over the Striebeck velocity). Based on this model, the limit cycles that occurs in mechatronic systems near Striebeck velocities can be predicted and studied using techniques from classical linear system theory.

[35] Wu Q, Sun M, Chen Z, et al. Tuning of active disturbance rejection attitude controller for statically unstable launch vehicle
Journal of Spacecraft and Rockets, 2017,54(6):1383-1389
[本文引用: 1]

[36] Zhong S, Huang Y, Guo L. A Parameter formula connecting PID and ADRC
Science China Information Sciences, DOI: 10.1007/s11432-019-2712-7
DOIURLPMID [本文引用: 2]
The current research progress and the existing problems of uncertain or imprecise knowledge representation and reasoning in description logics are analyzed in this paper. Approximate concepts are introduced to description logics based on rough set theory, and a kind of new rough description logic RDL AC (rough description logic based on approximate concepts) is proposed based on approximate concepts. The syntax, semantics and properties of the RDL AC are given. It is proved that the approximate concept satisfiability (definitely satisfiability and possibly satisfiability) reasoning problem and approximate concepts rough subsumption reasoning problem w.r.t. rough TBox in RDL AC may be reduced to the concept satisfiability reasoning problem in (almost) standard ALC (the description logic that provides the Boolean concept constructors plus the existential and universal restriction constructors). The works of this paper provide logic foundations for approximate ontologies and theoretical foundations for reasoning algorithms of more expressive rough description logics including approximate concepts, number restrictions, nominals, inverse roles and role hierarchies.

[37] Nayfeh AH, Balachandran B. Applied Nonlinear Dynamics: Analytical, Computational, and Experimental Methods
New Jersey: Wiley, 2004
[本文引用: 1]

[38] Fey RHB. Steady State Behaviour of Reduced Dynamic Systems with Local Nonlinearities
Eindhoven: Eindhoven University of Technology, 1992
[本文引用: 1]

[39] 贾宏杰, 余贻鑫, 李鹏. 电力系统环面分岔与混沌现象
中国电机工程学报, 2002,22(8):7-11


( Jia Hongjie, Yu Yixin, Li Peng. Torus bifurcation and chaos in power systems
Proceedings of the CSEE, 2002,22(8):7-11 (in Chinese))


[40] 邱宇, 邱勇, 邱家俊. 机电耦联系统余维3动态分岔研究
力学学报, 2006,38(3):421-428
[本文引用: 1]

( Qiu Yu, Qiu Yong, Qiu Jiajun. Study of electro mechanical coupling system by codimension-3 dynamical bifurcation
Chinese Journal of Theoretical and Applied Mechanics, 2006,38(3):421-428 (in Chinese))
[本文引用: 1]

[41] Clarke FA, Ledyaev YS, Stem RJ, et al. Nonsmooth Analysis and Control Theory
New York: Graduate Texts in Mathematics, 1998
[本文引用: 1]

[42] Leine RI, Wouw VD. Stability properties of equilibrium sets of non-linear mechanical systems with dry friction and impact
Nonlinear Dynamics, 2008,51(4):551-583
DOIURL [本文引用: 1]
In this paper, we will give conditions under which the equilibrium set of multi-degree-of-freedom non-linear mechanical systems with an arbitrary number of frictional unilateral constraints is attractive. The theorems for attractivity are proved by using the framework of measure differential inclusions together with a Lyapunov-type stability analysis and a generalisation of LaSalle’s invariance principle for non-smooth systems. The special structure of mechanical multi-body systems allows for a natural Lyapunov function and an elegant derivation of the proof. Moreover, an instability theorem for assessing the instability of equilibrium sets of non-linear mechanical systems with frictional bilateral constraints is formulated. These results are illustrated by means of examples with both unilateral and bilateral frictional constraints.

[43] Li Z, Cao Q, Leger A, et al. The equilibrium stability for a smooth and discontinuous oscillator with dry friction
Acta Mechanica Sinica, 2016,32(2):309-319
[本文引用: 1]

[44] Foias C, Georgiou TT, Smith MC. Robust stability of feedback systems: a geometric approach using the gap metric
SIAM Journal on Control and Optimization, 1993,31(6):1518-1537
[本文引用: 1]