张玉玲^*, 谷勇霞^?, 赵杰亮^*, 阎绍泽^,*,2)*清华大学 摩擦学国家重点实验室,北京 100084
^?北京工商大学 材料与机械工程学院,北京 100048

RESEARCH ON VIBRATION CHARACTERISTICS OF THE MANIPULATOR END UNDER ACTIVE CONTROL OF ARM STIFFNESS$^{\bf 1)}$

Zhang Yuling^*, Gu Yongxia^?, Zhao Jieliang^*, Yan Shaoze^,*,2)*State Key Laboratory of Tribology,Tsinghua University,Beijing 100084,China
^?School of Material and Mechanical Engineering,Beijing Technology and Business University,Beijing 100048,China

通讯作者: 2)阎绍泽,教授,主要研究方向：智能仿生与机械动力学. E-mail:yansz@mail.tsinghua.edu.cn

收稿日期:2020-03-5接受日期:2020-03-16网络出版日期:2020-07-18

基金资助:

1)国家自然科学基金.11872033 北京市自然科学基金.3172017

Received:2020-03-5Accepted:2020-03-16Online:2020-07-18
作者简介 About authors


摘要
机械臂在运动过程中会因臂杆柔性引发结构变形和弹性振动,降低机械臂末端的定位精度和运动稳定性,将结构振动控制方法用于机械臂的振动抑制研究具有重要意义. 基于变刚度主动控制的设计思想,提出了臂杆刚度主动控制方法,通过改变机械臂臂杆的轴向受力状况来主动改变机械臂的刚度. 采用变形耦合法描述了机械臂的非线性变形,进而结合假设模态法和拉格朗日方程建立了臂杆的变刚度动力学模型,并进行了数值仿真. 在此基础上,设计了基于臂杆刚度主动控制方法的单自由度实验台,分析了不同预紧力下机械臂末端的振动特性. 数值仿真和实验结果表明,随着预紧力的增加,机械臂末端的振动幅值得到衰减,验证了臂杆刚度主动控制方法的有效性. 通过采用响应面法建立了机械臂末端的振动响应与预紧力的关系,并基于内部映射牛顿法的子空间置信域法优化算法对预紧力进行了优化分析,得到了最优预紧力. 该研究可为机械臂的精细动力学建模和振动抑制提供一定的理论依据,并为研究经济型低刚度材料的刚化问题提供了方向,以利用廉价低刚度材料取代目前所应用的昂贵高刚度材料.
关键词： 臂杆刚度主动控制;预紧力;机械臂;动力学建模;振动特性

Abstract
The structural deformation and elastic vibration of the manipulator will be caused by the flexibility of the manipulator arm during the movement, which will reduce the positioning accuracy and motion stability of the manipulator end. It is of great significance to apply structural vibration control method to the vibration suppression of the manipulator. Based on the design idea of variable stiffness active control, an active control method of arm stiffness is proposed. The stiffness of the manipulator is actively changed by changing the axial force of the manipulator arm. The nonlinear deformation of the manipulator is described by the deformation coupling method, and then the variable stiffness dynamic model of the manipulator arm is established by using the assumption mode method and Lagrange equation. Further, numerical simulation is performed to solve the variable stiffness dynamic model of the manipulator arm. On this basis, a single degree of freedom experimental device based on the active control of arm stiffness method is designed, and the vibration characteristics of the manipulator end under different preloading forces are analyzed. Numerical simulation and experimental results show that the vibration amplitude of the manipulator end is suppressed with the increase of preloading force, which verifies the effectiveness of the active control of arm stiffness. The relationship between the vibration response of the manipulator end and the preloading force is established by using the response surface method. Then the preloading force is optimized by using the Subspace Trust-region algorithm based on Interior-reflective Newton Method, and the optimal preloading force is obtained. This study can provide a theoretical basis for the fine dynamic modeling and the vibration suppression of the manipulator, and provide a direction for the study of the rigidization of economical low-stiffness materials, so as to replace the currently used expensive high-stiffness materials with cheap low-stiffness materials.
Keywords：active control of arm stiffness;preloading force;manipulator;dynamic modeling;vibration characteristic


PDF (11923KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
张玉玲, 谷勇霞, 赵杰亮, 阎绍泽. 机械臂臂杆刚度主动控制下的末端振动特性研究$^{\bf 1)}$. 力学学报[J], 2020, 52(4): 985-995 DOI:10.6052/0459-1879-20-075
Zhang Yuling, Gu Yongxia, Zhao Jieliang, Yan Shaoze. RESEARCH ON VIBRATION CHARACTERISTICS OF THE MANIPULATOR END UNDER ACTIVE CONTROL OF ARM STIFFNESS$^{\bf 1)}$. Chinese Journal of Theoretical and Applied Mechanics[J], 2020, 52(4): 985-995 DOI:10.6052/0459-1879-20-075

引言

随着航天技术的发展,空间机械臂成为辅助甚至代替人类从事各种太空作业的重要在轨服务工具^[1]. 空间机械臂具有质量轻、工作半径大、高负载能力等特征,在运动过程中会因臂杆柔性引发结构变形和弹性振动,降低机械臂末端的定位精度和运动稳定性,成为机械臂研究中的突出问题^[2-3].

早期国内外****为了解决柔性机械臂的弹性振动问题对机械臂的动力学建模、控制策略及实验方面进行了大量的研究,理论模型不断得到完善,控制策略也趋于智能化,极大地提高了机械臂动力学特性的分析精度. 目前主要结合模态分析法等离散化方法等^[4]和经典建模方法建立理论模型,然后采用 PD 控制、鲁棒控制、奇异摄动等经典控制方法及神经网络控制、模糊控制等智能控制方法抑制振动及轨迹跟踪^[5-12]. Yang 等^[13]结合假设模态法和 Lagrange 方程建立了空间机械臂系统的动力学模型,并通过复合滑模控制方法对轨迹进行振动抑制. Pisculli 等^[14]采用有限元法和 Newton-Euler 及 Euler-Lagrange 的混合方程相结合建立了柔性空间机械臂系统的动力学模型,并采用反应零空间和雅可比矩阵转置控制策略相结合对机械臂系统进行控制. Gao 等^[15]利用假设模态法建立了两连杆柔性机械臂的 $N$ 维离散化模型,并基于全状态反馈控制和输出反馈控制实现了轨迹跟踪和振动抑制. 虽然这些控制算法相对成熟,但其依赖于模型的准确程度,较为复杂. 由于抗弯刚度、结构阻尼是柔性机械臂的两个主要结构参数,尤其影响弹性振动的响应,因此将结构振动控制方法用于机械臂的振动抑制研究具有重要意义.

结构振动控制方法有被动控制、半主动控制和主动控制三种,其中被动控制和主动控制因外部能源问题而应用受到限制^[16]. 半主动控制仅需较少的能量来调节结构的刚度、阻尼等参数,通过结构的振动能量产生控制力,其控制效果明显优于被动控制,接近主动控制^[17]. 半主动控制主要包括主动刚度控制和主动阻尼控制,刚度主动控制是结构振动控制方法中半主动振动控制技术的常用方法^[18-20]. 目前主动刚度控制在航空航天、微电子机械等技术领域得到一定程度的应用,Lew 等^[21]针对地震环境中的结构振动抑制问题,提出了一种结构自适应控制方法,并通过仿真验证了方法的有效性. Li 等^[22]提出了一种考虑非线性磁流变阻尼器模型的结构振动半主动控制方法,并采用模糊系统对模型进行逼近,通过控制器对抖振现象进行了控制. Mevada 等^[23]研究了被动刚度阻尼器和半主动刚度阻尼器的扭转耦合建筑的地震响应,结果表明半主动刚度阻尼器减小位移和加速度的效果要明显优于被动刚度阻尼器. 部分****对建筑结构层间的主动控制力特征进行研究,研究表明主动控制力除了阻尼项外,主要体现了负刚度控制特性,进而出现了负刚度控制方法^[24]. 汪志昊等^[25]对结构振动的负刚度控制进行了详细的研究,为负刚度控制在实际工程中的应用奠定了基础. 龚微等^[26]基于 Benchmark 隔振模型,提出了一种磁流变阻尼器的负刚度智能隔振控制策略,仿真结果表明负刚度控制集合了主动和半主动控制的优点,有效降低地震时隔震层的位移. 之后,随着变刚度主动控制算法的不断优化,刚度主动控制得到了广泛应用,耿士能等^[27]为避免机械臂碰撞过程中产生冲击与破坏,设计了一种利用温控记忆合金改变关节内摩擦力的变刚度方法,实验结果表明该连续型机械臂具有良好的运动控制精度和刚度调节能力. Petit 等^[28]提出了一种多关节变刚度机器人跟踪控制的后退方法,通过对变刚度关节和多关节变刚度机器人进行仿真和测量验证了该方法的有效性. Lin 等^[29]提出了采用变刚度的调谐质量阻尼器进行振动控制,数值结果表明该控制方法能够自动避免失调影响并有效抑制振动.

本文根据半主动控制中的变刚度主动控制的设计思想,通过改变机械臂臂杆的轴向受力状况来主动改变机械臂的刚度,进而达到振动抑制的目的,因此文中将该方法称为"臂杆刚度主动控制"方法. 在此基础上,采用变形耦合法来计算机械臂的非线性变形,并结合假设模态法和拉格朗日方程建立了臂杆的动力学模型;进而设计了基于臂杆刚度主动控制方法的单自由度实验台,分析了机械臂在不同预紧力下末端的振动特性,结合仿真和实验结果验证了方法的有效性;最后采用响应面法和基于内部映射牛顿法的子空间置信域法优化算法对预紧力进行了优化分析. 该研究可为机械臂的精细动力学建模和振动控制提供一定的参考.

1 基于臂杆刚度主动控制的机械臂动力学建模

1.1 臂杆刚度主动控制方法

空间机械臂因臂杆柔性在运动过程中产生的弹性变形与机械臂大范围刚性运动的耦合效应会导致机械臂在其弹性变形中的振动频率不一致,即产生刚化效应. 另外,机械臂在旋转运动过程中会受到离心力的作用,轴向的较大变形引起刚度减小,即产生软化效应^[30]. 刚化效应和软化效应相互作用,使机械臂在运动过程中的刚度发生变化,影响其动力学响应.

根据上述机械臂刚度变化效应产生的原理和结构振动控制中的刚度主动控制方法的设计思路,文中提出的臂杆刚度主动控制方法结构示意图如图 1 所示. 在管状机械臂的臂杆中置一弹性绳索,其两端分别连接拉力传感器与螺栓,拉力传感器用于测量绳索拉力大小,用螺母拧上螺栓以拉紧绳索,通过调节螺栓来调节臂杆受力进而调节臂杆刚度来抑制机械臂运动过程中产生的弹性振动.

图1

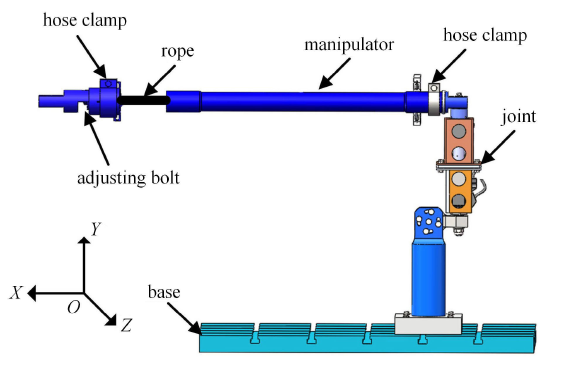新窗口打开|下载原图ZIP|生成PPT
图1机械臂臂杆刚化调节结构图

Fig.1The structure of manipulator arm stiffening adjustment



为建立图 1 中机械臂的变刚度动力学模型,将其简化为图 2 所示的平面管状悬臂梁模型,虚线为变形前的机械臂,实线为变形后的机械臂. 假设机械臂在运动过程中绳索与机械臂始终不接触,因此可将绳索对机械臂的作用力简化为一作用于机械臂末端面的集中力 ${\pmb F}$. 另外,机械臂的关节处作用有驱动力矩 ${\pmb \tau }$;$l_0 $,$D_0 $ 和 $\delta $ 分别为变形前机械臂的长度、外径和厚度尺寸. 为验证臂杆刚度主动控制的效果,在运动过程中同时考虑臂杆的纵向 (轴向) 变形和横向 (径向) 变形以及横向变形引起轴向变形的二次耦合效应.

图2

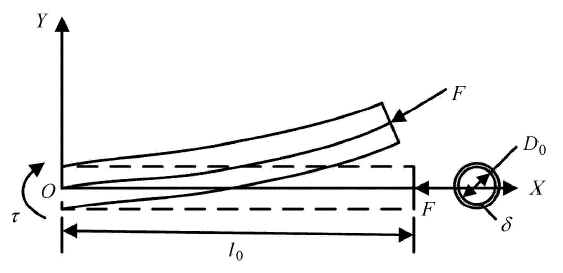新窗口打开|下载原图ZIP|生成PPT
图2机械臂臂杆刚度主动控制的简化模型

Fig.2The simplified model for active control of manipulator arm stiffness

1.2 臂杆结构参数分析

将臂杆刚度主动控制下的机械臂运动过程进行受力分析,如图 3 所示. 以机械臂关节端为坐标原点分别建立惯性坐标系 $OXY$ 和随动坐标系 $Oxy$. 机械臂在平面内运动产生刚性转角为 $\theta $,$F_1 $ 和 $F_2 $ 分别为绳索作用于机械臂末端面的集中力在惯性坐标系中的投影.

图3

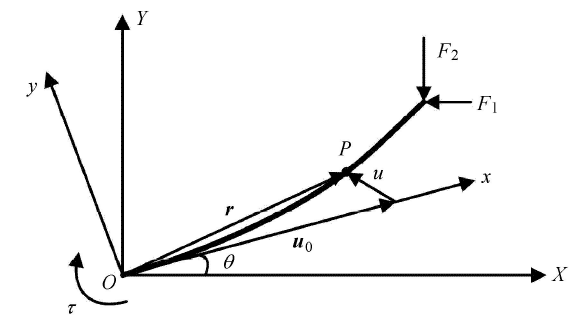新窗口打开|下载原图ZIP|生成PPT
图3机械臂运动过程中的受力分析图

Fig.3The force analysis during the movement of the manipulator



设在动坐标系中机械臂上 $x$ 处任一点 $P$ 变形前的坐标向量为 $u_0 $,总变形位移为 $u$,纵向和横向总变形量分别为 $u_x $ 和 $u_v $,则

(1)${\pmb u}_0 = \left[ {x} \ \ 0 \right]^{\rm T}, \quad {\pmb u} = \left[ {u}_{x} \ \ {u}_{y} \right]^ {\rm T}$
根据弹性梁的变形理论,考虑完全几何非线性变形,臂杆上 $P$ 点的纵向和横向变形位移分别为^[31]

(2)$u_x = v_1 - \dfrac{1}{2}\sum_{i = 1}^n {\sum_{j = 1}^n {e_{ij} q_i } } (t) q_j (t), \ \ u_y = v_2$
式中,$v_1 $ 和 $v_2 $ 分别为臂杆纵向振动和横向弯曲振动产生的变形;$ {e}_{ij} $ 为耦合形函数,其表达式为 $ {e}_{ij} = \int_0^x \dfrac{\partial \varphi _i \left( \varepsilon \right)}{\partial \varepsilon } \dfrac{\partial \varphi _j \left( \varepsilon \right)}{\partial \varepsilon } \text{d}\varepsilon $,$\varphi _i (x) $ 和 $\varphi _{j} ( x )$ 为臂杆横向弯曲振动的模态函数,$ {q}_i (t)$ 和 ${q}_{j} (t)$ 为与模态函数对应的模态坐标,$\varepsilon $ 为积分变量. 令 $ {v}_{\rm c} = - \dfrac{1}{2}\sum_{i = 1}^n \sum_{j = 1}^n e_{ij} q_i (t) q_j (t)$,$ {v}_{\rm c} $ 为考虑横向弯曲变形引起轴向变形的二次耦合变形量. 由此可得

(3)${\pmb u} = \left[ {v_1 + v_c } \ \ {v_2 } \right]^{\rm T}$
根据臂杆轴向变形和径向变形的关系,可计算得到臂杆变形后的外径 $D$ 为

(4)$D = D_0 + \Delta D = D_0 \left( {1 + \dfrac{\mu }{l_0 }u_x } \right)$
机械臂为管状构形,为了保证臂杆结构强度和稳定性要求,臂杆厚度与臂杆外径一般成正比关系

(5)$\delta = k_\delta D$
式中,$k_\delta $ 为机械臂截面厚度与外径的比例系数.

结合式 (4) 和式 (5) 可计算出变形后臂杆的横截面面积和惯性矩分别为

(6)$A ( x ) = \pi k_\delta \left( {1 - k_\delta } \right)D_0^2 \left( {1 + \dfrac{\mu }{l_0 }u_x } \right)^2$
(7)$I ( x ) = \dfrac{\pi }{8}k_\delta \left( {1 - k_\delta } \right)\left( {1 - 2k_\delta + 2 k_\delta ^2 } \right)D_0^4 \left( {1 + \dfrac{\mu }{l_0 }u_x } \right)^4$
由式 (6) 和式 (7) 可知,机械臂在运动过程中的横截面面积和惯性矩发生变化,引起机械臂在运动过程中的臂杆刚度不断发生变化.

1.3 臂杆动力学模型

如图 3 所示,${\pmb r}$ 为臂杆上点$P$在惯性坐标系 $OXY$ 中的位置向量,则

(8)${\pmb r} = \bar {\pmb u}_0 + \bar{\pmb u} = N{\pmb r}' = N\left( {{\pmb u}_0 + {\pmb u}} \right)$
式中,${\pmb r}'$ 为点 $P$ 在动坐标系中的位置向量,$\bar{\pmb u}_0 $ 和 $\bar {\pmb u}$ 分别为动坐标系中 ${\pmb u}_0 $ 和 ${\pmb u}$ 在惯性坐标系中的表示. $N$ 为从动坐标系 $Oxy$ 到惯性坐标系 $OXY$ 的旋转变换矩阵,即

(9)${\pmb N} = \left[ \!\! \begin{array}{cc} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{array} \!\!\right]$
由规范理论的基本思想,可得如下基本的运动学关系

(10)$\dot {\pmb r} = {\pmb N} \left( {\dfrac{\partial {\pmb r}' }{\partial t} + \tilde {\pmb \omega }'{\pmb r}'} \right) = {\pmb N}{\pmb D}_{t} {\pmb r}'$
式中

$\tilde {\pmb \omega }' = {\pmb N}^{\rm T}\left( {\dfrac{\partial {\pmb r}'}{\partial t} + \tilde {\pmb \omega }'{\pmb r}'} \right) = {\pmb N}{\pmb D}_{t} {\pmb r}'\\ \tilde {\pmb \omega }' = {\pmb N}^{\rm T} \dot {\pmb N} \left[ \begin{array}{cc} 0 & { - 1} \\ 1 & 0 \end{array} \right]\dot {\theta }, \ \ {\pmb D}_{ t} = \dfrac{\partial }{\partial t} + \tilde {\pmb \omega }' $

由此可计算出

(11)$ \dot{\pmb r}^{\rm T} \dot{\pmb r} = \left( { {\pmb N}{\pmb D}_t {\pmb r}' } \right)^{\rm T}\left( { {\pmb N}{\pmb D}_t {\pmb r}' } \right) = \left( {\dfrac{\partial {\pmb r}'}{\partial t} + \tilde {\pmb \omega }'{\pmb r}' } \right)^{\rm T}\left( {\dfrac{\partial {\pmb r}'}{\partial t} + \tilde {\pmb\omega }'{\pmb r}' } \right)$
结合式 (1)、式 (3) 及式 (8) 并考虑,可将上式表示为

(12)$\dot{\pmb r}^{\rm T} \dot{\pmb r} = \left( {\dfrac{\partial v_1 }{\partial t} + \dfrac{\partial v_c }{\partial t}} \right)^2 + \left( {\dfrac{\partial v_2 }{\partial t}} \right)^2 +\\ \qquad 2\dot {\theta }\left[ {\dfrac{\partial v_2 }{\partial t}\left( {v_1 + v_c + x} \right) - v_2 \left( {\dfrac{\partial v_1 }{\partial t} + \dfrac{\partial v_c }{\partial t}} \right)} \right] +\\ \qquad \dot {\theta }^2\left[ {\left( {v_1 + v_c + x} \right)^2 + v_2^2 } \right]$
基于假设模态法,采用前两阶模态对臂杆的弹性振动进行近似描述,则机械臂的纵向振动和向弯曲振动可表示为

(13)$v_1 \left( {x,t} \right) = a_1 (t) \varphi _{11} (x) + a_2 (t) \varphi _{12} (x) $
(14)$v_2 \left( {x,t} \right) = b_1 (t) \varphi _{21} (x) + b_2 (t) \varphi _{22} (x) $
式中,$\varphi _{1i} (x) $和$\varphi _{2i} \left( x \right)$ ($i =1, 2$) 分别为机械臂纵向振动和横向弯曲振动的模态函数,$a_i $ 和 $b_i $ ($i =1, 2$) 分别为与模态函数对应的模态坐标. 通过查阅资料可得悬臂梁的前两阶纵向振动和横向弯曲振动模态函数表达式^[32]

(15)$ \ \ \varphi _{11} (x) = \sin \dfrac{\pi }{2l}x, \ \ \varphi _{12} (x) = \sin \dfrac{3\pi }{2l}x$
(16)$\left.\begin{array}{c} \varphi _{21} (x) = \cosh \left( {\dfrac{1.875}{l}x} \right) - \cos \left( {\dfrac{1.875}{l}x} \right) -\\ \qquad 0.7341\sinh \left( {\dfrac{1.875}{l}x} \right) + 0.7341\sin \left( {\dfrac{1.875}{l}x} \right) \\ \varphi _{22} (x) = \cosh \left( {\dfrac{4.694}{l}x} \right) - \cos \left( {\dfrac{4.694}{l}x} \right) -\\\qquad 1.0185\sinh \left( {\dfrac{4.694}{l}x} \right) + 1.0185\sin \left( {\dfrac{4.694}{l}x} \right) \end{array}\!\!\right\}$
将式 (13)$\sim$ 式 (16) 代入式 (12) 可得其离散化后的表达式,进而得到机械臂的动能为

(17)$T = \dfrac{1}{2}\int_0^l \rho A(x) \dot {\pmb r}^{\rm T} \dot{\pmb r} \text{d}x = \dfrac{1}{2}\pi \rho k_\delta \left( {1 - k_\delta } \right)^2D_0^2 \int_0^l \left[ {1 + \dfrac{\mu }{l_0 }\left( {v_1 + v_{\rm c} } \right)} \right] ^2 \dot{\pmb r}^{\rm T} \dot{\pmb r}\text{d}x $
式中, $\rho $ 和 $\mu $ 分别为臂杆的密度和泊松比. 由式 (17) 可知,机械臂系统的动能不仅取决于其刚性运动,还与运动过程中产生的弹性变形密切相关.

机械臂在运动过程中的势能包括弹性势能和重力势能,其中弹性势能包括纵向振动和横向弯曲振动两部分变形能,总弹性势能表达式为

(18)$U_s = \dfrac{1}{2}\int_0^l EA(x) \left( {\dfrac{\partial v_1 \left( {x,t} \right)}{\partial x}} \right)^2 \text{d}x + \dfrac{1}{2}\int_0^l {EI(x) } \left( {\dfrac{\partial v_2^2 \left( {x,t} \right)}{\partial x^2}} \right)^2 \text{d}x$
将式 (6) 和式 (7) 及弹性变形的离散化表达式 (13) 和式 (14) 代入式 (18),并取系统的广义 坐标为 ${\pmb q} = \left[ \theta \ \ {a_1 } \ \ {a_2 } \ \ {b_1 } \ \ {b_2 } \right]^{\rm T}$,总弹性势能可表示为

(19)$U_s = \dfrac{1}{2}\sum_{i = 1}^5 \sum_{j = 1}^5 k_{ij} q_i q_j = \dfrac{1}{2}{\pmb q}^{\rm T}{\pmb K}{\pmb q}$
其中

$ k_{ij} = \int_0^l EA(x) \dfrac{\text{d}\varphi _{1i} ( x )}{\text{d}x}\dfrac{\text{d}\varphi _{1j} (x) }{\text{d}x}\text{d}x + \int_0^l EI ( x ) \dfrac{\text{d}^2\varphi _{1i} (x) }{\text{d}x^2}\dfrac{\text{d}^2\varphi _{1j} (x) }{\text{d}x^2}\text{d}x \ \ (i =1, 2; \ j =1, 2) $

式中,$E$ 为臂杆的弹性模量,${\pmb K} $ 为广义刚度矩阵. 由刚度矩阵的表达式可知,刚度项中存在纵向变形和横向弯曲变形之间的耦合,且机械臂运动过程中结构参数随臂杆受力发生变化,导致臂杆刚度不断发生变化. 同样分析可得重力势能的表达式为

(20)$U_g = \int_0^l {\rho A(x) } gu_x \sin \theta \text{d}x + \int_0^l {\rho A(x) } gv_2 \cos \theta \text{d}x =\\ \qquad \int_0^l {\rho A(x) } g(v_1 + v_{\rm c} )\sin \theta dx + \int_0^l {\rho A(x) } gv_2 \cos \theta \text{d}x $
整个机械臂系统所受非保守外力包括关节驱动力矩 ${\pmb\tau }$,绳索作用于机械臂末端面的集中力 ${\pmb F}$,根据虚 功原理可求得相应于外力的广义力为

(21)$\delta W = \tau \delta \theta +{\pmb F}\delta {\pmb r}_{\rm e} = \sum_{i = 1}^5 {Q_i } \delta q_i$
式中,${\pmb r}_{\rm e}$ 为机械臂末端点在惯性坐标系中的位置矢量. 机械臂末端处变形前位 置矢量为 ${\pmb u}_{\rm oe} = \left[ {l_0 } \ \ 0 \right]^{\rm T}$,变形总位移为 ${\pmb u}_{\rm e} = \left[ {v_{\rm 1e} + v_{\rm ce} } \ \ {v_{\rm 2e} } \right]^{\rm T}$,$v_{\rm 1e} $,$v_{\rm ce} $,$v_{\rm 2e} $ 分别为机械臂末端处的相应变形量. 由此 ${\pmb r}_{\rm e} $ 可表示

(22)${\pmb r}_{\rm e} = {\pmb N}\left( { {\pmb u}_{\rm oe} + {\pmb u}_{\rm e} } \right) ={\pmb N}\left[ {l_0 + v_{\rm 1e} + v_{\rm ce} } \ \ {v_{\rm 2e} } \right]^{\rm T}$
设弹性绳索的刚度为 $k$,调节螺栓的移动距离为 $\Delta x$. 由于机械臂在运动过程中绳索与臂杆始终不接触,则绳索作用于机械臂末端面的集中力可表示为

(23)${\pmb F} = \left[ { - F_1 } \ \ { - F_2 } \right]^{\rm T}, \ \ F = k\Delta x$
若机械臂末端横向弯曲变形的截面转角为 $\alpha $,则由小变形假设可得到如下近似结果

(24)$\sin \alpha = \dfrac{\partial v_2 }{\partial x}, \ \ \cos \alpha = 1$
由此可得绳索作用于机械臂末端面的轴向和径向分力大小分别为

(25)$F_1 = F\cos \left( {\theta + \alpha } \right), \ \ F_2 = F \sin \left( {\theta + \alpha } \right)$
将式 (22) 和式 (23) 代入式 (21) 可求得与广义坐标 $q_i $ 对应的广义力大小 $Q_i$ $(i = 1, 2, \cdots, 5)$.

根据第二类 Lagrange 方程

(26)$\dfrac{\text{d}}{\text{d}t}\left( {\dfrac{\partial T}{\partial \dot {\pmb q}} } \right) - \left( {\dfrac{\partial T}{\partial {\pmb q}} } \right) = {\pmb Q}_F$
式中, ${\pmb Q}_F = -{\pmb K}{\pmb q} + {\pmb Q}$,${\pmb Q}$ 为上述求得的作用于机械臂上,除变形引起的弹性力以外的全部主动力对应的广义力列阵,$ - {\pmb K}{\pmb q} $为弹性力对应的广义力. ${\pmb q} = \left[ \theta \ \ {a_1 } \ \ {a_2 } \ \ {b_1 } \ \ {b_2 } \right]^{\rm T}$为广义坐标列阵,$ \dot{\pmb q}$ 为广义速度列阵. 将式 (17)、式 (19) 及式 (20) 代入式 (26) 可得机械臂的臂杆变刚度动力学模型为

(27)${\pmb M}\left( {\pmb q} \right) \ddot{\pmb q} + {\pmb C}\left( {{\pmb q}, \dot{\pmb q}} \right) \dot{\pmb q} + {\pmb K}{\pmb q}+ \dfrac{\partial {\pmb U}_g }{\partial {\pmb q}} = {\pmb Q}$
式中,${\pmb M}\left( {\pmb q} \right)$ 为 $5\times 5$ 的对称、正定质量矩阵,${\pmb C}\left( {{\pmb q},\dot {\pmb q}} \right) \dot {\pmb q}$ 为包含科氏力、离心 力的 5 阶列向量,${\pmb Q}$ 为广义力组成的 5 阶列向量,${\pmb M}\left( {\pmb q} \right)$, ${\pmb C}\left( {{\pmb q}, \dot {\pmb q}} \right)$,${\pmb K}\left( {\pmb q} \right)$ 均存在纵向变形与横向弯曲变形的耦合项. 由此可知,机械臂臂杆的变刚度动力学模型呈现出较强的非线性、强耦合和时变特性.

2 预紧力对机械臂末端振动特性的影响

为了研究机械臂在不同绳索预紧力下的振动特性,对式 (27) 臂杆的变刚度模型进行了数值仿真求解. 系统的结构参数设置如下：$l_{0} =0.6$m,$D_{0} =0.038$m,$k_{\delta } =4/38$;机械臂的材料参数设置如下： $\rho =2.9 \times 10^{3}$kg/m$^{3}$,$E =68.9$GPa,泊松比 $\mu =0.33$;重力加速度为 $g=9.8$m/s$^{2}$,机械臂关 节的驱动力矩为 $\tau (t) = 0.1\sin (2\pi t) + 0.5$. 仿真初始条件为：${\pmb q} = \left[ 0 \ 0 \ 0 \ 0 \ 0 \right]^{\rm T}$,$ \dot{\pmb q} = \left[ 0 \ 0 \ 0 \ 0 \ 0 \right]^{\rm T}$. 设置仿真时间为1s,分别对预紧力为 0,10N,20N 及 30N 下机械臂末端的振动特性进行了分析,其中预紧力为 0 和 20N 时 $X$ 方向和 $Y$ 方向加速度曲线及其频谱分别如图 4 $\sim $ 图 7 所示.

图4

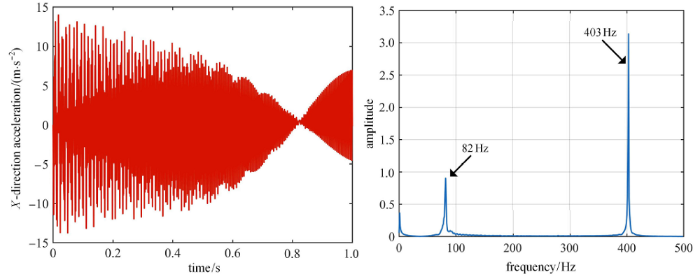新窗口打开|下载原图ZIP|生成PPT
图4预紧力为 0 时机械臂末端 $X$ 方向加速度及频谱图

Fig.4The $X$-direction acceleration and spectrum of manipulator end without preloading force

图5

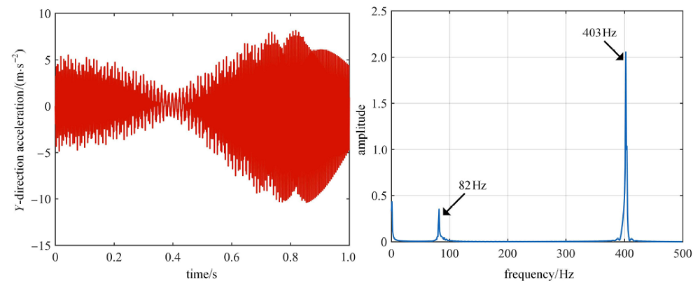
新窗口打开|下载原图ZIP|生成PPT
图5预紧力为 0 时机械臂末端 $Y$ 方向加速度及频谱图

Fig.5The $Y$-direction acceleration and spectrum of manipulator end without preloading force

图6

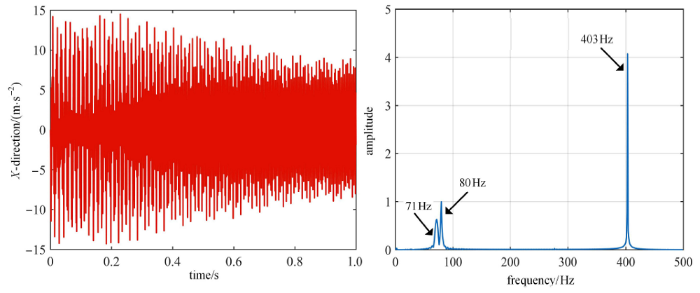
新窗口打开|下载原图ZIP|生成PPT
图6预紧力为 20N 时机械臂末端 $X$ 方向加速度及频谱图

Fig.6The $X$-direction acceleration and spectrum of manipulator end with 20N preloading force

图7

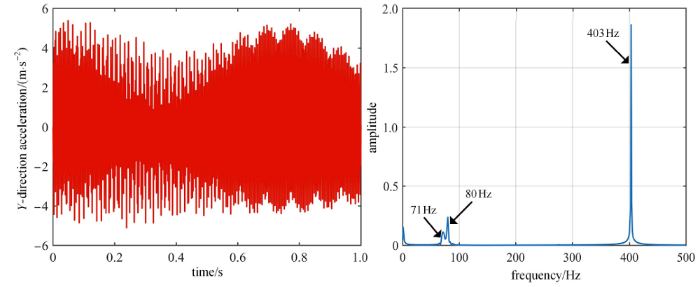
新窗口打开|下载原图ZIP|生成PPT
图7预紧力为 20N 时机械臂末端 $Y$ 方向加速度及频谱图

Fig.7The $Y$-direction acceleration and spectrum of manipulator end with 20N preloading force



根据图 4 和图 5 可知,预紧力为 0 时,机械臂末端 $X$ 方向的加速度振动范 围为 $-15$m/s$^{2}$$\sim $15m/s$^{2}$,而 $Y$ 方向的加速度振动范围为 $-10$m/s$^{2}$$\sim $8m/s$^{2}$,且两个方向的振动能量分别主要集中在 82Hz,403Hz 两个频率处. 由图 6 和图 7 可知,预紧力为 20N 时,机械臂末端 $X$ 方向的加速度振动范围为 $-15$m/s$^{2}$$\sim $15m/s$^{2}$,而 $Y$ 方向的加速度振动范围为 $-5$m/s$^{2}$$\sim $5m/s$^{2}$,两个方向的振动能量分别主要集中在 72Hz,80Hz,403Hz 三个频率处. 由此可知,随着预紧力的增大,臂杆的低阶频率略微减小,$X$ 方向的振动范围影响较小,而 $Y$ 方向的振动范围明显减小. 因此将不同预紧力下 $Y$ 方向加速度频谱进行对比分析,结果如表 1 所示.

Table 1
表1
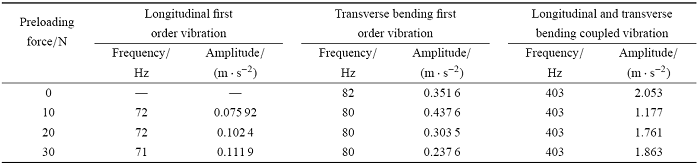
表1不同预紧力下 $Y$ 方向加速度的振动频率及其相应的幅值
Table 1The vibration frequency and corresponding amplitude of $Y$-direction acceleration under different preloading force

新窗口打开|下载CSV

由表 1 可知,预紧力存在时,低阶振动频率略微减小,高阶振动频率不变. 另外,随着预紧力的增加,纵向一阶振动及纵向和横向弯曲耦合振动的幅值略微增大,而横向弯曲一阶振动略微减小. 由于系统的振动能量主要取决于系统的低频振动,而 $Y$ 方向的振动主要为横向弯曲一阶振动,因此文中提出的基于臂杆刚度主动控制的方法在一定条件下可以抑制机械臂的弹性振动.

3 机械臂臂杆刚度主动控制下的末端振动测试

3.1 机械臂实验台设计

为验证臂杆刚度主动控制对机械臂弹性振动的抑制效果,本文设计了一种平面单自由度机械臂实验台,如图 8 所示. 该实验台主要包括基座和机械臂主体结构两大部分,其中基座具有 $90^\circ$ 的安装可调功能;机械臂的主体结构是臂杆刚化调节机构,主要含有机械臂臂杆、绳索、调节螺栓和加速度传感器等,其调节原理如图 1 所示. 在机械臂运动过程中,通过调节臂杆内绳索的预紧力来改变机械臂的受力状况,并采用拉力传感器和加速度传感器对绳索预紧力和机械臂末端加速度信号进行实时测量. 加速度传感器输入 INV-8 多功能抗混滤波放大器中,经过电荷放大器的放大作用将采集到的电信号放大,通过 INV3060F 智能信号采集分析仪采集. 拉力传感器选用蚌埠金力公司的 JL-L 型号,线性度为 0.1%,分辨率为 2000;加速度传感器选用美国 Dytran 公司的压电加速度传感器 3056C,测量频率范围为 0$\sim $5000Hz,重量为 10g,灵敏度为 15pC/g,最大加速度可达 600gpk,二者均满足机械臂的测量要求. 机械臂关节采用直流伺服电机驱动与谐波减速器传动的形式,臂杆采用铝合金型材,其意义在于研究经济型低刚度材料的刚化问题,以便利用廉价低刚度材料取代目前所应用的昂贵高刚度材料.

图8

新窗口打开|下载原图ZIP|生成PPT
图8机械臂实验装置图

Fig.8The experimental device of manipulator

3.2 机械臂末端振动特性分析

实验过程中保持电机以 400r/min 的转速稳定运行,通过调节绳索预紧力,使臂杆受力分别为 0,10N,20N,30N,40N,50N,60N,70N,测量上述 8 组绳索预紧力条件下机械臂的振动情况,可得不同预紧力下机械臂末端的加速度信号及其频谱图如图 9 所示.

图9

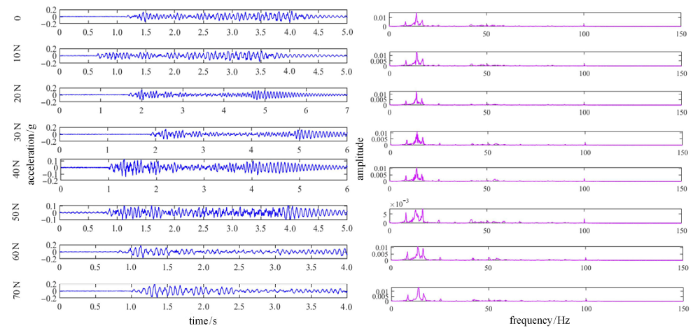新窗口打开|下载原图ZIP|生成PPT
图9不同预紧力下机械臂末端的加速度响应及其频谱图

Fig.9The acceleration and spectrum of manipulator end under different preloading force



由图 9 可知,在不同预紧力作用下,机械臂末端产生剧烈振荡,且加速度信号的振动能量主要 集中在 0$\sim $100Hz 之间,其中在频率分别为 5.8Hz,16.7Hz,25Hz 及 100Hz 附近出现4条比较明显的频谱. 根据电机的转速计算出其工频为 6.67Hz,而 5.8Hz,16.7Hz,25Hz 三种频率与电机工频的倍频接近,且由于机械臂系统各部件运动状况复杂,臂杆刚度随绳索预紧力的变化而发生变化,导致机械臂系统的频率发生变化,因此推测上述 3 种频率是由电机工频的倍频引起的. 另外,机械臂在各种预紧力下在 100Hz 处都出现幅值突变,而谐波减速的减速比为 100,故该频率是谐波减速器与外界激励产生了共振. 由以上可知,预紧力的存在对臂杆刚度影响较小,但可以使机械臂末端的振动得到一定的衰减. 不同预紧力下机械臂末端振动幅值变化范围如表 2 和图 10 所示.

Table 2
表2
表2不同预紧力情况下臂杆末端振动幅值的变化范围
Table 2The range of vibration amplitude of manipulator end under different preloading force

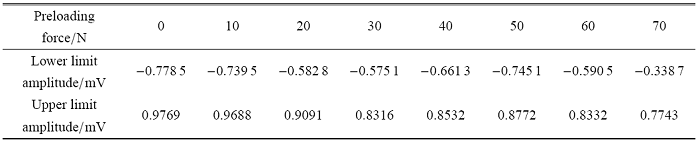新窗口打开|下载CSV

图10

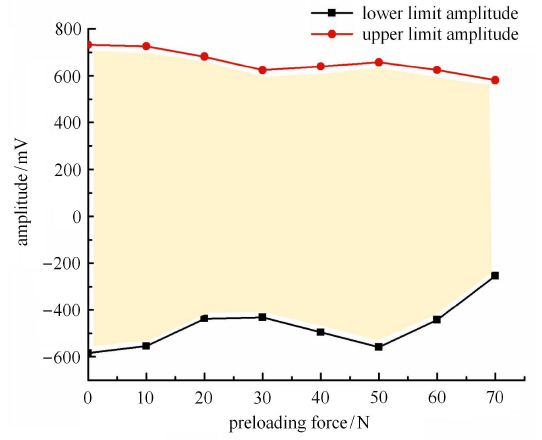新窗口打开|下载原图ZIP|生成PPT
图10机械臂末端振动幅值随预紧力的变化曲线

Fig.10The curve of vibration amplitude of manipulator end with preloading force



结合表 2 和图 10 可知,随着绳索预紧力的增加,机械臂的振动幅值变化范围呈现收拢趋势,且上限幅值和下限幅值的大小几乎都随着预紧力增加而减小.说明文中提出的臂杆刚度主动控制方法在一定条件下可以有效抑制机械臂末端的弹性振动.

4 预紧力的优化分析

绳索预紧力越大,会导致机械臂存在较大内应力,影响其结构性能,而实际机械臂在不同工况下需要满足不同的功能要求和精度要求,因此需要选择既满足精度要求又保证结构性能要求的预紧力,而不是无限增大预紧力.为了获取预紧力与机械臂末端振动响应的关系,采用响应面法来近似表示系统的极限状态函数^[33].为反映机械臂末端的振动剧烈程度,选择臂杆末端的振动幅值范围来表示性能函数,即

(28)$\phi = \sqrt {u^2 + d^2}$
式中,$\phi $ 为极限状态函数,$u$ 和 $d$ 分别上限幅值和下限幅值.为准确获得极限状态函数,采用二次多项式来近似 表示性能函数 $\tilde {\phi } ( f )$,即

(29)$\tilde {\phi } ( f) = a_0 + a_1 f + a_2 f^2$
式中,$f$ 为预紧力的大小,${\pmb a} = \left({a_0 ,} \ \ {a_1 ,} \ \ {a_2 } \right)^{\rm T}$ 为回归系数的矢量.

结合表 2 不同预紧力下机械臂末端振动的上限幅值和下限幅值,可得响应面函数的设计点和响应点如表 3 所示.

Table 3
表3
表3响应面函数的设计点和响应值
Table 3Design points and response values of the response surface function

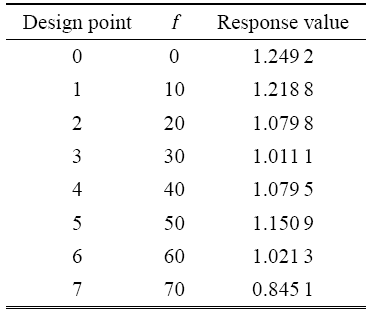新窗口打开|下载CSV

根据式 (29) 所示的响应面函数和表3所示的设计点及响应值,可以求得回归系数 ${ \pmb a}$,并由此可得响应面函数为

(30)$\tilde {\phi } ( f) = 1.249205 - 0.002298 f - 2.659379\times 10^{-5} f^2$
基于内部映射牛顿法 (interior-reflective Newton method) 的子空间置信域法 (subspace trust-region) 优化算法对式 (30) 的响应面函数进行寻优处理,将预紧力作为设计变量, 机械臂末端振动最小化作为目标函数,建立数学模型为

(31)$\left. \begin{array}{c} \min \ \ \tilde {\phi } ( f) \\ {\rm s.t.} \ \ 0 \leqslant f \leqslant 70 \end{array}\right\}$
根据式 (31) 获得的最优预紧力的大小为 70N,如图 11 所示. 说明在本文实验条件下,预紧力为 70N 时,机械臂末端的振动得到最大衰减,可以获得较高的末端精度.

图11

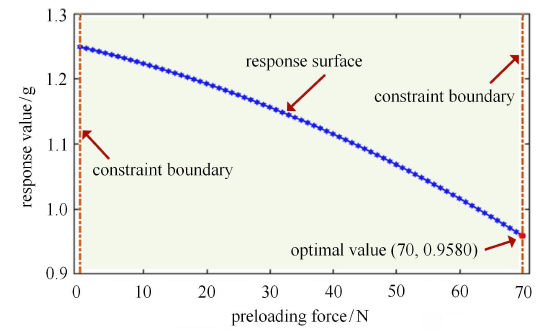新窗口打开|下载原图ZIP|生成PPT
图11预紧力与响应值关系曲线

Fig.11The curve of preloading forces and response values

5 结论

为抑制机械臂在运动过程中因臂杆柔性引发的结构变形和弹性振动,本文提出了臂杆刚度主动控制方法. 采用变形耦合法研究了机械臂运动过程中臂杆径向弯曲变形对轴向变形的影响,并基于假设模态法对柔性机械臂进行离散化描述,结合 Lagrange 方程建立了臂杆的变刚度动力学模型.

在此基础上,设计了基于臂杆刚度主动控制方法的单自由度实验台,通过调节臂杆内绳索预紧力来调节臂杆刚度,研究了机械臂在不同预紧力下末端的振动特性.

实验和仿真结果表明,随着预紧力的增加,本文提出的基于臂杆刚度主动控制的方法可以有效抑制机械臂末端的振动,提高机械臂的运动稳定性和末端定位精度.

采用响应面法建立了机械臂末端的振动响应与预紧力的关系,并基于内部映射牛顿法的子空间置信域法优化算法得到了响应面内的最优预紧力.

该研究可为机械臂的精细动力学建模提供一定的理论参考,并为研究经济型低刚度材料的刚化问题提供了方向,以利用廉价低刚度材料取代目前所应用的昂贵高刚度材料.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] Korayem MH, Shafei AM. Application of recursive Gibbs-Appell formulation in deriving the equations of motion of N-viscoelastic robotic manipulators in 3D space using Timoshenko beam theory
Acta Astronautica, 2013,83:273-294
DOIURL [本文引用: 1]

[2] Meng D, She Y, Xu W, et al. Dynamic modeling and vibration characteristics analysis of flexible-link and flexible-joint space manipulator
Multibody System Dynamics, 2018,43(4):321-347
DOIURL [本文引用: 1]

[3] Dwivedy SK, Eberhard P. Dynamic analysis of flexible manipulators, a literature review
Mechanism and Machine Theory, 2006,41(7):749-777
DOIURL [本文引用: 1]

[4] 范纪华, 章定国. 基于变形场不同离散方法的柔性机器人动力学建模与仿真
力学学报, 2016,48(4):843-856
DOIURL [本文引用: 1]
Dynamic modeling and simulation of flexible robots based on different discretization methods are investigated in this paper. Firstly, the physical model of flexible robots consisting of n links and n revolute joints is established. Secondly, the assumed mode method, finite element method, Bezier interpolation method and B-spline interpolation method are used to describe the deformation of the flexible link. Then, kinematics of both rotary-joint motion and link deformation is described by 4×4 homogenous transformation matrices, and the Lagrangian equations are used to derive the governing equations of motion of the system. The longitudinal deformation and the transverse deformation of the flexible link are considered, and the coupling term of the deformation which is caused by the transverse deformation is included in the total longitudinal deformation. Then, a software package for the dynamic simulation of the flexible robots based on the different discretization methods is developed, after that, the dynamic analysis for flexible robots are studied by three examples. The simulation results show that the computational efficiency of finite element method is the lowest, and the Bezier interpolation method and B-spline interpolation method are better than the assumed mode method in dealing with the large deformation dynamic problem. As new discretization methods, Bezier interpolation method and B-spline interpolation method can be used to describe the deformation of the flexible link, and they can be extended to the dynamic modeling for spatial flexible robots.
( Fan Jihua, Zhang Dingguo. Dynamic modeling and simulation of flexible robots based on different discretization methods
Chinese Journal of Theoretical and Applied Mechanics, 2016,48(4):843-856 (in Chinese))
DOIURL [本文引用: 1]
Dynamic modeling and simulation of flexible robots based on different discretization methods are investigated in this paper. Firstly, the physical model of flexible robots consisting of n links and n revolute joints is established. Secondly, the assumed mode method, finite element method, Bezier interpolation method and B-spline interpolation method are used to describe the deformation of the flexible link. Then, kinematics of both rotary-joint motion and link deformation is described by 4×4 homogenous transformation matrices, and the Lagrangian equations are used to derive the governing equations of motion of the system. The longitudinal deformation and the transverse deformation of the flexible link are considered, and the coupling term of the deformation which is caused by the transverse deformation is included in the total longitudinal deformation. Then, a software package for the dynamic simulation of the flexible robots based on the different discretization methods is developed, after that, the dynamic analysis for flexible robots are studied by three examples. The simulation results show that the computational efficiency of finite element method is the lowest, and the Bezier interpolation method and B-spline interpolation method are better than the assumed mode method in dealing with the large deformation dynamic problem. As new discretization methods, Bezier interpolation method and B-spline interpolation method can be used to describe the deformation of the flexible link, and they can be extended to the dynamic modeling for spatial flexible robots.

[5] Sabatini M, Monti R, Gasbarri P, et al. Adaptive and robust algorithms and tests for visual-based navigation of a space robotic manipulator
Acta Astronautica, 2013,83:65-84
DOIURL [本文引用: 1]

[6] Nanos K, Papadopoulos EG. On the dynamics and control of flexible joint space manipulators
Control Engineering Practice, 2015,45:230-243
DOIURL

[7] Hacioglu Y, Yagiz N. Fuzzy robust backstepping with estimation for the control of a robot manipulator
Transactions of the Institute of Measurement and Control, 2019,41(10):2816-2825
DOIURL

[8] Rahimi HN, Howard I, Cui L. Neural adaptive tracking control for an uncertain robot manipulator with time-varying joint space constraints
Mechanical Systems and Signal Processing, 2018,112:44-60
DOIURL

[9] Liu K, Wu Y, Zhu T, et al. Improved RBF network torque control in flexible manipulator actuated by PMAs
Robotica, 2019,37(2):264-28
DOIURL

[10] 朱安, 陈力. 配置柔顺机构空间机器人双臂捕获卫星操作力学模拟及基于神经网络的全阶滑模避撞柔顺控制
力学学报, 2019,51(4):1156-1169


( Zhu An, Chen Li. Mechanical simulation and full order sliding mode collision avoidance compliant control based on neural network of dual-arm space robot with compliant mechanism capturing satellite
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(4):1156-1169 (in Chinese))


[11] 谢立敏, 陈力. 漂浮基柔性空间机器人的鲁棒控制及振动抑制
力学学报, 2012,44(6):1057-1065
DOIURL
The dynamics modeling, algorithm design of motion control and step active suppression of joint-link double flexible vibration of free-floating flexible space robot are discussed. The system dynamic equations are established according to system momentum conservation, angular momentum conservation and Lagrange-assumed mode method. Based on singular perturbation method, the system is decomposed into a slow subsystem (represents the system's rigid motion), a fast subsystem 1 (represents the system's flexible motion caused by flexible-link), and a fast subsystem 2 (represents the system's flexible motion caused by flexible-joint). For the slow subsystem, a robust controller is proposed to compensate the uncertain parameters and rotation errors, and to realize the asymptotic tracking of the system's motion trajectory. For the fast subsystem 1, linear quadric regulator (LQR) is used to suppress the flexible vibration caused by flexible-link. For the fast subsystem 2, a feedback controller based on the velocity difference between the link and the motor is used to suppress the flexible vibration caused by flexible-joint. So the system's controller is a synthesize controller by the three controllers. The simulation results prove the controller's efficiency.
( Xie Limin, Chen Li. Robust control and vibration suppression of free-floating flexible space robot
Chinese Journal of Theoretical and Applied Mechanics, 2012,44(6):1057-1065 (in Chinese))
DOIURL
The dynamics modeling, algorithm design of motion control and step active suppression of joint-link double flexible vibration of free-floating flexible space robot are discussed. The system dynamic equations are established according to system momentum conservation, angular momentum conservation and Lagrange-assumed mode method. Based on singular perturbation method, the system is decomposed into a slow subsystem (represents the system's rigid motion), a fast subsystem 1 (represents the system's flexible motion caused by flexible-link), and a fast subsystem 2 (represents the system's flexible motion caused by flexible-joint). For the slow subsystem, a robust controller is proposed to compensate the uncertain parameters and rotation errors, and to realize the asymptotic tracking of the system's motion trajectory. For the fast subsystem 1, linear quadric regulator (LQR) is used to suppress the flexible vibration caused by flexible-link. For the fast subsystem 2, a feedback controller based on the velocity difference between the link and the motor is used to suppress the flexible vibration caused by flexible-joint. So the system's controller is a synthesize controller by the three controllers. The simulation results prove the controller's efficiency.

[12] 戈新生, 陈凯捷. 自由漂浮空间机器人路径优化的 Legendre 伪谱法
力学学报, 2016,48(4):823-831
DOIURL [本文引用: 1]
Based on the Legendre pseudospectral method, the optimal control of free floating space robots path planning problems are studied. Free floating is the working status for the space robots in task and path planning is the foundation for them to fulfil a complex space task. Because the space robots have no fixed pedestal and there are nonholonomic constraints between the manipulator and the carrier, and it makes the path planning for free floating space robots different from those on the ground. In this paper, the Legendre pseudospectral method which can realize the optimal control of free floating space robots path planning problem is presented. Firstly, a dynamic model of free floating space robots is established by using multi-body dynamics theory. The path planning problem of Bolza with certain initial and terminal stance is then obtained. Here, we select the minimum joint dissipation as performance index and consider the actual control input saturation. Then, by applying the Legendre pseudospectral method, the state and control variables are discretized at Legendre-Gauss-Lobatto (LGL) point and Lagrange interpolation polynomials are constructed to approximate the state and control variables. The problem of continuous path optimization is discretized to solve a nonlinear programming problem. Finally, results of the numerical simulation show that using the application of Legendre pseudospectral method to solve the problem of free floating space robot path planning can get the optimal trajectory of manipulator and carrier. It can fit various constraint conditions well. And this method is with fast simulation calculation, high accuracy and good real-time performance.
( Ge Xinsheng, Chen Kaijie. Path planning of free floating space robot using legendre pseudospectral method
Chinese Journal of Theoretical and Applied Mechanics, 2016,48(4):823-831 (in Chinese))
DOIURL [本文引用: 1]
Based on the Legendre pseudospectral method, the optimal control of free floating space robots path planning problems are studied. Free floating is the working status for the space robots in task and path planning is the foundation for them to fulfil a complex space task. Because the space robots have no fixed pedestal and there are nonholonomic constraints between the manipulator and the carrier, and it makes the path planning for free floating space robots different from those on the ground. In this paper, the Legendre pseudospectral method which can realize the optimal control of free floating space robots path planning problem is presented. Firstly, a dynamic model of free floating space robots is established by using multi-body dynamics theory. The path planning problem of Bolza with certain initial and terminal stance is then obtained. Here, we select the minimum joint dissipation as performance index and consider the actual control input saturation. Then, by applying the Legendre pseudospectral method, the state and control variables are discretized at Legendre-Gauss-Lobatto (LGL) point and Lagrange interpolation polynomials are constructed to approximate the state and control variables. The problem of continuous path optimization is discretized to solve a nonlinear programming problem. Finally, results of the numerical simulation show that using the application of Legendre pseudospectral method to solve the problem of free floating space robot path planning can get the optimal trajectory of manipulator and carrier. It can fit various constraint conditions well. And this method is with fast simulation calculation, high accuracy and good real-time performance.

[13] Yang X, Ge SS, He W. Dynamic modelling and adaptive robust tracking control of a space robot with two-link flexible manipulators under unknown disturbances
International Journal of Control, 2018,91(4):969-988
DOIURL [本文引用: 1]

[14] Pisculli A, Gasbarri P. A minimum state multibody/FEM approach for modeling flexible orbiting space systems
Acta Astronautica, 2015,110:324-340
DOIURL [本文引用: 1]

[15] Gao H, He W, Zhou C, et al. Neural network control of a two-link flexible robotic manipulator using assumed mode method
IEEE Transactions on Industrial Informatics, 2018,15(2):755-765
DOIURL [本文引用: 1]

[16] Soong TT, Costantinou MC. Passive and active structural vibration control in civil engineering
Springer, 2014
[本文引用: 1]

[17] Housner GW, Bergman LA, Caughey TK, et al. Structural control: past, present, and future
Journal of Engineering Mechanics, 1997,123(9):897-971
DOIURL [本文引用: 1]

[18] Casciati F, Rodellar J, Yildirim U. Active and semi-active control of structures-theory and applications: A review of recent advances
Journal of Intelligent Material Systems and Structures, 2012,23(11):1181-1195
DOIURL [本文引用: 1]
It is internationally recognized that structural control was introduced in civil engineering through a pioneering article by Yao and through the implementations promoted by Kobori. The concepts of active and semi-active structural control in civil and infrastructure engineering date back 40 years and much progress has been recorded during these four decades. Periodically, state-of-the-art manuscripts have been published and technical books were also printed to testify the maturation of the topic. This article only covers the period from the second semester of 2009 to the first semester of 2011, emphasizing the developments in terms of theoretical, numerical and experimental studies, as well as the use of control algorithms and devices in actual implementations. It is observed that there are still several operational limitations to prevent from the expected growth of the applications in standard design. Nevertheless, some innovative concepts help to foresee future developments within special sectors of applications.

[19] Lin CC, Lu LY, Lin GL, et al. Vibration control of seismic structures using semi-active friction multiple tuned mass dampers
Engineering Structures, 2010,32(10):3404-3417
DOIURL

Abstract

An energy dissipation mechanism is an indispensable part of a tuned mass damper system, since it reduces the mass stroke of a system to a manageable level. Dry friction is a natural source of energy dissipation for tuned mass dampers. Nevertheless, there is no difference between a friction-type tuned mass damper and a dead mass added to the primary structure if static friction force inactivates the mass damper. To overcome this disadvantage, this paper proposes a novel semi-active friction-type multiple tuned mass damper (SAF-MTMD) for vibration control of seismic structures. Using variable friction mechanisms, the proposed SAF-MTMD system is able to keep all of its mass units activated in an earthquake with arbitrary intensity. A comparison with a system using passive friction-type multiple tuned mass dampers (PF-MTMDs) demonstrates that the SAF-MTMD effectively suppresses the seismic motion of a structural system, while substantially reducing the strokes of each mass unit, especially for a larger intensity earthquake. This means that applying the SAF-MTMD requires less installation space than a PF-MTMD system. The current study also shows that the SAF-MTMD performs well in a low-intensity earthquake, in which the PF-MTMD is inactivated due to friction.

[20] Bian Y, Gao Z, Hu J, et al. A semi-active control method for decreasing longitudinal torsional vibration of vehicle engine system: Theory and experiments
Journal of Sound and Vibration, 2019,439:413-433
DOIURL [本文引用: 1]

[21] Lew JS, Juang JN, Loh CH. Adaptive vibration control of structures under earthquakes//Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2017, Portland, Oregon, United States
International Society for Optics and Photonics, 2017,10168:101682D
[本文引用: 1]

[22] Li L, Liang H. Semiactive control of structural nonlinear vibration considering the MR damper model
Journal of Aerospace Engineering, 2018,31(6):1-9
[本文引用: 1]

[23] Mevada SV, Jangid RS. Seismic response of torsionally coupled building with passive and semi-active stiffness dampers
International Journal of Advanced Structural Engineering (IJASE), 2015,7(1):31-48
DOIURL [本文引用: 1]

[24] Pu H, Yuan S, Peng Y, et al. Multi-layer electromagnetic spring with tunable negative stiffness for semi-active vibration isolation
Mechanical Systems and Signal Processing, 2019,121:942-960
DOIURL [本文引用: 1]

[25] 汪志昊, 杨亚彬. 结构振动的负刚度控制
华北水利水电学院学报, 2012,33(2):26-30
[本文引用: 1]

( Wang Zhihao, Yang Yabin. Negative Stiffness Control of Structural Vibration
Journal of North China Institute of Water Conservancy and Hydroelectric Power, 2012,33(2):26-30 (in Chinese))
[本文引用: 1]

[26] 龚微, 熊世树. 拟负刚度隔震 Benchmark 模型减震效果及适应性
华中科技大学学报(自然科学版), 2015,43(8):7-11
[本文引用: 1]

( Gong Wei, Xiong Shishu. Effectiveness and adaptability analysis of smart base isolated benchmark model with pseudo-negative stiffness control
J Huazhong Univ of Sci & Tech (Natural Science Edition), 2012,33(2):26-30 (in Chinese))
[本文引用: 1]

[27] 耿仕能, 王友渔, 陈丽莎 等. 变刚度连续型机械臂设计与控制
宇航学报, 2018,39(12):1391-1400
[本文引用: 1]

( Geng Shineng, Wang Youyu, Chen Lisha, et al. Design and control of a continuum arm with variable stiffness
Journal of Astronautics, 2018,39(12):1391-1400 (in Chinese))
[本文引用: 1]

[28] Petit F, Daasch A, Albu-Sch?ffer A. Backstepping control of variable stiffness robots
IEEE Transactions on Control Systems Technology, 2015,23(6):2195-2202
DOIURL [本文引用: 1]

[29] Lin GL, Lin CC, Chen BC, et al. Vibration control performance of tuned mass dampers with resettable variable stiffness
Engineering Structures, 2015,83:187-197
DOIURL [本文引用: 1]

[30] Martins JM, Mohamed Z, Tokhi MO, et al. Approaches for dynamic modelling of flexible manipulator systems
IEE Proceedings-Control Theory and Applications, 2003,150(4):401-411
[本文引用: 1]

[31] 方建士, 章定国, 王宏伟. 旋转柔性悬臂梁的固有频率分析
机械强度, 2013,35(3):242-248
[本文引用: 1]

( Fang Jianshi, Zhang Dingguo, Wang Hongwei. Natural frequencies analysis of a rotating flexible cantilever beam
Journal of Mechanical Strength, 2013,35(3):242-248 (in Chinese))
[本文引用: 1]

[32] 郭振锋, 金国光, 畅博彦 等. 刚-柔性机械臂动力学建模及其动力学特性研究
天津工业大学学报, 2013,32(1):70-74
[本文引用: 1]

( Guo Zhenfeng, Jin Guoguang, Chang Boyan, et al. Research of dynamic modeling and performance for rigid-flexible manipulators
Journal of Tianjin Polytechnic University, 2013,32(1):70-74 (in Chinese))
[本文引用: 1]

[33] Zhang Y, Gu Y, Liu T, et al. Dynamic behavior and parameter sensitivity of the free-floating base for space manipulator system considering joint flexibility and clearance
Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2019,233(3):895-910
[本文引用: 1]