 ,*,?,2), 张莉**
,*,?,2), 张莉**MULTI-MODE OSCILLATIONS AND HAMILTON ENERGY FEEDBACK CONTROL OF A CLASS OF MEMRISTOR NEURON$^{\bf 1)}$
An Xinlei ,*,?,2), Zhang Li**
,*,?,2), Zhang Li**通讯作者: 2)安新磊,副教授,主要研究方向:非线性动力学. E-mail:anxin1983@163.com
收稿日期:2020-02-11接受日期:2020-04-19网络出版日期:2020-07-18
| 基金资助: |
Received:2020-02-11Accepted:2020-04-19Online:2020-07-18
作者简介 About authors

摘要
根据法拉第电磁感应定律,在离子穿越细胞膜或者在外界电磁辐射下,细胞内外的电生理环境会产生电磁感应效应,继而会影响神经元的电活动行为. 基于此,本文考虑电磁感应影响下的 Hindmarsh-Rose (HR) 神经元模型,研究了其混合模式振荡放电特征,并设计一个 Hamilton 能量反馈控制器,将其控制到不同的周期簇放电状态. 首先,通过理论分析发现磁通 HR 神经元系统的 Hopf 分岔使其平衡点的稳定性发生了改变,并产生极限环,进而研究了 Hopf 分岔点附近膜电压的放电特征. 基于双参数数值仿真发现该系统具有丰富的分岔结构,在不同的参数平面上存在倍周期分岔、伴有混沌的加周期分岔、无混沌的加周期分岔以及共存的混合模式振荡. 最后,为了有效控制膜电压的混合模式振荡,利用亥姆霍兹理论计算出磁通 HR 神经元系统的 Hamilton 能量函数并设计 Hamilton 能量反馈控制器,通过数值仿真分析了膜电压在不同反馈增益下的簇放电状态,发现该控制器能够有效地控制膜电压到不同的周期簇放电模式. 本文的研究结果为探究电磁感应下神经元的分岔结构及其能量控制领域提供了有用的理论支撑.
关键词:
Abstract
According to Faraday's electromagnetic induction law, the electrophysiological environment in and out the cell will produce electromagnetic induction effects in the case of ions penetrating the cell membrane or in the case of being exposed to external electromagnetic radiation, which will affect the electrical activity behavior of neural systems. Based on this principle, this paper studies the mixed-mode oscillation discharge characteristics of the Hindmarsh-Rose(HR) neuron model (here we call it as magnetic flux HR neuron model) with the influence of electromagnetic induction, and designs a Hamilton energy feedback controller to manage the mode to different periodic cluster discharge states. First, through theoretic analysis, it is found that the stability of equilibrium point in the magnetic flux HR neuron model is changed by the occurrence of Hopf bifurcation in the magnetic flux HR neuron model and a limit cycle is generated. Besides, some discharge characteristics of the membrane voltage near the Hopf bifurcation point are also discussed in detail. Then, it is also displayed there are abundant bifurcation structures in the magnetic flux HR neuron model based on the two-parameter numerical simulations, which includes multi-period bifurcation, period-adding bifurcation with chaos, period-adding bifurcation without chaos and co-existing mixed-mode oscillations in different initial conditions. At last, with the purpose of controlling the mixed-mode oscillation of membrane voltage, the Hamilton energy function is calculated by utilizing the Helmholtz theorem, and a Hamilton energy feedback controller is designed further. Additionally, it can be seen that the controller can effectively control the membrane voltage in different periodic clustering discharge modes, with the analysis of the discharge states of membrane voltage under different feedback gains in view of the numerical simulation. The results of this paper provide a useful theoretical support for the study of bifurcation structure in artificial neuron system under electromagnetic induction and the field of energy control related to the neurons.
Keywords:
PDF (31779KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
安新磊, 张莉. 一类忆阻神经元的电活动多模振荡及Hamilton 能量反馈控制$^{\bf 1)}$. 力学学报[J], 2020, 52(4): 1174-1188 DOI:10.6052/0459-1879-20-035
An Xinlei, Zhang Li.
引言
神经系统以神经元的不同放电活动对信息进行编码、传递和解码,由此实现神经系统信息的产生、整合和传输[1]. 神经元即神经细胞,是神经系统传输信息的最基本的元素,只有清晰地了解其各种环境下的放电模式,才能更好地理解神经网络以及各组织细胞的运行规律. 各种神经元的建立在很大程度上有助于了解神经元的放电机理,Hodgkin 和 Huxley 在 1952 年提出的 Hodgkin-Huxley (HH) 模型开创了神经元模型建立的新纪元,此后各种改进的数学模型如 Morris-Lecar (ML)、FitzHugh-Nagumo (FHN)、HR 神经元系统相继建立. ****们可以从数学和物理的角度分析神经元的放电行为[2-6].目前研究表明,外界电磁场对神经系统接收、处理和传递生理信息有着重要的影响[7-8],研究外界电磁场对生物神经元的作用机制已成为近年来备受关注的课题. 马军教授在文献[9] 中考虑到离子穿越细胞膜以及外界电磁辐射下,细胞内外的电生理环境会发生改变而产生电磁感应,进而会影响神经元的放电模式,首次提出用磁通来描述电磁场的作用,改进了一个四维 HR 神经元模型,并进行了初步讨论. 随后,其团队讨论了该模型的动力学性质[10-11],通过改变初始状态可以观察到多种电活动模式,如静息态、峰放电态、簇放电态、混沌放电等,同时指出,该改进模型的网络也可用于研究大脑和中枢神经系统神经元的集体行为,并可以解释电磁辐射诱发疾病的潜在机制.
神经元模型在各种不同的放电活动中,加周期分岔是重要的分岔和神经放电节律转迁类型之一[12],对其深入研究将为认识节律转迁的理论框架及理解神经编码的机制提供了一定的依据. 因此运用非线性理论及其数值仿真探究电磁场下神经元膜电压的放电活动有着重要的实际意义[13-16]. Chen 等[13]提出了一种具有线平衡点的三维耦合神经元磁控忆阻 HNN 模型,研究了在双参数平面上 Fold 和 Hopf 分岔集和不同的稳定性区域,发现具有不同振幅吸引子共存现象. Bao 等[14]利用阈值磁控忆阻器产生的电磁感应电流代替二维 (HR) 神经元模型中的外电流,建立了具有全局隐藏模式振荡的三维HR神经元模型,并进行了相应的数值模拟,研究发现,该模型存在单稳态和双稳态的隐藏簇放电模式. 混合模式振荡是一种复杂的振荡模式,是神经科学的一个研究热点[17-18]. 文献[17] 介绍了神经元系统中混合模式振荡的研究情况和研究方法,并介绍了几种神经元模型中混合振荡模式的研究进展. 文献[18] 研究了在反馈参数和外界刺激电流变化下时具有磁流作用的 Chay 神经元放电,并发现了丰富的复杂混合模式振荡. 因此,对神经元系统多种模式放电行为的研究可以使我们进一步了解神经元的节律变化,本文借助双参数分岔对电磁感应下的HR神经元系统中的复杂加周期振荡和混合模式振荡进行深入研究.
神经元不同模式的放电状态离不开外界能量的触发,神经元信号的传输、转化和迁移需要能量消耗[19-22]. 持续的能量供应对维持系统的振荡是至关重要的,否则振荡行为将会减弱直至消失[19]. 磁通 HR 神经元模型在各种外界刺激下具有不同的分岔模式及其能量特性,研究发现 Hamilton 能量函数中的负反馈能有效地稳定混沌运动轨迹[20]. 此外,可以对具有不同吸引子的混沌系统进行哈密顿能量计算,并利用能量反馈有效控制系统中的混沌态[21]. 文献[23] 中提出了一种 Hamilton 能量反馈控制方法,可以在控制非线性系统到期望状态的同时,控测系统能量的转换和迁移.
基于上述讨论,本文主要从数学的角度对磁通 HR 神经元模型的多模式放电行为进行全面分析,发现了磁通 HR 神经元模型具有丰富的分岔结构并对其进行 Hamilton 能量控制. 通过数值仿真在双参数空间上的分岔结构,发现该系统存在含混沌的倍周期分岔、无混沌的加周期分岔、混合模式振荡以及共存模式振荡. 其次,对磁通 HR 神经元模型构建 Hamilton 能量反馈控制器,研究结果发现该控制器可以有效地将混合模式振荡控制到多种周期的簇放电态. 这些都是神经元异常放电研究领域的前沿课题,因此有必要对其进行深入研究.
1 模型描述及其分岔分析
根据电磁感应定理,引入磁通后的HR神经元模型如下 (本文称为磁通 HR 神经元系统)式中,变量 $x, y, z, \phi $ 分别表示神经元的膜电位、恢复变量的慢电流、自适应电流和穿过细胞膜的磁通量. 参数 $a, b$ 表示快速离子通道的激活和失活,$r$ 为自适应电流变化速度的控制,与钙离子浓度有关,$s$ 描述了慢离子通道的激活. $\chi _0 $ 表示钙离子静息电位,$I$ 表示外界的刺激电流. $k_1 x, k_2 \phi $ 分别表示膜电压与外界磁通量电磁感应的变化速率和漏磁通,$k_1 , k_2 $ 为变化系数. $k_0 W(\phi )x$ 表示磁通量对膜电压的反馈电流,$k_0 $ 为调制强度. $W(\phi ) = \alpha + 3\beta \phi ^2$ 是磁控忆阻器的忆导,其中 $\alpha ,\beta $ 是确定的常数. 常规地,$a,b,c,d,s$ 取 1984 年 Hindmarsh 和 Rose[24]建立 HR 神经元系统时设定的基准值 $a = 1.0$,$b = 3.0$,$c = 1.0$,$d = 5.0$,$s = 4$. $r,\chi _0 ,\alpha ,\beta ,k_1 ,k_2 $ 可微调,其中 $r$ 一般在 $10^{ - 3}$ 量级取值,本文取值为 $r = 0.006$,$\chi _0 = - 1.61$,$\alpha = 0.2$,$\beta = 0.03$,$k_1 = 0.9$,$k_2 = 0.5$. $I$ 经常被用来作为分岔参数来研究HR神经元的放电模式,通常在 $[ - 10,10]$ 内取值.
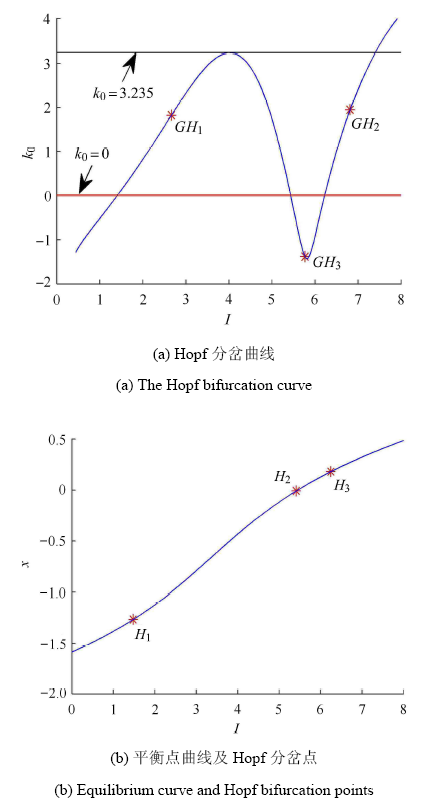
正常情况下,系统 (1) 膜电压的放电活动会受到刺激电流 $I$ 及其反馈增益 $k_0 $ 变化的影响. 本文基于 Matcont 软件分析了随着参数 $I,k_0 $ 同时变化时的 Hopf 分岔点的分布,如图 1(a) 所示. 由图可知,随着外界刺激电流 $I$ 的变化,当 $0 \leqslant k_0 < k_0^* = 3.235$ 时,系统 (1) 存在 3 个 Hopf 分岔点. 当 $k_0 = k_0^* $ 时,系统 (1) 存在两个 Hopf 分岔点. 当 $k_0 > k_0^* $ 时,系统 (1) 将出现一个 Hopf 分岔点. 不妨取 $k_0 = 0.16$, 此时系统 (1) 的平衡点随外界刺激电流 $I$ 的变化曲线如图 1(b) 所示,图中的蓝色曲线表示系统的平衡点,红色点 $H_i (i = 1,2,3)$ 表示 Hopf 分岔点. 通过数值计算得出在分岔点 $H_1 ,H_2 ,H_3$ 处的平衡点及其相应的特征根分别为
$I_{H_1 } = 1.519729 $
$ p_{H_1 } = ( - 1.240054, - 6.688672, 1.479783, - 2.232098)$
$\lambda _{H_1 }^{1,2} = \pm 0.042391i $
$ \lambda _{H_1 }^3 = - 0.494445,\lambda _{H_1 }^4 = - 13.168829$
$I_{H_2 } = 5.398755 $
$ p_{H_2 } = ( - 0.010282, 0.999471, 6.398874, - 0.018507)$
$\lambda _{H_2 }^{1,2} = \pm 0.147547i $
$ \lambda _{H_2 }^3 = - 0.499992,\lambda _{H_2 }^4 = - 1.100019$
$\lambda _{H_2 }^{1,2} = \pm 0.147547i, \lambda _{H_2 }^3 = - 0.499992 $
$ \lambda_{H_2 }^4 = - 1.100019, \lambda _{H_3 }^{1,2} = \pm 0.949442i $
$ \lambda _{H_3 }^3 = - 0.032424,\lambda_{H_3 }^4 = - 0.500731$
由此可知,系统 (1) 在平衡点 $p_{H_1 } , p_{H_2 } , p_{H_3 }$ 处都有一对实部为零的共轭特征根,从而验 证了系统 (1) 在分岔点 $H_1 ,H_2 ,H_3 $ 处发生了 Hopf 分岔.此外,由 Matcont 软件可以计算出相应的第一 Lyapunov 系数[25]
$ L_{H_1 } = 0.000623 > 0 \\ L_{H_2 } = - 3.416041 < 0 \\ L_{H_3 } = 0.852002 > 0 $
当第一 Lyapunov 系数小于零时,其 Hopf 分岔是超临界的;反之,Hopf 分岔是亚临界的. 因此,系统 (1) 在分岔点 $H_1 ,H_3 $ 处发生亚临界 Hopf 分岔,在分岔的 $H_2$ 处发生超临界 Hopf 分岔. 由于系统 (1) 的 Hopf 分岔使其平衡点的稳定性发生了改变,并产生相应的极限环,因此有必要研究 Hopf 分岔点附近膜电压的放电特征.
图1
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图1系统 (1) Hopf 分岔曲线、平衡点曲线和 Hopf 分岔点
Fig.1The Hopf bifurcation curve, equilibrium curve and Hopf bifurcation points
2 双参数变化下伴有混沌的倍周期分岔模式
由于系统 (1) 在外界刺激发生改变时,很难保持系统参数固定不变,通常情况下系统 (1) 中的几个或者多个参数同时在特定范围内发生变化. 因此,研究双参数平面上膜电压的放电活动将更具有现实意义. 在本节中,主要分析了双参数平面上系统 (1) 的膜电压分岔行为,根据不同的双参数组合,系统 (1) 在两个参数空间中的分岔图如图 2 所示,图中用不同的颜色绘制膜电压的不同的放电状态,并且图中右侧颜色栏用相应的数字进行标记 (如用 0 表示静息态,数值 1 表示尖峰放电,数值 2 表示周期 2 簇放电态,白色区域表示周期大于等于 20 簇放电或者混沌放电态).图2
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图2系统 (1) 关于 $x$ 的双参数分岔图
Fig.2Two-parameter bifurcation diagram of system (1) versus $x$
图 2(a)$\sim$图 2(e) 显示的是伴有混沌窗口的倍周期分岔模式. 当以 $d$ 和 $I$ 作为参数变量时,在 $d \in [4.4,5.8],I \in [2.6,4]$ 的参数平面上,相应的周期分岔图如图 2(a) 所示,系统 (1) 呈现出丰富而复杂的放电特性. 沿着图 2(a) 中黑线从左下到右上的方向,膜电压 $x$ 的倍周期分岔模式为:从周期 1 的尖峰放电由倍周期分岔通向混沌态 $ \to $ 从周期 3 簇放电由倍周期分岔通向混沌态 $ \to $ 从周期 4 簇放电由倍周期分岔通向混沌态 $ \to \cdots \to $ 从周期 19 簇放电由倍周期分岔通向混沌态. 此外,从图 2(a) 中不难看出,在上述分岔模式过程中,随着周期数的增加,相应的周期的颜色带的宽度而逐渐变窄,并且相应的混沌窗口宽度也逐渐变小. 图 2(b) $\sim$ 图 2(e) 所示的参数平面上也具有类似分岔结构,都存在"梳子状"的混沌区域,并且有规律地分布着"舌形"周期窗口,这些周期窗口通过倍周期分岔结构与混沌区域相连接. 在图 2(f) 和图 2(g) 中,分岔结构比较复杂,即都存在一个半环形的混沌区域,并且包括着半圆形的周期 5 簇放电区域,其外围有规律地分布着"舌形"周期窗口,这些周期窗口也是通过倍周期分岔结构与混沌区域相连接.
图 2(h) 为无混沌窗口的加周期分岔结构. 在参数 $c \in [0.2,0.9]$, $d \in [5,6.2]$ 的平面上,参数 $c$ 对系统 (1) 分岔结构影响不大,此时膜电压分岔模式取决于参数 $d$ 的取值,当参数 $d$ 由小变大时,膜电压 $x$ 分岔模式为:周期 2 簇放电态 $ \to $ 周期 3 簇放电态 $ \to \cdots \to $ 周期 18 簇放电态. 随着这些周期数的增大,其周期窗口的颜色带的宽度逐渐减小.
以参数 $d$ 为变量时,当保持参数 $I = 1.0769d + 2.1384$ 不变,沿图 2(a) 中的黑线所示的方向,此时系统 (1) 膜电压峰峰间期 (ISI) 分岔图和变量 $x$ 的分岔图如图 3 所示. 从图中可直观看出,随着参数 $d$ 的增大,膜电压 $x$ 放电模式为:尖峰放电态 $ \to $ 由倍周期分岔通向混沌 $ \to $ 周期 3 簇放电态 $ \to $ 由倍周期分岔通向混沌 $ \to $ 周期 4 簇放电态 $ \to $ 由倍周期分岔通向混沌放电态 $ \to \cdots \to $ 加周期簇放电态. 系统 (1) 每经历一次混沌放电,放电的周期比混沌放电前的周期大 1,并且随着周期的增大,相应的周期窗口及其混沌窗口逐渐变窄. 从图 3 中还可以观察到,当放电周期大于 15 时,混沌窗口几乎消失,此时系统 (1) 的膜电压进入加周期分岔模式,图 4 为图 3 所对应的最大 Lyapunov 指数图.
图3
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图3系统 (1) 关于参数 $d$ 的分岔图
Fig. 3Bifurcation diagram of system (1) versus parameter $d$
图4
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图4对应于
Fig. 4The maximum Lyapunov exponent graph corresponds to
3 混合模式振荡及其共存模式震荡
3.1 混合模式振荡
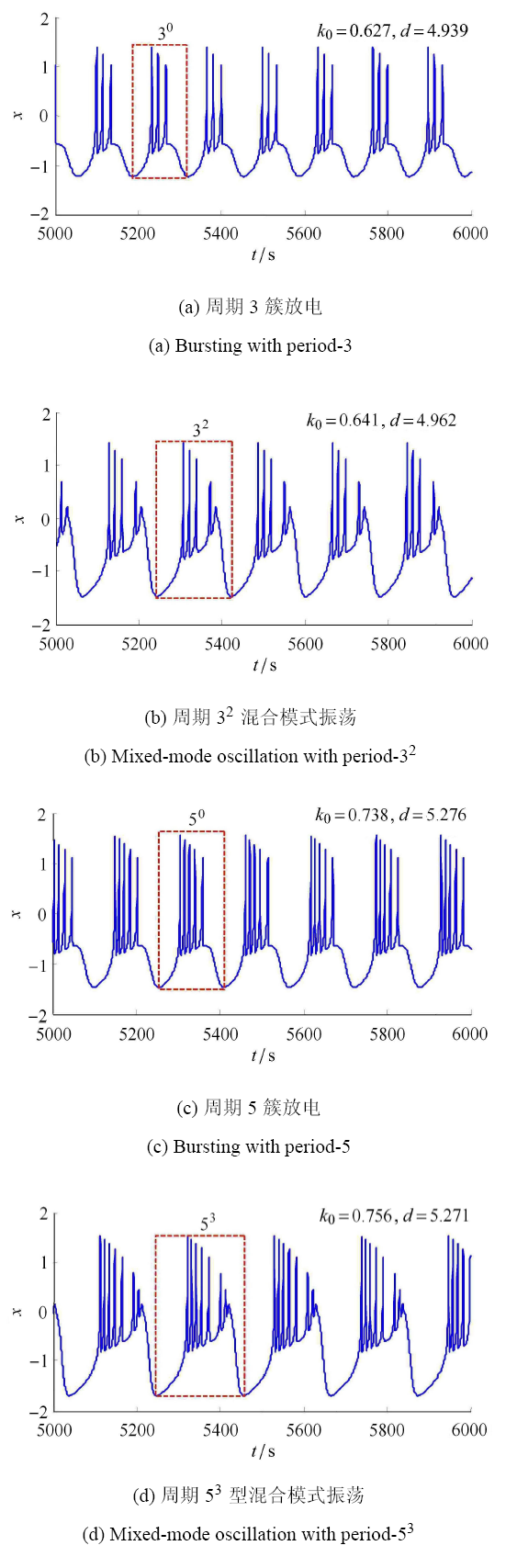
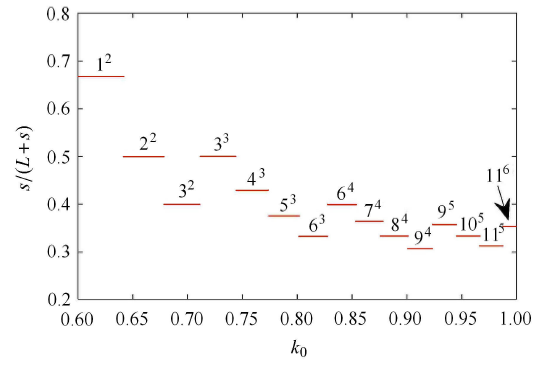
混合模式振荡是非线性动力系统中特有的复杂模式振荡[26],常常存在神经元系统中,即在一个周期振荡内,它是由一系列的大振幅振荡和小振幅振荡组成的,一般用符号 $L^s$ 来描述这种振荡模式,其中 $L$ 表示大振幅的数目,$s$ 表示小振幅的数目,而 $L^0$ 型的振荡模式表示没有小振幅振荡周期为 $L$ 簇发电模式.图 5 显示了含有混合模式振荡的周期分岔图,与图 2 中各图相比较,图 5 出现了"周期层错位"特有的现象. 在图 5 所示的 左侧区域,参数 $(k_0 ,d)$ 分别取值 $(0.627,4.939)$ 和 $(0.738,5.276)$ 时,系统 (1) 中膜电压分别处于周期 3、周期 5 簇放电态,其相应膜电压 $x$ 时间响应分别如图 6(a) 和图 6(c) 所示. 在图 5 中"周期层错位"的右侧区域,当参数 $(k_0 ,d)$ 分别取值 $(0.641, 4.962)$ 和 $(0.756,5.271)$ 时,系统 (1) 中膜电压 $x$ 分别处于周期$3^2$和周期 $5^3$ 的混合模式振荡放电态,其相应膜电压 $x$ 时间响应分别如图 6(b) 和图 6 (d) 所示. 当保持参数 $d = 3.5k_0 + 2.5$ 不变,以参数 $k_0 $ 为变量,沿图 5 中白线所示的方向,系统 (1) 膜电压 $x$ 的发放数 (在一个周期内小振幅数占总振幅数的比例) 随参数 $k_0 $ 变化如图 7 所示,由此可知,膜电压 $x$ 的混合振荡模式变化为: $1^2 \to 2^2 \to 3^2 \to 3^3 \to 4^3 \to 5^3 \to 6^3 \to 6^4 \to 7^4 \to 8^4 \to 9^4 \to 9^5 \to 10^5 \to 11^5 \to 11^6$. 由于神经元相关的疾病通常都是神经元异常振荡模式放电引起的,这与本节研究的系统 (1) 存在混合模式振荡放电具有一定的相关性,因此控制系统 (1) 振荡模式放电到期望的放电状态具有重要的实际意义.
图5
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图5$k_0 \in [0,1],d \in [4.6,6]$ 时系统 (1) 关于 $x$ 的双参数分岔图
Fig.5Two-parameter bifurcation diagram of system (1) versus $x$ when $k_0 \in [0,1],d \in [4.6,6]$
图6
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图6系统 (1) 的时间响应图
Fig.6Time response diagram of system (1)
图7
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图7膜电压的发放数关于参数 $k_0 $ 分岔图
Fig.7The spike count of membrane voltage versus parameter $k_0 $
3.2 共存混合模式振荡
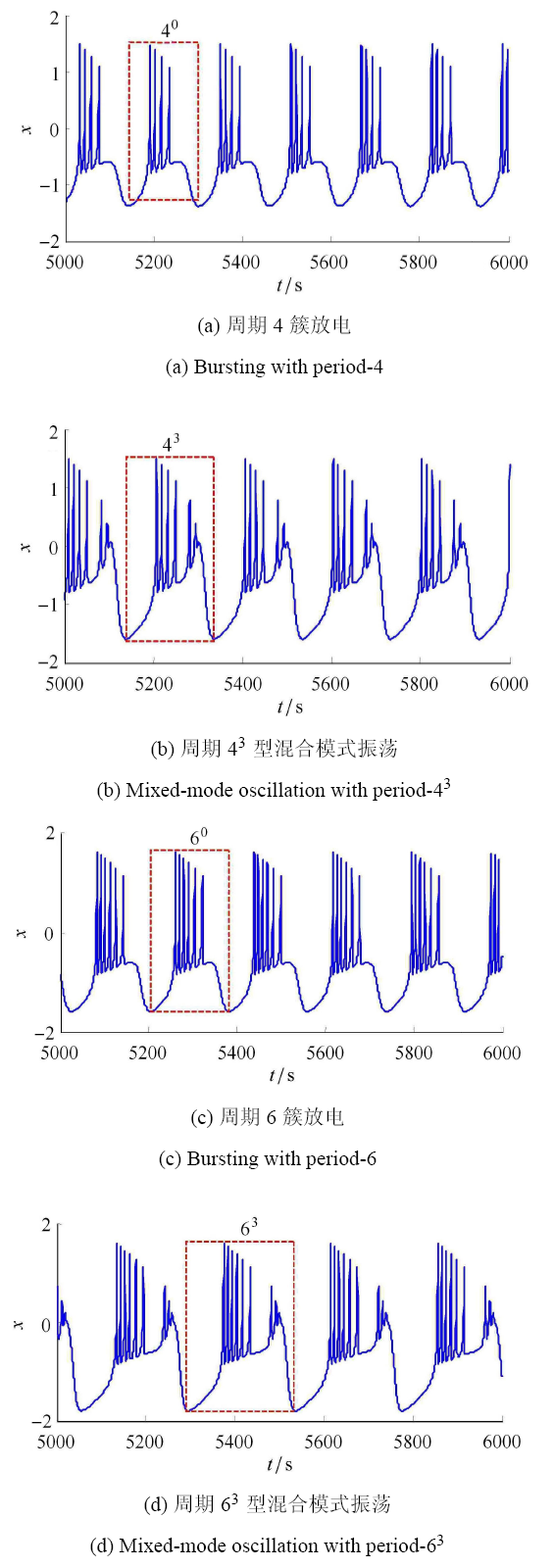
通过数值模拟发现, 这些"周期层错位"现象 是由于系统 (1) 发生了混合模式振荡产生的,即在图 5 中左侧区域 为簇放电模式,右侧区域为混合振荡模式. 此外,在这些"周期层错位"处,膜电压处于簇放电模式和混合模式振荡共存状态.当参数 $(k_0 ,d)$ 取 $(0.6994, 5.1330)$ 时,系统 (1) 将出现初值为 $(0.1,0,0,0.1)$ 时的周期 4 和初值为 $(2,0,0,0.1)$ 时的周期 $4^3$ 混合模式振荡共存状态,其膜电压 $x$ 的时间响应如图 8(a) 和图 8(b) 所示. 当参 数 $(k_0,d)$ 取 $(0.7948,5.4140)$ 时,系统 (1) 将出现初值为 $(0.1,0,0,0.1)$ 时的周期 6 和初值为 $(2,0,0,0.1)$ 时的周期 $6^3$ 的混合模式振荡共存状态,其膜电压 $x$ 的时间响应如图 8(c) 和图 8(d) 所示. 当参数 $(k_0 ,d)$ 取两种不同的值时,系统 (1) 的两种初值在 $x - \phi $ 和 $y - \phi$ 平面上的吸引域如图 9 所示.
图8
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图8系统 (1) 的时间响应图
Fig.8Time response diagram of the system (1)
图9
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图9系统 (1) 在不同初值时的吸引域
Fig.9The attractive basins of system (1) under different initial values
4 基于 Hamilton 能量的反馈控制
神经元系统中膜电压的不同放电模式、膜电位的迁移和转换都需要能量来维持,持续的能量供应对神经元系统 的放电是至关重要的,否则振荡行为将会减弱或者消失. 对于任意自治的动力系统式中,${\pmb X} \in {\pmb R }^n$ 为状态向量,$f({\pmb X} ) \in {\pmb R }^n$ 为连续非线性函数.
王春妮等[21]基于亥姆霍兹理论论证了一般广义动力学系统的哈密顿能量计算方法,对无量纲动力学系统以及非线性 振荡电路的 Hamilton 能量函数的计算进行了详细介绍. 基于亥姆霍兹理论可知,向量函数 $f({\pmb X})$ 可分解为
式 (3) 可以利用狄拉克- $\delta $ 和矢量的运算规则来证明,其中 $f_{\rm c} ({\pmb X} )$ 表示漩涡场,它与系统的 Hamilton 能量函数$H$的关系满足:$\nabla{\pmb H }^{\rm T}f_{\rm c} ({\pmb X }) = 0$. 而 $f_{\rm d} ({\pmb X })$ 表示梯度场,它可以对系统运行的相轨迹进行约束,并且满足 Hamilton 能量导数
能量的改变来自源于力场的做功,能量函数$H$满足式 (3) 和式 (4). 由此对于系统 (1) 可表示为
$ \dot{\pmb X} = \left[ \begin{array}{l} \dot {x} \\ \dot {y} \\ \dot {z} \\ \dot {\phi } \end{array} \right] = f({\pmb X} ) = \left[ \begin{array}{c} {y - z + I} \\ {c - bx^2} \\ {rs(x - \chi _0 )} \\ {k_1 x} \end{array} \right] + \left[ \begin{array}{c} {bx^2 - ax^3 - k_0 W(\phi )x} \\ { - y} \\ { - rz} \\ { - k_2 \phi } \end{array} \right] = f_{\rm c} ({\pmb X }) + f_{\rm d} ({\pmb X }) $
由关系式 $\nabla {\pmb H }^{\rm T}f_{\rm c} ({\pmb X }) = 0$ 可得到
从物理角度看,在神经元电路中,电容器和感应线圈是主要的电子元件,电容可以存储电场能量 $(1 /2CV^2)$,感应线圈可以存储磁场能量 $(1/ 2LI^2)$,这些物理场能量 $(H = 1/2CV^2 + 1/2 LI^2)$ 经过标度变换后就是无量纲的 Hamilton 能量. 通过式 (5) 计算可得系统 (1) 的 Hamilton 能量为
为验证关系式 $\dot {H} = \nabla {\pmb H}^{\rm T}f_{\rm d} ({\pmb X})$,由此对 Hamilton 能量 $H$ 求导可得
$ \dot {H} = (bx^2 - 1 + rs(x - \chi _0 ) + k_1 x)\dot {x} + \\ \qquad (y - z + I - \phi )(\dot {y} - \dot {z} - \dot {\phi }) =\\ \qquad [bx^2 - 1 + rs(x - \chi _0 ) + k_1 x]\cdot \\ \qquad [y + bx^2 - ax^3 - z + I - k_0 W(\phi )x]+ \\ \qquad (y - z + I - \phi )[c - dx^2 - y - \\ \qquad r(s(x - \chi _0 ) - z) - k_1 x + k_2 \phi ]= \\ \qquad [bx^2 - 1 + rs(x - \chi _0 ) + k_1 x]\cdot \\ \qquad [bx^2 - ax^3 - k_0 W(\phi )x]+ \\ \qquad (y - z + I - \phi )( - y) - (y - z + I - \phi )( - rz) - \\ \qquad (y - z + I - \phi )( - k_3 \phi ) =\\ \qquad \nabla {\pmb H}^{\rm T}F_{\rm d} ({\pmb X}) $
由此可知, 式 (6) 正是所求的 Hamilton 能量函数. 本文作者在文献[23] 中提出了一种基于 Hamilton 能量的反馈控制方法,即将控制输入项 $kH$ 作用到受控系统的某一项上去调控系统的群体变量. 为了得到更丰富的振荡模式,这里将 $kH$ 作用到系统 (1) 的第二项,受控下的磁通神经元系统如下
式中,$k$ 表示 Hamilton 能量 $H$ 的反馈增益,用于控制能量流的反馈强度,一般在 $[ - 1,1]$ 内取值. 当系统参数固定时,系统的能量靠反馈增益 $k$ 来改变,即利用控制输入项 $kH$ 来调制系统的动力学. 受控系统 (7) 中 的 Hamilton 能量调制器为
$ \dot {H} = [bx^2 - ax^3 - k_0 W(\phi )x]\cdot [bx^2 - 1 + rs(x - \chi _0 ) + k_1 x] + (y - z + I)( - y + rz + k_3 \phi ) $
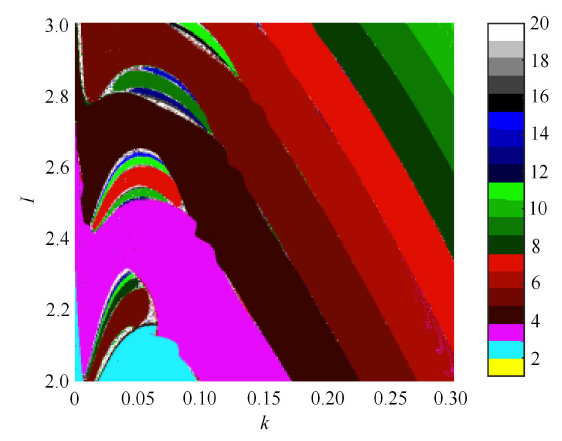
下面讨论系统 (1) 的膜电压受 Hamilton 能量控制后的放电行为. 图 10 为反馈增益 $k$ 和外界刺激电流 $I$ 的双参分岔图,从图中可以直观地看到反馈增益 $k$ 能有效地控制系统 (1) 到不同的簇放电状态.
图10
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图10$k \in [0,0.3],I \in [2,3]$ 时系统 (1) 关于 $x$ 的双参数分岔图
Fig.10Two-parameter bifurcation diagram of system (1) versus $x$ when $k \in [0,0.3],I \in [2,3]$
当 $I = 3$ 时,关于反馈增益 $k$ 的 ISI 分岔和在膜电压平面上的分岔如图 11(a) 和图 11(b) 所示. 明显地,系统 (1) 的膜电压在原始的周期 4 簇放电状态可以被 Hamilton 能量控制器控制到典型的周期簇放电状态. 图 12 和图 13 为加周期的簇放电状态,当取不同的反馈增益时,其周期放电模式为: $4^0 \to 5^0 \to \cdots \to 10^0 \to 11^0$.
图11
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图11系统 (1) 关于反馈增益 $k$ 的 ISI 分岔和单参分岔
Fig.11The ISI bifurcation and one-parameter bifurcation of system(7) versus feedback gain $k$
图12
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图12周期簇放电和相应的 Hamilton 能量曲线
Fig.12The period bursting states and corresponding Hamilton energy curves
图13
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图13在 $z-x -w$ 平面上的 3 维相轨迹
Fig.13The 3-dimensional phase diagrams in $z - x - w$ plane
簇放电是神经元系统中非常重要的放电模式,它能强化神经元之间的信息传输. 另外,从图 11 中也可以看出,磁通神经元系统 (1) 存在不规则的放电行为,其时间响应如图 14 所示. 当能量反馈增益分别取 $k = 0.075$ 和 $k = 0.083$ 时, 磁通神经元系统 (1) 均展现了如下的不规则混合振荡模式
图14
 新窗口打开|下载原图ZIP|生成PPT
新窗口打开|下载原图ZIP|生成PPT图14复杂混合模式簇放电和相应的 Hamilton 能量曲线
Fig.14The complexmixed-mode bursting states and corresponding Hamiltonian energy curves
$5^0 \to 5^0 \to 1^0 \to 5^0 \to 5^0 \to 5^0 \to 1^0 \to [ 0,1 ] 5^0 \to$
$ 5^0 \to 1^0 \to 5^0 \to 5^0 \to 5^0 \to 1^0 \to \cdots $
$5^0 \to 5^0 \to 1^0 \to 5^0 \to 5^0 \to 1^0 \to 5^0 \to 5^0 \to$
$1^0 \to 5^0 \to 5^0 \to 1^0 \to 5^0 \to 5^0 \to \cdots $
通过以上讨论可知,Hamilton 能量控制器可以有效地将磁通神经元系统控制到周期簇放电以及不规则的簇放电状态. 同时,也可以从图 12 中观察到膜电压簇放电时的能量迁移.
从 式 (6) 可以看出,Hamilton 能量受到系统参数和初值的制约,同时又是基于无量纲的系统变量得到的,Hamilton 能量反馈从动力学角度来看是对相空间进行压缩或者放大,从而达到对系统所有变量群体调控的目的,最终达到对系统动力学的控制. 从图 14 可以看出,周期 5 簇放电要比峰放电耗能多,大幅值峰放电要比小幅值峰放电耗能多. 同时, 可以设计合适的控制器,以期用最小的代价达到控制目的.
能量反馈控制是通过反馈增益调节能量控制输入的强度而去调制神经元系统的膜电压振荡,进而动力学行为可以被调节. 本文中,当反馈增益$k$取不同的值时,系统 (1) 能被很好地控制到不同的周期簇振荡状态. 同时,我们也能清楚地看到膜电压在簇振荡和静息状态时 Hamilton 能量的波动过程. 这是因为神经元数学模型中的 Hamilton 能量的变化趋势取决于模型中振荡模态的转变和外加电流,但主要依赖于振荡模态的变化. 同时,由于神经元可以自行编码能量,Hamilton 能量的变化会稍滞后于电活动的变化[28]. 从图 12 和图 14 中可以看到,改进的 HR 系统的 Hamilton 能量函数曲线有正有负,正的 Hamilton 能量为膜电压振荡提供能量,负的 Hamilton 能量暂时不会被消耗,而是为后续膜电压振荡的能量储备被储存下来. 这是由于神经元不仅是个耗能元件也是一个储能元件,从一个动作电位来看,神经元的能量由两部分组成,一部分是从血流中获得氧合的血红蛋白,表现为负的能量,用于能量的储存. 一部分将脱氧的血红蛋白释放到血流中,表现为正的能量,用于能量的消耗[29-30]. 另外,在两个簇振荡之间的静息状态下,能量通常接近于 0,但仍然有较低水平的振荡,故仍有少量能量释放,直到下一个簇振荡或峰振荡开始.
对无量纲后的神经元系统来说,膜电压的振荡都需要一定的能量,因此 Hamilton 能量的吸收和释放与膜电压紧密相关. 对 Hamilton 能量的研究为理解神经元电活动的信息编码和能量迁移提供了思路,也对分析振动模态转换过程中能量转移有一定的参考.
5 结论
本文通过研究磁通 HR 神经元系统在双参数空间上的分岔结构,发现该系统存在丰富的分岔结构,即含混沌的倍周期分岔、无混沌的加周期分岔及其混合模式振荡. 为了控制磁通 HR 神经元系统的放电模式,本文通过建立 Hamilton 能量反馈控制器,可以有效地将磁通 HR 神经元系统中的膜电压控制到不同周期的簇放电状态,同时,在控制过程中,可以探测到膜电压簇放电时能量的变化状态. 上述的研究为进一步探索磁通神经元的分岔模式和了解电磁场下神经元的能量控制提供了有益的探讨.参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[本文引用: 1]
[本文引用: 1]
URLPMID
DOIURL
URL
URL
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]

This paper presents the mathematical model of membrane current of neuron resulting from electromagnetic radiation based on the foundation of neuronal energy theory; and the effect of electromagnetic radiation on the dynamic behaviors of single neuron and the firing activities of two neurons coupled with gap connection are investigated. Results show that the neuronal firing rate is lowered as the radiation intensity increases, and finally reaches a stable value. As the radiation intensity increases, the periodical spiking of neuron is transformed into bursting firing, which is well explained based on the dynamic bifurcation theory. It turns out that the bursting firing induced by the electromagnetic radiation could spread out in neuronal network through an electrical gap junction.
DOIURL [本文引用: 1]

This paper presents the mathematical model of membrane current of neuron resulting from electromagnetic radiation based on the foundation of neuronal energy theory; and the effect of electromagnetic radiation on the dynamic behaviors of single neuron and the firing activities of two neurons coupled with gap connection are investigated. Results show that the neuronal firing rate is lowered as the radiation intensity increases, and finally reaches a stable value. As the radiation intensity increases, the periodical spiking of neuron is transformed into bursting firing, which is well explained based on the dynamic bifurcation theory. It turns out that the bursting firing induced by the electromagnetic radiation could spread out in neuronal network through an electrical gap junction.
URLPMID [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
URLPMID [本文引用: 1]
DOIURL [本文引用: 1]

Neural firing rhythm plays an important role in achieving the function of a nervous system. Neurons with autapse, which starts and ends in the same cell, are widespread in the nervous system. Previous results of both experimental and theoretical studies have shown that autaptic connection plays a role in influencing dynamics of neural firing patterns and has a significant physiological function. In the present study, the dynamics of a neuronal model, i.e., Rulkov model with inhibitory autapse and time delay, is investigated, and compared with the dynamics of neurons without autapse. The bifurcations with respect to time-delay and the coupling strength are extensively studied, and the time series of membrane potentials is also calculated to confirm the bifurcation analysis. It can be found that with the increase of time-delay and/or the coupling strength, the period-adding bifurcation of neural firing patterns can be induced in the Rulkov neuron model. With the increase of the period number of the firing rhythm, the average firing frequency increases. When time-delay and/or coupling strength are/is greater than their/its corresponding certain thresholds/threshold, the average firing frequency is higher than that of the neuron without autapse. Furthermore, new bursting patterns, which appear at suitable time delays and coupling strengths, can be well interpreted with the dynamic responses of an isolated single neuron to a negative square current whose action time, duration, and strength are similar to those of the inhibitory coupling current modulated by the coupling strength and time delay. The bursts of neurons with autapse show the same pattern as the square negative current-induced burst of the isolated single neuron when the time delay corresponds to the phase. The bifurcation structure of the neural firing rhythm of the neuron without autapse can be obtained with the fast-slow dissection method. The dynamic responses of the isolated bursting neuron to the negative square current are acquired by using the fast-slow variable dissection method, which can help to recognize the new rhythms induced by the external negative pulse current applied at different phases. The new rhythm patterns are consistent with those lying in the period-adding bifurcations. The results not only reveal that the inhibitory autapse can induce typical nonlinear phenomena such as the period-adding bifurcations, but also provide the new phenomenon that the inhibitory autapse can enhance the firing frequency, which is different from previous viewpoint that inhibitory effect often reduces the firing frequency. These findings further enrich the understanding of the nonlinear phenomena induced by inhibitory autapse.
DOIURL [本文引用: 1]

Neural firing rhythm plays an important role in achieving the function of a nervous system. Neurons with autapse, which starts and ends in the same cell, are widespread in the nervous system. Previous results of both experimental and theoretical studies have shown that autaptic connection plays a role in influencing dynamics of neural firing patterns and has a significant physiological function. In the present study, the dynamics of a neuronal model, i.e., Rulkov model with inhibitory autapse and time delay, is investigated, and compared with the dynamics of neurons without autapse. The bifurcations with respect to time-delay and the coupling strength are extensively studied, and the time series of membrane potentials is also calculated to confirm the bifurcation analysis. It can be found that with the increase of time-delay and/or the coupling strength, the period-adding bifurcation of neural firing patterns can be induced in the Rulkov neuron model. With the increase of the period number of the firing rhythm, the average firing frequency increases. When time-delay and/or coupling strength are/is greater than their/its corresponding certain thresholds/threshold, the average firing frequency is higher than that of the neuron without autapse. Furthermore, new bursting patterns, which appear at suitable time delays and coupling strengths, can be well interpreted with the dynamic responses of an isolated single neuron to a negative square current whose action time, duration, and strength are similar to those of the inhibitory coupling current modulated by the coupling strength and time delay. The bursts of neurons with autapse show the same pattern as the square negative current-induced burst of the isolated single neuron when the time delay corresponds to the phase. The bifurcation structure of the neural firing rhythm of the neuron without autapse can be obtained with the fast-slow dissection method. The dynamic responses of the isolated bursting neuron to the negative square current are acquired by using the fast-slow variable dissection method, which can help to recognize the new rhythms induced by the external negative pulse current applied at different phases. The new rhythm patterns are consistent with those lying in the period-adding bifurcations. The results not only reveal that the inhibitory autapse can induce typical nonlinear phenomena such as the period-adding bifurcations, but also provide the new phenomenon that the inhibitory autapse can enhance the firing frequency, which is different from previous viewpoint that inhibitory effect often reduces the firing frequency. These findings further enrich the understanding of the nonlinear phenomena induced by inhibitory autapse.
DOIURL [本文引用: 2]
DOIURL [本文引用: 1]
[博士论文].
[PhD Thesis].
[博士论文].
[本文引用: 1]
[PhD Thesis].
[本文引用: 1]
[本文引用: 2]
[本文引用: 2]
[本文引用: 2]
[本文引用: 2]
DOIURL [本文引用: 2]
DOIURL [本文引用: 1]
DOIURL [本文引用: 2]

The Helmholtz theorem confirms that any vector field can be decomposed into gradient and rotational field. The supply and transmission of energy occur during the propagation of electromagnetic wave accompanied by the variation of electromagnetic field, thus the dynamical oscillators and neurons can absorb and release energy in the presence of complex electromagnetic condition. Indeed, the energy in nonlinear circuit is often time-varying when the capacitor is charged or discharged, and the occurrence of electromagnetic induction is available. Those nonlinear oscillating circuits can be mapped into dynamical systems by using scale transformation. Based on mean field theory, the energy exchange and transmission between electronic field and magnetic field can be estimated by appropriate nonlinear dynamical equations for oscillating circuits. In this paper, we investigate the calculation of Hamilton energy for a class of dimensionless dynamical systems based on Helmholtz's theorem. Furthermore, the scale transformation can be used to develop dynamical equations for the realistic nonlinear oscillating circuit, so the Hamilton energy function could be obtained effectively. These results can be greatly useful for self-adaptively controlling dynamical systems.
DOIURL [本文引用: 2]

The Helmholtz theorem confirms that any vector field can be decomposed into gradient and rotational field. The supply and transmission of energy occur during the propagation of electromagnetic wave accompanied by the variation of electromagnetic field, thus the dynamical oscillators and neurons can absorb and release energy in the presence of complex electromagnetic condition. Indeed, the energy in nonlinear circuit is often time-varying when the capacitor is charged or discharged, and the occurrence of electromagnetic induction is available. Those nonlinear oscillating circuits can be mapped into dynamical systems by using scale transformation. Based on mean field theory, the energy exchange and transmission between electronic field and magnetic field can be estimated by appropriate nonlinear dynamical equations for oscillating circuits. In this paper, we investigate the calculation of Hamilton energy for a class of dimensionless dynamical systems based on Helmholtz's theorem. Furthermore, the scale transformation can be used to develop dynamical equations for the realistic nonlinear oscillating circuit, so the Hamilton energy function could be obtained effectively. These results can be greatly useful for self-adaptively controlling dynamical systems.
DOIURL [本文引用: 1]
DOIURL [本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL
DOIURL [本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
