陈少林^,2), 孙杰, 柯小飞南京航空航天大学土木与机场工程系, 南京 210016

ANALYSIS OF WATER-SEABED-STRUCTURE DYNAMIC INTERACTION EXCITED BY PLANE WAVES ¹⁾

Chen Shaolin^,2), Sun Jie, Ke XiaofeiDepartment of Civil Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China

通讯作者: 2)陈少林, 教授, 主要研究方向: 地震工程. E-mail:icmcsl@nuaa.edu.cn

收稿日期:2019-12-14接受日期:2020-02-9网络出版日期:2020-03-18

基金资助:

1)国家自然科学基金资助项目.51978337

Received:2019-12-14Accepted:2020-02-9Online:2020-03-18
作者简介 About authors


摘要
海洋工程结构的地震反应分析是保证海洋工程结构地震安全的重要环节.由于其所处的复杂环境, 该问题涉及到流固耦合和土-结相互作用.本文基于海水、饱和海床、基岩流固耦合统一计算框架,采用Davidenkov模型和修正的Masing准则考虑饱和海床的非线性,在脉冲SV波垂直入射下, 进行了海域场地和海洋工程结构的动力响应分析. 首先,对比分析了线性自由场和非线性自由场输入情形的海域场地非线性反应,结果表明线性自由场输入时反应不合理,自由场分析和场地分析应该采用相一致的本构模型. 然后,对比分析了海床分别为线性和非线性情形时,海域场地以及海水-海床-结构体系的反应特征. 与线性海床情形相比,非线性对海床反应的影响主要由如下两方面因素控制: 一方面,非线性导致饱和海床模量减小, 饱和海床与基岩间的波阻抗比减小,由基岩到饱和海床间的反射系数和透射系数增加, 导致反应增大; 另一方面,非线性导致阻尼加大, 使海床反应减小. 对于本文算例而言,阻尼对非线性海床结果的影响占主导作用.
关键词： 海水-海床-结构相互作用;土体非线性;自由场分析;饱和多孔介质;人工边界

Abstract
The seismic response analysis of marine engineering structures is important to ensure the seismic safety of these structures. Marine engineering structures are always built in a complex environment where there are both water and soil. So both fluid-structure interaction and soil-structure interaction need to be considered in seismic response analysis of marine engineering structures. This paper is based on the unified calculation framework for wave motion in water-saturated seabed-bedrock system, and uses the Davidenkov model and modified Masing rule to describe the nonlinear characteristics of saturated seabed. The dynamic responses of marine sites and marine engineering structures when the pulse SV wave incident vertically are analyzed. First, the nonlinear responses of marine sites under the input of linear free field and nonlinear free field are analyzed comparatively. The results show that the nonlinear response of the marine site under the input of the linear free field is unreasonable. So it means the consistent constitutive model should be used for the free field analysis and finite element analysis of marine site. Then, the characteristics of responses of the marine site and water-saturated seabed-bedrock system when the seabed is linear or nonlinear are analyzed comparatively. Compared with the case that the seabed is linear, the influence of nonlinearity on response of seabed is mainly controlled by the following two factors: on the one hand, the modulus of saturated seabed decreases because of nonlinearity, so the wave impedance ratio between saturated seabed and bedrock decreases, and then, the reflection coefficient and transmission coefficient from bedrock to saturated seabed increase, resulting in the increase of response; on the other hand, the nonlinearity of saturated seabed causes the increase of damping, resulting in the decrease of response. For the example in this paper, the effect of damping dominate the result when seabed is nonlinear.
Keywords：seawater-seabed-structure interaction;soil nonlinearity;free field analysis;saturated porous media;artificial boundary


PDF (18558KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
陈少林, 孙杰, 柯小飞. 平面波输入下海水-海床-结构动力相互作用分析 ¹⁾. 力学学报[J], 2020, 52(2): 578-590 DOI:10.6052/0459-1879-19-354
Chen Shaolin, Sun Jie, Ke Xiaofei. ANALYSIS OF WATER-SEABED-STRUCTURE DYNAMIC INTERACTION EXCITED BY PLANE WAVES ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2020, 52(2): 578-590 DOI:10.6052/0459-1879-19-354

引言

随着我国海洋战略的实施, 将要建造大量近海工程结构, 如何保证近海工程结构在服役期的地震安全性是目前面临的重要科技问题.要保证近海工程结构的地震安全性, 首先要对其在潜在地震作用下的反应进行准确的分析预测^[1-9]. 目前, 受水下振动台设备的限制, 采用试验方法对海工结构的地震反应分析还很少.而在数值分析方面, 其属于半无限域地震波散射问题(如图1所示), 涉及到海域场地自由场分析(为散射问题提供输入)、海水-饱和海床-结构间的相互耦合分析, 以及半无限海域场地的人工边界条件, 问题十分复杂.

图1

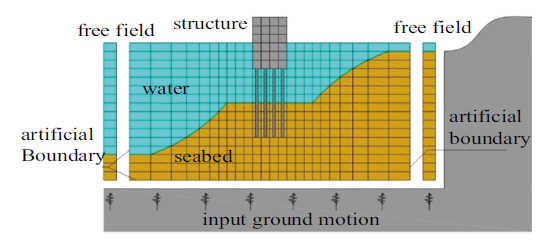新窗口打开|下载原图ZIP|生成PPT
图1海洋工程结构地震反应分析示意图

Fig. 1Seismic response analysis of marine engineering structure



其中, 海水、饱和海床、结构间的流固耦合问题, 若采用常规的流固耦合求解思路, 须分别采用流体声波方程、饱和多孔介质方程和固体波动方程的求解器, 各求解器在每一时步进行界面耦合, 十分不便, 目前还没有成熟方法和软件能高效地解决此问题. 因此, 发展一种海洋地震工程中海水-饱和海床-结构耦合分析的高效方法, 考虑海床的非线性, 揭示强震作用下海床液化失稳机理和海工结构的灾害模式十分必要.

对于海域场地非线性地震响应分析, 可以采用等效线性化分析方法^[10-11]或时域非线性分析方法^[12-18].一般认为, 等效线性化方法适合于弱非线性, 对于强非线性, 宜采用时域非线性分析方法. 当采用时域非线性方法分析场地地震响应时, 需要先进行水平成层场地的自由场分析, 作为边界的输入. 目前, 一般采用传递矩阵方法^[19-21]进行自由场分析, 适合于线性或等效线性化情形, 可以考虑地震波斜入射;-也可采用有限元数值分析方法^[22-24], 根据Snell定律, 将二维自由场分析一维化, 采用数值方法实现一维分析, 再根据视速度将一维波场外推至二维、三维, 这种外推只适合于波速恒定的线性情形.因此, 若采用数值方法求解非线性自由场, 只能获得一维自由场, 即垂直入射情形.在考虑饱和海床的非线性时, 理论上, 自由场计算也需采用与内域计算同样的本构, 若与内域分析的本构不一致, 对结果的影响值得讨论.

本文在海域场地自由场分析^[20]和海洋地震工程流固耦合问题统一计算框架^[25-26]的基础上, 首先考虑饱和海床的非线性, 分析海域场地的非线性反应特征, 并讨论了采用线性自由场和非线性自由场对结果的影响.进一步分析了海域场地和海水-海床-结构体系在地震作用下的动力响应, 对比了线性海床和非线性海床情形时响应的差异, 为海洋工程结构的抗震设计提供理论基础和分析手段.

1 基本理论

如图2所示, 从场地中截取有限土体, 采用八结点三维实体单元对其进行空间离散, 整个计算区域的有限元节点可以分为两类: 内节点与人工边界节点.内节点又分为一般内节点(包括自由表面节点)与不同介质交界面上的界面节点.场地介质为饱和多孔介质, 海水、基岩均可视为饱和多孔介质的特殊情形.

图2

新窗口打开|下载原图ZIP|生成PPT
图2场地-结构相互作用分析模型示意图

Fig. 2Site-structure interaction analysis model

1.1 一般内节点运动

对于饱和多孔介质, 其固相平衡方程^[27-28]

(1)$ \begin{eqnarray} {L}_{\rm s}^{\rm T} \sigma'-(1-\beta ){L}_{\rm w}^{\rm T} P+b({\dot{{U}}}-{\dot{{u}}})=(1-\beta )\rho _{\rm s} {\ddot{{u}}} \end{eqnarray}$
液相平衡方程

(2)$ \begin{eqnarray} -\beta {L}_{\rm w}^{\rm T} P+b({\dot{{u}}}-{\dot{{U}}})=\beta \rho _{\rm w} {\ddot{{U}}} \end{eqnarray}$
相容方程(考虑初始孔压和初始体应变为零时)

(3)$ \begin{eqnarray} \tau =-\beta P=E_{\rm w} [\beta e^{\rm w}+(1-\beta )e^{\rm s}] \end{eqnarray}$
其中, ${L}_{\rm s}$, ${L}_{\rm w}$为微分算子矩阵, $ \sigma'$为有效应力矢量, $\tau $为平均孔压, $P$为孔隙水压, ${\dot{{u}}}$, $\dot{{U}}$为固、液相的速度, ${\ddot{{u}}}$, ${\ddot{{U}}}$为固、液相的加速度, $\rho _{\rm s} $, $\rho _{\rm w}-$分别为固、液相的密度, $\beta $为孔隙率, $b={\beta ^2\mu _0 } / k_0 $, $k_0$为流体渗透系数, $\mu _0 $为动黏度系数, $E_{\rm w} $为流体的体变模量, $e^{\rm s}$, $e^{\rm w}$分别为固相和液相的体应变.

以上方程当孔隙比$\beta =1$时, 可退化为理想流体方程; 当孔隙比$\beta =0$时, 可退化为弹性波动方程. 因此, 流体、弹性固体、饱和多孔介质可统一由广义饱和多孔介质($0\leqslant \beta \leqslant 1)$方程描述, 仅是材料参数不同. 因此, 海域场地中地震波传播问题可由广义饱和多孔介质方程统一描述.

对方程(1)和(2)采用伽辽金方法离散, 并考虑相容方程(3)及边界条件, 可得任一结点$i$的运动平衡方程为^[26]

(4a)$ \begin{eqnarray} {\ddot{{u}}}_i {M}_{{\rm s}i} +{F}_i^{\rm s} +{T}_i^{\rm s} -{S}_i^{\rm s} ={\bf 0} \end{eqnarray} $
(4b)$ \begin{eqnarray} {\ddot{{U}}}_i {M}_{{\rm w}i} +{F}_i^{\rm w} +{T}_i^{\rm w} -{S}_i^{\rm w} ={\bf 0} \end{eqnarray} $
其中, ${M}_{{\rm s}i} $, ${M}_{{\rm w}i} $分别为固、液相质量; ${F}_i^{\rm s}$, ${F}_i^{\rm w} $分别为固、液相本构力,本文采用Davidenkov模型考虑固相的非线性, 具体见1.4节; ${T}_i^{\rm s} $, ${T}_i^{\rm w} $分别为固、液相黏性阻力; ${S}_i^{\rm s}$, ${S}_i^{\rm w}$分别为固、液相边界力, 当节点$i$为一般内节点时, 界面力为零.

对式(4a), (4b)进行时步积分, 可得到一般内节点$i$的固、液相位移递推公式

(5a) $ \begin{eqnarray} {u}_i^{(p+1)} =2{u}_i^p -{u}_i^{(p-1)} -\frac{(\Delta t)^2}{m_i^{\rm s} }({F}_i^{\rm s} +{T}_i^{\rm s} ) \end{eqnarray} $
(5b) $ \begin{eqnarray} {U}_i^{(p+1)} =2{U}_i^p -{U}_i^{(p-1)} -\frac{(\Delta t)^2}{m_i^{\rm w} }({F}_i^{\rm w} +{T}_i^{\rm w} ) \end{eqnarray} $

1.2 界面节点运动

对于界面节点, 如图2中的$j(k)$, 根据文献^[26], 采用隔离体概念, 对式(4a), (4b)进行时步积分得

(6a) $ \begin{eqnarray} {u}_i^{(p+1)} ={\hat{{u}}}_i^{(p+1)} +\Delta {u}_{{\rm N}i}^{(p+1)}+\Delta {u}_{{\rm T}i}^{(p+1)} \end{eqnarray} $
(6b) $ \begin{eqnarray} {U}_i^{(p+1)} ={\hat{{U}}}_i^{(p+1)} +\Delta {U}_{{\rm N}i}^{(p+1)}+\Delta {U}_{{\rm T}i}^{(p+1)} \end{eqnarray} $
其中, $i = j, k$

(7a) $ \begin{eqnarray} {\hat{{u}}}_i^{(p+1)} =2{u}_i^p -{u}_i^{(p-1)} -\frac{(\Delta t)^2}{m_i^{\rm s} }({F}_i^{{\rm s}p} +{T}_i^{{\rm s}p} ) \end{eqnarray} $
(7b) $ \begin{eqnarray} {\hat{{u}}}_i^{(p+1)} =2{u}_i^p -{u}_i^{(p-1)} -\frac{(\Delta t)^2}{m_i^{\rm s} }({F}_i^{{\rm s}p} +{T}_i^{{\rm s}p} ) \end{eqnarray} $
(7c) $ \begin{eqnarray} \Delta {u}_{{\rm N}i}^{(p+1)} =\frac{(\Delta t)^2}{m_i^{\rm s} }{S}_{{\rm N}i}^{{\rm s}p} \end{eqnarray} $
(7d) $ \begin{eqnarray} \Delta {u}_{{\rm T}i}^{(p+1)} =\frac{(\Delta t)^2}{m_i^{\rm s} }{S}_{{\rm T}i}^{{\rm s}p} \end{eqnarray} $
(7e) $ \begin{eqnarray} \Delta {U}_{{\rm N}i}^{(p+1)} =\frac{(\Delta t)^2}{m_i^{\rm w} }{S}_{{\rm N}i}^{{\rm w}p} \end{eqnarray} $
(7f) $ \begin{eqnarray} \Delta {U}_{{\rm T}i}^{(p+1)} =\frac{(\Delta t)^2}{m_i^{\rm w} }{S}_{{\rm T}i}^{{\rm w}p} \end{eqnarray} $
其中, $\Delta {u}_{{\rm N}i}^{(p+1)} $是由法向界面力${S}_{{\rm N}i}^{{\rm s}p} $引起的固相位移, $\Delta {u}_{{\rm T}i}^{(p+1)} $是由切向界面力${S}_{{\rm T}i}^{{\rm s}p} $引起的固相位移, $\Delta {U}_{{\rm N}i}^{(p+1)}$是由法向界面力${S}_{{\rm N}i}^{{\rm w}p} $引起的液相位移, $\Delta {U}_{{\rm T}i}^{(p+1)} $是由切向界面力${S}_{{\rm T}i}^{{\rm w}p} $引起的液相位移.

由式(6)、式(7), 以及界面连续条件, 经推导,可得

(8a) $ \begin{eqnarray} {S}_{{\rm N}j}^{{\rm s}p} =\frac{A_{22} B_1 -A_{12} B_2 }{A_{22} A_{11} -A_{12} A_{21} } \end{eqnarray} $
(8b) $ \begin{eqnarray} {S}_{{\rm N}j}^{{\rm w}p} =\frac{A_{21} B_1 -A_{11} B_2 }{A_{21} A_{12} -A_{11} A_{22} } \end{eqnarray} $
其中

(9a) $ \begin{eqnarray} A_{11} =(\Delta t)^2\left( {\frac{1}{m_j^{\rm s} }+\frac{1}{m_k^{\rm s} }} \right) \end{eqnarray} $
(9b) $ \begin{eqnarray} A_{12} =\left( {1-\frac{\bar{{\beta }}}{\beta }} \right)\frac{(\Delta t)^2}{m_k^{\rm s} }\end{eqnarray} $
(9c) $ \begin{eqnarray} B_1 ={n}_j \left[ {{n}_j \cdot \left( {{\hat{{\bar{{u}}}}}_k^{(p+1)} -{\hat{{u}}}_j^{(p+1)} } \right)} \right] \end{eqnarray} $
(9d) $ \begin{eqnarray} A_{21} =(\Delta t)^2\left( {-\frac{\bar{{\beta }}}{m_k^{\rm s} }+\frac{\beta }{m_k^{\rm s} }} \right) \end{eqnarray} $
(9e) $ \begin{eqnarray} A_{22} =(\Delta t)^2\left[ {\frac{\beta }{m_j^{\rm w} }+\frac{\bar{{\beta }}^2}{\beta m_k^{\rm w} }+\frac{\left( {\bar{{\beta }}-\beta} \right)\left( {\bar{{\beta }}-\beta } \right)}{\beta m_k^{\rm s} }} \right] \end{eqnarray} $
(9f) $ \begin{eqnarray} B_2 ={n}_j \left\{{n}_j \cdot \left[\bar{{\beta }}({\hat{{\bar{{U}}}}}_k^{(p+1)} -{\hat{{\bar{{u}}}}}_k^{(p+1)} )-\beta ({\hat{{U}}}_j^{(p+1)} -{\hat{{\bar{{u}}}}}_k^{(p+1)} )\right]\right\} \end{eqnarray} $
由式(8a)、式(8b)求得${S}_{{\rm N}j}^{{\rm s}p} $, ${S}_{{\rm N}j}^{{\rm w}p} $后, 可进一步由界面连续条件解得${\bar{{S}}}_{{\rm N}k}^{{\rm s}p} $, ${\bar{{S}}}_{{\rm N}k}^{{\rm w}p} $. 再由固相位移连续条件,可得

(10)$ \begin{eqnarray} \label{eq10} {S}_{{\rm T}j}^{{\rm s}p} =\frac{\left( {{\hat{{\bar{{u}}}}}_k^{(p+1)} +\Delta {\bar{{u}}}_{{\rm N}k}^{(p+1)} -{\hat{{u}}}_j^{(p+1)} -\Delta {u}_{{\rm N}j}^{(p+1)} } \right)m_j^{\rm s} m_k^{\rm s} }{(\Delta t)^2(m_j^{\rm s} +m_k^{\rm s} )} \end{eqnarray}$
由界面连续条件, 可得${\bar{{S}}}_{{\rm T}k}^{{\rm s}p} $. 液相切向界面力${S}_{{\rm T}i}^{\rm w}$, $\bar{{S}}_{{\rm T}k}^{\rm w} $为0. 有了界面力, 则可由式(6)求得界面点的位移响应.

1.3 人工边界节点运动

为了有效地模拟外行波穿过人工边界的运动状态, 我们采用多次透射公式^[29]

(11)$ \begin{eqnarray} \label{eq11} u_0^{p+1} =\sum\limits_{m=1}^N {\left( {-1} \right)^{j+1}C_j^N u_j^{p+1-j} } \end{eqnarray}$
其中

(12)$ \begin{eqnarray} \label{eq12} C_j^m =\frac{m!}{\left( {m-j} \right)!j!} \end{eqnarray}$
该局部人工边界条件具有普适性, 与具体波动方程无关, 可直接用于饱和多孔介质中的波动^[30]. 分别将式(11)应用于广义饱和多孔介质的固相和液相位移, 可得到边界点在$p+1$时刻的散射波场位移, 再叠加上边界点的自由场位移,即可得到边界点的固、液相总位移.

1.4 饱和土骨架非线性

在强震作用下, 土体将进入非线性, 本文采用三参数的Davidenkov本构模型, 通过对饱和土体固相剪切模量实时修正, 可以较为有效地描述饱和土体的非线性动力特性^[14-15].

由Martin和Seed^[18]提出的Davidenkov本构模型骨架曲线的表达式为

(13)$ \begin{eqnarray} \label{eq13} \tau \left( \gamma \right)=G\gamma =G_{\max } \gamma \left[ {1-H\left( \gamma \right)} \right] \end{eqnarray}$
其中

(14)$ \begin{eqnarray} \label{eq14} H\left( \gamma \right)=\left[ {\frac{\left( {\gamma / {\gamma _0 }} \right)^{2B}}{1+\left( {\gamma / {\gamma _0 }} \right)^{2B}}} \right]^A \end{eqnarray}$
式中, $\tau $, $\gamma$分别为剪应力、剪应变; $G_{\max}$为初始剪切模量; $A$, $B$, $\gamma _{0}$可由土体动三轴实验数据进行拟合得到.

经Masing法则修正后滞回曲线如图3所示, 依据Pyke提出的"$n$倍法", 应力-应变滞回曲线服从下述关系

(15)$ \begin{eqnarray} \label{eq15} \tau-\tau _{\rm c} =G_{\max } \left( {\gamma -\gamma _{\rm c} } \right)\left[{1-H\left( {\frac{\left| {\gamma -\gamma _{\rm c} } \right|}{2n}} \right)}\right] \end{eqnarray}$
分别对式(13)、式(15)求导, 可得到初始骨架曲线段、滞回曲线段的时变切线剪切模量

(16)$ \begin{eqnarray} \label{eq16} &&G^{t+\Delta t}=\frac{{\rm d}\tau }{{\rm d}\gamma }=G_{\max} \left[ 1-\left(1+\frac{2AB\gamma _0^{2B} }{\gamma_0^{2B} +\gamma^{2B}} \right)H\left( \gamma \right) \right] \end{eqnarray}$
(17)$ \begin{eqnarray} G^{t+\Delta t}=\frac{{\rm d}\left( {\tau -\tau _{\rm c} } \right)}{{\rm d}\left( {\gamma -\gamma _{\rm c} } \right)} = \\&&\qquad G_{\max } \left\{ {1-\left[ {1+\frac{2AB\left( {2n\gamma _0 } \right)^{2B}}{\left( {2n\gamma _0 } \right)^{2B}+\left| {\gamma -\gamma _{\rm c} } \right|^{2B}}} \right]H\left( {\frac{\left| {\gamma -\gamma _{\rm c} } \right|}{2n}} \right)} \right\} \end{eqnarray}$
式中参数$\left( {2n\gamma _0 }\right)^{2B}$根据当前拐点及历史上最大(小)点确定. 上述本构模型是依据实验室得到的主空间上的主剪切应力-主剪切应变曲线而建立的, 通常假定该本构模型同样适合于复杂三维情形的主剪切应力-主剪切应变关系, 因此将其用于三维计算分析时, 需根据应变分量, 求出主剪切应变,再根据式(16)和式(17)更新剪切模量.

图3

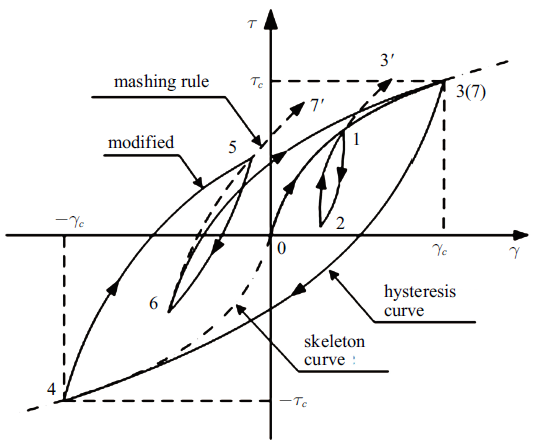新窗口打开|下载原图ZIP|生成PPT
图3不规则加卸载准则修正的Davidenkov本构模型曲线

Fig. 3Davidenkov mode modified by irregular loading and unloading criterion

2 算例分析

2.1 自由场对海域场地非线性响应的影响

考虑如图4所示的三维海水-饱和土-基岩海域场地模型, 整体尺寸为62 m $\times$ 62 m $\times$ 60 m, 单元尺寸为1 m $\times $ 1 m $\times $ 1 m, 各层介质参数如表1所示. 其中, 饱和土层采用三参数的Davidenkov非线性本构模型,参数$A=1.1$, $B=0.2$, $\gamma _0 =0.000 4$; 海水层和基岩层考虑为线性. 考虑SV波垂直入射, 输入如图5所示的单位脉冲, 步距为0.000 2 s, 步数为8000步.

图4

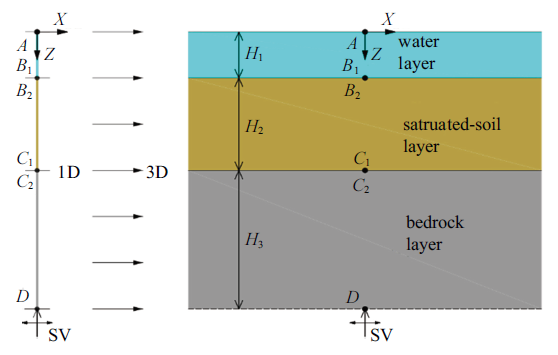新窗口打开|下载原图ZIP|生成PPT
图4海水-饱和土-基岩场地模型示意图

Fig. 4Water-saturated soil-bedrock site model



Table 1
表1
表1模型参数
Table 1Parameters of the model

新窗口打开|下载CSV

图5

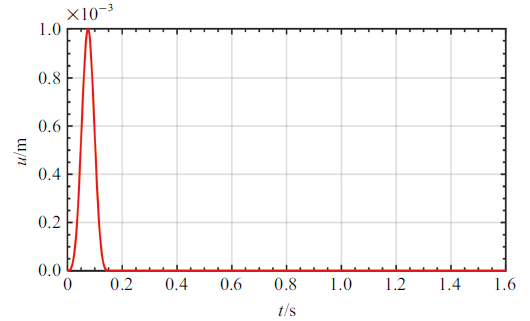新窗口打开|下载原图ZIP|生成PPT
图5脉冲时程图

Fig. 5Pulse time history



分别采用如下两种方案计算自由场: (1)方案I采用传递矩阵方法, 得到线性自由场; (2)方案II采用一维有限元方法, 饱和土层采用Davidenkov非线性本构模型, 参数与三维模型相同, 底边界采用透射边界, 得到非线性自由场. 将自由场作为输入, 并在5个边界面(左、后、右、前、底)上施加透射边界, 进行三维非线性海域场地分析.

理论上, 本模型为水平成层场地, SV波从底部垂直入射, 忽略海水黏性, 因此SV波不能在海水层传播, 海水层$X$向位移应为0. 从图6(a)、图6(b)中可以看到,方案II海水层表面$A$点$X$向位移为0, 与理论相符; 而方案I中, $A$点$X$向位移明显, 幅值量级与输入脉冲波相同, 与理论不符.

图7为方案II中, 一维与三维模型中饱和土层和基岩层各监控点(见图4)的响应, 从图中可以看出, 一维模型和三维模型的响应完全一致,验证了非线性自由场输入的可靠性.

图6

新窗口打开|下载原图ZIP|生成PPT
图6方案I、II海水层监控点$X$向位移对比

Fig. 6Comparison of $X$-direction displacement of water layer monitoring points in scheme I and II

图6

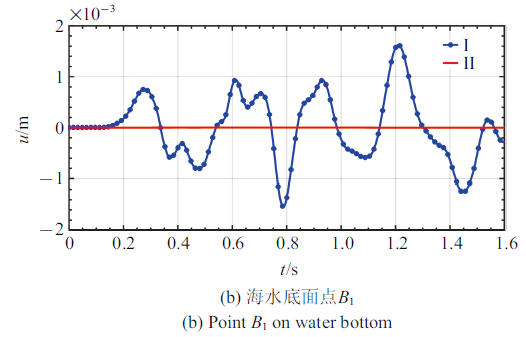新窗口打开|下载原图ZIP|生成PPT
图6方案I、II海水层监控点$X$向位移对比(续)

Fig. 6Comparison of $X$-direction displacement of water layer monitoring points in scheme I and II (continued)

图7

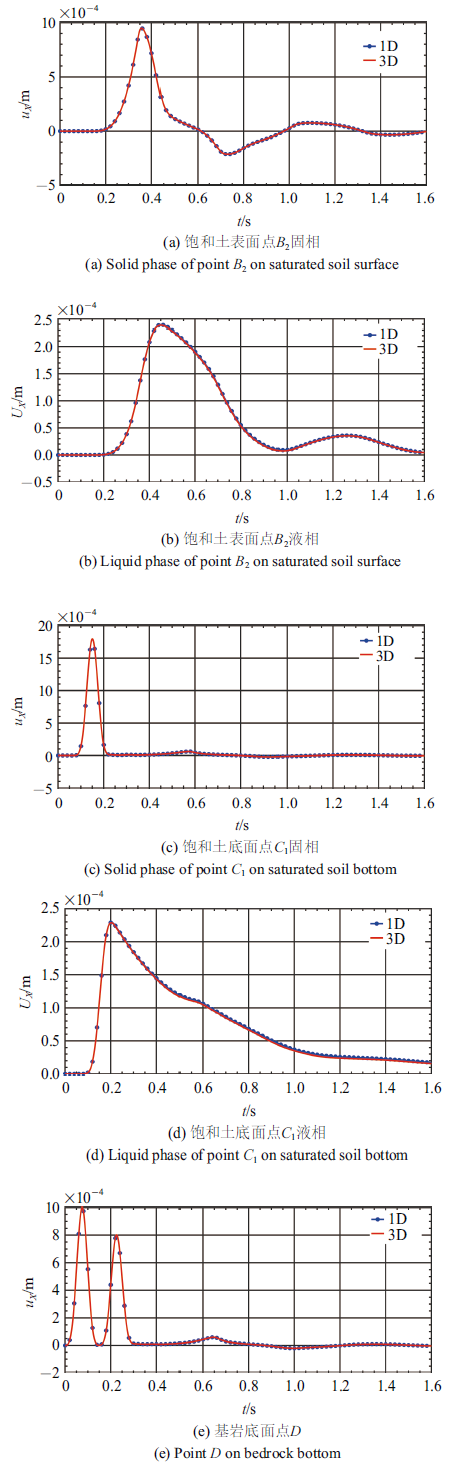新窗口打开|下载原图ZIP|生成PPT
图7方案II一维模型与三维模型$X$向位移对比

Fig. 7Comparison of $X$-direction displacement between 1D model and 3D model in scheme II

2.2 海域场地非线性响应特性分析

采用与2.1节中相同的模型、脉冲输入, 分别考虑饱和土层线性和非线性情形, 分析饱和土层非线性对海域场地响应的影响.

对于线性情形, SV波在场地中的传播过程如图8所示, 根据基岩层剪切波速$c_{3}$和土层剪切波速$c_{2}$估算各波峰到时, $\Delta t_3 =H_3/c_3 =0.075 0$ s, $\Delta t_2 =H_2 /c_2 =0.084 4$ s.

图8

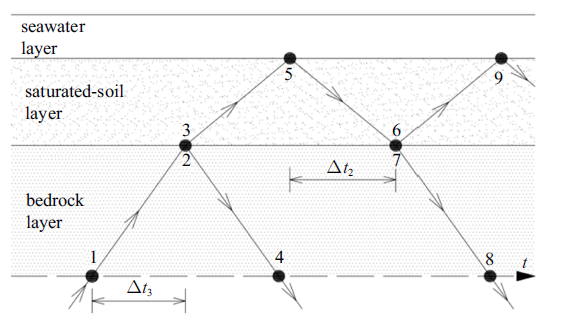新窗口打开|下载原图ZIP|生成PPT
图8SV波传播过程示意图

Fig. 8Schematic diagram of SV wave propagation



根据文献^[31,32], 得SV波垂直入射时, 略去高阶项后, 基岩层-饱和土层分界面上行波反射系数

(18)$ \begin{eqnarray} \label{eq18} R_1 =\frac{1-\psi }{1+\psi } \end{eqnarray}$
其中波阻抗比$\psi ={\rho _2 c_2 } /({\rho _3 }c_3)$, $\rho _2 =\rho _{\rm s2} (1-\beta _2 )$, $\rho _3 =\rho _{\rm s3}$, 得$R_1 =0.547$.

上行波透射系数

(19)$ \begin{eqnarray} \label{eq19} T_1 =\frac{2}{1+\psi } \end{eqnarray}$
得基岩分界面处透射系数为$T_1 =1.547$; 基岩层-饱和土层分界面下行波反射系数

(20)$ \begin{eqnarray} \label{eq20} R_2 =\frac{1-\psi '}{1+\psi '} \end{eqnarray}$
其中波阻抗比$\psi '={\rho _3 c_3 } /({\rho _2 }c_2)$, 得$R_2 =-0.547$; 下行波透射系数

(21)$ \begin{eqnarray} \label{eq21} T_2 =\frac{2}{1+\psi '} \end{eqnarray}$
得基岩分界面处透射系数为$T_2 =0.453$; 类似地, 得饱和土层-海水层分界面上行波反射系数为1.

表2与表3对波峰到时及幅值的实际值与理论值进行对比, 结果误差较小, 证明了线性情形模拟准确.

考虑饱和海床为非线性时, 当SV波传至饱和土层时, 土骨架进入非线性状态, 剪切模量$G_2 $减小, 则剪切波速$c_2 $减小, 因此波阻抗比$\psi $减小, 且$0<\psi <1$, 根据式(18)、式(19), 反射系数$R_1 $增大, 透射系数$T_1 $也增大, 因此图9中波峰$2'$, $3'$, $4'$峰值比线性情形的要大; 图9(a)中波峰$5'$峰值本应随波峰$3'$峰值增大而增大, 但由于饱和土层非线性阻尼效应的影响, 峰值反而减小; 同时, 由于剪切波速$c_2$减小, 图9中波峰$5'$, $6'$, $7'$, $8'$到时相比线性情形有延迟; 另一方面, 剪切波速$c_2 $减小, 则$\psi '$增大, 且$\psi '>1$, 根据式(21), 基岩层-饱和土层交界面下行波透射系数$T_2 $减小, 再加上饱和土层非线性的阻尼效应的影响, 波峰$6'$, $7'$, $8'$峰值减小明显.

此外, 对于饱和土层液相, 黏性力与惯性力相比, 占主导作用. 因此, 图9(b)和图9(d)中液相位移时程表现为明显的扩散过程.

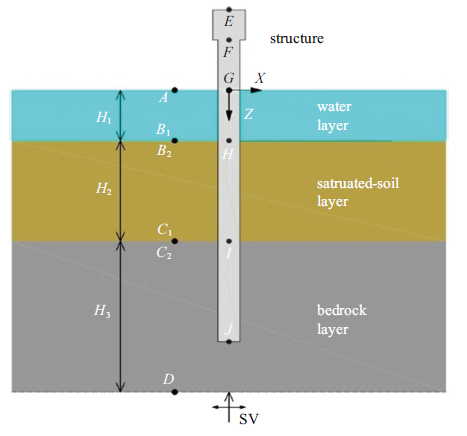
2.3 场地-结构模型

考虑如图10所示的三维场地-结构模型, 场地尺寸为62 m $\times $ 62 m $\times $ 60 m,桩总长60 m, 海水以上部分长10 m, 截面尺寸为4 m $\times $ 4 m,上部承台尺寸为6 m $\times $ 6 m $\times $ 6 m. 单元尺寸为1 m $\times $ 1 m $\times $ 1 m.饱和土层分别按线性、非线性两种情形计算, 场地、桩和承台参数见表1.输入图5所示的的SV脉冲波.

Table 2
表2
表2波峰到时
Table 2Arrival time of wave crest

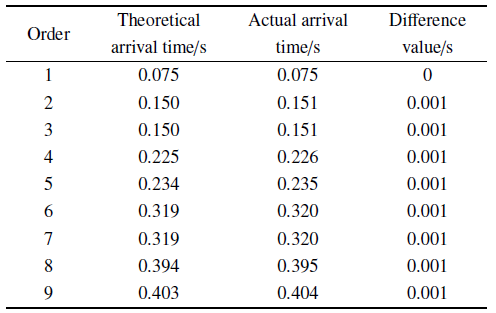新窗口打开|下载CSV

Table 3
表3
表3波峰幅值
Table 3Amplitude of wave crest

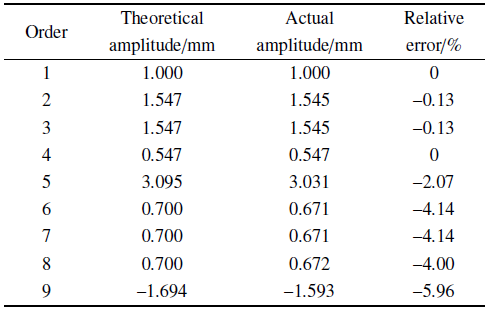新窗口打开|下载CSV

图9

新窗口打开|下载原图ZIP|生成PPT
图9线性和非线性情形各监控点$X$向位移对比

Fig. 9Comparison of $X$-direction displacement of monitoring points in linear and nonlinear cases

图9

新窗口打开|下载原图ZIP|生成PPT
图9线性和非线性情形各监控点$X$向位移对比(续)

Fig. 9Comparison of $X$-direction displacement of monitoring points in linear and nonlinear cases (continued)

图10

新窗口打开|下载原图ZIP|生成PPT
图10三维场地-结构模型示意图

Fig. 103D site-structure model



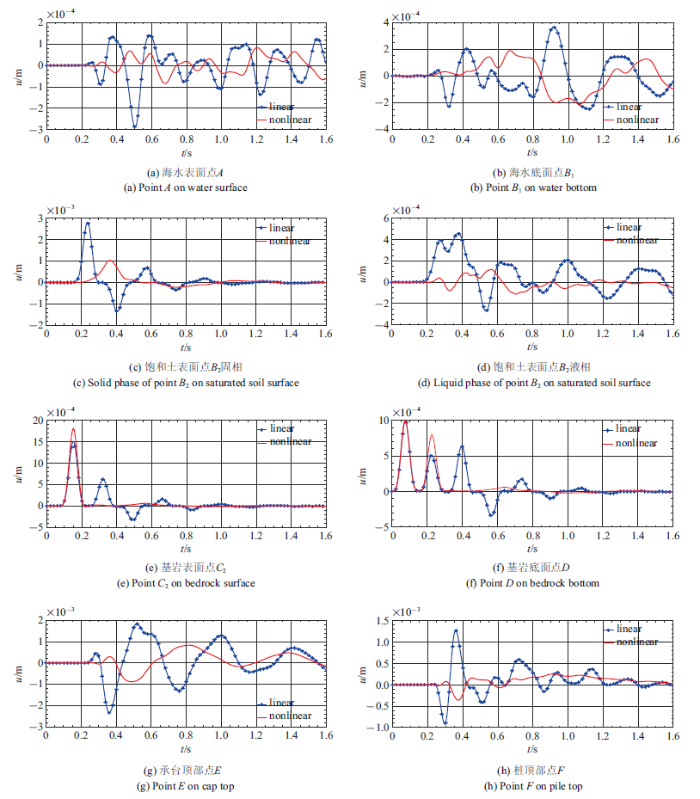
由于桩与结构的存在, 桩的运动会引起海水的运动, 从图11(a)和图11(b)中可以看到, 海水层存在一定位移.

从图11(c) $\sim\!$图11(f)可以看出, 相比线性情形, 非线性情形饱和土层位移幅值要小, 衰减更快; 非线性情形基岩层位移主要是初始的入射波及其在基岩层-饱和土层界面的反射波, 来自饱和土层的透射波幅值很小, 原因与2.2节中的分析相同.

从图11(g) $\sim\!$图11(j)可以看出, 由于饱和土层位移影响, 非线性情形承台顶部、桩上部位移幅值要比线性情形小. 从图11(l)可以看出, 由于基岩层位移影响, 非线性情形桩底部0.3 s后位移较小.

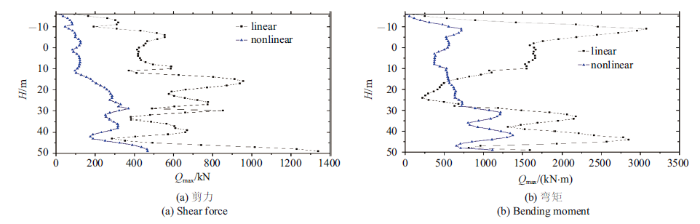
根据桩单元节点的位移, 可以得到不同高度处桩水平截面上的剪力和弯矩, 如图12所示. 从图中可看出, 非线性饱和海床与线性饱和海床情形相比,沿桩身的最大剪力和最大弯矩整体上要小. 无论是线性还是非线性情形, 桩头的弯矩($-$10 m处)均较大, 且在土层界面(10 m和30 m处)附近弯矩为极大值, 桩端附近弯矩也较大.

本算例中饱和土层厚20 m, 在饱和土层中间处水平截取一个平面, 监控该截面不同时刻的孔压. 图13为饱和土层为非线性情形下, SV波垂直入射时,不同时刻该截面的孔压云图.

考虑SV波沿$X$-$Z$平面垂直入射时, 主要反应为$X$方向, 由于模型对称, 则位移关于桩基$X$轴、$Y$轴对称分布. 孔压值主要受速度散度变化的影响,孔压的分布关于桩基$X$轴对称, 关于$Y$轴反对称分布, 如图13所示. 经计算地震波从基岩层入射, 响应峰值0.25 s左右到达监控面处. 下图中可以看出0.05$\sim$0.25 s阶段, 由于桩-土位移差异, 桩周围孔压逐渐集中; 0.25 s左右桩周围孔压到达峰值; 0.25$\sim$1.6 s高压区逐渐由桩周围向四周扩散, 孔压逐渐减小, 整个截面孔压趋于均匀.

图11

新窗口打开|下载原图ZIP|生成PPT
图11监测点$X$向位移对比

Fig. 11Comparison of $X$-direction displacement of monitoring points in linear and nonlinear cases

图11

新窗口打开|下载原图ZIP|生成PPT
图11监测点$X$向位移对比(续)

Fig. 11Comparison of $X$-direction displacement of monitoring points in linear and nonlinear cases (continued)

图12

新窗口打开|下载原图ZIP|生成PPT
图12桩截面内力最大值随深度变化曲线

Fig. 12Maximum of internal force with depth

图13

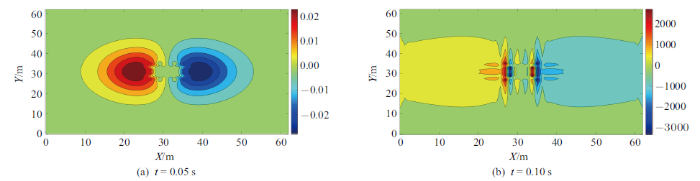新窗口打开|下载原图ZIP|生成PPT
图13不同时刻监控截面孔压云图(单位为Pa)

Fig. 13Distribution of pore water pressure on monitoring section (unit: Pa)

图13

新窗口打开|下载原图ZIP|生成PPT
图13不同时刻监控截面孔压云图(单位为Pa) (续)

Fig. 13Distribution of pore water pressure on monitoring section (unit: Pa) (continued)

3 结语

本文发展了一套海域场地和海水-饱和海床-结构体系地震响应的分析方法, 内域节点采用海水、饱和海床、基岩流固耦合分析的统一计算框架, 采用透射边界模拟无限域的影响, 分析了SV波垂直入射时, 海域场地和海水-饱和海床-结构体系的响应. 讨论了海域场地非线性响应分析时, 自由场对结果的影响, 分析了线性饱和海床和非线性饱和海床情形时响应的差异. 得到如下结论:

(1)就本文算例而言, 计算海域场地非线性地震响应时, 线性自由场将引起较大的误差, 应采用非线性自由场, 且自由场分析的本构应与海域场地分析的本构一致.

(2)由于饱和土层进入非线性, 模量减小, 由基岩入射到饱和土层的反射系数和透射系数均增大, 基岩的响应比线性情形时要大. 透射系数增大, 饱和土层的反应理应增大, 但由于非线性时阻尼增大, 导致饱和土层的非线性响应比线性情形时要小, 且持时要短.

(3)就本文算例而言, 非线性饱和海床情形沿桩身的最大弯矩和剪力要比线性饱和海床情形的小, 非线性饱和海床引起的结构破坏可能主要体现在海床液化引起的基础失效方面.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] 房营光, 孙钧 . 平台-群桩-水流-土体系统的地震反应分析
土木工程学报, 1998(5):56-64
[本文引用: 1]

( Fang Yingguang, Sun Jun . Earthquake response analysis of platform-pile group-water-soil system
China Civil Engineering Journal, 1998(5):56-64 (in Chinese))
[本文引用: 1]

[2] 李忠献, 黄信 . 地震和波浪联合作用下深水桥梁的动力响应
土木工程学报, 2012(11):134-140


( Li Zhongxian, Huang Xin . Dynamic responses of bridges in deep water under combined earthquake and wave actions
China Civil Engineering Journal, 2012(11):134-140 (in Chinese))


[3] 崔杰, 周鹏, 李亚东 等. 地震作用下海底沉管隧道的动力响应分析
地震工程与工程振动, 2016,36(4):96-102


( Cui Jie, Zhou Peng, Li Yadong , et al. Earthquake dynamic response analysis of seabed under the action of immersed tunnel
Earthquake Engineering and Engineering Vibration, 2016,36(4):96-102 (in Chinese))


[4] 李伟华 . 考虑水-饱和土场地-结构耦合时的沉管隧道地震反应分析
防灾减灾工程学报, 2010,30(6):607-613


( Li Weihua . Seismic Response analysis of immersed tube tunnels considering water saturated soil site structure coupling
Journal of Disaster Prevention and Mitigation Engineering, 2010,30(6):607-613 (in Chinese))


[5] Goyal A, Chopra AK . Earthquake analysis of intake-outlet towers including tower-water-foundation-soil interaction
Earthquake Engineering and Structural Dynamics, 1989(18):325-344


[6] Spyrakos CC, Xu C . Soil-structure-water interaction of intake-outlet towers allowed to uplift
Soil Dynamics & Earthquake Engineering, 1997,16(2):151-159


[7] Arablouei A, Gharabaghi ARM, Ghalandarzadeh A , et al. Effects of seawater-structure-soil interaction on seismic performance of caisson-type quay wall
Computers & Structures, 2011,89(23):2439-2459


[8] Ye JH, Wang G . Seismic dynamics of offshore breakwater on liquefiable seabed foundation
Soil Dynamics and Earthquake Engineering, 2015,76:86-99


[9] Wang P, Zhao M, Du X L , et al. Wind, wave and earthquake responses of offshore wind turbine on monopile foundation in clay
Soil Dynamics & Earthquake Engineering, 2018,113:47-57
[本文引用: 1]

[10] Idriss IM, Seed HB . Seismic response of horizontal soil layers.
Journal of the Soil Mechanics and Foundation Division, ASCE, 1968,94(SM4):1003-1031
[本文引用: 1]

[11] 李小军 . 一维土层地震反应线性化计算程序//廖振鹏. 地震小区化-理论与实践. 北京: 地震出版社, 1989: 250-265
[本文引用: 1]

( Li Xiaojun. A computer program for calculating earthquake response of ground layered soil//Liao Zhenpeng. Seismic Microzonation——Theory and Practice. Beijing: Seismological Press, 1989: 250-265(in Chinese))
[本文引用: 1]

[12] 张克绪, 李明宰, 王治琨 . 基于非曼辛准则的土体弹塑性模型
地震工程与工程振动, 1997,17(2):74-81
[本文引用: 1]

( Zhang Kexu, Li Mingzai, Wang Zhikun . Dynamic elastic-plastic models of soils basing on non-mansing's rule
Earthquake Engineering and Engineering Vibration, 1997,17(2):74-81 (in Chinese))
[本文引用: 1]

[13] 陈国兴, 庄海洋 . 基于Davidenkov骨架曲线的土体动力本构关系及其参数研究
岩土工程学报, 2005,27(8):860-864


( Chen Guoxing, Zhuang Haiyang . Developed nonlinear dynamic constitutive relations of soils based on Davidenkov skeleton curve
Chinese Journal of Geotechnical Engineering, 2005,27(8):860-864 (in Chinese))


[14] 赵丁凤, 阮滨, 陈国兴 等. 基于Davidenkov骨架曲线模型的修正不规则加卸载准则与等效剪应变算法及其验证
岩土工程学报, 2017,39(5):888-895
[本文引用: 1]

( Zhao Dingfeng, Ruan Bin, Chen Guoxing , et al. Validation of the modified irregular loading- reloading rules based on Davidenkov skeleton curve and its equivalent shear strain algorithm implemented in ABAQUS
Chinese Journal of Geotechnical Engineering, 2017,39(5):888-895 (in Chinese))
[本文引用: 1]

[15] 陈少林, 朱学江, 赵宇昕 等. 考虑土骨架非线性的饱和土-结构相互作用分析
地震工程与工程振动, 2019,39(1):114-127
[本文引用: 1]

( Chen Shaolin, Zhu Xuejiang, Zhao Yuxin , et al. Analysis of saturated soil-structure interaction considering nonlinearity of soil skeleton
Earthquake Engineering and Engineering Vibration, 2019,39(1):114-127 (in Chinese))
[本文引用: 1]

[16] Hashash YMA, Groholski DR, Phillips CA , et al. DEEPSOIL 5.0 User Manual and Tutorial.
2011


[17] Lee MKW, Finn W . DESRA-2: Dynamic Effective Stress Response Analysis of Soil Deposits with Energy Transmitting Boundary Including Assessment of Liquefaction Potential.
The University of British Columbia, Faculty of Applied Science, Vancouver, British Columbia, 1978


[18] Martin PP, Seed HB . One-dimensional dynamic ground response analyses.
Journal of Geotechnical Engineering, ASCE, 1982,108(7):935-952
[本文引用: 2]

[19] 赵宇昕, 陈少林 . 关于传递矩阵法分析饱和成层介质响应问题的讨论
力学学报, 2016,48(5):1145-1158
[本文引用: 1]

( Zhao Yuxin, Chen Shaolin . Discussion on the matrix propagator method to analyze the response of saturated layered media
Chinese Journal of Theoretical and Applied Mechanics, 2016,48(5):1145-1158 (in Chinese))
[本文引用: 1]

[20] 柯小飞, 陈少林, 张洪翔 . P-SV波入射时海水-层状海床体系的自由场分析
振动工程学报, 2018, 录用
[本文引用: 1]

( Ke Xiaofei, Chen Shaolin, Zhang Hongxiang . Freefield analysis of seawater-layered seabed system at P-SV wave incident
Journal of Vibration Engineering, 2018, accepted (in Chinese))
[本文引用: 1]

[21] 陈少林, 宗娟 . 平面波任意角度入射时波动散射问题输入的一种实现方法
固体力学学报, 2018,39(1):80-89
[本文引用: 1]

( Chen Shaolin, Zong Juan . Wave input method for three-dimensional wave scattering simulation of an incident wave in an arbitrary direction
Chinese Journal of Solid Mechanics, 2018,39(1):80-89 (in Chinese))
[本文引用: 1]

[22] 李山有, 廖振鹏 . 地震体波斜入射情形下台阶地形引起的波型转换
地震工程与工程振动, 2002,22(4):9-15
[本文引用: 1]

( Li Shanyou, Liao Zhenpeng . Wave-type conversion caused by a step topography subjected to inclined seismic body wave
Earthquake Engineering and Engineering Vibration, 2002,22(4):9-15 (in Chinese))
[本文引用: 1]

[23] 刘晶波, 王艳 . 成层半空间出平面自由波场的一维化时域算法
力学学报, 2006,38(2):219-225


( Liu Jingbo, Wang Yan . A 1-D time-domain methed for 2-D wave motion in elastic layers half-space by antiplane wave oblique incidence
Chinese Journal of Theoretical and Applied Mechanics, 2006,38(2):219-225 (in Chinese))


[24] 黄璟奇 . 岩体隧道非线性地震响应分析. [博士论文]
北京: 北京工业大学, 2015
[本文引用: 1]

( Huang Jingqi . Study on nonlinear seismic response of rock tunnels. [PhD Thesis]
Beijing: Beijing University of Technology, 2015 (in Chinese))
[本文引用: 1]

[25] 陈少林, 柯小飞, 张洪翔 . 海洋地震工程流固耦合问题的统一计算框架
力学学报, 2019,51(2):594-606
[本文引用: 1]

( Chen Shaolin, Ke Xiaofei, Zhang Hongxiang . A unified computational framework for fluid-solid coupling in marine earthquake engineering
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(2):594-606 (in Chinese))
[本文引用: 1]

[26] 陈少林, 程书林, 柯小飞 . 海洋地震工程流固耦合问题的统一计算框架-不规则界面情形
力学学报, 2019,51(5):1517-1529
[本文引用: 3]

( Chen Shaolin, Cheng Shulin, Ke Xiaofei . A unified computational framework for fluid-solid coupling in marine earthquake engineering: irregular interface case
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(5):1517-1529 (in Chinese))
[本文引用: 3]

[27] Biot MA . Theory of propagation of elastic waves in a fluid-saturated porous solid
Acoust Soc Am, 1956,28:168-191
[本文引用: 1]

[28] Biot MA . Mechanics of deformation and acoustic propagation in porous media
Journal of Applied Physics, 1962,33(4):1482-1498
[本文引用: 1]

[29] Liao ZP, Wong HL . A transmitting boundary for the numerical simulation of elastic wave propagation
Soil Dynamics and Earthquake Engineering, 1984,3:174-183
[本文引用: 1]

[30] Chen SL, Liao ZP . Multi-transmitting formula for attenuating waves
Acta Seismologica Sinica, 2003,16(3):283-291
[本文引用: 1]

[31] Deresiewicz H, Rice JT . The effect of boundaries on wave propagation in a liquid-filled porous solid: V. Transmission across a plane interface
Bulletin of the Seismological Society of America, 1964,54(1):409-416
[本文引用: 1]

[32] Deresiewicz H . The effect of boundaries on wave propagation in a liquid-filled porous solid: VII. Surface waves in a half-space in the presence of a liquid layer
Bulletin of the Seismological Society of America, 1964,54(1):425-430
[本文引用: 1]