复合材料水翼水动力与结构强度特性数值研究 1)

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-01

陈倩^*, 张汉哲^*, 吴钦^,^*^,²⁾, 傅晓英^?, 张晶^*, 王国玉^*

* 北京理工大学，北京 100081

? 四川大学，成都 610000

THE NUMERICAL INVESTIFATION ON HYDRODYNAMIC AND STRUCTURAL STRENGTH OF A COMPOSITE HYDROFOIL ¹⁾

Chen Qian^*, Zhang Hanzhe^*, Wu Qin^,^*^,²⁾, Fu Xiaoying^?, Zhang Jing^*, Wang Guoyu^*

* Beijing Institute of Technology，Beijing 100081，China

? Sichuan University，Chengdu 610000，China

通讯作者: 2)吴钦，助理教授，主要研究方向：空化流固耦合. E-mail:wuqin919@bit.edu.cn

收稿日期:2019-04-26网络出版日期:2019-09-18

基金资助:

1)国家自然科学基金.51839001
国家自然科学基金.91752105

四川大学水力学与山区河流开发保护国家重点实验室开放基金资助项目

Received:2019-04-26Online:2019-09-18
作者简介 About authors

摘要
针对复合材料水翼存在的流固耦合求解问题,结合其自身特有属性,对复合材料水翼结构变形特性进行了数值仿真计算研究.研究建立了复合材料水翼流固耦合数值计算模型,并将数值计算结果与Zarruk等的实验结果进行对比,验证模型的正确性,得出复合材料水翼尖端扭转角随雷诺数的增加而增加的研究结论.基于数值计算模型,系统地研究了不同铺层角对复合材料水翼水动力特性及强度特性的影响,结果表明：不同铺层角复合材料水翼的尖端扭转角,随铺层角的增大而减小,而其尖端位移量随铺层角的增大先减小后增大.为了削弱工程常数的影响对复合材料水翼变形的影响,研究提出了无量纲扭转角和无量纲位移量,进一步探究复合材料水翼结构的弯扭耦合作用对其变形特性的影响.最后利用蔡$\!$-$\!$-$\!$吴失效准则进行复合材料水翼强度特性的判断和分析,结果表明：不同铺层角复合材料水翼的蔡$\!$-$\!$-$\!$吴系数,随铺层角的增大呈现先减小后增大的趋势,其中0$^\circ$铺层时的复合材料水翼蔡$\!$-$\!$-$\!$吴系数最小,50$^\circ$铺层时的复合材料水翼的蔡$\!$-$\!$-$\!$吴系数最大.
关键词： 复合材料水翼;铺层角度;流固耦合;强度特性

Abstract
This paper investigates systematically the structural deformation characteristics of composite hydrofoils with own unique properties by numerical method to solve the fluid structure interaction problem on the composite hydrofoils. It establishes a numerical model of composite hydrofoils with fluid structure interaction in this study, which verifies the correctness of the numerical model by comparing the calculated results to the experimental results of Zarruk, and the numerical results show that the tip torsion angle of the composite hydrofoils increases with the increase of the Reynolds number. This paper investigates and analyses systematically the influence of the ply angle on the hydrodynamic performance and strength performance of composite hydrofoils in view of the numerical method. The results illustrate that the tip torsion angle of composite hydrofoils decreases with increasing the ply angle, while the tip displacement of composite hydrofoils decrease firstly and then increase with increase of ply angle. The study proposes two dimensionless, the dimensionless torsion angle and the dimensionless displacement, to eliminate the effect of engineering constants of composite on the structure deformation of composite hydrofoils, which is used to further investigate the influence of the bending-torsion coupling effect on the deformation characteristics of the composite hydrofoils. The strength of the composite hydrofoils is judged and studied by using the Tsai-Wu failure criterion. The numerical results show that the Tsai-Wu coefficient of composite hydrofoils decreases firstly and then increases with the increase of the ply angle, where the lowest Tsai-Wu coefficient and the largest Tsai-Wu coefficient appears in the 0$^\circ$layered composite hydrofoil and the 50$^\circ$layered composite hydrofoil, respectively.
Keywords：composite hydrofoil;ply angle;fluid structure interaction;strength

PDF (24814KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex 收藏本文
本文引用格式
陈倩, 张汉哲, 吴钦, 傅晓英, 张晶, 王国玉. 复合材料水翼水动力与结构强度特性数值研究 ¹⁾. 力学学报[J], 2019, 51(5): 1350-1362 DOI:10.6052/0459-1879-19-107
Chen Qian, Zhang Hanzhe, Wu Qin, Fu Xiaoying, Zhang Jing, Wang Guoyu. THE NUMERICAL INVESTIFATION ON HYDRODYNAMIC AND STRUCTURAL STRENGTH OF A COMPOSITE HYDROFOIL ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2019, 51(5): 1350-1362 DOI:10.6052/0459-1879-19-107

引言

水力机械作为重要的工业装备,在水电开发、农业灌溉、海洋运输等领域起着重要的作用^[1,2]. 在传统水力机械设计中多采用金属材料制造叶片,由于其固有频率低、振动模态复杂,流动容易引起结构振动甚至导致共振^[3],水力机械的安全高效稳定运行一直是困扰行业发展的关键问题. 同时,在船舶工程领域,复杂的海洋环境及空化^[4-5]现象会造成水力机械的严重腐蚀^[6],致使其使用寿命降低. 近年来,由于先进复合材料具有良好的适应性、减重效果显著、抗腐蚀性强等特点^[7],被广泛应用于螺旋桨^[8-9]、喷水推进器等水力机械设备中^[10-12],为提高水力机械安全稳定性以及拓宽运行高效区提供了重要契机.

复合材料最早应用于航空航天等领域,主要用来提高结构的综合性能^[13].从神舟一号到神舟九号,从无人到载人,飞船推进分系统的主承力构件主要采用哈尔滨玻璃钢研究院制造的碳纤维复合材料^[14],同时空客A380和波音B757设计的民航客机中采用先进复合材料分别占飞机总体重量的25%和50%.复合材料不仅具有显著的减重效果,在气动力学的研究中也体现出良好的气动性能.Ganguli和Chopra^[15],Soykasap和Hodges^[16]将气动弹性剪裁技术应用于复合材料直升机和旋翼叶片设计过程,有效提高了结构稳定性,减小了叶片动载荷及其振动.1995年美国国防部基于16%的F/A-18机翼模型风洞试验表明,自适应机翼增加了5% $\sim$8%的升力,机翼结构平均减重20%.

在水动力学方面,由于复合材料的流固耦合现象十分显著^[17-18],对水力机械的水动力特性会产生不同的影响.Zarruk等^[19]对金属材料钢、铝和铺层角为0$^\circ$和30$^\circ$的复合材料水翼进行水动力性能和结构响应的研究,结果表明：0$^\circ$铺层复合材料水翼产生正扭转变形,水翼有效攻角增大,而30$^\circ$铺层由于弯扭耦合特性的存在,使复合材料水翼呈现出负扭转变形,水翼有效攻角减小. Motley等^[20]和Young等^[21]研究了不同来流条件下叶片倾角随水动力载荷的变化情况,结果表明：复合材料结构的弯扭耦合效应有效提高了结构系统在非设计工况下的水力性能.并根据复合材料属性的研究结果,进一步给出了复合材料螺旋桨新的设计理念,即利用材料设计提高螺旋桨自适应性.Berthelet等^[22]研究复合材料铺层角度对结构的影响,结果表明,当铺层角度与所受载荷不一致时,产生的阻尼力较大.张汉哲等^[23]通过数值计算方法,研究复合材料水翼的变形特性,并提出复合材料水翼尖端扭转角和中面扭转曲率之间的关系.

随着计算机的出现及实际工程的需求,数值计算方法迅速发展^[24-25]. Murray等^[26]利用有限元方法,研究复合材料有限元模型(finite element model,FEM)的准确性,结果表明,复合材料FEM可以精确计算实验模型的变形,且吻合度较高. Brandon 等^[27]使用有限元方法及实验模型,分析不同复合材料水翼的模态,结果表明,材料类型及材料的铺层序列对模态均有显著影响.吴钦等^[28-29]基于完全耦合算法分别对二维水翼和弹性水翼的流固耦合特性进行了数值研究,探究Theodorsen模型对水翼结构的水弹性相应的影响,并得出柔性水翼空泡演化规律等结论.

已有研究表明,复合材料与金属材料相比具有比强度高、减重效果显著、抗腐蚀性强等优点,被广泛应用于航空航天、交通运输等领域.不同铺层角复合材料的工程常数存在明显差异,现有研究较少涉及不同铺层角复合材料在水动力学领域中的水动力性能、结构稳定性、变形特性等流固耦合特性的研究.本工作采用复合材料水翼流固耦合数值计算方法,研究了不同铺层角复合材料水翼在不同流动工况下的流固耦合特性,获得了复合材料水翼的水动力性能和尖端变形量,并提出无量纲变形量来表征复合材料结构的弯扭耦合效应,并基于蔡吴失效准则对复合材料水翼的强度特性进行了分析,以期为复合材料螺旋桨的设计提供了参考依据.

1 数值计算方法

1.1 流固耦合数值计算方法

流固耦合问题的求解需要同时考虑流场和结构场的求解及其之间数据的传递,为了较好地研究这种相互作用,本文基于ANSYS Workbench软件平台的System Coupling模块,采用紧耦合^[30]的流固耦合计算方法,其计算流程如图1所示.首先对流体域进行初值计算;然后,利用流固耦合交界面将流体域的信息传递至结构场,进行有限元结构分析;之后,结构场变形信息再通过流固耦合交界面传递于流场中,对流域的网格进行更新并求解.经过每一时间步内子迭代步的不断交叉求解,实现收敛,完成计算.

图1

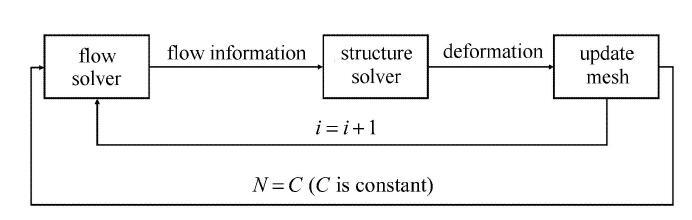新窗口打开|下载原图ZIP|生成PPT
图1流固耦合计算求解流程图

Fig. 1Flowchart of the fluid structure interaction

在流场计算中,N-S方程^[31]的求解是计算的关键和核心,通过对方程的求解,得出流场离散化时间、空间上的流体信息,从而根据流场性能参数获得流场流动特性. 在数值计算中,不考虑能量的相互转换,基本控制方程组如下所示

(1)$\dfrac{\partial v_j }{\partial x_j } = 0 $

(2)$\dfrac{\partial \left( {\rho v_i } \right)}{\partial t} + \dfrac{\partial \left({\rho v_i v_j } \right)}{\partial x_j } = - \dfrac{\partial p}{\partial x_i } + \mu \dfrac{\partial ^2v_i}{\partial x_i \partial x_j } $

式中,$v$为来流速度,$P$为流场压力, $\rho $为流体密度, $\mu $为流体运动黏度,下标$i,j$分别为$x$,$y$坐标.

计算选用由Launder和Spalding^[32]于1972年提出的标准$k$-$\varepsilon $湍流模型,其控制方程如下

(3)$\rho \dfrac{Dk}{Dt} = \dfrac{\partial }{\partial x_i }\left[ {\left( {\mu + \dfrac{\mu_t }{\sigma _k }} \right)\dfrac{\partial k}{\partial x_i }} \right] + G_k + G_{\rm b} - \rho \varepsilon -Y_{\rm M} $

$\rho \dfrac{D\varepsilon }{Dt} = \dfrac{\partial }{\partial x_j }\left[ {\left( {\mu +\dfrac{\mu _t }{\sigma _k }} \right)\dfrac{\partial \varepsilon }{\partial x_i }} \right] + $

(4)$\qquad C_{1\varepsilon } \dfrac{\varepsilon }{k}\left( {G{ }_k + C_{3\varepsilon } G_b} \right) - C_{2\varepsilon } \rho \dfrac{\varepsilon ^2}{k} $

式中,$k$和$\varepsilon$分别是湍动能和耗散率,$G_{k}$是由于平均速度梯度引起的湍动能产生项,$G_{b}$是由于浮力影响引起的湍动能产生项,$Y_{\rm M}$是可压速湍流脉动膨胀对总的耗散率的影响. 湍流黏性系数$\mu_t = \rho C_\mu k^2/\omega $,其中$C_{1\varepsilon }$, $C_{2\varepsilon }$, $C_{\mu }$, $\sigma_{k}$, $\sigma _{\varepsilon }$均为常数项.

利用有限元对复合材料水翼结构场进行分析,复合材料水翼在水动力作用下的动力学方程^[33]定义为

(5)$${\pmb M}_{\rm s} \ddot{\pmb X} +{\pmb C}_{\rm s} \dot{\pmb X} + {\pmb K}_{\rm s} {\pmb X } = {\pmb F}_{\rm HE} $$

式中, ${\pmb M}_{\rm s}$为结构质量矩阵, ${\pmb C}_{\rm s}$为结构阻尼矩阵, ${\pmb K}_{\rm s}$为结构刚度矩阵, ${\pmb X} $为结构位移、$\dot{\pmb X}$为结构速度、$\ddot{\pmb X}$为结构加速度,${\pmb F}_{\rm HE}$代表流固耦合作用下结构所受流场力.

1.2 流场计算模型

数值计算采用与文献^[19]实验一致的梯形水翼,截面形状为尾缘截断型NACA000,9翼型,几何方程为

(6)$\dfrac{y}{c_0 } = 0.45\Bigg [ 0.296,9\left( {\dfrac{x}{c_0 }} \right)^{0.5} - 0.126\left( {\dfrac{x}{c_0 }}\right) - 0.351,6\left( {\dfrac{x}{c_0 }} \right)^2 +$$\qquad 0.284,3\left( {\dfrac{x}{c_0 }} \right)^3 - 0.088,90\left( {\dfrac{x}{c_0 }}\right)^4\Bigg ] $

式中,$x$和$y$分别为翼型的横坐标值和厚度值,$c_{0}$为平均弦长,修正后的水翼在90%弦长处垂直截断后形成钝形尾部,其基线形状与坐标系定义如图2所示. 水翼展长为$d =0.3$,m,尖端弦长为$c_{1} =0.06$,m,根部弦长为$c_{2}=0.12$,m.

图2

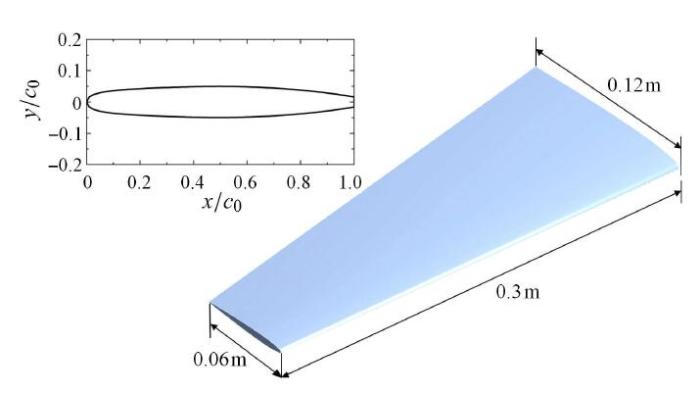新窗口打开|下载原图ZIP|生成PPT
图2修正型NACA0009水翼几何结构示意图

Fig. 2Schematic of geometry of trapezoidal hydrofoil with modified

计算流域边界条件的相应设置与文献^[19]实验保持一致,如图3所示,计算流域长2.6,m,宽0.6,m,高0.6,m,复合材料水翼中心距入口处0.7,m位置. 来流速度根据雷诺数$Re=v_{\rm c}/\nu _{\rm f}$计算得出,其中$v$表示来流速度,$c$表示平均弦长(0.09,m),$\nu _{\rm f}$表示流体动力黏度.对计算流域进行网格划分,如图4所示,为了提高计算精度,对水翼周边网格进行局部加密,网格总数约为352万,水翼近壁面区$y$+值约为25.

图3

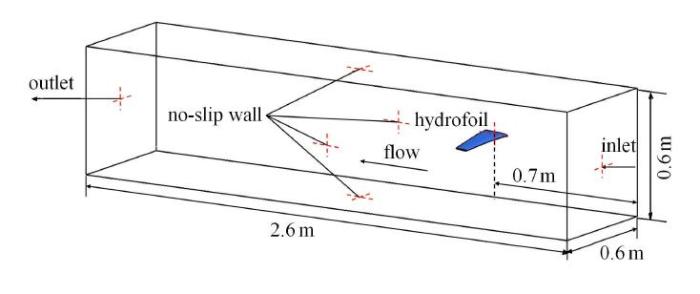新窗口打开|下载原图ZIP|生成PPT
图3流域边界条件设置

Fig. 3Boundary conditions of fluid domain with global coordinates

图4

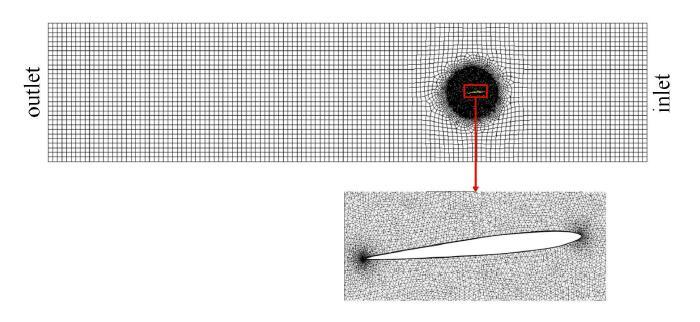新窗口打开|下载原图ZIP|生成PPT
图4计算流域网格划分

Fig. 4Mesh distribution of the fluid domain

1.3 复合材料水翼结构模型

复合材料选型及铺层方式与文献^[19]一致. 采用对称铺层,其铺层顺序为[(0$^{\circ}$/90$^{\circ })_{\rm g\hbox{-}basket}$, (0$^{\circ }$/90$^{\circ })_{\rm g\hbox{-}biaxial}$, $(\alpha )_{\rm 5c}$, (0$^{\circ }$/90$^{\circ })_{\rm 2g\hbox{-}biaxial}$, $(\alpha )_{\rm 4c}]_{\rm s}$,如图5(a)所示,其中下标g和c分别表示玻璃纤维和碳纤维,下标s表示铺层方式为对称铺层,下标数字表示纤维层数, $\alpha $表示铺层角,定义为纤维方向和与$x$轴正方向之间的夹角,如图5(b)所示. 各部分铺层的材料属性如表1所示.

图5

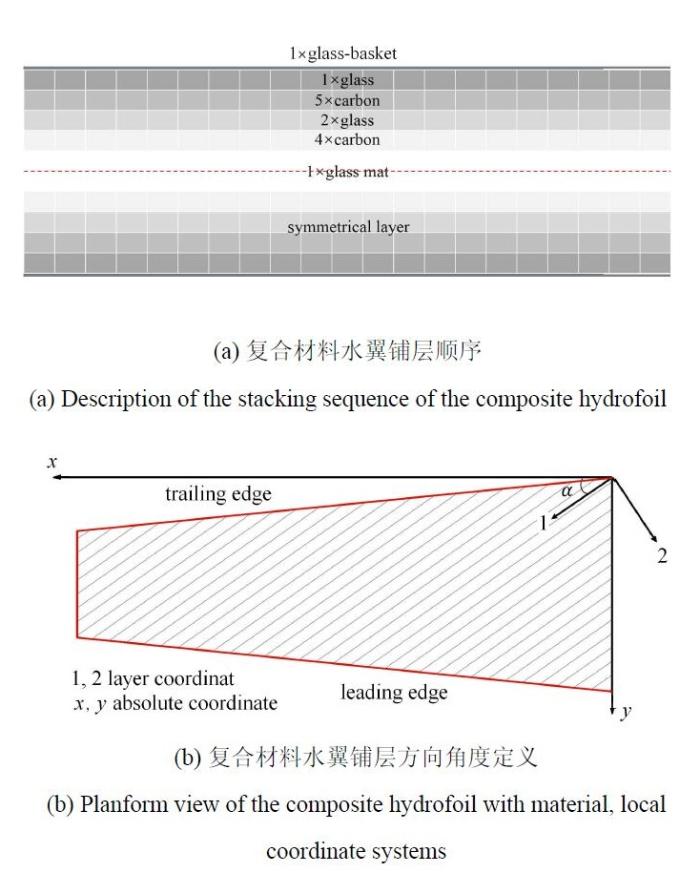新窗口打开|下载原图ZIP|生成PPT
图5复合材料水翼基本铺层顺序和角度示意图

Fig. 5The stacking sequence and planform view of the composite hydrofoil

Table 1
表1
表14种材料属性
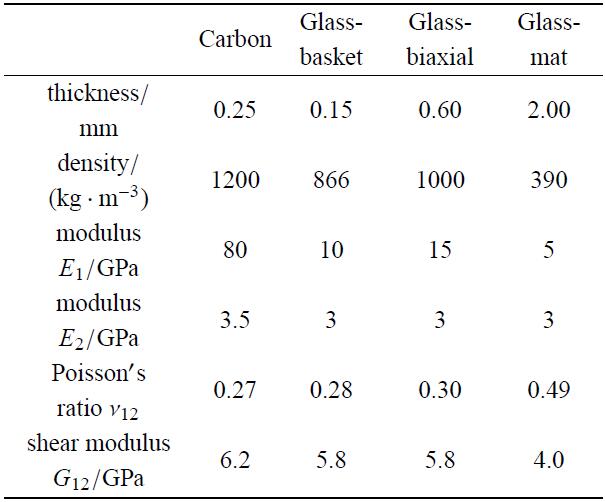Table 1Structural properties of the fabric layers

新窗口打开|下载CSV

由于水动力载荷本身具有较大的压力梯度和非线性载荷等特性,同时分析问题为实体水翼结构,因此选用三维20节点的具有准确变形效果的SOLID186单元体作为复合材料水翼结构的有限元单元体,复合材料水翼结构场的网格划分及边界条件如图6所示,复合材料水翼根部设置为固定端面,其余表面均定义为流固耦合交界面.

2 结果与讨论

2.1 流固耦合数值计算方法验证

为了验证紧耦合流固耦合数值计算方法的稳定性和可靠性,对铺层角$\alpha=0^\circ$,雷诺数${Re}=1.0\times 10^{6}$,初始攻角$\beta _{0}=2^\circ$的复合材料水翼进行流场计算残差收敛情况进行说明.

图6

新窗口打开|下载原图ZIP|生成PPT
图6复合材料水翼结构场网格划分及边界条件

Fig. 6Structure mesh and boundary conditions of composite hydrofoil

在耦合设置中迭代步控制为2步,子迭代步范围控制为2$\sim $10步,耦合数据残差收敛目标值为0.01.图7给出了流场与结构场耦合变量残差曲线图,由图7可知,在第1个迭代步中进行了4次子迭代计算,即可实现流场与结构场传递1/2的载荷,且流场与结构场信息变量传递的残差值均小于残差收敛目标0.01.在第2个迭代步中进行了3次子迭代计算,即完成了流场与结构场剩余载荷的传递,且残差值满足残差收敛目标0.01.因此,认为本文采用的紧耦合计算方法在计算不可压缩流体流固耦合时,具有较好的收敛性,其计算结果稳定可靠.

图7

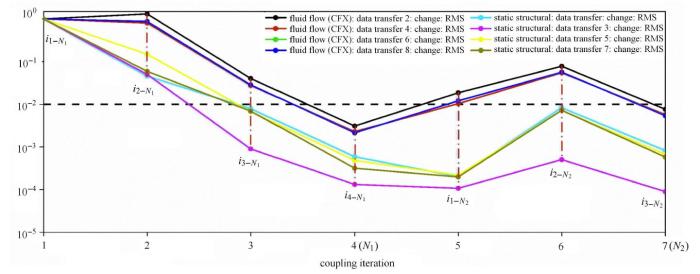新窗口打开|下载原图ZIP|生成PPT
图7流固耦合变量传递残差曲线图

Fig. 7Residual of variable in fluid-solid interaction

为了验证数值计算方法的准确性,对铺层角分别为$\alpha =0^\circ$和$\alpha=30^\circ$的复合材料水翼进行数值计算,其中雷诺数${Re}=1.0 \times 10^{6}$,初始攻角分别为 $\beta_{0}=2^\circ$,4$^\circ$和6$^\circ$.

图8给出了数值计算的复合材料水翼尖端速度云图及变形量示意图,并与文献^[19]实验结果进行对比,数值结果与实验结果吻合度较高.对比同一铺层角复合材料水翼在不同初始攻角下的速度云图发现,随着初始攻角$\beta_{0}$的增大,复合材料水翼尖端前缘吸力面的高速区域逐渐增大,且扭转角$\theta $和尖端位移量$\delta $也呈现上升趋势.对比不同铺层角复合材料水翼在同一初始攻角下的速度云图发现, 铺层角$\alpha=0^\circ$时的复合材料水翼的尖端扭转角 $\theta $均为正值,而铺层角$\alpha=30^\circ$时的复合材料水翼的尖端扭转角 $\theta $均为负值.当铺层角 $\alpha=0^\circ$时,复合材料水翼尖端发生逆时针扭转, 即在来流作用下复合材料水翼的有效攻角增加;当铺层角 $\alpha=30^\circ$时,复合材料水翼尖端产生顺时针的扭转,即在来流作用下复合材料水翼的有效攻角减小.

图8

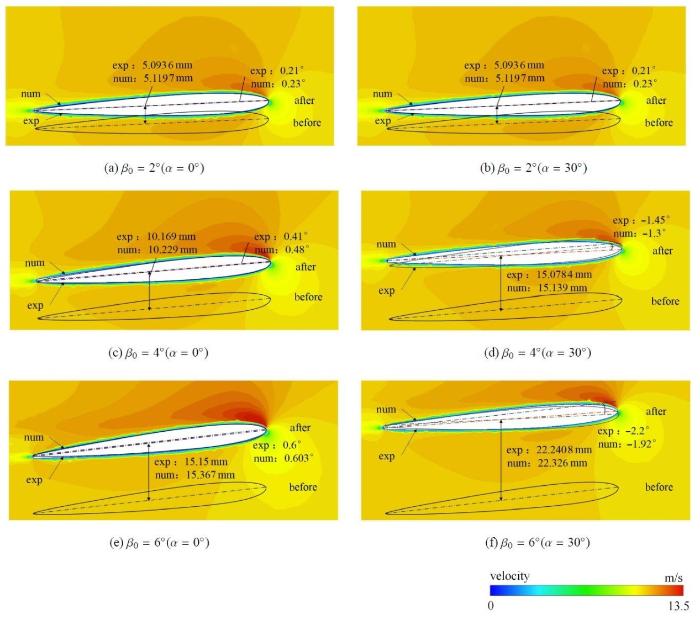新窗口打开|下载原图ZIP|生成PPT
图8复合材料水翼尖端流场速度云图及尖端变形量示意图

Fig. 8Velocity contours and deformation of composite hydrofoil

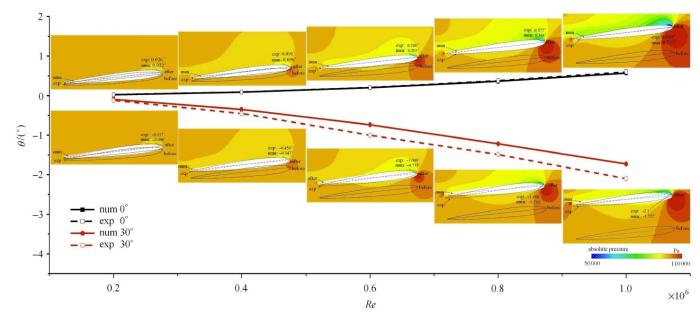
进一步针对上述复合材料水翼进行不同雷诺数工况数值计算,其中初始攻角均为 $\beta _{0}=6^\circ$.图9给出了不同铺层角复合材料水翼($\alpha =0^\circ$和 $\alpha=30^\circ$)尖端扭转角随雷诺数的变化曲线图及压力云图,其中黑线实框表示复合材料水翼尖端变形前位置,白色区域表示复合材料水翼尖端变形后位置,并与文献^[19]实验结果进行对比,发现0$^\circ$铺层复合材料水翼的数值结果与实验结果一致,30$^\circ$铺层符合材料水翼与实验吻合度较好.

图9

新窗口打开|下载原图ZIP|生成PPT
图9不同铺层角复合材料水翼($\alpha =0^\circ$和$\alpha =30^\circ$)尖端扭转特性曲线图及压力云图

Fig. 9Absolute pressure contours and twist angles at tip of composite hydrofoil with two ply angles ($\alpha $)

由图9可知,随着雷诺数${Re}$的增大,不同铺层角复合材料水翼($\alpha =0^\circ$和$\alpha =30^\circ$)的尖端扭转角 $\theta $在绝对值上均呈现上升趋势,且30$^\circ$铺层复合材料水翼的增长速率明显大于0$^\circ$铺层. 其中,0$^\circ$铺层复合材料水翼均产生正值扭转角,即在来流作用下,水翼的有效攻角增加;30$^\circ$铺层复合材料水翼均产生负值扭转角,即在来流作用下,水翼的有效攻角减小. 对比同一铺层角水翼在不同雷诺数条件下的压力云图可知,随着雷诺数$Re$的增大,不同铺层角复合材料水翼($\alpha =0^\circ$和 $\alpha =30^\circ$)尖端前缘压力面的高压区域逐渐增大. 对比不同铺层角复合材料水翼( $\alpha =0^\circ$和$\alpha =30^\circ$)在同一雷诺数条件下的压力云图可知,0$^\circ$铺层复合材料水翼的尖端前缘压力面的高压区域大于30$^\circ$铺层,这是由于0$^\circ$铺层复合材料水翼产生的尖端扭转角有效攻角增大,而30$^\circ$铺层复合材料水翼产生的尖端扭转角有效攻角减小.

2.2 不同铺层复合材料水翼水动力特性分析

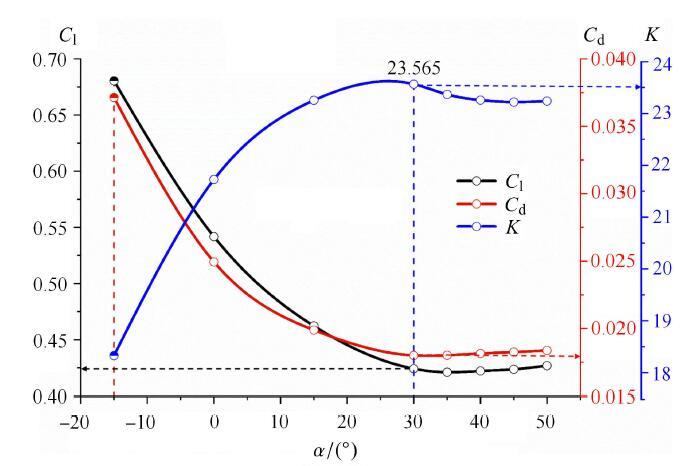
为了探究不同铺层角复合材料水翼的水动力特性,本文针对典型工况下不同铺层角复合材料水翼进行数值计算,其中雷诺数${Re}=1.0\times 10^{6}$,初始攻角$\beta _{0}=6^\circ$.

图10给出了不同铺层角复合材料水翼的水动力特性及水动效率变化曲线,其中$K$表示升阻比,升阻力系数定义如下

(7)$C_{\rm l} = \dfrac{2L}{\rho lv^2cd} $

(8)$C_{\rm d} = \dfrac{2D}{\rho lv^2cd} $

式中,$L$,$D$分别表示升力和阻力,$v$表示来流速度,$c$,$d$分别表示复合材料水翼平均弦长(0.09,m)和展长(0.3,m).

图10

新窗口打开|下载原图ZIP|生成PPT
图10不同铺层角复合材料水翼的水动力特性及水动效率曲线图

Fig. 10Lift and drag coefficients and lift-drag ratio of composite hydrofoil with different ply angles

由图10可知,在相同初始攻角条件下,随铺层角$\alpha $的增加,复合材料水翼的升力系数$C_{\rm l}$先呈现出下降趋势,当铺层角约为35$^\circ$铺层时,升力系数$C_{\rm l}$达到最小值,之后升力系数$C_{\rm l}$呈现小幅缓慢回升趋势;复合材料水翼的阻力系数$C_{\rm d}$同样先表现出下降趋势,当铺层角约为30$^\circ$铺层时,阻力系数$C_{\rm d}$达到最小值,随后阻力系数$C_{\rm d}$出现小幅缓慢回升趋势;复合材料水翼的升阻比$K$先呈现出上升趋势,当铺层角为30$^\circ$铺层时,升阻比$K$达到最大值,表明此时复合材料水翼具有最高的水动效率.对比$-15^\circ$铺层和15$^\circ$铺层可知,不同铺层角复合材料水翼的升阻力系数几乎关于0$^\circ$铺层的升阻力系数呈现反对称关系,同时$-15^\circ$铺层具有最大的升阻力系数和最小的升阻比.

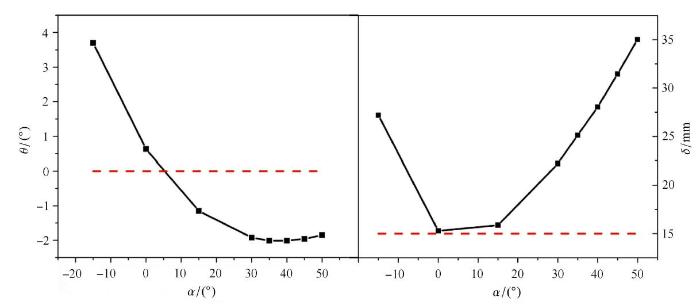
图11给出了不同铺层角复合材料水翼的尖端扭转角$\theta $和位移量$\delta $的变化曲线.由图11中尖端扭转角$\theta $曲线可知,当铺层角$\alpha <0^\circ$时,复合材料水翼尖端扭转角均为正值,即在来流作用下,,复合材料水翼的有效攻角增大,且随着铺层角$\alpha $的增大,复合材料水翼尖端扭转角$\theta$逐渐减小,即复合材料水翼的有效攻角逐渐减小;当铺层角$\alpha>0^\circ$时,复合材料水翼尖端扭转角均为负值,即在来流作用下,复合材料水翼的有效攻角减小,且随着铺层角$\alpha$的增大,复合材料水翼尖端扭转角$\theta $的绝对值逐渐增大,则水翼的有效攻角持续减小;当铺层角$\alpha$增大到约为35$^\circ$时,复合材料水翼尖端扭转角$\theta $的绝对值开始小幅下降,水翼的有效攻角开始增大.由图11中尖端位移量$\delta $曲线可知,复合材料水翼尖端位移量均在15,mm以上,当铺层角$\alpha<0^\circ$时,随着铺层角$\alpha $的增大,复合材料水翼尖端位移量$\delta$持续下降,在铺层角为0$^\circ$时,复合材料水翼尖端位移量$\delta$取得最小值;当铺层角$\alpha>0^\circ$时,随着铺层角$\alpha $的增大,复合材料水翼尖端位移量$\delta $持续上升.

不同铺层角复合材料水翼呈现出不同的变形特性,而铺层角的变化,一方面影响弹性模量等结构属性,另一方面使复合材料水翼结构的弯扭耦合效应发生变化. 根据经典层合板理论^[34]可知,层合板拉伸刚度矩阵${\pmb A}$、耦合刚度矩阵${\pmb B}$及弯曲刚度矩阵${\pmb D}$计算公式如下

(9)$$\left.\begin{matrix} A_{ij} = \sum_{k = 1}^{13} \left( {\overline Q _{ij} } \right)_k \left( {z_k - z_{k - 1} } \right) \\ B_{ij} = \dfrac{1}{2}\sum_{k = 1}^{13} \left( {\overline Q _{ij} } \right)_k \left( {z^2_k - z^2_{k - 1} } \right) \\ D_{ij} = \dfrac{1}{3}\sum_{k = 1}^{13} \left( {\overline Q _{ij} } \right)_k \left( {z^3_k - z^3_{k - 1} } \right) \end{matrix} \right \} $$

式中,$z_{k}$表示复合材料层合板的第$k$层复合材料单层板($z =0$面称为复合材料层合板中面),$\overline Q _{ij} $,$i$,$j=1$, 2, 6表示第$k$层刚度矩阵的转换矩阵,其与刚度矩阵和铺层角度有关.

图 11

新窗口打开|下载原图ZIP|生成PPT
图 11不同铺层角复合材料水翼的尖端扭转角$\theta $和位移量$\delta $的变化曲线

Fig. 11eformation at tip of composite hydrofoil with different ply angles

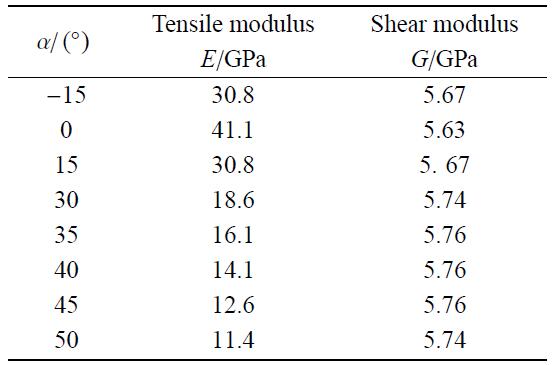
由于复合材料水翼采用了对称铺层方式,其耦合刚度矩阵${\pmb B}$为零矩阵,即拉弯耦合效应对水翼结构变形无影响. 水翼结构仅有拉伸刚度矩阵${\pmb A}$产生的拉剪耦合作用和弯曲刚度矩阵${\pmb D}$产生的弯扭耦合作用. 同时表2给出了不同铺层角复合材料水翼的工程常数,对比铺层角为$-15^\circ$和15$^\circ$的复合材料水翼可发现,尽管$-15^\circ$和15$^\circ$铺层复合材料水翼的工程常数相同,但各自的尖端变形量呈现明显的差异,如图11所示,这是由于复合材料结构的弯扭耦合效应改变了结构的变形特性,而拉剪耦合效应并未在图中体现.

Table 2
表2
表2不同铺层角复合材料水翼的工程常数
Table 2Engineering constants of composite hydrofoil

新窗口打开|下载CSV

为了进一步分析弯扭耦合效应对复合材料结构变形的作用,削弱工程常数的影响, 建立了无量纲位移量$\delta_{0}$与拉伸弹性模量$E$, 无量纲扭转角$\theta _{0}$与剪切弹性模量$G$的关系

(10)$\delta _{0}=\delta EI \big / ,(F_{\rm N}d^{3}) $

(11)$\theta_{0}=\theta GJ \big / ,(Pd) $

式中, $\delta $为尖端位移量,$E$为拉伸弹性模量,$I$为惯性矩,$F_{\rm N}$为垂直于复合材料水翼弦长的合力(简称垂弦力), $\theta$为尖端扭转角,$G$为面内剪切弹性模量,$J$为转动惯量,$P$为复合材料水翼的俯仰力矩,$d$为复合材料水翼的展长.

对于各向同性的金属材料,若载荷分布$F_{\rm N}, P$相同,则无量纲数相同.而对于各向异性的复合材料,由于弯扭耦合作用的影响, 将会导致无量纲数的变化. 图12给出了不同铺层角复合材料水翼的无量纲尖端位移量$\delta _{0}$和无量纲尖端扭转角$\theta _{0}$变化曲线图.

图 12

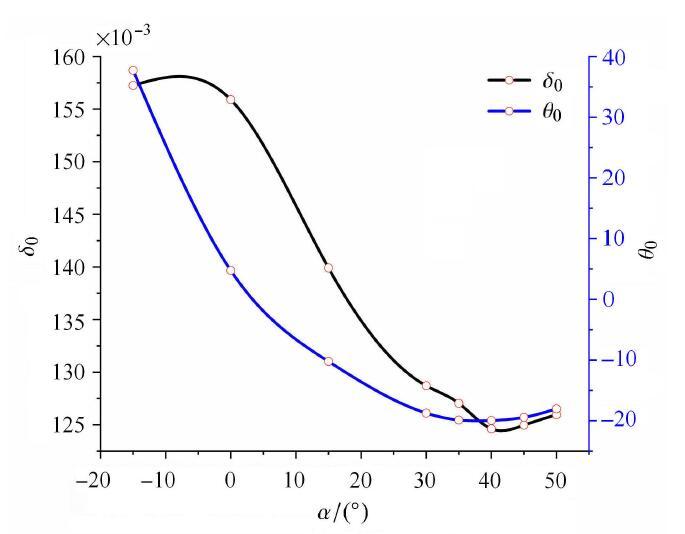新窗口打开|下载原图ZIP|生成PPT
图 12不同铺层角复合材料水翼的无量纲$\delta _{0}$和无量纲$\theta _{0}$变化曲线图

Fig. 12The dimensionless torsion angle and displacement of composite hydrofoil with different ply angles

由图 12可知,随着铺层角$\alpha $的增大,无量纲$\delta _{0}$逐渐下降,当铺层角增大到约40$^\circ$时,无量纲$\delta_{0}$缓慢回升. 随着铺层角的$\alpha$的增大,无量纲$\theta_{0}$逐渐下降,当铺层角度数增大到约35$^\circ$时,无量纲$\theta_{0}$开始小幅缓慢回升,其变化趋势与直接测量的复合材料水翼尖端扭转角$\theta $变化趋势一致.

2.3 不同铺层角复合材料水翼强度特性分析

为了进一步探究复合材料水翼在不同铺层角下的强度特性,图13给出了不同铺层角复合材料水翼最大应力应变随铺层角的变化曲线. 由图13可知,不同铺层角复合材料水翼的最大应变曲线与图11中的复合材料水翼尖端位移量 $\delta $变化趋势一致. 当铺层角 $\alpha =-15^\circ \sim15^\circ$时,复合材料水翼的最大应力随着铺层角的增大而减小;当铺层角 $\alpha =15^\circ \sim35^\circ$时,复合材料水翼的最大应力随着铺层角的增大而增大;当铺层角 $\alpha =35^\circ \sim50^\circ$时,复合材料水翼的最大应力随着铺层角的增大逐渐降低.

图 13

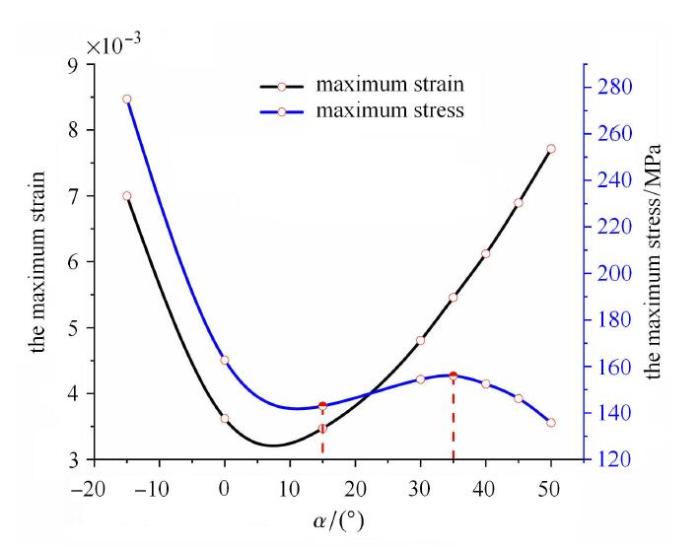新窗口打开|下载原图ZIP|生成PPT
图 13不同铺层角复合材料水翼最大应力$\!$-$\!$-$\!$应变变化曲线图

Fig. 13Maximun stress and strain of composite hydrofoil with different ply angles

图14给出了典型铺层复合材料水翼($\alpha =-15^\circ$, 0$^\circ$, 15$^\circ$,35$^\circ$)的变形后的应力$\!$-$\!$-$\!$应变云图.由图14可知,最大应力区域均出现在复合材料水翼根部吸力面处,且随着铺层角的增大,最大应力点逐渐由水翼根部吸力面前缘向尾缘处移动,最大应力区域也逐渐减小.同时最大应变与最大应力出现位置一致,当铺层角大于0$^\circ$时,最大应变值和区域逐渐增大.

图 14

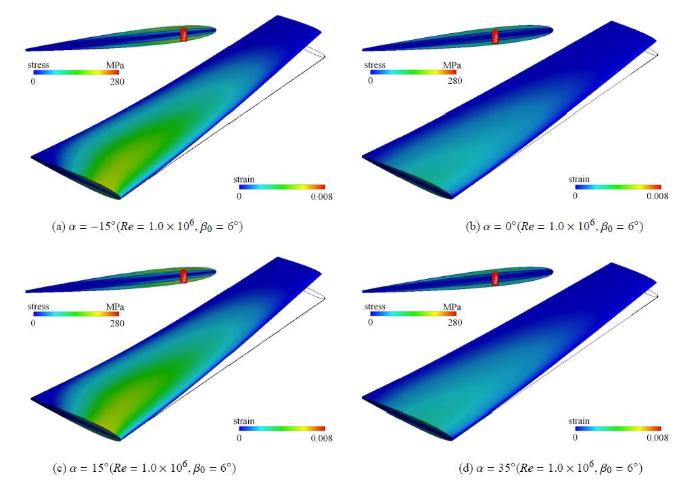新窗口打开|下载原图ZIP|生成PPT
图 14典型铺层复合材料水翼变形应力应变云图

Fig. 14Stress and strain contours of composite hydrofoil with typical ply angles

图 15基于蔡$\!$-$\!$-$\!$吴失效准则,给出了不同铺层角复合材料水翼的蔡$\!$-$\!$-$\!$吴系数随铺层角的变化曲线.其中蔡$\!$-$\!$-$\!$吴失效准则^[35]表达式如下

(12)$$FI = F_1 \sigma _1 + F_2 \sigma _2 + F_3 \sigma _3 + F_{11} \sigma _1^2 + F_{22} \sigma _2^2 + \\ F_{33} \sigma _3^2 + F_{44} \sigma _4^2 +F_{55} \sigma _5^2 + F_{66} \sigma _6^2 + 2F_{12} \sigma _1 \sigma _2 + \\ 2F_{13} \sigma _1 \sigma _3 + 2F_{23} \sigma _2 \sigma _3 \geqslant 1 $$

式中

$$F_1 = \dfrac{1}{S_1^{\rm t} } + \dfrac{1}{S_1^{\rm e} },, \ \ F_2 = \dfrac{1}{S_2^{\rm t} } + \dfrac{1}{S_2^{\rm e} },, \ \ F_3 = \dfrac{1}{S_3^{\rm t} } + \dfrac{1}{S_3^{\rm e} } \\ F_{11} = - \dfrac{1}{S_1^{\rm t} S_1^{\rm c} },, F_{22} = - \dfrac{1}{S_2^{\rm t} S_2^{\rm c} },, \ \ F_{33} = - \dfrac{1}{S_3^{\rm t} S_3^{\rm c} } \\ F_{44} = \dfrac{1}{S_4^2 },, F_{55} = \dfrac{1}{S_5^2 },, F_{66} = \dfrac{1}{S_6^2 } \\ F_{12} = - \dfrac{\sqrt {F_{11} F_{22} } }{2},, \ \ F_{13} = - \dfrac{\sqrt {F_{11} F_{33} } }{2} \\ F_{23} = - \dfrac{\sqrt {F_{22} F_{33} } }{2} $$

${FI}$为得到的蔡$\!$-$\!$-$\!$吴失效系数,大于1时,表示材料发生失效. 1, 2, 3分别表示$x$, $y$, $z$方向.$\sigma_{1}$, $\sigma_{2}$, $\sigma_{3}$, $\sigma_{4}$, $\sigma_{5}$, $\sigma_{6}$分别为1, 2,3方向上的正应力和2-3, 3-1, 1-2平面内的剪切应力. $S_1^{\rm t}, S_1^{\rm e}, S_{2}^{\rm t}, S_{2}^{\rm e},S_3^{\rm t}, S_3^{\rm e} $分别为材料1, 2, 3方向的拉伸、压缩强度(负号表压缩),$S_{4}$, $S_{5}$,$S_{6}$分别为材料2-3, 3-1, 1-2平面内剪切强度. 因为蔡$\!$-$\!$-$\!$吴失效准则考虑了 $\sigma_{1}$,$\sigma _{2}$项系数的正确取值,使其更具有普适性.

图 15

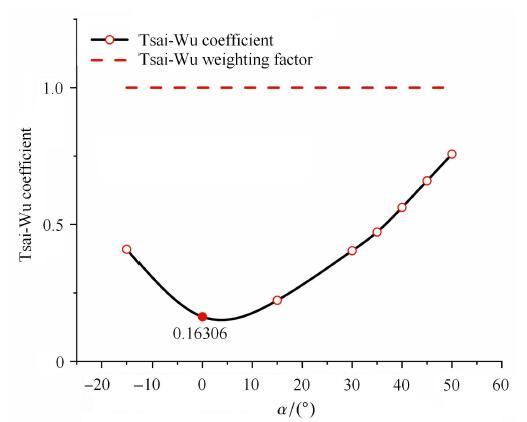新窗口打开|下载原图ZIP|生成PPT
图 15不同铺层角复合材料水翼蔡$\!$-$\!$-$\!$吴系数曲线图

Fig. 15Tsai-Wu coefficient of composite hydrofoil with different ply angles

由图 15可知,8种铺层方式的复合材料水翼的蔡$\!$-$\!$-$\!$吴系数均小于1,未发生失效.其中0$^\circ$铺层的复合材料水翼蔡$\!$-$\!$-$\!$吴系数最小,则其抵抗拉伸破坏的能力最强;50$^\circ$铺层的复合材料水翼的蔡$\!$-$\!$-$\!$吴系数最大,则其抗拉伸破坏的能力最弱. 当铺层角$\alpha<0^\circ$时,蔡$\!$-$\!$-$\!$吴系数随着铺层角而减小;当铺层角$\alpha>0^\circ$时,蔡$\!$-$\!$-$\!$吴系数随着铺层角的增大而增大.

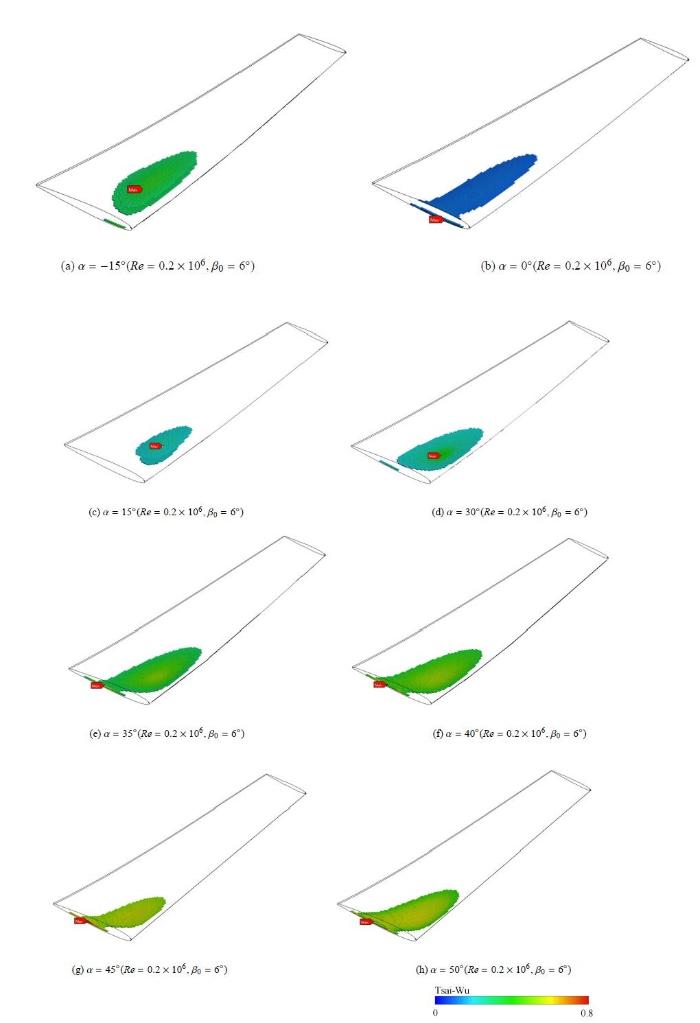
基于图 15蔡$\!$-$\!$-$\!$吴系数的变化曲线,图16给出了不同铺层角复合材料水翼的蔡$\!$-$\!$-$\!$吴系数分布云图.由图16可知, 铺层角$\alpha =0^\circ$, $35^\circ \sim 50^\circ$时,最大的蔡$\!$-$\!$-$\!$吴系数均分布在复合材料水翼根部压力面处,且随着铺层角的增大,最大蔡$\!$-$\!$-$\!$吴系数出现点由复合材料水翼根部压力面前缘端向尾缘端移动;铺层角$\alpha=-15^\circ$,15$^\circ$和30$^\circ$时,最大的蔡$\!$-$\!$-$\!$吴系数均分布在靠近复合材料水翼根部和前缘的中截面上.

图 16

新窗口打开|下载原图ZIP|生成PPT
图 16不同铺层角复合材料水翼蔡$\!$-$\!$-$\!$吴系数分布云图

Fig. 16Tsai-Wu contours of composite hydrofoil with different ply anglesNACA0009 section profile

3 结论

本文针对采用对称铺层方式的复合材料水翼,结合复合材料的结构特性,通过流固耦合数值计方法,对不同雷诺数、不同铺层角工况下的复合材料水翼进行了研究分析,并与文献^[19] 中相同工况的实验结果进行对比,得出以下结论：

(1)雷诺数的改变会影响对称铺层复合材料水翼的变形,对不同雷诺数、不同铺层角工况下的尖端扭转角在绝对值上均呈现上升趋势,且0$^\circ$铺层复合材料水翼产生正值扭转角,30$^\circ$铺层复合材料水翼产生负值扭转角.

(2)铺层角的改变会影响对称铺层复合材料水翼的变形. 当铺层角$\alpha<0^\circ$时,复合材料水翼尖端扭转角均为正值,且随着铺层角的增大,复合材料水翼尖端扭转角和尖端位移量均逐渐减小;当铺层角 $\alpha >0^\circ$时,复合材料水翼尖端扭转角均为负值,且随着铺层角的增大,复合材料水翼尖端扭转角的绝对值和尖端位移量均逐渐增大.

(3)采用无量纲变形量和扭转角分析了弯扭耦合效应对对称铺层复合材料水翼结构变形的作用.随着铺层角的增大,无量纲变形量和无量纲扭转角均下降;当铺层角度数增大到约35$^\circ$时,无量纲扭转角开始小幅增大;当铺层角度数增大到约40$^\circ$时,无量纲变形量逐渐增大.

(4)采用对称铺层的不同铺层角$(-15^\circ \sim 50^\circ$)复合材料水翼均未发生失效.根据蔡$\!$-$\!$-$\!$吴失效准则判定得出0$^\circ$铺层的复合材料水翼抵抗拉伸破坏的能力最强;当铺层角$\alpha<0^\circ$时, 蔡$\!$-$\!$-$\!$吴系数随着铺层角的增大而减小;当铺层角$\alpha>0^\circ$时,蔡$\!$-$\!$-$\!$吴系数随着铺层角的增大而增大.

参考文献原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]

陆力, 彭忠年, 王鑫等. 水力机械研究领域的发展
中国水利水电科学研究院学报, 2018,16(5):442-450