邢子康^*, 申永军^,*,?,2), 李向红^*** 石家庄铁道大学机械工程学院，石家庄 050043
? 交通工程结构力学行为与系统安全国家重点实验室，石家庄 050043
** 石家庄铁道大学数理系，石家庄 050043

PERFORMANCE ANALYSIS OF GROUNDED THREE-ELEMENT DYNAMIC VIBRATION ABSORBER¹⁾

Xing Zikang^*, Shen Yongjun^,*,?,2), Li Xianghong^*** Department of Mechanical Engineering，Shijiazhuang Tiedao University，Shijiazhuang 050043，China
? State Key Laboratory of Mechanical Behavior and System Safety of Traffic Engineering Structures，Shijiazhuang Tiedao University， Shijiazhuang 050043，China
** Department of Mathematics and Physics，Shijiazhuang Tiedao University，Shijiazhuang 050043，China

通讯作者: 2)申永军，教授，主要研究方向：机械系统的动力学与振动控制. E-mail:shenyongjun@126.com

收稿日期:2019-06-17网络出版日期:2019-09-18

基金资助:

1)国家自然科学基金项目.11772206 河北省高等学校创新团队领军人才计划.LJRC018 河北省高等学校高层次人才科学研究项目资助.GCC2014053

Received:2019-06-17Online:2019-09-18
作者简介 About authors


摘要
利用固定点理论优化接地类型的动力吸振器得到的结果可能不是全局最优参数,在选择其他参数时主系统可以获得更小的振幅, 接地类型动力吸振器的优化问题值得进一步研究. 因此,以一种接地式三要素型动力吸振器为对象,通过研究系统参数变化对固 定点位置与主系统最大振幅的影响,得到了此吸振器的局部最优参数并分析了它的性能. 首先建立了此系统模型的运动微分方程, 得到了主系统振幅放大因子,发现系统存在3个与阻尼无关的固定点. 固定点中幅值较大点随系统参数变化的趋势可以代表最大振 幅随系统参数变化的趋势,因此利用盛金公式得到了固定点幅值的表达式. 为了更加精确,进一步使用数值算法得到了最大振幅与 系统参数的关系图,发现系统中存在局部最优参数. 通过对比接地式吸振器与接地三要素型吸振器的最大振幅随系统参数变化的趋 势,得到了接地式三要素型吸振器的局部最优参数,并发现当固有频率比小于局部最优频率比时,接地式三要素型吸振器模型主系 统的最大振幅要远小于接地式动力吸振器模型.
关键词： 振动控制;动力吸振器;固定点理论;参数优化

Abstract
In grounded dynamic vibration absorbers (DVA), the changing tendencies of the fixed-point amplitude with the natural frequency ratio are not monotonous. Thus, the results obtained by optimizing this type DVA based on classical fixed-point theory may be the local optimum parameters. The primary system can obtain smaller amplitudes when selecting other parameters. The optimization of grounded type DVAs are worthy to further study. In addition, the damper of the DVA inevitably has some elasticity. Accordingly, a grounded three-element DVA is studied by analyzing the influence of system parameters on fixed-point positions and maximum amplitude in this paper. The local optimum parameters of the DVA are obtained and the performance is investigated. Firstly, the motion differential equation of the system is established, and the amplitude amplification factor of the primary system is obtained. It is found that there are three fixed-points independent of damping on the amplitude-frequency response curve. In most cases, by optimizing the damping ratio, the tendency of the larger of the fixed point changing with the system parameters can represent the tendency of the maximum amplitude changing with the system parameters. Therefore, the expressions of the fixed-point are obtained by using the Shengjin's formula. For more accuracy, the numerical algorithm is used to obtain the relationship between the maximum amplitude and the system parameters, and it is found that there are local optimum parameters in the system. Finally, in order to obtain the local optimum parameters the grounded three-element DVA is compared with the grounded DVA. The study shows that the local optimum parameters of the two DVAs are the same except the stiffness ratio. When the natural frequency is smaller than local optimum frequency ratio, the maximum amplitude of the primary system of the grounded three-element DVA model is much smaller than that of the grounded DVA.
Keywords：vibration control;dynamic vibration absorber;fixed-point theory;parameters optimization


PDF (17559KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
邢子康, 申永军, 李向红. 接地式三要素型动力吸振器性能分析¹⁾. 力学学报[J], 2019, 51(5): 1466-1475 DOI:10.6052/0459-1879-19-154
Xing Zikang, Shen Yongjun, Li Xianghong. PERFORMANCE ANALYSIS OF GROUNDED THREE-ELEMENT DYNAMIC VIBRATION ABSORBER¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2019, 51(5): 1466-1475 DOI:10.6052/0459-1879-19-154

引言

机械振动不仅会导致机器本身的性能和可靠性降低,而且还会危害人体的健康. 动力吸振器(dynamic vibration absorber,DVA)是一种 能够抑制共振的减振装置,与其他减振装置相比,动力吸振器的优点是小型轻量与便于安装.1911年,Frahm^[1]提出了仅由弹簧与质量构成的无阻尼动力吸振器,虽然在特定的激励力频率下这种吸振器可以使主系统(被控对象)的振幅为零,但是当激励力频率变化时吸振器的性能会显著恶化. 1928年,Ormondroyd和DenHartog^[2]在Frahm发明的吸振器中加入阻尼,拓宽了吸振器的减振频带,使吸振器能够适用于激励力频率变化的情况,这种吸振器就是目前广为所知的Voigt式动力吸振器.在附加质量一定时,吸振器的减振效果与弹簧的刚度和阻尼的大小都有关,根据不同的减振要求,通过参数优化可以使吸振器的性能最佳.1932年, Hahnkamm^[3]提出了在H$_{\infty }$准则下优化动力吸振器的条件.1946年,Brock^[4]根据此条件推导出了H$_{\infty }$准则下最优参数的设计公式. 1956年,DenHartog^[5]在他的著作中详细地总结了利用固定点理论优化动力吸振器的方法,至此根据固定点理论优化动力吸振器的方法已经成熟.在H$_{\infty }$优化准则下设计动力吸振器可以使主系统在简谐激励时的最大振幅最小. 除H$_{\infty}$优化以外,还存在其他优化准则,如1963年Crandall和Mark^[6]提出了H$_{2}$优化准则,优化后可以使输入主系统的功率最小;1988年Yamaguchi^[7]提出最大稳定性优化准则,从而可以使主系统瞬态响应最快衰减.

除了Voigt式动力吸振器以外,****们对其他吸振器模型也进行了大量的研究. Ren^[8]和Liu等^[9]对接地式动力吸振器进行了研究,这种模型是将阻尼与地面或固定位置连接,虽然在理论上接地式动力吸振器可以获得比Voigt式动力吸振器更好的减振效果,但是因为阻尼接地,接地式吸振器的安装限制也较大.Cheung和Wong^[10]对接地式动力吸振器进一步分析后发现,利用固定点理论得到的最优参数只是在一定质量比范围内的局部最优参数,当系统的频率比超过某一定值时,主系统的最大振幅可以更小.Asami和Nishihara^[11-12]对三要素式动力吸振器进行了详细的研究,这种吸振器是将Voigt式动力吸振器中的阻尼替换为黏弹性材料,经过H$_{\infty }$优化和H$_{2}$优化后发现这种吸振器的性能优于Voigt式动力吸振器.王孝然等^[13]对接地式三要素型动力吸振器进行了参数优化,得到了在固定点等高时的最优参数.申永军等^[14-15]研究了4种半主动动力吸振器的近似解析解,并分析了半主动吸振器的参数设计和时滞对半主动控制规律的影响.

近年来将负刚度器件以及惯容器件应用于减振设备是研究的热点.文献^{[16,17,18,19]}在动力吸振器中引入负刚度器件,发现含有负刚度器件的吸振器能使主系统振幅大幅度降低,减振效果明显优于传统的吸振器.Hu等^[20-21]与王孝然等^[22]研究了含有惯容器件的动力吸振器,利用固定点理论与数值算法对几种惯容式动力吸振器进行了优化,发现将惯容器安装在合适的位置可以提升动力吸振器的性能.非线性隔振以及含有时滞的振动系统也是研究中的热点与难点^[23-24].赵艳影与徐鉴^[25-27]研究了时滞动力吸振器的性能,通过调节反馈增益系数与时滞量可以使动力吸振器获得更好的控制效果.李帅等^[28]提出了一种时变参数时滞减振控制方法,进一步改善了时滞动力吸振器的性能.申永军等^[29]研究了含时滞的半主动悬架系统,证明了时滞半主动悬架系统的性能优势.时滞系统在受到随机激励时很难得到精确的闭合解,刘俊等^[30]利用迭代加权残值法得到了Bouc-Wen滞迟系统的稳态响应概率密度函数的近似解. 公徐路与许鹏飞^[31]研究了含有时滞反馈与质量涨落的记忆阻尼系统的随机共振.吕小红和罗冠炜^[32]分析了一种冲击渐进振动系统模型,通过协同仿真得到了系统的各类周期振动在参数平面内的分布规律.Zang等^[33]提出一种杠杆式非线性能量阱,与传统非线性能量阱相比能在较小附着质量时获得优异的减振性能.Zhang等^[34]提出了一种含有惯容的非线性能量阱,这种模型能够更有效的抑制主系统的振动,并且存在最优的惯容系数.

本文将研究接地式三要素型动力吸振器的最优参数并分析其性能. 通过建立了系统的数学模型,得到振幅放大因子的表达式.对振 幅放大求解得到固定点振幅与系统参数的表达式,并使用数值算法得到最大振幅与系统参数的关系图.通过分析最大振幅随系统参数变化的趋势,得到此模型的局部最优参数.将接地三要素型动力吸振器与接地式动力吸振器进行比较,进一步分析其性能.

1 接地式三要素型动力吸振器

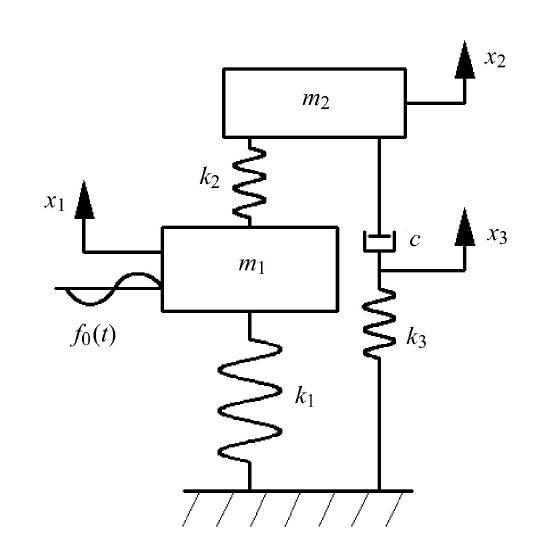
图1为接地式三要素型动力吸振器,$m_{1}$与$k_{1}$分别为主系统的质量与刚度,$m_{2}$与$k_{2}$为动力吸振器的质量与刚度,$c$与$k_{3}$分别为动力吸振器中串联型黏弹性模型的阻尼和刚度,$x_{1}$,$x_{2}$和$x_{3}$分别为主系统、动力吸振器和串联 阻尼弹簧分割点的位移,作用在主系统的简谐激振力$f_0 (t) = F\cos(\omega t)$.

图1中振动系统的运动微分方程为

(1)$$\left. \!\!\begin{array}{l} m_1 \ddot {x}_1 + k_1 x_1 + k_2 (x_1-x_2 ) = F\cos (\omega t) \\ m_2 \ddot {x}_2 + k_2 (x_2-x_1 ) + c(\dot {x}_2-\dot {x}_3 ) = 0 \\ c(\dot {x}_3-\dot {x}_2 ) + k_3 x_3 = 0 \end{array}\!\!\right\} $$

图1

新窗口打开|下载原图ZIP|生成PPT
图1接地式三要素型动力吸振器

Fig. 1Grounded three-element DVA



根据式(1)可以得到振幅放大因子$A$

(2)$$A = \left| {\dfrac{X_1 }{X_{\rm st} }} \right| = \sqrt {\dfrac{A_1^2 + \xi ^2B_1^2 }{C_1^2 + \xi ^2D_1^2 }} $$

其中

(3)$$\left.\!\!\begin{array}{l} A_1 = \nu \alpha (\nu ^2-\lambda ^2) \\ B_1 = 2\lambda (\lambda ^2-\nu ^2-\alpha \nu ^2) \\ C_1 = \nu \alpha (\nu ^2-\lambda ^2)(\lambda ^2-1) + \mu \alpha \lambda ^2\nu ^3 \\ D_1 = 2\lambda \{\lambda ^2-\lambda ^4-\mu \alpha \nu ^4 + \\ \nu ^2[(1 + \alpha )(\lambda ^2-1) + \mu \lambda ^2]\} \end{array}\!\! \right\} $$

式(2)与式(3)中 $X_{1}$为主系统的振幅;$X_{\rm st} = F/k $为主系统的静位移;$\nu = {\omega _2 }/{\omega _1}$为固有频率比;$\lambda = {\omega }/{\omega _1 }$为归一化频率;$\mu = {m_2 }/{m_1 }$为质量比;$\omega _1 =\sqrt { {k_1 }/{m_1 }} $为主系统固有频率;$\omega _2 = \sqrt { {k_2 }/{m_2 }} $为动力吸振器固有频率;$\alpha = {k_3 }/{k_2 }$为动力吸振器刚度比;$\xi = {c}/(2m_2 \omega _2)$为临界阻尼比.

2 两种经典模型中固定点位置与最大振幅的关系

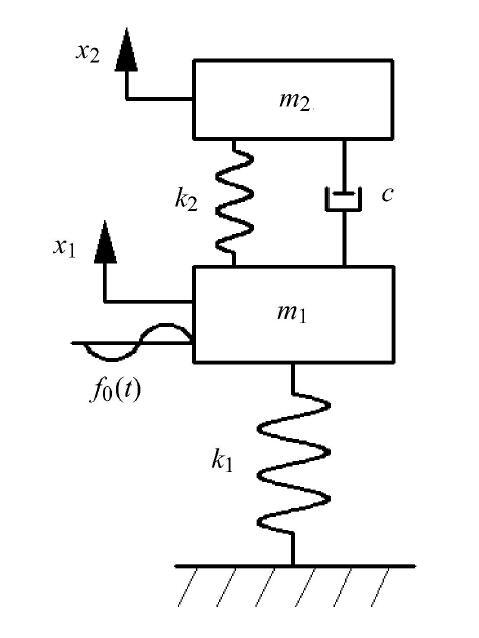
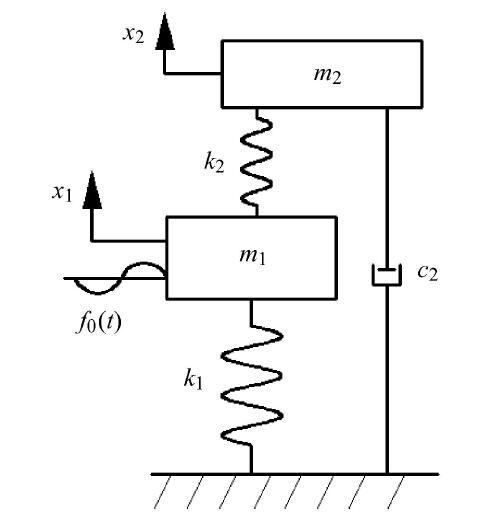
由文献^[5]中固定点理论可知,固定点是幅频响应曲线中与阻尼无关的点,调整阻尼比可以使幅频响应曲线的峰值位于固定点附近.而固定点在幅频响应曲线的位置只与固有频率比有关,因此固有频率比决定了主系统可能的最大振幅的最小值.调整固有频率比使固定点幅值最小可以得到动力吸振器的最优固有频率比,此时固定点处的幅值为主系统可能的最大振幅的最小值.为了简便,以下将取得最优参数时最小的最大振幅简称为最大振幅.

图2与图3分别为含有Voigt式动力吸振器与接地式动力吸振器的振动系统,两系统中固有频率比与固定点($P$,$Q$点)幅值的关系式可从文献^[10]中得到,如式(4)与式(5)所示

(4)$\left.\begin{array}{l} A_{D\left( P \right)} = (2 + \mu )\Bigg /, \Bigg \{ 2 + \mu-\left( {1 + \mu } \right)\Big [ 1 + \nu ^2\left( {1 + \mu } \right)- \\ \sqrt {1-2\nu ^2 + \nu ^4\left( {1 + \mu } \right)^2}, \Big ] \Bigg\} \\ A_{D\left( Q \right)} = (-2-\mu ) \Bigg / ,\Bigg \{ 2 + \mu-\left( {1 + \mu } \right)\Big [ 1 + \nu ^2\left( {1 + \mu } \right) + \\ \sqrt {1-2\nu ^2 + \nu ^4\left( {1 + \mu } \right)^2} ,\Big ] \Bigg\} \end{array} \!\! \right \} $

(5)$\left.\begin{array}{l} A_{Rn\left( P \right)} = {2}\Big / ,\Big [ 1 + \nu ^2\left( {\mu-1} \right) + \\ \sqrt {1 + 2\nu ^2\left( {\mu-1} \right) + \nu ^4\left( {1 + \mu ^2} \right)} ,\Big ] \\ A_{Rn\left( Q \right)} = {2}\Big / ,\Big [-1-\nu ^2\left( {\mu-1} \right) + \\ \sqrt {1 + 2\nu ^2\left( {\mu-1} \right) + \nu ^4\left( {1 + \mu ^2} \right)} ,\Big ] \end{array} \!\! \right \} $

图2

新窗口打开|下载原图ZIP|生成PPT
图2Voigt式动力吸振器

Fig. 2Voigt DVA

图3

新窗口打开|下载原图ZIP|生成PPT
图3接地式动力吸振器

Fig. 3Grounded DVA



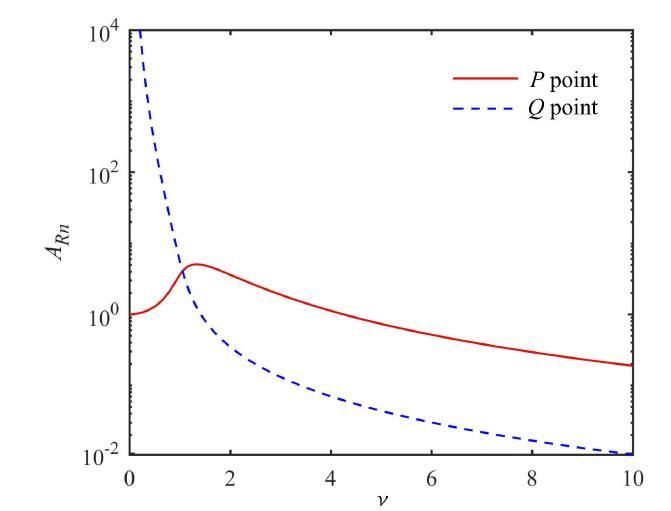
根据上式可以得到在两系统中固定点幅值与固有频率比的关系图,如图4, 图5所示. 从图4与图5中可以看出,在含有Voigt式动力吸 振器的振动系统中,当$P$, $Q$点位于同一高度时(即$P$,$Q$相交点),可以在全局范围内使固定点在幅频响应曲线中的高度最小, 因此$P$,$Q$相交点对应的固有频率比为全局最优固有频率比. 而在含有接地式动力吸振器的振动系统中,令$P$,$Q$点位于同一高度时只能得到局部的最优固有频率比,当固有频率比较大时, 固定点可 以在曲线中位于更低的位置,从而得到更小的最大振幅.

图4

新窗口打开|下载原图ZIP|生成PPT
图4Voigt式动力吸振器中固定点幅值与固有频率比关系图

Fig. 4The relationship between the amplitude of fixed points and natural frequency ratio in Voigt DVA

图5

新窗口打开|下载原图ZIP|生成PPT
图5接地式动力吸振器中固定点幅值与固有频率比关系图

Fig. 5The relationship between the amplitude of fixed points and natural frequency ratio in grounded DVA



在经典的固定点理论优化方法中,令两固定点等高获得最优固有频率比的方法只适用于阻尼连接在主系统与子系统之间的情况(即Voigt式动力吸振器).当阻尼连接在子系统与地面或固定位置时(即接地式动力吸振器),用经典的优化方法得到的固有频率比只是局部最优结果.在接地式动力吸振器中当固有频率比趋向于无穷大时,此系统的模型近似于单自由度阻尼系统,阻尼越大最大振幅越小.

3 接地式三要素型动力吸振器固定点位置与最大振幅

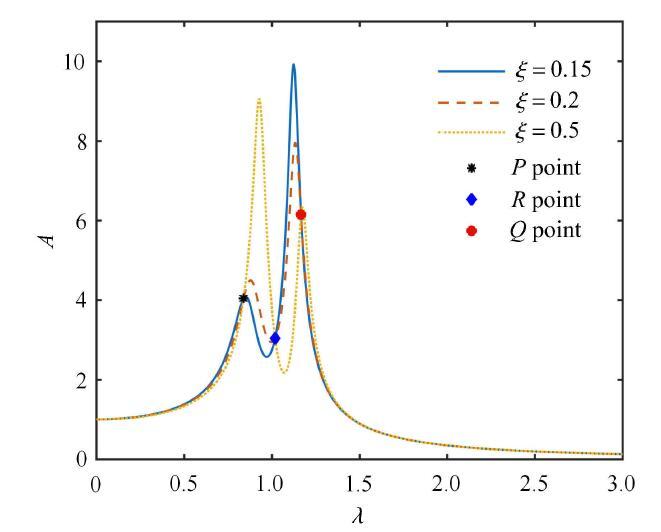
经过以上分析可知,固定点位置与主系统最大振幅关联密切,下面通过求解接地式三要素型动力吸振器固定点的表达式对此吸振器模型进行分析.

根据式(2)可以得到主系统的幅频响应曲线图,图6为选取相同的系统参数而阻尼比取值不同时的幅频响应曲线图,从图6中可以看出无论阻尼取值大小,曲线都通过3个固定点($P$, $Q$, $R$点). 推导式(2)可知当$\left( {A_1 / C_1 } \right)^2 =\left( {B_1 / D_1 } \right)^2$时,$\xi $的取值与$A$无 关, 即

(6)$$\left| {\dfrac{\nu \alpha (\nu ^2-\lambda ^2)}{\nu \alpha (\nu ^2- \lambda ^2)(\lambda ^2-1) + \mu \alpha \lambda ^2\nu ^3}} \right| = \\ \left| {\dfrac{\nu \alpha (\nu ^2-\lambda ^2)(\lambda ^2-1) + \mu \alpha \lambda ^2\nu ^3}{2\lambda [\lambda ^2-\lambda ^4-\mu \alpha \nu ^4 + \nu ^2(\lambda ^2 + \alpha \lambda ^2 + \mu \lambda ^2-1-\alpha )]}} \right| $$

图6

新窗口打开|下载原图ZIP|生成PPT
图6阻尼比取值不同时的幅频响应曲线(系统参数$\mu = 0.1, \nu = 0.9, \alpha = 0.5)$

Fig. 6The amplitude-frequency response curves for different damping ratios with the parameters as $\mu = 0.1, \nu = 0.9, \alpha = 0.5$



根据式(6)可以将$P$, $Q$, $R$三点处横坐标(即$\lambda $的值)求出. 将式(6)两端去掉绝对值符号,并在其中一端添加$\pm $号. 当取负号时,化简等式(6)得到$\lambda ^2 =0$,这表示当激振频率为0时,振幅总是等于固定值,此结果对求解无用,舍去即可. 当取正号时,化简式(6)可得到

(7)$$\lambda ^6 + \lambda ^4a_1 + \lambda ^2a_2 + a_3 = 0 $$

其中

(8)$$\left. a_1 =-1-\nu ^2(2 + \alpha + \mu ) \\ a_2 = \nu ^2[2 + \alpha + \nu ^2(1 + \alpha )(1 + \mu )] \\ a_3 =-\nu ^4[1 + 0.5\alpha (2 + \nu ^2\mu )] \!\!\right\} $$

令$\lambda ^2 = \varLambda $可以将式(7)转换为一个一元三次方程.因为用盛金公式求解一元三次方程得到的表达式较为简洁,不存在开立方,这里利用它对式(7)求解^[35],固定点处横坐标公式如下

(9)$$\left.\!\!\begin{array}{l} \lambda _P^2 = \dfrac{1}{3}\left[ {1 + J-2G\sin \left( {\dfrac{\pi }{6} + \dfrac{\arccos (H)}{3}} \right)} \right] \\ \lambda _Q^2 = \dfrac{1}{3}\left[ {1 + J-2G\sin \left( {\dfrac{\pi }{6}- \dfrac{\arccos (H)}{3}} \right)} \right] \\ \lambda _R^2 = \dfrac{1}{3}\left[ {1 + J + 2G\cos \left( {\dfrac{\arccos (H)}{3}} \right)} \right] \end{array}\!\! \right \} $$

其中

(10)$\left.\begin{array}{l} J = \nu ^2(2 + \alpha + \mu ) \\ H = \dfrac{-2 + \nu ^2(2 + \alpha-2\mu )\left[ {-2 + 2\nu ^2(2 + \alpha-2\mu ) + \nu ^4\left( {-2 + 2\alpha-\mu } \right)\left( {1 + 2\alpha + 2\mu } \right)} \right]}{4\sqrt {\left\{ {-3\nu ^2\left[ {2 + \alpha + \nu ^2(1 + \alpha )(1 + \mu )} \right] + \left[ {1 + \nu ^2(2 + \alpha + \mu )} \right]^2} \right\}^3} } \\ G = \sqrt {1-\nu ^2(2 + \alpha-2\mu ) + \nu ^4(1 + \alpha + \alpha ^2 + \mu-\alpha \mu + \mu ^2)} \end{array}\!\!\right\} $

阻尼比为零时的振幅放大因子为

(11)$$A = \left| {\dfrac{\nu ^2-\lambda ^2}{(\nu ^2-\lambda ^2)(\lambda ^2-1)+ \mu \lambda ^2\nu ^2}} \right| $$

因为固定点位置与阻尼比无关,将式(9)代入式(11)可以得到固定点在幅频响应曲线中的幅值,如式(12)所示

(12)$\left.\!\!\begin{array}{l} A_P = \left| {\dfrac{3}{-2 + J-3\nu ^2\mu-2G\cos \left( {\dfrac{\pi }{6} + \dfrac{\arcsin H }{3}} \right) + \dfrac{9\nu ^4\mu }{-1-J + 3\nu ^2 + 2G\cos \left( {\dfrac{\pi }{6} + \dfrac{\arcsin H }{3}} \right)}}} \right| \\ A_Q = \left| {\dfrac{3}{-2 + J-3\nu ^2\mu-2G\sin \left( {\dfrac{\arcsin H }{3}} \right)-\dfrac{9\nu ^4\mu }{1 + J-3\nu ^2-2G\sin \left( {\dfrac{\arcsin H }{3}} \right)}}} \right| \\ A_R = \left| {\dfrac{3}{-2 + J-3\nu ^2\mu + 2G\cos \left( {\dfrac{\arccos H }{3}} \right)-\dfrac{9\nu ^4\mu }{1 + J-3\nu ^2 + 2G\cos \left( {\dfrac{\arccos H }{3}} \right)}}} \right| \end{array}\!\! \right \} $

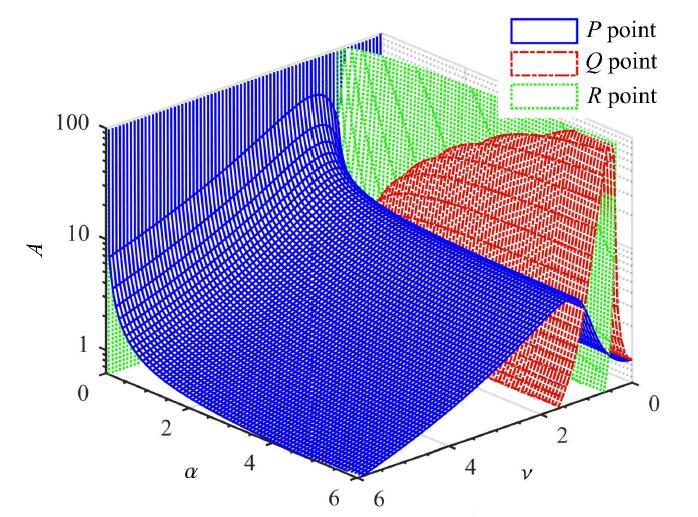
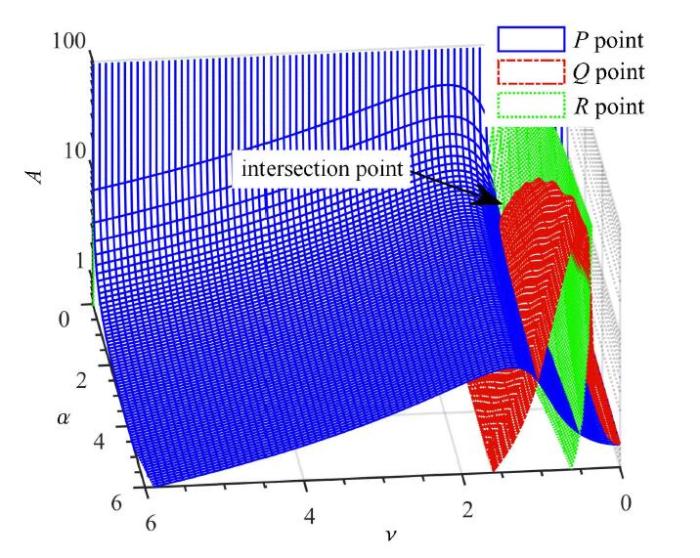
在图6中3个固定点的位置可以由式(9)与 式(12)得到,这也验证了求解的正确性. 图7与图8为质量比$\mu =0.1$时根 据式(12)得到的固定点处幅值与固有频率比和刚度比的关系图,不难看出,图中不存在最小点,当$\nu$与$\alpha $增大$P$点一直减小.文献^[13]中利用固定点理论得到了三点相交处的固有频率比、刚度比以及在此参数下使振幅最小的近似阻尼比, 公式如下

(13)$\left.\begin{array}{l} \nu _{\rm opt\_I} = \sqrt { {1}\Big / ,\Big ( 1 + \sqrt \mu-\mu \Big ) } \\ \alpha _{\rm opt\_I} = 2\sqrt \mu \\ \xi _{\rm opt\_I} = \sqrt { {\mu }\Big / ,\Big ( 1 + \sqrt \mu \Big )} \end{array} \!\! \right \} $

图7

新窗口打开|下载原图ZIP|生成PPT
图7接地式三要素型动力吸振器中固定点幅值与固有频率比和刚度比的关系

Fig. 7The relation between the amplitude of fixed point and the natural frequency ratio and stiffness ratio in grounded three-element DVA

图8

新窗口打开|下载原图ZIP|生成PPT
图8接地式三要素型动力吸振器中固有频率比和刚度比与固定点位置关系图

Fig. 8The relation between the amplitude of fixed point and the natural frequency ratio and stiffness ratio in grounded three-element DVA



在Voigt式与接地式动力吸振器中,系统存在两个与阻尼无关的固定点,文献^[5]与文献^[8]中利用求导的方法使幅频响应曲线的峰值在固定点附近.然而在三要素型动力吸振器中存在3个固定点,无论黏弹性材料安装在主系统与子系统之间还是安装在子系统与地面之间,当3个固定点的幅值相近时,很难使曲线峰值位于固定点附近^[11].图9为在三固定点幅值相等并选择最优阻尼比时的幅频响应曲线图,从图中可以看出调整阻尼只能使3个固定点位于两共振峰之间峰谷位置.而固定点幅值相差较大时,曲线峰值位于固定点中较大点附近,如图10所示.根据以上可知图7与图8能大致反应最大振幅的变化趋势,但在固定点幅值相近的区域上是不精准的.因此为了得到最大振幅与固有频率比和刚度比的准确关系,利用数值算法对式(2)最大振幅的最 小值进行求解,即

(14)$$A_{\max } (\mu ,\lambda ,\nu ,\alpha ,\xi _{\rm opt} ) = \\ \min \{\mathop {\max}\limits_\xi [A(\mu ,\lambda ,\nu ,\alpha )]\} $$

图9

新窗口打开|下载原图ZIP|生成PPT
图9固定点幅值相等且取最优阻尼比时主系统的幅频响应曲线图

Fig. 9Amplitude frequency response curve of the prime system when the amplitude of the fixed point is equal and the optimal damping ratio is taken

图10

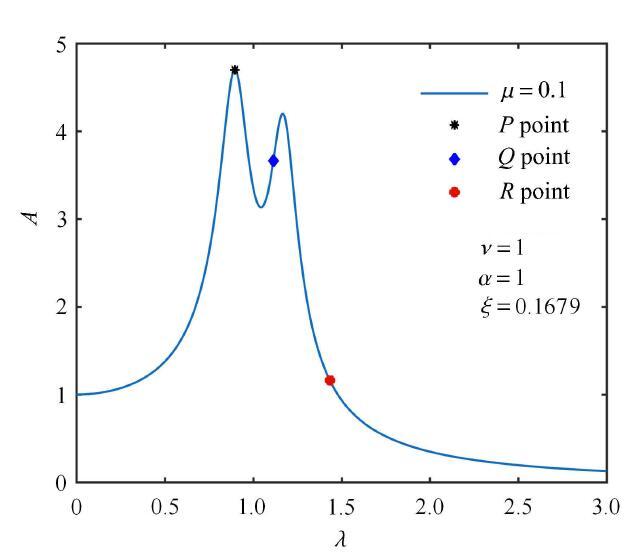新窗口打开|下载原图ZIP|生成PPT
图10固定点幅值相差较大且取最优阻尼比时主系统的幅频响应曲线图

Fig. 10Amplitude frequency response curve of the prime system when the amplitude difference of the fixed point is large and the optimal damping ratio is taken



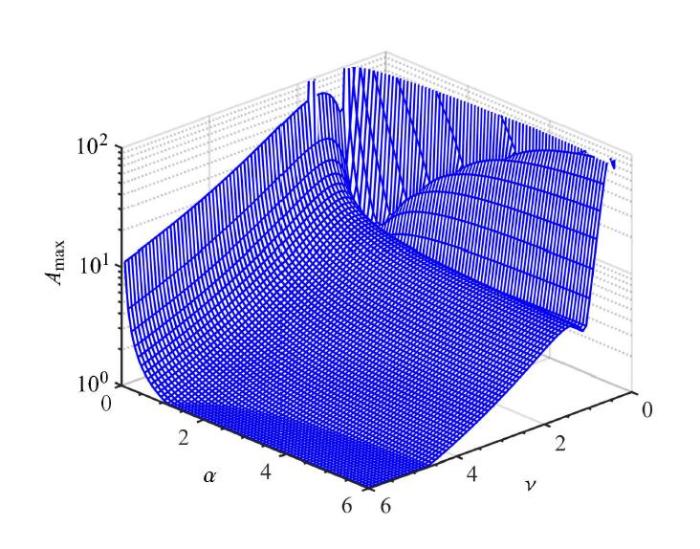
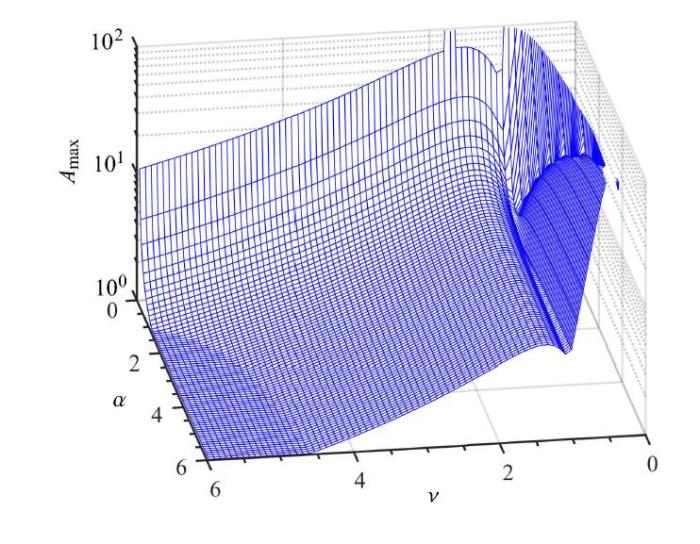
依据$\mu $的值与$\lambda $的范围而选取不同的$\nu $和$\alpha $时,利用序列二次规划法对式(14)求解可以得到每一个$\nu $和$\alpha $对应的最大振幅. 图11与图12为$\nu $和$\alpha $在0$\sim$6范围内对应的最大振幅,其中$\mu = 0.1$,$0 \le qslant \lambda \le qslant 3$,$\nu $和$\alpha$步长为0.08,$\lambda$步长为0.001. 比较图7、图8与图11、图12可发现最大振幅与3个固定点中较大点的变化趋势相同.在进一步利用数值算法分析后发现,接地式三要素型动力吸振器存在局部最优参数,但不在3个固定点相交处.图13为图11中$\nu $和$\alpha $在0$\sim$1.5范围内的局部放大图,其中$I$点为固定点相交时对应的最大振幅,可以看出在此点附近存在幅值更小的点,下面将通过与接地式吸振器比较来说明局部最优参数的位置.

图11

新窗口打开|下载原图ZIP|生成PPT
图11固有频率比和刚度比所对应的最大振幅

Fig. 11The maximum amplitude to the natural frequency ratio and stiffness ratio

图12

新窗口打开|下载原图ZIP|生成PPT
图12固有频率比和刚度比所对应的最大振幅

Fig. 12The maximum amplitude to the natural frequency ratio and stiffness ratio

图13

新窗口打开|下载原图ZIP|生成PPT
图13固有频率比和刚度比所对应的最大振幅

Fig. 13The maximum amplitude to the natural frequency ratio and stiffness

4 接地式三要素型吸振器与接地式吸振器比较

比较图1与图3中模型可知,当图1中$k_{3}$刚度为无穷大时,两模型没有区别,接地式吸振器模型是接地式三要素型动力吸振器模型在黏弹性材料刚度为无穷时的特例.从图7与图8中可以看出,当刚度比取值较大时固定点中较大点的趋势与图5相同,但刚度比较小时则不然.下面将接地式三要素型吸振器与接地式吸振器在选取相同固有频率比时的最大振幅进行比较.

接地式动力吸振器振幅放大因子的形式可从文献^[8]中得到,如式(15)所示

(15)$$A_{Rn} = \sqrt {\dfrac{A_2^2 \xi ^2 + B_2^2 }{C_2^2 \xi ^2 + D_2^2 }} $$

其中

(16)$$\left.\begin{array}{l} A_2 = 2\lambda \nu \\ B_2 = \nu ^2-\lambda ^2 \\ C_2 = 2\lambda \nu \left( {1-\lambda ^2 + \mu \nu ^2} \right) \\ D_2 = \left( {\lambda ^2-1} \right)\left( {\lambda ^2-\nu ^2} \right)- \mu \nu ^2\lambda ^2 \end{array}\!\! \right \} $$

对式(2)与式(15)在选定固有频率比时的最大振幅进行求解,即

(17)$$\left.\!\!\begin{array}{l} A_{\max } (\mu ,\lambda ,\nu ,\alpha _{\rm opt} ,\xi _{\rm opt} ) = \min \{\mathop {\max }\limits_{\alpha ,\xi } [A(\mu ,\nu ,\lambda )]\} \\ A_{Rn\max } (\mu ,\lambda ,\nu ,\xi _{\rm opt} ) = \min \{\mathop {\max }\limits_\xi [A_{Rn} (\mu ,\nu ,\lambda )]\} \end{array} \!\! \right \} $$

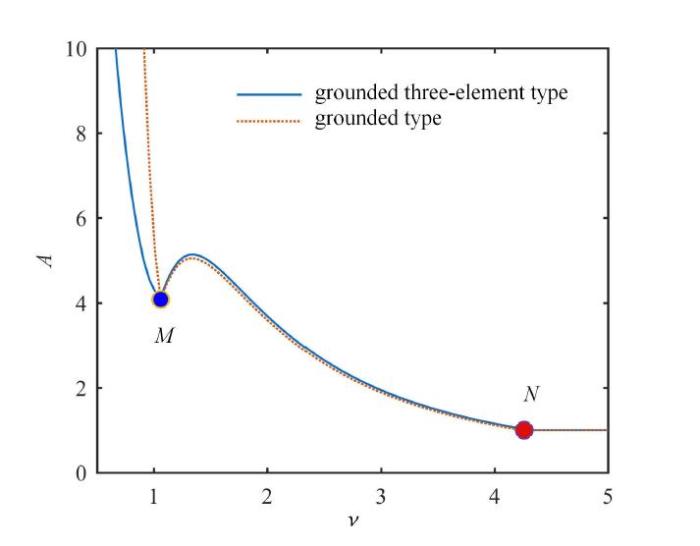
依据$\mu $的值与$\lambda $的范围而选取不同的$\nu $时,利用序列二次规划法对式(17)求解可以得到每一个$\nu$对应的最大振幅. 图14为两种吸振器固有频率比$\nu $在0.5$\sim $5范围内对应的最大振幅,其中$\mu = 0.1$,$\nu$的步长为0.1,$0 \le qslant \lambda \le qslant 3$且步长为0.05,限制刚度比$0 \le qslant \alpha \le qslant 30$.可以看出图中$M$点对应的固有频率比为接地式吸振器中与接地式三要素型的局部最优频率比,对应的公式以及局部最优阻尼比在文献^[11]中已给出,如下

(18)$$\left.\begin{array}{l} \nu _M = \dfrac{1}{\sqrt {1-\mu } } \\ \xi _M = \sqrt {\dfrac{3\mu }{8-4\mu }} \end{array} \right \} $$

图14

新窗口打开|下载原图ZIP|生成PPT
图14最大振幅与固有频率比的关系

Fig. 14The relationship between the maximum amplitude and natural frequency ratio



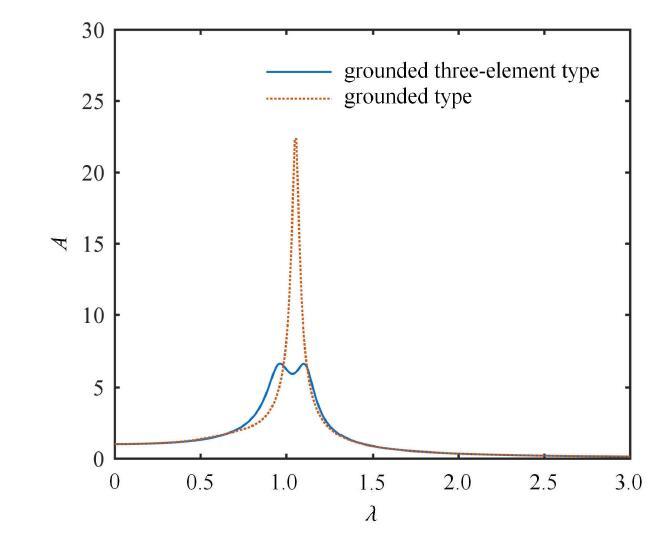
另外当质量比$\mu > 0.267,9$时将不存在局部最优频率比,文献^[10]中已经进行了详细的说明这里不再赘述.图中在$M$点左侧接地式三要素型动力吸振器的最大振幅要远小于接地式动力吸振器的最大振幅,随着固有频率比继续增大,在$M$点右侧两条曲线会重合,并且在$N$点以后最大振幅点为归一化频率$\lambda = 0$时的点,此时最大振幅为1.图15为固有频率比小于局部最优频率比而其他参数取最优值时的幅频响应曲线图,可以看出接地式三要素型吸振器在固有频率较小时的性能优势,图中接地式三要素型吸振器的刚度比$\alpha = 0.881,1$,阻尼比$\xi =0.597,1$,接地式吸振器的阻尼比为$\xi = 0.269,0$.

图15

新窗口打开|下载原图ZIP|生成PPT
图15$\mu = 0.1$与$\nu = 0.8$时接地式三要素型与接地式吸振器幅频响应曲线对比

Fig. 15Comparison of amplitude frequency response curves between grounded three-element type and grounded type with $\mu = 0.1$\\ and $\nu = 0.8$



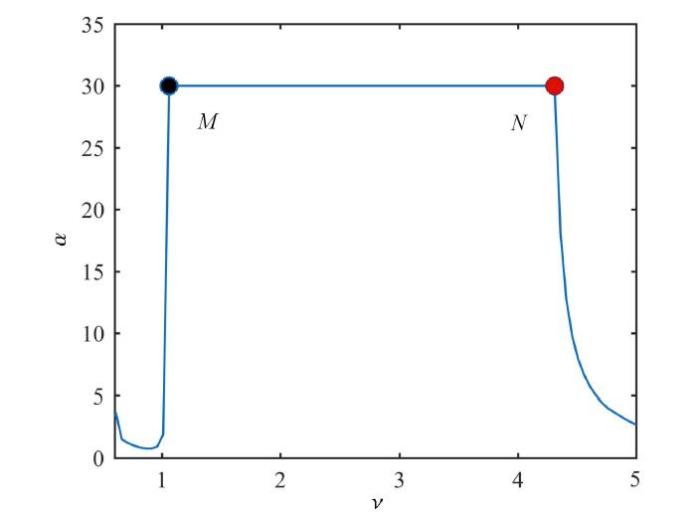
在利用序列二次规划法对式(17)求解得到图14的同时,也可以得到每一个固有频率比对应的最优刚度比,如图16所示.从图中 可以看出在$M$点左侧存在合适的刚度比能使最大振幅最小,而在$M$点与$N$点之间时,由式(17)得到的最优刚度比为限制范围内的最大值,这说明在此时合适的刚度比应趋向于无穷,刚度比取值越大,接地式三要素型动力吸振器的最大振幅与接地式吸振器最大振幅越吻合.

图16

新窗口打开|下载原图ZIP|生成PPT
图16质量比$\mu = 0.1$时固有频率比对应的最优刚度比

Fig. 16The relationship between the optimal stiffness ratio and the natural frequency ratioratio



通过以上分析可知,除刚度比$\alpha $以外,接地式三要素型动力吸振器的局部最优参数$\nu $和$\xi$与接地式动力吸振器局部最优参数相同,而局部最优刚度比理论上应取无穷大值. 假如刚度比取无穷大值时,图14中$N$点以后 可以得到主系统全局最小的最大振幅,此时的最大振幅为1. 另外,接地式三要素型动力吸振器的固有频率比小于$\nu _M $时,最大振幅远小于接地式动力吸振器. 在固有频率比大于$\nu _M$时,接地式三要素型动力吸振器需要较大的刚度比才能达到与接地式动力吸振器相同的最大振幅.

5 结论

研究了一种接地式三要素型动力吸振器的性能和最优参数.根据固定点理论,最优频率比可以通过固定点在幅频响应曲线等高位置时获得,但是这一方法并不适用于接地类型的吸振器.在接地型动力吸振器中阻尼与地面连接,当吸振器刚度值较大时系统的模型近似于一个单自由度阻尼系统,所以通过固定点理论优化得到的最优参数是局部最优参数;因此,当吸振器的弹簧刚度较大时,接地型吸振器阻尼越大主系统的振幅越小,接地型的动力吸振器不存在所谓的最优参数;在接地三要素型动力吸振器中,固定点等高时对应的最优参数既不是局部最优参数也不是全局最优参数.通过对比接地式吸振器与接地三要素型吸振器的最大振幅发现,两吸振器的局部最优频率比与局部最优阻尼比相同,而接地三要素型吸振器的最优刚度比理论上应为无穷;接地式三要素型动力吸振器的优势在于固有频率比小于局部最优参数的情况,当固有频率比较小时接地式三要素型动力吸振器的最大振幅远小于接地式动力吸振器.

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] Frahm H. Device for damping vibrations of bodies: U.S. Patent 989958
1911 -04-18
[本文引用: 1]

[2] Ormondroyd J, Den Hartog JP . The theory of the dynamic vibration absorber.
Trans ASME, J Appl Mech, 1928,50:9-22
[本文引用: 1]

[3] Hahnkamm E . The damping of the foundation vibrations at varying excitation frequency
Master of Architecture, 1932,4:192-201
[本文引用: 1]

[4] Brock JE. A note on the damped vibration absorber
Trans ASME, J Appl Mech , 1946, 13(4): A-284
[本文引用: 1]

[5] Den Hartog JP . Mechanical vibrations
Courier Corporation, 1985
[本文引用: 3]

[6] Crandall SH, Mark WD. Random vibration in mechanical systems. Academic Press, 1963: 71-72
[本文引用: 1]

[7] Yamaguchi H . Damping of transient vibration by a dynamic absorber
Trans Jpn Soc Mech Eng, 1988,54(499):561
[本文引用: 1]

[8] Ren MZ . A variant design of the dynamic vibration absorber
Journal of Sound Vibration, 2001,245:762-770
[本文引用: 3]

[9] Liu K, Liu J . The damped dynamic vibration absorbers: revisited and new result
Journal of Sound and Vibration, 2005,284(3-5):1181-1189
[本文引用: 1]

[10] Cheung YL, Wong WO . H-infinity optimization of a variant design of the dynamic vibration absorber---Revisited and new results
Journal of Sound and Vibration, 2011,330(16):3901-3912
[本文引用: 3]

[11] Asami T, Nishihara O . Analytical and experimental evaluation of an air damped dynamic vibration absorber: design optimizations of the three-element type model
Journal of Vibration and Acoustics, 1999,121(3):334-342
[本文引用: 3]

[12] Asami T, Nishihara O . H$_{2}$optimization of the three-element type dynamic vibration absorbers
Journal of Vibration and Acoustics, 2002,124(4):583-592
[本文引用: 1]

[13] 王孝然, 申永军, 杨绍普 . 接地式三要素型动力吸振器的H$_{\infty }$优化
动力学与控制学报, 2016,14(5):448-453
[本文引用: 2]

( Wang Xiaoran, Shen Yongjun, Yang Shaopu . H$_{\infty }$optimization of the grounded three element type dynamic vibration absorber
Journal of Dynamics and Control, 2016,14(5):448-453 (in Chinese))
[本文引用: 2]

[14] Shen YJ, Wang L, Yang SP , et al. Nonlinear dynamical analysis and parameters optimization of four semi-active on-off dynamic vibration absorbers
Journal of Vibration and Control, 2013,19(1):143-160
[本文引用: 1]

[15] Shen Y, Ahmadian M . Nonlinear dynamical analysis on four semi-active dynamic vibration absorbers with time delay
Shock and Vibration, 2013,20(4):649-663
[本文引用: 1]

[16] 彭海波, 申永军, 杨绍普 . 一种含负刚度元件的新型动力吸振器的参数优化
力学学报, 2015,47(2):320-327
[本文引用: 1]

( Peng Haibo, Shen Yongjun, Yang Shaopu . Parameter optimization of a new type of dynamic vibration absorber with negative stiffness
Chinese Journal of Theoretical and Applied Mechanics, 2015,47(2):320-327 (in Chinese))
[本文引用: 1]

[17] 邢昭阳, 申永军, 邢海军 等. 一种含放大机构的负刚度动力吸振器的参数优化
力学学报, 2019,51(3):894-903
[本文引用: 1]

( Xing Zhaoyang, Shen Yongjun, Xing Haijun , et al. Parameters optimization of a dynamic absorber with amplifying mechanism and negative stiffness
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(3):894-903 (in Chinese))
[本文引用: 1]

[18] 王孝然, 申永军, 杨绍普 等. 含负刚度元件的三要素型动力吸振器的参数优化
振动工程学报, 2017,30(2):177-184
[本文引用: 1]

( Wang Xiaoran, Shen Yongjun, Yang Shaopu , et al. Parameter optimization of three-element type of dynamic vibration absorber with negative stiffness
Journal of Vibration Engineering, 2017,30(2):177-184 (in Chinese))
[本文引用: 1]

[19] Shen Y, Peng H, Li X , et al. Analytically optimal parameters of dynamic vibration absorber with negative stiffness
Mechanical Systems and Signal Processing, 2017,85:193-203
[本文引用: 1]

[20] Hu Y, Chen MZQ . Performance evaluation for inerter-based dynamic vibration absorbers
International Journal of Mechanical Sciences, 2015,99:297-307
[本文引用: 1]

[21] Hu Y, Chen MZQ, Zhan S , et al. Analysis and optimisation for inerter-based isolators via fixed-point theory and algebraic solution
Journal of Sound and Vibration, 2015,346(1):17-36
[本文引用: 1]

[22] Wang X, Liu X, Shan Y , et al. Analysis and optimization of the novel inerter-based dynamic vibration absorbers
IEEE Access, 2018,6:33169-33182
[本文引用: 1]

[23] 陆泽琦, 陈立群 . 非线性被动隔振的若干进展
力学学报, 2017,49(3):550-564
[本文引用: 1]

( Lu Zeqi, Chen Liqun . Some recent progresses in nonlinear passive isolations of vibrations
Chinese Journal of Theoretical and Applied Mechani, 2017,49(3):550-564 (in Chinese))
[本文引用: 1]

[24] 张舒, 徐鉴 . 时滞耦合系统非线性动力学的研究进展
力学学报, 2017,49(3):565-587
[本文引用: 1]

( Zhang Shu, Xu Jian . Review on nonlinear dynamics in systems with coupling delays
Chinese Journal of Theoretical and Applied Mechanics, 2017,49(3):565-587 (in Chinese))
[本文引用: 1]

[25] 赵艳影, 徐鉴 . 时滞非线性动力吸振器的减振机理
力学学报, 2008,40(1):98-106
[本文引用: 1]

( Yanying Zhao Jian Xu . Mechanism analysis of delayed nonlinear vibration absorber
Chinese Journal of Theoretical and Applied Mechanics, 2008,40(1):98-106 (in Chinese))
[本文引用: 1]

[26] Zhao YY, Xu J . Effects of delayed feedback control on nonlinear vibration absorber system
Journal of Sound and Vibration, 2007,308(1-2):212-230


[27] 赵艳影, 徐鉴 . 利用时滞反馈控制自参数振动系统的振动
力学学报, 2011,43(5):894-904
[本文引用: 1]

( Zhao Yanying, Xu Jian . Using the delayed feedback to control the vibration of the auto-parametric dynamical system
Chinese Journal of Theoretical and Applied Mechanics, 2011,43(5):894-904 (in Chinese))
[本文引用: 1]

[28] 李帅, 周继磊, 任传波 等. 时变参数时滞减振控制研究
力学学报, 2018,50(1):99-108
[本文引用: 1]

( Li Shuai, Zhou Jilei, Ren Chuanbo , et al. The research of time delay vibration control with time-varying parameters
Chinese Journal of Theoretical and Applied Mechanics, 2018,50(1):99-108 (in Chinese))
[本文引用: 1]

[29] 申永军, 赵永香, 田佳雨 等. 一类含时滞的半主动悬架系统的动力学分析
力学学报, 2013,45(5):755-762
[本文引用: 1]

( Shen Yongjun, Zhao Yongxiang, Tian Jiayu , et al. Dynamical analysis on a kind of semi-active suspension with time delay
Chinese Journal of Theoretical and Applied Mechanics, 2013,45(5):755-762 (in Chinese))
[本文引用: 1]

[30] 刘俊, 陈林聪, 孙建桥 . 随机激励下滞迟系统的稳态响应闭合解
力学学报, 2017,49(3):685-692
[本文引用: 1]

( Liu Jun, Chen Lincong, Sun Jianqiao . The closed-form solution of steady state response of hysteretic system under stochastic excitation
Chinese Journal of Theoretical and Applied Mechanics, 2017,49(3):685-692 (in Chinese))
[本文引用: 1]

[31] 公徐路, 许鹏飞 . 含时滞反馈与涨落质量的记忆阻尼系统的随机共振
力学学报, 2018,50(4):880-889
[本文引用: 1]

( Gong Xulu, Xu Pengfei . Stochastic resonance of a memorial-damped system with time delay feedback and fluctuating mass
Chinese Journal of Theoretical and Applied Mechanics, 2018,50(4):880-889 (in Chinese))
[本文引用: 1]

[32] 吕小红, 罗冠炜 . 冲击渐进振动系统相邻基本振动的转迁规律
力学学报, 2017,49(5):1091-1102
[本文引用: 1]

( Lü Xiaohong, Luo Guanwei . Transition law of adjacent fundamental motions in vibro-impact system with progression
Chinese Journal of Theoretical and Applied Mechanics, 2017,49(5):1091-1102 (in Chinese))
[本文引用: 1]

[33] Zang J, Yuan TC, Lu ZQ , et al. A lever-type nonlinear energy sink
Journal of Sound and Vibration, 2018,437:119-134
[本文引用: 1]

[34] Zhang YW, Lu YN, Zhang W , et al. Nonlinear energy sink with inerter
Mechanical Systems and Signal Processing, 2019,125:52-64
[本文引用: 1]

[35] 范盛金 . 一元三次方程的新求根公式与新判别法
海南师范学院学报(自然科学版), 1989,2(2):91-98
[本文引用: 1]

( Fan Shengjin . A new extracting formula and a new distinguishing means on the one variable cubic equation
Natural Science Journal of Hainan Normal College, 1989,2(2):91-98 (in Chinese))
[本文引用: 1]