多稳态串联折纸结构的非线性动力学特性 1)

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-01

邱海^*, 方虹斌^,^?^,²⁾, 徐鉴^*

* 同济大学航空航天与力学学院,上海 200092

?复旦大学智能机器人研究院,上海 200433;

NONLINEAR DYNAMICAL CHARACTERISTICS OF A MULTI-STABLE SERIES ORIGAMI STRUCTURE ¹⁾

Qiu Hai^*, Fang Hongbin^,^?^,²⁾, Xu Jian^*

* School of Aerospace Engineering and Applied Mechanics, Tongji University,Shanghai 200092,China

? Institute of AI and Robotics, Fudan University, Shanghai 200433,China

通讯作者: 2) 方虹斌,研究员,主要研究方向：折纸超材料,仿生移动机器人,非线性动力学. E-mail:fanghongbin@fudan.edu.cn

收稿日期:2019-05-5接受日期:2019-05-23网络出版日期:2019-07-18

基金资助:

1) 国家自然科学基金资助项目.11772229
国家自然科学基金资助项目.11572224
国家自然科学基金资助项目.91748203

Received:2019-05-5Accepted:2019-05-23Online:2019-07-18
作者简介 About authors

摘要
折纸结构和折纸力学超材料由于其无穷的设计空间、出色的变形能力、超常规力学特性和广泛的应用前景,最近受到了学术界和工程界的广泛关注.特别地,某些折纸结构单胞由于具有独特的双稳态特性而获得深入研究.注意到折纸结构和折纸超材料通常由多胞构成,但多胞结构的多稳态特性及其诱发的动力学行为尚不清晰,相关的研究还较少.本文在双稳态Miura-ori堆叠结构单胞的基础上,研究由两个异构双稳态单胞基于力平衡串联而成的结构.静力学分析指出,双胞串联结构具有4个定性不同的稳定构型,呈现出多稳态特征.动力学分析指出,双胞串联结构在4个稳定构型处具有显著不同的固有频率特征. 逐渐增大激励幅值,双胞串联结构的多稳态特性诱发出类型丰富的复杂非线性动力学响应,包括亚谐、超谐甚至混沌的阱内和阱间振动. 根据幅值特征,我们将稳态动力学响应分为九类,并开展了动力学响应的吸引盆和吸引盆稳定性分析.结果表明,不同类型动力学响应的吸引盆稳定性(即出现概率)显著不同,且与激励幅值密切相关.本文得到的多稳态双胞串联结构的静力学特性、动力学响应的分类,以及吸引盆稳定性相对于激励幅值的演化规律,对深入认识多稳态折纸结构的非线性动力学特性,调控非线性动力学响应具有参考价值和指导意义.
关键词： 折纸结构;机械超材料;多稳态;吸引盆;吸引盆稳定性

Abstract
Recently, origami structures and origami mechanical metamaterials receive extensive attention from the science and engineering communities due to the infinite design space, excellent deformability, extraordinary mechanical properties, and wide application potentials. In particular, some origami structures have been well studied due to their unique bistability. Note that origami structures and origami metamaterials are always composed of multiple cells; however, for multi-cell origami structures, their multistability characteristics and the induced dynamical behaviors have not been well understood. On the basis of the bistable stacked Miura-ori structure, this paper studies an origami structure connected by two heterogeneous cells in series based on force balance. Static analysis suggests that the two-cell series structure have four different stable configurations, exhibiting a multi-stable profile. Dynamical analysis reveals that the two-cell series origami structure presents significantly different natural frequencies at the four stable configurations. With the increase of the excitation amplitude, the multistability of the two-cell series structure could induce complex nonlinear dynamical responses, including intrawell and interwell oscillations that are sub-harmonic, super-harmonic, or even chaotic. They can be classified into nine types based on the response amplitude characteristics. Moreover, the basin of attraction and the basin stability of these dynamical responses are examined. The results indicate that the basin stabilities (i.e., the appearing probabilities) of these types of dynamical response are significantly different and closely relate to the excitation amplitude. In summary, the outcomes of this paper, i.e., the static characteristics of the two-cell series structure, the classification on dynamical responses, and the evolution rule of the basin stabilities with respect to the excitation amplitude, would contribute to the understanding on the nonlinear dynamics of multi-stable origami structures, and provide the basis for controlling the nonlinear dynamical responses.
Keywords：origami structure;mechanical metamaterials;multistability;basin of attraction;basin stability

PDF (20171KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex 收藏本文
本文引用格式
邱海, 方虹斌, 徐鉴. 多稳态串联折纸结构的非线性动力学特性 ¹⁾. 力学学报[J], 2019, 51(4): 1110-1121 DOI:10.6052/0459-1879-19-115
Qiu Hai, Fang Hongbin, Xu Jian. NONLINEAR DYNAMICAL CHARACTERISTICS OF A MULTI-STABLE SERIES ORIGAMI STRUCTURE ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2019, 51(4): 1110-1121 DOI:10.6052/0459-1879-19-115

引言

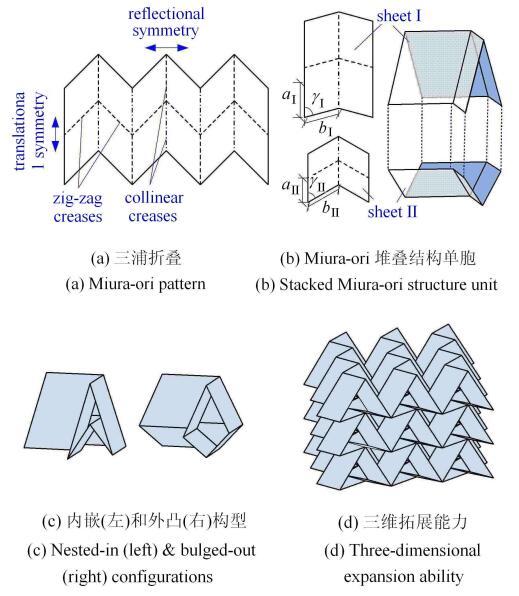
折纸(origami)作为古老的民间艺术,由于其出色的折叠变形能力和无穷的设计空间,最近受到了科学界和工程界的广泛关注^[1-10]. 日本科学家三浦公亮(Koryo Miura)于1985年提出了一种可以应用于卫星太阳能电池帆板的折叠模式,被称为三浦折叠(Miura-ori或Miura Fold)^[11]. 如图1(a)所示, Miura-ori的折痕图由平行四边形填充而成.在一个方向上,折痕共线,两侧的平行四边形关于共线折痕镜射对称;在另一个方向,折痕成锯齿状,平行四边形穿过锯齿折痕并具有平移对称.由于其设计参数较少且具备刚性可折性(rigid-foldability)和可折平性(flat-foldability),Miura-ori得到了较为深入的研究,其应用场景也日益拓展,例如：基于Miura-ori开发的机器人旋翼飞机^[12]、含有Miura-ori结构的防冲击夹芯板的核心^[13-14]、Miura-ori声学传感器阵列^[15]、Miura-ori结构引导的可变构型声屏障^[16-18]以及基于Miura-ori的可编程曲面^[19]等.

最近一段时间,Miura-ori又在力学超材料(以下简称超材料)的开发中发现了它的价值^[20-25].折纸超材料的研究一般从两个角度展开："刚性折面+理想铰链折痕"模式(即刚性折叠(rigid-folding))和"弹性折面(facet)+虚拟折痕(crease)"模式.前者主要研究由折叠引起的构型变化和拓扑变化及其带来的静力学特性;后者着重研究由折面弯曲变形所诱发的特有力学特性.例如, Schenk和Guest^[23]对Miura-ori超材料进行了系统的几何学分析和折叠运动学分析.基于刚性折面假设,研究揭示了由刚性折叠带来的负泊松比特征;基于弹性折面假设,研究给出了其面外变形的模式. Filippov等^[26-27]研究了由Miura-ori构成的大刚度可重构折纸管道,基于弹性折面假设,研究得到了折纸管道的变形模态和在三个特征方向的刚度.

图1

新窗口打开|下载原图ZIP|生成PPT
图1Miura-ori折痕及Miura-ori堆叠结构

Fig. 1Miura-ori and the stacked Miura-ori (SMO) structure

最近,通过进一步分析Miura-ori中的几何非线性,****们发现Miura-ori结构有可能呈现出独特的双稳态特性.在弹性折面假设下, Silverberg等^[22] 指出Miura-ori超材料中的每一个单元都可以在两种稳定构型间切换,利用此特性,超材料的刚度具有再编程性(re-programmability). 在刚性折面假设下,方虹斌等发现Miura-ori堆叠结构(stacked Miura-ori (SMO) structure)也可以呈现出双稳态特性. SMO单胞是由两个不同尺寸的Miura-ori单元在满足几何和运动学约束条件下堆叠而成的 (图1(b)).通过赋予折痕合适的旋转刚度,SMO单胞具有两种稳定构型：内嵌(nested-in)构型和外凸(bulged-out)构型(图1(c)). 值得指出的是,SMO单胞的双稳态来源于几何非线性,在稳定构型间切换时SMO单胞保持刚性可折叠性,即刚性折面不发生变形,仅相对于理想铰链折痕旋转;相反,Silverberg等^[22]所揭示的双稳态则打破了刚性可折叠性,双稳态来源于折面的弹性变形. SMO单胞还可以在三个方向平铺,具有出色的三维拓展能力(图1(d)).在上述研究的基础上,Li和Wang^[28]还提出了通过在单元内部施加压力以获得SMO结构的多稳态特性.研究发现,通过调节气压,多胞并联SMO结构可以在单稳态和多稳态之间切换.

除了上述几何学、运动学和静力学研究,最近对折纸结构和折纸超材料的研究也逐渐向动力学拓展.开展折纸结构的动力学研究具有重要的意义.首先,实际工程应用对折叠速度和加速度具有一定要求,这就对折叠过程中结构或超材料的动力学稳定性提出了要求. 其次,折纸结构和折纸超材料在工作时将不可避免地受到已知和未知的动力学激励,例如基础振动、冲击和碰撞等,明确在外激励下的动力学响应是折纸结构和折纸超材料投入实际应用的前提.最后,折纸结构和折纸超材料本身有可能呈现出优异的动力学特性,从而可以应用于隔振^[29-30]、俘能、波传导^[31-32]等领域并实现性能提升.尽管具有强烈的需求,相比于发展迅速且成果丰硕的折纸几何学、折纸运动学和折纸静力学,目前折纸动力学的研究还停留在起步阶段. Rodrigues等^[33]利用形状记忆合金制作了可自适应展开的折纸支架,并通过数值方法研究了该折纸支架在形状记忆合金热力学载荷下的复杂非线性动力学响应情况;类似的动力学研究也拓展到了具有多稳态特性的纸球(origami ball)结构. Yasuda等^[34]对弹性波在多单元串联的Tachi-Miura 链中的传播进行了研究,为了建模的便利性,他们将Tachi-Miura结构简化为多连杆结构.方虹斌等^[35]对具有双稳态特性的SMO单胞在简谐激励作用下的动力学行为进行了系统的理论、数值和实验研究.他们发现,双稳态作为一种全局强非线性, 可以诱发出复杂的动力学响应,包括阱内周期振动、阱间亚谐波振动和阱间混沌振动等;有些动力学响应可以衰减激励,而有些响应则显著地放大激励.研究发现,在相同外激励条件下,初始条件的细微调整可以显著地影响动力学响应;数值和实验结果观察到了丰富的稳态响应切换情况,包括小幅值阱内振动响应和大幅值阱间振动响应间的切换.为了解释这些动力学响应和切换行为,方虹斌等基于势阱的相似性,将双稳态SMO单胞等效建模为Helmholtz-Duffing振子.刘作林等^[36]从几何关系出发,建立了双稳态SMO单胞的动力学模型,并通过动力学辨识方法精确得到了折痕刚度和初始张开角度等重要参数.

注意到,折纸结构或折纸超材料在实际应用中通常由多胞构成.当这些构成单胞具有异构特征,或多胞间采用不同的连接形式时,折纸结构或折纸超材料整体的特性将与单胞具有显著差异.例如,方虹斌等^[37]研究了由两个异构SMO单胞构成的串联结构及其多稳态特性.当两个单胞之间没有变形约束时,串联结构是一个两自由度系统;当两个单胞受到较强的变形协调约束时,串联结构将呈现出力学二极管效应,即结构的拉、压刚度呈现出量级上的差异.研究给出了变形协调约束强弱与刚度特性之间的关系,并通过实验予以验证.尽管明确了静力学特征,双胞串联结构的动力学还没有得到研究,其在外激励作用下可能呈现的动力学响应尚不明了,不同类型稳态动力学响应出现的概率也没有得到评估.对这些问题开展深入研究,有助于进一步掌握多稳态折纸结构的动力学特性,有助于推动折纸动力学这一研究方向的发展,也可以促进折纸结构和折纸超材料应用于实际动力学场景.

为此,本文将研究由两个异构双稳态SMO单胞构成的串联结构在外激励作用下的非线性动力学特性. 第一节介绍双胞SMO串联结构的构成方式、静力学模型和静力学特性,明确其势能阱特征和力-位移关系,重点研究双胞串联结构的多稳态特性.第二节将建立多稳态双胞串联结构的两自由度等效动力学模型,并通过数值方法分析其在简谐激励下的动力学行为,重点关注由多稳态特征引起的复杂非线性动力学响应. 第三节进一步开展双胞串联结构的吸引盆分析和吸引盆稳定性分析,揭示稳态响应对初始条件的敏感性及不同类型稳态响应出现概率相对于激励幅值的演化规律.第四节总结本文的工作和结果.

1 双胞SMO串联结构及其多稳态特性

1.1 SMO单胞结构

SMO单胞结构的静力学和运动学分析已经较为完善,本文不再赘述具体推导过程,仅列出后续将要使用的关系. SMO单胞由两个不同尺寸的Miura-ori单元堆叠构成(图1(b)),两个单元需要满足几何约束条件$b_{I} = b_{{II}} $和$a_{II} \cos \gamma _{II}= a_{I} \cos \gamma _{I} $. SMO单胞的变形可以用单元${ II}$的折面与坐标平面$x-o-y$的夹角$\theta $来描述. 当$\theta > 0$时,该结构呈现出内嵌构型,当$\theta < 0$时为外凸构型(图1(c)).

在"刚性折面+理想铰链折痕"模式下,SMO单胞的折叠只有一个自由度,即可以用一个参数来描述单胞的折叠.本文选取SMO单胞在$z$轴方向的长度$L$作为变量,于是每条折痕处两个折面之间的二面角都可以通过$L$的代数方程来表示. SMO单胞共含有12个二面角,其中部分二面角在折叠过程中始终相同,仅有5个二面角$(\rho_i$, $i=1,2,3,4,5$)独立(图2(a)). 其中

(1)$\rho _1 = 2\arccos \left( {\dfrac{L^2 + a_{I} ^2-a_{II} ^2}{2La_{I} \sin \gamma _{I} }} \right) $

(2)$ \rho _4 = 2\arccos \left( {\dfrac{L^2-a_{I} ^2 + a_{II} ^2}{2La_{II} \sin \gamma _{II} }} \right) $

其他角度可以由$\alpha _1 $和$\alpha _4 $表示为

(3)$ \rho _2 = 2\arcsin \dfrac{\sin ({\rho _1 }/2)}{\sqrt {1-\cos ^2({\rho _1 } /2)\sin ^2\gamma _{I} } } $

(4)$ \rho _3 = \pi-{(\rho _1 + \rho _4 )}/ 2 $

(5)$\rho _5 = 2\arccos \dfrac{\cos \gamma _{II} \cos ({\rho _4 }/2)} {\sqrt {1-\cos ^2 ( \rho _4 / 2)\sin ^2\gamma _{II} } } $

(6)$\psi = 2\arcsin \left[ {\sin \gamma _{I} \sin (\rho _2 / 2)} \right] $

通过给折痕赋予旋转刚度, 可以调控SMO 单胞的势能阱特征和静力学特性.具体地,令$k_{II}$为对应于二面角$\rho_2 $的折痕的单位长度旋转刚度,$k_{I}$为其余折痕的单位长度旋转刚度.于是每一条折痕的刚度可以表示为$K_1 = 2b_{I}k_{I}$,$K_2 = 2a_{I} k_{II}$,$K_3 = 4b_{I} k_{I}$,$K_4 = 2b_{{II}} k_{I}$和$K_5 = 2a_{II} k_{I}$.据此,结构的总弹性势能可以得到

(7)$$ \varPi = \dfrac{1}{2}\sum_{i = 1}^5 K_i \left( {\rho _i-\rho _i^0 } \right)^2 $$

其中$\rho _i^0 $为结构初始无内应力状态时的折痕角度.将势能方程对位移求导,可以得到相应方向的恢复力-位移关系

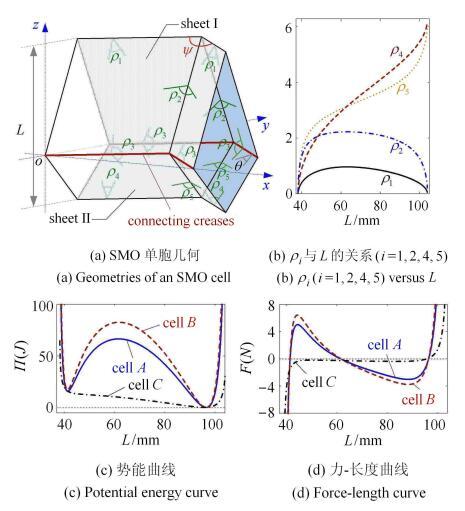
(8)$$ F_L = \dfrac{d\varPi }{dL} = \sum_{i = 1}^5 {K_i \left( {\alpha _i-\alpha _i^0 } \right)} \left( {\dfrac{d\rho _i }{dL}} \right) $$

图2(b)给出了二面角$\rho _1 $, $\rho _2 $, $\rho _4 $及$\rho _5 $与长度$L$的关系. 注意到$\rho _1 $和$\rho _2 $与$L$之间不是一一对应的,即一个二面角可以对应于两个不同的单胞长度$L$; 仅有的例外发生在$\rho _1 $和$\rho _2 $的最大值处,其对应于一个临界构型,即单元II处于水平.这样的几何非一一对应关系是SMO单胞双稳态特性的根本来源.因此,对应于$\rho _1 $和$\rho _2 $的折痕刚度对于结构的双稳态具有决定性作用.根据方虹斌等^[31]的实验结果和刘作林等^[32]给出的参数辨识结果, 设计了3个异构的SMO单胞(见表1),它们具有相同的几何参数,但是折痕的刚度系数不一样. 根据式(7)和式(8), 可以得到3个单胞的势能曲线(图2(b))和力-长度本构曲线(图2(c)). 对于单胞A和单胞B,$k_{II} $的值高出$k_{I} $两个量级,单胞呈现出双稳态特征,即势能曲线包含两个阱,对应的力-长度曲线两次正向穿越水平轴;对于单胞C,$k_{ II} $的值仅高出$k_{I} $一个量级,单胞丢失了双稳特征.这证明了折痕刚度的量级差异对于单胞势能和稳定性特征的影响.值得指出的是,除了单胞的折痕刚度,无内应力状态时的折痕角度$\rho _i^0 $也会显著影响SMO单胞的势能和稳定性特征^[28,35].

图2

新窗口打开|下载原图ZIP|生成PPT
图2SMO单胞的几何、势能、和静力学特征

Fig. 2Geometry, potential energy, and statics characteristics of SMO units

Table 1
表1
表1SMO单胞结构的几何和刚度参数
Table 1The geometric and stiffness parameters of SMO units

新窗口打开|下载CSV

1.2 双胞SMO串联结构

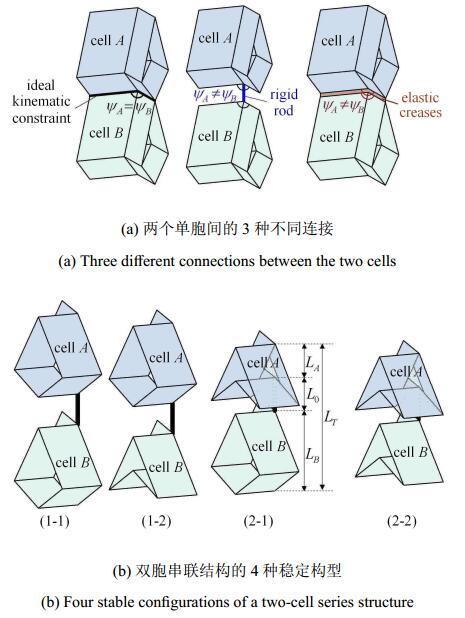
力学折纸超材料通常包含数量众多的基本单元,这就要求我们将研究重点从单胞结构发展到多胞结构.这里我们关注由两个异构SMO单元串联而成的结构.异构可以是为实现特定目标而人为设计的,也可以是由于制造误差等引起的.具体地,我们用表1给出的异构双稳态单胞$A$和双稳态单胞$B$来组建串联结构.通过采用不同的连接形式,两个单胞将受到不同的变形协调约束.例如,如果两个单胞在折痕处通过理想运动学约束连接,它们的折痕角$\psi _A $和$\psi _B $将完全一致,它们的变形也将保持完全同步,该串联结构为单自由度系统(图3(a));如果两个单胞通过刚性连杆约束,它们的折痕角完全自由,它们的变形也不受约束,该串联结构将成为一个两自由度系统(图3(b));如果两个单胞在折痕处通过弹性约束连接,折痕角的差值$\Delta \psi = \psi _A-\psi _B $会产生额外的弹性势能,影响串联结构整体的势能特征和静力学特性(图3(c)).

图3

新窗口打开|下载原图ZIP|生成PPT
图3双胞串联结构的连接形式和4种稳定构型

Fig. 3Different connections between the two cells and the four stable configurations of a two-cell series structure

本文考虑两个双稳态单胞$A$和$B$通过刚性连杆连接的情况(图3(a)),即两个单胞的变形不受约束独立折叠. 将两个单胞的长度表示为$L_A $和$L_B $,连杆的长度表示为常数$L_0 $.由于刚性连杆在折叠过程中不变形,不失一般性,我们令$L_0 = 0$. 于是,串联结构的总长度为$L_{T} = L_A + L_B $.由于单胞$A$和单胞$B$分别具有两个稳定构型,串联结构有可能呈现出4个稳定构型(图3(b)). 我们把单胞的外凸稳定构型表示为 "1",内嵌稳定构型表示为 "2",则串联结构的4个稳定构型可以分别表示为"(1-1)", "(1-2)", "(2-1)"和"(2-2)",其中两个数字分别表示单胞$A$和单胞$B$的构型. 基于式(7), 可以计算两个单胞的弹性势能$\varPi_A $和$\varPi _B $,双胞串联结构的总势能为$\varPi _{T} = \varPi _A + \varPi _B $.

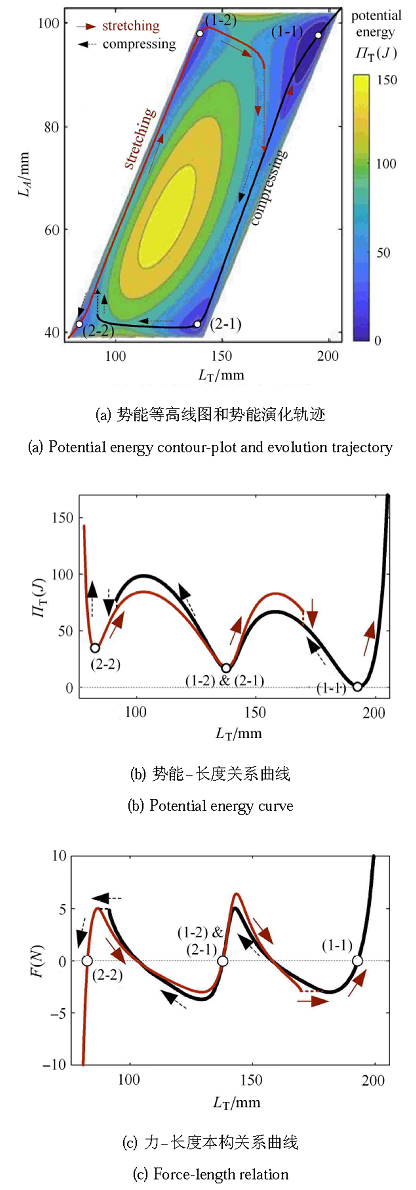
基于表1所列的单胞$A$和$B$的参数, 计算了双胞串联结构的总势能,如图4(a)所示.与预测的一致,势能超曲面具有4个阱,说明双胞串联结构具有4个稳定构型. 通过寻找每一个$L_{T}$值所对应的局部势能最小值, 可以在势能图上得到双胞串联结构准静态拉伸和压缩过程的势能演化轨迹(图4(a)和图4(b)). 对应于该轨迹, 可以得到基于位移控制的双胞串联结构的力-长度本构曲线(图4(c)). 注意到,尽管双胞串联结构具有4个势能局部极小值点,对应于4个稳定构型,但是,准静态拉伸或压缩不能遍历4个稳定构型.在拉伸过程中,双胞串联结构的构型从(2-2)变到(1-2),随后发生了一次跳跃并逐渐变到(1-2),却没有经过(2-1)构型;在压缩过程中, 构型从(1-1)变到(2-1),随后发生了一次跳跃并回到(2-2),却没有经过(1-2)构型. 在上述势能演化轨迹上,两个单胞之间力平衡的关系可以得到满足. 值得指出的是,通过调整构成单胞的几何或刚度参数, 有可能得到定性不同的势能演化轨迹和力-长度本构关系.

图4

新窗口打开|下载原图ZIP|生成PPT
图4双胞串联结构的势能特征和力-长度关系

Fig. 4Potential energy landscape and force-length relation of the two-cell series structure

2 双胞SMO串联结构及其多稳态特性

2.1 动力学模型与固有频率特征

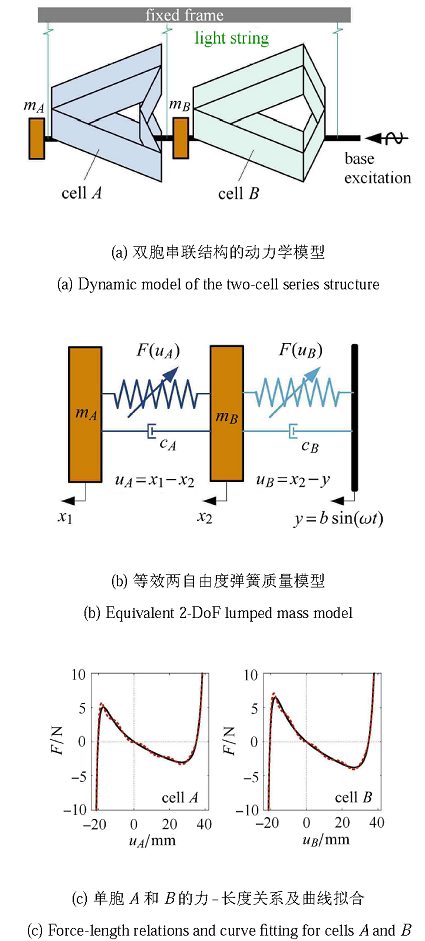
本节建立双胞SMO串联结构在基础激励下的动力学模型,并探讨在弱激励条件下的固有频率特征. 如图5(a)所示,串联结构中单胞$A$和单胞$B$的一个端部分别连有集中质量$m_A $和$m_B $,并假设集中质量的重量远大于单胞结构本身;整个系统通过细绳水平地悬挂于固定支架上,并使双胞结构的4个顶点和集中质量中心位于同一条水平线上.系统的端部受到简谐基础位移激励.由于两个SMO单胞的折叠相互独立,每个单胞和与其固结的集中质量可以被等效建模为一个单自由度双稳态弹簧质量系统,双胞串联结构整体则可以被等效建模为一个两自由度弹簧质量系统(图5(b)).

具体地,两个单胞的几何和刚度参数由表1给出,它们的力-位移关系如图5(c)中实线所示.引入$u_i = L_i-L_{i0} (i = A,B)$, 其中$L_{A0} = 61.55$ mm和$L_{B0} = 61.71$ mm是两个单胞处于不平衡构型(势能最高点),即力-长度本构曲线以负斜率穿越$F_i = 0$轴时的长度.因此,$u_i > 0$表示单胞处于外凸构型,$u_i < 0$表示单胞处于内嵌构型. 由于力-长度关系无显示表达,为了后续分析的方便, 采用十二次多项式曲线进行拟合, 如图5(c)中虚线所示. 系统中两个集中质量的重量相同$m_A = m_B = 0.15$ kg. 注意到,折纸结构的折痕通常含有一定的阻尼效应,在动力学建模时阻尼项不可忽略. 这里我们假设两个单胞具有相同的黏性结构阻尼,阻尼系数$c = 1.0kg/s$. 整个串联结构受到基础位移激励$y = bsin(\omega t)$,其中$b$为激励幅值,$\omega $为激励频率.集中质量$m_A $和$m_B $的绝对位移可表示为$x_1 = y + u_B + u_A $,$x_2 = y + u_B $.于是,双胞串联结构的两自由度等效动力学模型的控制方程为

(9)$$ \left.\begin{array} m_A \ddot {u}_A + F(u_A ) + c\dot {u}_A =-m_A (\ddot {u}_B + \ddot {y}) \\ m_B \ddot {u}_B + F(u_B )-F(u_A ) + c\dot {u}_B-c\dot {u}_A =-m_B \ddot {y} \end{array}\!\!\right\} $$

我们首先研究串联结构在4个稳定构型处的固有频率特征.设定外激励幅值$b = 0.01$ mm,我们在[0, 50]Hz区间内以0.1 Hz为间隔对双胞串联结构进行离散扫频,并考察均方根意义下结构整体的位移传递率$T_{d { RMS}} $

(10)$ T_{d {RMS}} = \dfrac{X_{1 RMS} }{Y_{RMS} } = \dfrac{\sqrt {\left( {x_{11}^2 + x_{12}^2 + \cdots + x_{1n}^2 } \right) / n} }{\sqrt {\left( {y_1^2 + y_2^2 + \cdots+ y_n^2 } \right) / n} } $

图5

新窗口打开|下载原图ZIP|生成PPT
图5双胞串联结构的动力学模型

Fig. 5Dynamic model of the two-cell series structure

图6给出了串联结构在4个稳定构型处位移传递率$T_{d_{RMS}} $的频谱曲线,它们总体上呈现出线性特征,但是差异显著. 在(1-1)构型,由于两个单胞的力-长度本构关系接近且具有相同的外凸构型,频谱曲线上出现了两个固有频率非常接近的情况,分别为12.9 Hz和15.0 Hz. 在(1-2)和(2-1)构型, 由于两个单胞构型不一致,串联结构的第一阶和第二阶固有频率差异较大.在(1-2)构型,第一阶和第二阶固有频分别为12.9 Hz和39.2 Hz;在(2-1)构型,分别为15.3 Hz和35.8 Hz.在(2-2)构型,由于两个单胞具有相同的内嵌构型,频谱曲线上再次出现了两个固有频率非常接近的情况,分别为35.9 Hz和39.0 Hz.

图6

新窗口打开|下载原图ZIP|生成PPT
图6弱激励条件下双胞串联结构在4个稳定构型处位移传递率$T_{d_ {RMS}}$的频谱曲线

Fig. 6The $T_{d_ {RMS}} $ frequency-amplitude curves of the two-cell series structure corresponding to the four stable configurations under weak excitations

为了解释上述现象,我们采用类似的离散扫频方法研究了两个构成单胞的固有频率特征.单胞$A$在外凸构型和内嵌构型的固有频率分别是12.8 Hz和35.6 Hz;单胞$B$在外凸构型和内嵌构型的固有频率分别是15.2 Hz和38.9 Hz. 因此串联结构在某一稳定构型处的两阶固有频率与两个构成单胞在对应构型处的固有频率非常接近. 这是由于在激励幅值很弱的情况下,单胞折叠变形很小,非线性特征尚没有被激发;同时,两个单胞之间的连接没有运动学约束,它们独立折叠,当激励频率与某一构成单胞的固有频率接近时,其振动幅值被明显放大,但另一个单胞却几乎没有发生折叠变形,呈现出刚性特征.

串联结构在4个稳定构型出呈现显著不同的固有频率,对于实现动力学特性的可调性具有重要意义.例如,将该串联结构作为机械超材料的基本构成单胞,通过切换其稳定构型可以实现阻带/通带位置和宽度的调控.

2.2 非线性动力学响应

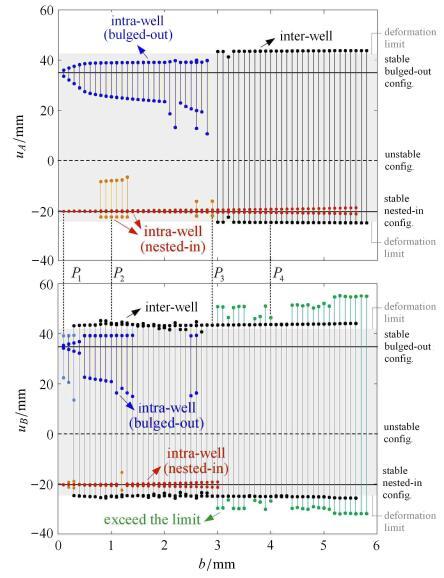
在上述动力学模型的基础上,本节研究双胞SMO串联结构在基础位移激励下的非线性动力学行为,着重探讨有可能出现的复杂动力学响应. 我们对串联结构的动力学控制方程进行了系统的数值分析.具体地,基础位移激励的频率设为12.9 Hz,接近于单胞$A$在外凸构型时的固有频率;激励幅值在[0.1,6] mm内以0.1 mm为步长离散变化. 在初始时刻,单胞$B$被固定在外凸稳定构型,即$u_{B0} = 34.79$ mm,$\dot {u}_{B0} = 0$ mm/s;由于单胞本构具有全局强非线性(双稳态),为了抓住尽可能多的动力学响应, 在$u_{A0} \in [-23,41]$ mm和$\dot {u}_{A0} \in [-1000, 1000]$ mm/s范围内按网格布置$100\times 100$个单胞$A$ 的初始条件. 基于四阶龙格库塔方法, 可以得到$u_A $和$u_B $的动力学响应. 图7给出了$u_A $和$u_B $响应的峰峰值与激励幅值$b$之间的关系.总的来说,两个单胞的响应可以分为两大类,即围绕某一个稳定平衡构型的阱内振动响应(intra-well responses)和围绕3个平衡点的阱间振动响应(inter-well responses). 进一步分析可知,阱内振动响应可以分为非共振阱内振动和共振阱内振动,体现为振动幅值的差异^[40];阱间振动也可以具有不同的幅值.图7同时标出了两个单胞的平衡构型位置和变形极限. 注意到部分阱间振动响应的幅值超出了单胞的变形极限,这是因为通过多项式拟合的单胞本构具有一定的误差,尤其是,其不能体现单胞趋向于折叠极限时所受的运动学约束. 事实上,趋向于折叠极限时的运动学约束对应了力学本构上的非光滑特征,也具有强非线性;将其纳入折纸结构的动力学模型,对于动力学响应的定量描述具有重要意义,是未来研究的重要方向. 考虑到本节研究的目的是揭示可能的动力学响应类型,因此,图7给出的结果依然具有价值.

图7

新窗口打开|下载原图ZIP|生成PPT
图7$u_A $和$u_B $响应的幅值(峰峰值)与激励幅值$b$的关系

Fig. 7Relations between the peak-peak response amplitude of $u_A $, $u_B $ and the excitation amplitude $b$

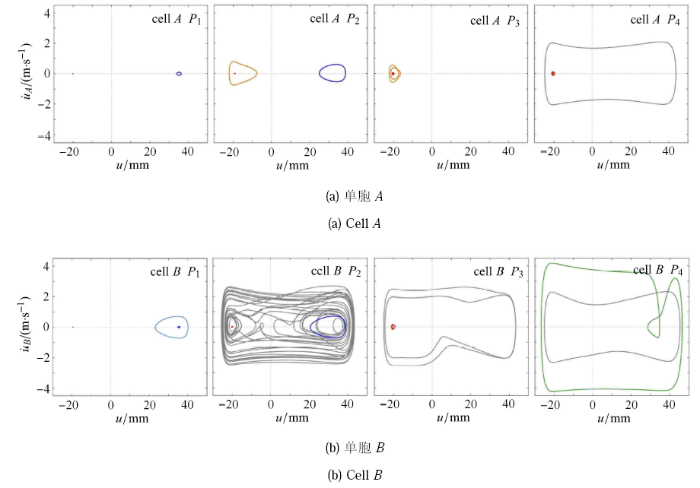
需要注意的是,图7给出的分类不区分振动响应的谐波特征,而只关注了响应的幅值特征.事实上,上述观察到的响应有可能具有丰富的谐波成分.为此, 选取了4个激励幅值(图7,$P_1 \sim P_4 )$： $P_1 $ (0.1 mm),$P_2 $ (1.0 mm),$P_3 $ (2.9 mm)和$P_4 $ (4.0 mm),并在图8中分别展示单胞$A$和单胞$B$动力学响应的相图. 单胞$A$和单胞$B$都有可能呈现阱内振动和阱间振动,且这两类响应可以在同一激励条件下共存.例如,当外激励振幅为4.0 mm ($P_4 )$时,取决于不同的初始条件,单胞$A$有可能呈现出小振幅的阱内振动和大振幅的阱间振动.图8也清晰地表明,阱内振动和阱间振动具有丰富的谐波形式.例如,当振幅为2.9 mm ($P_3 )$时,单胞$A$可以呈现出超谐波(具有显著的$2\omega $和$3\omega $频率成分)的阱内振动,单胞$B$却可以呈现出亚谐波的阱间振动(具有显著的$\omega / 2$频率成分);当外激励振幅为1.0 mm ($P_2 )$,单胞$B$呈现出具有混沌特征的阱间振动.上述响应中的倍频和分数频成分是由单胞本构中的关键非线性因素诱发的. 方虹斌等^[35]曾对双稳SMO单胞的动力学测试数据进行频谱分析,也发现了响应中的$2\omega $,$3\omega $和$\omega / 2$频率成分,并通过数值分析证实了平方和立方非线性对诱发这些超谐波和亚谐波响应的重要意义. 对于本文研究的串联结构, 上述复杂的动力学行为也要求我们开展更为细致的频谱分析,从而明确结构非线性特征与动力学响应特征间的关系. 由于篇幅限制, 频谱分析将另文分析.

图8

新窗口打开|下载原图ZIP|生成PPT
图8单胞$A$和单胞$B$在图7所示$P_1 , P_2 , P_3 $和$P_4 $处可能动力学响应的相图

Fig. 8Phase diagrams of cell $A$ and cell $B$'s dynamic responses at $P_1 , P_2 , P_3 $ and $P_4 $ shown in Fig.7

3 吸引盆稳定性分析

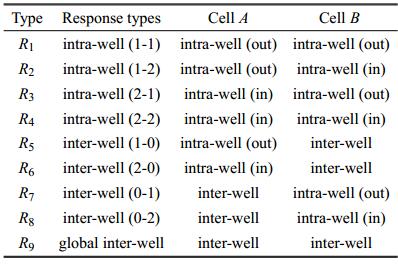
图7和图8清晰地指出,单胞$A$和单胞$B$在相同的激励频率和幅值下,有可能呈现出多种类型定性不同的动力学响应. 根据单胞$A$和单胞$B$响应的幅值特征(即是否是围绕外凸和内嵌稳定构型的阱内振动,还是阱间振动), 可以将双胞串联结构的响应类型分为9类,如表2所示.其中,数字`1'和`2'分别表示构成单胞围绕稳定构型`1'和`2'的阱内振动;数字`0'表示构成单胞的阱间振动. 这就要求我们深入探讨双胞串联结构不同类型动力学响应的出现概率及其随基础位移激励幅值的演化规律.

本文使用"吸引盆稳定性(basin stability)"指标来衡量不同类型动力学响应出现的概率. 2013年,Menck等^[41]提出了利用吸引盆稳定性指标来表征某一稳定吸引子的"稳定性",即该吸引子在多维相空间中吸引盆的体积.具体地,吸引盆稳定性是通过计算在随机初始条件下到达某一吸引子的概率而得到的. 为此,令双胞串联结构受到的基础位移激励的频率为12.9 Hz,激励幅值在[0.1, 6] mm内以0.1 mm为步长离散变化.单胞$B$在初始时刻被固定在外凸稳定构型,即$u_{B0} = 34.79$ mm, $\dot {u}_{B0} = 0$ mm/s;单胞$A$的初始条件在$u_{A0} \in [-23, 41]$ mm和$\dot {u}_{A0} \in [-1000, 1000]$ mm/s范围内可以随机取值. 针对每一个激励幅值, 随机取$N_{T} = 10 000$个单胞$A$的初始条件$(u_{A0}, \dot {u}_{A0} )$,通过四阶龙格-库塔法分别求得系统的稳态响应,并判断单胞$A$和单胞$B$的响应类型. 通过统计最终收敛到某一类型吸引子的初始条件的个数$N(R_i )$,$i = 1,2,\cdots,9$, 可以得到该类型动力学响应的吸引盆稳定性,即

(11)$$ S_B (R_i ) = \dfrac{N(R_i )}{N_T } $$

$S_B (R_i ) \in [0,1]$,其值越高表明该类型吸引子的吸引区域越大,即该类型动力学响应出现的概率越高.

Table 2
表2
表2双胞串联结构的动力学响应分类
Table 2Classification of the two-cell series structure's dynamical responses

新窗口打开|下载CSV

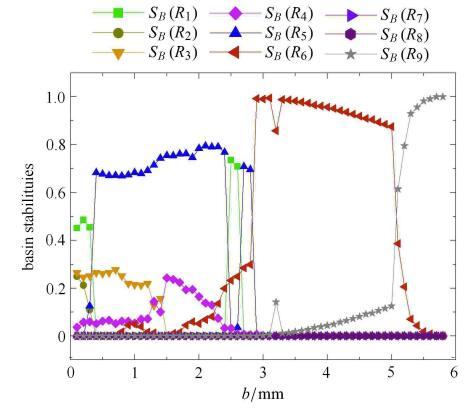
图9给出了上述9种动力学响应类型的吸引盆稳定性随激励幅值的演化规律. 我们注意到,吸引盆稳定性与激励幅值密切相关.当激励幅值很小($b < 0.3$ mm)时,两个单胞主要执行阱内振动;由于每个单胞的两个势阱具有不同的深度和宽度,4种阱内振动的吸引盆稳定性(即$S_B (R_i )$ $(i = 1,2,3,4))$具有明显差异.随着输入能量的增大,更靠近激励源的单胞$B$开始执行阱间振动,而单胞$A$仍然维持阱内振动(外凸构型), 其临界点发生在$b = 0.3$ mm到0.4 mm之间,表现为$S_B (R_5 )$的突然增大.在$b \in (0.3,2.8)$ mm范围内,动力学响应类型$R_5 $占主导,但两个单胞仍可以继续发生阱内振动. 当激励幅值进一步增大时,单胞$A$也可以突破能障跳入另一个对应于内嵌构型的势阱, 而单胞$B$继续执行阱间振动,其临界点发生在$b = 2.8$ mm到2.9 mm之间,表现为$S_B (R_5 )$的突然降低和$S_B (R_6 )$的突然升高. 继续增大激励幅值,当$b > 5$ mm时,$S_B (R_9 )$突然升高,表明两个单胞都开始执行阱间振动.注意到,在$ b \in [0.1,6.0]$ mm 范围内,$R_7$ 和$R_8$ 类型的动力学响应一直没有出现.

图9

新窗口打开|下载原图ZIP|生成PPT
图99种类型动力学响应的吸引盆稳定性(单胞$B$的初始条件固定)

Fig. 9Basin stabilities of the nine types of dynamical responses (with fixed initial conditions of cell $B$)

为了更清晰地展示吸引盆稳定性随激励幅值的演化规律,同时展示动力学响应对初始条件的敏感性,我们选取了6个激励幅值($b = 0.2$,1.0,2.8,3.5,5.0,5.5 mm)并绘制了相应的吸引盆,如图10所示.这里,绿色表示响应类型$R_1 $,黄色表示响应类型$R_2 $和$R_3 $ (由于定性特征相图,不作区分),紫色表示响应类型$R_4 $,蓝色表示响应类型$R_5 $,红色表示响应类型$R_6 $,$R_7 $和$R_8 $类型的动力学响应没有出现,灰色表示响应类型$R_9 $.图10清晰地展示了在$u_A-\dot {u}_A $相平面上不同类型动力学响应吸引盆的演化. 图10(a)中,全局吸引到双胞阱内振动($R_1 , R_2 , R_3 , R_4 )$;图10(b) $\sim $图10(d)中,单胞$B$执行阱间振动 ($R_5 , R_6 )$的吸引域出现并不断扩大至全局,图10(d) $\sim $图10(f)中,双胞阱间振动($R_9 )$的吸引域出现并不断扩大至全局.

图10

新窗口打开|下载原图ZIP|生成PPT
图10在6个激励幅值处的吸引盆($u_A-\dot {u}_A $相平面)

Fig. 10Basin of attractions (on the $u_A-\dot {u}_A $ phase plane) corresponding to six excitation amplitudes

上述吸引盆和吸引盆稳定性结果清晰地说明了不同类型动力学响应出现的概率具有高度不一致性,且与激励幅值密切相关. 吸引盆稳定性相对于激励幅值的演化规律也为我们控制双胞串联结构的动力学响应并从而获得动力学性能的提升提供了依据. 例如,具有大振幅的阱间振动可以利用于振动能量俘获或动力学吸振,这就要求阱间振动响应具有较高的出现概率,在本文给出的例子中, 即$S_B (R_5 )$,$S_B (R_6 )$或$S_B (R_9 )$的值较高;相反,具有小振幅的阱内振动则有希望应用于动力学隔振,其要求$S_B (R_5 )$,$S_B (R_6 )$或$S_B (R_9 )$的值较小.

4 结论

具有多稳态特性的折纸结构和折纸超材料具有广阔的应用前景.本文研究了由两个异构双稳态折纸SMO单胞基于力平衡串联而成的结构. 静力学分析指出,双胞串联结构具有4个定性不同的稳定构型;准静态拉伸和压缩将经历不同的路径,且不能遍历4个稳定构型. 动力学分析指出,在小振幅激励下,双胞串联结构在4个稳定构型处呈现出显著不同的固有频率特征.逐渐增大激励幅值,多稳态双胞串联结构将呈现出类型丰富的复杂非线性动力学响应,包括双胞阱内振动、阱内-阱间耦合振动、双胞阱间振动等.通过初步的频谱分析, 我们发现这些响应可以是超谐的、亚谐的,甚至可以是混沌的. 根据幅值特征,我们将稳态动力学响应分为9类. 为了研究他们出现的概率特征,我们开展了动力学响应的吸引盆和吸引盆稳定性分析.结果表明,不同类型的动力学响应的吸引盆大小(即出现概率)显著不同,且与激励幅值密切相关.本文得到的多稳态双胞串联结构的静力学特性、动力学响应的分类以及吸引盆稳定性相对于激励幅值的演化规律,对于深入认识多稳态折纸结构的非线性动力学特性,调控其非线性动力学响应具有参考价值和指导意义.

参考文献原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]

Perazahernandez

, Hartl

, Malak

RJJ

, et al. Origami-inspired active structures: a synthesis and review
Smart Materials & Structures, 2014,23(9):094001

[本文引用: 1]

[2]

Lebée

. From folds to structures, a review
International Journal of Space Structures, 2015,30(2):55-74

DOI URL

[3]

Ning

, Wang

, Zhang

, et al. Assembly of advanced materials into 3D functional structures by methods inspired by origami and Kirigami: A review
Advanced Materials Interfaces, 2018,1800284

[4]

Turner

, Goodwine

, Sen

. A review of origami applications in mechanical engineering
Journal of Mechanical Engineering Science, 2016,230(14):2345-2362

DOI URL

[5]

Park

, Won

, Ko

. A review on hierarchical origami and kirigami structure for engineering applications.
International Journal of Precision Engineering and Manufacturing-Green Technology, 2019,6(1):147-161

DOI

[6]

Rus

, Tolley

. Design, fabrication and control of origami robots
Nature Reviews Materials, 2018,3:101-112

DOI

[7]

陈仕魁, 顾险峰 . 心脏支架、折纸艺术与超材料设计
科技导报, 2017(10):107

( Chen

Shikui

, Gu

Xianfeng

. Heart stent, origami and metamaterial design
Science & Technology Review, 2017(10):107 (in Chinese))

[8]

李笑, 李明 . 折纸及其折痕设计研究综述
力学学报, 2018,50(3):23-32

( Li

Xiao

, Li

Ming

. A review of origami and its crease design
Chinese Journal of Theoretical and Applied Mechanics, 2018,50(3):23-32 (in Chinese))

[9]

常若菲, 张一慧, 宋吉舟 . 可延展结构的设计及力学研究新进展
固体力学学报, 2016,37(2):95-106

( Chang

Roufei

, Zhang

Yihui

, Song

Jizhou

. Recent advances in mechanics of stretchable designs
Chinese Journal of Solid Mechanics, 2016,37(2):95-106 (in Chinese))

[10]

冯慧娟, 杨名远, 姚国强等. 折纸机器人
中国科学: 技术科学, 2018,48(12):5-20

[本文引用: 1]

( Feng

Huijuan

, Yang

Mingyuan

, Yao

Guoqiang

, et al. Origami robots
Scientia Sinica Technologica, 2018,48(12):5-20 (in Chinese))

[本文引用: 1]

[11]

Miura

. Method of packaging and deployment of large membranes in space
Title The Institute of Space and Astronautical Science Report, 1985,618:1

[本文引用: 1]

[12]

Sareh

, Chermprayong

, Emmanuelli

, et al. Rotorigami: A rotary origami protective system for robotic rotorcraft
Science Robotics, 2018,3:5228

DOI URL [本文引用: 1]

[13]

Gattas

, You

. Geometric assembly of rigid-foldable morphing sandwich structures
Engineering Structures, 2015,94:149-159

DOI URL [本文引用: 1]

[14]

Karagiozova

, Zhang

, Lu

, et al. Dynamic in-plane compression of Miura-ori patterned metamaterials
International Journal of Impact Engineering, 2019,129:80-100

DOI URL [本文引用: 1]

[15]

Harne

, Lynd

. Origami acoustics: Using principles of folding structural acoustics for simple and large focusing of sound energy
Smart Materials and Structures, 2016,25(8):085031

DOI URL [本文引用: 1]

[16]

Thota

, Wang

. Reconfigurable origami sonic barriers with tunable bandgaps for traffic noise mitigation
Journal of Applied Physics, 2017,122(15):154901

DOI URL [本文引用: 1]

[17]

Thota

, Wang

. Tunable waveguiding in origami phononic structures
Journal of Sound and Vibration, 2018,430:93-100

DOI URL

[18]

Thota

, Li

, Wang

. Lattice reconfiguration and phononic band-gap adaptation via origami folding
Physical Review B, 2017,95:064307

DOI URL [本文引用: 1]

[19]

Dudte

, Vouga

, Tachi

, et al. Programming curvature using origami tessellations
Nature Materials, 2016,15:583-588

DOI [本文引用: 1]

[20]

Boatti

, Vasios

, Bertoldi

. Origami metamaterials for tunable thermal expansion
Advanced Materials, 2017,29:1700360

DOI URL [本文引用: 1]

[21]

, Evans

, Bae

, et al. Programming reversibly self-folding origami with micropatterned photo-crosslinkable polymer trilayers
Advanced Materials, 2015,27(1):79-85

DOI URL

[22]

Silverberg

, Evans

, McLeod

, et al. Using origami design principles to fold reprogrammable mechanical metamaterials
Science, 2014,345(6197):647-650

DOI URL [本文引用: 2]

[23]

Schenk

, Guest

. Geometry of Miura-folded metamaterials
Proceedings of the National Academy of Sciences, 2013,110(9):3276-3281

DOI URL [本文引用: 1]

[24]

, Fang

, Sadeghi

, et al. Architected origami materials: How folding creates sophisticated mechanical properties
Advanced Materials, 2018,31(5):1805282

[25]

Fang

, Chu

, Xia

, et al. Programmable self-locking origami mechanical metamaterials
Advanced Materials, 2018,30(15):1706311

DOI URL [本文引用: 1]

[26]

Filipov

, Tachi

, Paulino

. Origami tubes assembled into stiff, yet reconfigurable structures and metamaterials//
Proceedings of the National Academy of Sciences of the United States of America, 2015

[本文引用: 1]

[27]

Filipov

, Paulino

, Tachi

. Origami tubes with reconfigurable polygonal cross-sections.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science, 2016,472(2185):20150607

DOI URL [本文引用: 1]

[28]

, Wang

. Fluidic origami with embedded pressure dependent multi-stability: A plant inspired innovation
Journal of The Royal Society Interface, 2015,12(111):20150639

DOI URL [本文引用: 2]

[29]

陆泽琦, 陈立群 . 非线性被动隔振的若干进展
力学学报, 2017,49(3):550-564

[本文引用: 1]

( Lu

Zeqi

, Chen

Liqun

. Some recent progresses in nonlinear passive isolations of vibrations
Chinese Journal of Theoretical and Applied Mechanics, 2017,49(3):550-564 (in Chinese))

[本文引用: 1]

[30]

曹登庆, 白坤朝, 丁虎等. 大型柔性航天器动力学与振动控制研究进展
力学学报, 2019,51(1):1-13

[本文引用: 1]

( Cao

Dengqing

, Bai

Kunchao

, Ding

, et al. Advances in dynamics and vibration control of large-scale flexible spacecraft
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(1):1-13 (in Chinese))

[本文引用: 1]

[31]

刘坚, 雷济荣, 夏百战 . 基于Chebyshev展开的区间穿孔板超材料分析
力学学报, 2017,49(1):137-148

DOI Magsci [本文引用: 2]

<p>目前对于声学超材料的传输特性分析和优化大多是基于确定的数值和确定的模型，然而在实际工程和结构设计中存在大量材料自身特性和几何物理参数的不确定性.如果忽略这些不确定变量对声学超材料传输特性分析和优化过程的影响，得到的结果可能不正确.针对这一现状，拟将切比雪夫区间模型引入多层穿孔板超材料，提出多层穿孔板超材料声学透射率的区间切比雪夫展开——蒙特卡洛模拟法（interval Chebyshev expansionMonte Carlo simulation method，ICE-MCSM）.该方法采用截断切比雪夫多项式近似拟合多层穿孔板超材料的声学透射率响应曲线，构造声学透射率响应曲线的切比雪夫代理模型；然后采用蒙特卡洛模拟法（Monte Carlosimulation method，MCSM）随机生成一定数量的不确定区间变量的样本数据点，并将生成的不确定区间变量样本数据点代入切比雪夫代理模型，预测单个不确定区间变量和多个不确定区间变量条件下的多层穿孔板超材料声学透射率区间的上界和下界.数值分析结果表明，ICE-MCSM预测的声学透射率变化区间的上界和下界与直接蒙特卡洛法（direct Monte Carlo simulation method，DMCSM）预测的声学透射率上界和下界的结果非常接近.与DMCSM相比，ICE-MCSM具有更高的计算效率.因此，ICE-MCSM可有效且高效地分析不确定区间变量条件下多层穿孔板超材料声学透射率传输特性，具有良好的工程应用前景.</p>

( Liu

Jian

, Lei

Jirong

, Xia

Baizhan

. The interval analysis of multilayer-meramaterials with perforated apertures based on Chebyshev expansion
Chinese Journal of Theoretical and Applied Mechanics, 2017,49(1):137-148 (in Chinese))

DOI Magsci [本文引用: 2]

修晨曦, 楚锡华 . 基于微形态模型的颗粒材料中波的频散现象研究
力学学报, 2018,50(2):315-328

[本文引用: 2]

( Xiu

Chenxi

, Chu

Xihua

. Study on dispersion behavior and band gap in granular materials based on a micromorhpic model
Chinese Journal of Theoretical and Applied Mechanics, 2018,50(2):315-328 (in Chinese))

[本文引用: 2]

[33]

Rodrigues

, Fonseca

, Savi

, et al. Nonlinear dynamics of an adaptive origami-stent system
International Journal of Mechanical Sciences, 2017,133:303-318

DOI URL [本文引用: 1]

[34]

Yasuda

, Chong

, Charalampidis

, et al. Formation of rarefaction waves in origami-based metamaterials
Physical Review E, 2016,93(4):043004

DOI URL [本文引用: 1]

[35]

Fang

, Li

, Ji

, et al. Dynamics of a bistable Miura-origami structure
Physical Review E, 2017,95(5):052211

DOI URL [本文引用: 3]

[36]

Liu

, Fang

, Wang

, et al. A parameter identification method for continuous-time nonlinear systems and its realization on a Miura-origami structure
Mechanical Systems and Signal Processing, 2018,108:369-386

DOI URL [本文引用: 1]

[37]

Fang

, Wang

, Li

. Asymmetric energy barrier and mechanical diode effect from folding multi-stable stacked-origami
Extreme Mechanics Letters, 2017,17:7-15

DOI URL [本文引用: 1]

[38]

Kuribayashi

, Tsuchiya

, You

, et al. Self-deployable origami stent grafts as a biomedical application of Ni-rich TiNi shape memory alloy foil
Materials Science & Engineering A, 2006,419(1):131-137

[39]

Fonseca

, Rodrigues

, Savi

, et al. Nonlinear dynamics of an origami wheel with shape memory alloy actuators.
Chaos, Solitons & Fractals, 2019,122:245-261

[40]

Lenci

, Rega

. Forced harmonic vibration in a duffing oscillator with negative linear stiffness and linear viscous damping//
The Duffing Equation: Nonlinear Oscillators and their Behaviour, John Wiley & Sons Ltd, 2015

[本文引用: 1]

[41]

Menck

, Heitzig

, Marwan

, et al. How basin stability complements the linear-stability paradigm
Nature Physics, 2013,9(2):89-92

DOI [本文引用: 1]