,2), 王毅泓华东理工大学理学院认知神经动力学研究所, 上海 200237ENERGY CODING OF HEMODYNAMIC PHENOMENA IN THE BRAIN 1)
Peng Jun, Wang Rubin,2), Wang YihongThe Institute for Cognitive Neurodynamics,School of Science,East China University of Science and Technology,Shanghai 200237, China通讯作者: 2) 王如彬,教授,主要研究方向：认知神经动力学.E-mail:rbwang@163.com
收稿日期:2019-01-7接受日期:2019-04-6网络出版日期:2019-07-18
| 基金资助: |
Received:2019-01-7Accepted:2019-04-6Online:2019-07-18
作者简介 About authors
摘要
神经信息的编码与解码是神经科学中的核心研究内容,同时又极具挑战性.传统的编码理论都具有各自的局限性,很难从脑的全局运行方式上给出有效的理论.而由于能量是一个标量具有可叠加性,因此能量编码理论可以从神经元活动的能量特征出发来研究脑功能的全局神经编码问题,取得了一系列的研究成果.本研究以王-张神经元能量计算模型为基础,构建了一个多层次结构的神经网络,通过计算机数值模拟得到了神经网络的能量消耗和血液中葡萄糖供能的变化情况.计算结果显示,和网络的神经活动达到峰值的时间相比,血液中葡萄糖的供能达到峰值的时间延迟了约5.6s.从定量的角度再现了功能性核磁共振(fMRI)中的血液动力学现象：大脑某个脑区的神经元集群被激活以后经过5~7 s的延迟,脑血流的变化才会大幅增加.模拟结果表明先前发表的由王-张神经元模型所揭示的负能量机制在控制大脑的血液动力学现象中起着核心的作用,预测了刺激条件下大脑的能量代谢与血流之间变化的本质是由神经元在发放动作电位过程中正、负能量之间的非平衡、不匹配性质所决定的.本文的研究结果为今后进一步探究血液动力学现象的生理学机制提供了新的研究方向,在神经网络的建模与计算方面给出了一个新的视角和研究方法.
关键词：
Abstract
The coding and decoding of neural information is the core research content in neuroscience, and it is also very challenging. The traditional neural coding theories have their own limitations, and they are difficult to provide effective theory from the global operation mode of the brain. Since energy is a scalar and has superposition, the theory of energy coding can study the global neural coding problem of the brain function from the prospective of energy characteristics of neuron activities, and has achieved a series of research results. Based on the Wang-Zhang neuron energy calculation model, this paper constructed a multi-level neural network, and we obtained the changes of the energy consumption of the neural network and energy supply of glucose in the blood by numerical simulation. The calculation results showed that the time of peak supply of glucose in the blood is delayed about 5.6 seconds compared to the time when the neural activity of the network reaches its peak, which reproduced hemodynamic phenomena in functional nuclear magnetic resonance (fMRI) from a quantitative perspective: after a five to seven seconds delay in the activation of a brain region, the change in cerebral blood flow increases dramatically. The simulation results showed that negative energy mechanism, which was previously reported by our group using Wang-Zhang neuronal model, played a central role in controlling the hemodynamics of the brain. Also, it predicted the neural coupling mechanism between the energy metabolism and blood flow changes in the brain under the condition of stimulation, which was determined by imbalance and mismatch between the positive and negative energy during the spike of neuronal action potentials. The research results in this paper provided a new research direction for further exploring the physiological mechanism of hemodynamic phenomena in the future, and gave a new perspective and research method in the modeling and calculation of neural networks.
Keywords：
PDF (1113KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
彭俊, 王如彬, 王毅泓. 大脑血液动力学现象中的能量编码 1). 力学学报[J], 2019, 51(4): 1202-1209 DOI:10.6052/0459-1879-19-010
Peng Jun, Wang Rubin, Wang Yihong.
引言
神经信息编码与解码是神经科学中非常重要,却又极具挑战性的研究内容[1-4],有许多十分困难的问题亟需解决[5-6].目前还没有一套能够从全局角度解释大脑是如何编码和解码的有效理论,这是因为一方面是由于受到实验神经科学技术水平等的限制,另一方面也缺少相关的可供参考的详细的实验数据的分析[7].从神经科学发展的历史来看,理论研究与实验分析是相辅相成的,理论建模与数值模拟已经给实验神经科学带来了许多新的研究思想和研究方向[8].大脑的神经结构是复杂和多层次的,而且认知功能的实现也是多层次的耦合和各个脑区协调的结果.因此,要揭示大脑皮层的神经编码,需要在各个不同的视角,不同的层面以及不同层面的结合上展开研究.特别是应当从大脑神经活动的全局观点出发,给出神经编码的有效理论,因此集群编码脱颖而出.然而大规模神经元集群的神经编码目前还没有一个能够为大家所普遍接受的成熟理论[9],更没有一个能够用于识别和解读脑内神经活动的全局编码理论.在神经系统的全局编码研究领域,基于神经元的电活动需要消耗脑内大量的神经能量,而大脑工作时的运筹方式又必须服从两个基本原则[10]：(1)经济性--阈上刺激和阈下刺激情况下的神经元活动应当符合能量最小化原则;(2)高效率--在神经网络中信号的传输效率应当符合能量利用率最大化的原则.在这两个基本原则的约束下,神经能量是如何来控制脑的运作和信息编码的呢?为此在神经电生理实验数据的基础上Wang等[11]提出了一个耦合神经元电特性的生物物理模型(王-张模型),继而提出了能量编码的理论与方法[12-16].利用这个耦合模型,能够模拟神经元的动作电位及兴奋性突触后电位(EPSP)和抑制性突触后电位(IPSP)的形状,与实验记录结果完全一致[11].
王-张模型的一个重要特点是得到了神经元膜电位的函数,并发现这个膜电位函数与对应的能量函数有唯一的对应的关系[11].这个重要的发现在H-H模型中也得到了证明[13].由于神经元是通过膜电位的各种发放模式来编码神经信息的,又因为动作电位和能量函数有唯一的对应关系,这就有可能利用能量的演化模式来编码神经信息.已经发现,用能量方法可以编码不同的刺激信息,不仅可以编码单个神经元的发放,也可以编码神经网络水平上不同频率的神经振荡[12,14,16].因为能量是一个标量,所以集群神经元中每个神经元消耗的能量是可以相互叠加[15].利用这样一种计算方法,可以避免其他编码理论中需要处理的高维非线性耦合这个难点.在单个神经元能量函数的基础上,还研究了网络模型中集群神经元能量消耗的演化规律.当网络中能够对一个刺激产生一种能量分布模式,就说这种特定的能量分布编码了这个刺激[12,14,16].
在实验方面,神经活动伴随着大脑血流量(CBF)和血氧饱和度的变化而变化,这种变化可用功能磁共振成像(fMRI)技术检测.现在的实验神经科学可以根据功能性核磁共振成像中记录到的血氧水平依赖对比信号(BOLD),在定量的层面上对大脑血流所供给的能量需求变化情况进行评估[1-23].根据脑血流上升和耗氧比例的不同,会引起的磁通率的变化,从而功能核磁共振成像通常在刺激之后的数秒时间内能够检测到其对应脑区局部血流的活动变化.这就是所谓的血液动力学现象,神经系统的血流总是在皮层神经元受到刺激大约5~7 s后才会显著增加[24].就所了解到的文献资料来看[25],目前神经科学界并没有提出一个有效的理论对这一现象的神经机制给出科学合理的解释,同时也没有看到相关的从神经建模到计算这两个方面对这一实验现象进行计算机模拟并再现血液动力学现象的研究报道.
为了模拟fMRI磁共振成像中的血流延迟现象,本文以王-张神经元模型为基础,通过构造一个多层次结构的神经网络,用能量编码的方法给出产生血液动力学现象的神经能量变化,从定量的角度再现功能性磁共振成像技术中脑血流的大幅增加滞后神经元激活区5$\sim $7s的血液动力学现象.由于该研究是建立在神经元活动的负能量机制的基础之上[11],预测大脑血液动力学现象的本质是神经活动过程中负能量机制的存在.因此这项研究的重要意义在于能够为今后探究血液动力学现象的生理机制提供了新的视野,从而与以前发表的研究成果一起为今后建立脑理论研究框架提供了重要的支撑[11-16,26- 29].
1 模型和方法
1.1 神经元的能量计算模型
为了近似的计算出神经元网络的能量消耗,Wang等[11,13,28]对单个神经元提出了一个生物物理模型,其结构见图1.图1
新窗口打开|下载原图ZIP|生成PPT图1王-张神经元生物物理模型
Fig. 1Wang-Zhang biophysical model of a neuron
图1中,$C_{m}$表示膜电容,$I_{m}$为外部神经元输入的总电流,$U$为电压源.$r_{m}$表示跨越$I_{m}$的电阻,$r_{0m}$表示跨越$U$的电阻,将膜电阻分为了三部分$r_{1m}$,$r_{2m}$和$r_{3m}$.此外,钠离子、钾离子、钙离子等各种带电离子在离子通道中流进流出,会形成一个回路电流,引起自感应效果,等效于一个电感元件$L_{m}$.网络中第$m$个神经元和周围神经元的耦合关系由所有与之相连的神经元输入电流的总和$I_{m}$表达如下
其中,$i_{1m}$表示维持静息膜电位所需要的电流,$i_{0m}$表示在阈下活动时神经元受周围神经元电流刺激而产生的总效应,$\omega_m $表示动作电位发放的频率.
图1的电路方程为 \begin{equation} \label{eq2} \left.{\begin{array}{l} U_m = r_{0m} I_{0m} + r_{1m} I_{1m} + L_m \dot {I}_{1m} \\ I_{0m} = I_{1m}-I_m + \dfrac{U_{im} }{r_m } + C_m \dot {I}_{1m} \\ U_{im} = C_m r_{3m} \dot {U}_{0m} + U_{0m} \\ \end{array}} \right\}(2) \end{equation}又 \begin{equation} \label{eq3} L_m \dot {I}_{1m} + r_{1m} I_m = K_{1m} \dot {U}_{0m} + K_{2m} U_{0m}-r_{2m} I_m(3) \end{equation} 其中, $ K_{1m} = C_m \left(r_{2m} + r_{3m} + {r_{2m} r_{3m} }/{r_m }\right)$, $k_{2m} = 1 + {r_{2m} }/{r_m }$. 通过解上述方程组,可得到膜电位$U_{0m} $的解析
$$\begin{align*}& U_{0m} =-\frac{\hat {g}_1 }{\lambda ^2_m }-\frac{\hat {g}_2{ e}^{-a(t-t_n )}}{\lambda ^2_m-a^2} -\\&\qquad \frac{1}{\lambda _m ^2 + \omega _m ^2}\bigg\{\hat {g}_3 \sin [\omega _m (n)(t-t_n )] +\\ &\qquad \hat {g}_4 \cos [\omega _m (n)(t-t_n )]\bigg(U_{0m} (t_n ) + \frac{\hat {g}_1 }{\lambda ^2_m } +\\&\qquad \frac{\hat {g}_2 }{\lambda ^2_m-a^2} + \frac{\hat {g}_4 }{\lambda _m ^2 + \omega _m ^2(n)}\bigg)\bigg\}{e}^{-\lambda _m (t-t_n )} (4) \end{align*} $$
其中第$m$个神经元的消耗功率为
其中,$d_{1m}$,$d_{2m}$,$d_{3m}$,$d_{4m}$,$d_{5m}$,$d_{6m}$可由文献[11]得到.根据物理学中的概念,功率是指在单位时间内的能量消耗.下文所涉及到的能量指的就是功率,除非需要否则将不再特别说明.
式(4)是用能量方法得到的动作电位,其数值解如图2(a)所示.将式(4)的解析解代入第$m$个神经元的功率表达式(5)中,可得到如图2(b)所示的功率$P_{m}$.从图2中可以观察到,通过王-张神经元模型模拟得到的神经元动作电位与实验记录结果完全一致[11,13];然而,这样得到的动作电位的能量变化与神经能量的传统理论并不一致.传统的编码理论认为在动作电位的发放过程中,神经元一直处于能量消耗状态即只有正的能量部分;而由王-张神经元模型模拟得到的动作电位的能量变化是由两部分组成.神经元首先从与之相连的微动脉和微血管中汲取能量(脑血流中氧气和葡萄糖),因此从图2中可以观察到当神经元动作电位达到峰值之前(去极化),对应的能量函数是负的用于能量的储存.当动作电位从峰值开始下跌进入复极化阶段时,对应的能量状态表现为正的能量函数即神经元开始耗散能量,被神经元吸收的血流中的氧合血红蛋白,只有在这个时候才变成了脱氧的血红蛋白[11-16].
图2
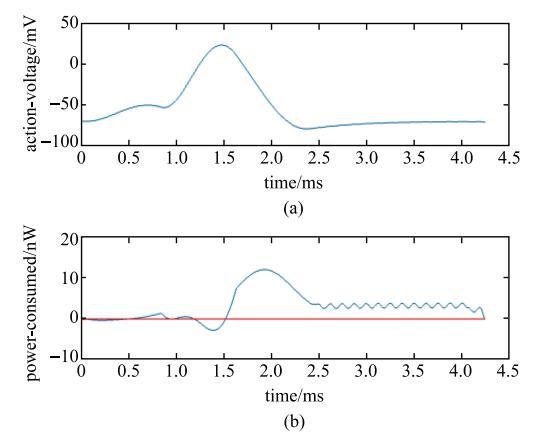新窗口打开|下载原图ZIP|生成PPT图2动作电位和对应的能量函数
Fig. 2Action potential and the corresponding energy function
这个能量计算结果表明,神经元不仅是个耗能元件也是一个储能元件.从一个动作电位来看,神经元先从血流中吸收能量,然后再将吸收的能量消耗,这样周而复始,达到一个动态平衡,这表明单个神经元的能量储备能力是有限的.从血流的葡萄糖和氧气供应来看,在血流的葡萄糖和氧气供应充足且神经元的储能未达上限的情况下,神经元进行能量储备,即在产生动作电位的过程中,出现的"负能量"(即储存的能量)不会被消耗,此时神经元所消耗的能量完全由血流中的葡萄糖提供,而"负能量"则作为后续神经活动的能量储备被神经元储存下来,这说明单个神经元储存的能量应该是在一个动作电位中存储能量的整数倍.这里用$e_{0}$表示单个神经元在一个动作电位中存储的能量,$e_{a}$表示神经元平均储存的能量,$e_{i}$表示第$i$个神经元储存的能量,$E_{0}$表示一个神经网络初始储存的能量,则有\begin{equation} \label{eq6} e_{a} = k_1 e_0(6) \end{equation} \begin{equation} \label{eq7} E_0 = \sum {e_i }(7) \end{equation}其中,$k_{1}$为可调参数,$e_{i}$服从均值为$e_{ a}$的高斯分布：$e_i \sim N(e_{a},\sigma ^2)$.
1.2 网络结构和计算模型
生物体在接受到外界刺激时,该刺激信息会通过反射弧传递到大脑皮层中的相关区域,这会迅速激活一部分神经元,对外界信息进行加工处理.当一部分相关的神经元被激活发放动作电位后,相应的神经脉冲通过传递,引起更大范围的神经网络活动;接着更大范围的神经脉冲会继续扩散传播,直到所有相关神经元构成的网络全部被激活.大脑皮层的许多区域,特别是感知和运动皮层,具有明显的分层结构[30-31].所以本文考虑把相关神经元构成的网络分为五层(其结构如图3所示),考虑到网络传播的特点以及神经电生理的实验现象,每层网络的神经元数量随层数的增加而显著增大[30].首先是第一层的少数神经元受到外界刺激,进而通过第一层神经元间的耦合作用激发该层其他神经元的活动;同时第一层的部分神经元因与第二层的部分神经元耦合而将神经活动传递到第二层,进而第二层神经网络因层内耦合作用逐渐达到激活状态;如此传递下去直到最后一层较大规模的神经网络被激活(本文假设层间传递是单向的).
图3
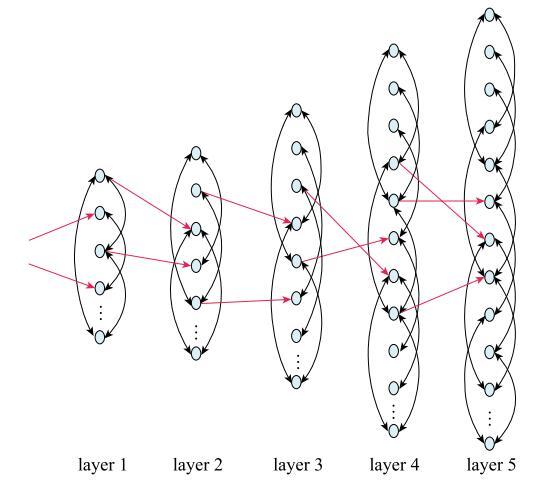新窗口打开|下载原图ZIP|生成PPT图3神经网络的多层次结构
Fig. 3Multi-level structure of neural networks
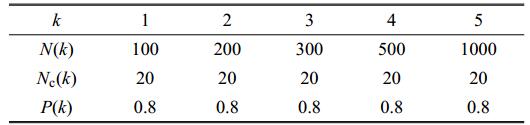
适当选择各种网络参数,如表1所示.其中,$k$表示神经元处于网络中的层数,$N(k)$为第$k$层网络中的神经元数量,第$k$层神经元之间的耦合概率记为$P(k)$,第$k$层神经元受前一层网络(第一层时是指受到外界刺激)影响的神经元数量记为$N_{ c}(k)$.
在神经信息进行传递的过程中,网络中相互耦合的神经元的信号传递通过化学突触连接,存在有突触延迟[32],大约为0.5到2 ms. 用$\tau _{ij} $表示突触前神经元$j$将信息传递到突触后神经元$i$的传递时滞. 假设网络中的神经元均为兴奋性神经元,从统计意义上可知神经元之间突触耦合强度的取值范围服从均匀分布的随机值[33],在下文的计算中,取耦合强度为0.1~0.3之间的均匀分布. 此外,根据赫布可塑性原理[34],在神经信号的传递过程中,每当突触前神经元$j$发放动作电位,与其相连的突触后神经元的耦合作用将会增强. 本文简化突触的这种可塑性特点,假定每次耦合强度的值增加原来的$k_{2}$倍,即：$\omega = \omega (1 + k_2 )$,其中$k_{2}$表示突触学习率,在下面的模拟计算中取为0.02. 不过,突触强度可塑性存在适当的阈值[35],即当增大到一定强度的时候就不会再有明显变化了,本文取耦合强度的上限为1.5.
Table 1
表1
表1网络参数
Table 1
 |
新窗口打开|下载CSV
网络的运行方式
其中,$S(t) = [S_1 (t),S_2 (t),\cdots ,S_j (t),\cdots, S_n (t)]^{ T}$表示$t$时刻各个神经元受到周围神经元的影响,$I_{j}(t)$代表$t$时刻第$j$个神经元收到电流刺激总和;$S_{j}(t)$表示$t$时刻第$j$个神经元受到周围神经元的影响,$I_{ ext}(t)$表示外界刺激对神经元的影响. $W = \left[ {{\begin{array}{*{20}c} {w_{1,1} } & {w_{1,2} } & {\cdots } & {w_{1,n} } \\ {w_{2,1} } & \ddots & & {w_{2,n} } \\ \vdots & & \ddots & \vdots \\ {w_{n,1} } & {w_{n,2} } & \cdots & {w_{n,n} } \\ \end{array} }} \right]$表示网络中神经元间的耦合矩阵,$w_{i,j}$表示第$j$个神经元到第$i$个神经元的耦合强度,$n$表示神经网络中的神经元个数. $Q(t-\tau ) = [Q_1 (t-\tau ),Q_2 (t-\tau ),\cdots ,Q_j (t-\tau ),\cdots, Q_n (t-\tau )]$代表$t-\tau $时刻各个神经元的动作电流发放状态. 其中,神经元静息时对应的$Q_j (t-\tau )$值为0,发放动作电位时对应的$Q_j (t-\tau )$为1;因此刺激信息被简化为0或1的脉冲发放.
将$I_{j}(t)$代入方程式(3)解得膜电位$U_{j}(t)$,并通过功率公式(5)可计算出神经元的功率消耗$P_{j}(t)$. 在$t$时刻,神经网络消耗的总能量$P(t)$为 \begin{equation} \label{eq10} P(t) = \sum P_j (t)(10) \end{equation} 神经网络消耗的能量来源分为两部分：主要部分由血液中的葡萄糖分解直接提供,记为$P_{g}(t)$;其余部分消耗的能量由储存的能量提供,记为$P_{ s}(t)$. 则有 \begin{equation} \label{eq11} P(t) = P_{g} (t) + P_{s} (t)(11) \end{equation} 其中
$$ P_{s} (t) = bP(t)\mbox{sgn}(E(t))$$
这里$E(t)$表示$t$时刻,整个神经网络储存的能量,由式(7)计算可得其初值$E_{0}$. 在本文的模拟中,依据相关实验结果[36]对模型参数进行取值：$b$=3/23.
2 模型计算结果与分析
按表1设置相关网络参数,同时对网络中各个神经元编号. 整个网络的神经元数量一共有$N=2100$个,依次对应于1到2100号. 其中,第1号至第100号对应的是第一层网络中的神经元,第101号至第300号对应的是第 二层网络中的神经元,以此类推,最后1000号对应于最后一层即第五层网络中的神经元. 根据上述数学模型,在Matlab计算软件中进行模拟. 对网络中的小部分神经元(第一层中1到20号神经元)持续施加电流刺激,刺激强度为$I_{ ext}$=70.7 $\mu$A,得到整个网络的神经活动情况和血液中葡萄糖的供能变化情况如图4所示. 其中,横坐标表示时间;图4(a)的纵坐标表示的是整个网络的发放率$R(t) = \dfrac{n(t)}{N}$,$n(t)$表示$t$时刻整个神经网络产生动作电位发放的神经元的总数;图4(b)的纵坐标表示的是在整个网络的运行过程中,血液中葡萄糖供能的功率曲线.对照图4中的(a)图和(b)图可知,网络的神经活动仅在刺激之后的短暂时间内呈明显的阶梯状变化,很快在0.9 s左右时就达到峰值并之后趋于稳定振荡状态. 而血液中葡萄糖的供能则出现两次明显的变化,一开始血液中葡萄糖的供能随着网络的神经活动逐渐增强而呈阶梯状上升,并在0.9 s之后趋于稳定振荡状态;直到5.6 s左右时,血液中葡萄糖的供能又开始大幅度增大,到6.5 s左右时达到峰值并重新趋于稳定振荡状态,此过程中,网络的神经活动一直处于稳定振荡状态. 由此可知,和神经活动达到峰值的时间相比,血液中葡萄糖的供能达到峰值的时间慢了约5.6 s.
图4
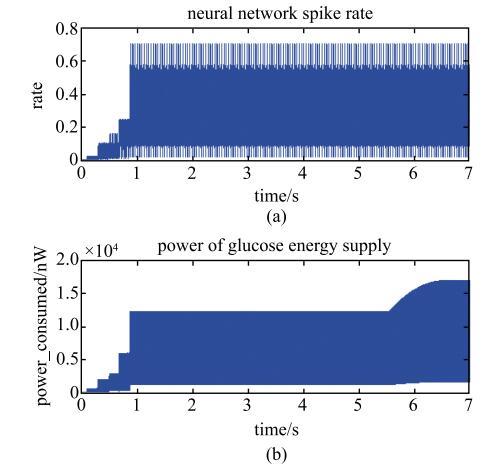新窗口打开|下载原图ZIP|生成PPT图4神经网络的神经活动以及对应时刻血液中葡萄糖的供能变化
Fig. 4Neural activity of the visual neural network and energy supply of blood glucose at the corresponding time points
图5是前1.2 s神经网络的所有神经元的动作电位的发放记录. 在图5中,横坐标表示时间,纵坐标表示的是网络中各个神经元的编号,如果第$i$号神经元在$t$时刻发放了动作电位,则在图中在相应的坐标($t$,$i)$位置处用一个小黑点标记. 观察图5可知,神经网络的神经元被逐层激活,在0.9 s左右时,整个网络的神经元均被激活并很快达到同步振荡状态,这与信息随网络逐层传递相符. 对照图4(a)记录的神经活动可知,网络的神经活动随神经元被逐层激活而呈阶梯状变化,当整个神经网络的神经元都被激活时,网络的神经活动达到峰值,而之后神经活动的稳定振荡对应于多层次神经网络中不同层次神经元之间的同步振荡. 由于血液中葡萄糖供能达到峰值的时间比神经活动的达到峰值的时间慢了约5.6 s,这意味着神经网络被激活之后需经过约5.6 s的延迟,血液中葡萄糖的供能才达到 峰值.
另一方面,血液中葡萄糖的供能可以间接反映血流量的变化[37]. 结合两次血液中葡萄糖供能的大幅上升可知,第一次葡萄糖供能随网络能量消耗上升而上 升到正常血流条件下的最大值,但仍不能完全满足神经网络的能量需求. 在5.6 s左右时,葡萄糖供能出现第二次大幅度增大,这里正好可以间接反映血流的大幅增加,直到6.5 s左右时达到峰值并之后趋于稳定. 所以图4的模拟结果表明和整个神经网络被激活的时间相比,血流大幅上升的时间延迟了约5.6 s,从而再现了fMRI的血液动力学现象：脑区某个神经元集群被激活5~7 s后,脑血流才会大幅上升.
图5
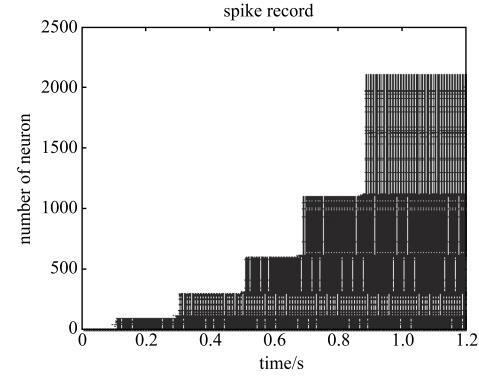新窗口打开|下载原图ZIP|生成PPT图5神经网络在持续刺激下的动作电位的发放记录
Fig. 5The spikes record of the action potential of the neural network under continuous stimulation
为了探究产生上述延迟的原因,同时记录整个过程中网络的神经活动和能量消耗的变化情况如图6所示. 其中,图6(a)记录的是整个网络发放率的变化情况;图6(b)记录的是整个网络对应时刻的能量消耗. 从图可知,网络的能量消耗随神经活动的变化而变化,两者之间具有一一对应的关系. 前0.9 s,网络的能量消耗随神经活动逐渐增强而增加;在0.9 s之后,网络的能量消耗随神经活动趋于稳定振荡而趋于稳定. 结合图4可知,在5.6 s左右时,血液中葡萄糖供能的大幅度上升不是神经网络耗能增加的结果,说明血液动力学现象中血流延迟上升不是神经网络耗能增加的结果.
从神经元模型的角度分析,王-张神经元模型的能量计算结果揭示的一个负能量机制. 与神经能量的传统理论不同,在一个动作电位的产生过程中,王-张神经元模型计算得到的神经元的能量变化由两部分组成(如图2(b)所示),一部分是从血流中获得氧合的血红蛋白,表现为负的能量,用于能量的储存. 而另一部分是将脱氧的血红蛋白释放到血流中,表现为正的能量,用于能量的消耗. 这个新颖的能量计算结果表明,神经元不仅是个耗能元件也是一个储能元件. 基于该机制的基础之上,用能量编码的方法再现了fMRI的血液动力学现象,说明了负能量机制在血液动力学现象中起着重要 作用.
图6
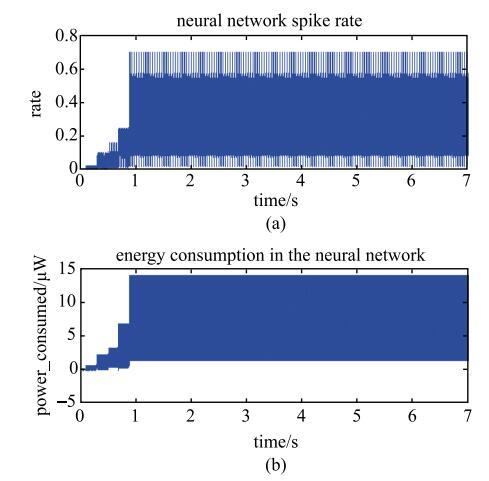新窗口打开|下载原图ZIP|生成PPT图6网络的神经活动和能量消耗的变化情况
Fig. 6Neural activity and energy consumption in the network
3 总结
本研究以王-张神经元模型为基础,构建了一个多层次结构的神经网络,从能量的角度再现了fMRI的血液动力学现象. 通过计算机数值模拟得到了7 s内网络中神经元的神经活动和网络能量消耗的变化情况. 计算结果表明施加刺激后的0.9 s内,网络中神经元的神经活动和网络的能量消耗随时间呈阶梯状变化,在0.9 s左右时达到峰值并趋于稳定. 而血液中葡萄糖的供能出现了两次大幅度上升,第一次随神经活动增强而呈阶梯状上升,在0.9 s左右时达到正常血流条件下供能的最大值;在5.6 s左右时出现第二次大幅度增加,直到6.5 s达到峰值并重新趋于稳定. 由于血液中葡萄糖的供能可以间接反映脑血流的变化,因此在5.6 s左右时的血糖供能的大幅度增加反映了脑血流的大幅度上升,从而再现了fMRI的血液动力学现象： 脑区被激活5$\sim $7 s后,脑血流才会大幅上升.能量编码方法是从脑的活动的全局角度出发而提出的一种新的编码理论,这种方法最重要的一个特点是可叠加性,并且是线性叠加[14,16,28, 38]. 一方面,对于由大规模神经元组成的神经网络来说,这种能量的可叠加性为计算分析带来了极大的简便. 另一方面,叠加后神经网络的总能量在某一时刻的分布,可以用来反映整个网络在该时刻同步振荡的状态,而皮层各区域网络大范围同步振荡的状态与知觉认知的形成过程有密切关系[39-42]. 因此从神经能量的角度来建立大脑皮层知觉认知的神经网络,可以极大地简化对错综复杂的知觉认知的分析.
此外,神经能量编码的另一个特点是,神经能量可以是神经信息处理与脑血流变化之间关系的一个载体. 神经信息处理与脑血流变化之间存在一定的耦合关系[17]. 因此,通过对网络神经能量和血糖供能的计算分析,可以间接反映脑神经网络的信息处理的能力与脑血流变化之间的关系,从而间接为fMRI BOLD信号改变给出定量的解释.
本文考虑了神经元的神经活动和能量供应之间的关系,从能量的角度再现了血液动力学现象. 血液动力学现象不仅直观地反映了脑区激活区与脑血流之间的关系,还反映了脑血流与能量代谢之间的关系. 本文给出的网络模型是很一般的层次网络结构,但是体现了大脑网络的分层结构,作为探讨大脑血流的延迟现象,这样的网络结构主要是被用来模拟大脑在刺激条件下的血液动力学现象的. 模拟结果预测了大脑血液动力学现象的本质是神经活动过程中负能量机制的存在,这就为我们今后进一步探索血液动力学现象的生理机制提供了科学的基础,在建模与计算方面给出了一个新的视角和研究方法.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
DOI [本文引用: 2]
DOIURL
DOIURL
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
DOI [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 9]
URL [本文引用: 3]
URL [本文引用: 3]
DOIURL [本文引用: 3]
DOIURL [本文引用: 1]
URL [本文引用: 6]
DOIURL [本文引用: 1]
DOIURL
DOIURL
DOIURL
DOI
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
URL [本文引用: 1]
URL
DOIURL [本文引用: 2]
DOIURL [本文引用: 1]
DOIURL [本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIMagsci [本文引用: 1]
<p>微循环是血液和组织之间发生物质交换的主要场所，它可以通过改变管径实现对血压、血流量的局部调节.血管内皮层对小动脉运动有重要的调节作用.本文基于连续介质假设，建立了内皮调节过程中主要活性物质在管壁中的扩散——反应动力学模型，并分析了非线性黏弹性血管的径向运动特性.利用该模型首先得到了内皮舒张因子一氧化氮（NO）、平滑肌细胞内钙离子（Ca<sup>2+</sup>）以及磷酸化肌球蛋白（actin-myosin complexes，AMC）在管壁内的的径向浓度分布；为分析内皮调节的动态过程，进一步对小动脉的被动舒张、血流量发生扰动时的管径响应分别进行了模拟.研究结果显示：当没有活性物质参与调节小动脉被动舒张时，管径无振荡发生；当血流量变化引起内皮调节时，内皮舒张因子NO浓度和管径均出现衰减振荡，振荡周期约60 s.分析认为内皮调节对壁面剪切力的反馈控制，可能是NO浓度和管径产生周期性振荡的原因.内皮调节过程呈现的频谱特征可以为血管内皮功能障碍的诊断提供帮助.</p>
DOIMagsci [本文引用: 1]
<p>微循环是血液和组织之间发生物质交换的主要场所，它可以通过改变管径实现对血压、血流量的局部调节.血管内皮层对小动脉运动有重要的调节作用.本文基于连续介质假设，建立了内皮调节过程中主要活性物质在管壁中的扩散——反应动力学模型，并分析了非线性黏弹性血管的径向运动特性.利用该模型首先得到了内皮舒张因子一氧化氮（NO）、平滑肌细胞内钙离子（Ca<sup>2+</sup>）以及磷酸化肌球蛋白（actin-myosin complexes，AMC）在管壁内的的径向浓度分布；为分析内皮调节的动态过程，进一步对小动脉的被动舒张、血流量发生扰动时的管径响应分别进行了模拟.研究结果显示：当没有活性物质参与调节小动脉被动舒张时，管径无振荡发生；当血流量变化引起内皮调节时，内皮舒张因子NO浓度和管径均出现衰减振荡，振荡周期约60 s.分析认为内皮调节对壁面剪切力的反馈控制，可能是NO浓度和管径产生周期性振荡的原因.内皮调节过程呈现的频谱特征可以为血管内皮功能障碍的诊断提供帮助.</p>
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOI
DOIURL
DOIURL [本文引用: 1]
