,*,2), 梅雨辰*, 任永亮?AN INTEGRAL DIFFERENTIATION PROCEDURE FOR DYNAMIC TIME-HISTORY RESPONSE ANALYSIS OF STRUCTURES1)
Li Hongjing,*,2), Mei Yuchen*, Ren Yongliang?通讯作者: 2)李鸿晶, 教授, 主要研究方向: 地震工程学. E-mail：hjing@njtech.edu.cn
收稿日期:2019-04-26网络出版日期:2019-09-18
| 基金资助: |
Received:2019-04-26Online:2019-09-18
作者简介 About authors
摘要
传统采用微分求积(differential quadrature,DQ)法求解动力问题时都是以位移响应作为基本未知量,而将速度响应和加速度响应表示为位移响应的加权和的形式.如此做法需要处理线性方程组或者矩阵方程(Sylvester方程)才能求得动力响应,导出的算法一般为有条件稳定算法.本文利用动力响应的Duhamel积分解,逆用DQ原理,提出了一种计算卷积的高精度显式算法.该算法可以逐时段地求解出动力时程响应,当各时段内DQ节点分布完全一致时,仅须进行一次Vandermonde矩阵求逆计算即可应用于各个时段,一次性获得时段内多个时刻的位移响应值,因而具有计算效率高的优点.通过分析动力方程积分格式,证明本文动力算法传递矩阵的谱半径恒等于1,因而该算法具有无条件稳定特性,且计算过程中不会产生数值耗散. 本文算法的数值精度取决于分析时段内布置的DQ节点数量$N$,具有$N-1$阶代数精度.实际操作时可以取10个甚至更多的DQ节点数,从而获得比较高的数值精度.
关键词：
Abstract
Traditionally, the response of displacement is selected to be the basic unknown and the responses of velocity and acceleration are usually expressed by linear weighted sum of the displacement when the differential quadrature (DQ) method is applied to the solution of dynamic problems. Either the linear equations or matrix equations (Sylvester equation) has to be processed in such procedure for dynamic solutions and the derived algorithm is conditionally stable in general. In this paper,the DQ principle is used in the inverse way to implement a high-accuracy explicit algorithm for the operation of convolution, and the algorithm is applied to dynamic analysis via the solution of Duhamel's integral. The dynamic response can be solved over a finite time interval according to this procedure, so that the total time-history of response could be obtained step by step. The inverse of Vandermonde matrix is required only once if the distribution of DQ nodes are completely consistent in each time interval and the response at several time instants during the interval can be obtained simultaneously. Hence, the procedure for dynamic solutions numerically achieves a high computational efficiency. It is proved that the spectral radius of the transfer matrix in the dynamic algorithm is always equal to 1, so the algorithm has unconditional stability and no numerical dissipation occurs during the calculation. The numerical accuracy of this algorithm depends on $N$, the number of DQ nodes within the analyzing time interval, and an algebraic accuracy with the order of $N-1$can be achieved. In practice, 10 and even more DQ nodes of $N$are suggested in order to gain high accuracy for dynamic problems.
Keywords：
PDF (963KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
李鸿晶, 梅雨辰, 任永亮. 一种结构动力时程分析的积分求微方法1). 力学学报[J], 2019, 51(5): 1507-1516 DOI:10.6052/0459-1879-19-105
Li Hongjing, Mei Yuchen, Ren Yongliang.
引言
结构动力响应分析是认识动态系统性态和行为的基础性工作,应用广泛[1-3].传统的结构动力响应分析方法大致可以分为两种类型,即变换方法和直接积分方法.其中振型叠加法[4-5]、频域分析法[5]等变换方法应用了叠加原理,所以原则上仅适用于线弹性体系的动力响应分析,且只能处理经典阻尼问题.直接积分法则是直接对体系运动方程进行求解,未引入任何数学变换,所以线性和非线性动力响应分析都可以应用.目前已提出多种直接积分法,如中心差分法[4-5]、Houbolt法[6]、Newmark-$\beta$法[4-5,7]、Wilson-$\theta$法[8]等,当体系质量矩阵和阻尼矩阵为对角阵时,中心差分法还表现为显式计算格式.这些直接积分法的一般思路是将动力时程划分为一系列足够小的有限时步,并在每个时步内建立起加速度、速度和位移之间的关系,然后将这些关系代入运动微分方程,以时步始点响应作为初始条件推知末点的响应.有别于传统直接积分法的求解模式,精细时程积分法[9]则是致力于对动力方程解析解进行求解,将问题转化为数值积分问题,并创立了一种高精度的数值解法.显然,从结构动力学的角度出发,结构动力响应分析方法可以有多种,但是不是所有的动力学解法都能适用于实际结构动力分析的需求.例如,对于超大规模自由度数目的大型复杂结构或者超高频振动问题,除了所有动力分析方法都要面对的数值稳定性问题外,计算效率的矛盾将上升成为动力算法能否实施的关键. 发展稳定性好、计算效率高的动力分析算法始终是一种非常现实的需要.利用振型的正交性和完备性,结构动力响应可以分解为各阶振型响应的叠加.在每阶振型下,广义坐标方程同单自由度体系运动微分方程具有相同的形式,其解可以表示为外载荷与单位脉冲响应函数的卷积(Duhamel积分)运算.精细时程积分法针对这一解析积分解建立数值算法,为动力响应分析创立了另外一条求解路径.显然,可用于结构动力响应卷积计算的数值算法存在多种选择,而建立能够兼顾数值稳定性、数值精度和计算效率的算法则是追求的目标.为了实现上述目标,本文尝试利用微分求积(differential quadrature,DQ)原理建立Duhamel积分计算的高精度、高效率算法,并将其应用于结构动力响应分析.
DQ法[10-11]被认为是一种仅需较小的计算工作量即可获得偏微分方程高精度解答的数值方法,无论是将其用于静力分析或特征值分析(边值问题)[12-21],还是用于动力响应分析(初值问题)[22-31],一般做法都是以基本响应量(变形、位移等)的加权和表示它们的导数值,进而将微分方程转换为线性方程进行求解的.但是,这种做法并不总是方便的,对于某些具有特殊性质的问题,因未能很好地利用这些问题的特性使得导出的算法没有具备高计算效率.本文将推广文献[32]发展的卷积计算方法,利用Duhamel积分的导数容易计算的特点,逆用DQ原理,构建一种高效率的结构动力分析算法.因卷积积分是通过求导数的方式计算的,故称之为积分求 微法.
1 体系状态方程
在动力载荷向量$\{ {\pmb p}(t)\}$激励下,多自由度体系响应可以分解为各阶振型响应的叠加.在振型坐标下,振型响应方程与单自由度体系运动方程形式一致,故这里借助单自由度体系动力响应进行推导,对于多自由度体系仅需以各阶振型下的广义坐标替换单自由度响应量即可.单自由度体系运动方程写为
式中,$m$, $c$, $k$分别为体系的质量、阻尼和刚度特性;$u(t)$, $\dot {u}(t)$, $\ddot{u}(t)$分别为体系位移响应、速度响应和加速度响应.
引入状态向量
$$y = \left\{ \!\! \begin{array}{c} {y_1 } \\ {y_2 } \end{array} \!\! \right\} = \left\{ \!\! \begin{array}{c} u \\ \dot {u} \end{array} \!\! \right\} (2) $$
则方程(1)可改写成状态空间方程形式
其中
$${\pmb M} = \left[\!\! \begin{array}{cc} {-k} & 0 \\ 0 & m \end{array} \!\! \right],,\quad {\pmb K} = \left[\!\! \begin{array}{cc} 0 & k \\ k & c \end{array}\!\! \right],, \quad {\pmb P} = \left\{\!\! \begin{array}{c} 0 \\ p \end{array}\!\! \right\} $$
状态方程(3)的初始条件为
$${\pmb y} ={\pmb y}(0) = \left\{ \!\! \begin{array}{c} {u_0 } \\ {\dot {u}_0 } \end{array} \!\! \right\} (4) $$
其中$u_0 $和$\dot {u}_0 $分别为体系的初始位移和初始速度.
将体系状态方程写成式(3)的形式可使系数矩阵${\pmb M}$和${\pmb K}$均保持对称性,求解广义特征值问题
式中,$\lambda $和${\pmb\varphi }$分别为体系复特征值和复特征向量. 求解特征方程(5),可得特征值为
其中,$\bar {\lambda }_2 $表示$\lambda _2 $的共轭复数;$\omega _{\rm n}$和$\xi$分别为体系的固有频率和阻尼比;$\omega _{\rm D} $为体系有阻尼固有频率,$\omega _{\rm D} = \omega _{\rm n}\sqrt {1-\xi ^2} $.
复特征向量为
容易证明,复特征向量具有加权正交性,即
将体系状态响应表示为复振型叠加的形式
将式(9)代入状态方程(3),并在方程两边前乘${\pmb\varphi}_j^{\rm T} (j = 1,2)$,利用正交条件(8),可得
其中
$$m_j^ * = {\pmb\varphi}_j^{\rm T} {\pmb M}{\pmb\varphi}_j =-k + m\lambda _j^2 \\ k_j^ * ={\pmb\varphi}_j^{\rm T} {\pmb K}{\pmb\varphi}_j = 2k\lambda _j + c\lambda _j^2 =-\lambda _j m_j^ * \\ p^ * (t) = {\pmb\varphi} _j^{\rm T} {\pmb P}(t) = \lambda _j p(t) $$
方程(10)的解为
式中
为广义坐标$q_j (t)$的初始值.
显然,若想求得广义坐标$q_j (t)$的解就必须进行卷积运算.当外载荷$p(t)$的特性复杂(例如地震引起的地面运动时程)时,获得形如式(11)积分式的解析解答是非常困难的,一般需要借助于数值解.
2 动力响应DQ分析
考察非耦联方程组(10)中的一个方程,略去各变量的下标"$j$",如果令则式(11)的广义坐标改写为
由此可见,求得$q(t)$的关键是计算出函数$D(t)$,即计算式(13)所表达的积分式. 对$D(t)$求导,有
假定外载荷$p(t)$的持时为$T$,在时间区间[0, $T$]内取离散点$t_k \;(k = 0,1, \cdots ,N)$,并记
和
这里,$N$为持时的离散分段数,若计及始末端点,则$[0, T]$内离散点总数为$N+1$.
根据DQ原理,导数值$\dot {D}_k \;(k = 0,1, \cdots,N)$可以用定义域内所有函数值$D_0 ,,D_1 ,, \cdots ,,D_N $的加权和表示,即
或记为
式中,${\pmb A}$为权系数矩阵,它由离散时刻值(即离散时间点的坐标)决定,可表示为
其中,${\pmb V}$和${\pmb G}$分别为Vandermonde矩阵和导数转换矩阵,分别写为
$${\pmb V} = \left[ \begin{array}{cccc} 1 & {t_0 } & \cdots & {t_0^N } \\ 1 & {t_1 } & \cdots & {t_1^N } \\ \vdots & \vdots & \ddots & \vdots \\ 1 & {t_N } & \cdots & {t_N^N } \end{array} \right],,\quad G = \left[ \begin{array}{cccc} 0 & 1 & & \\ & 0 & \ddots & \\ & & \ddots & N \\ & & & 0 \end{array} \right] $$
式(18)亦可以写为
其中
$${\pmb D}_\nu ^{\rm T} = \left\{ {D_1 } {D_2 } \cdots {D_N } \right\} \\ {\pmb A}_{\mu \nu } = \left\{ {a_{01} } {a_{02} } \cdots {a_{0N} } \right\} \\ {\pmb A}_{\nu \mu }^{\rm T} = \left\{ {a_{10} } {a_{20} } \cdots {a_{N0} } \right\} \\ {\pmb A}_{\nu \nu } = \left[ \!\! \begin{array}{cccc} {a_{11} } & {a_{12} } & \cdots & {a_{1N} } \\ {a_{21} } & {a_{22} } & \cdots & {a_{2N} } \\ \vdots & \vdots & \ddots & \vdots \\ {a_{N1} } & {a_{N2} } & \cdots & {a_{NN} } \end{array} \!\! \right] $$
由式(16)和式(17)可知,$D_0 = 0$和$\dot {D}_0 = p_0 $,这里$p_0 = p(0)$为零时刻外载荷值. 将$D_0 $和$\dot {D}_0 $代入式(20b),可得
故有
通过推导可以得到
由式(22)可知,各离散时刻的函数值$D_1 ,,D_2 ,, \cdots ,,D_N$可以通过转换矩阵${\pmb B}$由其导数向量$\dot {D}_\nu $转换而得,而$\dot {D}_\nu$由式(17)非常容易计算得到. 注意到式(23)中需要对Vandermonde矩阵求逆,故逆矩阵必定存在,但其阶数$N$不宜过高,否则可能导致病态.
如果需要分析的动力响应持续时间$T$过长,则可将整个持时$T$划分为若干个时段$[t_j,\;t_k ]$,这里$t_j $和$t_k $分别为时段的始、末时刻,有$t_j < t_k$. 在每个时段$[t_j ,\;t_k]$内执行上述DQ分析程序,求得该时段内的动力响应. 只要从零时刻开始逐个时段地重复求解,即可获得整个持时内的全部动力响应. 需要注意的是,各时段的初始条件(初始位移和初始速度)为前一个时段末时刻的响应,已在前一个时段动力分析时求得.
3 稳定性和精度
3.1 数值格式的稳定性
动力方程积分格式的稳定性可以由传递矩阵的谱半径进行判断[33-35]. 考虑动力响应分时段执行DQ分析程序的情形,选择各时段内DQ节点数量以及分布方式完全相同,如此做法可以确保DQ权系数矩阵${\pmb A}$和转换矩阵${\pmb B}$均保持不变,即仅需执行一次权系数矩阵计算和Vandermonde矩阵求逆运算即可应用于所有时段. 在此情形下,式(22)应改写为式中,$\tau $为时段$\left[ {t,\;t + \Delta t} \right]$内设置的局部坐标,$D_t$表示函数$D(t)$在该时段的初始值,即
$$D_t = \int_0^t {\rm e}^{-\lambda \tau }p(\tau ) \tau$$
注意到实际计算时上述各时段可以选择不同的长度,但各时段DQ节点数量及其分布宜相同,这样可以减小计算工作量.考察时段$\left[ {t,\;t + \Delta t} \right]$始末时刻的结构响应,有递推关系
式中,${\pmb H}$和${\pmb L}$分别代表传递矩阵和载荷逼近算子,按照下式计算
这里${\pmb \gamma} = \left\{ {0,\;0,\; \cdots ,\;1}\right\}$. 在本文情形下,${\pmb H}$和${\pmb L}$均退化为1$\times$1维.
由式(18a)可知,若令$D\left( t \right) = 1$,则可得
$$\left[ \begin{array}{cccc} {a_{00} } & {a_{01} } & \cdots & {a_{0N} } \\ {a_{10} } & {a_{11} } & \cdots & {a_{1N} } \\ \vdots & \vdots & \ddots & \vdots \\ {a_{N0} } & {a_{N1} } & \cdots & {a_{NN} } \end{array} \right]\left\{ \begin{array}{c} 1 \\ 1 \\ \vdots \\ 1 \end{array} \right\} = \left\{ \begin{array}{c} 0 \\ 0 \\ \vdots \\ 0 \end{array} \right\} $$
据此,有
$$\left\{ \begin{array}{c} {a_{10} } \\ \vdots \\ {a_{N0} } \end{array} \right\} =-\left[ \begin{array}{ccc} {a_{11} } & \cdots & {a_{1N} } \\ \vdots & \ddots & \vdots \\ {a_{N1} } & \cdots & {a_{NN} } \end{array} \right]\left\{ \begin{array}{c} 1 \\ \vdots \\ 1 \end{array} \right\} $$
即
式中${\pmb\theta}^{\rm T} = \left\{ {1,\;1,\; \cdots ,\;1} \right\}$.
利用式(23)和式(28),传递矩阵${\pmb H}$的谱半径即可求得,即
由稳定性判别准则$R\left( {\pmb H} \right) \le qslant 1$可知,上述动力响应DQ分析方法为无条件稳定算法,意味着该方法不会因为时段长度$\Delta t$或时段内离散点数$N$的变化而产生失稳.
3.2 数值格式的代数精度
DQ法的本质是多项式插值逼近,为了计算函数$D(t)$的导数$\dot {D}(t)$,构造近似函数式中,$f_j (t)$, $\alpha _j (j = 0,\;1,\; \cdots,\;N)$分别为($N$+1)维向量空间中的一组基函数和相应的基下坐标.
对式(30)中函数$d(t)$求导,得
对于各DQ节点$t_0 ,\;t_1 ,\; \cdots ,\;t_N $,根据式(31),有
式中
$$\dot {\pmb d} = \left\{ \!\! \begin{array}{c} {\dot {d}_0 } \\ {\dot {d}_1 } \\ \vdots \\ {\dot {d}_N } \end{array} \!\! \right\} = \left\{ \!\! \begin{array}{c} {\dot {d}(t_0 )} \\ {\dot {d}(t_1 )} \\ \vdots \\ {\dot {d}(t_N )} \end{array}\!\! \right\},, \ \ {\pmb\alpha} = \left\{ \!\! \begin{array}{c} {\alpha _0 } \\ {\alpha _1 } \\ \vdots \\ {\alpha _N } \end{array} \!\! \right\} \\ \dot {\pmb f} = \left[\!\! \begin{array}{cccc} {\dot {f}_{00} } & {\dot {f}_{10} } & \cdots & {\dot {f}_{N0} } \\ {\dot {f}_{01} } & {\dot {f}_{11} } & \cdots & {\dot {f}_{N1} } \\ \vdots & \vdots & \ddots & \vdots \\ {\dot {f}_{0N} } & {\dot {f}_{1N} } & \cdots & {\dot {f}_{NN} } \end{array} \!\! \right] $$
这里记$\dot {f}_{ji} = \dot {f}_j (t_i )$.
由式(30),有${\pmb d} ={\pmb f}{\pmb\alpha }$,故
将式(33)代入式(32),得
若以$d(t)$替代$D(t)$,基函数取为$f(t) = 1,\;t,\; \cdots,\;t^N$,则式(34)即为式(18)表示的DQ法基本公式.
显然,式(34)给出的是$\dot{D}(t)$的近似值,其精确值应该按照式(15)计算. 设$R(t) = \dot {D}(t)-\dot{d}(t)$表示逼近余项,有
这里$\xi \in [0,\;T]$且依赖于$t$,$r(t)$为式(13)中被积函数,即$r(t) = \dot {D}(t) ={\rm e}^{-\lambda t}p(t)$,$r^{(N)}(\xi )$表示$r(t)$在$t = \xi $处的$N$阶导数.
由式(35)可知,在计算积分$D(t)$的过程中,当$r(t)$为小于等于$N-1$阶多项式时,余项$R(t) = 0$,积分精确成立.而当$r(t)$为大于$N-1$阶多项式时,$R(t) \ne 0$,积分为近似结果. 因此,采用$N +1$个节点对于不大于$N-1$次的被积函数精确成立,即本文算法具有$N-1$阶代数精度.
需要说明的是,上述关于代数精度的讨论是在Duhamel积分数值计算的基础上进行的,即实际上是数值积分的代数精度.观察其推导过程,可以发现没有包含任何关于节点(积分点)位置的信息.也就是说,无论采用何种节点方案,方法都能达到上述精度,严格来说这是该方法精度的下限.如果选择一些特殊的节点,积分精度有可能进一步提高,这将是另外一个研究问题.
4 算例
考察单自由度体系,质量$m =150$,kg,刚度$k =600$,N/m,不计阻尼.外载荷考虑两种情形,一种是有限长度的简谐载荷, 另一种是三角形载荷,分别记为$$p_1 (t) = 5\sin \left( {\frac{2}{15}\pi t} \right),\quad t \in \left[{0,\;30} \right] \\ p_2 (t) = 3-\left| {3-0.2t} \right|,\quad t \in \left[ {0,\;30} \right]$$
两种载荷曲线如图1所示.
图1
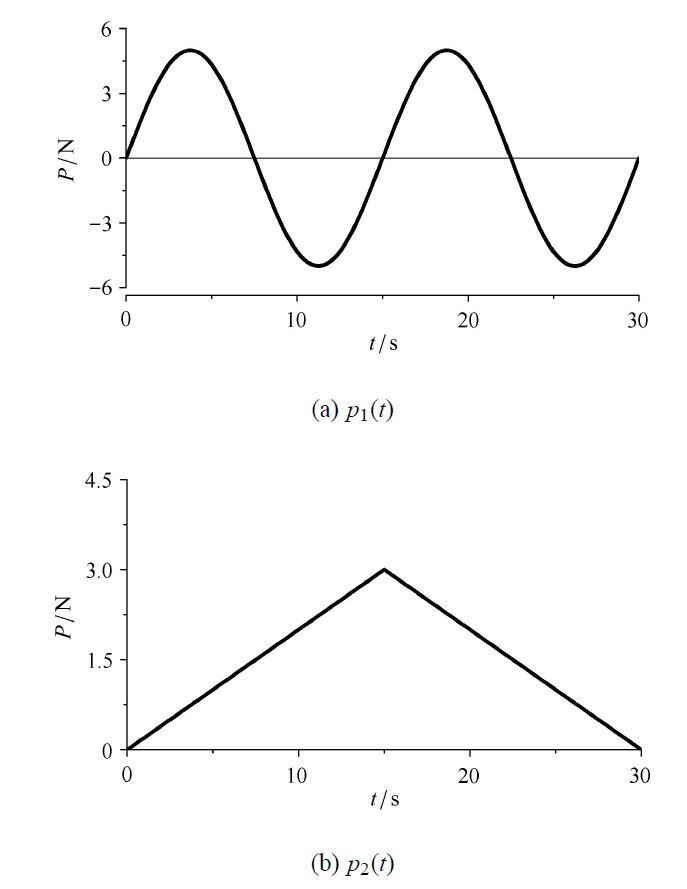新窗口打开|下载原图ZIP|生成PPT图1外载荷时程曲线
Fig. 1Time history of the forces
两种载荷的持时均为30,s,采取逐时段DQ分析的方式计算结构动力响应.按照两种方案划分时段,即将持时分别划分为30段和10段的 等长度时段,则每个时段长度分别为$\Delta t =1$,s和$\Delta t = 3$,s.以各时间节点下位移响应相对误差的平均值${Err}$作为定量地度量数值解与理论解逼近程度的指标,当时段长度一定时,${Err}$与$N$的关系如图2所示.
图2
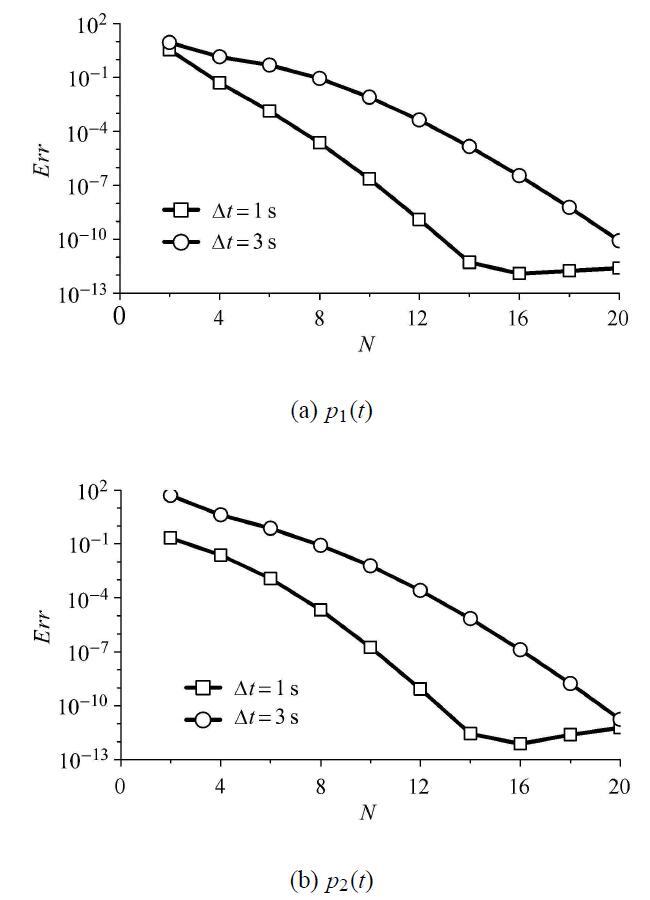新窗口打开|下载原图ZIP|生成PPT图2DQ法计算动力响应的平均相对误差与DQ节点数的关系
Fig. 2The relationship between average relative error and the number of the DQ time instants
从上述两种载荷激励下的相对误差(图2)中可以清晰地看出,DQ法的计算精度与时段长度$\Delta t$及时段内DQ节点数量$N$两个参数密切相关. 当$\Delta t$一定时,随着$N$的增大相对误差将急剧减小并最终接近于0.另一方面,通过比较误差图中的两条曲线可以发现, 当$N$一定时,DQ结果与精确解的相对误差将随着$\Delta t$的减小而减小. 事实上,$\Delta t$与$N$两个参数本质上影响的是DQ节点的间距,上述误差计算结果反映了DQ节点间距越小,计算结果越精确,这满足了一般数值计算方法的收敛性原则. 因此,本文的DQ方法是合理可行的,且能收敛到精确解.由于在实际结构分析中比较关心体系的峰值位移响应,表1和表2给出了不同参数下体系的最大节点位移响应计算结果,单位为cm.
Table 1
表1
表1$p_1 (t)$激励下体系的最大节点位移响应
Table 1
 |
新窗口打开|下载CSV
Table 2
表2
表2$p_2 (t)$激励下体系的最大节点位移响应
Table 2
 |
新窗口打开|下载CSV
表1和表2同样显示,随着节点步距的减小,动力响应逐渐逼近精确解. 受迫段内体系动力响应DQ分析结果与精确解的比较示于图3和图4中,计算时统一取$N =10$. 可以发现,即便取$\Delta t =3$,s时,DQ解与精确解仍然高度吻合,显示本文算法具有较高的数值精度. 实际动力计算时,可通过调节或匹配$\Delta t$和$N$这两个参数取值,在保证计算精度的前提下大幅度降低总体计算工作量,达到提高计算效率的目标.
图3
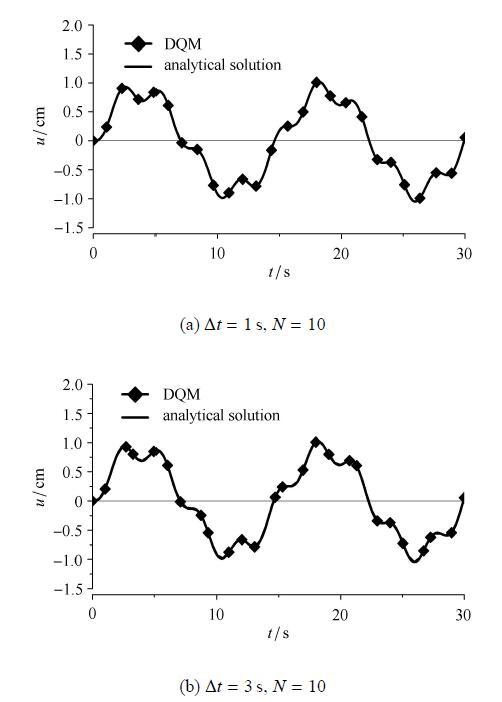新窗口打开|下载原图ZIP|生成PPT图3$p_1 (t)$激励下体系动力响应时程与精确解对比
Fig. 3Comparison of the dynamic response of the system under $p_1 (t)$with analytical solutions
图4
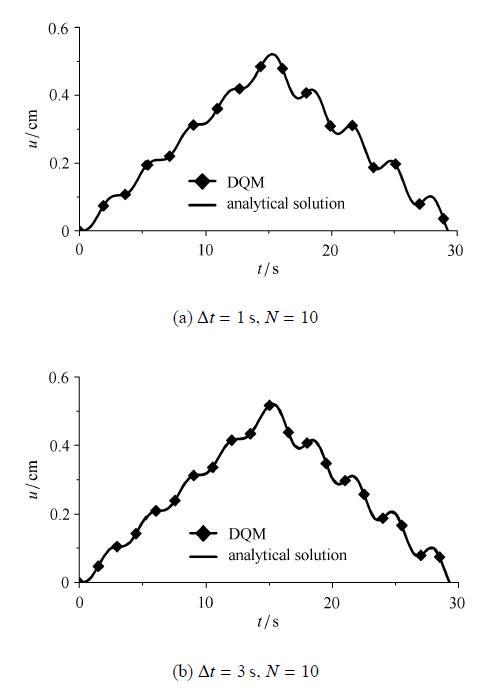新窗口打开|下载原图ZIP|生成PPT图4$p_2 (t)$激励下体系动力响应时程与精确解对比
Fig. 4Comparison of the dynamic response of the system under $p_2 (t)$with analytical solutions
5 讨论与结论
对实际结构开展动力分析时,稳定性、精度和计算效率是评价算法优劣的主要内容. 关于本文算法的稳定性和精度已在前面进行讨论,下面主要探讨该算法的计算效率.如果实际结构动力分析的外载荷持时较长,或者结构响应的频率较高,则一般需要划分若干时段,然后逐时段地应用本文DQ分析程序,最终获得全部响应时程.由式(22)可知,在待求解时段内,$N$个时刻处的动力响应可以通过转换矩阵${B}$直接一次性计算出来,所以计算工作量主要来自$N$阶Vandermonde矩阵求逆运算.关于Vandermonde矩阵求逆问题已有较多研究,提出了多种有效的算法. 计算${B}$时可以利用这些算法,但Vandermonde矩阵阶数不宜过高,以避免因条件数大而引起病态.事实上,对于动力时程分析问题,划分的分析时段一般不可能很大,故在每个时段内布置的DQ节点数$N$亦没有必要设置过大.文献[36]在总结DQ法解决结构静力问题时给出结论,即DQ节点取为9$\sim $11个是比较适宜的.本文针对结构动力问题开展了大量数值试验,当DQ节点取为10个左右时即可以获得比较满意的数值结果.另外,实际动力问题分析时一般是逐时段实施的,假设任意时段$[t_j ,\;t_k ]$的长度为$\Delta t_j = t_k-t_j$,实际计算时各段$\Delta t_j $不必取为相等,但各时段内DQ节点布置得一致比较有利,包括节点数$N$和分布方式.因为这样做法可以使转换矩阵${\pmb B}$仅计算一次即可应用到所有时段,从而大大减少计算工作量.若在分析时段内设立局部坐标$\tau $,则有$\tau \in [0,\;\Delta t_j ]$,这时只要取${\tau }' = \tau / {\Delta t_j}$,则时段$\tau \in [0,\;\Delta t_j ]$即可变换为${\tau }' \in[0,\;1]$,可知当DQ节点布置一致时式(23)中Vandermonde矩阵亦完全一致,故不必每个时段都重复计算转换矩阵${B}$.
进一步探究式(23)中关于转换矩阵${\pmb B}$的计算,可以发现其结果仅与节点在时段内分布的相对位置有关,而与结构体系的特性(如刚度特性、质量特性等)参数无关,其实质上可视为一种广义的积分权系数. 因此,当待求解时段内DQ节点方案设定为固定不变时,可根据$N$值事先将转换矩阵${\pmb B}$计算出来,制作成表在计算中直接取用.这样整个计算过程中就可避免对 方程的求解,而使得动力计算成为一种显式的时程分析.与中心差分法等传统的显式单步法相比,本文方法一次能计算多个时刻的响应值,属于一种显式多步方法,其计算效率大大提高.
DQ节点分布对稳定性和精度影响很大,这方面已有很多研究,提出了多种DQ节点分布方式,这里不对此进行专门讨论. 值得注意的是,本文方法传递矩阵的谱半径恒等于1,这意味着在时程计算过程中对于任何形式的时间节点方案都不会导致发散,亦不会产生数值耗散. 这是本文方法拥有的一个非常理想的性能.
对于本文关于动力问题的DQ分析,离散节点即为待求标准时段$[0,\;1]$内离散时点$\tau _k \;(k = 0,1, \cdots,N)$的分布. DQ法多采用不等距节点方案,如GCL节点(Gauss-Chebyshev-Lobatto节点),其节点位置由下式确定
本文前述2个算例即是按照这种节点方案进行计算的,这是一类能够获得较高精度的节点. 但是,对于动力时程分析不等距时间离散方式会带来不便,因为需要通过插值才能获得等距时刻的动力响应,虽然对于有限时段而言额外增加的计算工作量并不是很严重.前面关于数值稳定性和精度分析已经表明,本文算法在待求时段内离散时点的分布不会影响稳定性,而且都能够达到较高的计算精度,故可以直接采用与动力时程分析相匹配的等距时点进行DQ计算,而不必引入额外的插值计算.图5和表3给出了前述简谐载荷算例分别选择GCL节点和等距节点时的计算结果,其中取时段长度$\Delta t =1$,s,时段内离散时点数取为10,其他条件保持不变.由于时段内两种离散时点不重合,表3中列出的是一些时段始末端点时刻处的响应值.
Table 3
表3
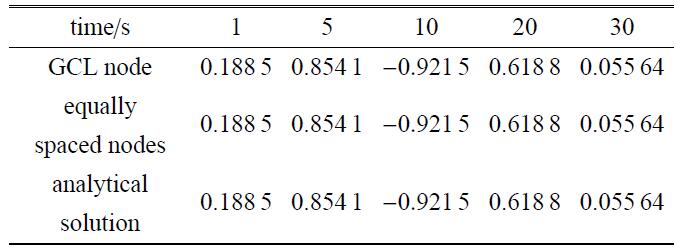
表3不同时间离散方案下位移响应比较(单位：cm)
Table 3
 |
新窗口打开|下载CSV
图5
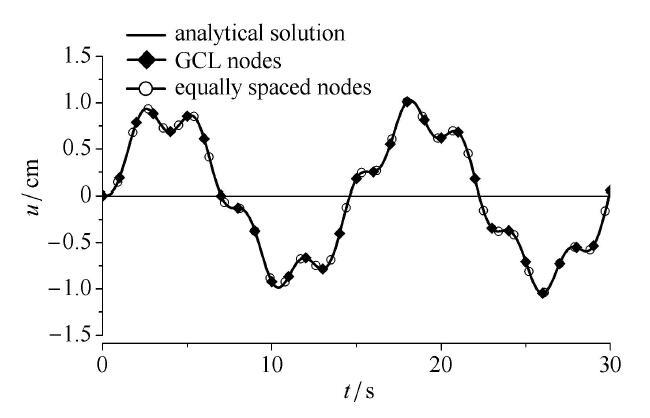
新窗口打开|下载原图ZIP|生成PPT图5位移响应时程比较
Fig. 5Comparison of displacement response due to different discrete time
观察图5可以清晰地发现,GCL节点与等距节点的计算结果与解析解几乎完全重合,而表3定量展现的一些时刻的动力响应计算结果在4位小数内是完全相同的,充分说明了采用均匀节点时也同样能够达到很高的计算精度,实际动力分析时不必采用不等距的GCL节点而直接选择等距时点即可.
需要说明的是,如果在待求时段内选择等距时点方案,对离散时点数不宜过大的限制不仅是前述的Vandermonde矩阵求逆的客观要求,而且对于等距节点插值时节点过多还会发生Runge现象而出现不收敛的情形,同样需要限制节点的数量. 通过数值试验,发现如果节点数控制在15个以内时,Runge现象不明显,计算结果仍然是可靠的且精度较高. 这同前述讨论的结论即节点数宜控制在9$\sim$11个是可以匹配起来的. 故建议将本文的积分求微法应用于实际动力问题分析时待求时段内的离散时点数$N$(不包含时段的起始点)取为10个左右.
本文通过将DQ原理应用于动力响应卷积计算,建立了一种动力时程分析算法,主要结论如下：
(1)本文将动力分析归结为简单的矩阵变换,仅需操作一次Vandermonde矩阵求逆运算即可快速求得各时段内多个时刻上的动力响应值,因而具有很高的计算效率. 本文算法相当于动力响应分析多步法,并且是显式算法.
(2) 在逐时段实施DQ分析程序的过程中,无论时段长度$\Delta t$和时段内DQ节点数$N$如何变化,传递矩阵的谱半径都恒等于1,既不存在任何失稳放大现象,也不会产生数值耗散,因而本文方法为无条件稳定方法.
(3) 本文动力DQ分析程序的数值精度取决于待求解时段内设置的DQ节点数量$N$,其代数精度为$N-1$阶.
某些DQ节点的特殊布置方式(多为不等间距布置)可以一定程度地提高计算精度,实际动力分析时可依需求进行选取,但不影响本文方法的实施.
(4)建立本文方法的关键环节在于对DQ原理的逆用. 对于Duhamel积分这类形式的卷积,其导数计算非常容易,逆用DQ原理后动力响应分析无需进行方程求解,从而大大降低了计算工作量.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 3]
[本文引用: 4]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
