,*,?,2), 刘飞?, 刘冬洁?PROGRESS IN MOLECULAR DYNAMICS SIMULATIONS OF SURFACTANT SOLUTION FOR TURBULENT DRAG REDUCTION 1)
Wei Jinjia,*,?,2), Liu Fei?, Liu Dongjie?通讯作者: 2) 魏进家,教授,主要研究方向：表面活性剂减阻及强化传热.E-mail:jjwei@mail.xjtu.edu.cn
收稿日期:2018-11-7接受日期:2019-04-8网络出版日期:2019-07-18
| 基金资助: |
Received:2018-11-7Accepted:2019-04-8Online:2019-07-18
作者简介 About authors
摘要
减阻用表面活性剂在能源动力及化工领域有着广泛应用,在管道流体中加入少量表面活性剂可以使流动阻力大大降低从而节约能源,对于表面活性剂减阻机理的讨论也是近些年****关注的热点之一.本文不仅对课题组前些年在表面活性剂溶液流变性、湍流减阻、减阻与传热的相关性、布朗动力学模拟方面的工作进行了概述,而且详细介绍了近三年来在表面活性剂粗粒化分子动力学模拟方面的研究成果.粗粒化模拟是近年来发展起来的方法,目前已广泛应用于化学、生物等诸多领域.在粗粒化分子动力学模拟方面的工作包括：表面活性剂溶液的流变性能与微观结构、表面活性剂溶液湍流减阻机理研究、湍流减阻失效分析三个部分.通过对表面活性剂溶液分子动力学模拟研究进展的回顾,作者认为,利用粗粒化分子动力学模拟方法可以合理揭示表面活性剂胶束的结构与流变性的对应关系,对胶束的断裂与再连接能力进行多维度的评价,如胶束的拉伸能、断裂能、最大拉伸长度、结合能、$\zeta$电势、疏水基驱动作用等方面.并对"黏弹说"减阻机理进行分子模拟层面的验证,对实际应用中的湍流减阻失效原理进行初步分析.最后,根据对近几年分子动力学模拟工作的总结,展望了未来粗粒化分子动力学模拟在表面活性剂方面的研究方向.
关键词：
Abstract
Surfactant additives for turbulent drag reduction have been widely used in energy power and chemical industry. The addition of a small amount of surfactant additives in the pipeline fluid can greatly reduce the flow friction resistance and save energy. In recent years, the research on the mechanism of surfactant drag reduction is also a hot scientific topic. This paper not only summarized our work on the rheology of surfactant solution, surfactant drag reduction, the correlation with surfactant drag reduction and heat transfer, Brownian dynamics simulations in the latest years, but also concerning some works based on the coarse grained molecular dynamics (CGMD) simulations in the past three years, which will be elaborated in detail. The CGMD simulation is developed these years and now widely used in chemistry, biology and many other aspects. Our CGMD simulation work includes three parts, which are the rheology properties and its microstructures of the surfactant solution, the mechanism of turbulent drag reduction by surfactant additives, the analysis of turbulent drag reduction failure phenomenon on the pipeline transportation system. Through reviewing the progress in our CGMD simulation work, we believe that the CGMD simulation method can reasonably explain the rheological behavior of surfactant solutions, and the relationship between the rheology and the surfactant micelle structure can be well studied by using the coarse grained model. The breakage and the recombination behaviors of surfactant micelles can be evaluated from a multidimensional system including the extensional energy, the breakage energy, the maximum reasonable stretching distance, coalescence energy, zeta potential, or hydrophobic driving effect. Besides, the "viscoelasticity theory" can be proved from a molecular scale. Last but not least, the mechanism of turbulent drag reduction failure phenomenon can also be analyzed by CGMD simulation by simulating different failure reasons. At last, we summarize the CGMD simulation work on surfactant in recent years and then the direction of the future work about CGMD simulation work on surfactant is predicted.
Keywords：
PDF (61824KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
魏进家, 刘飞, 刘冬洁. 减阻用表面活性剂溶液分子动力学模拟研究进展 1). 力学学报[J], 2019, 51(4): 971-990 DOI:10.6052/0459-1879-18-372
Wei Jinjia, Liu Fei, Liu Dongjie.
引言
在集中供热系统与管道流体长距离运输中,管道运输阻力造成的能耗约为80%,这是一个极为重要的能量损失. 面对我国能源紧张的现状,除了对新能源的开发和利用之外,对已有能源的节约和高效利用也是一个不可忽视的问题. 通过添加减阻剂、对管路进行壁面处理等方法可以有效降低流动阻力,减少能耗. 但是考虑到方法的实用性,添加减阻剂是最便捷且最有效的措施. 相对于高分子的机械降解性以及微气泡的低效,表面活性剂具有高效以及机械降解可逆性[1]的特点,因此在高剪切力场合及封闭式循环系统中应用更为广泛[2-4].表面活性剂受到温度、浓度、剪切力等多方面影响,在溶液中会形成不同的胶束结构,如球状、蠕虫状、囊泡状、网状等[5]. 不同的结构能够影响溶液的流变性能,进而影响溶液的减阻性能. 因此对表面活性剂微观结构及流变性能的影响一直是****们研究的重点. 国内外****借助流变仪等测量表面活性剂的流变性能,借助透射电子显微镜(TEM)等拍摄表面活性剂内部微观结构. 这些实验方法能够从一定程度上认识表面活性剂的特性,但是受制于实验条件,****们无法从中获得更微观层面的结构,这也对流变特性甚至减阻特性的机理解释蒙上了一层阴影.
当表面活性剂发生减阻作用时,表面活性剂会形成剪切诱导结构,从而改变流体内部湍流涡的结构.在剪切过程中,胶束的形态结构一直在发生变化,实时跟踪胶束结构变化,对表面活性剂减阻的机理解释显的尤为重要.
综上所述,为了从更深层次认识表面活性剂内部微观结构,并对胶束在剪切作用中的结构变化实时跟踪,众多****选择了分子动力学模拟方法,对表面活性剂进行平衡态及非平衡态模拟,从而获得表面活性剂在分子层面的具体结构,并实时跟踪胶束形态变化,以此解释宏观层面上表面活性剂的流变特性及减阻特性.
本文对近年来在减阻用表面活性剂方向的最新研究进展进行概括,并对其他****的同类研究进行分析总结.首先总结分析了表面活性剂溶液的实验及模拟研究现状.从表面活性剂溶液的流变特性、减阻特性、传热特性、直接数值模拟以及布朗动力学方法模拟四个方向进行了概述.接下来,以分子动力学模拟为基础,从表面活性剂的微观结构及流变特性、表面活性剂的湍流减阻机理、表面活性剂湍流减阻失效分析三个方向进行概述.最后对表面活性剂减阻今后的研究重点提出建议.
1 减阻用表面活性剂实验及模拟研究现状
1.1 表面活性剂溶液的流变特性
表面活性剂的流变特性受流动状态、溶液温度、溶质浓度等多方面因素影响.表面活性剂的流变性不仅仅是溶液内部结构特征的反应,更是表面活性剂减阻特性的体现.近年来,****们针对不同的表面活性剂体系进行了一系列流变测试.近几年,课题组针对温度、浓度、剪切等多方面影响因素对十六烷基三甲基氯化铵与水杨酸钠(CTAC/NaSal)等表面活性剂体系进行了测试,尤其是针对表面活性剂的临界温度[6]、表面活性剂在剪切作用下随时间的变化过程[7-9]、表面活性剂的二次增稠现象[10]进行了测试和分析.魏进家 等[6]对20~30°C温度范围内的CTAC/NaSal水溶液进行了剪切黏度测量,发现杰塞库斯(Giesekus)模型可以描述其剪切黏度.马宁等[7-8]测试了中等浓度CTAC/NaSal水溶液的流变特性,发现溶液黏度随表面活性剂浓度增大而增大,随着剪切率的增大,剪切黏度分为剪切稀化、剪切增稠、剪切稀化三阶段.Xu等[9-10]重点研究了表面活性剂流变性随时间的变化.研究发现,表面活性剂黏度呈现出弱剪切增稠、弱剪切稀化和稳定、急剧增稠、震荡调整以及基本稳定五个阶段.在温度和剪切的双重作用下,表面活性剂溶液可出现二次增稠现象.该现象产生的原因是由于胶束结构尺寸变化速度随测试条件多次正负转变形成的.除此之外,针对一些新兴的表面活性剂类型,如双子型表面活性剂,王青会等[11]也进行了流变性的测试和分析.通过对25°C下不同剪切速率范围内高低浓度双子型表面活性剂溶液黏度的测量,发现高剪切速率下溶液黏度变化趋势简单,低剪切速率下黏度曲线复杂,胶束受到剪切的初始阶段展现的"应激响应过程"使得溶液黏度在初始阶段到达峰值.
1.2 表面活性剂溶液的减阻特性
除了对表面活性剂进行流变特性的测试,表面活性剂的减阻特性一直是****关注的重中之重[12-14].对此,本课题组也做了相应的研究[15-16].通过对表面活性剂减阻效率的测量,发现表面活性剂可以实现60%以上的减阻效率.粒子图像测速技术(PIV)等测量手段也被用来获得湍流减阻内部的湍流结构以及流场信息,从而揭示表面活性剂湍流减阻机理.近年来,表面活性剂的湍流减阻研究有了新的想法和方向.一方面是增加了新型槽道内湍流减阻的研究.比如庞明军等[17]针对小槽道进行了表面活性剂湍流减阻的测量,蔡书鹏等[18]针对突扩流段进行了阻力特性的测量.研究结果认为,突扩流的阻力行为与胶束网状结构的形成以及松弛时间密切相关.另一方面,****们把更多注意力放在了表面活性剂减阻与其他减阻方法耦合减阻上.
Bixler等[19]由鲨鱼皮肤表面启发制造了微结构表面,表面有V形、U形、L形三种不同的几何形状,采用了几种不同的材料,分别在明渠和暗渠两种环境下对水、油、空气三种不同的流体进行减阻实验的研究.Chen等[20]鲨鱼表面的微结构与聚合物减阻添加剂结合到一起,实验结果发现减阻率高达80%.
考虑到聚合物减阻的机械降解性,Huang等[21]对表面活性剂与微沟槽耦合的减阻的特性进行了实验研究.图1为实验中采用的微沟槽横截面示意图.实验发现,纵向微沟槽的尺寸和粗糙度对减阻性能有明显影响.在表面活性剂溶液中,不同尺寸的微沟槽对减阻的强化率为5%~8%.通过PIV对流场的观察,作者发现纵向微沟槽的减阻机理与近壁湍流涡的尺度和纵向微沟槽对湍流涡的约束有关.
图1
新窗口打开|下载原图ZIP|生成PPT图1微沟槽横截面示意图
Fig. 1Microgrooves in the experiment
表面活性剂与微沟槽耦合减阻虽然能够取得比单独使用表面活性剂更为理想的减阻效果,但是考虑到微沟槽加工工艺的困难,以及在后期使用过程中沟槽的清洗及磨损等多方面因素,将沟槽与表面活性剂耦合减阻应用到实际生活中还是有明显难度的.所以很多****将目光转换到了使用上更便捷的多种添加剂减阻耦合上,以求获得更佳的减阻效果.Mohsenipour等[22]对十八烷基三甲基氯化铵(OTAC)与聚合物聚氧化乙烯(PEO)的混合溶液进行了减阻测试.Matras等[23]针对表面活性剂十六烷基三甲基溴化铵(CTAB)与聚合物PEO的混合减阻性能进行了研究.二者均发现表面活性剂与聚合物的混合溶液可以在某一雷诺数内对减阻率有明显提高.
王青会等[24]将表面活性剂十六烷基三甲基氯化铵与非离子型聚丙烯酰胺(PAM)混合,以水杨酸钠作为反离子盐的情况下,对混合溶液的减阻特性进行了实验研究.结果表明,加入聚合物之后,混合溶液的减阻临界温度均低于相应纯表面活性剂溶液的减阻临界温度,聚合物的加入可以明显提升溶液在超过临界雷诺数的减阻破坏区的减阻效率.
1.3 表面活性剂溶液的传热特性
表面活性剂具有优良的减阻性能,但是提高减阻性能的提升的同时导致了传热性能恶化.究其原因,主要是发生减阻现象的同时,表面活性剂形成的剪切诱导结构使得流体内部尤其是近壁面湍流涡受到极大抑制,近壁处湍流脉动减弱,导致传热性能下降.为了提高表面活性剂在换热领域的应用价值,解决提高换热带来的压损升高的问题,魏进家等[25]提出了利用拉伸流场破坏胶束结构,从而提升表面活性剂传热效果的方法.利用拉伸流场避免了流体粒子的旋转能耗,保证了粒子破碎的高效,该方法能够在有效强化换热的同时保证较小的压力损失,为表面活性剂的强化换热提供了新的思路.
1.4 表面活性剂溶液的直接数值模拟
针对表面活性剂的流变特性、减阻特性以及传热特性****们做了众多的实验研究.但是针对流场内部的流动信息以及胶束的微观结构,****们需要借助模拟的方法来获得相应的信息.直接数值模拟在表面活性剂减阻研究中有着重要应用. Yu等[26-28]在此方面做了大量的工作.Huang等[29-30]借助直接数值模拟方法,对表面活性剂与微沟槽耦合减阻进行了模拟.模拟结果不仅验证了实验中发现的微沟槽对减阻的强化作用,而且验证了微沟槽对湍流涡的抑制作用.通过模拟结果提出了利用涡密度和旋转半径互相关,并结合涡半径分布预测微沟槽减阻的最佳尺寸的方法.
2 表面活性剂溶液的流变性能与微观结构
2.1 分子动力学模拟简介
表面活性剂的微观结构一直是****们研究的重点,因为通过对微观结构的研究可以直观的对流变特性以及减阻特性进行分析解释.但是受制于现有的实验条件,没有办法获得分子层面的微观结构.借助直接数值模拟方法虽然可以获得流场的整体性流动信息以及流畅内部结构的部分信息,但是这种模拟方法无法获得更深层次的结构形态,对此,需要借助分子动力学对表面活性剂溶液进行模拟研究,以此获得分子层面的微观结构,从而更为准确地解释其流变特性及减阻机理.分子动力学模拟借助计算机,通过求解经典牛顿方程得到粒子的运动轨迹,进而得到粒子的位移、速度、能量等各方面的信息.如今,分子动力学已经广泛应用在化学、生物等各个学科领域中[31-33].
在分子动力学模拟中,首先要确定力场.如果需要精确定义体系中每一个原子的力场参数,则需使用原子力场.如果需要简化计算量,可以使用粗粒化力场.粗粒化力场可以自定义,也可以使用经过实验校准的参数化力场.基于自定义力场进行的粗粒化分子动力学模拟研究存在一个很大的缺陷,就是力场的设置很大程度上取决于作者的偏好,所使用的力场参数没有与全原子模型或者实验进行校准,所以研究得到的结论往往是定性的,粗糙的.使用合适的力场可以得到更为准确的计算结果,甚至减少计算量.针对表面活性剂溶液体系,Marrink等[34-35]提出了一个针对脂质系统及表面活性剂系统的参数化粗粒化力场——马丁尼(Martini)力场,该力场后期被有效地推广到其他系统如聚合物系统中[36],其准确性得到了广泛的验证.
2.2 表面活性剂溶液
采用分子动力学模拟方法可以获得表面活性剂分子层面的微观结构,有助于分析其流变特性及减阻机理.魏进家等[37-38]早期采用了组合势作用模型WK模型来描述溶液内部胶束之间的相互作用,并成功地模拟了表面活性剂内部的网状结构.在此基础上,Zhang等[39]对上述模型进行了优化,采用刚性棒状模型,并结合了布朗动力学方法,对拉伸流黏度进行计算并获得了稳态拉伸黏度.该模型能较为准确的预测稀疏表面活性剂溶液的流变性.随着粗粒化力场的发展,粗粒化分子动力学逐渐应用在表面活性剂等溶液的模拟中,并取得了不错的成果.粗粒化分子动力学模拟方法最早应用在聚合物熔体流变性质计算上,比较有代表性的是Xu等[40]在1995年对库埃特流动情况下的聚合物熔体进行的剪切黏度计算,模拟结果验证了聚合物熔体剪切变稀的流变学特性.Castillo-Tejas等[41]使用自定义力场的粗粒化分子动力学模拟方法计算了CTAC水溶液的剪切黏度及法向应力差等非牛顿流体特征,并且随后将自己的计算拓展到了表面活性剂-水-油混合溶液中,同样得到了剪切变稀的性质,并且对胶束在溶剂中的微观结构与剪切黏度的关联性进行了分析.刘飞等[42]利用自定义力场对表面活性剂溶液进行了库埃特流动模拟,结果验证了表面活性剂的剪切稀化特征,并且发现剪切速率有助于胶束形态的平衡.其中Sangwai等[43]使用基于马丁尼力场的粗粒化分子动力学方法对表面活性剂溶液中反离子盐浓度与表面活性剂胶束形状的关系进行了模拟研究,发现随着反离子盐水杨酸钠浓度的升高,胶束与水界面的界面张力会大幅度的降低,从而使胶束从球状向柱状转变.他们同时研究了反离子盐NaSal和NaCl对胶束间作用力的影响,发现在同种浓度下NaSal相比于NaCl更容易降低胶束之间的排斥力,其中一个原因是Sal$^{-}$能够嵌入到CTA$^{+}$分子基团的尾基中,屏蔽了胶束表面及胶束之间的排斥力,更加有利于胶束之间的融合[44].
综上所述,在使用马丁尼力场的粗粒化分子动力学模拟进行的表面活性剂研究中,****们局限于静态溶液自然弛豫的研究范围内.为了更清楚地了解表面活性剂溶液流变性质与微观结构之间的关系,Liu等[45]对表面活性剂溶液在不同剪切速率库埃特流动情况下的流变性质和相对应的胶束微结构进行了研究.具体研究的表面活性剂为表面活性剂CTAC和反离子盐NamSal/NaSal/NaCl的水溶液,系统盒子大小为20 nm $\times $ 20 nm$\times $ 20 nm. 其他基础设定为：温度$T$ = 300K,表面活性剂CTAC浓度 $C_{CTAC}$ =0.1 mol/L,盐与表面活性剂摩尔比$R$ =0.8,反离子盐为NaSal,剪切速率从低到高分别设定为4.0$\times$10$^{8}$s$^{-1}$, 5.0$\times$10$^{8}$ s$^{-1}$, 6.0$\times$10$^{8}$s$^{-1}$, 1.0$\times$10$^{9}$ s$^{-1}$,3.0$\times$10$^{9}$ s$^{-1}$, 5.0$\times$10$^{9}$ s$^{-1}$,6.6$\times$10$^{9}$ s$^{-1}$.
为了研究剪切速率与剪切黏度在不同温度、表面活性剂和反离子盐浓度、摩尔比、反离子盐之间的关系,使温度、浓度、摩尔比和反离子盐分别设置为$C_{ CTAC}$ = 0.3 mol/L,$R$ = 2,$T$ = 320K,反离子盐分别为NaCl和NamSal,与基础设定所得到的剪切黏度进行比较,上述条件下剪切黏度计算结果如图2所示.
从图2可以看出,在低剪切速率范围内(从4.0$\times$10$^{8}$s$^{-1}$到1.0$\times$10$^{9}$ s$^{-1})$,剪切黏度基本保持不变;而在高剪切速率时,溶液具有剪切变稀的特性.这个计算结果与Helgeson等[46]实验吻合良好,并且优于Castillo-Tejas等[38]模拟结果,因为后者的黏度分布没有黏度保持不变区域.此外,可以明显看出,当溶液温度从300 K 升高到320K时,剪切黏度降低;而当溶液浓度从0.1 mol/L变化到0.3mol/L时,剪切黏度增大,该结论也与本课题组Xu等[47]的实验结论有很好的一致性.同时发现,当反离子盐为NamSal时的剪切黏度在相同浓度下大于反离子盐为NaSal,对现象的合理解释为：在马丁尼力场中,Sal$^{-}$和mSal$^{-}$均可以刺入CTA$^{ +}$分子团簇表面而作为表面活性剂胶束的组成部分,而mSal$^{-}$在苯环第五点位上的甲基能够比Sal$^{-}$中的苯环刺入CTA$^{ +}$疏水基更多,从而结合力更强.反映到马丁尼力场中,NamSal环形链三个粗粒化分子中的一个分类为SC2,区别于NaSal中三个粗粒化分子均为SC4,而SC2对CTA$^{+}$中的4个疏水基粗粒化分子(粗粒化分子类型分别为两个C1和两个C2)的吸引力比SC4要强很多,导致mSal$^{-}$与CTA$^{ +}$的胶束结合更紧密,高剪切率下形成的蠕虫状胶束比CTA$^{ + }$/Sal$^{-}$的组合更加难以破坏,导致CTAC/NamSal溶液的剪切黏度相对较大.
表面活性剂溶液摩尔比$R$与剪切黏度的关系,如图3所示.
图2
新窗口打开|下载原图ZIP|生成PPT图2剪切速率与剪切黏度关系
Fig. 2Shear rate versus shear viscosity
图3
新窗口打开|下载原图ZIP|生成PPT图3摩尔比与剪切黏度关系
Fig. 3Concentration molar ratio versus shear viscosity
从图3可以看出当$R$从0.3逐步增大到1.0时,剪切黏度逐渐变大;但当$R$大于1.0之后,随着$R$的增大,剪切黏度逐渐趋于稳定.这个结果刚好验证了Sangwai等[40]关于反离子盐离子Sal$^{-}$最大搭载量的判断,CTA$^{ + }$最大吸附等摩尔的Sal$^{-}$.
表面活性剂溶液黏度与其胶束微结构之间有很强的相关性,本课题组研究了在高剪切速率,低剪切速率,静态自然弛豫情况下表面活性剂溶液中典型的分子自组装过程,如图4所示.表面活性剂为CTAC,反离子盐为NaSal,表面活性剂浓度$C_{CTAC}$ =0.3 mol/L,盐与表面活性剂摩尔比$R$ = 0.8.
从图4可以看出,在静态自然弛豫、低剪切率和高剪切率情况下,初始状态为CTAC和NaSal分子随机散布在水溶液中(图4(a));无论是有剪切或者是静态自然弛豫,表面活性剂和反离子盐分子都会在随后很短的时间内自组装为小球状胶束(图4(b));随后在静态自然弛豫状态下小胶束团逐渐合并成蠕虫状胶束(图4(c)),因为静态自然弛豫与低剪切状态下在这个阶段蠕虫状胶束形态基本一致,所以就省略了低剪切率情况下该阶段的状态图.在最终的静态自然弛豫平衡阶段和高低剪切率状态下的动态平衡阶段,胶束结构呈现出完全不同的形态特征.在静态自然弛豫状态下,模拟系统中最大胶束呈现出枝状结构(图4(e));而对于低剪切率状态,最大胶束呈现出多节点互相连接的网状结构(图4(f));然而在高剪切速率状态下,最大胶束呈现出蠕虫状(图4(d)),并且沿剪切流动方向排布.
图4
新窗口打开|下载原图ZIP|生成PPT图4胶束典型自组装过程
Fig. 4Typical self-assemble processes of micelles
表面活性剂溶液中的胶束形态与流变性质有着深刻的关联,在低剪切速率状态下形成的网状胶束能够抵抗溶剂的剪切力,相比于静态自然弛豫和高剪切速率状态下的树枝状胶束和沿流向分布的蠕虫状胶束, 具有更高的剪切黏度,这个结论也同样得到了文献${[48]的实验验证.
进一步研究了在静态自然弛豫和高低剪切速率三种表面活性剂溶液库埃特流动状态下,模拟盒子系统中最大胶束所包括CTA$^{+ }$数目随时间变化规律,如图5所示.
从图5可以看出,最大胶束所含表面活性剂分子数目随时间延长而增加.对于静态自然弛豫和低剪切速率状态下的溶液,最大胶束所含表面活性剂分子数目变化经历了七个阶段;而对于高剪切速率状态下的溶液,有六个阶段.前五个阶段最大胶束的形成时间大小顺序为：$T_{\mbox{高剪切}}<T_{\mbox{低剪切}}<T_{\mbox{静态自然弛豫}}$,最大胶束中所包含表面活性剂分子数目排列顺序为：$N_{\mbox{高剪切}}>N_{\mbox{低剪切}}>N_{\mbox{静态自然弛豫}}$.可以看出,随着剪切速率的增大,同样大小的胶束形成时间逐渐减小.因此对于低剪切速率和高剪切速率状态的库埃特流动,与静态自然弛豫状态相比,剪切作用可以提升溶液中胶束的生长速率.
2.3 表面活性剂与聚合物混合溶液的流变特性及微观结构
刘冬洁等[49]对表面活性剂与聚合物混合体系CTAC/PAM进行了粗粒化分子动力学模拟.图6为该研究采用的粗粒化模型. 其中CTAC溶于水之后分散成CTA$^{ +}$和Cl$^{-}$,NaSal溶于水之后分散成Na$^{ +}$以及Sal$^{-}$,Cl$^{-}$和Na$^{ + }$分别用相应的带电荷粒子表示.CTA$^{+}$由C2粒子和C1粒子组成的疏水尾基与Q0代表的亲水头基构成.Sal$^{-}$由Qa代表的带电荷粒子以及三个SC4粒子构成的环状物组成.PAM的碳链骨架由SC1粒子代替,侧链的亲水酰胺基由P5代替,聚合物的聚合物为50.图5
新窗口打开|下载原图ZIP|生成PPT图5最大胶束所含CTA$^{ + }$数目随时间变化规律
Fig. 5The CTA$^{ + }$ number of the largest micelle at different simulation times
图6
新窗口打开|下载原图ZIP|生成PPT图6CTAC和PAM的粗粒化拓扑模型
Fig. 6Topology of CTAC, PAM, NaSal, water and antifreeze water
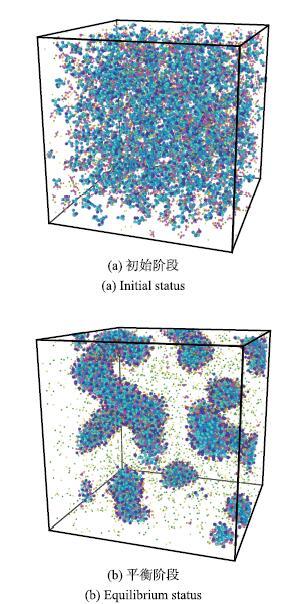
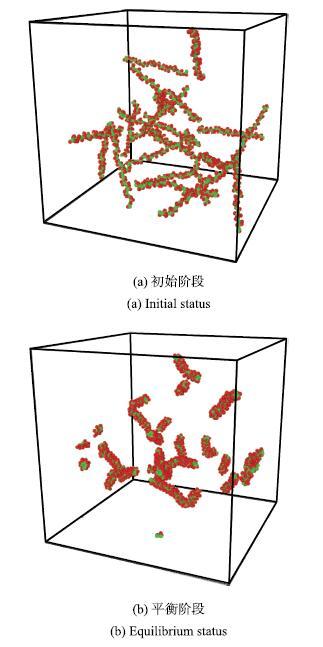
首先对CTAC/NaSal溶液以及PAM溶液进行了平衡态模拟.模拟结果发现,对于CTAC/NaSal溶液,初始时刻粒子均匀散乱分布,经过充分弛豫之后CTAC在溶液中形成了明显的棒状胶束.其中,CTA$^{ + }$粒子亲水基朝向外侧,疏水基隐藏在胶束内部,Sal$^{-}$粒子插入在胶束头基之间,屏蔽头基之间的静电排斥作用,使得胶束结构更为紧密,如图7所示.对于PAM溶液,在模拟的初始时刻,PAM链为伸展状态,弛豫一段时间后,在PAM碳链骨架的疏水性与侧链酰胺基的亲水性的双重作用下,PAM分子链蜷缩变短,侧链酰胺基裸露在外侧,屏蔽了碳链骨架与水分子的接触,如图8所示.
图7
新窗口打开|下载原图ZIP|生成PPT图7CTAC/NaSal 溶液模拟不同阶段内部结构
Fig. 7Snapshots of CTAC/NaSal system at different status
图8
新窗口打开|下载原图ZIP|生成PPT图8PAM溶液模拟不同阶段内部结构
Fig. 8Snapshots of PAM system at different status
为了探讨反离子盐NaSal对CTAC/PAM混合溶液内部结构的影响,作者对CTAC/NaSal/PAM体系以及CTAC/PAM体系进行了分子动力学模拟.
图9中展示了CTAC/PAM体系的模拟结果.从图中可以看到,由于没有反离子盐的存在,CTAC不能形成棒状胶束,在溶液中以球状胶束存在.PAM链依旧为蜷缩形态.但是在溶液中可以明显观察到CTAC球状胶束与PAM链相互缠结,但是溶液中仍有部分游离态没有与PAM缠结的CTAC胶束.
图9
新窗口打开|下载原图ZIP|生成PPT图9CTAC/PAM体系平衡态内部结构
Fig. 9Snapshots of CTAC/PAM system at equilibrium status
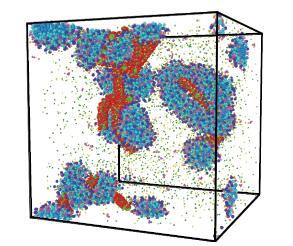
从图10中可以看出,在NaSal存在的条件下,CTAC明显形成了蠕虫状胶束,CTAC与PAM的相互纠缠更为紧密,溶液中已经没有游离态的CTAC胶束存在,CTAC与PAM完全形成了复合交联结构.由此看出,反离子盐的加入不仅会使得CTAC发生形态上的转变,有利于CTAC形成蠕虫状胶束,也会促进CTAC与PAM的结合.
图10
新窗口打开|下载原图ZIP|生成PPT图10CTAC/NaSal/PAM溶液平衡态内部结构
Fig. 10Snapshots of CTAC/NaSal/PAM system at equilibrium status
为了更准确地探讨反离子盐在表面活性剂与聚合物混合溶液中的作用,计算了在CTAC/PAM体系与CTAC/NaSal/PAM体系中,CTAC与PAM所含粒子之间的径向分布函数.通过径向分布函数的计算可以直观的看到各个粒子之间的分布关系.结果如图11所示. 图11(a)为CTAC/PAM体系中粒子的径向分布函数结果.从结果中可以看到,CTAC胶束中的Q0粒子与PAM中的P5粒子接触最为紧密,也就是说胶束的最外侧亲水头基与PAM外侧亲水侧链酰胺基紧密贴合.除此之外,CTAC胶束的疏水尾基粒子C2及C1与PAM的SC1粒子及P5粒子均有接触,但是接触程度相对较弱,这说明有部分PAM链深入到CTAC胶束内部,即CTAC的疏水尾基与PAM的疏水碳链有一定的吸引作用.从图11(b)中可以看出,加入反离子盐之后,除了CTAC的亲水头基与PAM的亲水酰胺基的作用之外,其他粒子之间的距离都近似为零,即加入反离子盐之后,CTAC与PAM之间作用只剩下亲水基之间的相互吸引.
图11
新窗口打开|下载原图ZIP|生成PPT图11不同体系中粒子的径向分布函数
Fig. 11Radial distribution function in of CTA$^{ + }$ and PAM in different systems
除了利用分子动力学模拟方法对溶液内部结构进行模拟之外,还对溶液的流变特性进行了测试.从之前的实验结果中可以得到[24],表面活性剂与聚合物的混合溶液可以获得更高的减阻率,尤其是在超过临界雷诺数之后.刘冬洁等[46]利用分子动力学模拟的方法,对CTAC/NaSal溶液、PAM溶液以及CTAC/NaSal/PAM溶液进行了RNEMD方法进行了黏度模拟.RNEMD方法通过交换粒子速度获得流场[50-51],相较于NEMD模拟结果更为准确.模拟结果如下图所示(图12).
从图中可以看出,三种溶液在剪切率较小时都呈现出类似牛顿流体的性质,出现了黏度的平台期.后期随着剪切率的增大,黏度明显减小,此模拟结果与实验测试定性上吻合良好[46,52].而且从图中发现,CTAC/NaSal/PAM组成的混合溶液无论在任何时候都具有最高的黏度.为了解释混合溶液黏度升高的原因,截取了CTAC/NaSal/PAM溶液与CTAC/NaSal溶液受到剪切之后的结构形态图进行对比分析,结果如图13与图14所示.
图12
新窗口打开|下载原图ZIP|生成PPT图12黏度随剪切速率的变化
Fig. 12Shear viscosity versus shear rate in different systems
图13
新窗口打开|下载原图ZIP|生成PPT图13CTAC/NaSal/PAM溶液剪切结构变化图
Fig. 13Snapshots of the shearing process for CTAC/NaSal/PAM system
图14
新窗口打开|下载原图ZIP|生成PPT图14CTAC/NaSal溶液剪切结构变化图
Fig. 14Snapshots of the shearing process for CTAC/NaSal system
通过对比图13和图14内部结构,可以看出：对于表面活性剂与聚合物混合溶液来说,溶液中已经完全形成了复合交联结构,受到剪切作用时,该结构更有能力抵抗剪切作用的破坏.同时,PAM因为其具有的特殊的长链特征,可以有效地吸收剪切力的能量并转化成长链的弹性势能,使得PAM链伸长.PAM链承担了大部分的剪切力,保护了溶液中的CTAC胶束,是胶束免受剪切力破坏.相反,对于CTAC/NaSal溶液,由于溶液中只有胶束的存在,在剪切力的作用下长蠕虫状胶束被剪断,胶束结构遭到破坏.所以相较之下,混合溶液具有较高的黏度.同理,针对表面活性剂与聚合物的减阻实验,正是因为溶液中的复合交联结构的存在,以及PAM链的保护作用,使得混合溶液具有更高的减阻效果.
3 表面活性剂溶液湍流减阻机理
3.1 表面活性剂胶束断裂与再连接行为
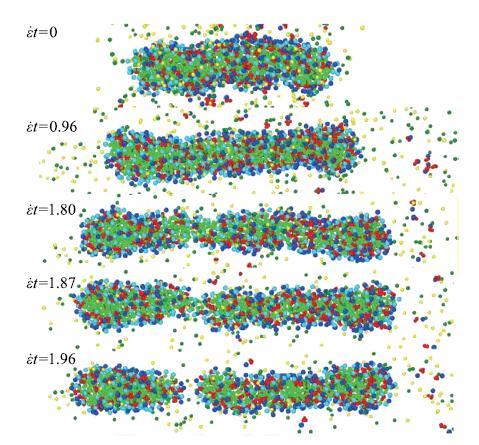
表面活性剂相比较于高分子聚合物在管道流体运输中的优点就是具有可逆机械降解的特性,更加适用于高剪切以及封闭的循环回路的减阻.而作为表面活性剂溶液中自组装成的胶束,其断裂和再连接性能直接关系到减阻效果的优劣,所以研究表面活性剂胶束的断裂与再连接行为很有必要.魏进家课题组Liu等[53]对单根表面活性剂胶束的断裂与再连接行为进行了研究,主要回答了以下三个基本问题：(1)溶液温度、反离子盐浓度和不同类型的反离子盐是如何影响蠕虫状胶束的柔韧性的?(2)胶束的断裂和再连接能量的精确值是多大?(3)胶束之间的结合能是受什么因素影响的?Liu等使用Packmol[54]首先在12 nm$\times $12 nm$\times $40nm的盒子中心预组装了四个不同长度的蠕虫状胶束(表面活性剂为CTAC,反离子盐为NaSal),分别为14nm,19 nm,23 nm和28 nm.随后对胶束溶液系统在Z轴方向进行单轴拉伸,而盒子通过压力平衡调整$X$和$Y$方向的长度使盒子总体积保持不变[55],从初始状态直至断裂,如图15所示.
图15
新窗口打开|下载原图ZIP|生成PPT图15表面活性剂胶束断裂过程
Fig. 15The breakage processes of a wormlike micelle
通过对胶束断裂过程分析可以发现,胶束断裂时胶束长度约为初始长度的140%,这也为有限可伸长非线性弹性FENE或者简谐式模型中1.5倍初始长度设定提供了理论解释.
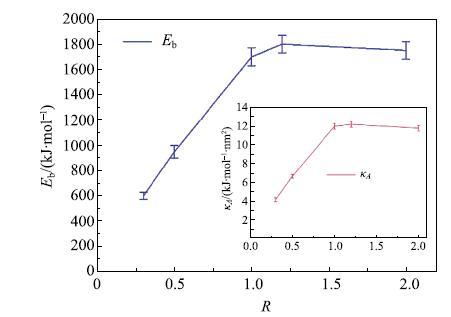
在胶束逐渐拉伸到断裂过程中,胶束拉伸能量随累积拉伸量的变化规律,如图16所示.
从图16可以看出,胶束的拉伸是近乎均匀的,胶束的拉伸能量几乎是一个完美的抛物线,胶束拉伸能$E_{{extension}} $ 可以近似表达为$F_0 \Delta x + \kappa _A\Delta x^2$. 其中$\kappa _A $可以看作是胶束的弹性模量.经过计算发现,所计算工况表面活性剂蠕虫状胶束的弹性模量约为12$\mbox{kJ$\cdot$(mol}\mbox{$\cdot$nm}^{ {2}})$.胶束完全可以被认为是一个有弹性的弹簧,因为它比较完美的吻合胡克弹簧模型.而弹性模量越大,胶束的柔韧性就越好,在湍流减阻过程中能够吸收的湍流小涡的能量就越多,越有利于湍流减阻过程.
图16
新窗口打开|下载原图ZIP|生成PPT图16胶束能量与累积拉伸量
Fig. 16Micelle extension energy versus the accumulated strains
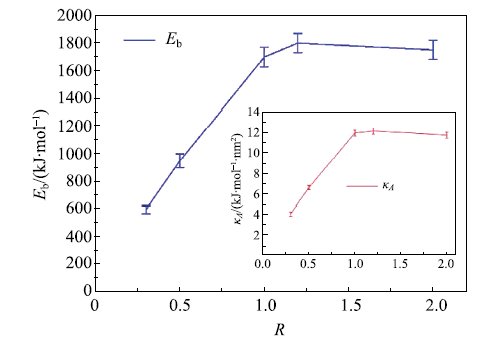
胶束的断裂能$E_{b}$就是最大拉伸能,选取28nm蠕虫状胶束为研究对象,研究摩尔比$R$分别为0.3,0.5,1.0,1.2,2.0情况下胶束的断裂能变化规律,如图17所示.
图17
新窗口打开|下载原图ZIP|生成PPT图17胶束断裂能与摩尔浓度比
Fig. 17The effect of concentration molar ratio on the breakage energy
从图17可以看出,在$R$$<$1.0时,随着$R$的增大,胶束断裂能从600kJ/mol增 大到1700kJ/mol,对应于胶束弹性模量$\kappa _A $为4.23$\mbox{kJ/(mol}\mbox{$\cdot$nm}^{ {2}})$到12$\mbox{kJ/(mol}\mbox{$\cdot$nm}^{{2}})$;当$R$$>$1.0时,随着$R$的增大,断裂能基本维持在$R$ =1.0时的数值附近,这与在工业应用中选择$R$ =1.0作为反离子盐添加量相吻合.根据魏进家等报道,表面活性剂溶液湍流减阻能力在$R$$<$1.0时会有显著下降[56].
胶束断裂能随溶液温度的变化规律,如图18 所示.
图18
新窗口打开|下载原图ZIP|生成PPT图18胶束断裂能与溶液温度
Fig. 18The effect of solution temperature on the breakage energy
从图18可以看出,溶液的温度从280 K增大到320K,胶束断裂能维持在一个很小的区间内 (1750$\pm $100$\mbox{kJ/mol})$,这说明溶液温度对胶束断裂能的影响很小.
通过研究不同种类反离子盐NaSal,NamSal和NaCl对胶束断裂能的影响,发现可穿透胶束表面的有机反离子盐NaSal和NamSal溶液中胶束断裂能远远大于同等摩尔数的无机盐NaCl,这是因为NaCl在水中电离成Na$^{+ }$和Cl$^{-}$,无法被阳离子胶束所有效搭载,从而无法减小胶束表面的静电排斥力,导致胶束容易断裂.
在工业应用中的表面活性剂胶束网状结构一般持续1~10 $\mu$m范围内[57],对于湍流流动来说,湍流涡对整个胶束网状结构造成的撕裂现象可以简化为网状胶束结构中单根胶束的拉伸撕裂,所以本课题组目前主要讨论了单根胶束的拉伸断裂问题,至于一个完整的胶束网状结构的断裂现象,有待于下一步的研究.
湍流小尺度涡在使胶束发生断裂之后,减阻能力的恢复主要依靠胶束之间再连接作用,重新组装在一起.在胶束/反离子盐系统中,胶束直径基本维持在一个固定的数值,所以在湍流网状胶束被破坏后的再连接过程中,根据破碎胶束的大小形状,从单个胶束的再连接角度来看,可分为三种再连接类型(如图19所示)：(1)两个球状胶束合并成一个短棒状胶束;(2)一个球状/短棒状胶束与一个短棒状/蠕虫状胶束合并成一个枝状胶束;(3)两个蠕虫状胶束合并成一个X形胶束.
图19
新窗口打开|下载原图ZIP|生成PPT图19胶束的再连接过程
Fig. 19The recombination processes of two individual micelles
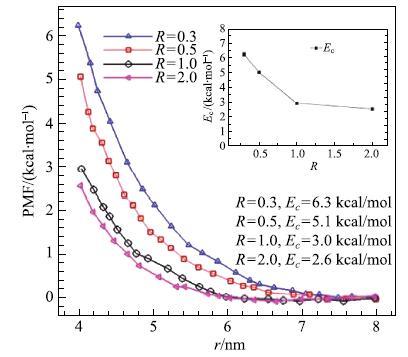
这三种类型的合并有一个共同的特征,就是他们的合并点均可以简化为两个球形胶束的合并.所以可以用两个球形胶束的合并来简化胶束的合并过程,通过计算他们的结合能来研究胶束的合并行为,根据文献${[58],结合能可以被认为是平均力势PMF之差,而PMF可以通过Gromacs软件包[59]中的伞状抽样[60]和直方图分析方法[61]来计算.PMF以及结合能随摩尔比$R$的变化,如图20所示.
从图20可以看出,PMF始终为正值,说明两个胶束始终是相互排斥的.从结合能大小来看,随着$R$的增大胶束之间的结合能逐渐变小,胶束越来越容易融合在一起.另外还发现结合能随着温度升高而降低,说明温度有利于胶束之间的融合;反离子盐NamSal,NaSal和NamSal使胶束之间的融合比NaCl更容易.以28nm胶束为例,从数值上来看,每个分子所平均的断裂能和结合能分别为3.54kJ/mol和0.154kJ/mol,而实际上两则差距可能更大,因为实际工况中胶束是弯曲状态的[62],湍流小尺度涡应该首先使胶束"拉直",然后才能拉伸断裂.说明相比较于结合能,在实际工业应用中如何提高胶束断裂能更应该被优先考虑.
图20
新窗口打开|下载原图ZIP|生成PPT图20平均力势PMF及结合能随$R$变化(1 cal=4.185 J)
Fig. 20PMF and the coalescence energy versus $R$
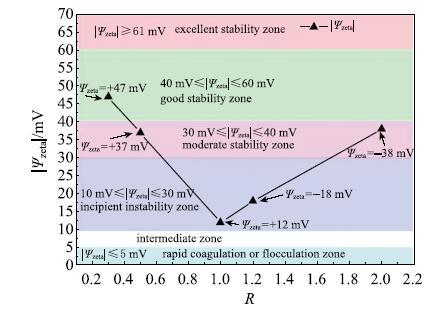
由于表面活性剂胶束在水溶液中可以看成是一个带电的胶体[43],所以根据Derjaguin-Landau-Verwey-Overbeek(DLVO)理论[63-64],两个阳离子表面活性剂胶束之间的排斥力可以归功于胶束表面的库仑排斥力和扩散层排斥力的总和.而$\zeta$电势是描述胶体稳定性的很好的指标.两个胶束之间的$\zeta$势能随摩尔比$R$变化的关系,如图21所示.
图21
新窗口打开|下载原图ZIP|生成PPT图21$\zeta$电势随$R$变化
Fig. 21The $\zeta$ potential versus $R$
从图21可以看出,当反离子盐浓度逐渐增大时,即摩尔比$R$从0.3逐步增大到1.0时,胶束越来越容易融合.这个结论与结合能随摩尔比的变化趋势一致,说明两者具有同步效应.而同样有同步效应的还有$\zeta$电势与溶液温度的关系,当温度升高时候,$\zeta$电势逐渐降低,胶束易于融合~,如图22所示.这个与结合能与温度升高的关系也具有同步性,这说明当反离子盐浓度和温度增大时候,不仅胶束表面电荷之间的排斥力减小了,而且胶束外面扩散层的排斥力也减小了,更有利于胶束融合.
图22
新窗口打开|下载原图ZIP|生成PPT图22$\zeta$电势随溶液温度变化 (1 kcal=4.18 kJ)
Fig. 22The $\zeta$ potential versus solution temperature
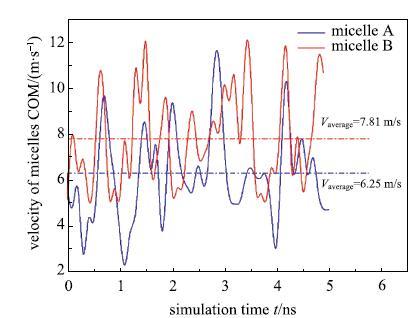
因为反离子盐离Sal$^{-}$在CTA$^{ +}$表面分布的不均匀性[65],所以会导致胶束表面疏水基团与水接触面积的不均匀分布,而疏水基驱动力是蛋白质折叠的主要驱动力[66-67],所以可以猜想CTA$^{+ }$/Sal$^{-}$胶束同样存在疏水基的驱动作用,为了证明这个猜想,可以设计两个Sal$^{-}$均匀度不同,但是尺寸相同且拥有同样的疏水基与水接触面积的两个胶束,其中胶束A表面的Sal$^{-}$是近乎均匀分布的,而B为不均匀分布的.两个胶束质心的平均速度随时间变化,如图23所示.
图23
新窗口打开|下载原图ZIP|生成PPT图23两个胶束质心速度随时间变化
Fig. 23The velocity of the COMs of the two micelles versus the simulation time
从图23可以看出,尽管胶束A和胶束B的平均速度随时间变化波动幅度很大,但是从总体时间平均速度来看,胶束B的平均速度是大于胶束A的,这个结论验证了表面活性剂胶束疏水基驱动效应假说的正确性.即加入有机反离子盐Sal$^{-}$之后胶束存在疏水基驱动作用,这个驱动作用叠加到胶束因温度产生的布朗随机运动上,提高了胶束的再连接可能性.
3.2 表面活性剂湍流减阻"黏弹说"分子尺度验证
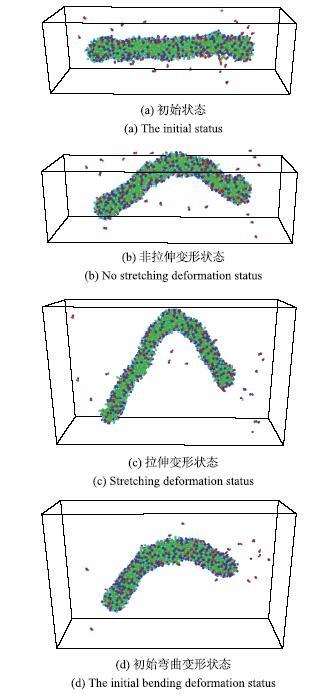
在****们基于实验观测提出了一些合理假说来解释表面活性剂溶液湍流减阻机理,其中诺贝尔奖获得者DeGennes等[68]所提出的"黏弹说"获得了很好的认可度.该假说的主要思想是,表面活性剂溶液中的胶束微观网状/条带状结构可以吸收并存储湍流小尺度涡的能量,待储能的胶束网状/条带状结构扩散或对流到低应变速率区域后,再将其存储的能量以弹性切应力波的形式释放给大尺度湍流涡,从而减小了流体的湍动能耗散,达到减阻的目的.然而该假说很难被直接证明,一个很重要的原因就是PIV的实验观测或者湍流直接数值模拟方法都只能在宏观尺度下得到湍流涡结构、湍流脉动等信息[69],无法直接观测到湍流过程中胶束的微观运动.而微观尺度却提供了验证"黏弹说"的可能性,因为表面活性剂溶液中的条带状/网状胶束微结构可以在微观尺度下被观察和测量出来.粗粒化分子动力学模拟、小角中子散射、光的双折射、核磁共振等模拟和实验方法均发现了剪切条带状微观结构[70-71].采用粗粒化分子动力学模拟,Dhakal等[65]在静态溶液中发现了胶束的网状结构,而条带状与网状胶束微结构则为支持黏弹说提供了可储存能量的微单元.尽管从粗粒化分子动力学模拟和实验上对表面活性剂胶束研究均有了一些进展,但是从分子尺度证实黏弹说的正确性,仍然面临着挑战.魏进家课题组Liu等[50]使用非平衡态粗粒化分子模拟中的Muller-Plathe算法,使一个蠕虫状胶束产生非拉伸弯曲变形和拉伸弯曲变形,改变交换原子的个数和频率以实现单根胶束的非拉伸变形和拉伸变形,通过对胶束自身能量和水分子溶剂的能量分析,试图在分子角度上为表面活性剂溶液湍流减阻"黏弹说"提供直接证据.
Liu等[50]首先研究了表面活性剂胶束与水之间的能量传递规律,在分子尺度上,小尺度涡可以使胶束发生拉伸变形和非拉伸变形,而当胶束扩散或对流到大尺度涡所在的低应变速率区域时,胶束就会自然弛豫到稳定状态.在12 nm$\times $12 nm$\times $40nm的模拟盒子中预组装一个表面活性剂胶束,胶束初始构型状态如图24(a)所示;使用LAMMPS软件对Muller-Plathe方法中交换原子的个数和频率大小控制[72],可以得到胶束的非拉伸变形状态(图24(b))和拉伸变形状态(图24(c)),随后再对两种非平衡稳态系统进行静态自然弛豫,稳定之后的胶束形态如图24(d)所示.显示所用的软件为OVITO[73],为了更清楚地显示,隐藏了盒子系统中的水分子和游离态的离子.
图24
新窗口打开|下载原图ZIP|生成PPT图24四种典型的胶束形态
Fig. 24Four typical micelle morphologies
从初始状态(图24(a))到初始弯曲变形状态(图24(d)),胶束能量随模拟时间的变化,如图25所示.
从图25可以看出,胶束在非拉伸变形(紫色区域)和拉伸变形过程中(绿色区域),均会从水分子的剪切流场中吸收能量;而在静态自然弛豫阶段,无论是非拉伸变形和拉伸变形后的胶束,自身的能量都会逐渐减小(蓝色区域和黄色区域),直至恢复到初始低能量状态.从吸收能量的大小来看,胶束拉伸变形后吸收的能量远大于胶束非拉伸变形吸收的能量.
图25
新窗口打开|下载原图ZIP|生成PPT图25胶束能量随时间变化规律
Fig. 25The micelle energy versus simulation times
为了追踪胶束被最大拉伸变形后自然弛豫过程中胶束耗散的能量去向,胶束拉伸变形和非拉伸变形情况下的水分子的势能变化,如图26所示.
图26
新窗口打开|下载原图ZIP|生成PPT图26水分子势能随时间变化规律
Fig. 26The pair potential of water molecules versus simulation times
从图26可以看出,在拉伸变形胶束自然弛豫的2669ps内,水分子势能从-261 610 kJ/mol增大到-260 680 kJ/mol,增大了930 kJ/mol.这说明胶束释放的大部分能量都传递给了水分子,能量传递效率约为75%(930/1248).
为了更好地理解胶束与水之间的能量传递规律,把胶束沿轮廓方向分成了20个等份,计算了胶束四种状态下"对势能"的大小分布规律,如图27所示.
图27
新窗口打开|下载原图ZIP|生成PPT图27胶束"对势能"沿胶束轮廓分布规律
Fig. 27The pair potential energy along the contour of the micelle
从图27可以看出,胶束在最大拉伸变形状态时,沿胶束轮廓各个等份的"对势能"大于另外三种状态,这说明表面活性剂胶束内各个粗粒化基团之间的平均距离变大.由于胶束在拉伸过程中可以近似看作为线性胡克弹簧模型[53],因此在胶束断裂前的拉伸长度内,当剪切/拉伸流场消失而转为自然弛豫时,胶束就会沿着轮廓收缩到它的初始长度.被拉伸胶束的收缩效应可以被更直观的观察到,图28为胶束在四种状态下其轮廓附近的水分子瞬态速度分布.
从图28可以看出,胶束从最大拉伸变形状态开始自然弛豫时,胶束轮廓附近有很多的水分子沿着胶束轮廓收缩的方向运动.
在另外三种状态(初始状态,非拉伸变形和初始弯曲变形状态)时,沿胶束轮廓的水分子的运动是杂乱无章的,可以被认为是随机运动.所以胶束存储能量-释放能量的过程发生在胶束被拉伸变形后的自然弛豫阶段.
图28
新窗口打开|下载原图ZIP|生成PPT图28胶束轮廓附近水分子速度分布
Fig. 28The velocity distribution of water molecules around the micelle contour
4 表面活性剂湍流减阻失效分析
在实验中可以发现,表面活性剂溶液经历一个月或者更久时间,减阻能力开始缓慢减弱;而在实际应用中,甚至只有三天时间湍流减阻效果就会完全失去[56].因为试验中的集中供热/制冷系统管道经常为透明玻璃状[69],而实际应用中管道则为普通碳钢,管道容易生锈.而生锈的主要原因是水中电离态氢离子的消耗,氢氧根离子会与铁发生化合反应导致的,因为氢氧根离子与铁化合的生锈过程非常缓慢,水中就滞留了一些氢氧根离子,这样在生锈的管道中pH值就会略微升高.因为管道是封闭系统,所以生成的铁锈一部分会分散在流体中,另一部分会保留在管道壁面上.因为生锈过程是一直在发生的,所以铁锈表面也带有一些电荷.本课题组目前尝试用粗粒化分子动力学模拟方法对减阻失效问题进行解释,从三个方面进行分析.
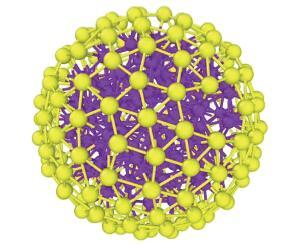
(1)氢氧根离子的存在会造成表面活性剂自组装胶束团簇形态的变化.Quan等[74]在马丁尼力场中使用胶束头部改性来表征pH值降低,基于这个思路,根据马丁尼力场的设定[38],溶液中有氢氧根离子时,可以把CTA$^{+ }$头基的分类由Q0改为Nda. 部分CTA$^{ +}$已经改性后的胶束结构如图29所示.
图29
新窗口打开|下载原图ZIP|生成PPT图29表面活性剂溶液中的胶束
Fig. 29Surfactant micelles in aqueous solution
从图29可以看出,胶束形态不再符合均匀的,直径为4.5nm左右的网状结构[43,65],而成为不规则的胶束团,失去了减阻时具有的网状构造.在实际工业应用中,反映为絮凝状沉淀,随着铁锈的增加,头部改性的表面活性剂分子越多,表面活性剂减阻效果就会大大减弱,直至完全失效.
(2)管道内微小的铁锈颗粒与胶束的相互作用.微小的铁锈颗粒可以近似看作纳米颗粒,在粗粒化分子动力学模拟中,纳米颗粒有几种常用的构建方式[75-77],选择键连接的方式可以使纳米颗粒的带电层各个带电点位的位置更稳定[78],如图30所示.
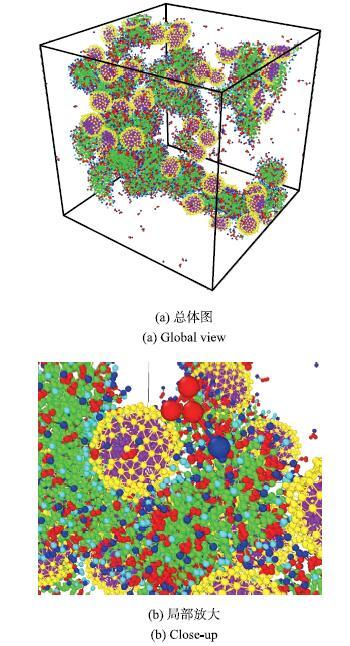
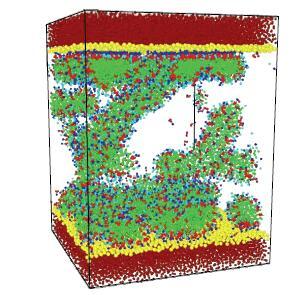
纳米颗粒在高分子聚合物溶液中通常被认为是连接聚合物的节点[79],使高分子聚合物胶束的网状结构更紧密的连接.但是在表面活性剂溶液中,表面活性剂小分子自组装胶束与带电纳米颗粒的连接却使胶束的网格结构遭到了破坏,如图31所示.
从图31可以看出,带电的纳米颗粒使胶束在纳米颗粒附近产生了弯曲,并且纳米颗粒填充了正常胶束网格结构中的空格位置,使网状结构的胶束变成一团吸附在纳米颗粒上的絮凝物,在实际工业应用中,造成湍流减阻的部分失效或者全部失效.
图30
新窗口打开|下载原图ZIP|生成PPT图30键连接方式的纳米颗粒
Fig. 30Nanoparticle composed by bond connection
图31
新窗口打开|下载原图ZIP|生成PPT图31表面活性剂溶液中的胶束
Fig. 31Surfactant micelles in aqueous solution
(3) 管道壁面上的铁锈颗粒与胶束的相互作用.管道壁面上的带电铁锈颗粒,跟纳米颗粒一样,也会对表面活性剂胶束有吸附作用,使一部分表面活性剂胶束吸附在了管道壁面,如图32所示.
图32
新窗口打开|下载原图ZIP|生成PPT图32带电壁面对表面活性剂胶束的吸附
Fig. 32The absorption effect of charged wall on surfactant micelles
从图32可以看出,带电壁面对表面活性剂胶束具有吸附作用.吸附的机理为,当壁面带电为正电时,壁面通过吸附CTA$^{ +}$上面搭载的反离子盐Sal$^{-}$对表面活性剂胶束进行吸附;而带负电壁面主要吸附CTA$^{ +}$的头基,使胶束粘附在壁面上.
综上所述,对于表面活性剂减阻失效问题,粗粒化分子动力学模拟可以从机理上出发给出有说服力的解释.
5 结论与展望
本文回顾本课题组在表面活性剂溶液流变性实验测量与模型建立,湍流减阻模拟,布朗动力学模拟的工作,重点介绍了表面活性剂溶液粗粒化分子动力学模拟方面的研究工作,得到了表面活性剂溶液流变性与胶束微结构的关系、分子尺度上对表面活性剂湍流减阻机理的认识、湍流减阻失效的机理解释三个方面的模拟数据与结论.表面活性剂溶液在高剪切速率、低剪切速率和静态自然弛豫三种状态下对应的胶束微结构分别为蠕虫状、树枝状和网状,增大剪切速率和溶液温度都能提升胶束的生长速度.而表面活性剂与PAM混合溶液中的复合交联结构的存在,使混合溶液具有更好的减阻效果.对于表面活性剂胶束的断裂与再连接行为,胶束可以看成一个符合胡克弹性模型的弹簧,胶束断裂行为可以通过拉伸能、断裂能与最大拉伸长度进行描述;而胶束再连接行为可以通过结合能、$\zeta$电势与疏水基驱动作用三个因素来进行评价.通过对胶束和水分子之间能量传递规律的研究,可以从分子角度验证表面活性剂湍流减阻假说"黏弹说"的正确性.表面活性剂在实际湍流减阻应用中的失效问题来自三个方面的原因：溶液弱碱性、溶液中微小的铁锈颗粒与管道铁锈壁面.溶液呈现弱碱性导致表面活性剂胶束由网状结构变为团簇状结构,溶液中微小铁锈表面的带电性使其与胶束相互吸附而填充了胶束网格结构之间的空隙,管道铁锈壁面吸附部分表面活性剂胶束而使溶液中总体胶束网状构造变少,这三种情况均破坏了表面活性剂溶液中胶束的网状剪切诱导结构,造成表面活性剂溶液湍流减阻效果部分失效或者完全失效.
未来的粗粒化分子动力学模拟研究工作将侧重于以下三个方面：(1)采用粗粒化分子动力学模拟方法,对表面活性剂与其他添加剂进行模拟研究,解释表面活性剂与其他添加剂的相互作用机理;(2)将单根胶束拓展为一个完整的胶束网状结构,进一步研究湍流减阻机理,并且对网状结构胶束进行SANS模拟和小角度X射线散射实验测定,确定表面活性剂胶束网格的尺寸特征,为耗散粒子动力学模拟提供更好的理论基础;(3)对可能的湍流减阻失效模式进行化学反应层面的更深入研究,并且对目前分子动力学模拟所得出的结论进行透射电镜等实验测定,验证粗粒化分子动力学模拟的可靠性.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
[本文引用: 1]
[本文引用: 1]
Magsci [本文引用: 2]
利用ARES流变仪对具有湍流减阻作用的阳性界面活性剂CTAC/NaSal水溶液的剪切黏度进行了测量。溶液的质量浓度范围为5×10-5 ～2×10-4，温度范围为20～40℃。对实验数据的分析发现，Giesekus模型可较好地拟合不同浓度和温度下界面活性剂溶液的剪切黏度。得到了不同溶液浓度下Giesekus模型参数与温度的关联式，从而揭示了溶液减阻特性与其流变特性的内在联系。利用对向喷嘴装置RFX流变仪对CTAC/NaSal水溶液的拉伸黏度进行了测量。
Magsci [本文引用: 2]
利用ARES流变仪对具有湍流减阻作用的阳性界面活性剂CTAC/NaSal水溶液的剪切黏度进行了测量。溶液的质量浓度范围为5×10-5 ～2×10-4，温度范围为20～40℃。对实验数据的分析发现，Giesekus模型可较好地拟合不同浓度和温度下界面活性剂溶液的剪切黏度。得到了不同溶液浓度下Giesekus模型参数与温度的关联式，从而揭示了溶液减阻特性与其流变特性的内在联系。利用对向喷嘴装置RFX流变仪对CTAC/NaSal水溶液的拉伸黏度进行了测量。
Magsci [本文引用: 2]
在25℃条件下,测量了质量分数w=0.007%～0.15%范围内表面活性剂水溶液的流变特性。实验结果表明,表面活性剂稀溶液在剪切作用下出现剪切增稠转变,随着溶液浓度的增加,剪切增稠转变越来越弱。当浓度达到某一临界饱和浓度时,不再有剪切增稠转变发生,该浓度所对应的流变曲线称为最大黏度线;对于表面活性剂稀溶液,剪切诱导时间和剪切平衡时间均是剪切速率的幂函数,幂指数为-1.0;剪切增稠转变结束后,表面活性剂稀溶液的稳态黏度随浓度增大而增大,当w>0.05%时,稳态黏度逼近最大黏度线,继续增大浓度,稳态黏度几乎保持不变。
Magsci [本文引用: 2]
在25℃条件下,测量了质量分数w=0.007%～0.15%范围内表面活性剂水溶液的流变特性。实验结果表明,表面活性剂稀溶液在剪切作用下出现剪切增稠转变,随着溶液浓度的增加,剪切增稠转变越来越弱。当浓度达到某一临界饱和浓度时,不再有剪切增稠转变发生,该浓度所对应的流变曲线称为最大黏度线;对于表面活性剂稀溶液,剪切诱导时间和剪切平衡时间均是剪切速率的幂函数,幂指数为-1.0;剪切增稠转变结束后,表面活性剂稀溶液的稳态黏度随浓度增大而增大,当w>0.05%时,稳态黏度逼近最大黏度线,继续增大浓度,稳态黏度几乎保持不变。
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
Magsci
为阐明表面活性剂水溶液的减阻作用，使用LDV对零压梯度的二维湍流平板边界层中的CTAB表面活性剂水溶液的湍流特性进行了实验研究. 结果表明：与牛顿流体相比，CTAB水溶液边界层的粘性底层增厚；主流时均速度分布有被层流化的趋势，对数分布域上移；主流方向速度湍动强度峰值减小，且远离壁面，在靠近边界层中部，出现第2峰值；垂直于主流方向的速度湍动强度受到了大幅度抑制，雷诺应力沿着边界层厚度方向几乎为零. 结果说明CTAB水溶液具有减弱湍流湍动各个成分相关度的作用，从而能够使雷诺应力降低、湍流能量生成项减小最终降低流体的输送动力.
Magsci
为阐明表面活性剂水溶液的减阻作用，使用LDV对零压梯度的二维湍流平板边界层中的CTAB表面活性剂水溶液的湍流特性进行了实验研究. 结果表明：与牛顿流体相比，CTAB水溶液边界层的粘性底层增厚；主流时均速度分布有被层流化的趋势，对数分布域上移；主流方向速度湍动强度峰值减小，且远离壁面，在靠近边界层中部，出现第2峰值；垂直于主流方向的速度湍动强度受到了大幅度抑制，雷诺应力沿着边界层厚度方向几乎为零. 结果说明CTAB水溶液具有减弱湍流湍动各个成分相关度的作用，从而能够使雷诺应力降低、湍流能量生成项减小最终降低流体的输送动力.
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
Magsci [本文引用: 1]
对不同的浓度和温度下阳性离子表面活性剂十六烷基三甲基氯化铵(CTAC)在循环回路系统中的减阻特性进行了实验研究。表面活性剂呈现明显减阻特性,且各浓度条件下均存在一个临界温度,并表现出温度效应。本文从微观尺度和能量分析角度来解释这种温度效应。通过分析该表面活性剂溶液阻力减小和传热性能降低之间的关系,提出了通过对溶液温度的控制来改变减阻溶液的传热特性的方法。
Magsci [本文引用: 1]
对不同的浓度和温度下阳性离子表面活性剂十六烷基三甲基氯化铵(CTAC)在循环回路系统中的减阻特性进行了实验研究。表面活性剂呈现明显减阻特性,且各浓度条件下均存在一个临界温度,并表现出温度效应。本文从微观尺度和能量分析角度来解释这种温度效应。通过分析该表面活性剂溶液阻力减小和传热性能降低之间的关系,提出了通过对溶液温度的控制来改变减阻溶液的传热特性的方法。
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 2]
[本文引用: 1]
[本文引用: 1]
DOIURL
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 3]
DOIURL [本文引用: 1]
DOIURL [本文引用: 2]
DOIURL [本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 3]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 3]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
[本文引用: 3]
[本文引用: 1]
DOIURL [本文引用: 1]
[本文引用: 2]
[本文引用: 1]
DOIURL [本文引用: 1]
[本文引用: 2]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 3]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
[本文引用: 1]
[本文引用: 2]
[本文引用: 2]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
DOIURL [本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
[本文引用: 1]
DOIURL
DOIURL [本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
